Robust Load Frequency Control in Cyber-Vulnerable Smart Grids with Renewable Integration
Abstract
1. Introduction
- water distribution systems (e.g., SCADA-based flow control);
- natural gas pipelines (e.g., pressure and flow regulation);
- district heating or HVAC networks.
- spatiotemporal dependencies (pressure, flow, demand over time);
- vulnerabilities to FDI, DoS, replay attacks;
- telemetry data suitable for wavelet decomposition and forecasting.
- Standards and Certification: Update NERC CIP and IEC 61850 standards [14] to recognize AI/ML-based intrusion detection systems (IDS) alongside traditional rule-based FDD. Establish benchmarks and certification bodies for AI-based anomaly detection tools to ensure reliability and explainability.
- Cybersecurity Incentives: Encourage utility participation through regulatory sandboxes where new detection technologies can be piloted without financial or compliance risks. Introduce financial incentives or tax credits for adopting certified AI-driven cybersecurity tools.
- Data-Sharing Policies: Enable secure, anonymized telemetry sharing across utilities to improve the training of generalized AI models while preserving privacy and compliance. Mandate event logging and incident sharing (e.g. DOE Cybersecurity Risk Information Sharing Program—CRISP) to build resilient AI threat models.
- Interoperability Requirements: Ensure detection frameworks can integrate with existing energy management systems (EMS), SCADA platforms, and digital twins through open APIs or OPC-UA/MQTT protocols.
- A fuzzy rule-based LADRC (F-LADRC) scheme is proposed for frequency regulation (FR) under stochastic load conditions, with controller parameters optimized using the quasi-opposition-based reptile search algorithm (QORSA).
- A modified IEEE 39-bus system incorporating renewable energy and electric vehicles is developed to simulate and analyze the impact of cyberattacks.
- A novel cyberattack detection and mitigation framework is introduced, combining wavelet transform (WT) for feature extraction and long short-term memory (LSTM) networks for predictive analysis, targeting false data injection (FDI) and time delay attacks (TDA).
2. Problem Formulation
2.1. Frequency Regulation in Smart Grids
2.2. Cyberattack Approaches Employed in the Smart Grid LFC System
- (i)
- FDIA Model
- (a)
- Stealthy FDIA model: Originally put forth in [15], and according to the literature, FDIA targeting state estimation can bypass conventional FDD thanks to the following theorem.
- (b)
- Scaling attack FDIA model: The model entails the process of multiplying real measurements by a constant, causing them to increase or decrease, depending on the scaling attack parameter. The three possible assault targets for scaling and exogenous events, together with their ACE formulations, are shown below.
- Assault on the frequency measurement data of the kth area may be described as (10).
- Assault on the tie-line measurement data between kth and lth areas may be described as (11).
- Assault on ACE measurement data may be described as (12)
- Publicly available data: many utilities and independent system operators (ISOs) publish planning and operational data (e.g., one-line diagrams, base load/generation profiles, system operating conditions) that can be exploited by sophisticated attackers to estimate system topology or parameters.
- Insider threats: employees or contractors with legitimate access to SCADA or EMS systems may inadvertently or maliciously leak sensitive information such as Jacobian structures or model parameters.
- Reconnaissance and machine learning: attackers can perform probing attacks and use system responses to learn the Jacobian structure over time using statistical or machine learning techniques.
- Prior research: this assumption is consistent with the prevailing literature on stealthy FDIAs, such as in subsequent studies, where even partial or estimated Jacobian information can be sufficient to bypass conventional bad data detection (BDD) mechanisms.
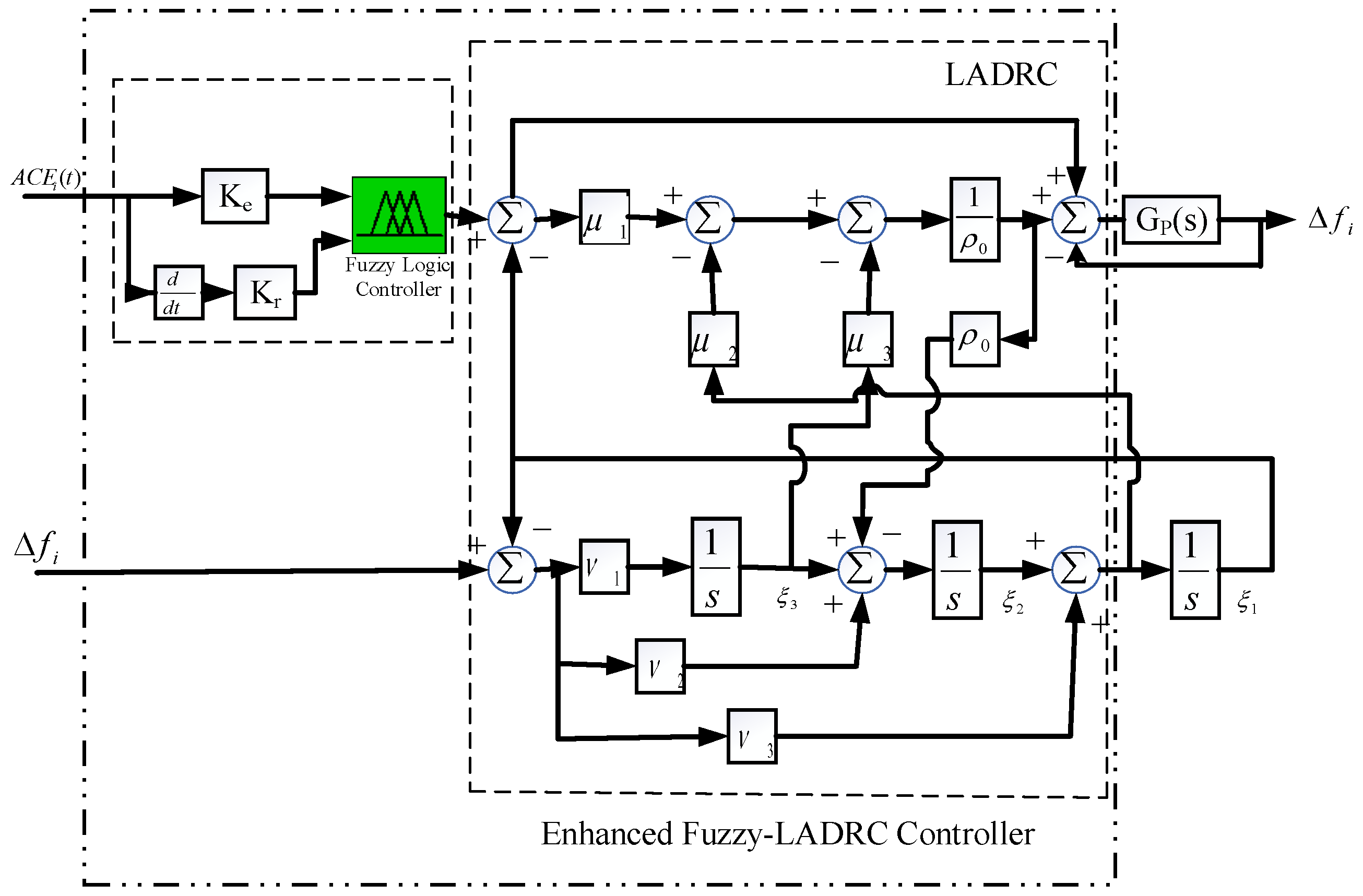
3. Design Methodology of the Proposed Adaptive Fuzzy-LADR Controller
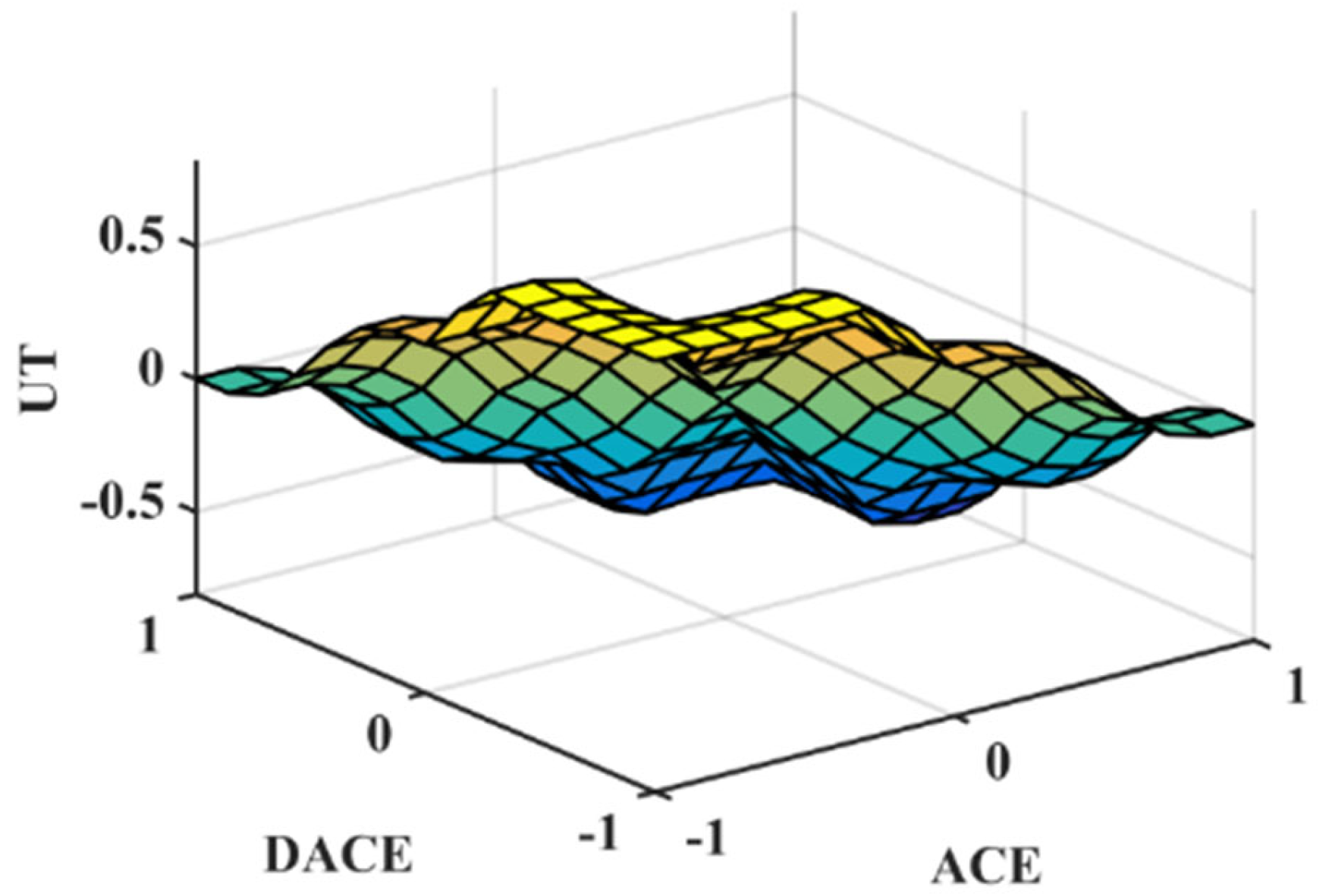
3.1. Proposed Control Strategy
- Fuzzy logic inference: The fuzzy controller requires the evaluation of membership functions and rule bases in real time. However, the inference mechanism used in our implementation is based on a Mamdani-type system with a small number of rules (typically fewer than 10), and triangular membership functions. This keeps the computational load relatively low and suitable for real-time execution on standard microcontrollers or DSP platforms.
- Extended state observer (ESO): The LADRC framework includes an ESO for disturbance estimation, which involves solving a set of differential equations. This is computationally light and requires only a few arithmetic operations per control cycle.
- Natural disturbances (e.g., load changes) typically align with the system’s physical model and occur within expected bounds. The ESO within LADRC adapts to such changes as part of the normal control behavior.
- FDI attacks, especially scaling-type injections, introduce structured deviations that do not conform to the model dynamics or expected measurement residuals over time. The LADRC’s ESO detects these as unmodeled disturbances, and the fuzzy adaptation enhances sensitivity by adjusting gains dynamically.
3.2. Proposed Optimization Algorithm
3.3. Examination of Designed Controller’s Effectiveness
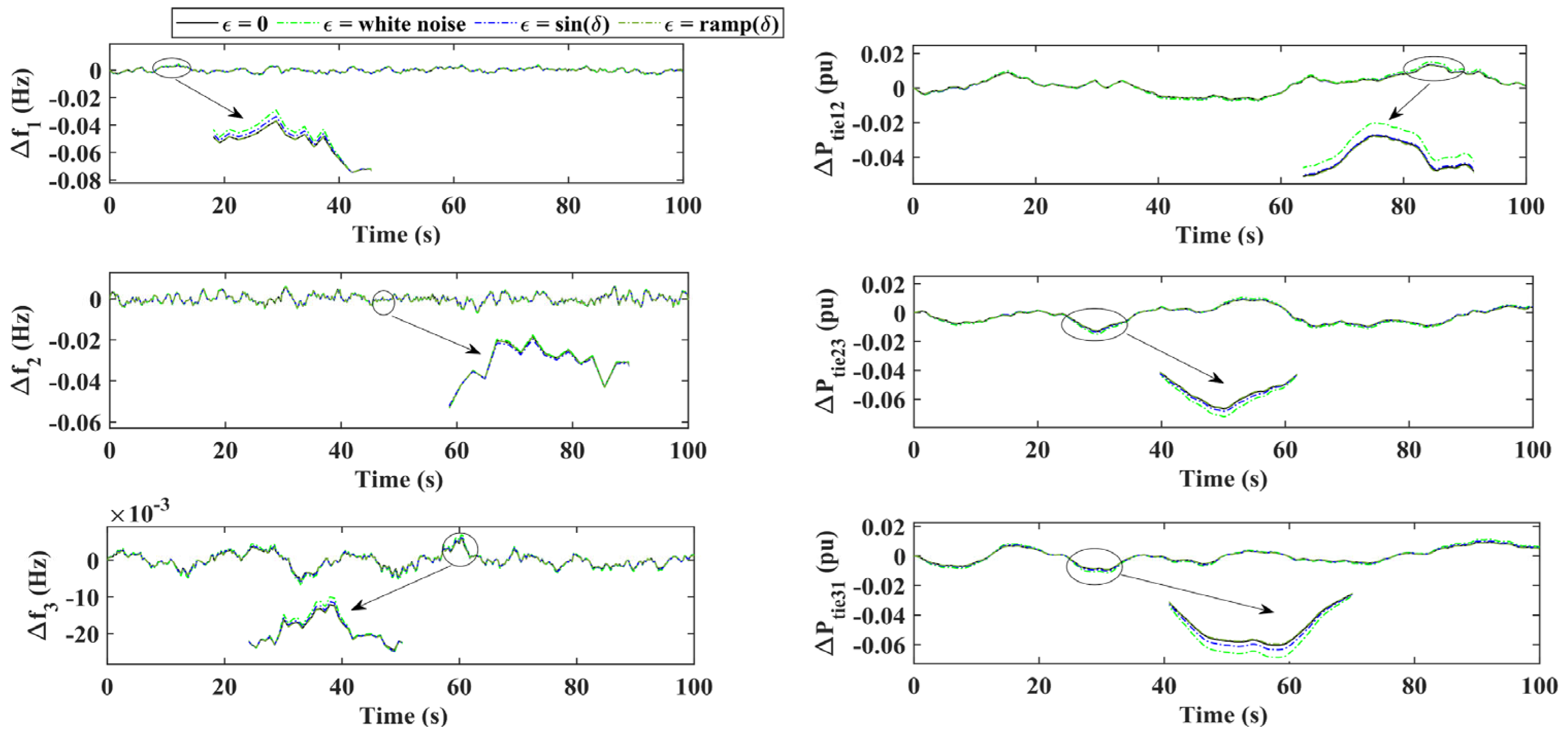
3.4. Sensitivity Analysis
4. Proposed Cyber-Threat Detection and Mitigation Model
4.1. Wavelet-Based Attack Detector
4.2. Long Short-Term Memory
- Capture correlated behaviors: for example, simultaneous ramp FDIAs across interconnected areas will cause synchronized anomalies in ACE patterns, which the LSTM can recognize through learned temporal patterns.
- Predict cross-area ACE values: during attacks, the LSTM estimates the expected ACE signal based on the joint evolution of all areas. Deviations between the predicted and actual ACE help isolate and suppress anomalous inputs.
- Activate a mitigation mechanism: when a correlated attack is detected, the LSTM-predicted ACE acts as a surrogate signal for controller input, ensuring continuity of control. Additionally, its training includes mixed-scenario datasets with uncorrelated and correlated attacks, improving generalization.
- missing or delayed data packets;
- sudden communication drops.
- training is based on local historical ACE data;
- LSTM captures temporal dependencies, irrespective of the underlying source.
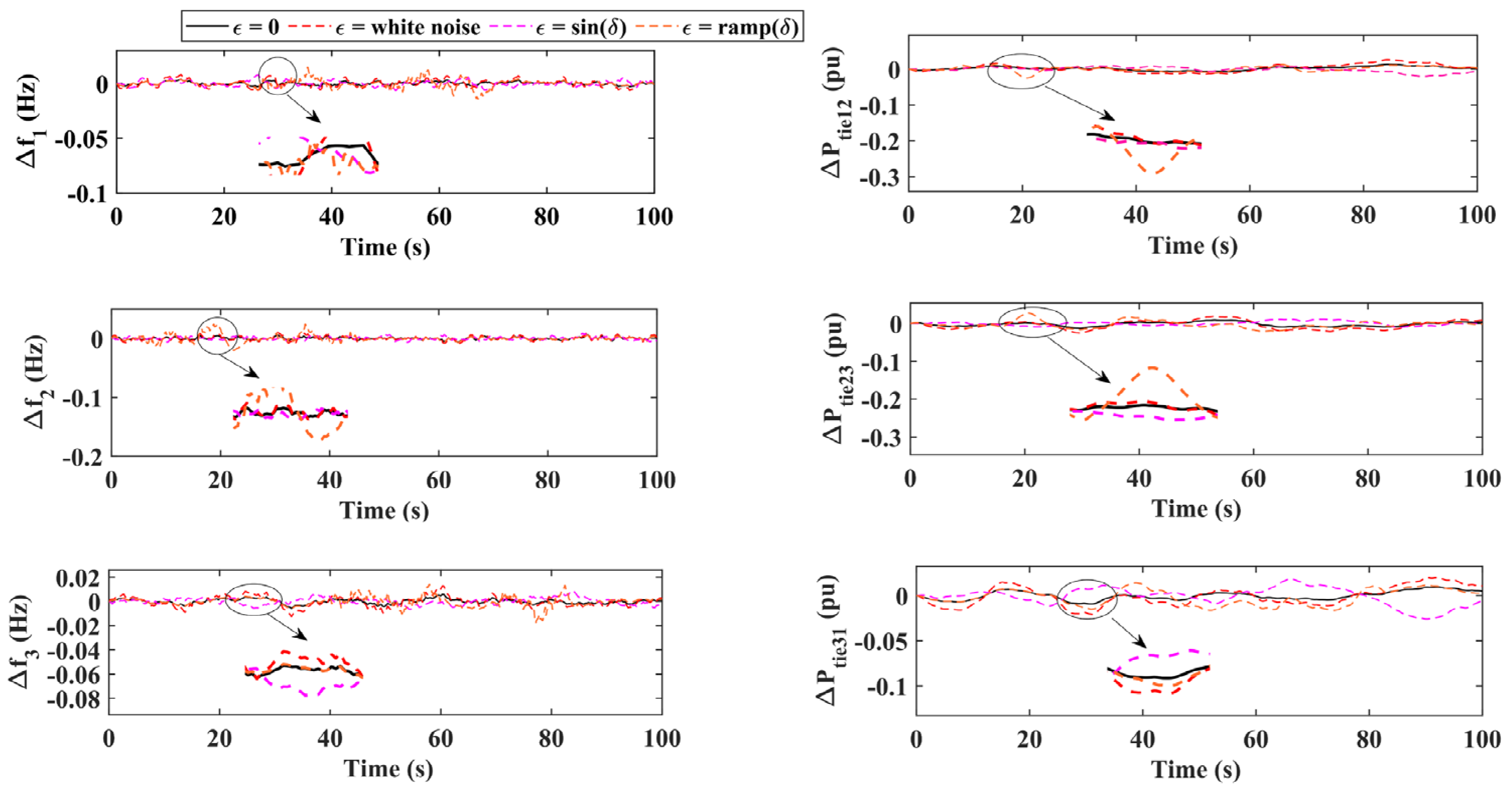
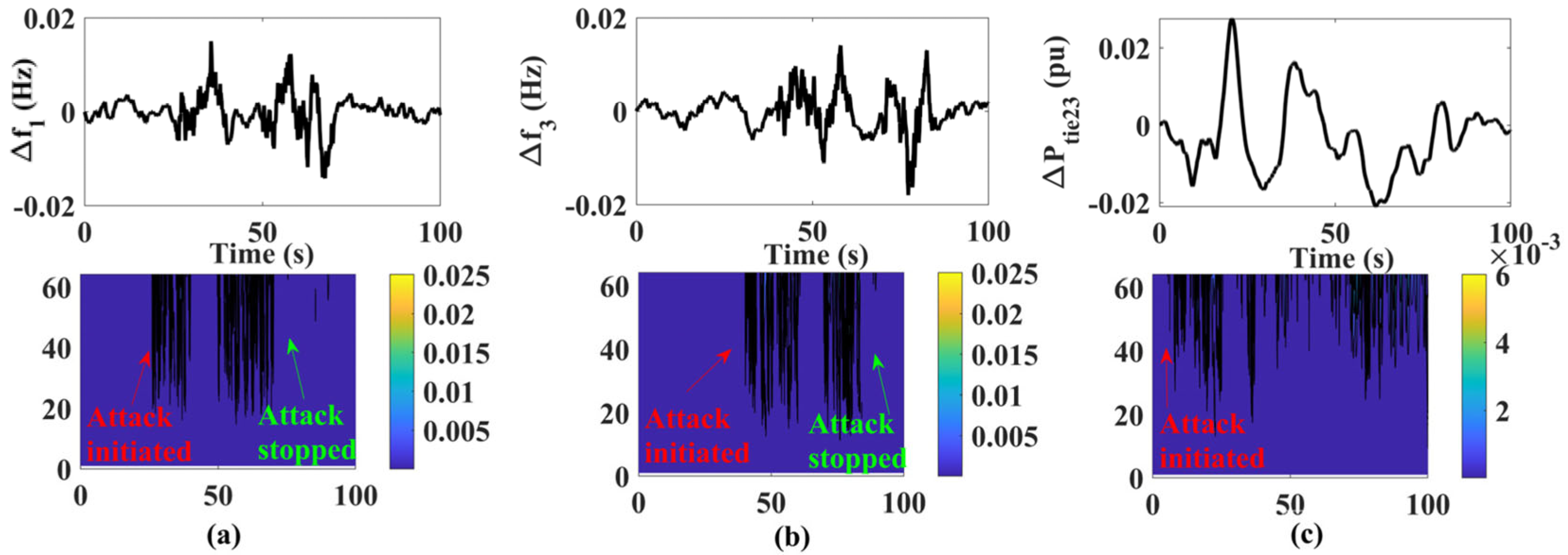
5. Results
- S1: normal operation without an attack.
- S2: FDI attack without cyber defense.
- S3: FDI attack with the proposed detection and mitigation system.
Case-1: FDI Attack
- WT transform and thresholding: ~5 ms;
- LSTM prediction (1-step ahead): ~15–20 ms on a standard CPU (Intel i7, 2.8 GHz);
- Total latency: ~20–25 ms per sampling interval.
- Durations: each attack spans 5–15 s to capture the transient response, which is the most critical window for LFC and detection systems.
- Intensities: scaling factors and signal amplitudes (e.g., 10–30% of nominal ACE or tie-line power) were selected to remain stealthy (i.e., bypass threshold detection), while still significantly perturbing system dynamics.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| F-LADRC | Fuzzy Linear Active Disturbance Rejection Controller |
| DoS | Denial of service |
| FDI | False data injection |
| GDB | Governor dead band |
| GRC | Generation rate constraint |
| QORSA | Quasi-Opposition-based Reptile Search Algorithm |
| LSTM | Long Short-Term Memory |
| WT | Wavelet Transform |
| NSG | Networked Smart Grid |
Appendix A
References
- Dong, M.; Liu, K.; He, J.; Li, X.; Qiao, L.; Zhao, X. Power grid load frequency control based on Fractional Order PID combined with pumped storage and battery energy storage. Energy Rep. 2023, 9, 1402–1411. [Google Scholar] [CrossRef]
- Raj, U.; Shankar, R. Deregulated Automatic Generation Control using Novel Opposition-based Interactive Search Algorithm Cascade Controller Including Distributed Generation and Electric Vehicle. Iran. J. Sci. Technol. Trans. Electr. Eng. 2020, 44, 1233–1251. [Google Scholar] [CrossRef]
- Bošković, M.Č.; Šekara, T.B.; Rapaić, M.R. Novel tuning rules for PIDC and PID load frequency controllers considering robustness and sensitivity to measurement noise. Int. J. Electr. Power Energy Syst. 2020, 114, 105416. [Google Scholar] [CrossRef]
- Gobinda, D.; Majhi, S. A new control scheme for PID load frequency controller of single-area and multi-area power systems. ISA Trans. 2013, 52, 242–251. [Google Scholar] [CrossRef]
- Ranjan, M.; Shankar, R. A literature survey on load frequency control considering renewable energy integration in power system: Recent trends and future prospects. J. Energy Storage 2022, 45, 103717. [Google Scholar] [CrossRef]
- Khan, M.; Sun, H.; Xiang, Y.; Shi, D. Electric vehicles participation in load frequency control based on mixed H2/H∞. Int. J. Electr. Power Energy Syst. 2021, 125, 106420. [Google Scholar] [CrossRef]
- Chen, C.; Chen, Y.; Zhao, J.; Zhang, K.; Ni, M.; Ren, B. Data-Driven Resilient Automatic Generation Control Against False Data Injection Attacks. IEEE Trans. Ind. Inform. 2021, 17, 8092–8101. [Google Scholar] [CrossRef]
- Khalili, J.; Dehkordi, N.M.; Hamzeh, M. Distributed event-triggered secondary frequency control of islanded AC microgrids under cyber attacks with input time delay. Int. J. Electr. Power Energy Syst. 2022, 143, 108506. [Google Scholar] [CrossRef]
- Ameli, A.; Hooshyar, A.; El-Saadany, E.F.; Youssef, A.M. Attack Detection and Identification for Automatic Generation Control Systems. IEEE Trans. Power Syst. 2018, 33, 4760–4774. [Google Scholar] [CrossRef]
- Tabassum, T.; Lim, S.; Khalghani, M.R. Artificial intelligence-based detection and mitigation of cyber disruptions in microgrid control. Electr. Power Syst. Res. 2024, 226, 109925. [Google Scholar] [CrossRef]
- Raj, U.; Shankar, R.; Rani, S.; Ranjan, M. Enhanced load frequency regulation in cyberattack triggered grids with renewable energy and electric vehicles. Electr. Eng. 2024. [Google Scholar] [CrossRef]
- Mishra, A.K.; Mishra, P.; Mathur, H.D. A deep learning assisted adaptive nonlinear deloading strategy for wind turbine generator integrated with an interconnected power system for enhanced load frequency control. Electr. Power Syst. Res. 2023, 214, 108960. [Google Scholar] [CrossRef]
- Sah, S.V.; Prakash, V.; Pathak, P.K.; Yadav, A.K. Virtual inertia and intelligent control assisted frequency regulation of time-delayed power system under DoS attacks. Chaos Solitons Fractals 2024, 188, 115578. [Google Scholar] [CrossRef]
- IEEE Recommended Practice for Implementing an IEC 61850-Based Substation Communications, Protection, Monitoring, and Control System. In IEEE Std 2030.100-2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–67. [CrossRef]
- Zhang, G.; Li, J.; Bamisile, O.; Xing, Y.; Cai, D.; Huang, Q. An H∞ Load Frequency Control Scheme for Multi-Area Power System Under Cyber-Attacks and Time-Varying Delays. IEEE Trans. Power Syst. 2023, 38, 1336–1349. [Google Scholar] [CrossRef]
- Wang, Q.; Tai, W.; Tang, Y.; Ni, M. Review of the false data injection attack against the cyber-physical power system. IET Cyber-Phys. Syst. Theory Appl. 2019, 4, 101–107. [Google Scholar] [CrossRef]
- Liu, K.; He, J.; Luo, Z.; Shen, X.; Liu, X.; Lu, T. Secondary Frequency Control of Isolated Microgrid Based on LADRC. IEEE Access 2019, 7, 53454–53462. [Google Scholar] [CrossRef]
- Yuan, C.; Zhou, X.; Ma, Y. DC Bus Voltage Control of Wind Power Inverter Based on First-Order LADRC. IEEE Access 2022, 10, 3263–3274. [Google Scholar] [CrossRef]
- An, L.; Yang, G.H. Decentralized Adaptive Fuzzy Secure Control for Nonlinear Uncertain Interconnected Systems Against Intermittent DoS Attacks. IEEE Trans. Cybern. 2019, 49, 827–838. [Google Scholar] [CrossRef] [PubMed]
- Abualigah, L.; Abd Elaziz, M.; Sumari, P.; Geem, Z.W.; Gandomi, A.H. Reptile Search Algorithm (RSA): A nature-inspired meta-heuristic optimizer. Expert Syst. Appl. 2022, 191, 116158. [Google Scholar] [CrossRef]
- Raj, U.; Shankar, R. Optimally enhanced fractional-order cascaded integral derivative tilt controller for improved load frequency control incorporating renewable energy sources and electric vehicle. Soft Comput. 2023, 27, 15247–15267. [Google Scholar] [CrossRef]







| Parameter | Symbol | Value |
|---|---|---|
| Governor constant | Tg1, Tg2, Tg3 | 0.15, 0.10, 0.10 |
| Turbine constant | Tt1, Tt2, Tt3 | 0.30, 0.30, 0.30 |
| Droop constant | R1, R2, R3 | 0.05, 0.05, 0.05 |
| Frequency bias factor | B1, B2, B3 | 30, 28, 34 |
| Inertia constant | M1, M2, M3 | 35.8, 26.4, 34.5 |
| Damping coefficient | D1, D2, D3 | 10, 8, 14 |
| Area capacity factor | a12, a23, a31 | 1.33, 1.00, 0.75 |
| Controller Parameter | PID | TID | I-PD | LADRC | F-LADRC |
|---|---|---|---|---|---|
| Area-1 | |||||
| KP1 | 0.58 | - | 0.28 | - | - |
| KI1 | 0.66 | 0.14 | 0.21 | - | - |
| KD1 | 0.45 | 0.64 | 0.32 | - | - |
| KT1 | - | 0.12 | - | - | - |
| b1 | - | - | - | 8.62 | 4.51 |
| w1 | - | - | - | 1.38 | 1.47 |
| Area-2 | |||||
| KP2 | 0.61 | - | 0.41 | - | - |
| KI2 | 0.54 | 0.19 | 0.11 | - | - |
| KD2 | 0.24 | 0.27 | 0.17 | - | - |
| KT2 | - | 0.37 | - | - | - |
| b2 | - | - | - | 8.14 | 4.11 |
| w2 | - | - | - | 1.44 | 1.36 |
| Area-3 | |||||
| KP3 | 0.81 | - | 0.24 | - | - |
| KI3 | 0.35 | 0.15 | 0.29 | - | - |
| KD3 | 0.14 | 0.13 | 0.13 | - | - |
| KT3 | - | 0.22 | - | - | - |
| b3 | - | - | - | 9.63 | 5.19 |
| w3 | - | - | - | 1.61 | 1.57 |
| Aspect | WT-LSTM Framework | Model-Based Observers |
|---|---|---|
| Detection Accuracy | High accuracy for nonlinear/time-varying anomalies; learns from data patterns | Moderate-to-high accuracy but sensitive to model mismatches |
| Adaptability | Easily adaptable to changing operating conditions (retrainable) | Fixed structure; needs re-tuning under system changes |
| Robustness to Noise | Haar wavelet preprocessing improves robustness | Kalman filters may degrade under unmodeled noise |
| Model Dependency | Model-free (requires only historical ACE data) | Requires accurate system modeling and parameters |
| Computation | Moderate (20–25 ms latency) | Very low (1–5 ms) but may lack generalization |
| Aspect | WT-LSTM Framework | Blockchain-Based Approaches |
|---|---|---|
| Detection Latency | ~25 ms per sampling interval | High (seconds to minutes due to consensus delays) |
| Resource Usage | Requires only local computation and storage | High storage/computation due to distributed ledger overhead |
| Scalability | Scalable to many areas with parallel LSTM units | Limited by network and consensus bottlenecks |
| Security Focus | Detects anomalies in real-time ACE behavior | Ensures data integrity and non-repudiation, but not real-time detection |
| Implementation Complexity | Moderate (data + neural model) | High (smart contracts, cryptographic protocols, node trust) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, R.; Kumar, R.; Raj, U.; Shankar, R. Robust Load Frequency Control in Cyber-Vulnerable Smart Grids with Renewable Integration. Energies 2025, 18, 2899. https://doi.org/10.3390/en18112899
Singh R, Kumar R, Raj U, Shankar R. Robust Load Frequency Control in Cyber-Vulnerable Smart Grids with Renewable Integration. Energies. 2025; 18(11):2899. https://doi.org/10.3390/en18112899
Chicago/Turabian StyleSingh, Rambaboo, Ramesh Kumar, Utkarsh Raj, and Ravi Shankar. 2025. "Robust Load Frequency Control in Cyber-Vulnerable Smart Grids with Renewable Integration" Energies 18, no. 11: 2899. https://doi.org/10.3390/en18112899
APA StyleSingh, R., Kumar, R., Raj, U., & Shankar, R. (2025). Robust Load Frequency Control in Cyber-Vulnerable Smart Grids with Renewable Integration. Energies, 18(11), 2899. https://doi.org/10.3390/en18112899






