Research on Torque Modeling of the Reluctance Spherical Motor Based on Magnetic Equivalent Circuit Method
Abstract
1. Introduction
2. RSPM Structure and Working Principle
2.1. Basic Structure
2.2. Working Principle
3. MEC of the RSPM
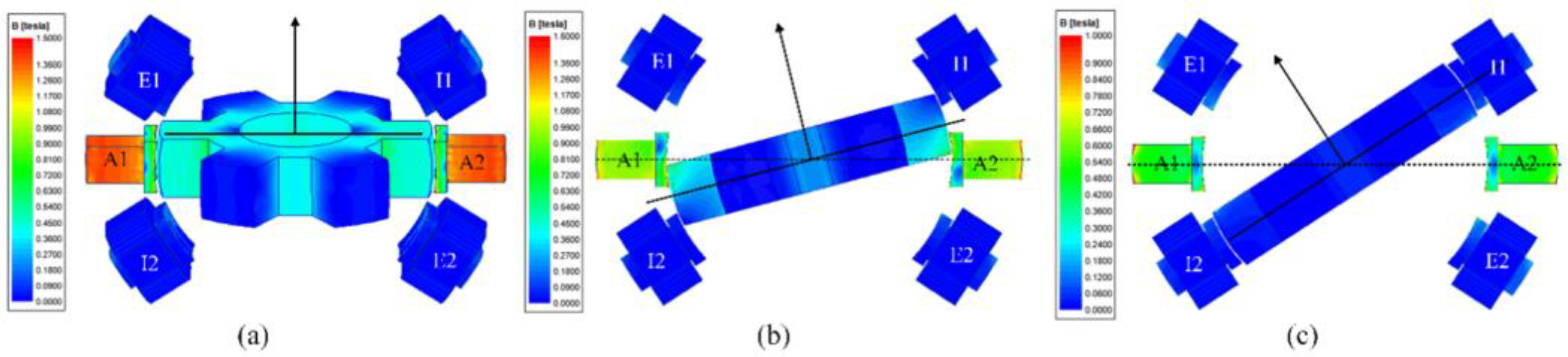
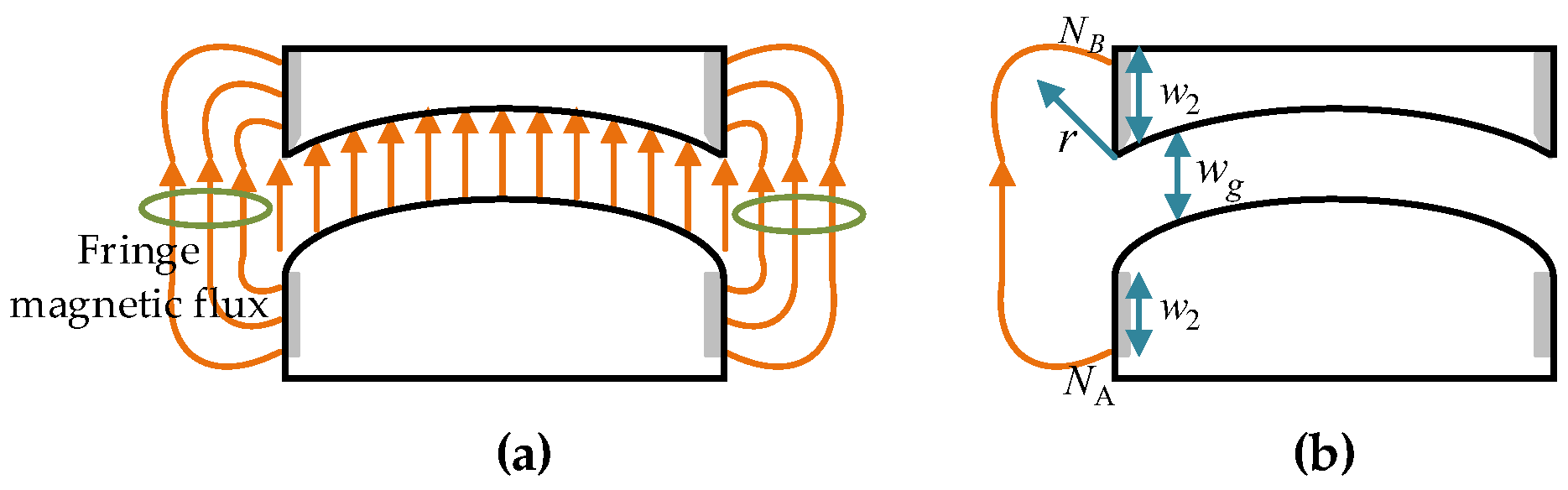
3.1. Magnetic Flux Path of the RSPM
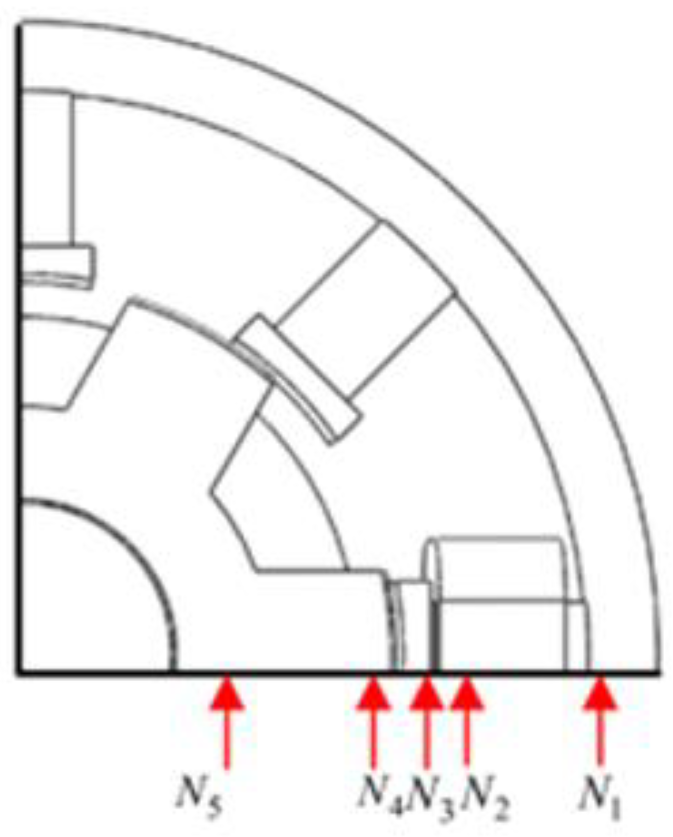
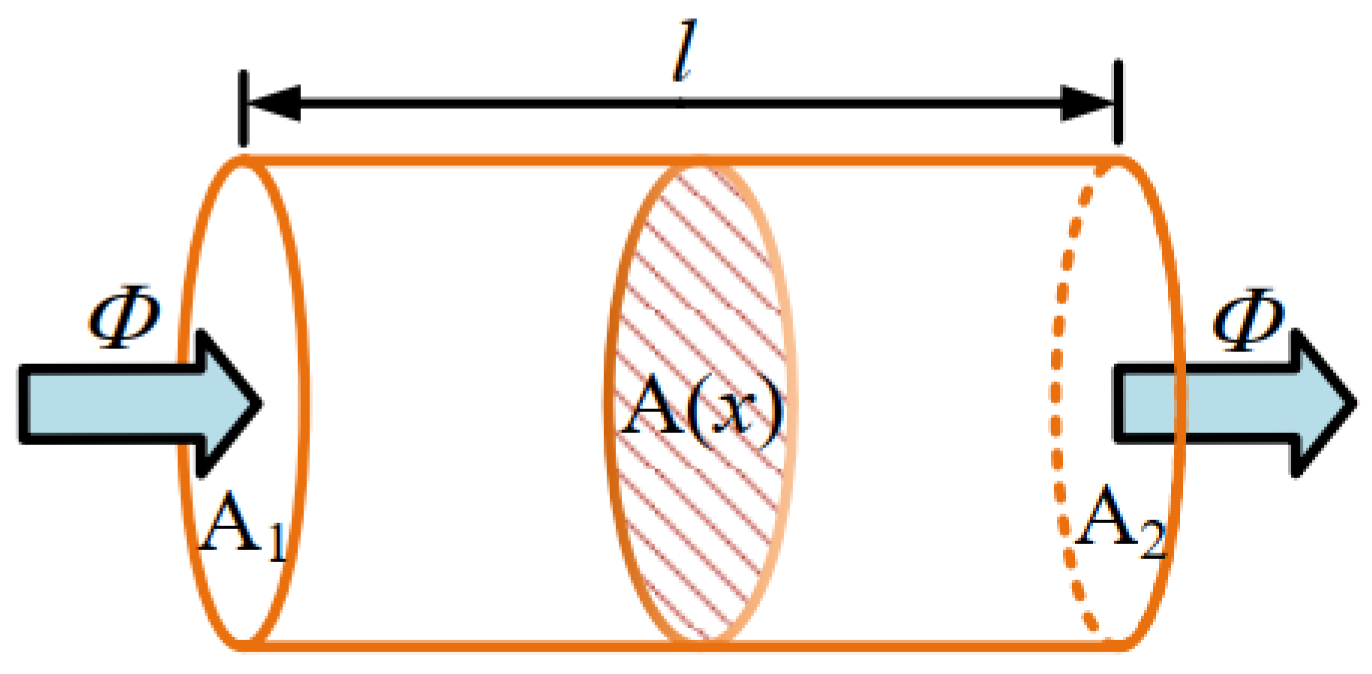
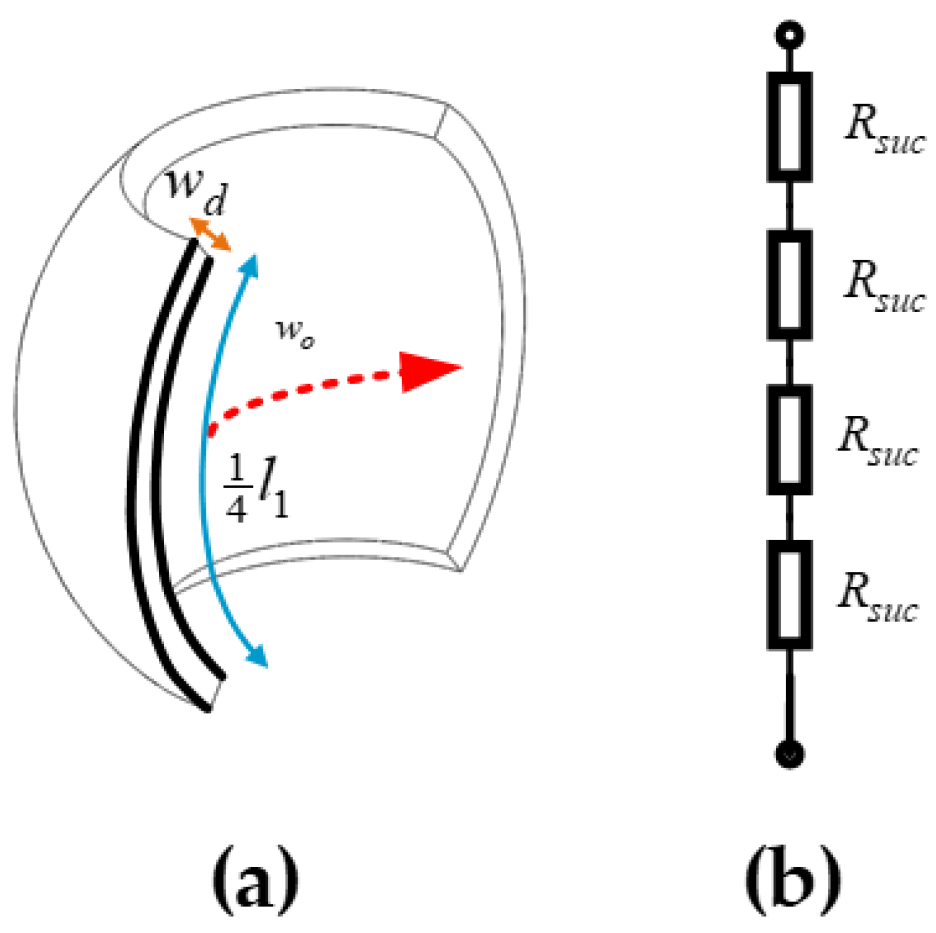
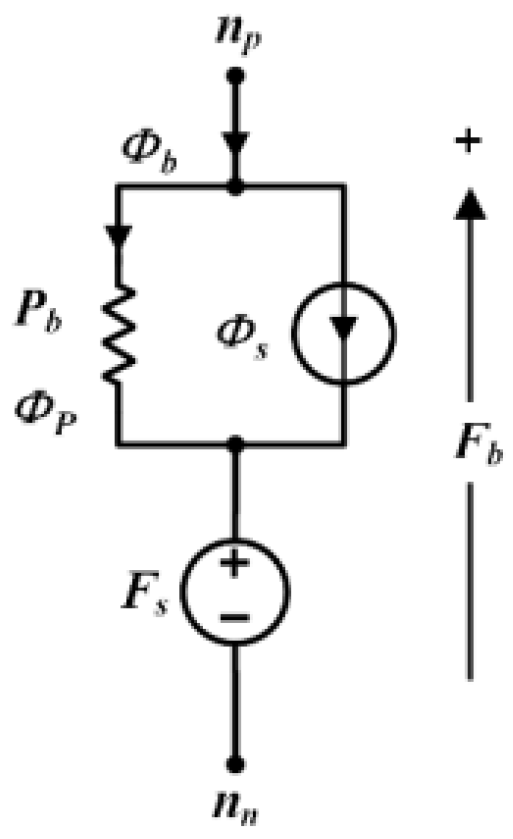
3.2. Calculation of Magnetic Reluctance Based on Equivalent Flux Tube
- (1).
- The reluctance network of the stator.
- (2).
- The reluctance network of the rotor.
- (3).
- The reluctance of the air gap.
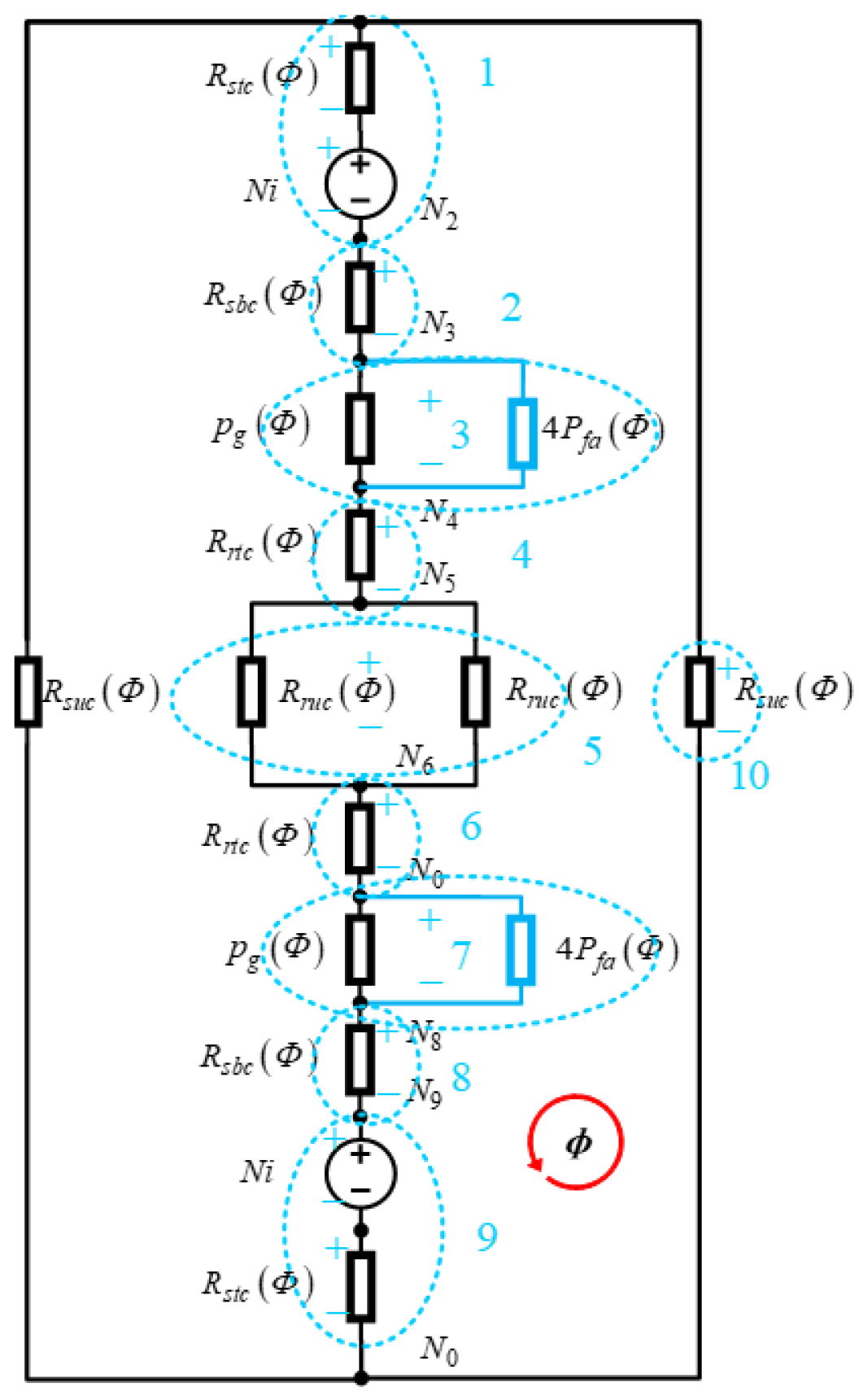
3.3. MEC Topology of the RSPM
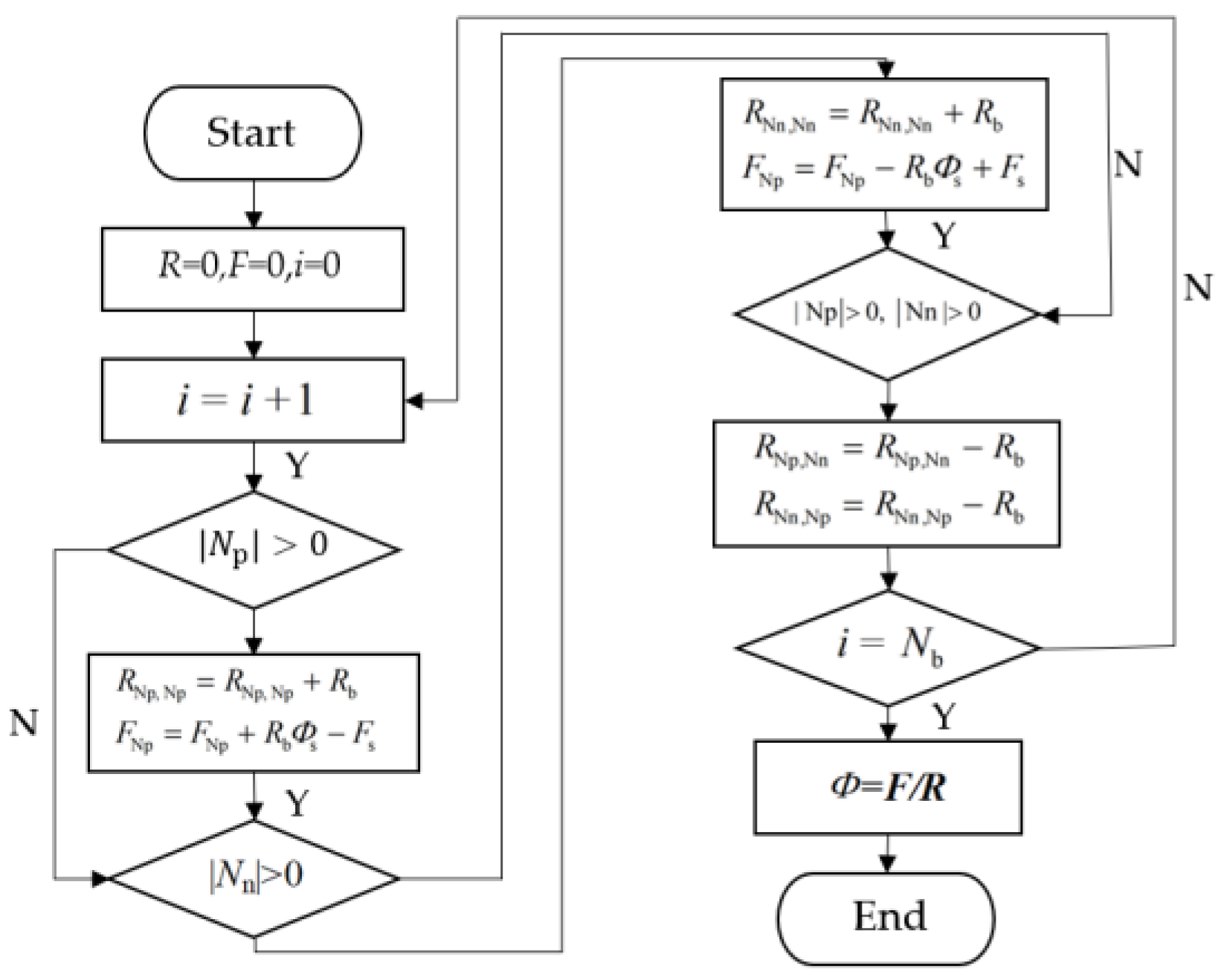
4. Torque Modeling of Nonlinear MEC
4.1. Mesh Analysis Method
4.2. Torque Calculation Based on Energy Storage
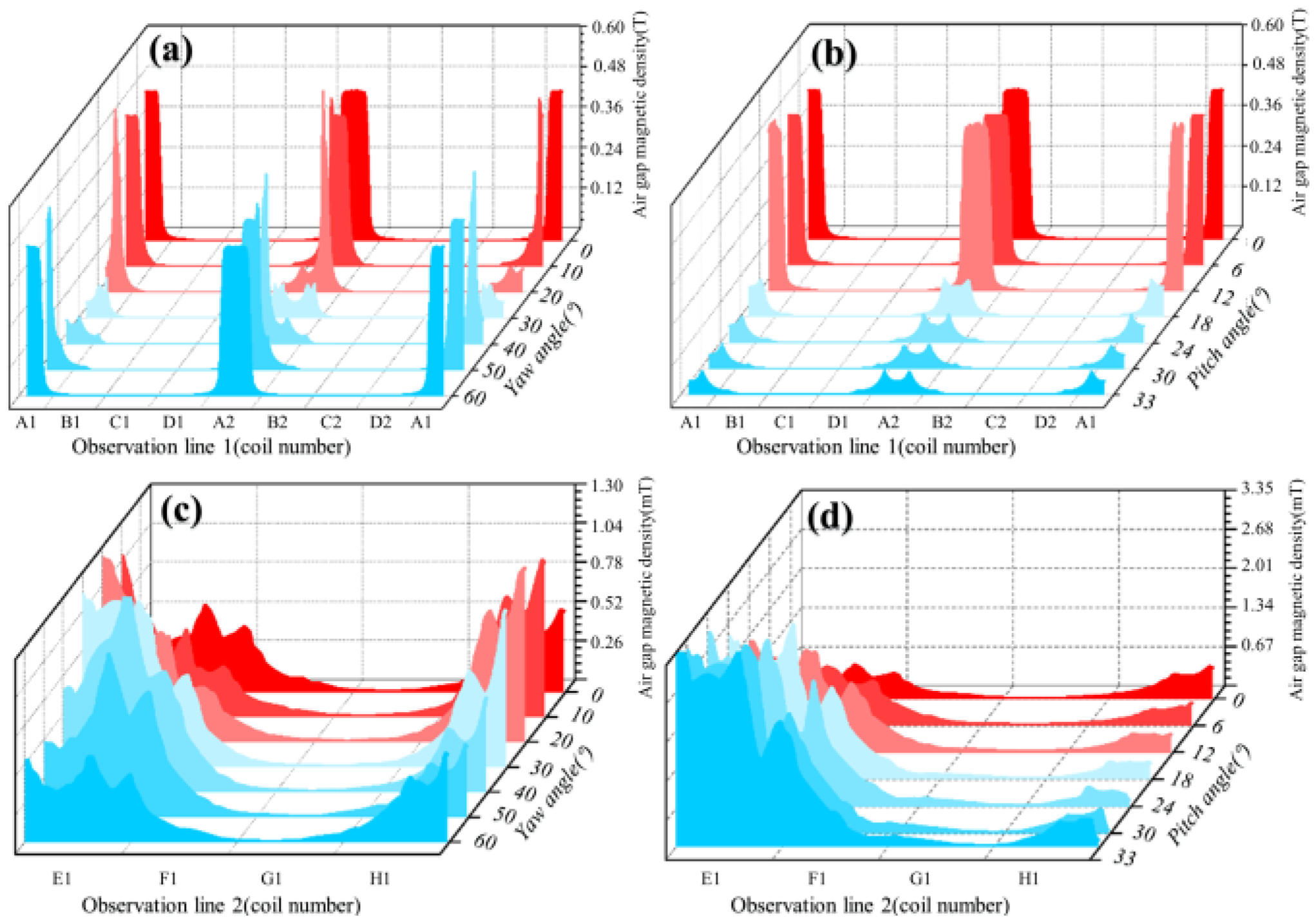
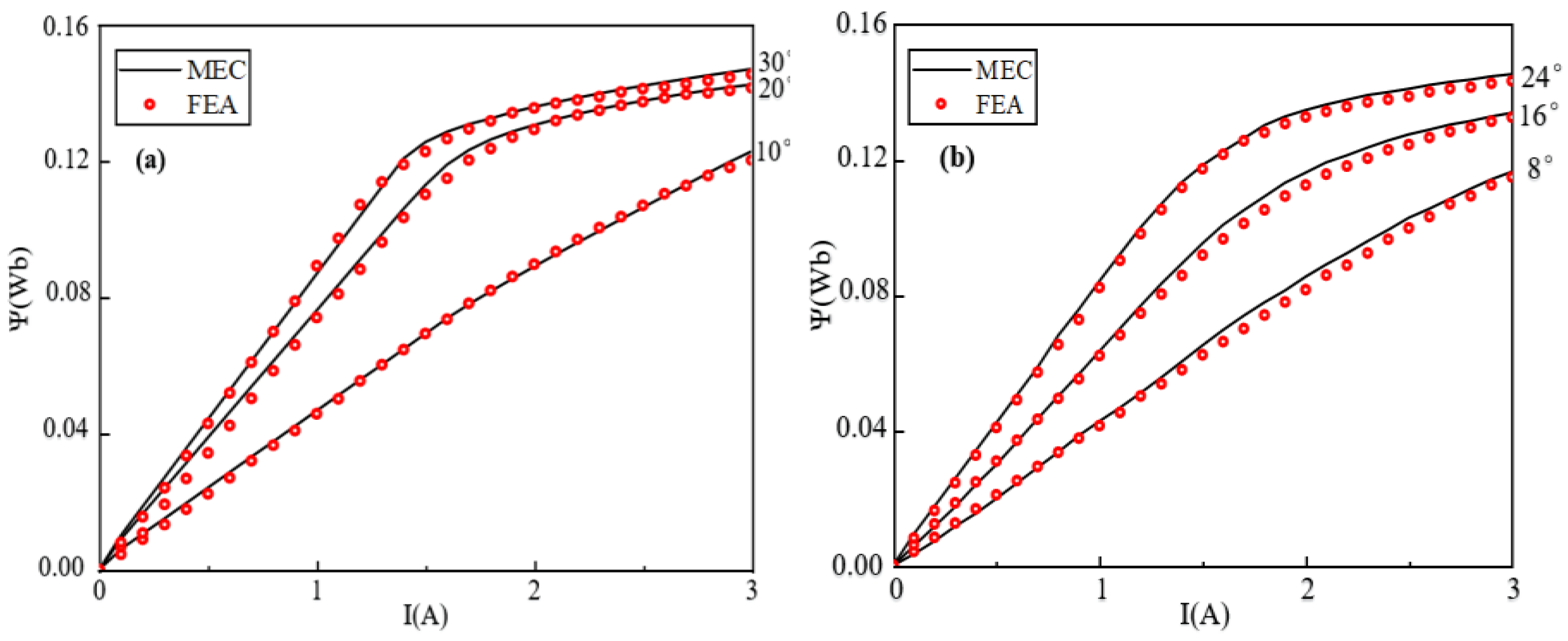
5. Verification of the Torque Model Based on MEC Method
- (1).
- A pair of stator winding coils are energized by the motor drive circuits, and the rotor is locked.
- (2).
- The rotor is driven by a stepper motor at a speed of 3 r/min, and the motion control handle is used to control the forward and reverse rotation of the stepper motor.
- (3).
- The motion torque of the RSPM is measured through the torque sensor.
- (1)
- Errors exist in the sensors during the rotor’s spinning and tilting motions.
- (2)
- Due to the supporting structure of the reluctance-type spherical motor, friction generated during rotor movement can also affect torque measurement.
- (3)
- The gravitational effect of the detection device may cause deviations in the torque measurement results.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tao, W.; Li, G.; Ju, L.; Zhou, R.; Hu, C. Design and analysis of a novel spherical motor based on the principle of reluctance. In Proceedings of the 2018 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, 4–7 December 2018; pp. 1–6. [Google Scholar]
- Lee, K.M.; Pei, J.; Roth, R. Kinematic analysis of a three degree-of-freedom spherical wrist actuator. In Proceedings of the Fifth International Conference on Advanced Robotics ‘Robots in Unstructured Environments, Pisa, Italy, 19–22 June 1991; pp. 72–77. [Google Scholar]
- Lee, K.-M.; Wang, X.-A. Dynamic modeling and control of a Ball-Joint-Like variable-reluctance spherical motor. In Proceedings of the 1992 American Control Conference, Chicago, IL, USA, 24–26 June 1992; pp. 2463–2467. [Google Scholar]
- Lee, K.-M.; Sosseh, R.A.; Wei, Z. Effects of the torque model on the control of a VR spherical motor. Control Eng. Pract. 2004, 12, 1437–1449. [Google Scholar] [CrossRef]
- Chen, X.; Hu, J.; Chen, K.; Peng, Z. Modeling of electromagnetic torque considering saturation and magnetic field harmonics in permanent magnet synchronous motor for HEV. Simul. Model. Pract. Theory 2016, 66, 212–225. [Google Scholar] [CrossRef]
- Nakao, N.; Akatsu, K. A simple unipolar excitation strategy for switched reluctance motors by using PWM current control. In Proceedings of the 2013 IEEE ECCE Asia Downunder, Melbourne, VIC, Australia, 3–6 June 2013; pp. 1111–1117. [Google Scholar]
- Shao, J.; Deng, Z.; Gu, Y. Sensorless control for switched reluctance motor based on special position detection. ISA Trans. 2017, 70, 410–418. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Zhang, S.; Habetler, T.G.; Harley, R.G. Modeling, Design optimization, and Applications of switched reluctance machines—A Review. IEEE Trans. Ind. Appl. 2019, 55, 2660–2681. [Google Scholar] [CrossRef]
- Hou, J.; Geng, W.; Li, Q.; Zhang, Z. 3-D equivalent magnetic network modeling and FEA verification of a novel axial-flux hybrid-excitation in-wheel motor. IEEE Trans. Magn. 2021, 57, 8106912. [Google Scholar] [CrossRef]
- Li, H.; Zhao, Y.; Li, B.; Li, G.; Cui, L. Torque Calculation of permanent magnet spherical motor based on virtual work method. IEEE Trans. Ind. Electron. 2020, 67, 7736–7745. [Google Scholar] [CrossRef]
- Zhao, S.; Che, Y.; Li, H. Three-dimensional Interval Identification of Permanent Magnet Spherical Motor Based on Improved Deep Neural Network. J. Electr. Eng. Technol. 2024, 19, 419–431. [Google Scholar] [CrossRef]
- Shi, M.; Wang, Q.; Li, G.; Xu, J.; Han, Q.; Ye, Q. A new adaptive analytical model for the spherical reluctance motor based on hybrid trigonometric function-power function. IEEE Trans. Ind. Electron 2023, 70, 6099–6109. [Google Scholar] [CrossRef]
- Sun, X.; Xiong, Y.; Yao, M.; Tang, X. A hybrid control strategy for multimode switched reluctance motors. IEEE/ASME Trans. Mechatron. 2022, 27, 5605–5614. [Google Scholar] [CrossRef]
- Cai, Y.; Wang, Y.; Xu, H.; Sun, S.; Wang, C.; Sun, L. Research on rotor position model for switched reluctance motor using neural network. IEEE/ASME Trans. Mechatron. 2018, 23, 2762–2773. [Google Scholar]
- Chai, F.; Gan, L.; Pei, Y. Torque Characteristic of a Novel Tiered Type Permanent Magnet Spherical Motor. IEEE Trans. Ind. Appl. 2020, 56, 6338–6347. [Google Scholar] [CrossRef]
- Ostović, V. Dynamics of Saturated Electric Machines; Springer Nature: Dordrecht, The Netherlands, 1989; p. 107134341. [Google Scholar]
- Sudhoff, S.D.; Shane, G.M.; Suryanarayana, H. Magnetic-equivalent-circuit-based scaling laws for low-frequency magnetic devices. IEEE Trans. Energy Convers. 2013, 28, 746–755. [Google Scholar] [CrossRef]
- ManaaBarhoumi, E.; Wurtz, F.; Chillet, C.; Ben Salah, B. Reluctance network model for linear switched reluctance motor. In Proceedings of the 2015 IEEE 12th International Multi-Conference on Systems, Signals & Devices (SSD15), Mahdia, Tunisia, 16–19 March 2015; pp. 1–4. [Google Scholar]
- Ju, L.; Zha, K.; Wang, Q.; Li, G.; Zhou, R.; Wen, Y. A Torque Modeling Method of Spherical Reluctance Motor Based on the Magnetic Circuit Method. IEEE/ASME Trans. Mechatron. 2024, 1–9. [Google Scholar] [CrossRef]
- Shi, M.; Wang, Q.; Li, G.; Zhou, R.; Liu, Y.; Gao, S. A new analytical method for modelling of a spherical reluctance motor based on a small amount of measured flux linkage. Measurement 2023, 208, 112447. [Google Scholar] [CrossRef]
- Miller, T. Electronic Control of Switched Reluctance Machines; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Sudhoff, S.D. Power Magnetic Devices: A Multi-Objective Design Approach; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Vince, J. Quaternions for Computer Graphics; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
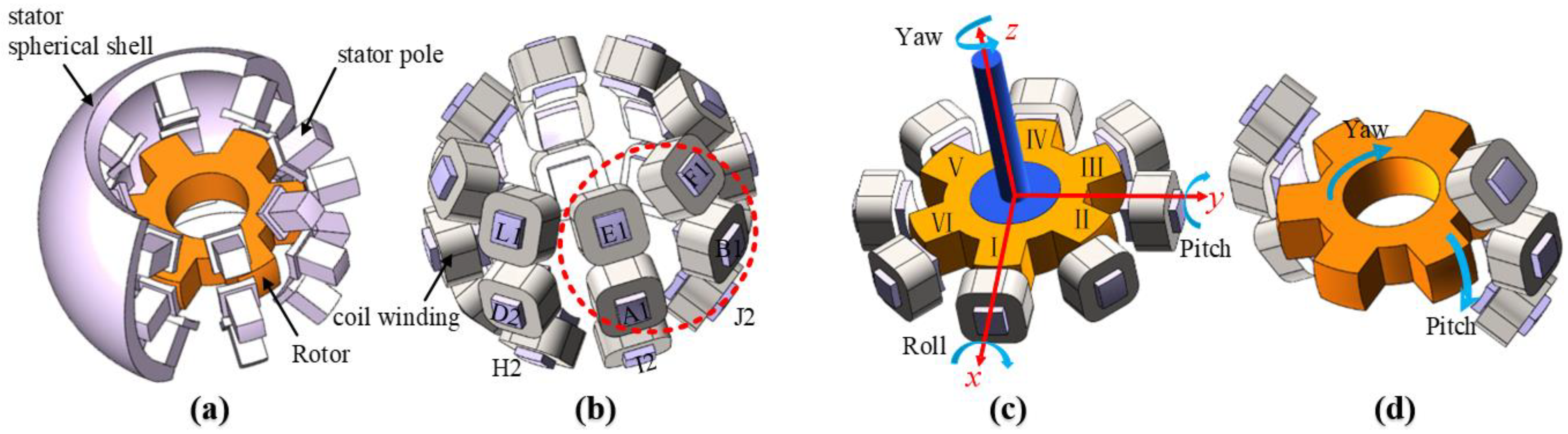










| Upper poles | E1 | F1 | G1 | H1 | I1 | J1 | K1 | L1 |
| Middle poles | A1 | B1 | C1 | D1 | A2 | B2 | C2 | D2 |
| Lower poles | I2 | J2 | K2 | L2 | E2 | F2 | G2 | H2 |
| Parameters | Value (mm) | Parameters | Value (mm) |
|---|---|---|---|
| wo | 45.95 | l2 | 10 |
| wd | 7 | l3 | 14 |
| w1 | 15 | l4 | 16 |
| w2 | 2 | l5 | 9 |
| ws | 12 | w3 | 12.1 |
| wg | 1 | w4 | 20.42 |
| l1 | 102.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ju, L.; Liu, H.; Li, G.; Wang, Q.; Zha, K. Research on Torque Modeling of the Reluctance Spherical Motor Based on Magnetic Equivalent Circuit Method. Energies 2025, 18, 2882. https://doi.org/10.3390/en18112882
Ju L, Liu H, Li G, Wang Q, Zha K. Research on Torque Modeling of the Reluctance Spherical Motor Based on Magnetic Equivalent Circuit Method. Energies. 2025; 18(11):2882. https://doi.org/10.3390/en18112882
Chicago/Turabian StyleJu, Lufeng, Honglei Liu, Guoli Li, Qunjing Wang, and Kangjian Zha. 2025. "Research on Torque Modeling of the Reluctance Spherical Motor Based on Magnetic Equivalent Circuit Method" Energies 18, no. 11: 2882. https://doi.org/10.3390/en18112882
APA StyleJu, L., Liu, H., Li, G., Wang, Q., & Zha, K. (2025). Research on Torque Modeling of the Reluctance Spherical Motor Based on Magnetic Equivalent Circuit Method. Energies, 18(11), 2882. https://doi.org/10.3390/en18112882





