Study on Fracture Interference and Formation Mechanisms of Complex Fracture Networks in Continental Shale Oil Horizontal Well Staged Fracturing
Abstract
1. Introduction
2. Materials and Methods
2.1. Mechanism of Natural Fracture Generation
2.2. Fundamentals and Establishment of Numerical Models
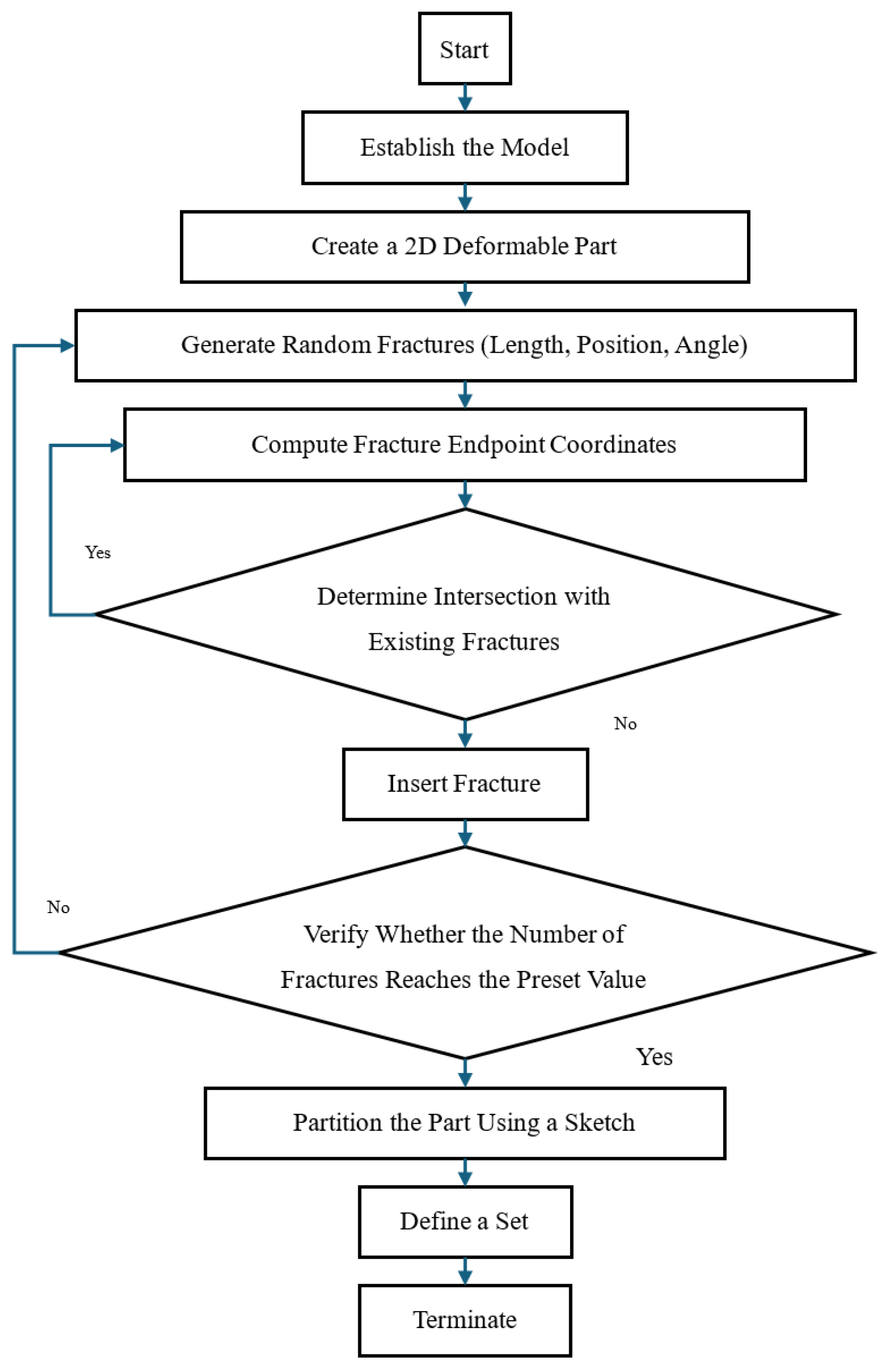
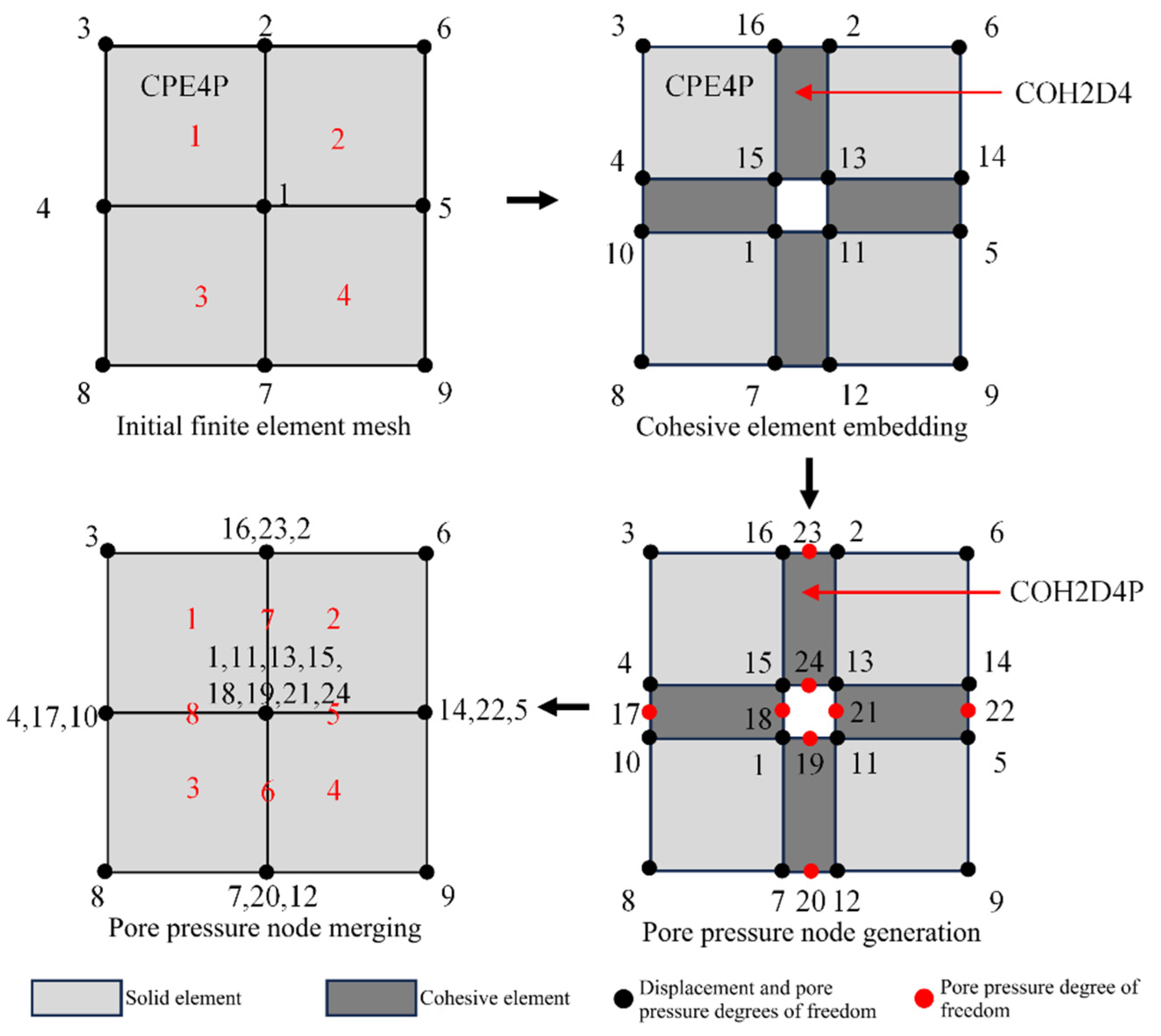
2.2.1. Principle and Method of Globally Embedding Zero-Thickness Cohesive Elements
- (1)
- Extract the information of all model elements and nodes. By rearranging the sequence of the element nodes, ensure that each element does not share nodes with other elements. The sequence follows the right-hand rule. If there are n solid elements, there will be 4n nodes.
- (2)
- Discretize the finite element mesh. Assume that the model consists of n CPE4P elements. Redefine the 4n nodes, and after discretization, set the coordinates of the newly generated nodes equal to the coordinates of the original nodes to ensure that the thickness of the embedded cohesive elements is zero.
- (3)
- Search for any two elements and determine whether they share two pairs of nodes with identical positions. If they do, embed a zero-thickness cohesive element (COH2D4) between each pair of CPE4P elements. If not, no embedding is needed.
- (4)
- Generate pore pressure nodes. To ensure fluid flow between the newly generated interface surfaces, an additional pore pressure node is added at the center of the interface between each adjacent element. At this point, the cohesive element is COH2D4P.
- (5)
- Merge seepage nodes at intersecting points. By merging nodes, the fluid flow can be transmitted smoothly through the shared pore pressure nodes to the surrounding cohesive pore pressure elements.
2.2.2. Establishment of the Numerical Model
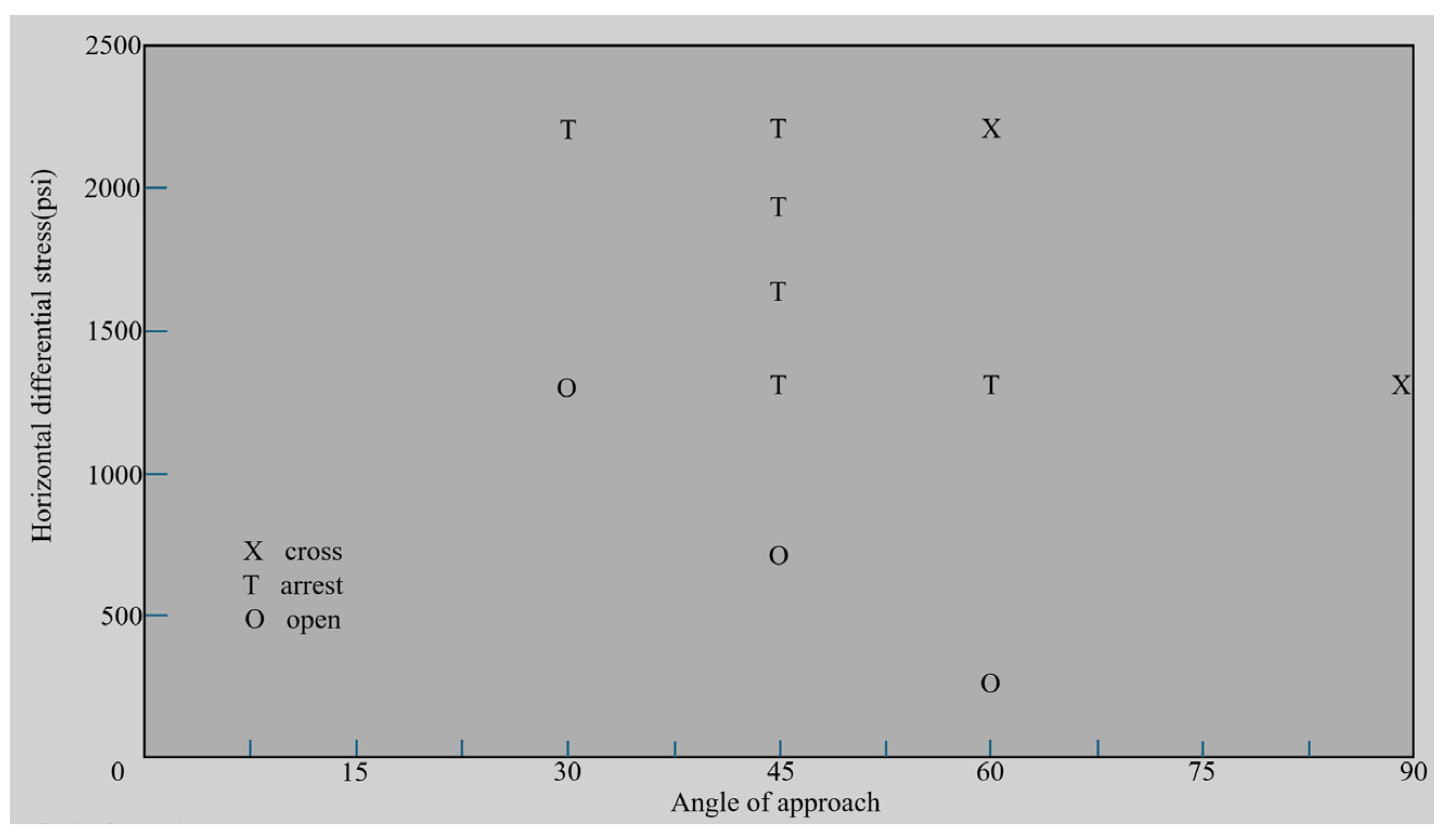
2.2.3. Numerical Model Validation
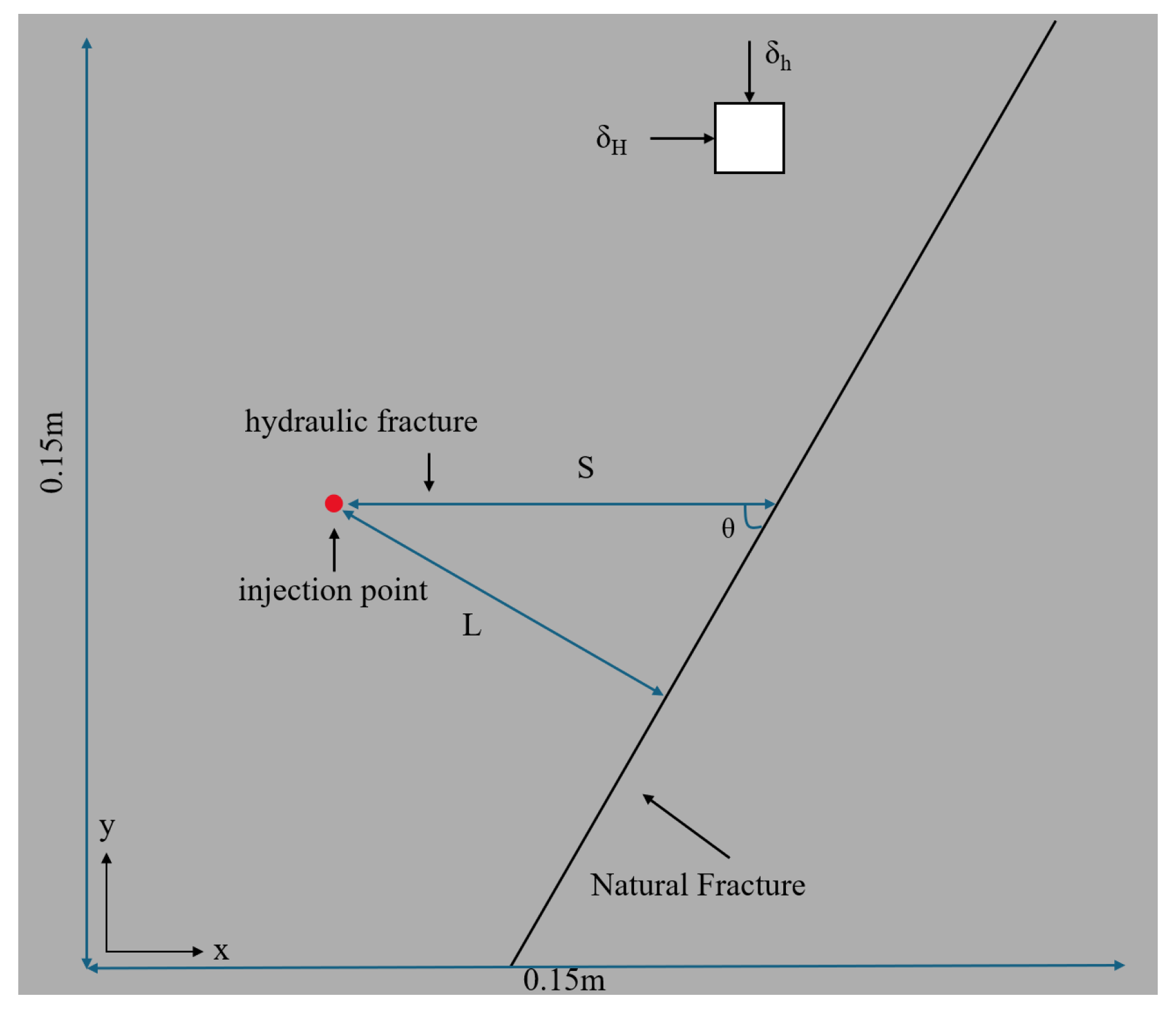
2.3. Model Parameters
2.4. Boundary Condition Setup
3. Numerical Simulation Study of Fracture Evolution in Horizontal Well Staged Fracturing
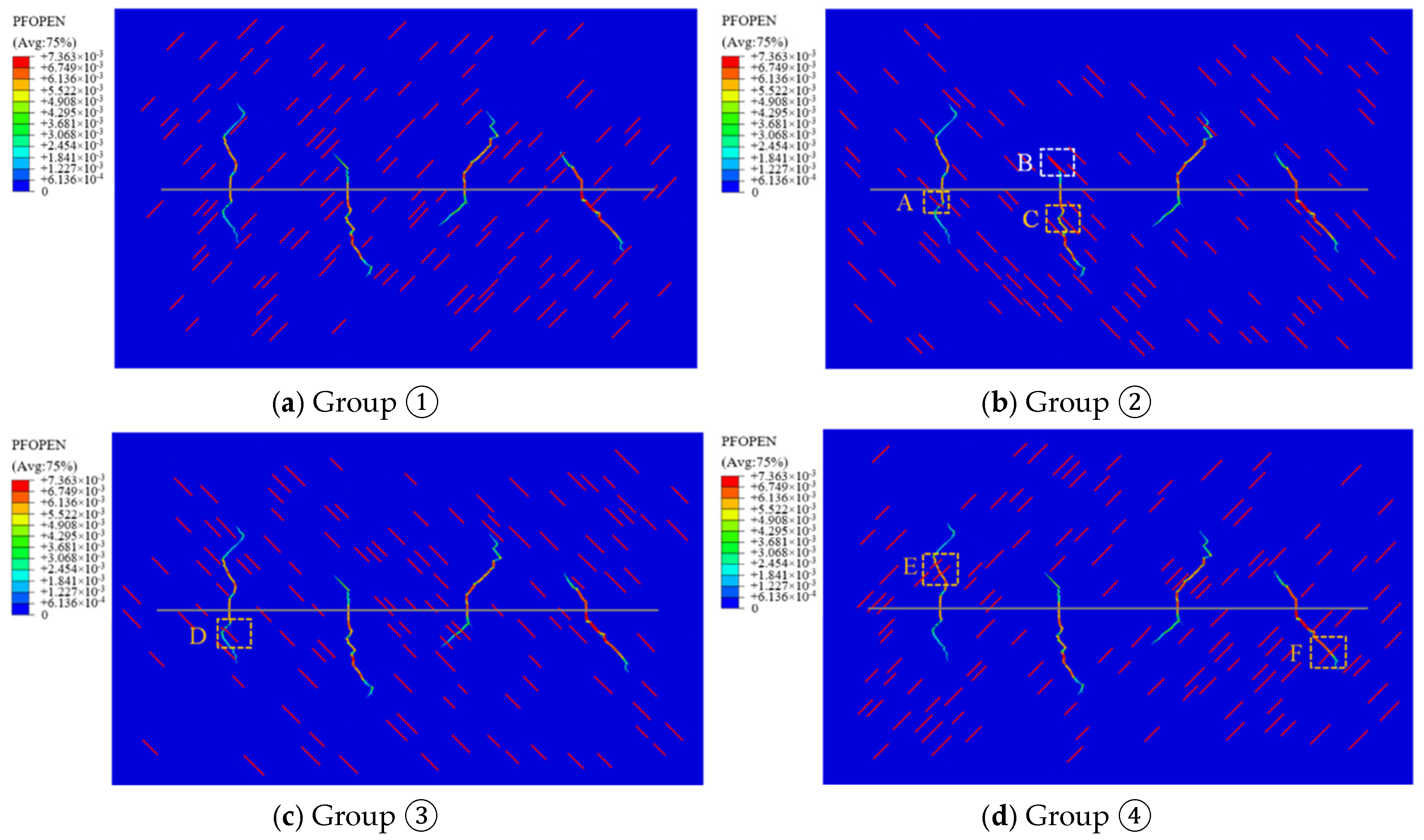
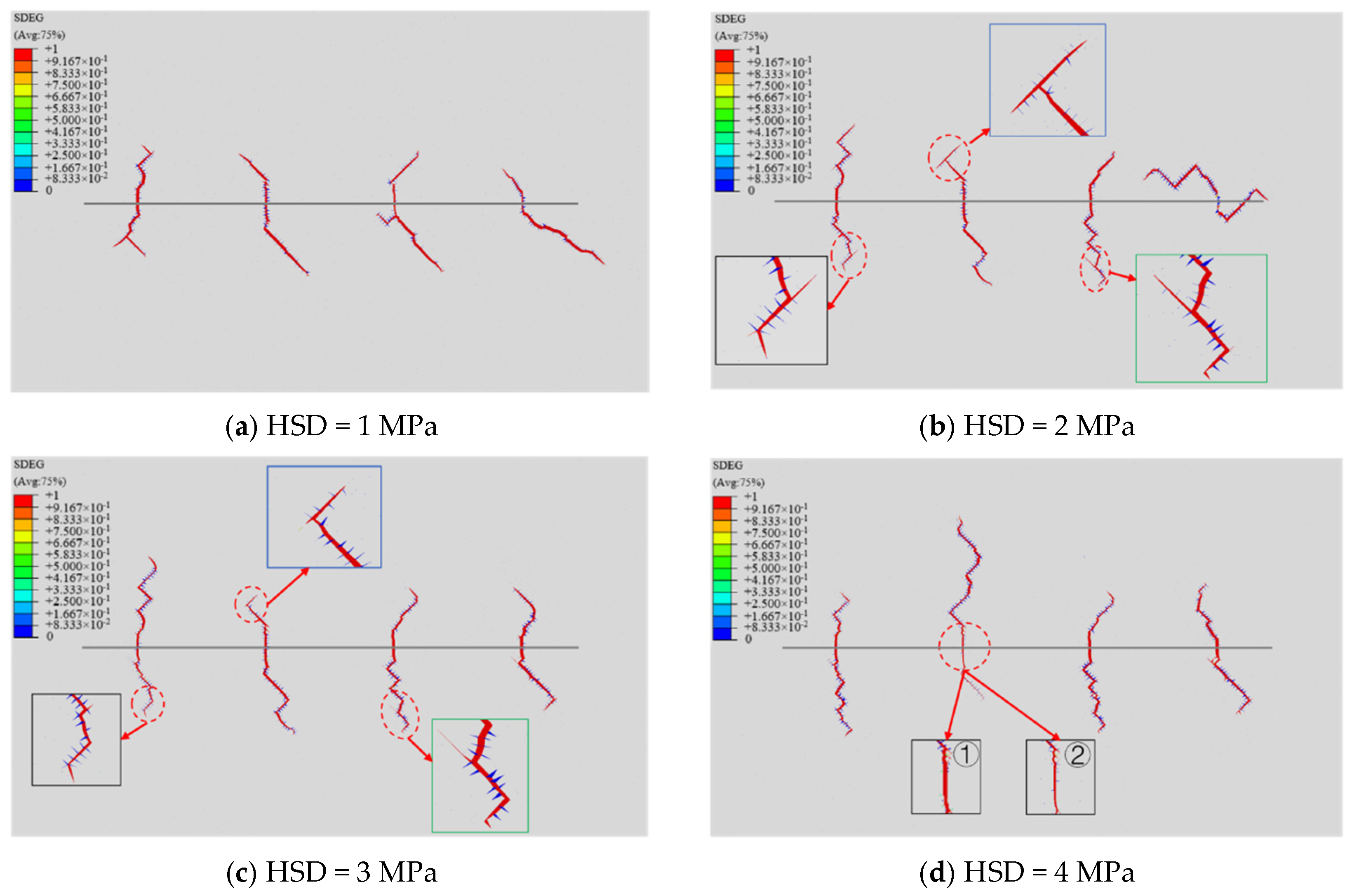
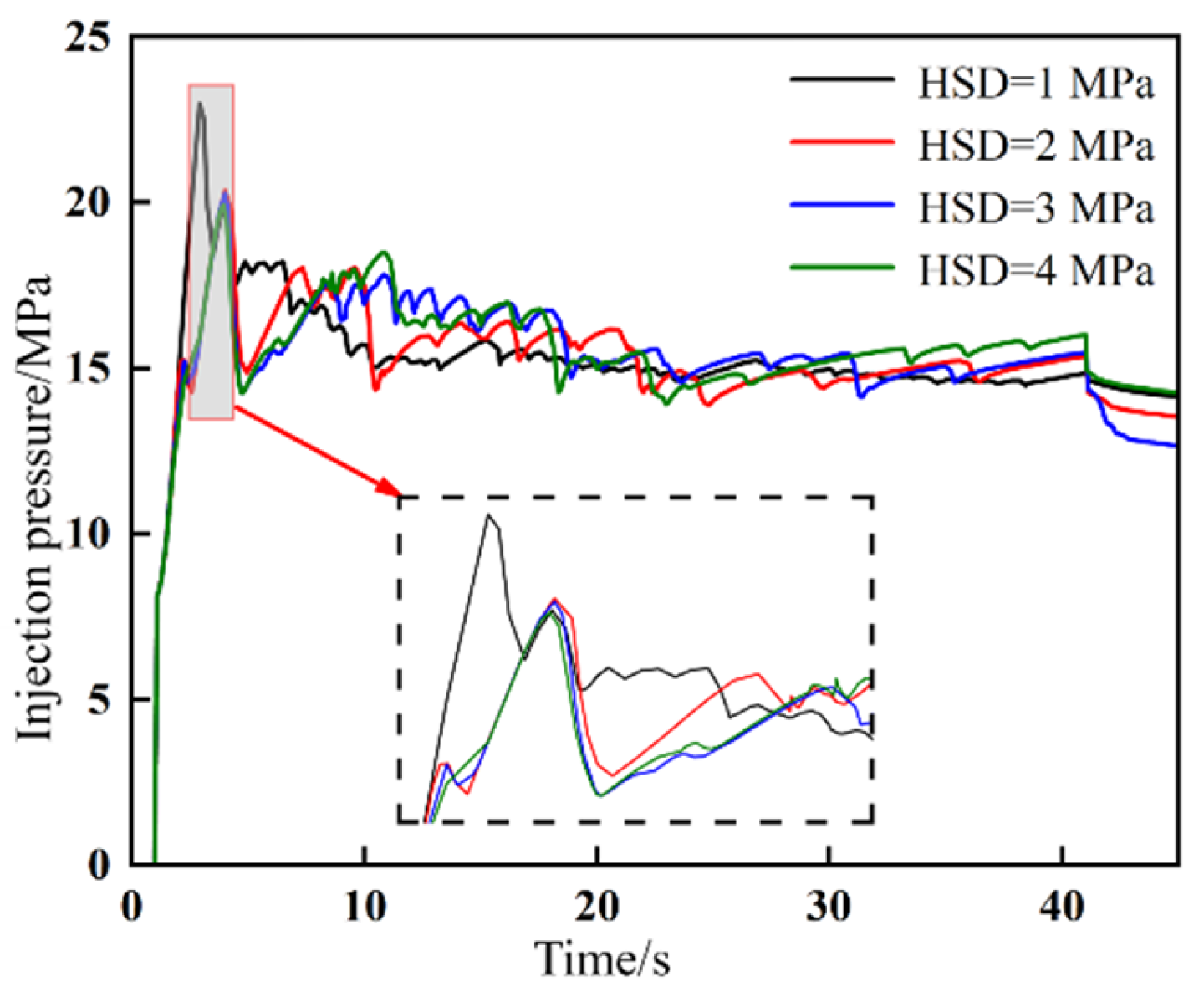
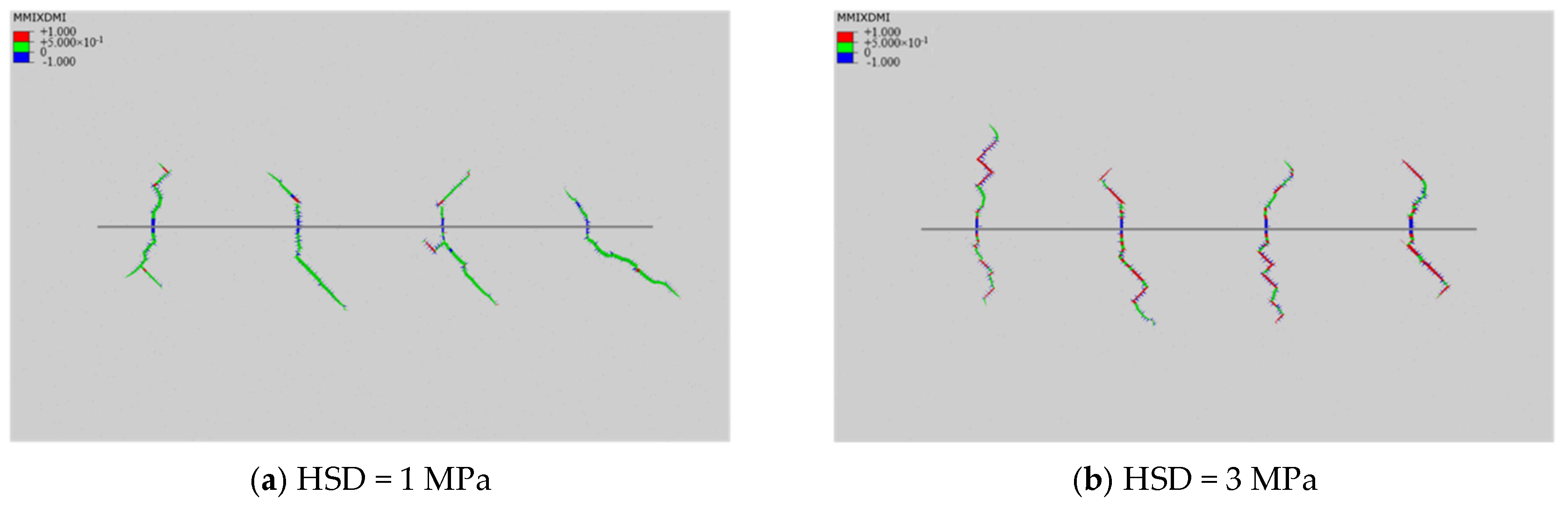
3.1. Evolution Mechanism of Fracture Network Under Different Natural Fracture Cementation Strength
3.2. The Fracture Network Evolution Mechanism Under Different Horizontal Stress Differences
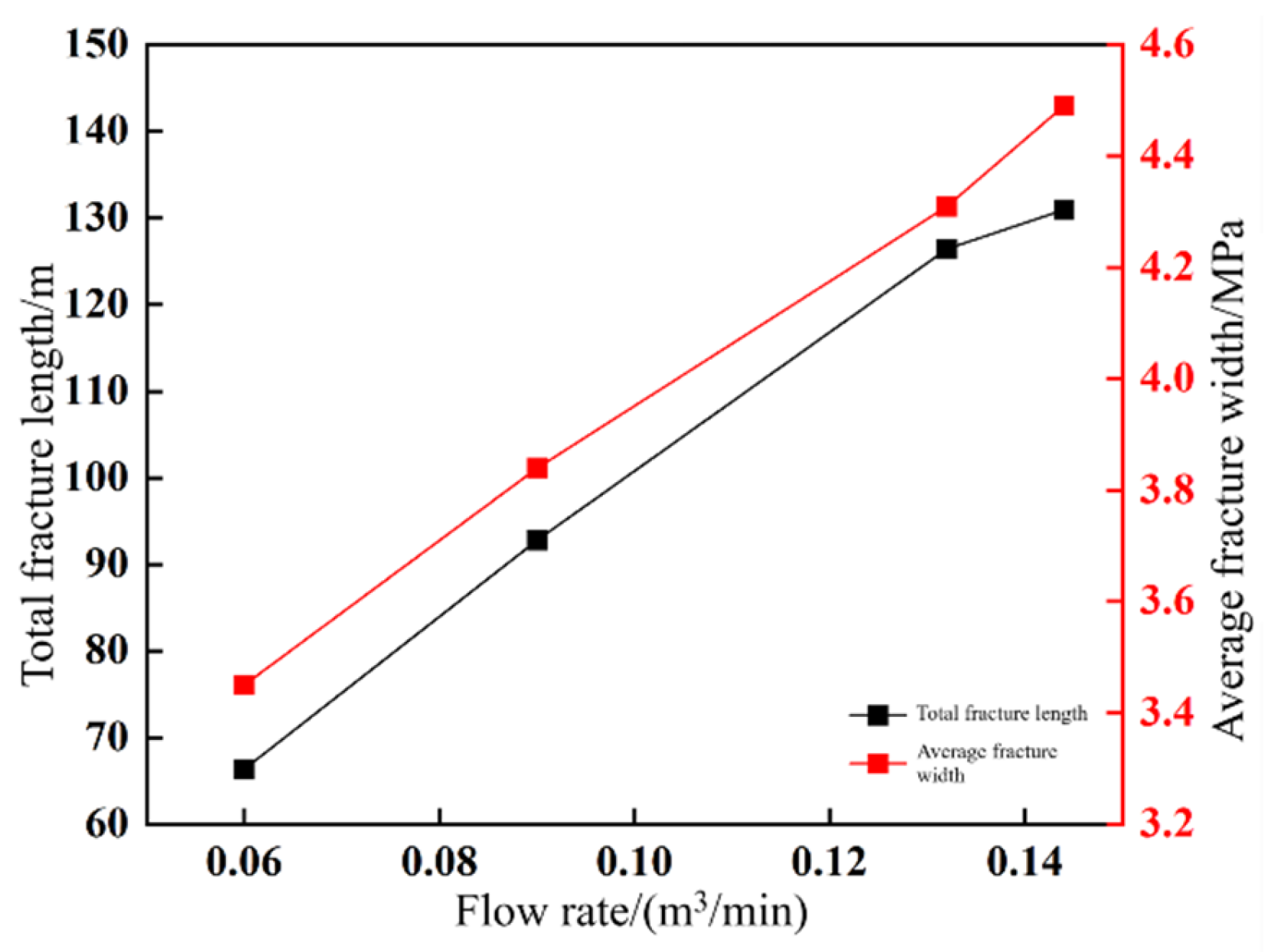
3.3. Fracture Network Evolution Mechanism Under Different Fracturing Fluid Displacement Rates
4. Discussion
5. Conclusions
- Natural fracture cementation strength: Weakly cemented natural fractures exhibit higher activation potential. Increasing the cementation strength coefficient from 0.4 to 0.9 reduces natural fracture communication probability by 5.0% and significantly decreases hydraulic fracture tortuosity.
- Horizontal in situ stress differentials (Δσ): Higher stress differentials amplify normal stress on natural fractures, increasing fracture initiation resistance and promoting elongated, narrow fractures. Optimal production occurs at Δσ = 4 MPa, where fracture networks balance length-width ratios for maximized drainage efficiency.
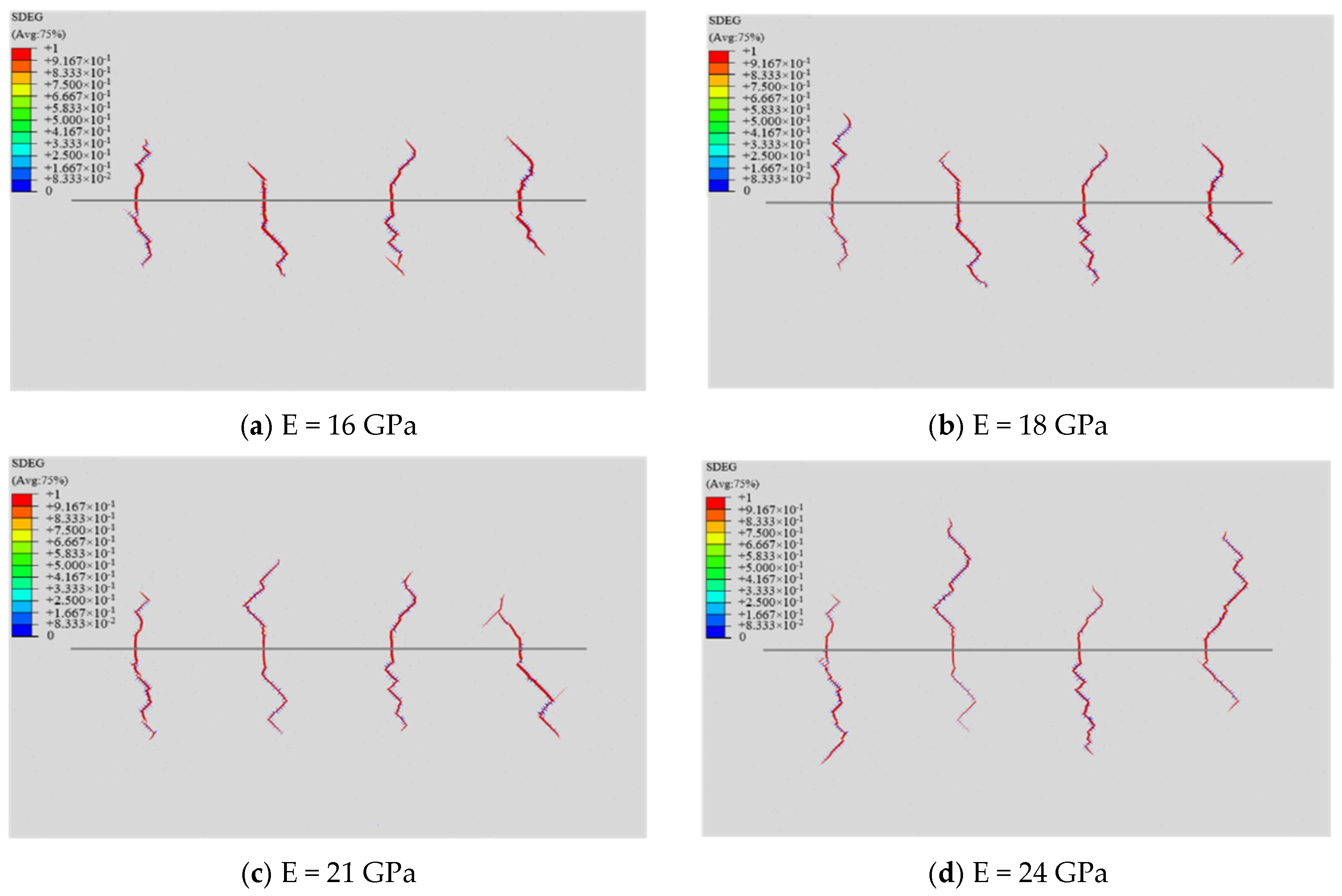
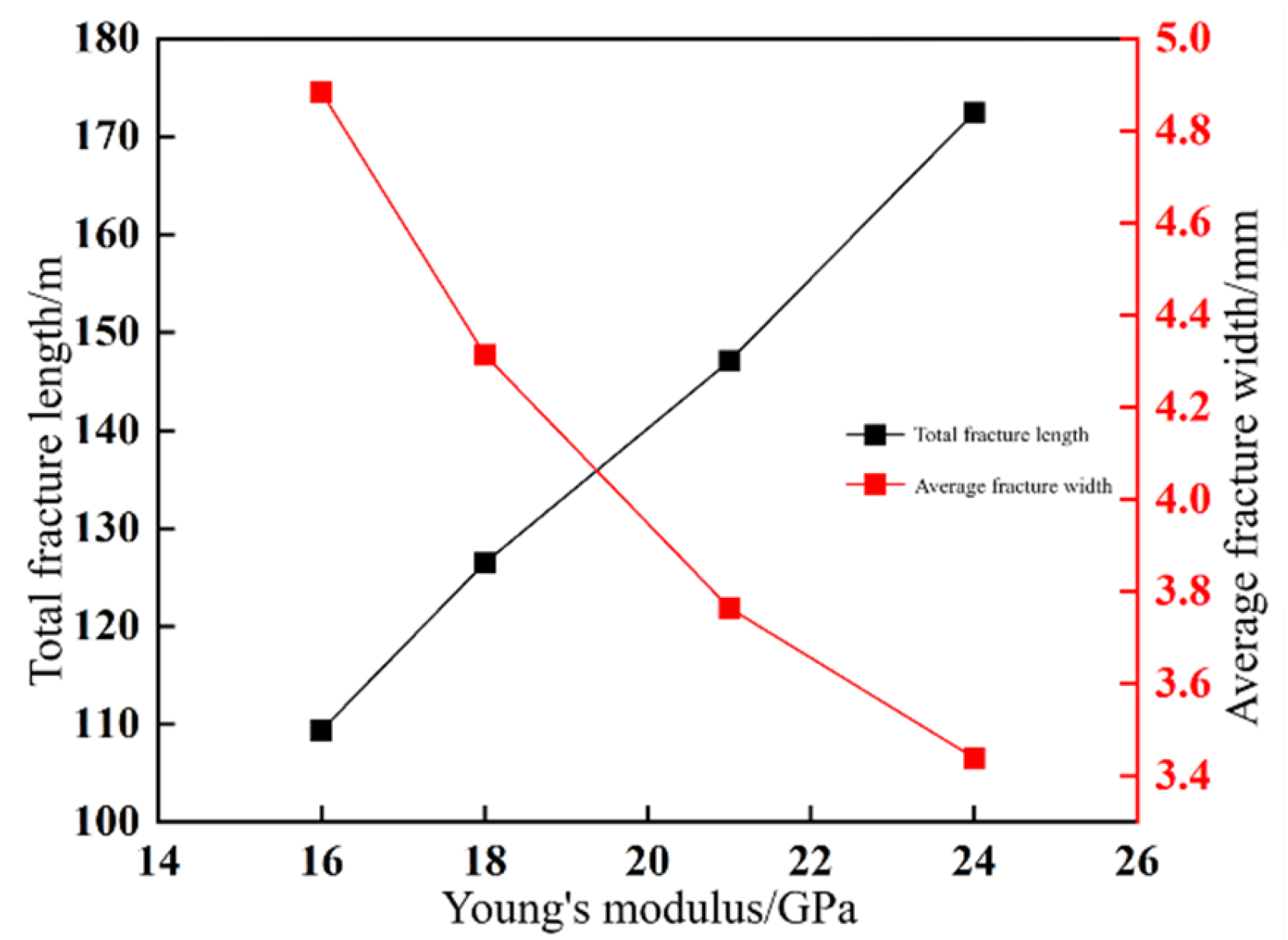
- Young′s modulus (E): Young′s modulus critically governs fracture network complexity. Increasing E from 16 GPa to 24 GPa enhances total fracture length by 57.7% and tortuosity by 33.2%, achieving peak cumulative production at E = 24 GPa due to optimized stimulated reservoir volume (SRV).
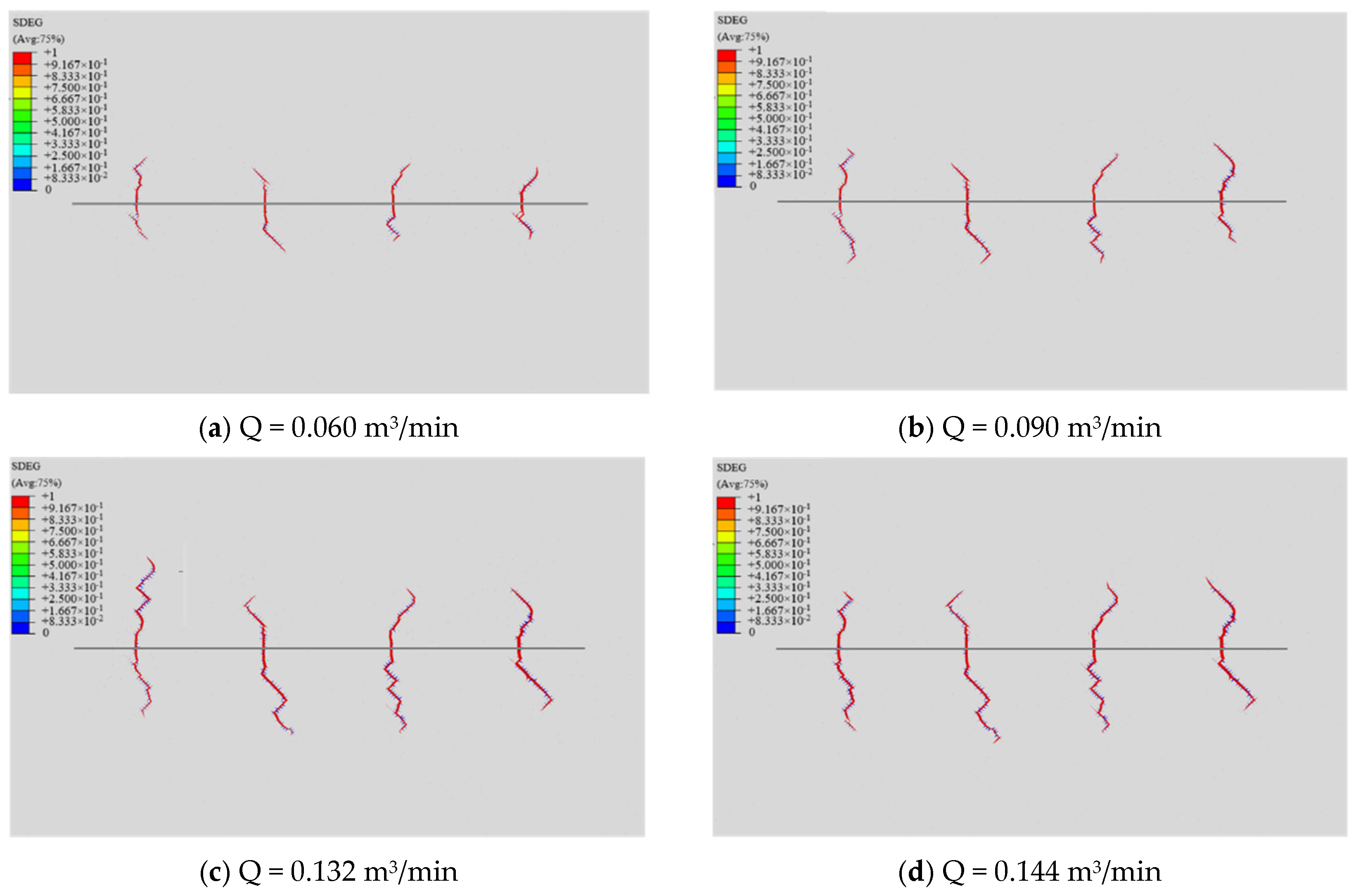
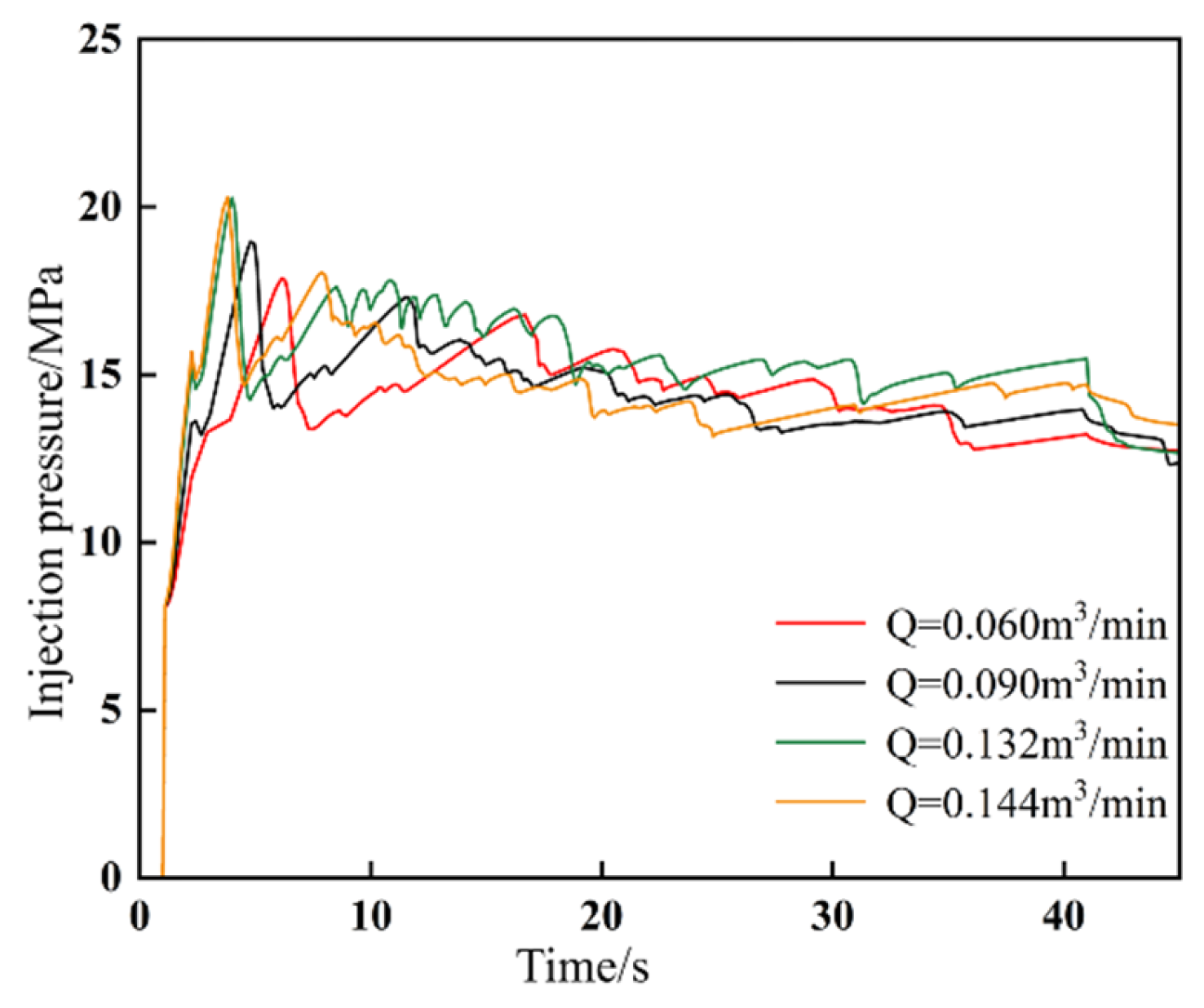
- Injection rate (Q): Elevated injection rates (0.060 → 0.144 m3/min) enhance energy delivery for fracture propagation, increasing total length by 90.6% and network complexity by 41.5%. Higher rates reduce breakdown pressure attainment time by 38%, improving operational efficiency.
- When simulating multiple fracture intersections using globally embedded zero-thickness cohesive elements, the fluid distribution and mass balance within fracture networks become critically intricate, making hydraulic fracturing models challenging to achieve accurate and stable convergence. Therefore, the next phase of research should focus on developing efficient numerical algorithms and fluid partitioning strategies to enhance model performance and computational robustness;
- Future studies should develop multiphysics-coupled models integrating thermodynamic and stochastic bedding effects. Specifically, a novel numerical simulation framework should be established to address thermal–hydraulic–mechanical coupling mechanisms in shale reservoirs, incorporating formation thermal stress evolution, heterogeneous bedding interface distributions, and stochastic geological characteristics;
- Continental shale formations contain multi-scale impurities and pore structures beyond natural fractures, whose distinct structural features influence hydraulic fracture propagation. Subsequent investigations should therefore conduct comprehensive research on the mechanical interactions between these multi-scale heterogeneities and fracture development dynamics.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ding, Y.T. Domestic Oil and Gas Production Equivalent to Exceed 400 Million Tons for the First Time in 2024; Tongfang Knowledge Network (Beijing) Technology Co., Ltd.: Beijing, China, 2025; p. 002. [Google Scholar] [CrossRef]
- Jia, C.Z.; Wang, Z.G.; Jiang, L.; Zhao, W. Research Progress and Scientific Challenges in Shale Oil Exploration and Development in China. World Pet. Ind. 2024, 31, 1–11. [Google Scholar] [CrossRef]
- Chen, B.; Barboza, B.R.; Sun, Y.; Bai, J.; Thomas, H.R. A Review of Hydraulic Fracturing Simulation. Arch. Comput. Methods Eng. 2022, 29, 1–58. [Google Scholar] [CrossRef]
- Barati, R.; Liang, J.T. A Review of Fracturing Fluid Systems Used for Hydraulic Fracturing of Oil and Gas Wells. J. Appl. Polym. Sci. 2014, 131, 318–323. [Google Scholar] [CrossRef]
- Osiptsov, A.A. Fluid Mechanics of Hydraulic Fracturing: A Review. J. Pet. Sci. Eng. 2017, 156, 513–535. [Google Scholar] [CrossRef]
- Zhang, J.; Lian, L.; Wang, P.; Li, G.; Liu, Z.; Zou, G.; Tian, L.; Huang, X. Application of Hydraulic Fracture Propagation and Production Simulation Technology for Multi-Stage Optimization—A Case Study from Unconventional Reservoir. In Proceedings of the SPE EOR Conference at Oil and Gas West Asia, Muscat, Oman, 16–18 April 2024; p. D031S036R005. [Google Scholar]
- Huang, L.; Liao, X.; Fan, M.; Wu, S.; Tan, P.; Yang, L. Experimental and Numerical Simulation Technique for Hydraulic Fracturing of Shale Formations. Adv. Geo-Energy Res. 2024, 13, 83–88. [Google Scholar] [CrossRef]
- Guo, X.; Yu, Z. Experimental and Numerical Simulation Study on Hydraulic Fracture Propagation Law of Coal Seam. Pet. Sci. Technol. 2024, 42, 2063–2085. [Google Scholar] [CrossRef]
- Yu, H.; Xu, W.; Li, B.; Huang, H.; Micheal, M.; Wang, Q.; Huang, M.; Meng, S.; Liu, H.; Wu, H. Hydraulic Fracturing and Enhanced Recovery in Shale Reservoirs: Theoretical Analysis to Engineering Applications. Energy Fuels 2023, 37, 42. [Google Scholar] [CrossRef]
- Li, G.Y. Improved Water Security for China’s Efforts to Build Itself into a Stronger Country and Rejuvenate the Chinese Nation on All Fronts by Pursuing Chinese Modernization—Speech at the 2024 National Water Conservancy Work Conference. Water Resour. Dev. Res. 2024, 24, 1–10. [Google Scholar] [CrossRef]
- Li, G.Y. Thoroughly Implemented the Spirit of the 20th National Congress of the Communist Party of China and Solidly Promoted the High-Quality Development of Water Conservancy in the New Stage Speech at the National Water Conservancy Work Conference in 2023. Water Resour. Dev. Res. 2023, 23, 1–11. [Google Scholar] [CrossRef]
- Wu, F.C. Effectiveness, Scientific and Technological Support, and Prospects for Water Pollution Control and Management in China. Water Resour. Dev. Res. 2023, 23, 1–8. [Google Scholar] [CrossRef]
- Zhu, D.; Zhang, L.; Song, X.; Lian, H.; Niu, D. Propagation Mechanism of the Hydraulic Fracture in Layered-Fractured-Plastic Formations. Int. J. Fract. 2023, 241, 189–210. [Google Scholar] [CrossRef]
- Wang, H.; Xiao, P.; Zhou, D.; Wang, Q. Numerical Modeling of the Interaction of Cemented Natural Fractures and Hydraulic Fractures. Sci. Rep. 2024, 14, 32050. [Google Scholar] [CrossRef] [PubMed]
- Shi, S.; Wang, M.; Tang, W.; Pan, Y.; Jin, H.; He, J.; Hou, L.; Xie, B.; Chen, X.; Lv, Z. Study of Stress Field Induced by Natural Fracture and Its Influence on Hydraulic Fracture Propagation. J. Pet. Explor. Prod. Technol. 2024, 14, 1085–1099. [Google Scholar] [CrossRef]
- Fu, H.; Huang, L.; Hou, B.; Weng, D.; Guan, B.; Zhong, T.; Zhao, Y. Experimental and Numerical Investigation on Interaction Mechanism Between Hydraulic Fracture and Natural Fracture. Rock Mech. Rock Eng. 2024, 57, 10571–10582. [Google Scholar] [CrossRef]
- Yan, C.; Zheng, H.; Sun, G.; Ge, X. Combined finite-discrete element method for simulation of hydraulic fracturing. Rock Mech. Rock Eng. 2016, 49, 1389–1410. [Google Scholar] [CrossRef]
- Yan, C.Z.; Zheng, H. FDEM-flow 3D: A 3D hydro-mechanical coupled model considering the pore seepage of rock matrix for simulating three-dimensional hydraulic fracturing. Comput. Geotech. 2017, 81, 212–228. [Google Scholar] [CrossRef]
- Nguyen, V.P.; Lian, H.; Rabczuk, T.; Bordas, S. Modelling hydraulic fractures in porous media using flow cohesive interface elements. Eng. Geol. 2017, 225, 68–82. [Google Scholar] [CrossRef]
- Duan, G.; Mou, J.; Liu, Z.; Han, L.; Cui, H. Study on the Induced Effect of Bedding Weakness in Deep Shale Gas Reservoir on Hydraulic Fractures Propagation. Front. Energy Res. 2024, 12, 1392298. [Google Scholar] [CrossRef]
- Jiang, M.; Wei, Y.; Li, T.; Dong, K. Influence of Horizontal Multi-Bedding on Hydraulic Fracture Propagation in Shale Reservoirs. Processes 2023, 11, 2846. [Google Scholar] [CrossRef]
- Ma, Y.; Li, J. Utilization Law of Shale Gas in Hydraulic Fracturing with the Changning-Weyuan Block in China as an Example. Phys. Fluids 2024, 36, 102020. [Google Scholar] [CrossRef]
- Kukharova, T.; Maltsev, P.; Novozhilov, I. Development of a Control System for Pressure Distribution During Gas Production in a Structurally Complex Field. Appl. Syst. Innov. 2025, 8, 51. [Google Scholar] [CrossRef]
- Zhao, Y.G.; Zhang, X.Y.; Li, Z.; Wang, Z.L.; Shen, L.F. Study on the Influence of Stochastic Microcracks on Macroscopic Crack Propagation in Rocks. Eng. Mech. 2024, 41, 103–115. [Google Scholar]
- Li, J.; Zhai, W.B.; Chen, C.W.; Liu, G.H.; Zhou, Y.C. Research on Stochastic Propagation Method of Hydraulic Fractures Based on Zero-Thickness Cohesive Elements. Rock Soil Mech. 2021, 42, 265–279. [Google Scholar] [CrossRef]
- Li, Z.Y.; Lin, T.; Ouyang, W. Numerical Simulation of Staged Fracturing in Horizontal Wells. Yunnan Chem. Technol. 2024, 51, 125–128+131. [Google Scholar]
- Blanton, T.L. An experimental study of interaction between hydraulically induced and pre-existing fractures. In Proceedings of the SPE Unconventional Gas Recovery Symposium, Pittsburgh, PA, USA, 16–18 May 1982; p. SPE-10847-MS. [Google Scholar]
- Zhang, H.Y. Evolution Mechanisms of Intensive Volume Fracturing-Induced Fracture Networks in Continental Shale Oil Reservoirs. Master’s Thesis, Xi’an Shiyou University, Xi’an, China, 2023. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, J.Z.; Hu, Y.Q.; Zhao, C.N.; Fu, C.H. Morphology and Activation Mechanisms of Hydraulic Fracture Networks in Shale. J. Southwest Pet. Univ. (Nat. Sci. Ed.) 2022, 44, 71–86. [Google Scholar]
- He, M.Q. Fracture Propagation Behavior and Microscopic Mechanisms of CO2 Fracturing in Shale Reservoirs. Ph.D. Thesis, China University of Petroleum (Beijing), Beijing, China, 2022; pp. 40–42. [Google Scholar]
- Cai, X. Cohesive Zone Modeling of Fluid-Solid Coupling Considering Complex Hydraulic Fracture Morphologies. Ph.D. Thesis, China University of Petroleum (East China), Qingdao, China, 2021; pp. 55–63. [Google Scholar]

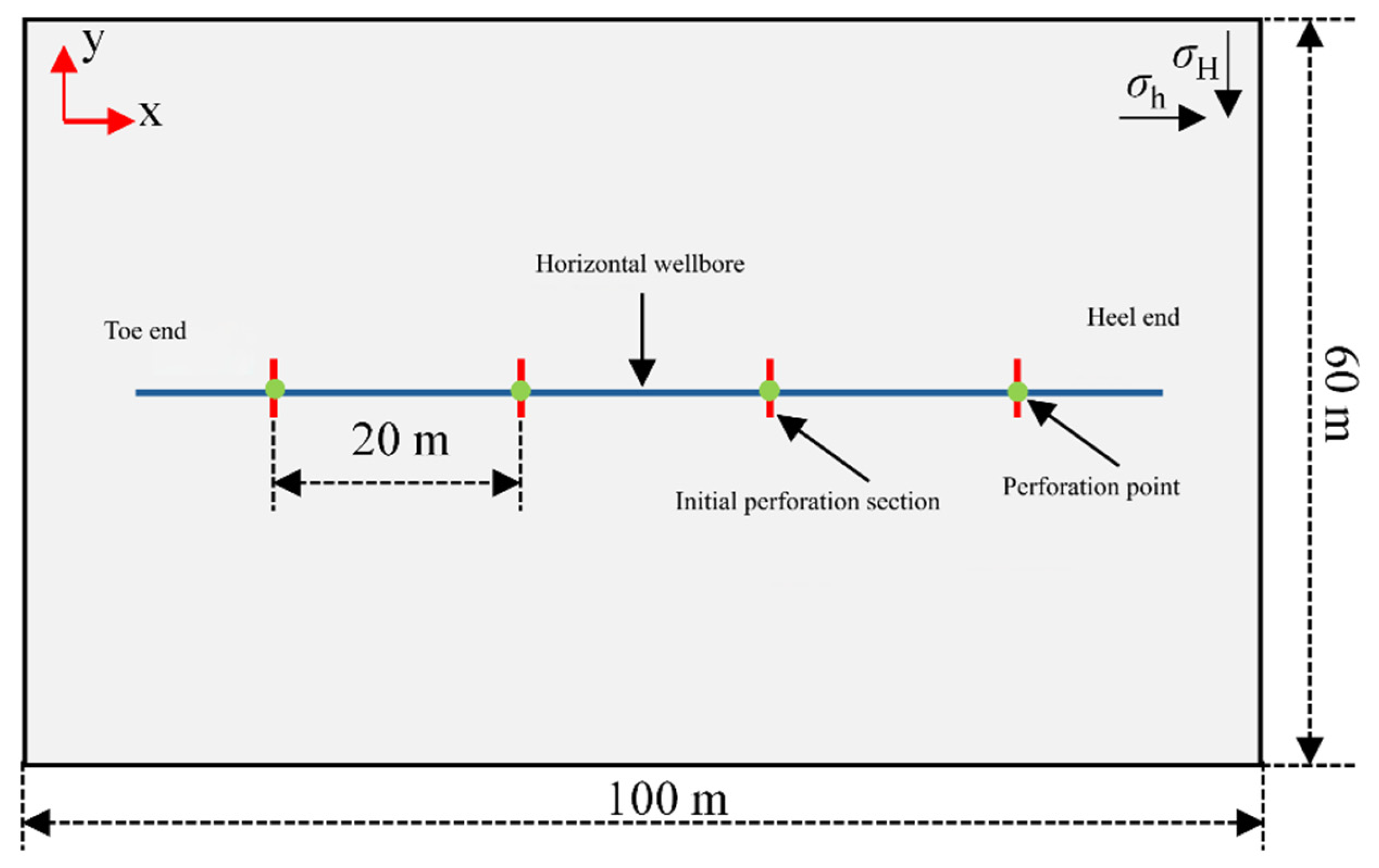



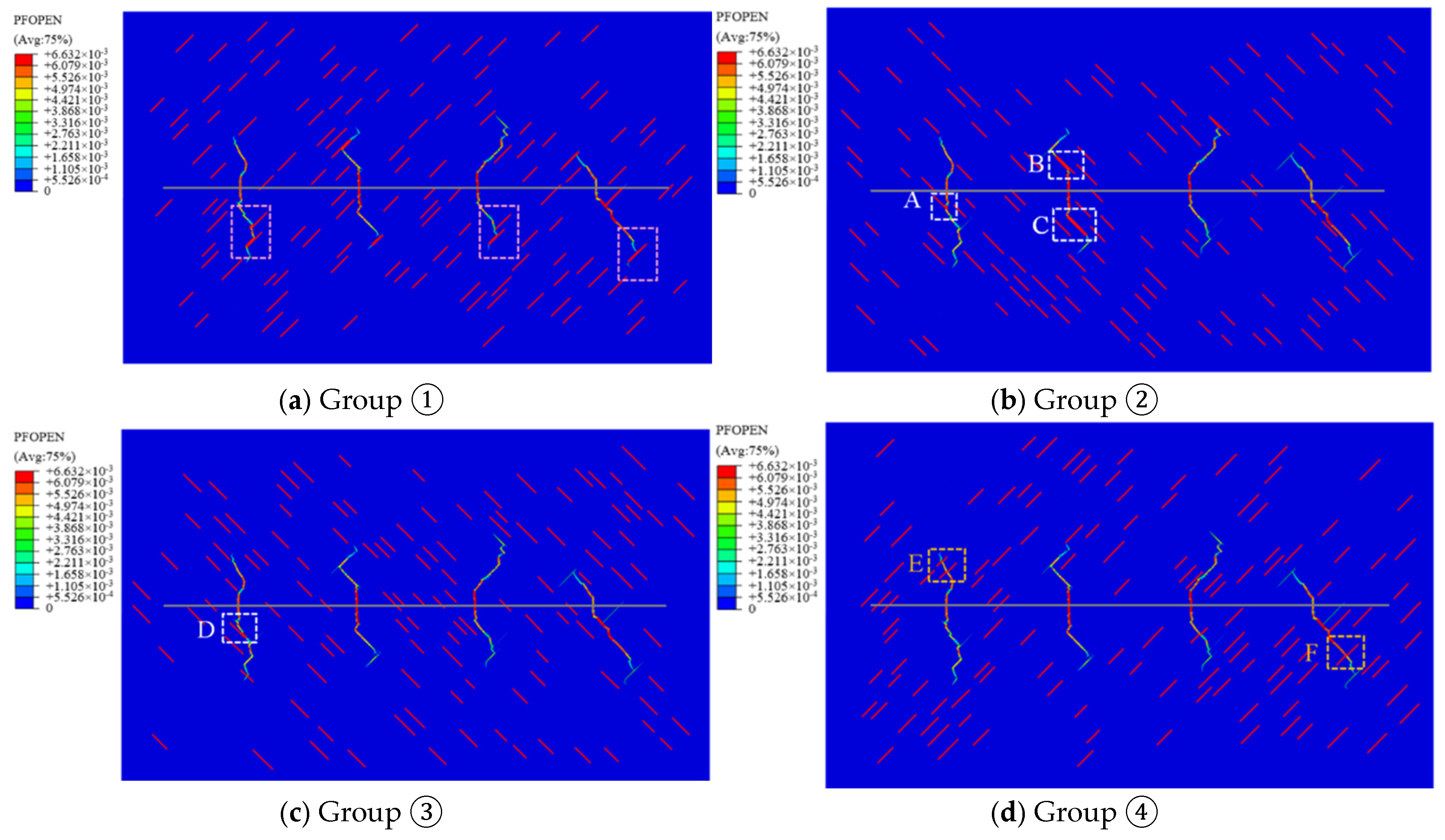

| Number of Groups | Length/m | Angle/° | Quantity/Fracture Count |
|---|---|---|---|
| ① | 3–5 | 45° | 100 |
| ② | 3–5 | −45° | 100 |
| ③ | 3–5 | −45° | 100 |
| ④ | 3–5 | 45° | 100 |
| Name | Parameter | Unit | Value |
|---|---|---|---|
| Injection Parameters | Fracturing Fluid Viscosity | Pa·s | 0.001 |
| Fracturing Fluid Injection Rate | m3/min | 0.132 | |
| Injection Time | s | 40 | |
| In situ stress field | Maximum Horizontal Principal Stress | Pa | 11 × 106 |
| Minimum Horizontal Principal Stress | Pa | 8 × 106 | |
| Matrix | Young’s Modulus | GPa | 18 |
| Poisson’s Ratio | / | 0.14 | |
| Initial Porosity | / | 0.1 | |
| Pore Pressure | MPa | 20 | |
| Permeability Coefficient | m/s | 1 × 10−7 | |
| Rock Cohesion Zone | Bedrock Tensile Strength | Pa | 8 × 106 |
| Rock Shear Strength | Pa | 2 × 107 | |
| Bedrock Tensile Fracture Energy | N/m | 2000 | |
| Bedrock Shear Fracture Energy | N/m | 4500 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, S.; Gong, D.; Li, Z.; Chen, J.; Chen, X.; Song, W. Study on Fracture Interference and Formation Mechanisms of Complex Fracture Networks in Continental Shale Oil Horizontal Well Staged Fracturing. Energies 2025, 18, 2862. https://doi.org/10.3390/en18112862
Lin S, Gong D, Li Z, Chen J, Chen X, Song W. Study on Fracture Interference and Formation Mechanisms of Complex Fracture Networks in Continental Shale Oil Horizontal Well Staged Fracturing. Energies. 2025; 18(11):2862. https://doi.org/10.3390/en18112862
Chicago/Turabian StyleLin, Shiqi, Diguang Gong, Ziyan Li, Junbin Chen, Xi Chen, and Wenying Song. 2025. "Study on Fracture Interference and Formation Mechanisms of Complex Fracture Networks in Continental Shale Oil Horizontal Well Staged Fracturing" Energies 18, no. 11: 2862. https://doi.org/10.3390/en18112862
APA StyleLin, S., Gong, D., Li, Z., Chen, J., Chen, X., & Song, W. (2025). Study on Fracture Interference and Formation Mechanisms of Complex Fracture Networks in Continental Shale Oil Horizontal Well Staged Fracturing. Energies, 18(11), 2862. https://doi.org/10.3390/en18112862





