Charging Incentive Design with Minimum Price Guarantee for Battery Energy Storage Systems to Mitigate Grid Congestion
Abstract
1. Introduction
- ✓
- For BESS owners, improvements in both profitability and price predictability can be expected via charging shifts as the most cost-effective charging periods are identified in advance;
- ✓
- For system operators, as the market prices during congestion periods tend to be at their lowest, the additional payment required to compensate BESS owners (i.e., the difference between the market and minimum prices) can be minimized.
- A novel incentive design method is proposed to guide BESS charging for congestion mitigation by leveraging the alignment between day-ahead market prices and congestion periods.
- The proposed method aims to balance two potentially conflicting objectives, namely promoting BESS charging during congestion periods and avoiding increased social costs due to excessive incentives, offering benefits to both BESS owners and system operators.
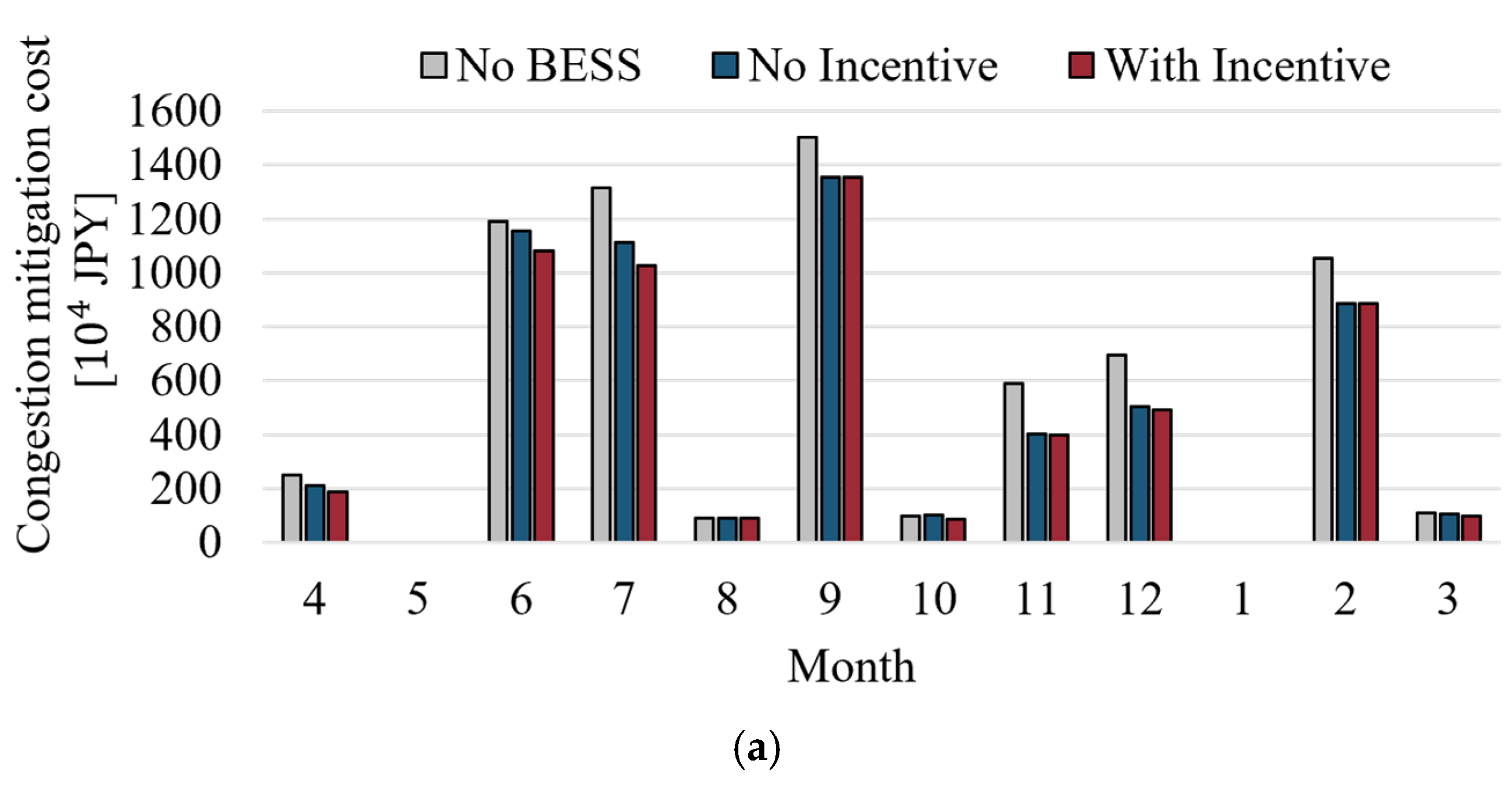
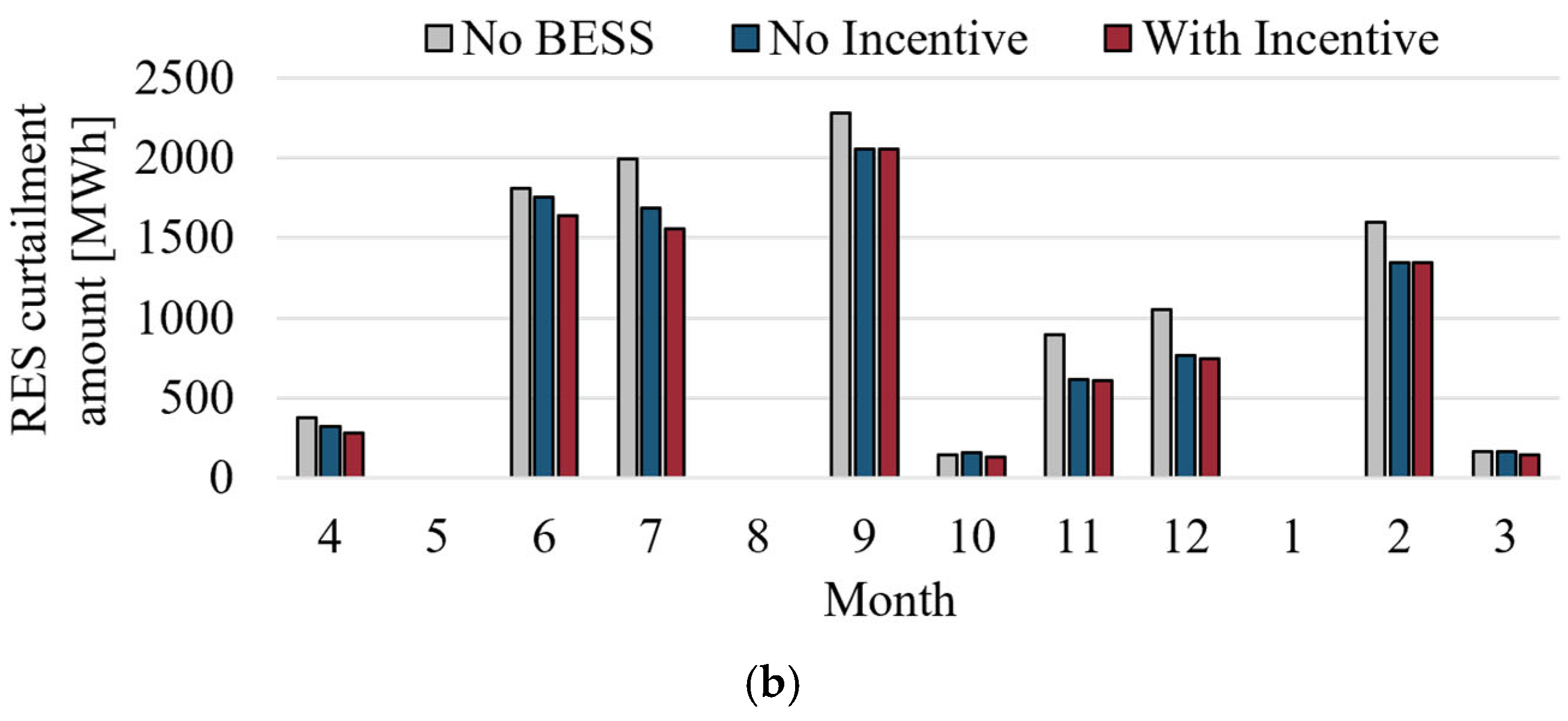
- Congestion management simulations based on a Japanese power system model confirm that the proposed method reduces both the congestion mitigation costs and renewable energy curtailment compared to the case without incentives. Furthermore, the additional payments to BESS owners under the proposed scheme were smaller than the corresponding reduction in the congestion mitigation costs, demonstrating a net decrease in the total system operating costs.
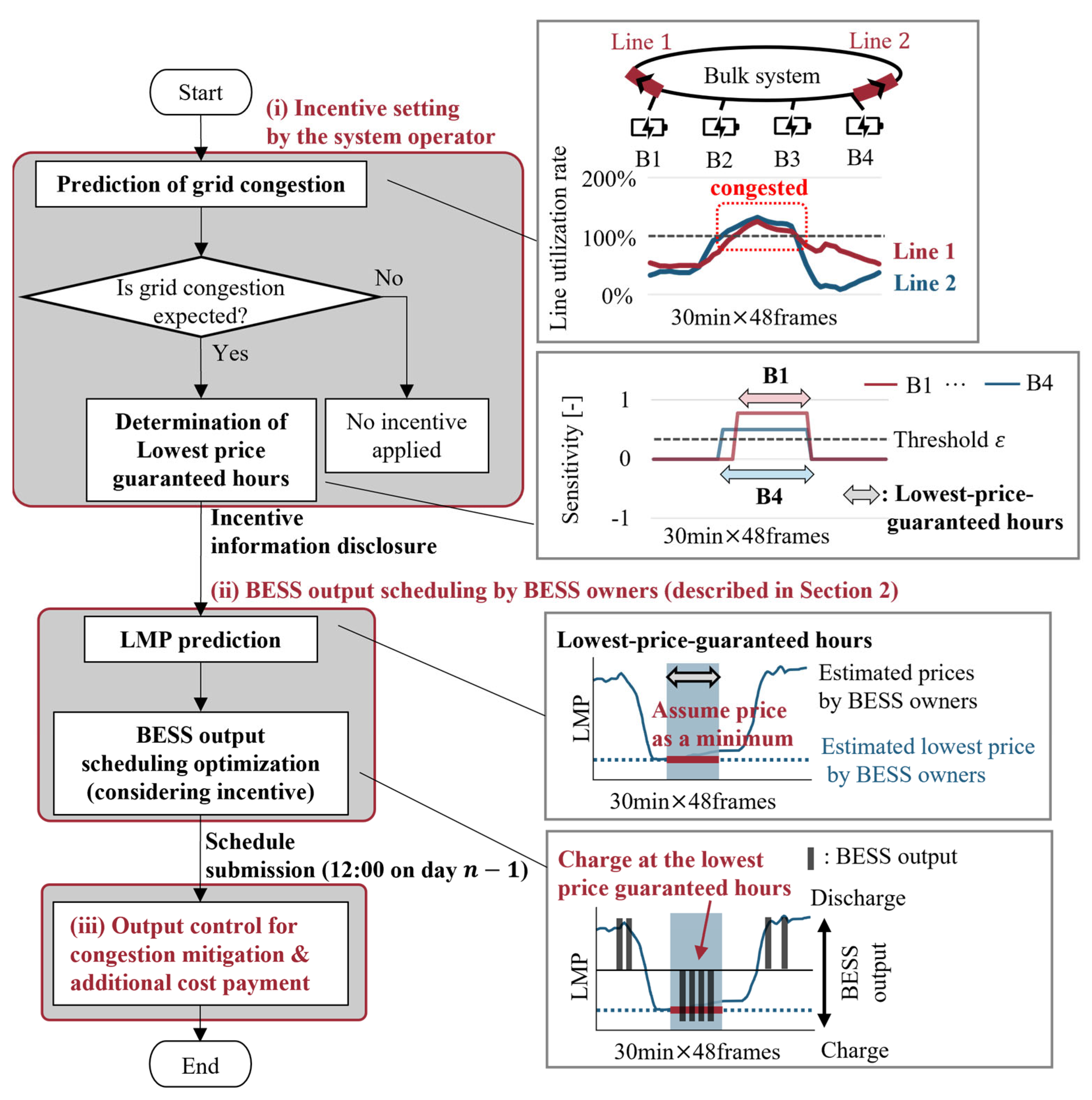
2. Definition of Grid Congestion Management
2.1. BESS Operation Planning
2.2. Grid Congestion Management and LMP Calculation
3. Charging Incentive Design with Minimum Price Guarantee for BESSs
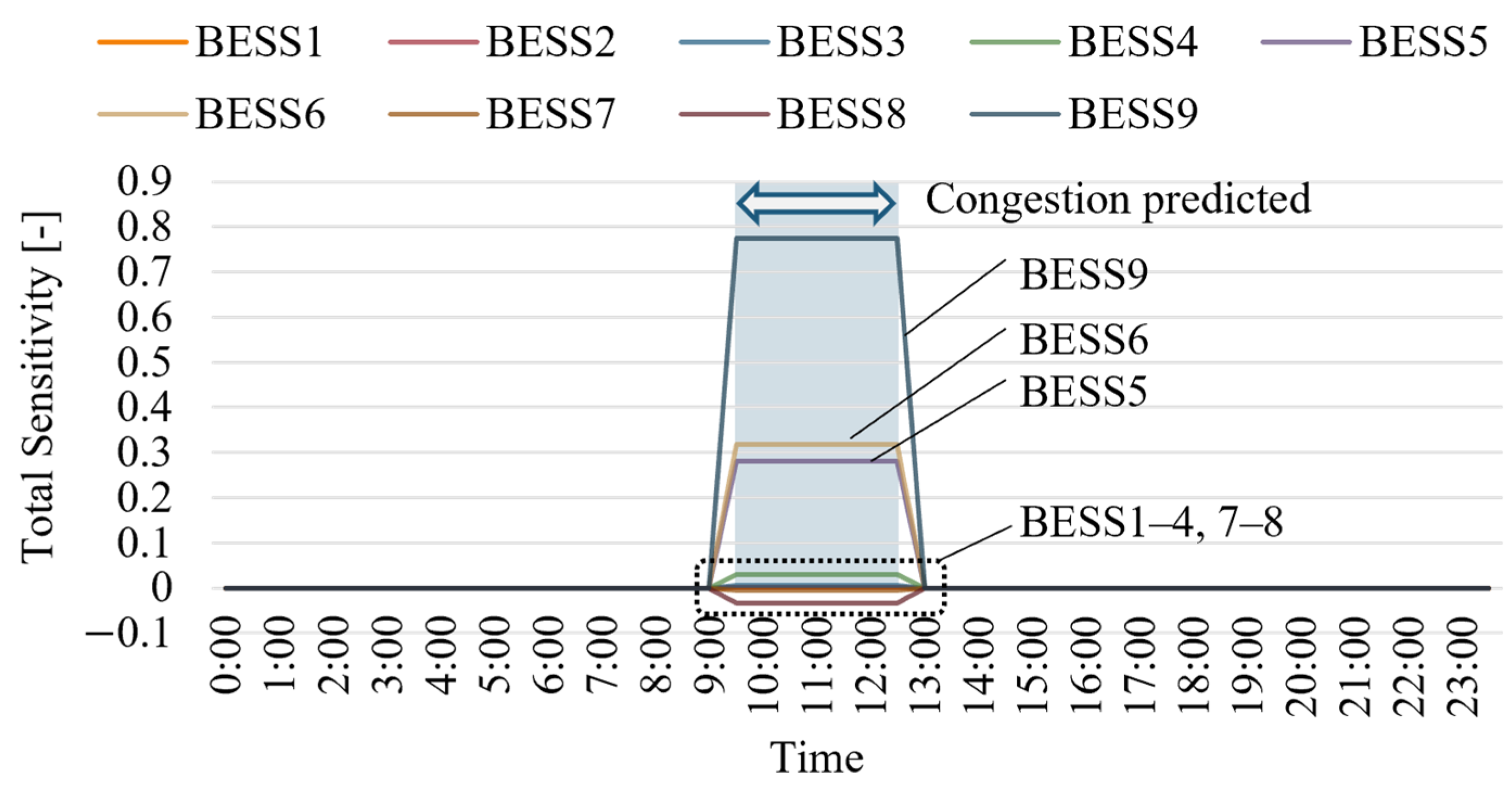
3.1. BESS and Period Identification for Incentive Application
3.2. Additional Payment Cost Calculation
4. Numerical Simulations
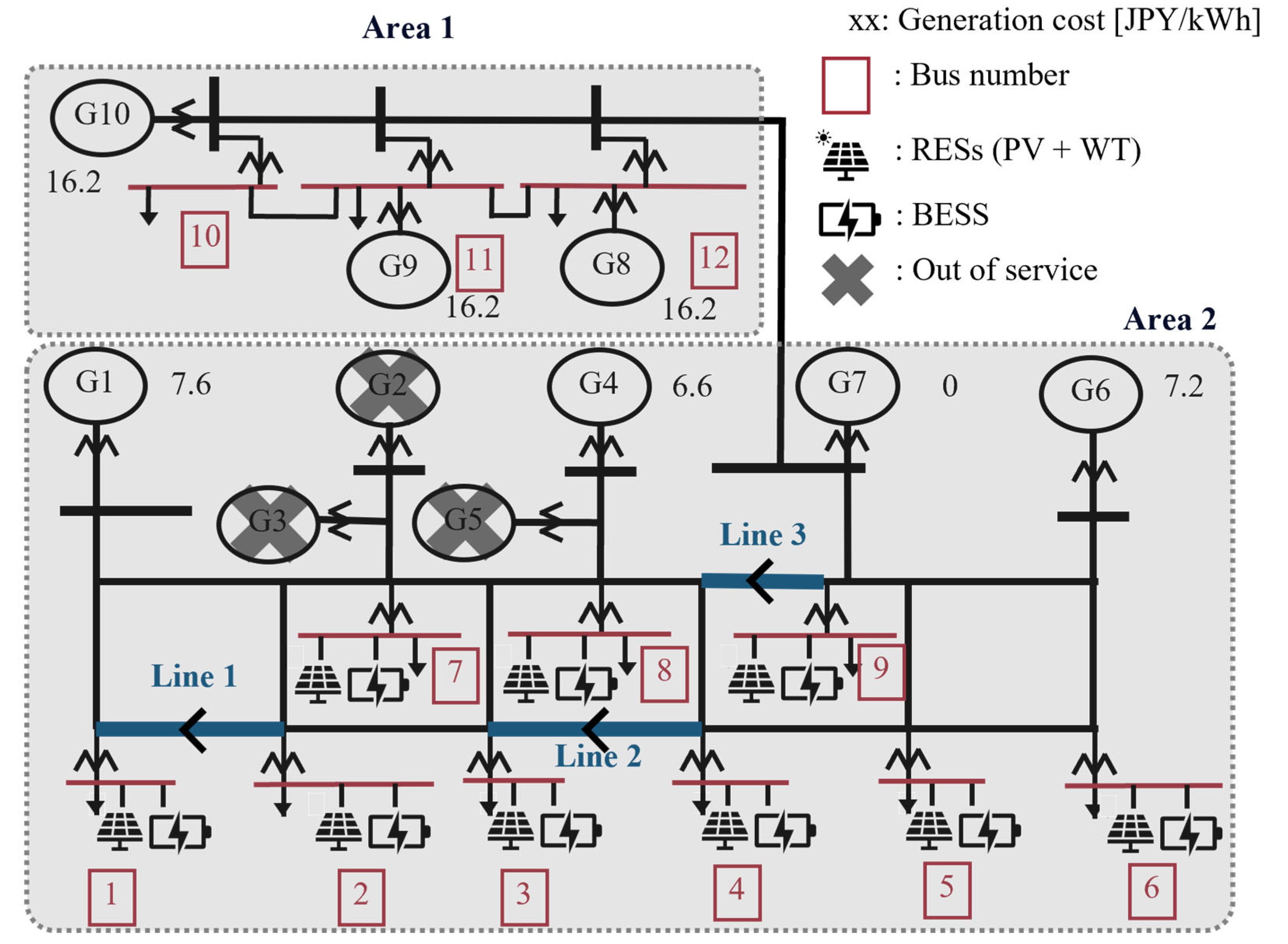
4.1. Simulation Settings
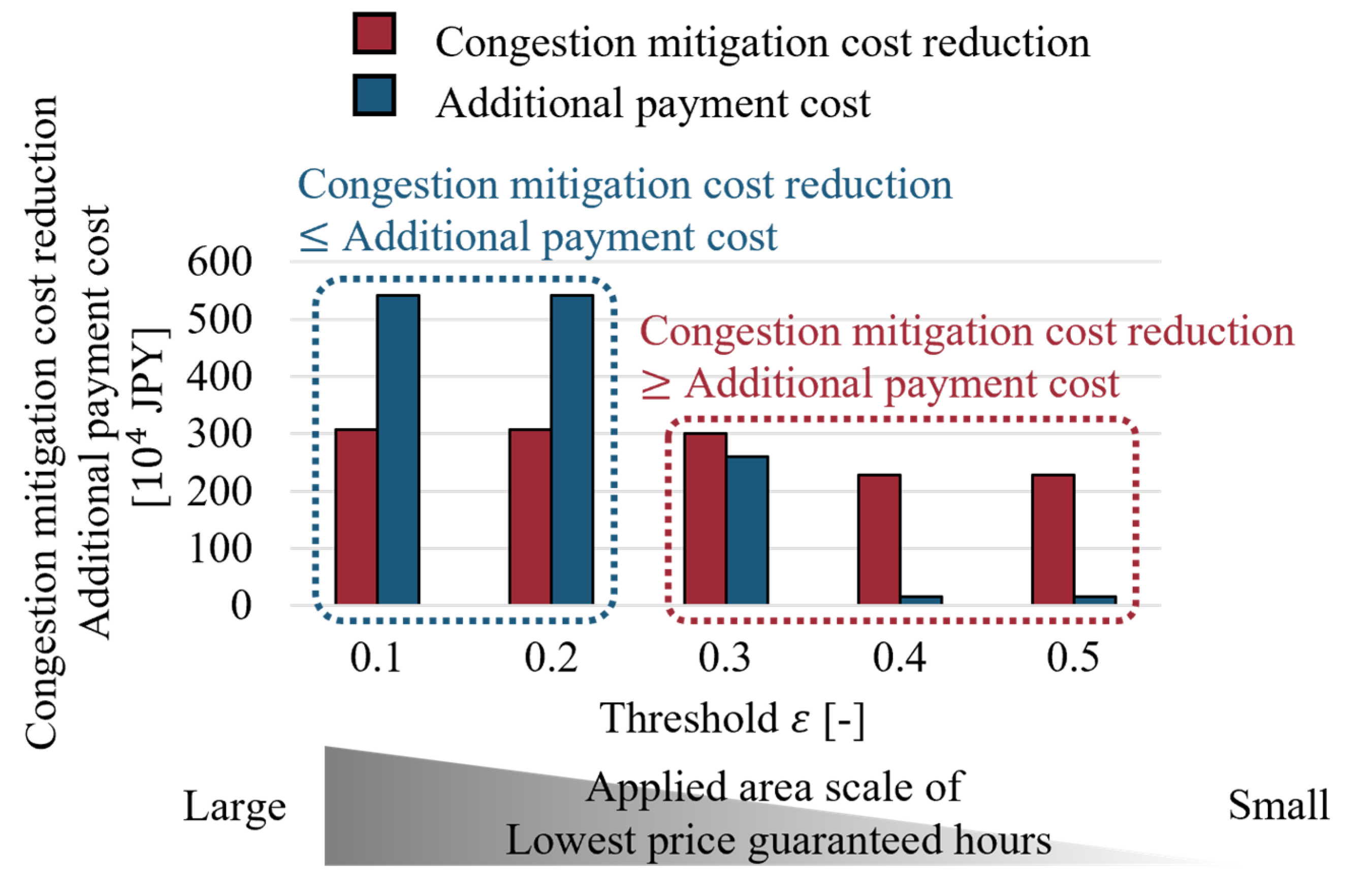
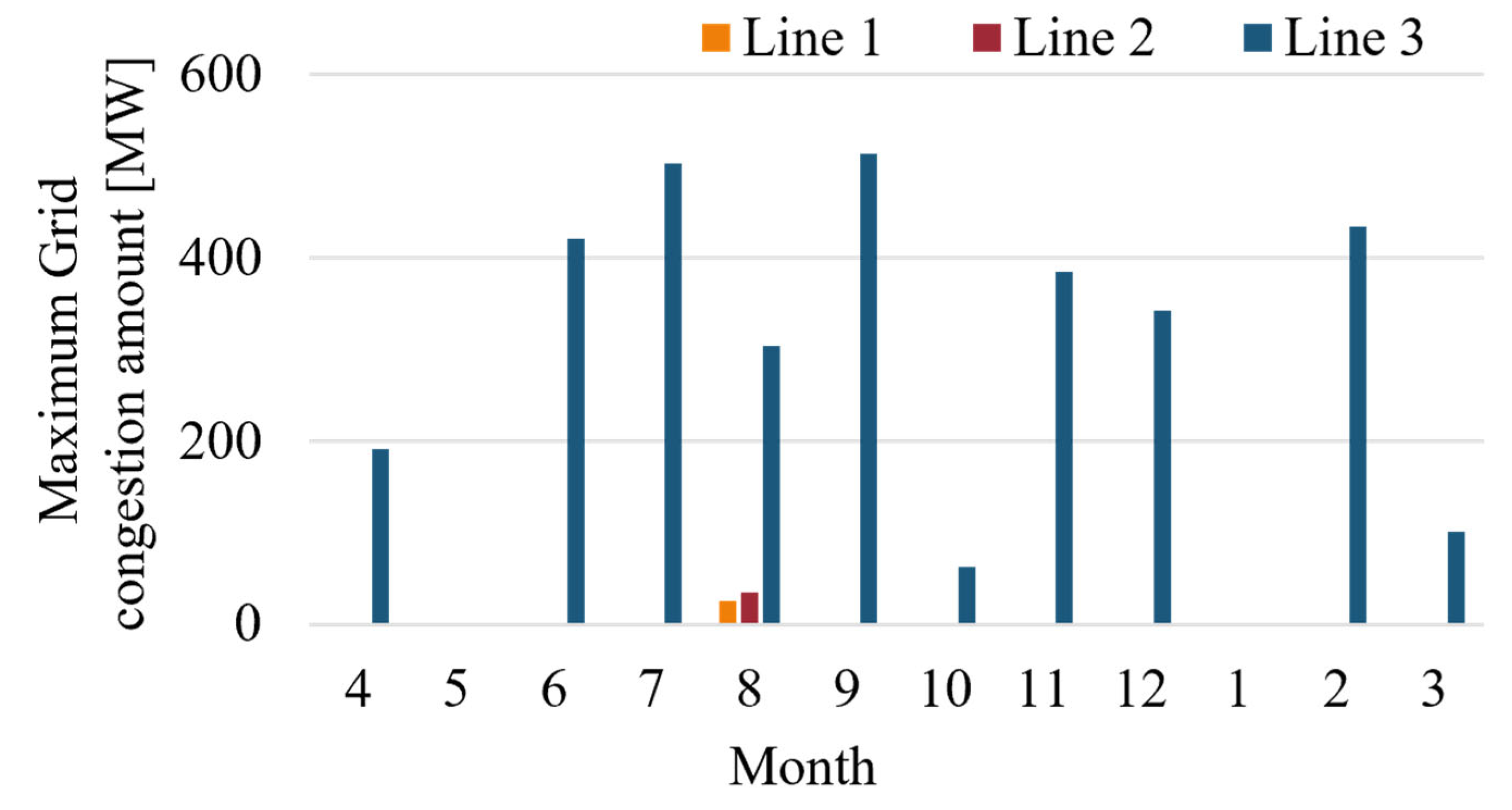
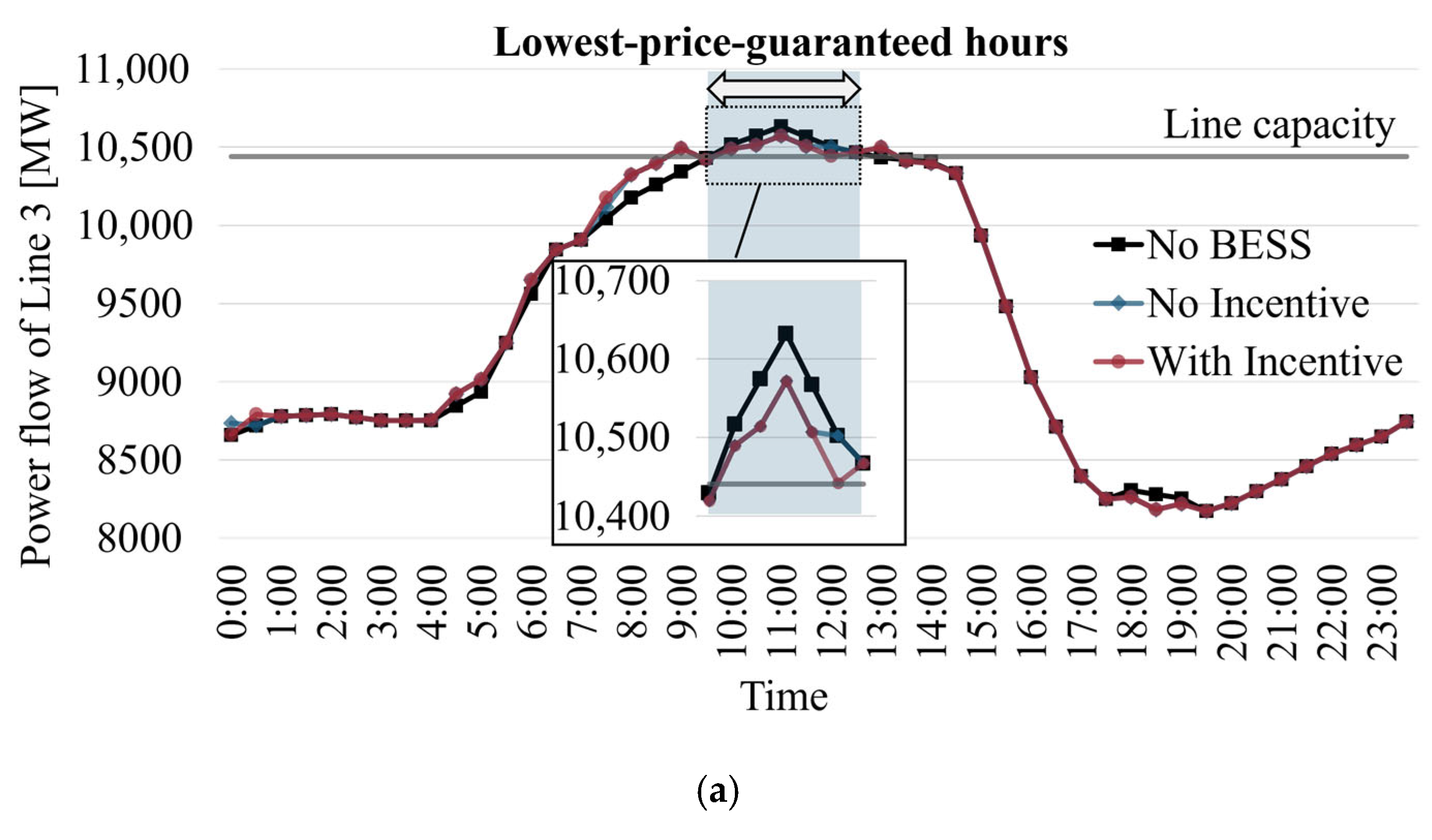
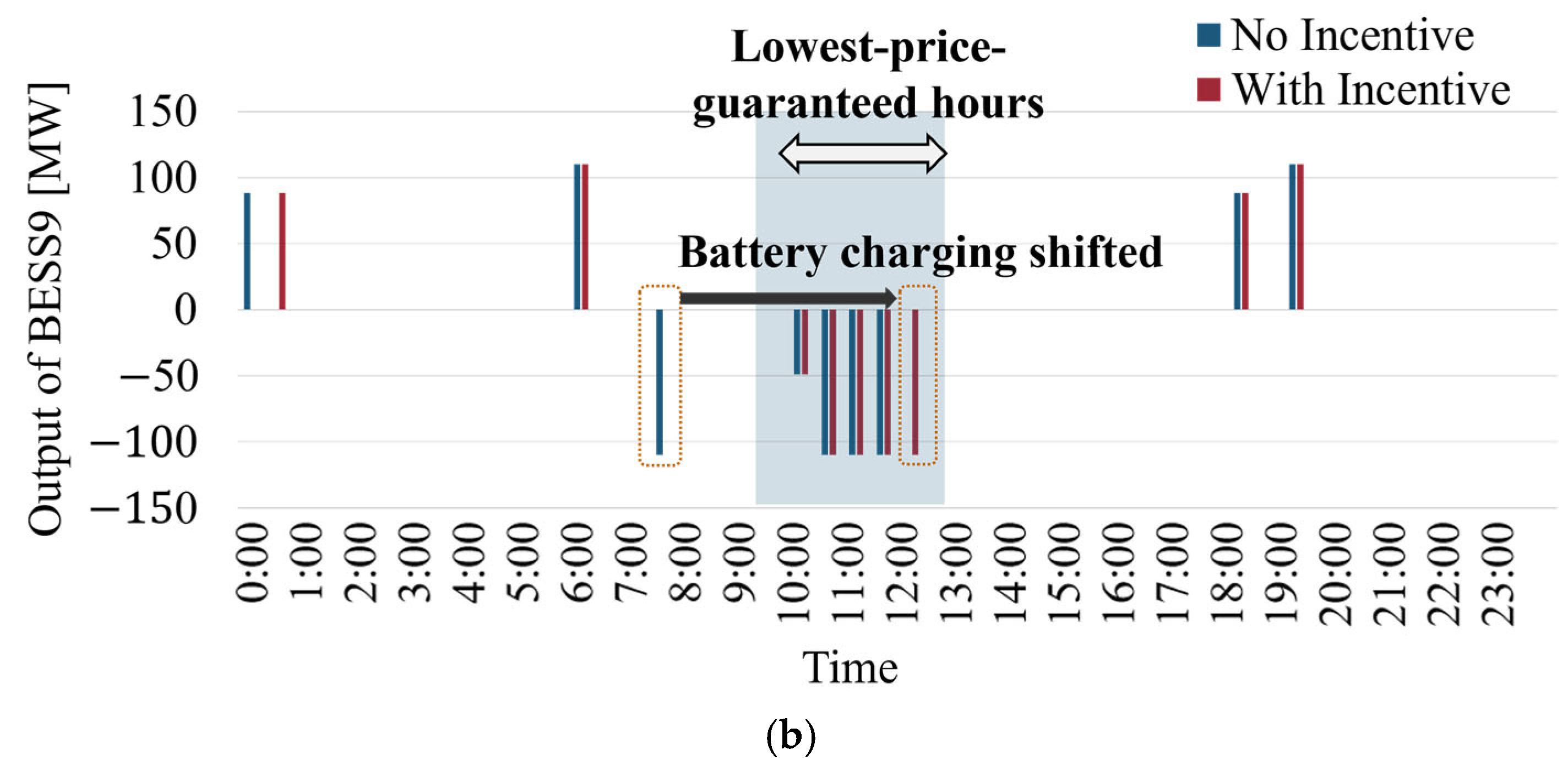
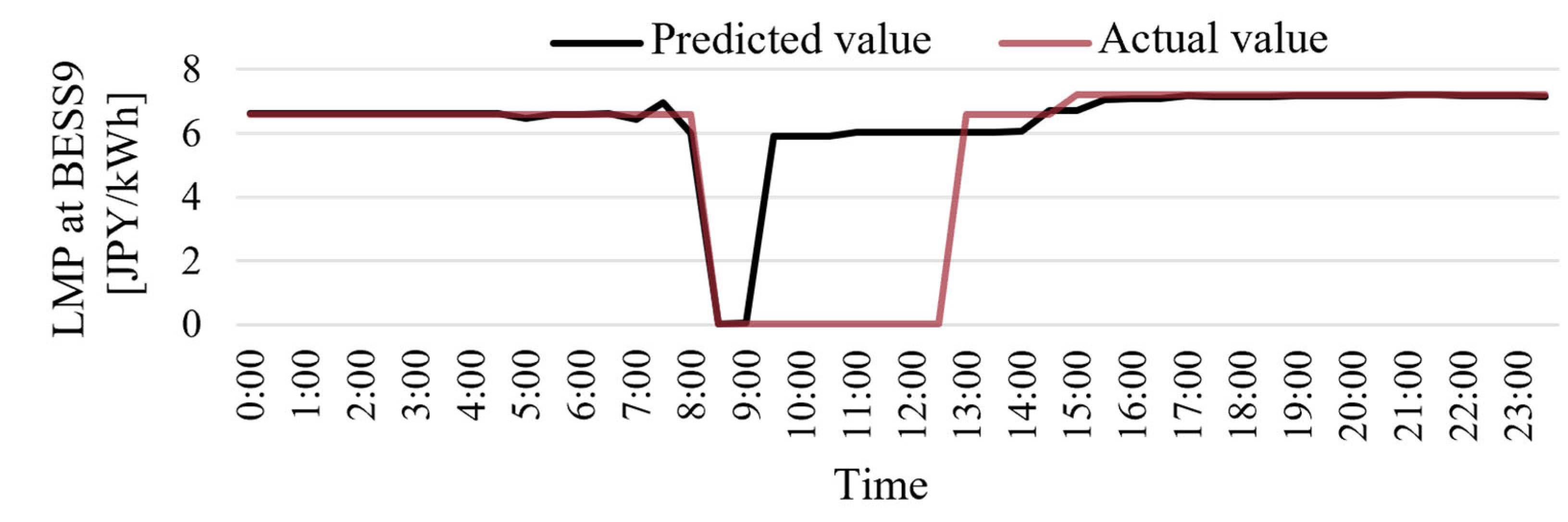
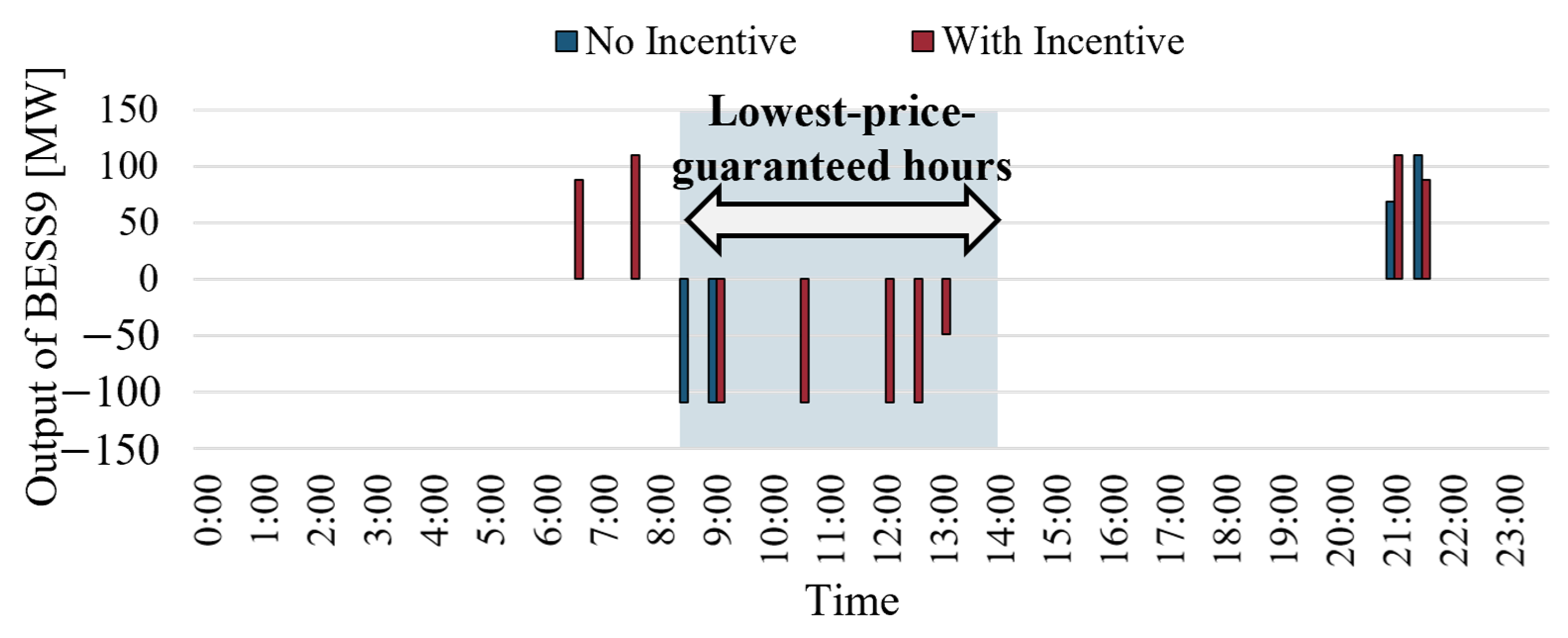
4.2. Simulation Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Parameter Tuning in the Proposed Method

References
- Agency for Natural Resources and Energy Japan. Basic Energy Plan. Available online: https://www.meti.go.jp/shingikai/enecho/denryoku_gas/saisei_kano/pdf/052_01_00.pdf (accessed on 13 February 2025). (In Japanese).
- Kilthau, M.; Mannari, T.; Tadokoro, T.; Hatta, H.; Fay, A.; Gehlhoff, F. A Generalized Distributed Energy Dispatch and Congestion Management Approach Applied to German and Japanese Grid Systems. IEEE Access 2025, 13, 5380–5395. [Google Scholar] [CrossRef]
- Hazra, J.; Padmanaban, M.; Zaini, F.; De Silva, L.C. Congestion Relief Using Grid Scale Batteries. In Proceedings of the 2015 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 18–20 February 2015; pp. 1–5. [Google Scholar]
- Agüero, M.; Peralta, J.; Quintana, E.; Velar, V.; Stepanov, A.; Ashourian, H.; Mahseredjian, J.; Cardenas, R. Virtual Transmission Solution Based on Battery Energy Storage Systems to Boost Transmission Capacity. J. Mod. Power Syst. Clean Energy 2024, 12, 466–474. [Google Scholar] [CrossRef]
- Muqbel, A.; Al-Awami, A.T.; Parvania, M. Optimal Planning of Distributed Battery Energy Storage Systems in Unbalanced Distribution Networks. IEEE Syst. J. 2022, 16, 1194–1205. [Google Scholar] [CrossRef]
- Agency for Natural Resources and Energy Japan. Toward Rapid Grid Interconnection of Battery Energy Storage Systems. Available online: https://www.meti.go.jp/shingikai/enecho/shoene_shinene/shin_energy/keito_wg/pdf/053_02_00.pdf (accessed on 13 February 2025). (In Japanese).
- Sang, L.; Xu, Y.; Long, H.; Hu, Q.; Sun, H. Electricity Price Prediction for Energy Storage System Arbitrage: A Decision-Focused Approach. IEEE Trans. Smart Grid 2022, 13, 2822–2832. [Google Scholar] [CrossRef]
- Parisio, A.; Rikos, E.; Glielmo, L. A Model Predictive Control Approach to Microgrid Operation Optimization. IEEE Trans. Control Syst. Technol. 2014, 22, 1813–1827. [Google Scholar] [CrossRef]
- Sustainable Open Innovation Initiative. Preliminary Study Project for the Introduction of an Energy Storage System to Reduce Congestion on the Hokkaido Grid, Conducted by Hokkaido Electric Power Networks, Inc. and NGK Insulators, Ltd. Available online: https://sii.or.jp/chikudenchi05/uploads/R5kess_j_seikahoukoku.pdf (accessed on 13 February 2025). (In Japanese).
- Agency for Natural Resources and Energy Japan. Discussion on the Use and Grid Integration of Battery Energy Storage Systems. Available online: https://www.meti.go.jp/shingikai/enecho/shoene_shinene/shin_energy/keito_wg/pdf/046_05_00.pdf (accessed on 13 February 2025). (In Japanese).
- Nair, U.R.; Sandelic, M.; Sangwongwanich, A.; Dragičević, T.; Costa-Castelló, R.; Blaabjerg, F. Grid Congestion Mitigation and Battery Degradation Minimisation Using Model Predictive Control in PV-Based Microgrid. IEEE Trans. Energy Convers. 2021, 36, 1500–1509. [Google Scholar] [CrossRef]
- Nair, U.R.; Sandelic, M.; Sangwongwanich, A.; Dragičević, T.; Costa-Castelló, R.; Blaabjerg, F. An Analysis of Multi Objective Energy Scheduling in PV-BESS System Under Prediction Uncertainty. IEEE Trans. Energy Convers. 2021, 36, 2276–2286. [Google Scholar] [CrossRef]
- Nair, U.R.; Costa-Castelló, R. A Model Predictive Control-Based Energy Management Scheme for Hybrid Storage System in Islanded Microgrids. IEEE Access 2020, 8, 97809–97822. [Google Scholar] [CrossRef]
- Pingxu, G.; Daogui, T.; Yuji, Y.; Josep, M.G.; Enrico, Z. A hierarchical multi-objective co-optimization framework for sizing and energy management of coupled hydrogen-electricity energy storage systems at ports. Appl. Energy 2025, 384, 125451. [Google Scholar]
- Li, J.; Danzer, M.A. Optimal Charge Control Strategies for Stationary Photovoltaic Battery Systems. J. Power Sources 2014, 258, 365–373. [Google Scholar] [CrossRef]
- Bahramipanah, M.; Torregrossa, D.; Cherkaoui, R.; Paolone, M. A Decentralized Adaptive Model-Based Real-Time Control for Active Distribution Networks Using Battery Energy Storage Systems. IEEE Trans. Smart Grid 2018, 9, 3406–3418. [Google Scholar] [CrossRef]
- James, H.K.; Dev, M.; Ryan, W.; Julie, M. Renewable-battery hybrid power plants in congested electricity markets: Implications for plant configuration. Renew. Energy 2024, 232, 121070. [Google Scholar]
- Ni, L.; Wen, F.; Liu, W.; Meng, J.; Lin, G.; Dang, S. Congestion Management with Demand Response Considering Uncertainties of Distributed Generation Outputs and Market Prices. J. Mod. Power Syst. Clean Energy 2017, 5, 66–78. [Google Scholar] [CrossRef]
- Ponoćko, J.; Dang, S. Cross-border DSM as a Complement to Storage and RES in Congestion Management Markets. Int. J. Electr. Power Energy Syst. 2023, 148, 108917. [Google Scholar] [CrossRef]
- Bjarghov, S.; Kalantar-Neyestanaki, M.; Cherkaoui, R.; Farahmand, H. Battery Degradation-Aware Congestion Management in Local Flexibility Markets. In Proceedings of the 2021 IEEE Madrid PowerTech, Madrid, Spain, 28 June–2 July 2021; pp. 1–6. [Google Scholar]
- Khomami, H.P.; Fonteijn, R.; Geelen, D. Flexibility Market Design for Congestion Management in Smart Distribution Grids: The Dutch Demonstration of the Interflex Project. In Proceedings of the 2020 IEEE PES Innovative Smart Grid Technologies Europe (ISGT-Europe), The Hague, The Netherlands, 26–28 October 2020; pp. 1191–1195. [Google Scholar]
- Netheler, I.L.; Schuldt, F.; Maydell, K.V.; Agert, C. Technical and Economic Analysis of Curative Actions in Distribution Networks Utilizing Battery Energy Storage Systems. IET Gener. Transm. Distrib. 2021, 16, 724–736. [Google Scholar] [CrossRef]
- Goyal, A.; Bhattacharya, K. Design of Multi-Settlement Electricity Markets Considering Demand Response and Battery Energy Storage Systems Participation. IEEE Trans. Energy Mark. Policy Regul. 2024, 2, 226–239. [Google Scholar] [CrossRef]
- Banaei, M.; D’Ettorre, F.; Ebrahimy, R.; Almassalkhi, M.R.; Madsen, H. Procuring Flexibility in Power Systems with Incentive-Based Grid Access Requests. Int. J. Electr. Power Energy Syst. 2024, 156, 109745. [Google Scholar] [CrossRef]
- Dey, B.; Sharma, G.; Bokoro, P.N.; Dutta, S. An Intelligent Incentive-Based Demand Response Program for Exhaustive Environment Constrained Techno-Economic Analysis of Microgrid System. Sci. Rep. 2025, 15, 894. [Google Scholar] [CrossRef] [PubMed]
- Hassan, A.S.; Cipcigan, L.; Jenkins, N. Optimal Battery Storage Operation for PV Systems with Tariff Incentives. Appl. Energy 2017, 203, 422–441. [Google Scholar] [CrossRef]
- Yaniv, A.; Beck, Y. Optimal Battery Scheduling in Solar-Plus-Storage Grid-Connected Microgrid for Profit and Cost Efficiency: A Use Case on an Israeli Microgrid. J. Energy Storage 2024, 77, 109697. [Google Scholar] [CrossRef]
- Ali, E.N.; Toktam, T.S.; Ravindra, P.J. Coordinated TSO-DSO operational planning for congestion management in day-ahead and real-time markets. E-Prime-Adv. Electr. Eng. Electron. Energy 2025, 12, 100981. [Google Scholar]
- Xiang, G.; Jiahao, Z.; Jiang, C.; Shuqing, W.; Ziao, S.; Zhiying, M. Employing battery energy storage systems for flexible ramping products in a fully renewable energy power grid: A market mechanism and strategy analysis through multi-Agent Markov games. Energy Rep. 2024, 12, 5066–5082. [Google Scholar]
- Günter, N.; Marinopoulos, A. Energy Storage for Grid Services and Applications: Classification, Market Review, Metrics, and Methodology for Evaluation of Deployment Cases. J. Energy Storage 2016, 8, 226–234. [Google Scholar] [CrossRef]
- Merve, B.; Evrencan, Ö. How to build a state-of-the-art battery energy storage market? Challenges, opportunities, and future directions. J. Energy Storage 2024, 86, 111174. [Google Scholar]
- The Institute of Electrical Engineers of Japan. Japanese Power System Models. Available online: https://www.iee.jp/en-pes/japanese/ (accessed on 13 February 2025).
- Organization for Cross-Regional Coordination of Transmission Operators Japan. About the Connection Rules of the Grid ~Non-Firm Access~. Available online: https://www.occto.or.jp/grid/business/documents/matome.pdf (accessed on 27 February 2025).
- Hotz, M.; Utschick, W. The Hybrid Transmission Grid Architecture: Benefits in Nodal Pricing. IEEE Trans. Power Syst. 2018, 33, 1431–1442. [Google Scholar] [CrossRef]
- TEPCO Power Grid, Inc. Area Supply and Demand Performance Data. Available online: https://www.tepco.co.jp/forecast/html/area_jukyu_p-j.html (accessed on 6 March 2025). (In Japanese).
- Agency for Natural Resources and Energy Japan. Toward Rapid Grid Interconnection of Battery Energy Storage Systems. Available online: https://www.meti.go.jp/shingikai/enecho/shoene_shinene/shin_energy/keito_wg/pdf/052_03_00.pdf (accessed on 6 March 2025). (In Japanese).
- Generation Cost Working Group. Report on Verification of Electricity Generation Costs and Other Costs to the Sub-Committee on the Long-Term Energy Supply and Demand Outlook (Draft). Available online: https://www.enecho.meti.go.jp/committee/council/basic_policy_subcommittee/mitoshi/cost_wg/006/pdf/006_05.pdf (accessed on 6 March 2025). (In Japanese).
- Agency for Natural Resources and Energy Japan. Verification of the Generation Cost. Available online: https://www.enecho.meti.go.jp/committee/council/basic_policy_subcommittee/mitoshi/cost_wg/2024/data/01_07.pdf (accessed on 6 March 2025). (In Japanese).
- TEPCO Power Grid, Inc. Publication of Medium-and Long-Term Forecasts for Grid Congestion in 2029. Available online: https://www.tepco.co.jp/pg/consignment/system//keitoukonzatu/2029konzatumitoosi.html (accessed on 6 March 2025). (In Japanese).
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ‘16), New York, NY, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]








| References | [11,12,13,14,15,16] | [17] | [18] | [19,20,21,22,23,24,25,26,27,28,29] | Proposed Method |
|---|---|---|---|---|---|
| Benefits for BESS owners | Self-consumption and battery degradation are incorporated into output control | Revenue maximization | Financial compensation | Market revenue | Lowest price guarantee |
| Reliable utilization of BESSs for grid constraint mitigation | ✓ | - | ✓ | - | ✓ |
| Motivation of BESS owners to contribute to grid constraint mitigation | - | - | ✓ | ✓ | ✓ |
| Avoiding excessive additional payments to BESS owners | ✓ | ✓ | - | - | ✓ |
| Content | Settings |
|---|---|
| Inputs (explanatory variables) | Total RES generation output and demand on the target day (30 min intervals from 0:00–23:30) |
| Output | LMP at each bus or power flow at each line on the target day (30 min intervals from 0:00–23:30) |
| Maximum depth of a tree | 3 |
| Number of trees | 100 |
| Learning rate | 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tanno, Y.; Kaneko, A.; Fujimoto, Y.; Hayashi, Y.; Hanai, Y.; Koseki, H. Charging Incentive Design with Minimum Price Guarantee for Battery Energy Storage Systems to Mitigate Grid Congestion. Energies 2025, 18, 2840. https://doi.org/10.3390/en18112840
Tanno Y, Kaneko A, Fujimoto Y, Hayashi Y, Hanai Y, Koseki H. Charging Incentive Design with Minimum Price Guarantee for Battery Energy Storage Systems to Mitigate Grid Congestion. Energies. 2025; 18(11):2840. https://doi.org/10.3390/en18112840
Chicago/Turabian StyleTanno, Yujiro, Akihisa Kaneko, Yu Fujimoto, Yasuhiro Hayashi, Yuji Hanai, and Hideo Koseki. 2025. "Charging Incentive Design with Minimum Price Guarantee for Battery Energy Storage Systems to Mitigate Grid Congestion" Energies 18, no. 11: 2840. https://doi.org/10.3390/en18112840
APA StyleTanno, Y., Kaneko, A., Fujimoto, Y., Hayashi, Y., Hanai, Y., & Koseki, H. (2025). Charging Incentive Design with Minimum Price Guarantee for Battery Energy Storage Systems to Mitigate Grid Congestion. Energies, 18(11), 2840. https://doi.org/10.3390/en18112840







