Study on Seepage Characteristics and Production Capacity Characteristics of Complex Structural Wells in Non-Homogeneous Gas Reservoirs Based on Hydroelectric Simulation
Abstract
1. Introduction
2. Hydropower Simulation Experiment Principle and Device
2.1. Experimental Materials
2.2. Experimental Principles
2.3. Experimental Setup and Procedures
2.3.1. Composition of the Experimental Setup
2.3.2. Experimental Step
3. Experimental Parameters and Program Design
3.1. Experimental Parameters
3.2. Experimental Program
4. Analysis of Results
4.1. Comparison of Seepage and Capacity Characteristics of Different Well Types in Homogeneous Reservoirs
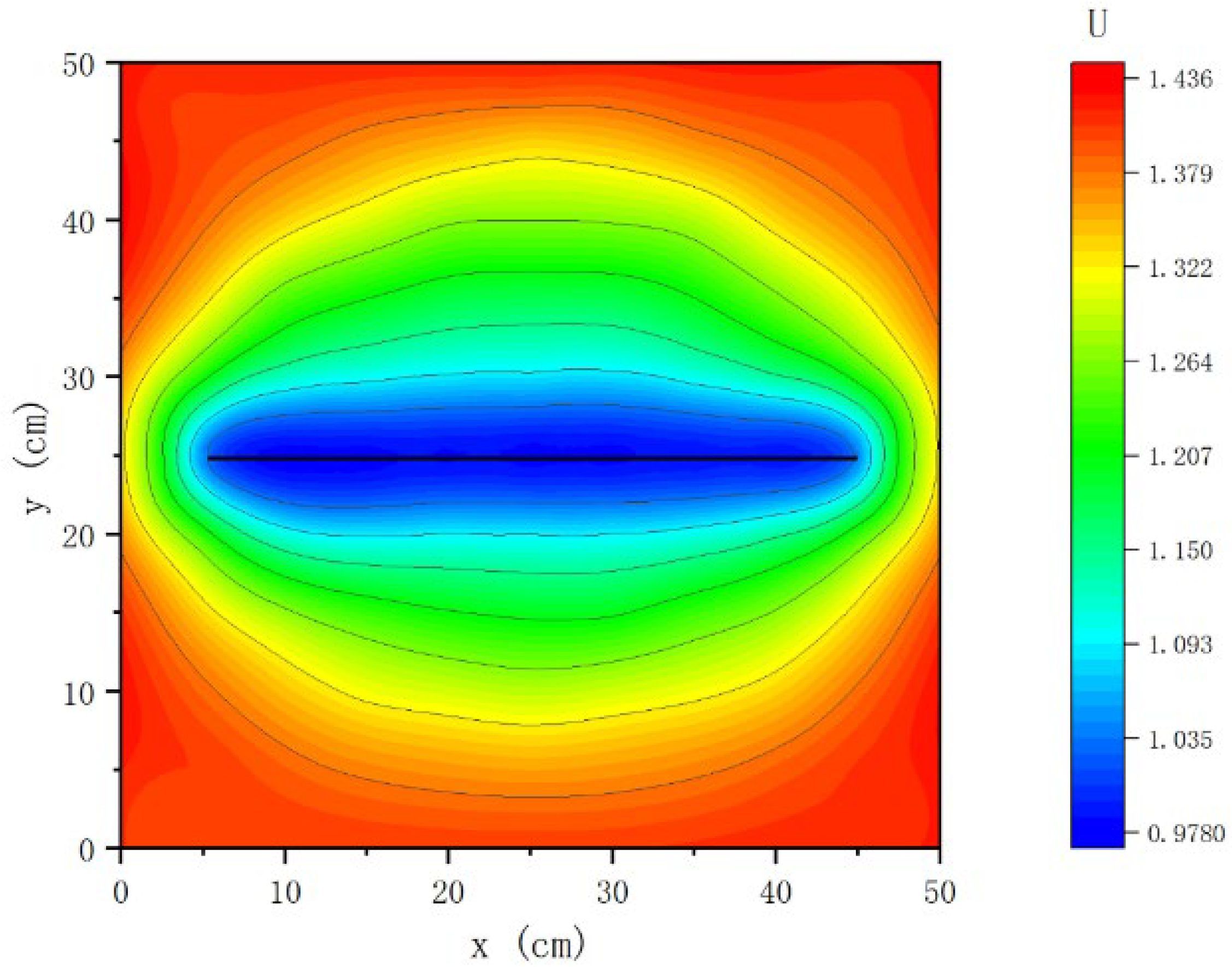
4.1.1. Seepage Characterization
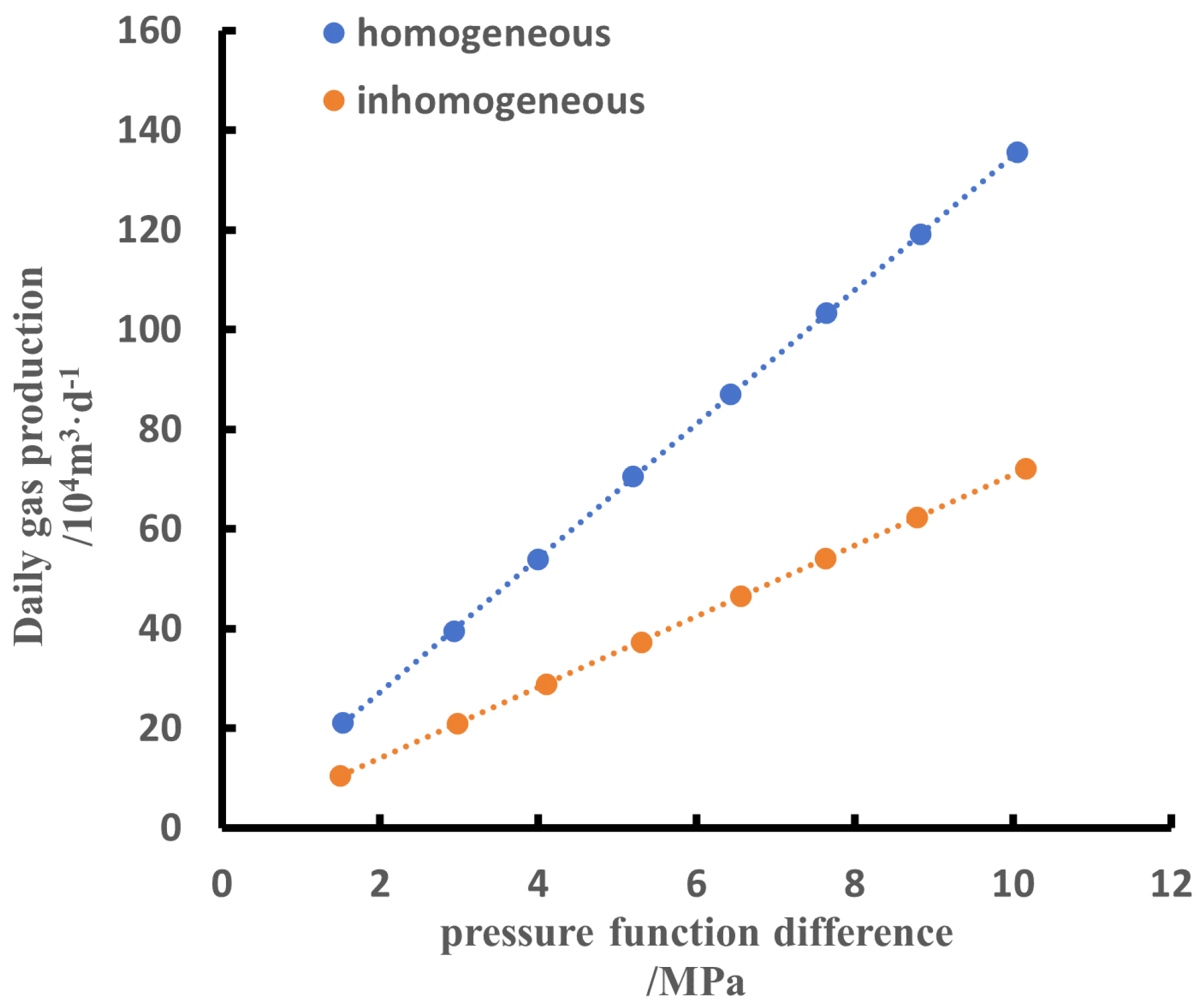
4.1.2. Characterization of Production Capacity
4.2. Comparison of Seepage and Capacity Characteristics of Different Well Types in Non-Homogeneous Reservoirs
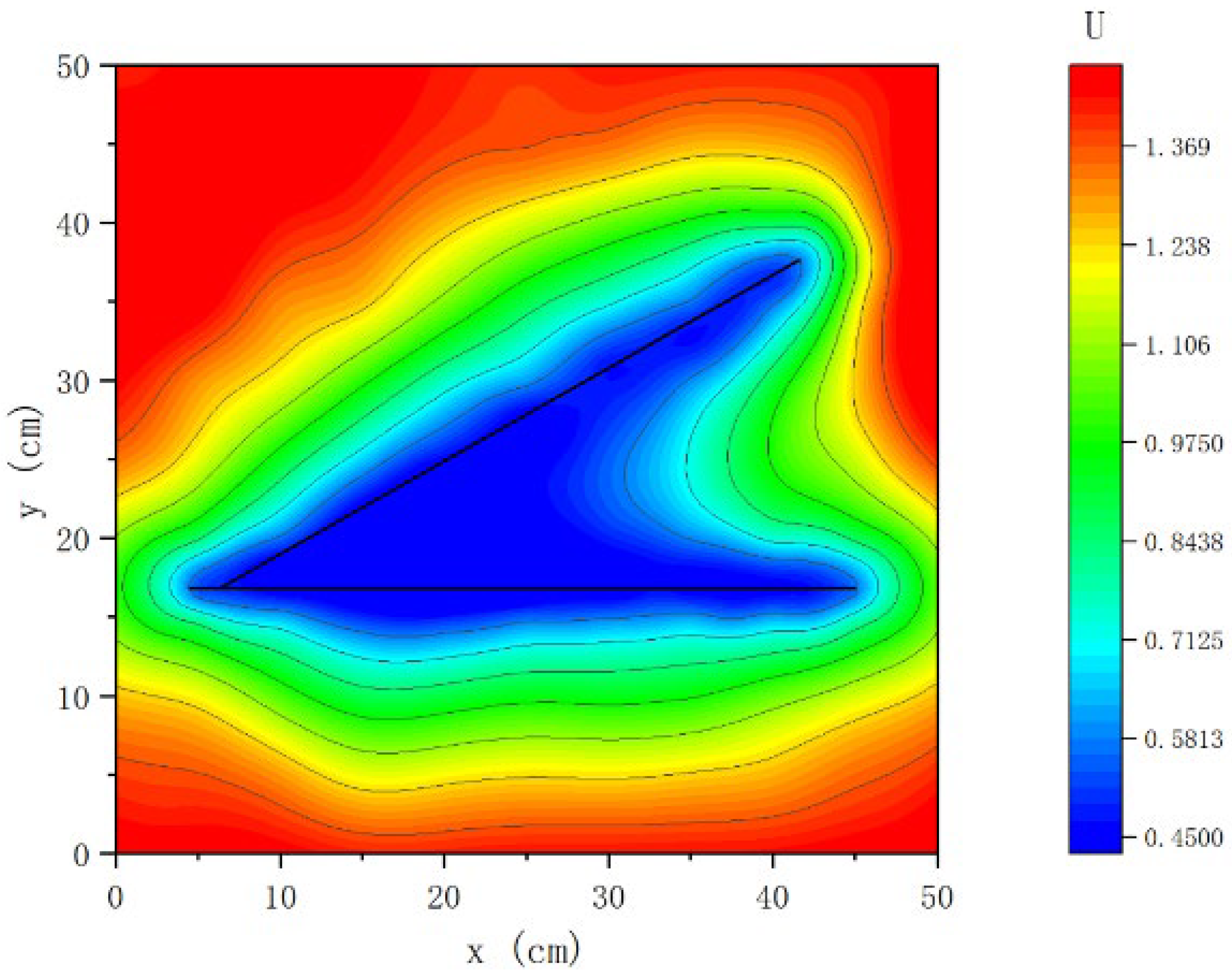
4.2.1. Seepage Characterization
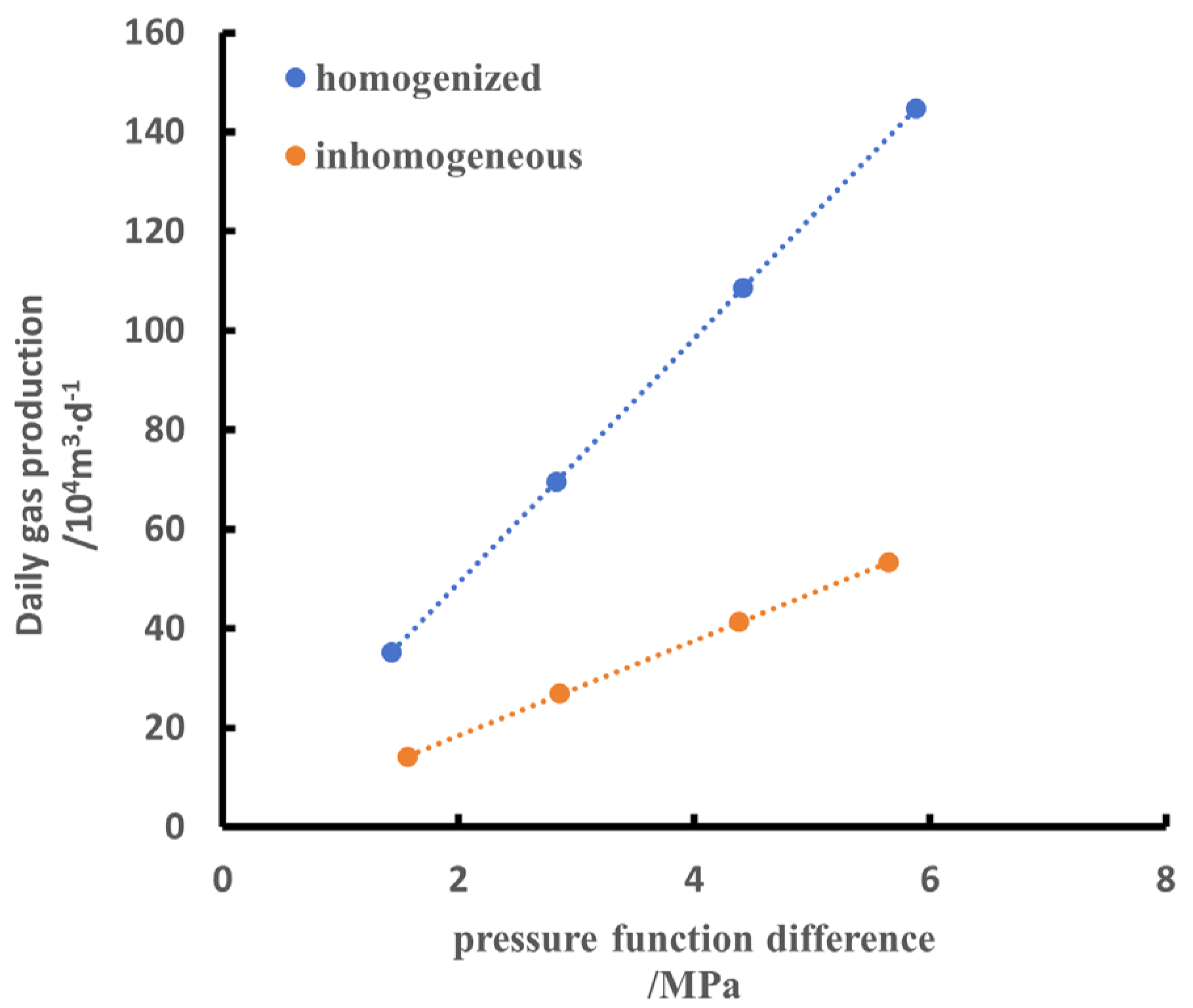
4.2.2. Characterization of Production Capacity
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, X.D.; Sui, X.F.; An, Y.S.; Zhang, F.X.; Chen, Y.G. Electrolytic simulation experiment of fractured horizontal well. J. Pet. 2009, 30, 740–743. [Google Scholar]
- Mao, C.X. Electric Simulation Test and Seepage Study; Water Resources Press: Beijing, China, 1981. [Google Scholar]
- Gao, F.; Han, G.Q.; Wu, X.D.; Zhu, M.; Wang, Y.N.; Cen, X.Q.; Zhang, R. The Research of Experimental Method about Hydroelectric Simulation. Sci. Technol. Eng. 2012, 12, 3839–3843. [Google Scholar]
- Wang, T.Q.; Huang, Y. Electrical Simulation Experiment of the Seepage of Zone Near the Borehole in Symmetric Herringbone Wells. Contemp. Chem. Ind. 2017, 46, 54–56. [Google Scholar]
- Han, G.Q.; Li, X.F.; Wu, X.D. Experiment research of electric analogy for multi—Branch wells. Nat. Gas Ind. 2004, 24, 99–101. [Google Scholar]
- Huang, S.J.; Cheng, L.S.; Zhao, F.L.; Li, C.L. Experimental research of flow mechanism of near wellbore area of fishbone wells. Oil Drill. Process 2006, 28, 58–60. [Google Scholar]
- Qu, Z.Q.; Xu, X.; Liu, J.M.; Yang, X.Y. Electric analogy experiment of the productivity of radial-distributing multi-branch horizontal wells. J. Xi’an Pet. Univ. (Nat. Sci. Ed.) 2007, 22, 65. [Google Scholar]
- Liu, H.; Shi, C.P.; Pan, Y.; Leng, J.; Xu, Z.J. Electrolytic simulation experiment of fractured multilateral horizontal well. J. Liaoning Univ. Petrochem. Technol. 2015, 35, 43–46. [Google Scholar]
- Ozawa, M.; Suzuki, S. Microstructural development of natural hydroxyapatite originated from fish-bone waste through heat treatment. J. Am. Ceram. Soc. 2002, 85, 1315–1317. [Google Scholar] [CrossRef]
- Jiang, M.C. Study on Interbranch Pressure and Productivity Interference of Multi-branch Wells. Master’s Thesis, China University of Petroleum, Beijing, China, 2023. [Google Scholar] [CrossRef]
- Ji, G.F.; Liu, Z.Q.; Zhao, W.W.; Nan, C.Y. Similarity simulation of tight oil horizontal well post-fracturing productivity based on principle of hydropower similarity. J. Heilongjiang Univ. Sci. Technol. 2024, 34, 440–445. [Google Scholar]
- Yin, J.W. Experimental study on hydraulic fracturing simulation of horizontal well fracturing on well production. Energy Environ. Prot. 2017, 39, 167–170. [Google Scholar]
- Su, G.D.; Zhang, P.; Gu, X.; Han, B.Y.; Yi, P.; Li, M.Y. Design of Virtual Teaching Platform for Hydroelectric Simulation Experiment. Lab. Res. Explor. 2018, 37, 105–109. [Google Scholar]
- Ji, G.F.; Zhou, Y.; Wang, M.; Xu, C.Z. Electric simulation of seepage flow for tight-oil horizontal well staged fracturing and considering start-up pressure. Energy Environ. Prot. 2019, 41, 64–67. [Google Scholar]
- Sun, X.C.; Liu, Z.L.; Ji, G.F.; Liu, Z.T.; Xu, Z. Hydro-electric Simulation of the Influence of Fracture Parameters on Seepage in Horizontal Wells After Fracturing in Tight Oil Reservoirs. Contemp. Chem. Ind. 2020, 49, 2736–2741. [Google Scholar]
- Lu, T.D. Study on Flow Law of Complex Fracture Network in Tight Reservoir. Master’s Thesis, China University of Petroleum, Beijing, China, 2020. [Google Scholar]
- Liu, H.L. Similarity Experiment Study on Directional Pinnate Multi-branch Horizontal Wells of Coalbed Methane. Master’s Thesis, Liaoning University of Engineering and Technology, Fuxin, China, 2021. [Google Scholar]
- Zhai, L.; Yang, M.; Yan, C.; Tian, T.; Huang, S. Dynamic distribution characteristics of oil and water during water flooding in a fishbone well with different branch angles. ACS Omega 2022, 7, 27206–27215. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.Q. Study on the Productivity Evaluation of Refracturing in Tight Oil Horizontal Wells Based on Hydroelectric Simulation. Master’s Thesis, Yangtze University, Jingzhou, China, 2024. [Google Scholar] [CrossRef]
- Li, Y.C.; Liu, H.L.; Jia, J.Z. Hydroelectric simulation test of coalbed methane in symmetric multi branch horizontal wells. Coal Sci. Technol. 2022, 50, 135–142. [Google Scholar] [CrossRef]
- Kukharova, T.; Maltsev, P.; Novozhilov, I. Development of a Control System for Pressure Distribution During Gas Production in a Structurally Complex Field. Appl. Syst. Innov. 2025, 8, 51. [Google Scholar] [CrossRef]

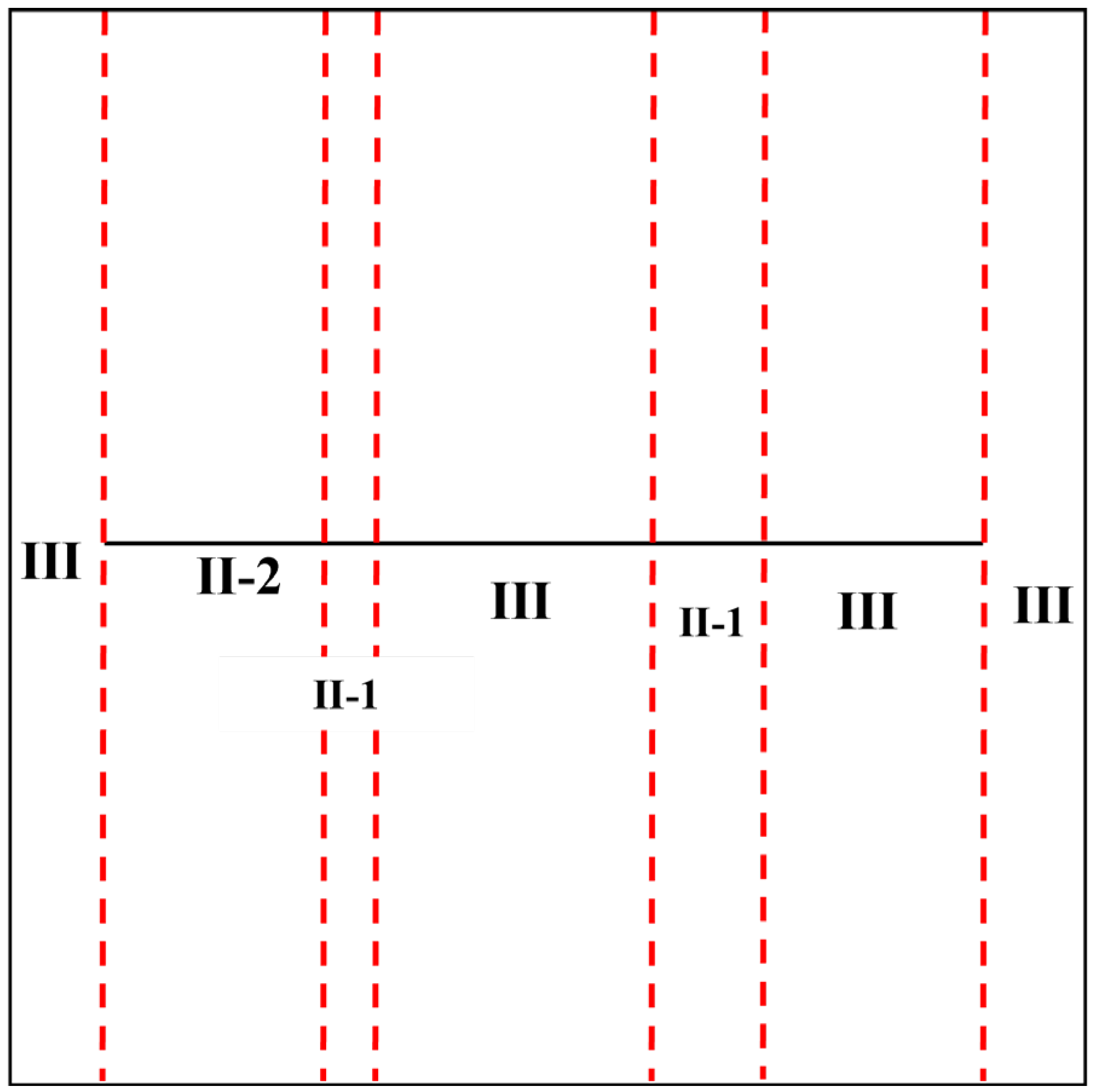
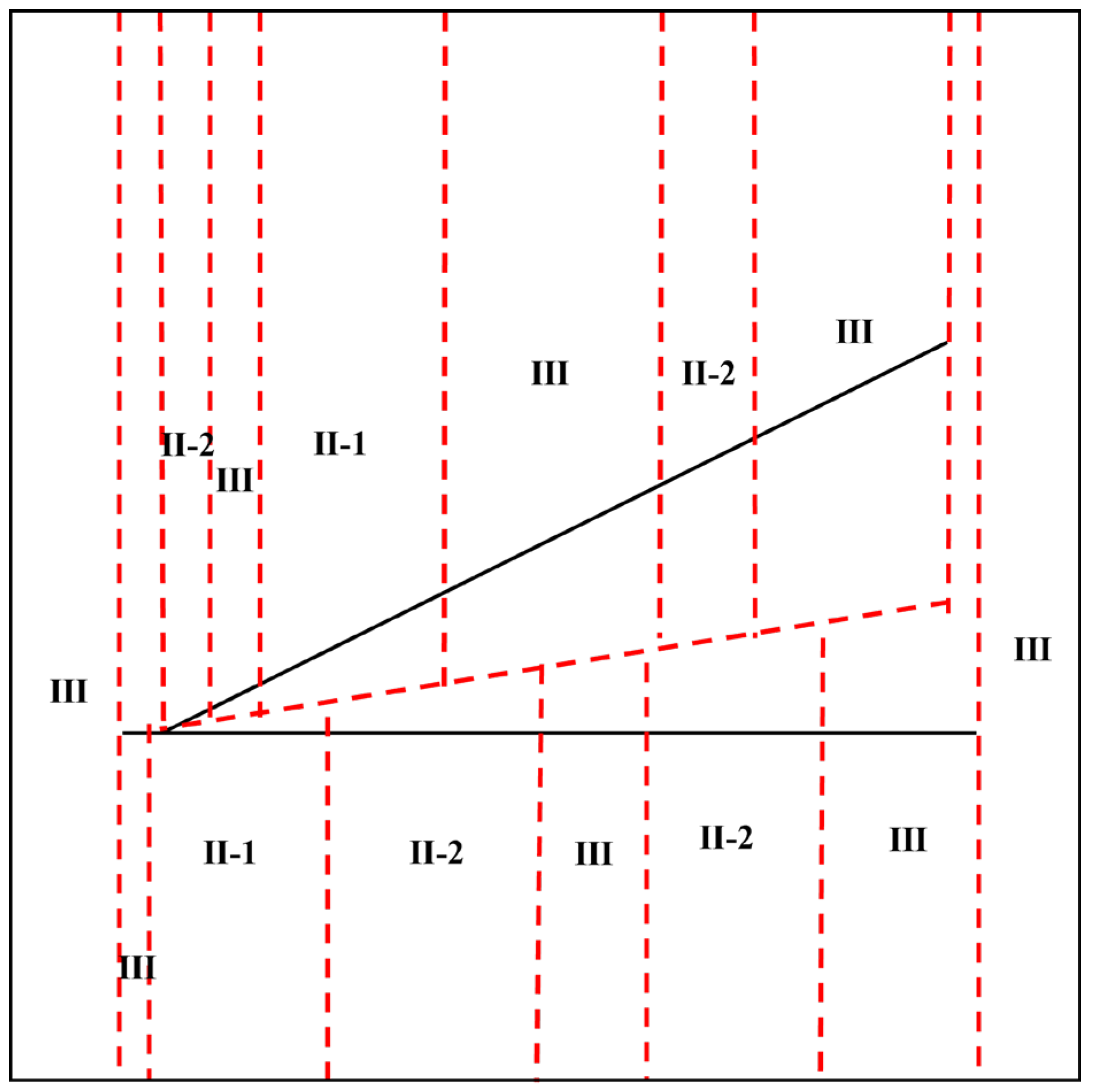
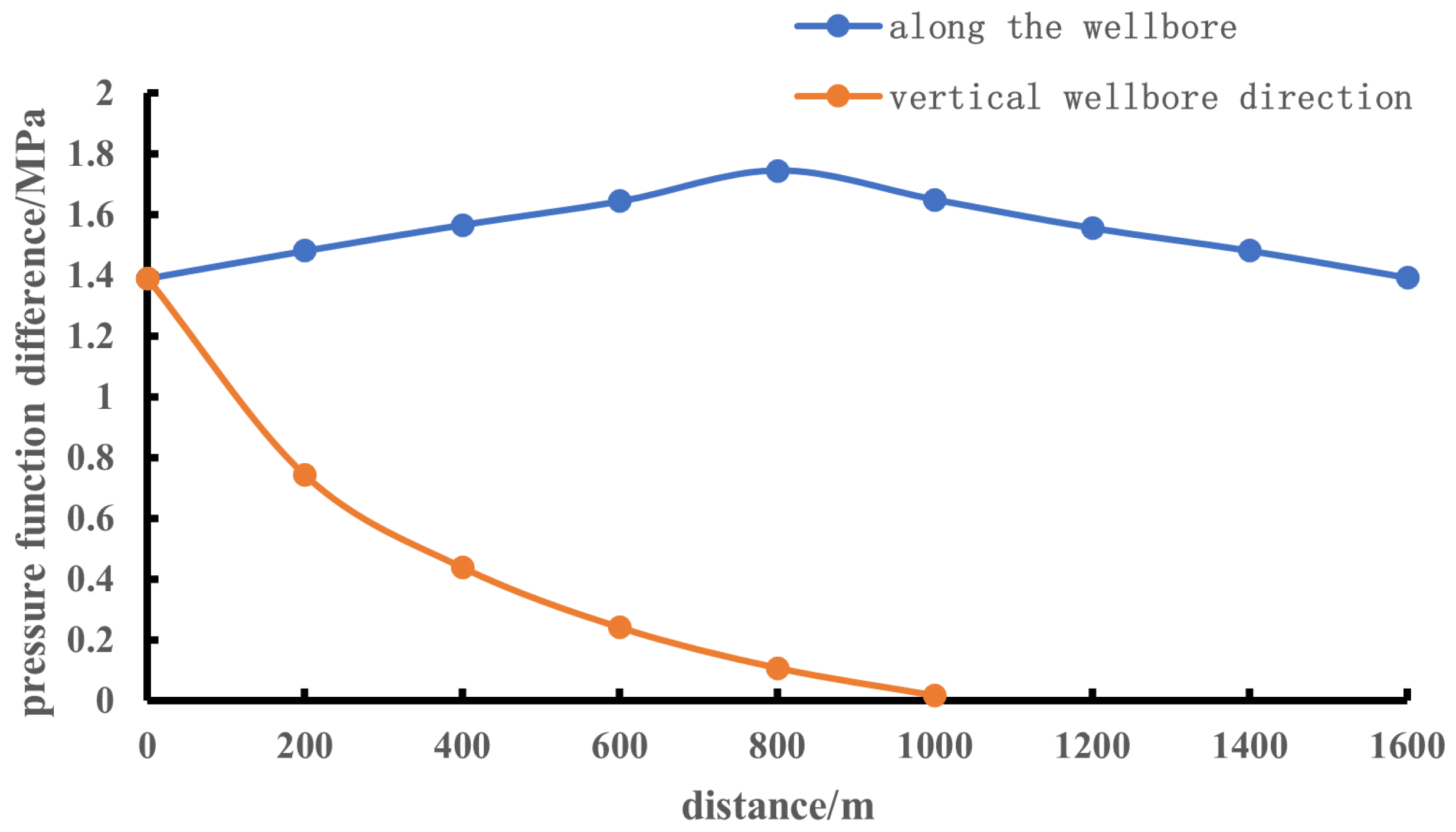
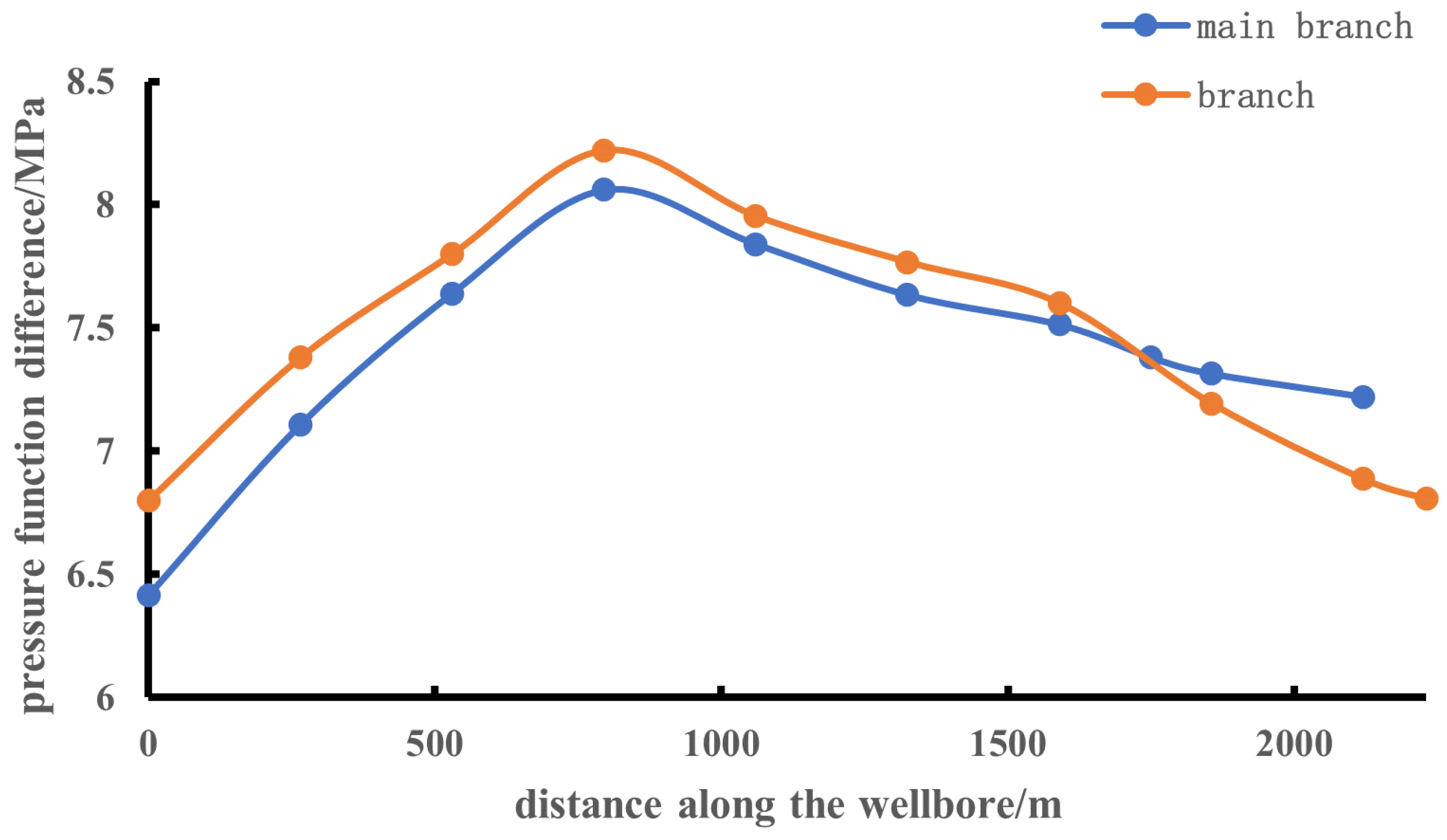


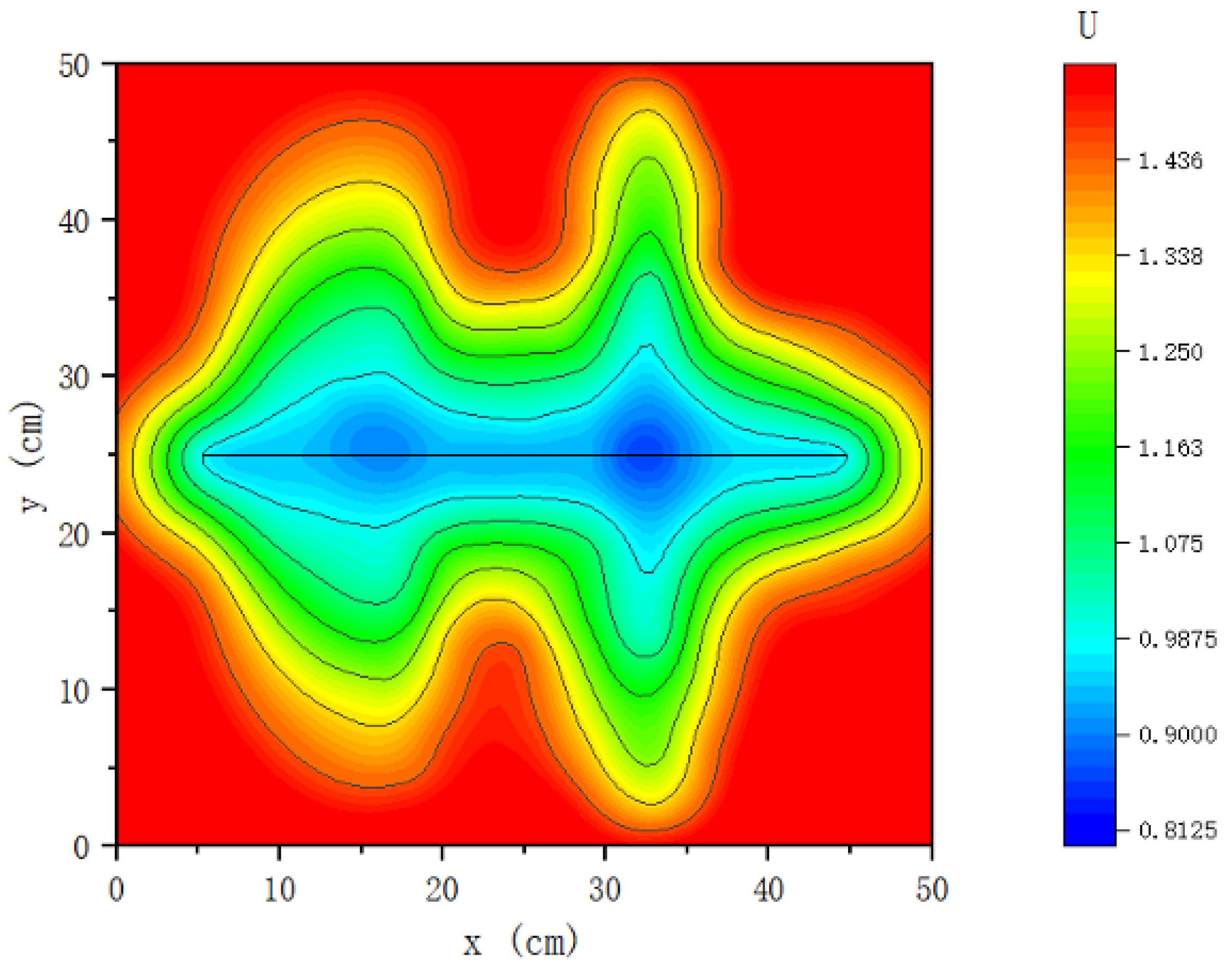


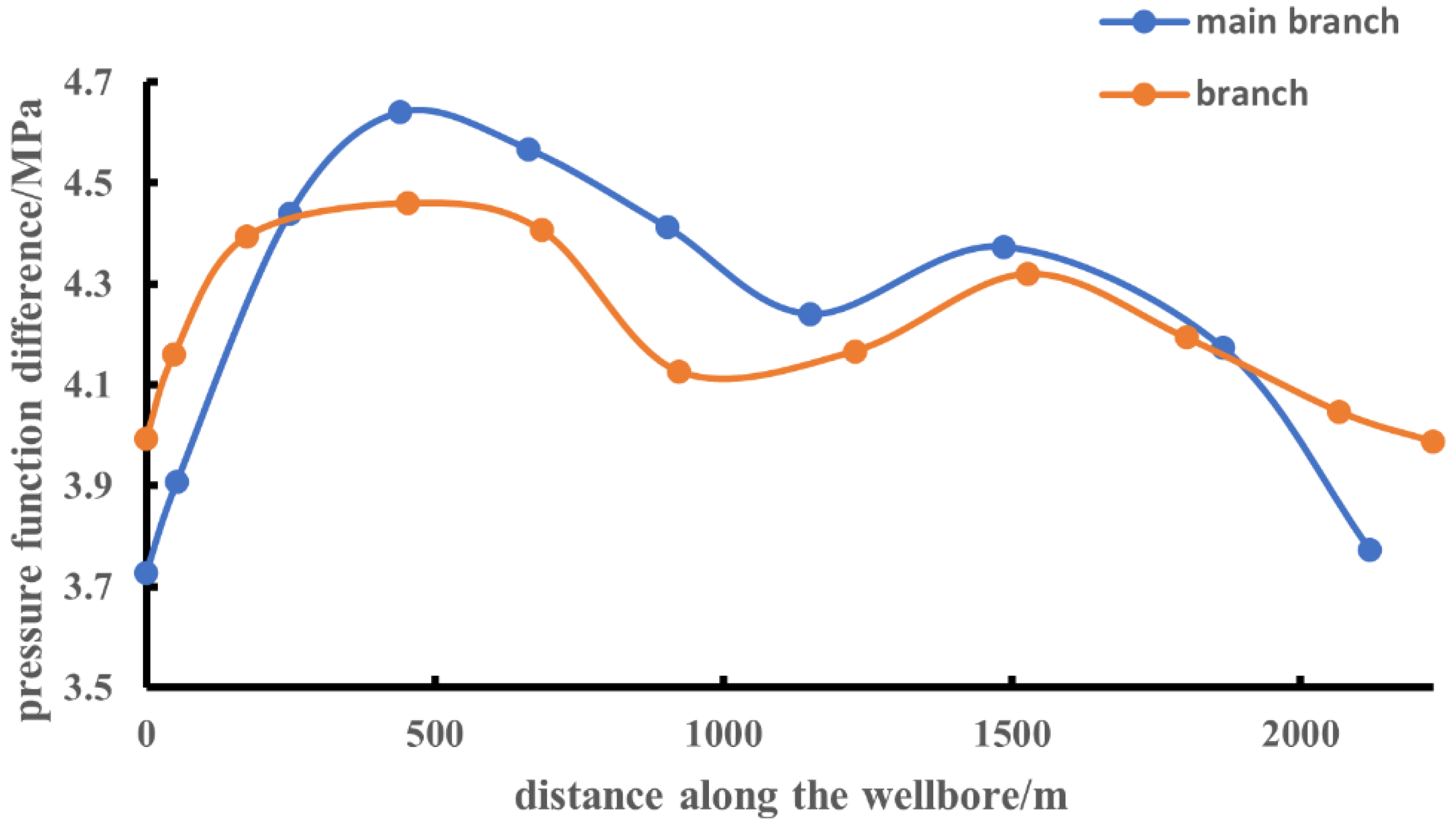
| Stratigraphic Model Parameters | Numerical Value | Experimental Model Parameters | Numerical Value |
|---|---|---|---|
| Horizontal well length/m | 1600 | Copper wire length/m | 0.4 |
| Production differential pressure/MPa | 4 | Experimental voltage/V | 1.5 |
| Viscosity/mPa·s | 2.4 × 10−2 | Geometric similarity coefficient CL | 2.5 × 10−4 |
| Pressure similarity coefficient Cp/V·(MPa)−1 | 0.375 | Resistance similarity coefficient Cr/μm2·[(mPa·s)·(μs/cm)]−1 | 93.22 |
| Flow similarity coefficient Cq/mA·(m3/d)−1 | 4 × 10−3 | Mobility similarity coefficient Cρ/(μs/cm)·[mPa·s·(10−3 μm2)−1] | 42.91 |
| Stratigraphic Model Parameters | Numerical Value | Experimental Model Parameters | Numerical Value |
|---|---|---|---|
| Length of horizontal section of main branch/m | 2120 | Length of main branch copper wire/m | 0.4 |
| Length of branch horizontal section/m | 2230 | Branch copper wire length/m | 0.42 |
| Production differential pressure/MPa | 10 | Experimental voltage/V | 1.5 |
| Viscosity/mPa·s | 2.4 × 10−2 | Geometric similarity coefficient CL | 1.89 × 10−4 |
| Pressure similarity coefficient Cp/V·(MPa)−1 | 0.15 | Resistance similarity coefficient Cr/μm2·[(mPa·s)·(μs/cm)]−1 | 73.49 |
| Flow similarity coefficient Cq/mA·(m3/d)−1 | 2 × 10−3 | Mobility similarity coefficient Cρ/(μs/cm)·[mPa·s·(10−3 μm2)−1] | 72 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, H.; Ji, Q.; Jiang, Z.; Yuan, B. Study on Seepage Characteristics and Production Capacity Characteristics of Complex Structural Wells in Non-Homogeneous Gas Reservoirs Based on Hydroelectric Simulation. Energies 2025, 18, 2794. https://doi.org/10.3390/en18112794
Liao H, Ji Q, Jiang Z, Yuan B. Study on Seepage Characteristics and Production Capacity Characteristics of Complex Structural Wells in Non-Homogeneous Gas Reservoirs Based on Hydroelectric Simulation. Energies. 2025; 18(11):2794. https://doi.org/10.3390/en18112794
Chicago/Turabian StyleLiao, Hengjie, Quanzhi Ji, Zhehao Jiang, and Bin Yuan. 2025. "Study on Seepage Characteristics and Production Capacity Characteristics of Complex Structural Wells in Non-Homogeneous Gas Reservoirs Based on Hydroelectric Simulation" Energies 18, no. 11: 2794. https://doi.org/10.3390/en18112794
APA StyleLiao, H., Ji, Q., Jiang, Z., & Yuan, B. (2025). Study on Seepage Characteristics and Production Capacity Characteristics of Complex Structural Wells in Non-Homogeneous Gas Reservoirs Based on Hydroelectric Simulation. Energies, 18(11), 2794. https://doi.org/10.3390/en18112794





