An Electric Vehicle Charging Simulation to Investigate the Potential of Intelligent Charging Strategies

Abstract

As electric vehicle (EV) adoption grows, efficient and accessible charging infrastructure is essential. This paper introduces a modular simulation environment to evaluate charging point configurations and operational strategies. The simulation incorporates detailed models of electrical consumers and user behaviour, leveraging real-world data to simulate charging scenarios. A rule-based control strategy is applied to assess six configurations for a supermarket parking lot charging point. Key findings include the highest profit being achieved with two fast chargers. In scenarios with a 50 kW grid connection limit, combining fast chargers with stationary battery storage proves effective. Conversely, mobile charging robots generate lower revenue, though grid peak limitations have minimal impact. The study highlights the potential of the simulation environment to optimise charging layouts, refine operational strategies, and develop energy management algorithms. This work demonstrates the utility of the simulation framework for analyzing diverse charging solutions, offering insights into cost efficiency and user satisfaction. The results emphasise the importance of tailored strategies to balance grid constraints, profitability, and user needs, paving the way for intelligent EV charging infrastructure development.

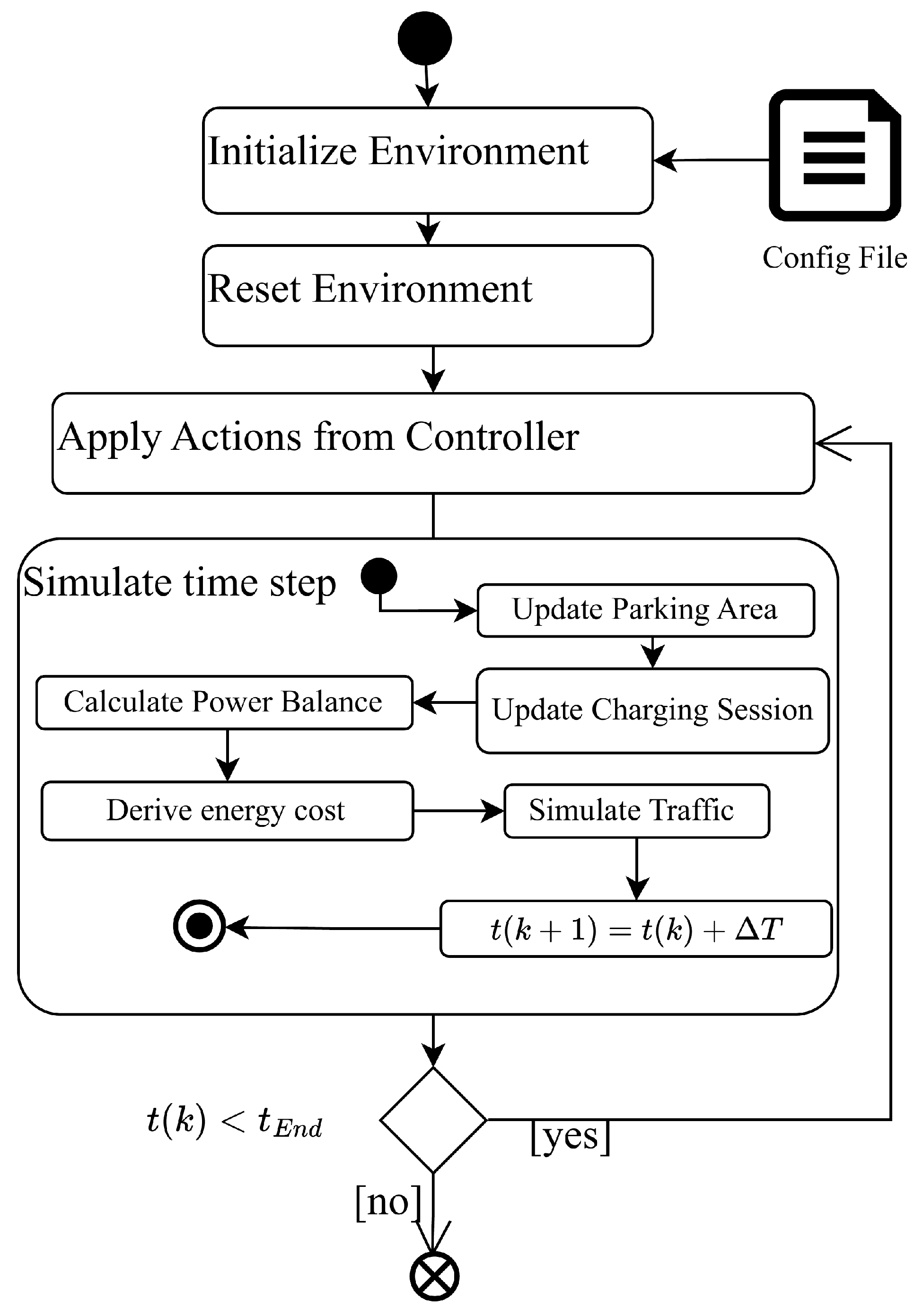
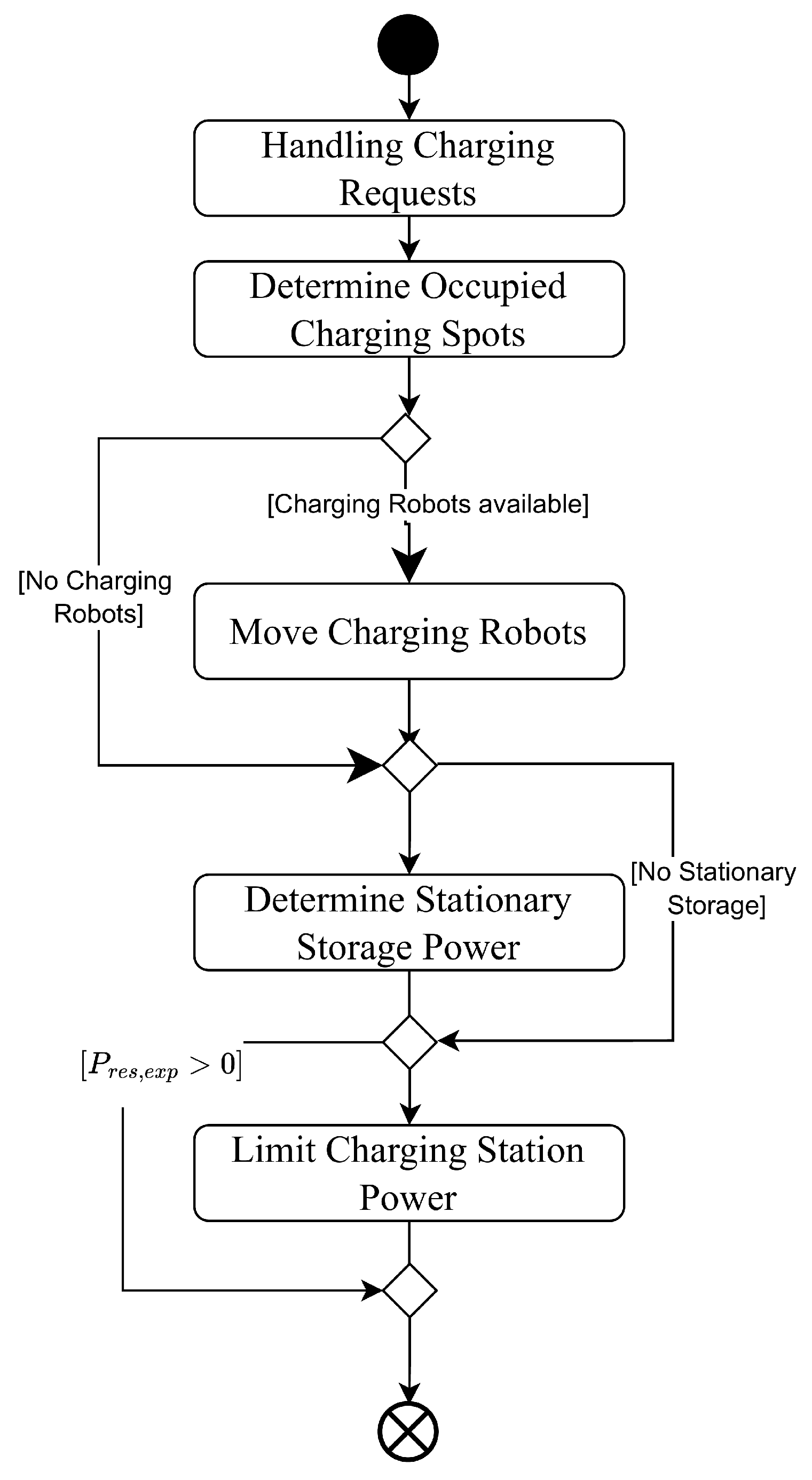
1. Introduction

In order to achieve the Paris-aligned climate goals and reduce greenhouse gas emissions, a transformation in the mobility and transport sector is necessary. Already, it can be observed that E-mobility gains importance [1]. One main challenge associated with E-mobility is the charging infrastructure. While users expect charging to be convenient, reliable, and fast, the charge point operator (CPO) focuses on the return-on-investment (ROI), and the grid operator needs to ensure the stability of the grid.

The increasing adoption of electric vehicles (EVs) has also elevated the role of public charging infrastructure. According to the International Energy Agency [2], public charging solutions are expected to play a key role in the global EV ecosystem, complementing home and fleet charging options by addressing the needs of EV users in urban and high-traffic environments. Recently, many solutions have been proposed that take into account the different stakeholders. Smart charging and bi-directional charging strategies are becoming increasingly important in fleet management and home use cases. In public and semi-public environments, there is a growing interest in concepts that utilise battery storage to reduce the need for grid reinforcement while still providing high charging power and, consequently, fast charging. Nevertheless, the issue persists: although a stationary battery-supported charging solution offers flexibility to the grid, it does not provide the same flexibility to the users. This is because, in the event that all the charging ports are occupied, the user will be unable to charge or will have to return at a later time.

The deployment of mobile charging robots, such as the GINI robot presented by Wessel et al. [3], offers several key advantages over stationary solutions. Mobile robots provide flexibility in charging location, potentially increasing user satisfaction by reducing wait times and better utilising charging infrastructure. They can also help distribute the load more evenly by charging their own batteries during off-peak times and using that stored energy during peak times, reducing strain on the grid. However, mobile charging robots come with higher initial investment and operational costs compared to stationary solutions. While they can increase revenue by serving more vehicles, the higher costs need to be considered to determine their overall financial viability. Detailed simulations are necessary to evaluate the potential of these charging solutions, including modelling of the charging solution, grid connection, power flows, user behaviour, and smart charging strategies.

The following section presents an overview of publications that incorporate modelling of charging points. In many publications, simulation models have been setup, either to evaluate potentials of a specific application, verify a control strategy, find an optimal design and sizing or train an RL agent. Sandhu et al. [4] describes a model for evaluating the potential of smart charging and Vehicle-to-Grid (V2G) charging strategies for an EV fleet. Self-consumption increase is considered as well as market integration of the EVs by participating into balancing services such as frequency containment reserve (FCR) and automatic frequency restoration reserve (aFRR).

Dorokhova et al. [5] model a microgrid containing a building, one charging point, an EV and the grid connection point. Based on this model, different optimisation strategies are compared with regard to how well a target SOC of the EV is reached and the level of self-consumption. The main focus is on reinforcement learning based algorithms, which are compared with rule-based and optimisation-based approaches.

For the application of reinforcement learning, many approaches for EV charging management can be found. Chu et al. [6] target the fleet management problem in a residential community containing PV and additional energy storage. The phenomenon of range anxiety experienced by electric vehicle (EV) users when charging their vehicles is subjected to a modelling process. Similarly, Fang et al. [7] model a microgrid with renewable energies. The objective is to optimise the energy cost. For that, access of the microgrids to an auction-based market is modelled. The problem is solved by a multi-agent reinforcement learning (MARL) approach. Jiang et al. [8] looks at a single parking lot, with EV arrival times derived from historical data. A combination of a data-based learning and an RL approach is used to smoothen the load at the parking lot. Lee et al. [9] use a non-parametric density function to model the usage pattern of a charger at a specific location. The model is used for a deep reinforcement learning approach targeting real-time charging and discharging control. The authors conclude that the combination of deep reinforcement learning with data-driven approaches to reflect the characteristics of a charging location are very effective.

While the aforementioned publications build a separate model for their use case, Liu et al. [10] use the SUMO framework [11] and combine it with OpenAI Gym [12]. The paper focuses on an electric vehicle fleet management problem and leverages multi-agent reinforcement learning to solve it.

Examining algorithms for charging management or evaluating the potential of new charging paradigms, such as V2G, is one use case for a charging point model. Another present research field is evaluating different charging point configurations, considering Battery Energy Storage System (BESS). BESS specifically refers to a stationary battery storage in this context.

Rafi and Bauman [13] provide a comprehensive overview of DC fast charging in conjunction with BESS as well as other energy storage options. They present various topologies and elucidate their respective advantages. Bartolucci et al. [14] and Datta et al. [15] analyze the integration of PV and BESS into electric vehicle charging stations. While Bartolucci et al. [14] target the coupling of the design and sizing, Datta et al. [15] rather focus on the control aspect. Similarly, Engelhardt et al. [16] develops an EMS algorithm for the coordination between BESS, PV, and EVSEs and validate the efficiency with the Monte Carlo simulation in different scenarios. Another publication focuses on the sizing of battery storage for a charging hub, so a larger battery supported high power charging points [17].

BESS are attractive, because they offer additional flexibility with regard to the time of production and consumption of electricity at a charging point. This idea is taken even further with mobile charging stations that contain BESS. Afshar et al. [18] classifies mobile charging stations into three categories: truck mobile charging stations, portable charging, and vehicle-to-vehicle power transfer. The truck mobile charging stations (TMCS) are further classified into four sub-categories. One of them are the battery-integrated TMCS, which are equipped with an energy storage system and can visit EVs at a requested location. Wang et al. [19] describe a concept of Single-Port and Multi-Port Vans, that would fall into this category. In contrast to that, the work presented by Zhang et al. [20] would fall in the battery-less TMCS, where only the charging stations are transported as mobile units.

Afshar et al. [21] set up an optimisation model to determine the optimal mixture of charging solutions. Stationary fast charging stations and mobile charging stations are considered for this purpose. Other publications focus on optimal routing for mobile charging stations [22] or the optimal placement [23,24].

Afshar et al. [18] further presents robot-like TMCS, which are useful at places with high demand and short distances between parking lots. These mobile charging robots have gained interest in the recent years and concepts as well as prototype products have been presented for example by Kong [25], Walzel et al. [26], Ulrich [27] and Volkswagen Group [28]. Wessel et al. [3] present a prototype of a mobile charging robot, named GINI. Battery capacities and power limits are provided. These will be taken as a reference for the studies performed in this work.

The advent of a more sophisticated and comprehensive array of charging solutions has rendered open frameworks that facilitate the selection, sizing, and testing of operating strategies a necessity. While many models exist for the power and energy system [29], the focus is often more on a bigger scale. Open-source models have been presented that focus on modelling of electricity markets such as the ones presented by Bussar et al. [30], Schimeczek et al. [31] and Hirth et al. [32]. Others are supporting planning of the transmission grid, especially with regard to renewable energy sources [33,34,35]. Moreover, there are models that take into account the interrelationships between different energy sectors [36,37]. Although these models provide valuable contributions, with regard to modelling, simulating, and developing control strategies, for charging point level energy systems, they do not seem suitable.

Recently, advanced open-source models have been developed for modelling charging points. In

Table 1. Overview of existing EV simulators focusing on smart charging strategies.

Simulator Name	RL Ready	Programming Language	BESS Integration	Capable of Modelling Mobile Chargers	Comments on Features
V2G-Sim [41]	No	Python	Yes	No	Large-Scale customizable V2G simulations
EVLib [42]	No	Java	No	No	Supports charging, discharging, battery swapping and inductive charging
EV-EcoSim [40]	No	Python	Yes	No	Charging infrastructure optimisation considering BESS
evsim [43]	No	R	No	No	Analyze charging behaviourof EVs
OPEN [44]	No	Python	Yes	No	Modelling, control, and simulations of local energy systems, no explicit focus on EVs
ACN-Sim [45]	Yes	Python	No	No	Data-driven charging simulator including three-phase system
SustainGym [46]	Yes	Python	No	No	RL benchmark platform for sustainable applications with EV charging based on ACN-Sim presented as one example
Chargym [47]	Yes	Python	No	No	Comparing RL algorithms for smart charging
FleetRL [38]	Yes	Python	No	No	RL for fleet charging management applications
EV2Gym [39]	Yes	Python	No	No	Simulator for different control strategies featuring V2G application
GiniSim (Ours)	Yes	Python	Yes	Yes	Custom simulator focusing on mobile charging robots via spatial modelling of charging location

a comprehensive summary that highlights their specific focus is given. Examining the most recently presented models, Cording and Thakur [38] present a model for training reinforcement learning strategies for EV fleets, while Orfanoudakis et al. [39] propose a framework specifically designed for V2G strategies using RL. Additionally, Balogun et al. [40] address the design and optimisation of electric vehicle charging infrastructure with their EV-EcoSim model. In contrast to existing tools (e.g., EV-EcoSim), our framework uniquely combines spatial modelling of mobile chargers (GINIs), battery storage, and grid constraints in a modular, RL-compatible design. This fills a critical gap in assessing flexible and mobile charging configurations at parking-lot scale.

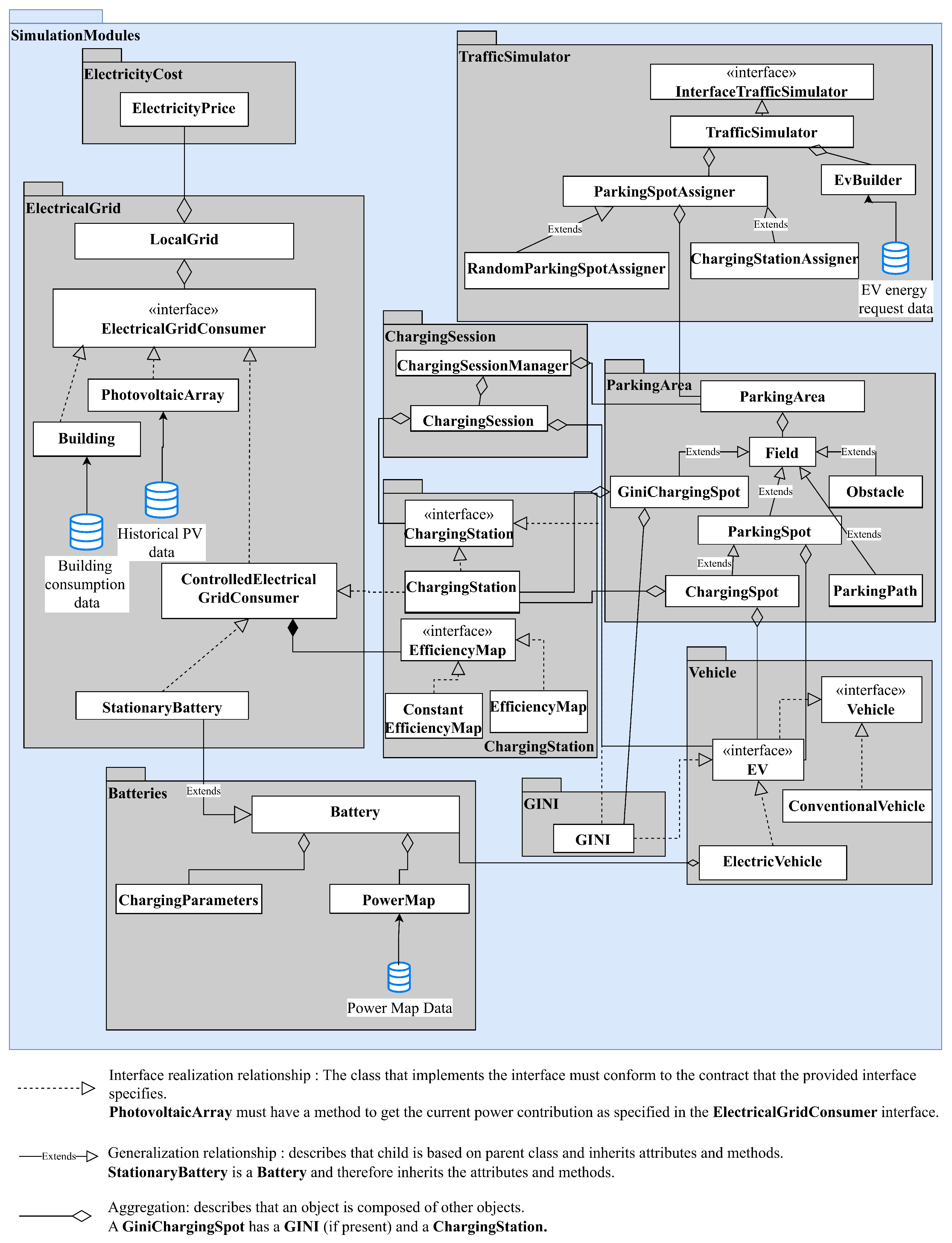
As presented, there is a lot of research examining charging management and new charging strategies for different charging points. Often, these include buildings, PV, and a grid connection. The concept of combining charging solutions with BESS is becoming increasingly prominent in research, with investigations extending to include mobile charging robots. In order to facilitate the research in this area, this work presents an open-source framework for the modelling of charging points. The contributions can be described as follows:

• An open-source library for modelling of charging points is presented, that allows for spatial resolution and hence the modelling of mobile charging robots.
• The integration of (smart) charging strategies and their interaction with the simulation environment is elaborated and shown for a rule-based strategy, which is compatible for charging points with BESS and/or mobile charging robots.
• An exemplary study of different charging point configurations considering BESS, mobile charging robots and grid limitations, respectively, is conducted.

2. Methodology

The following chapter discusses the model created for simulating power flows on charging point level considering the option of a mobile charging robot (in the following referred to as GINI). The simulation model consists of three main packages shown in Figure 1 which will be introduced. Firstly, in Section 2.1 the packages of the overall environment are introduced. The functionality and their role in the overall simulation environment is presented. Further, the usage of data within the package, if applicable, is described and the limitations of the models are shortly discussed. Next, Section 2.2 introduces how the environment is composed based on the models introduced in Section 2.1. The logical flow of the environment is presented and the interaction with the controller is described. Finally, in Section 2.3 the package containing controllers that interact with the environment is introduced. Controller refers in this context to an algorithm that outputs control values or actions to influence the environment. An exemplary use case is shown for the application of GINI charging robots.

2.1. Simulation Modules

In this section, the packages created for the simulation environment are presented. As shown in bottom part of Figure 1, there are nine main packages that are composed of multiple classes. In order to get a better understanding how the low level objects are aggregated into complex objects that the environment uses, the elaboration will go from low-level packages towards high-level packages. A more detailed look at the class architecture of the simulation modules is given in Figure A1 in Appendix C.

2.1.1. Battery

The Battery package consists of the battery model, which itself contains charging parameters and a power map. For a battery object the stored energy and the overall capacity of the battery can be defined. Based on the present energy and the the overall capacity the state of charge (SoC) is defined as in Equation (1). Since the model is only based on power, not on current and charge, the SoC is used analogously to the State of Energy (SoE).

$$SoC={\displaystyle \frac{E_{Bat}\left(t\right)}{E_{Bat,total}}}$$

(1)

The battery allows adding energy (charging) and drawing energy (discharging) the battery. The power limits for the charging and discharging are part of the ChargingParameters class and can be determined based on the PowerMap class. The PowerMap class allows setting a SoC dependent maximum charging and discharging power. In the case of unidirectional use of an electric vehicle, only the charging case is relevant. In contrast, for a BESS or a GINI that can be both charged and discharged, the discharging power curve is also relevant.

The pre-configured power maps have been derived from typical EVs that can be found in the market today [49]. An overview of some selected models is given in Figure 2.

As can be seen, every vehicle shows a decreasing maximum charging power for high SoCs. The absolute values of the maximum charging power over the whole SoC range can differ, though. Since the battery energy capacity $E_{Bat,total}$ has a high impact on the maximum charging power, it is often referred to the C-Rate $C_{Ch}$, which puts the power in relation to the energy (Equation (2)).

$$C_{Ch}={\displaystyle \frac{P_{Ch}}{E_{Bat,total}}},$$

(2)

In order to represent the variety of shapes of charging curves, different relative power curves are provided within the simulation environment. The absolute curve for charging and discharging is then created based on the $C_{max/min,ch/dch}$ and the total battery energy capacity $E_{Bat,total}$.

It should be noted that temperature effects are not explicitly modelled. In real-world systems, battery charging limits and degradation strongly depend on temperature. The literature shows that, especially at extreme temperatures below 0 °C and above 40 °C, the charging performance is deteriorated [50,51]. As this simulation assumes operation in moderate ambient conditions, extreme temperature cases are not considered, which may limit the accuracy for hot or cold climates. Incorporating thermal effects is a relevant future extension of the model.

The parameters that can be provided to the battery module are summarised in

Table 2. Parameters for battery module.

Parameter	Description	Default
$E_{Bat,total}$	Total battery energy capacity	50 kWh
$E_{Bat,Act}$	Actual battery energy capacity (at start)	30 kWh
$C_{max,ch}$	C-Rate for point with maximum charging power	1.5 $\mathrm{C}$
$C_{min,ch}$	C-Rate for point with minimum charging power (typically at SoC = 100%)	0.15 $\mathrm{C}$
$C_{max,dch}$	C-Rate for point with maximum discharging power	1.5 $\mathrm{C}$
$C_{min,dch}$	C-Rate for point with minimum discharging power	1 $\mathrm{C}$

.

2.1.2. Vehicle

In order to keep the model generic and allow for extension, a general vehicle interface and a concrete class for conventional vehicles is introduced. In theory this can be used in cases where some interaction between EVs and conventional vehicles should be modelled, e.g., when there is a scarcity of total parking spots. So far this has not been considered; therefore, this part is solely introduced for completeness and extensibility.

An EV is represented as an object containing a battery. The state of the EV is modelled as described in Equation (3).

$$s_{EV}\in \left\{\begin{array}{cc}\hfill & \mathrm{IDLE}\hfill \\ \hfill & \mathrm{CONNECTED}\hfill \\ \hfill & \mathrm{CHARGING}\hfill \\ \hfill & \mathrm{INTERRUPTING}\hfill \end{array}\right\}$$

(3)

When an EV parks at a parking spot it is in $s_{EV}=IDLE$. If it parks at a charging station or a GINI is at the same parking spot, it can be $s_{EV}=CONNECTED$. Once power is flowing into the EV, it is $s_{EV}=CHARGING$. It can change to $s_{EV}=INTERRUPTING$ once the departure time of the vehicle has passed.

In the context of the simulation environment, every vehicle has an arrival time and a stay time. Based on those, a departure time is derived. The attributes are provided by the EvBuilder of the TrafficSimulator module.

2.1.3. Charging Station

The charging station package defines the interface for a charging station. The functionalities range from connecting and disconnecting of an EV to providing the power limits of the charging station. Since the charging station is usually connected to the grid, it also implements the interface of an ElectricalGridConsumer, which allows the provision of the actual power for calculating the general power balance in the local grid. More specifically, the ChargingStation implements the ControlledElectricalGridConsumer, which ensures that the charging power can be set by an external entity. Similarly to the EV, the Charging Station (CS) implements different states (Equation (4)).

$$s_{CS}\in \left\{\begin{array}{cc}\hfill & \mathrm{IDLE}\hfill \\ \hfill & \mathrm{CONNECTED}\hfill \\ \hfill & \mathrm{CHARGING}\hfill \end{array}\right\}$$

(4)

During the charging process, losses occur between the power that is provided from the grid and the power that is actually charged into the battery. The magnitude of the losses depends on different parameters such as battery SoC, charging current, power electronics topology and others [52]. Additionally, the location or component where the losses occur differs [53]. A detailed model of the losses or efficiency of each contributing component is out of scope. The assumption here is that all losses are realised within the charging station and typical rectifier maps are used to represent these losses in the EfficiencyMap. In cases where the impact of current on the magnitude of the losses is deemed negligible, a class for a constant efficiency is provided: ConstantEfficiencyMap.

2.1.4. GINI

The GINI package contains the GINI class, which implements the EV and the charging station interface. This is due to the fact that the mobile charging robot GINI shares the characteristics of an EV in a way that it is mobile and can be recharged at a charging station, but it can also act as a charging station itself.

Similarly to the EV, the GINI has a battery. The default parameterisation has been done according to the first prototype. Therefore, the GINIs are parameterised with $E_{Batt}=35\mathrm{kWh}$, $C_{max}=1.5\mathrm{C}$ and $C_{min}=0.15\mathrm{C}$ for charging and discharging.

2.1.5. Charging Session

The charging session package consists of the ChargingSession and the ChargingSessionManager class. While the charging session class is responsible for the energy exchange between an object that implements the EV interface and an object that implements the charging station interface, the charging session manager controls the start and end of sessions and handles requests for charging of parked EVs. Within every charging session, the charging power is negotiated according to the Equations (5)–(10).

$$\begin{array}{cc}\hfill P_{max,cap}& ={\displaystyle \frac{E_{total,Batt}-E_{act}}{\mathrm{\Delta }T}}\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill P_{max}& =min(P_{CS,max},P_{EV,max},P_{max,cap})\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill P_{min,cap}& ={\displaystyle \frac{E_{act}}{\mathrm{\Delta }T}}\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill P_{min}& =min(P_{CS,min},P_{EV,min},P_{max,cap})\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill P_{chrg,EV,tar}& =min(max(P_{min},P_{tar}),P_{max})\hfill \end{array}$$

(9)

$$P_{chrg,EV}=\left\{\begin{array}{cc}{P}_{max}\hfill & \mathrm{if}\mathrm{no}{P}_{tar}\hfill \\ P_{chrg,EV,tar}\hfill & \mathrm{else}\hfill \end{array}\right.$$

(10)

Equations (5) and (7) represent the fact that if the battery is almost fully charged or discharged, not more then the remaining energy can be added or removed. Assuming a constant power during one time step, this leads to a limit for charging or discharging $P_{max/min,cap}$.

The maximum charging power is then calculated according to Equation (6) under consideration of the maximum charging power capability of the CS $P_{CS,max}$ and the EV or more specifically the battery of the EV $P_{EV,max}$. In case bidirectional charging is considered the Equation (8) also limits the discharging power. Setpoints are considered according to Equation (9). If no setpoint is provided, $P_{max}$ is applied (Equation (10)).

Since the GINI implements the EV and the CS interface, it can participate in a charging session as an EV which usually consumes the energy (except from bidirectional charging use cases) and a CS which usually donates energy. The role depends on the respective counterpart. In real-world applications, charging sessions may occasionally fail due to technical malfunctions or user-related issues [54]. However, such failure scenarios are not captured within the scope of the simulation model, which assumes that all charging sessions proceed successfully.

The model shall also allow simulating the availability of a BESS. Therefore, a StationaryStorageChargingSession is provided which generally behaves like a normal charging session but with the subtle difference that it is always active, since a BESS usually does not disconnect from the grid. Further, the BESS has no “partner” in the session. Within the session, only the set-point is compared to the power limits of the BESS.

The ChargingSessionManager is responsible for starting and stopping the charging session based on EVs arriving and leaving CS or the movement from the GINI to an EV or a CS.

2.1.6. Electrical Grid

The power balance of the consumers and generators available at the charging point is represented by the electrical grid package. The main class is the LocalGrid. It is a container for all elements that implement the ElectricalGridConsumer interface or the derived interface ControlledElectricalGridConsumer. The Building and the PhotovoltaicArray classes implement the ElectricalGridConsumer. This means that their behaviour is solely dependent on time and based on available (potentially historical) data. The power contribution of PhotovoltaicArray is taken from [55]. The power contribution from Building is based on standard load profiles [56]. For the Building, the data is scaled by a yearly consumption, so the general shape of the power trajectory over time can be attained with different yearly consumptions.

The ControlledElectricalGridConsumer is implemented by ChargingStation as well as by the StationaryBatteryStorage. This means that a target power can be provided which is taken into account during a charging session. Initially, all electrical grid consumers are registered within the local grid. During simulation, the energy balance is calculated according to Equation (11). The sign convention used for the calculations can be seen in Figure 3. The photovoltaic array can only serve as a source. Therefore, this direction is treated as positive for $P_{PV}$. In contrast, since the building is only a power sink, this is the direction which is used as positive for $P_{Building}$. Although charging stations can be operated bidirectionally, the operating mode in which the CS charges an EV has been assumed as positive for $P_{CS,i}$. For $P_{BESS}$, charging is positive and discharging negative. Lastly, a positive grid power $P_{Grid}$ is interpreted as drawing energy from the grid.

$$P_{Grid}=P_{Building}+\sum _{i=1}^n{P}_{CS,i}+P_{BESS}-P_{PV}$$

(11)

2.1.7. Electricity Cost

In the ElectricityCost package, the cost for the energy is calculated based on prices. So far, a simple dynamic tariff based on the day-ahead market price has been implemented. The dynamic price is represented by $p\left(t\right)$ and the cost $c_{E,buy}$ is calculated according to Equation (12).

$$c_{E,buy}=\left\{\begin{array}{cc}p\left(t\right)·P_{Grid}·\mathrm{\Delta }t\hfill & \mathrm{if}{P}_{Grid}>0\hfill \\ 0\hfill & \mathrm{else}\hfill \end{array}\right.$$

(12)

2.1.8. Parking Area

The main class of the parking area package is the ParkingArea class. The parking area is composed of many fields, which can have different properties and behaviour. The different types of fields and their characteristics are list in

Table 3. Different parking area field classes.

Class	Description
ParkingSpot	field where vehicles can park
ChargingSpot	field that contains a charging station
GiniChargingSpot	field that contains a charging station where only the GINI is allowed to recharge
ParkingPath	path along which the GINIs can move
Obstacle	path around which the GINIs need to navigate

.

2.1.9. Traffic Simulator

Finally, there is the TrafficSimulator package. The module is responsible for controlling the arrival and assignment of vehicles. For this purpose, the main class TrafficSimulator is composed of the EvBuilder and the ParkingSpotAssigner. The TrafficSimulator carries out three main steps:

• Calculate number of new EVs arriving: based on open available data [57] or data provided by a charge point operator (CPO) a distribution is created. The distribution represents the likelihood of an EV arriving at a time step. From this distribution, the number of EVs arriving at each time step is sampled.
• Build an EV instance for each EV arriving: distributions for the stay time and battery characteristics of the EV are determined based on the aforementioned datasets as well and sampled for each EV that has virtually arrived at the parking area.
• Assign the EV to a parking spot: there are two different classes that can be used for the assignment of a parking spot. A random parking spot can be assigned (RandomParkingSpotAssigner) or a charging spot will be assigned if one is available, otherwise, it is defaulted to a random parking spot (ChargingStationParkingSpotAssigner). The first one would be suitable for a case where the charging relies on the GINI moving towards the EVs parking positions, while the second one would represent a classic charging scenario with stationary charging infrastructure.

So far, two different data sources have been used for generating the distributions for the EVs. While the data set provided by Hecht et al. [57] covers a very high number of charging stations in Germany (22,200), it does not provide the granularity to distinguish by location. Therefore, a second data distribution has been derived from a (not openly available) dataset, which was recorded at three charging stations located at a supermarket parking lot in the city of Aachen, Germany.

2.2. Simulation Environment

The simulation packages are used to create a configurable simulation environment. The simulation environment is build based on OpenAI gym, to be suitable for reinforcement learning applications. As can be seen in Figure 4 the simulation environment consists of five main steps:

• Read Configuration
• Initialise Environment
• Reset Environment
• Apply actions from the agent
• Simulate one time step in environment

In the following, the steps will be elaborated in more detail.

2.2.1. Configuration

The environment shall allow to simulate different scenarios. One of the main requirements derived from this is to have a simple way to change the environment setup. Therefore, all configuration is provided via config-files. Within these files, it can be defined at which time and date the simulation starts. This will impact the for example the power contribution of the photovoltaic object to the local grid. Further, the duration and step size can be configured. In addition, the parking lot layout as well as the number of GINIs within the environment can be configured within this file.

2.2.2. Initialisation

During initialisation the elements of the environment are initialised and the observation and action spaces created. The environment directly contains a ParkingArea, a ChargingSessionManager, a TrafficSimulator and a LocalGrid object. These are initialised with the specific configuration provided.

The observation and action spaces have been designed in a way to serve a high amount of use cases and allow to be used with many different control algorithms. The observation space contains the power contributions of the different grid consumers, power, and energy states of the BESS, information about the electric vehicles present at the parking area and others.

The action space contains, for example, the requested field where the GINI is supposed to move to, target powers for GINI, BESS, and charging stations.

A complete overview of the observation space is provided in Appendix A and for the action space is provided in Appendix B.

Figure 4. Flow chart describing the conducted steps within the simulation environment.

Figure 4. Flow chart describing the conducted steps within the simulation environment.

2.2.3. Reset

In order to facilitate the training of an RL agent within a simulation environment, it is necessary to reset the environment after each episode. This functionality has, therefore, been provided.

2.2.4. Agent Action

The environment interacts in each step with an agent or controller. The actions are determined based on the observations. Based on the actions, the following operations are performed:

• answer requests from EVs
• set the target field for all GINIs
• set the requested charging/discharging power for GINIs
• set charging/discharging targets for charging stations
• set charging/discharging targets for the BESS

More details about how the existing agents’ work are provided in Section 2.3.

2.2.5. Simulation Step

In each simulation step, the elements of the simulation environment are updated. Firstly, the parking area is updated to include a list of available parking spots and free charging points. Further, the state of the GINI is adjusted based on the action provided by the controller.

Secondly, charging sessions are started and ended based on the status and position of EVs and GINIs.

Subsequently, the power contribution of each consumer is calculated, and based on that, the power at the grid connection point is calculated. This is used to calculate the electricity cost for the current time step.

Consecutively, the traffic is simulated, meaning that new EVs are created and registered at the parking area and EVs that reached their departure time are leaving. Additionally, the position of the GINI is updated based on the action provided by the controller. Finally, the time step is increased and the new observation created.

For better understanding, a rendering from the simulation environment has been added as a video (Appendix D).

2.3. Controller-Agent

As described in the last section, a controller can interact with the environment by providing actions. Generally, different types of control algorithms can be used with the environment through the observation and action interface. For the purpose of this work, a rule-based controller is implemented. The general steps, which are performed by the controller, are depicted in Figure 5. It contains five main steps for generating the complete action set:

• handle unanswered requests from EVs
• determine occupied charging spots
• request moving GINIs
• determine charging/discharging power of BESS
• limit CS charging power if required

In the following sections, the steps will be explained in more detail.

2.3.1. Request Handling

If there are requests from EVs for being charged, the controller can either confirm or deny the request. This is only relevant if there are GINIs at the parking area. Otherwise, the EVs will directly move towards the charging stations they want to charge at.

2.3.2. Occupied Charging Spots

In order to facilitate subsequent control logic and the limitation of the charging power, it is essential to ascertain which charging locations are currently in use. Therefore, this information is extracted from the given observations.

2.3.3. Moving GINIs

With the rule-based strategy, the GINIs movement is based on three main rules. Firstly, if the SoC of a GINI $So{C}_{GINI,i}$ is below a threshold $So{C}_{GINI,min}$, the GINI will go to a charging spot if there is one available.

Secondly, if the SoC of a GINI $So{C}_{GINI,i}$ is above $So{C}_{GINI,min}$ and there are confirmed charging requests but no GINI is at the requesting EV already, the GINI will move to the field of the EV.

Finally, if the GINI is sufficiently charged ($So{C}_{GINI,i}>So{C}_{GINI,suff}$), the GINI will clear the charging station and move to a free field.

Figure 5. Flow chart describing the steps and decisions conducted by the rule-based controller.

Figure 5. Flow chart describing the steps and decisions conducted by the rule-based controller.

In the subsequent study, the thresholds were set to $So{C}_{GINI,\min }=10\%$ and $So{C}_{GINI,\mathrm{suff}}=95\%$, representing a balanced compromise. Discharging the battery close to 0 leads to a significant drop in output power, resulting in slow EV recharging. With the configured power map, the discharging power of the GINI is only 5% of its maximum power capability. Conversely, charging the GINI to near 100% is inefficient, as the maximum charging power decreases substantially at high SoC levels. For the GINI battery model, less than 20 kW is available at 95% SoC, decreasing even further towards 100% SoC.

In cases where no GINIs are present in the scenario, this step is simply skipped, and default values are returned.

2.3.4. Charging Power BESS

The control strategy for the BESS is based on [58]. The proposed approach contains multiple charging and discharging strategies, which are varied based on the power produced at the charging point $P_{Prod}$, the load at the charging point $P_{Load}$ and the power limit for the grid connection $P_{grid,max}$, as well as the SoC of the BESS $So{C}_{BESS}$. Furthermore, the battery limits for charging $P_{Batt,chrg,max}$ and discharging $P_{Batt,dischrg,max}$ are considered. Namely, the following strategies are implemented:

• Optimising self-consumption (Discharging option): the battery is discharged when the local consumption exceeds the local production.
• Limiting peak load (Discharging option): the battery is discharged when the local consumption, minus any local production, exceeds a defined maximum power. The discharge power corresponds to the power difference between (net) consumption and maximum power.
• Surplus charging (Charging option): the battery is charged when the electricity production is higher than the local consumption.
• Local charging (Charging option): the battery is charged using the surplus energy generated by the PV system, ensuring that the total power consumption does not exceed the maximum grid connection limit $P_{grid,max}$.
• Grid charging (Charging option): the battery charges from the grid when there is available capacity, up to the maximum allowable charging power.

The authors further define SoC thresholds that trigger transitions between different control strategies and a methodology to determine the parameters for a specific scenario. In this work, a transition SoC of 95% was found to be effective for discharging strategies, while transition thresholds of 95% and 70% proved effective for charging strategies. For the details, it refers to [58].

If no BESS is foreseen in a scenario, this step is skipped.

2.3.5. CS Charging Power Limiting

Lastly, the power of the charging stations is controlled. This is only done in case, the power limit for the grid connection $P_{grid,max}$ would be exceeded otherwise. If the power limit would be exceeded, the residual power is taken into account and split evenly between all charging sessions.

$$\begin{array}{cc}\hfill P_{res}& =P_{Building}+P_{BESS}-P_{PV}\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill P_{res,\mathrm{\Delta }Grid,max}& =P_{Grid,max}-P_{res}\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill P_{CS,tar,i}& ={\displaystyle \frac{P_{res,\mathrm{\Delta }Grid,max}}{n_{Session}}},\forall i\in {\mathcal{I}}_{active}\hfill \end{array}$$

(15)

Based on Equation (13), the residual power $P_{res}$ is calculated. This represents the power difference between the locally consumed and generated power, without considering the charging stations. The difference between the maximum grid power $P_{Grid,max}$ and the residual power $P_{res}$ results in $P_{res,\mathrm{\Delta }Grid,max}$ and indicates how much power is left to be consumed by the charging stations. $P_{res,\mathrm{\Delta }Grid,max}$ is split evenly between the charging stations and assigned as the target power $P_{CS,tar,i}$. This is only done for charging stations with active charging sessions (${\mathcal{I}}_{active}$).

3. Results

This section will provide exemplary results generated with the model presented in Section 2. In particular, the charging concept with a fleet of GINI robots shall be compared to concepts with solely fast chargers and a concept integrating a BESS.

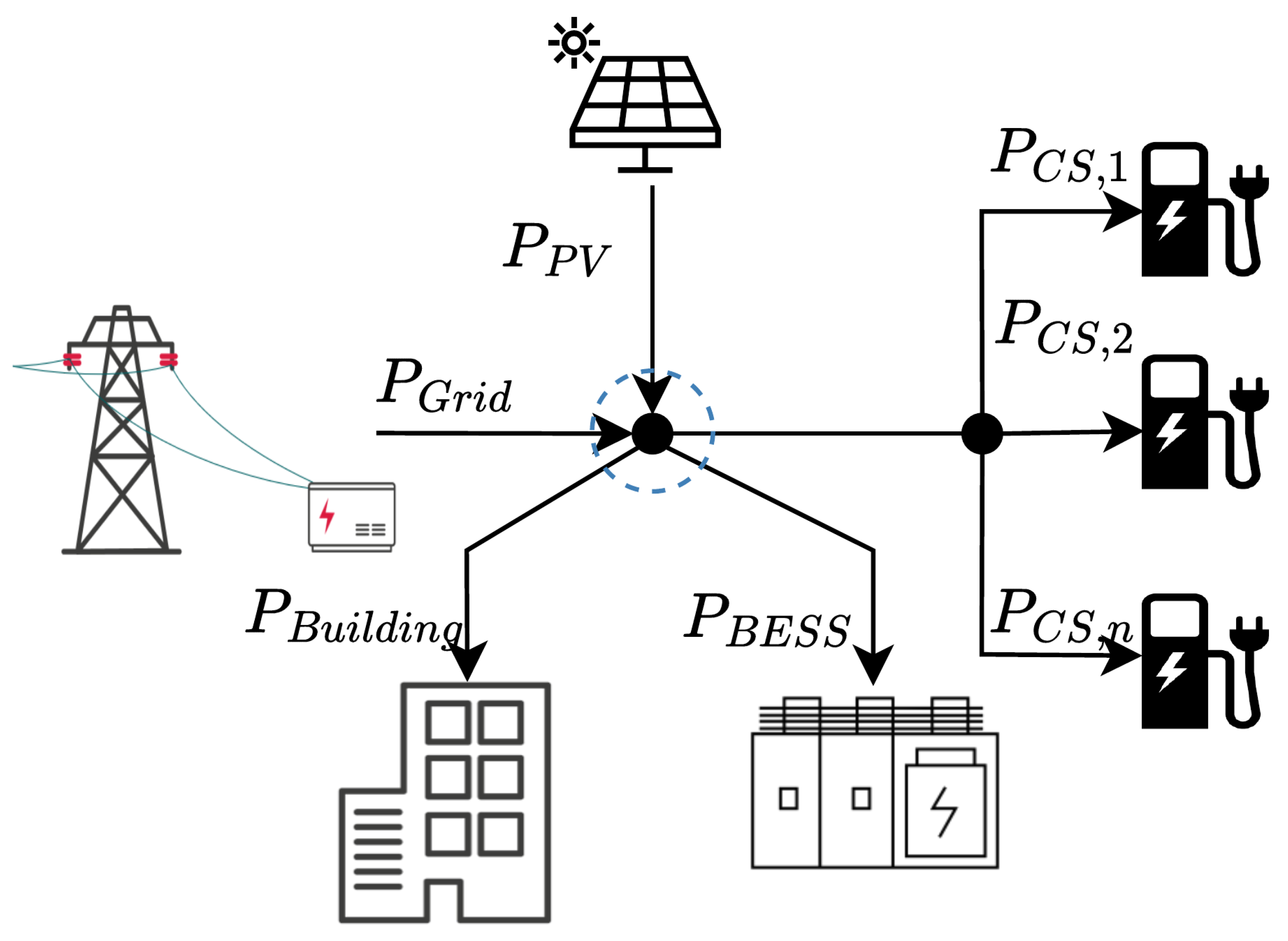
The overarching use case is that of a supermarket with installed charging infrastructure. This use case has been selected as one example satisfying the requirements set out in International Energy Agency [2] of chargers in publicly accessible areas, which also enable the adoption of EVs outside urban and suburban areas. This use case means in general that relatively short staying times are expected. The arrival times are sampled from the traffic simulator model as presented in Section 2.1.9. The expectation for the number of EVs to arrive per day is set to 48 (two per hour). Further, many supermarkets nowadays have a rooftop PV, which has been integrated in the environment. For all scenarios, a selling price for charged energy $p_{energy}$ has been set to 0.5 €/kWh. In the scenarios, that include GINI robots (Scenario 2, 3, 5), the charging stations can only be used by the GINIs. In these scenarios, the EVs park at a randomly assigned parking field and wait for a GINI. In the event of power being fed back into the grid, it is assumed that there will be no remuneration for it.

In

Table 4. Configuration parameters for compared scenarios.

Scenario	${\mathit{n}}_{\mathbf{CS}}/-$	${\mathit{n}}_{\mathbf{GINI}}/-$	${\mathit{P}}_{\mathbf{grid},\mathbf{max}}$/kW	${\mathit{P}}_{\mathbf{CS}}$/kW	${\mathit{E}}_{\mathbf{BESS}}$/kWh
1	2	0	200	55	0
2	2	3	200	11	0
3	2	3	200	55	0
4	2	0	50	55	0
5	2	3	50	55	0
6	2	0	50	55	80

, the most important parameters of the configuration are listed. It is important to note that these results do not represent a detailed study on the optimal charging solution for a specific location, but should rather highlight how the model can be used to compare different solutions. For all runs, a summer day with the solar irradiance data and electricity prices from the 2 June 2022 is assumed.

Importantly, the profit values presented in the following scenarios reflect only operational margins-revenue from charging EVs minus cost for buying energy. Capital expenditures (e.g., BESS and GINI purchase), maintenance costs, and battery degradation effects are not included. These aspects are essential for a full techno-economic analysis and should be evaluated in future site-specific studies.

In the following, the results from the different scenarios are presented and a short comparison summary of the results is provided afterwards (Section 3.7).

3.1. Scenario 1

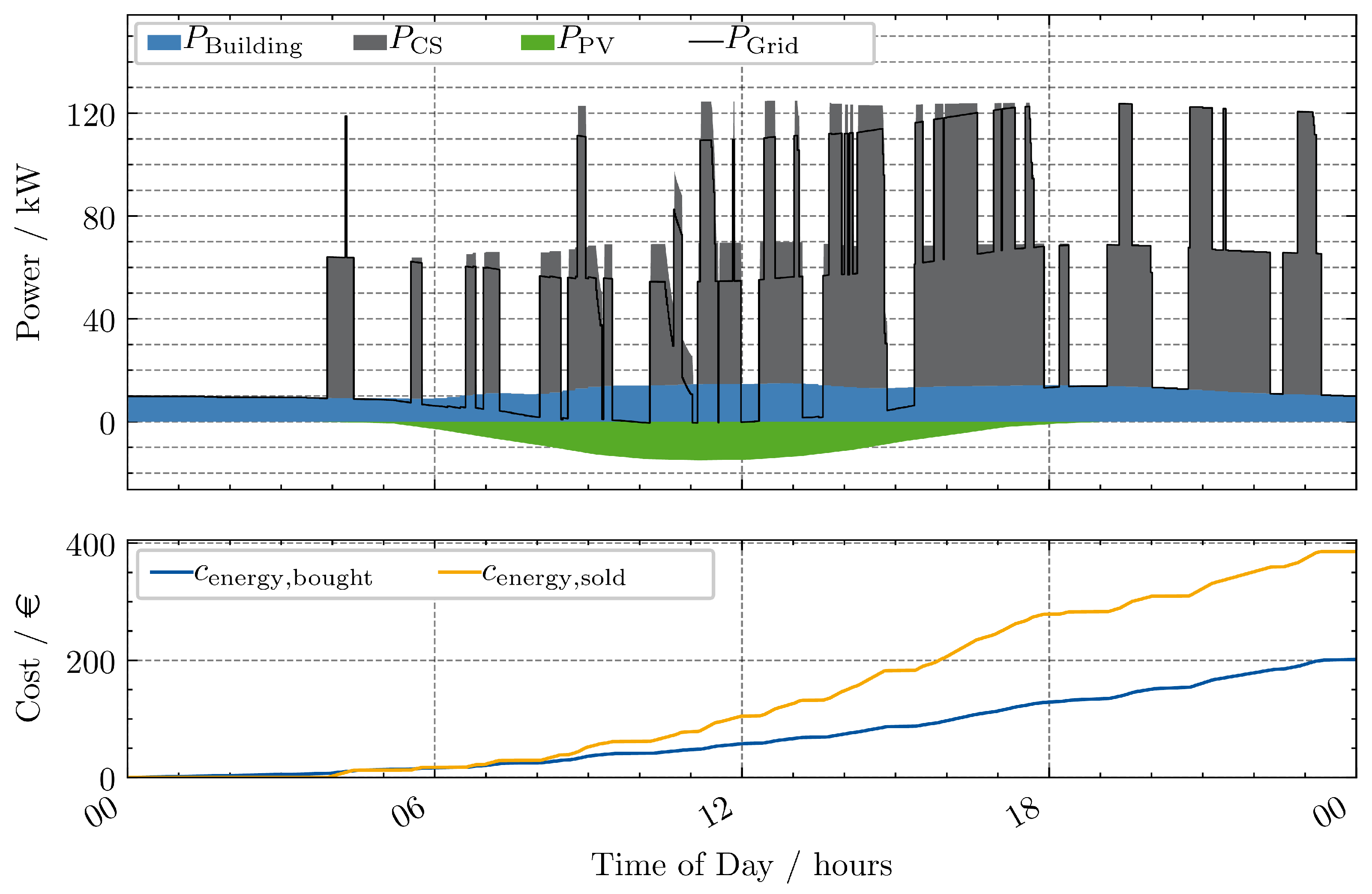
In the first scenario, the grid limit $P_{grid,max}$ is set to $200\mathrm{kW}$, which cannot be reached with the consumers installed. Therefore, this limit is practically irrelevant for the scenario. The power trajectory and cost are shown in Figure 6. In the upper graph, the PV power is depicted as negative and the building and CS power as positive in the stacked form. The resulting power drawn from the grid is depicted as a line. If $P_{\mathrm{Grid}}$ is negative, it means that power is fed back into the grid. In the bottom graph the accumulated cost and revenue are shown. The difference is the profit, only considering the operational expenses in regard to energy cost. In cases, where GINIs are present, the revenue results from the GINIs charging EVs. In cases only with CSs, the revenue results from the EVs charging at the CSs. As there is no storage system (GINI or BESS) in this scenario, no SoC is shown.

As most EVs can charge with maximum power above the limit of the CS up to a high SoC, two distinct power levels can be observed in the top graph. If one EV is charging at the parking area it results in a grid power of around 60 kW and if there are two it is around 120 kW. The full magnitude also depends on the building and PV power at the respective time step. Although, compared to the high charging powers these are almost negligible in the configured scenarios.

Especially in the afternoon hours, where often both CSs are occupied by an EV, the revenue increases much steeper compared to the cost, due to the spread between buying and selling price.

Figure 6. Scenario 1: Two fast chargers and no power limit; Profit €184.27 (Cost: €201.575-Revenue: €385.85).

Figure 6. Scenario 1: Two fast chargers and no power limit; Profit €184.27 (Cost: €201.575-Revenue: €385.85).

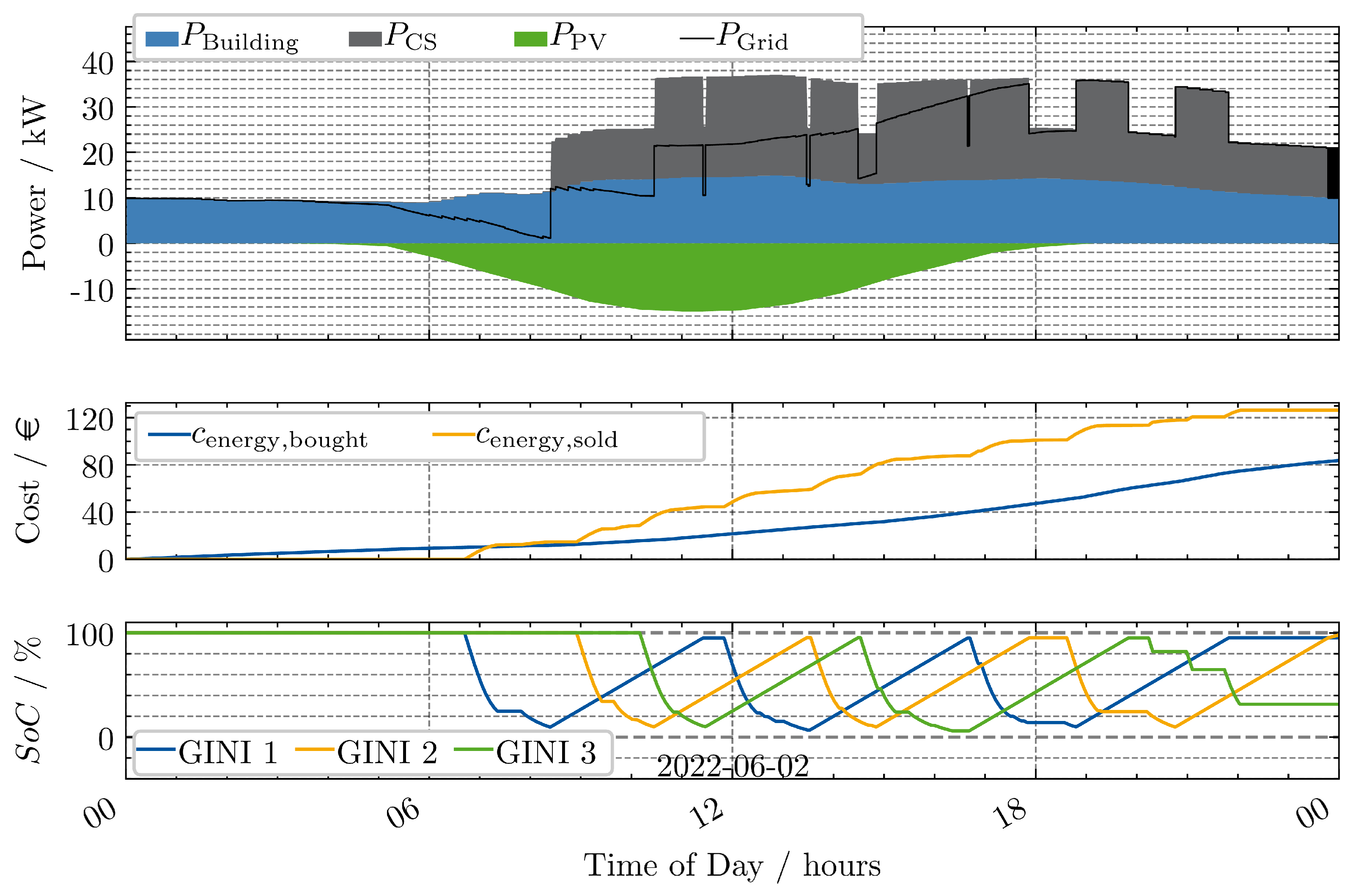
3.2. Scenario 2

In the second scenario, three GINIs are introduced into the environment and charged on two slow chargers with 11 kW. The SoC of the batteries integrated in the GINIs are shown in Figure 7 in addition to the cost and the power trajectories, that have already been introduced for the first scenario.

In the bottom graph, it can be seen that GINI 1 and GINI 2 recharged three times and the third GINI recharges two times and end the day with a SoC of around 50%. It becomes evident that the grid load is much lower compared to scenario 1. Instead of reaching more than 120 kW, only around 35 kW peak grid power is observed. This is due to the significantly lower charging power of the CSs in this scenario. Consequently, it results in lower revenue and hence lower profit, as the number of EVs the GINIs can service, depends on the recharging time (see Table 5).

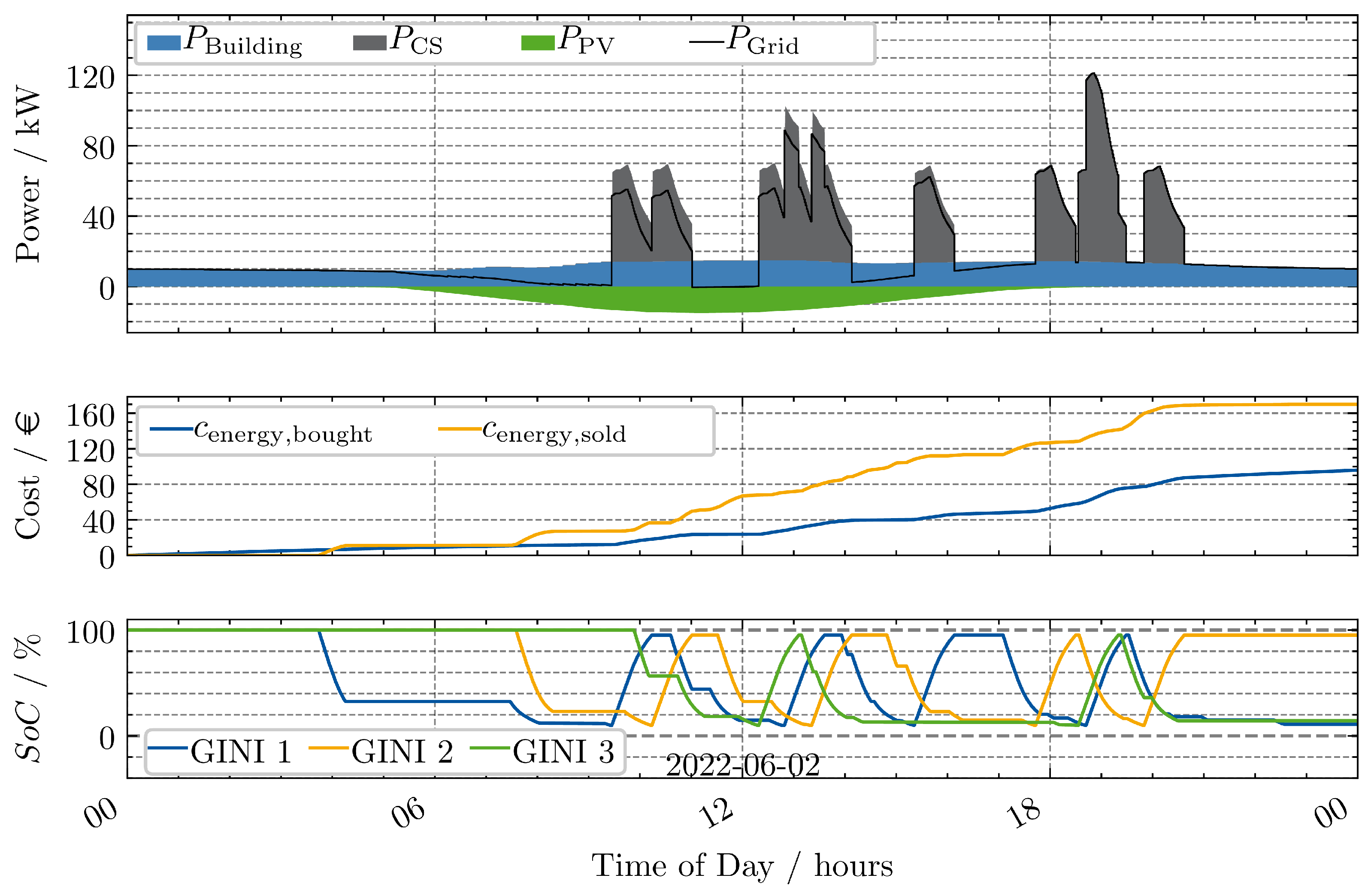
3.3. Scenario 3

Scenario 3 presents a combination of Scenario 1 and 2. The same number of GINIs is used, but with the same configuration of charging stations from Scenario 1 (see Figure 8).

The results show that the GINIs are able to charge more often compared to Scenario 2. The peak load is higher compared to Scenario 2, but still lower in comparison to Scenario 1. Accordingly, the profit is higher compared to Scenario 2, but still significantly lower compared to Scenario 1 as highlighted in Table 5. It can be observed that at high SoCs the charging power is reduced. This indicates recharging to 100% SoC might not be the most profitable strategy. Additionally, in many cases, the energy of the GINIs battery is only sufficient for a single EV. In particular, the cost of travelling to and from an electric vehicle (EV) and then back to the charging station (CS) to recharge, followed by travelling to the next EV, can be significant, especially for large parking spots. This cost could be reduced by using battery sizes that allow for servicing multiple EVs and potentially only a single recharging throughout the day, with the main recharging occurring during the night.

Table 5. Summary of key metrics for all scenarios (single-day simulations).

Scenario	Profit/	Cost/	Revenue/	EVs Arrived	EVs Fully Charged	Charged Energy/kWh	Avg. kWh/EV
1	184.27	201.58	385.85	56	19	771.70	13.80
2	42.44	83.78	126.22	40	7	252.44	6.31
3	74.16	95.87	170.03	43	7	340.06	7.90
4	89.85	126.27	216.11	45	7	422.85	9.40
5	76.50	89.72	166.21	43	3	332.23	7.73
6	138.13	172.08	310.21	54	11	620.42	11.49

Table 5. Summary of key metrics for all scenarios (single-day simulations).

Scenario	Profit/	Cost/	Revenue/	EVs Arrived	EVs Fully Charged	Charged Energy/kWh	Avg. kWh/EV
1	184.27	201.58	385.85	56	19	771.70	13.80
2	42.44	83.78	126.22	40	7	252.44	6.31
3	74.16	95.87	170.03	43	7	340.06	7.90
4	89.85	126.27	216.11	45	7	422.85	9.40
5	76.50	89.72	166.21	43	3	332.23	7.73
6	138.13	172.08	310.21	54	11	620.42	11.49

3.4. Scenario 4

Scenario 4 and the following introduce a power limit $P_{Grid,max}=50\mathrm{kW}$. In practice, the grid connection is frequently insufficient, to handle the maximum charging power of all CSs installed in combination with the building load. Hence, charging management solutions, which curtail the CS power are used. This is simulated within Scenario 4 and the results are shown in Figure 9.

As depicted in the upper graph, the power limit is effective in reducing the peak load. In cases where the power limit is reached, the charging power of all CSs is equally reduced. As a result profit is reduced significantly compared to Scenario 1, but still exceeds the profit of Scenario 3.

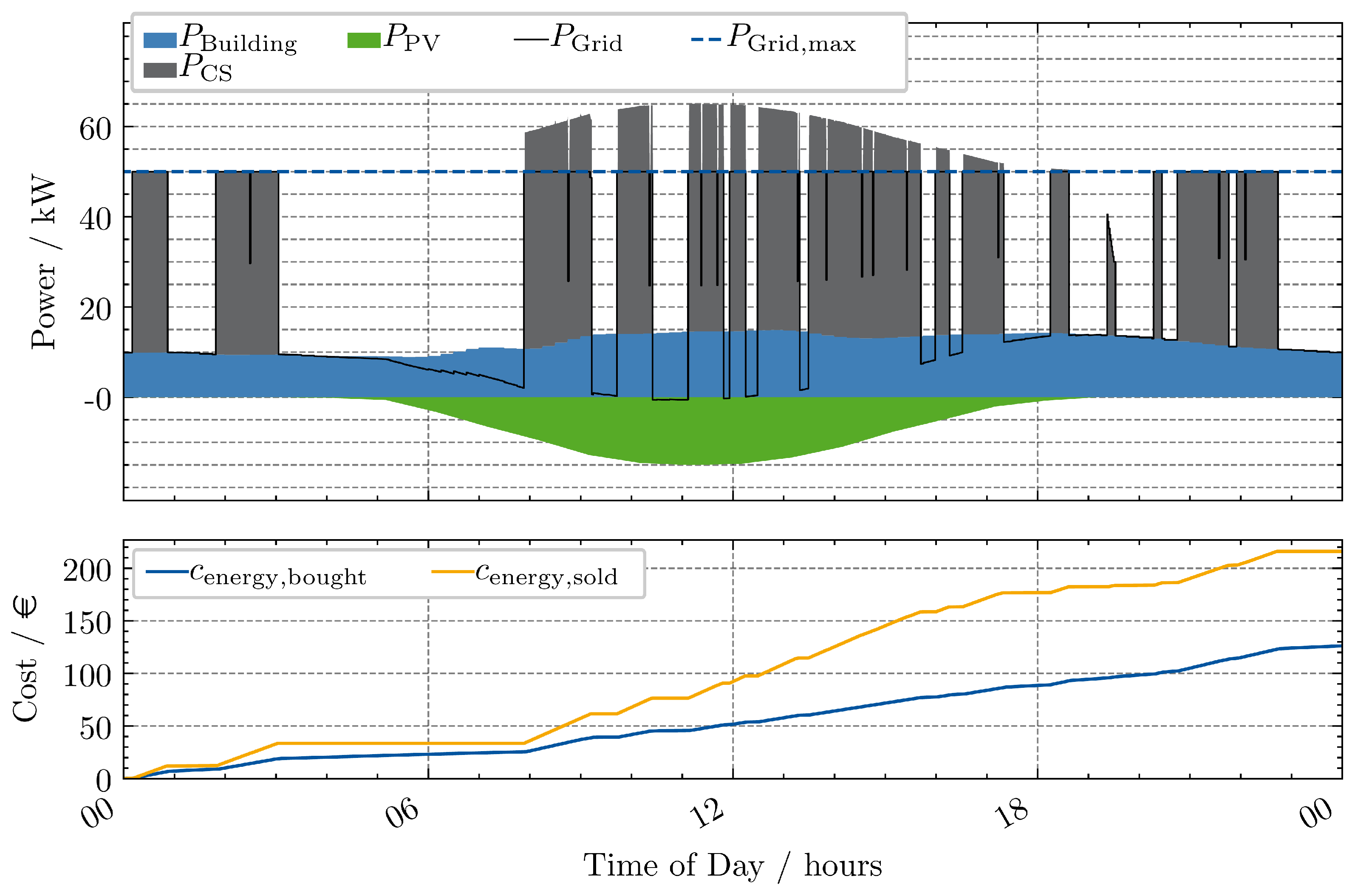
3.5. Scenario 5

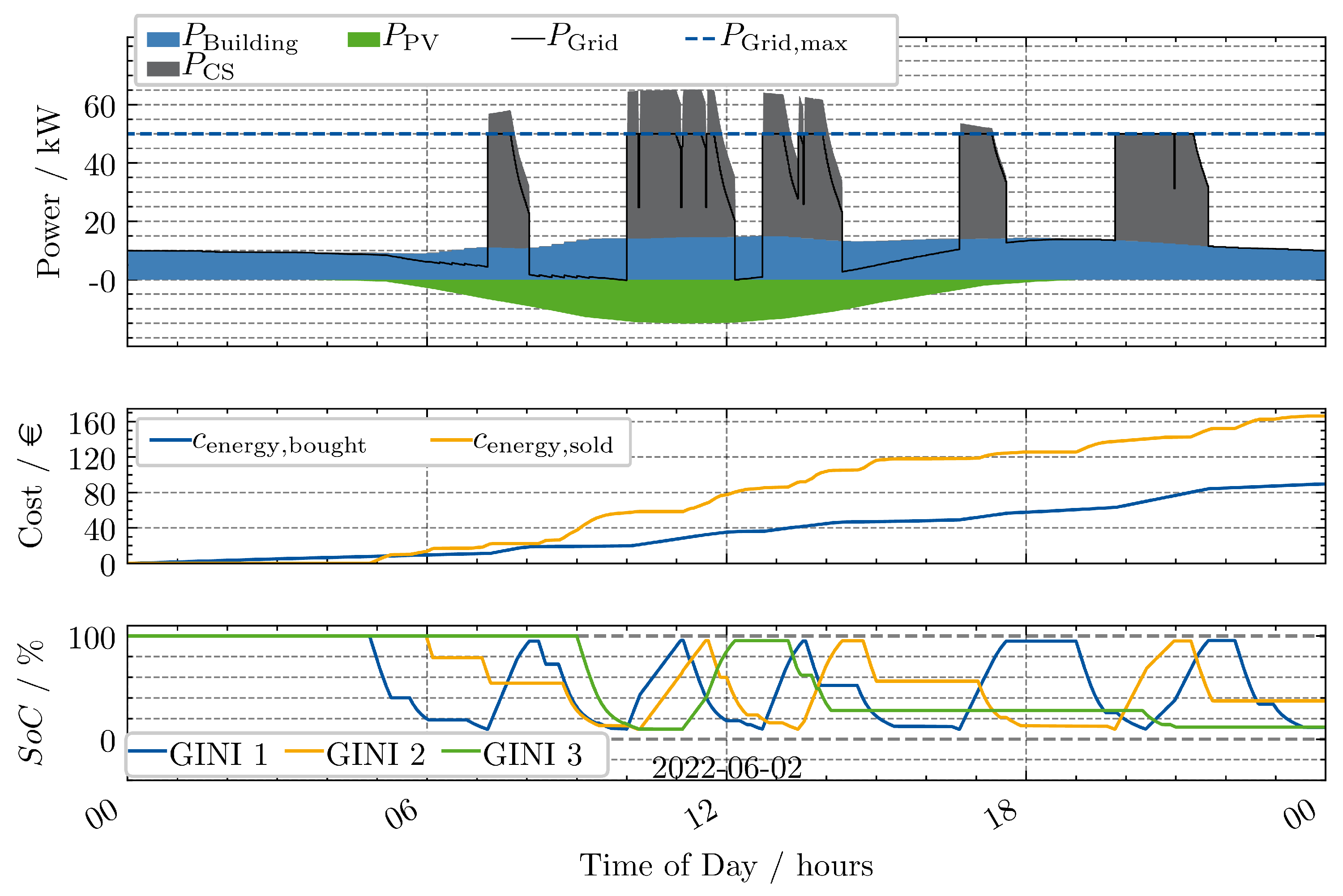
Scenario 5 introduces a power limit $P_{Grid,max}=50\mathrm{kW}$ to the setup from Scenario 3. The resulting power, cost, and SoC trajectories are shown in Figure 10.

The power limit is effective in reducing the peak load. This is also visible in the SoC trajectories of the GINIs. For example, at 10:00 the GINIs are not able to charge with full power, as the power limit is reached, resulting in a more flat increase in SoC for GINI 1. Interestingly, the profit stays quite stable compared to Scenario 3.

The lower sensitivity to a maximum grid power limit can be explained with the temporal seperated recharging and charging of EVs and the starting SoC of 100% for the GINIs.

A limitation that can be observed is that there are times where the power limit is not reached, but the GINIs are not recharging. This is due to the simple rule-based control strategy. This can for example be observed in the afternoon after 15:00.

Figure 10. Scenario 5: Two fast chargers, three GINIs and grid limitation; Profit €76.50 (Cost: €89.72-Revenue: €166.21).

Figure 10. Scenario 5: Two fast chargers, three GINIs and grid limitation; Profit €76.50 (Cost: €89.72-Revenue: €166.21).

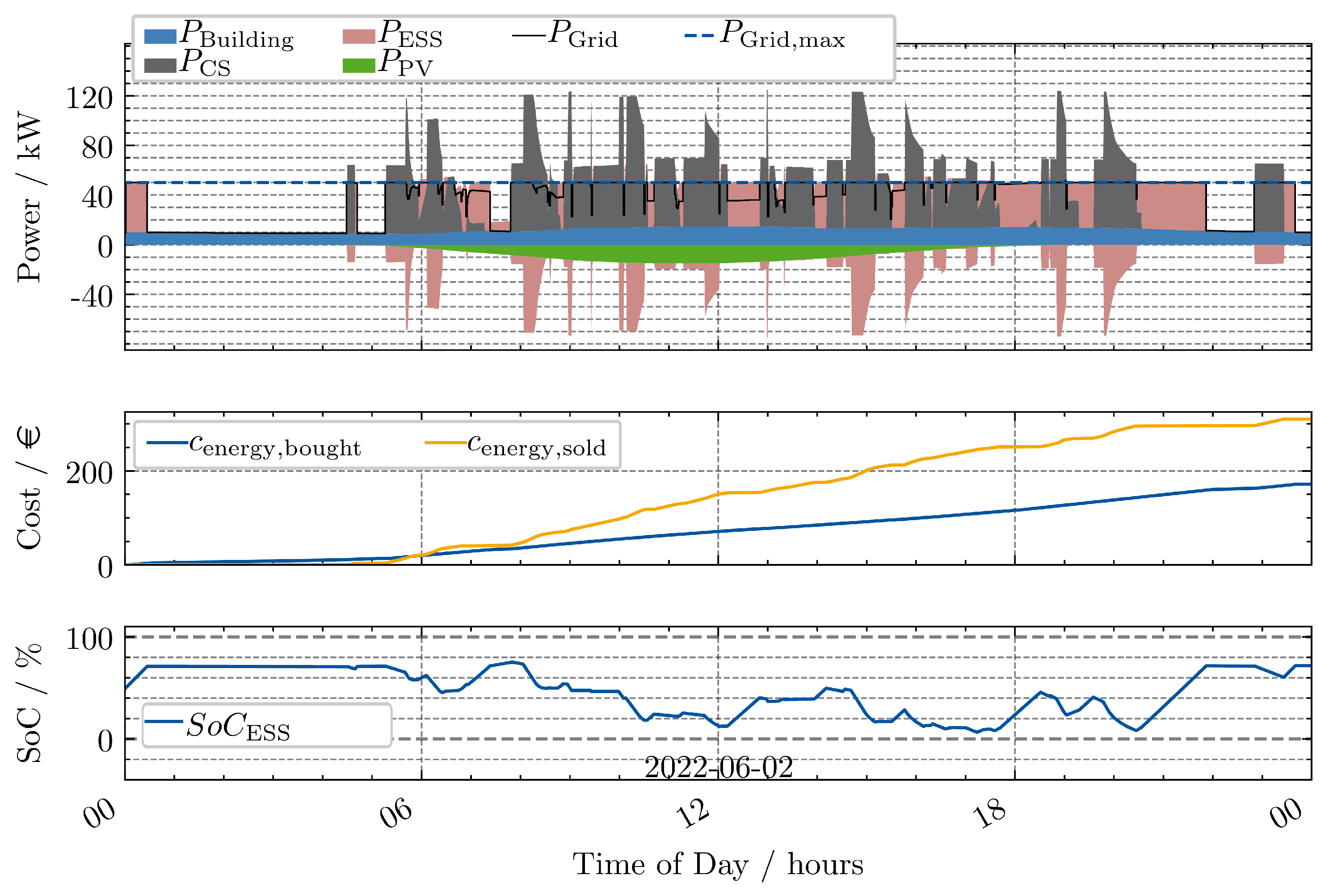
3.6. Scenario 6

While with a load management system it is ensured that the power limit of the grid connection is not exceeded, the installation of a BESS can support high power charging in peak times, if the storage is recharged in off-peak times. Scenario 6 introduces a BESS with a capacity of 80 kWh to the setup from Scenario 5. The resulting power, cost, and SoC trajectories are shown in Figure 11.

In addition to the previous scenarios, $P_{\mathrm{BESS}}$ is shown in the top graph. Discharging of the BESS is depicted in the negative part of the y-axis and charging in the positive. The BESS has an SoC of 50% at the beginning of the simulation run. During the first couple of minutes, the BESS charges with the maximum permissible power to not exceed the grid limit. The BESS only charges to 70% due to the configured thresholds for the different operating strategies. Similar behaviourcan be observed at the end of the day, after 20:00. Throughout the day, the BESS mainly charges during times, where no EVs are charging, e.g., at 12:15, or 17:45. The BESS allows for higher charging power by discharging during times, where the grid power is already high, e.g., at 10:00.

3.7. Comparison Single-Day Simulations

Table 5 summarises the key operational results for all simulated scenarios over a single day. Scenario 1 achieves the highest profit, driven by unconstrained access to grid power and fast charging capabilities. In contrast, Scenario 2 yields the lowest profit due to the limited charging power of the 11 kW chargers, which significantly reduces the number of EVs that can be serviced by the GINIs.

The addition of fast chargers in Scenario 3 improves GINI utilisation and profit compared to Scenario 2, though the logistical overhead and limited battery capacity of the GINIs still constrain performance relative to stationary CSs. Introducing a 50 kW grid constraint in Scenario 4 reduces profit compared to Scenario 1 but remains higher than GINI-based setups, highlighting the impact of power availability on throughput and revenue.

Scenario 5, which combines GINIs and a grid constraint, achieves a profit similar to Scenario 3, indicating that the GINIs’ temporal flexibility can partially mitigate grid limitations. Scenario 6 demonstrates that integrating a BESS allows for substantial profit recovery despite the grid constraint, nearly closing the gap to the unconstrained Scenario 1.

Overall, the comparison underscores the importance of available charging power. Although, the results indicate that a BESS can help maintaining high operational margins, with less available power at the grid connection point. GINI-based systems offer flexibility but require careful coordination and likely benefit from larger battery capacities or optimised dispatch strategies to reach their full potential.

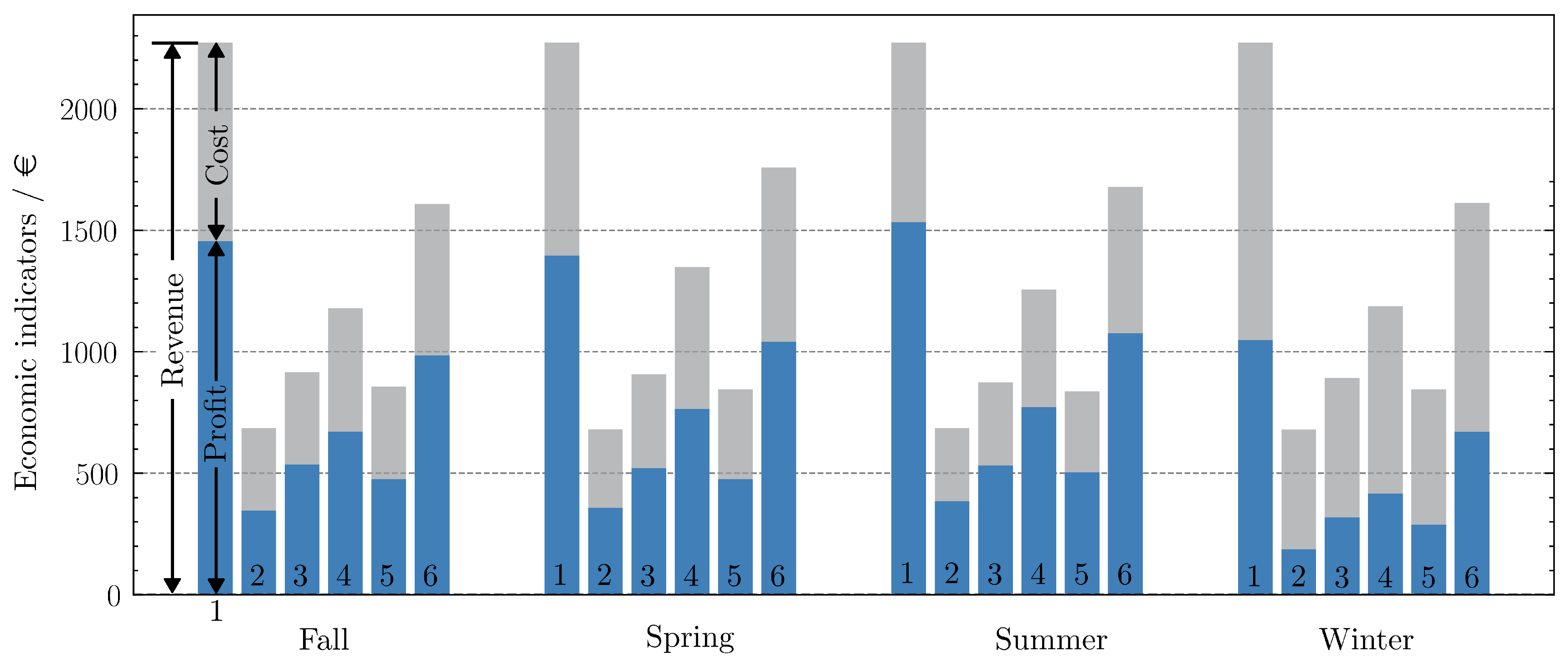
3.8. Seasonal Analysis

While the previous results primarily served to illustrate the capabilities of the simulation environment under specific daily conditions, this section aims to assess the sensitivity of different charging point layout scenarios to seasonal variations. To this end, the marginal operational profit is analysed over four representative weeks, one for each season of the year. The same EV arrival scheme is used across all runs to ensure comparability. The time frames selected for each season are as follows:

• Winter: 2023-01-19 00:00 to 2023-01-25 24:00
• Spring: 2023-04-03 00:00 to 2023-04-09 24:00
• Summer: 2023-08-14 00:00 to 2023-08-20 24:00
• Fall: 2023-10-16 00:00 to 2023-10-22 24:00

The results are shown in Figure 12.

Overall, the ranking of profit across the scenarios remains consistent across all seasons. Scenario 1 yields the highest profit, followed by scenarios 6 and 4. Scenarios 3, 5, and 2 show the lowest profits, with scenario 2 performing significantly worse due to the limited charging power of its charging stations (CSs). Notably, the overall revenue from EV charging in scenario 1 remains constant across all seasons. This results from the use of a fixed EV model in all simulations, with consistent EV-specific parameters, arrival times, and dwell durations.

The high profit in scenario 1 is primarily attributed to the high charging power available at the CSs and the absence of a grid connection constraint requiring peak shaving. Among all 24 runs, the summer scenario of scenario 1 achieves the highest profit, exceeding €1500. When a weaker grid connection is introduced in scenario 4, profit decreases significantly across all seasons. The addition of a BESS in scenario 6 improves profitability compared to scenario 4, although it does not match the profit levels of scenario 1 without grid constraints. This observation is in accordance with the findings from the single-day simulations.

Figure 12. Seasonal comparison of marginal operational profit across all charging point layout scenarios.

Figure 12. Seasonal comparison of marginal operational profit across all charging point layout scenarios.

As observed in single-day simulations, adding a grid constraint in the scenario with GINIs and fast chargers (scenario 5, based on scenario 3) does not lead to a significant profit reduction. This can be explained by the flexibility of the GINIs, which can recharge at times when grid power availability is higher and thus are less impacted by peak limitations. While the GINI-based scenarios (3 and 5) offer greater flexibility, their overall revenue remains lower compared to scenarios with stationary CSs. This can be attributed to two main factors:

• the operational overhead of recharging and moving the GINIs, which can be significant, especially in larger parking areas.
• the comparably small battery capacity of the GINIs, which not only limits the number of EVs that can be serviced before recharging but also results to lower charging power as the power capability depends on the C-rate and hence the battery capacity.

4. Discussion

In the preceding Section 3, the capability of the presented simulation framework to analyze different charging scenarios has been demonstrated. The findings are discussed in this section. Special attention is paid to the integration of mobile charging robots (GINIs) into the charging locations. Further, the limitations and possible extensions to the simulation model and the performed study are presented. Lastly, the practical implications of the results are discussed and the impact of capital costs is highlighted.

4.1. Discussion of Results

In general, reducing the maximum grid power limit leads to a decrease in profit. As this is expected, the main focus is on how different charging concepts can mitigate this disadvantage. Under the highlighted scenarios with grid limitation, Scenario 6 shows the most promising results by integrating a BESS. The decrease in profit is significantly lower compared to the scenarios with GINIs and the one only with CSs. This is due to the BESS being able to store energy during off-peak times and discharge it during peak times. This allows for higher charging power during peak times, while still not exceeding the grid limit. While the GINIs have the theoretical potential to store energy during off-peak times and discharge it during peak times, the results demonstrate that, in the given configuration, they are unable to fully exploit this potential. The causes of this include an operating strategy that is not optimal, a battery energy capacity that necessitates numerous recharging sessions during the day, and a comparably large parking area that causes long travelling durations. It is encouraging to note that the profit margin with GINIs remains stable despite the grid limit (compare Section 3.3 and Section 3.5).

In general, maintaining a low level of power consumption from the main grid is crucial for grid stability. This is particularly important in scenarios where grid expansion cannot keep up with the increasing number of EVs, as described by the European Network of Transmission System Operators for Electricity [59].

4.2. Model Limitations and Possible Extensions

With regard to the limitations of the simulation framework, several simplifying assumptions should be explicitly acknowledged. Most notably, the energy selling price is fixed at €0.50 per kWh across all scenarios, while the purchase price varies dynamically based on day-ahead electricity market data. This fixed pricing strategy does not account for time-of-use tariffs or user-specific pricing models, which could significantly affect revenue.

Additionally, the model does not incorporate the effects of temperature on battery performance and charging efficiency. These factors can significantly influence the operational performance of BESS, GINIs, and EVs. Particularly extreme temperatures can lead to lower charging power and increased auxiliary consumption for cooling or heating the battery system. The incorporation of a temperature-dependent behaviour into the battery model has the potential to enhance the relevance of the simulation model, particularly in regions and seasons characterised by extreme temperature conditions. Therefore, future work should consider integrating temperature effects into the simulation framework.

Furthermore, the simulation excludes capital expenditures and operational costs, such as investment, maintenance, and battery degradation. Hence, it only focuses on operational margins not a full techno-economic study.

In Section 2.1.3, we assume that all charging losses occur at the CS, abstracting from whether AC or DC charging is used. This simplification facilitates an efficient and generalizable energy flow model between CS and EV. However, it does not capture the nuanced loss mechanisms of different charging technologies. As part of future work, this assumption could be revisited through a sensitivity analysis using more detailed, mode-specific efficiency models. If significant sensitivity to charging mode or power level is observed, extending the current map-based model to include differentiated loss models may improve accuracy.

With regard to profit optimisation, especially regarding BESS and GINI scenarios, considering the dynamic price more explicitly or investigating electricity market products such as demand side management or frequency balancing is another field that could be explored based on the simulation framework.

4.3. Practical Implications

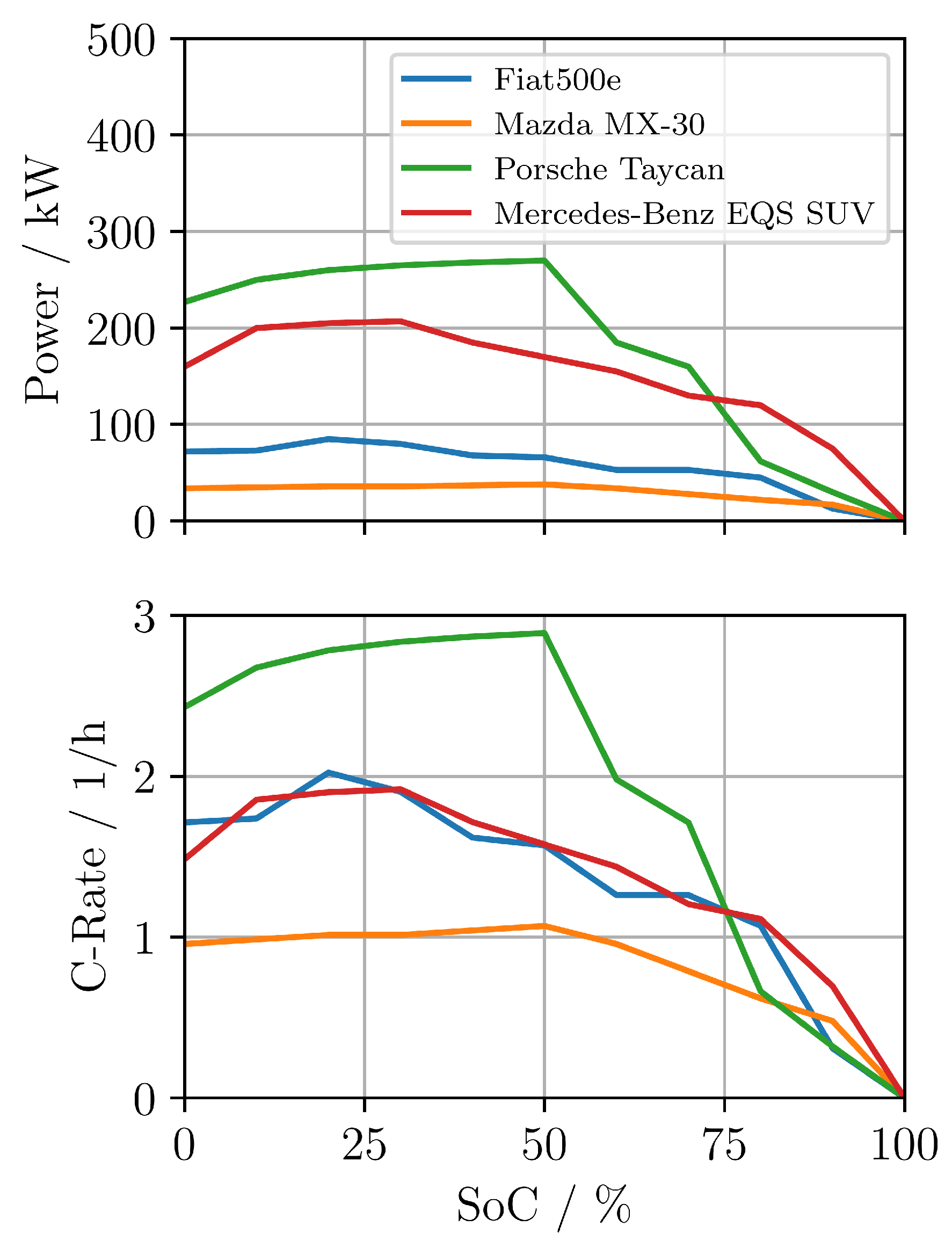
The analysis suggests that GINIs could become economically viable in situations where flexible charging is required but grid expansion is infeasible or prohibitively expensive. For instance, GINIs may provide value at locations with high EV turnover, spatially distributed charging needs, and limited grid access. However, profitability depends heavily on efficient routing and charging strategies. It has been shown that with the battery configuration used in the first prototypes (35 kWh and maximum of roughly 1.5 C), the operational margins fall behind other concepts.

Optimised battery sizing appears critical. Larger batteries may reduce the need for frequent recharging trips and allow faster recharging of GINIs themselves as well as EVs. In Germany, in public charging sessions, the average amount of energy charged can be estimated to around 20 kWh for AC charging and 40 kWh for DC charging [57]. Hence, integrating batteries with a capacity of 80 kWh or more could be beneficial and guarantee multiple charging sessions before the GINI needs to recharge. Furthermore, a larger battery would allow for higher charging power at the same C-rate. With high performance battery systems with adequate cooling, even higher C-rates could allow for even more profitable operation, but with increased capital cost.

4.4. Impact of Capital Costs

Although a techno-economic analysis is beyond the scope of this work, some qualitative conclusions can be drawn. As demonstrated in the report by Wessel et al. [3], the architecture of a mobile charging robot is intricate and sophisticated, necessitating substantial investment. High CAPEX associated with GINIs due to high performance battery systems and demanding robotic functions might offset operational profits unless high utilisation rates or additional revenue streams (e.g., grid services) are achieved. Further, sophisticated operating strategies and adequate battery sizing, as discussed in the previous section, are essential. In contrast, expansion of conventional charging infrastructure may require costly grid enhancements. Similarly, the installation of BESS necessitates a substantial initial investment. Depending on the circumstances, numerous fast chargers may be required to meet user expectations. The central question is whether the multiplicative capabilities of mobile charging robots (sequential EV charging and staggered recharging at shared stations) can economically justify their higher investment costs compared to a system based on BESS and multiple fast chargers.

In order to provide a rigorous response to this question, future research should incorporate techno-economic modelling approaches such as net present value (NPV), total cost of ownership (TCO) analysis, and scenario-based sensitivity studies. The utilisation of these tools would facilitate the quantification of trade-offs between capital investment, operational performance, and long-term cost efficiency, thereby supporting evidence-based investment decisions.

5. Conclusions

In this work, an open-source model for simulating charging points has been presented. The main components of the model were elaborated in detail. The model consists of the SimulationModules, the SimulationEnvironment and the ControllerAgent. The SimulationModules contain many modules which allow to set up different configurations of environments containing charging solutions. While the modules represent the physical and logical behaviourof relevant components, they are enriched by openly available data, or probability distributions derived from such data. The SimulationEnvironment composes these modules based on a configuration file and sets up the interface towards a controller. The ControllerAgent provides the blueprint for integrating control strategies for optimal charging behaviour. An exemplary control strategy has been implemented. While the model can be used to simulate traditional charging points with multiple CS, one main contribution is that it further allows for the simulation of concepts with mobile charging robots. In Section 3 the model has been used to compare different charging scenarios. The results show that for a setup with two fast chargers, the disadvantage of a power limit at grid connection can be compensated to some extend by integrating a BESS. While the scenarios with GINIs show lower peak loads and still some profits, these are significantly lower compared to the fast charging scenarios. This motivates future research where the framework can be used to investigate how higher energy capacities and higher charging powers of mobile charging robots impact these revenues. Further concepts such as battery swapping could be investigated, which could lead to fast “recharging” of the mobile charging robots.

Future work will focus on using the simulation environment to assess AI-supported charging management strategies. Specifically, two approaches will be compared. The first will be a reinforcement learning-based approach, which will address the challenge of learning effective policies despite the high observation and action spaces in this problem. To this end, hierarchical and multi-agent RL approaches will be investigated. The second area of focus will be on optimisation-based strategies, where the problem is formulated as a mixed-integer linear program. This approach will be supported by deep learning predictions, for example, with recurrent neural networks.