Investigation on Pressure Drop Characteristics During Refrigerants Condensation Inside Internally Threaded Tubes

Abstract

This study investigates the influence of geometric parameters of internally threaded tubes on heat transfer and resistance characteristics. Experimental analyses were conducted on pressure drop for 9.52 mm outer diameter tubes with various industry-standard geometric parameter combinations. Using R410A as the working fluid under turbulent flow conditions (Re = 20,000–60,000), experimental parameters included the following: mass velocity 50–600 kg/(m²·s), condensation temperature 45 ± 0.2 °C, and geometric ranges of thread height (e = 0.0001–0.0003 m), helix angle (α = 17–46°), crest angle (β = 16–53°), and number of ribs (Ns = 50–70). Results demonstrate that the newly developed correlation based on Webb and Ravigururajan friction factor models shows improved prediction accuracy for R410A condensation pressure drop in ribbed tubes. Model II achieved a mean absolute percentage error (MAPE) of 7.08%, with maximum and minimum errors of 27.66% and 0.76%, respectively. The standard deviation decreased from 0.0619 (Webb-based Model I) to 0.0362. Integration of SVR machine learning further enhanced tube selection efficiency through optimized correlation predictions.

1. Introduction

With the increasing severity of energy shortages and environmental issues, improving the heat transfer efficiency of heat exchange equipment has become a core demand for industrial energy conservation and consumption reduction. Heat transfer enhancement technology, which significantly increases the heat transfer capacity per unit volume by optimizing the geometric structure or flow characteristics of heat transfer surfaces, has been widely applied in refrigeration, chemical engineering, energy, and other fields. Researchers have emphasized the integrated application of active and passive enhancement techniques to optimize heat transfer performance [1]. Internally threaded copper tubes, for instance, have been extensively used in air conditioning and refrigeration systems due to their excellent heat transfer performance, making research on their enhancement mechanisms particularly significant. In 1966, Lawson and Webb first proposed the concept of heat transfer enhancement using threaded tubes, which quickly garnered global attention and spurred extensive research [2]. Champagne and Bergles [3] further categorized heat transfer enhancement into active and passive technologies, noting that threaded tubes exhibit high rationality through increased pressure drop and play a critical role in enhancing turbulent flow heat transfer. However, the improvement in heat transfer is often accompanied by increased flow resistance, resulting in elevated pressure drop and pump power loss. This inherent trade-off has become a critical bottleneck limiting technological development and widespread adoption. Consequently, achieving simultaneous minimization of pressure drop and enhancement of heat transfer efficiency in internally threaded tubes has emerged as a key research focus in current studies [4]. Wu et al. [5] suggested that incorporating turbulence-enhancing structures in internally threaded tubes, such as modifying the number of ribs, increasing thread height, and inserting turbulators could effectively intensify heat transfer. Nonetheless, a critical balance must be maintained between mitigating flow resistance and enhancing thermal performance.

Although enhanced heat transfer technologies such as internally threaded tubes can significantly improve heat exchange efficiency, their complex geometric structures exacerbate flow separation and turbulent fluctuations, making pressure drop characteristics challenging to predict [6]. Traditional empirical formulas, primarily developed for smooth tubes or simple rough surfaces, show limited applicability to the asymmetric helical grooves and multi-scale vortices in internally threaded tubes. Furthermore, the dispersion of resistance coefficients caused by experimental condition variations (e.g., Reynolds number, rib height, helix angle, and crest angle) and the inadequate accuracy of turbulence models in numerical simulations for capturing complex swirling flows both hinder the establishment of reliable resistance correlations. Achieving precise prediction of pressure drop characteristics in internally threaded tubes while balancing heat transfer enhancement and flow resistance requires a systematic analysis of how geometric parameters influence resistance mechanisms. Naphon et al. [7] conducted an in-depth investigation of heat transfer and flow characteristics in horizontally arranged double-pipe configurations with internally threaded tubes. Their research demonstrated that helical ribs significantly affect heat transfer and pressure drop, leading to the proposal of non-isothermal correlations for heat transfer and friction coefficients. Liu and Jensen [8] numerically studied the impact of geometric parameters on turbulent flow and heat transfer in ribbed tubes, finding that both the Nusselt number and friction factor increase with higher fin counts and helix angles. Increasing fin height enhances both parameters, while helix angles exceeding 20° cause substantial increases in heat transfer and pressure drop. Kim [9] analyzed that micro-fin and low-fin tubes share similar enhancement mechanisms, with low-fin tube performance mainly influenced by front-edge oscillation effects while rear-edge impacts are minimal. Circular teeth exhibit lower friction coefficients and Nusselt numbers compared to rectangular teeth, but higher tooth counts lead to increased friction in circular teeth configurations. These findings highlight the potential for geometric optimization to enhance heat transfer performance in turbulent flows while managing pressure drop impacts. Sethumadhavan and Rao [10] investigated the effect of thread pitch on friction and heat transfer coefficients, revealing that ribbed tubes achieve 15–100% higher heat transfer coefficients than smooth channels, with reduced pitch and increased thread count raising friction coefficients by 30–200%. Di Piazza and Ciofalo [11] numerically simulated turbulent flow and heat transfer in helical heat exchanger tubes, comparing k-ε and SST k-ω models. Their results showed that the SST k-ω model better matched experimental pressure drop data, whereas the k-ε model exhibited deviations in heat transfer predictions.

Current research on the flow resistance characteristics of internally threaded tubes primarily relies on experimental testing, numerical simulation, and data-driven modeling. Experimental methods obtain pressure drop data through parametric analysis [12], but suffer from high costs and limited coverage of full operating conditions. Numerical simulations (e.g., CFD) can resolve local flow field details but exhibit strong dependence on grid quality and turbulence models [13]. While machine learning-based black-box models [14] can fit complex nonlinear relationships, they lack physical interpretability. Therefore, there is an urgent need to establish a resistance correlation formula integrating geometric parameters and flow conditions by combining experimental data with theoretical analysis. Constructing a high-precision resistance prediction model for key geometric parameters (including thread height, helix angle, crest angle, and number of ribs) will not only provide theoretical support for heat exchanger design but also guide heat transfer–flow synergy optimization through quantitative pressure drop analysis, thereby promoting engineering applications of enhanced heat transfer technology. For internally threaded copper tubes specifically, research on resistance characteristics mainly employs two approaches: experimental studies and numerical simulations. Experimental investigations measure pressure drop and flow rate under various operating conditions through dedicated test platforms to calculate flow resistance coefficients. Numerical simulations utilize CFD software to establish three-dimensional models of ribbed copper tubes and simulate fluid flow processes to obtain resistance characteristic data. Based on experimental and simulation results, researchers have proposed multiple resistance correlation formulas for threaded copper tubes, which can be broadly classified into two categories:

The first category is empirical correlations, which are derived from experimental data fitting. Common forms include power functions and logarithmic expressions. For instance, Webb [15] investigated heat transfer and friction in single-phase flow within 15.54 mm ID internally threaded tubes, extending linear multivariate regression to predict heat transfer coefficients and friction factors as functions of enhanced dimensions. Ravigururajan and Bergles [16] developed generalized correlations for friction and heat transfer coefficients in single-phase turbulent flow through enhanced tubes, validated through linear modeling to establish normalized correlations with roughness corrections. Results showed applicability across broad roughness types and Prandtl numbers. However, such empirical correlations face limitations: narrow applicability (dependent on specific experimental conditions, incompatible with novel thread structures or diverse fluids), lack of physical mechanisms (purely data-driven without explaining flow resistance fundamentals), high data dependency (accuracy constrained by experimental data quality and quantity), and poor universality (non-uniform formula formats hinder cross-scale applications). Improvements may involve integrating theoretical models, machine learning, or segmented fitting to enhance prediction accuracy and generalizability. While valuable for preliminary engineering design, these correlations require more precise models for complex operating conditions. The second category comprises semi-empirical and semi-theoretical correlations combining theoretical analysis with experimental data while considering multiple influencing factors. Notable examples include Cavallini et al.’s correlation [17] and the widely adopted Gnielinski equation [18], recognized as an accurate formula for predicting average turbulent convective heat transfer in smooth pipes and channels [19]. Derived from high Reynolds and Prandtl number experiments, Gnielinski’s equation predicts heat/mass transfer coefficients within ±20% deviation. Ji [20] modified it by replacing the friction factor in the numerator with experimentally measured values for fully developed flow regions, achieving ±10% deviation in threaded tube heat transfer predictions. De Chazal [21] established semi-empirical correlations through in-depth analysis of turbulent heat transfer and resistance coefficient relationships. Petukhov [22] developed temperature coefficient correction expressions validated by gas heat transfer experiments and simplified turbulent heat transfer governing equations. Nakayama [23,24] systematically investigated fully developed flow heat transfer and resistance characteristics in ribbed tubes, formulating high-Reynolds-number correlations through model simplification. Lee S.C. [25] studied single-phase heat transfer and pressure loss in horizontal serrated rib tubes, finding eightfold heat transfer enhancement over smooth tubes at identical Reynolds numbers, with derived formulas for laminar/turbulent flow coefficients. Harleβ [26] established experimental Nu and resistance coefficient correlations for 18 single/triple-start ribbed tubes with varying geometric parameters (pitch: 0.00027~0.00153 m, thread height: 0.0002~0.00056 m, helix angle: 9.2°~37.0°), providing design references. Nevertheless, current models inadequately explain the coupling mechanisms between complex geometric parameters (thread height, helix angle, crest angle, number of ribs) and pressure drop characteristics in internally threaded tubes. Most existing correlations oversimplify geometric variables or operating conditions, failing to reveal resistance evolution under multi-parameter synergy, thus the theoretical support for heat-flow collaborative optimization in engineering design is insufficient.

Based on the aforementioned context, this study focuses on the pressure drop characteristics of internally threaded copper tubes. Through systematic experimentation and theoretical modeling, we investigate the variation patterns of resistance coefficients with geometric parameters and flow conditions, ultimately developing a physically meaningful resistance correlation formula to provide practical insights for designing and optimizing high-efficiency, low-resistance heat exchangers. The research initially examines the resistance generation mechanism resulting from the coupling between geometric features of internally threaded tubes and turbulent flow. By employing parametric experimentation combined with Support Vector Regression (SVR) model assistance, we systematically analyze the influence of key geometric parameters on pressure drop in internally threaded tubes. Subsequently, through designed condensation experiments for internally threaded tubes, we establish a staged resistance prediction framework based on existing empirical correlations, culminating in a novel resistance correlation formula that incorporates geometric parameter expressions.

This work aims to overcome the limitations of traditional correlation formulas in adapting to complex geometries, offering a theoretical tool with both physical interpretability and engineering applicability for low-resistance, high-efficiency design of internally threaded tube heat exchangers. The outcomes are expected to enhance the prediction accuracy of resistance coefficients and improve selection efficiency for internally threaded tubes.

2. Methods

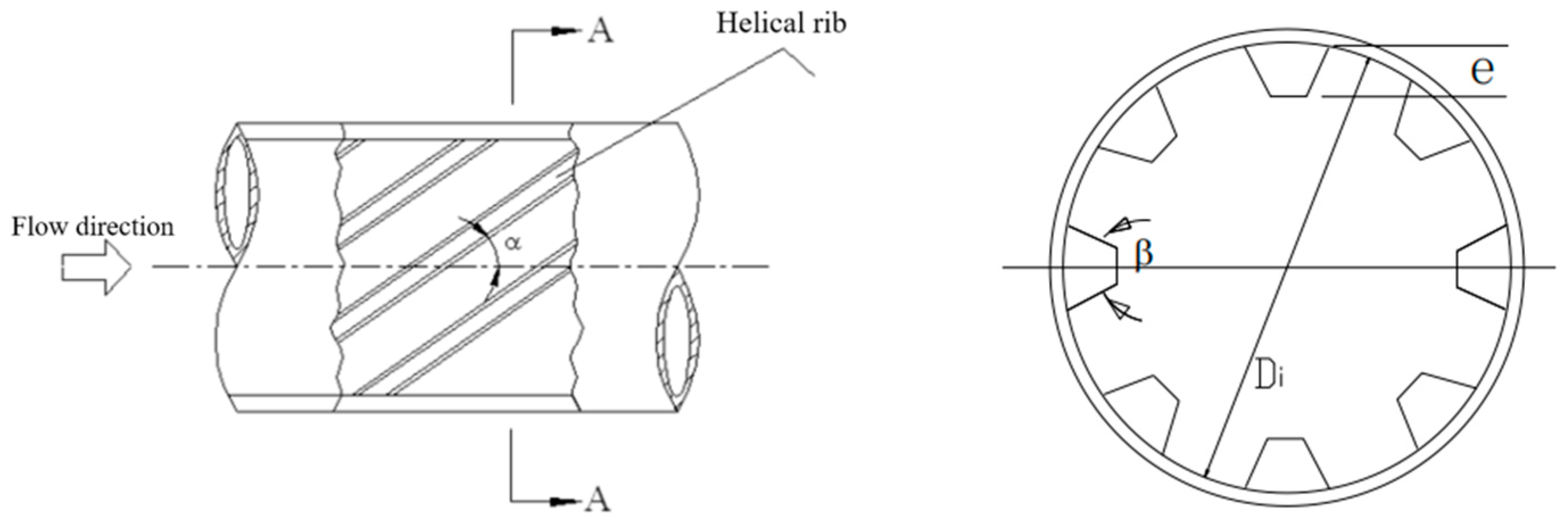
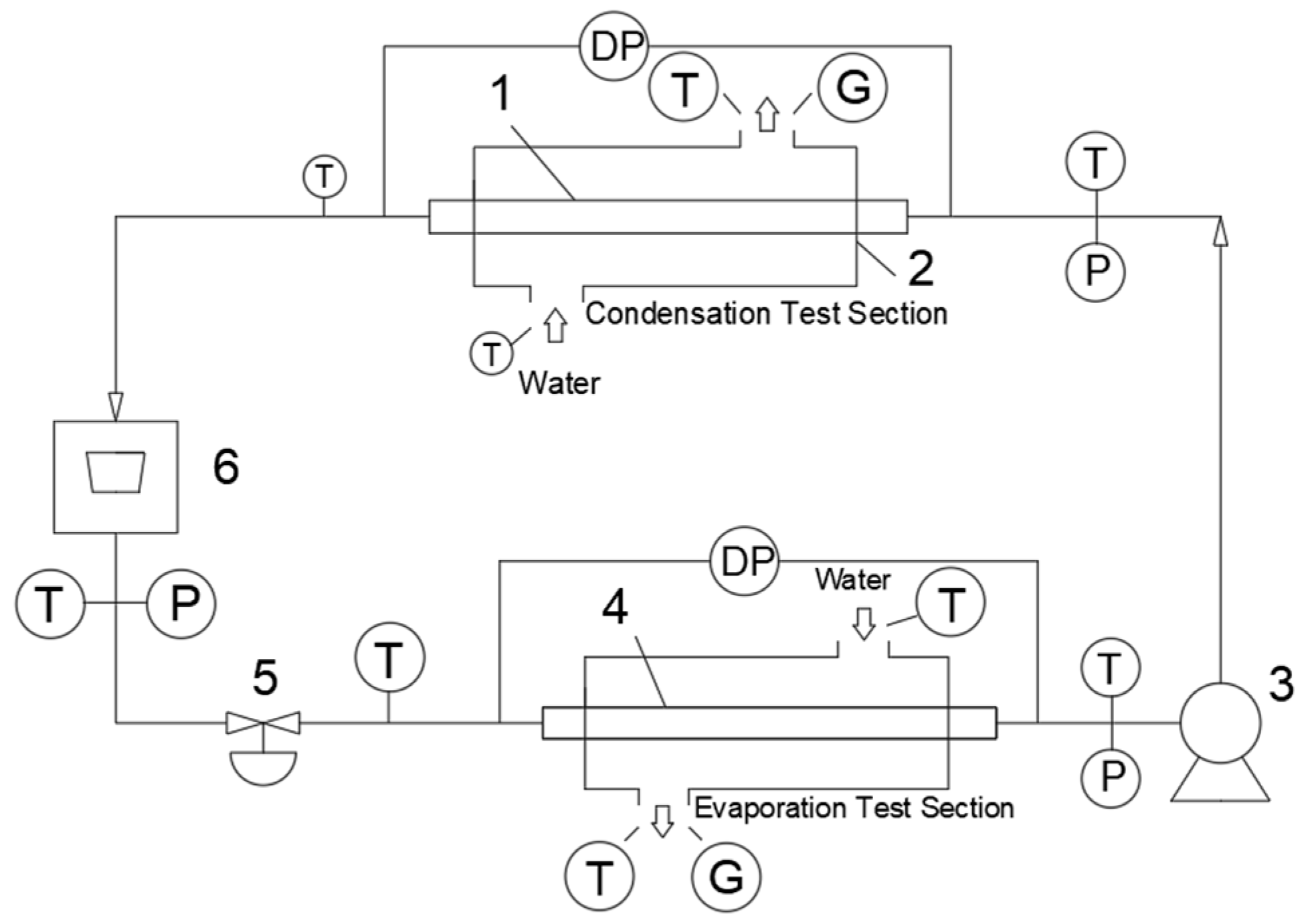
2.1. Experimental Setup for Internally Threaded Tubes

The present study focuses on the trapezoidal ribbed internally threaded tube, with schematic, physical, and microscopic cross-sectional views of the tooth structure illustrated in Figure 1 and Figure 2. The key geometric parameters of the investigated internally threaded tube are defined as follows: e represents the actual height of the helical ribs, α indicates the helix angle between the rib orientation and horizontal plane, Ns specifies the total number of uniformly distributed internal ribs along the circumferential direction, and β designates the included angle between the two flank surfaces at the rib crest.

The present experiment was conducted at Xinxiang Longxiang Precision Copper Tube Co., Ltd., located in Xinxiang City, Henan Province, China. Photographs of the experimental setup and a schematic diagram of the testing apparatus are presented in Figure 3. The single-tube test rig for internally threaded tubes primarily consists of a vapor compression refrigeration system and a double-pipe heat exchanger. The vapor compression refrigeration section comprises four key components: a compressor, condenser, expansion valve, and evaporator, which are interconnected via piping to form a hermetically sealed system. Both the evaporator and condenser employ double-pipe heat exchanger configurations. In this arrangement, the inner tube serves as the test specimen where refrigerant undergoes a phase change (evaporation or condensation), while the annulus between the inner and outer tubes contains water as the secondary medium flowing counter-currently.

Experimental parameters including flow rate, temperature, and pressure at both water-side and refrigerant-side inlets/outlets are systematically measured. Subsequent data processing enables the determination of the heat transfer capacity and flow resistance loss of the test specimen.

The experimental procedure follows these steps:

• Install the test specimen with pressure transducers mounted at both ends to measure pressure differentials.
• Regulate compressor frequency through a variable-frequency drive and adjust refrigerant flow rate using an electronic expansion valve, while monitoring flow parameters with high-precision flow meters to ensure system stability.
• Establish predetermined test conditions through the aforementioned control mechanisms. Maintain steady-state operation for sufficient duration before recording measurements. Collect at least five data points per test group and compute arithmetic means.
• Modify operational parameters (flow rates or temperatures) to conduct repetitive experiments across the target research range.
• Terminate testing by deactivating heating elements and water pumps, discontinue data acquisition, and evacuate residual refrigerant from the system.

The schematic diagram of the experimental system is presented in Figure 4.

2.2. Experimental Measurement Device

To ensure the accuracy and reliability of experimental data, all instrumentation employed in the inner-threaded tube performance testing system must comply with stringent performance specifications and technical standards. The measurement precision and operational stability of core components—including high-precision sensors, constant-voltage power supply units, and temperature control systems—critically determine the scientific validity of experimental outcomes. Equipment selection shall conform to relevant national or industry standards, with mandatory pre-use calibration and debugging procedures. The primary measurement devices encompass temperature, pressure differential, and flow rate instrumentation.

2.2.1. Thermometric Instruments

The temperature measurement instrument employed in the experiments was a PT100 sensor. Its operational principle relies on the thermal resistance thermometry mechanism, which measures fluid temperature by utilizing the temperature-dependent resistance characteristics of platinum (Pt). The PT100 platinum resistance sensor adopted in this experimental system features a four-wire configuration. Compared to two-wire and three-wire setups, the four-wire configuration demonstrates superior measurement accuracy and stability. In this design, two wires deliver excitation current, while the remaining two measure voltage signals. Such a configuration effectively eliminates lead resistance interference, thereby enhancing measurement accuracy.

The experimental system incorporates eight strategically distributed temperature monitoring positions, specifically configured as follows: refrigerant inlet and outlet temperature measurement points in the preheating unit (with the outlet temperature corresponding to the test section’s inlet temperature), circulating water supply and return temperature monitoring points in the preheating section, circulating water inlet/outlet temperature measurement points in the test section, refrigerant outlet temperature measurement point in the test section, and liquid storage device inlet temperature measurement point. This rational distribution ensures comprehensive acquisition of critical thermodynamic parameters during experimentation, providing a reliable foundation for subsequent data analysis.

2.2.2. Pressure and Differential Pressure Measuring Instrument

The experimental pressure and differential pressure measurements were conducted using absolute pressure transmitters and differential pressure transmitters. Absolute pressure transmitters were installed at the inlet and outlet of the inner-threaded tube to measure absolute pressures, while the differential pressure transmitter, which incorporates dual pressure sensors connected to two measurement points, calculates pressure drops by determining the difference between paired pressure values. This configuration is particularly suited to monitoring pressure gradients across pipeline segments or localized regions. The pressure measurement system employs a two-wire configuration, where sensors output standardized 4–20 mA current signals. These signals are transmitted to a computer via data acquisition devices for processing, enabling precise computation of measurements from both absolute and differential pressure transmitters. Four pressure monitoring points were strategically positioned along the internal pipeline: upstream of the liquid storage device, at the test section inlet, test section outlet, and preheating section inlet. The differential pressure transmitter was connected across the test section inlet and outlet to monitor real-time pressure loss during fluid flow through the heat exchange tube. This instrumentation layout ensures comprehensive characterization of pressure distribution patterns at critical locations, providing robust data support for hydrodynamic analysis.

2.2.3. Flow Measurement Instrument

In the performance testing experiments of inner-threaded tubes, flow rate measurement serve as one of the critical parameters for evaluating heat transfer efficiency and hydrodynamic characteristics. Accurate quantification of flow parameters is essential for obtaining reliable experimental data. Given the involvement of two working media in the system—circulating water in the preheating section and refrigerant—distinct measurement methodologies were implemented. For the circulating water system, volumetric flow meters were employed to directly measure flow rates, as liquid water density exhibits minimal pressure dependence. Common volumetric flow metering devices include positive displacement meters, turbine flow meters, rotameters, and electromagnetic flow meters. The experimental system adopted an electromagnetic flow meter, operating on Faraday’s law of electromagnetic induction. Its operational principle relies on generating an induced electromotive force within conductive fluids subjected to a magnetic field, enabling precise calculation of flow velocity and volumetric rate through voltage measurement. Characterized by obstruction-free flow channels, this design eliminates pressure loss while maintaining measurement accuracy unaffected by fluid property variations, thereby ensuring high-precision quantification. The electromagnetic flow meter’s bidirectional detection capability, facilitating accurate measurements in both forward and reverse flow directions, rendered it an optimal selection for the experimental configuration. Owing to its superior metrological performance and multidirectional adaptability, this instrument was designated as the primary flow measurement device in the study.

Given the insufficient electrical conductivity of the refrigerant, which renders it unsuitable for electromagnetic flow metering, alternative measurement methodologies were required. Due to the refrigerant’s heightened sensitivity of thermophysical properties (e.g., density) to temperature and pressure variations under operational conditions, a mass flow meter was adopted to directly quantify refrigerant mass flow rates. This approach circumvents measurement inaccuracies arising from thermophysical property fluctuations, thereby ensuring experimental data reliability. A Coriolis flow meter was selected as the primary instrumentation for refrigerant mass flow measurement. Its operational principle exploits the Coriolis effect: when fluid flows through a vibrating tube, the resultant Coriolis force induces phase displacement between inlet and outlet vibration signals. By monitoring this subtle deformation via electromagnetic sensors, the meter calculates mass flow rates with exceptional precision.

2.2.4. Error Analysis

Error analysis constitutes a systematic study of potential errors or uncertainties in measurement processes. The objectives of this analytical section are threefold: (1) to investigate the sources of measurement deviations, (2) to optimize experimental conditions for improved result accuracy, and (3) to provide comprehensive uncertainty quantification. Given that the drag coefficient in this experimental study is derived through indirect calculations involving multiple measured parameters (temperature, pressure, and flow rate), inherent uncertainties persist due to compounded measurement errors.

The direct error of a directly measured quantity is defined as follows:

$$\epsilon ={\displaystyle \frac{∆x}{x_0}}$$

(1)

According to the error propagation theorem, if an indirect measurement y is defined by a deterministic functional relationship with n mutually independent directly measured quantities, the following is true:

$$y=f(x_1,x_2,\dots x_n)$$

(2)

According to the relative error propagation formula, the equation for relative uncertainty is expressed as follows:

$${\epsilon }_y=\sqrt{{{\displaystyle \sum _{i=1}^m\left(\frac{\partial y}{\partial x_i}\right)}}^2{\epsilon }_{xi}^2}$$

(3)

The measuring instruments and their accuracy comply with the regulations as shown in

Table 1. Measurement instruments and accuracy grades.

Measuring Instrument	Accuracy Level	Instrument Range
Thermometer	±0.10 °C	−20–150 °C
Volume flowmeter	±0.20%	0–10 L/min
Mass flowmeter	±0.5%	0–100 kg/h
Absolute pressure transmitter	±0.04%	0–4 MPa
Pressure differential transmitter	±0.065%	0–100 kPa

:

(1)

Analysis of temperature error

The measurement error of temperature is determined by the PT100 thermistor, which employs a four-wire configuration and meets the AA accuracy class specification. The temperature measurement uncertainty is maintained within ±0.1 °C. Under the design operating conditions specified in this study, with the minimum measurement temperature setpoint at 30 °C, the calculated maximum relative error of temperature is as follows:

$${\displaystyle \frac{\delta T}{T}}={\displaystyle \frac{0.1}{30}}\times 100\%=0.33\%$$

(4)

(2)

Analysis of pressure errors

The pressure sensor implemented in the experimental system features a measurement range of 0–4 MPa with an accuracy of ±0.04% of full scale (FS). By substituting the saturated vapor pressure (2.4 MPa) at a condensation temperature of 40 °C into the computational analysis, the maximum relative error of pressure is determined as follows:

$${\displaystyle \frac{\delta P}{P}}={\displaystyle \frac{4\times 0.04\%}{2.4}}=0.067\%$$

(5)

(3)

Analysis of flow error

The refrigerant (R410A) and water flow measurements in the experimental system employ different flowmeters: a Coriolis mass flowmeter with ±0.50% accuracy (measuring mass flow rate in kg/h) is implemented for R410A, while an electromagnetic flowmeter demonstrating ±0.20% FS error tolerance (providing volumetric flow rate in L/min) is utilized for water. Given the Coriolis flowmeter’s operational range of 0–100 kg/h and the minimum recorded mass flow rate of 11.9 kg/h during testing, the maximum relative error for refrigerant flow measurement is calculated as follows:

$${\displaystyle \frac{\delta m}{m}}={\displaystyle \frac{100\times 0.5\%}{11.9}}=4.2\%$$

(6)

The electromagnetic flowmeter operates with a measurement range of 10 L/min. During the preheating phase of the experiment, the minimum recorded water flow rate is 3 L/min. Consequently, the maximum relative error for water flow measurement during the preheating phase is calculated as follows:

$${\displaystyle \frac{\delta m}{m}}={\displaystyle \frac{10\times 0.2\%}{3}}=0.67\%$$

(7)

The minimum recorded water flow rate in the test section is 5 L/min. The maximum relative error for water flow measurement in the test section is therefore determined as follows:

$${\displaystyle \frac{\delta m}{m}}={\displaystyle \frac{10\times 0.2\%}{5}}=0.40\%$$

(8)

(4)

Error analysis of the friction factor

As indicated by Equation (10), the drag coefficient is an indirectly measured quantity. Since the maximum relative error of the flow velocity u is identical to that of the refrigerant flow rate measurement, the maximum relative error of the drag coefficient can be derived as follows:

$${\displaystyle \frac{\delta f}{f}}=2∆u=2\times 4.2\%=8.4\%$$

(9)

2.3. Main Experimental Parameters

The test tubes used in the experiment were internally threaded tubes with an outer diameter of 9.52 mm. The refrigerant was R410A. The geometric parameters of the tested tubes were within the following ranges: e = 0.0001~0.0003 m, α = 17~46°, β = 16~53°, and Ns = 50~70, all of which are typical for industrially manufactured ribbed tubes. The operating conditions for the condensation experiments are listed in

Table 2. Condensation test conditions.

Parameter	Experimental Condition
Saturation temperature at inlet pressure	45 °C
Inlet superheat	20 K
Outlet subcooling	5 K
The pressure difference across the test section	0~100 kPa
Refrigerant mass velocity	50~600 kg/(m2·s)

.

2.4. Data Processing

This study employs refrigerant R410A as the working fluid to conduct condensation experiments on internally threaded tubes with varying geometric configurations. The primary structural parameters investigated include the following: fin height (e) = 0.00013–0.0002 m, helix angle (α) = 15–30°, crest angle (β) = 25–53°, and number of ribs (Ns) = 50–70. To investigate the flow resistance characteristics of internally threaded tubes under turbulent flow conditions, particular attention is given to pressure drop and friction factor analysis.

The data processing primarily focuses on two key parameters: friction factor and area enhancement ratio. The Darcy friction factor adopted in this study quantifies the energy loss caused by viscous effects during fluid flow through pipes. Based on fluid mechanics principles, the friction factor for viscous fluid flow in channels is defined through the pressure gradient using the Darcy–Weisbach equation.

$$f={\displaystyle \frac{-\left(\mathrm{dp}/\mathrm{dx}\right)D\mathrm{e}}{\rho {\mathrm{u}}^2/2}}$$

(10)

In the equation, dp/dx represents the pressure drop per unit pipe length (Pa/m), De denotes the outer diameter (in meters), ρ stands for the density (kg/m³), and u indicates the flow velocity (m/s).

The area enhancement ratio [27] is defined as the ratio of the actual heat transfer surface area inside the tube to the circular area calculated based on the root diameter. As a comprehensive parameter integrating internal thread structural characteristics, it serves to evaluate the heat transfer performance of internally threaded tubes. This study employs this parameter to indirectly characterize the influence of resistance characteristics, which can be mathematically expressed as follows:

$$A_{\mathrm{ai}}/A_{fr}=1+2e\left[\sec \left(\alpha /2\right)-\tan \left(\alpha /2\right)\right]/p_f$$

(11)

In the formula, A_ai denotes the actual heat transfer area inside the tube (m²); A_fr represents the area based on the root inner diameter of the fin (m²); p_f indicates the fin pitch perpendicular to the fin direction (m).

3. Experimental Results and Analysis

3.1. Resistance Characteristics of Internally Threaded Tubes

3.1.1. Pressure Drop Comparison Between R22 and R410A

The condensation pressure drop performances of R22 and R410A in a 9.52 mm-diameter test tube are shown in Figure 5. The thermophysical properties of R22 and R410A are listed in

Table 3. Thermophysical properties of R22 and R410A.

	Temperature (°C)	Liquid Density (kg/m3)	Vapor Density (kg/m3)	Liquid Dynamic Viscosity (Pa·s)	Vapor Dynamic Viscosity (Pa·s)
R22	45	1106.0	75.7	0.000149	0.0000137
R410A	45	942.9	120.4	0.0000888	0.0000154

.

Table 4. Specific parameters of internal threaded tubes.

Number	Root Wall Thickness (m)	Thread Height (m)	Crest Angle	Helix Angle	Number of Ribs
1#	0.0003	0.0002	53	18	60
2#	0.0003	0.00017	25	18	70
3#	0.0003	0.0002	30	18	50

presents the geometric parameters of internally threaded tubes required for pressure drop comparison. Analysis reveals that among the three selected internally threaded tubes, R22 consistently exhibited higher pressure drops than R410A. As indicated in Table 3, while the physical properties of R22 and R410A are similar, R22 demonstrates a greater density difference between gas and liquid phases. According to Equation (12), this leads to a correspondingly higher slip ratio, resulting in more significant velocity differences between the gas and liquid phases. Equation (13) shows that R22 generates greater axial shear forces, and Equation (14) reveals intensified interfacial friction between phases. These combined effects enhance fluid disturbance and increase energy dissipation. Furthermore, under identical temperatures, R22 exhibits higher liquid-phase viscosity than R410A while maintaining comparable gas-phase viscosity. This viscosity characteristic not only amplifies the frictional resistance between the fluid and tube wall but also intensifies interphase friction between gas and liquid flows, ultimately contributing to greater pressure loss. Consequently, R410A demonstrates lower pressure drops compared to R22 under equivalent operating conditions.

The partial geometric parameter specifications of the internal threaded tubes involved in the following content are as follows:

The velocity difference between gas and liquid phases can be characterized by the slip ratio, which is defined as the ratio of gas phase velocity to liquid phase velocity:

$$S={\displaystyle \frac{u_g}{u_l}}$$

(12)

This interphase velocity difference induces shear stress at the phase interface. The interfacial shear stress can be described using Newton’s law of internal friction:

$$\tau =\mu {\displaystyle \frac{du}{dy}}$$

(13)

The interfacial friction is typically quantified through a dimensionless friction factor f. The relationship between the friction factor and shear stress is expressed as follows:

$$\tau =f\times {\displaystyle \frac{1}{2}}\rho u^2$$

(14)

In the formula, $u_g$ denotes the gas-phase velocity; $u_l$ represents the liquid-phase velocity; τ is the shear stress; μ indicates the dynamic viscosity; du/dy stands for the velocity gradient.

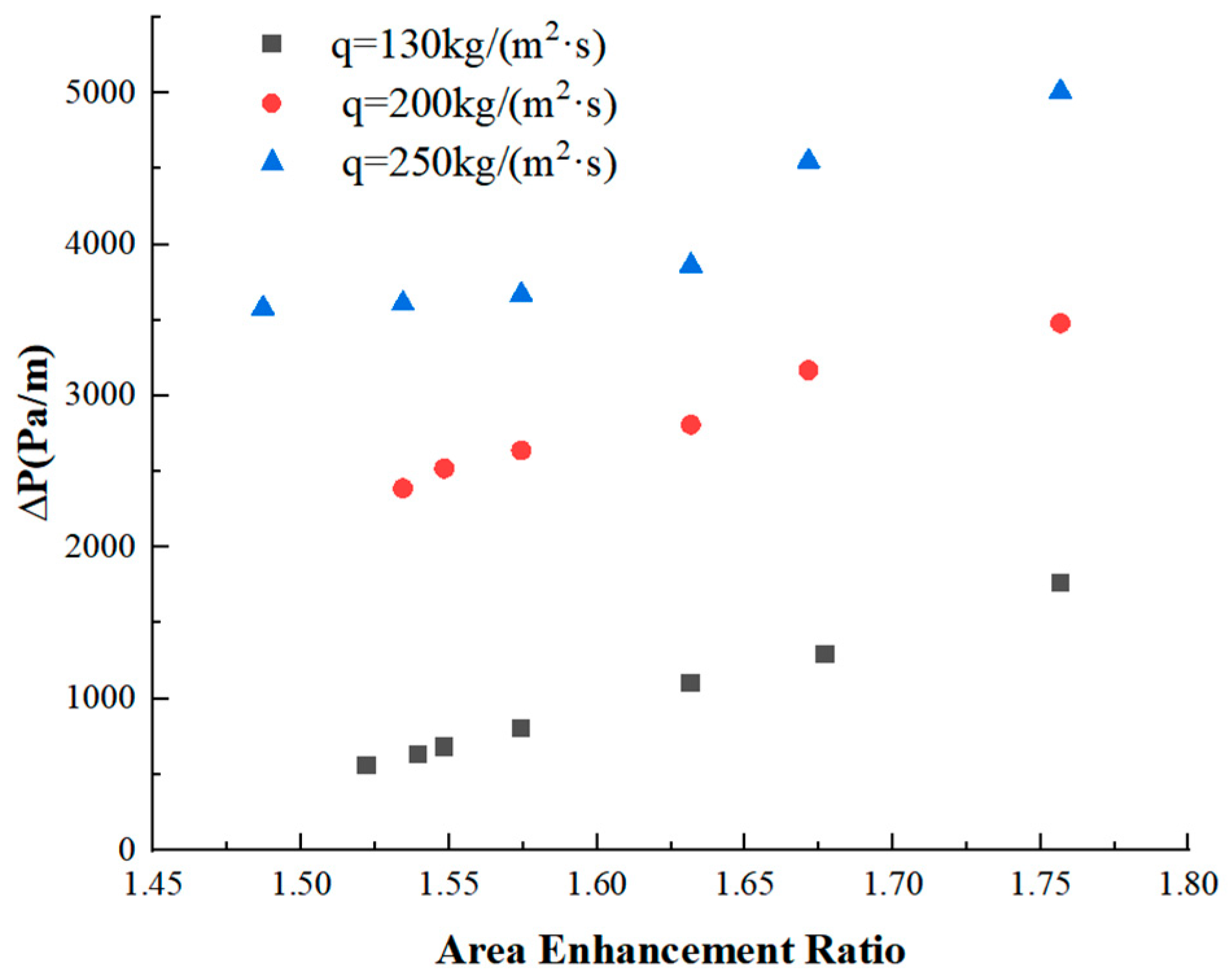
3.1.2. Relationship Between Area Enhancement Ratio and Pressure Drop

To investigate the combined effects of the area enhancement ratio and mass velocity on the pressure drop of internally threaded tubes and reveal their flow resistance characteristics, this study selected tubes with area enhancement ratios ranging from 1.48 to 1.76, which are commonly used in industrial applications. The refrigerant R410A was tested at mass velocities of 130, 200, and 250 kg/(m²·s). As shown in Figure 6, the pressure drop of the internally threaded tube increases with a higher area enhancement ratio, and significant variations in pressure drop are observed under different mass velocities. This phenomenon can be attributed to the geometric parameters of the tube (e.g., fin height, helix angle, crest angle, and number of ribs), which determine the area enhancement ratio. Tubes with a higher area enhancement ratio exhibit stronger flow resistance, particularly at elevated mass velocities. The intensified disturbance within the tube enhances turbulence, amplifies interfacial friction between phases, and increases wall-fluid friction, thereby leading to greater frictional losses.

The linear fitting of experimental data points using a straight-line equation reveals the following characteristics: At relatively low mass velocity conditions (below 200 kg/(m²·s)), the experimental results demonstrate a linear relationship between area enhancement ratio and pressure drop. However, when mass velocity increases from 130 kg/(m²·s) to 200 kg/(m²·s), the slope of the fitted curve decreases from 5097 to 4850. This phenomenon may be attributed to the turbulence enhancement induced by increased flow velocity remaining insufficient to match the accelerated growth rate of pressure drop, resulting in a decelerating pressure drop increment with increasing mass velocity under constant area enhancement ratio conditions.

When mass velocity further increases beyond this range, the relationship between area enhancement ratio and pressure drop exhibits significant nonlinear fluctuations that deviate from linear fitting suitability. Potential mechanisms include the following: The area enhancement ratio improves heat transfer efficiency through increased internal surface area while simultaneously generating additional flow resistance. Under high mass velocity conditions, the turbulence intensity undergoes nonlinear variations, leading to unstable growth rates of pressure drop. Particularly, larger area enhancement ratios intensify the nonlinear effects of turbulence, resulting in more pronounced pressure drop fluctuations [27]. These complex interactions warrant further systematic investigation.

3.2. Study on Resistance Coefficient Correlations

3.2.1. Resistance Coefficient Model

Existing research methodologies for resistance coefficient correlations demonstrate significant diversity. In engineering practice, conventional approaches involve manufacturing internally threaded tubes with various parameter combinations followed by empirical calculations to obtain corresponding resistance coefficients. While this method yields intuitive numerical results, it requires substantial time and effort for repeated debugging and validation processes to evaluate performance. Ultimately, such approaches may fail to produce tubes meeting practical requirements due to cost and efficiency constraints. It is imperative to establish resistance coefficient correlations corresponding to different geometric parameter combinations of internally threaded tubes, enabling pre-production assessment of whether prospective tubes will satisfy specified requirements. Currently, the most widely adopted formulas are the Webb resistance coefficient formula [15] and the Ravigururajan resistance coefficient formula [16], The working conditions of the two models and this experiment are shown in

Table 5. Operating conditions of the two models and experimental setup.

Model	Operating Parameters
Webb model	Re = 20,000~80,000	0.024 ≤ e/De ≤ 0.041
	25° ≤ α ≤ 45°	10 ≤ Ns ≤ 45
Ravigururajan model	Re = 5000~250,000	0.01 ≤ e/De ≤ 0.2
	27° ≤ α ≤ 90°	0.1 ≤ p/d ≤ 7.0
Current experimental conditions	Re = 20,000~60,000	e = 0.13~0.20 mm
	α = 15~30°, β = 25~53°	Ns = 50~70

.

The Webb resistance coefficient formula is expressed as follows:

$$f=0.108\times R{e}^{-0.283}\times N{s}^{0.221}\times {({\displaystyle \frac{e}{D_{\mathrm{i}}}})}^{0.785}\times {\alpha }^{0.78}$$

(15)

The Ravigururajan resistance coefficient formula is expressed as follows:

$$\begin{gathered} f_s={\left(1.58\ln Re-3.28\right)}^{-2} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{f}_a/f_s=1+29.1R{e}^{(0.67-0.006p/d-0.49\alpha /90)} \\ \hspace{1em}\hspace{1em}\times {\left(e/d\right)}^{1.37-0.157p/d} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\times {\left(p/d\right)}^{-1.66\times {10}^{-6}R\mathrm{e}-0.33\alpha /90} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\times {\left(\alpha /90\right)}^{4.59+4.11\times {10}^{-6}R\mathrm{e}-0.15p/d} \end{gathered}$$

(16)

In the equation, f_s represents the resistance coefficient of the smooth tube; f_a denotes the resistance coefficient of the enhanced tube; and p stands for the pitch of thread (m).

The Ravigururajan model, as a widely applicable resistance coefficient model, exhibits relatively larger errors yet maintains stability, making it suitable for qualitative research. While the Webb model can accurately reflect the variation trends of resistance coefficients with changes in Reynolds number, rib count, rib height, and helix angle, its narrow applicable range and the critical research parameter of crest angle necessitate further model modification. This requires establishing experimental correlations with broader parameter ranges to enhance verification accuracy.

Regarding the flow states and operational condition applicability of both models, both correlation formulas can serve as a reference for resistance coefficient prediction in this experiment. It should be particularly noted that both Webb and Ravigururajan models were developed based on water as the working fluid, whereas this study focuses on refrigerant R410A. Given the significant differences in thermophysical properties between refrigerants and water, the original formulas cannot be directly applied to R410A. Therefore, this study modifies the original formulas specifically for refrigerant flow characteristics to better adapt them for calculating flow resistance in refrigerant-carrying tubes.

3.2.2. Optimization Based on Webb Model

The Webb model was optimized by incorporating the discriminability parameter of crest angle β. Through nonlinear least squares problem solving using MATLAB 2022a experimental data, this modified approach was established as Model I.

$$f=C_{0}R{e}^{C_1}N{s}^{C_2}{({\displaystyle \frac{e}{d}})}^{C_3}{\alpha }^{C_4}{\beta }^{C_5}$$

(17)

The fitted resistance correlation is expressed as follows:

$$f=0.703\times R{e}^{-0.2445}\times N{s}^{0.2235}\times {({\displaystyle \frac{e}{d}})}^{0.1731}\times {\alpha }^{0.3545}\times {\beta }^{0.2277}$$

(18)

Figure 7 presents the comparison between experimental values and predicted values of resistance coefficients for R410A condensation in tubes using Model I, based on 69 experimental samples. The test conditions included a saturated inlet temperature of 45 °C and a subcooling degree of 5 °C in the condensation section. Results demonstrate that the relative errors between predicted values from Model I (established based on the Webb model) and experimental measurements are primarily within 30%. The mean absolute percentage error (MAPE) reaches 8.21%, with maximum and minimum prediction errors of 31.08% and 0.62%, respectively. These findings indicate that the proposed model can essentially predict resistance coefficients in internally threaded tubes under these operating conditions. Explanation: The points on the red solid line represent that the experimental values are close to the predicted values. The two black dashed lines indicate that the error values range from −30% to 30%.

While the Webb-based model exhibits structural simplicity and facilitates modification of exponential terms corresponding to geometric parameters, its limitations lie in its oversimplified attribution of friction factor variations to individual geometric parameters of internally threaded tubes with fixed influence coefficients. In reality, the actual interaction mechanisms differ significantly.

3.2.3. Parameter-Coupled Model Integrating Ravigururajan Approach

Specifically, the impact of exponential terms containing structural parameters on the friction factor varies across different internally threaded tube configurations. Consequently, Model I demonstrates restricted applicability and lacks predictive capability for friction characteristics under complex coupling effects of structural parameters. To address these limitations inherent in Model I, we propose Model II by incorporating Ravigururajan’s methodology that introduces parameter coupling through exponential term interactions. This enhanced model achieves deeper interdependency among structural parameters by embedding them into exponential terms rather than maintaining constant coefficients, thereby better representing their mutual influences. The mathematical formulation of Model II is expressed as follows:

$$f=CR{e}^{g(N\mathrm{s},e,\alpha ,\beta )}N{s}^{g(R\mathrm{e},e,\alpha ,\beta )}{({\displaystyle \frac{e}{d}})}^{g(Re,Ns,\alpha ,\beta )}{\alpha }^{g(Re,Ns,e,\beta )}{\beta }^{g(Re,Ns,e,\alpha )}$$

(19)

The original resistance correlation equation failed to converge through direct least squares optimization in MATLAB due to the involvement of over twenty optimization parameters. To address this computational challenge, the model was refined through stepwise modifications of exponential terms based on Model I. Sequential optimizations were implemented for the exponential terms of Re, Ns, e/d, α, β. Specifically, a functional form of −0.2445 + Cx (where C represents correction coefficients and x denotes each of the remaining four parameters) was introduced into the Re exponential term to incorporate cross-parameter coupling effects. The selection of parameter coupling forms was determined through systematic evaluation of whether introducing new parameter terms could reduce the mean relative error between experimental measurements and theoretical predictions. This optimization methodology was subsequently applied to other exponential terms through analogous procedures. The final optimized resistance correlation equation obtained through this hierarchical optimization approach is presented as follows:

$$\begin{gathered} f=0.0349\times R{e}^{-0.2445+0.007824e/d-0.000005123\beta }\times N{s}^{0.07896-1.609\times {10}^{-7}R\mathrm{e}+0.0001157\alpha +0.00003161\beta } \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\times {({\displaystyle \frac{e}{d}})}^{-0.3889+0.00001106N\mathrm{s}-0.00003784\alpha }\times {\alpha }^{0.7886+1.807\times {10}^{-8}Re-0.01676e/d}\times {\beta }^{0.2277-4.332\times {10}^{-8}Re+0.0402e/d} \end{gathered}$$

(20)

The newly developed correlation demonstrates that the updated formulation incorporates the following coupling relationships: Reynolds number with thread height and crest angle coupling; rack count coupled with Reynolds number, helix angle, and crest angle; thread height interacting with rack count and helix angle; helix angle showing interdependence with Reynolds number and tooth height; and crest angle exhibiting coupling with Reynolds number and tooth height. When evaluated on test samples consistent with Model 1, the new model achieves a mean absolute percentage error (MAPE) of 7.08% in resistance coefficient prediction, with maximum and minimum prediction errors of 27.66% and 0.76%, respectively. The prediction standard deviation decreases from 0.0619 in Model 1 to 0.0362, indicating enhanced precision in resistance coefficient modeling. As evidenced in Figure 8, the predictive stability of the new model shows significant improvement compared to its predecessor. Explanation: The points on the red solid line represent that the experimental values are close to the predicted values. The two black dashed lines indicate that the error values range from −30% to 15%.

Model II demonstrates superior predictive accuracy with a smaller prediction standard deviation in the flow resistance coefficient, which aligns closely with engineering practice considering the cross-influence of geometric parameters. While Model I, based on the Webb model, offers simplicity and ease of modification, it exhibits significant limitations by treating the resistance coefficient as a monotonic function of flow and structural parameters while neglecting parameter coupling. In contrast, Model II substantially enhances prediction accuracy through comprehensive consideration of parameter coupling effects.

Table 6. Comparison of drag coefficients between two models’ mean absolute.

	Mean Absolute Percentage Error (MAPE)	Standard Deviation (SD)	Maximum Error	Minimum Error
Model I	8.21%	0.0619	31.08%	0.62%
Model II	7.08%	0.0362	27.66%	0.76%

presents the comparison of error rates for the resistance coefficients of the two models. It is clearly evident that the resistance coefficient prediction ability of Model II is significantly superior.

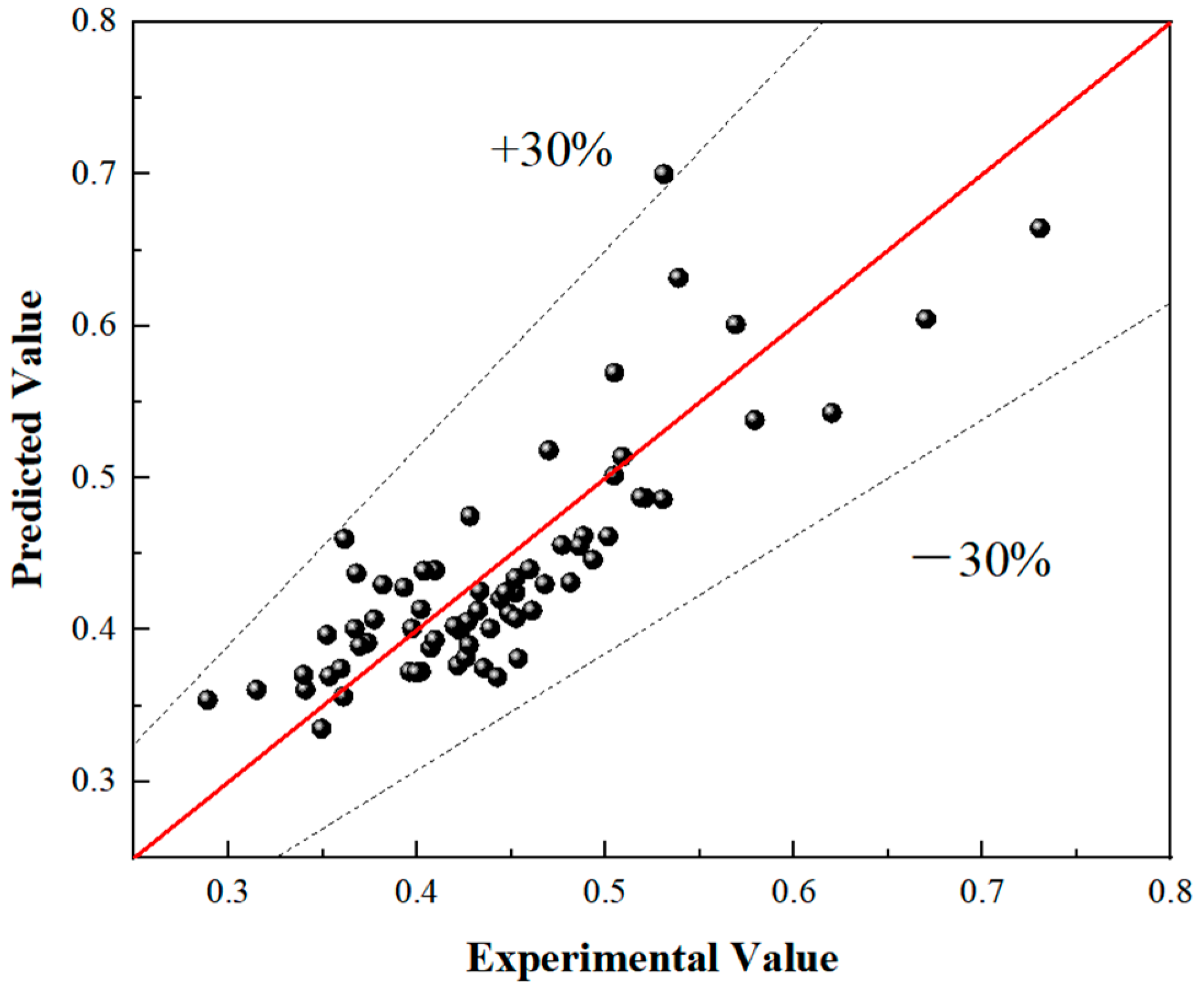
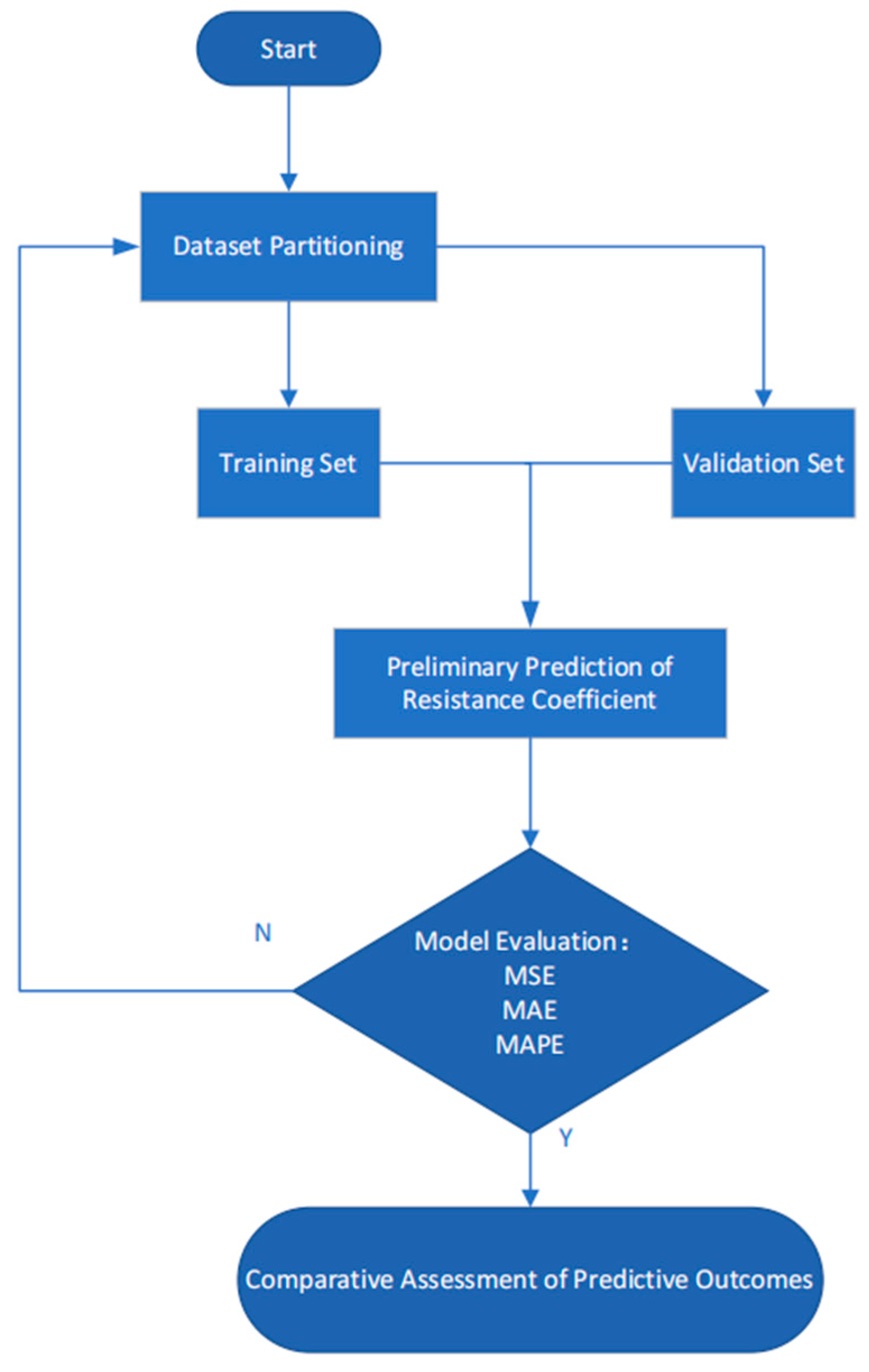
3.3. Prediction and Validation of the SVR Model

The SVR model, as a robust machine learning method, demonstrates exceptional efficacy in handling regression problems [28]. In this study, the SVR model is employed to enhance data processing and improve the stability of the fitting formula. Specifically, experimental data are introduced into the SVR model for training, aiming to establish the mapping relationship between geometric parameters of internal threaded tubes (as primary input features) and drag coefficient (as the output target). The trained SVR model subsequently generates predicted values of a drag coefficient.

Figure 9 illustrates the application strategy of the SVR model in this article: The processed dataset is first partitioned into training and validation sets. Subsequently, the trained model conducts preliminary predictions of drag coefficients. These predictions are then evaluated using the drag coefficient correlation formula derived from Model II fitting and corresponding evaluation metrics. If the evaluation results meet the predefined criteria, the model will be applied to new data prediction and assessment. Otherwise, the dataset will be re-partitioned to optimize data allocation and enhance prediction accuracy.

The prediction accuracy of the model was evaluated using three metrics: Root Mean Square Error (RMSE, Equation (21)), Mean Absolute Error (MAE, Equation (22)), and mean absolute percentage error (MAPE, Equation (23)). These metrics were calculated based on the discrepancies between the predicted values from the SVR model and the experimental data of drag coefficients. The validation criteria required RMSE to be below 30%, while the standard mean error must fall within ±10%. Both RMSE and MAE quantitatively reflect the magnitude of prediction errors, with smaller values indicating higher model accuracy.

$$RMSE=\sqrt{{\displaystyle \frac{{\displaystyle \sum _{i=1}^n{\left({\widehat{y}}_i-{\overline{y}}_i\right)}^2}}{n}}}$$

(21)

$$MAE={\displaystyle \frac{1}{\mathrm{n}}}{\displaystyle \sum _{i=1}^n\left|{\widehat{y}}_i-y_i\right|}$$

(22)

$$MAPE={\displaystyle \frac{1}{\mathrm{n}}}{\displaystyle \sum _{i=1}^n\left|\frac{{\widehat{y}}_i-y_i}{y_i}\right|}$$

(23)

In the equation, $y_i$ denotes experimental value, ${\widehat{y}}_i$ represents predicted value, and ${\overline{y}}_i$ stands for the mean experimental value.

Figure 10 shows the comparison between the experimental values and the predicted values after the training of the SVR model: 58.8% of the relative errors in SVR predictions are predominantly distributed within the range of 20–30%, with a root mean square error (RMSE) of 0.0949 and a mean absolute error (MAE) of 0.08931. The mean absolute percentage error (MAPE) reaches 20.4%. Although the predictive accuracy of the SVR model is inferior to that of the nonlinear fitting method based on least squares optimization, it aligns fundamentally with the prediction trends observed in both Model I and Model II. Furthermore, the SVR model demonstrates effective predictive capability for resistance coefficients corresponding to diverse geometric parameter combinations. Explanation: The points on the red solid line represent that the experimental values are close to the predicted values. The two black dashed lines indicate that the error values range from −30% to 30%.

The integration of physics-informed machine learning models with experimental data for friction factor prediction in the geometric parameter space of internally threaded tubes enables enhanced dataset construction, thereby facilitating rapid identification of desired tube geometries that satisfy production-specified friction factor requirements.

The SVR model, as a representative physics-informed machine learning approach, demonstrates superior generalization capability. By synergizing SVR models with experimental measurements, this methodology effectively eliminates outlier data while expediting the determination of operational friction factor ranges through hybridized fitting correlations. Such a strategy not only addresses data scarcity by augmenting limited experimental datasets (which are typically costly to acquire) with extensive numerical predictions but also incorporates physical features and domain knowledge—an innovation particularly valuable for industrial applications involving high-cost experimental scenarios. This dual approach significantly enhances selection efficiency in production practice while maintaining engineering reliability.

4. Conclusions

This study selected a series of industrially prevalent internally threaded tubes with an outer diameter of 9.52 mm to conduct pressure drop analysis. Using R410A as the working fluid, condensation pressure drop experiments were performed under operating conditions including Reynolds numbers (Re) of 20,000–60,000, mass velocity of 50–600 kg/(m²·s), and a condensation temperature of 45 °C. Through systematic integration and analysis of experimental data, the conclusions are as follows:

• R410A demonstrates comparable thermophysical properties to R22 while exhibiting superior operational characteristics as an alternative refrigerant. Under the investigated conditions, R410A generated lower pressure drops compared to R22. This phenomenon is attributed to the greater vapor–liquid density disparity in R22, which amplifies velocity differences between phases, enhances axial shear forces, intensifies interfacial friction, and consequently elevates flow disturbance and energy dissipation.
• For R410A flow, the pressure drop in internally threaded tubes increases proportionally with the area enhancement ratio. A linear correlation between area enhancement ratio and pressure drop was observed at mass velocity below 200 kg/(m²·s), with the slope of this relationship diminishing as flow velocity increases. However, pronounced nonlinear fluctuations emerge at higher velocities, rendering linear regression inadequate. Tubes with higher area enhancement ratios exhibit stronger flow resistance, particularly under elevated mass velocity conditions. This results in intensified flow turbulence enhanced interfacial and wall friction, and consequently increased frictional losses.
• Two friction factor prediction models were developed based on the Webb and Ravigururajan correlations. Model, I (Webb-based) demonstrated a mean absolute percentage error of 8.21%, with maximum and minimum prediction errors of 31.08% and 0.62%, respectively. Model II (Ravigururajan-based) showed improved performance with a mean absolute percentage error of 7.08%, maximum error of 27.66%, minimum error of 0.76%, and reduced standard deviation from 0.0619 to 0.0362. The enhanced predictive accuracy of Model II satisfies engineering application requirements.
• Implementation of an SVR model enabled effective outlier removal and rapid determination of resistance coefficient ranges when combined with empirical correlations. This hybrid strategy addresses data scarcity issues in high-cost experimental scenarios by integrating physical characteristics with domain knowledge, while simultaneously improving selection efficiency in industrial applications. The methodology demonstrates broad applicability to various experimental configurations requiring substantial resource investment.

5. Future Works

This study investigates the geometric parameters, resistance characteristics, and correlation fitting of copper internally threaded tubes, systematically analyzes intrinsic relationships between parameters, and develops a novel resistance coefficient correlation. Future research could focus on the following aspects:

• The selected industrially prevalent internally threaded tubes in this study could potentially accommodate expanded geometric parameter ranges (e.g., rib numbers of 50–70). The coupled effects of low rib counts with other parameters on flow resistance merit further investigation.
• The coupled interactions among geometric parameters of internally threaded tubes present inherent complexity. While the developed friction factor correlation in this work partially integrates parametric interdependencies, its extrapolation beyond experimental conditions requires empirical validation through extensive datasets to progressively refine the coupled relationships, thereby enhancing coupling coherence and predictive accuracy. Furthermore, implementing functional transformations (e.g., logarithmic scaling, power-law modifications) to the correlation architecture could optimize parametric coupling effects. This demands that investigators possess sophisticated analytical capabilities to discern critical hydrodynamic mechanisms governing friction factor evolution.