Predicting Thermal Performance of Aquifer Thermal Energy Storage Systems in Depleted Clastic Hydrocarbon Reservoirs via Machine Learning: Case Study from Hungary †
Abstract
1. Introduction
2. Glossary of Terms
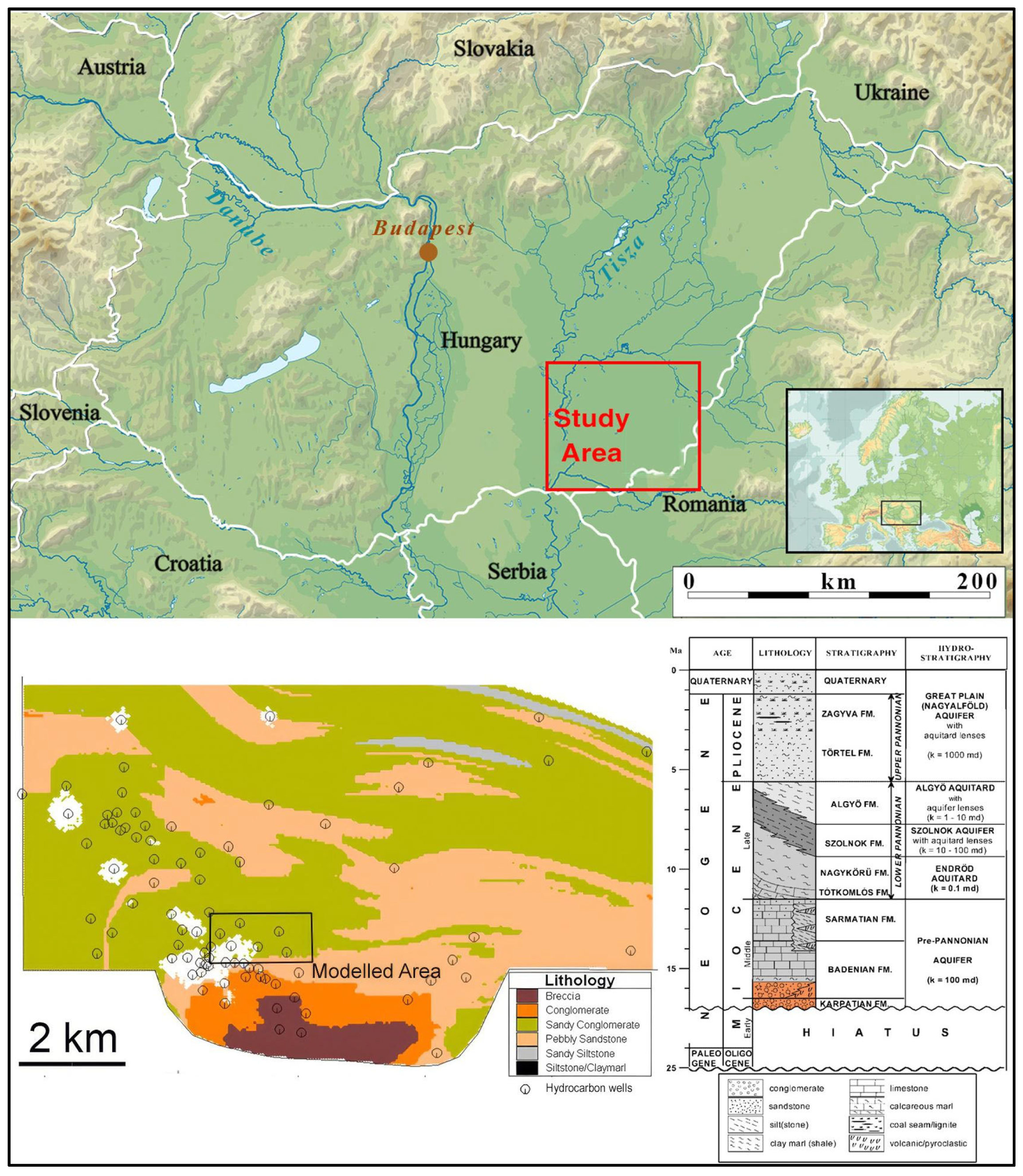
3. Background and Regional
3.1. Geological and Hydrogeological Setting of the Békés Basin
3.2. Hydrodynamic Systems and Pressure Regimes
3.3. Reservoir Properties and Geothermal Potential
3.4. Hydrocarbon History and Well Infrastructure
3.5. Relevance to Seasonal Heat Storage
4. Materials and Methods
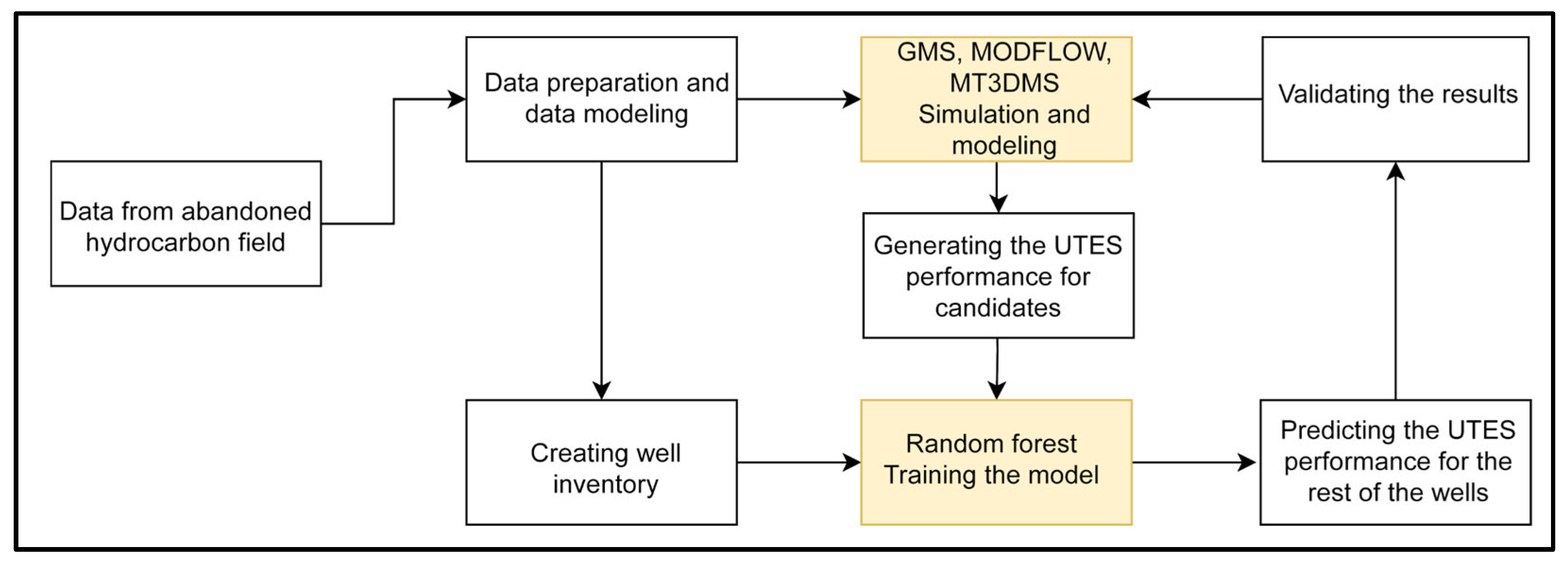
4.1. Methodological Framework
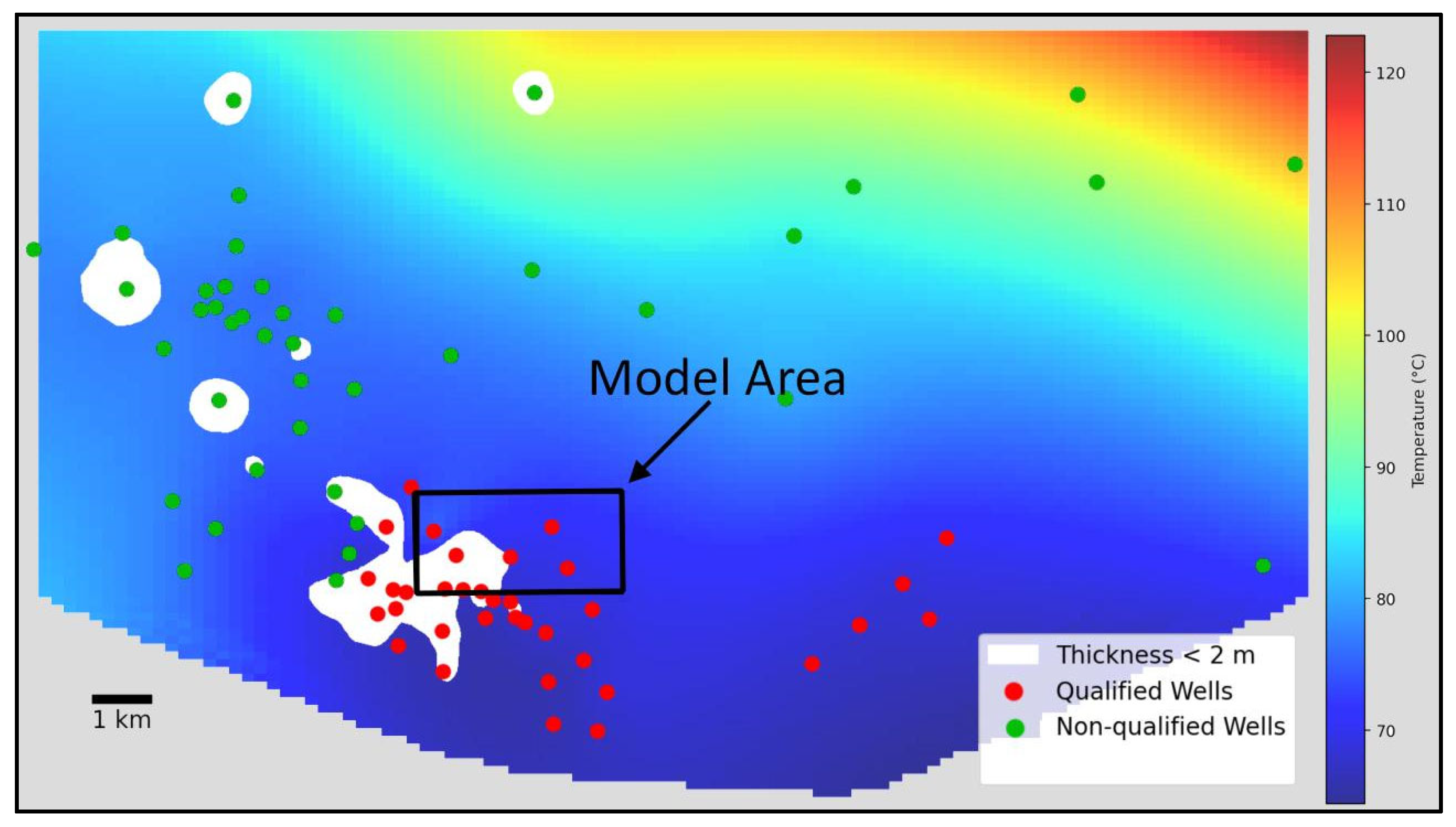
4.2. Data Collection and Data Preparation
4.3. Hydrogeological Modeling
4.4. Heat Transport Modeling
4.5. Simulation Setting
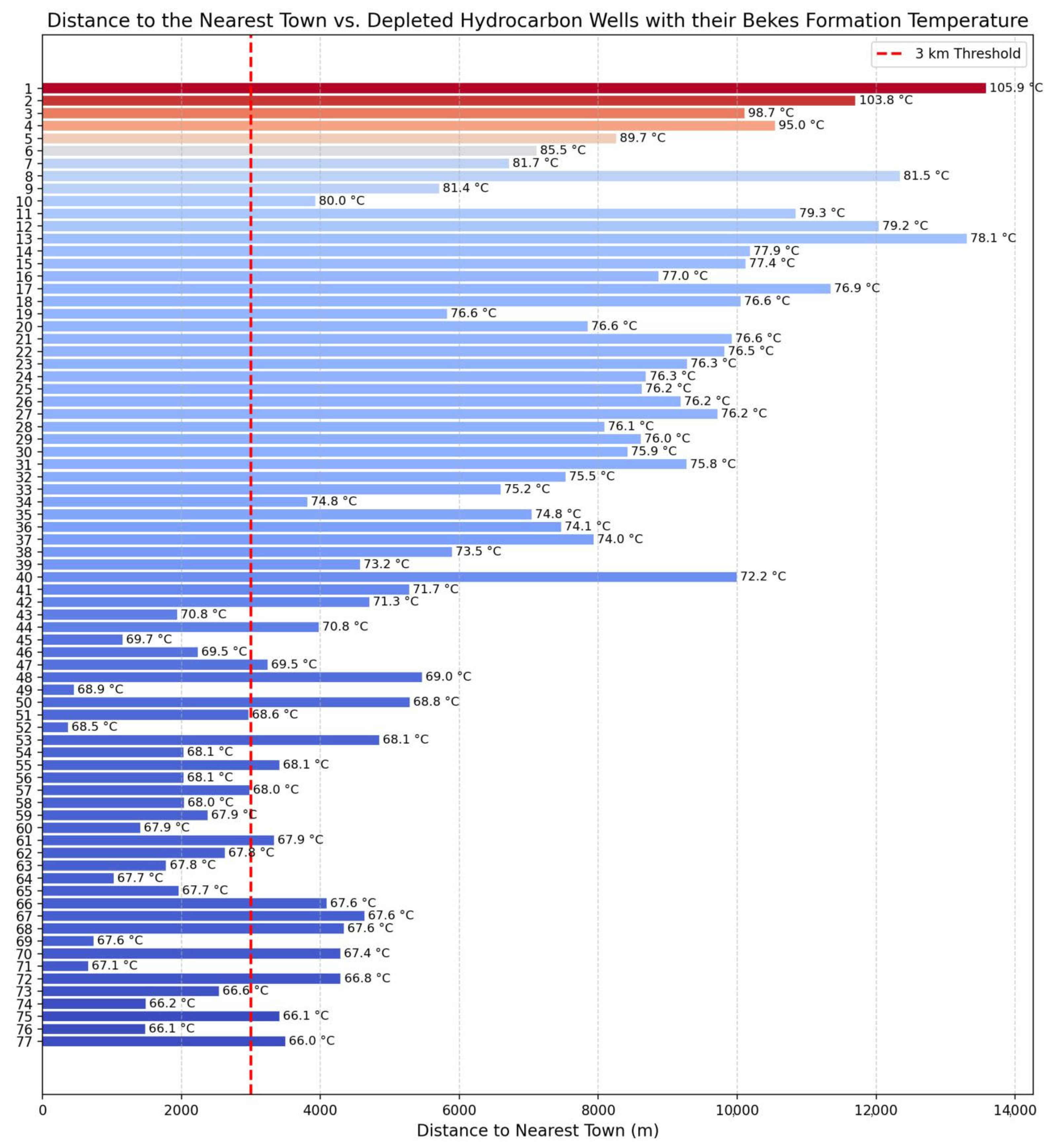
4.6. Training Data for Machine Learning
4.7. Model Calibration and Validation
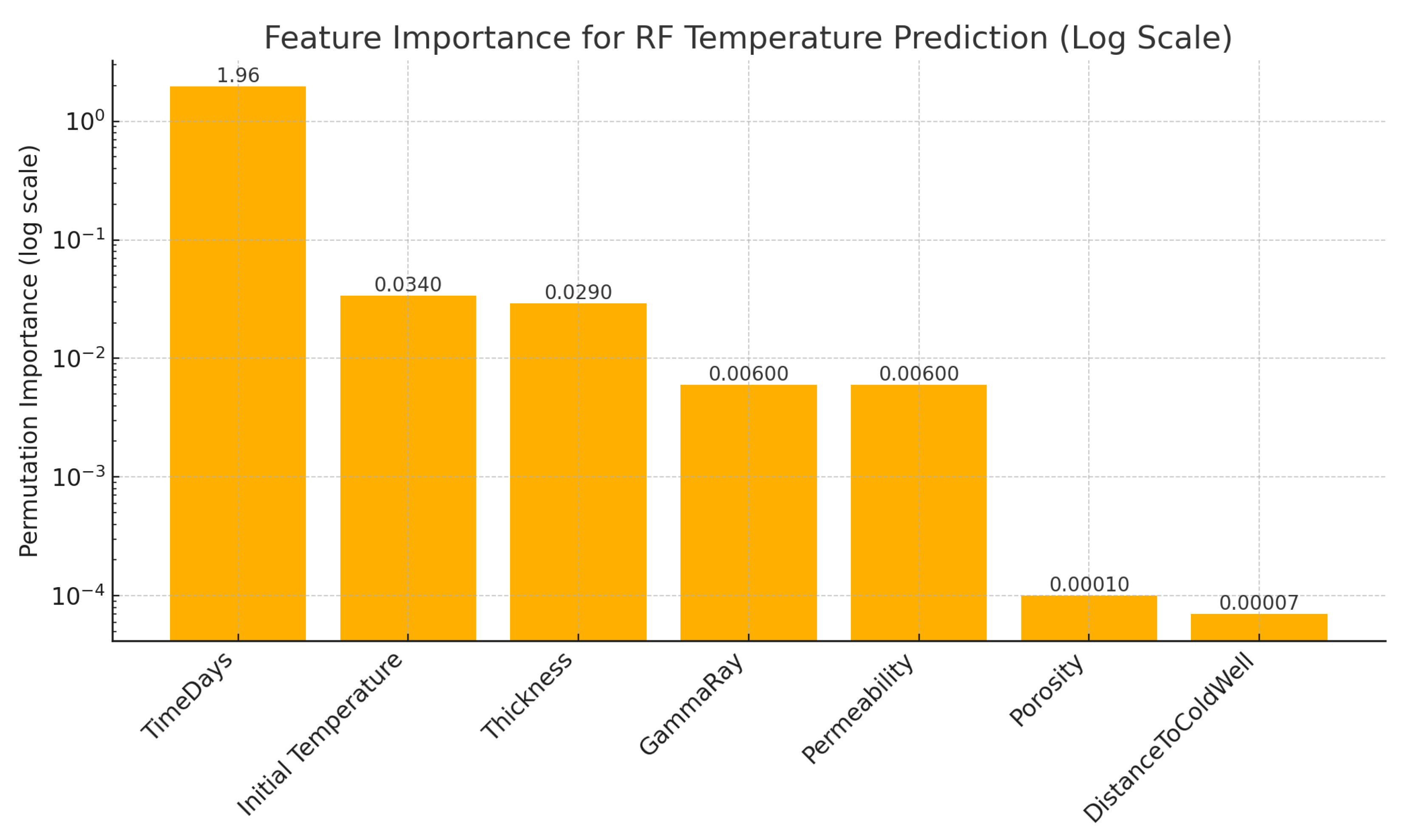
4.8. Sensitivity Analysis
5. Results
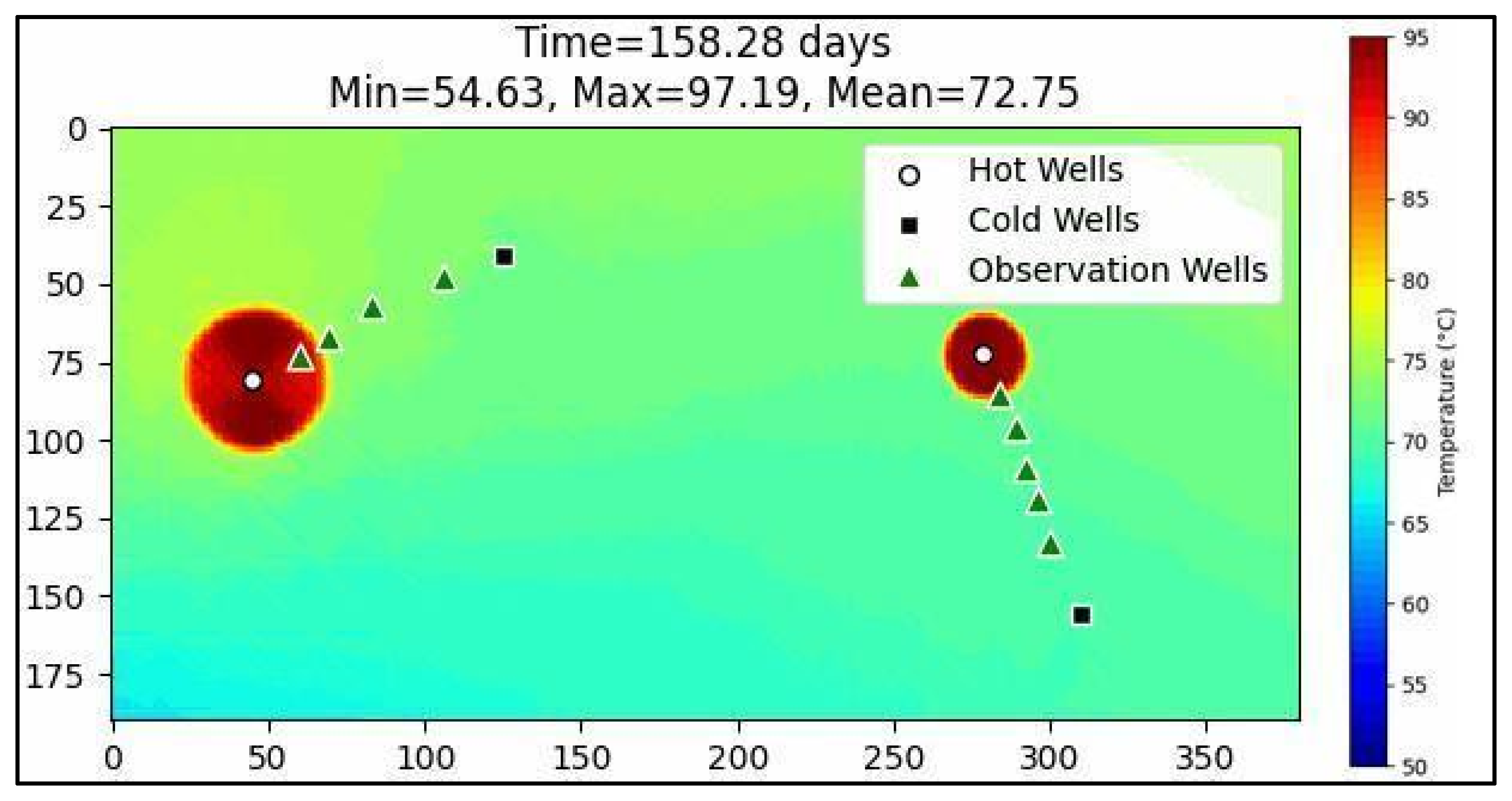
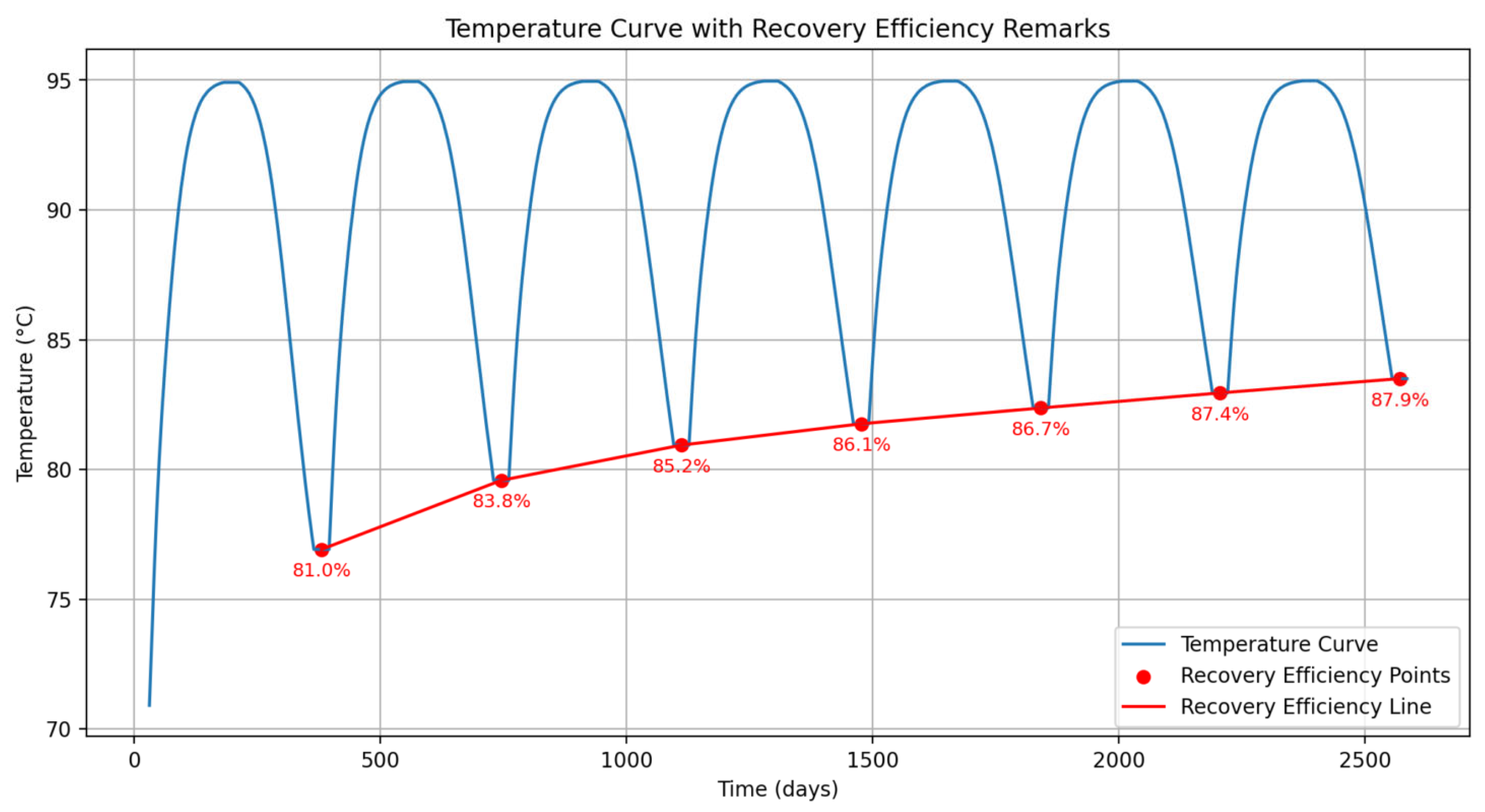
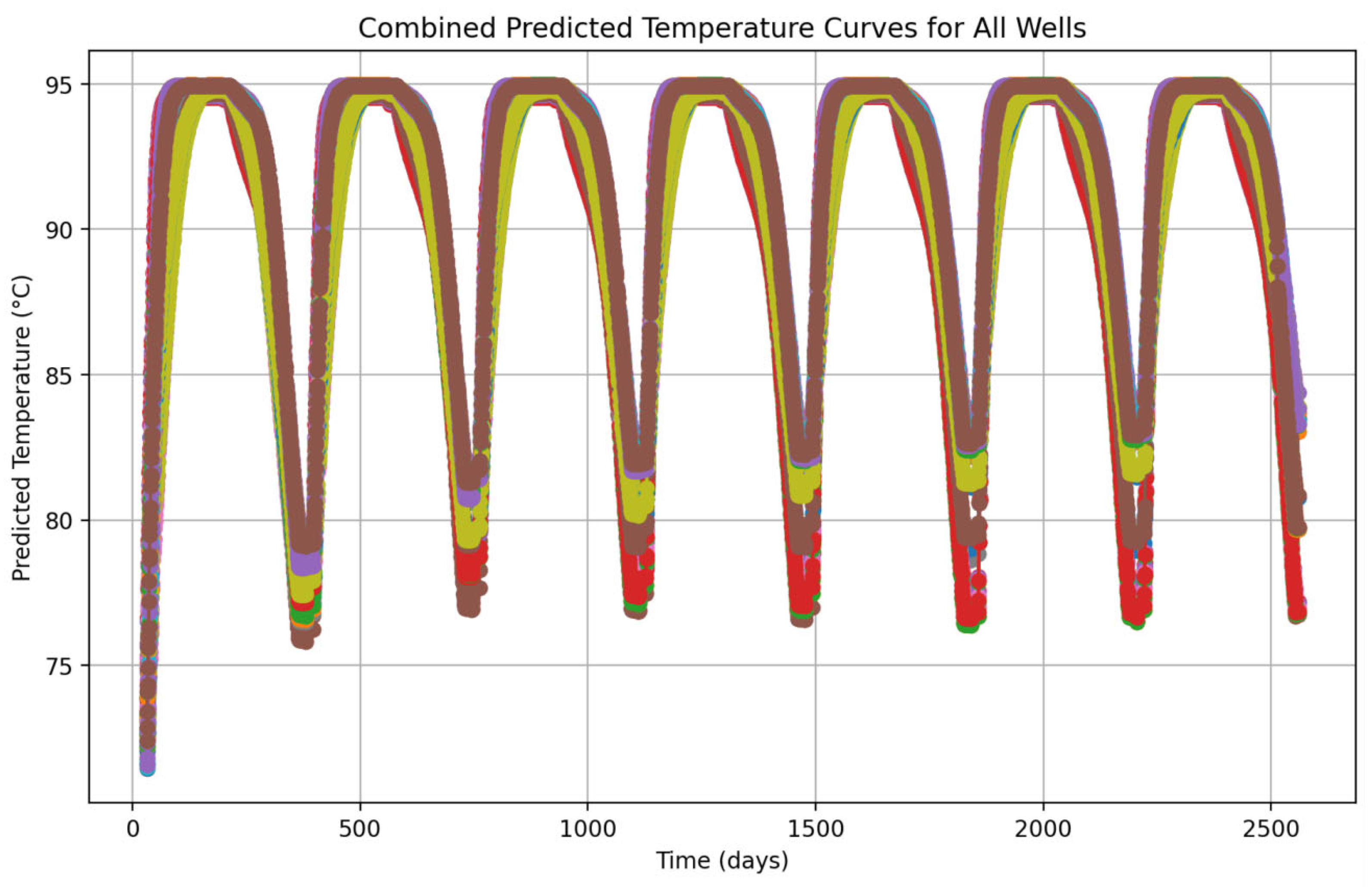
5.1. Heat Simulation Result
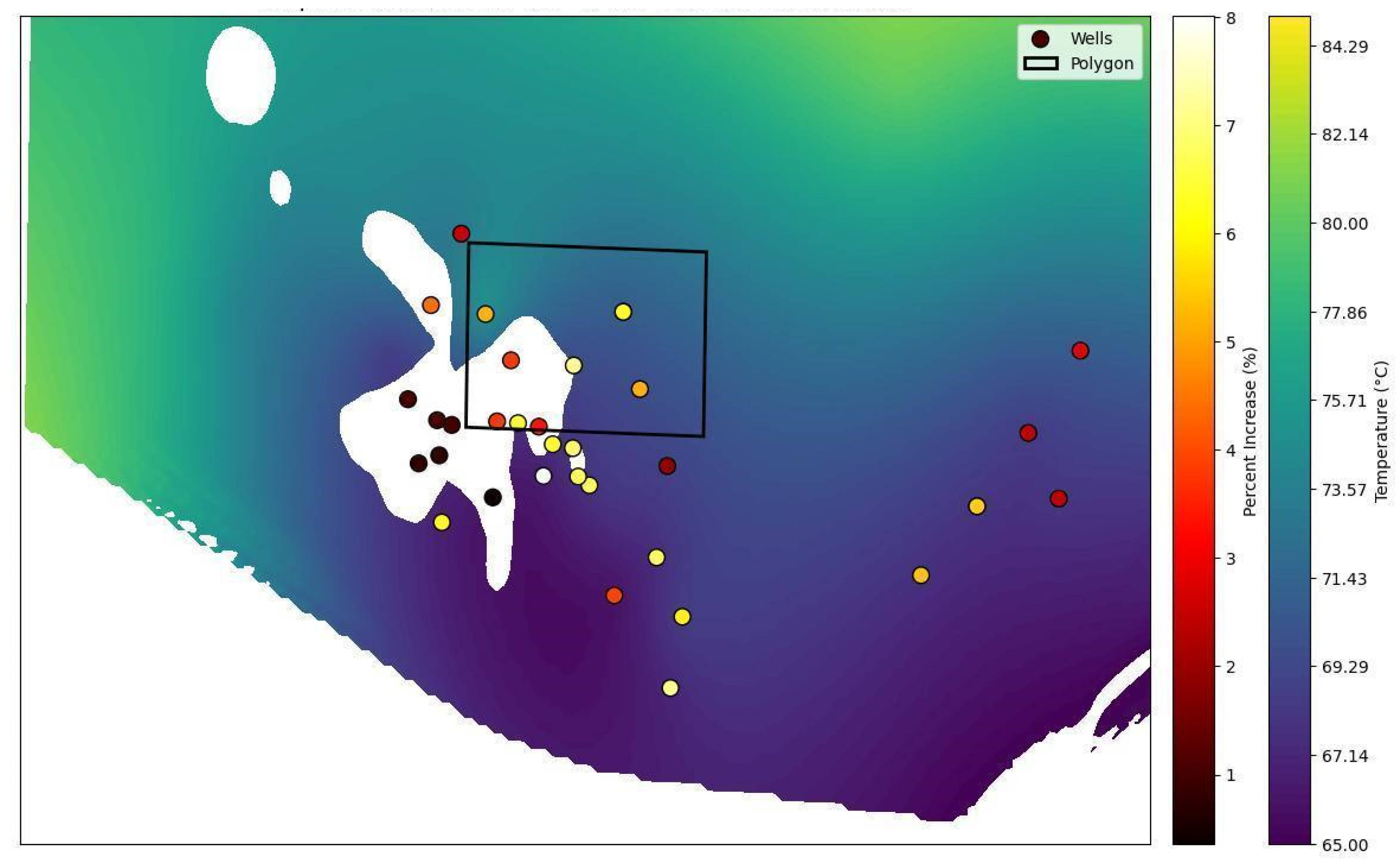
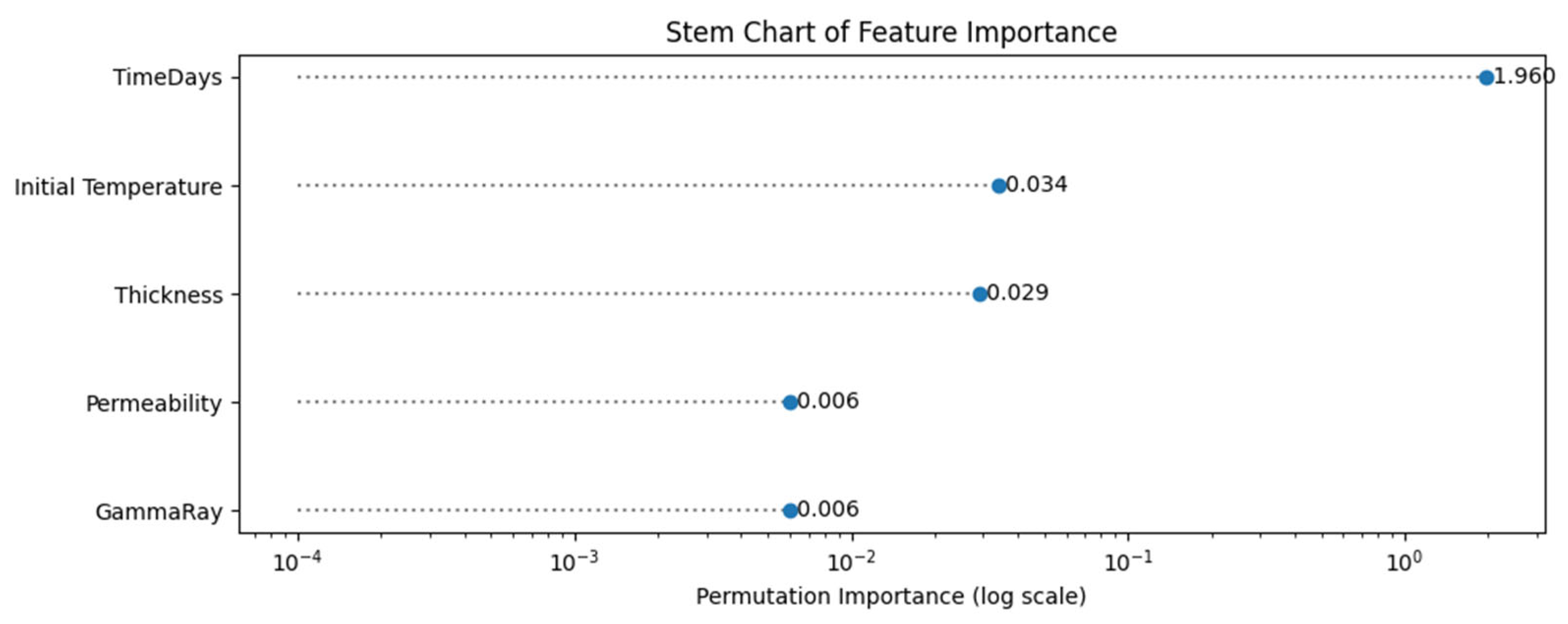
5.2. Machine Learning Result
6. Discussion
6.1. Alignment with Previous Studies and Theoretical Outcomes
6.2. Key Influencing Parameters
6.3. Strengths and Limitations of Hydrogeological Model Calibration
6.4. Enhancing Decision-Making for UTES Site Selection
6.5. Implications for Scaling Geothermal Storage Projects
6.6. Assumptions and Simplifications
6.7. Uncertainties in Input Data
6.8. Recommendations and Future Work
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Raimi, D.; Krupnick, A.J.; Shah, J.-S.; Thompson, A. Decommissioning Orphaned and Abandoned Oil and Gas Wells: New Estimates and Cost Drivers. Environ. Sci. Technol. 2021, 55, 10224–10230. [Google Scholar] [CrossRef] [PubMed]
- Vass, I. (MOL Hungary, Algyő, Hungary). Well Abandonment Cost Estimates for Hungary. Personal Communication. 2025. [Google Scholar]
- IPCC. Climate Change Widespread, Rapid, and Intensifying—IPCC—IPCC. 2021. Available online: https://www.ipcc.ch/2021/08/09/ar6-wg1-20210809-pr/ (accessed on 10 May 2025).
- Kang, M.; Mauzerall, D.L.; Ma, D.Z.; Celia, M.A. Reducing methane emissions from abandoned oil and gas wells: Strategies and costs. Energy Policy 2019, 132, 594–601. [Google Scholar] [CrossRef]
- Osundare, O.; Teodoriu, C.; Falcone, G.; Ichim, A. Estimation of Plugging and Abandonment Costs Based on Different EU Regulations with Application to Geothermal Wells. In Proceedings of the 43rd Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 12–14 February 2018. [Google Scholar]
- Duplyakin, D.; Beckers, K.F.; Siler, D.L.; Martin, M.J.; Johnston, H.E. Modeling Subsurface Performance of a Geothermal Reservoir Using Machine Learning. Energies 2022, 15, 3. [Google Scholar] [CrossRef]
- Jin, W.; Atkinson, T.A.; Doughty, C.; Neupane, G.; Spycher, N.; McLing, T.L.; Dobson, P.F.; Smith, R.; Podgorney, R. Machine-learning-assisted high-temperature reservoir thermal energy storage optimization. Renew. Energy 2022, 197, 384–397. [Google Scholar] [CrossRef]
- Rohmer, J.; Armandine Les Landes, A.; Loschetter, A.; Maragna, C. Fast prediction of aquifer thermal energy storage: A multicyclic metamodelling procedure. Comput. Geosci. 2023, 27, 223–243. [Google Scholar] [CrossRef]
- Duggal, R.; Rayudu, R.; Hinkley, J.; Burnell, J.; Wieland, C.; Keim, M. A comprehensive review of energy extraction from low-temperature geothermal resources in hydrocarbon fields. Renew. Sustain. Energy Rev. 2022, 154, 111865. [Google Scholar] [CrossRef]
- Gayayev, I. Conversion of Abandoned Hydrocarbon Structures into Geothermal Wells for Sustainable Energy Production in Sedimentary Basins [Laurea, Politecnico di Torino]. 2023. Available online: https://webthesis.biblio.polito.it/29039/ (accessed on 10 May 2025).
- IEA. Energy Technology Perspectives 2017—Analysis; IEA: Paris, France, 2017; Available online: https://www.iea.org/reports/energy-technology-perspectives-2017 (accessed on 10 May 2025).
- REN21. Renewables 2019 Global Status Report. 2019. Available online: https://www.ren21.net/gsr-2019 (accessed on 10 May 2025).
- WEF. 5 Green Energy Milestones from Around the World. World Economic Forum. 2021. Available online: https://www.weforum.org/agenda/2021/04/renewables-record-capacity-solar-wind-nuclear/ (accessed on 10 May 2025).
- Dincer, I.; Rosen, M.A. Thermal Energy Storage: Systems and Applications, 2nd ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Van Der Roest, E.; Beernink, S.; Hartog, N.; Van Der Hoek, J.P.; Bloemendal, M. Towards Sustainable Heat Supply with Decentralized Multi-Energy Systems by Integration of Subsurface Seasonal Heat Storage. Energies 2021, 14, 7958. [Google Scholar] [CrossRef]
- Green, S.; McLennan, J.; Panja, P.; Kitz, K.; Allis, R.; Moore, J. Geothermal battery energy storage. Renew. Energy 2021, 164, 777–790. [Google Scholar] [CrossRef]
- Lee, K.S. Underground Thermal Energy Storage; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Li, G. Sensible heat thermal storage energy and exergy performance evaluations. Renew. Sustain. Energy Rev. 2016, 53, 897–923. [Google Scholar] [CrossRef]
- Qin, J.; Song, J.; Tang, Y.; Rui, Z.; Wang, Y.; He, Y. Well applicability assessment based on fuzzy theory for CO2 sequestration in depleted gas reservoirs. Renew. Energy 2023, 206, 239–250. [Google Scholar] [CrossRef]
- Zhu, S.; Shi, X.; Yang, C.; Bai, W.; Wei, X.; Yang, K.; Li, P.; Li, H.; Li, Y.; Wang, G. Site selection evaluation for salt cavern hydrogen storage in China. Renew. Energy 2024, 224, 120143. [Google Scholar] [CrossRef]
- Matos, C.R.; Carneiro, J.F.; Silva, P.P. Overview of Large-Scale Underground Energy Storage Technologies for Integration of Renewable Energies and Criteria for Reservoir Identification. J. Energy Storage 2019, 21, 241–258. [Google Scholar] [CrossRef]
- Stricker, K.; Grimmer, J.C.; Egert, R.; Bremer, J.; Korzani, M.G.; Schill, E.; Kohl, T. The Potential of Depleted Oil Reservoirs for High-Temperature Storage Systems. Energies 2020, 13, 24. [Google Scholar] [CrossRef]
- Khosravi, R.; Simjoo, M.; Chahardowli, M. A new insight into pilot-scale development of low-salinity polymer flood using an intelligent-based proxy model coupled with particle swarm optimization. Sci. Rep. 2024, 14, 29000. [Google Scholar] [CrossRef]
- Liu, A.; Li, J.; Bi, J.; Chen, Z.; Wang, Y.; Lu, C.; Jin, Y.; Lin, B. A novel reservoir simulation model based on physics informed neural networks. Phys. Fluids 2024, 36, 116617. [Google Scholar] [CrossRef]
- Menear, K.; Duplyakin, D.; Oliver, M.C.; Shah, M.; Martin, M.J.; Martinek, J.; Nithyanandam, K.; Ma, Z. One System, Many Models: Designing a Surrogate Model for Sulfur Thermal Energy Storage; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2023. [Google Scholar]
- Dickinson, J.S.; Buik, N.; Matthews, M.C.; Snijders, A. Aquifer thermal energy storage: Theoretical and operational analysis. Géotechnique 2009, 59, 249–260. [Google Scholar] [CrossRef]
- Fleuchaus, P.; Schüppler, S.; Bloemendal, M.; Guglielmetti, L.; Opel, O.; Blum, P. Risk analysis of High-Temperature Aquifer Thermal Energy Storage (HT-ATES). Renew. Sustain. Energy Rev. 2020, 133, 110153. [Google Scholar] [CrossRef]
- Kastner, O.; Norden, B.; Klapperer, S.; Park, S.; Urpi, L.; Cacace, M.; Blöcher, G. Thermal solar energy storage in Jurassic aquifers in Northeastern Germany: A simulation study. Renew. Energy 2017, 104, 290–306. [Google Scholar] [CrossRef]
- Van Heekeren, V.; Bakema, G. The Netherlands Country Update on Geothermal Energy. In Proceedings of the Stichting Platform Geothermie, World Geothermal Congress, Melbourne, Australia, 19–25 April 2025. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Holstenkamp, L.; Meisel, M.; Neidig, P.; Opel, O.; Steffahn, J.; Strodel, N.; Lauer, J.J.; Vogel, M.; Degenhart, H.; Michalzik, D.; et al. Interdisciplinary Review of Medium-deep Aquifer Thermal Energy Storage in North Germany. Energy Procedia 2017, 135, 327–336. [Google Scholar] [CrossRef]
- HEATSTORE. 2025. Available online: https://www.heatstore.eu/national-project-netherlands.html (accessed on 10 May 2025).
- Oerlemans, P.; Drijver, B.; Koenen, M.; Koornneef, J.; Dinkelman, D.; Godschalk, B. First field results on the technical risks and effectiveness of mitigation measures for the full scale HT-ATES demonstration project in Middenmeer. In Proceedings of the European Geothermal Congress 2022, Berlin, Germany, 17–21 October 2022. [Google Scholar]
- Akindipe, D.; McTigue, J.; Dobson, P.; Atkinson, T.; Witter, E.; Kumar, R.; Sonnenthal, E.; Umbro, M.; Lederhos, J.; Adams, D.; et al. Techno-Economic Analysis and Market Potential of Geological Thermal Energy Storage (GeoTES) Charged With Solar Thermal and Heat Pumps; (NREL/TP–5700-91225, 2474842, MainId:93003; p. NREL/TP--5700-91225, 2474842, MainId:93003); National Renewable Energy Laborator: Golden, CO, USA, 2024. [Google Scholar] [CrossRef]
- IEA. World Energy Outlook 2021—Analysis; IEA: Paris, France, 2021; Available online: https://www.iea.org/reports/world-energy-outlook-2021 (accessed on 10 May 2025).
- Anttila, A. Techno-Economic Comparison of Thermal Energy Storage Solutions for Decarbonizing Heat in Espoo by 2025. 2021. Available online: https://aaltodoc.aalto.fi/server/api/core/bitstreams/a65b9c93-33d1-4975-8a97-af3fdf3d39b1/content (accessed on 10 May 2025).
- Bloemendal, M.; Hartog, N. Analysis of the impact of storage conditions on the thermal recovery efficiency of low-temperature ATES systems. Geothermics 2018, 71, 306–319. [Google Scholar] [CrossRef]
- Sommer, W.; Valstar, J.; van Gaans, P.; Grotenhuis, T.; Rijnaarts, H. The impact of aquifer heterogeneity on the performance of aquifer thermal energy storage. Water Resour. Res. 2013, 49, 8128–8138. [Google Scholar] [CrossRef]
- Pellegrini, M.; Bloemendal, M.; Hoekstra, N.; Spaak, G.; Andreu Gallego, A.; Rodriguez Comins, J.; Grotenhuis, T.; Picone, S.; Murrell, A.J.; Steeman, H.J. Low carbon heating and cooling by combining various technologies with Aquifer Thermal Energy Storage. Sci. Total Environ. 2019, 665, 1–10. [Google Scholar] [CrossRef]
- Abdulhaq, H. Predicting Thermal Performance of Aquifer Thermal Energy Storage Systems in Depleted Clastic Hydrocarbon Reservoir via Machine Learning: Case Study from Hungary. The 16th European Geothermal PhD Days Book of Abstracts. 2025. Available online: https://www.egpd2025.com (accessed on 15 April 2025).
- Nádor, A.; Kujbus, A.; Tóth, A. Geothermal Energy Use, Country Update for Hungary. Eur. Geotherm. Congr. 2022, 2022, 1–13. [Google Scholar]
- Szanyi, J.D.; Kovács, B.; Abdulhaq, H.A. Harnessing geothermal energy in Hungary. Geol. Soc. Lond. Spec. Publ. 2025, 555, SP555-2024. [Google Scholar] [CrossRef]
- Topór, T.; Słota-Valim, M.; Kudrewicz, R. Assessing the Geothermal Potential of Selected Depleted Oil and Gas Reservoirs Based on Geological Modeling and Machine Learning Tools. Energies 2023, 16, 13. [Google Scholar] [CrossRef]
- Horváth, F.; Musitz, B.; Balázs, A.; Végh, A.; Uhrin, A.; Nádor, A.; Koroknai, B.; Pap, N.; Tóth, T.; Wórum, G. Evolution of the Pannonian basin and its geothermal resources. Geothermics 2015, 53, 328–352. [Google Scholar] [CrossRef]
- Juhász, G. Lithostratigraphical and sedimentological framework of the Pannonian (sl) sedimentary sequence in the Hungarian Plain (Alföld), Eastern Hungary. Acta Geol. Hung. 1991, 34, 53–72. [Google Scholar]
- U.S. Geological Survey. Mineral Commodity Summaries 2023; U.S. Geological Survey: Reston, VA, USA, 2023. [Google Scholar] [CrossRef]
- Abdulhaq, H.A.; Geiger, J.; Vass, I.; Tóth, T.M.; Medgyes, T.; Szanyi, J. Transforming Abandoned Hydrocarbon Fields into Heat Storage Solutions: A Hungarian Case Study Using Enhanced Multi-Criteria Decision Analysis–Analytic Hierarchy Process and Geostatistical Methods. Energies 2024, 17, 16. [Google Scholar] [CrossRef]
- Haas, J. (Ed.) Geology of Hungary; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Mádl-Szőnyi, J.; Tóth, J. A hydrogeological type section for the Duna-Tisza Interfluve, Hungary. Hydrogeol. J. 2009, 17, 961–980. [Google Scholar] [CrossRef]
- Tóth, J.; Almási, I. Interpretation of observed fluid potential patterns in a deep sedimentary basin under tectonic compression: Hungarian Great Plain, Pannonian Basin. Geofluids 2001, 1, 11–36. [Google Scholar] [CrossRef]
- Bálint, A.; Szanyi, J. A half century of reservoir property changes in the Szentes geothermal field, Hungary. Cent. Eur. Geol. 2015, 58, 28–49. [Google Scholar] [CrossRef]
- Korim, K. A szentesi hévízmező feltárásának és termelésének három évtizedes története (Three decades of research and utilization in the Szentes Geothermal Field). Bányászati és Kohászati Lapok 1991, 124, 179–184. [Google Scholar]
- Szanyi, J.; Kovacs, B.; Scharek, P. Geothermal energy in Hungary: Potentials and barriers. Eur. Geol. 2009, 27, 15–19. [Google Scholar]
- Szanyi, J.; Medgyes, T.; Kóbor, B.; Pál-Molnár, E. Technologies of Injection into Sandstone Reservoirs: Best Practices, Case Studies; GeoLitera; Institute of Geosciences, University of Szeged: Szeged, Hungary, 2015; Available online: https://publicatio.bibl.u-szeged.hu/13471/ (accessed on 10 May 2025).
- Lenkey, L.; Mihályka, J.; Paróczi, P. Review of geothermal conditions of Hungary. Földtani Közlöny 2021, 151, 65. [Google Scholar] [CrossRef]
- Harbaugh, A.W. MODFLOW-2005: The U.S. Geological Survey Modular Ground-Water Model–the Ground-Water Flow Process; Techniques and Methods 2005, 6-A16; US Department of the Interior, US Geological Survey: Reston, VA, USA, 2005. [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Kovács, A.; Teleki, P.G. History of Oil and Natural Gas Production in the Békés Basin. In Basin Analysis in Petroleum Exploration; Teleki, P.G., Mattick, R.E., Kókai, J., Eds.; Springer: Dordrecht, The Netherlands, 1994; pp. 237–256. [Google Scholar] [CrossRef]
- Varga, A.; Bozsó, G.; Garaguly, I.; Raucsik, B.; Bencsik, A.; Kóbor, B. Cements, Waters, and Scales: An Integrated Study of the Szeged Geothermal Systems (SE Hungary) to Characterize Natural Environmental Conditions of the Thermal Aquifer. Geofluids 2019, 2019, 4863814. [Google Scholar] [CrossRef]
- Kun, É.; Zilahi-Sebess, L.; Szanyi, J. Battonya–Pusztaföldvári-hát térségének nagy entalpiájú geotermikusenergia-vagyona (I. rész): Hidrodinamikai és hőtranszportmodell. Földtani Közlöny 2022, 152, 53–75. [Google Scholar] [CrossRef]
- Gelhar, L.W.; Welty, C.; Rehfeldt, K.R. A Critical Review of Data on Field-Scale Dispersion in Aquifers. Water Resour. Res. 1992, 28, 1955–1974. [Google Scholar] [CrossRef]
- Langevin, C.D.; Provost, A.M.; Panday, S.; Hughes, J.D. Documentation for the MODFLOW 6 Groundwater Transport Model. U.S Geological Survey Techniques and Methods, Book 6. 2022; Chapter A61; 56p. Available online: https://pubs.usgs.gov/publication/tm6A61 (accessed on 10 May 2025).
- ModelMuse: A Graphical User Interface for Groundwater Models|U.S. Geological Survey. 2024. Available online: https://www.usgs.gov/software/modelmuse-a-graphical-user-interface-groundwater-models (accessed on 10 May 2025).
- Vass, I.; Tóth, T.M.; Szanyi, J.; Kovács, B. Hybrid numerical modelling of fluid and heat transport between the overpressured and gravitational flow systems of the Pannonian Basin. Geothermics 2018, 72, 268–276. [Google Scholar] [CrossRef]
- Abdulhaq, H. Machine Learning Model for Predicting Thermal Performance of High-Temperature Aquifer Thermal Energy Storage (HT-ATES) in Depleted Clastic Reservoirs. Zenodo 2025 (Version v1). Available online: https://zenodo.org/records/15294847 (accessed on 10 May 2025).
- Anderson, M.P.; Woessner, W.W.; Hunt, R.J. (Eds.) Front Matter. In Applied Groundwater Modeling, 2nd ed.; Academic Press: Cambridge, MA, USA, 2015; p. iii. [Google Scholar] [CrossRef]
- Fisher, A.; Rudin, C.; Dominici, F. All Models are Wrong, but Many are Useful: Learning a Variable’s Importance by Studying an Entire Class of Prediction Models Simultaneously. arXiv 2019, arXiv:1801.01489. [Google Scholar] [CrossRef]
- Ishikawa, T.; Morita, A.; Fukushima, T.; Ono, H. Three-Dimensional Cerebral Aneurysm Models for Surgical Simulation and Education—Development of Aneurysm Models with Perforating Arteries and for Application of Fenestrated Clips. Open J. Mod. Neurosurg. 2014, 4, 59–63. [Google Scholar] [CrossRef]
- Abdulhaq, H. Thermal Performance Analysis and Visualization App for UCN-Based Heat Simulations. Zenodo 2025 (Version V1). Available online: https://zenodo.org/records/15294958 (accessed on 10 May 2025).
- Collignon, M.; Klemetsdal, Ø.S.; Møyner, O.; Alcanié, M.; Rinaldi, A.P.; Nilsen, H.; Lupi, M. Evaluating thermal losses and storage capacity in high-temperature aquifer thermal energy storage (HT-ATES) systems with well operating limits: Insights from a study-case in the Greater Geneva Basin, Switzerland. Geothermics 2020, 85, 101773. [Google Scholar] [CrossRef]
- Drijver, B.; van Aarssen, M.; de Zwart, B. High-temperature aquifer thermal energy storage (HT-ATES): Sustainable and multi-usable. In Proceedings of the 12th International Conference on Energy Storage, Lleida, Spain, 16–18 May 2012. [Google Scholar]
- Winterleitner, G.; Schütz, F.; Wenzlaff, C.; Huenges, E. The Impact of Reservoir Heterogeneities on High-Temperature Aquifer Thermal Energy Storage Systems. A Case Study from Northern Oman. Geothermics 2018, 74, 150–162. [Google Scholar] [CrossRef]
- Tang, D.W.S.; Rijnaarts, H.H.M. Dimensionless Thermal Efficiency Analysis for Aquifer Thermal Energy Storage. Water Resour. Res. 2023, 59, e2023WR035797. [Google Scholar] [CrossRef]
| Parameters | Value/Description | Source |
|---|---|---|
| Initial Prescribed Hydraulic Head | Varies spatially | Derived from [60] |
| Horizontal Hydraulic Conductivity | Derived from permeability modeling | Estimated from well log data |
| Vertical Hydraulic Conductivity | Assumed as 50% of horizontal conductivity | Based on lithological assumptions |
| Specific Storage | 0.001 m−1 | Literature-based estimate |
| Effective Porosity | Derived from porosity modeling | Estimated from well log data |
| Specific Yield | 0.15 | Literature-based estimate |
| Bulk Density | Calculated via gamma ray log surface simulation | Derived from natural gamma ray log simulation |
| Parameter | Value/Description | Justification |
|---|---|---|
| Initial Temperature | Varies spatially | Derived from drill stem tests and bottom-hole temperature data |
| Advection Package | Third order TVD scheme Ultimate | Selected for numerical stability and accuracy |
| TRPT | 0.1 | Assumed based on typical sedimentary conditions [61] |
| TRVT | 0.01 | Assumed based on typical sedimentary conditions [62] |
| DMCOEF (Effective Molecular Diffusion Coefficient) | 0.01 m2/day | Literature-based estimate [63] |
| longitudinal Dispersivity | Varies with lithology | Based on the Rock Type Calculation and thermal conductivity of Bekes Fm. from [64] |
| Sorption | Linear isotherm | Common assumption for initial reactive transport modeling |
| Kinetic Rate Reaction | Zero order reaction | Assumed for simplification of reactive processes |
| Preconditioner | Jacobi | Default iterative solver preconditioner |
| Hyperparameter | Description of Tuning Performed |
|---|---|
| Number of estimators (n_estimators) | Increased to reduce variance and stabilize predictions. |
| Maximum depth (max_depth) | Limited to prevent overfitting and improve generalization. |
| Minimum samples per split (min_samples_split) | Adjusted to balance model complexity and predictive accuracy. |
| Minimum samples per leaf (min_samples_leaf) | Increased slightly to ensure robust generalization. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdulhaq, H.A.; Geiger, J.; Vass, I.; Tóth, T.M.; Medgyes, T.; Bozsó, G.; Kóbor, B.; Kun, É.; Szanyi, J. Predicting Thermal Performance of Aquifer Thermal Energy Storage Systems in Depleted Clastic Hydrocarbon Reservoirs via Machine Learning: Case Study from Hungary. Energies 2025, 18, 2642. https://doi.org/10.3390/en18102642
Abdulhaq HA, Geiger J, Vass I, Tóth TM, Medgyes T, Bozsó G, Kóbor B, Kun É, Szanyi J. Predicting Thermal Performance of Aquifer Thermal Energy Storage Systems in Depleted Clastic Hydrocarbon Reservoirs via Machine Learning: Case Study from Hungary. Energies. 2025; 18(10):2642. https://doi.org/10.3390/en18102642
Chicago/Turabian StyleAbdulhaq, Hawkar Ali, János Geiger, István Vass, Tivadar M. Tóth, Tamás Medgyes, Gábor Bozsó, Balázs Kóbor, Éva Kun, and János Szanyi. 2025. "Predicting Thermal Performance of Aquifer Thermal Energy Storage Systems in Depleted Clastic Hydrocarbon Reservoirs via Machine Learning: Case Study from Hungary" Energies 18, no. 10: 2642. https://doi.org/10.3390/en18102642
APA StyleAbdulhaq, H. A., Geiger, J., Vass, I., Tóth, T. M., Medgyes, T., Bozsó, G., Kóbor, B., Kun, É., & Szanyi, J. (2025). Predicting Thermal Performance of Aquifer Thermal Energy Storage Systems in Depleted Clastic Hydrocarbon Reservoirs via Machine Learning: Case Study from Hungary. Energies, 18(10), 2642. https://doi.org/10.3390/en18102642









