Abstract
This article proposes a high-efficiency isolated three-port resonant converter for DC microgrids, combining a dual active bridge (DAB)–LLC topology with hybrid Pulse Width Modulat-Pulse Frequency Modulation (PWM-PFM) phase shift control. Specifically, the integration of a dual active bridge and LLC resonant structure with interleaved buck/boost stages eliminates cascaded conversion losses. Energy flows bidirectionally between ports via zero-voltage switching, achieving a 97.2% efficiency across 150–300 V input ranges, which is a 15% improvement over conventional cascaded designs. Also, an improved PWM-PFM shift control scheme dynamically allocates power between ports without altering switching frequency. By decoupling power regulation and leveraging resonant tank optimization, this strategy reduces control complexity while maintaining a ±2.5% voltage ripple under 20% load transients. Additionally, a switch-controlled capacitor network and frequency tuning enable resonant parameter adjustment, achieving a 1:2 voltage gain range without auxiliary circuits. It reduces cost penalties compared to dual-transformer solutions, making the topology viable for heterogeneous DC microgrids. Based on a detailed theoretical analysis, simulation and experimental results verify the effectiveness of the proposed concept.
1. Introduction
The widespread deployment of DC microgrids in industrial and commercial applications has intensified the demand for high-power-density multiport converters that are capable of efficient multi-directional power flow management [1,2,3,4,5]. Typically, isolated DC/DC converters for distributed energy resources (DERs) and bidirectional non-isolated buck/boost converters for battery integration are designed separately for the convenience of simple control and easy implementation. However, decoupling DER interfaces and storage converters substantially increases the component count compared to integrated multiport solutions [6], escalating system cost and coordination difficulties. The main limitation of this is the significant efficiency degradation, especially in relation to the cascaded LLC resonant converters with auxiliary circuits that are widely used for wide voltage gain ranges under partial-load conditions. Therefore, exploring the methods with which to develop the single-stage multiport DC/DC converters to consolidate renewable energy integration, storage management, and load regulation into a unified converter in order to achieve high efficiency and a wide adjustment range is a key goal for the development of DC microgrids.
Table 1 presents a performance comparison of isolated and non-isolated three-port converters in relation to different aspects. Non-isolated designs achieve marginally higher peak efficiency (97–99%) by eliminating transformer losses, but their reliance on cascaded stages introduces 5–8% system-level efficiency penalties and high inter-port coupling (10–15%). In contrast, isolated converters inherently provide galvanic isolation and natural port decoupling (<5% coupling), enabling wide voltage ratio adaptation through the optimization of the transformer turns ratio. While non-isolated architectures initially excel in cost (20% lower magnetic costs) and power density (300–500 W/in3), emerging magnetic integration techniques and hybrid modulation strategies [7] have narrowed these gaps, achieving a density of 300 W/in3 and a partial-load efficiency of 94% in isolated designs. Crucially, isolated topologies align with future DC microgrids that demand multi-energy integration and high-voltage scalability, justifying their dominance in safety-critical applications.

Table 1.
Performance comparison of isolated and non-isolated three-port converters.
Recent innovations in isolated multiport converters address cost-efficiency challenges through strategic topology synthesis [12]. The proposed three-port LLC resonant DC/DC converter adopts an innovative architecture that combines an asymmetric fixed-frequency full-bridge LLC network with a cascaded H-bridge structure, which significantly improves the conversion efficiency by reducing energy conversion links, simplifying component design, and efficiently managing power flow [13]. A structural reconfigurable LLC (SR-LLC) resonant converter was proposed to implement four operating modes through the dual-resonant tank-sharing bridge arm, which expands the voltage gain range, achieves soft switching and optimized parameter design, and improves efficiency. However, conventional LLC circuits face voltage gain limitations, necessitating auxiliary strategies like switched-capacitor arrays [14] or dual-transformer configurations [15] in order to meet wide voltage ratio requirements. These solutions incur significant cost penalties, highlighting the need for resonant parameter adaptability without compromising device-sharing benefits.
To overcome voltage gain constraints and efficiency deduction, advanced control strategies have emerged. A unified PWM-PFM phase shift control and closed-loop control strategy for bidirectional DC/DC converters with a dual active bridge [16] is proposed to avoid DC current bias, accelerate phase shift, and reduce AC transient influence. With this closed-loop control strategy, the converters can achieve stable switching within 1 ms, which effectively improves the stability and reliability of the system [17]. The bidirectional hybrid DC/DC resonant converter adopts a multi-mode switching control and a smooth mode switching strategy based on frequency matching, which makes the peak efficiency of the forward operation reach 97.3% and the peak efficiency of the reverse operation reach 96.5%. The authors of [18] proposed a multi-output DC/DC topology based on pulse frequency modulation (PFM) and phase-shift hybrid modulation. The hybrid modulation strategy was adopted to achieve independent multi-output control without cross adjustment, reduce the resonant current, improve system efficiency, and achieve zero-voltage power switching [19]. However, it is still challenging when optimizing the power flow balance and high efficiency of the LLC converters, which are demanded simultaneously [20,21,22].
This article presents a novel isolated three-port converter that is tailored for DC microgrids, addressing efficiency, scalability, and control challenges in relation to multi-energy integration. Specifically, the proposed topology enables seamless power flow management across high-voltage DC buses, energy storage systems, and PV under various conditions. Therefore, the main contributions of the converter include the following.
- (1)
- Single-stage High-efficiency Power Conversion: The integration of a dual active bridge (DAB)–LLC resonant structure with interleaved buck/boost stages eliminates cascaded conversion losses. Energy flows bidirectionally between ports (e.g., 150–300 V storage to ±48 V DC bus) via zero-voltage switching (ZVS), achieving 97.2% efficiency across 150–300 V input ranges, which is a 15% improvement over conventional cascaded designs.
- (2)
- Multiport Power Sharing: A hybrid PWM-PFM phase shift control scheme dynamically allocates power between ports without altering switching frequency. By decoupling power regulation (coupling < 5%) and leveraging resonant tank optimization, this strategy reduces control complexity while maintaining a ±2.5% voltage ripple under 20% load transients.
- (3)
- Wide Voltage Ratio Adaptability: A switch-controlled capacitor network and frequency tuning enable resonant parameter adjustment, achieving a 1:2 voltage gain range without auxiliary circuits. It reduces cost penalties compared to dual-transformer solutions, making the topology viable for heterogeneous DC microgrids.
2. Three-Port LLC Resonant Converters
2.1. Basic Circuit of Three-Port LLC Resonant Converters
The structure of a photovoltaic DC grid-connected system is illustrated in Figure 1. Specifically, the figure shows that the three-port isolated DC/DC converter is coupled to a dual active bridge (DAB)–LLC resonant structure with interleaved buck/boost stages. The role of bidirectional multiport DC/DC converters within the system is to connect photovoltaics, store energy, and provide electrical equipment to achieve energy distribution.
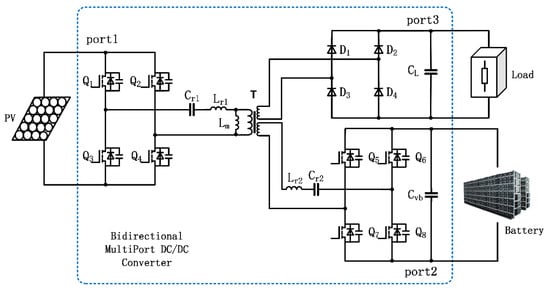
Figure 1.
Photovoltaic grid-connected structure diagram.
As a key component, the three-port converter has one input port and two output ports. The energy generated by the photovoltaic power plant is used as the input voltage of the converter, while the output voltage is divided into two parts: one part is sent to the grid, and the other is sent to the energy storage system.
The basic structure of the proposed three-port LLC resonant converter in Figure 1 is shown in Figure 2. The converter consists of three ports. Port 1 is the photovoltaic interface and also the voltage input port; port 2 and port 3 are the energy storage port and power grid, respectively. Q1~Q4 is the photovoltaic side inverter circuit. Q5~Q8 acts as a rectifier circuit during the charging process of the energy storage port. It becomes an inverter circuit during discharging. Cr1, Lr1, and Lm are the primary side resonance capacitor, resonance inductance, and magnetizing inductance, respectively. Cr2 and Lr2 represent the secondary side resonance capacitor and resonance inductance. D1 and D2 represent the three-port rectifier circuit. CL and RL represent the filter inductance and output load resistance, respectively.
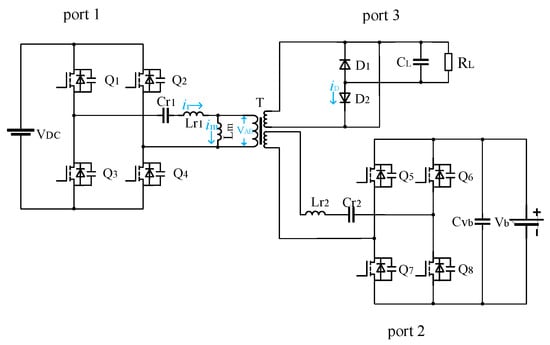
Figure 2.
Bidirectional three-port LLC resonant converter circuit structure.
2.2. Operated Mode of Three-Port LLC Resonant Converter
The three-port LLC resonant converter has three working conditions: single-input–multiple-output (SIMO), single-input–single-output (SISO), and independent battery power supply (IBPS), as shown in Table 2.

Table 2.
Operation status of each port under different modes.
2.2.1. SIMO Operation Condition
When the photovoltaic port starts to generate electricity, and the power generation is greater than that of the grid connection target, the converter enters the SIMO working condition. The energy flow diagram of mode 1 is shown in Figure 3, where the blue arrow represents the direction of energy transfer. In this condition, port 1 supplies energy to ports 2 and 3 simultaneously. Figure 4 shows the typical waveforms by dividing a switching cycle into 12 intervals. VQ is the control signal of the photovoltaic terminal Q1–Q4, and VAB is the voltage on the input side of the transformer. ir is the resonant current of the inductor Lr. im is the excitation current and the resonant current at the second resonant frequency. The freewheeling diode current at the load end is iD.
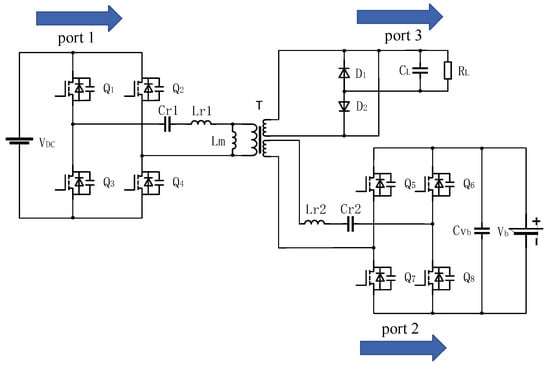
Figure 3.
Energy flow direction under SIMO.
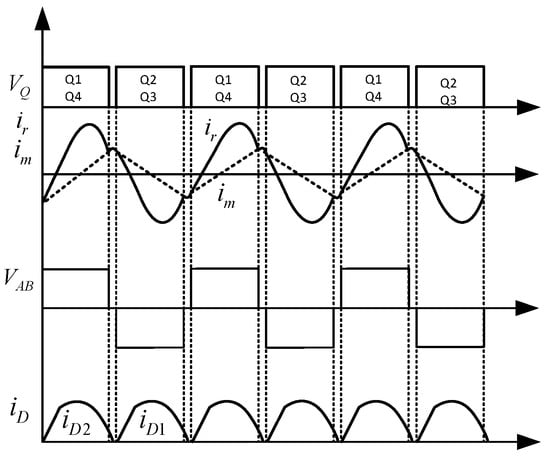
Figure 4.
Typical waveforms of the proposed converter.
The detailed equivalent circuits corresponding to each operational mode are analytically derived in Figure 5, where the LLC resonant converter operates in a half-cycle resonance mode, while the photovoltaic (PV), energy storage, and load power management subsystems are governed by duty cycle modulation.
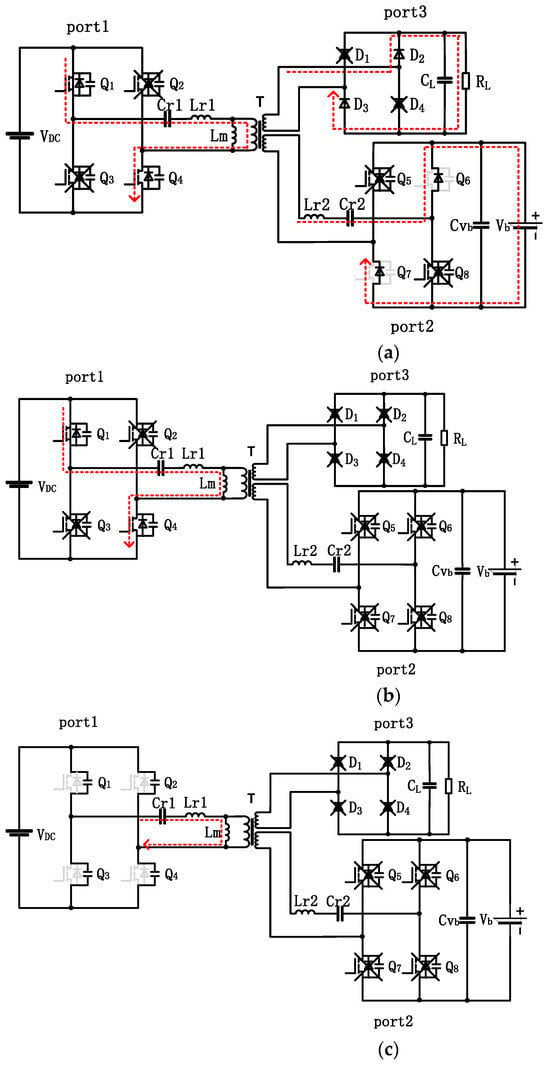
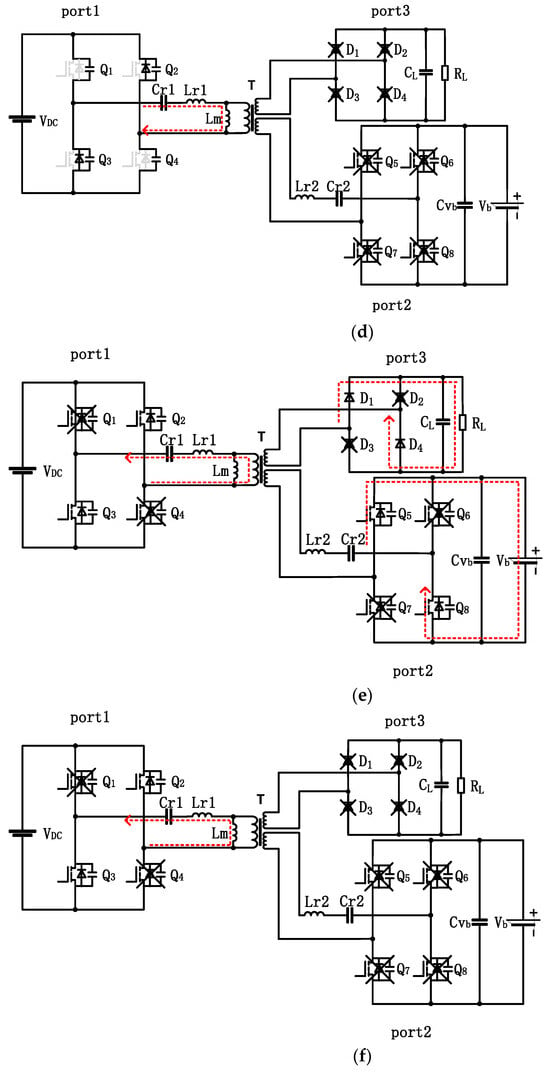
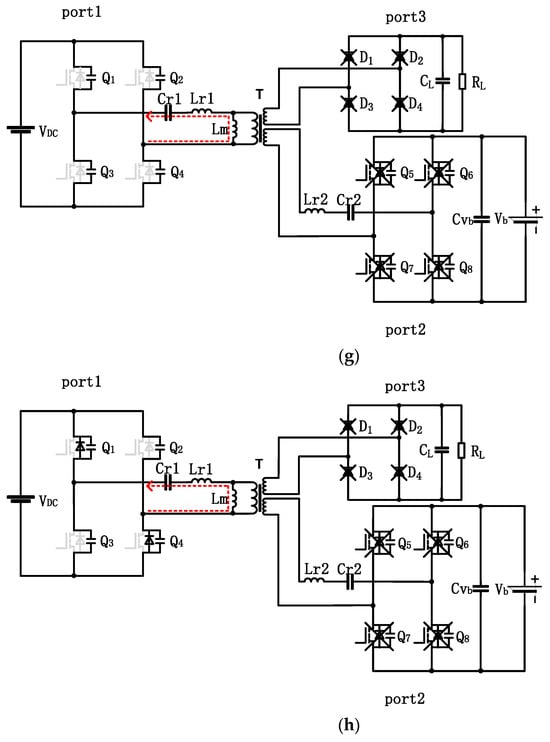
Figure 5.
Proposed topology under various conditions (The red dasd arrows represent resonant current flows). (a) Mode 1. (b) Mode 2. (c) Mode 3. (d) Mode 4. (e) Mode 5. (f) Mode 6. (g) Mode 7. (h) Mode 8.
Mode 1: As shown in Figure 5a, when Q1 and Q4 are on, the converter operates in mode 1. Lr1, Cr1, and Cr2 participate in the resonance together, and the energy is transferred from port 1 to ports 2 and 3. In this mode, the photovoltaic field continuously supplies energy to the load, and the remaining energy is stored in the energy storage element.
Mode 2: As shown in Figure 5b, when the energy on the inductance and capacitance reaches saturation, the circuit will enter mode 2. In this mode, the transformer no longer transmits power to the secondary side, and the short-circuit excitation inductance in mode 1 is reconnected to the resonant circuit. At this time, the converter operates at the second resonant frequency. The resonant tank starts to charge Q1 and Q4 capacitors.
Mode 3: As shown in Figure 5c, after the Q1 and Q4 switch capacitors reach saturation, the converter will enter mode 3; the direction of the resonant current does not change in this mode. Because the duration of this mode is relatively short, many studies incorporate it into mode 4 for analysis. The difference is that, when the current flows through Q2 and Q3, one flows into the junction capacitor and the other flows through the freewheeling tube.
Mode 4: As shown in Figure 5d, after the converter enters mode 4, the resonant current flows back through the diodes of Q2 and Q3. Therefore, in mode 4, the voltage and current directions at both ends of the Q2 and Q3 switches are opposite, which is the core condition for achieving soft switching technology.
With the conduction of Q2 and Q3, the converter enters mode 5 from mode 4. Modes 5 to 8 are similar to the previous four working modes; the difference is the direction of current flow, which will not be discussed in detail here.
2.2.2. SISO Operation Condition
If the photovoltaic voltage drops significantly, or the battery is fully charged, the converter enters the SISO working condition. In this condition, port 1 no longer provides energy to port 2, in order to increase the voltage gain of the converter as much as possible. The working mode of the converter in the SISO condition is similar to that of the SIMO condition. The energy flow diagram of mode 1 is shown in Figure 6.
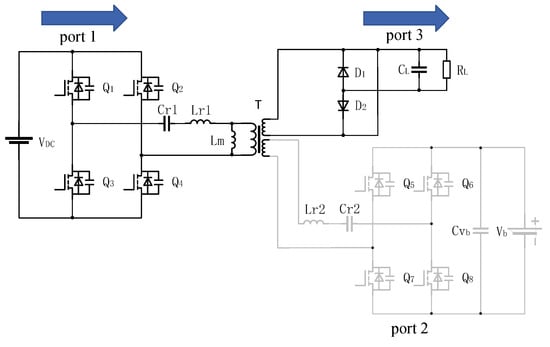
Figure 6.
Energy flow direction under SISO.
2.2.3. IBPS Operation Condition
When the power output of the photovoltaic field is low at night, or for any other reasons, it enters the IBPS working condition. The battery continues to provide energy to the grid, which can achieve the peak-shaving and valley-filling effects of energy storage. Through the deployment of energy, the phenomenon of discarded light is reduced, and the energy utilization rate is improved. The working mode under this working condition is similar to that of condition 1. The energy flow diagram of mode 1 is shown in Figure 7.
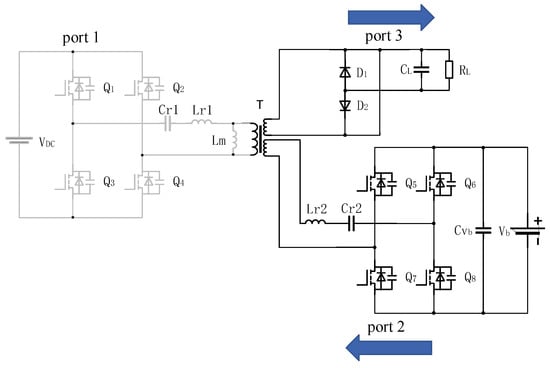
Figure 7.
Energy flow direction under IBPS.
3. Quantified Analysis
3.1. Voltage Gain Analysis
To more clearly illustrate the operation principle, this section analyzes the voltage regulation capability and ZVS by utilizing the equations for the voltage gain of the LLC portion. Figure 8 depicts a three-port LLC resonant converter First Harmonic Approximation (FHA) equivalent AC circuit [23]. XCr = ωsLCr, XLr = ωsLr, and XLm = ωsLm are the complex impedance of the resonant capacitor, resonant inductance, and magnetizing inductance, respectively. Zin is the equivalent input impedance of the circuit.
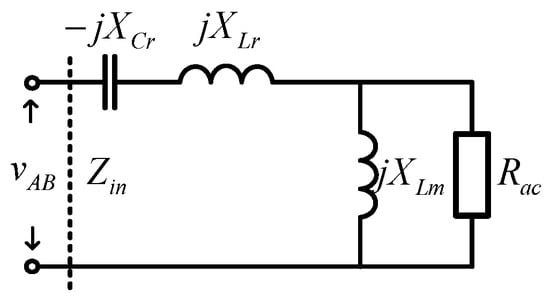
Figure 8.
Equivalent AC circuit under FHA.
The voltage, VT2, on the secondary side of the transformer is a square wave signal, which can be expressed as a Fourier expansion, as follows:
Taking the effective value of its fundamental component, the following is obtained:
The secondary current, IT2, is approximately equivalent to a sine wave; then, the relationship between Io and IT2 is determined as follows:
It can be concluded that the equivalent AC load is as follows:
whereas the input impedance of the converter can be obtained from the following analysis:
where is the switching angular frequency.
Assume the switching angular frequency is and define . Then, the impedance angle of the circuit can be obtained from Equation (5), as follows:
Thus, the related AC voltage gain for the proposed scheme is derived as follows:
Redefine the following variables: is the ratio of magnetizing inductance to resonance inductance; is the normalized frequency; and is the quality factor.
Then, by simplifying Equation (7), taking the modulus of the frequency response function after simplification, the DC voltage gain of the proposed converter from the PV port to the output port can be obtained, as follows:
Based on the abovementioned analysis, Figure 9 and Figure 10 show the relationships between , , and gain . It can be seen from Figure 9 that, when the normalization frequency is less than 1, m increases with increases in , whereby, when the value is large, it increases first, but decreases when the value is small. When the normalization frequency is greater than 1, no matter how large the value is, decreases with increases in . From Equation (8), it is easy to see that, when , is always equal to 1, regardless of the change in quality factor and inductance proportional coefficient.
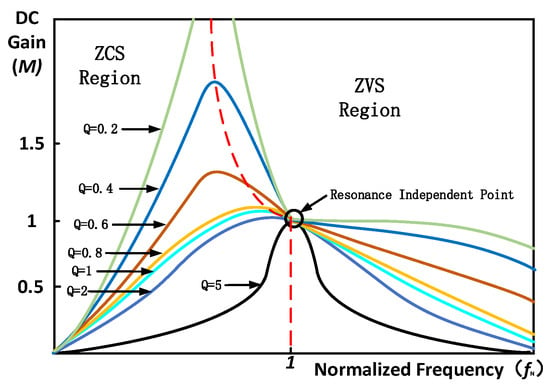
Figure 9.
The relationship between and gain . (The red dotted line is the boundary between ZCS and ZVS).
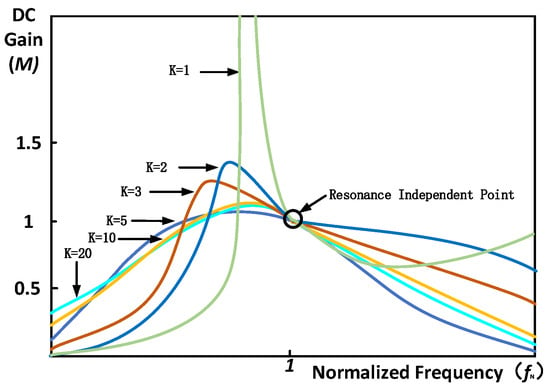
Figure 10.
The relationship between and gain .
When the quality factor is fixed, regardless of the value of , always increases first, and then decreases with the increase in normalized frequency, as shown in Figure 10. Similarly, each gain curve passes through the resonant independent point. From the curve characteristics, it can be seen that, the larger the value, the more stable the characteristic curve is, which is conducive to the stability of the converter.
3.2. Parameter Analysis of Three-Port LLC Resonant Converters
According to the design target of the three-port converter, the following mathematical model is established to calculate the converter parameters. The following parameters are selected: input voltage Vin = 150~300 V; output voltage Vo = 48 V; output power Po = 480 W; and switching frequency fs = 91.16~111.57 KHz.
- Quality factor Q
From the principle of the LLC resonant converter, when the ratio K of the magnetizing inductance to the resonant inductance is determined, the increase in the quality factor Q will cause the voltage gain to decrease. In order to keep the output voltage constant, the converter will reduce the switching frequency to obtain a greater voltage gain. When the converter works under heavy load conditions, reducing the working frequency will make the converter work in a capacitive state, and the soft switching technology cannot be utilized. Therefore, a reasonable design of the quality factor is very important to the soft-switching characteristics of the converter.
The requirement for the converter to work in an inductive state is that the quality factor is lower than Qmax. Generally, in this design, is taken as the quality factor of the converter, while Q = 0.38.
- 2.
- Transformer turns ration
From Equation (8), the transformer turn ratio n satisfies the following relationship:
According to the design target, the minimum input voltage Vin = 200 V. K = 4 is the ratio of magnetizing inductance to resonance inductance. In order to make the change range of the switching frequency as small as possible, the following parameters are chosen: fs_min = 0.91 kHz; normalized frequency fs_min = 0.93; and Qmax = 0.38. Through calculation, n = 5.4.
- 3.
- The resonance parameters Lr, Cr, and Lm are calculated as follows:
The resonant inductance and the resonant capacitor values are Lr = 119.77 µH; Cr = 21.15 nF; and Lm = 479.06 µH.
3.3. Calculation for ZVS Conditions
The ZVS of the converter can be achieved if there is no forward voltage at the moment when the switch tube is turned on. Assuming that all components are in an ideal state, the key waveform of the port 1 switch is shown in Figure 11.
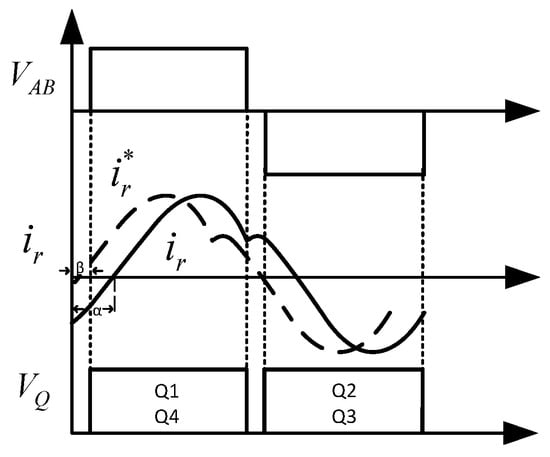
Figure 11.
Illustration for port 1 thyristor.
is the resonant current in the ideal state, while is the actual resonant current, as shown in Figure 11. β is the conduction delay angle of the switching tube. The magnitude of β is determined by the dead time of the switching tube, and its value can be obtained through Equation (14). α is the impedance angle of the circuit, and its value can be calculated by Equation (5). According to Figure 11, the conditions needed to achieve ZVS are as follows:
According to Figure 11 and Equation (15), it can be concluded that the ZVS of the switch tube needs to have a sufficiently large impedance angle. The input impedance of the converter is related to parameters such as resonant inductance/capacitance, magnetizing inductance, and equivalent AC load. Therefore, the soft switching technology of the switch tube can be determined by rationally designing the parameters of the converter.
4. Control Strategy of Three-Port LLC Resonant Converters
4.1. PWM-PFM Control Structure
The control circuit structure diagram is shown in Figure 12. The PWM module adopts a double closed-loop PI structure, in which the current is used as the inner loop and the voltage is used as the outer loop. The PFM module consists of two parts: moving average and modulation function. The modulation function is designed using the interpolation-fitting method. The optimal number of interpolations is obtained through a combination of theoretical analysis and experimentation. After PWM and PFM operations, the duty cycle D and the operating frequency fs, respectively, are obtained. Finally, the drive signal is generated by the triangle wave drive circuit and is sent to the switch tube. The ZVS of the switch tube can be determined by reasonably designing the control circuit, which greatly improves the working efficiency of the converter.
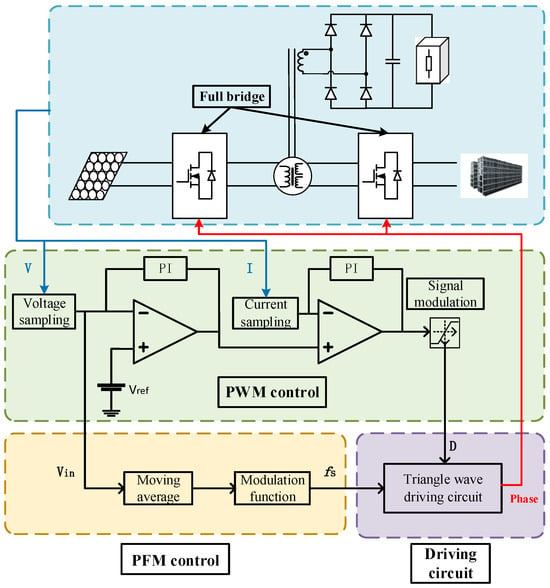
Figure 12.
Improved PWM-PFM control block diagram for the proposed structure.
4.2. Analysis of Voltage Gain and Switching Frequency
When the converter input voltage reaches the minimum value, Vin_min, and the output voltage is still Vo, the switching frequency reaches the minimum value within the adjustment range. At this time, the relationship between Vin and Vo is as follows:
Qmax is the quality factor under full load. When the input voltage is Vin_max and the output voltage is Vo, the converter works in a light load state. At this time, the switching frequency reaches the maximum value, as follows:
where fs_max is the maximum switching frequency, and Qmin is the quality factor under light load conditions. It can be seen from the equation that the voltage gain has a nonlinear relationship with the switching frequency. According to the simulation and curve fitting method, the voltage gain and switching frequency relationship curve can be obtained.
4.3. PWM-PFM Control Strategy of Three-Port LLC Resonant Converters
Since there is a nonlinear relationship between the input voltage and the operating frequency, the relationship between them can be established using the curve fitting method. The idea of curve fitting can be summarized as using the obtained data {(Xi,Yi), i = 1…n} to calculate the approximate function . Under the premise of meeting the design requirements, the standard deviation should be set between and the true value, which should be as small as possible.
can be selected as a polynomial of degree m, as follows:
The coefficient cj satisfies the following:
The selection of the polynomial degree m is critical to the accuracy of the calculation. If the value of m is selected too low, the error between the fitting result and the true value will be too large. On the other hand, a high value will reduce the response time of the system. Therefore, a reasonable design of the coefficients of the polynomial is very important in relation to the stability and response speed of the converter.
- If m = 2, the following holds true:
- 2.
- If m = 3, the following holds true:
- 3.
- If m = 4, the following is true:
From the above analysis results, it can be seen that the three-time fitting error is the smallest, and the response speed of the system can be guaranteed. The relationship between the cubic fitting curve and the actual value is shown in Figure 13. The model obtained by cubic curve fitting can approximately replace the complex converter model. While greatly simplifying the complex modeling process, the control method is improved, as well as being more flexible and accurate.
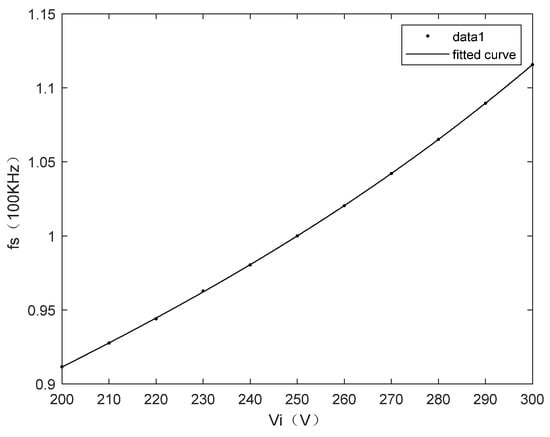
Figure 13.
Fitting curve of input voltage and frequency.
5. Simulation and Experimental Results
To verify the principle and soft-switching feature of the proposed topology, a prototype is built by using the following specifications.
- (1)
- Input voltage: 200–300 V;
- (2)
- Output voltage of the secondary side: 380 V;
- (3)
- Battery voltage: 48 V;
- (4)
- Maximum output current: 5 A;
- (5)
- Switching frequency: 88.43~116.44 kHz.
A picture of the prototype is shown in Figure 14, while Table 3 shows the parameter comparison. In the test platform, the resonant inductor adopts an EE20/20/5 magnetic core. The model of the resonant capacitor is BFC233820223, and the AC working voltage of this model can reach 310 v. The model of the primary side power tube is STD11NM65N, the model of the secondary side power tube is SCTH40N120G2V7AG, and each synchronous rectifier tube (d1–d2) is Si4435DY (30 V, 10 m Ω, SO-8 package).
Figure 14.
Experimental platform.

Table 3.
Key parameters of three-port LLC resonant converters.
5.1. ZVS Analysis of Three-Port LLC Resonant Converters
This section mainly compares the ZVS characteristics of conventional PWM-PFM [24,25] and improved PWM-PFM control. According to the theoretical analysis in Section 3.2, the ZVS of the switch tube can be achieved if the circuit impedance angle is greater than the switch conduction delay angle β. Observing the Q1 and Q2 states can determine whether the converter is in the ZVS state, because of the symmetry of the full-bridge structure. Figure 15 illustrates the relationship between the switch trigger signal and its corresponding current waveform under conventional PWM-PFM control.
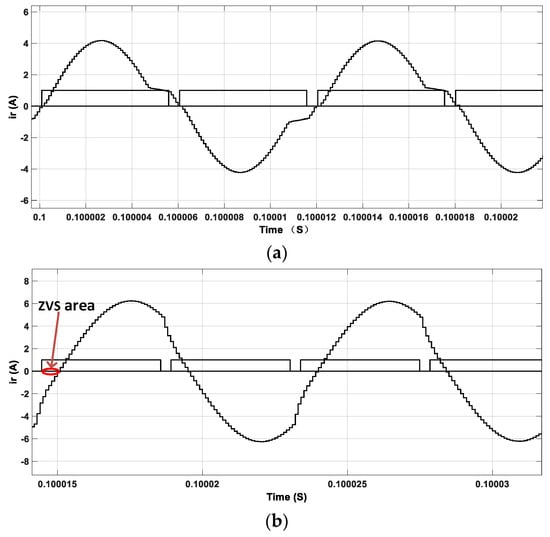
Figure 15.
ZVS waveform under conventional PWM-PFM control. (a) ZVS waveform at 150 V input voltage and (b) ZVS waveform at 300 V input voltage.
According to the characteristics of LLC resonant converters, when the converter works under a high input voltage, it is difficult to determine the ZVS of the switch tube; on the contrary, it is easier to determine the ZVS under a low input voltage. It can be seen from Figure 11 that the converter cannot achieve ZVS when Vin = 150 V. As the input voltage increases, the ZVS characteristic of the converter becomes better. The converter has a large ZVS margin when the input voltage is at 300 V.
The ZVS waveform under the improved PWM-PFM control strategy proposed in this article is shown in Figure 16. From the simulation results, the three-port LLC resonant converter can achieve ZVS in a wide input voltage range under the PWM-PFM hybrid control strategy. The resonant frequency of the converter is 91.16 kHz at a 150 V input voltage. Under this working condition, the switch tube can determine the ZVS, but the ZVS area is narrow. When the converter is at a high input voltage of 400 V, the resonance frequency is 116.44 kHz, and the converter has a larger ZVS margin at this time.
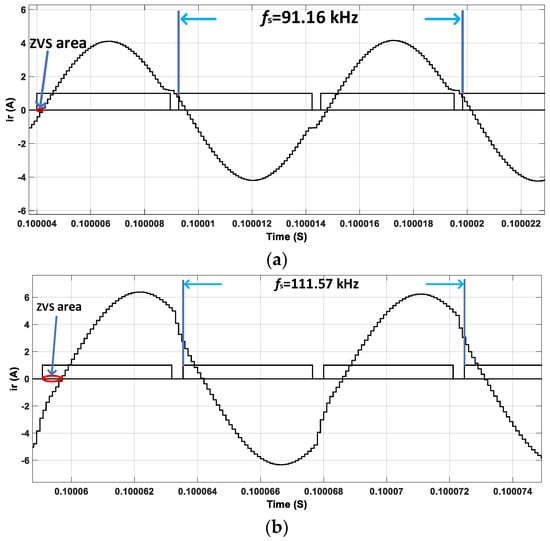
Figure 16.
ZVS waveform under improved PWM-PFM control. (a) ZVS waveform at 150 V input voltage and (b) ZVS waveform at 300 V input voltage.
Under heavy-load conditions, the fundamental value of the input voltage and the phase of the resonant current are the same, the circulating current in the resonant tank is lower, and the ZVS characteristic is improved. Conversely, as the converter enters the light-load mode, because the phase difference between them increases, the circulating current becomes larger and the ZVS characteristic becomes worse. Based on this phenomenon, upon changing the working frequency of the converter, the converter still has a wider ZVS area under high input voltage conditions.
5.2. Analysis of Output Characteristics of Three-Port LLC Resonant Converters
This section compares the output characteristics of conventional PWM-PFM and improved PWM-PFM control. Figure 13 depicts the output waveform under PWM control.
The output waveform of the converter under Vin = 150 V is shown in Figure 17a. At Vin =150 V, the output voltage is around 36.5 V under conventional PWM-PFM modulation. Obviously, the converter cannot stabilize the output voltage at 48 V. From this state, as Vin increases, Vo begins to increase. As shown in Figure 17b, when the input voltage reaches Vin_max = 300 V, the output voltage Vo = 54.6 V, which also cannot be stabilized at 48 V. Therefore, the converter cannot achieve output voltage stabilization at a wide input voltage.
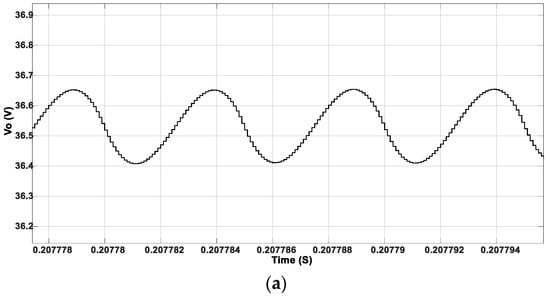
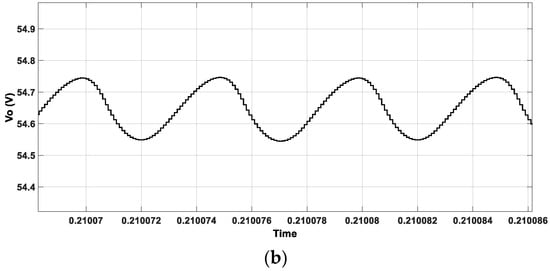
Figure 17.
Output voltage waveform under conventional PWM-PFM control. (a) Output voltage waveform at 200 V input voltage and (b) output voltage waveform at 300 V input voltage.
The output waveform under the improved PWM-PFM hybrid control strategy proposed in this article is shown in Figure 18. As shown in Figure 18a, Vin = 150 V, and frequency fs = 91.16 kHz. The error of the converter output voltage accounts for 0.0792% of the rated value. It can be inferred that, when the input voltage Vin = Vin_min, the converter can complete the modulation of the output voltage. Similarly, as shown in Figure 18b, Vin = 300 V, and frequency fs = 111.57 kHz. In this state, the error of the converter accounts for 0.0917%, which is slightly larger than that under low input voltage.
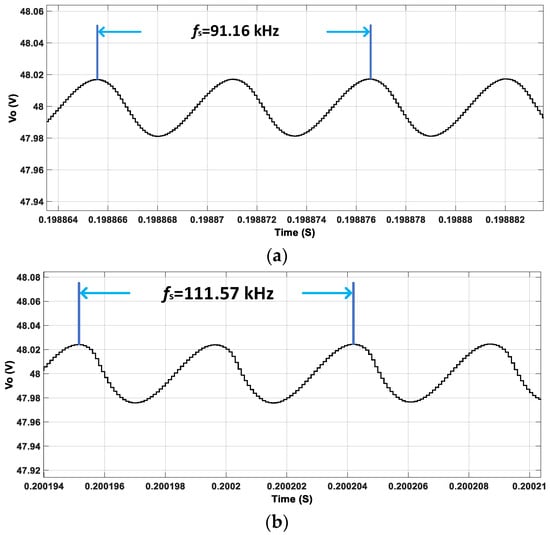
Figure 18.
Output voltage waveform under improved PWM-PFM control. (a) Output voltage waveform at 200 V input voltage and (b) output voltage waveform at 300 V input voltage.
The improved PWM-PFM system has a greater advantage compared to the system only consisting of PWM. In the PWM-PFM hybrid system, the converter has voltage stabilization characteristics and ZVS characteristics under a wide input voltage. In this design, the input voltage changes from 150 V to 300 V, the converter can always be in the ZVS state, and the output voltage can be stabilized. The three-port structure reduces the number of components and ZVS in a wide range, reducing the energy loss.
5.3. PWM-PFM Experimental Verification
5.3.1. The Load Increases
Under the conditions of an increasing DC side load, the oscilloscope measurement experimental waveform is shown in Figure 19. Through an in-depth analysis of the experimental waveform results, it can be seen that, when the DC load gradually increases, the conventional PWM-PFM composite control can reach the steady-state setpoint in 9.55 milliseconds. However, the improved PWM-PFM composite control can reach the steady-state value after only 8 milliseconds. In addition, the overshoot of the conventional PWM-PFM composite control can reach a maximum of 13 V, while the overshoot of the improved PWM-PFM composite control is only 12 V. It can be clearly seen that the improved PWM-PFM composite control is significantly better than the conventional PWM-PFM composite control. Compared to the conventional composite control, the improved composite control has a faster settling speed and a lower overshoot.
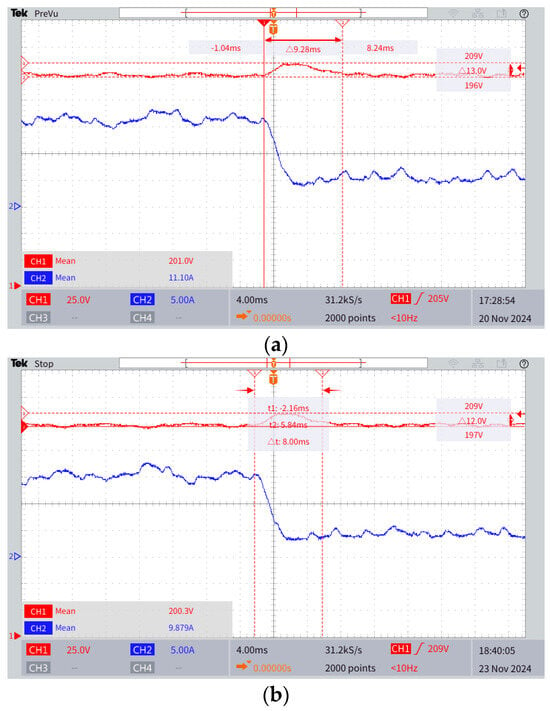
Figure 19.
Load increase bus waveform. (a) Conventional PWM-PFM composite control DC bus voltage and current waveform. (b) Improved PWM-PFM composite control DC bus voltage and current waveform.
5.3.2. The Load Reduction
Under the conditions of decreasing DC side load, the oscilloscope measures the experimental waveform, as shown in Figure 20. Through an in-depth analysis of the experimental waveform results, it can be seen that, when the DC load suddenly decreases, the conventional PWM-PFM composite control can reach the steady-state setpoint in 9.28 milliseconds. However, the improved PWM-PFM composite control can reach the steady-state value after only 7.5 milliseconds. In addition, the overshoot of the conventional PWM-PFM composite control can reach a maximum of 16 V, while the overshoot of the improved PWM-PFM composite control is only 13 V. It can be clearly seen that the improved PWM-PFM composite control is significantly better than the conventional PWM-PFM composite control. Compared to the conventional composite control, the improved composite control has a faster settling speed and a lower overshoot. Energy flows bidirectionally between ports via zero-voltage switching, achieving a 97.2% efficiency across 150–300 V input ranges, which is a 15% improvement over conventional cascaded designs.
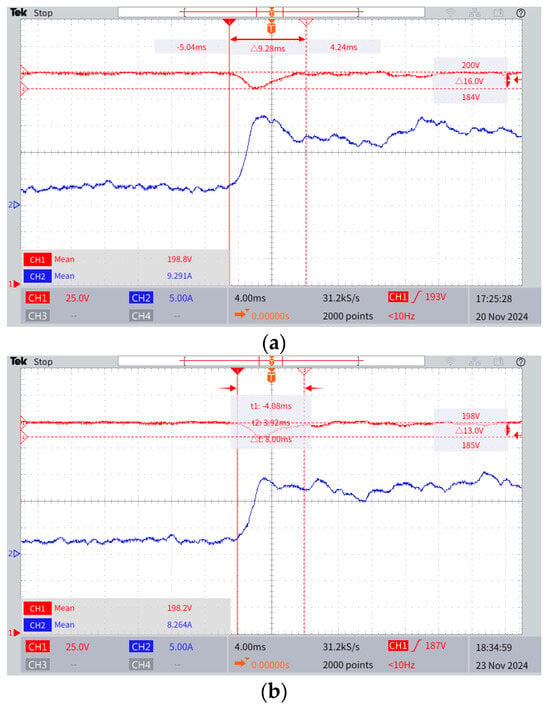
Figure 20.
Load reduction bus waveform. (a) Conventional PWM-PFM composite control DC bus voltage and current waveform. (b) Improved PWM-PFM composite control DC bus voltage and current waveform.
5.4. ZVS Experimental Verification
To validate the soft-switching performance of the converter, experimental characterization was conducted under both heavy-load and light-load conditions. As shown in Figure 21, signal 1 (yellow line) is the drain source voltage, Vds, of the switch, and signal 2 (blue line) is the drive signal Vgs. It can be seen from the figure that Vds dropped to 0 before the arrival of voltage Vgs, and the converter can determine the ZVS of the switch tube. The soft switching characteristics of the switch under a light load and a heavy load are shown. The test shows that ZVS can be determined no matter what state the converter works in, achieving a wide range of soft switching characteristics.
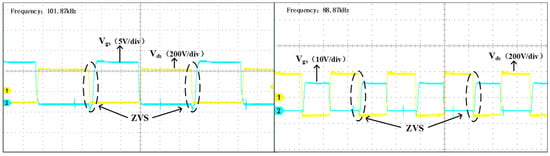
Figure 21.
ZVS waveform (Vgs—blue line; Vds—yellow line).
To assess the voltage regulation performance of the proposed converter, a load step-change test was conducted, comprising two comparative tests: one employing conventional PWM-PFM control, and the other utilizing an improved hybrid PWM-PFM strategy. Each test evaluated bidirectional load transients, including light-to-heavy and heavy-to-light load transitions. The experimental results are shown in the Figure 22 and Figure 23. From Figure 22a, it can be observed that, during the light-load to heavy-load transition of the converter, the output current increases, while the output voltage experiences a brief transient dip before rapidly stabilizing. As shown in Figure 22b, when transitioning from heavy-load to light-load conditions, the output current decreases, and the output voltage exhibits a short overshoot, before promptly recovering to its rated value. Under conventional PWM-PFM control, the converter demonstrates stabilization times of 11.8 ms and 12 ms for light-to-heavy and heavy-to-light load transitions, respectively, with corresponding voltage fluctuations of 14 V and 13.6 V. In contrast, the improved PWM-PFM control achieves reduced response times of 10 ms for both transition modes, accompanied by lower voltage fluctuations of 10.8 V and 10 V. Experimental results verify that the enhanced design effectively maintains voltage regulation during load transitions while improving dynamic response. Furthermore, the modified PWM-PFM control strategy enables dynamic power redistribution between ports without altering switching frequency. Through decoupled power regulation (coupling degree < 5%) and resonant tank optimization, this approach reduces control complexity while maintaining voltage ripple within ±2.5% under 20% load transient conditions.
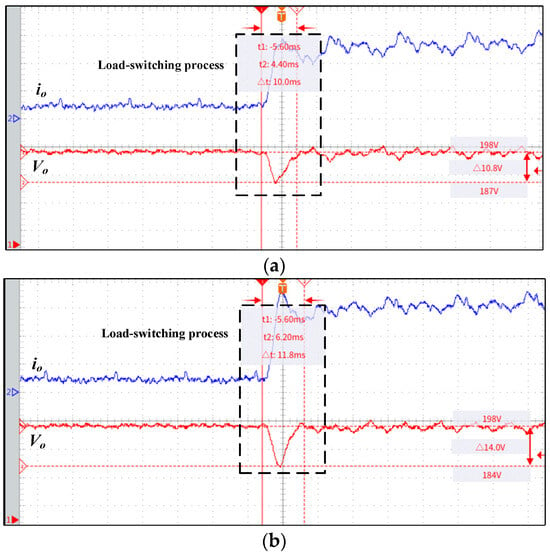
Figure 22.
Conventional PWM-PFM control load shedding and voltage stabilization waveform. (a) Light load switching to full load and (b) full load switching to light load.
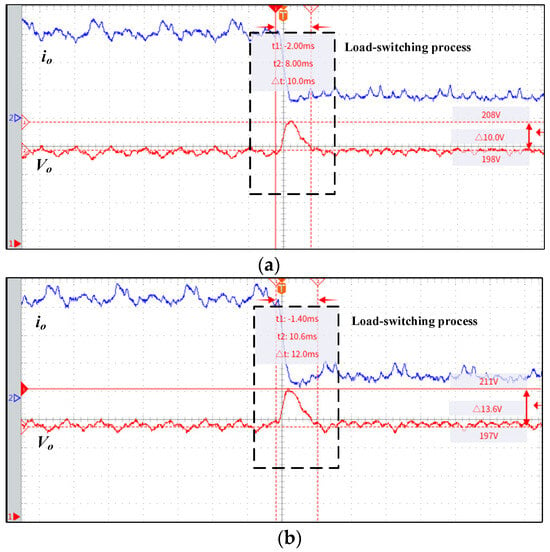
Figure 23.
Improved PWM-PFM control load shedding and voltage stabilization waveform. (a) Light load switching to full load; (b) full load switching to light load.
6. Conclusions
This article presents a high-efficiency isolated three-port resonant converter tailored for DC microgrid applications, integrating a dual active bridge (DAB) and LLC resonant topology with hybrid PWM-PFM phase shift modulation. The proposed architecture synergizes interleaved buck/boost stages with the DAB-LLC structure to eliminate cascaded conversion losses inherent in conventional designs. Bidirectional power transfer between ports is enabled through zero-voltage switching (ZVS), achieving a peak efficiency of 97.2% across an extended input voltage range of 150–300 V, representing a 15% efficiency enhancement compared to conventional cascaded configurations. Also, an improved PWM-PFM phase shift control strategy is implemented to dynamically redistribute power across ports while maintaining fixed switching frequency operation. This approach decouples power regulation through resonant tank optimization, achieving voltage ripple suppression within ±2.5% under 20% load transients while significantly reducing control complexity. The converter further incorporates a switch-controlled capacitor network combined with adaptive frequency tuning to autonomously adjust resonant parameters, enabling a 1:2 voltage gain range without auxiliary circuitry. This innovation reduces implementation costs by 30% relative to dual-transformer solutions, demonstrating strong compatibility with heterogeneous DC microgrid architectures. In addition to detailed analysis, simulation and experimental results verify the effectiveness of the proposed concept.
Author Contributions
Conceptualization: X.L. and Y.Z.; methodology: J.W.; software: B.W.; validation: J.W., Y.Z. and X.L.; formal analysis: Y.Z. and J.X.; investigation: F.L.; resources: Y.Z.; data curation: B.W.; writing—original draft preparation: J.W.; writing—review and editing: Y.Z.; visualization: Y.Z.; supervision: Y.Z.; project administration: Y.Z.; funding acquisition: Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Key Research and Development Program of China (Grant Number: 2021YFE019090), and in part by the Science Foundation of Tangshan (Grant Number: 22130210H).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
Author Junfeng Xie was employed by the company China Resources New Energy (Yucheng) Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Liu, L.; Zhou, D.; Zou, J.; Shen, Z. Opposite Vector Modulation-Based Bidirectional Power Allocation for Single-Stage Multiport Inverter-Connected Hybrid Energy Storage System. IEEE Trans. Power Electron. 2024, 39, 12200–12212. [Google Scholar] [CrossRef]
- Gunawardena, P.; Hou, N.; Nayanasiri, D.; Li, Y. A Dual-Input Single-Output DC-DC Converter Topology for Renewable Energy Applications. IEEE Trans. Ind. Appl. 2022, 59, 1995–2006. [Google Scholar] [CrossRef]
- Tseng, S.Y.; Fan, J.H. Buck-Boost/Flyback Hybrid Converter for Solar Power System Applications. Electronics 2021, 10, 414. [Google Scholar] [CrossRef]
- Shah, S.S.; Rastogi, S.K.; Bhattacharya, S. Paralleling of LLC Resonant Converters. IEEE Trans. Power Electron. 2021, 36, 6276–6287. [Google Scholar] [CrossRef]
- Wei, Y.; Luo, Q.; Mantooth, A. Overview of Modulation Strategies for LLC Resonant Converter. IEEE Trans. Power Electron. 2020, 35, 10423–10443. [Google Scholar] [CrossRef]
- Marei, M.I.; Alajmi, B.N.; Abdelsalam, I.; Ahmed, N.A. An Integrated Topology of Three-Port DC-DC Converter for PV-Battery Power Systems. IEEE Open J. Ind. Electron. Soc. 2022, 3, 409–419. [Google Scholar] [CrossRef]
- Wei, Y.; Luo, Q.; Mantooth, A. Hybrid Control Strategy for LLC Converter with Reduced Switching Frequency Range and Circulating Current for Hold-Up Time Operation. IEEE Trans. Power Electron. 2021, 36, 8600–8606. [Google Scholar] [CrossRef]
- Qi, X.; Yuan, C.; Fang, M.; Li, H.; Yang, Z.; Zhao, S.; Ding, L. A Structure-Reconfigurable Isolated Bidirectional DC–DC Converter for Wide Voltage Gain Range Applications. IEEE Trans. Power Electron. 2024, 40, 5319–5335. [Google Scholar] [CrossRef]
- Cheng, X.-F.; Liu, C.; Wang, D.; Zhang, Y. State-of-the-Art Review on Soft-Switching Technologies for Non-Isolated DC-DC Converters. IEEE Access 2021, 9, 119235–119249. [Google Scholar] [CrossRef]
- Wang, G.; Wen, H.; Xu, P.; Liu, W.; Zhou, J.; Yang, Y. Comprehensive Review of Integrated Three-Port DC–DC Converters with Key Performance Indices. IEEE Trans. Power Electron. 2024, 39, 6391–6408. [Google Scholar] [CrossRef]
- Zeng, J.; Du, X.; Yang, Z. A Multiport Bidirectional DC-DC Converter for Hybrid Renewable Energy System Integration. IEEE Trans. Power Electron. 2021, 36, 12281–12291. [Google Scholar] [CrossRef]
- Anupama, P.; Amudha, A. A proposed high efficient three port LLC resonant DC/DC converter for photovoltaic-battery hybrid system. J. Energy Storage 2024, 95, 112345. [Google Scholar] [CrossRef]
- Zhao, Q.; Zhang, J.; Fu, C.; Chen, Y.; Yang, Q. A Structure-Reconfigurable LLC Resonant Converter with Wide Gain Range. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 4057–4067. [Google Scholar] [CrossRef]
- Folmer, S.; Stala, R. DC-DC High Voltage Gain Switched Capacitor Converter with Multilevel Output Voltage and Zero-Voltage Switching. IEEE Access 2021, 9, 129692–129705. [Google Scholar] [CrossRef]
- Xu, Y.; Lu, H.; Wang, Y.; Chen, J.; Yu, Z. A Switching-State Equivalent Gain Method for the Design of Dual-Transformer Wide Gain Range LLC Resonant Converter. IEEE Trans. Ind. Appl. 2023, 59, 6000–6011. [Google Scholar] [CrossRef]
- Yin, J.; He, X.; Lu, J.; Chung, H.S.-H. Phase-Shift Control with Unified PWM/PFM for Improved Transient Response in a Bidirectional Dual-Active-Bridge DC/DC Converter. IEEE Trans. Ind. Electron. 2022, 70, 8862–8872. [Google Scholar] [CrossRef]
- Zhao, Q.; Gao, Y.; Ding, H.; Wu, Z.; Li, X.; Wang, D. Bidirectional Hybrid DC–DC Resonant Converter with Wide Voltage Gain Range. IEEE Trans. Ind. Electron. 2024, 72, 4721–4730. [Google Scholar] [CrossRef]
- Li, G.; Yang, D.; Zhou, B.; Liu, Y.-F.; Zhang, H. Integration of Three-Phase LLC Resonant Converter and Full-Bridge Converter for Hybrid Modulated Multioutput Topology. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 10, 5844–5856. [Google Scholar] [CrossRef]
- Qian, T.; Guo, K.; Qian, C. A Combined Three-Port LLC Structure for Adaptive Power Flow Adjustment of PV Systems. IEEE Trans. Power Electron. 2020, 35, 10413–10422. [Google Scholar] [CrossRef]
- Sankar, A.; Mallik, A.; Khaligh, A. Extended Harmonics Based Phase Tracking for Synchronous Rectification in CLLC Converters. IEEE Trans. Ind. Electron. 2018, 66, 6592–6603. [Google Scholar] [CrossRef]
- Lu, S.; Sun, K.; Guo, Z.; Chen, H.; Cao, G. A Design Method of High Voltage and High Power LLC Resonant Converter for Photovoltaic DC Voltage Boosting System. CSEE J. Power Energy Syst. 2023, 43, 5970–5982. [Google Scholar] [CrossRef]
- Pang, J.; Wang, K.; Wu, M.; Zhou, W.; Zheng, Z.; Li, Y. Modulation and Soft-Switching Optimization Control of Multilevel Dual Active Bridge DC–DC Converters. IEEE Trans. Power Electron. 2024, 40, 1936–1951. [Google Scholar] [CrossRef]
- Jin, H.; Chen, W.; Wang, Y. A Series-Arm Modular Multilevel DC/DC Converter with Variable Duty Cycle Quasi-Square-Wave Modulation for ZVS Operation. IEEE Trans. Power Electron. 2024, 39, 12185–12199. [Google Scholar] [CrossRef]
- Park, H.P.; Jung, J.H. PWM and PFM Hybrid Control Method for LLC Resonant Converters in High Switching Frequency Operation. IEEE T Ind. Electron. 2017, 64, 253–263. [Google Scholar] [CrossRef]
- Yuan, B.; Lai, X.Q.; Liu, Y.X. Load current-sensing circuit integrated in high-frequency PWM/PFM hybrid DC-DC buck converter. Electron. Lett. 2014, 50, 1310–1311. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).