Bounding Case Requirements for Power Grid Protection Against High-Altitude Electromagnetic Pulses
Abstract
1. Introduction
2. System Models
2.1. HEMP Insult Model
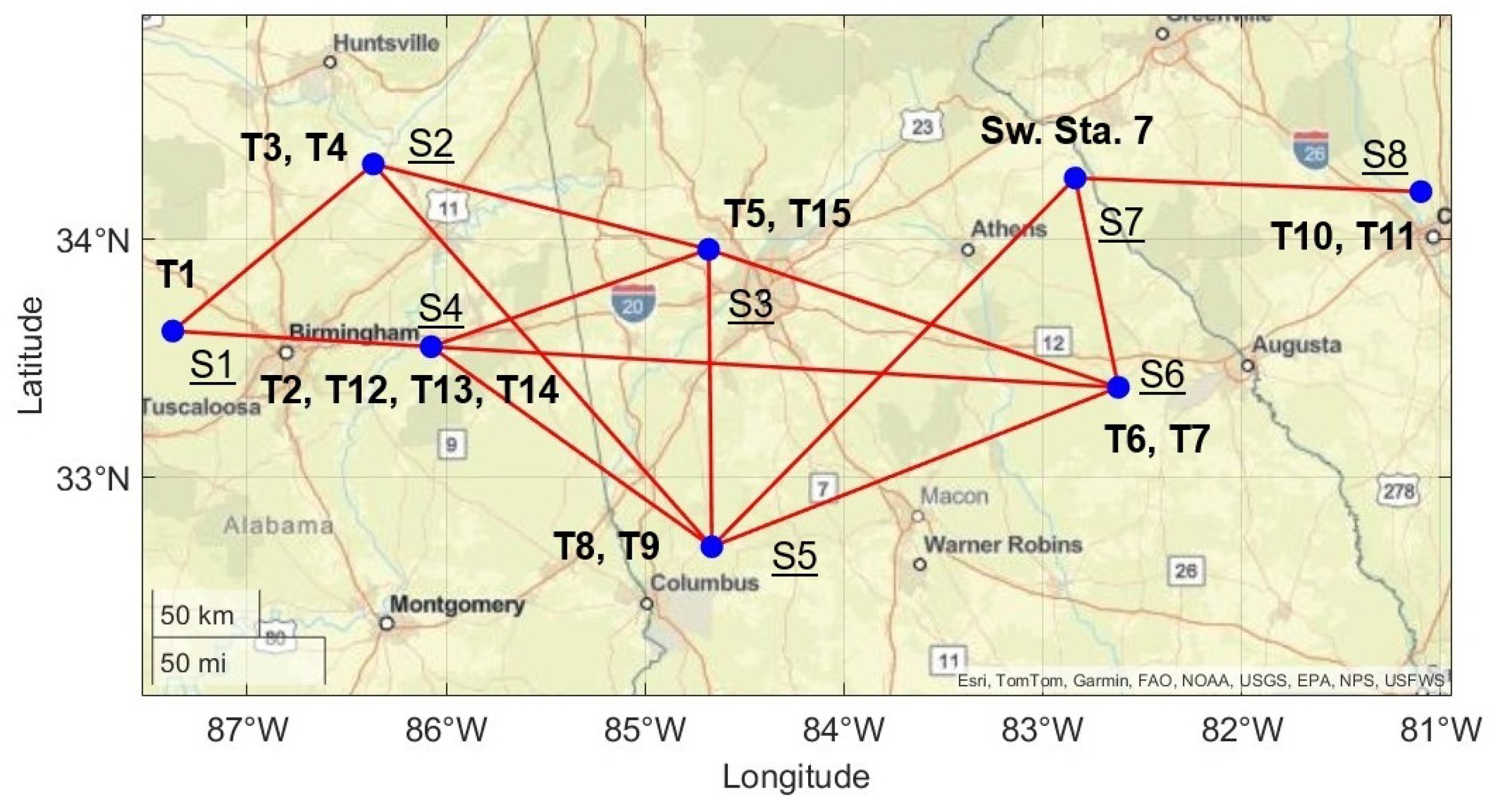
2.2. Horton et al. 20-Bus System
3. Controller Design
4. Controllability
4.1. Background
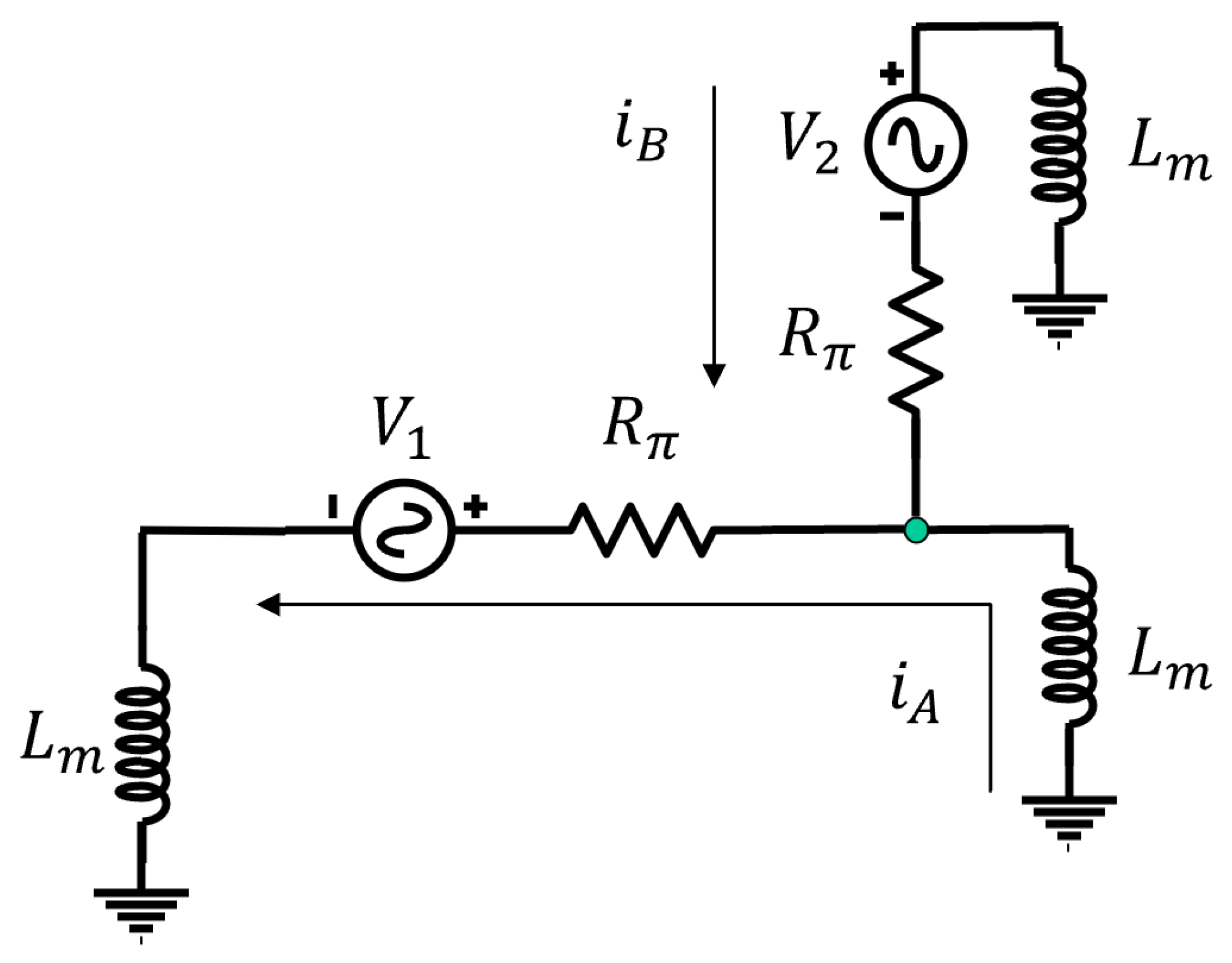
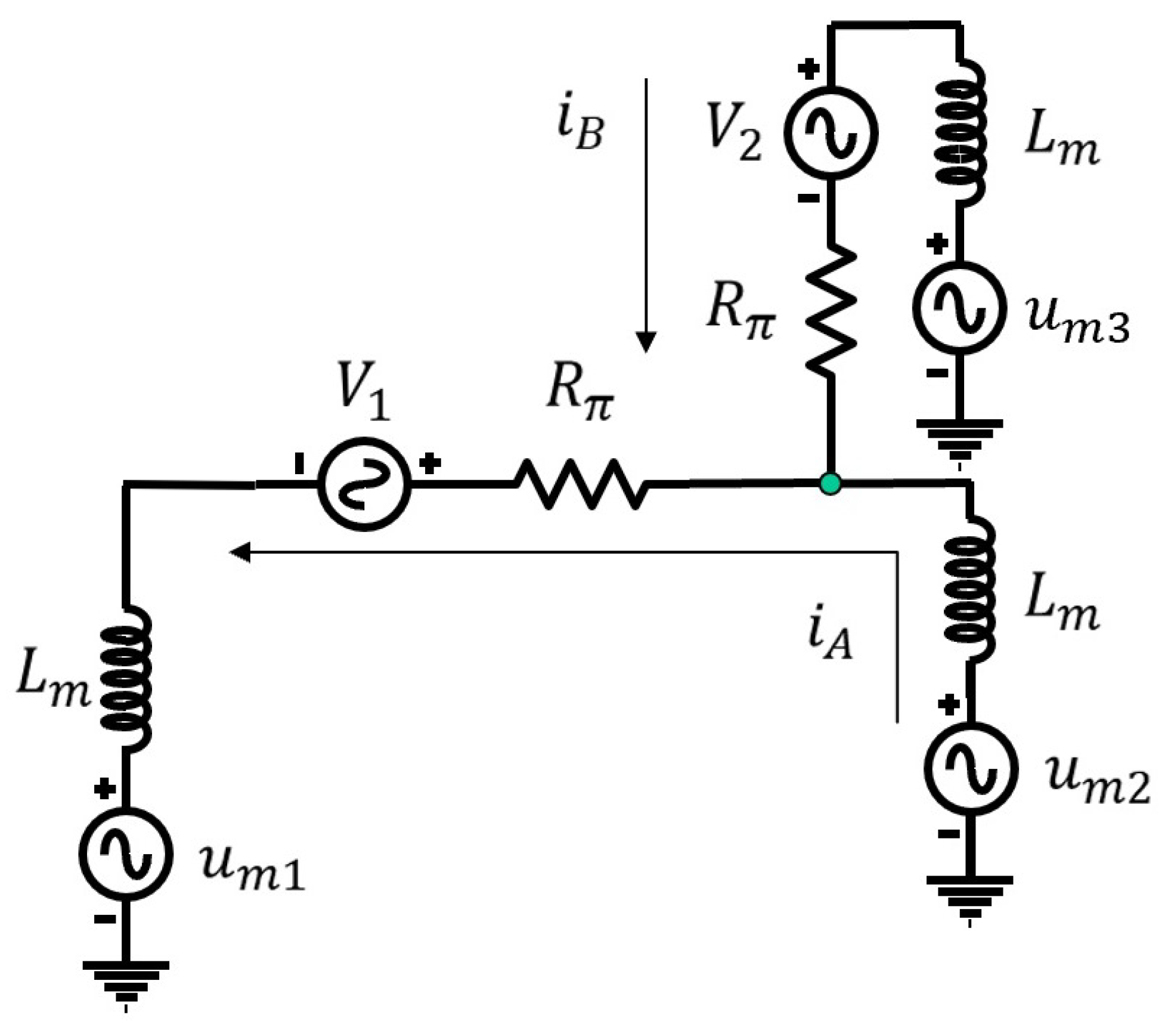
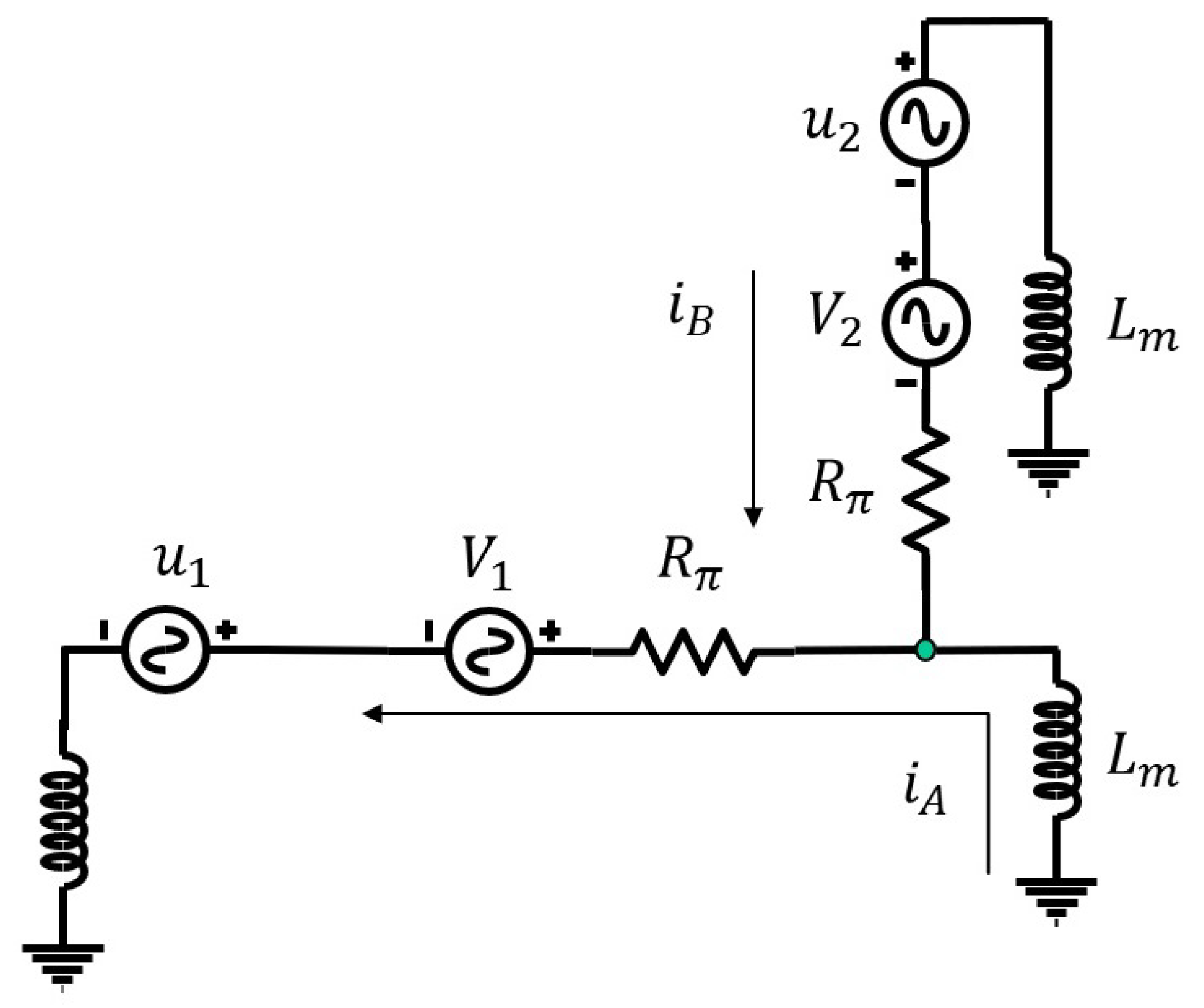
4.2. The Disturbance Influence Problem
5. Observability
5.1. Background
5.2. Observability of a Power Grid
6. Results
6.1. All Permutations Neutral Blocking Case
6.2. All Permutations Transmission Line Blocking Case
6.3. Discussion of Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HEMP | High-altitude electromagnetic pulse |
| SST | Solid state transformer |
| LQR | Linear quadratic regulator |
References
- Foster, R.A.; Frickey, S.J. Strategies, Protections and Mitigations for Electric Grid from Electromagnetic Pulse Effects; Technical Report; Idaho National Lab (INL): Idaho Falls, ID, USA, 2016.
- Baker, G.H. Electromagnetic Pulse Resilience of United States Critical Infrastructure: Progress and Prognostics. J. Crit. Infrastruct. Policy 2021, 2, 35–46. [Google Scholar] [CrossRef]
- SRI International. Starfish Prime, Santitized Version. 1962. Available online: https://apps.dtic.mil/sti/citations/ADA955694 (accessed on 15 May 2025).
- Vittitoe, C.N. Did High-Altitude EMP Cause the Hawaiian Streetlight Incident. System Design and Assessment Notes. 1989. Available online: https://ece-research.unm.edu/summa/notes/SDAN/0031.pdf (accessed on 15 May 2025).
- Barnes, A.K.; Mate, A.; Bent, R. A Review of the GIC Blocker Placement Problem. In Proceedings of the 2024 IEEE/IAS 60th Industrial and Commercial Power Systems Technical Conference (I&CPS), Las Vegas, NV, USA, 19–23 May 2024; pp. 1–6. [Google Scholar]
- Etemadi, A.H.; Rezaei-Zare, A. Optimal placement of GIC blocking devices for geomagnetic disturbance mitigation. IEEE Trans. Power Syst. 2014, 29, 2753–2762. [Google Scholar] [CrossRef]
- Liang, Y.; He, D.; Zhu, H.; Chen, D. Optimal blocking device placement for geomagnetic disturbance mitigation. IEEE Trans. Power Deliv. 2019, 34, 2219–2231. [Google Scholar] [CrossRef]
- Donnelly, T.J.; Wilson, D.G.; Robinett, R.D.; Weaver, W.W. Top-Down Control Design Strategy for Electric Power Grid EMP (E3) Protection. In Proceedings of the 2023 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 13–14 February 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, D.; Li, Y.; Dehghanian, P.; Wang, S. Power Grid Resilience to Electromagnetic Pulse (EMP) Disturbances: A Literature Review. In Proceedings of the 2019 North American Power Symposium (NAPS), Wichita, KS, USA, 13–15 October 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Kappenman, J. Low-Frequency Protection Concepts for the Electric Power Grid: Geomagnetically Induced Current (GIC) and E3 HEMP Mitigation; Metatech Corporation, FERC: Goleta, CA, USA, 2010. [Google Scholar]
- Tarditi, A.G.; Besnoff, J.S.; Duckworth, R.C.; Li, F.R.; Li, Z.; Liu, Y.; Mcconnell, B.W.; Olsen, R.G.; Poole, B.R.; Piesciorovsky, E.C.; et al. High-Voltage Modeling and Testing of Transformer, Line Interface Devices, and Bulk System Components Under Electromagnetic Pulse, Geomagnetic Disturbance, and Other Abnormal Transients; ORNL/TM-2019/1143; Oak Ridge National Laboratory (ORNL): Oak Ridge, TN, USA, 2019.
- Garrett, R.; Guttromson, R. A Survey of Preventive and Remediating Mitigations for High-Altitude Electromagnetic Pulse Impacts on the United States Electric Power Grid; Technical report; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 2021.
- Kappenman, J.; Norr, S.R.; Sweezy, G.; Carlson, D.; Albertson, V.; Harder, J.; Damsky, B. GIC mitigation: A neutral blocking/bypass device to prevent the flow of GIC in power systems. IEEE Trans. Power Deliv. 1991, 6, 1271–1281. [Google Scholar] [CrossRef]
- Zhang, S.M.; Liu, L.G. A mitigation method based on the principle of GIC-even distribution in whole power grids. IEEE Access 2020, 8, 65096–65103. [Google Scholar] [CrossRef]
- Lehman, C.A.; Donnelly, T.J.; Robinett, R.D., III; Weaver, W.W.; Wilson, D.G. Decoupled, decentralized, lqr-based controls for e3 hemp/gmd mitigation on the power grid. In Proceedings of the Annual Conference of the IEEE Industrial Electronics Society (IECON), Chicago, IL, USA, 3–6 November 2024. [Google Scholar]
- Lehman, C.A.; Robinett, R.D.; Weaver, W.W.; Wilson, D.G. Solid State Transformer Controls for Mitigation of E3a High-Altitude Electromagnetic Pulse Insults. Energies 2025, 18, 1055. [Google Scholar] [CrossRef]
- Bhela, S.; Kekatos, V.; Zhang, L.; Veeramachaneni, S. Enhancing observability in power distribution grids. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 4551–4555. [Google Scholar]
- You, M.; Jiang, J.; Tonello, A.M.; Doukoglou, T.; Sun, H. On statistical power grid observability under communication constraints. IET Smart Grid 2018, 1, 40–47. [Google Scholar] [CrossRef]
- Ryu, M.; Attia, A.; Barnes, A.; Bent, R.; Leyffer, S.; Mate, A. Heuristic algorithms for placing geomagnetically induced current blocking devices. Electr. Power Syst. Res. 2024, 234, 110645. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Z.; Xue, Y.; Chang, X.; Su, J.; Wang, P.; Guo, Q.; Sun, H. A stochastic bi-level optimal allocation approach of intelligent buildings considering energy storage sharing services. IEEE Trans. Consum. Electron. 2024, 70, 5142–5153. [Google Scholar] [CrossRef]
- Zhai, X.; Li, Z.; Li, Z.; Xue, Y.; Chang, X.; Su, J.; Jin, X.; Wang, P.; Sun, H. Risk-averse energy management for integrated electricity and heat systems considering building heating vertical imbalance: An asynchronous decentralized approach. Appl. Energy 2025, 383, 125271. [Google Scholar] [CrossRef]
- Legro, J.R.; Abi-Samra, N.C.; Crouse, J.C.; Hileman, A.R.; Kruse, V.J.; Taylor, E.R., Jr.; Tesche, F.M. Study to Assess the Effects of High-Altitude Electromagnetic Pulse on Electric Power Systems. Phase I, Final Report; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 1986. [CrossRef]
- IEC 61000-2-9; Electromagnetic Compatibility (EMC). IEC: Geneva, Switzerland, 1996.
- Brouillette, D. Physical Characteristics of HEMP Waveform Benchmarks for Use in Assessing Susceptibilities of the Power Grid, Electrical Infrastructures, and Other Critical Infrastructure to HEMP Insults; Department of Energy Memo: Washington, DC, USA, 2021.
- Lee, R.H.W.; Shetye, K.S.; Birchfield, A.B.; Overbye, T.J. Using detailed ground modeling to evaluate electric grid impacts of late-time high-altitude electromagnetic pulses (E3 HEMP). IEEE Trans. Power Syst. 2018, 34, 1549–1557. [Google Scholar] [CrossRef]
- Hutchins, T. Modeling, Simulation, and Mitigation of the Impacts of the Late Time (E3) High-Altitude Electromagnetic Pulse on Power Systems. Ph.D. Thesis, University of Illinois at Urbana–Champaign, Champaign, IL, USA, 2015. [Google Scholar]
- Tesche, F.M.; Barnes, P.R.; Meliopoulos, A.P. Magnetohydrodynamic Electromagnetic Pulse (MHD-EMP) Interaction with Power Transmission and Distribution Systems; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 1992. [CrossRef]
- Donnelly, T.J.; Wilson, D.G.; Robinett, R.D.; Weaver, W.W. Dynamic Model of a 20-Bus Power System for HEMP/GMD Controls-based Mitigation Design. In Proceedings of the 2023 North American Power Symposium (NAPS), Asheville, NC, USA, 15–17 October 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Horton, R.; Boteler, D.; Overbye, T.J.; Pirjola, R.; Dugan, R.C. A Test Case for the Calculation of Geomagnetically Induced Currents. IEEE Trans. Power Deliv. 2012, 27, 2368–2373. [Google Scholar] [CrossRef]
- Corzine, K.; Kuhn, B.; Sudhoff, S.; Hegner, H. An improved method for incorporating magnetic saturation in the q-d synchronous machine model. IEEE Trans. Energy Convers. 1998, 13, 270–275. [Google Scholar] [CrossRef]
- Dommel, H.; Yan, A.; Wei, S. Harmonics from transformer saturation. IEEE Trans. Power Deliv. 1986, 1, 209–215. [Google Scholar] [CrossRef]
- Bolduc, L.; Gaudreau, A.; Dutil, A. Saturation time of transformers under dc excitation. Electr. Power Syst. Res. 2000, 56, 95–102. [Google Scholar] [CrossRef]
- MathWorks. Pi Section Line. Available online: https://www.mathworks.com/help/sps/powersys/ref/pisectionline.html (accessed on 5 December 2024).
- Faxvog, F.; Fuchs, G.; Jensen, W.; Wojtczak, D.; Marz, M.; Dahman, S. HV power transformer neutral blocking device (NBD) operating experience in Wisconsin. In Proceedings of the MIPSYCON Conference November, St. Paul, MN, USA, 7–9 November 2017; Volume 7. [Google Scholar]
- Nazir, M.; Burkes, K.; Enslin, J.H. Electrical safety considerations of neutral blocker placements for mitigating DC. IEEE Trans. Ind. Appl. 2020, 57, 1113–1121. [Google Scholar] [CrossRef]
- Horton, R. Magnetohydrodynamic Electromagnetic Pulse Assessment of the Continental US Electric Grid; Electric Power Research Institute: Palo Alto, CA, USA, 2017. [Google Scholar]
- Nise, N.S. Control Systems Engineering, 7th ed.; Wiley: Hoboken, NJ, USA, 2015; pp. 157–235. [Google Scholar]
- Robinett, R.D., III; Wilson, D.G. Nonlinear Power Flow Control Design; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Baggini, A. Handbook of Power Quality; JohnWiley & Sons, Ltd.: Hoboken, NJ, USA, 2008. [Google Scholar]
- Lehman, C.A.; Robinett, R.D.; Weaver, W.W.; Wilson, D.G. Hamiltonian-Based Power Flow and Stability Analysis on a Passively Controlled Multi-Frequency Power System. In Proceedings of the 2024 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Napoli, Italy, 19–21 June 2024; pp. 242–247. [Google Scholar] [CrossRef]
- Argelaguet, R.; Pons, M.; Quevedo, J.; Aguilar, J. A New Tuning of PID Controllers Based on LQR Optimization. Ifac Proc. Vol. 2000, 33, 271–276. [Google Scholar] [CrossRef]
- Silva, E.I.; Erraz, D.A. An LQR Based MIMO PID Controller Synthesis Method for Unconstrained Lagrangian Mechanical Systems. In Proceedings of the 45th IEEE Conference on Decision and Control, San Diego, CA, USA, 13–15 December 2006; pp. 6593–6598. [Google Scholar] [CrossRef]
- Zhou, D.; Blaabjerg, F. Reliability evaluation of power capacitors in a wind turbine system. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; pp. 3264–3269. [Google Scholar] [CrossRef]
- Rezaei, M.A.; Fathollahi, A.; Akbari, E.; Saki, M.; Khorgami, E.; Teimouri, A.R.; Chronopoulos, A.T.; Mosavi, A. Reliability Calculation Improvement of Electrolytic Capacitor Banks Used in Energy Storage Applications Based on Internal Capacitor Faults and Degradation. IEEE Access 2024, 12, 13146–13164. [Google Scholar] [CrossRef]
- Ogata, K. Modern Control Engineering, 5th ed.; Prentice Hall: Hoboken, NJ, USA, 2010. [Google Scholar]
- Haynes, G.W.; Hermes, H. Nonlinear Controllability via Lie Theory. Siam J. Control 1970, 8, 450–460. [Google Scholar] [CrossRef]
- Whalen, A.J.; Brennan, S.N.; Sauer, T.D.; Schiff, S.J. Observability and Controllability of Nonlinear Networks: The Role of Symmetry. Phys. Rev. X 2015, 5, 011005. [Google Scholar] [CrossRef]
- Jacobson, N. Lectures in Abstract Algebra; D. Van Nostrand Company, Inc.: New York, NY, USA, 1953. [Google Scholar]
- Donnelly, T.J.; Wilson, D.G.; Robinett, R.D.; Weaver, W.W. Control Strategies for Large Power Transformer HEMP/GMD Protection. In Proceedings of the 2023 North American Power Symposium (NAPS), Asheville, NC, USA, 15–17 October 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Van Handel, R. Observability and nonlinear filtering. Probab. Theory Relat. Fields 2009, 145, 35–74. [Google Scholar] [CrossRef]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. Trans. ASME—J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Morris, K.; Yang, S. Comparison of actuator placement criteria for control of structures. J. Sound Vib. 2015, 353, 1–18. [Google Scholar] [CrossRef]
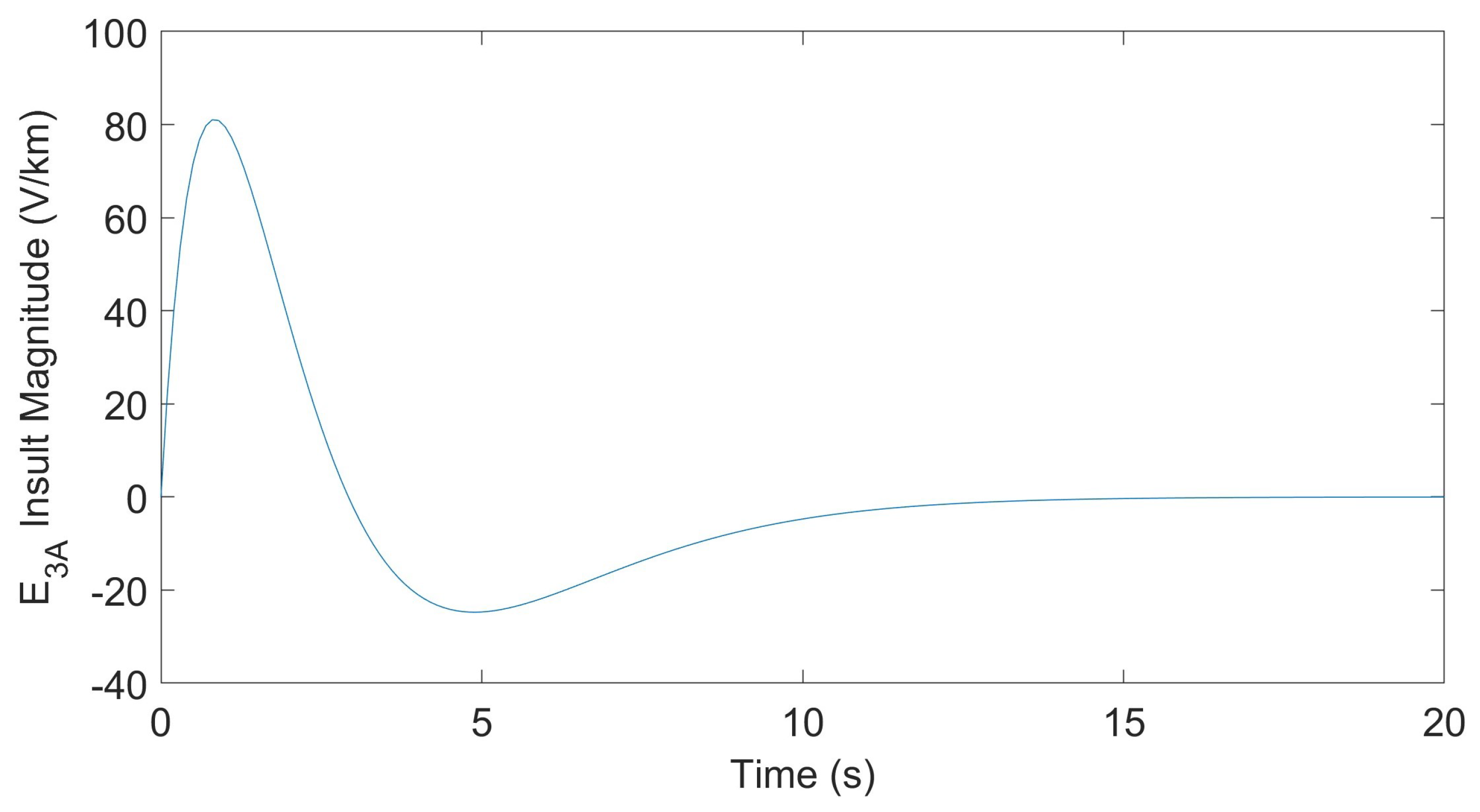
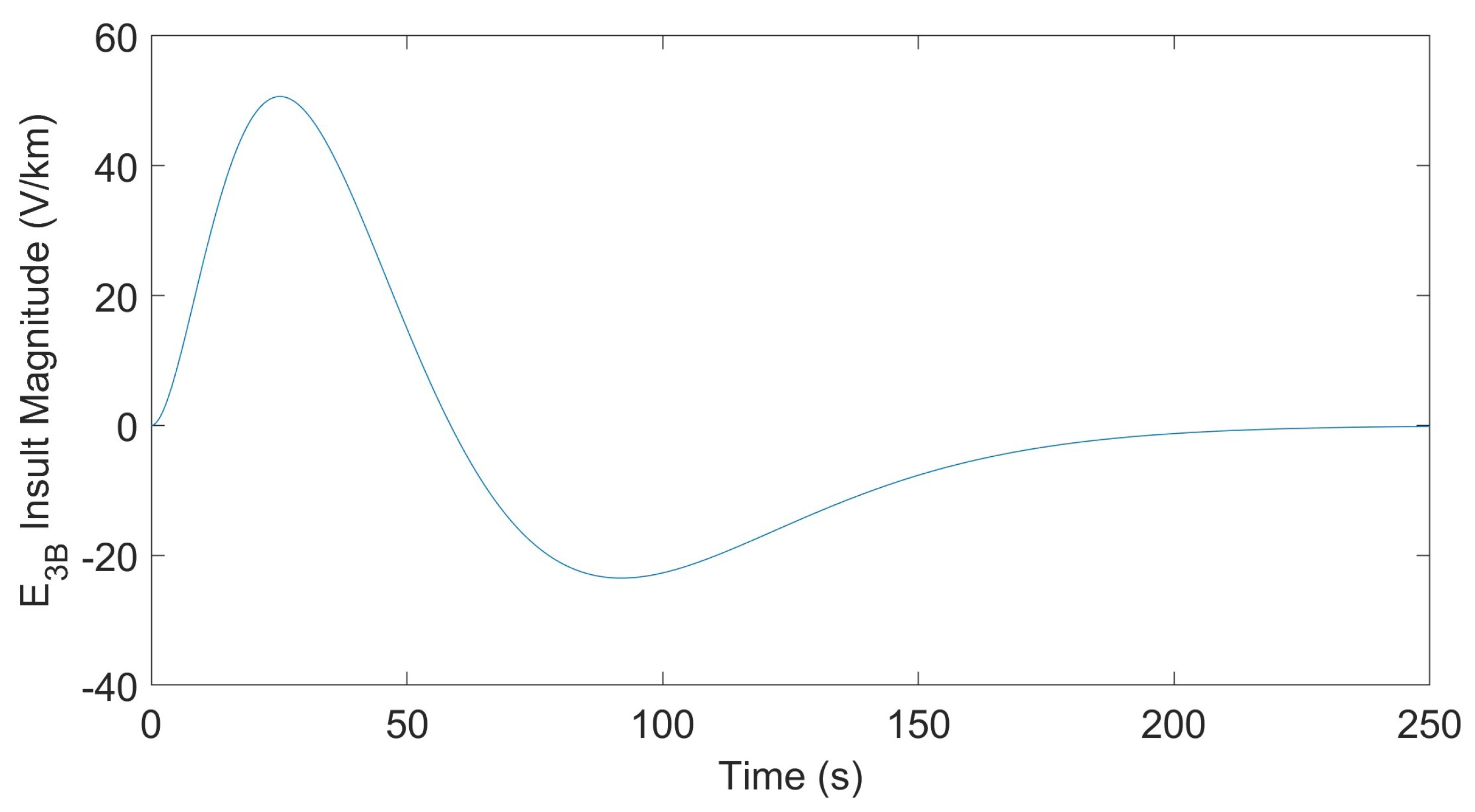
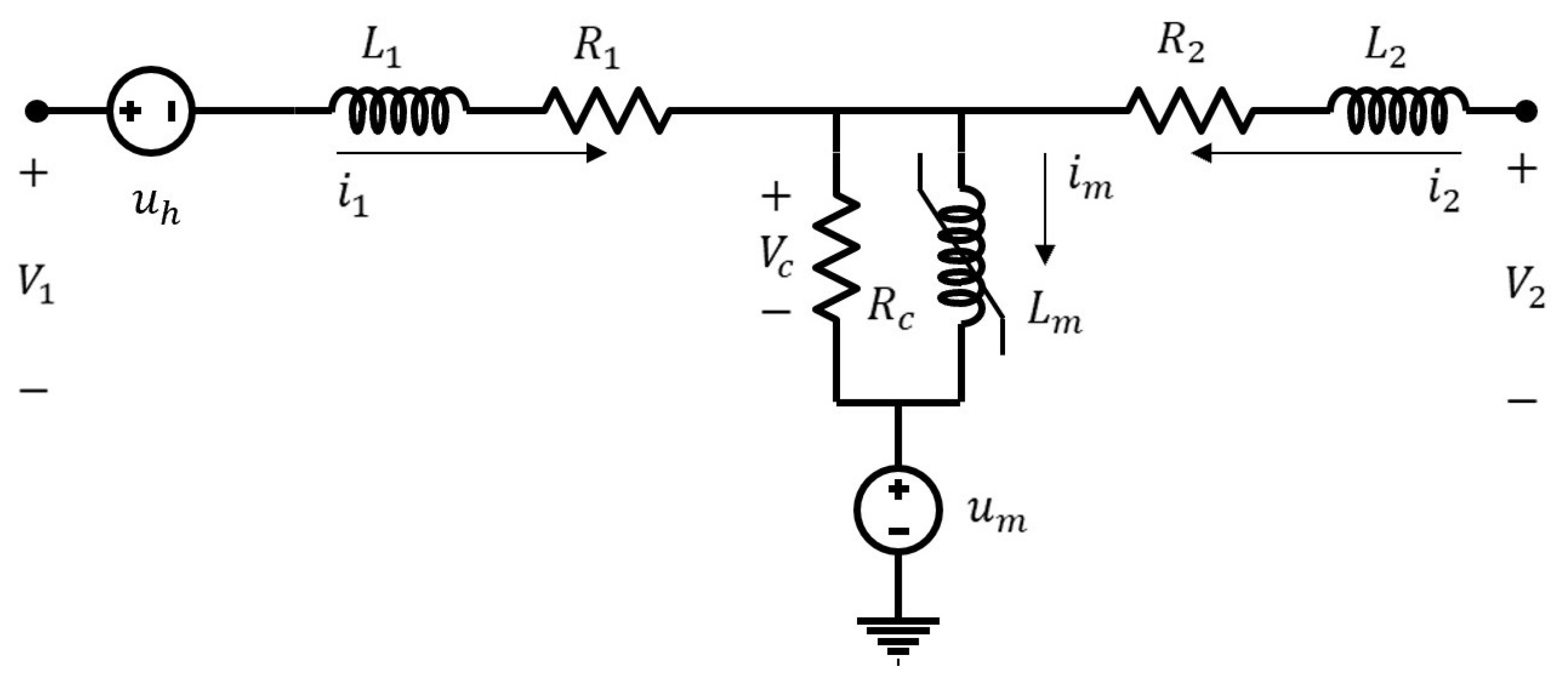
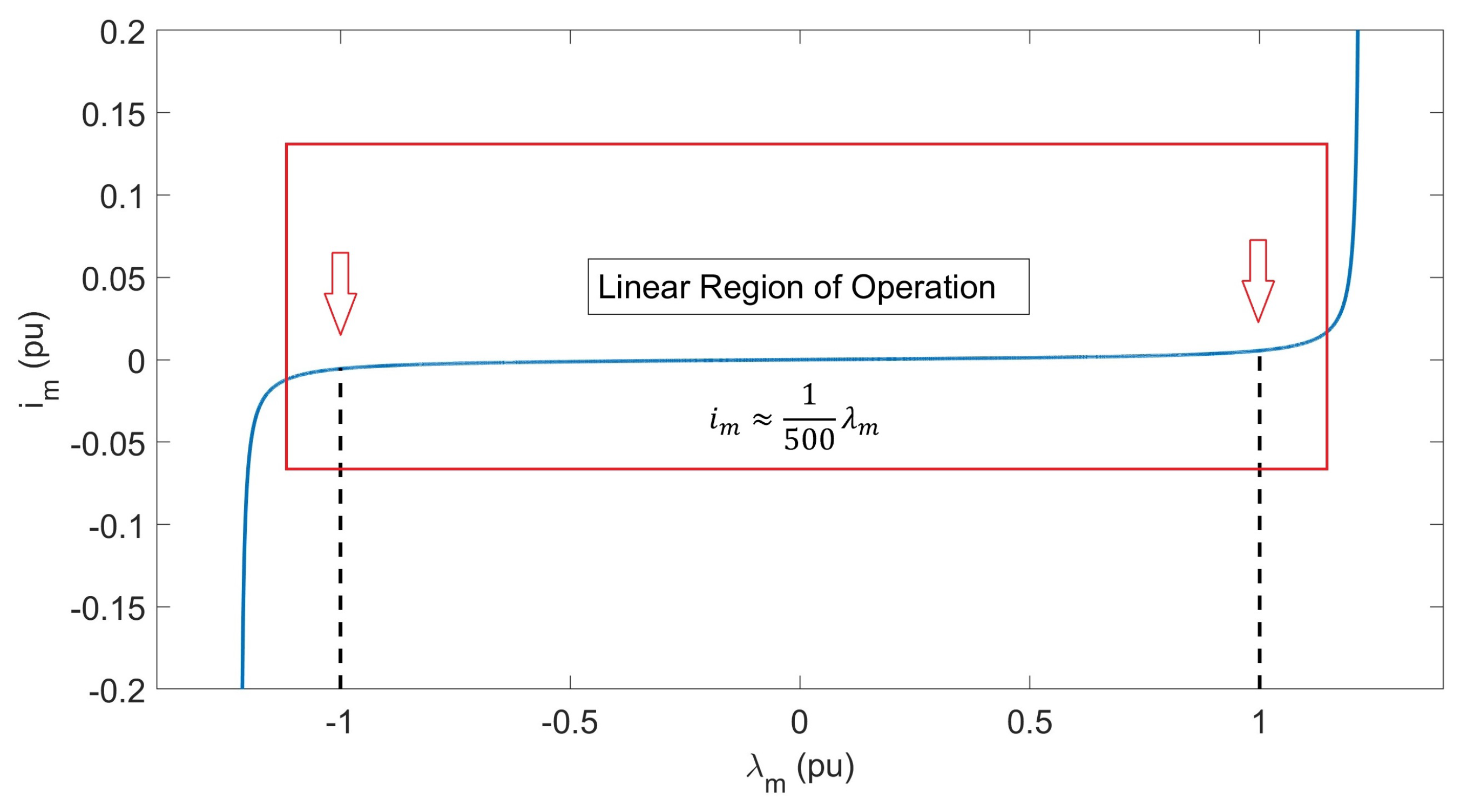
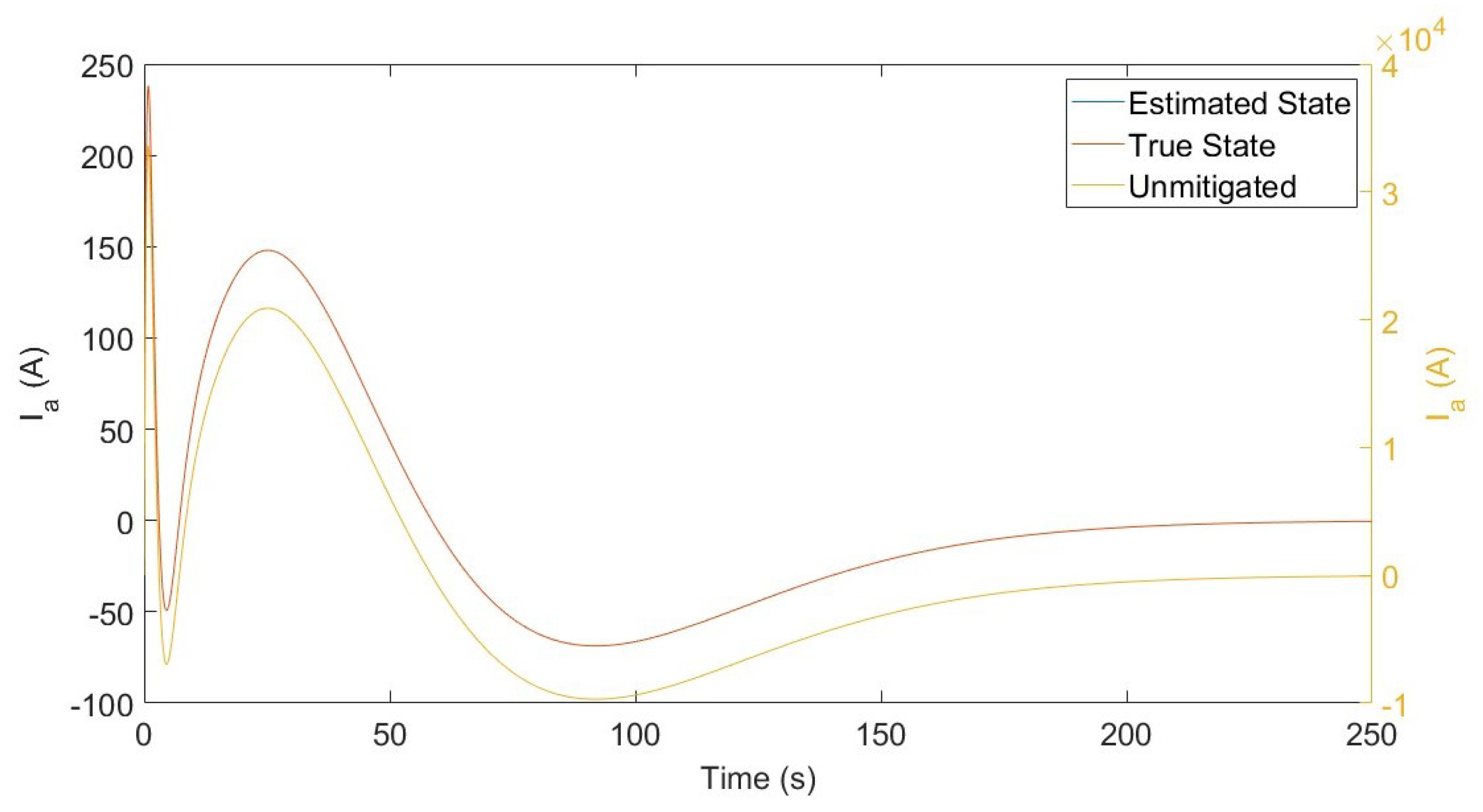
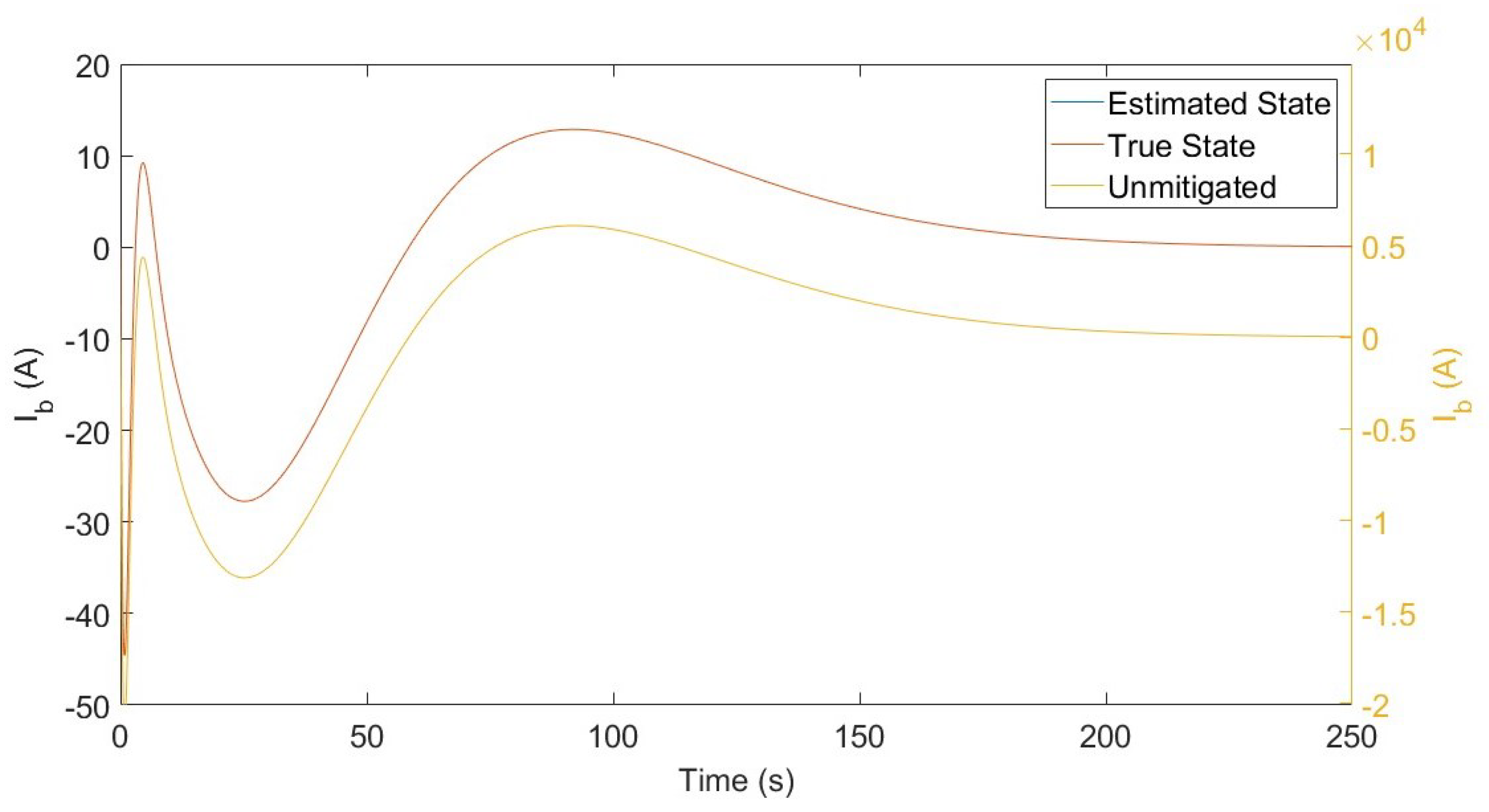
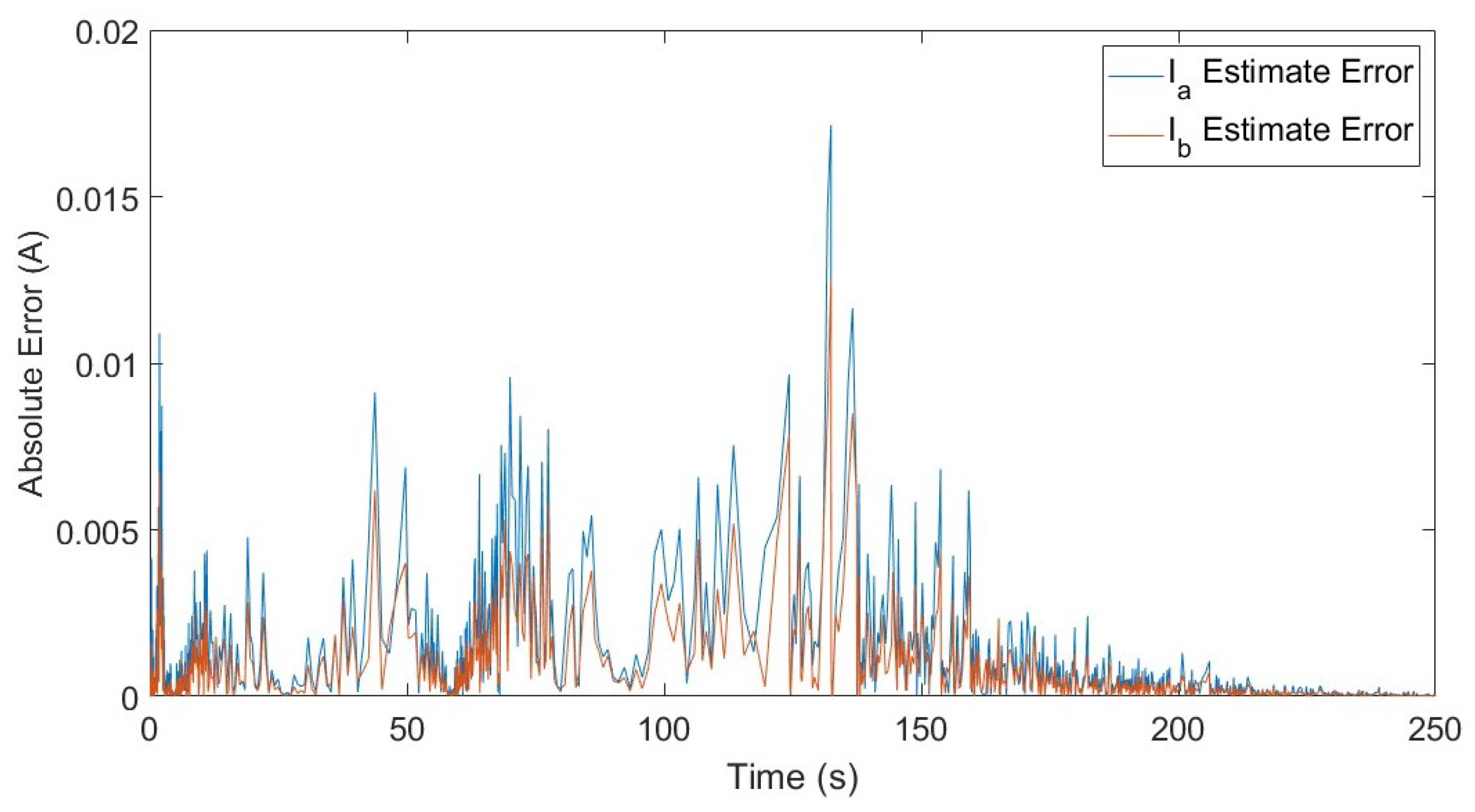
| # of Controllers | Transformer Number | Max. || (pu) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | ||
| 8 | X | X | X | X | X | X | X | X | 1.1053 | |||||||
| 9 | X | X | X | X | X | X | X | X | X | 0.6580 | ||||||
| 10 | X | X | X | X | X | X | X | X | X | X | 0.6414 | |||||
| 11 | X | X | X | X | X | X | X | X | X | X | X | 0.5990 | ||||
| 12 | X | X | X | X | X | X | X | X | X | X | X | X | 0.5785 | |||
| 13 | X | X | X | X | X | X | X | X | X | X | X | X | X | 0.4948 | ||
| 14 | X | X | X | X | X | X | X | X | X | X | X | X | X | X | 0.5015 | |
| 15 | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | 0.5228 |
| # of Controllers | Transformer Number | Max. || (pu) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | ||
| 9 | X | X | X | X | X | X | X | X | X | 0.4234 | ||||||
| 10 | X | X | X | X | X | X | X | X | X | X | 0.3890 | |||||
| 11 | X | X | X | X | X | X | X | X | X | X | X | 0.3890 | ||||
| 12 | X | X | X | X | X | X | X | X | X | X | X | X | 0.3618 | |||
| 13 | X | X | X | X | X | X | X | X | X | X | X | X | X | 0.3346 | ||
| 14 | X | X | X | X | X | X | X | X | X | X | X | X | X | X | 0.3346 | |
| 15 | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | 0.5233 |
| # of Controllers | Transmission Line (Subst. to Subst.) | Max. || (pu) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2→3 | 2→5 | 2→1 | 1→4 | 3→5 | 3→6 | 3→6 | 3→4 | 4→5 | 4→5 | 4→6 | 5→6 | 5→7 | 6→7 | 7→8 | ||
| 3 | X | X | X | 0.9342 | ||||||||||||
| 4 | X | X | X | X | 0.5528 | |||||||||||
| 5 | X | X | X | X | X | 0.4375 | ||||||||||
| 6 | X | X | X | X | X | X | 0.3427 | |||||||||
| 7 | X | X | X | X | X | X | X | 0.3204 | ||||||||
| 8 | X | X | X | X | X | X | X | X | 0.3117 | |||||||
| 9 | X | X | X | X | X | X | X | X | X | 0.3051 | ||||||
| 10 | X | X | X | X | X | X | X | X | X | X | 0.3010 | |||||
| 11 | X | X | X | X | X | X | X | X | X | X | X | 0.2971 | ||||
| 12 | X | X | X | X | X | X | X | X | X | X | X | X | 0.2947 | |||
| 13 | X | X | X | X | X | X | X | X | X | X | X | X | X | 0.2920 | ||
| 14 | X | X | X | X | X | X | X | X | X | X | X | X | X | X | 0.2918 | |
| 15 | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | 0.2918 |
| # of Controllers | Transmission Line (Subst. to Subst.) | Max. Flux (pu) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2→3 | 2→5 | 2→1 | 1→4 | 3→5 | 3→6 | 3→6 | 3→4 | 4→5 | 4→5 | 4→6 | 5→6 | 5→7 | 6→7 | 7→8 | ||
| 11 | X | X | X | X | X | X | X | X | X | X | X | 1.0755 | ||||
| 12 | X | X | X | X | X | X | X | X | X | X | X | X | 1.0713 | |||
| 13 | X | X | X | X | X | X | X | X | X | X | X | X | X | 1.0587 | ||
| 14 | X | X | X | X | X | X | X | X | X | X | X | X | X | X | 1.0535 | |
| 15 | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | 1.0535 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lehman, C.A.; Robinett, R.D., III; Weaver, W.W.; Wilson, D.G. Bounding Case Requirements for Power Grid Protection Against High-Altitude Electromagnetic Pulses. Energies 2025, 18, 2614. https://doi.org/10.3390/en18102614
Lehman CA, Robinett RD III, Weaver WW, Wilson DG. Bounding Case Requirements for Power Grid Protection Against High-Altitude Electromagnetic Pulses. Energies. 2025; 18(10):2614. https://doi.org/10.3390/en18102614
Chicago/Turabian StyleLehman, Connor A., Rush D. Robinett, III, Wayne W. Weaver, and David G. Wilson. 2025. "Bounding Case Requirements for Power Grid Protection Against High-Altitude Electromagnetic Pulses" Energies 18, no. 10: 2614. https://doi.org/10.3390/en18102614
APA StyleLehman, C. A., Robinett, R. D., III, Weaver, W. W., & Wilson, D. G. (2025). Bounding Case Requirements for Power Grid Protection Against High-Altitude Electromagnetic Pulses. Energies, 18(10), 2614. https://doi.org/10.3390/en18102614







