Unified Inductor Type Based Linear Resonant Hybrid Converter for Wide Voltage Range Applications
Abstract
:1. Introduction
- The resonant inductor and excitation inductor are unified, and the resonant tank with equal inductance ratio is realized. The wide voltage gain can be achieved within a very narrow frequency range;
- The type of inductor in the resonant tank is reduced. In addition, compared with the traditional LLC resonant converters, the magnetic flux and heat distribution are more uniform.
2. Proposed Topology and Operation Principle
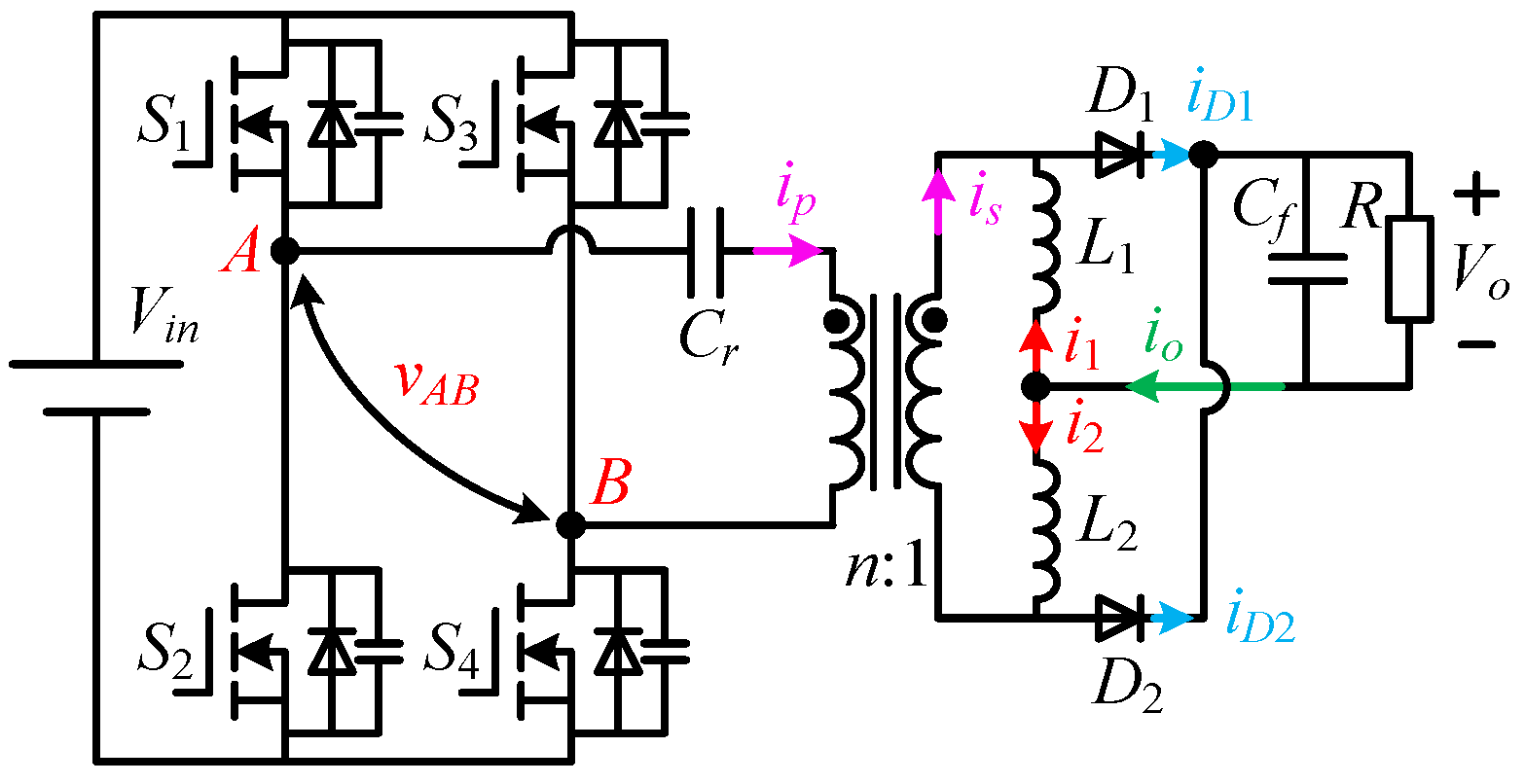
2.1. Topology of the Proposed UITBLRHC
2.2. Operation Principle
3. Characteristics of the UITBLRHC
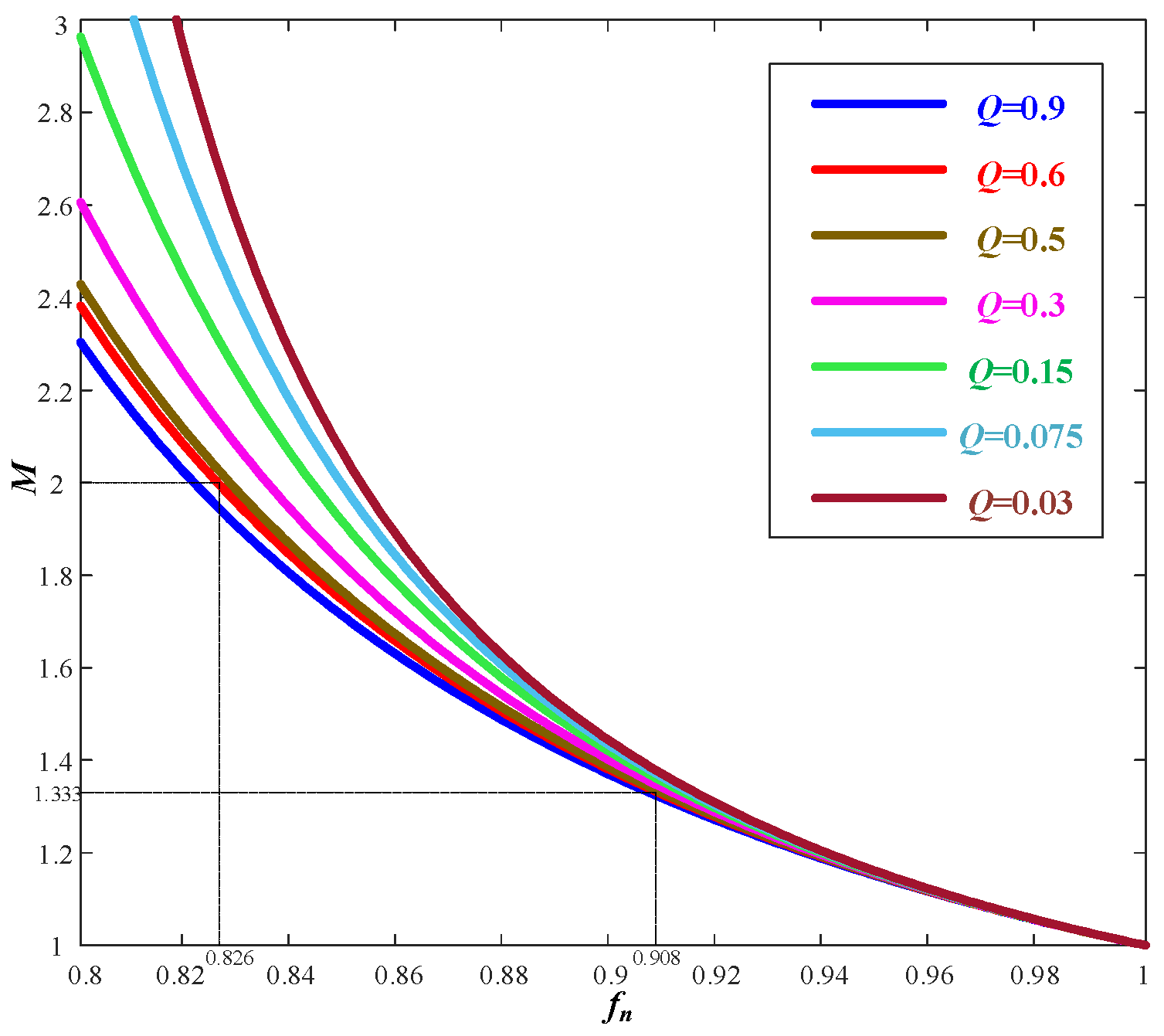
3.1. Voltage Gain Characteristic
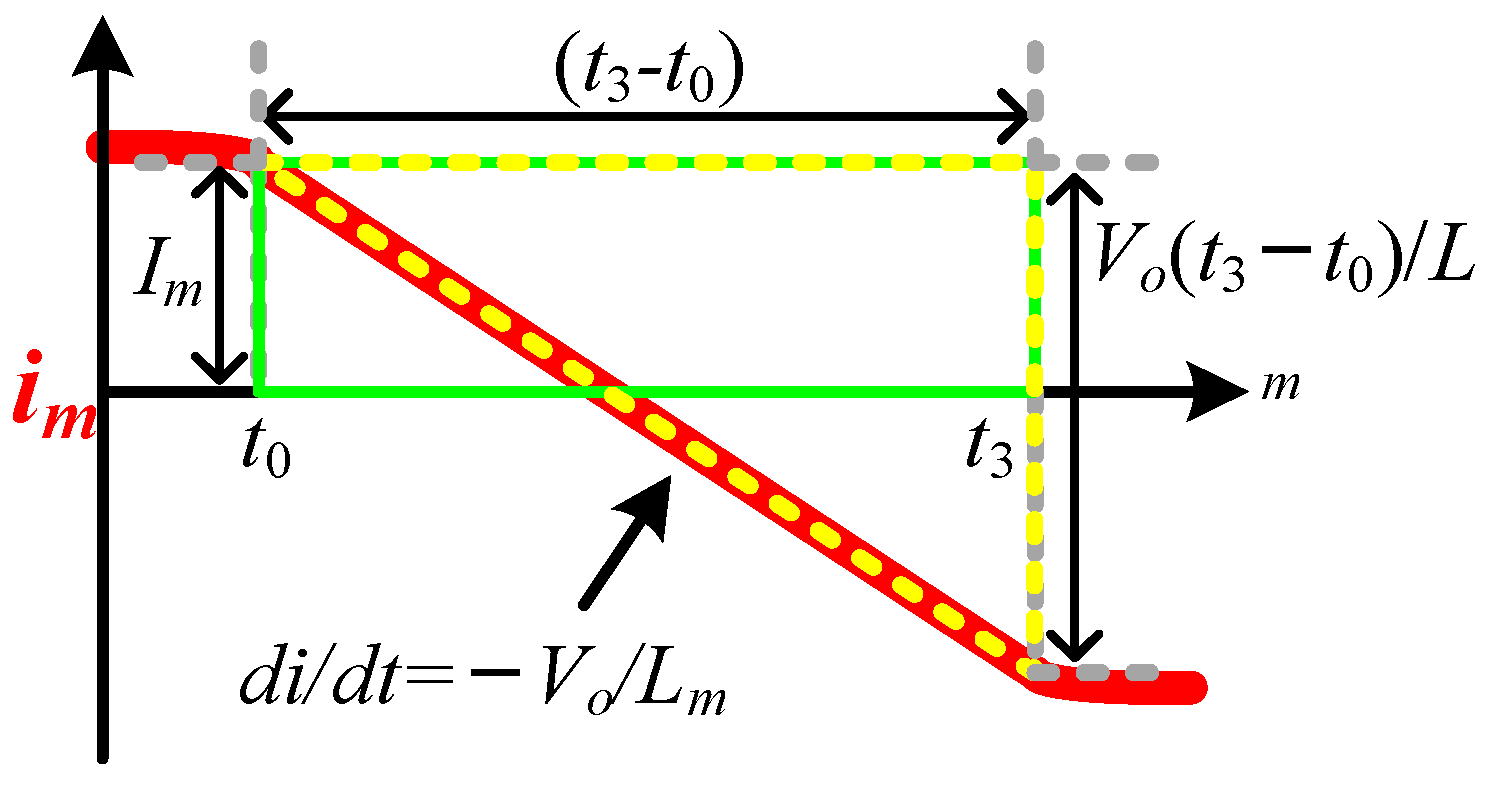
3.2. Soft Switching Performance
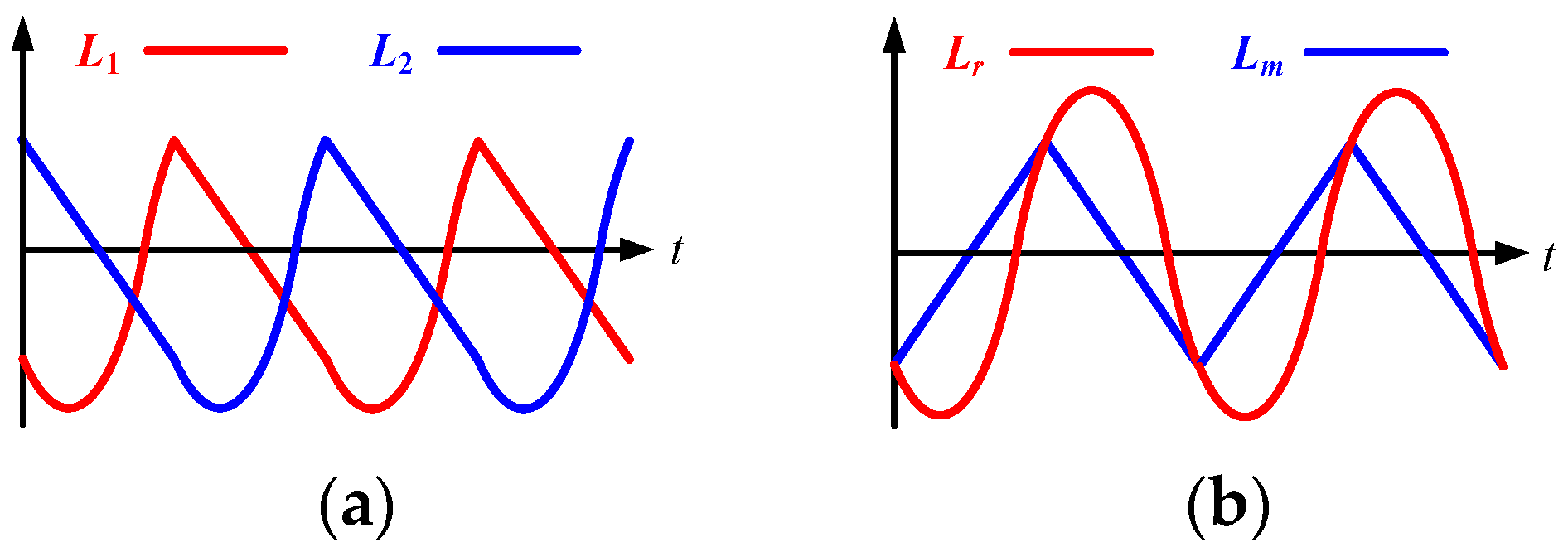
3.3. Magnetic Flux Analysis
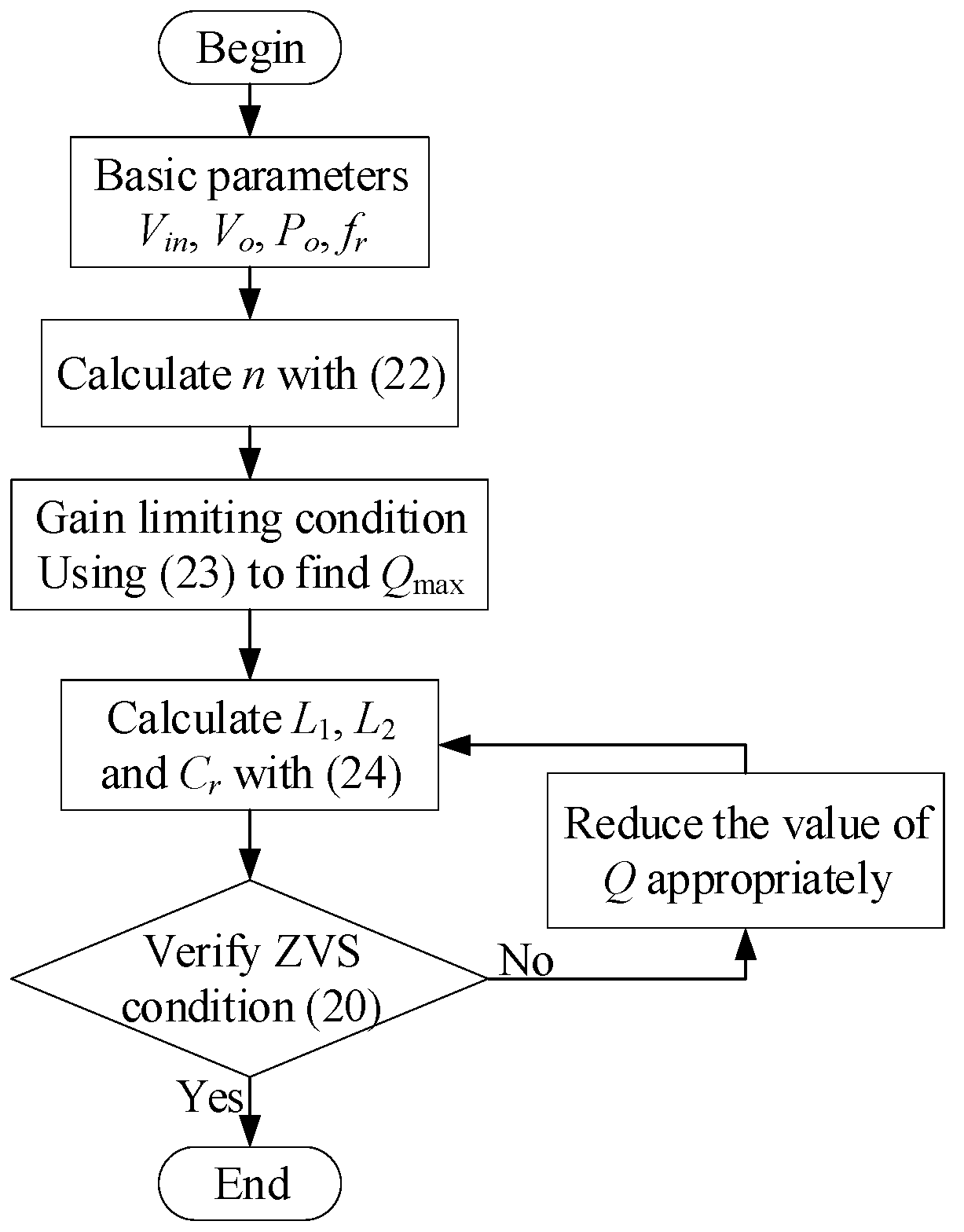
4. Proposed Converter Design Considerations
4.1. Turns Ratio of the Transformer
4.2. Factor Q
4.3. Resonant Tank
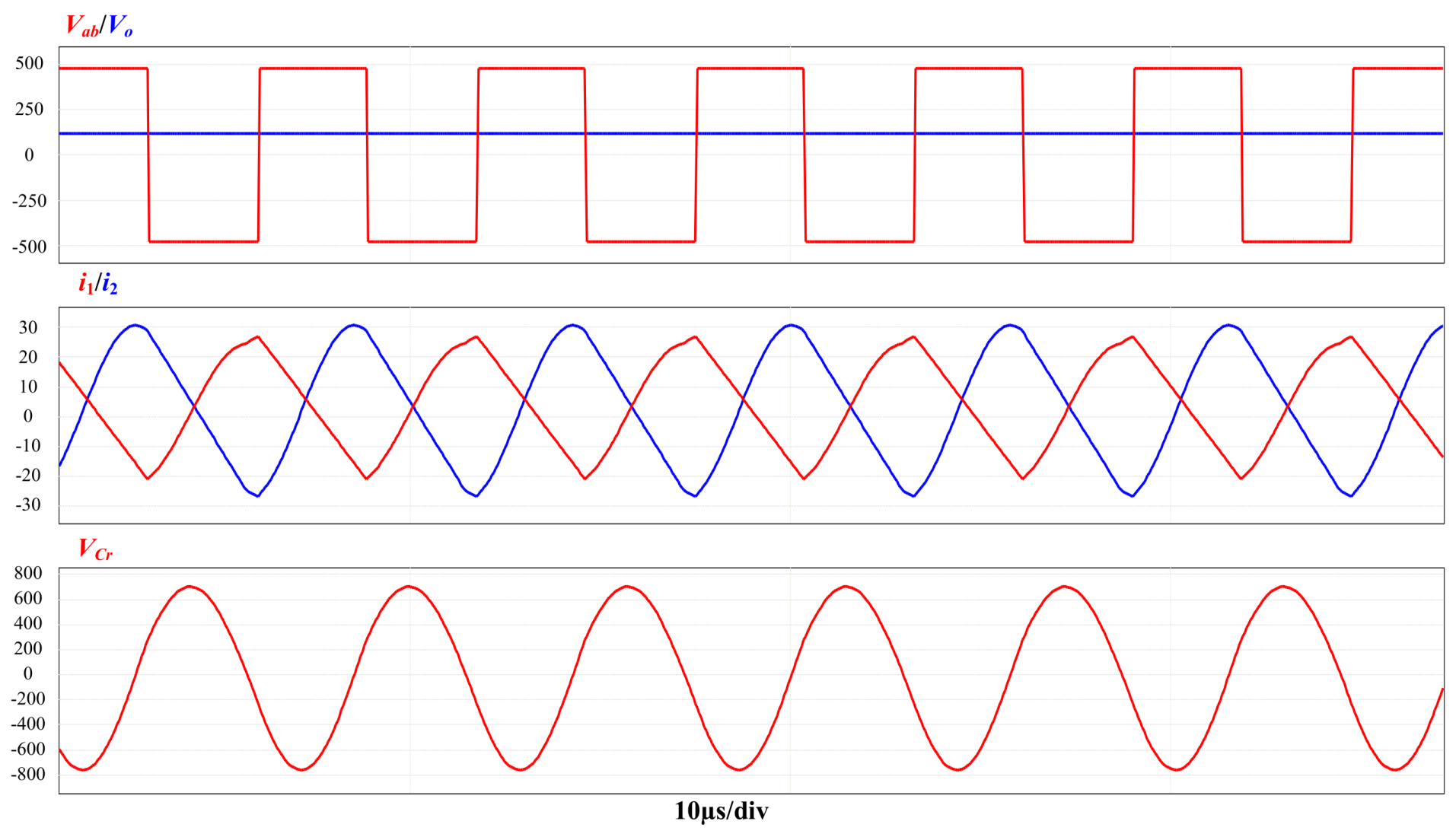
5. Experimental Verification and Comparison
5.1. Experimental Prototype
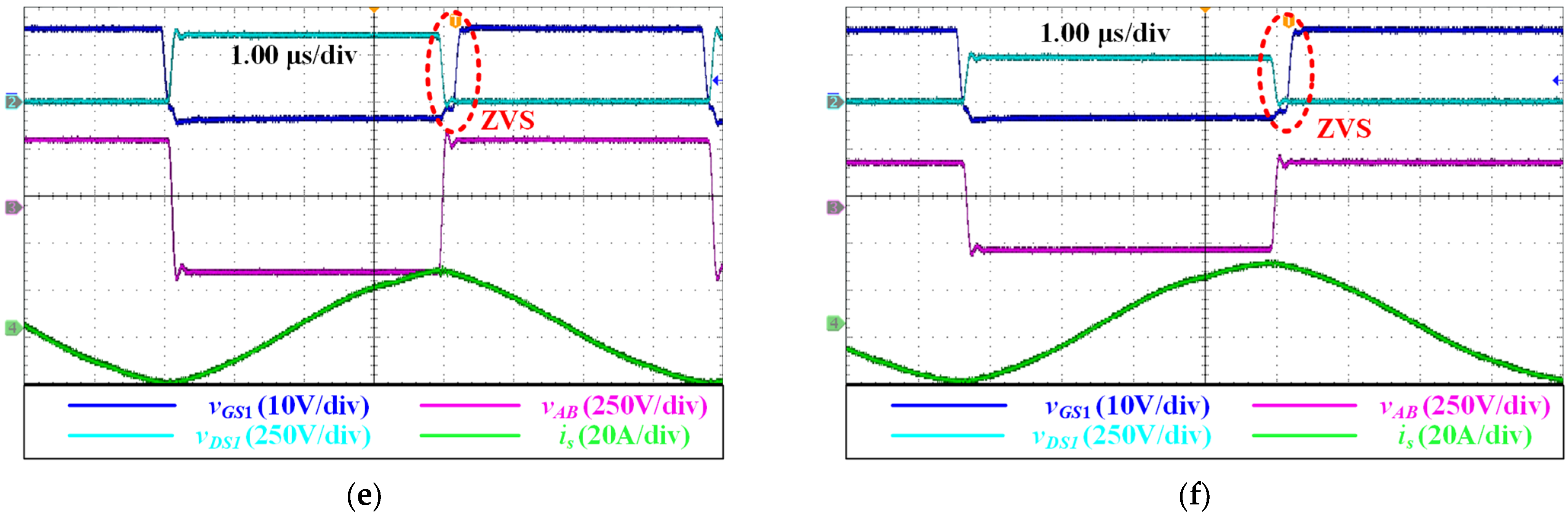
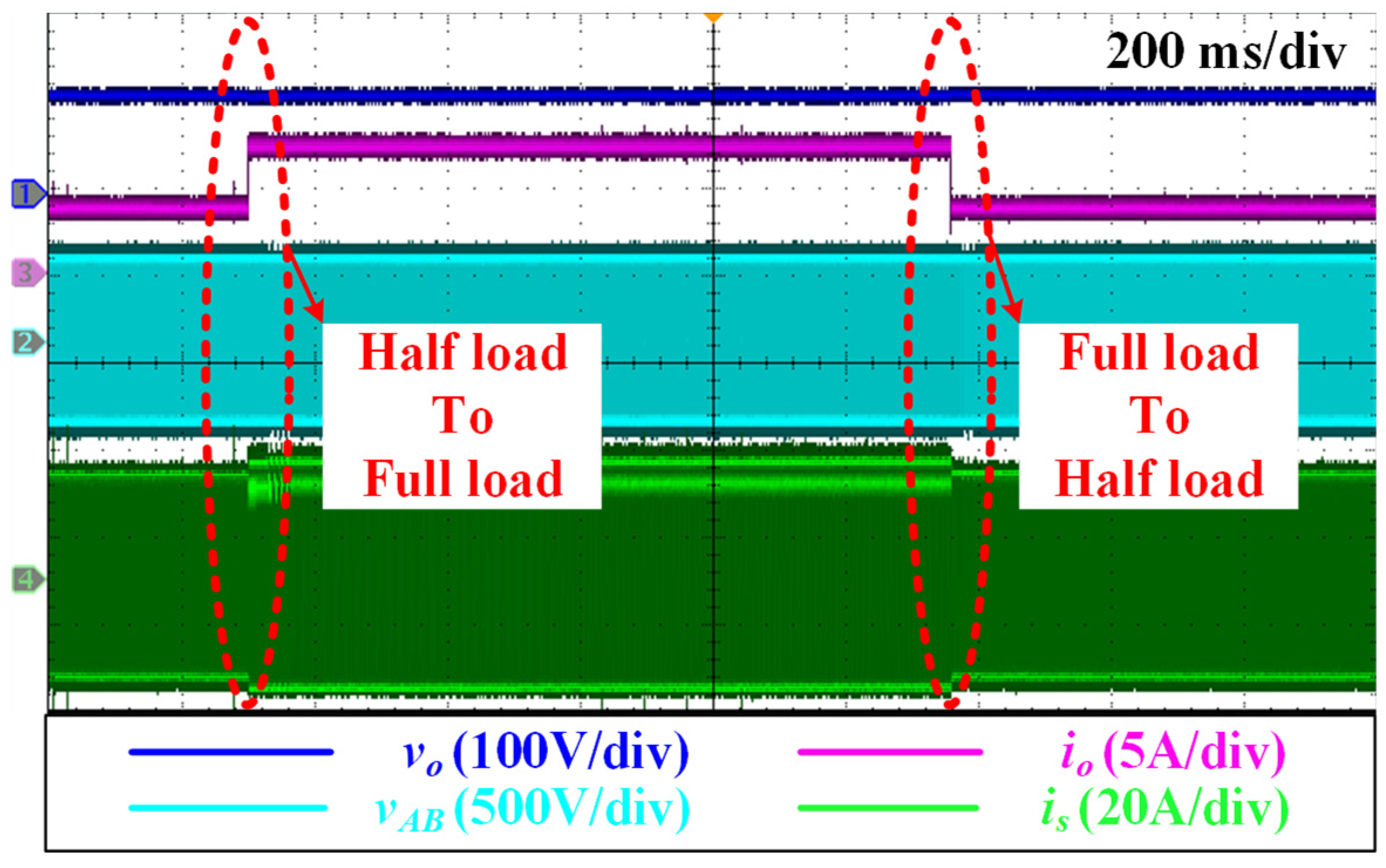
5.2. Experimental Results and Waveforms
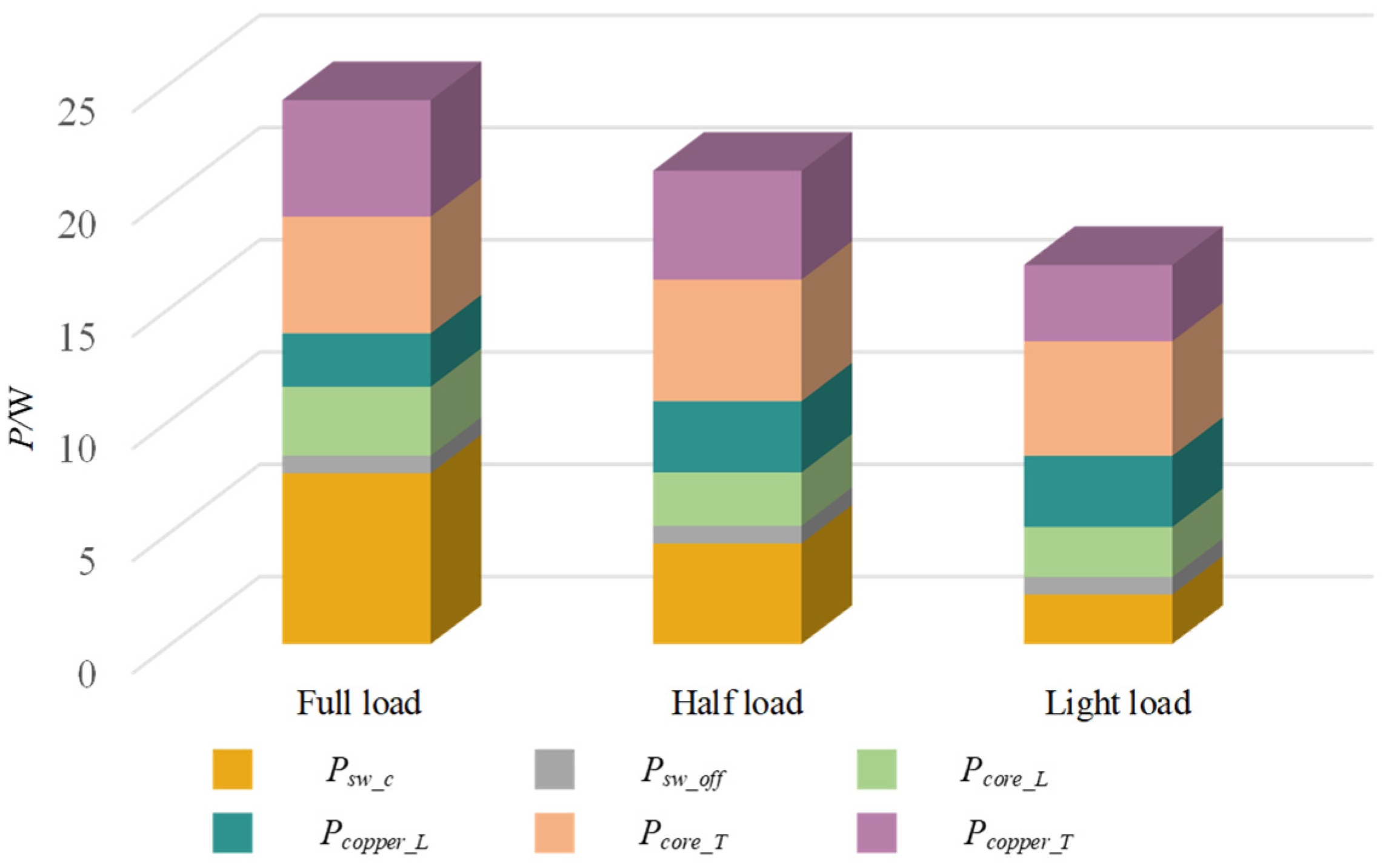
5.3. Loss Breakdown
5.4. Inductor Difference Analysis
5.5. Comparison
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, L.; Xu, G.; Sha, D.; Liu, Y.; Sun, Y.; Su, M. Review of Dual-Active-Bridge Converters with Topological Modifications. IEEE Trans. Power Electron. 2023, 38, 9046–9076. [Google Scholar] [CrossRef]
- Li, L.; Su, M.; Xu, G.; Jiang, L.; Liu, Y. A Soft-Switched Semi Dual Active Half Bridge Converter with Voltage Match Trapezoidal Modulation Control. IEEE Trans. Circuits Syst. II Express Briefs 2024, 72, 303–307. [Google Scholar] [CrossRef]
- Rocha, J.; Amin, S.; Coelho, S.; Rego, G.; Afonso, J.L.; Monteiro, V. Design and Implementation of a DC–DC Resonant LLC Converter for Electric Vehicle Fast Chargers. Energies 2025, 18, 1099. [Google Scholar] [CrossRef]
- Yin, M.; Luo, Q. Stepwise Multi-Objective Parameter Optimization Design of LLC Resonant DC-DC Converter. Energies 2024, 17, 1919. [Google Scholar] [CrossRef]
- Yang, B.; Lee, F.; Zhang, A.; Huang, G. LLC resonant converter for front end DC/DC conversion. In Proceedings of the APEC 2002—Applied Power Electronics Conference and Exposition, Dallas, TX, USA, 10–14 March 2002; pp. 1108–1112. [Google Scholar]
- Beiranvand, R.; Zolghadri, M.R.; Rashidian, B.; Alavi, S.M.H. Optimizing the LLC–LC Resonant Converter Topology for Wide-Output-Voltage and Wide-Output-Load Applications. IEEE Trans. Power Electron. 2011, 26, 3192–3204. [Google Scholar] [CrossRef]
- Wei, Y.; Luo, Q.; Mantooth, H.A. A Resonant Frequency Tracking Technique for LLC Converter-Based DC Transformers. IEEE J. Emerg. Sel. Top. Ind. Electron. 2021, 2, 579–590. [Google Scholar] [CrossRef]
- Wei, Y.; Luo, Q.; Du, X.; Altin, N.; Alonso, J.M.; Mantooth, H.A. Analysis and Design of the LLC Resonant Converter with Variable Inductor Control Based on Time-Domain Analysis. IEEE Trans. Ind. Electron. 2019, 67, 5432–5443. [Google Scholar] [CrossRef]
- Wei, Y.; Luo, Q.; Mantooth, H.A. An LLC Converter with Multiple Operation Modes for Wide Voltage Gain Range Application. IEEE Trans. Ind. Electron. 2020, 68, 11111–11124. [Google Scholar] [CrossRef]
- Zhang, J.; Cai, Z. Hybrid Control Switching Technology for LLC Resonant Converter. Energies 2024, 17, 6250. [Google Scholar] [CrossRef]
- Wu, H.; Mu, T.; Gao, X.; Xing, Y. A Secondary-Side Phase-Shift-Controlled LLC Resonant Converter with Reduced Conduction Loss at Normal Operation for Hold-Up Time Compensation Application. IEEE Trans. Power Electron. 2015, 30, 5352–5357. [Google Scholar] [CrossRef]
- Wang, H.; Li, Z. A PWM LLC Type Resonant Converter Adapted to Wide Output Range in PEV Charging Applications. IEEE Trans. Power Electron. 2017, 33, 3791–3801. [Google Scholar] [CrossRef]
- Bai, C.; Han, B.; Kwon, B.-H.; Kim, M. Highly efficient bidirectional series-resonant DC/DC converter over wide range of battery voltages. IEEE Trans. Power Electron. 2019, 35, 3636–3650. [Google Scholar] [CrossRef]
- Zhu, T.; Zhuo, F.; Zhao, F.; Wang, F.; Yi, H.; Zhao, T. Optimization of extended phase-shift control for full-bridge CLLC resonant converter with improved light-load efficiency. IEEE Trans. Power Electron. 2020, 35, 11129–11142. [Google Scholar] [CrossRef]
- Zuo, Y.; Pan, X.; Wang, C. A Reconfigurable bidirectional isolated LLC resonant converter for ultra-wide voltage-gain range applications. IEEE Trans. Ind. Electron. 2021, 69, 5713–5723. [Google Scholar] [CrossRef]
- Fang, Z.J.; Huang, Z.; Jing, H.; Liu, F. Hybrid Mode-Hopping Modulation for LLC Resonant Converter Achieving High Efficiency and Linear Behavior. IET Power Electron. 2020, 13, 1153–1162. [Google Scholar] [CrossRef]
- Zong, S.; Fan, G.; Yang, X. Double Voltage Rectification Modulation for Bidirectional DC/DC Resonant Converters for Wide Voltage Range Operation. IEEE Trans. Power Electron. 2018, 34, 6510–6521. [Google Scholar] [CrossRef]
- Dang, H.; Du, S.; Zhang, Y.; Liu, J. A Novel LLC Resonant Converter with Configurable Capacitors in Output Stage for Wide Output Voltage Range Operation. IEEE Trans. Power Electron. 2021, 37, 6233–6236. [Google Scholar] [CrossRef]
- Wu, H.; Li, Y.; Xing, Y. LLC Resonant Converter with Semiactive Variable-Structure Rectifier (SA-VSR) for Wide Output Voltage Range Application. IEEE Trans. Power Electron. 2015, 31, 3389–3394. [Google Scholar] [CrossRef]
- Li, C.; Wang, H.; Shang, M. A Five-switch bridge based reconfigurable LLC converter for deeply depleted PEV charging applications. IEEE Trans. Power Electron. 2018, 34, 4031–4035. [Google Scholar] [CrossRef]
- Yuan, Y.; Peng, N.; Liu, W.; Yi, C. A Linear-Resonant Hybrid Bridge DC–DC Converter. IEEE Trans. Ind. Electron. 2022, 70, 1478–1488. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, H.; Zou, J.; Tai, Y.; Ge, Z. CLL Resonant Converter with Secondary Side Resonant Inductor and Integrated Magnetics. IEEE Trans. Power Electron. 2021, 36, 11316–11325. [Google Scholar] [CrossRef]
- Hu, H.; Fang, X.; Chen, F.; Shen, Z.J.; Batarseh, I. A modified high-efficiency LLC converter with two transformers for wide input-voltage range applications. IEEE Trans. Power Electron. 2012, 28, 1946–1960. [Google Scholar] [CrossRef]
- Wei, Y.; Luo, Q.; Chen, J.; Mantooth, H.A. Analysis and design of LLC resonant converter with variable magnetising inductance control. IET Power Electron. 2020, 12, 3528–3536. [Google Scholar] [CrossRef]








| Symbol | Quantity | Value |
|---|---|---|
| Vin | Input Voltage | 240–480 V |
| Vo | Output Voltage | 110 V |
| Po | Rated Power | 800 W |
| n | Transformer Ratio | 28/6 |
| fs | Switching Frequency | 120–150 kHz |
| fr | Resonant Frequency | 150 kHz |
| L1, L2 | L-R Inductors | 6.34 μH |
| Cr | Resonant Capacitor | 11.2 nF |
| S1~S4 | MOSFETs | IPW60R070CFD7 |
| D1&D2 | Diodes | STTH30AC06C |
| Topologies | Traditional Full Bridge LLC Converter with Full-Wave Rectifier | Phase-Shift Controlled LLC Converter [10,11] | LLC Converter with Additional Components [18] | Variable Inductance LLC Converter [8,23] | Proposed UITBLRC |
|---|---|---|---|---|---|
| Number of switches and diodes | 4 MOSFETs + 2 Diodes | 6 MOSFETs + 2 Diodes | 6 MOSFETs + 2 Diodes | 2 MOSFETs + 4 Diodes | 4 MOSFETs + 2 Diodes |
| Additional components | - | 2 MOSFETs | 1 Switched capacitor + 2 MOSFETs + 2 Output capacitors | 1 Variable inductor | - |
| Magnetic components | 1 Resonant inductor + 1 Excitation inductor + 1 Transformer (center-tapped) | 1 Resonant inductor + 1 Excitation inductor + 1 Transformer | 1 Resonant inductor + 1 Excitation inductor + 1 Transformer | 1 Variable inductor + 1 Transformer | 2 L-R inductors + 1 Transformer |
| Inductor types | 2 | 2 | 2 | 2 | 1 |
| Modulation | PFM | PFM + PSM | PFM + PWM | PFM | PFM |
| Switching frequency range | Wide | Narrow | Wide | Variable | Narrow |
| Voltage regulation range | Narrow | Wide | Wide | Narrow | Wide |
| Input/output voltage | - | 200–400 V/48 V | 400 V/100–500 V | 190–210 V/48 V | 240–480 V/110 V |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Wang, H.; Liu, B. Unified Inductor Type Based Linear Resonant Hybrid Converter for Wide Voltage Range Applications. Energies 2025, 18, 2572. https://doi.org/10.3390/en18102572
Xu J, Wang H, Liu B. Unified Inductor Type Based Linear Resonant Hybrid Converter for Wide Voltage Range Applications. Energies. 2025; 18(10):2572. https://doi.org/10.3390/en18102572
Chicago/Turabian StyleXu, Jingtao, Hao Wang, and Bin Liu. 2025. "Unified Inductor Type Based Linear Resonant Hybrid Converter for Wide Voltage Range Applications" Energies 18, no. 10: 2572. https://doi.org/10.3390/en18102572
APA StyleXu, J., Wang, H., & Liu, B. (2025). Unified Inductor Type Based Linear Resonant Hybrid Converter for Wide Voltage Range Applications. Energies, 18(10), 2572. https://doi.org/10.3390/en18102572









