1. Introduction
New energy generation technologies such as wind power and photovoltaic power have become effective solutions for alleviating the global energy crisis and environmental problems. According to statistics, the amount of electricity generated by renewable energy has increased rapidly in recent years [
1]. With the continuous deepening of industrial structure adjustment in various countries, the demand for electricity has risen rapidly. Additionally, the balance between power supply and demand is facing great pressure [
2].
The large-scale grid-connected operation of new energy sources such as wind power and photovoltaic power has injected a large amount of clean energy into the power grid. China’s wind power and photovoltaic installed capacity will exceed 1.2 billion kilowatts by 2030, and will grow to 3.6 billion kilowatts by 2050 [
3]. However, the output of wind power and photovoltaic power generation shows strong power fluctuations. Exploring efficient peak-to-peak regulation methods is still one of the most urgent tasks of the current power grid [
4,
5,
6].
At present, the peak-shaving methods used by the power grid mainly include the peak shaving of pumped-storage power plants, the peak shaving of oil, gas and coal-fired units, the peak shaving of load-side management, the peak shaving of hydropower units, etc. The peak-shaving cost of oil-fired units is high [
7,
8,
9], gas-fired peak shaving is limited, deep coal-fired peak shaving also has certain requirements regarding the minimum technical output, and the peak shaving capacity is limited. Load-side management can guide users to reduce peak loads and fill valleys through time-of-use electricity prices and tiered electricity prices [
10,
11,
12], but the implementation of load-side management is still in the small-scale trial operation stage; researchers have explored the feasibility of nuclear power units participating in peak-shaving [
13,
14], but the frequent reduction and increase in power of nuclear power units would lead to insufficient fuel consumption and waste; safety and economy are also difficult to guarantee. Battery energy storage technology is a new technology that has been introduced in recent years [
15,
16]. Although this type of technology has developed rapidly, its application and promotion are limited by factors such as the large initial investment required and short battery lives. Hydropower units have excellent peak-shaving capabilities [
17,
18]. Compared with other peak-shaving methods, pumped-storage power plants have significant peak-shaving capabilities, but newly built pumped-storage power stations have high requirements regarding their location and generally take a long time to construct.
With the rapid development of electric vehicles in China [
19,
20,
21], EV charging stations are being built at an astonishing speed and have great development potential [
22,
23]. They have great peak-shaving potential and could thus promote the consumption of wind power and photovoltaic power and alleviate the pressure of hydropower peak shaving.
At present, some research has been carried out on the optimization of EV charging stations participating in grid operation. Mohammad et al. [
24] proposed a method able to find the best location for charging stations in urban areas using particle swarm optimization algorithm technology. Bokopane et al. [
25] proposed an optimization method and modeling framework for PV–grid integrated EV charging stations with battery storage and a point-to-point vehicle charging strategy, optimizing system reliability and profitability while minimizing operating costs. Luo et al. [
26] adopted and utilized the linearized Distflow equation and the exact second-order cone relaxation to obtain the allocation scheme with the minimum annualized social cost in polynomial time. Sortomme et al. [
27] developed an optimal scheduling algorithm for electric vehicles with Vehicle-to-grid (V2G) function that simultaneously considers the economic interests of customers and aggregators. Wang et al. [
28] proposed a novel agent-based coordinated scheduling strategy for EV and DGR to enable them to adapt to actual implementation in a more effective way. Mao et al. [
29] aimed to free V2G prices from market electricity prices, and on this basis, incentivize electric vehicle owners to participate in activities while ensuring the profits of aggregators. Zhang et al. [
30] established an orderly charging optimization model for electric vehicles, with the goal of minimizing the difference between system peak and valley loads and charging costs. Michele et al. [
31] proposed a method able to optimize the configuration of future energy centers for electric vehicle charging and renewable energy generation. Based on the intermittent output and reverse peak-shaving characteristics of wind power, Ju et al. [
32] proposed a multi-source peak-shaving trading optimization model that combines thermal power, energy storage, power generation and demand response. Hou et al. [
33] proposed a power system consisting of wind–solar–hydro–thermal energy and a hybrid demand response that improved the utilization of renewable energy and optimized the dispatch of the economic benefit system of each power generation unit.
For the innovative application of deep reinforcement learning in solving mixed-integer nonlinear programming problems, Zhang et al. [
34] designed a DRL (deep reinforcement learning)-based framework to solve the LFC (load frequency control) problem present in power systems. Di et al. [
35] proposed a method based on deep reinforcement learning to analyze the optimal power flow (OPF) of a distribution network (DN) embedded with renewable energy and storage devices. The proposed method makes full use of historical data and reduces the impact of prediction errors on the optimization results. The proposed real-time control strategy can provide more flexible decisions and achieve better performance than the predetermined strategy. The algorithm proposed by Antonio et al. [
36] is based on a hybrid storage system with supercapacitors and lithium-ion batteries, and performs several analyses based on technical and economic parameters.
This paper proposes an innovative fine-tuning model for the participation of EV charging stations in the peak shaving of the integrated hydro–wind–solar system to enhance the peak-shaving effect of the power grid and promote a higher level of renewable energy regulation. By choosing deep reinforcement learning as the core optimization method, this paper mainly targets the special challenges faced by the hydro–wind–solar multi-energy system in dynamic coupling and uncertainty coordination. Traditional optimization methods (such as stochastic programming and mixed-integer linear programming) find it difficult to effectively handle multi-time-scale coupled decision-making problems in seconds, minutes and hours, and are prone to dimensionality problems in the high-dimensional state space where the strong randomness of the wind and solar output, time-varying hydropower ecological flow constraints and the heterogeneity of EV behavior coexist. DRL can autonomously explore the rules of cross-energy space–time complementarity through the end-to-end mapping of “system state–optimization action”. Its dual advantages are reflected in the following: (1) its ability to perform time series decision-making based on value function approximation can dynamically coordinate the coordinated rhythm of hydropower rapid regulation (minutes) and the EV cluster response in seconds; (2) through the policy gradient adaptive avoidance of complex constraints (such as vibration zone crossing and SOC safety boundary), it avoids the suboptimal solution problem caused by the linearization/relaxation of traditional methods. The main contributions of this study are as follows:
- (1)
Considering the detailed production characteristics, comprehensive cost characteristics, controllability and safety constraints of EV charging stations, this article proposes a refined peak-shaving model. The model ensures that charging stations can participate in grid regulation safely and reliably and meet the charging needs of car owners.
- (2)
By establishing a collaborative optimization model, it combines the regulation of EV charging stations with the dispatch of conventional hydropower stations. The model determines the peak regulation state while considering the comprehensive cost, economic feasibility and contribution to the consumption of new energy associated with hydropower regulation.
- (3)
Taking the actual power grid as a case, the effectiveness of the proposed model is verified under the actual operation scenario. The results show that adjusting the power of EV charging stations and hydropower stations can bring huge comprehensive benefits to the entire social power system while meeting production characteristics and safety constraints.
3. A Hierarchical Optimization Model for Water–Wind–Solar Integration Considering EV Charging Station Regulation and Hydropower Deep Regulation
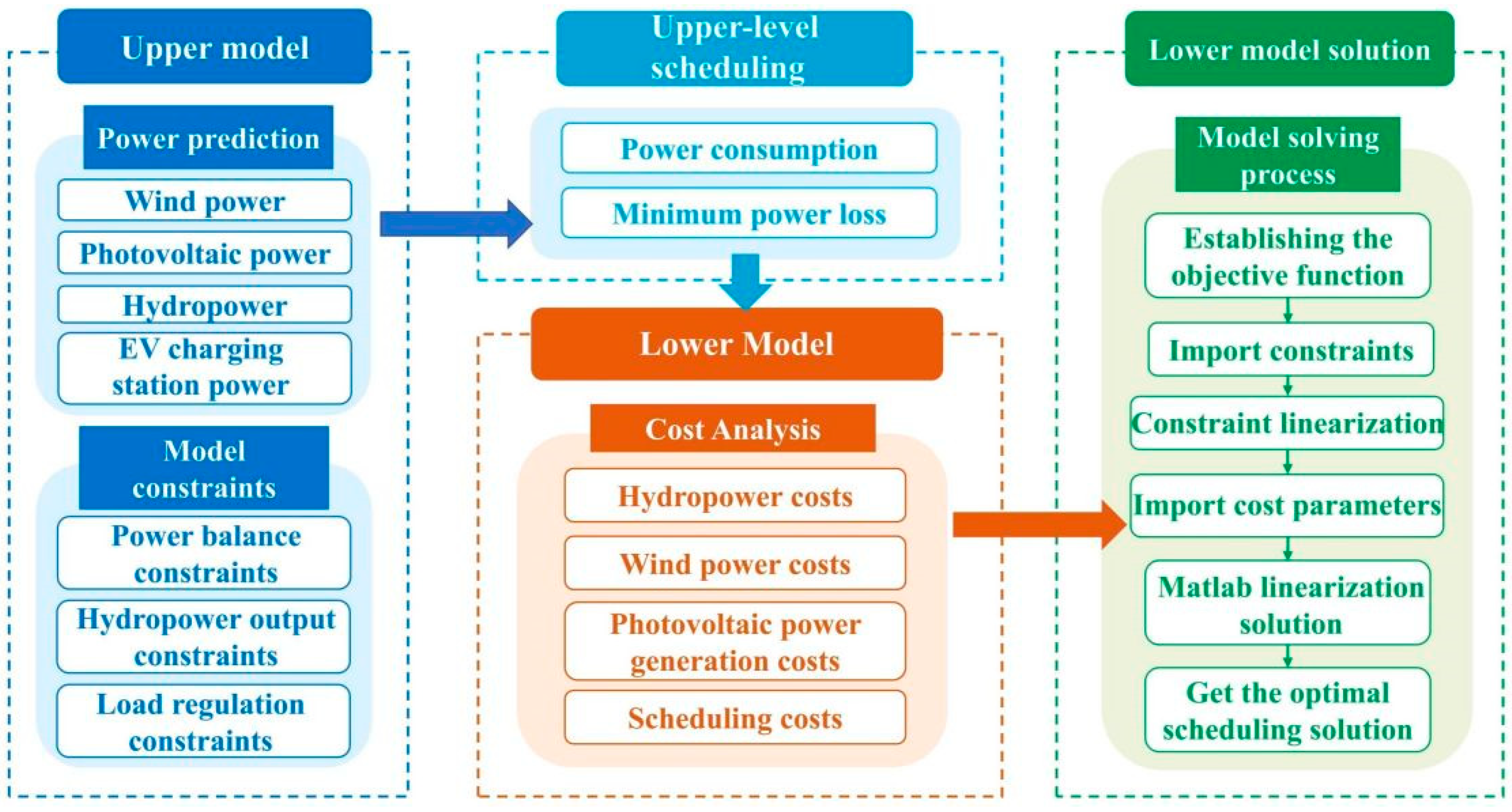
The hierarchical optimization model proposed in this paper is a hierarchical relationship between the upper and lower layers, as shown in
Figure 2; this gives full play to the role of charging stations’ load and hydropower deep peak regulation in absorbing wind power and photovoltaic power, and optimizes the system peak regulation structure.
3.1. Upper Model
In the upper-level model, the power of the EV charging station’s load and the total output of the hydropower units are arranged in order to minimize the total amount of abandoned electricity to maximize the use of peak-shaving resources.
The constraints of the upper model are mainly system power balance constraints, wind power and photovoltaic output constraints, total hydropower output and ramp constraints, and positive and negative spinning reserve constraints.
A schematic diagram of the hierarchical optimization model is shown in
Figure 2.
3.1.1. System Power Balance Constraints
In order to ensure the reliable operation of the regional power system, it is essential to maintain a balance between power supply and demand at each time interval. The system power balance constraint reflects the fundamental requirement that the sum of renewable generation, dispatchable power sources, and EV charging/discharging must match the regional load demand. This relationship is mathematically described as follows:
where
is the total output of hydropower units in the region;
is the conventional load forecast in the region; and
is the number of EV charging stations in the region.
3.1.2. Wind Power Output Constraints
Wind power output is inherently variable and largely dependent on real-time meteorological conditions, particularly wind speed. To accurately reflect the generation capabilities of wind turbines, a set of constraints is introduced to model the relationship between wind speed, turbine efficiency, and power output. These constraints ensure that the wind power output remains within feasible operating limits and accounts for the nonlinear characteristics of wind turbine performance. The detailed formulation is given below:
where
is the wind power output at time
and
is the maximum wind power output.
is a piecewise function that represents the effect of wind speed
on the wind power output.
3.1.3. Photovoltaic Power Output Constraints
Photovoltaic power generation is influenced by solar irradiance, temperature, and panel efficiency, leading to time-varying output profiles. To model the operational limits of PV systems, constraints are imposed to ensure that the actual PV output does not exceed its theoretical maximum under given environmental conditions:
where
is the photovoltaic output at time
, and
is the maximum photovoltaic output.
3.1.4. Total Hydropower Output and Climbing Constraints
Hydropower units play a crucial role in balancing power supply due to their high flexibility and fast response characteristics. However, their operation is still subject to physical and environmental limitations, such as maximum and minimum output levels, as well as ramping constraints that restrict how quickly output can increase or decrease over time. The following equations define these operational boundaries to ensure safe and realistic dispatch of hydropower resources:
where
and
are the upper and lower limits of the total hydropower output, and
and
are the ramp-up and ramp-down rates of the total hydropower output.
3.1.5. Positive and Negative Spinning Reserve Constraints
To maintain the reliability and stability of the power system in the face of renewable generation uncertainties and load fluctuations, spinning reserve requirements must be considered. These reserves ensure that sufficient upward or downward capacity is available to respond to real-time deviations from forecasts. The following constraints define the minimum positive and negative spinning reserves that hydropower units must provide, based on the forecasted loads and renewable generation levels:
where
is the photovoltaic output at time
, and
is the maximum photovoltaic output.
and
are the spinning reserve coefficients for the wind power and photovoltaic power forecast.
3.1.6. Hydropower Station Water Balance Constraints
The actual operation and regulation characteristics of the hydropower station are taken into account [
46].
where
is the final storage capacity,
,
and
are the power generation flow, abandoned water flow and inflow flow,
is the hydropower stations that have a direct hydraulic connection with the station
, and
is the water flow time lag from upstream station
to downstream station
.
3.1.7. Hydropower Reservoir Capacity Constraints
The water storage level of each hydropower station must remain within its operational limits to ensure safe and efficient operation. This constraint is defined as follows:
where
and
are the minimum and maximum storage capacities allowed by hydropower station
.
3.1.8. Hydropower Shipping and Irrigation Constraints
In addition to power generation, hydropower stations must meet water demand for shipping and irrigation. The total discharge must therefore stay within specified limits, as shown below:
where
and
are the minimum and maximum discharge flows of hydropower station
, respectively.
3.1.9. Hydropower Maintenance Constraints
To account for maintenance schedules and operational conditions, the output of each hydropower station is constrained within allowable maintenance limits, as follows:
where
and
are the minimum and maximum outputs allowed by hydropower station
, respectively.
3.1.10. The Current Storage Capacity and the Storage Capacity Control Constraints
To ensure long-term water resource planning and operational continuity, the reservoir storage levels must meet predefined targets at the start and end of the dispatch period. The constraint is expressed as follows:
where
and
are the control storage capacities at the beginning and end of the dispatching period of hydropower station
.
3.1.11. Hydropower Output Limit Area Constraints
The formula used to determine the power station output limit area constraints in the unit vibration area is shown as follows:
where
is the set of output limit ranges for hydropower station
;
is the minimum allowable output (lower limit) of the
-th unit when it enters the vibration zone; and
is the maximum allowable output (upper limit) of the
-th unit when it leaves the vibration zone.
3.2. Lower Layer Optimization Model
The lower model mainly optimizes the peak load regulation of each hydropower unit from the perspective of the system’s operation cost, based on the output results of the upper model when maximizing the consumption of wind power and photovoltaic power, taking into account the cost of the deep peak load regulation of hydropower units, and considering the minimum system operation cost as the goal.
3.2.1. Cost Model of Deep Peak Regulation of Hydropower Units
The cost of providing peak load regulation services mainly includes the fixed costs, which mainly include the mechanical losses caused by the unit’s participation in peak load regulation and the costs of various behaviors required during the unit’s peak load regulation process, and the opportunity costs, which refer to the profit loss caused by the unit’s reduced power generation due to its peak load regulation services.
The peak-shaving cost of thermal power units is relatively clear [
47]. Through actual research on hydropower stations [
48], the fixed cost of peak shaving in hydropower units is mainly the mechanical loss caused by frequent output adjustment in the peak-shaving process.
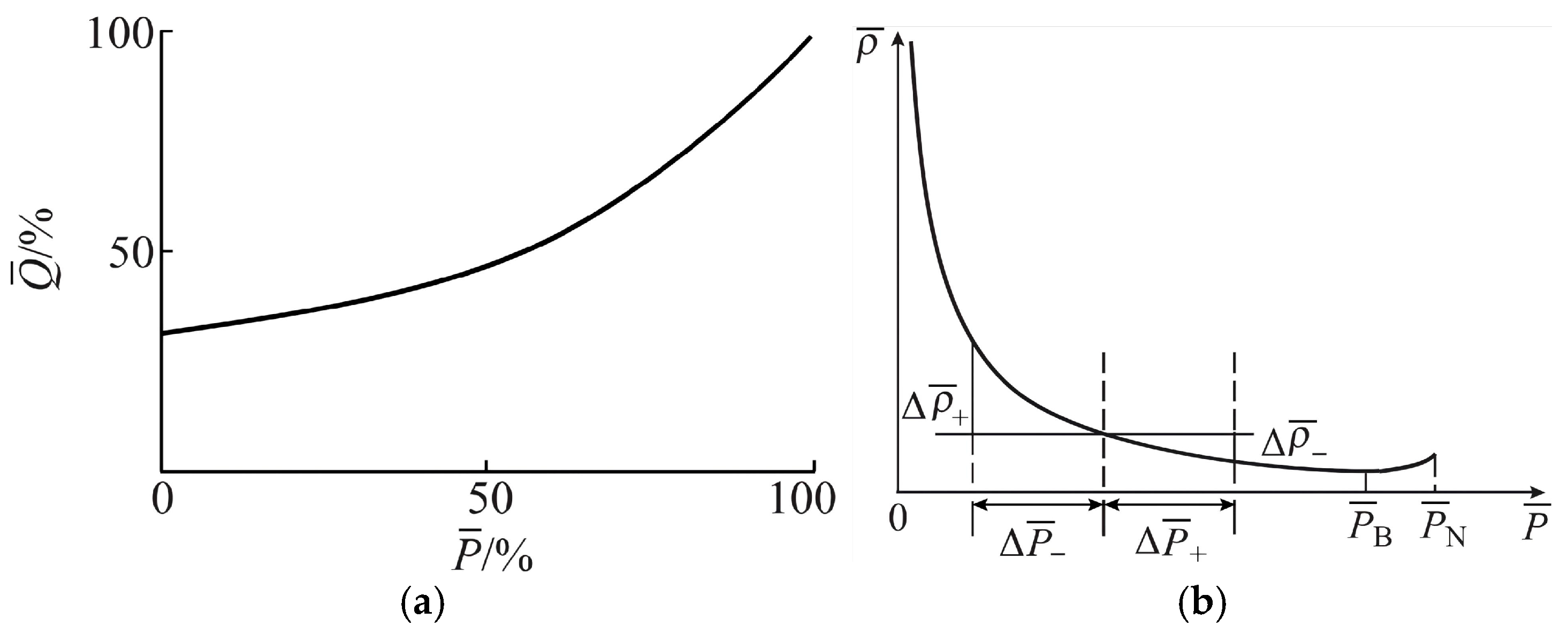
The relative output
is the ratio of the actual output
of the unit to the rated output
of the unit, and the relative flow
is the ratio of the actual flow
to the maximum flow
, as shown in
Figure 3a [
49].
The water consumption rate
is an important parameter used to characterize the efficiency of a hydropower unit. The relative value of the water consumption rate
is the ratio of the actual water consumption rate
to the minimum water consumption rate
, as shown in
Figure 3b [
49].
The process used to calculate the peak load compensation for hydropower units is listed below:
- (1)
Integrate the gap of and obtain the corresponding peak load .
- (2)
Based on the water consumption rate
, the peak load
is converted into the water consumption
under the rated water head using the following formula:
- (3)
Using the water consumption rate corresponding to the output of the basic peak load limit , is converted into the minimum power generation using the following formula when no downward peak load regulation is performed:
Assuming that the unit power generation revenue of the hydropower unit is
, the compensation fee is
:
Combining Equations (32) and (33), we can obtain the following:
3.2.2. The Objective Function of the Lower Model
The lower model optimizes the peak load structure of each hydropower unit based on the minimum power abandonment of the upper model, according to the optimized wind power and photovoltaic power consumption, load power of the EV charging station, and total hydropower output. The goal is to maximize the profitability of system operation:
where
is the conventional load power consumption,
is the conventional load electricity price,
is the electric vehicle charging amount,
is the electric vehicle charging price,
is the compensation amount,
is the cost of power generation for the hydropower station,
is the cost of photovoltaic power generation,
is the cost of wind power generation, and
is the total dispatch cost of the system.
3.3. Model Solving
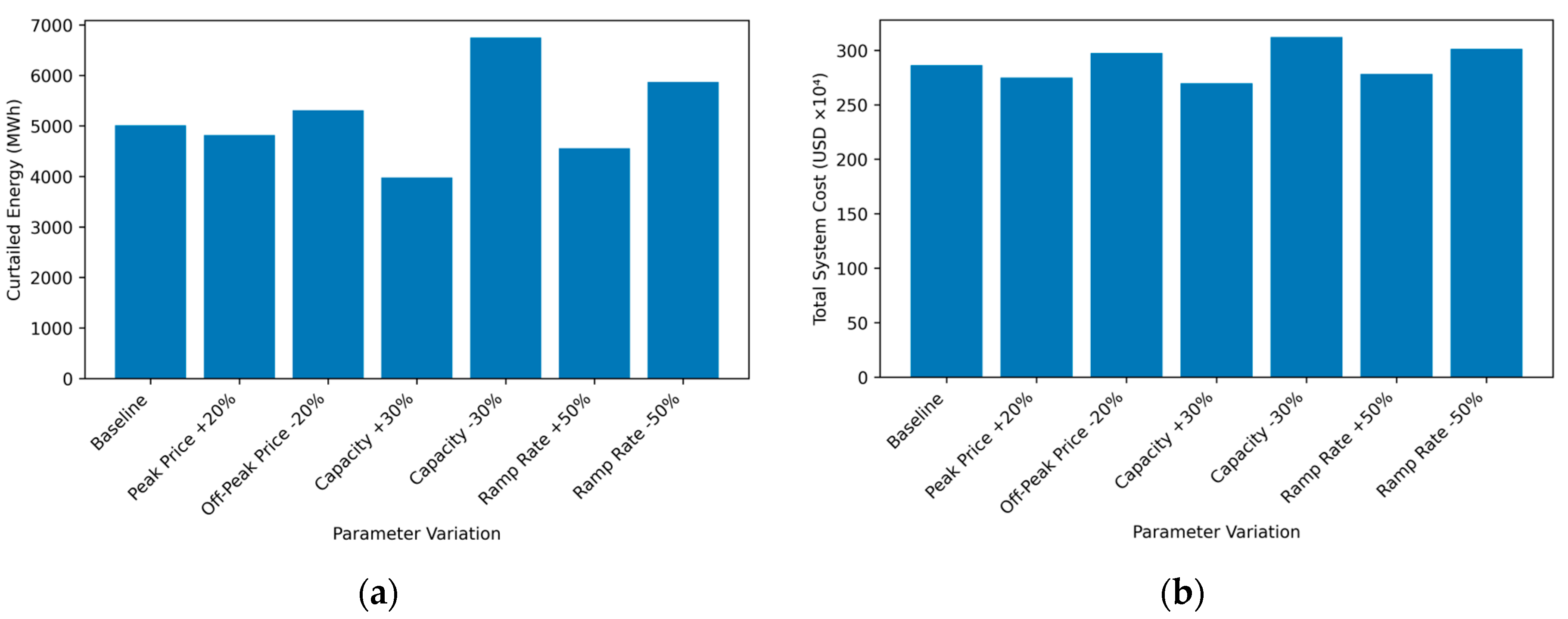
The upper and lower layers of the hierarchical optimization model established in this paper belong to mixed-integer nonlinear programming problems. In order to reduce computational complexity, linearization processing is required. Equations (14)–(30) in the upper model and Equations (34)–(38) in the lower model are both linearized piecewise. Finally, taking an actual regional system containing a large number of EV charging stations and hydropower stations as an example, a deep reinforcement learning (DRL) algorithm is used to solve and analyze the problem, thereby calculating the maximum operating profit and various parameters to verify the effectiveness of the proposed scheme.
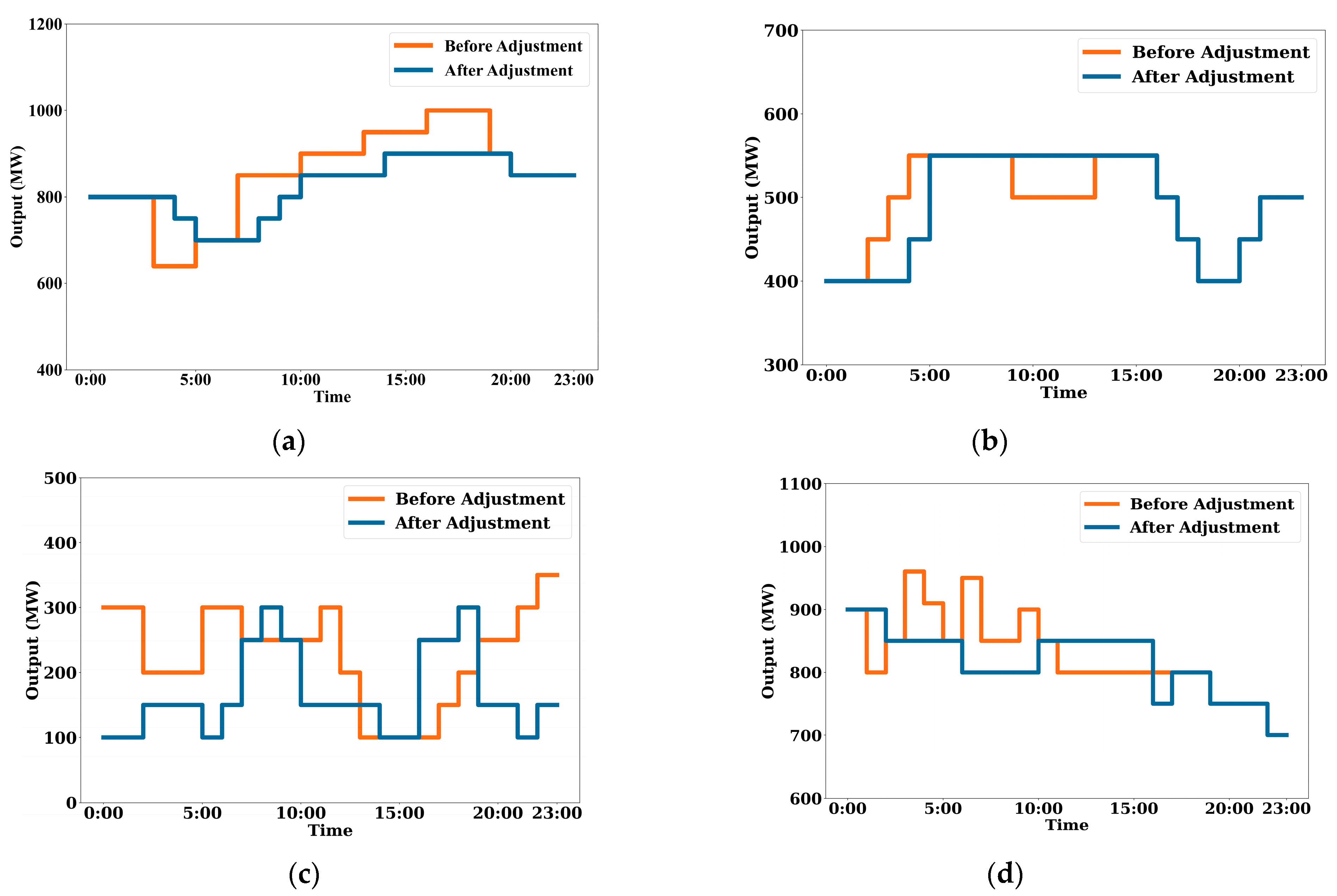
In actual operation, in order to balance economy and the dispatch flexibility, we stipulate that the hydropower station receives a power dispatch instruction from the power grid once an hour and that each power adjustment is made in multiples of 50 MW.
In order to ensure the strict implementation of the constraint listed above and thus ensure the safety of the adjustment process, we organize the formulas listed above into a constraint function (CF) and control it in combination with the input in the deep reinforcement learning algorithm [
50]. The training algorithm of the DRL-CF network is summarized as follows.
The examined DRL-CF control method was implemented in Python (version 3.7) through PyTorch (version 2.0). The training processes were executed on a Windows system with an AMD Ryzen 7 7840HS with Radeon 780M Graphics 3.80 GHz and 32 GB of RAM. The hardware was sourced from AMD, CA, USA. The actor and critic networks included two hidden layers, with 256 hidden units, which were trained using the Adam optimizer. The tanh activation was adopted for the output layer. Other system input parameters of the RL agent are summarized in
Table 1.The DRL-CF algorithm is shown as Algorithm 1.
| Algorithm 1: DRL-CF algorithm |
![Energies 18 02566 i001]() |
5. Conclusions
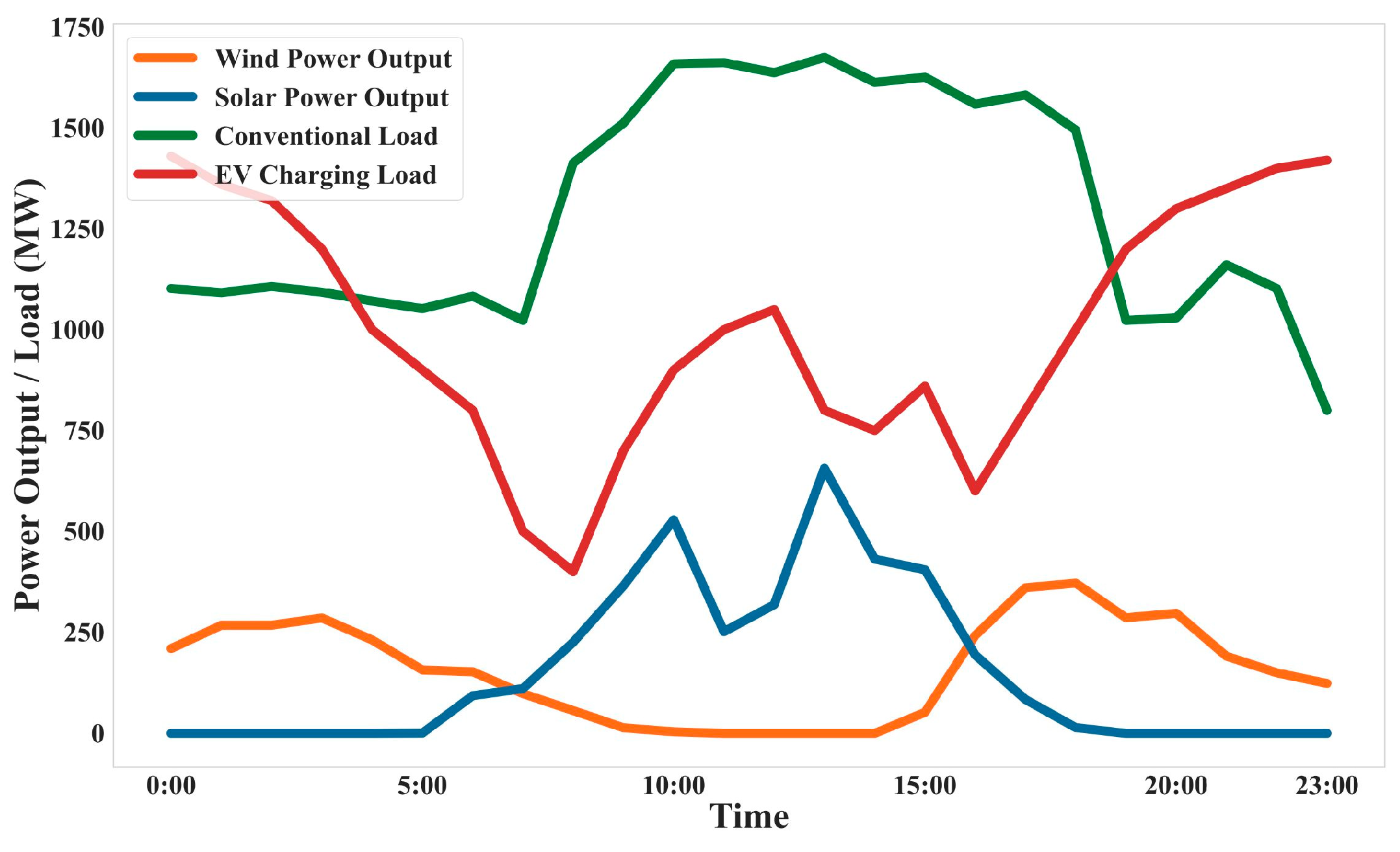
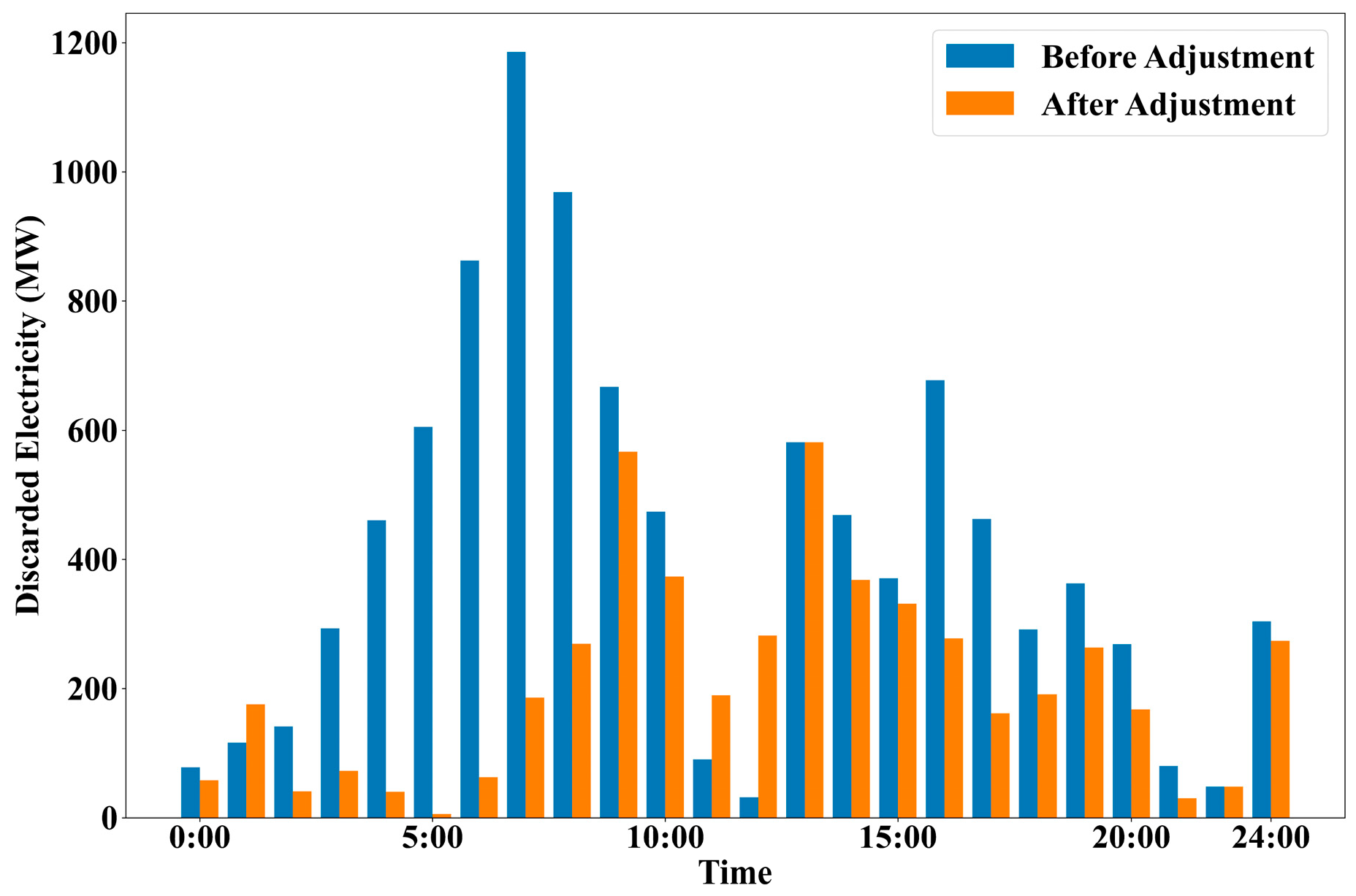
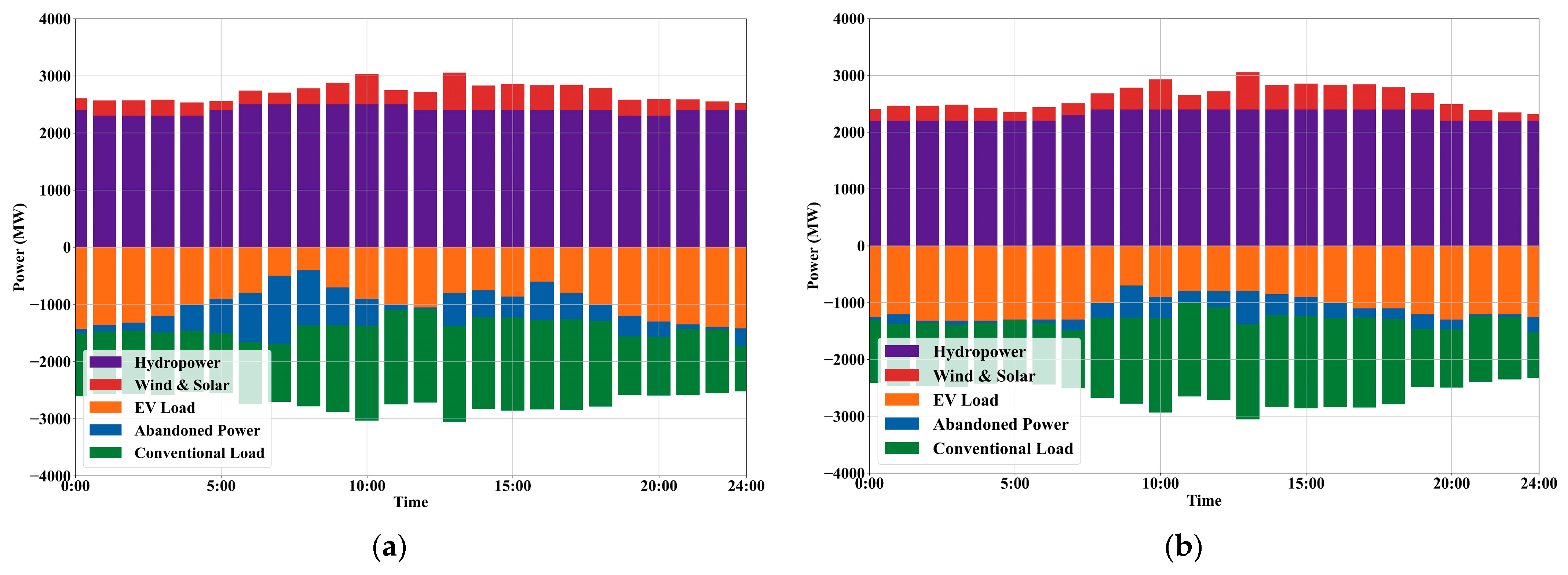
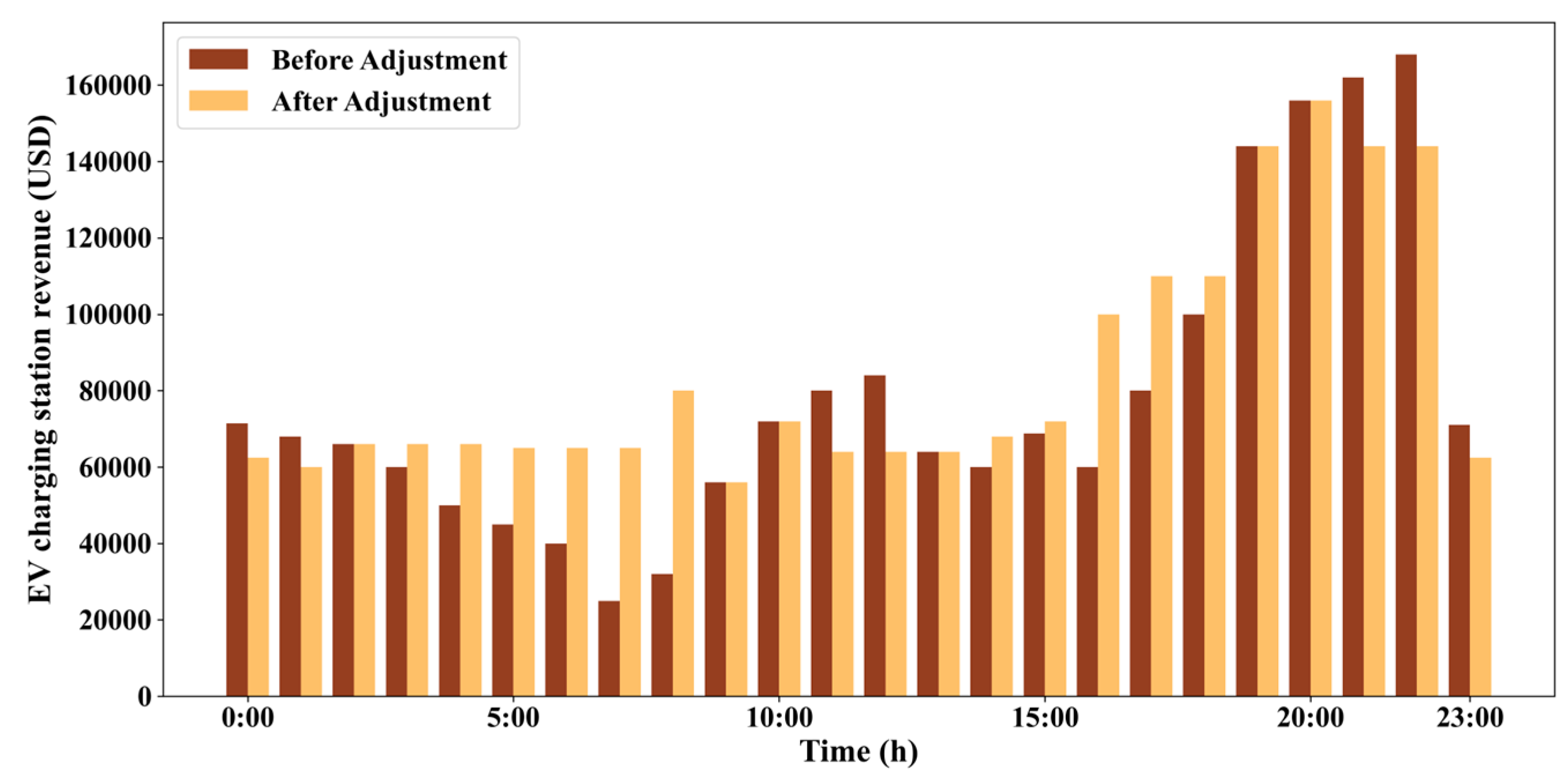
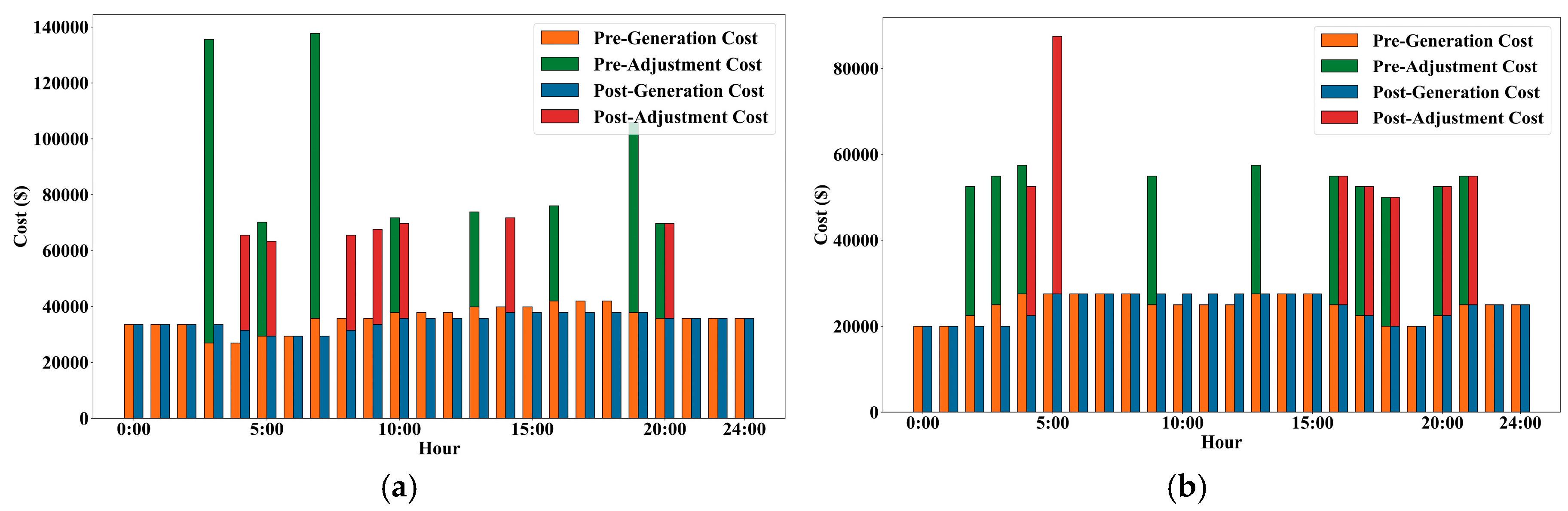
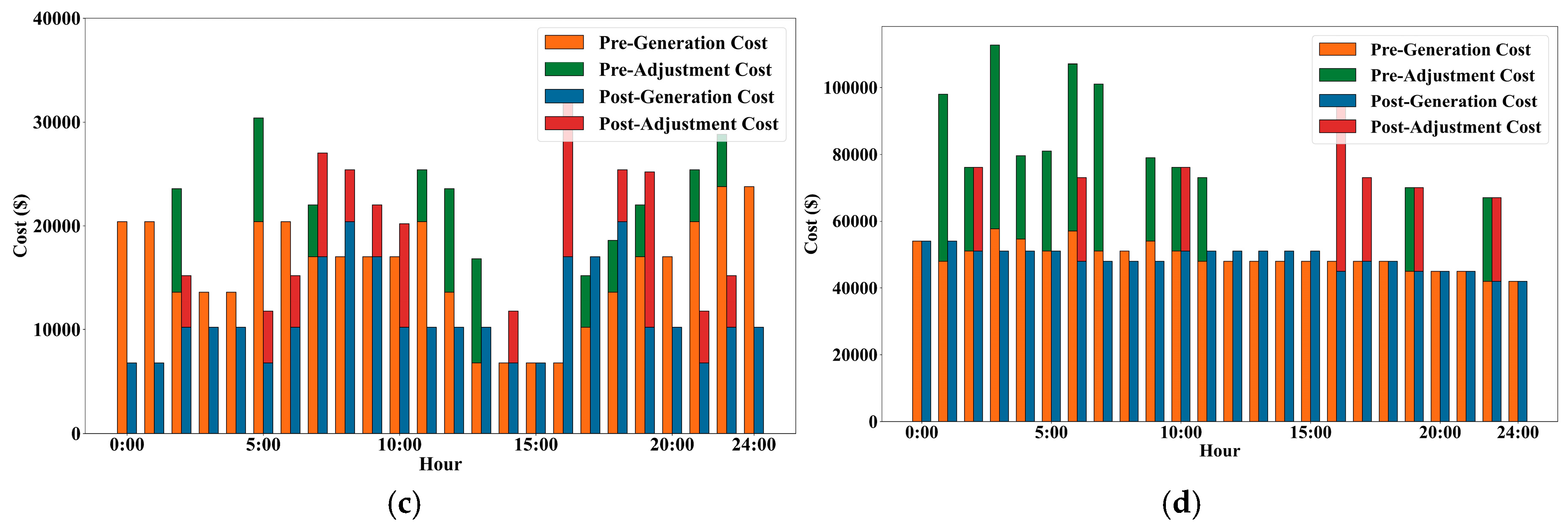
This paper considers incorporating the load of EV charging stations into the optimal dispatching of the power grid, and jointly participates in the peak-shaving operation of the integrated water–wind–solar system with the deep peak shaving of hydropower units; it also establishes a hierarchical optimization model with the minimum system power abandonment and the minimum operating cost. Finally, taking a real regional system with a high proportion of wind power and photovoltaic power and rich hydropower resources as an example, the effectiveness of the proposed strategy is verified, the economic and technical impact of the deep peak shaving of hydropower units is analyzed, and the following conclusions are obtained:
- (1)
The proposed scheme can effectively improve the comprehensive peak-shaving effect of the system, and reduce the cost of hydropower in the regional example system by 4.34% and the system operation costs by 5.67%, respectively; the load regulation of EV charging stations and the hierarchical coordination of deep hydropower regulation promote wind power consumption, which relatively reduces the abandoned wind volume by 46.8%.
- (2)
Under the proposed scheme, the economic and technical performance of hydropower units participating in the peak shaving of the power grid is improved. The participation of the load of EV charging stations in grid regulation significantly alleviates the peak-shaving pressure of hydropower units, reduces the regulation of hydropower units and the amount of electricity, optimizes the deep peak-shaving structure of hydropower units, and reduces the cost of hydropower regulation and total hydropower generation, which lowers the cost of generating hydropower.
- (3)
The proposed hierarchical optimization model focuses on verifying the support potential and effect of the load of charging stations on the system’s peak shaving in the regional power grid, and has a significant effect on the integrated water–wind–solar regional system with a high proportion of wind power and photovoltaic power and a high proportion of charging stations; this is especially true for the coordination of peak-shaving strategies with hydropower peak-shaving resources, which has great significance for practical guidance.
In the future, the model can be combined with the secondary control of DC microgrids to utilize fast control dynamics to achieve large-scale communication, networked sensor sampling and computing loads [
52]. At the same time, decentralized operation methods that avoid risks should be considered to effectively limit the systemic risks existing in the joint system [
53]. For the distribution of benefits, the random double-level optimal allocation method can be considered to ensure the distribution of the benefits of different entities in the joint system when electricity prices are uncertain [
54].