Two-Stage Dynamic Partitioning Strategy Based on Grid Structure Feature and Node Voltage Characteristics for Power Systems
Abstract
1. Introduction
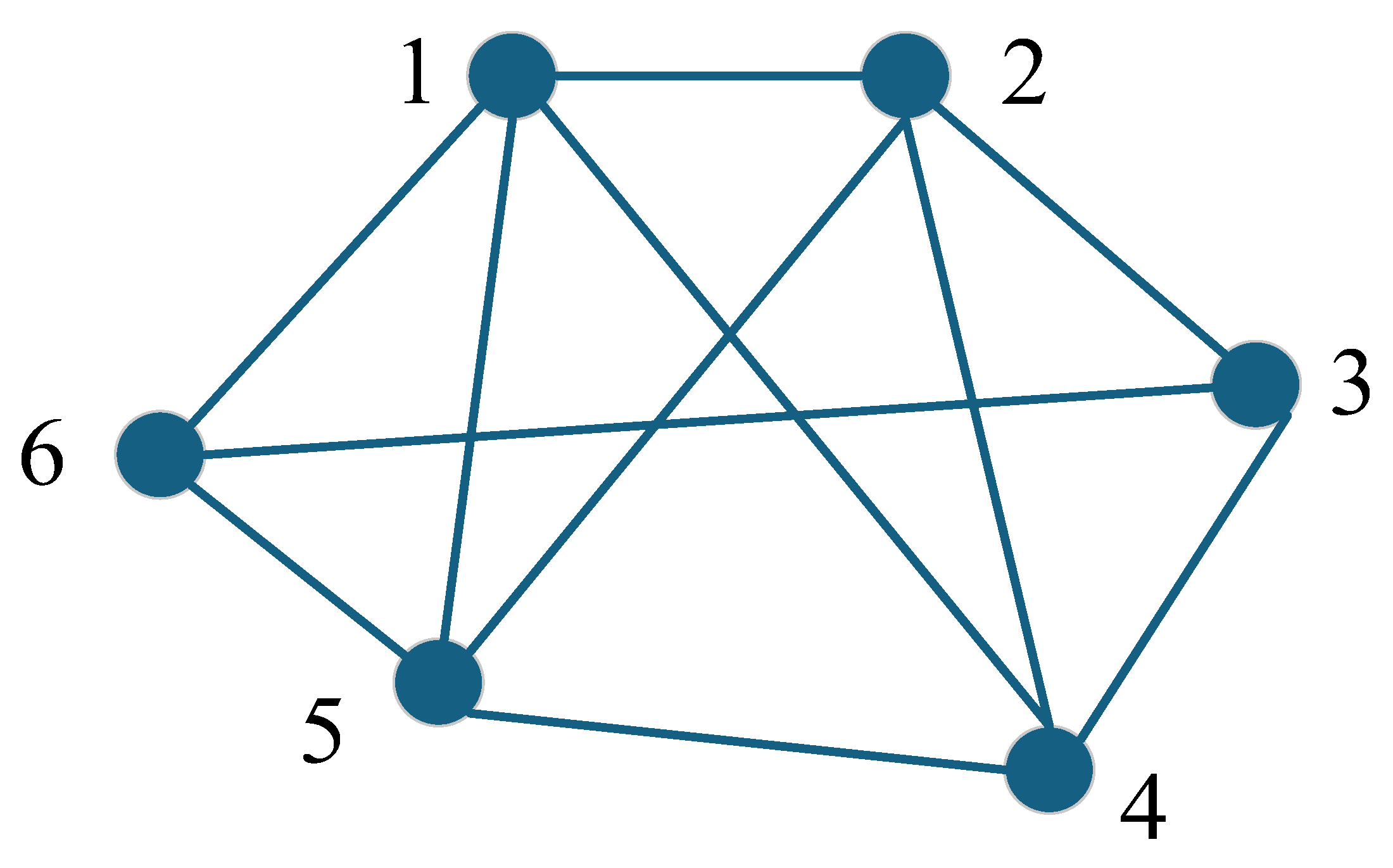
2. The Complex Network Based on Structure–Function Coupling
2.1. Complex Network Features of Electrical Grid
2.2. Electrical Functional Features of Electrical Grid
2.2.1. Electrical Coupling Strength
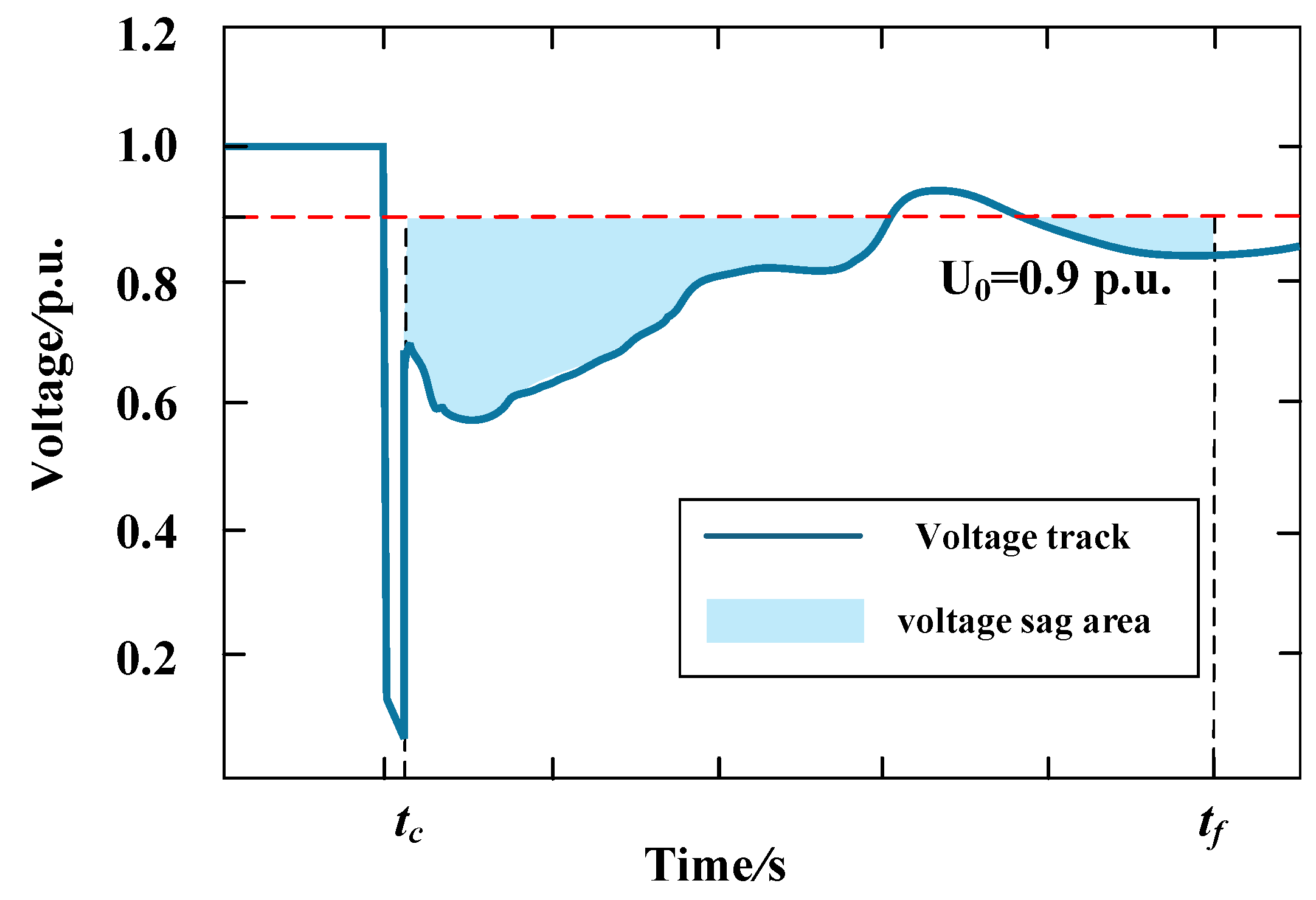
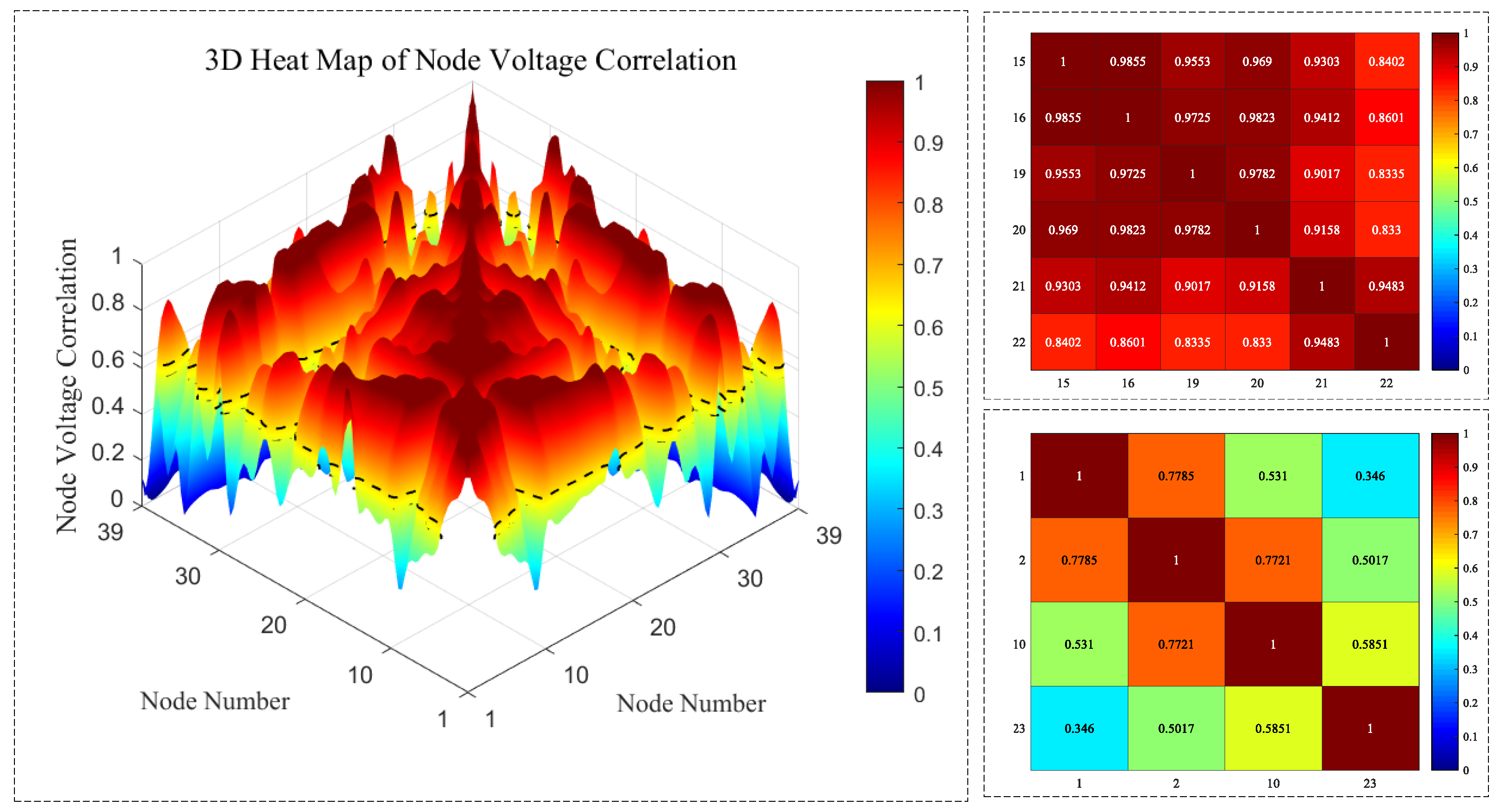
2.2.2. Node Voltage Fluctuation Index
2.3. Weighted Network Considering Node Voltage Correlation
- (1)
- Value Range: The modularity value Q lies in the interval (0, 1).
- (2)
- Topological Interpretation: Modularity captures the extent to which connections are concentrated within communities rather than between them. A high Q value indicates that the network exhibits dense intra-community links, while values closer to 0 imply weaker or insignificant community organization.
- (3)
- Extended Functional Meaning: By adjusting the weights of network edges, modularity can incorporate additional system-level features beyond topology. For example, assigning weights based on electrical correlations allows Q to reflect the functional coupling strength between nodes, rather than just the structural proximity.
3. Two-Stage Grid Dynamic Partitioning Strategy
3.1. Pre-Partitioning Based on Electrical Coupling Strength
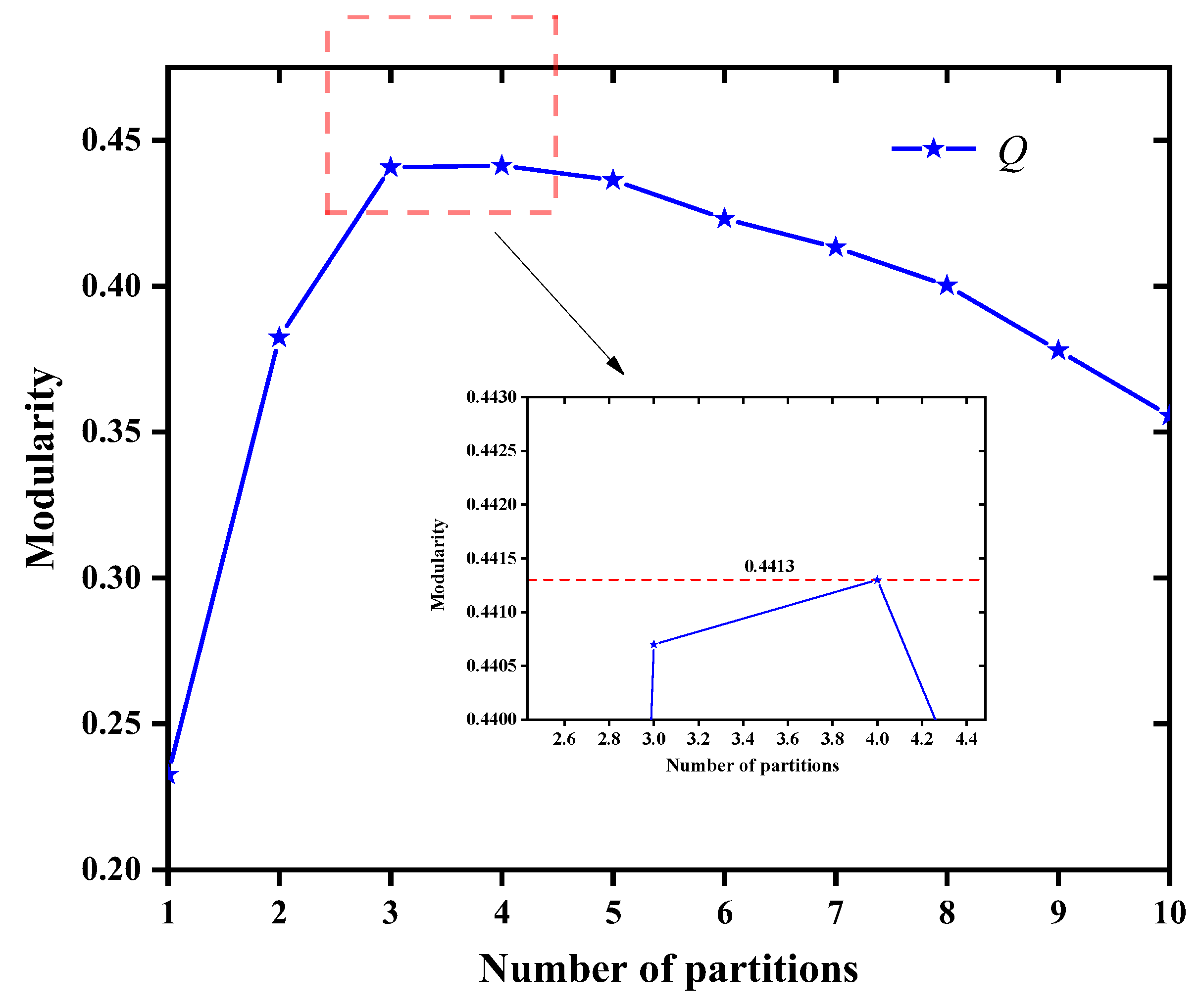
3.2. Second-Stage Partitioning Based on Modularity Optimization
4. Case Study
4.1. Example Setting
- (1)
- The load level is increased in increments of 10% based on the reference level of 90% to 110%.
- (2)
- The set of assumed faults is an N − 1 three-phase permanent fault, occurring on a total of 35 buses throughout the system.
- (3)
- The fault occurs at 0%, 30%, 60%, and 90% of the distance from the line’s starting point.
- (4)
- The fault clearance time is set to 0.1, 0.2, and 0.3 s after the fault occurs.
4.2. Validation of the Proposed Method
4.3. Comparison and Analysis
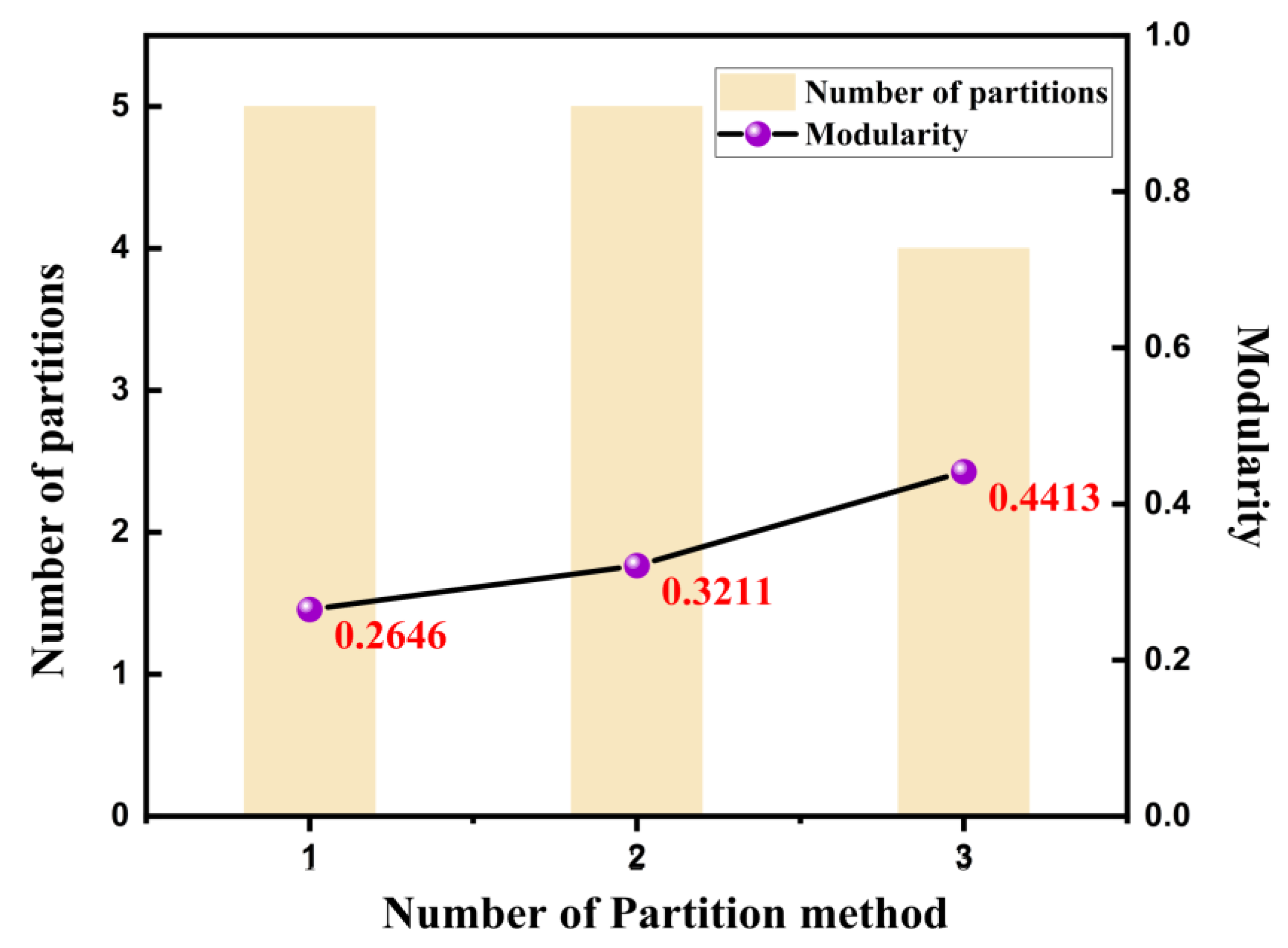
4.3.1. Modularity
4.3.2. Regional Decoupling Rate
4.3.3. Maximum Voltage Deviation
4.4. Limitations and Prospects
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Acronyms | |
| AVC | Automatic Voltage Control |
| PV | Photovoltaic |
| DC | Direct Current |
| PSD-BPA | Power System Data—Bonneville Power Administration |
| Variables | |
| C | clustering coefficient |
| Crandom | clustering coefficient of random network |
| L | average path of the network |
| Lrandom | average path of the random network |
| A | adjacency matrix |
| aij | element of adjacency matrix A |
| ki | degree of node |
| sij | sensitivity of reactive power and voltage between reactive source node j and load node i |
| Zij | short-circuit impedance between reactive source node j and load node i |
| lij | short-circuit impedance distance between reactive source node j and load node i |
| Eij | electrical coupling strength between reactive source node j and load node i |
| Uη | voltage fluctuation index |
| tc | fault clearing moment |
| Tth | permissible duration below the transient voltage threshold |
| T | duration for which the bus voltage is below the threshold in an actual fault |
| U0 | steady voltage amplitude after fault disappearance |
| Fi | transient voltage behavior of node i across n scenarios |
| ρij | node voltage correlation index between node j and node i |
| m | total number of edges |
| a’ij | element of modified adjacency matrix A |
| Q | modularity index |
| err | degree of internal lines within the r-th |
| ar | degree of lines associated with the r-th region |
| I | regional decoupling rate |
References
- Liu, L.; Cheng, H.Z.; Wu, Y.W. Research Progress and Prospects of Transmission Expansion Planning Method for High Proportion of Renewable Energy. Autom. Electr. Power Syst. 2021, 45, 176–183. [Google Scholar]
- Ruan, H.; Gao, H.; Liu, Y.; Wang, L.; Liu, J. Distributed Voltage Control in Active Distribution Network Considering Renewable Energy: A Novel Network Partitioning Method. IEEE Trans. Power Syst. 2020, 35, 4220–4231. [Google Scholar] [CrossRef]
- Duan, J.; Li, F.; Xue, B.; Zhu, D.; Wang, H.; Cheng, W. Power Grid Partitioning Methods Based on Improved GN Splitting Algorithm. In Proceedings of the 18th International Conference on AC and DC Power Transmission (ACDC 2022), Virtual, 2–3 July 2022; pp. 725–730. [Google Scholar]
- Yang, Y.; Sun, Y.; Wang, Q.; Liu, F.; Zhu, L. Fast Power Grid Partition for Voltage Control with Balanced-Depth-Based Community Detection Algorithm. IEEE Trans. Power Syst. 2022, 37, 1612–1622. [Google Scholar] [CrossRef]
- Chen, J.; Wei, X.; Zhang, T. Advanced Methodology for Optimal Allocation of Reactive Voltage Control Utilizing Sensitivity Matrix Analysis and Distance Evaluation Metrics. In Proceedings of the 2024 IEEE 7th Student Conference on Electric Machines and Systems (SCEMS), Macao, China, 6–8 November 2024; pp. 1–6. [Google Scholar]
- Li, T.; Xue, F. Power Network Partitioning Method Based on Dijkstra Algorithm. Power Syst. Prot. Control 2018, 46, 159–165. [Google Scholar]
- Zou, S.H.; Cao, Y.J.; Liu, Z.W. Identification of Grid Weak Link Considering Voltage Instability Patterns at Multiple Time Scales. Power Syst. Prot. Control 2024, 52, 35–49. [Google Scholar]
- Li, Y.; Cao, Z.; Zhang, Z. Voltage Stability Index-Based Synchronous Condenser Capacity Configuration Strategy of Sending End System Integrated Renewable Energies. In Proceedings of the 2022 IEEE Sustainable Power and Energy Conference (iSPEC), Perth, Australia, 4–7 December 2022; pp. 1–5. [Google Scholar]
- Jiang, D.; Ma, X.; Liu, Y.; Sun, X.; Chen, Q. Network Partition Method for Transient Voltage Control of the AC/DC Power System. In Proceedings of the 2023 Panda Forum on Power and Energy (Panda FPE), Chengdu, China, 27–30 April 2023; pp. 272–276. [Google Scholar]
- Liu, Z.; Li, Y.; Yao, L.; Wang, X.; Nie, F. Agglomerative Neural Networks for Multi-View Clustering. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 2842–2852. [Google Scholar] [CrossRef]
- Cao, X.; Han, M.X.; Ma, L.M.; Guo, Z.F.; Cai, W.T.; Zhang, X.H.; Wen, J. Segmentation Method of a Multi-Infeed LCC System Based on Local Fitness Measure. Adv. Technol. Electr. Eng. Energy 2021, 40, 32–42. [Google Scholar]
- Wang, Y.; Lebovitz, L.; Zheng, K.; Zhou, Y. Consensus Clustering for Bi-Objective Power Network Partition. CSEE J. Power Energy Syst. 2022, 8, 973–982. [Google Scholar]
- Sinaga, K.P.; Yang, M.S. Unsupervised K-Means Clustering Algorithm. IEEE Access 2020, 8, 80716–80727. [Google Scholar] [CrossRef]
- Mahdi, S.; Colombo, G.; Longo, M. K-Means and Alternative Clustering Methods in Modern Power Systems. IEEE Access 2023, 11, 119596–119633. [Google Scholar]
- Peng, X.Y.; Shen, Y.; Lu, Q.Y.; Shen, C. Robust Var-Voltage Control Partitioning for Power Grid Considering Wind Power Uncertainty. Power Syst. Technol. 2023, 47, 4102–4110. [Google Scholar]
- Zhao, C.; Zhao, J.; Wu, C.; Wang, X.; Xue, F.; Lu, S. Power Grid Partitioning Based on Functional Community Structure. IEEE Access 2019, 7, 152624–152634. [Google Scholar] [CrossRef]
- Liu, F.; Gu, B.; Qin, S. Power Grid Partition with Improved Biogeography-Based Optimization Algorithm. Sustain. Energy Technol. Assess. 2021, 46, 101267. [Google Scholar] [CrossRef]
- Zou, Y.; Li, H. Study on Power Grid Partition and Attack Strategies Based on Complex Networks. Front. Phys. 2022, 9, 790218. [Google Scholar] [CrossRef]
- Zheng, J.X.; Zhong, J. A Complex Network Theory Fast Partition Algorithm of Reactive Voltage Based on Node Type and Coupling of Partitions. Power Syst. Technol. 2020, 45, 223–230. [Google Scholar]
- Ling, R.; Shao, B.; Li, M.; Chen, X.; Cao, C.; Xue, C. Study of Power Grid Partition Based on the Similarity of Complex Network Communities. Zhejiang Electr. Power 2021, 40, 47–53. [Google Scholar]
- Wei, Z.B.; Guan, X.Y.; Liu, L.H. Overview of Power Community Structure Discovery Algorithms and Their Application in Power Grid Analysis. Power Syst. Technol. 2020, 44, 2600–2609. [Google Scholar]
- Massaoudi, M.; Ez Eddin, M.; Ghrayeb, A.; Abu-Rub, H.; Refaat, S.S. Advancing Coherent Power Grid Partitioning: A Review Embracing Machine and Deep Learning. IEEE Open Access J. Power Energy 2025, 12, 59–75. [Google Scholar] [CrossRef]
- Wang, X.; Xue, F.; Lu, S.; Jiang, L.; Bompard, E.; Masera, M. Understanding Communities from a New Functional Perspective in Power Grids. IEEE Syst. J. 2022, 16, 3072–3083. [Google Scholar] [CrossRef]
- Yan, W.; Wang, F.; Tang, W.Z. Network Partitioning for Reactive Power/Voltage Control Based on Power Sources Clustering and Short-Circuit Impedance Distance. Power Syst. Prot. Control 2013, 41, 109–115. [Google Scholar]
- Chen, Y.; Zeng, J.; He, R. Grid Partitioning Method for Medium Voltage Distribution Network Based on Improved K-Means Algorithm. In Proceedings of the 2024 6th International Conference on Eergy, Power and Grid (ICEPG), Guangzhou, China, 27–29 September 2024; pp. 959–962. [Google Scholar]
- Nguyen, Q.; Ke, X.; Samaan, N.; Holzer, J.; Elizondo, M.; Zhou, H.; Hou, Z.; Huang, R.; Vallem, M.; Vyakaranam, B.; et al. Transmission-Distribution Long-Term Volt-Var Planning Considering Reactive Power Support Capability of Distributed PV. Int. J. Electr. Power Energy Syst. 2022, 138, 107955. [Google Scholar] [CrossRef]








| Partition Number | Reactive Power Source | Load Node |
|---|---|---|
| 1 | 30 | 2, 3, 17, 18, 26, 27 |
| 2 | 31 | 4–7 |
| 3 | 32 | 10–15 |
| 4 | 33 | 19 |
| 5 | 34 | 20 |
| 6 | 35 | 16, 21, 22, 24 |
| 7 | 36 | 23 |
| 8 | 37 | 25 |
| 9 | 38 | 28, 29 |
| 10 | 39 | 1, 8, 9 |
| Partitioning Method | The Regional Decoupling Rate |
|---|---|
| Transient voltage-based method | 0.1702 |
| Complex network-based method | 0.2034 |
| Method proposed in this paper | 0.2654 |
| Partitioning Method | The Maximum Voltage Deviation |
|---|---|
| Transient voltage-based method | 0.0852 |
| Complex network-based method | 0.0852 |
| Method proposed in this paper | 0.0759 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, L.; Sha, X.; Zhang, S.; Wang, J.; Yu, Y. Two-Stage Dynamic Partitioning Strategy Based on Grid Structure Feature and Node Voltage Characteristics for Power Systems. Energies 2025, 18, 2544. https://doi.org/10.3390/en18102544
Sun L, Sha X, Zhang S, Wang J, Yu Y. Two-Stage Dynamic Partitioning Strategy Based on Grid Structure Feature and Node Voltage Characteristics for Power Systems. Energies. 2025; 18(10):2544. https://doi.org/10.3390/en18102544
Chicago/Turabian StyleSun, Lixia, Xianxue Sha, Shuo Zhang, Jiahao Wang, and Yiping Yu. 2025. "Two-Stage Dynamic Partitioning Strategy Based on Grid Structure Feature and Node Voltage Characteristics for Power Systems" Energies 18, no. 10: 2544. https://doi.org/10.3390/en18102544
APA StyleSun, L., Sha, X., Zhang, S., Wang, J., & Yu, Y. (2025). Two-Stage Dynamic Partitioning Strategy Based on Grid Structure Feature and Node Voltage Characteristics for Power Systems. Energies, 18(10), 2544. https://doi.org/10.3390/en18102544






