Research on Shale Oil Well Productivity Prediction Model Based on CNN-BiGRU Algorithm
Abstract
1. Introduction
2. Methods
2.1. Bidirectional Gated Recurrent Unit
- (a)
- Enter the update gate:
- (b)
- Enter the reset gate:
- (c)
- Output of GRU unit
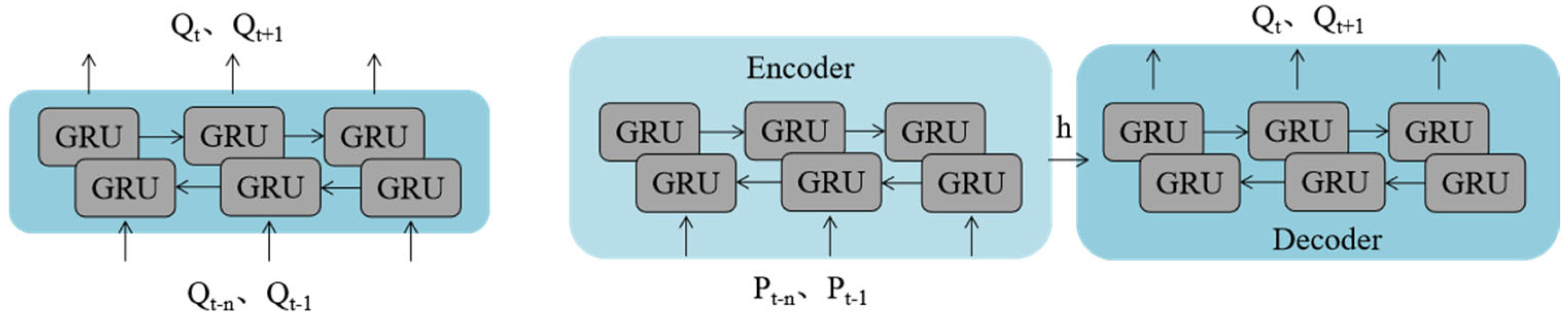
2.2. Sequence to Sequence
- Cross-domain sequence mapping: we implement a sequence-to-sequence (seq2seq) architecture with dedicated encoder–decoder modules.
- Physical signal embedding: we establish pressure-to-production transformation pathways through intermediate latent states (h).
- Multiscale feature fusion: w combines convolutional operations for local pressure pattern extraction with bidirectional GRU for global temporal context modeling.
2.3. Sliding Windows
2.4. CNN-BiGRU Modeling
- Temporal dynamic features: production time series via BiGRU networks.
- High-dimensional static constraints: two-dimensional spatial parameters (e.g., Horizontal stress, Young’s modulus, Poisson’s ratio, etc., distributed along the depth) through CNN-based feature extraction.
- Scalar engineering parameters: one-dimensional static variables (e.g., fracturing scale, reservoir parameters, etc.) using fully connected layers.
2.5. Model Evaluation Metric
3. Model Performance Discussion
3.1. Optimization of Sliding Window and Output Step Length
3.2. Reliability Assessment
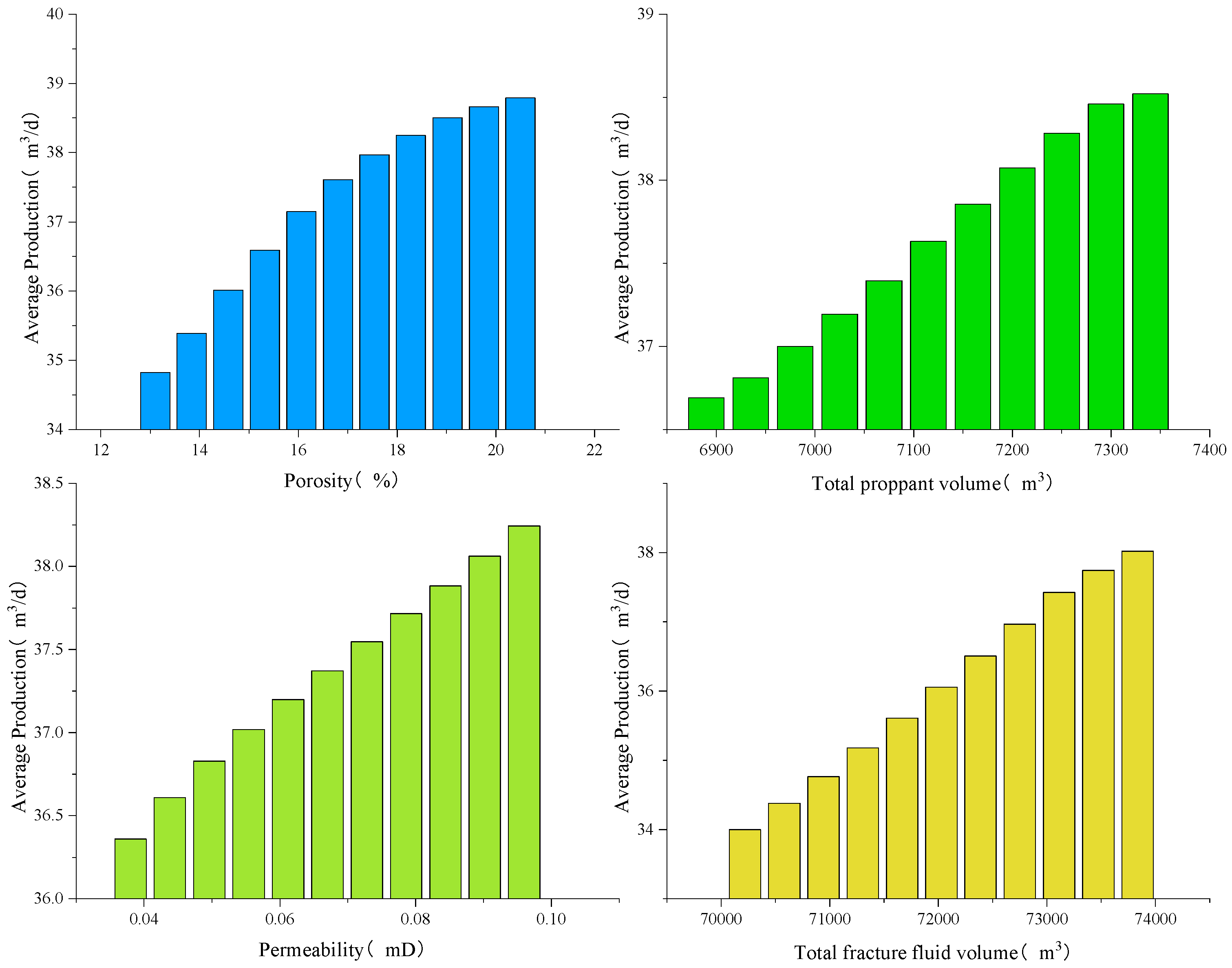
- Parameter space discretization: uniform sampling of 11 points across normalized ranges for key features.
- Univariate perturbation: holding other variables at baseline values while systematically varying target parameters through discretized levels.
- Production prediction: aggregating predicted production across test set samples through ensemble averaging.
- Geological controls: production scales positively with ϕ (storage capacity) and k (fluid conductivity), aligning with Darcy’s law and capillary pressure theory.
- Completion efficiency: hyperbolic growth patterns emerge for and , reflecting fracture conductivity enhancement and drainage volume expansion mechanisms.
3.3. Input Feature Analysis
- Geological features: petrophysical parameters derived from logging interpretation (e.g., porosity, permeability).
- Engineering features: completion and hydraulic fracturing parameters (e.g., proppant volume, stage spacing).
- Temporal features: wellhead pressure time series data.
- Geological parameters encode reservoir flow capacity, heterogeneity, and fracture network geometry.
- Engineering parameters reflect stimulation intensity and fracture conductivity potential.
- Temporal features capture transient flow behavior and pressure propagation.
- Geological/engineering features constrain production trend baselines.
- Temporal features resolve short-term production fluctuations.
- Combined inputs establish multiphysics-constrained predictions.
4. Case Study
4.1. Dataset Construction
- Geological attributes: length of horizontal section, penetration rate, porosity, permeability, oil saturation, “Dessert” thickness, Young’s modulus, Poisson’s ratio.
- Completion parameters: number of stages, number of clusters, proppant loading intensity, fluid volume per stage, cluster spacing.
- The wellhead pressure sequence—this sequence serves as the input sequence (production sequence) for the model.
- The oil production sequence—this sequence serves as the output sequence (target sequence) of the model.
4.2. Superparametric Optimization
- Objective function: mean squared error (MSE) as both a loss metric and an evaluation criterion.
- Data partitioning: stratified 70:20:10 training–validation–test split ratio.
- Activation functions: ReLU, Sigmoid, Tanh (input layer selection)
- Convolutional architecture:
- BiGRU configuration:
- 1D static features: processed as 3D tensor (3158, 6, 11)
- 2D static features: structured as 4D tensor (3158, 6, 11, 4)
- Temporal features: formatted as 3D tensor (3158, 6, 1)
- 1D feature processing:
- 2D feature processing:
- Temporal feature processing:
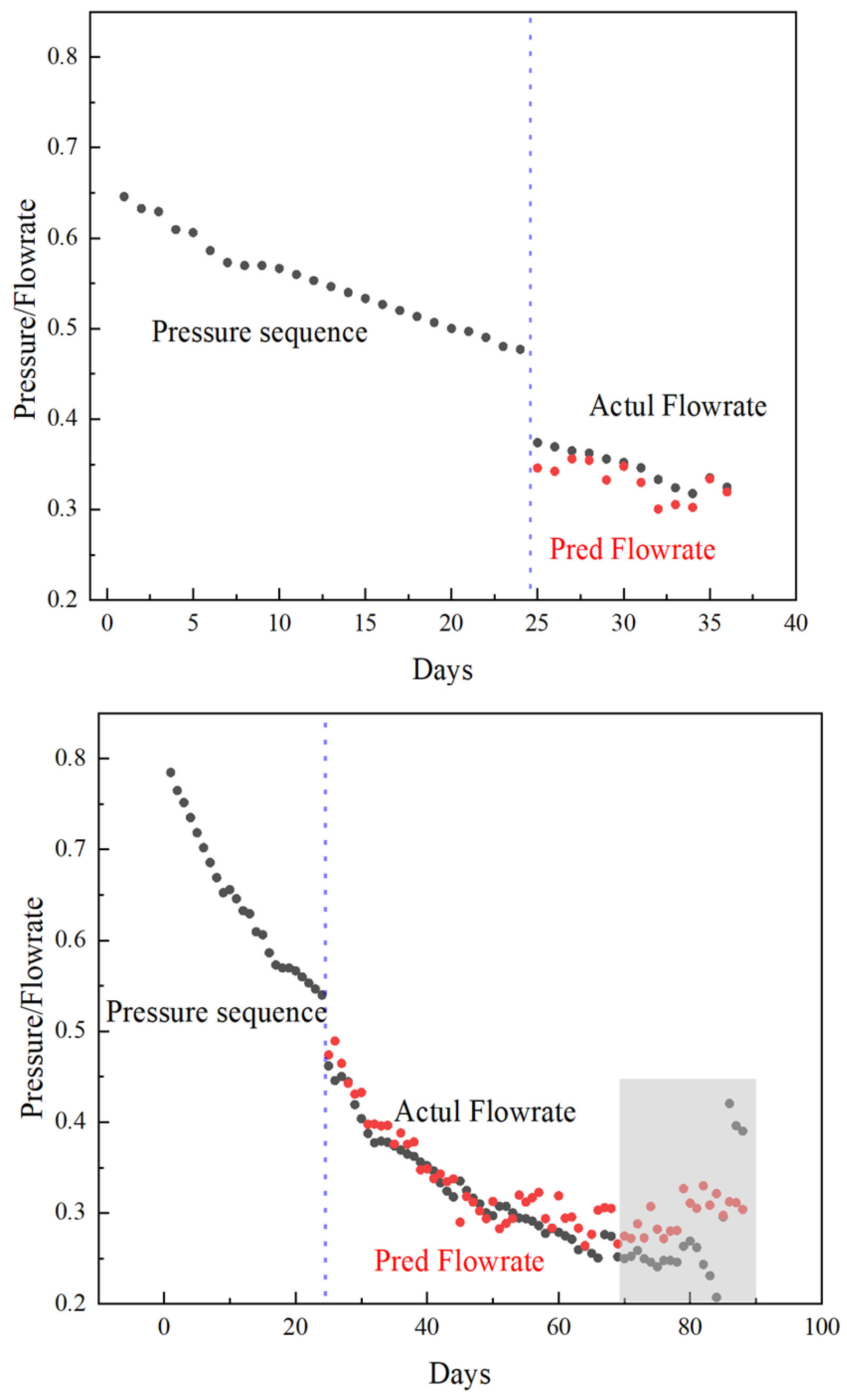
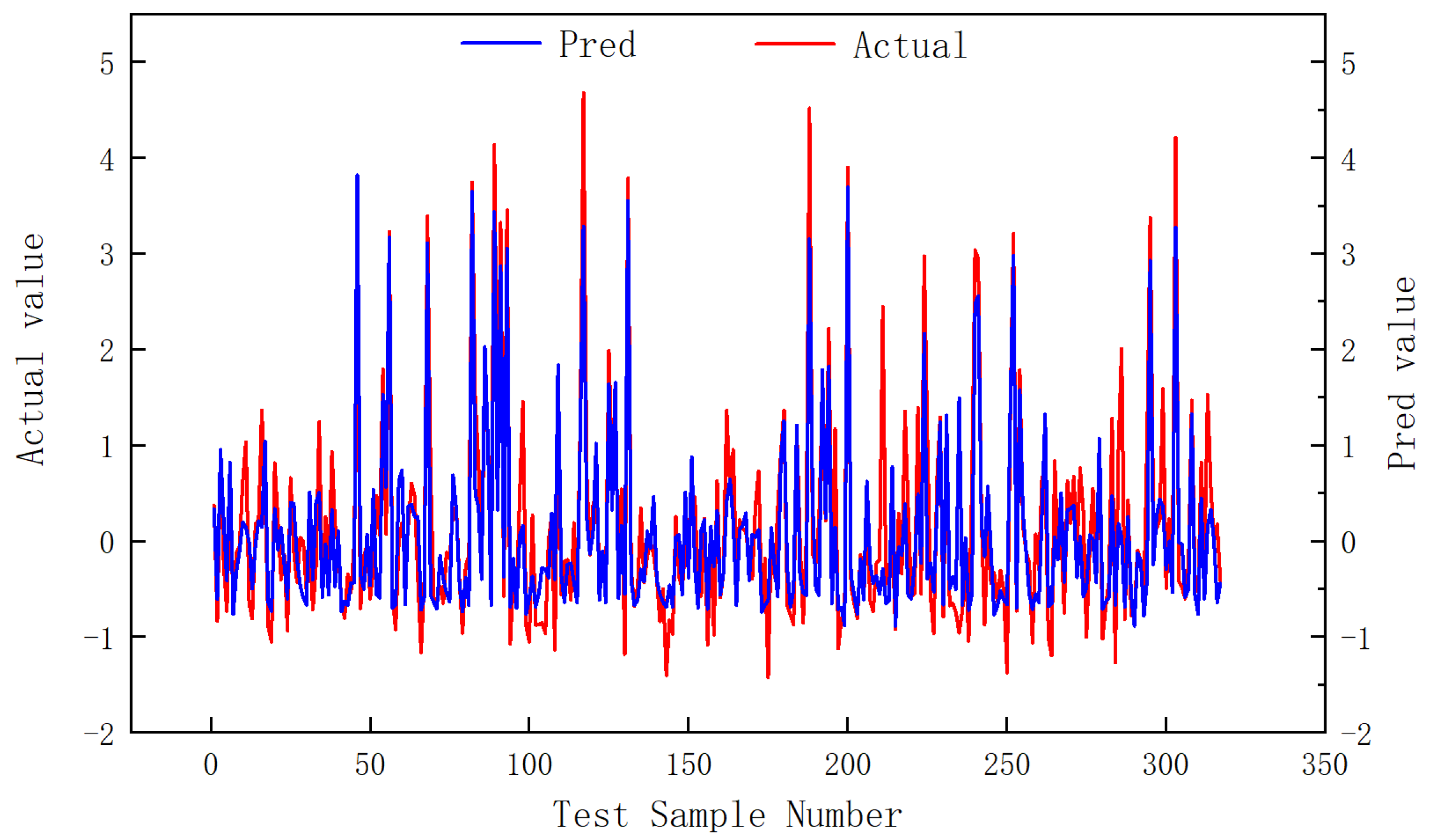
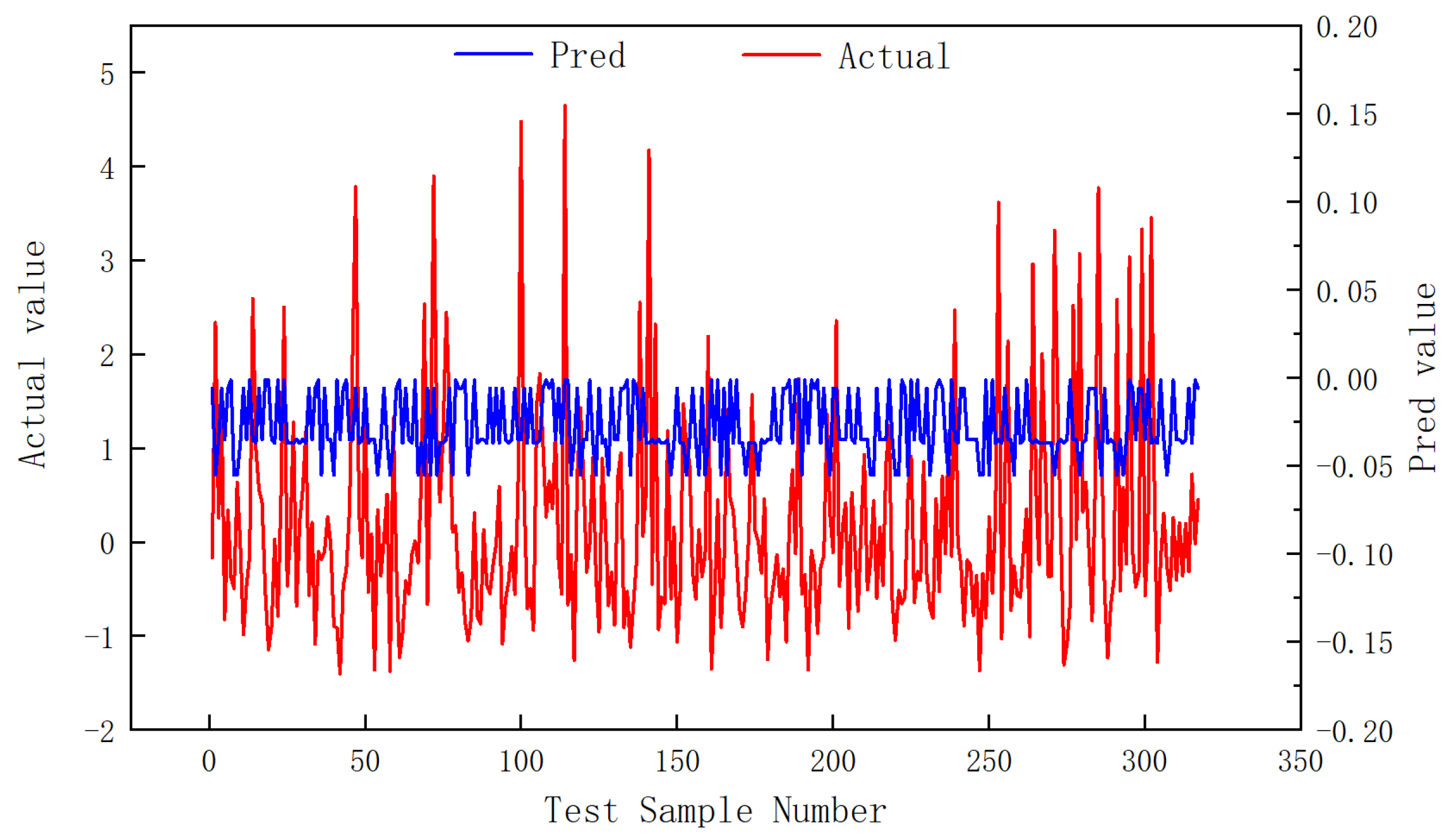
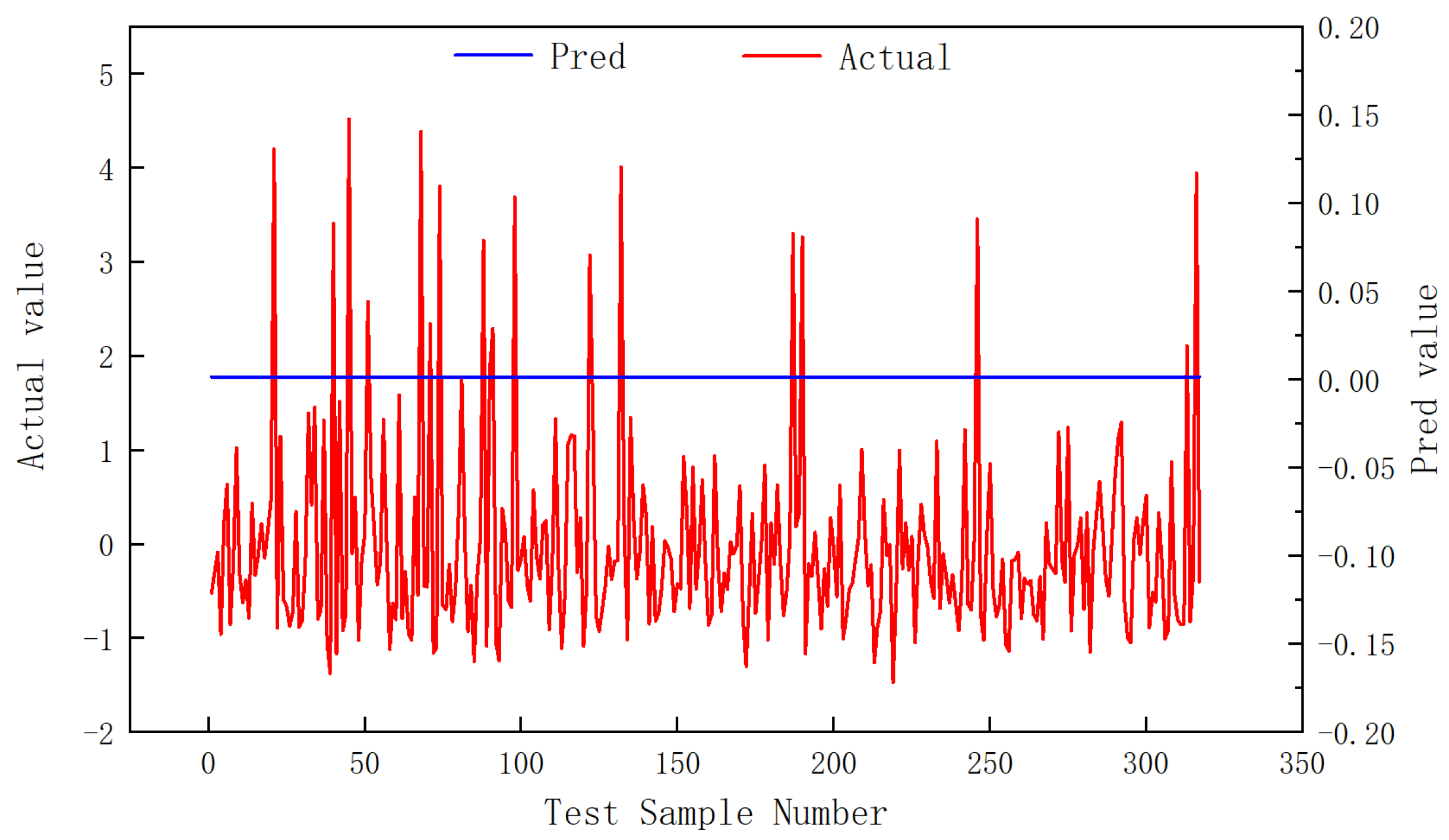
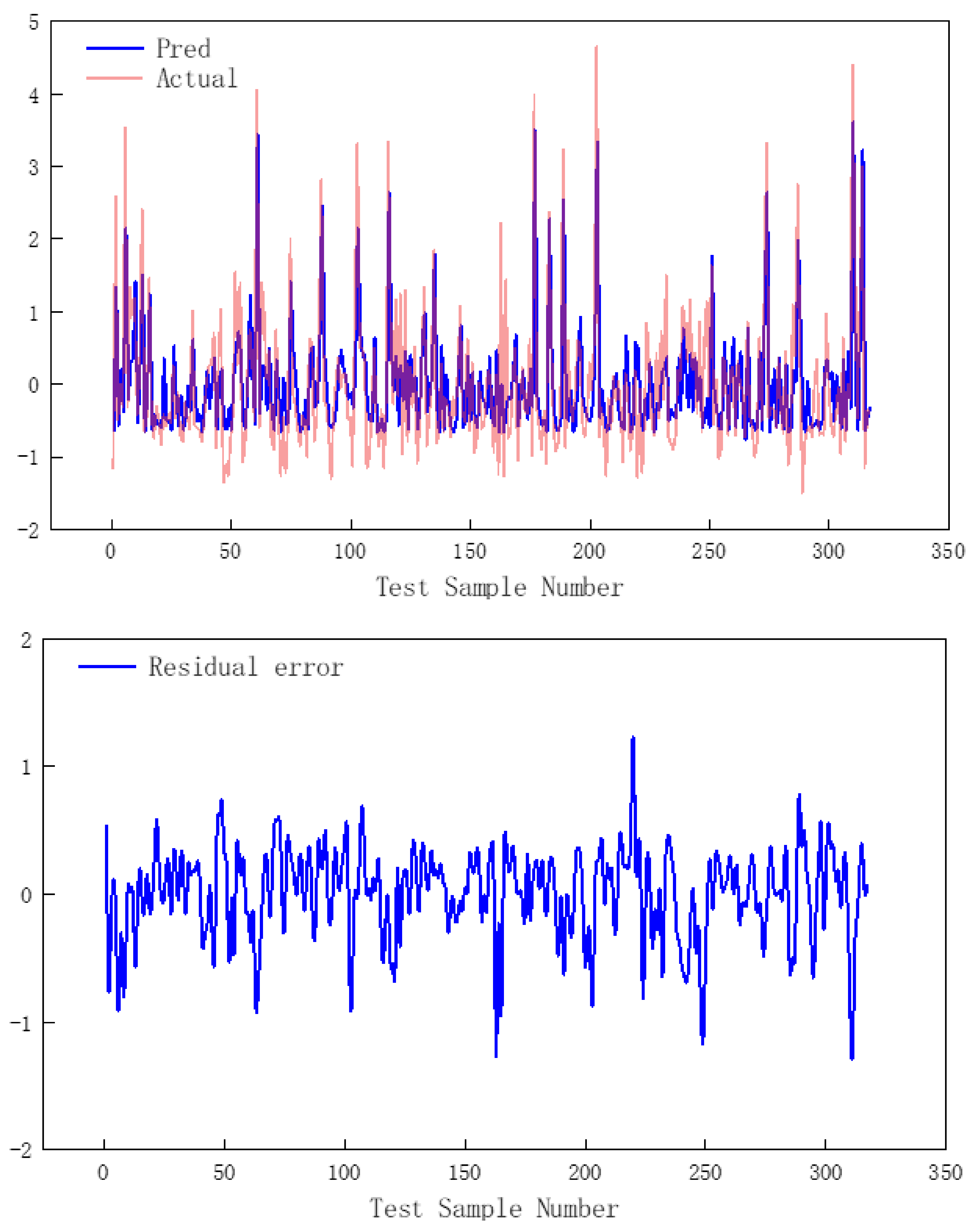
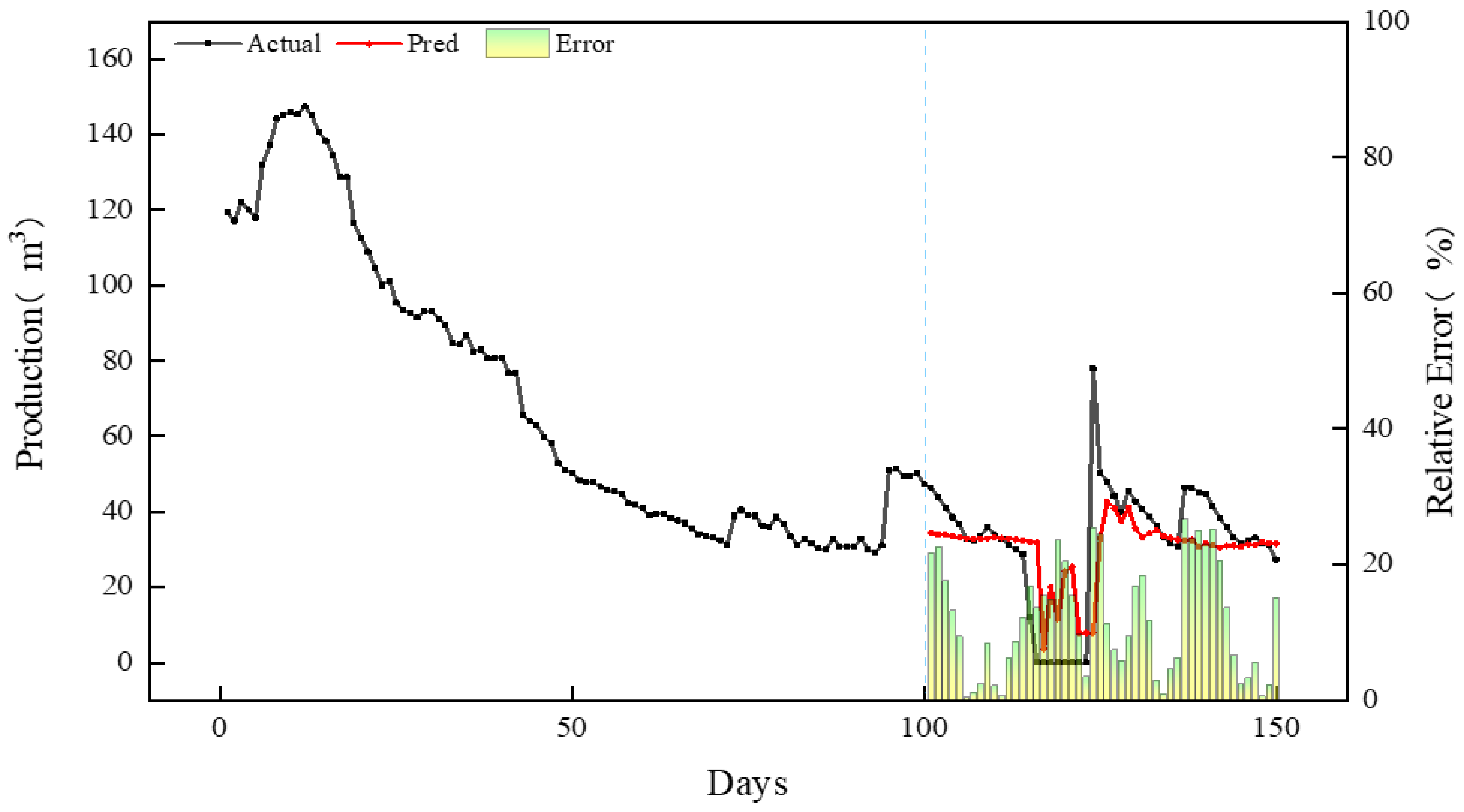
4.3. CNN-BiGRU Model Application
5. Conclusions
- (1)
- The CNN-BiGRU productivity prediction framework was successfully implemented on the TensorFlow deep learning platform. Systematic analysis revealed optimal temporal context configurations: sliding window—6/24/128/256 days; corresponding optimal forecast horizons—1/1/32/64/128 days.
- (2)
- Controlled-variable experiments demonstrated physical consistency with established reservoir engineering principles. The model effectively reconciles geological constraints, completion impacts, temporal dynamics.
- (3)
- Feature ablation studies quantified distinct physical roles. The results show that geological and engineering characteristics are responsible for constraining the overall trends in production, while time series characteristics are used to study the subtle fluctuations during production, which can comprehensively constrain production.
- (4)
- The hyperparameters of the model were optimized based on Bayesian optimization method. The results showed that the number of BiGRU neurons was 64 × 2, the number of CNN convolution cores was 11, and the size of convolution cores was 3. The mean square error of the model test set is 0.46 and the average residual error is 0.004, indicating that the model can be used for learning tasks between different sequences. In addition, the application results of the model show that the average relative error of the actual production prediction is 16.11%, and the prediction accuracy is high.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guo, J.; Ren, W.; Zeng, F.; Luo, Y.; Li, Y.; Du, X. Unconventional oil and gas well fracturing parameter intelligent optimization: Research progress and future development prospects. Pet. Drill. Tech. 2023, 51, 1–7. [Google Scholar]
- Li, Y.; Zhao, Q.; Lyu, Q.; Xue, Z.; Cao, X.; Liu, Z. Evaluation technology and practice of continental shale oil development in China. Pet. Explor. Dev. 2022, 49, 955–964. [Google Scholar] [CrossRef]
- Li, Y. Study on Main Control Factors and Production Prediction of Single Well Production of Coalbed Methane Based on Machine Learning. Master’s Thesis, China University of Petroleum, Beijing, China, 2017. [Google Scholar]
- Clar, F.H.; Monaco, A. Data-driven approach to optimize stimulation design in Eagle Ford formation. In Proceedings of the Unconventional Resources Technology Conference, Denver, CO, USA, 22–24 July 2019. [Google Scholar]
- Kyungbook, L.; Jungtek, L.; Daeung, Y.; Hyungsik, J. Prediction of Shale-Gas Production at Duvernay Formation Using Deep-Learning Algorithm. SPE J. 2019, 24, 2423–2437. [Google Scholar]
- Pan, Y.; Wang, Y.; Che, M.; Liao, R.; Zheng, H. Post-fracturing production prediction and fracturing parameter optimization of horizontal wells based on grey relational projection random forest algorithm. J. Xi’an Shiyou Univ. Nat. Sci. Ed. 2021, 36, 71–76. [Google Scholar]
- Wan, X.; Zou, Y.; Wang, J.; Wang, W. Prediction of Shale Oil Production Based on Prophet Algorithm. In Proceedings of the 3rd International Conference on Polymer Synthesis and Application, Nanjing, China, 23–25 July 2021. [Google Scholar]
- Huang, C.; Tian, L.; Wang, H.; Wang, J.; Jiang, L. A Single Well Production Forecasting Model of Reservoir Based on Conditional Generative Adversarial Net. Chin. J. Comput. Phys. 2022, 39, 465–478. [Google Scholar]
- Zhang, D.; Zhang, L.; Tang, H.; Zhao, Y. Fully coupled fluid-solid productivity numerical simulation of multistage fractured horizontal well in tight oil reservoirs. Pet. Explor. Dev. 2022, 49, 338–347. [Google Scholar] [CrossRef]
- Ozkan, E.; Brown, M.L.; Raghavan, R.; Kazemi, H. Comparison of Fractured-Horizontal-Well Performance in Tight Sand and Shale Reservoirs. SPE Reserv. Eval. Eng. 2011, 14, 248–259. [Google Scholar] [CrossRef]
- Song, X.Y.; Liu, Y.T.; Ma, J.; Wang, J.Q.; Kong, X.M.; Ren, X.N. Productivity forecast based on support vector machine optimized by grey wolf optimizer. Lithol. Reserv. 2020, 32, 134–140. [Google Scholar]
- Hu, Q.; Liu, C.; Zhang, J.; Cui, X.; Wang, Q.; Li, J.; He, S. Machine learning-based coalbed methane well production prediction and fracturing parameter optimization. Pet. Reserv. Eval. Dev. 2025, 15, 266–273. [Google Scholar]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to Sequence Learning with Neural Networks. arXiv 2014, arXiv:1409.3215. [Google Scholar]
- Cho, K.; van Merrienboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Lecun, Y.; Bottou, L. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Liu, J.; Yang, Y.; Lv, S.; Wang, J.; Chen, H. Attention-based BiGRU-CNN for Chinese question classification. J. Ambient. Intell. Humaniz. Comput. 2019, 1, 1–12. [Google Scholar] [CrossRef]
- Shalabi, L.; Shaaban, Z.; Kasasbeh, B. Data mining: A preprocessing engine. J. Comput. Sci. 2006, 2, 735–739. [Google Scholar] [CrossRef]
- Huang, J. Modeling and Application of Horizontal Well Production Prediction Based on Machine Learning. Ph.D. Thesis, China University of Geosciences, Beijing, China, 2020. [Google Scholar]



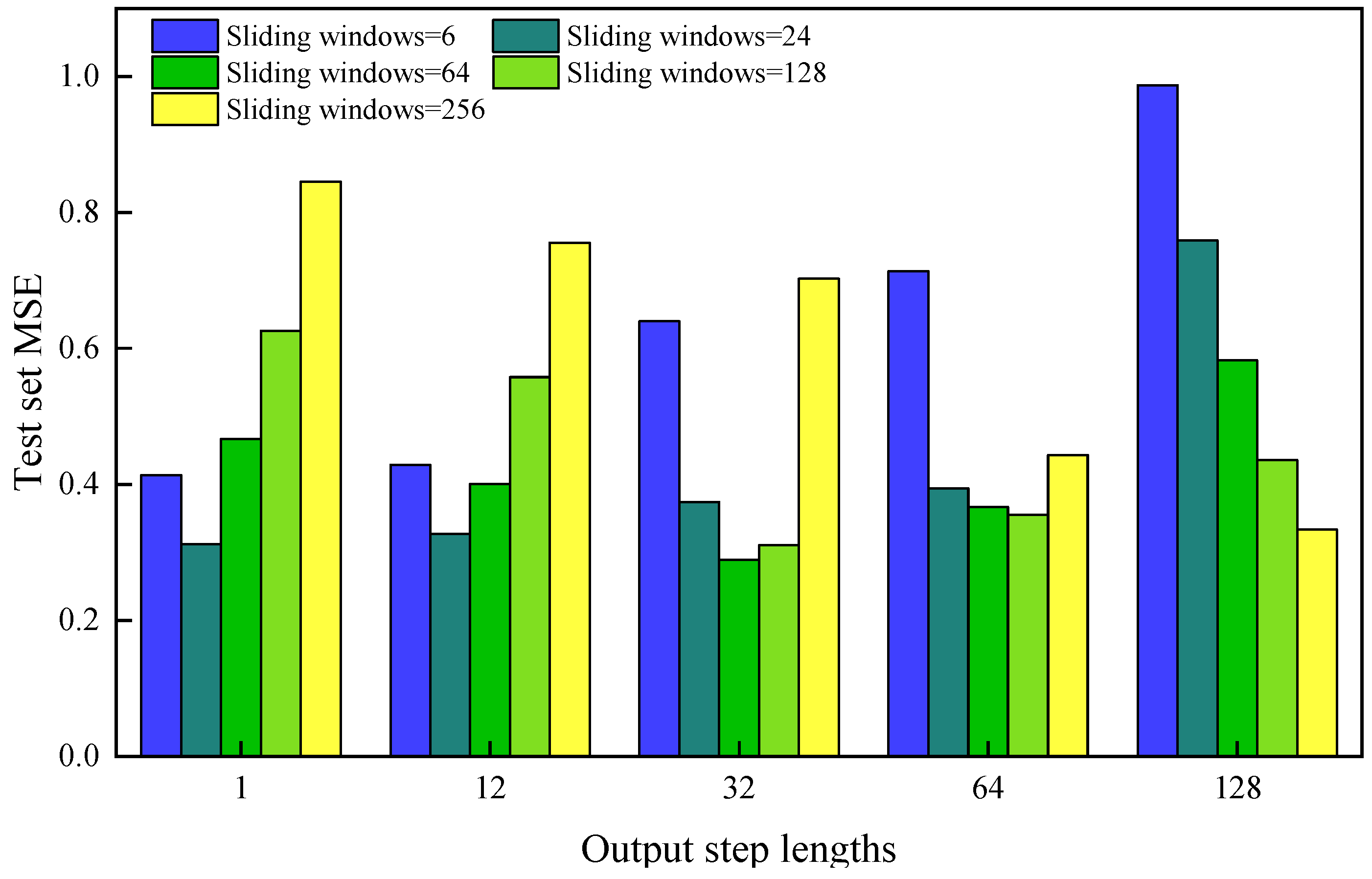



| Sliding Windows Size | The Best Output Step Length | Test Set MSE |
|---|---|---|
| 6 | 1 | 0.431 |
| 24 | 1 | 0.313 |
| 64 | 32 | 0.289 |
| 128 | 64 | 0.311 |
| 256 | 128 | 0.342 |
| Geological Features | Engineering Features | Time Series |
|---|---|---|
| Penetration rate (%) | Vertical depth (m) | Wellhead pressure (MPa) |
| Porosity (%) | Length of horizontal section (m) | |
| Permeability (mD) | Fracturing stages | |
| Oil saturation (%) | Fracturing clusters | |
| “Dessert” thickness (m) | Fracturing fluid volume (m3) | |
| Two-dimensional stress difference (MPa) | Proppant volume (m3) | |
| Young’s modulus (GPa) | ||
| Poisson’s ratio |
| Feature Type | Feature Name | Range | Average | Standard Deviation |
|---|---|---|---|---|
| 1D static characteristics | Vertical depth/m | 3561.0~3601.2 | 3582.7 | 15.1 |
| Length of horizontal section/m | 1800.0~1812.6 | 1698.7 | 254.1 | |
| Penetration rate/% | 86.8~99.4 | 91.6 | 5.4 | |
| Porosity/% | 13.1~20.5 | 16.5 | 2.5 | |
| Permeability/mD | 0.039~0.096 | 0.1 | 0.02 | |
| Oil saturation/% | 89.8~93.1 | 92.1 | 1.2 | |
| “Dessert” thickness/m | 797.0~1675.5 | 1408.1 | 311.9 | |
| Number of stages | 37.0~40.0 | 39.0 | 1.1 | |
| Number of clusters | 289.0~307.0 | 299.8 | 6.1 | |
| Fracturing fluid volume/m3 | 70,219.1~73,836.4 | 72,241.8 | 1215.8 | |
| Proppant volume/m3 | 6890.2~7340.5 | 7166.6 | 152.6 | |
| 2D static characteristics | Depth/m | 3561.2~3695.4 | 3628.5 | 33.04 |
| Two-dimensional stress difference/MPa | 16.8~17.8 | 27.3 | 0.2 | |
| Young’s modulus/GPa | 12.8~43.8 | 28.5 | 7.8 | |
| Poisson’s ratio | 0.2~0.3 | 0.2 | 0.01 | |
| Production sequence | Wellhead pressure/MPa | 0.1~29.3 | 4.2 | 5.9 |
| Target sequence | Daily production/m3 | 5.8~117.9 | 38.7 | 23.5 |
| Superparameter Type | Activation Function | Superparametric Optimization Value | ||
|---|---|---|---|---|
| Input layer | 1D static characteristics | ReLU | / | / |
| 2D static characteristics | ReLU | Convolution kernel size | 3 | |
| Number of convolution kernels | 11 | |||
| Production series | ReLU | Convolution kernel size | 3 | |
| Number of convolution kernels | 11 | |||
| Middle layer | Encoder | Sigmoid | Number of neurons | 64 × 2 |
| Tanh | ||||
| Decoder | Sigmoid | Number of neurons | 64 × 2 | |
| Tanh | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, Y.; Liu, X.; Tian, F.; Yang, L.; Gou, X.; Jia, Y.; Wang, Q.; Zhang, Y. Research on Shale Oil Well Productivity Prediction Model Based on CNN-BiGRU Algorithm. Energies 2025, 18, 2523. https://doi.org/10.3390/en18102523
Pan Y, Liu X, Tian F, Yang L, Gou X, Jia Y, Wang Q, Zhang Y. Research on Shale Oil Well Productivity Prediction Model Based on CNN-BiGRU Algorithm. Energies. 2025; 18(10):2523. https://doi.org/10.3390/en18102523
Chicago/Turabian StylePan, Yuan, Xuewei Liu, Fuchun Tian, Liyong Yang, Xiaoting Gou, Yunpeng Jia, Quan Wang, and Yingxi Zhang. 2025. "Research on Shale Oil Well Productivity Prediction Model Based on CNN-BiGRU Algorithm" Energies 18, no. 10: 2523. https://doi.org/10.3390/en18102523
APA StylePan, Y., Liu, X., Tian, F., Yang, L., Gou, X., Jia, Y., Wang, Q., & Zhang, Y. (2025). Research on Shale Oil Well Productivity Prediction Model Based on CNN-BiGRU Algorithm. Energies, 18(10), 2523. https://doi.org/10.3390/en18102523






