Oscillations of the Oil Pipeline Axis with Consideration of the Inertia Component When Pumping Diesel Fuel
Abstract
1. Introduction
2. Materials and Methods
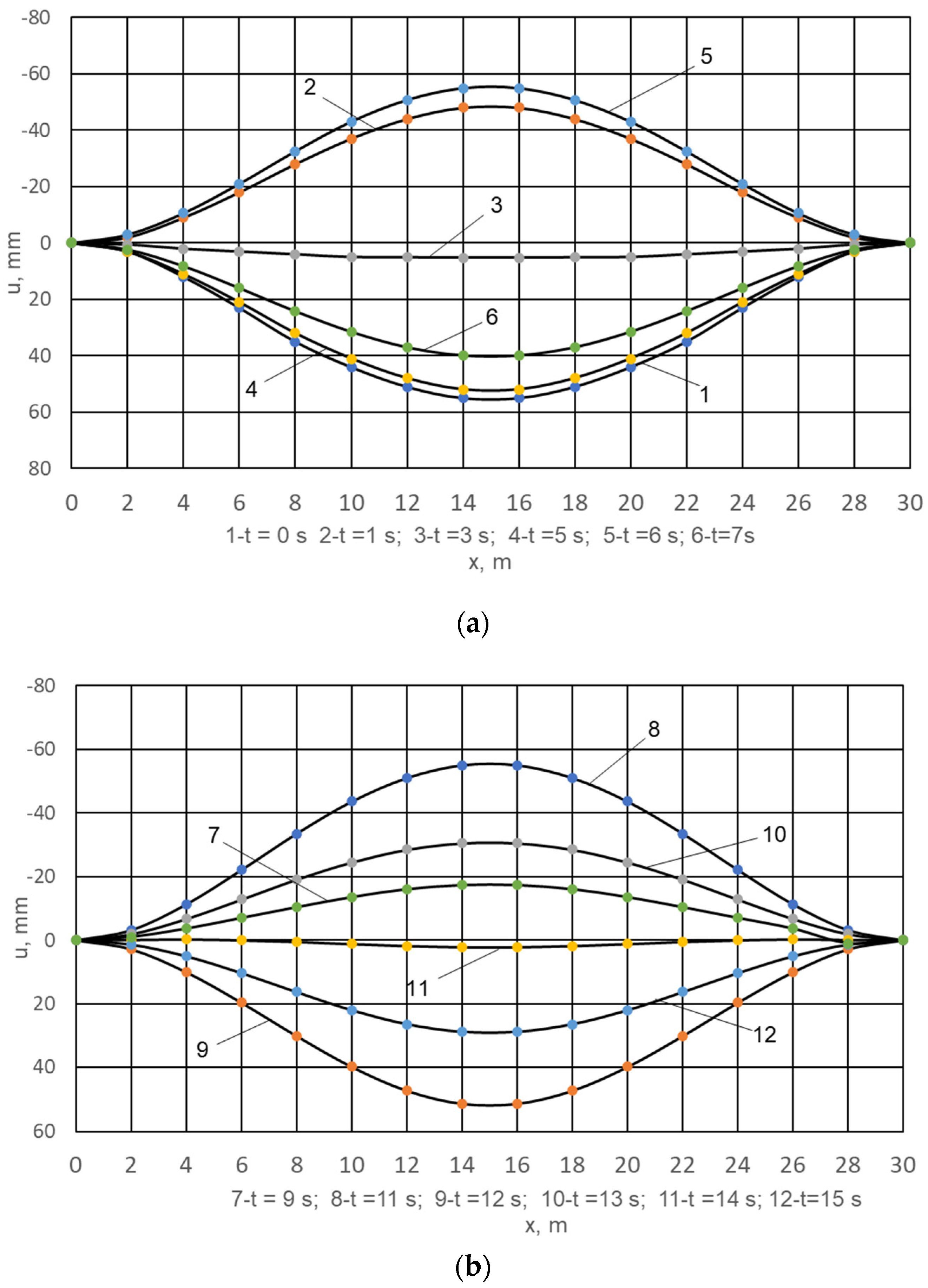
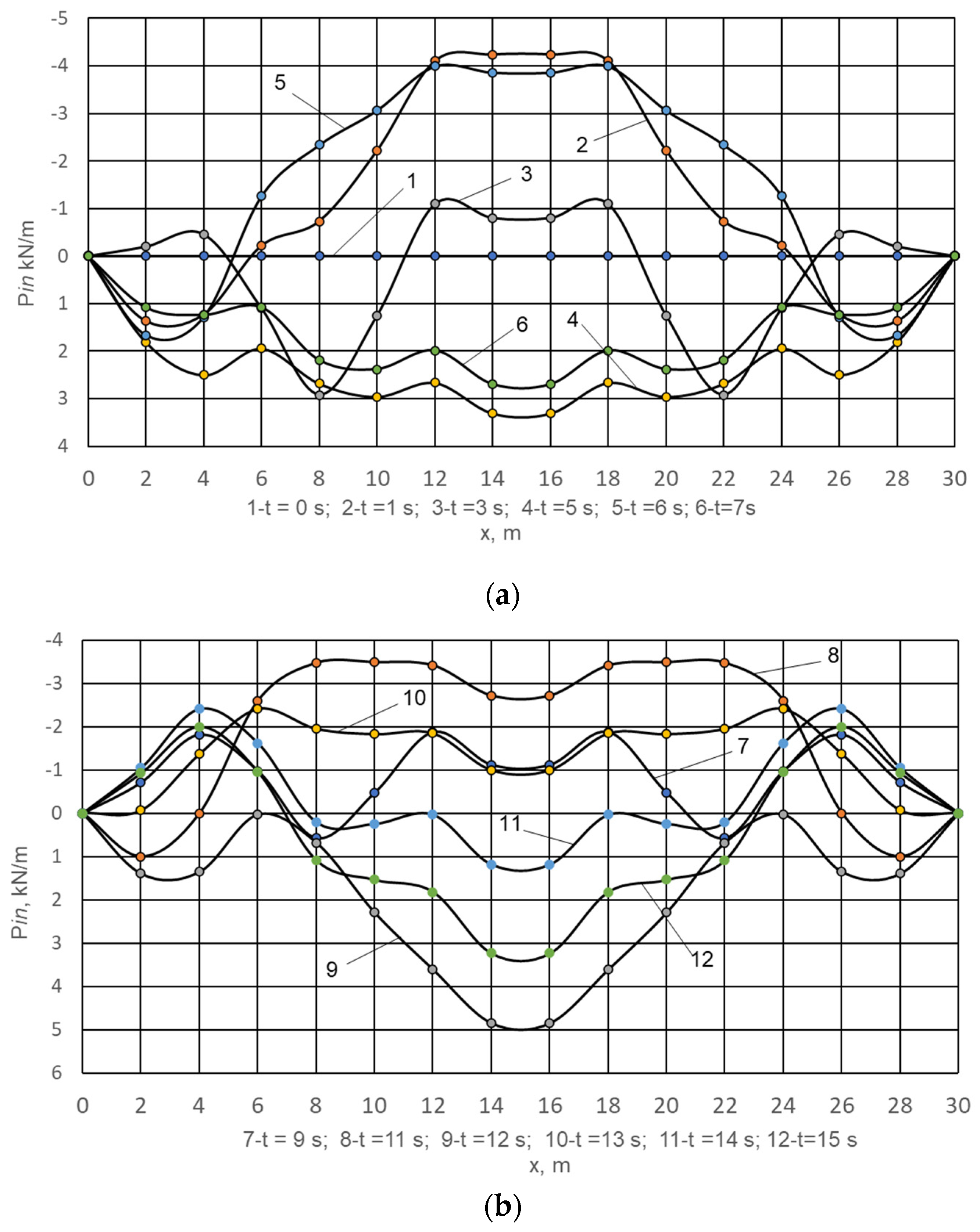
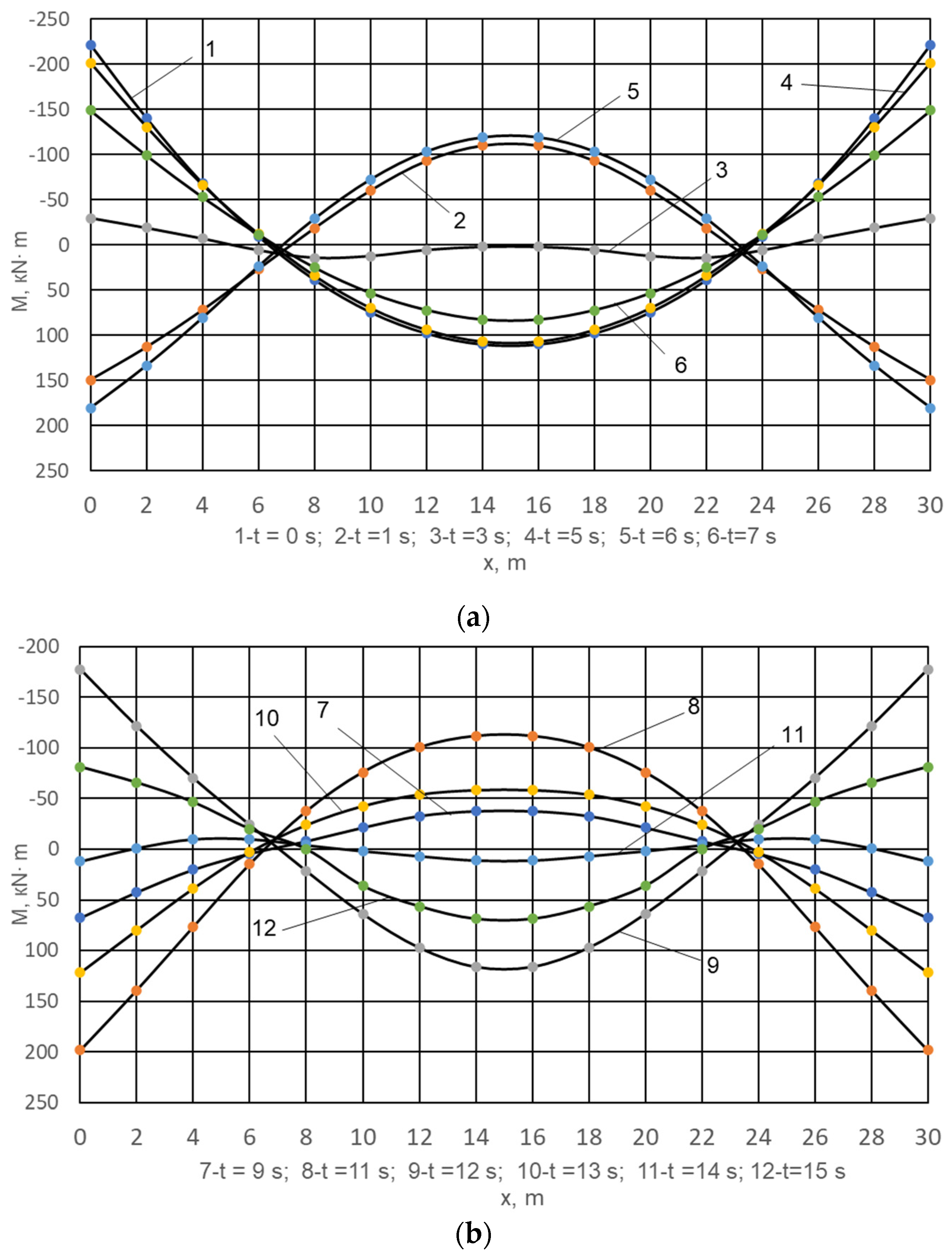
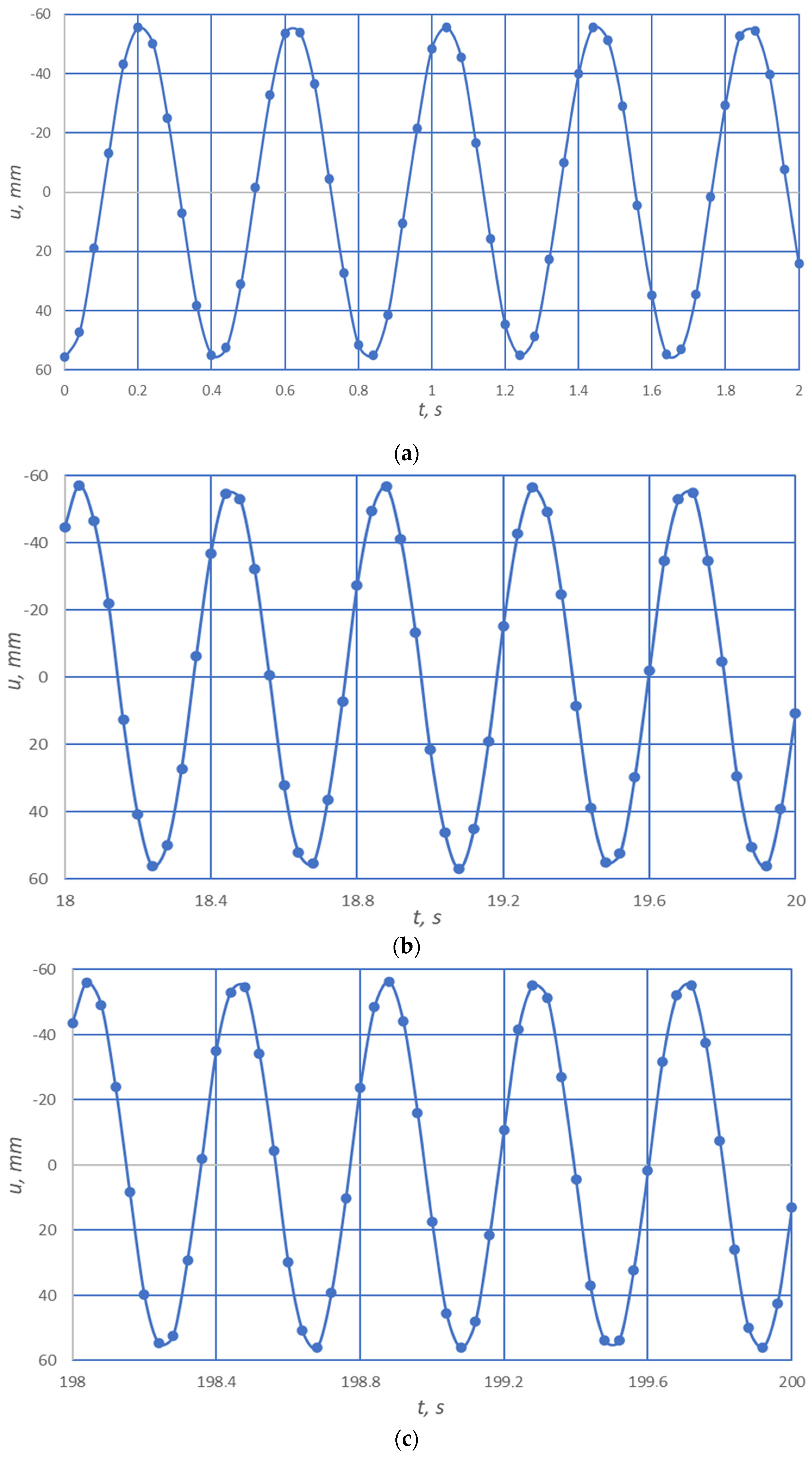
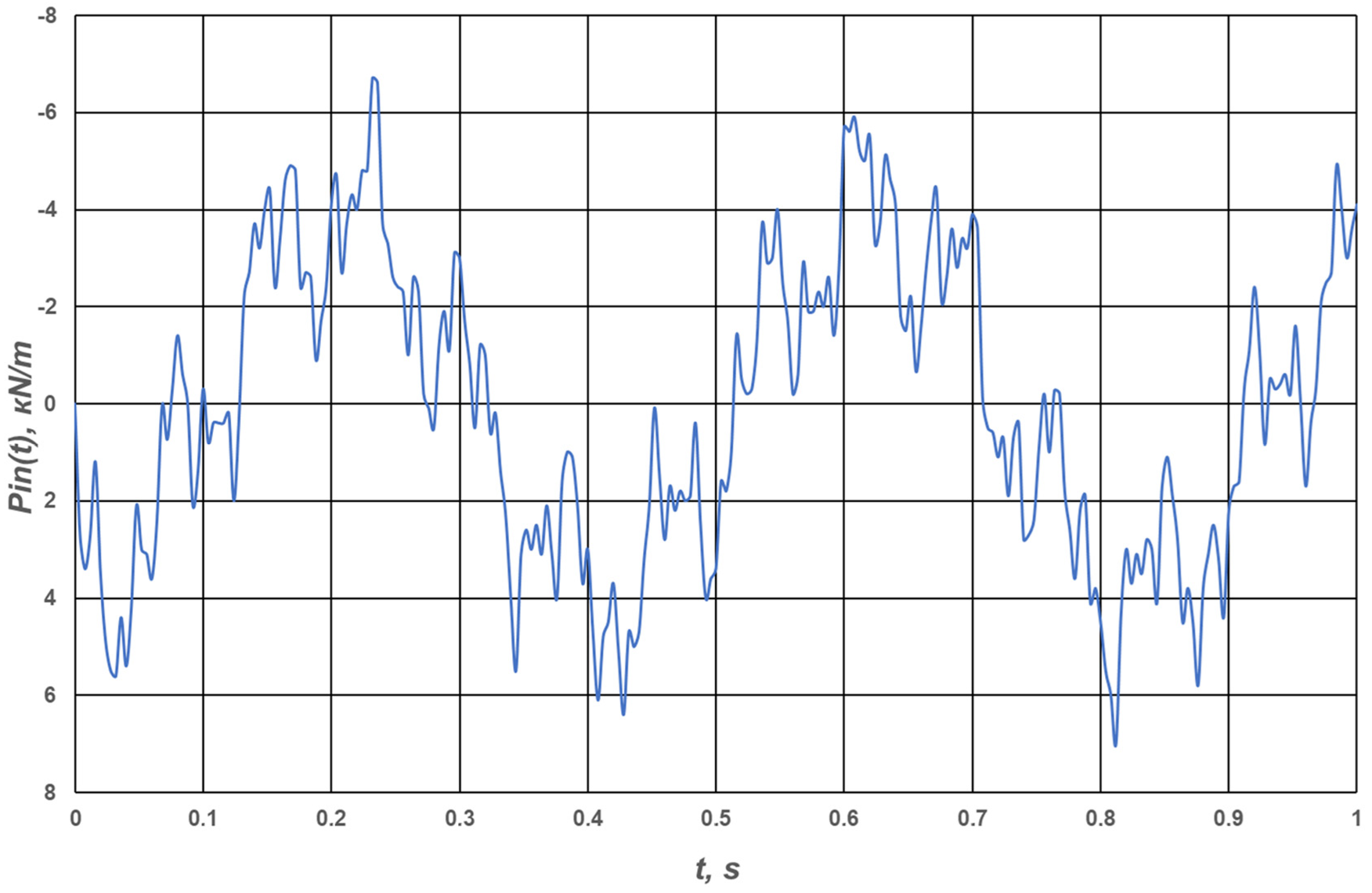
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Andrusiv, U.; Zelinska, H.; Galtsova, O.; Kupalova, H.; Goncharenk, N. The modeling and forecasting of fuel and energy resources usage in the context of the energy independence of Ukraine. Polityka Energ. 2021, 24, 29–47. [Google Scholar] [CrossRef]
- Zelinska, H.; Fedorovych, I.; Andrusiv, U.; Chernova, O.; Kupalova, H. Modeling and prediction of the gas pipelines reliability indicators in the context of energy security of Ukraine. CEUR Workshop Proc. 2020, 2713, 415–433. [Google Scholar]
- He, Z.; He, L.; Liu, H.; Wang, D.; Li, X.; Li, Q. Experimental and Numerical Study on Gas-Liquid Flow in Hilly-Terrain Pipeline-Riser Systems. Discrete Dyn. Nat. Soc. 2021, 2021, 5529916. [Google Scholar] [CrossRef]
- Hart, J.D.; Zulfiqar, N. Historical Perspective on Wind-Induced Vibration of Above-Ground Pipeline Configurations on the Alaskan North Slope. Proc. Biennial Int. Pipeline Conf. 2024, 2A, v02AT03A030. [Google Scholar] [CrossRef]
- Xu, W.; He, Z.; Zhai, L.; Wang, E. Vortex-induced vibration prediction of an inclined flexible cylinder based on machine learning methods. Ocean Eng. 2023, 282, 114956. [Google Scholar] [CrossRef]
- Satchithananthan, U.; Ullah, S.N.; Lee, F.H.; Chen, Z.; Gu, H. Centrifuge modeling of axial pipe-soil interaction of deep-water pipelines. Geotech. Test. J. 2020, 43, 94–112. [Google Scholar] [CrossRef]
- Pukish, A.; Mandryk, O.; Arkhypova, L.; Syrovets, S.; Hryniuk, D. Mathematical modeling of pollution of underground aquifers due to mining of minerals. Min. Miner. Depos. 2024, 18, 94–103. [Google Scholar] [CrossRef]
- Bazaluk, O.; Slabyi, O.; Vekeryk, V.; Velychkovych, A.; Ropyak, L.; Lozynskyi, V. A Technology of Hydrocarbon Fluid Production Intensification by Productive Stratum Drainage Zone Reaming. Energies 2021, 14, 3514. [Google Scholar] [CrossRef]
- Kubba, A.; Trabelsi, H.; Derbel, F. Enhanced Long-Range Network Performance of an Oil Pipeline Monitoring System Using a Hybrid Deep Extreme Learning Machine Model. Future Internet 2024, 16, 425. [Google Scholar] [CrossRef]
- Han, J.; Tian, L. Review of Construction Technology of Advanced Energy Infrastructure. Energies 2024, 17, 4157. [Google Scholar] [CrossRef]
- Popescu, C.; Gabor, M.R. Quantitative Analysis Regarding the Incidents to the Pipelines of Petroleum Products for an Efficient Use of the Specific Transportation Infrastructure. Processes 2021, 9, 1535. [Google Scholar] [CrossRef]
- Dai, L.; Wang, D.; Wang, T.; Feng, Q.; Yang, X. Analysis and Comparison of Long-Distance Pipeline Failures. J. Pet. Eng. 2017, 2017, 3174636. [Google Scholar] [CrossRef]
- Xie, M.; Tian, Z. A review on pipeline integrity management utilizing in-line inspection data. Eng. Fail. Anal. 2018, 92, 222–239. [Google Scholar] [CrossRef]
- Dutkiewicz, M.; Andrusyak, A.; Kychma, A.; Vytvytskyi, V.; Velychkovych, A. Numerical model of interaction of a mobile lift chain with a main gas pipeline pipe in the process of repair work. Ekspl. Niezawodn. 2024, 26, 187159. [Google Scholar] [CrossRef]
- Prysyazhnyuk, P.; Bembenek, M.; Drach, I.; Korzhov, A.; Romanyshyn, L.; Ropyak, L. Restoration of the Impact Crusher Rotor Using FCAW with High-Manganese Steel Reinforced by Complex Carbides. Manag. Syst. Prod. Eng. 2024, 32, 294–302. [Google Scholar] [CrossRef]
- Bembenek, M.; Mandziy, T.; Ivasenko, I.; Berehulyak, O.; Vorobel, R.; Slobodyan, Z.; Ropyak, L. Multiclass Level-Set Segmentation of Rust and Coating Damages in Images of Metal Structures. Sensors 2022, 22, 7600. [Google Scholar] [CrossRef]
- Shats’kyi, I.P. Closure of a longitudinal crack in a shallow cylindrical shell in bending. Mater. Sci. 2005, 41, 186–191. [Google Scholar] [CrossRef]
- Shats’kyi, I.P.; Makoviichuk, M.V. Analysis of the limiting state of cylindrical shells with cracks with regard for the contact of crack lips. Strength Mater. 2009, 41, 560–565. [Google Scholar] [CrossRef]
- Okodi, A.; Li, Y.; Cheng, R.; Kainat, M.; Yoosef-Ghodsi, N.; Adeeb, S. Crack Propagation and Burst Pressure of Pipeline with Restrained and Unrestrained Concentric Dent-Crack Defects Using Extended Finite Element Method. Appl. Sci. 2020, 10, 7554. [Google Scholar] [CrossRef]
- Zvirko, O.I.; Savula, S.F.; Tsependa, V.M.; Gabetta, G.; Nykyforchyn, H.M. Stress corrosion cracking of gas pipeline steels of different strength. Procedia Struct. Integr. 2016, 2, 509–516. [Google Scholar] [CrossRef][Green Version]
- Shatskii, I.P.; Makoviichuk, N.V. Effect of closure of collinear cracks on the stress-strain state and the limiting equilibrium of bent shallow shells. J. Appl. Mech. Tech. Phys. 2011, 52, 464–470. [Google Scholar] [CrossRef]
- Dutkiewicz, M.; Dalyak, T.; Shatskyi, I.; Venhrynyuk, T.; Velychkovych, A. Stress Analysis in Damaged Pipeline with Composite Coating. Appl. Sci. 2021, 11, 10676. [Google Scholar] [CrossRef]
- Shatskyi, I.; Makoviichuk, M.; Ropyak, L.; Velychkovych, A. Analytical Model of Deformation of a Functionally Graded Ceramic Coating under Local Load. Ceramics 2023, 6, 1879–1893. [Google Scholar] [CrossRef]
- Ropyak, L.; Shihab, T.; Velychkovych, A.; Dubei, O.; Tutko, T.; Bilinskyi, V. Design of a Two-Layer Al–Al2O3 Coating with an Oxide Layer Formed by the Plasma Electrolytic Oxidation of Al for the Corrosion and Wear Protections of Steel. Prog. Phys. Met. 2023, 24, 319–365. [Google Scholar] [CrossRef]
- Tutko, T.; Dubei, O.; Ropyak, L.; Vytvytskyi, V. Determination of Radial Displacement Coefficient for Designing of Thread Joint of Thin-Walled Shells. In Advances in Design, Simulation and Manufacturing IV, Proceedings of the 4th International Conference on Design, Simulation, Manufacturing: The Innovation Exchange, DSMIE 2021, Lviv, Ukraine, 8–11 June 2021; Lecture Notes in Mechanical Engineering; Springer: Cham, Switzerland, 2021; pp. 153–162. [Google Scholar] [CrossRef]
- Vynnykov, Y.; Kharchenko, M.; Manhura, S.; Aniskin, A.; Manhura, A. Neural network analysis of safe life of the oil and gas industrial structures. Min. Miner. Depos. 2024, 18, 37–44. [Google Scholar] [CrossRef]
- Matkivskyi, S. Near Wellbore Heavy Hydrocarbons Retrograde Condensation Study. Miner. Resour. Ukr. 2023, 3, 39–44. [Google Scholar] [CrossRef]
- Raimbekova, A.; Kapralova, V.; Dalbanbai, A.; Kubekova, S.; Popova, A. Effect of Various Phosphate Inhibitors on Corrosion of Low Carbon Steel in 3% Sodium Chloride Solution. Eng. J. Satbayev Univ. 2023, 145, 25–31. [Google Scholar] [CrossRef]
- Tatsiy, R.M.; Pazen, O.Y.; Vovk, S.Y.; Ropyak, L.Y.; Pryhorovska, T.O. Numerical study on heat transfer in multilayered structures of main geometric forms made of different materials. J. Serb. Soc. Comput. Mech. 2019, 13, 36–55. [Google Scholar] [CrossRef]
- Hamzawy, N.; Khedr, M.; Mahmoud, T.S.; EI-Mahallawi, I.; Khalifa, T.A. Investigation of Temperature Variation During Friction Drilling of 6082 and 7075 Al-Alloys. In Light Metal Technology symposium, Proceedings of the Light Metals Symposium, 149th Annual Meeting and Exhibition, TMS 2020, San Diego, CA, USA, 23–27 February 2020; Springer: Cham, Switzerland, 2020; pp. 471–477. [Google Scholar] [CrossRef]
- Doroshenko, Y.; Kogut, G.; Doroshenko, Y.; Tarayevs’kyy, O.; Pyrig, T. Numerical study on erosion wear and strength of main gas pipelines bends. Stroj. Cas. 2021, 71, 27–40. [Google Scholar] [CrossRef]
- Owoseni, O.D.; Orolu, K.O.; Oyediran, A.A. Dynamics of Slightly Curved Pipe Conveying Hot Pressurized Fluid Resting on Linear and Nonlinear Viscoelastic Foundations. J. Vib. Acoust. 2018, 140, 021005. [Google Scholar] [CrossRef]
- Kryzhanivs’kyi, E.I.; Rudko, V.P.; Shats’kyi, I.P. Estimation of admissible loads upon a pipeline in the zone of sliding ground. Mater. Sci. 2004, 40, 547–551. [Google Scholar] [CrossRef]
- Shats’kyi, I.P.; Struk, A.B. Stressed state of pipeline in zones of soil local fracture. Strength Mater. 2009, 41, 548–553. [Google Scholar] [CrossRef]
- Vazouras, P.; Dakoulas, P.; Karamanos, S.A. Pipe–soil interaction and pipeline performance under strike–slip fault movements. Soil Dyn. Earthq. Eng. 2015, 72, 48–65. [Google Scholar] [CrossRef]
- Han, J.; Bi, Y.; Hou, B.; Zhao, W.; El Naggar, M.H. Response of Corroded Steel Pipeline Without and with CFRP Reinforcement to Reverse Fault Movement. Appl. Sci. 2024, 14, 10896. [Google Scholar] [CrossRef]
- Landar, S.; Velychkovych, A.; Ropyak, L.; Andrusyak, A. A Method for Applying the Use of a Smart 4 Controller for the Assessment of Drill String Bottom-Part Vibrations and Shock Loads. Vibration 2024, 7, 802–828. [Google Scholar] [CrossRef]
- Filippov, A.N. Dynamic impact on a pipeline considering dry friction on its surface. Mech. Solids 2019, 54, 1144–1150. [Google Scholar] [CrossRef]
- Shatskyi, I.; Perepichka, V.; Vaskovskyi, M. Longitudinal waves in an elastic rod caused by sudden damage to the foundation. Theor. Appl. Mech. 2021, 48, 29–37. [Google Scholar] [CrossRef]
- Shatskyi, I.; Makoviichuk, M.; Vaskovkyi, M. Transversal Straining of Pressurized Pipeline Caused by Vibration of Damaged Foundation. Springer Proc. Math. Stat. 2024, 453, 501–508. [Google Scholar] [CrossRef]
- Zhang, Y.; Ye, J.; He, K.; Chen, S. Seismic Dynamics of Pipeline Buried in Dense Seabed Foundation. J. Mar. Sci. Eng. 2019, 7, 190. [Google Scholar] [CrossRef]
- Shatskii, I.P.; Perepichka, V.V. Shock-wave propagation in an elastic rod with a viscoplastic external resistance. J. Appl. Mech. Techn. Phys. 2013, 54, 1016–1020. [Google Scholar] [CrossRef]
- Moisyshyn, V.; Levchuk, K. Investigation on Releasing of a Stuck Drill String by Means of a Mechanical Jar. Oil Gas Sci. Technol. 2017, 72, 27–35. [Google Scholar] [CrossRef]
- Shatskyi, I.; Perepichka, V. Problem of dynamics of an elastic rod with decreasing function of elastic-plastic external resistance. In Dynamic Systems and Applications, Proceedings of the DSTA 2017, Łódź, Poland, 11–14 December 2017; Springer: Cham, Switzerland, 2018; Volume 249, pp. 335–342. [Google Scholar] [CrossRef]
- Begmatov, A.; Mamatova, N. Impact of rigid body and viscous-plastic rod of finite length. E3S Web of Conf. 2023, 401, 02003. [Google Scholar] [CrossRef]
- Bembenek, M.; Grydzhuk, Y.; Gajdzik, B.; Ropyak, L.; Pashechko, M.; Slabyi, O.; Al-Tanakchi, A.; Pryhorovska, T. An Analytical-Numerical Model for Determining “Drill String–Wellbore” Frictional Interaction Forces. Energies 2024, 17, 301. [Google Scholar] [CrossRef]
- Shatskyi, I.; Perepichka, V. Shock Torsion Wave in an Elastic Rod with Decreasing Function of Viscoplastic External Friction. Springer Proc. Math. Stat. 2024, 454, 585–592. [Google Scholar] [CrossRef]
- Bolonnyi, V.T.; Grudz, V.Y.; Grudz, Y.V.; Zapukhliak, V.B.; Dodyk, T.Y. Prediction of transient processes in oil pipelines with the purpose of emergency incident prevention. Nauk. Visn. Nats. Hirn. Univ. 2020, 1, 118–122. [Google Scholar] [CrossRef]
- Petryna, D.Y.; Kozak, O.L.; Shulyar, B.R.; Petryna, Y.D.; Hredil, M.I. Influence of alloying by rare-earth metals on the mechanical properties of 17g1s pipe steel. Mater. Sci. 2013, 48, 575–581. [Google Scholar] [CrossRef]
- Melnychenko, Y.; Poberezhny, L.; Hrudz, V.; Zapukhliak, V.; Chudyk, I.; Dodyk, T. Determination of preconditions leading to critical stresses in pipeline during lowering. In Degradation Assessment and Failure Prevention of Pipeline Systems; Lecture Notes in Civil Engineering; Springer: Cham, Switzerland, 2021; Volume 102, pp. 241–252. [Google Scholar] [CrossRef]
- Andreikiv, O.E.; Skal’s’kyi, V.R.; Dolins’ka, I.Y.; Dzyubyk, A.R. Influence of Corrosive Hydrogenating Media on the Residual Service Life of Structural Elements in the Maneuvering Mode of Operation. Mater. Sci. 2018, 54, 61–68. [Google Scholar] [CrossRef]
- Voloshyn, V.A.; Zvirko, O.I.; Sydor, P.Y. Influence of the compositions of neutral soil media on the corrosion cracking of pipe steel. Mater. Sci. 2015, 50, 44–47. [Google Scholar] [CrossRef]
- Kharchenko, L.E.; Kunta, O.E.; Zvirko, O.I.; Savula, R.S.; Duryahina, Z.A. Diagnostics of hydrogen macrodelamination in the wall of a bent pipe in the system of gas mains. Mater. Sci. 2016, 51, 530–537. [Google Scholar] [CrossRef]
- Khoma, M.; Vynar, V.; Chuchman, M.; Vasyliv, C. Corrosion-mechanical failure of pipe steels in hydrogen sulfide environments. In Degradation Assessment and Failure Prevention of Pipeline Systems; Lecture Notes in Civil Engineering; Springer: Cham, Switzerland, 2021; Volume 102, pp. 231–239. [Google Scholar] [CrossRef]
- Khoma, M.S.; Korniy, S.A.; Vynar, V.A.; Datsko, B.M.; Maksishko, Y.Y.; Dykha, O.V.; Bukliv, R.L. Influence of Hydrogen Sulfide on the Carbon-Dioxide Corrosion and the Mechanical Characteristics of High-Strength Pipe Steel. Mater. Sci. 2022, 57, 805–812. [Google Scholar] [CrossRef]
- Andreikiv, O.Y.; Dolins’ka, I.Y.; Shtoiko, I.P.; Raiter, O.K.; Matviiv, Y.Y. Evaluation of the Residual Service Life of Main Pipelines with Regard for the Action of Media and Degradation of Materials. Mater. Sci. 2019, 54, 638–646. [Google Scholar] [CrossRef]
- Vorobel, R.; Student, O.; Ivasenko, I.; Maruschak, P.; Krechkovska, H.; Zvirko, O.; Berehulyak, O.; Mandziy, T.; Tsybailo, I.; Solovei, P. Development of a method for computer processing of fractographic images to assess the cohesion of inclusions to the matrix in the weld metal after its operational degradation and hydrogenation. Materialia 2024, 34, 102074. [Google Scholar] [CrossRef]
- Mandziy, T.; Ivasenko, I.; Berehulyak, O.; Vorobel, R. Influence of Colour Restoration on Rust Image Segmentation. In Proceedings of the IEEE UKRCON 2021. 3rd Ukraine Conference on Electrical and Computer Engineering, Lviv, Ukraine, 26–28 August 2021; IEEE: Washington, DC, USA, 2021; pp. 68–73. [Google Scholar] [CrossRef]
- Stetsiuk, S.; Bondarenko, R.; Doroshenko, Y.; Holubenko, V. Experimental Studies on the Dynamics of the Movement of Cleaning Pigs through Tee Pipe Fittings. Stroj. Casopis. 2024, 74, 9–24. [Google Scholar] [CrossRef]
- Stetsiuk, S.; Shatskyi, I.; Doroshenko, Y.; Velychkovych, A. Analytical Study of Frictional Interaction of Elastic Cleaning Pig with Pipeline Wall. Arch. Mater. Sci. Eng. 2024, 129, 67–76. [Google Scholar] [CrossRef]
- Amandi, K.U.; Diemuodeke, E.O.; Briggs, T.A.; Pham, D. Model for remaining strength estimation of a corroded pipeline with interacting defects for oil and gas operations. Cogent Eng. 2019, 6, 1663692. [Google Scholar] [CrossRef]
- Vanitha, C.N.; Easwaramoorthy, S.V.; Krishna, S.A.; Cho, J. Efficient qualitative risk assessment of pipelines using relative risk score based on machine learning. Sci. Rep. 2023, 13, 14918. [Google Scholar] [CrossRef] [PubMed]
- Fan, T.; Liu, Z.; Li, M.; Zhao, Y.; Zuo, Z.; Guo, R. Development of cost-effective repair system for locally damaged long-distance oil pipelines. Constr. Build. Mater. 2022, 333, 127342. [Google Scholar] [CrossRef]
- Yu, J.; Chen, C.; Li, C. Safety analysis and emergency response of suspended oil and gas pipelines triggered by natural disasters. Sustainability 2022, 14, 17045. [Google Scholar] [CrossRef]
- Bazaluk, O.; Kuchyn, O.; Saik, P.; Soltabayeva, S.; Brui, H.; Lozynskyi, V.; Cherniaiev, O. Impact of Ground Surface Subsidence Caused by Underground Coal Mining on Natural Gas Pipeline. Sci. Rep. 2023, 13, 19327. [Google Scholar] [CrossRef]
- Nguyen, L.Q.; Le, T.T.T.; Nguyen, T.G.; Tran, D.T. Prediction of Underground Mining-Induced Subsidence: Artificial Neural Network Based Approach. Min. Miner. Depos. 2023, 17, 45–52. [Google Scholar] [CrossRef]
- Ding, Y.; Yang, H.; Xu, P.; Zhang, M.; Hou, Z. Coupling interaction of surrounding soil-buried pipeline and additional stress in subsidence soil. Geofluids 2021, 7941989. [Google Scholar] [CrossRef]
- Bazaluk, O.; Lozynskyi, V.; Falshtynskyi, V.; Saik, P.; Dychkovskyi, R.; Cabana, E. Experimental Studies of the Effect of Design and Technological Solutions on the Intensification of an Underground Coal Gasification Process. Energies 2021, 14, 4369. [Google Scholar] [CrossRef]
- Lozynskyi, V. Critical Review of Methods for Intensifying the Gas Generation Process in the Reaction Channel during Underground Coal Gasification (UCG). Min. Miner. Depos. 2023, 17, 67–85. [Google Scholar] [CrossRef]
- Petlovanyi, M.; Lozynskyi, V.; Saik, P.; Sai, K. Predicting the producing well stability in the place of its curving at the underground coal seams gasification. E3S Web Conf. 2019, 123, 01019. [Google Scholar] [CrossRef]
- Yu, H.; Li, S.; Wang, X. The Recent Progress China Has Made in the Backfill Mining Method, Part I: The Theory and Equipment of Backfill Pipeline Transportation. Minerals 2021, 11, 1274. [Google Scholar] [CrossRef]
- Petlovanyi, M.; Sai, K. Research into Cemented Paste Backfill Properties and Options for Its Application: Case Study from a Kryvyi Rih Iron-Ore Basin, Ukraine. Min. Miner. Depos. 2024, 18, 162–179. [Google Scholar] [CrossRef]
- Bazaluk, O.; Petlovanyi, M.; Zubko, S.; Lozynskyi, V.; Sai, K. Instability Asses during Underground Mining of Iron Ores. Minerals 2021, 11, 858. [Google Scholar] [CrossRef]
- Kopei, V.; Onysko, O.; Odosii, Z.; Pituley, L.; Goroshko, A. Investigation of the Influence of Tapered Thread Profile Accuracy on the Mechanical Stress, Fatigue Safety Factor and Contact Pressure. Lect. Notes Netw. Syst. 2021, 233, 177–185. [Google Scholar] [CrossRef]
- Kopei, V.; Onysko, O.; Barz, C.; Dašić, P.; Panchuk, V. Designing a Multi-Agent PLM System for Threaded Connections Using the Principle of Isomorphism of Regularities of Complex Systems. Machines 2023, 11, 263. [Google Scholar] [CrossRef]
- Velychkovych, A.; Andrusyak, A.; Pryhorowska, T.; Ropyak, L. Analytical model of oil pipeline overground transitions, laid in mountain areas. Oil Gas Sci. Technol. 2019, 74, 65. [Google Scholar] [CrossRef]
- Grudz, V.; Grudz, Y.; Pavlenko, I.; Liaposhchenko, O.; Ochowiak, M.; Pidluskiy, V.; Portechyn, O.; Iakymiv, M.; Włodarczak, S.; Krupińska, A.; et al. Ensuring the Reliability of Gas Supply Systems by Optimizing the Overhaul Planning. Energies 2023, 16, 986. [Google Scholar] [CrossRef]
- Bi, A.; Huang, S.; Zhang, Y.; Cao, Y. Reliability analysis of oil and gas pipelines based on step-down-stress testing in corrosive environments. Math. Probl. Eng. 2022, 4055779. [Google Scholar] [CrossRef]
- Chen, X.; Jeng, D.-S. Oscillatory Seabed Responses Around Two Pipelines in Tandem Under Combined Wave and Current Loading. Int. J. Offshore Polar Eng. 2022, 32, 321–329. [Google Scholar] [CrossRef]
- Soares, B.; Srinil, N. Capturing wake stiffness in wake-induced vibration of tandem cylinders. In Proceedings of the Int. Conf. Offshore Mech. Arctic Eng. (OMAE) 2020, Online, 3–7 August 2020; Volume 6A, p. V06AT06A011. [Google Scholar] [CrossRef]
- Dutkiewicz, M.; Velychkovych, A.; Andrusyak, A.; Petryk, J.; Kychma, A. Analytical model of an oil pipeline with a support of an overpass built in a mountainous area. Energies 2023, 16, 4464. [Google Scholar] [CrossRef]
- Dutkiewicz, M.; Shatskyi, I.; Martsynkiv, O.; Kuzmenko, E. Mechanism of casing string curvature due to displacement of surface strata. Energies 2022, 15, 5031. [Google Scholar] [CrossRef]
- Dey, S.; Tesfamariam, S. Structural performance of buried pipeline undergoing fault rupture in sand using Taguchi design of experiments. Soil Dyn. Earthq. Eng. 2022, 155, 107174. [Google Scholar] [CrossRef]
- Liu, E.; Li, W.; Cai, H.; Peng, S. Formation Mechanism of Trailing Oil in Product Oil Pipeline. Processes 2019, 7, 7. [Google Scholar] [CrossRef]
- Striletskyi, Y.; Ropyak, L.; Bandura, A. Method of oscillation excitation for investigation of inconsistency of coating deposition on long parts. Vibroeng. Procedia 2024, 57, 25–31. [Google Scholar] [CrossRef]
- Bandura, A.; Skaskiv, O. Analog of hayman’s theorem and its application to some system of linear partial differential equations. J. Math. Phys. Anal. Geom. 2019, 15, 170–191. [Google Scholar] [CrossRef]
- Bandura, A.; Skaskiv, O. Entire Functions of Bounded L-Index: Its Zeros and Behavior of Partial Logarithmic Derivatives. J. Complex Anal. 2017, 2017, 3253095. [Google Scholar] [CrossRef]
- Sheremeta, M.M.; Trukhan, Y.S. On a generalization of some Shah equation. Carpathian Math. Publ. 2024, 16, 259–266. [Google Scholar] [CrossRef]
- Sheremeta, M.M. Pseudostarlikeness and Pseudoconvexity of Multiple Dirichlet Series. Univ. J. Math. Appl. 2023, 6, 130–139. [Google Scholar] [CrossRef]
- Bandura, A.; Skaskiv, O.; Hural, I.; Shehda, L.; Smolovyk, L. Analytic functions in a unit polydisc: Conditions of directional boundedness of L-index for the sum of functions with directionally bounded L-index. J. Math. Sci. 2025, 288, 155–162. [Google Scholar] [CrossRef]
- Bandura, A.I.; Salo, T.M.; Skaskiv, O.B. Composition of entire function and analytic functions in the unit ball with a vanished gradient. Mat. Stud. 2024, 62, 132–140. [Google Scholar] [CrossRef]
- Gere, J.; Timoshenko, S. Mechanics of Materials. CL Engineering, 4th ed.; 912p, Available online: https://www.amazon.com/Mechanics-Materials-James-M-Gere/dp/0534934293 (accessed on 15 February 2025).
- Fridman, V. Theory of Elastic Oscillations. Equations and Methods; Springer Nature Pte Ltd.: Singapore, 2018. [Google Scholar] [CrossRef]
- Filippov, A. Oscillations of Mechanical Systems; Naukova Dumka: Kyiv, Ukraine, 1965. [Google Scholar]
- Peng, L.; Zhang, J.; Li, Y.; Du, G. A novel percussion-based approach for pipeline leakage detection with improved MobileNetV2. Eng. Appl. Artif. Intell. 2024, 133, 108537. [Google Scholar] [CrossRef]
- Akande, S.; Adetunla, A.; Olanrewaju, T.; Adeoye, A. UAV and Its Approach in Oil and Gas Pipeline Leakage Detection. J. Robot. 2021, 1300740. [Google Scholar] [CrossRef]
- Park, D.-Y.; Liang, J. Effects of Fatigue Parameters on Fatigue Crack Growth Rate of Pipe Steels and Girth Weld. J. Press. Vessel Technol. 2024, 146, 031701. [Google Scholar] [CrossRef]
- Yan, S.; Jia, K.; Xu, W.; Ma, Y. An experimental study on vortex-induced vibration suppression for submarine multispan pipelines. Ocean Eng. 2023, 271, 113678. [Google Scholar] [CrossRef]
- Liang, W.; Lou, M.; Fan, C.; Zhao, D.; Li, X. Coupling effects of vortex-induced vibration and local scour of double tandem pipelines in steady current. Ocean Eng. 2023, 286, 115495. [Google Scholar] [CrossRef]
- Tang, J.; Xu, J.; Zhou, D.; Huang, D.; Li, Y.; Chen, Z. Ground surface deformation caused by pipe jacking construction in a soft soil area: An experiment-based study. Buildings 2023, 13, 1628. [Google Scholar] [CrossRef]
- Wang, F.; Wu, G.; Chen, D.; Li, G.; Qian, Y.; Xi, F.; Wang, L. Mexanical response of a buried pipeline to permafrost trawing based on sequential coupling method. Atmosphere 2023, 14, 620. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, M.; Guo, Q.; Ma, W.; Zhang, Y.; Wu, W. Failure risk prediction model for girth welds in high-strength steel pipeline based on historical data and artificial neural network. Processes 2023, 11, 2273. [Google Scholar] [CrossRef]
- Zhang, Y.; Hou, S.; Lin, L.; Lou, Y.; Zhou, Y. Experimental study on the mechanical behavior of buried steel pipeline subjected to the local subsidence. Int. J. Press. Vessels Piping 2023, 206, 105037. [Google Scholar] [CrossRef]
- Li, X.; Wu, Q.; Jin, H.; Kan, W. A new stress monitoring method for mechanical state of buried steel pipelines under geological hazards. Adv. Mater. Sci. Eng. 2022, 2022, 4498458. [Google Scholar] [CrossRef]
- Arumugam, T.; Vijaya Kumar, S.D.; Karuppanan, S.; Ovinis, M. The influence of axial compressive stress and internal pressure on a pipeline network: A review. Appl. Sci. 2023, 13, 3799. [Google Scholar] [CrossRef]
- Witek, M. Structural integrity of steel pipeline with clusters of corrosion defects. Materials 2021, 14, 852. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, J.; Li, X.; Chen, F.; Guo, J.; Li, W.; Cai, J. Energy pipeline strength evaluation and reliability technology based on fuzzy deep learning network algorithm. Energy Rep. 2022, 8, 5129–5136. [Google Scholar] [CrossRef]
- Saraswat, R.; Patil, P.; Ciecko, E.; Koul, P. Identification of interacting free spans in subsea pipeline. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering (OMAE), Melbourne, Australia, 11–16 June 2023; Volume 3, p. v003t04a043. [Google Scholar]
- Liu, X.; Sun, Z.; Zhu, J.; He, Y.; Pan, Y. Study on stress-strain characteristics of pipeline-soil interaction under ground collapse condition. Geofluids 2022, 5778761. [Google Scholar] [CrossRef]
- Bao, Y.; Ma, T.; Zhang, Y.; Wang, L. Influence of vibration on transient flow characteristics of gas-liquid two-phase flow in inclined pipes. Chem. Eng. Res. Des. 2023, 196, 71–88. [Google Scholar] [CrossRef]
- Chudyk, I.; Raiter, P.; Grydzhuk, Y.; Yurych, L. Mathematical model of oscillations of a drill tool with a drill bit of cutting-scraping type. Nauk. Visn. Nats. Hirn. Univ. 2020, 2020, 52–57. [Google Scholar] [CrossRef]
- Chudyk, I.; Sudakova, I.; Dreus, A.; Pavlychenko, A.; Sudakov, A. Determination of the Thermal State of a Block Gravel Filter during Its Transportation along the Borehole. Min. Miner. Depos. 2023, 17, 75–82. [Google Scholar] [CrossRef]
- Moysyshyn, V.; Lyskanych, M.; Borysevych, L.; Vytyaz, O.; Voznyi, I. Experimental estimation of design and drilling regime option influence on drilling tool dynamics. Metallofiz. Adv. Technol. 2021, 43, 689–712. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tutko, R.; Lozynskyi, V. Oscillations of the Oil Pipeline Axis with Consideration of the Inertia Component When Pumping Diesel Fuel. Energies 2025, 18, 2472. https://doi.org/10.3390/en18102472
Tutko R, Lozynskyi V. Oscillations of the Oil Pipeline Axis with Consideration of the Inertia Component When Pumping Diesel Fuel. Energies. 2025; 18(10):2472. https://doi.org/10.3390/en18102472
Chicago/Turabian StyleTutko, Roman, and Vasyl Lozynskyi. 2025. "Oscillations of the Oil Pipeline Axis with Consideration of the Inertia Component When Pumping Diesel Fuel" Energies 18, no. 10: 2472. https://doi.org/10.3390/en18102472
APA StyleTutko, R., & Lozynskyi, V. (2025). Oscillations of the Oil Pipeline Axis with Consideration of the Inertia Component When Pumping Diesel Fuel. Energies, 18(10), 2472. https://doi.org/10.3390/en18102472






