Embedded Processor-in-the-Loop Implementation of ANFIS-Based Nonlinear MPPT Strategies for Photovoltaic Systems
Abstract
1. Introduction
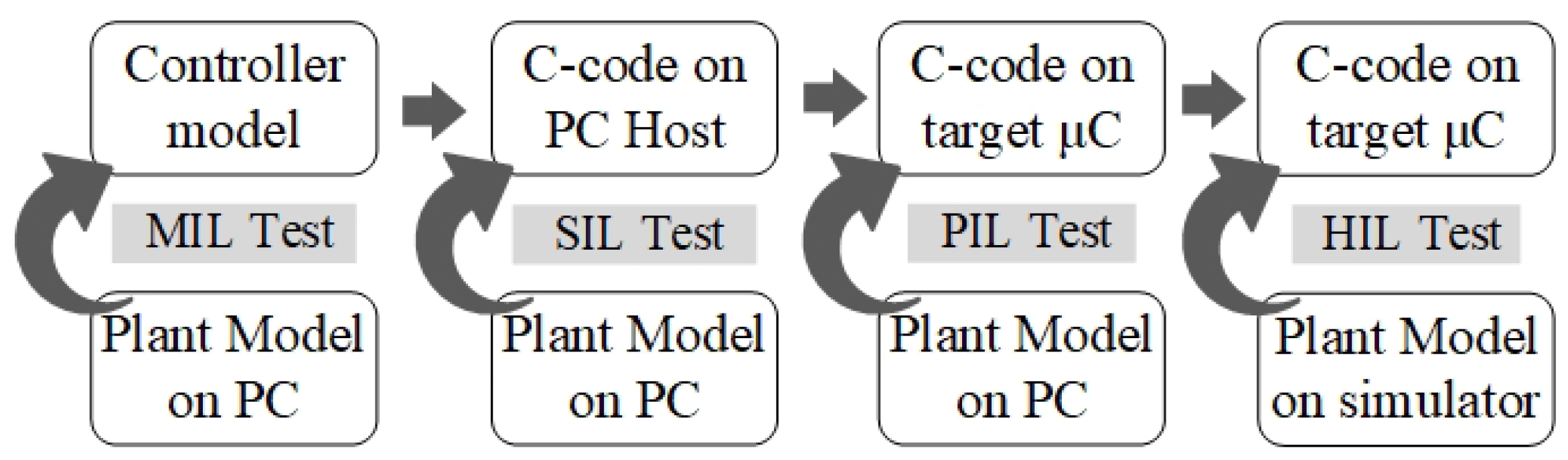
2. Model-Based Design and Validation Framework for MPPT Controllers
2.1. Model-Based Design Approach for MPPT Controllers
- Model-in-the-Loop (MIL) Testing: The initial validation stage, where the MPPT control algorithm is tested in a simulated environment to ensure that it meets system requirements. MIL testing verifies that the control model behaves as expected under different operating conditions before proceeding to code generation [32].
- Software-in-the-Loop (SIL) Testing: After MIL, the control algorithm is automatically converted into C code and tested within a software simulation environment to verify that the compiled code produces the same results as the original model, ensuring functional consistency [32].
- Processor-in-the-Loop (PIL) Testing: This stage bridges simulation and real hardware implementation. The MPPT algorithm is executed on the target microcontroller (STM32F4) while interfacing with a simulated PV system. PIL testing allows developers to evaluate real-time computational performance, software-hardware interactions, and potential integration challenges before full deployment [33].
2.2. V-Model Development Process for MPPT Validation
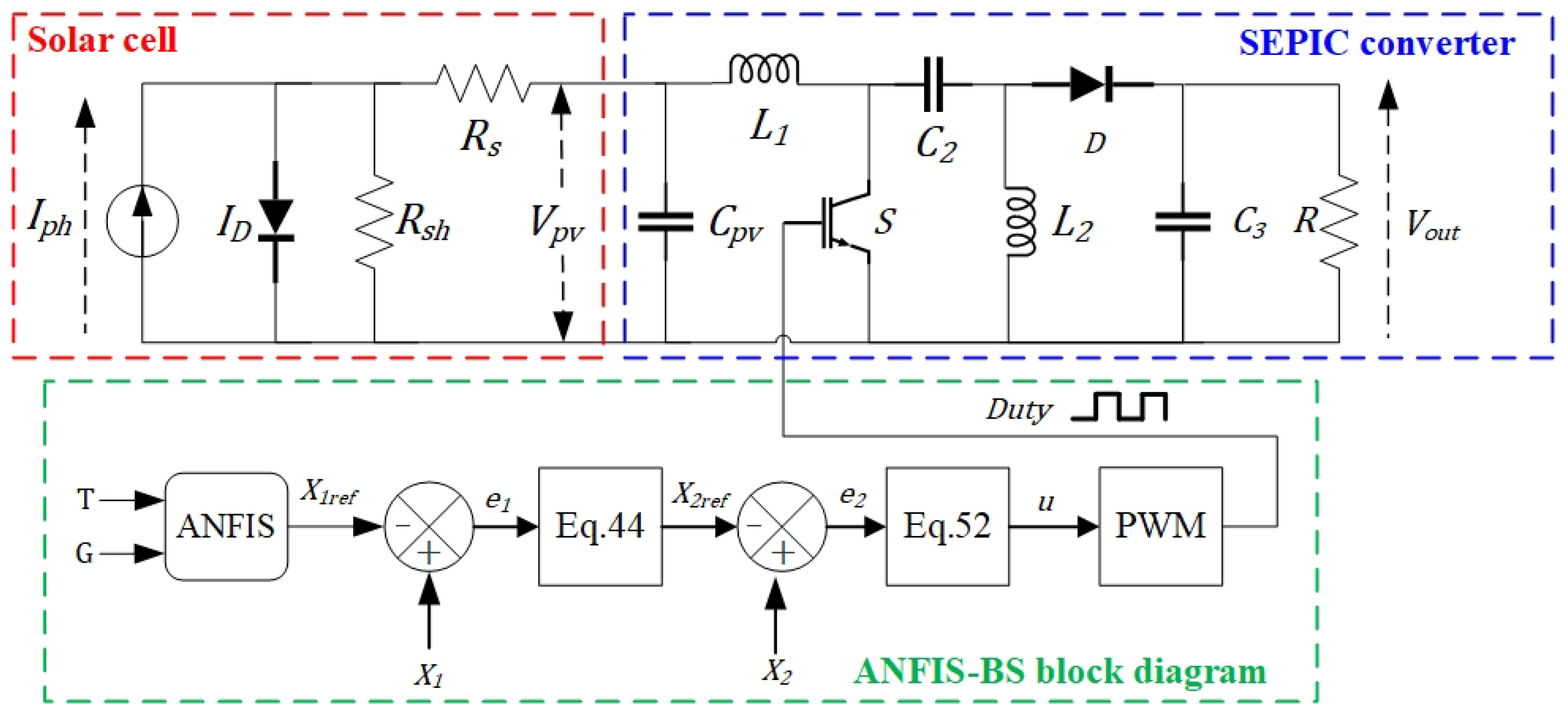
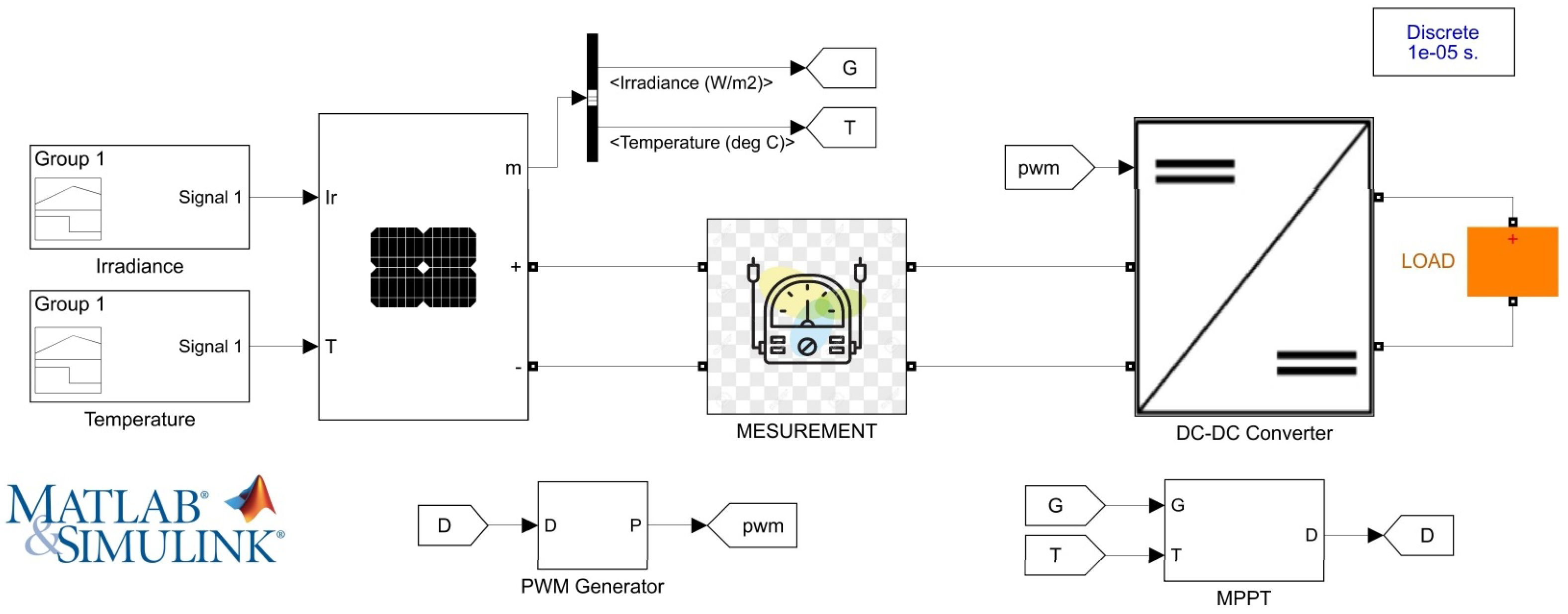
3. Photovoltaic System Modeling
3.1. PV Module
- : Photogenerated current, which depends on irradiance and temperature.
- : Diode current, responsible for the nonlinear characteristics of the PV cell.
- : Short-circuit current of the PV module.
- : Series resistance, which affects voltage and current.
- : Shunt resistance, often neglected for simplicity.
- : Number of series-connected cells in the PV module.
- : Thermal voltage, dependent on the cell temperature.
- : Boltzmann’s constant.
- e: Electron charge.
- : Energy bandgap of the semiconductor material.
3.2. DC-DC Converter
3.2.1. Boost Converter
- : Maximum power output of the PV panel.
- : Equivalent resistance of the converter.
- : PV panel voltage at MPP.
- : Desired duty cycle to maintain MPPT.
- : Inductor current.
- : PWM duty cycle.
- : Output voltage.
- R: Load resistance.
- : System uncertainties, satisfying:
3.2.2. SEPIC Converter
- : Inductor currents.
- : Capacitor voltage.
- : Output voltage.
- u: PWM duty cycle.
4. Proposed Control Methodology for Optimal Power Extraction
- Fast Terminal Synergetic Control, which ensures rapid convergence to the MPP with improved robustness.
- Nonlinear Backstepping Control, which guarantees adaptive regulation and enhances system stability.
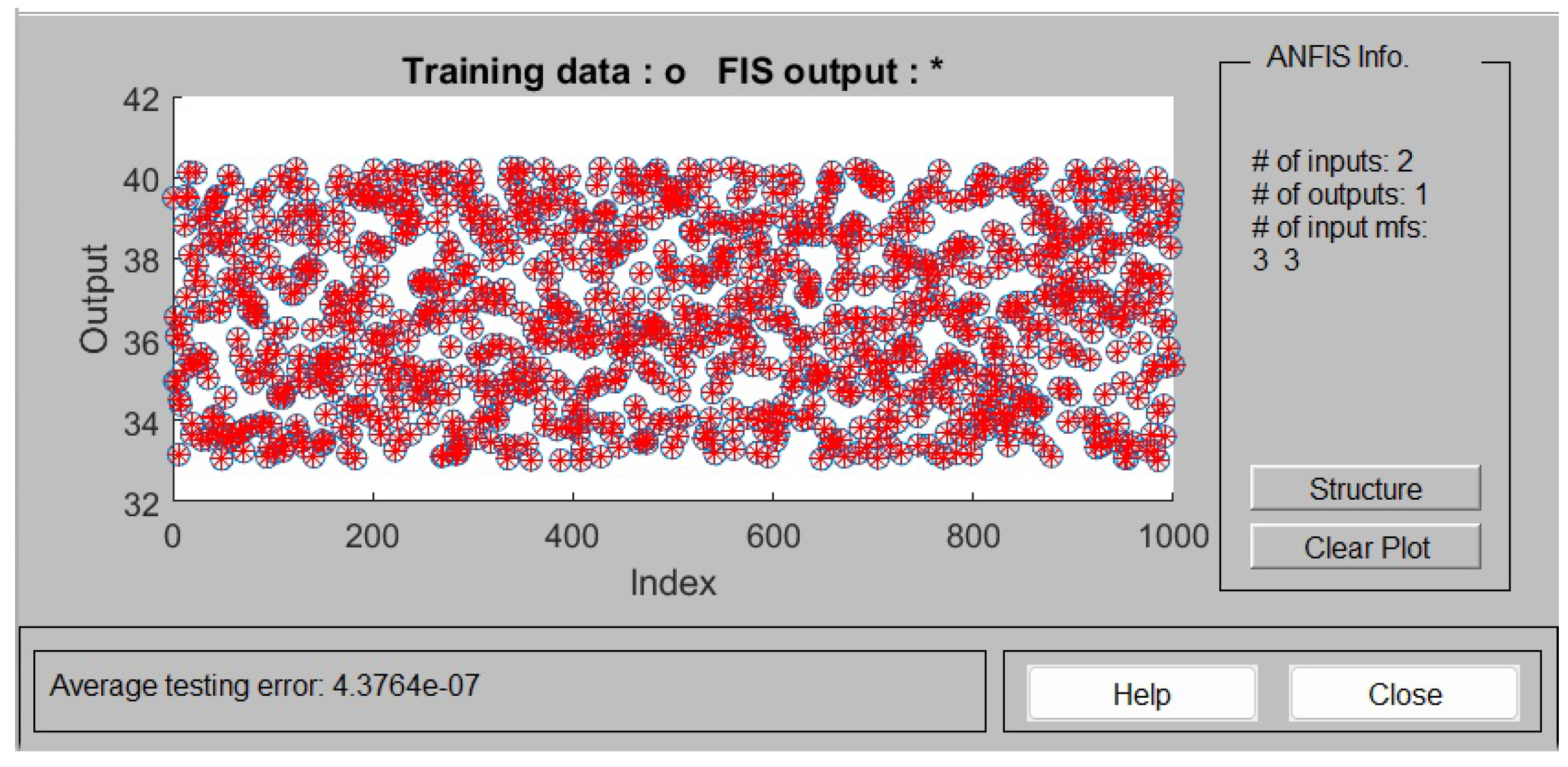
4.1. Reference Voltage Generation Using ANFIS
4.2. Fast Terminal Synergetic Control
4.3. Backstepping Control
5. Results
5.1. Model-in-the-Loop Testing
5.2. Software-in-the-Loop Testing
5.3. Processor-in-the-Loop Testing
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PV | Photovoltaic |
| MPPT | Maximum Power Point Tracking |
| ANFIS | Adaptive Neuro-Fuzzy Inference System |
| FTSC | Fast Terminal Synergetic Control |
| BS | Backstepping |
| SEPIC | Single-Ended Primary Inductor Converter |
| PIL | Processor-in-the-Loop |
| MBD | Model-Based Design |
| DC-DC | Direct Current to Direct Current |
| P&O | Perturb and Observe |
| INC | Incremental Conductance |
| FLC | Fuzzy Logic Control |
| ANNs | Artificial Neural Networks |
| PSO | Particle Swarm Optimization |
| GA | Genetic Algorithms |
| ACO | Ant Colony Optimization |
| MIL | Model-in-the-Loop |
| SIL | Software-in-the-Loop |
| ANFIS-FTSC | Adaptive Neuro-Fuzzy Inference System with Fast Terminal Synergetic Control |
| ANFIS-BS | Adaptive Neuro-Fuzzy Inference System with Backstepping |
| MPP | Maximum Power Point |
| V&V | Verification and Validation |
| Optimal Reference Voltage | |
| Actual PV Voltage | |
| G | Irradiance |
| T | Temperature |
References
- Zoungrana, R.; Çakmakci, M. From non-renewable energy to renewable by harvesting salinity gradient power by reverse electrodialysis: A review. Int. J. Energy Res. 2021, 45, 3495–3522. [Google Scholar] [CrossRef]
- Solarin, S.A.; Al-Mulali, U.; Ozturk, I. Validating the environmental Kuznets curve hypothesis in India and China: The role of hydroelectricity consumption. Renew. Sustain. Energy Rev. 2017, 80, 1578–1587. [Google Scholar] [CrossRef]
- Mekhilef, S.; Saidur, R.; Safari, A.; Mustaffa, W. Biomass energy in Malaysia: Current state and prospects. Renew. Sustain. Energy Rev. 2011, 15, 3360–3370. [Google Scholar] [CrossRef]
- Bollipo, R.B.; Mikkili, S.; Bonthagorla, P.K. Critical review on PV MPPT techniques: Classical, intelligent and optimisation. IET Renew. Power Gener. 2020, 14, 1433–1452. [Google Scholar] [CrossRef]
- Liu, Z.; Cheng, X.; Peng, X.; Wang, P.; Zhao, X.; Liu, J.; Jiang, D.; Qu, R. A review of common-mode voltage suppression methods in wind power generation. Renew. Sustain. Energy Rev. 2024, 203, 114773. [Google Scholar] [CrossRef]
- Killi, M.; Samanta, S. Modified perturb and observe MPPT algorithm for drift avoidance in photovoltaic systems. IEEE Trans. Ind. Electron. 2015, 62, 5549–5559. [Google Scholar] [CrossRef]
- Nkambule, M.S.; Hasan, A.N.; Ali, A.; Hong, J.; Geem, Z.W. Comprehensive evaluation of machine learning MPPT algorithms for a PV system under different weather conditions. J. Electr. Eng. Technol. 2021, 16, 411–427. [Google Scholar] [CrossRef]
- Yang, B.; Zhu, T.; Wang, J.; Shu, H.; Yu, T.; Zhang, X.; Yao, W.; Sun, L. Comprehensive overview of maximum power point tracking algorithms of PV systems under partial shading condition. J. Clean. Prod. 2020, 268, 121983. [Google Scholar] [CrossRef]
- Elbaset, A.A.; Ali, H.; Abd-El Sattar, M.; Khaled, M. Implementation of a modified perturb and observe maximum power point tracking algorithm for photovoltaic system using an embedded microcontroller. IET Renew. Power Gener. 2016, 10, 551–560. [Google Scholar] [CrossRef]
- Choi, H.; Ciobotaru, M.; Jang, M.; Agelidis, V.G. Performance of medium-voltage DC-bus PV system architecture utilizing high-gain DC-DC converter. IEEE Trans. Sustain. Energy 2015, 6, 464–473. [Google Scholar] [CrossRef]
- Houssein, E.H.; Mahdy, M.A.; Fathy, A.; Rezk, H. A modified Marine Predator Algorithm based on opposition based learning for tracking the global MPP of shaded PV system. Expert Syst. Appl. 2021, 183, 115253. [Google Scholar] [CrossRef]
- Liu, F.; Duan, S.; Liu, F.; Liu, B.; Kang, Y. A variable step size INC MPPT method for PV systems. IEEE Trans. Ind. Electron. 2008, 55, 2622–2628. [Google Scholar]
- Raza, M.A.; Zahra, S.; Raza, S.; Altimania, M.R.; Hassan, M.; Munir, H.M.; Zaitsev, I.; Kuchanskyy, V. Mitigating the Impact of Partial Shading Conditions on Photovoltaic Arrays Through Modified Bridge-Linked Configuration. Sustainability 2025, 17, 1263. [Google Scholar] [CrossRef]
- Celikel, R.; Yilmaz, M.; Gundogdu, A. A voltage scanning-based MPPT method for PV power systems under complex partial shading conditions. Renew. Energy 2022, 184, 361–373. [Google Scholar] [CrossRef]
- Awan; Javed, A.B.M.Y.; Asghar, A.B.; Ejsmont, K. Performance optimization of a ten check MPPT algorithm for an off-grid solar photovoltaic system. Energies 2022, 15, 2104. [Google Scholar] [CrossRef]
- Abidi, H.; Sidhom, L.; Chihi, I. Systematic literature review and benchmarking for photovoltaic MPPT techniques. Energies 2023, 16, 3509. [Google Scholar] [CrossRef]
- Chnini, K.; Jouini, H.; Allagui, H.; Mami, A. ANFIS-RTSMC based MPPT for a hybrid PV-diesel-battery water pumping system. Meas. Control 2024. [Google Scholar] [CrossRef]
- Chnini, K.; Jouini, H.; Allagui, H.; Mami, A. A Novel Nonlinear Intelligent Control Approach for Optimizing Solar PV Systems in Medical Applications Under Dynamic Conditions. In Proceedings of the 2024 IEEE 7th International Conference on Advanced Technologies, Signal and Image Processing (ATSIP), Sousse, Tunisia, 11–13 July 2024; pp. 553–558. [Google Scholar] [CrossRef]
- Sarang, S.A.; Raza, M.A.; Panhwar, M.; Khan, M.; Abbas, G.; Touti, E.; Altamimi, A.; Wijaya, A.A. Maximizing solar power generation through conventional and digital MPPT techniques: A comparative analysis. Sci. Rep. 2024, 14, 8944. [Google Scholar] [CrossRef] [PubMed]
- Fares, D.; Fathi, M.; Shams, I.; Mekhilef, S. A novel global MPPT technique based on squirrel search algorithm for PV module under partial shading conditions. Energy Convers. Manag. 2021, 230, 113773. [Google Scholar] [CrossRef]
- Motahhir, S.; Ghzizal, A.E.; Sebti, S.; Derouich, A. The most used MPPT algorithms: Review and the suitable low-cost embedded board for each algorithm. J. Clean. Prod. 2020, 246, 118983. [Google Scholar] [CrossRef]
- Ticona Coaquira, F.J.; Wang, X.; Vidaurre Torrez, K.W.; Mamani Quiroga, M.J.; Silva Plata, M.A.; Luna Verdueta, G.A.; Murillo Quispe, S.E.; Auza Banegas, G.J.; Antezana Lopez, F.P.; Rojas, A. Model-Based Design and Testbed for CubeSat Attitude Determination and Control System with Magnetic Actuation. Appl. Sci. 2024, 14, 6065. [Google Scholar] [CrossRef]
- Chtita, S.; Motahhir, S.; El Ghzizal, A. A New Design and Embedded Implementation of a Low-Cost Maximum Power Point Tracking Charge Controller for Stand-Alone Photovoltaic Systems. Energy Technol. 2024, 12, 2301324. [Google Scholar] [CrossRef]
- Rimouche, W.; Talha, A.; Boumaaraf, H. Comparative Analysis of Hardware Resource Utilization for MPPT Techniques: P&O, Incremental Conductance, and ANN Using Processor-in-the-Loop Testing on STM32F407. In Proceedings of the 2024 12th International Conference on Systems and Control (ICSC), Batna, Algeria, 3–5 November 2024; pp. 53–59. [Google Scholar] [CrossRef]
- Chnini, K.; dhifaoui, D.; Jouini, H.; Allagui, H. Enhancing PV power generation via an adaptive neuro-fuzzy and fast terminal synergetic MPPT approach. Meas. Control 2024, 58, 502–514. [Google Scholar] [CrossRef]
- Chnini, K.; Jouini, H.; Allagui, H.; Mami, A. Enhancing power generation via an adaptive neuro-fuzzy and backstepping maximum-power-point tracking approach for photovoltaic single-ended primary inductor converter system. Clean Energy 2024, 8, 34–44. [Google Scholar] [CrossRef]
- Cheddadi, B.; Errahimi, F.; Es-sbai, N. Design and verification of photovoltaic MPPT algorithm as an automotive-based embedded software. Sol. Energy 2018, 171, 414–425. [Google Scholar] [CrossRef]
- Karmouni, S.; Chouiekh, M.; Motahhir, S.; Qjidaa, H.; Jamil, M.O.; Sayyouri, M. A fast and accurate sine-cosine MPPT algorithm under partial shading with implementation using Arduino board. Clean. Eng. Technol. 2022, 9, 100535. [Google Scholar] [CrossRef]
- Boopathi, S.; Sujatha, R.; Senthil Kumar, C.; Narasimman, S. Quantification of software code coverage using artificial bee colony optimization based on Markov approach. Arab. J. Sci. Eng. 2017, 42, 3503–3519. [Google Scholar] [CrossRef]
- Coronado-Mendoza, A.; Camas-Náfate, M.; Artal-Sevil, J.S.; Domínguez-Navarro, J.A. Optimum Design of a Photovoltaic Inverter System Based on Ga, Pso and Gwo Algorithms with a Mppt Sliding Mode Control. Energies 2025, 18, 1911. [Google Scholar] [CrossRef]
- Strandberg, P.E. Automated System-Level Software Testing of Industrial Networked Embedded Systems. Ph.D. Thesis, Malardalen University, Västerås, Sweden, 2021. [Google Scholar]
- De Lemos, R.; Giese, H.; Müller, H.A.; Shaw, M. (Eds.) Software Engineering for Self-Adaptive Systems II. In International Seminar, Dagstuhl Castle, Germany, October 24–29, 2010 Revised Selected and Invited Papers; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2013; Volume 7475. [Google Scholar]
- Megrini, M.; Gaga, A.; Mehdaoui, Y. Processor in the loop implementation of artificial neural network controller for BLDC motor speed control. Results Eng. 2004, 23, 102422. [Google Scholar] [CrossRef]
- Hill, A.; de Beeck, J.O.; Baja, M.; Djemili, I.; Reuther, P.; Sutra, I. Use of V-cycle methodology to develop mechatronic fuel system functions. In SAE Technical Paper; SAE International: Warrendale, PA, USA, 2017. [Google Scholar]
- Hommes, U. Review and assessment of the ISO 26262 draft road vehicle-functional safety. In SAE Technical Paper; SAE International: Warrendale, PA, USA, 2012. [Google Scholar]
- Tao, H.; Ghahremani, M.; Ahmed, F.W.; Jing, W.; Nazir, M.S.; Ohshima, K. A novel MPPT controller in PV systems with hybrid whale optimization-PS algorithm based ANFIS under different conditions. Control. Eng. Pract. 2021, 112, 104809. [Google Scholar] [CrossRef]
- Chennoufi, K.; Ferfra, M.; Mokhlis, M. Design and implementation of efficient MPPT controllers based on SDM and DDM using backstepping control and SEPIC converter. In Proceedings of the 2021 9th International Renewable and Sustainable Energy Conference (IRSEC), Benguerir, Morocco, 23–27 November 2021; pp. 1–8. [Google Scholar]
- Chennoufi, K.; Ferfra, M. Maximum Power Point Tracking using SEPIC converter and double diode solar cell model. In Proceedings of the International Conference on Digital Technologies and Applications, Fez, Morocco, 29–30 January 2021; pp. 1159–1169. [Google Scholar]
- Ali, K.; Khan, L.; Khan, Q.; Ullah, S.; Ahmad, S.; Mumtaz, S.; Karam, F.W.; Naghmash. Robust integral backstepping based nonlinear MPPT control for a PV system. Energies 2019, 12, 3180. [Google Scholar] [CrossRef]
- Lasheen, M.; Abdel-Salam, M. Maximum power point tracking using Hill Climbing and ANFIS techniques for PV applications: A review and a novel hybrid approach. Energy Convers. Manag. 2018, 171, 1002–1019. [Google Scholar] [CrossRef]
- Zou, L.; Wang, L.; Xia, L.; Lin, A.; Hu, B.; Zhu, H. Prediction and comparison of solar radiation using improved empirical models and Adaptive Neuro-Fuzzy Inference Systems. Renew. Energy 2017, 106, 343–353. [Google Scholar] [CrossRef]
- Hachana, A.; Harmas, M.N. Terminal synergetic control for blood glucose regulation in diabetes patients. J. Dyn. Syst. Meas. Control 2018, 140, 100801. [Google Scholar] [CrossRef]
- Zerroug, N.; Harmas, M.N.; Benaggoune, S.; Bouchama, Z.; Zehar, K. DSP-based implementation of fast terminal synergetic control for a DC–DC Buck converter. J. Frankl. Inst. 2018, 355, 2329–2343. [Google Scholar] [CrossRef]
- Arsie, I.; Betta, G.; Capriglione, D.; Pietrosanto, A.; Sommella, P. Functional testing of measurement-based control systems: An application to automotive. Measurement 2014, 54, 222–233. [Google Scholar] [CrossRef]
- Kasoju, A.; Petersen, K.; Mäntylä, M.V. Analyzing an automotive testing process with evidence-based software engineering. Inf. Softw. Technol. 2013, 55, 1237–1259. [Google Scholar] [CrossRef]
- Ropp, M.; Cale, J.; Mills-Price, M.; Scharf, M.; Hummel, S.G. A test protocol to enable comparative evaluation of maximum power point trackers under both static and dynamic irradiance. In Proceedings of the 37th IEEE Photovoltaic Specialists Conference, Seattle, WA, USA, 19–24 June 2011; pp. 3734–3737. [Google Scholar]
- Beneder, R. Development of an OpenOCD Compatible Debugger for ARM-CMARMJTAG. Master’s Thesis, University of Applied Sciences Technikum Wien, Vienna, Austria, 15 June 2011. [Google Scholar]
- Manna, S.; Singh, D.K.; Alsharif, M.H.; Kim, M.K. Enhanced MPPT approach for grid-integrated solar PV system: Simulation and experimental study. Energy Rep. 2024, 12, 3323–3340. [Google Scholar] [CrossRef]
- Soon, T.K.; Mekhilef, S. A fast-converging MPPT technique for photovoltaic system under fast-varying solar irradiation and load resistance. IEEE Trans. Ind. Inform. 2014, 11, 176–186. [Google Scholar] [CrossRef]
- Faraji, R.; Rouholamini, A.; Naji, H.R.; Fadaeinedjad, R.; Chavoshian, M.R. FPGA-based real time incremental conductance maximum power point tracking controller for photovoltaic systems. IET Power Electron. 2014, 7, 1294–1304. [Google Scholar] [CrossRef]
- Loukriz, A.; Haddadi, M.; Messalti, S. Simulation and experimental design of a new advanced variable step size incremental conductance MPPT algorithm for PV systems. ISA Trans. 2016, 62, 30–38. [Google Scholar] [CrossRef] [PubMed]
- Motahhir, S.; Ghzizal, A.E.; Sebti, S.; Derouich, A. MIL and SIL and PIL tests for MPPT algorithm. Cogent Eng. 2017, 4, 1378475. [Google Scholar] [CrossRef]
- Diouri, O.; Gaga, A.; Senhaji, S.; Jamil, M.O. Design and PIL test of high performance MPPT controller based on P&O-backstepping applied to DC-DC converter. J. Robot. Control (JRC) 2022, 3, 431–438. [Google Scholar]
- El Haji, I.; Meriem, M.; Kchikach, M.; Ahmed, G.; El Hasnaoui, A. Design and PIL Implementation of Fuzzy Logic-based MPPT Control for Symmetrical Multilevel Boost Converter. WSEAS Trans. Power Syst. 2024, 19, 388–399. [Google Scholar] [CrossRef]





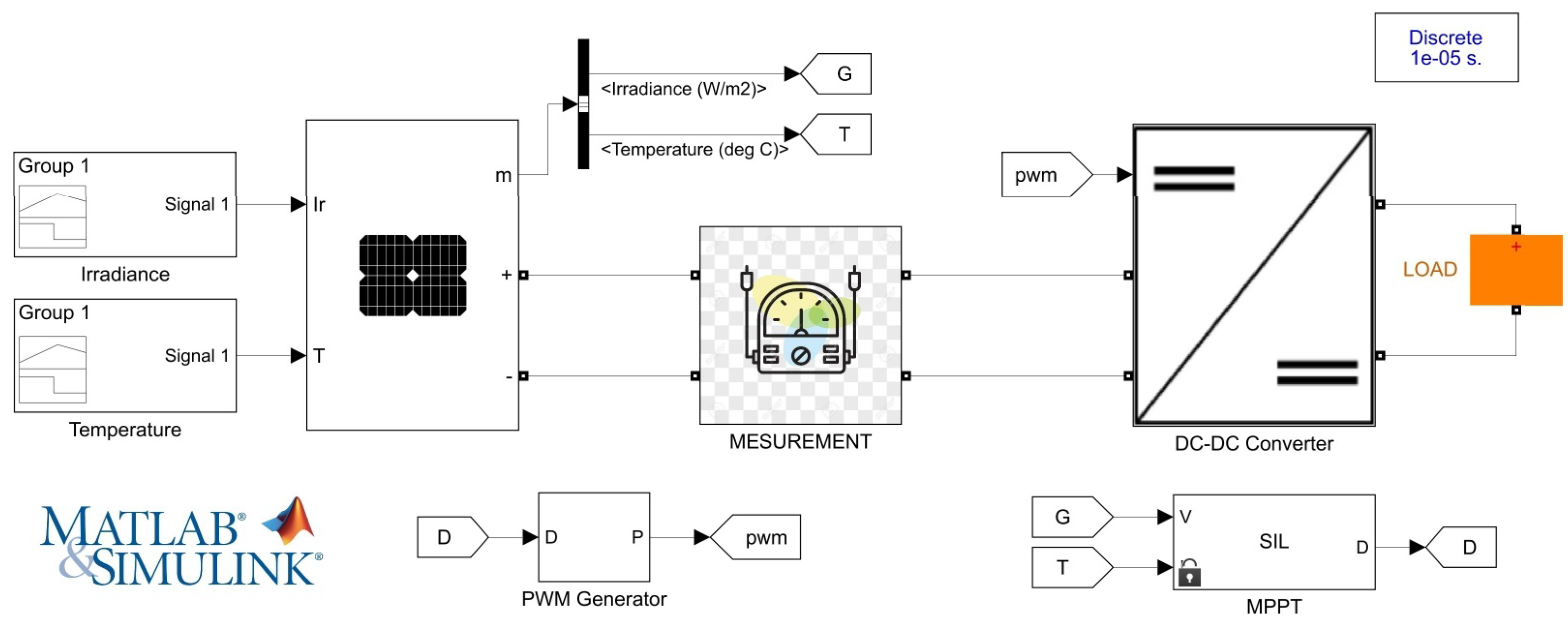
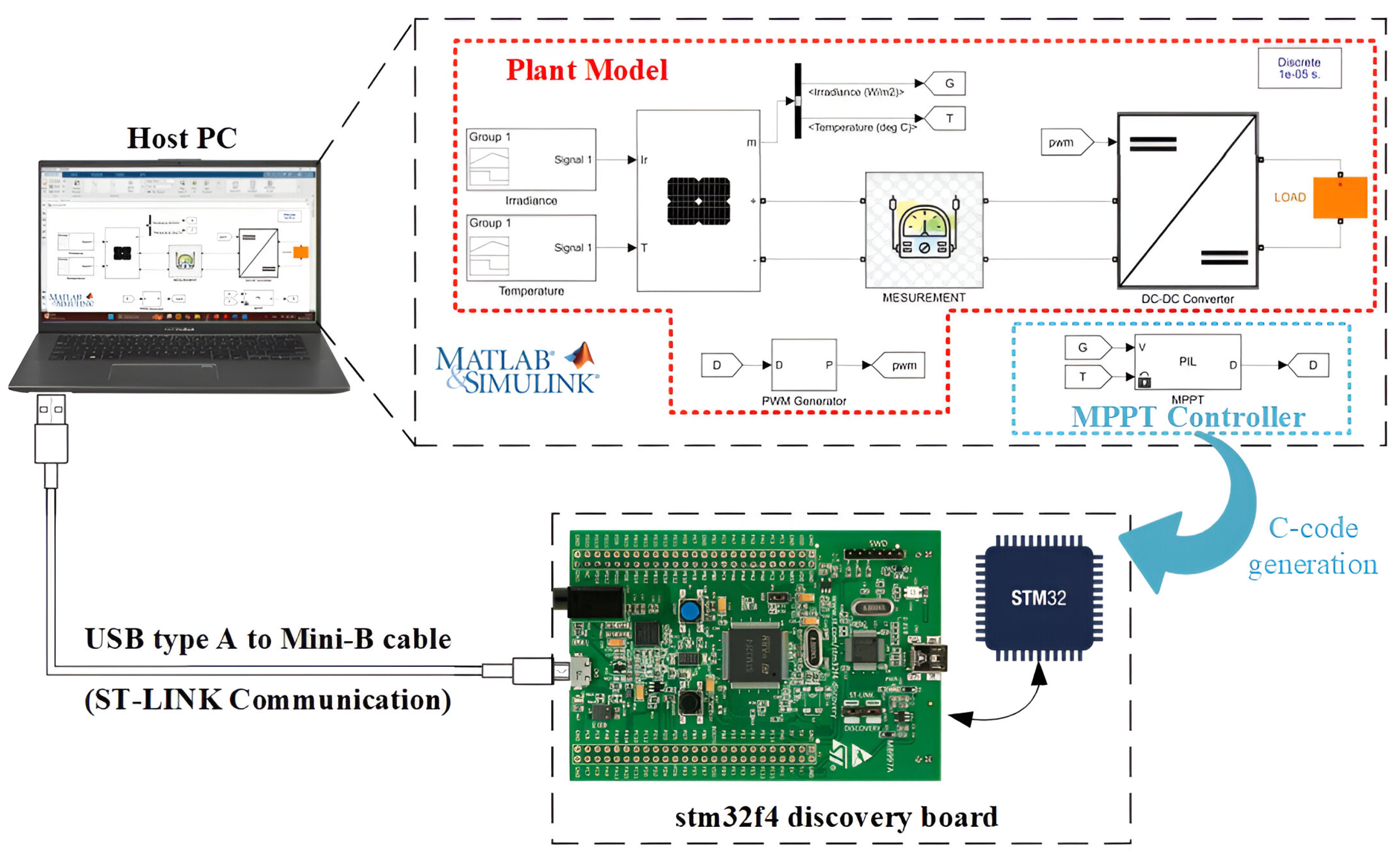
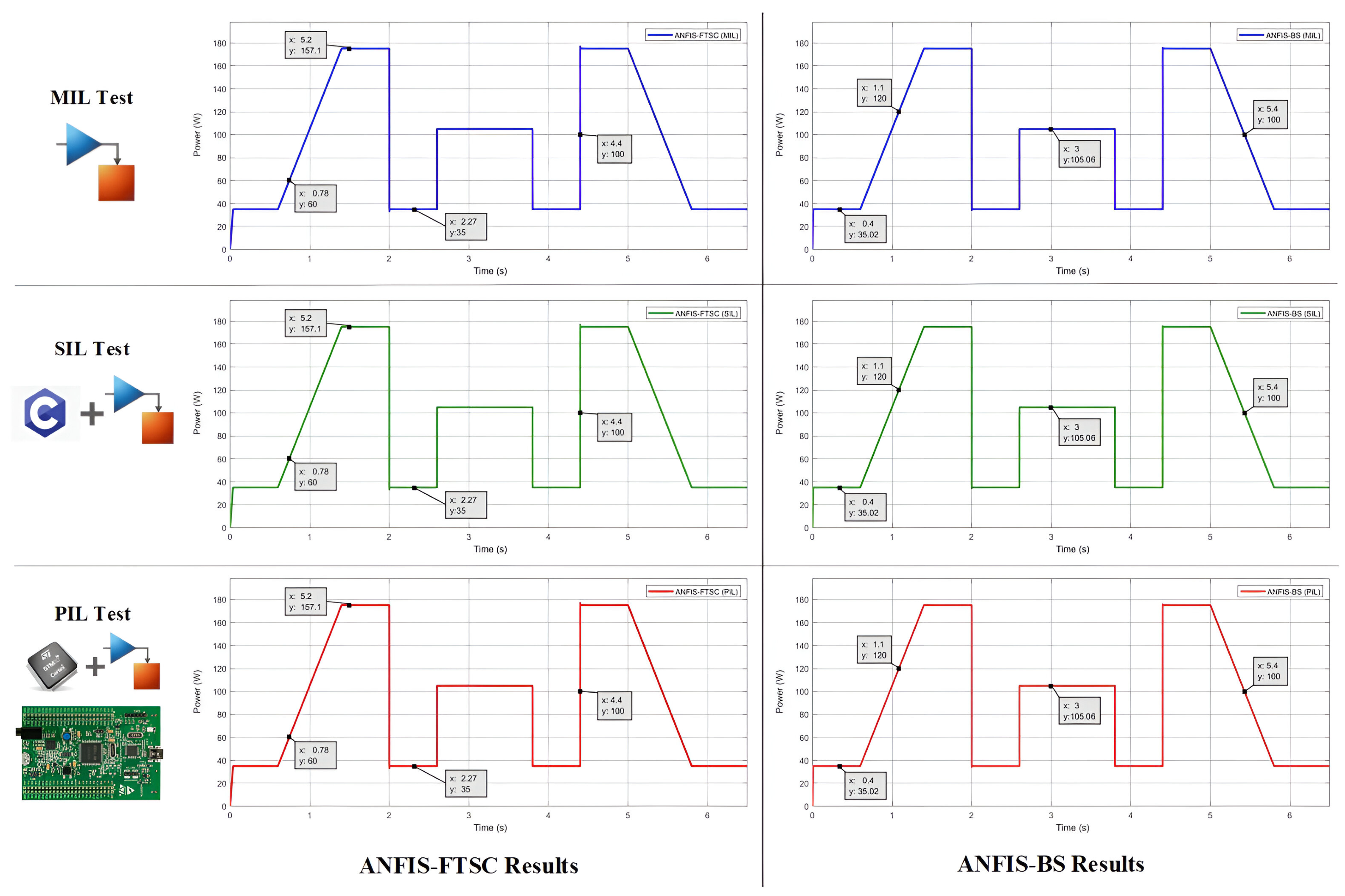
| Parameter | Symbol | Value |
|---|---|---|
| Maximum Power (W) | 175.1 | |
| Voltage at MPP (V) | 36.63 | |
| Current at MPP (A) | 4.78 | |
| Open Circuit Voltage (V) | 43.99 | |
| Short-Circuit Current (A) | 5.17 |
| Reference | Controller Used | Power Ripples | Efficiency | Response Time |
|---|---|---|---|---|
| Soon et al. (2014) [49] | PIC18F4520 | 2 W | 97.97% | 400 ms |
| Faraji et al. (2014) [50] | Xilinx XC3S400 FPGA | 2.7 W | 98.8% | 2.5 ms |
| Loukriz et al. (2016) [51] | dsPIC30F4011 | 2 W | 98% | 500 ms |
| Motahhir et al. (2017) [52] | STM32F407VG | Neglected | 98.8% | 20 ms |
| Diouri et al. (2022) [53] | STM32F4 | 1.2 W | 97.88% | 5 ms |
| El Haji et al. (2024) [54] | Arduino Mega 2560 | Neglected | 96% | 4.5 ms |
| EMRAC-MPPT [48] | dSPACE 1202 | Neglected | 98.28% | 110 ms |
| Fuzzy-PID [48] | dSPACE 1202 | Neglected | 97.9% | 120 ms |
| ANFIS-FTSC (proposed) | STM32F407VG | Neglected | 99.89% | 37 ms |
| ANFIS-BS (proposed) | STM32F407VG | Neglected | 99.6% | 9 ms |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chnini, K.; Abdou Tankari, M.; Jouini, H.; Allagui, H.; Ibrahim, M.A.; Touti, E. Embedded Processor-in-the-Loop Implementation of ANFIS-Based Nonlinear MPPT Strategies for Photovoltaic Systems. Energies 2025, 18, 2470. https://doi.org/10.3390/en18102470
Chnini K, Abdou Tankari M, Jouini H, Allagui H, Ibrahim MA, Touti E. Embedded Processor-in-the-Loop Implementation of ANFIS-Based Nonlinear MPPT Strategies for Photovoltaic Systems. Energies. 2025; 18(10):2470. https://doi.org/10.3390/en18102470
Chicago/Turabian StyleChnini, Khalil, Mahamadou Abdou Tankari, Houda Jouini, Hatem Allagui, Mostafa Ahmed Ibrahim, and Ezzeddine Touti. 2025. "Embedded Processor-in-the-Loop Implementation of ANFIS-Based Nonlinear MPPT Strategies for Photovoltaic Systems" Energies 18, no. 10: 2470. https://doi.org/10.3390/en18102470
APA StyleChnini, K., Abdou Tankari, M., Jouini, H., Allagui, H., Ibrahim, M. A., & Touti, E. (2025). Embedded Processor-in-the-Loop Implementation of ANFIS-Based Nonlinear MPPT Strategies for Photovoltaic Systems. Energies, 18(10), 2470. https://doi.org/10.3390/en18102470









