Statistical Foundations of Generative AI for Optimal Control Problems in Power Systems: Comprehensive Review and Future Directions

Abstract

With the rapid advancement of deep learning, generative artificial intelligence (Gen-AI) has emerged as a powerful tool, unlocking new prospects in the power systems sector. Despite the evident success of these methods and the rapid growth of this field in the power systems community, there is still a pressing need for a deeper understanding of how different evaluation metrics relate to the underlying statistical structure of the models. Another related important question is what tools can be used to quantify the different uncertainties, which are inherent in these problems, and stem not only from the physical system but also from the nature of the generative model itself. This paper attempts to address these challenges and provides a comprehensive review of existing evaluation metrics for generative models applied in various power system tasks. We analyze how these metrics align with the statistical properties of the models and explore their strengths and limitations. We also examine different sources of uncertainty, distinguishing between uncertainties inherent to the learning model, those arising from measurement errors, and other sources. Our general aim is to promote a better understanding of generative models as they are being applied in power systems to support this fascinating growing trend.

1. Introduction

With the rapid advancement of deep learning (DL), generative artificial intelligence (Gen-AI) has emerged as a powerful tool, unlocking new prospects in the power systems sector. Generative models, capable of learning from large amounts of data and generating new content, offer a paradigm shift in how we approach challenges within the energy industry. By synthesizing data, simulations, or designs that closely mimic real-world scenarios, generative AI creates new possibilities to address critical challenges, such as data augmentation, anomaly detection, system optimization, and synthetic energy market simulations. Unlike traditional deep learning algorithms, which primarily focus on pattern recognition and prediction, generative AI possesses the ability to generate diverse content and simulate various scenarios. This capability enables utilities to enhance decision-making processes, improve grid resiliency, and achieve more efficient and sustainable energy management. Currently, there is only one comprehensive review paper that analyzes and categorizes studies concerning generative AI applications for energy and power systems. This article, Ref. [1], provides a high-level statistical analysis of research trends and discusses open challenges in this domain.

When designing generative models, both researchers and engineers consider the underlying mathematical principles the model implements. Variational Autoencoders (VAEs), rooted in probability theory, employ variational inference and maximize the Evidence Lower Bound (ELBO) to learn latent representations by approximating the intractable posterior distribution; in contrast, Generative Adversarial Networks (GANs) are based on game theory concepts, specifically involving a minimax game between a generator and a discriminator. It is clear that each of the underlying statistical methods needs a different approach when evaluating the model’s performance and deals differently with variable sources of uncertainty. Thus, we aim to extend the previous review on this subject and better understand which current trends regarding evaluation methodologies and uncertainty quantification challenges are critical for applying these models to complex tasks like optimal control in power systems.

One key challenge in the application of generative AI to power system control lies in the absence of standardized evaluation benchmarks. This lack of standardization makes it difficult to objectively assess and compare the performance and accuracy of different generative models, especially when considering the unique characteristics of power system applications. Furthermore, the inherent uncertainty present in power systems, arising from various sources such as measurement errors and model stochasticity, complicates the evaluation process. Current methods often fail to adequately account for these diverse uncertainty sources, making it challenging to quantify their impact on model performance and to perform meaningful comparative analyses between different generative model architectures. A clear understanding of how evaluation metrics relate to the underlying statistical structure of these models is also lacking.

In this light, the current paper addresses these challenges by providing a comprehensive review of existing evaluation metrics for generative models applied in various power system tasks. We analyze how these metrics align with the statistical properties of the models and explore their strengths and limitations. We also examine different sources of uncertainty, distinguishing between uncertainties inherent to the learning model (e.g., stochastic policies in reinforcement learning), those arising from measurement errors, and other potential sources. We discuss methods for quantifying and characterizing these uncertainties, aiming to provide a more rigorous framework for evaluating generative models used in power systems applications and the new uncertainties they introduce. The main contributions of this work, outlined below, aim to bridge the existing gaps in this domain and provide new insights regarding possible applications of generative models for power systems tasks:

1.

This paper provides a comprehensive review and analysis of evaluation metrics for generative models, specifically applied to power system optimal control problems, addressing the current lack of standardized benchmarks. We examine the relationship between evaluation metrics and the underlying statistical properties of generative models and highlight the strengths and limitations in different assessment tasks.

2.

This paper also presents a systematic investigation and categorization of the primary sources of uncertainty in power system applications of generative AI, including model-inherent stochasticity and measurement errors, and discusses methods for quantifying these uncertainties.

2. Technical Background

Generative models are a class of unsupervised machine learning algorithms that learn the underlying probability distribution of a training dataset. Unlike discriminative models that predict labels, generative models aim to generate new data instances that plausibly originate from the same distribution as the training data. This is achieved by learning to model the complex dependencies and patterns within the data. Common examples include Variational Autoencoders (VAEs), Generative Adversarial Networks (GANs), General Purpose Transformers (GPTs), and Diffusion models, as presented in Figure 1.

2.1. Autoregressive Models

An autoregressive model is a representation of a type of random process. As such, it can be used to describe certain time-varying processes. The autoregressive model specifies that the output variable depends linearly on its own previous values and on a stochastic term; thus, the model is in the form of a stochastic difference equation. By modeling the conditional dependency between consecutive data points, autoregressive models enable sequential generation and prediction tasks. Modern autoregressive architectures like Transformers have significantly advanced the field by addressing challenges in capturing long-range dependencies. In the context of time series applications, autoregressive models predict values like stock prices, energy consumption, or weather data. For example, given a sequence $\{x_1,x_2,\dots ,x_t\}$, the task is to estimate $P\left(x_{t+1}\right|x_t,x_{t-1},\dots )$. These models are often combined with neural network structures that adapt to nonlinear patterns in the data.

Transformers are a widely used class of autoregressive architectures. The Transformer architecture, introduced in [3], is a deep learning model that relies on the self-attention mechanism to process input sequences in parallel. The encoder maps an input sequence of symbol representations $(x_1,\dots ,x_n)$ to a sequence of continuous representations $z=(z_1,\dots ,z_n)$. Given z, the decoder then generates an output sequence $(y_1,\dots ,y_m)$ of symbols one element at a time. The Transformer is composed of two modules, the encoder and the decoder. The encoder is composed of a stacked identical layers. Each layer has two sublayers, a multihead self-attention mechanism, and the second is a fully connected feed-forward network. Around each of the two sublayers a residual connection is added, followed by layer normalization. To facilitate these residual connections, all sublayers and embedding layers produce outputs of a constant size. The decoder is also composed of stacked identical layers. The structure of the decoder consists of the two sublayers in each encoder layer, and in addition, it has a third sublayer. The additional sublayer is used to perform multihead attention over the output of the encoder stack. Similar to the encoder, there are residual connections around each of the sublayers, followed by layer normalization.

The attention mechanism is based on an attention function. Essentially, this function maps a query and a set of pairs consisting of keys and values to an output. The attention function is computed on a set of queries simultaneously, packed together into a matrix Q. The keys and values are also packed together into matrices K and V. Intuitively, the query matrix Q represents the core of the question, highlighting what to pay attention to in the input. It typically corresponds to the input at a specific position in the sequence (e.g., a word or token). The keys serve as descriptors or tags of all inputs, encoding the features each position offers for potential attention. This is used to determine how relevant each input is to the query as a whole. Finally, the values represent the actual information contained at each position in the sequence. The output is computed as a weighted sum of the values, where the weight assigned to each value is computed by a compatibility function of the query with the corresponding key. This mechanism is illustrated in Figure 1.

Consider a simple example of the sentence “Renewable energy sources are unreliable”. For this toy example, each token will be coded depending on whether it is a subject or an object. Thus, $Q,K$ are binary vectors, their size will be denoted by $d=2$, and V is initialized randomly, as presented in

Table 1. Example of attention calculation for the sentence “Renewable energy sources are unreliable”. For each token (word or term in the sentence), the initial values of the vectors $Q,K,V$ are presented.

Token	Query	Key	Value
Renewable energy sources	[1, 0]	[1, 0]	[10, 0]
are	[0, 1]	[0, 1]	[5, 5]
unreliable	[1, 1]	[1, 1]	[0, 10]

.

Now we can compute the relevance of each input to the whole series, by performing a dot product between the queries and the keys. For instance, for the word “unreliable” with $Q=[1,1]$, the relevance will be computed as follows: $R=Q·K^{\mathrm{T}}=\left[\begin{array}{cc}1& 1\end{array}\right]·\left[\begin{array}{cc}1& 0\\ 0& 1\\ 1& 1\end{array}\right]=\left[\begin{array}{c}1\\ 1\\ 2\end{array}\right]$. This results in a relevance value of 1 for the tokens “Renewable energy sources” and “are” and a relevance value of 1 for the token “unreliable”. Next, the relevance values are scaled by the factor of $\sqrt{d}$, and then a softmax function is applied on these scaled weights. The resulting attention weights are $W=\mathrm{Softmax}\left({\displaystyle \frac{R}{\sqrt{d}}}\right)=\left[\begin{array}{c}0.25\\ 0.25\\ 0.5\end{array}\right]$. Fundamentally, this result means that the most focus (50%) is on “unreliable”, and the rest is divided equally between “renewable energy sources” and “are”. Finally, the output is computed by a dot product between the attention weights and the values $O=W·V=\left[\begin{array}{ccc}0.25& 0.25& 0.5\end{array}\right]·\left[\begin{array}{cc}10& 0\\ 5& 5\\ 0& 10\end{array}\right]=\left[\begin{array}{cc}5& 6.25\end{array}\right]$. The output vector O represents a processed semantic embedding for the word “unreliable”. In practice, the matrices $Q,K,V$ are learnable embeddings and are updated during the training process.

Transformers process fixed-length sequences, in which input tokens are first embedded into dense vector representations. Since the model processes sequences in parallel and lacks inherent order, positional encodings are added to these embeddings to encode the relative location of the tokens. Naturally, the self-attention mechanism can be extended to attend to multiple positions in the input sequence simultaneously. Each attention head processes a different part of the input sequence, and their outputs are concatenated and passed through a feed-forward layer. The Transformer architecture serves as the fundamental architecture for a family of contextual learning models. In particular, a well-known extension is the Generative Pretrained Transformer. This architecture uses the decoder structure present in the Transformer model, where there is causal relation between consecutive elements in the input series. This is achieved through autoregressive masking of the attention mechanism. The model is trained on large-scale data, with loss minimized over a sequence $x_{1:T}$ as $\mathcal{L}=-{\sum }_{t=1}^{T}logP\left(x_t\right|x_{1:t-1})$.

2.2. Variational Autoencoders

Variational Autoencoders (VAEs) are a class of probabilistic generative models designed to learn a latent representation of data while enabling data generation. Unlike standard autoencoders, VAEs incorporate a probabilistic framework to encode input data into a distribution, allowing for stochastic sampling from the learned latent space.

The latent space in VAEs is continuous, facilitating smooth interpolation and the generation of new samples. Each input x is mapped to a distribution in the latent space, typically modeled as a Gaussian with mean $\mu$ and standard deviation $\sigma$. The decoder then reconstructs data from sampled latent variables $z\sim \mathcal{N}(\mu ,\sigma )$.

The VAE algorithm aims to minimize the Evidence Lower Bound (ELBO). This metric takes into consideration reconstruction accuracy and a regularization term, encouraging the latent variables to follow a prior distribution. The ELBO is expressed as

$${\mathbb{E}}_{q\left(z\right|x)}[logp\left(x\right|z)]-\mathrm{KL}\left(q\left(z\right|x)\right|\left|p\left(z\right)\right),$$

(1)

where KL is the Kullback–Leibler divergence between the approximate posterior $q\left(z\right|x)$ and the prior $p\left(z\right)$. The fundamental operation mechanism of the VAE architecture is illustrated in Figure 1.

2.3. Generative Adversarial Networks

The structure of adversarial networks, first presented in [4], relies on interaction between two adversarial modules. These modules represent a generative model pitted against an adversary. This adversary is a discriminative model that learns to determine whether a sample is from the model distribution or the original data distribution.

We denote the generator by G and the discriminator by D. The generator creates synthetic data, while the discriminator distinguishes between real and generated data. The adversarial process pushes the generator to produce more realistic samples over time. This game-theoretic framework gives rise to a minimax optimization problem:

$$\underset{G}{min}\underset{D}{max}{\mathbb{E}}_{x\sim p_{\mathrm{data}}}[logD\left(x\right)]+{\mathbb{E}}_{z\sim p_z}[log(1-D\left(G\left(z\right)\right))],$$

(2)

where $p_{\mathrm{data}}$ is the distribution of real data and $p_z$ is the prior distribution (e.g., Gaussian) sampled by the generator. However, this architecture has some drawbacks. For instance, the generator may produce data with limited diversity, often referred to as “mode collapse”. Other challenges that require special care are nonconvergence, and vanishing gradients. The fundamental operation mechanism of the GAN architecture is illustrated in Figure 1.

2.4. Diffusion Models

Diffusion models are a class of generative models that are inspired by evolutionary processes to generate data [2,5]. They define a Markov chain of diffusion steps to slowly add random noise to data and then learn to reverse the diffusion process to construct desired data samples from the noise.

We are given a data point sampled from a real data distribution ${\mathbf{x}}_{0}q\left(\mathbf{x}\right)$ and a forward diffusion process in which we add noise to the sample in T steps. The amount of noise added at each time step is controlled by the variables ${\beta }_1,\dots ,{\beta }_T$. This process produces a sequence of noisy samples ${\mathbf{x}}_1,\dots ,{\mathbf{x}}_T$. Mathematically, this process may be described as

$$\begin{array}{cc}\hfill q({\mathbf{x}}_{1:T}\mid {\mathbf{x}}_0)& =\prod _{t=1}^{T}q({\mathbf{x}}_t\mid {\mathbf{x}}_{t-1}),\hfill \\ \hfill q({\mathbf{x}}_t\mid {\mathbf{x}}_{t-1})& =\mathcal{N}({\mathbf{x}}_t;\sqrt{1-{\beta }_t}{\mathbf{x}}_{t-1},{\beta }_t\mathbf{I}).\hfill \end{array}$$

(3)

A notable property of the forward process is that it admits sampling ${\mathbf{x}}_t$ at an arbitrary timestep t in closed form: using the notation ${\alpha }_t:=1-{\beta }_t$ and ${\overline{\alpha }}_t:={\prod }_{s=1}^t{\alpha }_s$ results in

$$q({\mathbf{x}}_t\mid {\mathbf{x}}_0)=\mathcal{N}({\mathbf{x}}_t;\sqrt{{\overline{\alpha }}_t}{\mathbf{x}}_0,(1-{\overline{\alpha }}_t)\mathbf{I}).$$

(4)

Diffusion models are probabilistic models where the observed data are explained using hidden variables, as illustrated in Figure 1. These latent variables capture some underlying structure or properties of the data that are not directly observable. Models of the form $p_{\theta }\left({\mathbf{x}}_0\right):=\int p_{\theta }\left({\mathbf{x}}_{0:T}\right)d{\mathbf{x}}_{1:T}$, where ${\mathbf{x}}_1,\dots ,{\mathbf{x}}_T$ are latent variables that describe the data as they transition through progressively noisier states in the forward process. These variables have the same dimensionality as the original data ${\mathbf{x}}_0\sim q\left({\mathbf{x}}_0\right)$. The joint distribution $p_{\theta }\left({\mathbf{x}}_{0:T}\right)$ is called the reverse process, and it is defined as a Markov chain with learned Gaussian transitions starting at $p\left({\mathbf{x}}_T\right)=\mathcal{N}({\mathbf{x}}_T;\mathbf{0},\mathbf{I})$:

$$\begin{array}{cc}\hfill p_{\theta }\left({\mathbf{x}}_{0:T}\right)& =p\left({\mathbf{x}}_T\right)\prod _{t=1}^T{p}_{\theta }({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t),\hfill \\ \hfill p_{\theta }({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t)& =\mathcal{N}({\mathbf{x}}_{t-1};{\mu }_{\theta }({\mathbf{x}}_t,t),{\Sigma }_{\theta }({\mathbf{x}}_t,t)).\hfill \end{array}$$

(5)

The training process aims to optimize the following loss function:

$${\mathbb{E}}_q\left[D_{\mathrm{KL}}(q({\mathbf{x}}_T\mid {\mathbf{x}}_0)\parallel p_{\theta }\left({\mathbf{x}}_T\right))\right]+\sum _{t=1}^T{\mathbb{E}}_q\left[D_{\mathrm{KL}}(q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t,{\mathbf{x}}_0)\parallel p_{\theta }({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t))\right]-log{p}_{\theta }({\mathbf{x}}_0\mid {\mathbf{x}}_1),$$

(6)

where conditionals can be written in closed form as

$$\begin{array}{cc}\hfill q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t,{\mathbf{x}}_0)& =\mathcal{N}({\mathbf{x}}_{t-1};{\tilde{\mu }}_t({\mathbf{x}}_t,{\mathbf{x}}_0),{\tilde{\beta }}_t\mathbf{I}),\hfill \\ \hfill {\tilde{\mu }}_t({\mathbf{x}}_t,{\mathbf{x}}_0)& ={\displaystyle \frac{\sqrt{{\overline{\alpha }}_{t-1}}{\beta }_t}{1-{\overline{\alpha }}_t}}{\mathbf{x}}_0+{\displaystyle \frac{\sqrt{{\alpha }_t}(1-{\overline{\alpha }}_{t-1})}{1-{\overline{\alpha }}_t}}{\mathbf{x}}_t,\hfill \\ \hfill {\tilde{\beta }}_t& ={\displaystyle \frac{1-{\overline{\alpha }}_{t-1}}{1-{\overline{\alpha }}_t}}{\beta }_t.\hfill \end{array}$$

(7)

Figure 2 demonstrates this idea.

2.5. Evaluation Metrics

The tasks machine learning models are engaged in in the context of power systems, may be sometimes less interpretable and intuitive in comparison to other domains such as vision or natural language processing. While in vision the goal is often clearly defined (e.g., accurate image classification), in power systems, the specific task can be more ambiguous and challenging to formulate. This ambiguity in task definition directly impacts the evaluation of the model’s performance. For instance, in vision, a simple accuracy metric might suffice, but in power systems, the “best” metric is often unclear. For example, when predicting grid instability, is it more important to minimize false positives (predicting instability when it does not occur) or false negatives (failing to predict actual instability)? The relative costs of these errors are vastly different, and the optimal balance depends on the specific application. Consequently, designing an appropriate loss function that reflects these priorities becomes a significant challenge. A loss function that simply minimizes prediction error might not adequately capture the critical aspects of power system operation, making it difficult to train a model that truly addresses the underlying problem. In light of this challenge, it is clear that selecting an appropriate error metric for evaluating generative models in power systems is important, as it directly impacts the model’s reliability and applicability. The choice of metric should align with the specific task, whether it is forecasting electricity demand, simulating power grid stability, or generating synthetic time series data for renewable energy profiles. Importantly, the error metric should be suited to the characteristics of the data the model receives, ensuring meaningful assessment and avoiding misleading conclusions. For instance, consider a generative model that simulates load demand profiles based on historical data. If the model is evaluated using Mean Squared Error (MSE) but the underlying objective is to match the probability distribution of the real data rather than minimizing pointwise errors, the evaluation may be misleading. In such cases, a distributional metric like the Wasserstein Distance or Maximum Mean Discrepancy (MMD) would be more appropriate. Using an inadequate metric might indicate a model performs well in a certain aspect (e.g., minimizing squared errors) but fails at capturing the variability and stochastic nature of power demand, making it unreliable for downstream applications. To systematically evaluate generative models in power systems, in this paper we classify the error metrics into six main categories, each suited to specific tasks and data characteristics. One class is error metrics that calculate the distance to the desired outcome pointwise. These are used for quantifying absolute or relative errors between generated and actual values, making them suitable for estimation and prediction tasks in power systems. They are commonly used when generative models are trained to predict time series energy demand or supply. An example is the Mean Squared Error (MSE), which measures the average squared difference between predicted and actual values, calculated by $(1/n)·{\sum }_{i=1}^n{(y_i-{\widehat{y}}_i)}^2$, where y is the real value and $\widehat{y}$ is the estimation. Another such metric is the RMSE, which provides the error in original units and is calculated as the square root of the MSE metric; furthermore, the MAE calculates the average absolute deviation and is calculated by $(1/n)·{\sum }_{i=1}^n|y_i-{\widehat{y}}_i|$ and the MAPE represents the percentage error and is given by $(1/n)·{\sum }_{i=1}^n|(y_i-{\widehat{y}}_i)/y_i|\times 100$. The second category, often used for measuring the quality of the fit and variability, uses statistical performance metrics. These metrics assess how well the generated data match the real data in terms of statistical properties. These are essential in time series reconstruction and validation. Metrics such as the coefficient of determination $R^2$ measure the proportion of variance explained by the model and are given by $R^2=1-\sum \left({(y_i-{\widehat{y}}_i)}^2\right)/(\sum {(y_i-\overline{y})}^2)$, where $\overline{y}$ is the mean of the labels y. In addition, Mean Deviation (MD) quantifies systematic bias. Using Autocorrelation helps assess dependencies in time series forecasting, while the Stationarity Measure (STA) evaluates the stability of the series over time. The third category includes classification metrics, which are useful for evaluating classification models in fault detection, event classification, and anomaly detection in power systems. These include the F1-score, which balances precision and recall as follows: $F1=2\times (\mathrm{Precision}\times \mathrm{Recall})/(\mathrm{Precision}+\mathrm{Recall})$. recall (true positive rate), precision, and the AUC (Area Under the Curve) assess the classification ability over different thresholds. Additionally, the Matthews Correlation Coefficient (MCC) is particularly useful for imbalanced datasets where traditional accuracy measures fail. The fourth category addresses probability-based metrics for distribution comparisons. This class of metrics focuses on uncertainty quantification and distribution matching, which is essential in probabilistic forecasting. Metrics like the Continuous Ranked Probability Score (CRPS) evaluate how well predicted distributions match actual outcomes, while the Kolmogorov–Smirnov (KS) test compares two cumulative distributions. Maximum Mean Discrepancy (MMD) and Wasserstein Distance measure the similarity between generated and real distributions, which is vital when assessing probabilistic generative models. The fifth category is mainly used for event-based analysis and is applicable for both decision-making and the simpler form of detection tasks. The metrics in this category are often used in applications such as power grid protection, fault detection, and stability control. These metrics assess decision-making accuracy and include Decision Accuracy (DA), Probability of False Alarm (PFA), and Threshold Utility Rate (TUR), which determine how well a model performs under real-world constraints. The final category aggregates metrics that are used for cross-validation. This class is used to evaluate model robustness under different data splits and training variations. Leave-One-Out Cross-Validation (LOO-CV) tests the model by excluding each sample individually, while the Diebold–Mariano (DM) test compares the forecast accuracy of two models, providing a statistical basis for selecting the best-performing approach. Rationally, the choice of the adequate evaluation metric should be driven by the specific application context. For instance, forecasting tasks may benefit from probabilistic evaluation measures such as CRPS and entropy-based criteria, which account for uncertainty in predictions. From another angle, synthetic data generation requires metrics that assess distributional similarity, such as Maximum Mean Discrepancy or Kullback–Leibler Divergence. An illustration presenting this categorical classification of evaluation metrics is presented in Figure 3.

2.6. Nature of Uncertainty and Uncertainty Classification

Uncertainty may be understood differently between power systems researchers and machine learning researchers. Thus, to bridge the gap between these two disciplines, there is a clear need to better understand how to categorize and quantify uncertainty. A natural question that comes to mind in this context is where different types of uncertainty arise. Essentially, for power experts, the nature of uncertainty is inherent in the physical system. The production, transmission, and distribution depend, naturally, upon the electricity demand. However, different consumers have their unique consumption patterns, which vary from day to day, and even they cannot always predict what it will look like. Moreover, the adoption of renewable energy sources and their increasing share in the overall production introduces additional uncertainty that stems from changing and unpredictable weather conditions, which make these sources intermittent and unreliable. Continuing this line of thinking, problems that are concerned with electricity price stability and policy design in energy markets also have a shade of uncertainty. In these scenarios, the market forces depend, again, on the behavior of many consumers, who are sometimes led by intuition, mood, and other factors that vary at each moment and cannot be anticipated. Furthermore, even in power system problems that have no inherent uncertainty, when gathering the data of different parameters such as voltage or current, the precision of measurement device limits our knowledge of the truth and gives us, in a sense, a partial observation of the real state of the system. Those types of uncertainties are often grouped together and categorized as “aleatoric uncertainty”.

The interpretation of uncertainty is somewhat different in the machine learning community, since machine learning experts will mostly link uncertainty to the scarcity of data. Due to security requirements, and several other reasons, the measurements of key properties of different power system problems are very limited. This causes a lack in high-fidelity data and quality data, which in turn creates a biased, and often unreliable, machine learning model due to limited training data and limited capability of generalization. This type of uncertainty is often referred to as “epistemic uncertainty”. This fact also causes another type of uncertainty, which arises due to a lack of data for rare faults or transients and is called “data-driven uncertainty”. Finally, it is often beneficial to use stochastic elements in the training process of a model, which may enhance its ability to generalize and avoid situations like overfitting. However, this may cause some errors in the output of the model. The uncertainty created by these errors, which the generative model itself introduces, is classified as “model-generated uncertainty”. These ideas are further illustrated in Figure 4.

3. Review of Existing Research Works

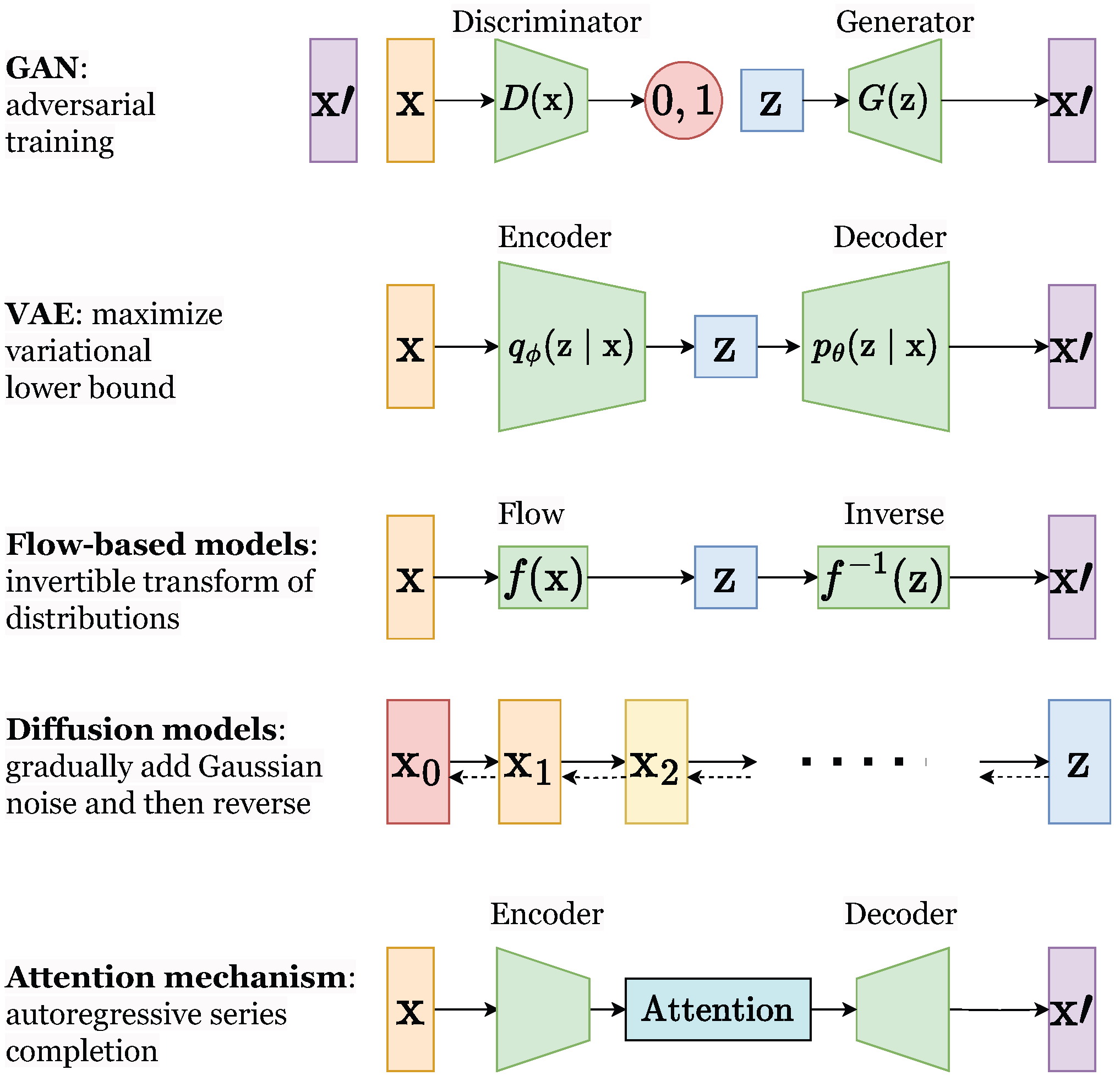
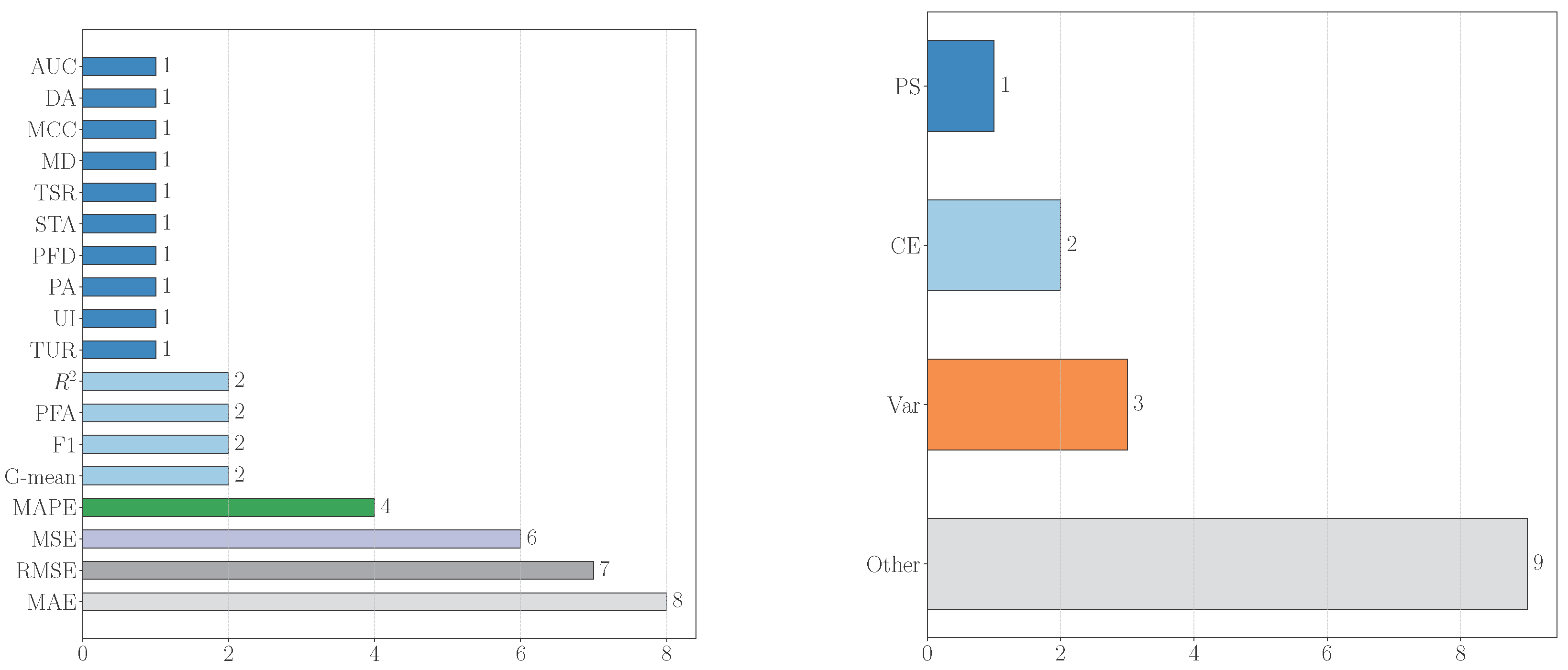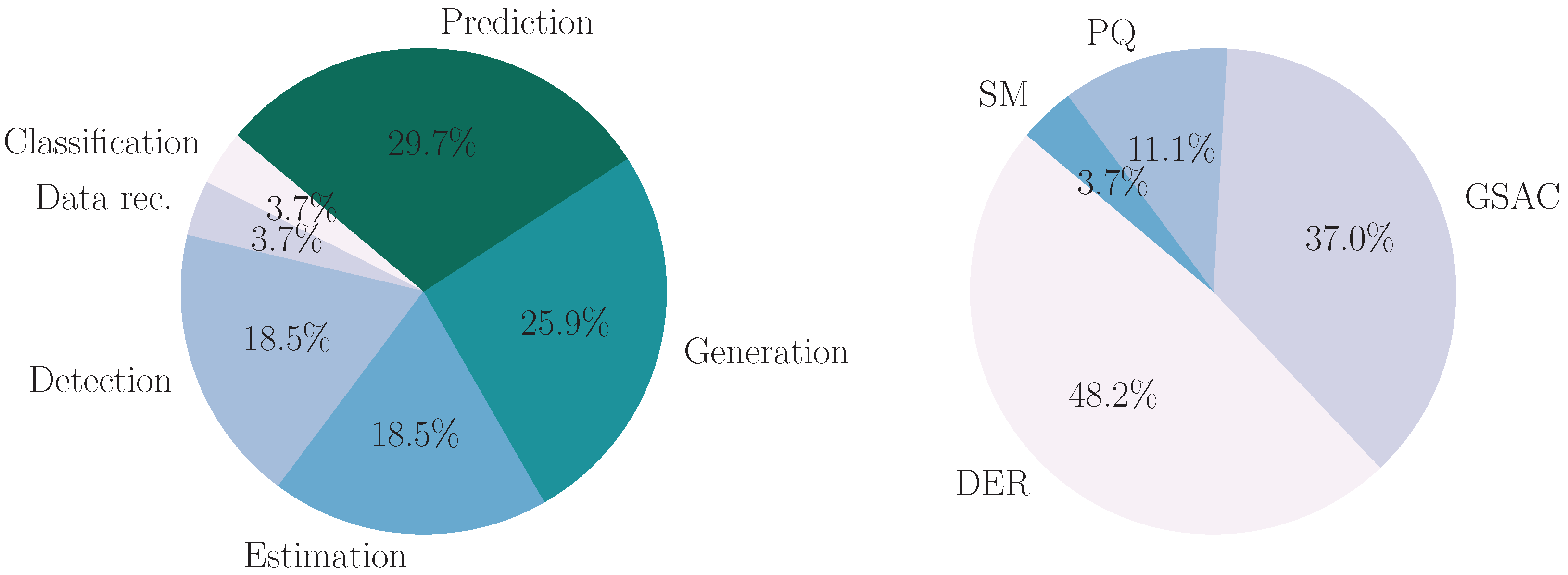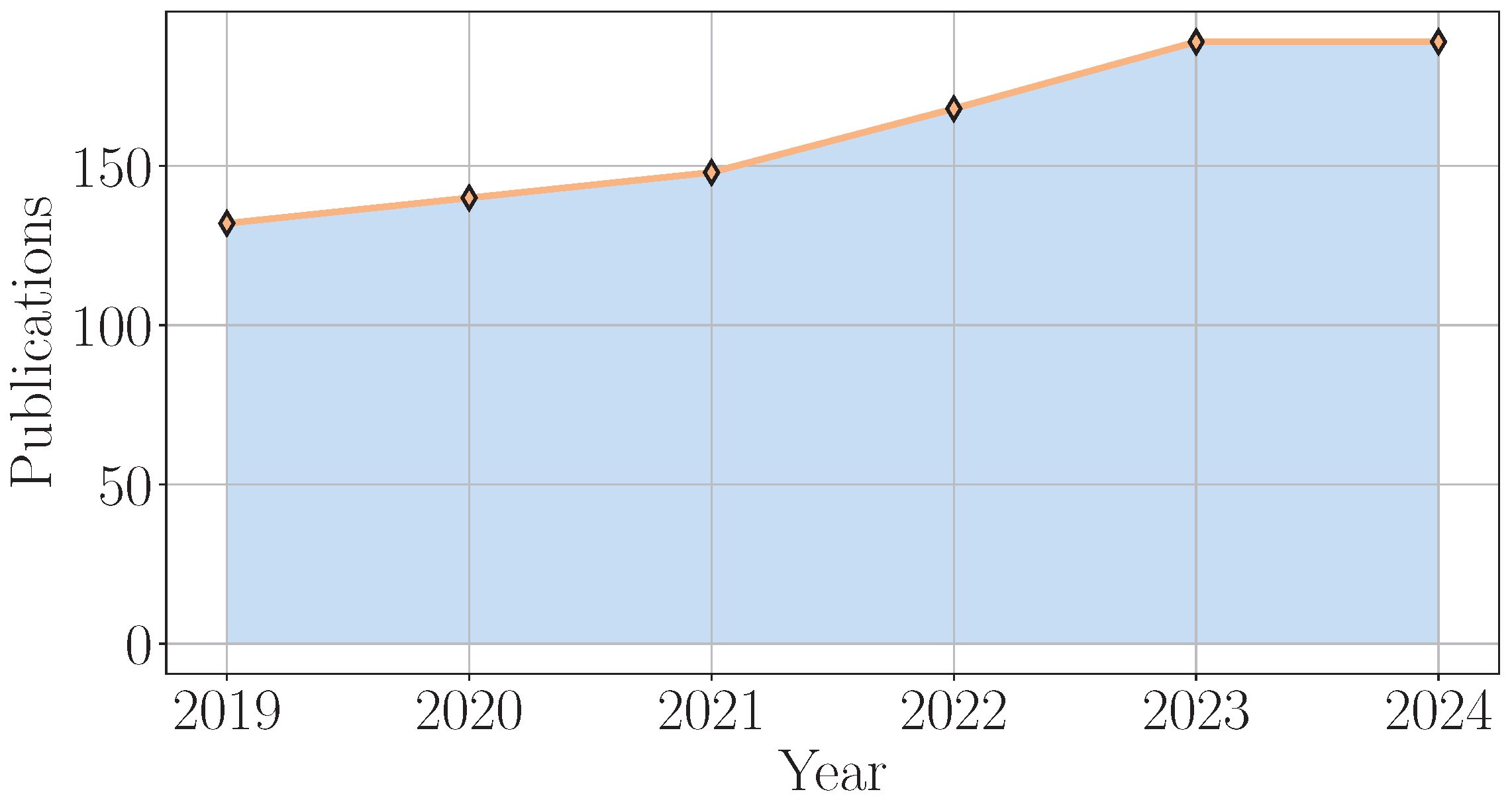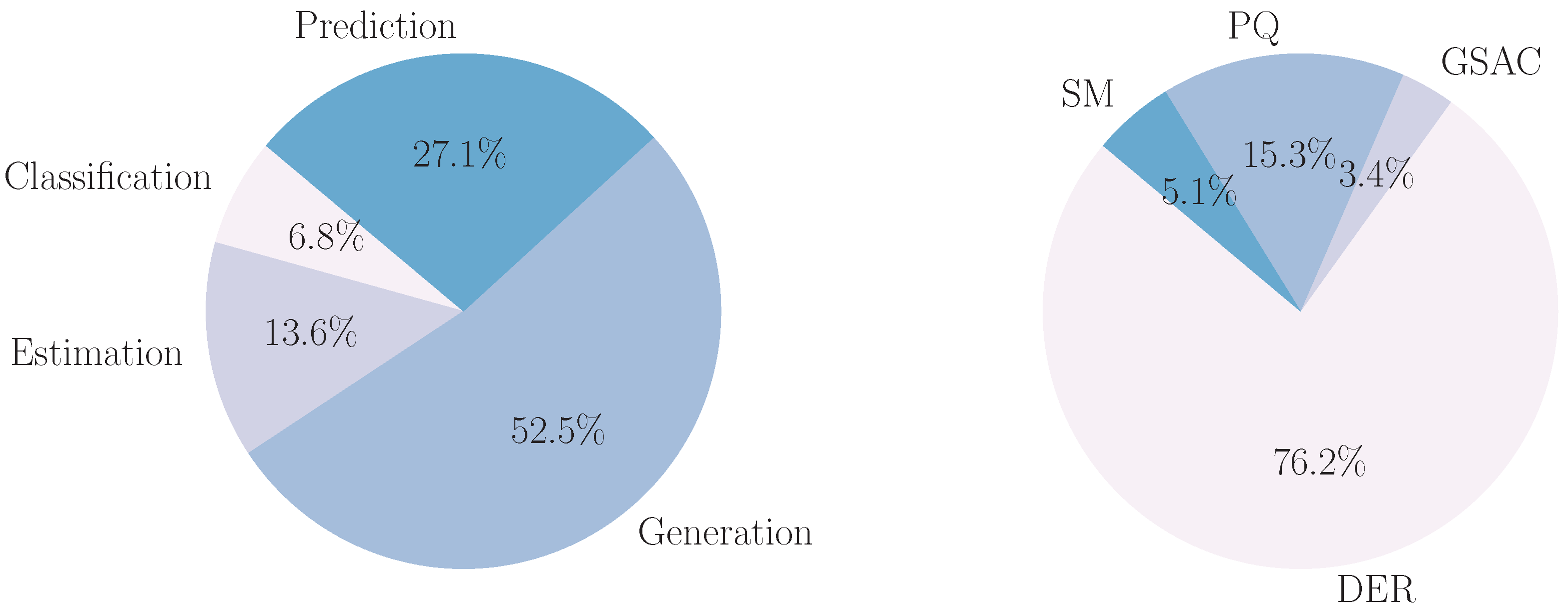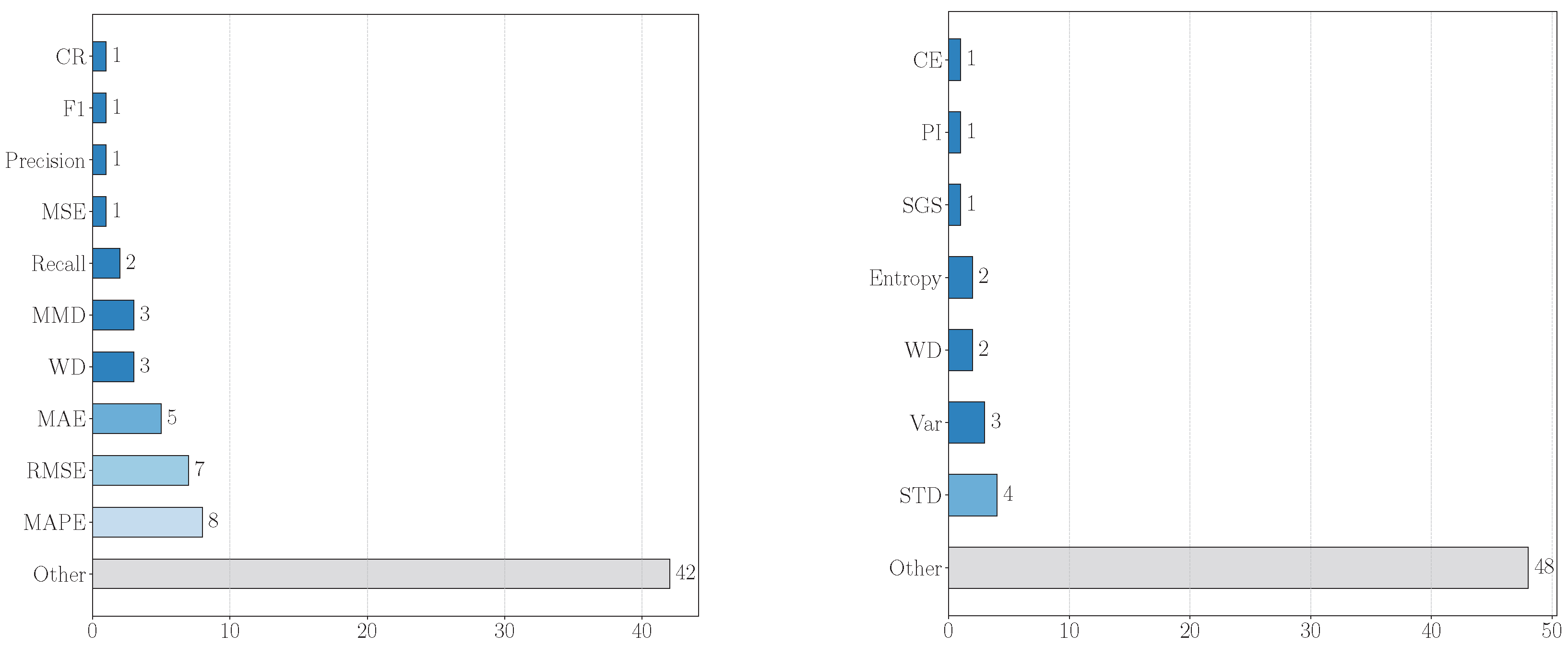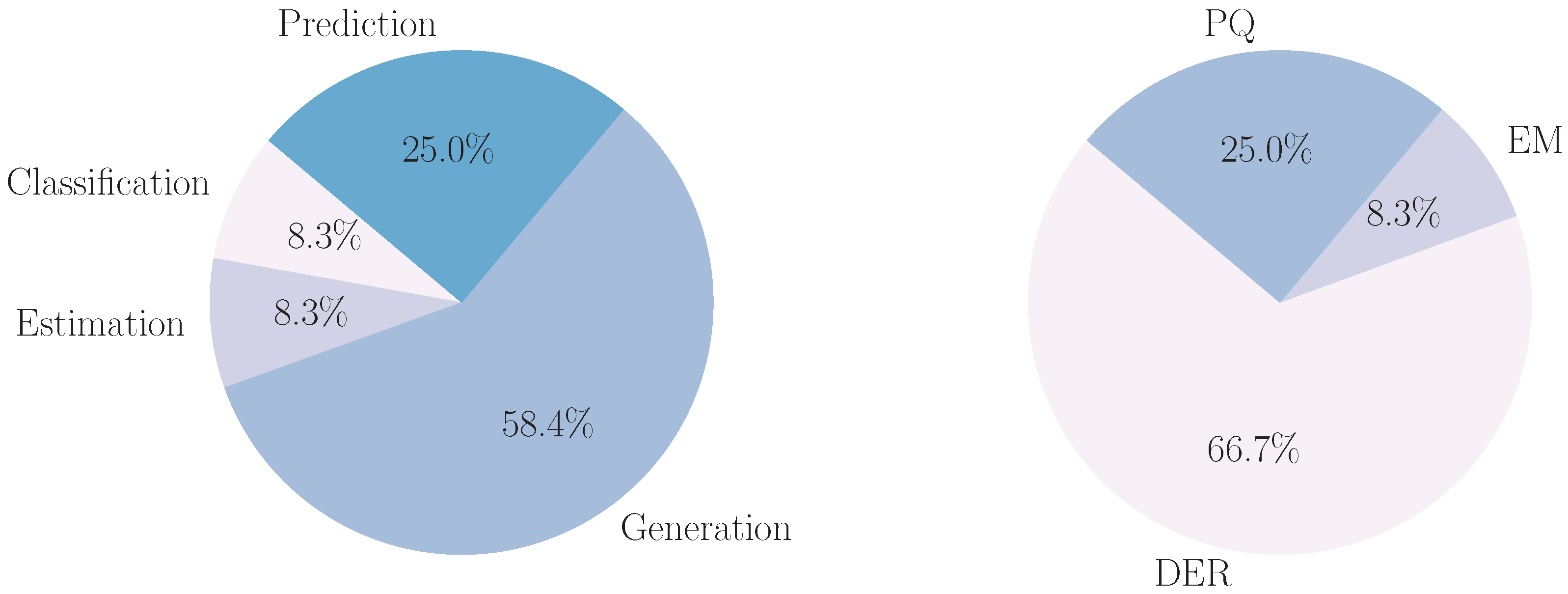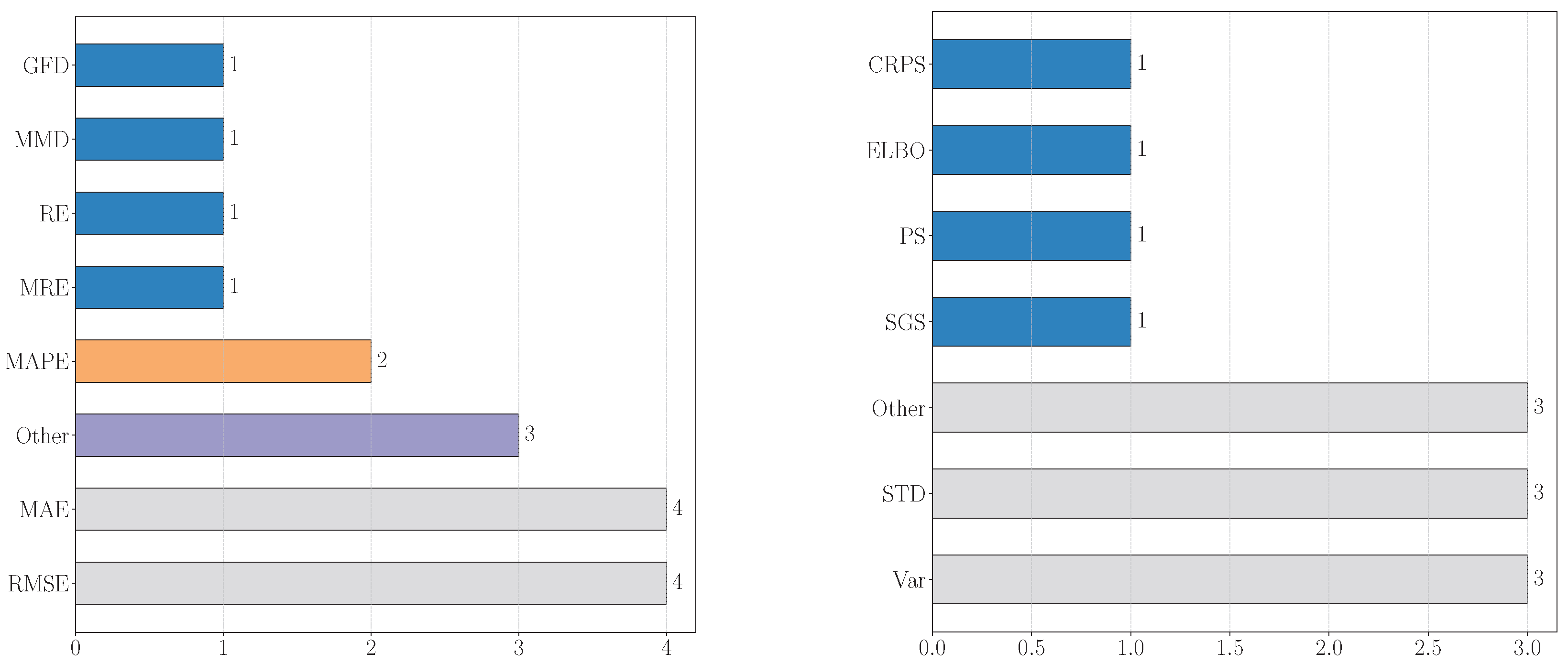3.1. Autoregressive Models

Autoregressive models, leveraging the chain rule of probability, decompose the joint distribution of a sequence into a product of conditional distributions. This approach allows for the generation of data points conditioned on preceding values, making them suitable for modeling time series data prevalent in power systems. This section reviews the application of autoregressive models, including specific architectures like Transformers, in addressing key challenges within the power domain.

Following the fundamentals of autoregressive modeling, several studies have investigated their application in generating synthetic power system data and scenarios for a variety of purposes. For instance, in [7], the authors describe an approach to real-time optimal power flow (OPF) that incorporates linguistic stipulations. This is achieved by integrating a Generative Pretrained Transformer (GPT) agent with deep reinforcement learning (DRL). The GPT agent interprets qualitative objectives and constraints based on linguistic stipulations as rewards, which are then optimized using a DRL process. This method allows traditionally unquantifiable linguistic stipulations expressed in natural language to be directly modeled as objectives and constraints in the OPF problem. The DRL agent can then solve the OPF model in real time, providing dispatch decisions that are interpretable with language outputs.

In addition to generating data, autoregressive models have been studied for prediction and forecasting tasks, which are of high interest for the efficient operation of power systems. Numerous studies have examined their application in this domain. One example is the work in [8], which proposes a CNN-LSTM model for enhancing the accuracy of steam turbine power prediction in co-generation systems. Short-term power load prediction is crucial for efficient energy management and should be more accurate. This model first uses a one-dimensional CNN to extract high-dimensional features from input data, then uses an LSTM layer to capture temporal correlations, and finally uses an attention mechanism to optimize the weights of the LSTM output. The model’s ability to focus on the most relevant features in the input data makes it robust to noise and missing data, and the results show more accurate and reliable predictions than traditional LSTM. In addition, study [9] proposes an attention-based CNN-LSTM-BiLSTM model for load forecasting in integrated energy systems (IESs). Load forecasting is becoming more difficult due to the combination of multiple energy sources and the nonlinear characteristics of the time series data. The CNN and attention block are used to extract the effective features of the model, and the LSTM-BiLSTM block is used to forecast the time-related data. The results have shown improved forecasting performance compared to CNN-BiLSTM, CNN-LSTM, BiLSTM, LSTM, BPNN, RFR, and SVR. Moreover, Ref. [10] presents a dual-stage attention-based Long Short-Term Memory (DA-QLSTM) network for short-term zonal electricity load probabilistic forecasting. The method integrates a feature attention-based encoder to identify the most relevant input features and a temporal attention-based decoder to capture temporal dependencies in load data. Utilizing the pinball loss function for probabilistic forecasting, the DA-QLSTM provides quantile-based predictions that capture uncertainties effectively. Case studies on the GEFCom2014 dataset demonstrate its superior performance in both point and probabilistic forecasting compared to state-of-the-art models. The model also automatically selects critical weather station data, enhancing accuracy while reducing irrelevant variables, making it robust under variable weather conditions and data uncertainties. In the same manner, work [11] introduces a novel method for short-term multienergy load forecasting in integrated energy systems (IESs). This method consists of a CNN-BiGRU model optimized by an attention mechanism to achieve more accurate load forecasting, one that considers fluctuations, randomness, and the coupling relationships of IESs. The model employs a one-dimensional CNN to extract complex features and a BiGRU to capture time dependencies from historical data. Attention modules are then applied to enhance key information, and a hard weight-sharing mechanism extracts multienergy coupling relationships. Finally, a multitask loss function with weight optimization is applied to balance the learning process across different energy types. The results indicate higher accuracy compared to LSTM models, especially in cooling, heat, and electrical load forecasting. Similarly, paper [12] introduces an innovative hybrid model, AMC-LSTM, for short-term wind power prediction. This model integrates an attention mechanism to dynamically assign weights to input physical features, Convolutional Neural Networks (CNNs) to extract short-term abstract features, and Long Short-Term Memory (LSTM) networks to identify long-term trends. By addressing redundancies in raw time series data and varying the importance of input features, the AMC-LSTM model achieves superior accuracy and stability compared to other models such as ARIMA, SVM, and CNN-LSTM. Tested on real-world wind turbine data from Inner Mongolia, the AMC-LSTM model demonstrated lower error rates and better alignment with actual wind power outputs, especially over extended forecasting horizons. This approach effectively supports grid management and decision-making in wind farms. On top of that, work [13] introduces a power forecast approach for centralized PV power plants based on a fusion LSTNet-Attn model. PV power forecasting is essential for the safe and economical operation of power systems, and prediction accuracy is important. This method combines a CNN, LSTM, attention mechanism, and autoregressive model to capture the short-term local dependencies and long-term trends in PV power data and weather factors. The effectiveness of the model is validated using data from a central PV plant, and the results demonstrate higher prediction accuracy and robustness compared to other methods. Correspondingly, work [14] proposes a new wind power forecasting system based on a dual-stage self-attention mechanism (DSSAM). An accurate and stable forecasting method is important for the optimized integration of large-scale wind power into the grid. This method consists of a feature decomposition module to remove noise, DSSAM to focus on important features, and GRU for forecasting with an ADAM-based optimization module. Results prove the developed feature decomposition module to be effective and the superiority of DSSAM over SSAM, of hybrid structures over single structures, and of deep learning models over linear ones. In a like manner, study [15] presents a hybrid ensemble deep learning framework for short-term photovoltaic (PV) power forecasting using Long Short-Term Memory (LSTM) networks with an attention mechanism. The method employs two LSTM models to process time series data on temperature and PV power output separately, followed by a fully connected layer to improve accuracy. The attention mechanism adaptively focuses on significant features within the LSTM hidden layers, enhancing forecasting performance. Experiments were conducted and compared with benchmark models like ARIMAX, Multilayer Perceptron (MLP), and traditional LSTM. The proposed method outperformed others across various time horizons, demonstrating superior accuracy and robustness.

From a different perspective, autoregressive models also contribute to estimation tasks, enabling the inference of critical system parameters. For instance, work [16] proposes a Graph Attention Network (GAT)-based node indispensability estimation (NIE) model to estimate the indispensability of specified nodes, which provides a risk early warning that the $n-1$ criterion is not satisfied under certain load conditions. Unlike existing methods, this mechanism uses partial state observations and does not require monitoring data from all system components. The model uses a GAT with a multihead attention mechanism and a residual structure, taking preprocessed node feature data as input to predict the indispensability of nodes in a power grid. A comparison between other models such as GCN and MLP is shown, and the model demonstrates superior accuracy and faster convergence. Another study concerning the same idea is [17], which proposes a new fault location model based on Bi-GRU and an attention mechanism that analyzes current data and extract fault features. Fault location techniques are used to maintain the stable operation of power systems and to quickly respond and restore the grid in case of a fault. Existing methods rely on the manual work of extracting the important features, a task that may not be performed accurately in large systems. The Bi-GRU is used in the method to retain the time characteristics in the signal, while the attention mechanism focuses on the signal changes near the fault, and a fault line location model is included as well to determine the fault position. The results show better accuracy of fault detection compared to traditional manual methods.

Furthermore, researchers have tried to employ autoregressive models for classification and detection tasks to aid in the identification of system events and anomalies. For example, work [18] introduces a Bi-LSTM attention mechanism model for transient stability assessment (TSA) in power systems, using voltage phasor data. The goal is to offer an improved TSA based on voltage phasor data in terms of accuracy and robustness. The method combines a Bi-LSTM network for feature extraction of time series voltage phasor data with an attention mechanism to weigh the importance of different time steps, improving the accuracy and robustness of the assessment. The results determine that the model outperforms other models (such as LSTM, Bi-LSTM, ANN, MLP, and SVM) in terms of accuracy and robustness. Furthermore, study [19] presents a novel method for classifying Power Quality Disturbances (PQDs) using a Cross-Attention Fusion of Temporal and Spatial Features (TSF-CAF) model. The method combines an improved SCINet architecture for temporal feature extraction and an adapted VGG16 model for spatial feature extraction, integrating these features with a cross-attention mechanism to enhance classification accuracy. PQD data were simulated and tested using a Python environment and hardware experiments, including synthetic and real-world disturbances. Results show an average classification accuracy of 95.01% under high noise (20 dB) conditions and 99.66% for hardware experiments. Comparative and ablation studies demonstrated the model’s superior performance in classification accuracy, convergence speed, and robustness to noise compared to other deep learning models. In addition, work [20] proposes a real-time transient stability early warning system for power grids using Graph Attention Networks (GATs) combined with Long Short-Term Memory (LSTM) networks. The system uses phasor measurement unit (PMU) data, including voltage phasors and frequency measurements, as inputs to predict transient instability. The network is trained and tested on synthetic data generated from simulations of the Nordic44 test system, incorporating variations in system topology and load. Results show that the proposed method achieves a missed detection rate of 2.21% and a false alarm rate of 8.20% under noisy conditions, with a maximum average early warning time of 9.61 cycles. The system’s performance is heavily influenced by the grid’s dynamic response to disturbances, demonstrating robustness under realistic conditions while offering significant potential for practical application in smart grids. Similarly, work [21] proposes an interpretable model based on the dual-attention mechanism and GRU for time-adaptive TSA. Deep learning use in TSA models can enhance their speed and accuracy, but their inexplicability makes them difficult to apply. This method uses a feature attention block to weigh the importance of input features and a time attention block to weigh the importance of different time steps, which are then fed into a GRU network. The model’s difficulty of training is reduced, the assessment speed is higher, and by the visualization of the feature attention block, instability patterns are identified, so the TSA rules learned by the proposed model can be understood. The results showed that the model outperforms other methods like GRU, DT, and SVM, with more than 95% of samples being evaluated at the first cycle after fault clearance. Moreover, work [22] proposes a data-driven framework for fault and abnormality detection in smart grids. Existing methods usually rely on a model and cannot capture complex temporal series. This method is based on a Bi-LSTM classifier with an attention mechanism to capture time-domain features and a 1D-CNN structure to extract frequency-domain features for prediction. Moreover, a frequency-based clustering algorithm is used to classify, in an unsupervised fashion, the signals into meaningful clusters. The method is also designed to be explainable, making it more suitable for real-world applications.

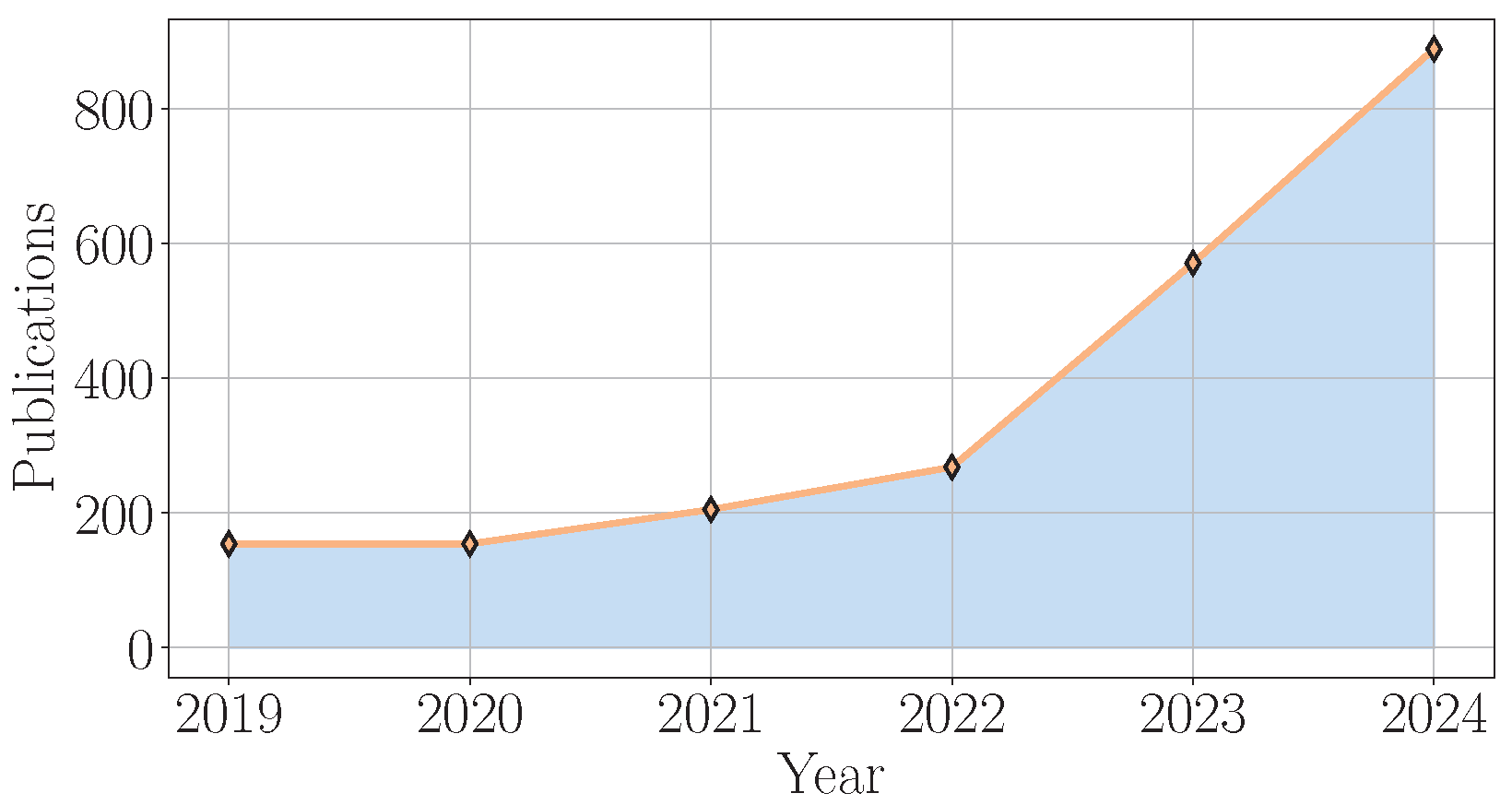
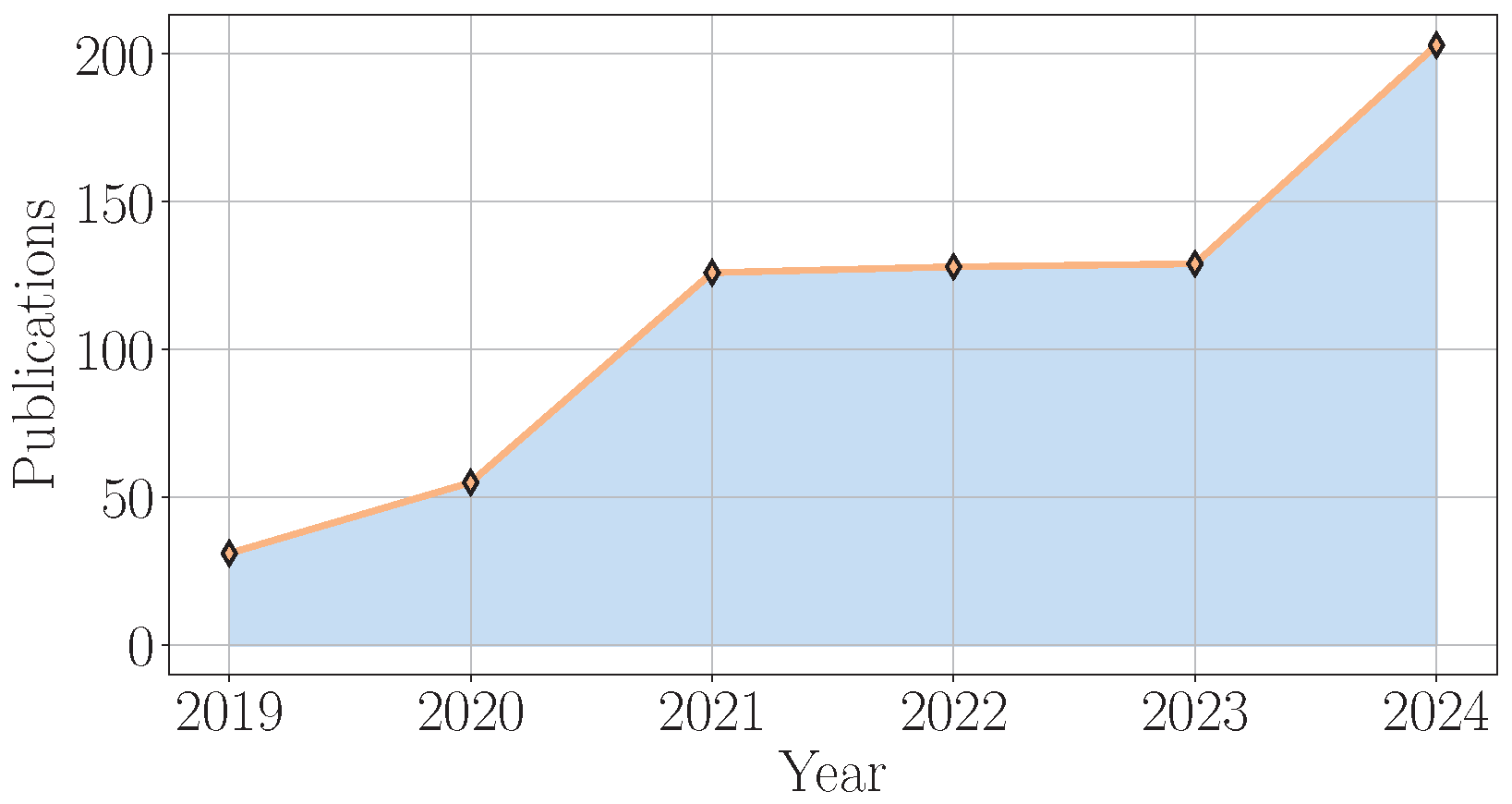
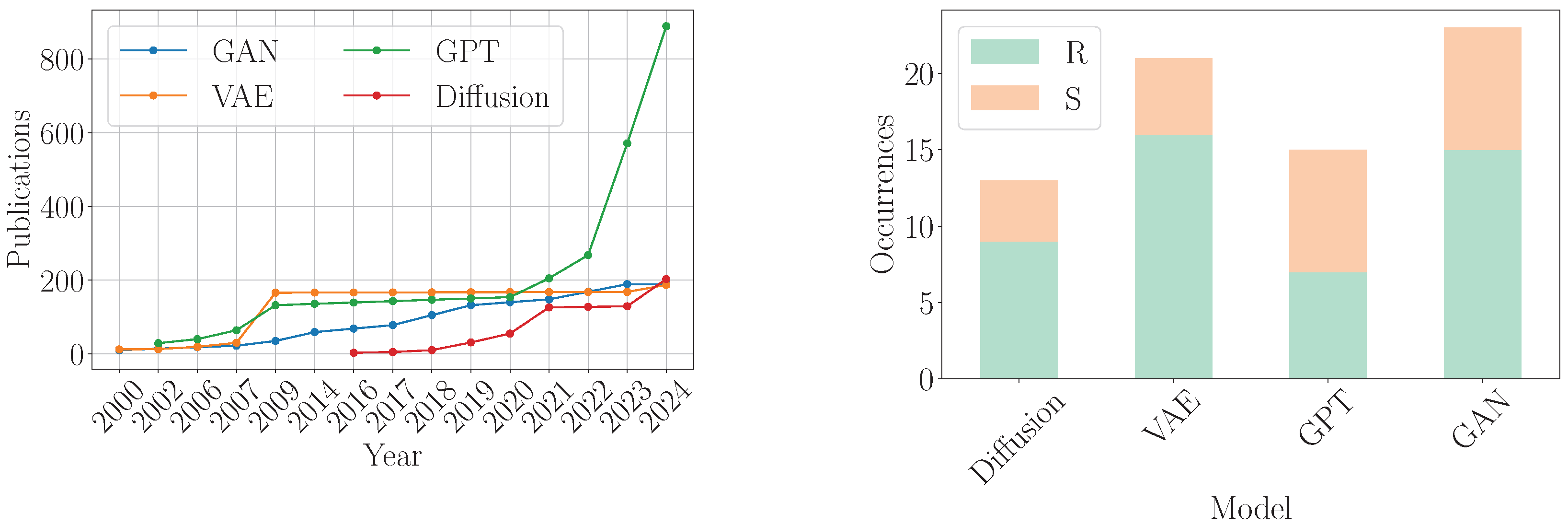
To conclude, as presented in Figure 5, there is an increasing interest, as shown by the growing number of research publications from 2019 to 2024, in applications of GPT models within the power systems domain. The number of publications shows a significant upward trend, starting at approximately 150 in 2019 and increasing to over 850 by 2024, indicating a growing interest and research activity in leveraging GPT models for power system challenges. 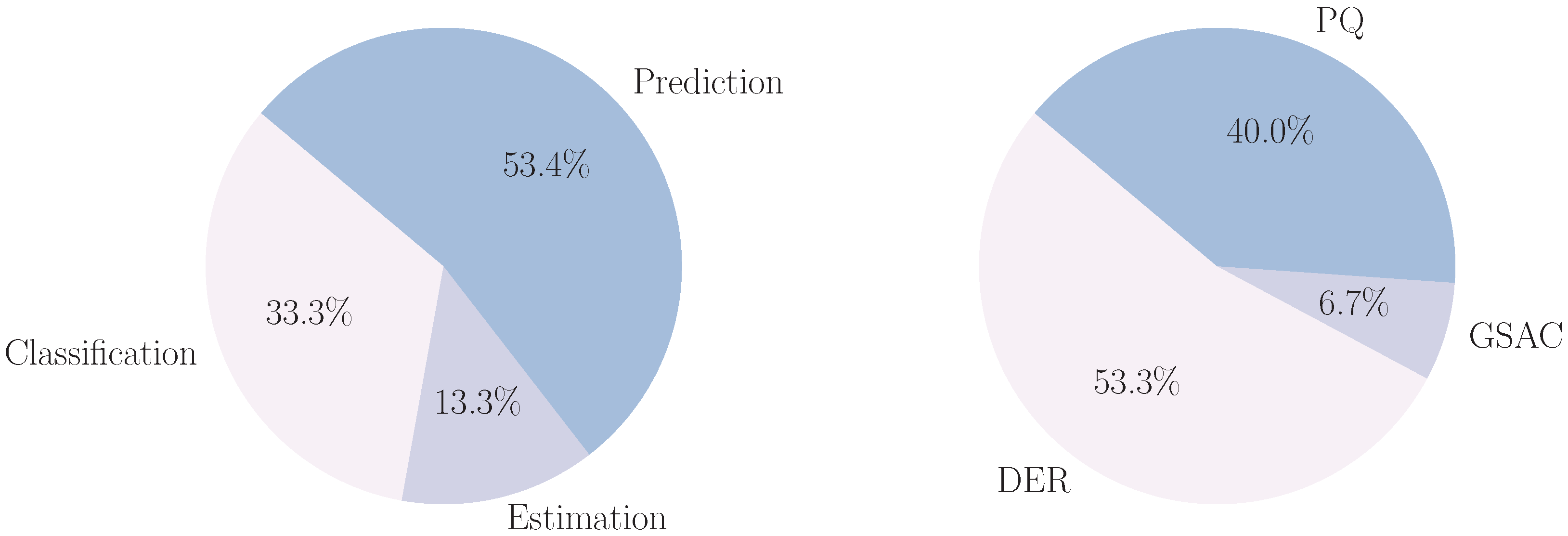Moreover, as shown in Figure 6, the left pie chart reveals the distribution of machine learning tasks where autoregressive models are employed in power systems, with prediction tasks being the most prevalent at 53.4%, followed by classification tasks at 33.3% and estimation tasks accounting for 13.3%. The right pie chart displays the distribution of power system applications utilizing autoregressive machine learning models, with DER (Distributed Energy Resources) representing the largest share at 53.3%, followed by PQ (Power Quality) at 40.0% and GSAC (Grid Stability and Control) at 6.7%. Finally, as may be viewed in Figure 7, the left bar chart shows that Mean Squared Error (MSE) is the most frequently used evaluation metric with a count of six, followed by Root Mean Squared Error (RMSE) with seven and Mean Absolute Error (MAE) with eight.The right bar chart indicates a relatively even distribution among the probability measurement metrics, with Cross Entropy, probability score, Variance, and a collection of other probability measurement metrics representing additional probability measurement metrics that were not covered in this review, each having a count of 10.

3.2. Variational Autoencoders

Variational Autoencoders (VAEs) are probabilistic generative models that learn latent representations of data using an encoder–decoder framework. By learning a compressed, probabilistic representation, VAEs can generate new samples and perform tasks such as dimensionality reduction and anomaly detection. This section explores the applications of VAEs in various power systems applications.

The generation of data, scenarios, and synthetic environments plays an important role in advancing power system research, development, and operation. Naturally, VAE architecture was explored for this category of applications, offering control over the generated samples through manipulation of the latent space. For instance, work [23] proposes a concentrating solar power (CSP) configuration method to determine the CSP capacity in multienergy power systems. CSP can provide flexibility for power systems, but due to its high construction cost, an evaluation of the configuration scheme is essential. The method employs a two-stage model, comprising a planning stage determining the capacity of CSP components and an operation stage evaluating costs in day-ahead and real-time periods using generated scenarios. To model uncertainty in the power system, the study utilizes an improved VAE (which has a hyperparameter that improves the performance), which learns from historical data and generates scenarios for the configuration model. The overall consideration of flexibility values makes CSP more economical in the configuration problem. Additionally, work [24] proposes a new VAE-BiLSTM method to reduce dimensionality arising from large volumes of data generation. The problem is derived from the growing use of advanced metering and smart sensing devices, leading to greater computing power and time for energy forecasting. This method generates encoded representations of given time series data to reduce computing resources and results in more accurate forecasting. A comparison between other variants of AEs and VAEs (including RNNs and LSTM) is shown, and in terms of forecasting accuracy, the method outperforms them. Another approach presented in [25] suggests the notion of a stochastic virtual battery (VB) model and a VAE-based algorithm to identify the probability distribution of the model’s parameters. VB models are used to represent flexible loads, which consist of uncertainties, making deterministic VB models impractical. As shown in the paper, the stochastic character of the method can better represent those flexible loads. Moreover, work [26] introduces an anomaly detection method that remains relatively insensitive to the moderate presence of anomalous data during training. Existing one-class-classifier-based methods suffer from performance degradation when training data contain anomalous samples, unlike this method. The method combines a VAE and LSTM-based RNN to utilize the data’s temporal relationships for unsupervised anomaly detection. To enhance the reparameterization trick in the VAE, an SVD of the wavelet coefficients found from the input’s high- and medium-frequency representation time series data is employed. Instead of an L2 norm-based cost function, a log cosh-based function is used. The effectiveness of generative models over clustering models in the context of anomaly detection for a sequential dataset is demonstrated, along with the proposed mechanism, whose results show improvement. Furthermore, the research in [27] addresses the challenge of generating representative multivariate load states for power systems when historical data are scarce. The proposed method utilizes a Conditional Variational Autoencoder (CVAE) to model high-dimensional dependencies and generate synthetic load data. Unlike traditional CVAE implementations, this approach incorporates sample-dependent noise during the generation process and co-optimizes noise parameters during training. Statistical tests and a multiarea adequacy case study on European load data demonstrate that the CVAE outperforms Gaussian copulas and Conditional GANs (cGANs) in reproducing multivariate dependencies and realistic tail distributions. The CVAE’s ability to condition generation on contextual variables, such as time of day, provides additional flexibility for targeted analysis. On top of that, work [28] introduces a VAE approach to generate electric vehicle (EV) loads. Existing methods rely on predefined probability distributions, and there is great significance in establishing an accurate load profile model of EV charging stations. This model, composed of deep convolution and transposed convolution networks, learns from original load profiles to encode and then decode data, generating new profiles. This method can generate EV loads of different times and spaces without manually specifying the probability distribution and setting many samples that fit this distribution. The method generates diverse profiles, which are classified, and only specific types remain, and from the results, the effective capture of the characteristics of the original data is shown. To continue this line of thinking, work [29] offers a VAE-based model for energy disaggregation—a tool for estimating the consumption of individual appliances from a single sensor that measures the total consumption of a building. This technique is called NILM (nonintrusive load monitoring), and although existing disaggregation algorithms are very accurate, they lack generalization capability, which is important for multistate appliances and different kinds of buildings. This model uses a probabilistic encoder to map information into a latent space and a decoder to reconstruct the power signal of the target appliance. The model uses an IBN-Net to enhance feature extraction and skip connections between the encoder and decoder to improve signal reconstruction. The proposed model was compared to state-of-the-art NILM approaches on the datasets and showed better results in detecting the target appliance and a more accurate reconstruction capability, especially for multistate appliances.

Another category of tasks in power systems concerns forecasting applications. In this context, VAEs can be utilized for probabilistic forecasting, which may provide not only point predictions but also uncertainty estimates. For instance, work [30] focuses on improving short-term solar photovoltaic (PV) power forecasting using a Variational Autoencoder (VAE)-based deep learning model, known for its strong performance in time series analysis and nonlinear modeling. The study compares the VAE approach against seven deep learning models, including LSTM, GRU, and RBM, and two traditional machine learning methods, logistic regression and support vector regression. Both single- and multistep-ahead forecasting are examined using data from two grid-connected PV systems in the US and Algeria. Results show that VAE consistently outperformed other methods in accuracy and robustness. This research highlights the potential of deep learning models, particularly VAEs, in enhancing solar power prediction to support efficient grid integration and management strategies. Study [31] introduces a novel approach for wind power forecasting using Variational Autoencoders (VAEs) combined with hybrid transfer learning for large-scale, multiregional wind farms. The method leverages pretrained features from one wind farm and fine-tunes them using small datasets from other wind farms, optimizing model training and reducing computational costs. The framework integrates MLP autoencoders for dimensionality reduction and feature extraction, followed by transfer learning to adapt models to diverse wind farm conditions. Empirical evaluations using three wind farm datasets demonstrate the method’s superior performance with MAE and RMSE. The model achieves high forecasting accuracy, reduces retraining runtime by 90×, and adapts effectively across varying regional conditions, showing potential for efficient and scalable wind power forecasting. In addition, work [32] presents a Convolutional Graph Rough Variational Autoencoder (CGRVAE) for forecasting photovoltaic (PV) power generation. PV power prediction is important for optimized management of the grid system, but the used methods suffer from uncertainty and inaccurate spatiotemporal representation. This method captures each PV site’s PDFs of future PV generation in a modeled weighted graph. A network of PV sites is modeled as a weighted graph, where nodes represent PV sites and edges reflect their correlations. The model incorporates rough set theory to handle uncertainties in the PV data and demonstrates superior performance compared to existing forecasting benchmarks. Yet another example is work [33], which introduces a deep learning framework for forecasting renewable electricity demands, combining Variational Autoencoders (VAEs) for data sampling and Bidirectional Long Short-Term Memory (Bi-LSTM) for prediction. The framework was tailored to South Korea’s energy context, aiming to support the Renewable Energy 3020 Plan by estimating future energy demands. Data preprocessing incorporated conversion factors and regional factors, while postprocessing addressed labeling inconsistencies. The VAE-Bi-LSTM model outperformed other techniques such as LSTM, GRU, ANN, and ARIMA, reducing RMSE, MAE, and MAPE compared to alternatives. The results provide insights into optimizing energy policies and emphasize the importance of data augmentation in enhancing forecasting accuracy for large-scale energy management. Furthermore, paper [34] introduces a data-driven Optimal Power Flow (OPF) solver leveraging unsupervised generative models to address the challenges of real-time computation, optimality, and feasibility in modern power grids. Unlike traditional solvers requiring labeled optimal datasets or heuristic assumptions, this method uses only feasible datasets to generate near-optimal solutions. The approach incorporates domain knowledge, information theory, and machine learning (ML) constructs to rapidly produce solutions that guarantee system constraint satisfaction without reliance on external tools like AC power flow solvers. Finally, work [35] proposes the use of a VAE-BiLSTM method for short-term load forecasting. Load forecasting is a significant tool for maximizing the economic efficiency of power producers in deregulated markets. Existing methods lack accuracy in modeling time-dependent patterns and removing noise from real-world data, making their forecasting not accurate enough. In this method, the VAEs preprocess and reconstruct the data (containing also historical, meteorological, and environmental data), creating a normalized, noise-free dataset for training the BiLSTM. To prevent overfitting, the training method is based on batch training, and the method is compared to SVR and LSTM. The forecasting operation was performed separately for all four seasons, and analyzing the results with various evaluation indicators showed the best performance with this method.

From a different perspective, there are many applications in power systems requiring accurate estimation. The latent representations learned by VAEs can be employed for parameter or state estimation in power systems, as may be seen in the following examples. Paper [36] introduces a novel data-driven method for long-term voltage stability assessment and monitoring in power systems using Variational Autoencoders (VAEs). Leveraging high-frequency PMU (Phasor Measurement Unit) data, the approach extracts low-dimensional latent features representing load and voltage levels, bypassing the need for prior system topology or control strategy knowledge. Unlike traditional methods, the VAE probabilistically regularizes latent features and uses variance reduction for better long-term stability evaluation. The method demonstrated high accuracy and efficiency in simulations across IEEE 14-bus, 57-bus, 118-bus, and European 1354-bus systems under diverse load scenarios, including single and multiple load increments. Results highlight its robustness, computational efficiency, and potential for real-time operation. In the same context, article [37] presents a novel approach for calibrating power plant model parameters using a Conditional Variational Autoencoder (CVAE) framework, ensuring computational efficiency and robustness in nonlinear dynamic systems. By combining Elementary Effects (EE) analysis for identifying critical parameters and the CVAE model for posterior distribution estimation, the method addresses challenges in traditional and machine learning-based calibration approaches. The framework was tested on a hydrogenerator model with 18 critical parameters under varying prior distributions and event scenarios. Results demonstrate that the proposed method achieves accurate parameter estimation, even when true values deviate from prior distributions. The method’s efficiency and generalizability make it suitable for real-world applications. Furthermore, article [38] proposes a novel method for fault detection and fault localization in power distribution networks using a Variational Autoencoder (VAE). The solution can handle massive amounts of multidimensional data collected by the power system combined with real-time dynamic distribution network status information to locate and detect anomalies. Simulations’ results demonstrate the correctness and accuracy of the model.

When focusing on classification and detection applications in power systems, VAEs may be applied to anomaly detection and classification tasks, as may be seen in several recent works. For example, work [39] proposes a data augmentation method for electricity theft detection based on a CVAE. Electricity theft detection is not accurate enough due to a lack of data samples, and this model can generate new data curves which can be used to train various classifiers. The method uses an encoder composed of convolutional layers to map power theft curves into low-dimensional latent variables and a decoder with deconvolutional layers to reconstruct new power theft curves. The proposed mechanism can consider both the shapes and distribution characteristics of samples, and when classifiers (such as CNN, MLP, SVM, and XGBoost) train with the augmented data, their detection performance is better than that achieved when trained with traditional augmentation mechanisms (ROS, SMOTE, CGAN, etc.), or with the original data.

From a slightly different perspective, study [26] focuses on detecting anomalies in electric vehicle (EV) power battery packs to ensure safety and prevent faults. The authors propose a semi-supervised model combining Gated Recurrent Units (GRUs) with a Variational Autoencoder (VAE), referred to as GRU-VAE. The model processes multivariate time series (MVTS) data, learning robust latent representations and reconstructing inputs to identify anomalies based on reconstruction errors. The Peaks Over Threshold (POT) model is employed to dynamically set anomaly thresholds. Experimental results on real EV datasets demonstrate GRU-VAE’s effectiveness, achieving a 24% improvement in F1-score over GRU-AE and outperforming traditional threshold-based methods. The approach is scalable and suitable for early detection, offering a significant advancement in battery anomaly detection technology. Moreover, work [40] focuses on anomaly detection for hydropower turbine units using a combination of a Variational Modal Decomposition (VMD) and a Deep Autoencoder (AE) based on a Convolutional Neural Network (CNN). The method first decomposes sensor signals into simpler subsignals using VMD, then employs a deep Autoencoder for unsupervised learning, using reconstruction residuals to detect anomalies. The dataset consists of sensor readings from a hydropower plant, including flow rate, guide vane opening, and oil level in tanks. The evaluation metrics include recall, precision, accuracy, specificity, and F1 score, where the proposed method improves recall by 0.140, precision by 0.205, and F1 score by 0.175 over traditional AE approaches. Wasserstein Distance is used for distributional comparison, highlighting improved convergence. The approach does not use transfer learning but benefits from self-supervised learning through AE training. The method significantly reduces reconstruction error, enhancing the separation of normal and abnormal data, making it a robust tool for anomaly detection in power systems. In addition, paper [41] addresses the challenge of anomaly detection in electric vehicle (EV) power batteries by introducing the Deep Variational AutoEncoder-Based Support Vector Data Description with Adversarial Learning (DVAA-SVDD) model. The method integrates a Variational Autoencoder (VAE) to regularize the feature space of normal samples, thereby mitigating hypersphere collapse issues common in Deep-SVDD methods. Adversarial learning complements the VAE, acting as a discriminator to enhance feature generation quality and define more robust classification boundaries. The model was validated on real-world datasets containing over 5 million samples, demonstrating superior performance compared to existing techniques in detecting anomalies with high accuracy, robustness, and efficiency. By achieving optimal metrics across diverse datasets, this framework ensures reliable and scalable deployment in real-world EV battery monitoring systems. The study highlights the effectiveness of unsupervised learning in addressing data imbalance and heterogeneity in battery fault detection. Consequently, Ref. [42] introduces a hybrid approach combining a physical model and an LSTM-based Variational Autoencoder (LSTM VAE) for anomaly detection in district heating substations. The physical model decomposes heat load data into regular components and residuals, while the LSTM VAE is trained on residuals to identify anomalies based on reconstruction errors. The approach was tested on real-world hourly heat energy data from a Swedish substation, partitioned into warm and cold months. Results demonstrate that the LSTM VAE outperforms baseline models (LSTM and LSTM Autoencoder) in terms of AUC and F1 score, particularly with optimized threshold settings. The study highlights the potential for improving energy system diagnostics through advanced machine learning techniques. Lastly, Ref. [43] proposes a novel method for anomaly detection in household appliances. Based on the analysis of their power signatures, the authors trained a VAE to model the normal operation of each appliance. Then, at test time, they compared the reconstruction error of the VAE to the anomaly threshold previously estimated from the training errors, looking for deviations. Finally, the paper shows that the VAE method outperforms traditional algorithms for anomaly detection.

Yet another core task in the power systems domain is data reconstruction. In this light, VAEs may be used for data imputation and reconstruction, filling in missing data points based on the learned latent representation. For instance, work [44] proposes an AT-GVAE-based FDIA detection framework based on data reconstruction. Existing FDIA detection methods can only tell if there is an attack without localizing the exact nodes injected, and their performance is not desirable under small attacks. The proposed mechanism consists of two multiple-layer GRU-based VAEs that act as the generator and discriminator. The VAE modules are enhanced with a self-attention mechanism to further characterize the latent feature variables for data reconstruction by decoders. This model outperforms other VAE-based methods, mainly because of two factors: capturing data distribution in both real data and latent vector space, and using the VAE-G to generate samples close to small abnormalities of FDIA attacks.

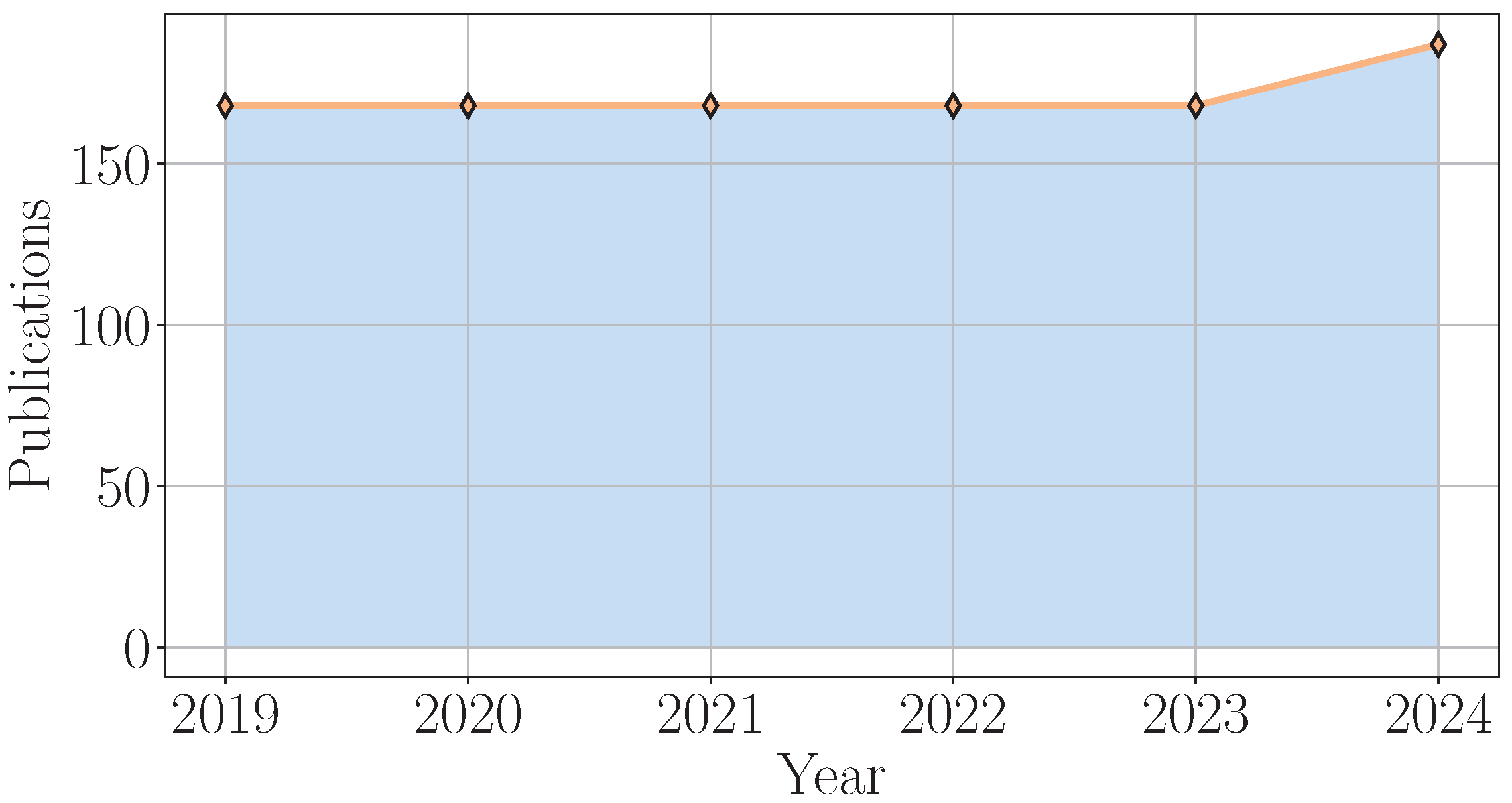
To conclude, VAEs are probabilistic generative models that learn compressed latent representations of data, enabling them to generate new samples and perform tasks like dimensionality reduction and anomaly detection. This section explored VAE applications in power systems, including tasks such as data generation, forecasting, estimation, classification, detection, and data reconstruction. As presented in Figure 8, there is a growing research interest, as may be inferred from the increasing number of publications, focusing on VAE models in power system applications from 2019 to 2024. The number of publications remained relatively stable around 160 from 2019 to 2023 before showing a noticeable increase to approximately 180 in 2024, suggesting a recent growth in research interest in VAEs for this domain. Moreover, as shown in Figure 9, the left pie chart indicates that prediction is the most common machine learning task for VAE models in power systems at 29.7%, followed by generation and estimation, both at 25.9%. The right pie chart shows that DER (Distributed Energy Resources) constitutes the largest application area for VAE models at 48.2%, with GSAC (Grid Stability and Control) following at 37.0%. 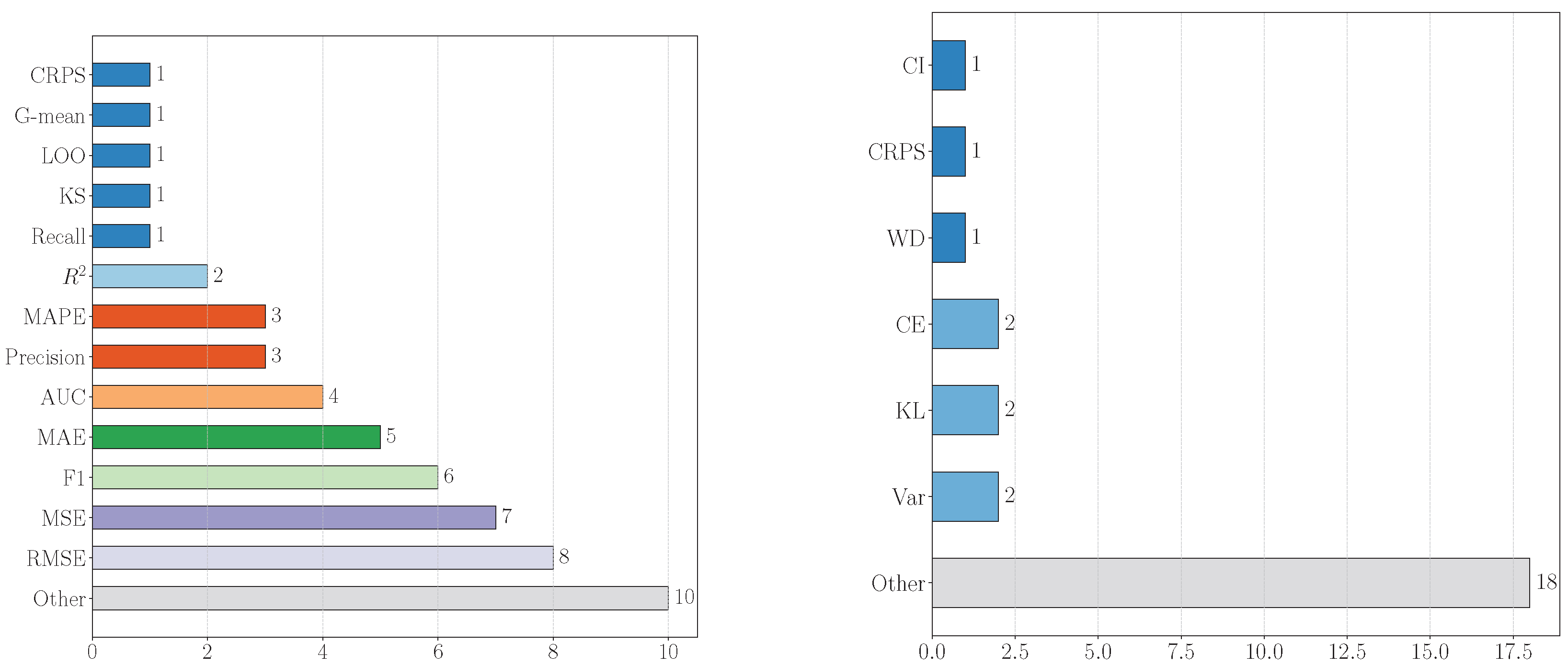Finally, as may be viewed in Figure 9, the left bar chart indicates that Root Mean Squared Error (RMSE) is the most frequent evaluation metric with a count of eight, closely followed by Mean Squared Error (MSE) with seven and F1-score with six. The right bar chart shows that the probability measurement metrics CRPS, Variance, WD, CI, CE, and KL each have a count of 10, while a collection of other metrics that were not covered in this review have a slightly higher count of 18. 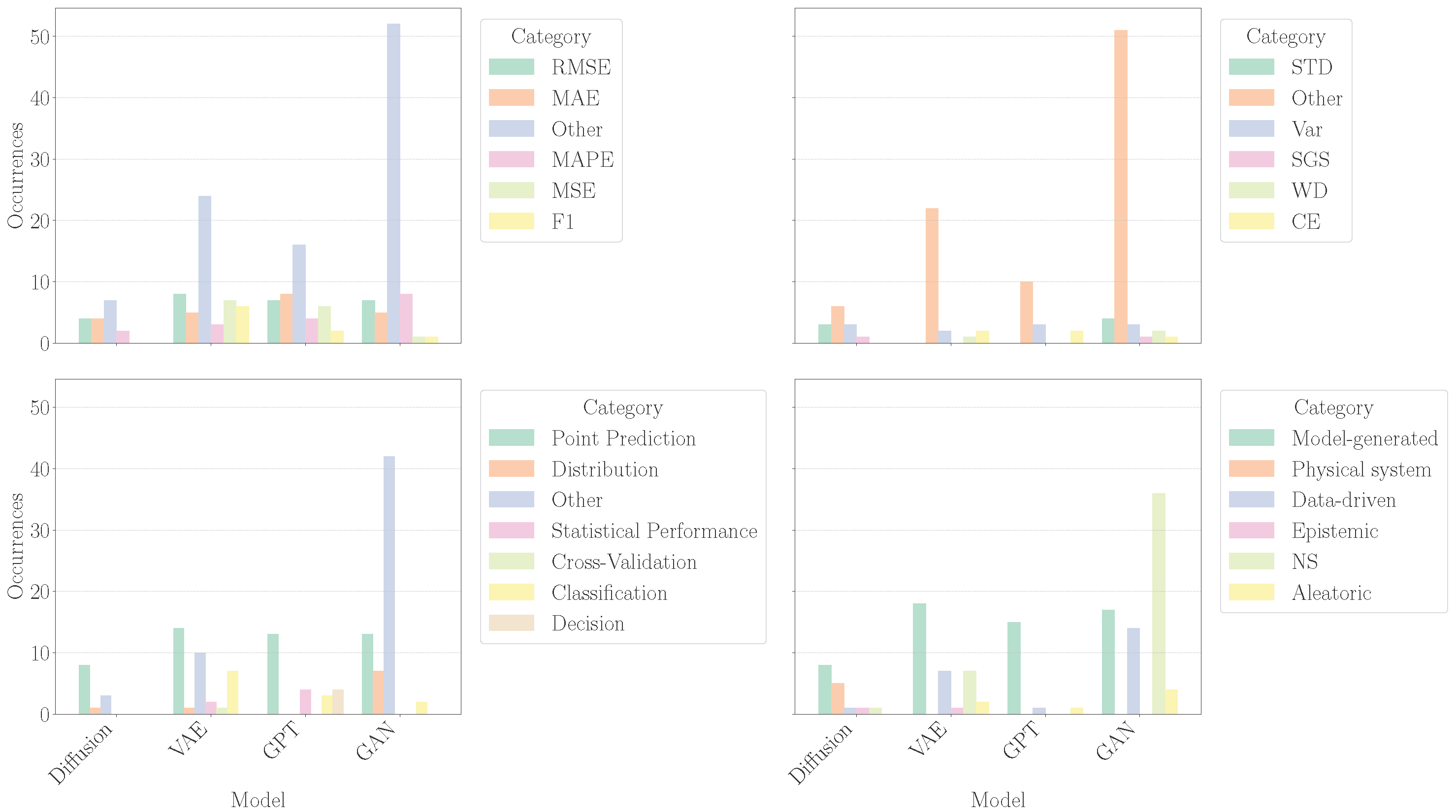Figure 10 shows the distribution of different evaluation metrics for machine learning tasks where Variational Autoencoder (VAE) models are used in power system applications. Right: The distribution of probability measurement metrics used to quantify uncertainty in power system applications involving VAE machine learning models. The left bar chart indicates that Root Mean Squared Error (RMSE) is the most frequent evaluation metric with a count of 8, closely followed by Mean Squared Error (MSE) with 7 and F1-score with 6. The right bar chart shows that the probability measurement metrics CRPS, Variance, WD, CI, CE, and KL each have a count of 10, while a collection of other metrics that were not covered in this review have a slightly higher count of 18.

3.3. Generative Adversarial Networks

Generative Adversarial Networks (GANs) employ a two-network architecture: a generator that creates synthetic data and a discriminator that distinguishes between real and generated samples. This adversarial training process enables GANs to learn complex data distributions and generate realistic synthetic data, offering potential benefits for power system analysis and simulation. This section examines the diverse applications of GANs in power systems, ranging from load forecasting to power grid security.

The generation of realistic and diverse scenarios is crucial for various power system applications. Several studies have explored the use of GANs for this purpose. For instance, article [45] explores the short-term optimal operation of a large-scale hydro–wind–solar hybrid system to address the challenges of renewable energy integration into power grids. A stochastic optimization model is proposed, utilizing an improved generative adversarial network (GAN) with variational inference (GAN-VI) to capture the spatial and temporal uncertainties of wind and photovoltaic (PV) power. A two-stage optimization approach is employed, combining a heuristic algorithm for unit commitment and a refined model for cascade hydropower stations. Case studies in Southwest China demonstrate the system’s capability to balance fluctuating renewable energy sources and meet power transmission demands efficiently. The results highlight that high-quality scenarios generated by GAN-VI improve operational strategies, reducing start–stop losses and enhancing renewable energy utilization by 2.5% compared to traditional methods. Furthermore, article [46] focuses on renewable scenario generation to address the uncertainty and variability in wind and photovoltaic energy. It introduces a data-driven, model-free approach utilizing Controllable Generative Adversarial Networks (ctrl-GANs) with a transparent latent space. The method incorporates orthogonal regularization and spectral normalization for training stabilization and establishes a link between the generated scenario features and the latent vectors. New evaluation metrics, including MMD, FID, and 1-NN scores, are used to assess the quality of generated scenarios. Results demonstrate the method’s effectiveness in generating realistic renewable energy scenarios, reflecting both temporal and spatial correlations while enabling controlled feature adjustments in the scenarios. The GAN-based approach outperforms traditional methods by capturing dynamic patterns and enabling flexible feature control. In addition, work [47] proposes a new method using an unsupervised labeling model and conditional WGAN-GP to model the uncertainties and variation in wind power. The method employs a cluster analysis to categorize wind forecast errors, a support vector classifier (SVC) to predict labels for these categories, and a conditional scenario generation process using an improved WGAN with a gradient penalty term. The generated scenarios try to capture both the marginal distribution of each category and the spatiotemporal relationships among multiple wind farms. The results show that the proposed model can generate scenarios that accurately reflect real-world wind power output patterns, including mode diversity and statistical reliability, and that the gradient penalty improves scenario quality compared to weight clipping. The paper also proposes a scenario reduction technique using the k-medoids algorithm to balance computational efficiency and reliability. Moreover, work [48] develops a distribution-free method for wind power scenario generation using SeqGAN. Power generation that can characterize the complex dynamics of wind power (and by that, it should avoid manual labeling) is necessary for the effectiveness of the generated datasets. The mechanism combines the SeqGAN with LSTM and GANs coupled with reinforcement learning. The model treats sequence generation as a stochastic sequential decision-making process, where a generative model acts as an agent guided by rewards from a discriminative model. This method’s performances are compared with Gaussian distributed, vanilla LSTM, and multivariate KDE models and show better results when applied to day-ahead scheduling. Similarly, study [49] explores a model-free, data-driven approach to renewable energy scenario generation using Generative Adversarial Networks. GANs leverage deep neural networks to generate realistic wind and solar power scenarios, capturing temporal and spatial correlations without explicit statistical modeling. Historical data from NREL datasets validated the method’s effectiveness, demonstrating its ability to produce diverse and statistically accurate renewable generation patterns. The method also supports conditional scenario generation, such as focusing on specific weather events or seasons, offering a scalable and efficient alternative to traditional probabilistic models. Evaluation metrics confirm the generated scenarios closely resemble real data in both statistical properties and diversity. Furthermore, study [50] addresses the challenge of real-time optimal power flow analysis, critical for efficient and reliable grid operation amidst uncertainties introduced by renewable generation, storage systems, and diverse loads. It proposes a novel data-driven machine learning approach that integrates generative learning, information theory, and domain-specific knowledge. This method only requires feasible data points for training and provides subsecond computation times, making it significantly faster than traditional and existing ML-based methods. The model guarantees both the feasibility and near-optimality of solutions without requiring grid topology or power flow equations post-training. Additionally, paper [51] introduces Recurrent Generative Adversarial Networks (R-GANs) for generating realistic energy consumption data to address the challenges of data scarcity and privacy in smart grids. By replacing CNNs with RNNs, the model captures temporal dependencies in time series data. The addition of a Wasserstein GAN (WGAN) and Metropolis–Hastings GAN (MH-GAN) improves the training stability and data quality. ARIMA and Fourier transform features further enhance the generated data’s realism and utility. The synthetic data were evaluated for training energy forecasting models, achieving results comparable to models trained on real data. Moreover, paper [52] explores the use of Generative Adversarial Networks for short-term load forecasting (STLF), addressing a gap in the use of GANs beyond data augmentation in energy systems. The study introduces a Conditional GAN (cGAN) architecture, leveraging minimal exogenous variables (temperature, day, and month) to predict daily load profiles. Various GAN architectures, including DCGAN, LSGAN, WGAN, and WGAN-GP, were tested, with cDCGAN achieving the best results (MAPE: 4.99%). The models were evaluated on one year of unseen data, demonstrating their capability to capture load variations and seasonality effectively. Future directions include enhancing the latent space and integrating multiple condition vectors to refine predictions. In addition, work [53] introduces a time series GAN controller for long-term smart generation control (LTSGC) in microgrids, aiming to address the uncoordinated problems of conventional control frameworks. The method replaces the typical combined framework of economic dispatch (ED), smart generation control (SGC), and generation commands dispatch (GCD) with a single-time-scale LTSGC. The proposed TSGAN controller utilizes reinforcement learning and deep generative adversarial networks (DGANs) to predict states from historical data. The TSGAN is trained using a min-max game system to generate data similar to real-life data. Results indicate the proposed TSGAN controller achieves higher control performance and smaller economic cost compared to conventional algorithms. Similarly, study [54] introduces a GAN-based robust optimization (GAN-RO) framework to improve the integration of photovoltaic systems into power grids by addressing variability and uncertainty in renewable energy. The proposed method combines GANs for generating realistic solar energy scenarios with a robust optimization model, allowing dynamic adjustments to operational strategies. The model was trained on historical energy and weather data and tested using IEEE 33-bus system simulations to optimize energy consumption and reduce operational costs. The results demonstrate a reduction in energy costs, a decrease in carbon emissions, and an increase in system efficiency. The study highlights the potential of AI-driven optimization techniques in enhancing grid stability, economic efficiency, and sustainability. In the same manner, work [55] proposes a strategy for electric vehicles (EVs) and thermostatically controlled loads (TCLs) in a distribution system, using a modified GAN. Intelligent energy strategy is important for not overloading the grid system with these flexible loads. This method models EVs as battery energy storage systems (BESSs) and TCLs as virtual energy storage systems (VESSs), and it integrates machine learning into a bilevel optimization problem to determine power dispatch and VESS control. A modified GAN is used to estimate power, voltage, and VESS energy storage states and to address missing data issues. Results demonstrate that the method outperforms conventional approaches in accuracy and voltage stability while also being less affected by incomplete datasets. The data-driven approach reduces computation time and enables a faster response to changes in the distribution system. Furthermore, study [56] addresses the challenge of transient stability assessment (TSA) in power systems, where data imbalance and limited unstable samples hinder the performance of data-driven classifiers. To overcome this, the authors propose a GAN-based case generation model that integrates a CNN-based regression model to guide the generation of realistic instability samples by shifting the data distribution towards prolonged instability moments. The model is trained and evaluated, where it successfully enhances dataset diversity. The performance is assessed using Fréchet Inception Distance (FID), Mean Absolute Percentage Error (MAPE), and classification accuracy across different TSA models (CNN, SVM, DBN, GCN). Results show that the proposed method outperforms conventional GAN-based approaches by improving the realism of generated cases and boosting classifier robustness in recognizing rare instability events. The study demonstrates the effectiveness of data augmentation in improving TSA performance, particularly in data-scarce scenarios. Another work concerning this idea is [57], which proposes a home energy management (HEM) system for minimizing bill cost. Unlike existing methods that assume probabilistic distribution, this method is model-free. It utilizes a WGAN to generate solar power scenarios and then applies mixed-integer linear programming (MILP) to schedule appliances and energy storage. The WGAN-generated solar power profiles closely match real solar data, and the results are compared to a Monte Carlo method for scenario generation, with the WGAN approach showing better performance in terms of accuracy and reduced computational time. Furthermore, the proposed system, when considering both PV and ESS, demonstrates a significant reduction in electricity costs. Additionally, paper [58] proposes a novel approach to generating synthetic time series data for smart grids using Conditional Generative Adversarial Networks (GANs). This method addresses the challenges of data availability, scale, and privacy in distribution-level datasets. The approach models time series data as a combination of “Level” (high-level statistics) and “Pattern” (behavioral trends), which are normalized and learned via GANs. The generated datasets preserve statistical properties and are evaluated using Maximum Mean Discrepancy (MMD), clustering, and load forecasting tasks. Experimental results using the Pecan Street Dataset demonstrate the synthetic data’s indistinguishability from real data, enabling privacy-preserving research and applications in smart grid scenarios. Moreover, article [59] introduces a weakly supervised Generative Adversarial Network (GAN) framework to enhance the detection and generation estimation of distributed solar photovoltaics (PVs) in power grids with limited labeled data. The method leverages GAN-based image augmentation to generate diverse labeled satellite images, embed PV-specific characteristics, and integrate PV detection and classification into a feedback loop for mutual improvement. The approach combines geographic data, weather conditions, and historical generation patterns for robust output estimation, validated through tests in Arizona and California. This solution addresses data scarcity and achieves high accuracy in PV localization and generation forecasting. From a slightly different perspective, work [60] suggests a method for synthesizing three-phase unbalanced active distribution networks, addressing the challenge of limited real-world data availability. The method employs an unbalanced graph Generative Adversarial Network (UG-GAN) to learn the distribution of random walks over a single real-world network and across phases, generating synthetic network connectivity. The framework also uses kernel density estimation (KDE) to generate time series load data and an optimization-based approach to place standard grid components, considering the interaction between topology, loads, and electrical components. Case studies demonstrate that the generated synthetic networks mimic the characteristics of real-world networks while maintaining data privacy and autonomy. The proposed method provides a comprehensive approach to generating realistic distribution system test cases using minimal real-world data. In a similar context, work [61] proposes a GAN-based reconstruction of low-frequency electrical measurement data in smart grids. This is important for realizing two-way communication of energy and data flow between various agents. This method begins by transforming electrical measurement data into electrical images, where different measurement types are stored in different color channels. Then, a GAN-based super-resolution reconstruction method is used to enhance the images’ resolution, effectively increasing the sampling frequency of the data. Results demonstrate that the model can restore high-frequency details with less error and can be generalized to different datasets with satisfactory accuracy.

Beyond scenario generation, GANs have also found significant application in prediction and forecasting tasks within power systems. Several studies have explored their potential in this domain. For example, work [62] presents a novel cross-modal method for generating scenarios of renewable energy, specifically addressing the issue of data quality and multimodality via cGAN. The method fuses spatial information from GPS data and temporal information from power output data using a spatiotemporal Transformer within the cGAN framework, which formulates scenario generation as a probability approximation problem. The results show that with a spatial Transformer, the model performed better than with a temporal Transformer and that it provides more training stability. This model’s generated data closely match real-world data and achieve state-of-the-art (SOTA) scenario generation performance. Furthermore, work [63] introduces TraceGAN, a novel method for generating synthetic appliance power signatures using a conditional, progressively growing, one-dimensional Wasserstein GAN. For accurate NILM, a significant amount of labeled data are needed, but collecting such data is challenging. This method involves training a generator and a discriminator in an alternating fashion, where the generator produces realistic power signals from a random input, while the discriminator tries to distinguish between the generated and real signals. TraceGAN can synthesize truly random and realistic appliance power data signatures. In addition, work [64] designs an attention-based cycle consistent (ABC)-GAN model for generating IoT data in intelligent systems. The goal is to better capture the important temporal features and the distribution of the data, as more quality generated data are essential for the operation of those systems. This method employs an encoder–decoder architecture with an improved attention-based LSTM variant to capture temporal features and a CycleGAN to learn distributions between different data patterns. It consists of two generators and two discriminators, which help it learn the cross-mapping between different domains, trying to overcome domain gaps. The training is performed with two adversarial loss functions and a cycle consistency loss function, which helps ensure that the generated data are close to the real time series. Results exhibit high consistency with the original data, although there is a potential limit to the pattern diversity of the augmented data, probably due to their dependency on the distribution of the training samples. Moreover, work [65] proposes a novel time series forecasting based on CGANs (TSF-CGANs) designed for PV power prediction. PV power forecasting is a solution for efficient management of the system, but existing deep learning methods have reached a development limit in extracting the inherent features of the input data. The method employs a CGAN framework combined with a CNN and Bi-LSTM. The generator within TSF-CGANs functions as a regression prediction mode and then employs Bi-LSTM to produce the predicted value. The discriminator concurrently assesses the authenticity of the generated datasets, with the generator’s parameters iteratively optimized through adversarial training. Model performances are compared with LSTM, RNN, BP, SVM, and the Persistence model and indicate better accuracy. Similarly, work [66] proposes an electric vehicle (EV) demand modeling called EV-GANs, which uses 3D CGANs to capture the nature of EV charging. Existing methods are based on Monte Carlo simulation and are unable to grasp the correlation between EV demand characteristics. This method maps EV demand characteristics into a 3D space and by that extracts the correlation between these dimensions. Results illustrate the effectiveness of the model, outperforming MC and Copula methods. In the same manner, study [67] explores the use of Generative Adversarial Networks (GANs) to improve cyber-attack detection in smart grids by addressing the challenge of limited attack sample availability. Traditional deep learning-based detection models struggle due to data scarcity, leading to overfitting and reduced robustness. The proposed approach utilizes a GAN to generate synthetic attack messages, which are then integrated into the training dataset to enhance model performance. The evaluation, conducted on a simulated smart grid environment, demonstrates a 4% improvement in attack detection accuracy when using GAN-augmented datasets. The results indicate that increasing the volume of attack samples enhances generalization, particularly for rare attack types such as R2L and U2R. Overall, the research provides a novel AI-driven approach to improving cybersecurity in smart grids, making detection models more resilient against emerging threats. Additionally, paper [68] presents a data-driven approach for detecting outages in partially observable distribution systems using smart meter (SM) data and Generative Adversarial Networks (GANs). The proposed method first decomposes the network into multiple zones using a breadth-first search (BFS)-based mechanism to enhance outage location accuracy. A GAN is then trained in each zone to learn the temporal–spatial distribution of normal operation data, and an anomaly scoring technique is applied to detect deviations indicating outages. The study validates the method using real AMI (Advanced Metering Infrastructure) data and evaluates performance using recall, precision, and F1 score. Results demonstrate that the proposed method effectively detects outages with high accuracy, even in cases of limited smart meter deployment, and achieves better detection performance than traditional support vector machine-based approaches. Likewise, study [69] addresses short-term wind power forecasting using a Conditional Generative Adversarial Network (CGAN) combined with Convolutional Neural Networks (CNNs) to improve day-ahead prediction accuracy. The method incorporates historical wind farm data, which are clustered using K-means based on weather factors such as wind speed and direction. Gray Relational Analysis (GRA) is employed to identify similar past conditions, providing labeled guidance for CGAN training. The results demonstrate that CGAN enhances prediction performance by generating realistic synthetic wind power samples, reducing the forecasting error compared to traditional methods like the ANN, SVM, and ELM. Further, study [70] introduces Informer-TimeGAN, a model for day-ahead wind power scenario generation, addressing the stochasticity and uncertainty of wind power forecasting. By integrating probSparse self-attention from Informer with time series generative adversarial networks (TimeGANs), the model effectively captures temporal correlations, seasonal patterns, and prediction error characteristics. An error stratification block categorizes errors based on ramping characteristics and power levels, allowing more targeted scenario generation. Evaluated on two real-world wind farm datasets in China, the model outperforms SeqGAN, RNN-GAN, and TimeGAN in maintaining autocorrelation, capturing volatility, and improving scenario accuracy, as shown by higher Coverage Rate (CR), lower Power Interval Width (PIW), and improved RMSE. The results demonstrate that Informer-TimeGANs enhance uncertainty modeling, making them a valuable tool for economic dispatch and power system planning. On top of that, paper [71] proposes a hybrid forecasting model leveraging a semi-supervised Generative Adversarial Network (GAN) for short-term wind power and ramp event forecasting. The method employs Variational Mode Decomposition (VMD) to preprocess wind power time series data into intrinsic mode functions (IMFs) and uses GANs to generate virtual samples for training, enhancing prediction accuracy. The discriminative model integrates a semi-supervised regression layer for point forecasting, while a self-tuning strategy with multilabel classification improves ramp event prediction. Testing on datasets from wind farms in Belgium and China demonstrated superior forecasting performance compared to traditional statistical and machine learning methods. The GAN-based approach reduced errors significantly, achieving high accuracy and adaptability across various conditions. Correspondingly, article [72] addresses the challenge of integrating renewable energy sources, particularly wind and solar, into power systems due to their inherent unpredictability and variability. The authors propose an improved Generative Adversarial Network (GAN)-based model for scenario forecasting, leveraging convolutional neural networks (CNNs) for robust feature extraction. This model captures the spatial–temporal correlations and stochastic dynamics of renewable power generation, allowing the generation of realistic time series trajectories. Experimental results demonstrate that the model effectively represents uncertainties, preserves statistical and spatial correlations, and achieves faster convergence compared to traditional methods. The approach is validated using 7 years of high-resolution wind and solar data from multiple sites in Washington State, showing its potential for application in renewable energy planning and operation.

GANs are also proving useful in classification tasks within power systems, particularly when dealing with imbalanced datasets or complex feature spaces. Several studies have explored their application in this area. For instance, work [73] introduces a novel method for detecting high impedance faults (HIFs) in distribution networks using a cGAN and a CNN classifier. HIFs can be mistaken for other transient events, which presents a challenge in the protection of distribution systems. Existing methods’ efficiency relies on the size of the training data, and acquiring a large amount of datasets is time-consuming. This method begins by extracting the third harmonic angle (THA) of the current using an adaptive linear neuron (ADALINE). The cGAN then generates a large amount of pseudo-data from a small set of real data. Finally, a CNN classifier separates HIF data from other transient events. The method achieves high accuracy despite a low quantity of data input. In addition, study [74] introduces a self-attention generative adversarial network (SA-GAN)-enhanced deep reinforcement learning (DRL) method to improve the resilience of networked microgrids (MGs) during sequential extreme events (SEEs). By generating credible data with sequential features, the SA-GAN addresses data scarcity and integrates into a double deep Q-network (DDQN) framework for adaptive MG reconfiguration. Tests on 7-bus and IEEE 123-bus systems show that this method enhances learning, adaptability, and resilience, ensuring continuous critical load survival. The approach outperforms conventional DRL methods, offering a robust, data-driven solution for power grid operations under extreme weather. Furthermore, work [75] proposes a new generative adversarial framework for learning from skewed class distributions called ACIL (adversarial class imbalance learner). The model tries to learn the minority class distributions along with the majority class distribution to find cyber-attacks and physical faults. The ACIL has been tested and compared to various class imbalance learning models, showing superior performance.

Finally, GANs are being investigated for estimation tasks in power systems, offering potential improvements in accuracy and robustness, particularly when dealing with incomplete or noisy data. For example, Ref. [76] introduces a fully data-driven approach for prefault dynamic security assessment (DSA) using phasor measurement unit (PMU) data with incomplete measurements. The method employs generative adversarial networks (GANs), an unsupervised deep learning technique, to address missing data, eliminating reliance on PMU observability and network topologies. Unlike traditional methods, which are constrained by PMU placement and require complete data inputs, the proposed approach is generalized and extensible, capable of handling various missing data scenarios. Simulation results demonstrate that this method maintains high DSA accuracy under all PMU missing conditions, with significantly reduced computational complexity. This innovation enhances the robustness of DSA for power systems facing uncertainties from renewable energy integration and data imperfections. The findings provide a practical and efficient solution for real-time dynamic security assessments in modern power grids. By the same token, study [77] addresses the challenges of high-resolution state estimation (SE) in power distribution networks caused by increasing renewable generation and incomplete or inaccurate measurements. To tackle these issues, a spatiotemporal estimation generative adversarial network (ST-EGAN) is proposed, which generates high-resolution pseudo-measurements by extracting temporal patterns and leveraging residual structures to bridge spatial and temporal data gaps. The method eliminates the need for additional equipment and improves the robustness of SE in noisy and uncertain conditions. Validation on the IEEE 33-bus test network demonstrates that ST-EGAN outperforms existing interpolation and deep learning methods, reducing the mean RMSE by 4.78% compared to interpolation techniques and achieving superior accuracy and robustness under various noise levels. This approach effectively supports high-resolution SE, enhancing reliability and operational efficiency without increasing computational demands. In addition, the article [78] proposes the CVAE method for modeling the probabilistic wind power curve. To achieve better modeling performance, they introduced the latent random variable. They use it to characterize underlying unobservable weather conditions and inconsistent wind turbine conditions. Their experimental results showed that CVAE gained better results over previous methods in terms of lower CRPS and PI reliability and sharpness.

To conclude this section, we have shown the diverse applications of Generative Adversarial Networks in power systems, spanning tasks such as data generation, prediction, classification, and estimation. An interesting trend is the popularity of GAN models for synthetic data and scenario generation. This opens avenues for addressing data scarcity issues and improving the training of other machine learning models in power system applications. Future research directions may include exploring novel GAN architectures specifically tailored for power system challenges, investigating methods for improving the stability and interpretability of GANs, and developing standardized evaluation metrics for assessing the performance of GAN-based power system solutions. As presented in Figure 11, there is an increasing interest, as shown by the growing number of research publications, focusing on GAN models in power system applications from 2019 to 2024. The number of publications shows a steady increase over the years, starting at approximately 140 in 2019 and reaching over 180 by 2024, indicating a growing research interest in utilizing GANs in this domain. 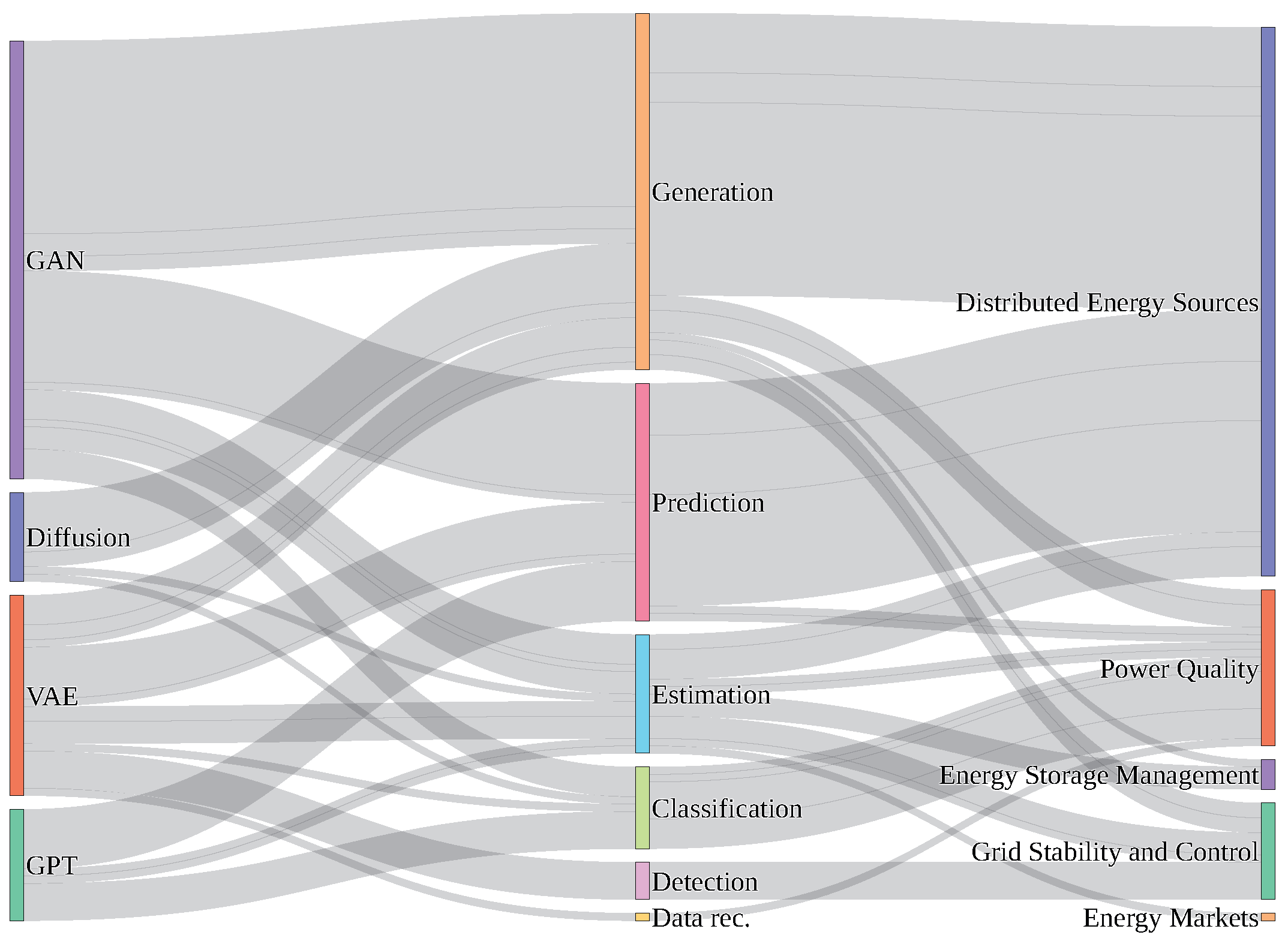Moreover, as shown in Figure 12, the left pie chart reveals that generation is the most common machine learning task for GAN models in power systems at 52.5%, followed by prediction at 27.1%. The right pie chart indicates that DER (Distributed Energy Resources) represents the dominant application area for GAN models at 76.2%, with PQ (Power Quality) accounting for 15.3%. Finally, as may be viewed in Figure 12, the left bar chart shows that a collection of other evaluation metrics that were not covered in this review have the highest count at 42, followed by Mean Absolute Percentage Error (MAPE) at 8 and Root Mean Squared Error (RMSE) at 7. The right bar chart indicates that a collection of other probability measurement metrics that were not covered in this review are most frequent with a count of 48, while CRPS, Entropy, SGS, PI, CE, STD, WD, and Variance each have a count of 10. Figure 13 shows the distribution of different evaluation metrics for machine learning tasks where Generative Adversarial Network (GAN) models are used in power system applications. Right: The distribution of probability measurement metrics used to quantify uncertainty in power system applications involving GAN models. The left bar chart shows a collection of other evaluation metrics that were not covered in this review have the highest count at 42, followed by Mean Absolute Percentage Error (MAPE) at 8 and Root Mean Squared Error (RMSE) at 7. The right bar chart indicates that a collection of other probability measurement metrics that were not covered in this review are most frequent with a count of 48, while CRPS, Entropy, SGS, PI, CE, STD, WD, and Variance each have a count of 10.

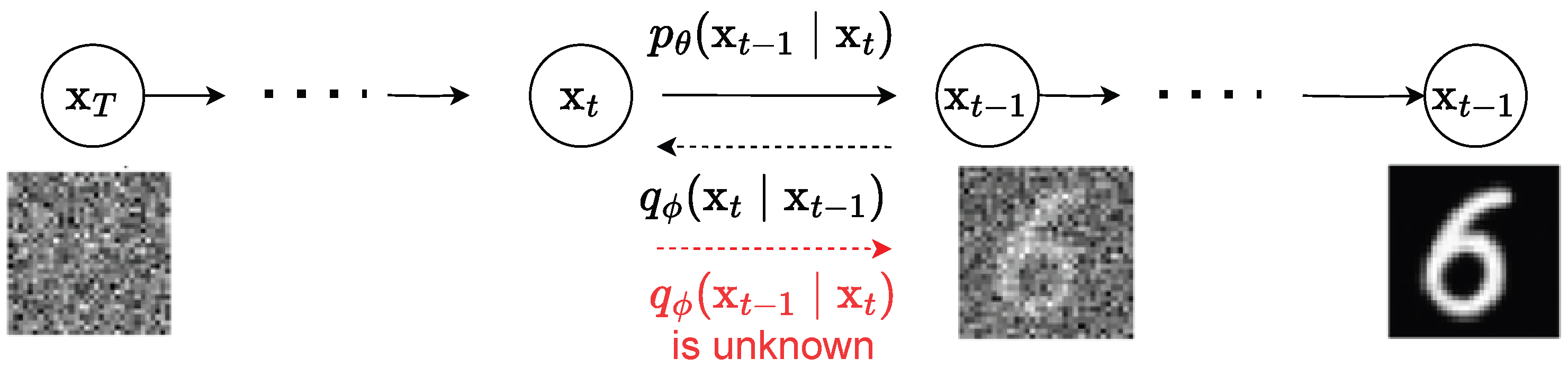
3.4. Diffusion Models

Diffusion models progressively add noise to data until they become pure noise and then learn to reverse this process to generate new data samples. This approach has recently achieved impressive results in various generative tasks and is gaining traction in the power systems domain. This section reviews the emerging applications of Diffusion models in power systems, focusing on their potential for data generation and probabilistic modeling.

One area of focus for Diffusion models is addressing data scarcity and generating synthetic data for various power system applications. This may be seen in several works, such as [79], which addresses the problem of limited training data offered to train a load forecasting model and proposes a two-step generative model-assisted approach for forecasting under small sample scenarios. First, the dataset is augmented, and then a regressor is trained on the augmented data. Two augmentation models are compared, TimeGAN and TS-Diffusion, and four regressor models, XGBoost, CatBoost, RandomForest, and ExtraTree. The results show that augmenting the dataset is effective for better forecasting when using a Diffusion model and that the best regressor for the model is ExtraTree. Furthermore, work [80] addresses the dynamics of electricity prices in power markets by analyzing irregular time series data and defining stochastic models to describe their behavior. The proposed methodology includes filling data gaps, detecting Gaussian components, and estimating a Diffusion model of power prices across two different time periods. The jump amplitude used in the Diffusion model is described by a normal random variable and a truncated Lévy distribution, enabling the reproduction of the first four moments of the log-returns distribution. The analysis is applied to markets such as SP15 and Palo Verde, demonstrating alignment between the model and empirical data. Results distinguish between normal market periods and price spikes, offering a comprehensive analytical tool for studying power price dynamics. In addition, study [81] offers a new method to mitigate parameter degeneracy in system dynamics. They undertake it by using a JCDI model and a Transformer encoder-based denoise neural network. In order to choose the sensitive parameters for identification, they use the Sobol method. This method can reveal the sensitivity discrepancies under different fault events, produce for specific disturbances multiple parameter sets, and enhance parameter estimation accuracy in degenerate cases. Moreover, paper [82] introduces a Conditional Latent Diffusion Model (CLDM) for short-term wind power scenario generation, addressing uncertainty in renewable energy forecasting. The model combines deterministic forecasting with forecast error scenario generation, utilizing an embedding network to extract relevant features from Numerical Weather Prediction (NWP) data. By performing the diffusion process in a latent space, the model reduces denoising complexity and generates high-quality scenarios with fewer diffusion steps. Compared to state-of-the-art methods like GANs and VAEs, CLDM demonstrates superior performance in accuracy and efficiency, validated through rigorous numerical studies. The proposed method provides a practical tool for power system operators to improve forecasting accuracy, aiding in unit commitment, market trading, and economic dispatch of renewable energy systems. Similarly, work [83] offers a universal data generation framework for energy time series data called EnergyDiff. The generated data the model creates are supposed to resolve the lack of high-resolution data. This framework is based on DDPM with a Marginal Calibration technique (which calibrates the inaccurate DDPM marginal distribution) that increases the accuracy and yields precise marginal distributions in various domains. Another related study is [84], which constructs a hybrid model based on DDPM and GAN for the load sample generation tasks in a DHS (District Heating System) and establishes the relationship between load samples and indoor temperature. It provides a complete data chain from “production to users” for DHS operation optimization and fault diagnosis. The study compares a GAN and DDPM and shows that the GAN is more accurate, while DDPM is more generic, robust, and easier to train, and the hybrid model suggested tries to use the advantages of both methods. To evaluate the effectiveness of the generated samples, an indoor temperature response model, is built. The entire model guides a more efficient and convenient operation of a DHS. Furthermore, work [85] proposes an FDIA (False Data Injection Attacks) data recovery framework comprising two key models: the FDIA localization model and the data recovery model. The increasing integration of renewable energy sources and power electronic devices introduces significant randomness in both power generation and loads, leading to significant power fluctuations that challenge the accuracy of existing FDIA detection and recovery methods. The first stage of the mechanism consists of an LMPNN and a hidden space that produce an input for the second stage. This one consists of a DDGM model that uses the input, DDIM, and physical constraints, allowing it to recover valid data. This method shows robustness compared to alternative techniques, as well as high FDIA localization and data recovery performance even under uncertain high-level power fluctuations. Finally, work [86] develops an SSSD-based transient trajectory generation framework to tackle the data insufficiency problem for power system applications. That is because real system simulations are mostly unavailable, and even if available, they are very time-consuming. The algorithm is designed based on a conditional time series Diffusion model that adds random noise and denoises it to create new data samples. Those samples are taken to reproduce multivariable trajectories so that their generation is guided to a desired dynamic behavior. The proposed framework can be used on a detailed system model to simplify the generation of dynamic response data. Furthermore, article [87] proposes a data-driven method for scenario generation of renewable energy production. They introduce a controllable GAN model with a latent controllable vector in manifold space, enabling deliberate modification of generated scenarios. This solution can also generate new scenarios which can be statistically characterized and explored. In addition, work [88] proposes the usage of a Conditional GAN to craft false data that can be injected as measurements to attack and circumvent the smart grid’s BDDs (bad data detectors). The CGAN and algorithm introduced only need access to the grid’s measurement data and to know what data types to inject to produce the threat model. Simulation results showed that the CGAN-based FDIA can bypass the BDD with a very high probability (0.99). Next, article [89] proposes a deep learning framework for predicting power consumption (PC) and RES power generation (PG) in residential and commercial buildings. Since PC and PG data are usually insufficient, they also introduce a method to use a GAN-based methodology to enlarge AI datasets for their work and future studies. Moreover, Ref. [90] proposes a novel PV system planning framework for distribution grids built as a two-stage stochastic optimization model. To address uncertainties in PV production and load demand, it introduces a GAN-based data-driven approach for scenario generation, which leads to comprehensive PV planning decisions. Additionally, the framework incorporates volt-var control using smart PV inverters to improve voltage regulation and reduce power losses. Next, Ref. [91] proposes a novel federated deep learning method for renewable scenario generation called Fed-LSGAN. This method enables learning on a central server, which receives parameters from different sites rather than collecting all their data. Each site captures spatiotemporal characteristics and sends them to the server. By that, the model preserves the sites’ privacy while learning and generating scenarios using shared inputs from all sites. Simulations show that the model outperforms other state-of-the-art centralized methods.

Beyond data generation, Diffusion models are also being explored for prediction and forecasting tasks, as may be seen in the following reviewed studies. For instance, work [92] analyzes wind power technology using the Generalized Bass Model (GBM) framework, incorporating both endogenous and exogenous dynamics, such as local incentive schemes. By comparing GBM with traditional Diffusion models, the study demonstrates GBM’s superior performance in model selection and forecasting accuracy across various metrics. A cross-country analysis highlights differences in wind power adoption, with specific focus on the US and Europe due to their comparable geographic areas. The findings emphasize the importance of integrating localized incentives into Diffusion models to enhance predictive reliability. Short-term forecasts generated through GBM offer practical insights for policymakers and industry stakeholders aiming to optimize wind power deployment strategies. This work bridges existing gaps in wind power diffusion studies and provides a robust methodological advancement for energy forecasting. In addition, paper [93] explores the application of denoising diffusion probabilistic models for energy forecasting, focusing on load, photovoltaic, and wind power time series. Using data from the Global Energy Forecasting Competition 2014, the authors evaluate DDPMs against state-of-the-art deep learning generative models, including generative adversarial networks (GANs), Variational Autoencoders (VAEs), and normalizing flows (NFs). The methodology employs a Markov chain framework trained via variational inference to model time series, offering scalable and robust performance. Results demonstrate that DDPMs outperform competing models in terms of quality and value, marking the first successful implementation of this approach in energy forecasting. The work bridges a critical gap in probabilistic scenario generation for renewable energy. The findings suggest that DDPMs hold significant potential for advancing power system applications and addressing renewable energy challenges. In a similar manner, paper [94] investigates the use of normalizing flows, a deep learning technique, to address the uncertainty in renewable energy generation and improve probabilistic forecasting for power systems. Unlike conventional statistical methods, normalizing flows directly learn the multivariate stochastic distribution of processes by maximizing likelihood, providing accurate scenario-based forecasts. The study evaluates this method using data from the Global Energy Forecasting Competition 2014 and compares its performance with state-of-the-art generative models such as GANs and VAEs. Results show that normalizing flows are competitive and effective in generating scenarios for wind, solar, and load forecasting, offering robust tools for energy applications like electricity market bidding and energy management. This methodology is also reproducible, encouraging further adoption by forecasting practitioners.

In the context of classification tasks, Diffusion models are being investigated for event classification uses, particularly in the presence of adversarial attacks. For example, work [95] tackles the issue of adversarial attacks on machine learning-based power system event classifiers by introducing a Diffusion model-based purification method. The approach adds noise to compromised PMU data and uses a pretrained neural network to remove both noise and adversarial perturbations. By employing Denoising Diffusion Implicit Models (DDIMs), the method achieves real-time efficiency while reducing discrepancies between original and compromised data. Tests on a large PMU dataset show the method improves classification accuracy and supports reliable, real-time power system monitoring.

To summarize, there is a growing interest in Diffusion models for power system applications. These models learn to reverse a process of progressively adding noise to data, and may be used for a variety of purposes. This section reviews their applications in data generation, including addressing data scarcity and creating synthetic data for various purposes, as well as their use in probabilistic modeling for prediction, forecasting, and classification tasks. As presented in Figure 14, there is an increasing interest, as shown by the growing number of research publications, focusing on Diffusion models in power system applications from 2019 to 2024. The number of publications shows a significant increase over the period, starting at a low of around 30 in 2019 and sharply rising to approximately 200 by 2024, indicating a substantial and growing interest in Diffusion models for this field. Moreover, as shown in Figure 15, the left pie chart indicates that generation is the most prevalent machine learning task for Diffusion models in power systems at 58.4%, followed by prediction at 25.0%. The right pie chart shows that DER (Distributed Energy Resources) represents the largest application area for Diffusion models at 66.7%, with PQ (Power Quality) and EM (Energy Markets) accounting for 25.0% and 8.3%, respectively. Finally, as may be viewed in Figure 15, the left bar chart reveals that Root Mean Squared Error (RMSE) is the most frequent evaluation metric with a count of four, followed by Mean Absolute Error (MAE) also at four, while a collection of other metrics that were not covered in this review account for a count of three. The right bar chart shows a relatively even distribution among the listed probability measurement metrics, with CRPS, ELBO, PS, SCS, STD, Variance, and a collection of other metrics that were not covered in this review each having a count of 10. Figure 16 presents the distribution of different evaluation metrics of machine learning tasks for which Diffusion models are used in different power systems applications. It also shows the distribution of probability measurement metrics that were used to quantify uncertainty in different power systems applications involving Diffusion-based machine learning models. The left bar chart reveals that Root Mean Squared Error (RMSE) is the most frequent evaluation metric with a count of 4, followed by Mean Absolute Error (MAE) also at 4, while a collection of other metrics that were not covered in this review account for a count of 3. The right bar chart shows a relatively even distribution among the listed probability measurement metrics, with CRPS, ELBO, PS, SCS, STD, Variance, and a collection of other metrics that were not covered in this review each having a count of 10.

4. Discussion and Prominent Trends

The analysis of publication trends, distribution and co-occurrence of different evaluation metrics, and uncertainty quantification methods for generative models used for power systems applications reveals several interesting trends. For instance, Figure 17 demonstrates a surge in research interest within this domain, evidenced by the steep growth in the number of publications over the past two decades. Furthermore, while Generative Adversarial Networks (GANs) and Variational Autoencoders (VAEs) have historically dominated the landscape, Diffusion models have emerged as an exciting area of research in recent years, exhibiting a steep climb in publication frequency. This ascendance suggests a growing interest in Diffusion-based methods, potentially driven by their reported advantages in terms of sample quality and training stability compared to earlier generative approaches.

Examining the evaluation practices, Figure 18 and Figure 19 highlight a reliance on established metrics like Root Mean Squared Error (RMSE) and Mean Absolute Error (MAE). These metrics, commonly used across various machine learning domains, remain dominant in assessing generative models’ performance in the context of power systems applications. However, the growing presence of probabilistic measures, including CRPS and entropy-based criteria, suggests a shift toward uncertainty-aware evaluation techniques. Moreover, the consistent prominence of “Other” within evaluation metrics suggests a diverse approach to performance assessment. This may indicate a lack of standardization in evaluation protocols or the necessity for domain-specific metrics that better capture the nuances of power system applications. The heatmap in Figure 18 further emphasizes the co-occurrence of RMSE and MAE, confirming their joint prevalence in evaluation studies.

The main challenge arising in this context is how to choose the best evaluation metric given the specific task and the generative model architecture. Can this process become standardized and systematic? To better understand the choice of the evaluation metric, we need to take into account, among other factors, the type of our data. For instance, when considering short-term load forecasting, it may be viewed as a series of points, and thus metrics such as MSE of RMSE seem like the best choice. However, by choosing a pointwise evaluation metric, the property of time is lost, and the correlations between the points in the series are overlooked. This discrepancy emphasizes the importance of the broader question of how to design or select evaluation metrics that accurately reflect the practical value of a generative model in a given task. Future work should consider the development of task-aware composite metrics that integrate both statistical accuracy and operational relevance—such as combining distributional similarity with lead time sensitivity, meaning how much the relevance of a prediction depends on how far in advance the prediction is made before the actual event occurs. Another example is combining reliability metrics that reflect the overall consistency of a model’s performance across different scenarios, time periods, and inputs with the frequency of false alarms. A model might exhibit a low false alarm rate, meaning it is rarely incorrect in its positive predictions. However, it could still be unreliable if its performance degrades significantly during high load periods or if it produces drastically different outputs in response to minor input variations. Moreover, metric selection should ideally be adaptive to the intended use case. For example, anomaly detection in power quality events may prioritize sensitivity and specificity, while synthetic data generation for training other models may emphasize distributional realism and diversity.

The investigation into uncertainty quantification methods, also presented in Figure 18 and Figure 19, reveals a less concrete methodology. While “Other” probabilistic measures again dominate, implying a wide array of approaches, standard deviation (STD) and Wasserstein Distance (WD) emerge as relatively more frequently utilized measures compared to others like Spectral Subtraction (SS), Minimum Subtraction (MS), Variance (Var), and Cross Entropy (CE). This suggests that while a variety of uncertainty quantification techniques are being explored, there is no clear consensus or dominant methodology established within the context of generative models deployment for power systems applications. Interestingly, Figure 19 further indicates that uncertainty quantification efforts in this field are more heavily biased towards addressing aleatoric uncertainty rather than epistemic uncertainty. This emphasis may reflect the inherent stochasticity and variability prevalent in power system data and operational environments, making the quantification of data-driven uncertainty a primary concern. Furthermore, it may be observed that across all model types, “Point Prediction” metrics, assessing direct accuracy in forecasting or estimation tasks, and the “Other” category, encompassing diverse domain-specific or less standardized measures, appear with significant frequency. This reinforces the earlier observation about the reliance on standard performance metrics while also highlighting the continued presence of varied, potentially less conventional evaluation approaches. Interestingly, Generative Adversarial Networks demonstrate a pronounced incline towards the “Other” category in evaluation, suggesting that for GANs, domain-specific or specialized metrics might be favored over more generic performance indicators. This could reflect the inherent complexities in evaluating the quality of GAN-generated synthetic data or the diverse applications of GANs in power systems demanding tailored assessment approaches. In contrast, Variational Autoencoders and GPT models exhibit a stronger emphasis on “Point Prediction” metrics, implying a focus on tasks where direct predictive accuracy is necessary. Diffusion models present a more balanced profile, with a relatively even distribution between “Point Prediction” and “Other” categories, and a notable, albeit smaller, usage of “Distribution” metrics. This might indicate the evolving field of Diffusion model evaluation, with researchers exploring a broader range of metrics including those capturing the distributional fidelity of generated samples. The less frequent occurrence of categories like “Statistical Performance”, “Cross-Validation”, “Classification”, and “Decision” across all models may suggest that these more specialized or computationally intensive evaluation approaches are currently less prevalent in the reviewed literature.

Nonetheless, the operational validity of these uncertainty quantification methods remains an open challenge. Most methods are evaluated in simulation environments or based on synthetic datasets, which, although useful for controlled benchmarking, do not capture the full complexity of real-world grid dynamics. For example, uncertainty arising from measurement noise, variability in production from renewable energy sources, and hidden system interactions is often far more volatile and correlated than what is typically assumed in modeling frameworks. As such, it remains unclear whether the uncertainty bounds produced by current methods are well-calibrated or trustworthy enough to support critical decisions like dispatch adjustments, fault detection, or contingency planning in live systems. In their current form, the proposed uncertainty quantification methods may not fully capture the complexity and variability of real-world power system operating environments. While they offer a structured framework for modeling different uncertainty sources—such as measurement noise, model stochasticity, and incomplete data—their accuracy and calibration often rely on assumptions (e.g., Gaussian noise, independent inputs) that may not hold in practical grid scenarios. Real systems are subject to correlated disturbances, nonstationary behaviors, and abrupt events like faults or market shifts, which are difficult to model or anticipate purely from training data. Therefore, although these methods provide valuable insights in simulation and controlled experiments, their ability to reliably reflect operational uncertainty in complex environments remains unproven without systematic validation. To be actionable in real-time grid applications, uncertainty estimates must be not only theoretically sound but also empirically aligned with observed outcomes—demonstrating calibration, robustness, and responsiveness under high-dimensional, dynamic, and data-scarce conditions.

In addition, the analysis of data types reveals a strong preference for utilizing real-world power system data in conjunction with generative models, as shown in Figure 17. This inclination towards real data underscores the practical orientation of research in this domain, aiming to develop models that are effective and reliable in real-world operational settings. The limited use of synthetic data may suggest that while synthetic datasets can be valuable for initial experimentation or stress-testing, the ultimate benchmark for generative models in power systems lies in their performance on authentic, real-world datasets. In conclusion, the reviewed literature demonstrates an emerging field focused on applying generative machine learning models for different tasks in the domain of power systems. Key trends include the rapid growth of research, particularly surrounding Diffusion models, a reliance on standard evaluation metrics (RMSE, MAE) alongside a diverse set of “Other” metrics, a varied landscape of uncertainty quantification methods with a focus on aleatoric uncertainty, and a strong emphasis on real-world data validation. Future research may consider addressing the potential need for standardized evaluation benchmarks and further explore the application and validation of diverse uncertainty quantification techniques, especially in coping with epistemic uncertainty. Figure 20 provides visualization of the relationships between specific generative model architectures, the types of tasks they are employed for, and the power system application domains they address. Notably, GANs exhibit a strong association with generation tasks, indicating their prevalent use in generating synthetic power system data, potentially for scenarios like data augmentation or simulation-based studies. Diffusion models, on the other hand, appear prominently linked to prediction and estimation tasks, suggesting their suitability for forecasting power system states or parameters and for state estimation processes. VAEs and, to a lesser extent, GPT models show connections to classification and data recovery tasks. This implies their utility in applications such as fault classification, anomaly detection, or completing missing data within power system datasets. Across task categories, prediction and estimation emerge as central application areas for generative models, while in terms of power system domains, the applications seem distributed across Distributed Energy Resources (DER), Storage Management (SM), Power Quality (PQ), Energy Markets (EM), and Grid Stability and Control (GSAC). This visualization underscores the diverse applicability of different generative model types within the power systems field.

Table 2. Summary of generative model tasks, used for various power systems applications, their benefits, and challenges.

Application Area	GenAI Tasks	Main Benefits	Main Challenges
Power Quality (PQ)	Detection, classification	Enhanced detection of voltage/current waveform distortions; adversarial robustness explored in classifiers	Susceptibility to adversarial attacks; lack of interpretability in safety-critical decisions
Distributed Energy Resources (DER)	Generation, prediction, estimation	Improved scenario generation for DER expansion planning; uncover synergies in multienergy planning	High computational costs; need for large and diverse training datasets
Grid Stability and Control (GSAC)	Detection, classification, estimation, prediction	Improved transient stability analysis with synthetic unstable case generation; data-driven security assessment	Limited robustness under real-time fluctuations; uncertainty bounds remain poorly quantified
Energy Markets (EM)	Prediction, estimation	Enhanced electricity price forecasting; facilitates market strategy evaluation under uncertainty	Lack of standardized benchmarks for model comparison; social bias in training data may affect fairness
Energy Storage Management (SM)	Generation, estimation, prediction	Efficient ESS operation through realistic demand simulations; support for risk-averse optimization	Integration with existing infrastructure is costly; explainability needed for decision transparency

summarizes generative model tasks, used for various power systems applications and their benefits and challenges. The keywords used for this search are presented in

Table 3. Keywords for different application areas in power systems and generative models.

First-Level Keywords	Second-Level Keywords	Third-Level Keywords
Deep learning	Diffusion models	Power systems
Deep learning	Power systems	Generative tasks
GPT
Attention
Large language models
Transformerencoder
Deep learning Transformer
Generative Adversarial Networks
Variational Autoencoder
Generative ai

.

While much of the research regarding uses of generative AI for power system applications remains academic, several projects and pilot implementations have already begun demonstrating practical value in real-world energy settings. For instance, the US Department of Energy’s Pacific Northwest National Laboratory published a report highlighting the integration of generative deep learning models for forecasting and grid anomaly detection. Specifically, they demonstrate that generative models can significantly reduce false positives in fault detection and improve energy demand forecasting by synthesizing realistic training data under limited data regimes [96]. On the industrial side, the Dutch grid operator “Alliander” has launched operational deployments involving synthetic data generation to improve anomaly detection and asset maintenance predictions. Using generative AI models, they simulate various Transformer failure scenarios to train classifiers without exposing real infrastructure to risk. Similarly, “Enexis” Group explores the application of generative AI for predictive maintenance by generating diverse stress-test conditions for critical grid components, especially in aging urban infrastructure [97,98]. Complementing these deployments, the “Grid-FM” project under “LF Energy” presents a concrete open-source initiative aimed at using generative models to simulate flexible grid topologies and load profiles. These simulations support planning and operation strategies under uncertain renewable integration scenarios [99]. On a broader European policy level, the “GenAI4EU” initiative, backed by the European Innovation Council, identifies generative AI as a strategic enabler for grid resilience, specifically promoting its use in dynamic market simulations and Digital Twins for national energy systems [100]. A pilot case within this program has focused on the automated generation of energy usage scenarios across smart building clusters to evaluate storage control strategies, showing substantial improvement in control robustness and energy balancing efficiency [101].

5. Challenges

5.1. Data Scarcity and Computational Complexity

One major challenge in applying generative AI for power systems applications is the scarcity and quality of available data. Generative models use statistical techniques for learning. Thus, to accurately mimic the real underlying statistics, they require large amounts of data for training. Obtaining enough balanced and diverse data samples can be difficult in many power systems areas. Additionally, the computational complexity of training large generative models, such as GANs and Diffusion models, can be significant, often requiring specialized hardware and software. Not only that, but integrating generative AI into existing power system infrastructures, which are not designed and planned to interact with local processing units, will require substantial monetary investment and time.

5.2. Robustness and Reliability

Generative models exhibit limited robustness and reliability in power system applications. The models must be able to generate accurate and realistic outputs, even under uncertain and dynamic conditions. For instance, for the application of power flow analysis, the model needs to generate a control sequence. However, the model also needs to take into considerations fluctuations caused by transient effect, which may not appear in the data it was trained on. The uncertainty inherent to different aspects of power system operations presents significant challenges for integrating generative models in real-time applications. Generating accurate and timely solutions or forecasts requires tailored algorithms, which are aware of the systems dynamics and stochastic nature, and advanced computing resources. To continue this line of thinking, there is not enough information about uncertainty bounds of these models. That is, we cannot quantify the amount of variability in the generated output of these algorithms. This puts in question the reliability of these models and may prevent power experts from using them. It is essential to understand the potential variability and uncertainty in generative outputs to ensure the systems integrity.

5.3. Safety and Interpretability

Adversarial attacks manipulate input data to mislead machine learning models and represent a significant security vulnerability in machine learning systems. These attacks pose a critical cyber–physical risk since by altering the model’s output, they may lead to incorrect functioning and jeopardize the integrity of the systems operation. For instance, they may alter the decision of a machine learning classifier regarding the type of Power Quality Disturbance it detected, as illustrated in Figure 21. This is particularly critical in the field of power systems, where decisions informed by deep learning directly influence physical processes. In this context, for example, an adversarial attack could manipulate sensor readings to a mislead fault detection algorithm or compromise load forecasting systems, resulting in equipment failures or blackouts.

Additionally, the interpretability of generative models might play an important role for operational decision-making. Generative models, while powerful in their ability to simulate, predict, or generate data, often lack the transparency needed for critical decision-making in fields such as power systems. This interpretability gap raises questions about the reliability and accountability of these models. For instance, in power systems, experts must understand why a model predicts certain failure probabilities or recommends specific energy dispatch strategies. Without a clear understanding of the model’s reasoning and underlying mechanisms, it may be difficult to justify actions or decisions based on the model’s outputs.

5.4. Social and Environmental Challenges

Deep learning models aim to learn the real underlying statistical distribution of data samples they train on. However, in some cases, the collected samples are not representative of the entire population or problem space. There are different factors that may affect the data variability, for instance, errors or inconsistencies in how data are collected or labels in the dataset that are biased due to human judgment. This bias in the training data may lead to incorrect modeling of the underlying probability function. This raises ethical concerns, since it may lead to unfair or discriminatory outcomes. For example, if the model is used for resource allocation, it may prioritize wealthier urban areas. This could lead to inequalities in power distribution and maintenance, as those in less affluent areas may face poor service quality.

Furthermore, generative models usually require extensive training on vast datasets to learn complex distributions of data. They typically necessitate thousands or even millions of iterations to learn. Each iteration involves performing operations on high-dimensional data, requiring substantial computational resources. However, the data centers which host specialized hardware needed to train and run deep learning models require an enormous amount of electricity to power the systems and keep them cool. These data centers are often located in regions that have access to cheap energy, since it is mainly sourced from fossil fuels. This reliance on nonrenewable energy sources contributes directly to carbon emissions and may have significant environmental effects. The high energy consumption of dedicated hardware used for deep learning, such as large farms of GPUs or TPUs in data centers located in places like Nevada, has significant environmental implications. These data centers, which host the specialized hardware needed to train and run deep learning models, require an enormous amount of electricity to power the systems and keep them cool. In regions like Nevada, where such facilities are often located due to favorable tax conditions and access to cheap energy, much of this electricity is still sourced from fossil fuels, particularly natural gas and coal. This reliance on nonrenewable energy sources contributes directly to carbon emissions.

The challenges presented in this section are summarized in

Table 4. Summary of challenges in applying generative AI for power systems.

Category	Challenges
Data scarcity and computational complexity	Difficulty obtaining large, balanced, and diverse datasets. High computational requirements for training generative models. Integration into existing power systems requires significant investment.
Robustness and reliability	Limited ability to handle uncertainty and dynamic conditions. Lack of quantifiable uncertainty bounds for generative outputs. Dependence on tailored algorithms and advanced computing resources.
Safety and interpretability	Vulnerability to adversarial attacks, risking system integrity. Lack of interpretability hinders critical decision-making. Challenges in understanding model predictions for operational decisions.
Social and environmental challenges	Bias in training data can lead to unfair outcomes (e.g., resource allocation). High energy consumption and environmental impact of training generative models, often reliant on fossil fuels in data centers.

.

6. Future Research Directions

6.1. Standardizing Data and Evaluation Frameworks

A significant barrier noted in this review is the lack of standardized evaluation benchmarks for generative models used in power system applications, particularly for control tasks. Establishing unified and reproducible testing frameworks is important for promoting the fair comparison and reliable evaluation of generative models in this important sector, even if only as an assisting tool. Naturally, a possible future research direction addresses practical measures that need to be taken for promoting standardized dataset libraries and unified evaluation protocols. To begin with, the surge in Internet of Things devices and advanced smart metering infrastructure presents an unprecedented opportunity to collect high-fidelity, real-world operational data at scale. Leveraging these technologies can help build comprehensive datasets reflecting diverse operating conditions and system dynamics. However, access to such data is often restricted due to privacy, security, and commercial sensitivities. Therefore, a significant push towards policy shifts is necessary, mirroring initiatives like those emerging in Europe, where policymakers encourage and fund collaborative projects between industry, academia, and government entities to create standardized, open-source datasets for research and benchmarking [100]. In addition, where real data remain scarce or insufficient, particularly for rare events or future scenarios, synthetic data generation is a viable alternative. One pathway involves developing standardized analytical models, perhaps based on well-understood mathematical approximations or principles that stem from the system’s dynamics, from which diverse and representative data samples can be derived. This ensures a degree of consistency and comparability across studies using synthetic data. Lastly, generative models themselves can be a powerful tool for creating high-fidelity synthetic datasets. However, this approach requires extreme caution and rigorous validation. Future work may examine methods for evaluating the performance and realism of these generated datasets, ensuring they correlate meaningfully with real-world phenomena and capture relevant statistical properties. Furthermore, as is discussed extensively in Section 6.3, enhancing the explainability of the generative models used for data synthesis may lead to a better understanding of the physical phenomena themselves. Understanding how these models learn from scarce real data to generate new samples can increase confidence in the synthetic datasets and ensure they capture the intended system behaviors rather than spurious correlations or biases. Developing these standardized datasets and associated evaluation protocols will be essential for comparing different generative models objectively and advancing their reliable integration into various power systems applications.

6.2. Combination of Deep Learning Models

The origin of the generative approaches reviewed in this work stems from different statistical methods. Some sprouted from signal processing methods for estimation, such as autoregressive models, while others evolved from statistical theory of Markov chains. However, these approaches are not contradicting but rather have distinct characteristics that can be combined to create hybrid models that leverage the advantages and properties of each method. For instance, Diffusion models rely on Markov chains, which is a stochastic process describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event. Combining it with an autoregressive model may allow us to attend to both short- and long-range dependencies in stochastic processes. These combinations may be adjusted to specific power system applications for which the statistical nature of these hybrid models is adequate. One important field of study that targets this exact objective focuses on control and management of shared services of energy storage devices for smart buildings. Several works address this subject. For instance, work [103] introduces a stochastic bilevel optimal allocation approach for intelligent buildings (IBs) that considers energy storage sharing (ESS) services to reduce investment costs and improve energy efficiency. The proposed model optimizes the planning of an ESS station at the upper level and the operating costs of individual IBs at the lower level, accounting for uncertainties in electricity prices and leveraging the thermal inertia of buildings. The results demonstrate that this approach can decrease the investment cost of energy storage, enhance the utilization of renewable energy, lower the annual operating costs for IBs while ensuring user comfort, and that considering building thermal inertia further improves economic benefits for both the ESS station and IBs. From a slightly different perspective, study [104] proposes a risk-averse decentralized energy management strategy for integrated electricity and heat systems with intelligent buildings. To achieve this, the authors formulate a thermal dynamic model for buildings that considers vertical height to represent heating conditions more accurately. The strategy incorporates a CVaR-based risk evaluation method to mitigate uncertainties in renewable energy sources and energy prices and employs a two-stage accelerated asynchronous decentralized ADMM algorithm to solve the energy management problem efficiently while preserving privacy. The results show that this approach effectively limits system risks, enhances solving efficiency, and accounts for vertical heating imbalances in buildings.

A natural link for generative models is the combination with reinforcement learning methods. These techniques are increasingly adopted in the power systems domain in various control tasks. There are several possible ways to communicate between these two distinct approaches, namely, by generating the environment for the reinforcement learning agent, generating the parameters of the agent’s network, or shaping the reward function to better suit the requirements of the power expert or user. From another perspective, the generative model can be used for explanation of the policy produced by the reinforcement learning agent. It can generate textual or visual output to clarify the reasoning of the reinforcement learning algorithm, adding a layer of transparency and enabling power experts and users to better understand and trust the suggestions produced by the model.

6.3. Explainability

Generative models show remarkable achievements in many disciplines and are highly suitable for power system applications, mainly due to their ability to process large amounts of serial data. However, it is not clear what the contextual connections they infer are and how their inner mapping generates the output from the input. The large scale of these models, with million of parameters connected by nonlinear functions, makes them uninterpretable by humans and unreliable. Their “black-box” nature makes it hard to trust these models both by power experts and users.

A possible approach to address this challenge is to add an aspect of explanation to these models. For instance, by applying explainability techniques, we can better understand the outcomes of the model without compromising its accuracy or making any structural changes. This layer of transparency will allow experts to detect contextual inaccuracies the model relies on and “guide” it so it will use more accurate reasoning, as demonstrated in Figure 22. This enables us to implicitly incorporate domain knowledge and human feedback, as discussed in Section 6.4. This concept started to emerge in the recent literature, as may be seen in works [105,106].

6.4. Incorporating Domain Knowledge

Generative models rely on statistical learning, meaning they analyze and find relations between large amounts of high-dimensional data. Nevertheless, the problems that arise in the context of power systems often have a structured dynamic behavior or some physical constraints that must be met. Using expert intuition and knowledge about the mathematical description, even if it is inaccurate, may substantially reduce the dimensions of the search space and significantly reduce training time. Moreover, the stability and proper operation of dynamic systems is fragile and affected by environmental signals, which may often cause unexpected behavior and add a stochastic element to the output of the mechanical system. This uncertainty might be predicted by power experts that investigate different transient effects of the system, and informing the generative model about variations in the input data or possible fluctuations that should be taken into consideration might result in robust and resilient models that generate more accurate data or produce more realistic simulations. On this basis, another possible improvement that needs to be considered is adjusting the model to process human feedback during its training. This possibility might serve as a heuristic and guide the training of the model, refining the hyperparameter tuning process and reducing training times.

6.5. Adaptive and Energy Efficient Models

Physical processes in power systems are inherently nonstationary and time variant. The optimal control policies evolve over time, subject to changes in system conditions. Hence, generative models must be aware of this variability in the systems dynamics and adjust their output accordingly. To address this challenge, they may take advantage of several concepts from other disciplines, such as signal processing and classical control theory. For example, concepts such as hierarchical decomposition, adaptive learning mechanisms, or domain-specific knowledge may aid in handling the nonstationary behavior of the environment. One approach is to decompose the complex dynamics into different hierarchical levels, such as varying time scales, frequency scales, or operational modes. By separating the input signal into these distinct levels, the generative model can examine each level in the context of itself and in the context of other levels and produce more accurate output. This structured analysis may also speed up training. In addition, general-purpose generative models are designed to be adapted to new tasks as they arrive. Incremental updates of models, by introducing them to new real-time data, improve their adaptability, allowing us to adjust these models to the changing systems conditions without training them from scratch.

In some cases, domain knowledge such as symmetries, conservation laws, and periodic behavior of the dynamics can be introduced and implicitly incorporated into the generative model. These properties may be used to reduce the dimensions of the time series the model processes. Moreover, in this manner, it allows us to incorporate knowledge about the possible variations of the signal due to known noise types. This knowledge can help the model in coping with the inherent uncertainty typical for power systems. Furthermore, utilizing techniques like the dq0 transformation may also reduce the dimensionality of the input series so that the model can look for temporal and spatial relations in a simplified domain where the input series elements exhibit linear or time-invariant properties. This domain-informed guidance can help focus the contextual relation search and may potentially improve both efficiency and robustness. The time dependency of the serial input to the model may also aid data augmentation. For instance, the generative model can create synthetic datasets with reduced dimensions by focusing on key time intervals or grid conditions that reflect system states. In addition, by applying temporal smoothing techniques, such as moving averages or exponential smoothing, generative models can reduce noise in time-varying data, which helps in learning more stable, long-term patterns. In this light, there are many future research directions toward more adaptable and efficient generative models suited for power system applications.

6.6. Integration with Digital Twins

The Digital Twin, a digital model of an intended or actual real-world physical system, serves as a digital counterpart for purposes such as simulation and monitoring. When combined with generative models, this digital representation can be used to predict and simulate a wide range of power system scenarios, including demand fluctuations, renewable energy generation, and grid faults. Generative models can learn from the vast amount of data generated by this virtual representation, allowing them to generate more accurate and reliable predictions about future system states and aid in decision-making processes. This integration could enable operators to foresee potential problems before they occur and test different operational strategies. Moreover, generative models can help simulate new conditions or forecast future grid behavior based on real-time data from the Digital Twin, even as the system evolves over time. This could be particularly useful in handling the uncertainties and complexities introduced by renewable energy sources, which have variable outputs. Over time, as the Digital Twin collects more data, the generative model can be updated to reflect new grid behaviors, thus allowing for more precise planning and more effective integration of decentralized energy resources.

6.7. Expansion Planning

The structural planning of the grid and development of the grid needs to adapt to the increase in electricity demand, new production sources, and technological advancements. In this light, generative models may serve as an advanced tool that may help decision-makers and engineers by generating plausible future scenarios that reflect uncertainties stemming from consumption profiles, unreliable renewable energy sources production, and transient effects. These models can synthesize diverse planning conditions, including extreme events and variable market dynamics, providing a rich set of alternatives for evaluating planning decisions. This approach contrasts with conventional scenario analysis, which often relies on manually crafted or limited synthetic scenarios and allows for more granular and probabilistic insights. Naturally, this wide topic, expansion planning, diverges into several important subjects in which generative models may assist as an advisory decision-making tool or, alternatively, point out specific problems in the designs. For instance, several examples include generation expansion planning, where generative models can simulate diverse demand and policy scenarios to identify optimal Distributed Energy Resources (DER) configurations, or energy storage expansion planning, in which models can evaluate the performance of various energy storage type deployment strategies under uncertain load and renewable profiles. Another subject concerns transmission or distribution expansion planning, where generative simulations can reveal infrastructure bottlenecks or the impact of extreme operating conditions. Additionally, in multiexpansion planning, such as the co-optimization of DER and energy storage, generative models can uncover synergies and trade-offs between different asset types, locations, and sizing. Finally, generative models can also enhance related tasks like energy storage localization and sizing within existing grids. These models can identify optimal grid locations and the maximum capacity of energy storage devices to most effectively improve local frequency stability, congestion mitigation, and resilience. In summary, generative AI holds significant promise for enriching and streamlining expansion planning processes. By leveraging its capacity for rapidly generating diverse and realistic scenarios and its ability to learn intricate statistical relationships within complex datasets, generative AI can provide planners with a more comprehensive and insightful understanding of potential future states and uncertainties. This enables more robust and adaptive long-term planning strategies.

6.8. Security and Safety of Information

An exciting and practical future research area concerns the challenges of secure and privacy-preserving information processing by generative models. Many power system applications involve sensitive operational data—such as load forecasts, fault logs, or control commands—that must be protected from manipulation, theft, or leakage. Given the distributed nature of modern smart grids, relying on centralized data repositories may pose risks to data integrity and system resilience. Therefore, research is exploring decentralized alternatives to address these vulnerabilities. For example, blockchain and federated learning offer a conceptual framework for enabling secure, decentralized learning environments in systems that aim to incorporate generative models. These approaches present a paradigm shift in how we think about and manage data, transactions, and trust, potentially offering solutions for secure and private processing of sensitive power system data.

Blockchain technology, initially developed for secure transaction verification in digital currencies, presents a promising solution for ensuring the integrity and transparency of generative learning processes within distributed power systems. Its inherent characteristics as an unchangeable and auditable record can be employed to track significant aspects of model development and deployment. For instance, the origin of training data used by generative models at various grid points can be securely documented, establishing a clear history and accountability. Furthermore, blockchain can facilitate the verification of model updates and the validation of agreement reached among distributed learning agents. Mechanisms like proof-of-stake or a novel “proof-of-learning” could be implemented on a blockchain to confirm the contributions of generative models trained locally at substations or microgrids, ensuring the quality and trustworthiness of the combined knowledge without needing the direct sharing of private operational data. This approach may aid in securing private energy infrastructure from unauthorized modifications and may improve the overall reliability of generative models, assisting in delicate power systems control and management.

Federated learning offers a complementary strategy for addressing data privacy concerns in collaborative generative model training across different power grid entities. By allowing utilities, prosumers, and distributed energy resource operators to train models on their local datasets without direct data exchange, federated learning inherently protects confidential operational information. The integration of blockchain with federated generative learning frameworks further strengthens security and trust in these collaborative environments. Blockchain’s immutable record can document the exchange of model parameters or gradients, creating auditable trails of the learning process. This transparency enhances verifiability and supports trust among participating nodes, potentially reducing the risk of malicious actors introducing data poisoning attacks or manipulating model updates. This research direction, combining federated learning and blockchain technology, offers a pathway towards improving scalability, security, and privacy protection when supporting the control and management of sensitive systems by using generative models. This may aid in advancing the incorporation of generative models as assisting tools for various applications, such as data augmentation and fault scenario synthesis, while adhering to stringent data protection regulations.

7. Conclusions

This review offers a detailed analysis of generative models used for different tasks in various power systems applications, notably highlighting the prevalent evaluation metrics and uncertainty quantification approaches and revealing key trends and gaps in their application.

Generative artificial intelligence (Gen-AI) methods are gaining increasing popularity in power system applications. However, the implementation of these models in the power system domain poses several interesting challenges. First and foremost, it is evident that the practical adoption of generative models is heavily dependent on the availability of high-quality, real-world datasets, as synthetic data alone may not always provide a sufficient benchmark for model validation. Furthermore, a comprehensive understanding of these models and their performance in power system-related tasks heavily depends on the statistical structure of the model itself, as is evident from the latest works reviewed above. In addition, power experts and machine learning scientists each perceive the nature of uncertainty, which is inherent in such problems, in a different way. Thus, a better understanding of the source of uncertainty, and its context may further promote the incorporation of generative models in power system applications. While a variety of uncertainty quantification methods—primarily focusing on data-driven uncertainty—are being explored, there is a need to better account for epistemic uncertainty.

The need for standardized evaluation benchmarks to be used as a reference of new and advanced models is imperative to promote the robustness of these models and their interpretability. Moreover, as highlighted in this review, the variety of evaluation techniques used for assessing a generative model’s performance is diverse. Generative models have demonstrated their utility across various power system applications, particularly in prediction and estimation tasks. Notably, Generative Adversarial Networks are commonly employed for data augmentation and synthetic data generation, while Diffusion models are increasingly used for forecasting and state estimation. In addition, Variational Autoencoders have shown promise in classification and data recovery tasks. Thus, this review underscores the importance of linking evaluation methodologies to the specific challenges posed by generative models in power systems, particularly in domains such as renewable energy integration, energy markets simulations, storage management, power quality assessment, and grid stability and control. Specifically, it is evident from this review that GANs often use diverse evaluation metrics from different categories, while VAEs and GPT models emphasize “Point Prediction”, which is important in tasks such as forecasting, in contrast to Diffusion models, which exhibit a more balanced approach.

One promising future research direction aims to establish standardized and system-specific evaluation benchmarks to ensure a correct and fair evaluation of the generative model’s performance. From the point of view of academic researchers, this may include developing mathematical assessment frameworks for performance evaluation or indicating specific properties of common statistical distributions and linking them to relevant applications in the power systems domain, such as stability impacts or economic benefits. Furthermore, another interesting direction concerns advancing uncertainty quantification techniques to effectively model epistemic uncertainty arising from model limitations and lack of complete knowledge. This could involve exploring hybrid methodologies that integrate statistical methods with power system domain expertise. Enhancing model interpretability through explainable AI (XAI) techniques is also important for building trust and facilitating the adoption of these models as advisory tools in sensitive infrastructure. Finally, investigating the synergistic integration of generative models with other advanced ML paradigms, such as reinforcement learning for adaptive control and optimization and Graph Neural Networks for modeling complex grid topologies, presents promising avenues for future innovation.

From the perspective of industry practitioners, a key actionable recommendation is to invest in the development and sharing of high-quality, real-world power system datasets, which are essential for training and validating robust generative models. Collaboration with academic institutions to evaluate the performance and uncertainty of these models on real-world scenarios may also promote this field. Furthermore, exploring and implementing privacy-preserving techniques like federated learning may impact greatly collaborative model development on sensitive operational data without compromising security or regulatory compliance. To conclude, the ongoing research on combining the remarkable abilities of generative models and applying them for power system uses is indeed an exciting and important subject, and although there are challenges to overcome, these models present interesting avenues for future research focusing on the application of generative models for power system optimization, forecasting, and control tasks.