A Multi-Objective Temperature Control Method for a Multi-Stack Fuel Cell System with Different Stacks Based on Model Predictive Control
Abstract
1. Introduction
2. PEMFC Dynamic Characterization Experiment
2.1. PEMFC and Test Platform
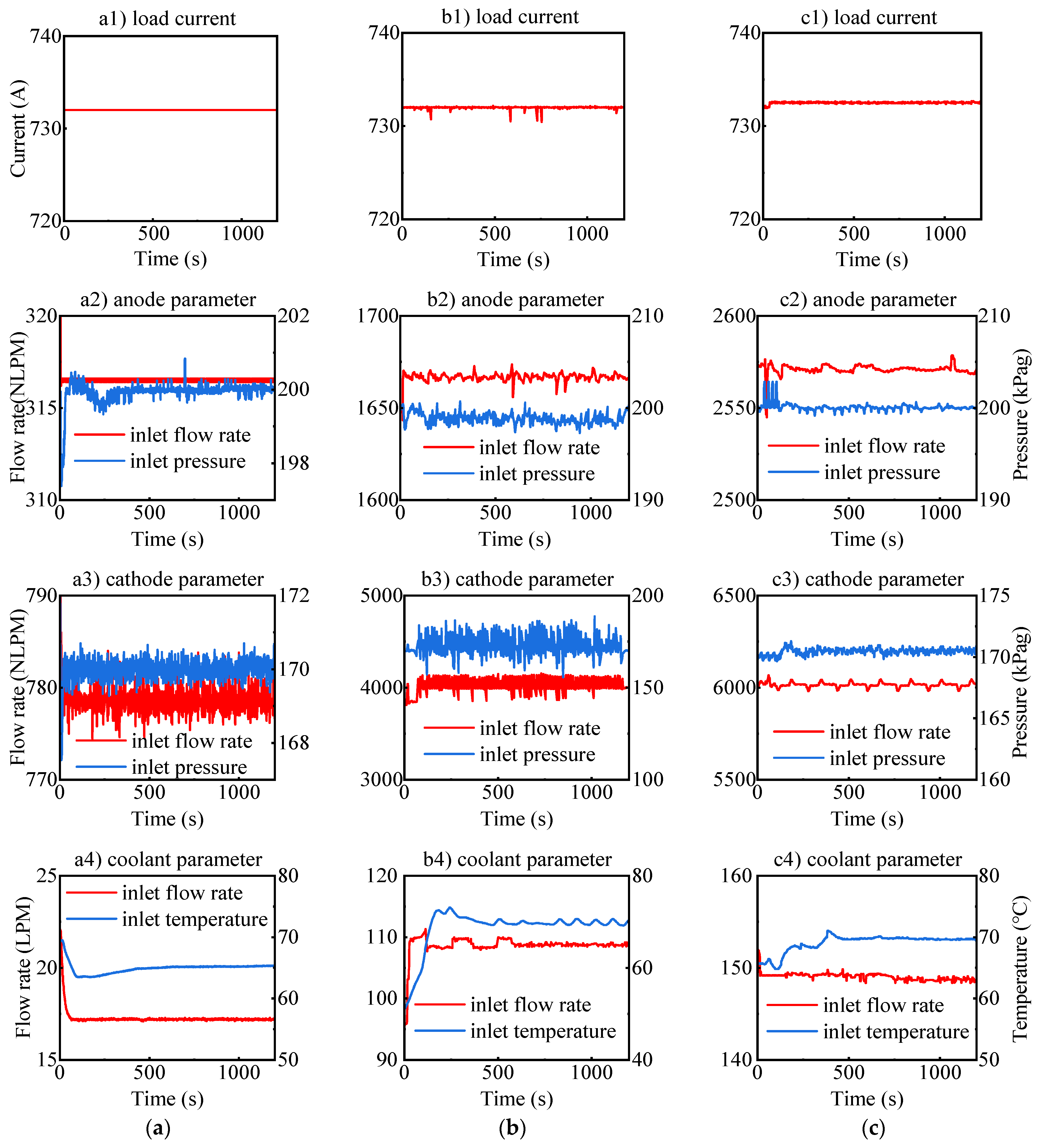
2.2. PEMFC Test Preparation
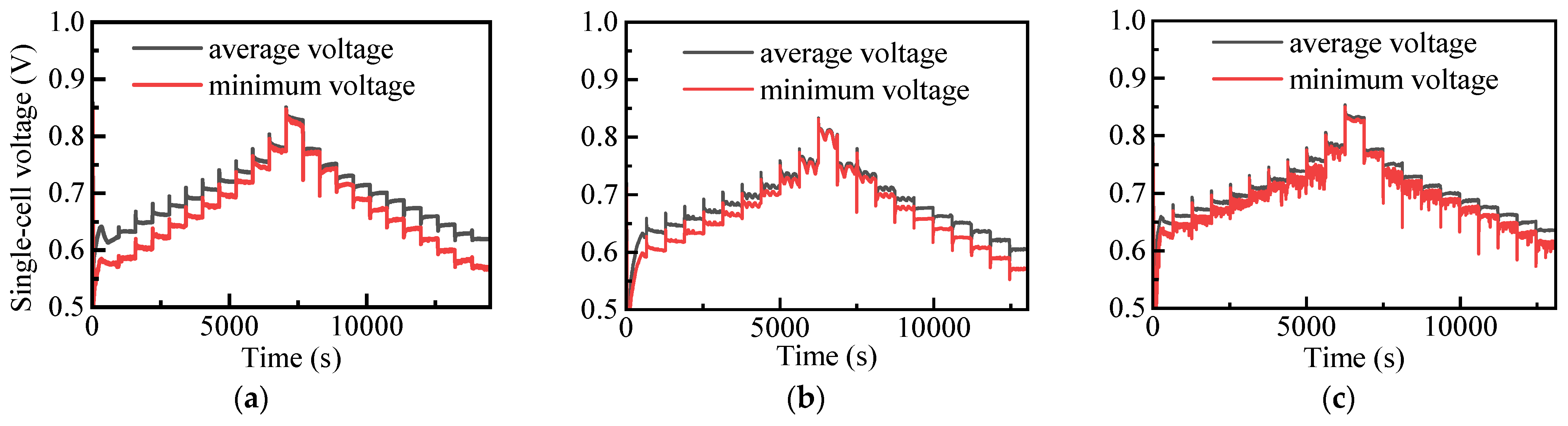
2.3. PEMFC Characterizations
3. MFCS Thermal Management System Model
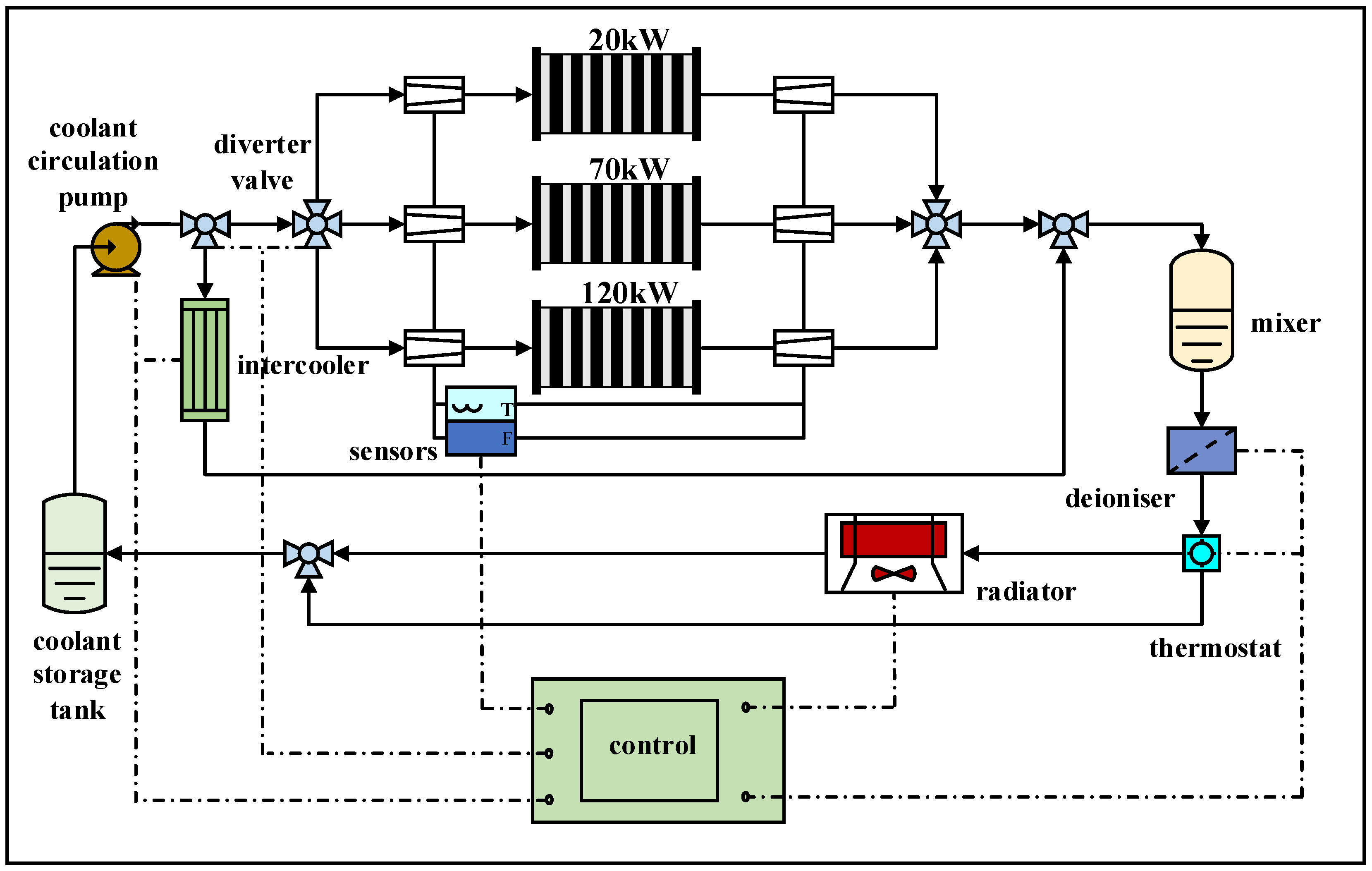
3.1. Thermal Management System Structure
3.2. Modeling of PEMFC Stack
3.3. Modeling of Thermal Balance
- (1)
- The gases involved in the electrochemical reaction are ideal gases;
- (2)
- Temperatures within each single cell are the same and in good consistency;
- (3)
- Each stack outlet coolant temperature is assumed to be the stack temperature;
- (4)
- Neglecting heat exchange between the circulating pipes and the environment.
4. Model Predictive Control of MFCS Stack Temperatures
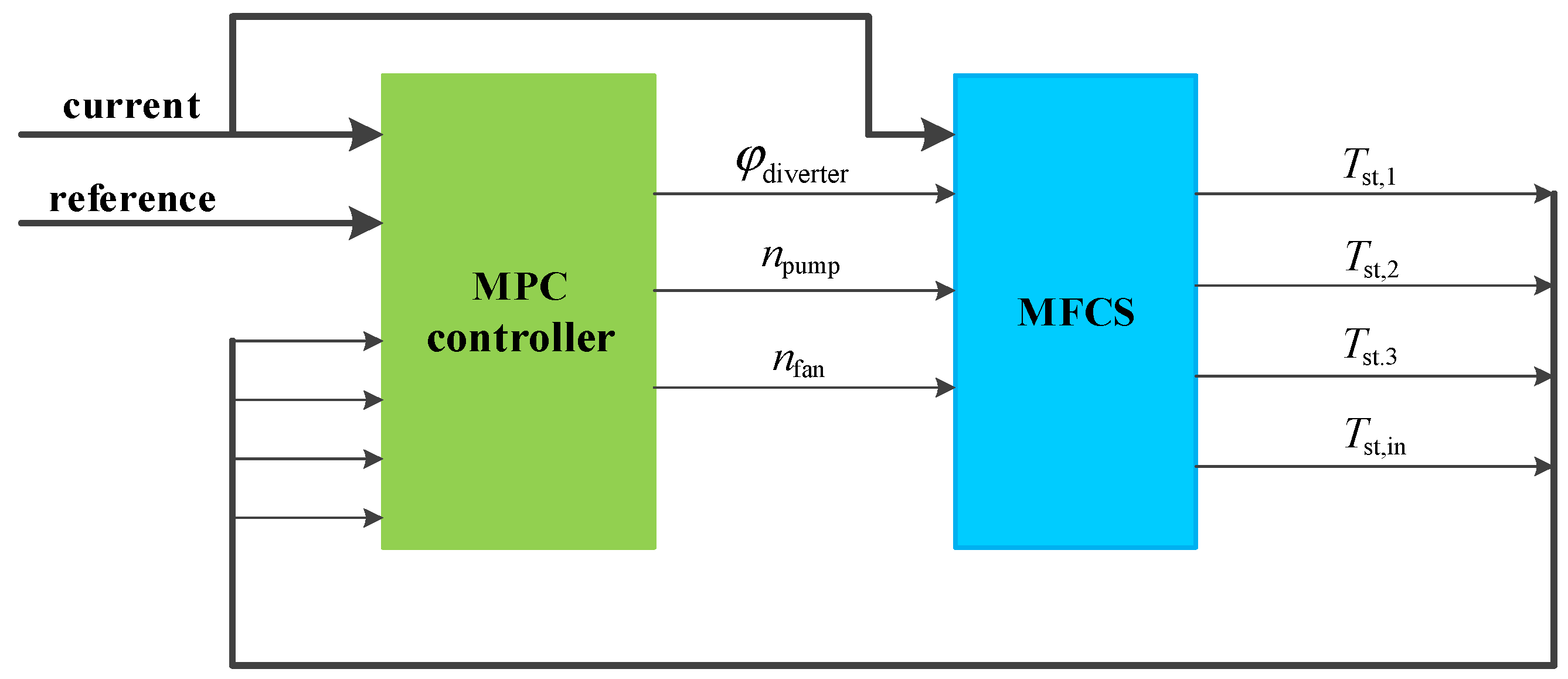
4.1. MFCS Thermal Management System Control Structure
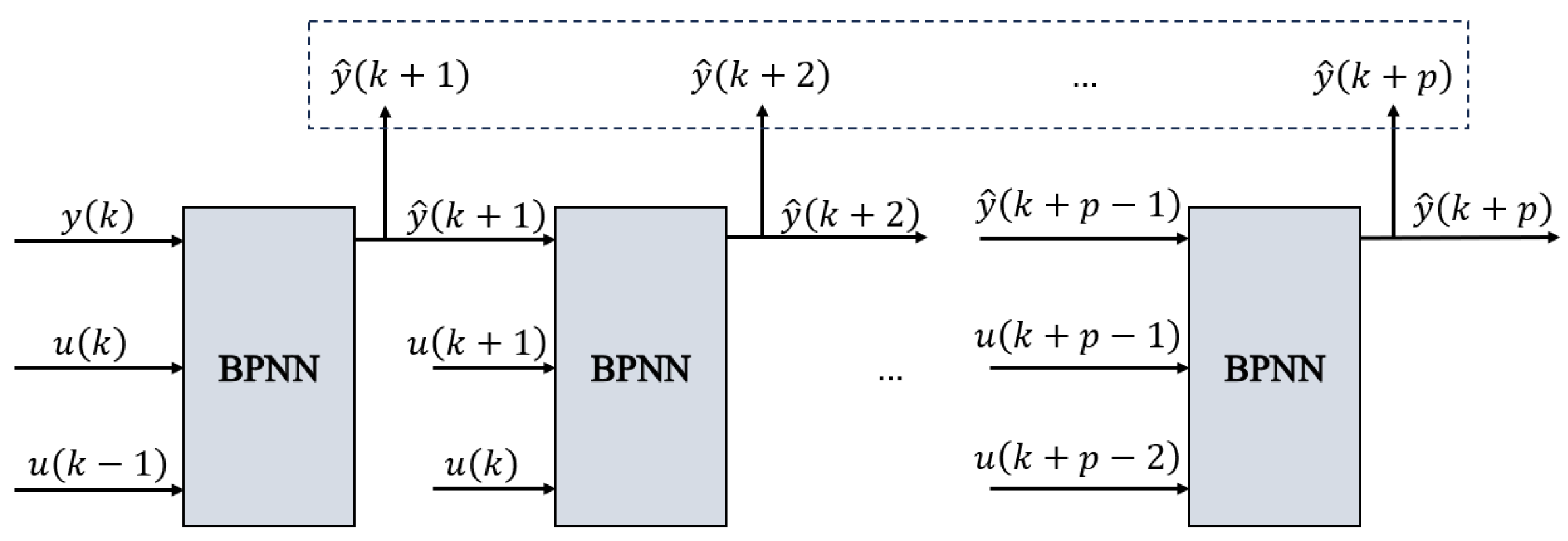
4.2. System Prediction Modeling of BP Neural Network
4.3. Design of the DMC
5. MPC Controller Simulation and Verification
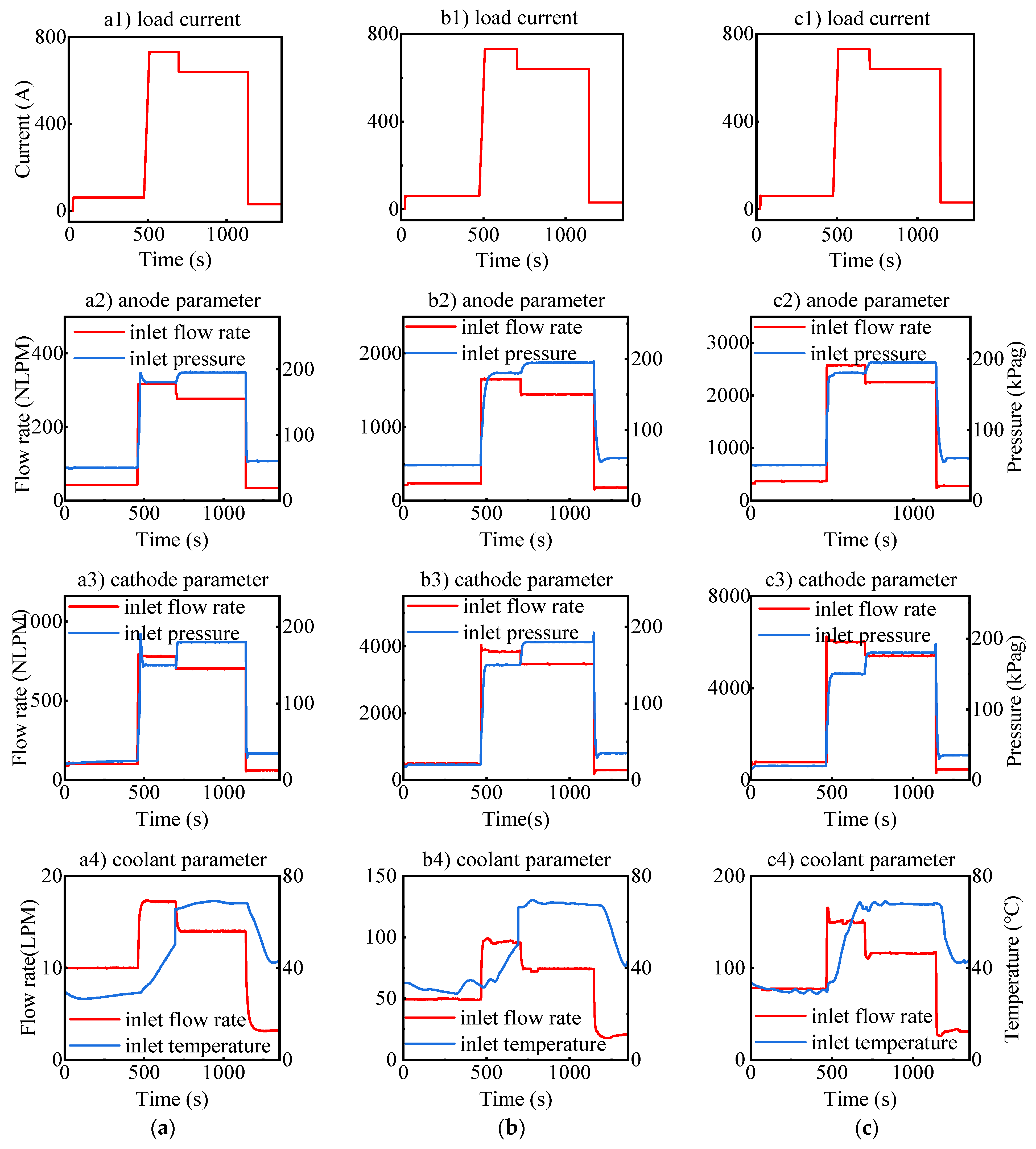
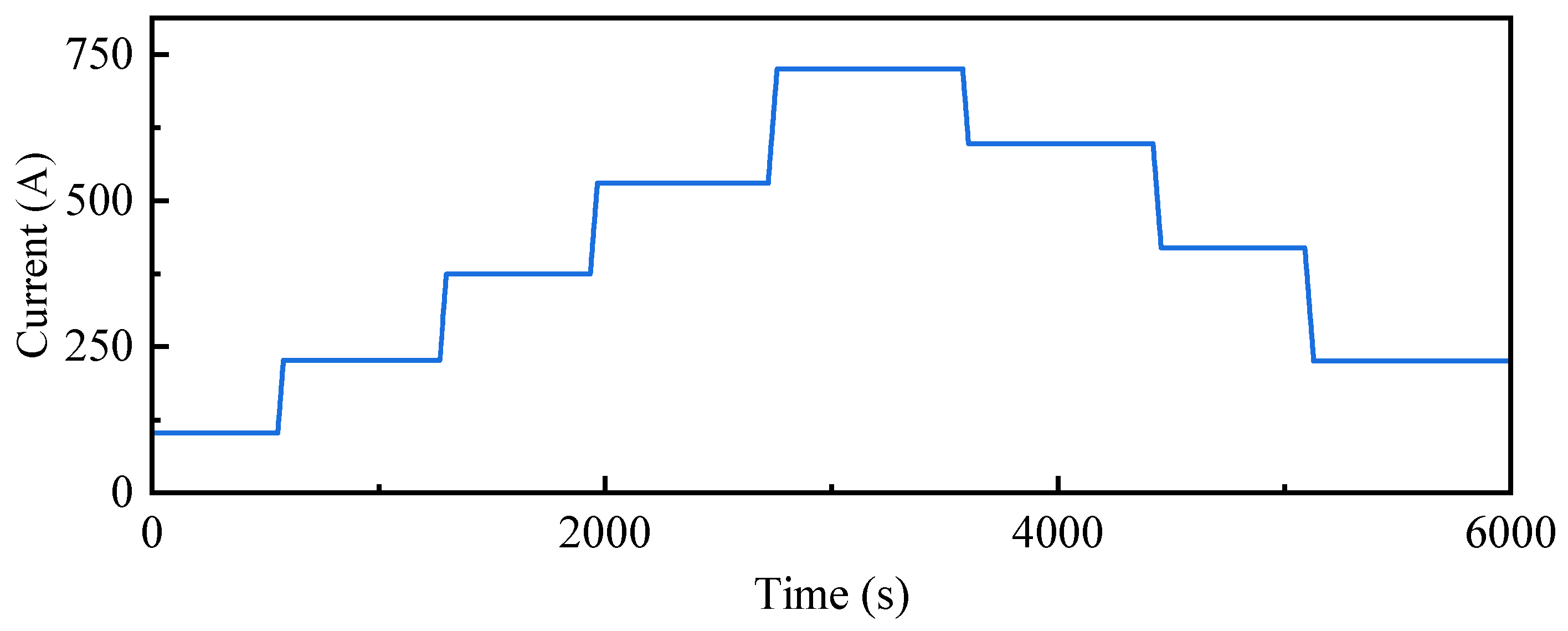
5.1. Design for Test Conditions
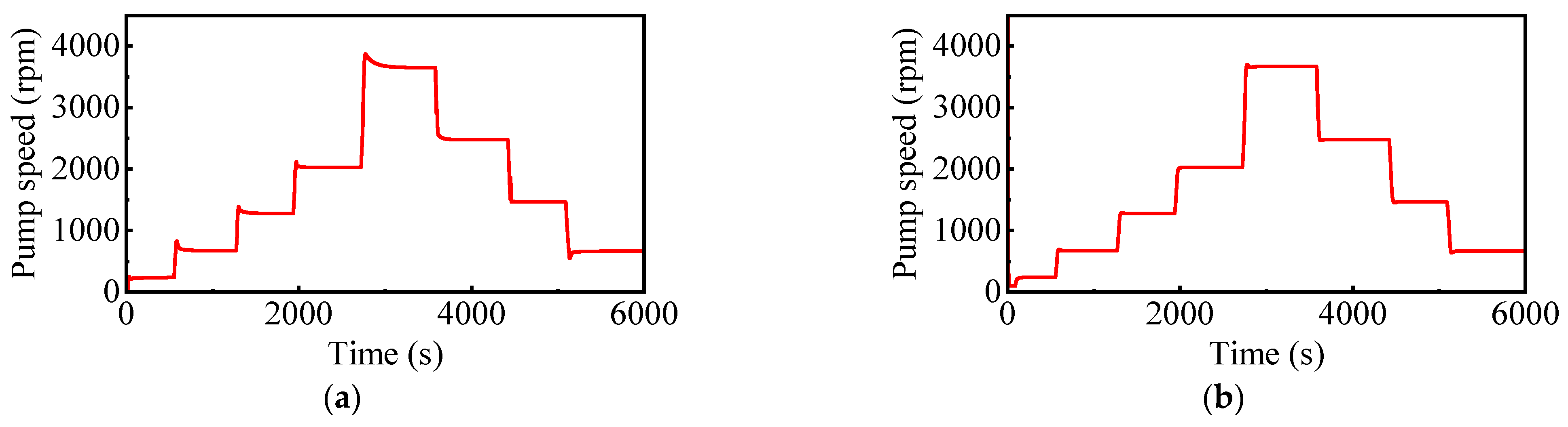
5.2. Analysis of Simulation Results Under Test Conditions
5.3. Verification of Dynamic Conditions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yu, X.; Wang, B.; Wang, W.; Guo, X.; Han, J.; Chen, X. Analysis of Renewable Resources in Central China under the “Double Carbon” Strategy. Energy Rep. 2022, 8, 361–373. [Google Scholar] [CrossRef]
- He, X.; Xiang, Q.; Jia, J.; Zhang, Z.; Yan, J.; Xu, Y.; Chen, D. Effect of Methyl Butyrate Blending on Soot Formation in Jet A Laminar Diffusion Flame. Fuel 2024, 376, 132598. [Google Scholar] [CrossRef]
- Aminudin, M.A.; Kamarudin, S.K.; Lim, B.H.; Majilan, E.H.; Masdar, M.S.; Shaari, N. An Overview: Current Progress on Hydrogen Fuel Cell Vehicles. Int. J. Hydrogen Energy 2023, 48, 4371–4388. [Google Scholar] [CrossRef]
- Roy, A.; Pramanik, S. A Review of the Hydrogen Fuel Path to Emission Reduction in the Surface Transport Industry. Int. J. Hydrogen Energy 2024, 49, 792–821. [Google Scholar] [CrossRef]
- Du, Y.; Li, Y.; Ren, P.; Zhang, L.; Wang, D.; Xu, X. Oxygen Transfer at Mesoscale Catalyst Layer in Proton Exchange Membrane Fuel Cell: Mechanism, Model and Resistance Characterization. Chem. Eng. J. 2024, 494, 153021. [Google Scholar] [CrossRef]
- Yang, X.-G.; Ye, Q.; Cheng, P. In-Plane Transport Effects on Hydrogen Depletion and Carbon Corrosion Induced by Anode Flooding in Proton Exchange Membrane Fuel Cells. Int. J. Heat Mass Transf. 2012, 55, 4754–4765. [Google Scholar] [CrossRef]
- de-Troya, J.J.; Álvarez, C.; Fernández-Garrido, C.; Carral, L. Analysing the Possibilities of Using Fuel Cells in Ships. Int. J. Hydrogen Energy 2016, 41, 2853–2866. [Google Scholar] [CrossRef]
- Jiao, K.; Xuan, J.; Du, Q.; Bao, Z.; Xie, B.; Wang, B.; Zhao, Y.; Fan, L.; Wang, H.; Hou, Z.; et al. Designing the next Generation of Proton-Exchange Membrane Fuel Cells. Nature 2021, 595, 361–369. [Google Scholar] [CrossRef]
- Shao, Y.; Xu, L.; Xu, L.; Zhang, X.; Wang, Z.; Zhao, G.; Hu, Z.; Li, J.; Ouyang, M. Water Management Issues during Load Cycling under High Temperature and Low Humidity Conditions Relevant for Heavy-Duty Applications of PEMFC. eTransportation 2023, 18, 100285. [Google Scholar] [CrossRef]
- Zhou, S.; Fan, L.; Zhang, G.; Gao, J.; Lu, Y.; Zhao, P.; Wen, C.; Shi, L.; Hu, Z. A Review on Proton Exchange Membrane Multi-Stack Fuel Cell Systems: Architecture, Performance, and Power Management. Appl. Energy 2022, 310, 118555. [Google Scholar] [CrossRef]
- Li, Y.; Yang, F.; Chen, D.; Hu, S.; Xu, X. Thermal-Physical Modeling and Parameter Identification Method for Dynamic Model with Unmeasurable State in 10-kW Scale Proton Exchange Membrane Fuel Cell System. Energy Convers. Manag. 2023, 276, 116580. [Google Scholar] [CrossRef]
- Liu, Y.; Gao, J.; Pei, P.; Yao, S.; Wang, F.; Qin, H. Effects of Dynamic Changes in Inlet Temperature on Proton Exchange Membrane Fuel Cell. J. Renew. Sustain. Energy 2019, 11, 044302. [Google Scholar] [CrossRef]
- Yang, L.; Nik-Ghazali, N.-N.; Ali, M.A.H.; Chong, W.T.; Yang, Z.; Liu, H. A Review on Thermal Management in Proton Exchange Membrane Fuel Cells: Temperature Distribution and Control. Renew. Sustain. Energy Rev. 2023, 187, 113737. [Google Scholar] [CrossRef]
- O’Keefe, D.; El-Sharkh, M.Y.; Telotte, J.C.; Palanki, S. Temperature Dynamics and Control of a Water-Cooled Fuel Cell Stack. J. Power Sources 2014, 256, 470–478. [Google Scholar] [CrossRef]
- Pei, Y.; Chen, F.; Jiao, J.; Ye, H.; Zhang, C.; Jiang, X. Fuel Cell Temperature Control Based on Nonlinear Transformation Mitigating System Nonlinearity. Renew. Energy 2024, 230, 120814. [Google Scholar] [CrossRef]
- Xu, J.-H.; Yan, H.-Z.; Ding, Q.; Zhu, K.-Q.; Yang, Y.-R.; Wang, Y.-L.; Huang, T.-M.; Chen, X.; Wan, Z.-M.; Wang, X.-D. Sparrow Search Algorithm Applied to Temperature Control in PEM Fuel Cell Systems. Int. J. Hydrogen Energy 2022, 47, 39973–39986. [Google Scholar] [CrossRef]
- Zhang, G.; Li, Q.; Chen, W.; Meng, X.; Deng, H. A Coupled Power-Voltage Equilibrium Strategy Based on Droop Control for Fuel Cell/Battery/Supercapacitor Hybrid Tramway. Int. J. Hydrogen Energy 2019, 44, 19370–19383. [Google Scholar] [CrossRef]
- Li, Q.; Yang, H.; Han, Y.; Li, M.; Chen, W. A State Machine Strategy Based on Droop Control for an Energy Management System of PEMFC-Battery-Supercapacitor Hybrid Tramway. Int. J. Hydrogen Energy 2016, 41, 16148–16159. [Google Scholar] [CrossRef]
- Zhou, S.; Gao, J.; Pan, Z.; Zhang, G.; Zhai, S.; Shen, W. Fault Diagnosis and Fault-Tolerant Control Method for a Multistack Fuel Cell Thermal Management Subsystem. Energy Technol. 2023, 11, 2300132. [Google Scholar] [CrossRef]
- Yuan, X.-H.; Wu, G.; Zhou, J.-G.; Xiong, X.; Wang, Y.-P. MPC-Based Thermal Management for Water-Cooled Proton Exchange Membrane Fuel Cells. Energy Rep. 2022, 8, 338–348. [Google Scholar] [CrossRef]
- Gao, J.; Zhou, S.; Lu, Y.; Shen, W. Simulation of a Novel Integrated Multi-Stack Fuel Cell System Based on a Double-Layer Multi-Objective Optimal Allocation Approach. Appl. Sci. 2024, 14, 2961. [Google Scholar] [CrossRef]
- Ma, M.; Shen, L.; Zhao, Z.; Guo, P.; Liu, J.; Xu, B.; Zhang, Z.; Zhang, Y.; Zhao, L.; Wang, Z. Activation methods and underlying performance boosting mechanisms within fuel cell catalyst layer. Escience/Dianhuaxue 2024, 4, 100254. [Google Scholar] [CrossRef]
- Rojas, J.D.; Ocampo-Martinez, C.; Kunusch, C. Thermal Modelling Approach and Model Predictive Control of a Water-Cooled PEM Fuel Cell System. In Proceedings of the IECON 2013—39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013. [Google Scholar] [CrossRef]
- Chen, M.; Xu, Z.; Zhao, J.; Shao, Z. Dynamic Matrix Control with Feed-Forward for Target Tracking. In Proceedings of the 2019 12th Asian Control Conference (ASCC), Kitakyushu, Japan, 9–12 June 2019. [Google Scholar]


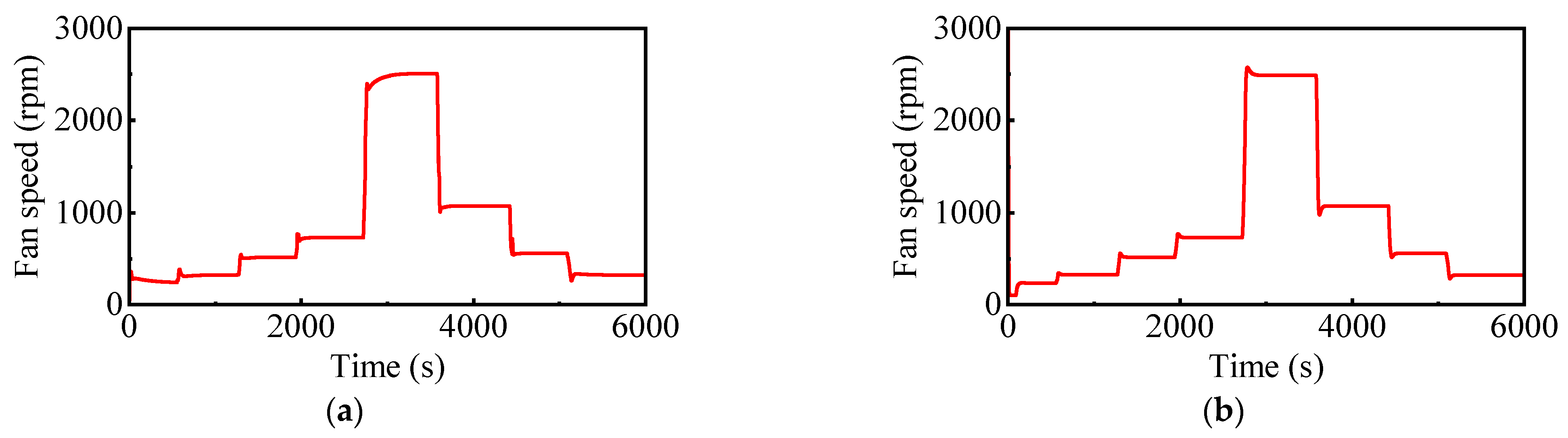

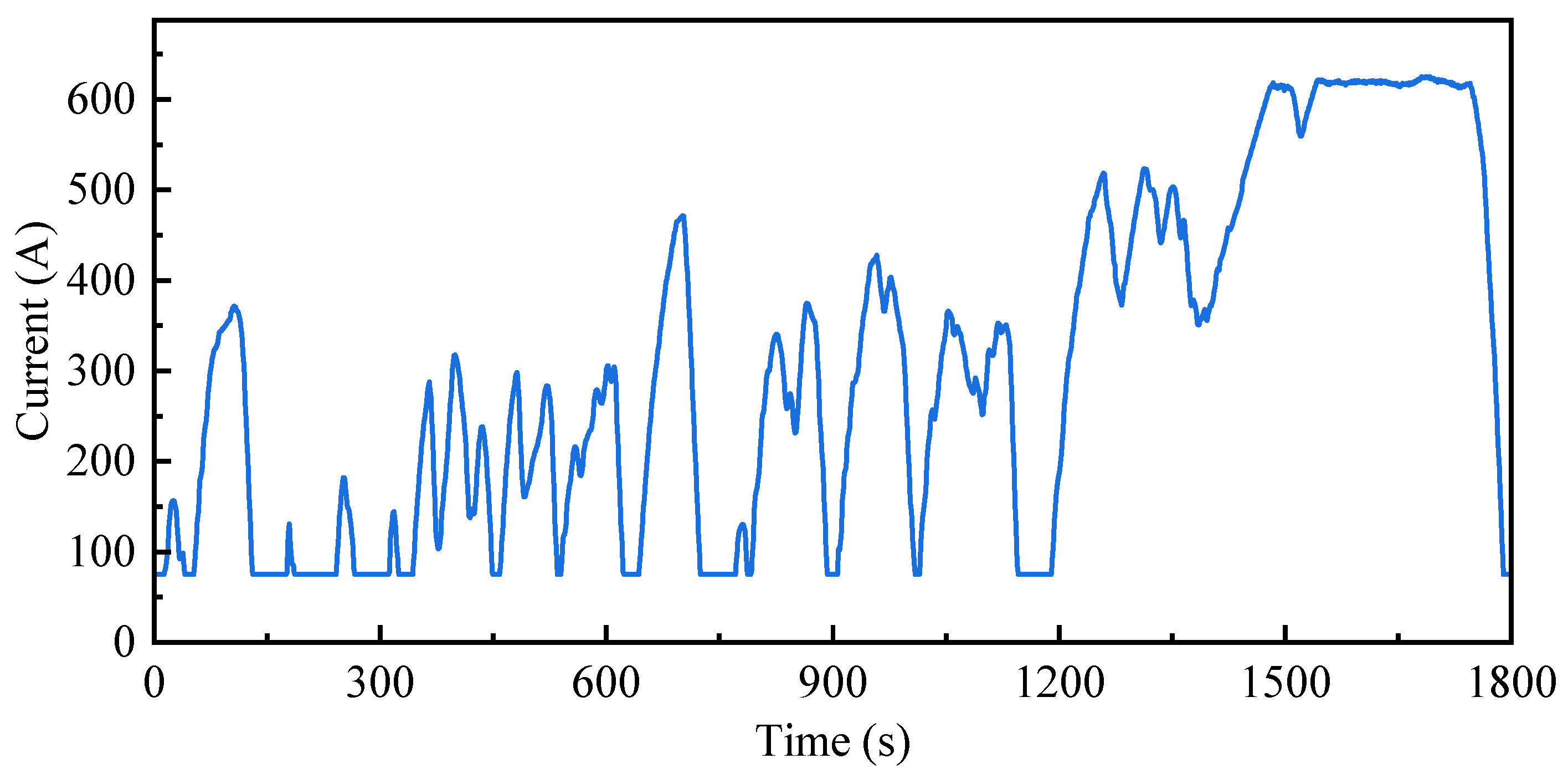
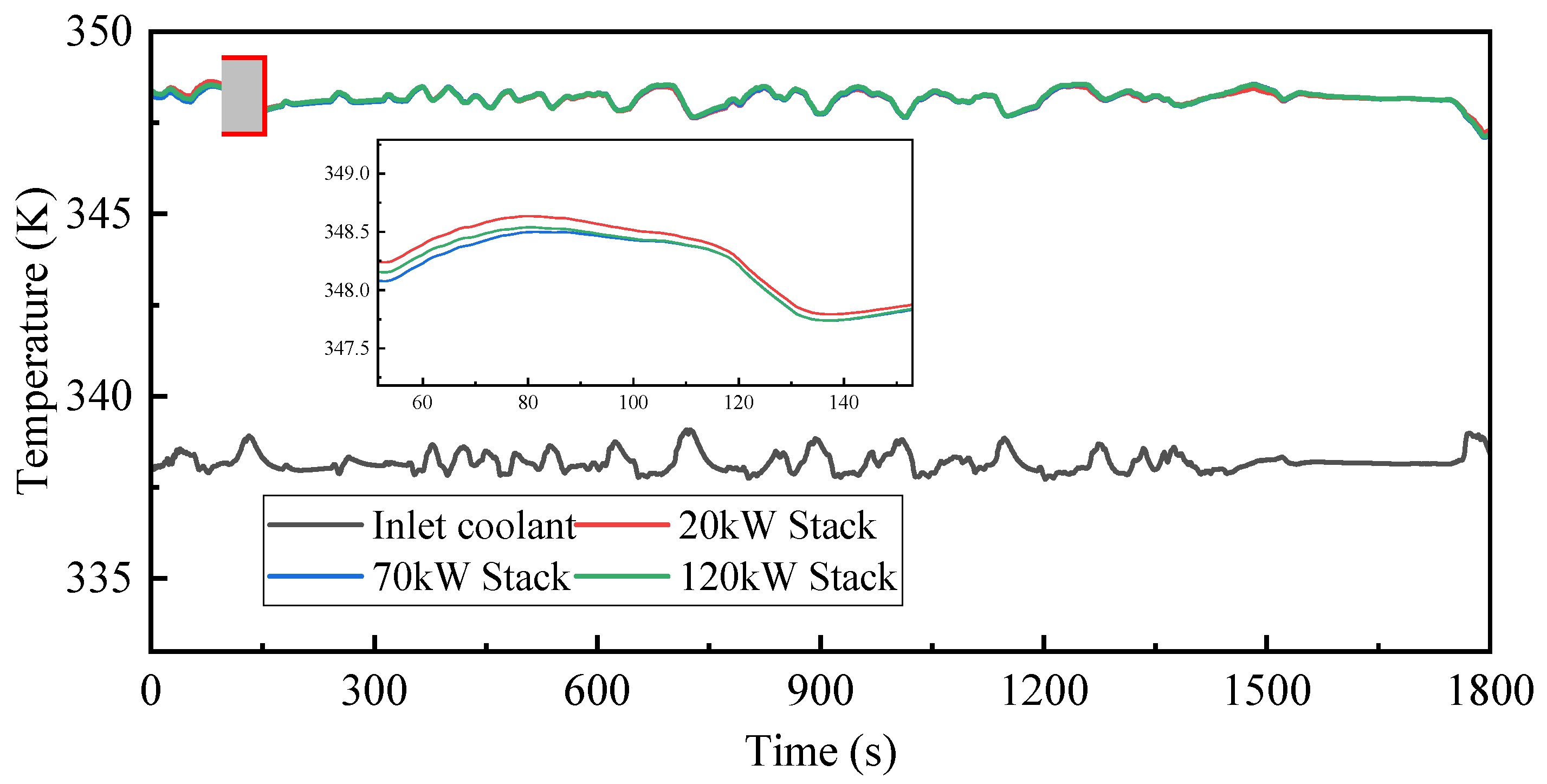
| Parameter | Network structure | Activation function | Number of trainings |
| Value | 18 × 13 × 4 | Sigmoid | 302 |
| Parameter | Minimum | Maximum | Type of Constraint |
|---|---|---|---|
| Coolant circulation pump speed (rpm) | 50 | 4500 | hard |
| Radiator fan speed (rpm) | 50 | 5000 | hard |
| Diverter valve opening | 0.1 | 0.95 | hard |
| Stack temperature (K) | 323 | 363 | soft |
| Inlet coolant temperature (K) | 343 | 353 | soft |
| Time/s | Prediction Model | 20 kW Stack | 70 kW Stack | 120 kW Stack | Inlet Coolant | ||||
|---|---|---|---|---|---|---|---|---|---|
| Overshoot/K | Stable Time/s | Overshoot/K | Stable Time/s | Overshoot/K | Stable Time/s | Overshoot/K | Stable Time/s | ||
| 1935 | BPNN | 0.318 | 120 | 0.483 | 120 | 0.446 | 120 | 0.284 | 120 |
| Linearization | 0.870 | 260 | 0.937 | 260 | 1.095 | 260 | 2.160 | 260 | |
| 2720 | BPNN | 0.728 | 165 | 1.473 | 165 | 1.146 | 165 | 0.799 | 165 |
| Linearization | 1.125 | 235 | 1.998 | 235 | 3.108 | 235 | 1.129 | 235 | |
| 3580 | BPNN | 0.665 | 125 | 1.321 | 125 | 1.005 | 125 | 0.568 | 125 |
| Linearization | 0.952 | 260 | 1.908 | 260 | 2.690 | 260 | 1.365 | 260 | |
| 4420 | BPNN | 0.392 | 115 | 0.611 | 115 | 0.541 | 115 | 0.320 | 115 |
| Linearization | 0.788 | 280 | 1.397 | 280 | 1.799 | 280 | 1.788 | 280 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, W.; Su, H.; Gao, J.; Fan, L.; Zhang, G.; Zhou, S. A Multi-Objective Temperature Control Method for a Multi-Stack Fuel Cell System with Different Stacks Based on Model Predictive Control. Energies 2025, 18, 2443. https://doi.org/10.3390/en18102443
Shen W, Su H, Gao J, Fan L, Zhang G, Zhou S. A Multi-Objective Temperature Control Method for a Multi-Stack Fuel Cell System with Different Stacks Based on Model Predictive Control. Energies. 2025; 18(10):2443. https://doi.org/10.3390/en18102443
Chicago/Turabian StyleShen, Wei, Hongtao Su, Jianhua Gao, Lei Fan, Gang Zhang, and Su Zhou. 2025. "A Multi-Objective Temperature Control Method for a Multi-Stack Fuel Cell System with Different Stacks Based on Model Predictive Control" Energies 18, no. 10: 2443. https://doi.org/10.3390/en18102443
APA StyleShen, W., Su, H., Gao, J., Fan, L., Zhang, G., & Zhou, S. (2025). A Multi-Objective Temperature Control Method for a Multi-Stack Fuel Cell System with Different Stacks Based on Model Predictive Control. Energies, 18(10), 2443. https://doi.org/10.3390/en18102443






