Research Progress on Nano-Confinement Effects in Unconventional Oil and Gas Energy—With a Major Focus on Shale Reservoirs
Abstract
1. Introduction
2. Physical Properties and Flow Characteristics of Fluids at the Nanoscale
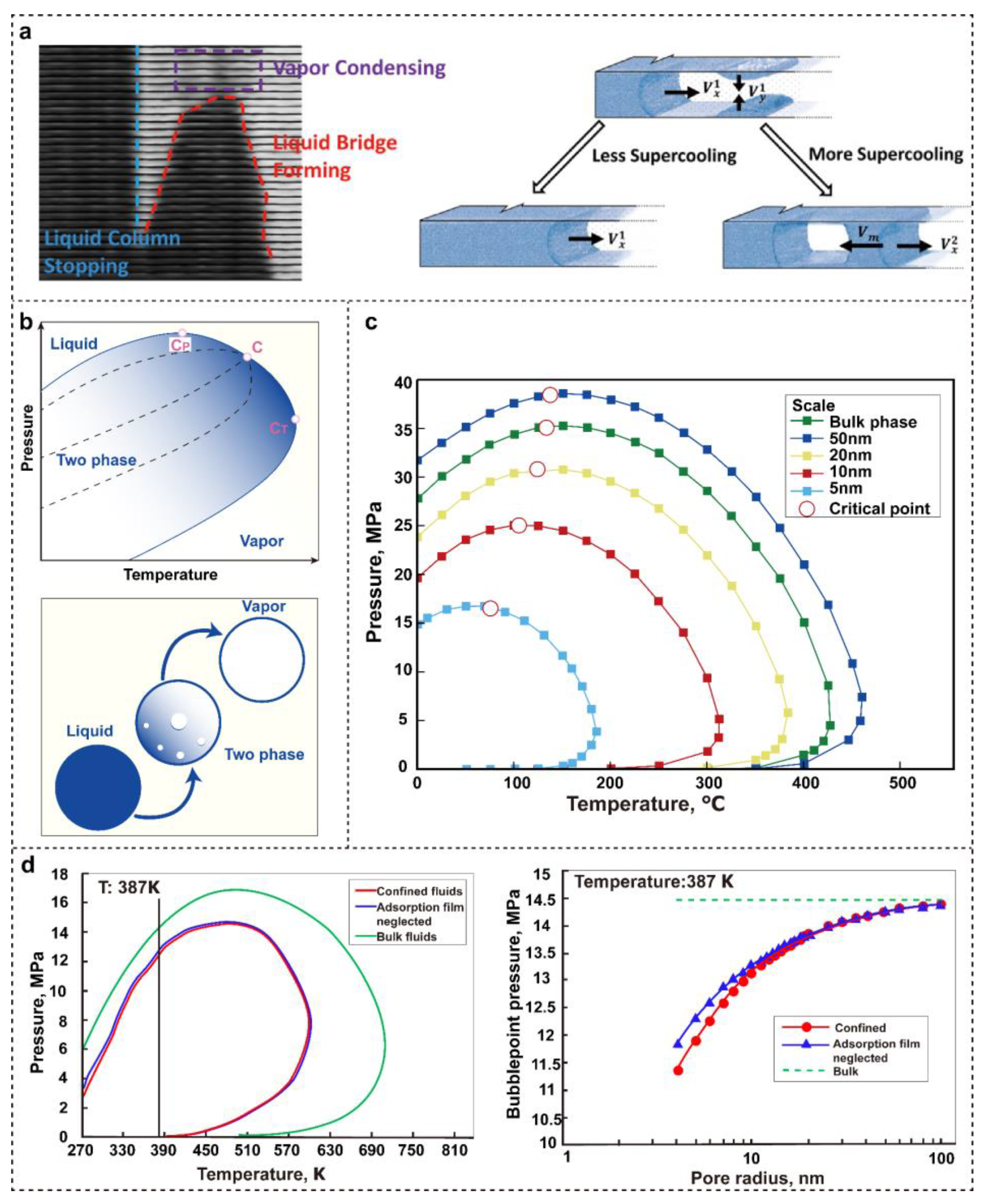
2.1. Phase Behavior of Fluids
2.2. Fluid Flow Mechanisms
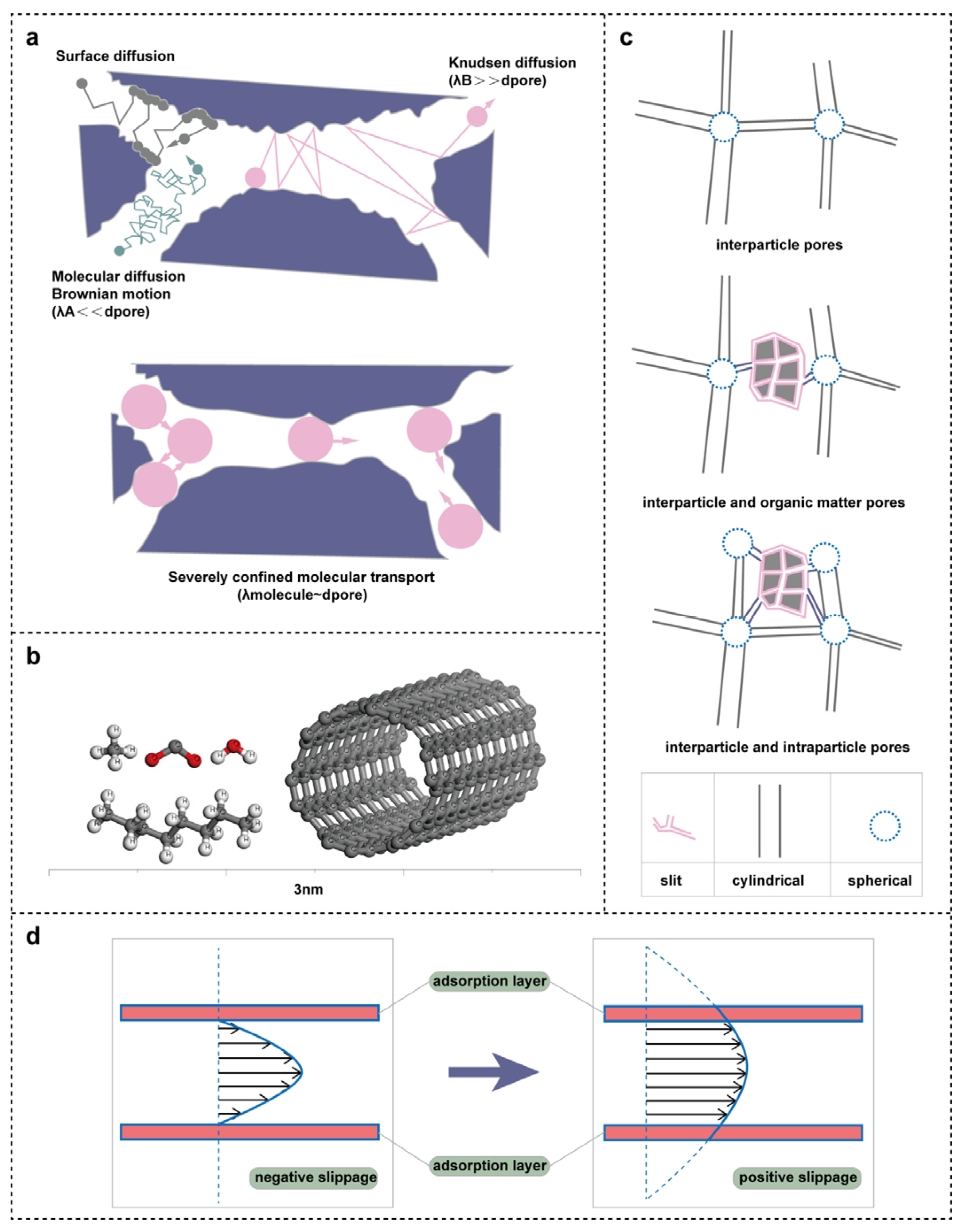
2.3. Changes in Other Areas
2.3.1. High-Viscosity Layer near the Wall
2.3.2. Imbibition
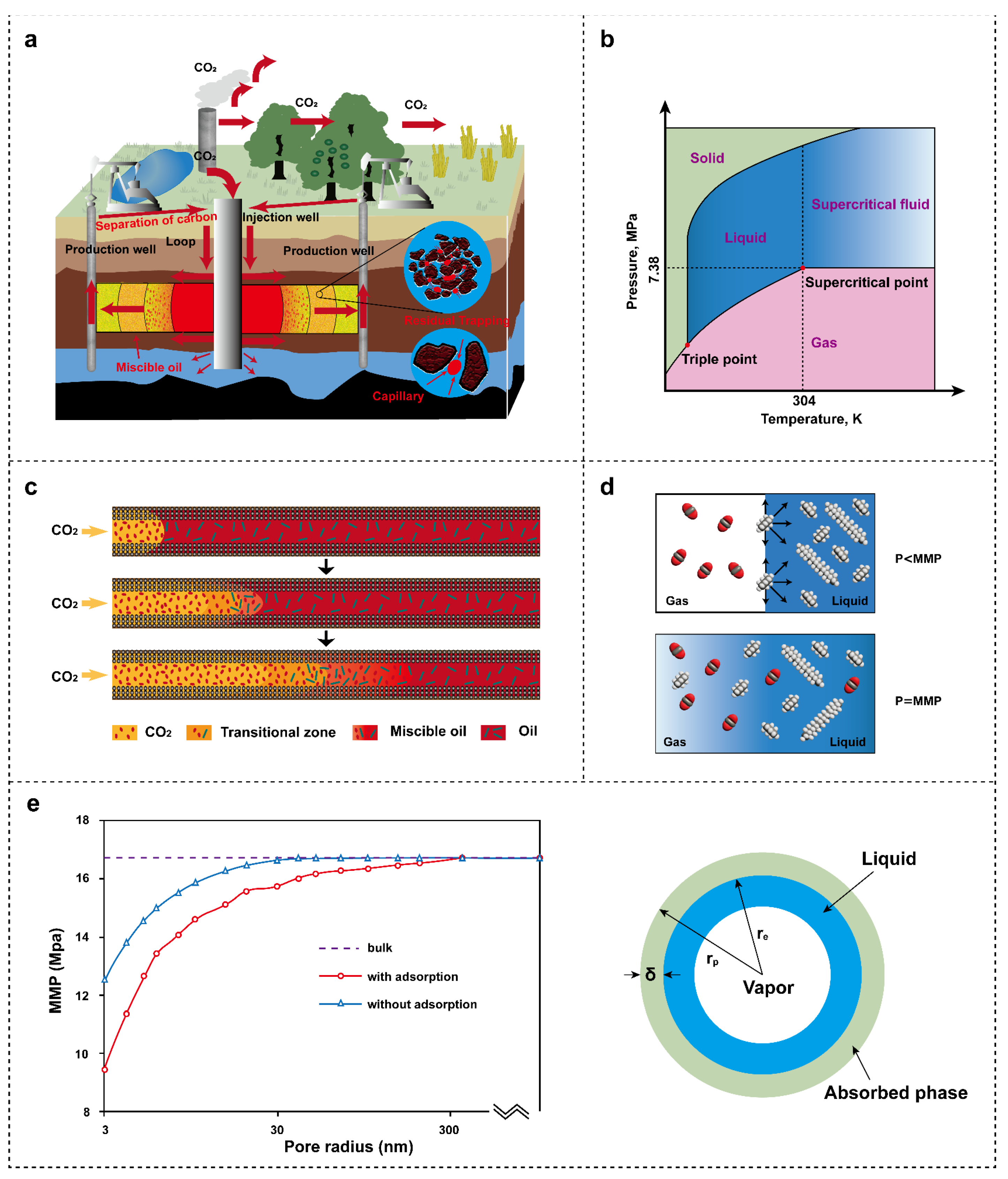
2.3.3. Minimum Miscibility Pressure
2.4. Summary
3. Physical Experimental Methods
3.1. Nanofluidic Technology
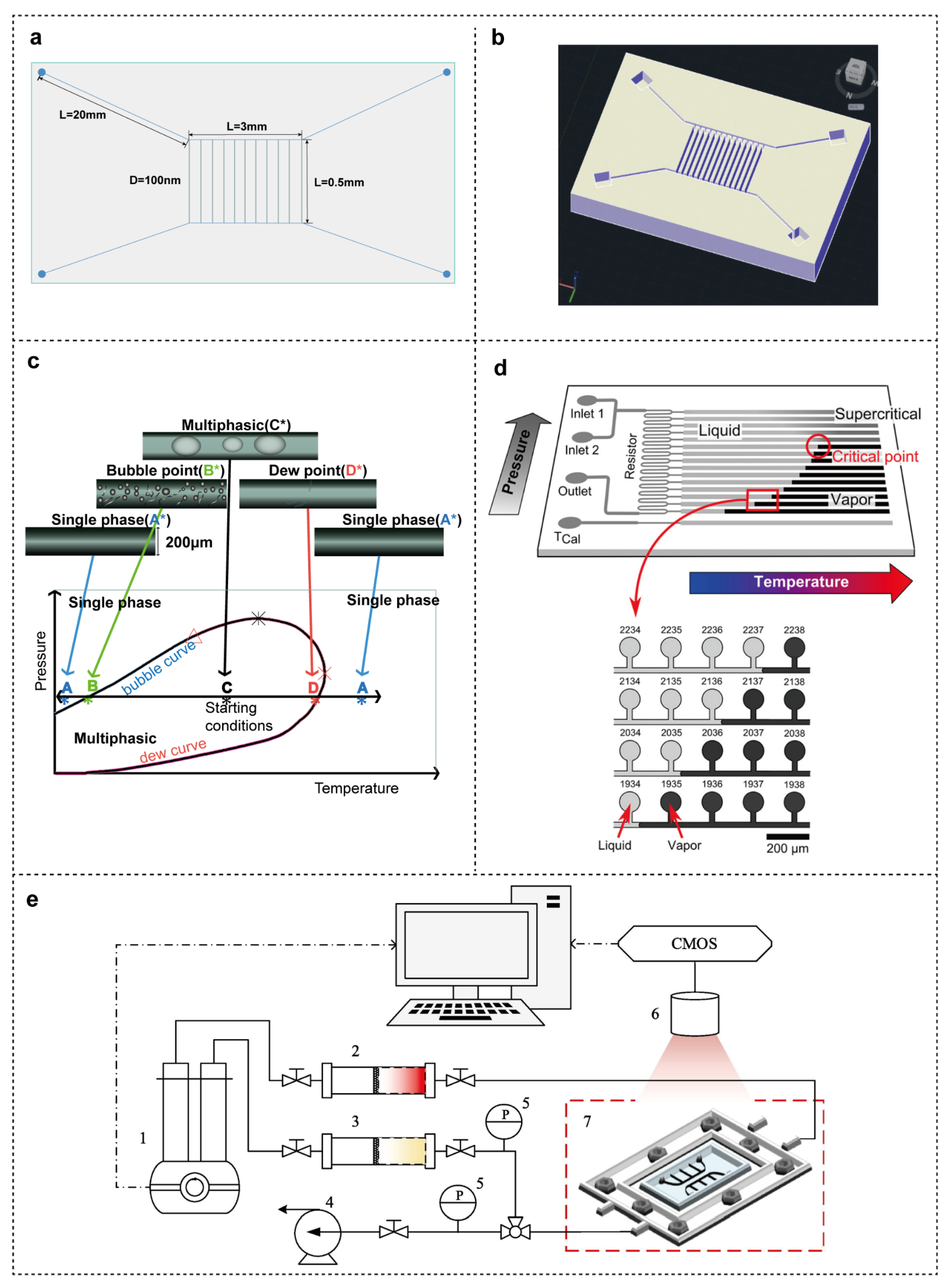
3.2. Nuclear Magnetic Resonance
3.3. Nano Computed Tomography
3.3.1. Pore and Fluid Characterization
3.3.2. Preprocessing for Numerical Simulations
3.4. Scanning Electron Microscopy
3.5. Summary
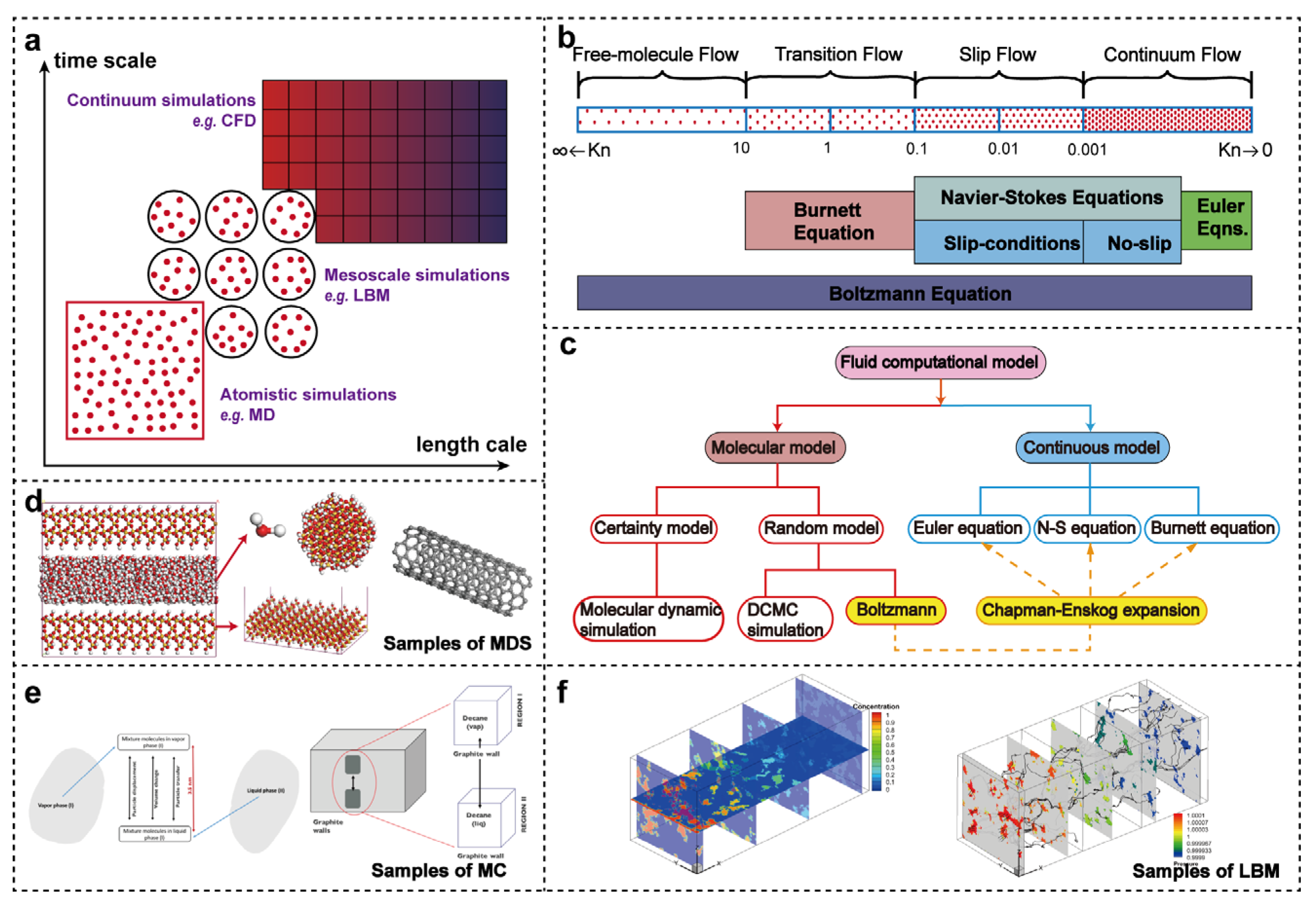
4. Numerical Simulation Methods
4.1. Molecular Dynamic Simulation
4.2. Monte Carlo Method
4.3. Lattice Boltzmann Method
4.4. Summary
5. Theoretical Calculation Methods
5.1. Equation of State
5.2. Density Functional Theory
5.3. Summary
6. Comparative Analysis of the Effects of Nano-Confinement on Fluid Properties
6.1. Influence on Fluid Phase Behavior
6.1.1. Phase Behavior
6.1.2. Pore Size Classification
6.2. Influence on Fluid Movement
6.2.1. Fluid Diffusion
6.2.2. Fluid Permeability
6.2.3. Surface Adsorption
6.3. Summary
7. Practical Application in the Industry
8. Current Challenges and Future Directions
9. Conclusions
- Fluid critical parameters in nanopores differ from those in the bulk phase, but there is no consensus on how these parameters change.
- Most studies suggest that nano-confinement effects cannot be ignored in pores smaller than 10 nm, becoming more pronounced as pore size decreases.
- The diffusion rate of fluids in nanopores decreases as the degree of confinement increases.
- Permeability also depends on pressure and other parameters like fluid–solid interactions.
- Fluid in nanopores forms a high-viscosity layer on the pore walls, and the number of layers depends on the nature of the fluid and the wall surface.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zou, C.; Dong, D.; Wang, S.; Li, J.; Li, X.; Wang, Y.; Li, D.; Cheng, K. Geological characteristics and resource potential of shale gas in China. Pet. Explor. Dev. 2010, 37, 641–653. [Google Scholar] [CrossRef]
- Sun, H.; Wang, H.; Yang, Y.; Lyu, Q.; Zhang, F.; Liu, Z.; Lyu, J.; Chen, T.; Jiang, T.; Zhao, P.; et al. Iteration And Evaluation of Shale Oil Development Technology for Continental Rift Lake Basins. Pet. Explor. Dev. 2024, 51, 993–1008. [Google Scholar] [CrossRef]
- BP. Statistical Review of World Energy. 2024. Available online: https://www.bp.com/content/dam/bp/business-sites/en/global/corporate/pdfs/energy-economics/energy-outlook/bp-energy-outlook-2024.pdf (accessed on 22 December 2024).
- Muther, T.; Qureshi, H.A.; Syed, F.I.; Aziz, H.; Siyal, A.; Dahaghi, A.K.; Negahban, S. Unconventional hydrocarbon resources: Geological statistics, petrophysical characterization, and field development strategies. J. Pet. Explor. Prod. Technol. 2022, 12, 1463–1488. [Google Scholar] [CrossRef]
- World Energy Resources; IEA: Paris, France, 2020.
- Annual Energy Outlook; EIA: Washington, DC, USA, 2021.
- Smith, M.B.; Montgomery, C. Hydraulic Fracturing, 1st ed.; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Zhao, J.; Ren, L.; Lin, C.; Lin, R.; Hu, D.; Wu, J.; Song, Y.; Shen, C.; Tang, D.; Jiang, H. A review of deep and ultra-deep shale gas fracturing in China: Status and directions. Renew. Sustain. Energy Rev. 2025, 209, 115111. [Google Scholar] [CrossRef]
- Liu, J.; Sheng, J.J. Experimental investigation of surfactant enhanced spontaneous imbibition in Chinese shale oil reservoirs using NMR tests. J. Ind. Eng. Chem. 2019, 72, 414–422. [Google Scholar] [CrossRef]
- Zou, C.; Zhu, R.; Wu, S.; Yang, Z.; Tao, S.; Yuan, X.; Hou, L.; Yang, H.; Xu, C.; Li, D.; et al. Types, Characteristics, Mechanisms and Prospects of Conventional and Unconventional Oil and Gas Aggregation—An Example of Tight Oil and Tight Gas in China. J. Pet. 2012, 33, 173–187. [Google Scholar]
- Recent IUPAC recommendations. Anal. Proc. 1989, 26, 142–145. [CrossRef]
- Phuong, V.T.; Chokbunpiam, T.; Fritzsche, S.; Remsungnen, T.; Rungrotmongkol, T.; Chmelik, C.; Caro, J.; Hannongbua, S. Methane in zeolitic imidazolate framework ZIF-90: Adsorption and diffusion by molecular dynamics and Gibbs ensemble Monte Carlo. Microporous Mesoporous Mater. 2016, 235, 69–77. [Google Scholar] [CrossRef]
- Chen, L.; Jiang, Z.X.; Jiang, S.; Liu, K.Y.; Yang, W.; Tan, J.Q.; Gao, F.L. Nanopore Structure and Fractal Characteristics of Lacustrine Shale: Implications for Shale Gas Storage and Production Potential. Nanomaterials 2019, 9, 390. [Google Scholar] [CrossRef]
- Wu, J.G.; Luo, C.; Zhong, K.S.; Li, Y.; Li, G.L.; Du, Z.M.; Yang, J.J. Innovative characterization of organic nanopores in marine shale by the integration of HIM and SEM. Energy 2023, 282, 128390. [Google Scholar] [CrossRef]
- Chandra, D.; Vishal, V. A critical review on pore to continuum scale imaging techniques for enhanced shale gas recovery. Earth-Sci. Rev. 2021, 217, 103638. [Google Scholar] [CrossRef]
- Dong, X.; Liu, H.; Hou, J.; Wu, K.; Chen, Z. Phase Equilibria of Confined Fluids in Nanopores of Tight and Shale Rocks Considering the Effect of Capillary Pressure and Adsorption Film. Ind. Eng. Chem. Res. 2016, 55, 798–811. [Google Scholar] [CrossRef]
- Zhong, J.; Zandavi, S.H.; Li, H.; Bao, B.; Persad, A.H.; Mostowfi, F.; Sinton, D. Condensation in One-Dimensional Dead-End Nanochannels. ACS Nano 2017, 11, 304–313. [Google Scholar] [CrossRef] [PubMed]
- Firincioglu, T.; Ozkan, E.; Ozgen, C. Thermodynamics of Multiphase Flow in Unconventional Liquids-Rich Reservoirs. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 8–10 October 2012; p. SPE–159869-MS. [Google Scholar]
- Tan, S.P.; Qiu, X.; Dejam, M.; Adidharma, H. Critical Point of Fluid Confined in Nanopores: Experimental Detection and Measurement. J. Phys. Chem. C 2019, 123, 9824–9830. [Google Scholar] [CrossRef]
- Feng, Q.; Xu, S.; Xing, X.; Zhang, W.; Wang, S. Advances and challenges in shale oil development: A critical review. Adv. Geo-Energy Res. 2020, 4, 406–418. [Google Scholar] [CrossRef]
- Song, Y.L.; Song, Z.J.; Chen, Z.X.; Zhang, L.C.; Zhang, Y.F.; Feng, D.; Wu, Z.B.; Wu, J.P. Fluid Phase Behavior in Multi-Scale Shale Reservoirs With Nano-Confinement Effect. Energy 2024, 289, 130027. [Google Scholar] [CrossRef]
- Yuan, S.; Lei, Z.; Li, J.; Yao, Z.; Li, B.; Wang, R.; Liu, Y.; Wang, Q. Key theoretical and technical issues and countermeasures for effective development of Gulong shale oil, Daqing Oilfield, NE China. Pet. Explor. Dev. 2023, 50, 638–650. [Google Scholar] [CrossRef]
- Bukowski, B.C.; Keil, F.J.; Ravikovitch, P.I.; Sastre, G.; Snurr, R.Q.; Coppens, M.-O. Connecting theory and simulation with experiment for the study of diffusion in nanoporous solids. Adsorpt.-J. Int. Adsorpt. Soc. 2021, 27, 683–760. [Google Scholar] [CrossRef]
- Knudsen, M. The laws of molecular flow and of inner friction flow of gases through tubes. J. Membr. Sci. 1995, 100, 23–25. [Google Scholar] [CrossRef]
- Ning, Z.; Wang, B.; Yang, F.; Zeng, Y.; Chen, J.e.; Zhang, L. Microscale effect of microvadose in shale reservoirs. Pet. Explor. Dev. 2014, 41, 492–499. [Google Scholar] [CrossRef]
- Wu, K.; Chen, Z.; Li, J.; Lei, Z.; Xu, J.; Wang, K.; Li, R.; Dong, X.; Peng, Y.; Yang, S.; et al. Nanoconfinement Effect on n-Alkane Flow. J. Phys. Chem. C 2019, 123, 16456–16461. [Google Scholar] [CrossRef]
- Yao, J.; Song, W.; Wang, D.; Sun, H.; Li, Y. Multi-scale pore network modelling of fluid mass transfer in nano-micro porous media. Int. J. Heat Mass Transf. 2019, 141, 156–167. [Google Scholar] [CrossRef]
- Geng, L.; Li, G.; Zitha, P.; Tian, S.; Sheng, M.; Fan, X. A diffusion–viscous flow model for simulating shale gas transport in nano-pores. Fuel 2016, 181, 887–894. [Google Scholar] [CrossRef]
- Goyal, I.; Srivastava, S.; Tankeshwar, K. Controlling Diffusion by Varying Width of Layers in Nano Channel. Nano-Micro Lett. 2012, 4, 154–157. [Google Scholar] [CrossRef]
- He, J.; Ju, Y.; Lammers, L.; Kulasinski, K.; Zheng, L. Tortuosity of kerogen pore structure to gas diffusion at molecular- and nano-scales: A molecular dynamics simulation. Chem. Eng. Sci. 2020, 215, 115460. [Google Scholar] [CrossRef]
- Wang, Y.; Xue, J.; Wang, D.; Xue, Q. Lattice Boltzmann method for simulation of shale gas flow in kerogen nano-pores considering temperature dependent adsorption. Int. J. Oil Gas Coal Technol. 2020, 23, 409–426. [Google Scholar] [CrossRef]
- Xu, R.; Prodanović, M. Effect of pore geometry on nitrogen sorption isotherms interpretation: A pore network modeling study. Fuel 2018, 225, 243–255. [Google Scholar] [CrossRef]
- Gibbs, J.W. On the equilibrium of heterogeneous substances. Am. J. Sci. Arts 1878, 3, 441–458. [Google Scholar] [CrossRef]
- Zeng, K.; Xu, R.; Lu, T.; Tian, Z.; Jiang, P. NMR Measurements for Gas Adsorption Characterization on Shale: State of the Art and Perspectives. Energy Fuels 2023, 37, 8824–8835. [Google Scholar] [CrossRef]
- Javadpour, F. Nanopores and Apparent Permeability of Gas Flow in Mudrocks (Shales and Siltstone). J. Can. Pet. Technol. 2009, 48, 16–21. [Google Scholar] [CrossRef]
- Javadpour, F.; Fisher, D.; Unsworth, M. Nanoscale Gas Flow in Shale Gas Sediments. J. Can. Pet. Technol. 2007, 46, PETSOC-07-10-06. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, X.; Li, H.; Lei, Q.; Luo, Y.; Wang, X. Analysis on the influencing factors of imbibition and the effect evaluation of imbibition in tight reservoirs. Pet. Explor. Dev. 2019, 46, 779–785. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, K.; Zhang, L.; Sun, H.; Zhang, K.; Ma, J. Pore-scale simulation of shale oil flow based on pore network model. Fuel 2019, 251, 683–692. [Google Scholar] [CrossRef]
- Arain, A.H.; Negash, B.M.; Yekeen, N.; Farooqi, A.S.; Alshareef, R.S. Synergising nanoparticles and low salinity waterflooding for enhanced oil recovery: A state-of-the-art review. J. Mol. Liq. 2024, 400, 124495. [Google Scholar] [CrossRef]
- Ahmadi, M.A.; Shadizadeh, S.R. Experimental investigation of a natural surfactant adsorption on shale-sandstone reservoir rocks: Static and dynamic conditions. Fuel 2015, 159, 15–26. [Google Scholar] [CrossRef]
- Zhang, Z.; Bai, M.; Xu, L.; Du, S.; Liu, Y.; Yang, E.; Shan, J. Study on Oil Extraction Characteristics in Micropores of a Typical Terrestrial Shale Reservoir in China by CO2 Injection and Surfactant Imbibition. Energy Fuels 2024, 38, 6927–6937. [Google Scholar] [CrossRef]
- Bao, B.; Riordon, J.; Mostowfi, F.; Sinton, D. Microfluidic and nanofluidic phase behaviour characterization for industrial CO2, oil and gas. Lab Chip 2017, 17, 2740–2759. [Google Scholar] [CrossRef]
- Salahshoor, S.; Fahes, M.; Teodoriu, C. A review on the effect of confinement on phase behavior in tight formations. J. Nat. Gas Sci. Eng. 2018, 51, 89–103. [Google Scholar] [CrossRef]
- Didar, B.R.; Akkutlu, I.Y. Pore-Size Dependence of Fluid Phase Behavior and Properties in Organic-Rich Shale Reservoirs. In Proceedings of the SPE International Symposium on Oilfield Chemistry, The Woodlands, TX, USA, 8–10 April 2013; p. SPE–164099-MS. [Google Scholar]
- Wang, S.; Feng, Q.; Javadpour, F.; Xia, T.; Li, Z. Oil adsorption in shale nanopores and its effect on recoverable oil-in-place. Int. J. Coal Geol. 2015, 147–148, 9–24. [Google Scholar] [CrossRef]
- Baek, S.; Yucel Akkutlu, I. CO2 Stripping of Kerogen Condensates in Source Rocks. SPE J. 2019, 24, 1415–1434. [Google Scholar] [CrossRef]
- Ambrose, R.J.; Hartman, R.C.; Diaz-Campos, M.; Akkutlu, I.Y.; Sondergeld, C.H. Shale Gas-in-Place Calculations Part I: New Pore-Scale Considerations. SPE J. 2011, 17, 219–229. [Google Scholar] [CrossRef]
- Su, Y.; Sun, Q.; Wang, W.; Guo, X.; Xu, J.; Li, G.; Pu, X.; Han, W.; Shi, Z. Spontaneous imbibition characteristics of shale oil reservoir under the influence of osmosis. Int. J. Coal Sci. Technol. 2022, 9, 69. [Google Scholar] [CrossRef]
- Yan, X.; Dai, C.; Wang, R.; Liu, H.; Meng, S.; Jin, X.; Hu, Y.; Wu, Y. Experimental study on countercurrent imbibition in tight oil reservoirs using nuclear magnetic resonance and AFM: Influence of liquid–liquid/solid interface characteristics. Fuel 2024, 358, 130026. [Google Scholar] [CrossRef]
- Jiang, T.; Shen, Z.; Wang, L.; Qi, Z.; Xiao, B.; Qin, Q.; Fan, X.; Wang, Y.; Qu, H. Optimization Method of fracturing fluid volume intensity for SRV fracturing technique in shale oil reservoir based on forced imbibition: A case study of well X-1 in Biyang Sag of Nanxiang Basin, China. Pet. Explor. Dev. 2024, 51, 674–683. [Google Scholar] [CrossRef]
- Dehghanpour, H.; Lan, Q.; Saeed, Y.; Fei, H.; Qi, Z. Spontaneous Imbibition of Brine and Oil in Gas Shales: Effect of Water Adsorption and Resulting Microfractures. Energy Fuels 2013, 27, 3039–3049. [Google Scholar] [CrossRef]
- Werder, T.; Walther, J.H.; Jaffe, R.L.; Halicioglu, T.; Koumoutsakos, P. On the water-carbon interaction for use in molecular dynamics simulations of graphite and carbon nanotubes. J. Phys. Chem. B 2003, 107, 1345–1352. [Google Scholar] [CrossRef]
- Tolman, R.C. The Effect of Droplet Size on Surface Tension. J. Chem. Phys. 1949, 17, 333–337. [Google Scholar] [CrossRef]
- Liu, J.; Sheng, J.J.; Wang, X.; Ge, H.; Yao, E. Experimental study of wettability alteration and spontaneous imbibition in Chinese shale oil reservoirs using anionic and nonionic surfactants. J. Pet. Sci. Eng. 2019, 175, 624–633. [Google Scholar] [CrossRef]
- Yao, Y.; Wei, M.; Bai, B. Descriptive statistical analysis of experimental data for wettability alteration with surfactants in carbonate reservoirs. Fuel 2022, 310, 122110. [Google Scholar] [CrossRef]
- Du, M.; Yang, Z.; Lyu, W.; Li, Z.; Wang, G.; Chen, X.; Qi, X.; Yao, L.; Zhang, Y.; Jia, N.; et al. Experiment of dynamic seepage of tight/shale oil under matrix fracture coupling. Pet. Explor. Dev. 2024, 51, 403–415. [Google Scholar] [CrossRef]
- Mei, Y.; Lv, W.; Zhou, X.; Huang, J.; Jia, N.; Wang, G. Current methods for measuring three-phase relative permeability and its influencing factors. Adv. Geo-Energy Res. 2023, 10, 21–38. [Google Scholar] [CrossRef]
- Nguyen, P.; Mohaddes, D.; Riordon, J.; Fadaei, H.; Lele, P.; Sinton, D. Fast Fluorescence-Based Microfluidic Method for Measuring Minimum Miscibility Pressure of CO2 in Crude Oils. Anal. Chem. 2015, 87, 3160–3164. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Liu, T.; Liu, S.; Jia, C.; Yao, J.; Sun, H.; Yang, Y.; Zhang, L.; Delshad, M.; Sepehrnoori, K.; et al. Adsorption Effects on CO2-Oil Minimum Miscibility Pressure in Tight Reservoirs. Energy 2024, 288, 129815. [Google Scholar] [CrossRef]
- Pan, X.; Sun, L.; Chen, F.; Huo, X.; Wang, Y.; Feng, C.; Zheng, X.; Zhang, Z. Minimum Miscibility Pressure of the CO2-Hydrocarbon System Based on Nanofluidics. Energy Fuels 2024, 38, 10904–10913. [Google Scholar] [CrossRef]
- Song, Y.L.; Song, Z.J.; Meng, Y.F.; Chen, Z.X.; Han, X.; Feng, D. Multi-Phase Behavior And Pore-Scale Flow in Medium-High Maturity Continental Shale Reservoirs With Oil, CO2, And Water. Chem. Eng. J. 2024, 484, 149679. [Google Scholar] [CrossRef]
- Sun, Q.; Zhang, N.; Zhu, P.; Liu, W.; Guo, L.; Fu, S.; Bhusal, A.; Wang, S. Confined Fluid Interfacial Tension and Minimum Miscibility Pressure Prediction in Shale Nanopores. Fuel 2024, 364, 130949. [Google Scholar] [CrossRef]
- Bocquet, L. Nanofluidics coming of age. Nat. Mater. 2020, 19, 254–256. [Google Scholar] [CrossRef]
- Bocquet, L.; Charlaix, E. Nanofluidics, from bulk to interfaces. Chem. Soc. Rev. 2010, 39, 1073–1095. [Google Scholar] [CrossRef]
- Sattari, A.; Hanafizadeh, P.; Hoorfar, M. Multiphase flow in microfluidics: From droplets and bubbles to the encapsulated structures. Adv. Colloid Interface Sci. 2020, 282, 102208. [Google Scholar] [CrossRef]
- Sinton, D. Energy: The microfluidic frontier. Lab Chip 2014, 14, 3127–3134. [Google Scholar] [CrossRef]
- Bonnet, J.; Lenormand, R. Ralisation de micromodles pour l’tude des coulements polyphasiques en milieux poreux. Oil Gas Sci. Technol. Rev. L Inst. Fr. Pet. 1977, 32, 477–490. [Google Scholar]
- Shim, J.-u.; Cristobal, G.; Link, D.R.; Thorsen, T.; Jia, Y.; Piattelli, K.; Fraden, S. Control and measurement of the phase behavior of aqueous solutions using microfluidics. J. Am. Chem. Soc. 2007, 129, 8825–8835. [Google Scholar] [CrossRef] [PubMed]
- Bao, B.; Zhao, S. A review of experimental nanofluidic studies on shale fluid phase and transport behaviors. J. Nat. Gas Sci. Eng. 2021, 86, 103745. [Google Scholar] [CrossRef]
- Zhang, K.; Jia, N.; Li, S.; Liu, L. Static and dynamic behavior of CO2 enhanced oil recovery in shale reservoirs: Experimental nanofluidics and theoretical models with dual-scale nanopores. Appl. Energy 2019, 255, 113752. [Google Scholar] [CrossRef]
- Sullivan, M.T.; Angelescu, D.E. Microfluidic Bubble Point Measurement Using Thermal Nucleation. Energy Fuels 2016, 30, 2655–2661. [Google Scholar] [CrossRef]
- Luther, S.K.; Schuster, J.J.; Leipertz, A.; Braeuer, A. Non-invasive quantification of phase equilibria of ternary mixtures composed of carbon dioxide, organic solvent and water. J. Supercrit. Fluids 2013, 84, 146–154. [Google Scholar] [CrossRef]
- Lefortier, S.G.R.; Hamersma, P.J.; Bardow, A.; Kreutzer, M.T. Rapid microfluidic screening of CO2 solubility and diffusion in pure and mixed solvents. Lab Chip 2012, 12, 3387–3391. [Google Scholar] [CrossRef]
- Wang, S.; Liang, Y.; Feng, Q.; Javadpour, F. Sticky layers affect oil transport through the nanopores of realistic shale kerogen. Fuel 2022, 310, 122480. [Google Scholar] [CrossRef]
- Bocquet, L.; Tabeling, P. Physics and technological aspects of nanofluidics. Lab Chip 2014, 14, 3143–3158. [Google Scholar] [CrossRef]
- Holt, J.K.; Park, H.G.; Wang, Y.; Stadermann, M.; Artyukhin, A.B.; Grigoropoulos, C.P.; Noy, A.; Bakajin, O. Fast Mass Transport Through Sub-2-Nanometer Carbon Nanotubes. Science 2006, 312, 1034–1037. [Google Scholar] [CrossRef]
- Mostowfi, F.; Molla, S.; Tabeling, P. Determining phase diagrams of gas–liquid systems using a microfluidic PVT. Lab Chip 2012, 12, 4381–4387. [Google Scholar] [CrossRef] [PubMed]
- Pinho, B.; Girardon, S.; Bazer-Bachi, F.; Bergeot, G.; Marre, S.; Aymonier, C. A microfluidic approach for investigating multicomponent system thermodynamics at high pressures and temperatures. Lab Chip 2014, 14, 3843–3849. [Google Scholar] [CrossRef] [PubMed]
- Bao, B.; Riordon, J.; Xu, Y.; Li, H.; Sinton, D. Direct Measurement of the Fluid Phase Diagram. Anal Chem 2016, 88, 6986–6989. [Google Scholar] [CrossRef] [PubMed]
- Lu, Z.; Wan, Y.; Xu, L.; Fang, D.; Wu, H.; Zhong, J. Nanofluidic Study of Multiscale Phase Transitions And Wax Precipitation in Shale Oil Reservoirs. Energies 2024, 17, 2415. [Google Scholar] [CrossRef]
- Liu, N.; Aymonier, C.; Lecoutre, C.; Garrabos, Y.; Marre, S. Microfluidic approach for studying CO2 solubility in water and brine using confocal Raman spectroscopy. Chem. Phys. Lett. 2012, 551, 139–143. [Google Scholar] [CrossRef]
- Alfi, M.; Nasrabadi, H.; Banerjee, D. Experimental investigation of confinement effect on phase behavior of hexane, heptane and octane using lab-on-a-chip technology. Fluid Phase Equilibria 2016, 423, 25–33. [Google Scholar] [CrossRef]
- Wang, Y.; Lei, Z.; Sun, L.; Pan, X.; Liu, Y.; Xu, Z.; Zheng, X.; Wang, Y.; Liu, P. Study on The Minimum Miscibility Pressure and Phase Behavior of CO2–Shale Oil in Nanopores. Chem. Eng. J. 2024, 497, 154493. [Google Scholar] [CrossRef]
- Zhang, Q.; Dong, Y.; Tong, S.; Li, X.; Wang, L. Nuclear magnetic resonance cryoporometry as a tool to measure pore size distribution of shale rock. Chin. Sci. Bull. 2016, 61, 2387–2394. [Google Scholar] [CrossRef]
- Zhang, X.; Wei, B.; You, J.; Liu, J.; Wang, D.; Lu, J.; Tong, J. Characterizing pore-level oil mobilization processes in unconventional reservoirs assisted by state-of-the-art nuclear magnetic resonance technique. Energy 2021, 236, 121549. [Google Scholar] [CrossRef]
- Petrov, O.V.; Furó, I. NMR cryoporometry: Principles, applications and potential. Prog. Nucl. Magn. Reson. Spectrosc. 2009, 54, 97–122. [Google Scholar] [CrossRef]
- Huang, J.; Xu, K.; Guo, S.; Guo, H. Comprehensive Study on Pore Structures of Shale Reservoirs Based on SEM,NMR and X-CT. Mod. Geol. 2015, 29, 198–205. [Google Scholar]
- Firouzi, M.; Rupp, E.C.; Liu, C.W.; Wilcox, J. Molecular simulation and experimental characterization of the nanoporous structures of coal and gas shale. Int. J. Coal Geol. 2014, 121, 123–128. [Google Scholar] [CrossRef]
- Fleury, M.; Fabre, R. Comparison of pore size distribution by nmr relaxation and nmr cryoporometry in shales. In Proceedings of the International Symposium of the Society of Core Analysts, St. John’s, NL, Canada, 16–21 August 2015. [Google Scholar]
- Tong, S.-q.; Dong, Y.; Zhang, Q.; Elsworth, D.; Liu, S. Quantitative Analysis of Nanopore Structural Characteristics of Lower Paleozoic Shale, Chongqing (Southwestern China): Combining FIB-SEM and NMR Cryoporometry. Energy Fuels 2017, 31, 13317–13328. [Google Scholar] [CrossRef]
- McDowell, B.; Tutuncu, A.; Yang, Y. High-Frequency (400 MHz) T2 Measurements Using a Custom-Built NMR Probe, Eagle Ford Shale, Gonzales and La Salle Counties, Texas. In Proceedings of the Unconventional Resources Technology Conference, Houston, TX, USA, 23–25 July 2018; Society of Exploration Geophysicists, American Association of Petroleum Geologists, Society of Petroleum Engineers: Houston, TX, USA, 2018; pp. 2315–2333. [Google Scholar]
- Xie, Z.H.; Gan, Z. Value of 20Mhz NMR Core Analysis for Unconventional Mudstones. In Proceedings of the SPWLA 59th Annual Logging Symposium, London, UK, 2–6 June 2018; p. D043S009R005. [Google Scholar]
- Zhang, P.; Lu, S.; Li, J.; Chang, X. 1D and 2D Nuclear magnetic resonance (NMR) relaxation behaviors of protons in clay, kerogen and oil-bearing shale rocks. Mar. Pet. Geol. 2020, 114, 104210. [Google Scholar] [CrossRef]
- Zhao, G.; Cheng, L.; Jia, P.; Liu, Y.; Feng, H.; Kuang, T.; Wang, Q. Initial Occurrence State and Movability Evaluation of the Gulong Shale Oil Reservoir, Songliao Basin. Energies 2024, 17, 1358. [Google Scholar] [CrossRef]
- Liu, D.; Ge, H.; Liu, J.; Shen, Y.; Wang, Y.; Liu, Q.; Jin, C.; Zhang, Y. Experimental investigation on aqueous phase migration in unconventional gas reservoir rock samples by nuclear magnetic resonance. J. Nat. Gas Sci. Eng. 2016, 36, 837–851. [Google Scholar] [CrossRef]
- Maojin, T.; Kun, W.; Youlong, Z.; Siyu, W.; Yuyang, F.; Xiangzhi, C. Nuclear magnetic resonance simulations of nano-scale cores and microscopic mechanisms of oil shale. Fuel 2019, 256, 115843. [Google Scholar] [CrossRef]
- Huang, X.; Li, X.; Zhang, Y.; Li, T.; Zhang, R. Microscopic production characteristics of crude oil in nano-pores of shale oil reservoirs during CO2 huff and puff. Pet. Explor. Dev. 2022, 49, 636–643. [Google Scholar] [CrossRef]
- Kausik, R.; Fellah, K.; Feng, L.; Simpson, G. High- and Low-Field NMR Relaxometry and Diffusometry of the Bakken Petroleum System. Petrophysics—SPWLA J. Form. Eval. Reserv. Descr. 2017, 58, 341–351. [Google Scholar]
- Kausik, R.; Minh, C.C.; Zielinski, L.; Vissapragada, B.; Akkurt, R.; Song, Y.; Liu, C.; Jones, S.; Blair, E. Characterization of Gas Dynamics in Kerogen Nanopores by NMR. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 30 October 2011; p. SPE–147198-MS. [Google Scholar]
- Liu, B.; Jiang, X.-W.; Bai, L.-H.; Lu, R.-S. Investigation of oil and water migrations in lacustrine oil shales using 20 MHz 2D NMR relaxometry techniques. Pet. Sci. 2022, 19, 1007–1018. [Google Scholar] [CrossRef]
- Zhong, J.; Yan, R.; Zhang, H.; Feng, Y.; Li, N.; Liu, X. A decomposition method of nuclear magnetic resonance T2 spectrum for identifying fluid properties. Pet. Explor. Dev. 2020, 47, 740–752. [Google Scholar] [CrossRef]
- Oschkinat, H.; Griesinger, C.; Kraulis, P.J.; Sørensen, O.W.; Ernst, R.R.; Gronenborn, A.M.; Clore, G.M. Three-dimensional NMR spectroscopy of a protein in solution. Nature 1988, 332, 374–376. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Xie, R.; Xiao, L. Pore-fluid characterizations and microscopic mechanisms of sedimentary rocks with three-dimensional NMR: Tight sandstone as an example. J. Nat. Gas Sci. Eng. 2020, 80, 103392. [Google Scholar] [CrossRef]
- Wang, P.; Jiang, Z.; Chen, L.; Yin, L.; Li, Z.; Zhang, C.; Tang, X.; Wang, G. Pore structure characterization for the Longmaxi and Niutitang shales in the Upper Yangtze Platform, South China: Evidence from focused ion beam–He ion microscopy, nano-computerized tomography and gas adsorption analysis. Mar. Pet. Geol. 2016, 77, 1323–1337. [Google Scholar] [CrossRef]
- Dunsmuir, J.H.; Ferguson, S.R.; D’Amico, K.L.; Stokes, J.P. X-Ray Microtomography: A New Tool for the Characterization of Porous Media. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 6–9 October 1991; p. SPE–22860-MS. [Google Scholar]
- Fang, Y.; Yang, E.; Guo, S.; Cui, C.; Zhou, C. Study on micro remaining oil distribution of polymer flooding in Class-II B oil layer of Daqing Oilfield. Energy 2022, 254, 124479. [Google Scholar] [CrossRef]
- Seright, R.S.; Prodanovic, M.; Lindquist, W.B. X-Ray Computed Microtomography Studies of Fluid Partitioning in Drainage and Imbibition Before and After Gel Placement: Disproportionate Permeability Reduction. SPE J. 2006, 11, 159–170. [Google Scholar] [CrossRef]
- Li, W.; Kuang, Y.; Lu, S.; Cheng, Z.; Xue, H.; Shi, L. Porosity Enhancement Potential through Dolomite Mineral Dissolution in the Shale Reservoir: A Case Study of an Argillaceous Dolomite Reservoir in the Jianghan Basin. Energy Fuels 2019, 33, 4857–4864. [Google Scholar] [CrossRef]
- Wu, S.; Zhu, R.; Cui, J.; Cui, J.; Bai, B.; Zhang, X.; Jin, X.; Zhu, D.; You, J.; Li, X. Characteristics of lacustrine shale porosity evolution, Triassic Chang 7 Member, Ordos Basin, NW China. Pet. Explor. Dev. 2015, 42, 185–195. [Google Scholar] [CrossRef]
- Akbarabadi, M.; Saraji, S.; Piri, M.; Georgi, D.; Delshad, M. Nano-scale experimental investigation of in-situ wettability and spontaneous imbibition in ultra-tight reservoir rocks. Adv. Water Resour. 2017, 107, 160–179. [Google Scholar] [CrossRef]
- Backeberg, N.R.; Iacoviello, F.; Rittner, M.; Mitchell, T.M.; Jones, A.P.; Day, R.; Wheeler, J.; Shearing, P.R.; Vermeesch, P.; Striolo, A. Quantifying the anisotropy and tortuosity of permeable pathways in clay-rich mudstones using models based on X-ray tomography. Sci. Rep. 2017, 7, 14838. [Google Scholar] [CrossRef]
- Liu, Q.; Sun, M.; Sun, X.; Liu, B.; Ostadhassan, M.; Huang, W.; Chen, X.; Pan, Z. Pore network characterization of shale reservoirs through state-of-the-art X-ray computed tomography: A review. Gas Sci. Eng. 2023, 113, 204967. [Google Scholar] [CrossRef]
- Jia, N.; Lv, W.; Liu, Q.; Wang, D.; Liu, F.; Hu, Z. Pore-Scale Modeling of Pressure-Driven Flow and Spontaneous Imbibition in Fracturing-Shut-In-Flowback Process of Tight Oil Reservoirs. Int. J. Energy Res. 2024, 2024, 3505763. [Google Scholar] [CrossRef]
- Wei, J.; Li, J.; Yang, Y.; Zhang, A.; Wang, A.; Zhou, X.; Zeng, Q.; Shang, D. Digital-Rock Construction of Shale Oil Reservoir and Microscopic Flow Behavior Characterization. Processes 2023, 11, 697. [Google Scholar] [CrossRef]
- Sun, H.; Tao, G.; Vega, S.; Al-Suwaidi, A. Simulation of gas flow in organic-rich mudrocks using digital rock physics. J. Nat. Gas Sci. Eng. 2017, 41, 17–29. [Google Scholar] [CrossRef]
- Adeleye, J.O.; Akanji, L.T. A quantitative analysis of flow properties and heterogeneity in shale rocks using computed tomography imaging and finite-element based simulation. J. Nat. Gas Sci. Eng. 2022, 106, 104742. [Google Scholar] [CrossRef]
- Wang, T.-Y.; Tian, S.-C.; Liu, Q.-L.; Li, G.-S.; Sheng, M.; Ren, W.-X.; Zhang, P.-P. Pore structure characterization and its effect on methane adsorption in shale kerogen. Pet. Sci. 2021, 18, 565–578. [Google Scholar] [CrossRef]
- Qie, Z.; Rabbani, A.; Liang, Y.; Sun, F.; Behnsen, J.; Wang, Y.; Wang, S.; Zhang, Y.; Alhassawi, H.; Gao, J.; et al. Multiscale investigation of pore network heterogeneity and permeability of fluid catalytic cracking (FCC) particles. Chem. Eng. J. 2022, 440, 135843. [Google Scholar] [CrossRef]
- Curtis, M.E.; Sondergeld, C.H.; Ambrose, R.J.; Rai, C.S. Microstructural investigation of gas shales in two and three dimensions using nanometer-scale resolution imaging. AAPG Bull. 2012, 96, 665–677. [Google Scholar] [CrossRef]
- Ambrose, R.J.; Hartman, R.C.; Diaz-Campos, M.; Akkutlu, I.Y.; Sondergeld, C.H. New Pore-scale Considerations for Shale Gas in Place Calculations. In Proceedings of the SPE Unconventional Gas Conference, Pittsburgh, PA, USA, 23–25 February 2010; p. SPE–131772-MS. [Google Scholar]
- Loucks, R.G.; Ruppel, S.C. Mississippian Barnett Shale: Lithofacies and depositional setting of a deep-water shale-gas succession in the Fort Worth Basin, Texas. Aapg Bull. 2007, 91, 579–601. [Google Scholar] [CrossRef]
- Sondergeld, C.H.; Ambrose, R.J.; Rai, C.S.; Moncrieff, J. Micro-Structural Studies of Gas Shales. In Proceedings of the SPE Unconventional Gas Conference, Pittsburgh, PA, USA, 23–25 February 2010; p. SPE–131771-MS. [Google Scholar]
- Slatt, R.M.; O’Brien, N.R. Pore types in the Barnett and Woodford gas shales: Contribution to understanding gas storage and migration pathways in fine-grained rocks. Aapg Bull. 2011, 95, 2017–2030. [Google Scholar] [CrossRef]
- Jiao, K.; Yao, S.; Liu, C.; Gao, Y.; Wu, H.; Li, M.; Tang, Z. The characterization and quantitative analysis of nanopores in unconventional gas reservoirs utilizing FESEM–FIB and image processing: An example from the lower Silurian Longmaxi Shale, upper Yangtze region, China. Int. J. Coal Geol. 2014, 128–129, 1–11. [Google Scholar] [CrossRef]
- Hou, Y.; He, S.; Yi, J.; Zhang, B.; Chen, X.; Wang, Y.; Zhang, J.; Cheng, C. Effect of pore structure on methane sorption potential of shales. Pet. Explor. Dev. 2014, 41, 272–281. [Google Scholar] [CrossRef]
- Wang, P.; Jiang, Z.; Ji, W.; Zhang, C.; Yuan, Y.; Chen, L.; Yin, L. Heterogeneity of intergranular, intraparticle and organic pores in Longmaxi shale in Sichuan Basin, South China: Evidence from SEM digital images and fractal and multifractal geometries. Mar. Pet. Geol. 2016, 72, 122–138. [Google Scholar] [CrossRef]
- Etminan, S.R.; Javadpour, F.; Maini, B.B.; Chen, Z. Measurement of gas storage processes in shale and of the molecular diffusion coefficient in kerogen. Int. J. Coal Geol. 2014, 123, 10–19. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, F.; Zhang, Q.; Li, Y.; Wang, K.; Xu, Q.; Yang, J.; Shang, Z.; Liu, J.; Wang, J.; et al. Recent Advances in Multiscale Digital Rock Reconstruction, Flow Simulation, and Experiments during Shale Gas Production. Energy Fuels 2023, 37, 2475–2497. [Google Scholar] [CrossRef]
- Pathak, M.; Kweon, H.; Deo, M.; Huang, H. Kerogen Swelling and Confinement: Its implication on Fluid Thermodynamic Properties in Shales. Sci. Rep. 2017, 7, 12530. [Google Scholar] [CrossRef]
- Mehmani, A.; Prodanović, M.; Javadpour, F. Multiscale, Multiphysics Network Modeling of Shale Matrix Gas Flows. Transp. Porous Media 2013, 99, 377–390. [Google Scholar] [CrossRef]
- Wang, Y.D.; Blunt, M.J.; Armstrong, R.T.; Mostaghimi, P. Deep learning in pore scale imaging and modeling. Earth-Sci. Rev. 2021, 215, 103555. [Google Scholar] [CrossRef]
- Wang, F.P.; Reed, R.M.; John, A.; Katherine, G. Pore Networks and Fluid Flow in Gas Shales. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 4–7 October 2009; p. SPE–124253-MS. [Google Scholar]
- Gad-el-Hak, M. The Fluid Mechanics of Microdevices—The Freeman Scholar Lecture. J. Fluids Eng. Trans. Asme 1999, 121, 5–33. [Google Scholar] [CrossRef]
- Roy, S.; Raju, R.; Chuang, H.F.; Cruden, B.A.; Meyyappan, M. Modeling gas flow through microchannels and nanopores. J. Appl. Phys. 2003, 93, 4870–4879. [Google Scholar] [CrossRef]
- Pathak, M.; Cho, H.; Deo, M. Experimental and Molecular Modeling Study of Bubble Points of Hydrocarbon Mixtures in Nanoporous Media. Energy Fuels 2017, 31, 3427–3435. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, L.; Kang, Q.; Viswanathan, H.S.; Yao, J.; Tao, W. Nanoscale simulation of shale transport properties using the lattice Boltzmann method: Permeability and diffusivity. Sci. Rep. 2015, 5, 8089. [Google Scholar] [CrossRef] [PubMed]
- Alder, B.J.; Wainwright, T.E. Studies in Molecular Dynamics. I. General Method. J. Chem. Phys. 1959, 31, 459–466. [Google Scholar] [CrossRef]
- Rahman, A. Correlations in the Motion of Atoms in Liquid Argon. Phys. Rev. 1964, 136, A405–A411. [Google Scholar] [CrossRef]
- Swai, R.E. A review of molecular dynamics simulations in the designing of effective shale inhibitors: Application for drilling with water-based drilling fluids. J. Pet. Explor. Prod. Technol. 2020, 10, 3515–3532. [Google Scholar] [CrossRef]
- Chen, X.; Cao, G.; Han, A.; Punyamurtula, V.K.; Liu, L.; Culligan, P.J.; Kim, T.; Qiao, Y. Nanoscale Fluid Transport: Size and Rate Effects. Nano Lett. 2008, 8, 2988–2992. [Google Scholar] [CrossRef]
- Riewchotisakul, S.; Akkutlu, I.Y. Adsorption-Enhanced Transport of Hydrocarbons in Organic Nanopores. SPE J. 2016, 21, 1960–1969. [Google Scholar] [CrossRef]
- Billemont, P.; Coasne, B.; De Weireld, G. Adsorption of Carbon Dioxide, Methane, and Their Mixtures in Porous Carbons: Effect of Surface Chemistry, Water Content, and Pore Disorder. Langmuir 2013, 29, 3328–3338. [Google Scholar] [CrossRef]
- You, J.; Tian, L.; Zhang, C.; Yao, H.; Dou, W.; Fan, B.; Hu, S. Adsorption behavior of carbon dioxide and methane in bituminous coal: A molecular simulation study. Chin. J. Chem. Eng. 2016, 24, 1275–1282. [Google Scholar] [CrossRef]
- Fazelabdolabadi, B.; Alizadeh-Mojarad, A. On the adsorption and hydrodynamics behavior of H2S and CO2 molecules in organic liquids inside nanoslit pores in vicinity of calcite {101¯4} surface. J. Nat. Gas Sci. Eng. 2016, 28, 106–120. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, J.; Yao, J.; Kou, J.; Li, Z.; Wu, T.; Zhang, K.; Zhang, L.; Sun, H. Adsorption behaviors of shale oil in kerogen slit by molecular simulation. Chem. Eng. J. 2020, 387, 124054. [Google Scholar] [CrossRef]
- Sun, L.; Jia, N.; Feng, C.; Wang, L.; Liu, S.; Lyu, W. Exploration of Oil/Water/Gas Occurrence State in Shale Reservoir by Molecular Dynamics Simulation. Energies 2023, 16, 7253. [Google Scholar] [CrossRef]
- Liu, J.; Yang, Y.; Sun, S.; Yao, J.; Kou, J. Flow behaviors of shale oil in kerogen slit by molecular dynamics simulation. Chem. Eng. J. 2022, 434, 134682. [Google Scholar] [CrossRef]
- Dubbeldam, D.; Snurr, R.Q. Recent developments in the molecular modeling of diffusion in nanoporous materials. Mol. Simul. 2007, 33, 305–325. [Google Scholar] [CrossRef]
- Jin, Z.; Firoozabadi, A. Flow of methane in shale nanopores at low and high pressure by molecular dynamics simulations. J Chem Phys 2015, 143, 104315. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Yu, H.; Fan, J.; Zhu, Y.; Wang, F.; Wu, H. Two-Phase Transport Characteristic of Shale Gas and Water through Hydrophilic and Hydrophobic Nanopores. Energy Fuels 2020, 34, 4407–4420. [Google Scholar] [CrossRef]
- Yu, H.; Fan, J.; Chen, J.; Zhu, Y.; Wu, H. Pressure-dependent transport characteristic of methane gas in slit nanopores. Int. J. Heat Mass Transf. 2018, 123, 657–667. [Google Scholar] [CrossRef]
- Zhang, H.; Moh, D.Y.; Wang, X.; Qiao, R. Review on Pore-Scale Physics of Shale Gas Recovery Dynamics: Insights from Molecular Dynamics Simulations. Energy Fuels 2022, 36, 14657–14672. [Google Scholar] [CrossRef]
- Wang, S.; Feng, Q.; Javadpour, F.; Yang, Y.-B. Breakdown of Fast Mass Transport of Methane through Calcite Nanopores. J. Phys. Chem. C 2016, 120, 14260–14269. [Google Scholar] [CrossRef]
- Sun, S.; Liang, S.; Liu, Y.; Liu, D.; Gao, M.; Tian, Y.; Wang, J. A review on shale oil and gas characteristics and molecular dynamics simulation for the fluid behavior in shale pore. J. Mol. Liq. 2023, 376, 121507. [Google Scholar] [CrossRef]
- Welch, W.R.W.; Piri, M. Pore diameter effects on phase behavior of a gas condensate in graphitic one-and two-dimensional nanopores. J. Mol. Model. 2016, 22, 22. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Zhang, H.; Jin, B.; Qiao, R.; Wen, X.-H. Molecular insights of condensate trapping mechanism in shale oil reservoirs and its implications on lean gas enhanced oil recovery. Chem. Eng. J. 2023, 476, 146366. [Google Scholar] [CrossRef]
- Jiang, J.; Sandler, S.I.; Schenk, M.; Smit, B. Adsorption and separation of linear and branched alkanes on carbon nanotube bundles from configurational-bias Monte Carlo simulation. Phys. Rev. B 2005, 72, 045447. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Gelb, L.D.; Gubbins, K.E.; Radhakrishnan, R.; Sliwinska-Bartkowiak, M. Phase separation in confined systems. Rep. Prog. Phys. 2000, 63, 727. [Google Scholar] [CrossRef]
- Singh, S.K.; Sinha, A.; Deo, G.; Singh, J.K. Vapor-Liquid Phase Coexistence, Critical Properties, and Surface Tension of Confined Alkanes. J. Phys. Chem. C 2009, 113, 7170–7180. [Google Scholar] [CrossRef]
- Sobecki, N.; Nieto-Draghi, C.; Di Lella, A.; Ding, D.Y. Phase behavior of hydrocarbons in nano-pores. Fluid Phase Equilibria 2019, 497, 104–121. [Google Scholar] [CrossRef]
- Malek, K.; Coppens, M.-O. Knudsen self- and Fickian diffusion in rough nanoporous media. J. Chem. Phys. 2003, 119, 2801–2811. [Google Scholar] [CrossRef]
- Coppens, M.-O.; Malek, K. Dynamic Monte-Carlo simulations of diffusion limited reactions in rough nanopores. Chem. Eng. Sci. 2003, 58, 4787–4795. [Google Scholar] [CrossRef]
- Malek, K.; Coppens, M.-O. Pore roughness effects on self- and transport diffusion in nanoporous materials. Colloids Surf. A: Physicochem. Eng. Asp. 2002, 206, 335–348. [Google Scholar] [CrossRef]
- Malek, K.; Coppens, M.-O. Effects of Surface Roughness on Self- and Transport Diffusion in Porous Media in the Knudsen Regime. Phys. Rev. Lett. 2001, 87, 125505. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Zhang, L.; Shao, Q.; Lu, L.; Lu, X.; Jiang, S.; Shen, W. Simulations of Binary Mixture Adsorption of Carbon Dioxide and Methane in Carbon Nanotubes: Temperature, Pressure, and Pore Size Effects. J. Phys. Chem. C 2007, 111, 11912–11920. [Google Scholar] [CrossRef]
- Wang, S.; Yao, X.; Feng, Q.; Javadpour, F.; Yang, Y.; Xue, Q.; Li, X. Molecular insights into carbon dioxide enhanced multi-component shale gas recovery and its sequestration in realistic kerogen. Chem. Eng. J. 2021, 425, 130292. [Google Scholar] [CrossRef]
- Falk, K.; Coasne, B.; Pellenq, R.; Ulm, F.-J.; Bocquet, L. Subcontinuum mass transport of condensed hydrocarbons in nanoporous media. Nat. Commun. 2015, 6, 6949. [Google Scholar] [CrossRef]
- McNamara, G.R.; Zanetti, G. Use of the Boltzmann Equation to Simulate Lattice-Gas Automata. Phys. Rev. Lett. 1988, 61, 2332–2335. [Google Scholar] [CrossRef]
- Shan, X.; Chen, H. Lattice Boltzmann model for simulating flows with multiple phases and components. Phys. Rev. E 1993, 47, 1815–1819. [Google Scholar] [CrossRef]
- Sukop, M.C.; Or, D. Lattice Boltzmann method for modeling liquid-vapor interface configurations in porous media. Water Resour. Res. 2004, 40, W01509. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, J.; Zhang, G.; Zhou, D.; Chen, L.; Viswanathan, H.; Kang, Q. Minireview on Lattice Boltzmann Modeling of Gas Flow and Adsorption in Shale Porous Media: Progress and Future Direction. Energy Fuels 2023, 37, 1511–1524. [Google Scholar] [CrossRef]
- Qian, Y.H.; Humières, D.D.; Lallemand, P. Lattice BGK Models for Navier-Stokes Equation. Europhys. Lett. 1992, 17, 479. [Google Scholar] [CrossRef]
- Cao, N.Z.; Shen, S.Y.; Jin, S.; Martinez, D. Physical symmetry and lattice symmetry in the lattice Boltzmann method. Phys. Rev. E 1997, 55, R21–R24. [Google Scholar] [CrossRef]
- Mei, R.W.; Shyy, W. On the finite difference-based lattice Boltzmann method in curvilinear coordinates. J. Comput. Phys. 1998, 143, 426–448. [Google Scholar] [CrossRef]
- Seta, T.; Kono, K.; Martinez, D.; Chen, S. Lattice Boltzmann Scheme for Simulating Two-Phase Flows. JSME Int. J. Ser. B 2000, 43, 305–313. [Google Scholar] [CrossRef]
- Sofonea, V.; Sekerka, R.F. Viscosity of finite difference lattice Boltzmann models. J. Comput. Phys. 2003, 184, 422–434. [Google Scholar] [CrossRef]
- He, X.Y.; Luo, L.S. Theory of the lattice Boltzmann method: From the Boltzmann equation to the lattice Boltzmann equation. Phys. Rev. E 1997, 56, 6811–6817. [Google Scholar] [CrossRef]
- Sofonea, V.; Sekerka, R.F. Boundary conditions for the upwind finite difference Lattice Boltzmann model: Evidence of slip velocity in micro-channel flow. J. Comput. Phys. 2005, 207, 639–659. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Guo, Z.L.; Zhao, T.S.; Shi, Y. Physical symmetry, spatial accuracy, and relaxation time of the lattice Boltzmann equation for microgas flows. J. Appl. Phys. 2006, 99, 074903. [Google Scholar] [CrossRef]
- Lee, T.; Lin, C.L. A characteristic Galerkin method for discrete Boltzmann equation. J. Comput. Phys. 2001, 171, 336–356. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Qin, R.S.; Emerson, D.R. Lattice Boltzmann simulation of rarefied gas flows in microchannels. Phys. Rev. E 2005, 71, 047702. [Google Scholar] [CrossRef]
- Gupta, N.; Fathi, E.; Belyadi, F. Effects of nano-pore wall confinements on rarefied gas dynamics in organic rich shale reservoirs. Fuel 2018, 220, 120–129. [Google Scholar] [CrossRef]
- Xu, R.; Prodanović, M.; Landry, C.J. Study of subcritical and supercritical gas adsorption behavior in different nanopore systems in shale using lattice Boltzmann method. Int. J. Coal Geol. 2019, 212, 103263. [Google Scholar] [CrossRef]
- Dupuis, A.; Kotsalis, E.M.; Koumoutsakos, P. Coupling lattice Boltzmann and molecular dynamics models for dense fluids. Phys. Rev. E 2007, 75, 046704. [Google Scholar] [CrossRef] [PubMed]
- He, Y.-L.; Tao, W.-Q. Numerical Solutions of Nano/Microphenomena Coupled With Macroscopic Process of Heat Transfer and Fluid Flow: A Brief Review. J. Heat Transf. 2015, 137, 090801. [Google Scholar] [CrossRef]
- Zhao, J.; Kang, Q.; Yao, J.; Zhang, L.; Li, Z.; Yang, Y.; Sun, H. Lattice Boltzmann simulation of liquid flow in nanoporous media. Int. J. Heat Mass Transf. 2018, 125, 1131–1143. [Google Scholar] [CrossRef]
- Zhang, T.; Li, X.; Yin, Y.; He, M.; Liu, Q.; Huang, L.; Shi, J. The transport behaviors of oil in nanopores and nanoporous media of shale. Fuel 2019, 242, 305–315. [Google Scholar] [CrossRef]
- Peng, D.-Y.; Robinson, D.B. A New Two-Constant Equation of State. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Robinson, D.B.; Peng, D.-Y.; Chung, S.Y.K. The development of the Peng—Robinson equation and its application to phase equilibrium in a system containing methanol. Fluid Phase Equilibria 1985, 24, 25–41. [Google Scholar] [CrossRef]
- Nojabaei, B.; Johns, R.T.T.; Chu, L. Effect of Capillary Pressure on Phase Behavior in Tight Rocks and Shales. SPE Reserv. Eval. Eng. 2013, 16, 281–289. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, W.; Sepehrnoori, K.; Di, Y. Investigation of nanopore confinement on fluid flow in tight reservoirs. J. Pet. Sci. Eng. 2017, 150, 265–271. [Google Scholar] [CrossRef]
- Song, Y.; Song, Z.; Guo, J.; Feng, D.; Chang, X. Phase Behavior and Miscibility of CO2–Hydrocarbon Mixtures in Shale Nanopores. Ind. Eng. Chem. Res. 2021, 60, 5300–5309. [Google Scholar] [CrossRef]
- Li, Y.; Li, X.; Teng, S.; Xu, D. Phase Equilibrium Calculations Considering Pore-Throat-Fluid-Molecule Interactions and Capillary Forces. J. Pet. 2015, 36, 511–515. [Google Scholar]
- Zhang, Y.; Zhang, M.; Liu, R.; Chen, J. Mechanism of CO2 oil drive considering the effect of micro- and nano-confinement effects on phase equilibrium. Geol. Front. 2023, 30, 306–315. [Google Scholar] [CrossRef]
- Dong, X.; Luo, Q.; Wang, J.; Liu, H.; Chen, Z.; Xu, J.; Zhang, G. Confined Behavior of Hydrocarbon Fluids in Heterogeneous Nanopores by the Potential Theory. In Proceedings of the SPE Annual Technical Conference and Exhibition, Huston, TX, USA, 11–14 October 2020; p. D022S061R040. [Google Scholar]
- Levy, M. Universal variational functionals of electron densities, first-order density matrices, and natural spin-orbitals and solution of the v-representability problem. Proc. Natl. Acad. Sci.USA 1979, 76, 6062–6065. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Xie, L.-H.; Li, J.-R.; Ma, Y.; Seminario, J.M.; Balbuena, P.B. CO2 Capture and Separations Using MOFs: Computational and Experimental Studies. Chem. Rev. 2017, 117, 9674–9754. [Google Scholar] [CrossRef]
- Qin, Q.; Liu, H.; Zhang, R.; Ling, L.; Fan, M.; Wang, B. Application of density functional theory in studying CO2 capture with TiO2-supported K2CO3 being an example. Appl. Energy 2018, 231, 167–178. [Google Scholar] [CrossRef]
- Qajar, A.; Daigle, H.; Prodanović, M. Methane dual-site adsorption in organic-rich shale-gas and coalbed systems. Int. J. Coal Geol. 2015, 149, 1–8. [Google Scholar] [CrossRef]
- Li, Z.; Jin, Z.; Firoozabadi, A. Phase Behavior and Adsorption of Pure Substances and Mixtures and Characterization in Nanopore Structures by Density Functional Theory. Spe J. 2014, 19, 1096–1109. [Google Scholar] [CrossRef]
- Jin, Z.; Firoozabadi, A. Thermodynamic Modeling of Phase Behavior in Shale Media. SPE J. 2016, 21, 190–207. [Google Scholar] [CrossRef]
- Teklu, T.W.; Alharthy, N.; Kazemi, H.; Yin, X.; Graves, R.M.; AlSumaiti, A.M. Phase Behavior and Minimum Miscibility Pressure in Nanopores. SPE Reserv. Eval. Eng. 2014, 17, 396–403. [Google Scholar] [CrossRef]
- Luo, S.; Nasrabadi, H.; Lutkenhaus, J.L. Effect of confinement on the bubble points of hydrocarbons in nanoporous media. AIChE J. 2016, 62, 1772–1780. [Google Scholar] [CrossRef]
- Wang, P. Prediction Method and Application of Heavy Organic Matter Deposition During CO2 Injection in Shale Oil Reservoirs. Ph.D. Thesis, China University of Petroleum, Beijing, China, 2022. [Google Scholar]
- Song, Z.; Deng, S.; Song, Y.; Liu, Y.; Xian, C.; Zhang, J.; Han, X.; Cao, S.; Fu, L.; Cui, H. High-Pressure Phase State And Mass Transfer Law of Oil-CO2 in Gulong Shale, Daqing Oilfield. J. Pet. 2024, 45, 390–402. [Google Scholar]
- Li, M.; Sun, M.; Mohammadian, E.; Ji, Y.; Blach, T.P.; Ostadhassan, M.; Wen, J.; Wu, C.; Pan, Z. Confinement effect in nanopores of shale and coal reservoirs: A review on experimental characterization methods. Gas Sci. Eng. 2024, 123, 205249. [Google Scholar] [CrossRef]
- Salama, A.; Amin, M.F.E.; Kumar, K.; Sun, S. Flow and Transport in Tight and Shale Formations: A Review. Geofluids 2017, 2017, 4251209. [Google Scholar] [CrossRef]
- Bazant, M.Z.; Storey, B.D.; Kornyshev, A.A. Double Layer in Ionic Liquids: Overscreening versus Crowding. Phys. Rev. Lett. 2011, 106, 046102. [Google Scholar] [CrossRef]
- Bazant, M.Z.; Kilic, M.S.; Storey, B.D.; Ajdari, A. Towards an understanding of induced-charge electrokinetics at large applied voltages in concentrated solutions. Adv. Colloid Interface Sci. 2009, 152, 48–88. [Google Scholar] [CrossRef]
- Gelb, L.D.; Gubbins, K.E. Pore Size Distributions in Porous Glasses: A Computer Simulation Study. Langmuir 1999, 15, 305–308. [Google Scholar] [CrossRef]
- Faucher, S.; Aluru, N.; Bazant, M.Z.; Blankschtein, D.; Brozena, A.H.; Cumings, J.; Pedro de Souza, J.; Elimelech, M.; Epsztein, R.; Fourkas, J.T.; et al. Critical Knowledge Gaps in Mass Transport through Single-Digit Nanopores: A Review and Perspective. J. Phys. Chem. C 2019, 123, 21309–21326. [Google Scholar] [CrossRef]
- Krishna, R. Describing the Diffusion of Guest Molecules Inside Porous Structures. J. Phys. Chem. C 2009, 113, 19756–19781. [Google Scholar] [CrossRef]
- Noordman, T.R.; Wesselingh, J.A. Transport of large molecules through membranes with narrow pores: The Maxwell–Stefan description combined with hydrodynamic theory. J. Membr. Sci. 2002, 210, 227–243. [Google Scholar] [CrossRef]
- Cui, R.; Feng, Q.; Chen, H.; Zhang, W.; Wang, S. Multiscale random pore network modeling of oil-water two-phase slip flow in shale matrix. J. Pet. Sci. Eng. 2019, 175, 46–59. [Google Scholar] [CrossRef]
- Zhang, P.; Hu, L.; Meegoda, J.N.; Gao, S. Micro/Nano-pore Network Analysis of Gas Flow in Shale Matrix. Sci. Rep. 2015, 5, 13501. [Google Scholar] [CrossRef] [PubMed]
- Goral, J.; Panja, P.; Deo, M.; Andrew, M.; Linden, S.; Schwarz, J.-O.; Wiegmann, A. Confinement Effect on Porosity and Permeability of Shales. Sci. Rep. 2020, 10, 49. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Jin, T.; Chai, Z.; Barrufet, M.; Killough, J. Compositional simulation of three-phase flow in mixed-wet shale oil reservoir. Fuel 2020, 260, 116361. [Google Scholar] [CrossRef]
- Jin, Z.; Firoozabadi, A. Phase behavior and flow in shale nanopores from molecular simulations. Fluid Phase Equilibria 2016, 430, 156–168. [Google Scholar] [CrossRef]
- Wang, Y.; Aryana, S.A. Coupled confined phase behavior and transport of methane in slit nanopores. Chem. Eng. J. 2021, 404, 126502. [Google Scholar] [CrossRef]
- Lee, J.H.; Lee, K.S. Investigation of asphaltene-derived formation damage and nano-confinement on the performance of CO2 huff-n-puff in shale oil reservoirs. J. Pet. Sci. Eng. 2019, 182, 106304. [Google Scholar] [CrossRef]
- Lee, J.H.; Jeong, M.S.; Lee, K.S. Comprehensive modeling of CO2 Huff-n-Puff in asphaltene-damaged shale reservoir with aqueous solubility and nano-confinement. J. Ind. Eng. Chem. 2020, 90, 232–243. [Google Scholar] [CrossRef]
- Du, F.; Nojabaei, B. A diffusion-based compositionally-extended black oil model to investigate produced gas re-injection EOR in Eagle Ford. Fuel 2021, 306, 121711. [Google Scholar] [CrossRef]
- Luo, S.; Lutkenhaus, J.; Nasrabadi, H. A novel and practical framework for incorporating nanopores in existing compositional simulators to model the unusually high GOR observed in shale reservoirs. J. Pet. Sci. Eng. 2020, 195, 107887. [Google Scholar] [CrossRef]
- Du, F.; Huang, J.; Chai, Z.; Killough, J. Effect of vertical heterogeneity and nano-confinement on the recovery performance of oil-rich shale reservoir. Fuel 2020, 267, 117199. [Google Scholar] [CrossRef]
- Jia, Z.; Cheng, L.; Feng, H.; Cao, R.; Jia, P.; Pu, B.; Pan, Q.; Shi, J. Full composition numerical simulation of CO2 utilization process in shale reservoir using projection-based embedded discrete fracture model (pEDFM) considering nano-confinement effect. Gas Sci. Eng. 2023, 111, 204932. [Google Scholar] [CrossRef]
- Jia, Z.; Cao, R.; Pu, B.; Cheng, L.; Li, P.; Awotunde, A.A.; Lin, Y.; Pan, Q.; Sun, Y. Effects of non-equilibrium phase behavior in nanopores on multi-component transport during CO2 injection into shale oil reservoir. Energy 2024, 307, 132614. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, L.; Wei, H.; Dai, Z.; Kang, Q.; Tao, W.-Q. Pore-scale study of mineral dissolution in heterogeneous structures and deep learning prediction of permeability. Phys. Fluids 2022, 34, 116609. [Google Scholar] [CrossRef]
- Zhou, L.; Sun, H.; Fan, D.; Zhang, L.; Imani, G.; Fu, S.; Yang, Y.; Zhang, K.; Yao, J. Flow Prediction of Heterogeneous Nanoporous Media Based on Physical Information Neural Network. Gas Sci. Eng. 2024, 125, 205307. [Google Scholar] [CrossRef]
- Liu, H.; Ren, Y.; Li, X.; Deng, Y.; Wang, Y.; Cao, Q.; Du, J.; Lin, Z.; Wang, W. Research Status and Application of Artificial Intelligence Large Models in the Oil and Gas Industry. Pet. Explor. Dev. 2024, 51, 1049–1065. [Google Scholar] [CrossRef]
- Santos, J.E.; Mehana, M.; Wu, H.; Prodanović, M.; Kang, Q.; Lubbers, N.; Viswanathan, H.; Pyrcz, M.J. Modeling Nanoconfinement Effects Using Active Learning. J. Phys. Chem. C 2020, 124, 22200–22211. [Google Scholar] [CrossRef]





| Country | Characteristics |
|---|---|
| USA | The total unproved technical recoverable tight/shale oil reserves are estimated to be 174.0 billion bbls, whereas the gas recoverable gas quantities are estimated to be 1611.1 TCF. |
| China | The geological resources of medium- and high-maturity shale oil are approximately 100 × 108 t, while tight oil resources are about 178.2 × 108 t, shale gas is 650.44 × 1012 m3, and tight gas is 95.16 × 1012 m3. |
| Australia | Shale gas reserves are 396 TCF, tight gas reserves are 20 TCF, and coalbed methane reserves are 235 TCF. |
| Types of Diffusion | Feature | Advantage | Disadvantage |
|---|---|---|---|
| Bulk diffusion | Primarily governed by molecular interactions. | The flow velocity is highest, with limited impact from pore walls, facilitating easier modeling and prediction [27]. | When the pore diameter approaches the molecular diameter, conventional research methods become inapplicable. |
| Knudsen diffusion | Molecules collide within the pores. | This mechanism is widely observed in the flow of fluids within nanopores, and its study contributes to a deeper understanding of microscopic flow mechanisms [24]. | The flow velocity is slower because of the high ratio of molecular mean free path to pore size [28]. |
| Surface diffusion | Predominantly influenced by interactions between molecules and pore walls. | Substantial studies show that adsorption layers constitute a considerable portion in nanopores [29]. Advances in this field can effectively enhance the recovery of unconventional oil and gas [30]. | The flow velocity is the slowest, primarily influenced by pore walls, which is unfavorable for enhancing oil and gas recovery [31]. |
| Numerical Simulation Methods | Feature | Advantage | Disadvantage |
|---|---|---|---|
| MD | Based on Newtonian mechanics, it investigates intermolecular interactions. | Enables the study of nanoscale microscopic mechanisms, primarily applied to simulating fluid adsorption and desorption, as well as fluid transport behavior in nanopores. | Limited by computational power, the simulation scale is relatively small. |
| MC | Based on probability theory, it examines the random distribution of molecules. | Requires fewer computational resources, making it relatively simple to simulate, and is primarily used for studying fluid phase behavior. | Exhibits randomness, resulting in reduced accuracy compared to MD simulations. |
| LBM | Based on the Boltzmann equation, it employs discrete solutions and focuses on particle groups. | Can simulate larger scales and is mainly used to study fluid flow behavior, including fluid transport in porous media under complex boundary conditions. | Compared to MD simulations, it cannot capture molecular-level interactions. |
| Reference | Methods | Simple | Pore Scale (nm) | Critical Temperature | Critical Pressure | ||
|---|---|---|---|---|---|---|---|
| Bubble Point (K) | Dew Point (K) | Bubble Point | Dew Point | ||||
| Singh, S. K. (2009) [160] | TMMC | light n-alkanes | 2 | 362.14 | 28.04 bar | ||
| 3 | 387.33 | 39.15 bar | |||||
| Didar, B. R. (2013) [44] | MC | C1 | 4.1 | from 190.6 to 177 | from 651 to 465 psi | ||
| 3.7 | from 190.6 to 170 | from 651 to 449 psi | |||||
| 2.9 | from 190.6 to 168 | from 651 to 221 psi | |||||
| 1.5 | from 190.6 to 150 | from 651 to 150 psi | |||||
| hydrocarbon mixtures | 2 3 | phase envelope shrinks inward | |||||
| Nojabaei, B. (2013) [192] | EOS | hydrocarbon mixtures | 10 | - | decrease | decrease or increase (depending on which part of the phase envelope is located) | |
| Teklu, T. W. (2014) [204] | modified conventional gas/liquid balance calculations | hydrocarbon mixtures | 3 and 10 | - | decrease | upper dew point increases, lower dew point | |
| Li, Z. (2014) [202] | DFT + PR-EOS | C3 | 10 | very small change | |||
| 3 | decrease | decrease | |||||
| Li, Y. (2015) [195] | PR-EOS | hydrocarbon mixtures | 2, 4, 5 and 10 | - | increase | decrease | |
| Alfi, M. (2016) [82] | nanofluidic technology | C6 | depth: 50 width: 50 | from 340.7 to 341.9 | - | ||
| C7 | from 374.4 to 373.3 | ||||||
| C8 | from 400.7 to 398.7 | ||||||
| Pathak, M. (2017) [129] | DSC + MD | C10 | 17.7 | decrease 7.8 °C | - | - | |
| hydrocarbon mixtures | decrease of about 50 °C | ||||||
| Pathak, M. (2017) [135] | GCMC | C10 | 3.5 | decrease 125 K (unable to capture critical parameters, using inferential estimation) decrease 85 K | decrease | ||
| C10:C10 = 9:1 | decrease | decrease | |||||
| Zhang, K. (2019) [70] | nanofluidic technology + modified PSD EOS | CO2–C10 | depth: 100 width: 100 | - | - | decrease (T = 25 °C, decreased 10.19%; T = 53 °C, decreased 7.26%) | - |
| Lu, Z. (2024) [80] | nanofluidic technology | crude oil | 100 | - | - | from 34.3 to 30.1 MPa (no-water) | - |
| 10 | from 28.2 to 24.9 MPa (water) | ||||||
| Methods | Advantages | Disadvantages | |
|---|---|---|---|
| Physical Experimental Methods | Nanofluidic | It makes microscopic visualization experiments possible and has been well-applied in the analysis of fluid phase behavior at the nanoscale. | The pore sizes of currently manufactured chips differ from those in actual unconventional reservoirs, making it difficult to study fluid properties at smaller scales. Currently, silicon-based chips are predominantly used, which differ from actual reservoir materials. |
| NMR | It can quantitatively characterize nanopores and fluids. | It cannot capture the distribution characteristics of samples. | |
| Nano-CT | It not only characterizes the pores of unconventional oil and gas reservoirs but also plays a role in pre-processing models for numerical simulations. | It has lower resolution than SEM. | |
| SEM | It can achieve higher resolution compared to nano-CT. | It cannot capture the three-dimensional characteristics of samples. | |
| Numerical Simulation Methods | MD | It primarily applied to study fluid adsorption and desorption in nanopores, as well as fluid motion within these pores. | It simulates molecular behavior on a microscopic scale, requiring substantial computational power, making the process time-consuming and limited by computational capacity. |
| MC | Compared to MD simulations, it is relatively simpler and requires fewer computational resources. | It is based on probability theory and statistical methods, and thus exhibits stochastic characteristics. | |
| LBM | It can not only simulate fluid flow at the mesoscale with complex boundary conditions but also enable parallel computing. | Particles serve as the smallest unit in its simulation, which constrains the precision of the results. | |
| Theoretical Calculation Methods | EOS | Researchers often modify the PR-EOS to study fluid phase behavior in nanopores. | Theoretical models to fully simulate real physical environments and their calculations are more complicated. |
| DFT | It has been widely used to study fluid adsorption behavior in nanopores. | Theoretical models to fully simulate real physical environments and their calculations are more complicated. | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Shen, R.; Xiong, S.; Mei, Y.; Dong, Q.; Chu, S.; Su, H.; Liu, X. Research Progress on Nano-Confinement Effects in Unconventional Oil and Gas Energy—With a Major Focus on Shale Reservoirs. Energies 2025, 18, 166. https://doi.org/10.3390/en18010166
Wang G, Shen R, Xiong S, Mei Y, Dong Q, Chu S, Su H, Liu X. Research Progress on Nano-Confinement Effects in Unconventional Oil and Gas Energy—With a Major Focus on Shale Reservoirs. Energies. 2025; 18(1):166. https://doi.org/10.3390/en18010166
Chicago/Turabian StyleWang, Guo, Rui Shen, Shengchun Xiong, Yuhao Mei, Qinghao Dong, Shasha Chu, Heying Su, and Xuewei Liu. 2025. "Research Progress on Nano-Confinement Effects in Unconventional Oil and Gas Energy—With a Major Focus on Shale Reservoirs" Energies 18, no. 1: 166. https://doi.org/10.3390/en18010166
APA StyleWang, G., Shen, R., Xiong, S., Mei, Y., Dong, Q., Chu, S., Su, H., & Liu, X. (2025). Research Progress on Nano-Confinement Effects in Unconventional Oil and Gas Energy—With a Major Focus on Shale Reservoirs. Energies, 18(1), 166. https://doi.org/10.3390/en18010166






