1. Introduction
Efficiency and reliability are paramount in helicopter turboshaft engine (TE) design and essential for both civilian and military applications. With advancing technology and increasing demands for performance, longevity, and safety, optimizing helicopter TE becomes crucial. This optimization is not only about economics but also important for environmental reasons, curbing emissions [
1]. Enhancing fuel combustion and energy utilization in helicopter TE workflows can drastically cut fuel usage and emissions. This optimization not only boosts engine performance and lifespan but also slashes maintenance costs and extends maintenance intervals [
2,
3]. Mathematical modelling is pivotal in analyzing and optimizing engine processes across various modes of helicopter TE operation, such as low gas mode, cruise modes, and emergency mode [
4,
5].
To solve the task of analysis and engine working processes optimization, the key task is the identification of its mathematical model [
6,
7]. In this context, it is also important to note that the energy efficiency of helicopter TE directly depends on the limitation of their power, which is regulated by the gas-generator rotor r.p.m., which is determined by the air needs to provide the necessary pressure and volume for fuel combustion.
Balancing power and gas-generator rotor r.p.m. is crucial for preventing fuel wastage and minimizing component stress, thereby optimizing engine efficiency. Regulating maximum power based on gas-generator rotor r.p.m. is important for achieving optimal efficiency and reducing fuel consumption [
8,
9]. Employing mathematical models and neural networks predicts parameter relations, enhancing system control and efficiency and aligning with aviation industry requirements for performance and energy efficiency [
10]. Neural networks approximate helicopter TE parameters, improving modelling precision, optimizing engine operation, and minimizing fuel consumption [
11]. This approach elevates flight efficiency, decreases emissions, and extends service life, which is pivotal in maintaining high standards in helicopter operations. The development of mathematical models and neural network analysis in helicopter TE operations offers new avenues in aviation engineering and maintenance. Accurate prediction and modelling reduce maintenance and repair costs, which is crucial for meeting flight safety standards across various operating conditions.
However, when describing TE processes analytically, a balance must be struck between complexity and model idealization. Mathematical models risk becoming impractical if overly complex or if essential relations defining work processes are overlooked [
12].
Mathematical models of helicopter turboshaft engines, derived from thermodynamic analyses, are intricate and challenging to manage, often resulting in discrepancies when linearized for wide operational modes [
13,
14,
15,
16]. Common models approximate experimental data from engine bench tests [
17]. However, this method lacks accuracy due to limited consideration of external factors and real operating conditions. Polynomial approximation of bench test results is another approach [
18,
19], requiring extensive data and resulting in a cumbersome model when different operating modes are approximated separately. Due to how costly, limited, and noisy experimental data are, fuzzy inference systems [
20,
21] and neural networks [
22,
23] are effective. Fuzzy approximation incorporates both bench and flight test results, while neural networks offer automated model identification and selective sensitivity [
24,
25]. Despite the complexity of analytical descriptions, mathematical models such as differential equations, polynomial approximations, and those based on fuzzy inference and neural networks are crucial for understanding helicopter TE operations across various conditions. The authors of [
26] focused on a universal flow resistance element to predict total energy consumption in engine secondary air systems, showing satisfactory accuracy but limited applicability with changing pressure and temperature. The authors of [
27] investigated heat transfer mechanisms and energy conversion in a pre-swirl system to enhance cooling efficiency. Although it develops a modified predictive model, its practical applicability is limited due to the challenge of accounting for all engine parameters in real conditions.
The closest approach to the method of neural network approximation of helicopter TE parameters proposed in this work for researching the dependence of engine power on the gas-generator rotor r.p.m. for efficient use of energy in helicopter TE are the results of research [
28], the main focus of which is the development of an engine hybrid model for detecting faults and diagnosing, which uses principal component analysis and artificial neural networks to improve diagnostic accuracy and efficiency for early fault detection. Condition monitoring and diagnostics not only help in engine detecting faults but also maximize energy use to ensure proper performance and minimize energy loss due to faults and sub-optimal operation. Principal component analysis and artificial neural networks are used to create a hybrid model that provides increased diagnostic accuracy and efficiency, ultimately leading to more efficient energy use and minimizing losses due to faults and suboptimal performance. The disadvantage of this method is the complexity of the hybrid model, which can lead to difficulties in its application in practice due to the need to configure a large number of engine parameters and the difficulty of interpreting the results. In addition, the shortcomings of the applied neural network training algorithm, such as the possibility of falling into a local minimum, limit the model’s ability to adequately reflect the dependence of engine power on the gas-generator rotor r.p.m. This, in turn, can affect the energy efficiency of the engine, as distorted or inaccurate power-speed data can lead to suboptimal energy use, loss of efficiency, and increased costs.
Thus, at the moment, a relevant scientific and practical issue is the development of a formal approach to the neural network approximation of helicopter TE characteristics, which will make it possible to accurately model the relations between engine power and gas-generator rotor r.p.m. to the helicopter TE operation optimize. The development of formal models based on neural networks will increase the accuracy of approximation in predicting engine operation under various operating conditions. This is a decisive aspect in creating reliable and efficient power control systems for helicopter TE while simultaneously increasing safety and productivity in aviation.
The work aims to develop a method for neural network approximation of helicopter TE parameters to research and optimize its characteristics, including limiting engine power depending on the gas-generator rotor r.p.m. to improve engine efficiency, reduce fuel consumption and ensure more reliable and safer helicopter operation.
To achieve this work aim, the following tasks are solved:
Development of helicopter TE mathematical model, which shows the relations between its thermogas-dynamic parameters.
Development of helicopter TE model parameters approximating method.
Justification for the choice of neural network architecture and its training algorithm for helicopter TE model neural network approximation.
Modification of the neural network training algorithm to avoid local minima, which is one of the tasks that arise when optimizing neural networks.
Conducting a computational experiment—solving the tasks of helicopter TE parameters neural network approximation based on the parameter values recorded on board the helicopter.
Research of the dependence of engine power on the gas-generator rotor r.p.m. for the efficient use of helicopter TE energy, optimizing their operation depending on the gas-generator rotor r.p.m.
Conducting a comparative analysis of the obtained results of solving the task of neural network approximation of helicopter TE parameters to demonstrate how the proposed neural network training algorithm stands out in the context of traditional ones.
The research results make a significant contribution to the development of control technologies and end-use energy in helicopter TE operations. They help optimize engine operation processes and regulate maximum power depending on the gas-generator rotor r.p.m., which ultimately contributes to more efficient fuel use and increased reliability and durability of helicopter TE.
2. Materials and Methods
Currently, there are no known methods for finding the optimal structure of neural networks when solving specific tasks of parameter approximation. At the same time, it is known that neural networks with one hidden and one output layer are capable of approximating an arbitrary continuous function on a compact set with any predetermined accuracy [
29,
30]. At the problem statement stage of helicopter TE model parameters neural network approximation, a mathematical model of helicopter TE is developed, which in general form represents a certain mathematical apparatus
, according to which, according to [
22] each vector of parameters recorded on board the helicopter
,
,
,
, where
nTC is the gas-generator rotor r.p.m.,
nFT is the free turbine rotor speed,
is the gas temperature in front of the compressor turbine assigned to the output vector
, where
y is the compressor parameters (it is noted that the parameters of other components of helicopter TE, for example, the combustion chamber, compressor turbine, free turbine, etc., can be presented similarly),
Gair is the airflow through the compressor,
NC is the power required to rotate the compressor,
is the degree of increase in total pressure in the compressor,
is the total air pressure behind the compressor,
is the air temperature behind the compressor,
ηC is the compressor efficiency.
At the first stage of researching the dependence of power on the gas-generator rotor r.p.m., the helicopter TE static properties using the hierarchical structure of a neural network that implements reflection:
The model operator
F must be, in a certain sense, the best approximation to the unknown operator of the object
F*. We will evaluate the proximity of operators solely by the proximity of their reactions to the same input influence. The process of identifying a mathematical model consists of determining the operator structure of model
F and the vector of model unknown parameters P [
31]:
The identification process should be based on experimentally obtained speed and load characteristics of helicopter TE, ensure ease of setting up the model for a specific type of engine, have sufficient noise immunity, and be automatic or automated [
22].
The paper proposes to research the helicopter’s TE characteristics, according to which the engine power is limited depending on the speed of the gas-generator rotor r.p.m. Limiting the helicopter’s TE power is necessary to ensure flight safety, engine service life, and fuel consumption optimization. The proposed characteristic is modelled using the dependence:
where
kp1 and
kp2 are the proposed control characteristic parameters.
To implement the mappings
F1 and
F2 in (1) and (2), according to (3), three-layer feed-forward neural networks (3LFNN) with linear neurons in the output layer are used [
31,
32]. Hyperbolic tangent functions were chosen as activation functions of hidden layer neurons [
31]:
where
N11,
N12,
N21, and
N22 are the output vectors of neurons of the first and second layers, respectively;
W11,
W12,
W13,
W21,
W22, and
W23 are the matrices of neuron weighting coefficients;
B11,
B12,
B13,
B21,
B22, and
B23 are the displacement vectors of neurons of the first, second, and third layers, respectively.
Normalization and denormalization of signals from the neural network
F1 are carried out according to the expressions
where min(
nTC), max(
nTC),
,
, min(
nFT), max(
nFT), min(
Gair), max(
Gair),
,
,
,
are respectively, the minimum and maximum values of the sets
nTC i,
,
nFT i,
Gair i,
,
,
,
K1 is the number of points (helicopter TE parameters values) dependencies
and
, respectively, analytically calculated and experimentally obtained helicopter TE static characteristics.
Normalization and denormalization of signals from the
F2 neural network are carried out according to the expressions:
where min(
Gair), max(
Gair),
,
,
,
,
,
, min(
NC), max(
NC), min(
ηC), max(
ηC) are respectively, the minimum and maximum values of the sets
Gair j,
,
,
,
NC j,
ηC j,
,
K2 is the number of points (helicopter TE parameters values) dependencies
and
, analytically calculated helicopter TE static characteristics.
The task of helicopter TE model structural identification can be parameterized, that is, a vector of structural parameters D can encode various structures [
31]:
In this case, the elements of vector D are the number of neurons in the hidden layers of the neural network F1 and F2, which determines the dimensions of the corresponding matrices of weight coefficients and neuron biases. In turn, the elements of the vector P of model unknown parameters are the elements of the matrices of weighting coefficients and displacements of neurons of the neural network F1 and F2, as well as the parameters of the adjustment characteristic kp1 and kp2.
At the next stage of solving the task of helicopter TE model parameters neural network approximation, it is accepted that as a result of the flight operation of helicopter TE with further analytical calculations, sets of points were obtained , , and , and , , which represent a representative sample of experimental data and quite accurately reflect the behaviour of helicopter TE working processes, indicators of their efficiency at , , .
If the parameters P = [
kp1,
kp2] of dependence (5) are specified, identification of the mathematical model of helicopter TE is reduced to determining the structure and parameters of the neural network
F1 and
F2 [
31]:
where the objective functionals have the form [
30]:
In turn, the discrepancy functions of the outputs of the model and the object at each point of the experimental characteristics are defined as [
31]:
To solve the task, the next step is to select a training algorithm for the proposed 3LFNN with linear neurons in the output layer. To train it, it is proposed to use the scaled conjugate gradient algorithm (SCG), which has demonstrated high performance in solving a similar task, and combines the concepts of summary methods and quasi-Newton methods [
33,
34]. According to this algorithm, the initial parameters of the model
θ0 are initialized, including weights and biases (bias). Next, the gradient of the cost function is calculated for all parameters of the model according to the finite difference method. The loss function
E(
θ) is assumed to be differentiable concerning each parameter
θi. Then the gradient of the loss function at point
θ0 is calculated by numerically approximating the derivative of the loss function concerning the
i-th parameter at point
θ0 as follows:
where
ε is the small positive number (for example,
ε = 10
−6), e
i is the vector whose
i-th component is equal to 1, and all other components are equal to 0.
Next, the gradients for each parameter are scaled to take into account its weight in the context of optimization:
where
D is the diagonal matrix containing scaling factors for each parameter.
Next, the optimal training step for each parameter is determined. Zoom is used to adaptively select the step size:
To avoid local minima, which is one of the problems that can arise when optimizing neural networks, a modification of the SCG algorithm is proposed when estimating new neural network parameters by introducing a torque coefficient:
where
β is the moment coefficient,
θ is the neural network parameter,
is the scalable gradient of the cost function at point
θk.
Next, by numerical approximation, a new gradient of the loss function at point
θk+1 is calculated according to the expression:
where
ε is the small positive number (for example,
ε = 10
−6), u is the unit vector in the parameter space.
Next, the model parameters are updated according to the scaled conjugate direction of the gradients:
where Δ
θk is calculated using the conjugate direction of the gradients and the scaled gradients:
where
αk is the optimization step at step
k, which is calculated using the optimal step length method,
is the scaled gradient of the loss function at step
k, which is calculated according to (19) as
and
.
Expression (23) allows you to determine how the parameters change between two successive iterations of the algorithm. The difference between the two scaled gradients is taken into account to adjust the parameter changes in the current iteration.
At the final stage of neural network training, the fulfilment of stopping criteria is checked at each optimization iteration. The two most common stopping criteria are achieving the required accuracy and achieving the maximum number of iterations.
To achieve the required accuracy, check how much the loss function
E(
θ) has decreased with each iteration and compare this decrease with some predetermined accuracy threshold
ϵ. Formally, this can be written as:
where
ϵ is the specified accuracy.
Reaching the maximum number of iterations involves stopping optimization after reaching a certain number of iterations
Nmax. This can be checked mathematically as follows:
where
k is the current iteration,
Nmax is the maximum number of iterations.
Thus, at each iteration of the proposed neural network training algorithm, both stopping criteria are checked. If at least one of the criteria is met, then the optimization is completed and the algorithm returns the found approximate solution. Based on the above, a theorem is proposed on the conditions for exiting local minima (Theorem 1).
Theorem 1. When the conditions of the modified optimization algorithm are met, the probability of exiting local minima increases, which helps to find more optimal solutions for neural networks.
Proof of Theorem 1. Let the loss function E(θ) be given, where θ is the vector of neural network parameters, and θ∗ is the global minimum of the loss function. It is assumed that the optimization algorithm that is used satisfies the conditions of the modified algorithm, namely:
The algorithm contains an element of randomness, which allows you to explore different parts of the parameter space.
The algorithm uses a variety of optimization parameters, such as training rate, initialization of weights, and other parameters.
Modification of the algorithm facilitates the exploration of various optimization paths and increases the probability of exiting local minima.
Thus, it is necessary to prove that the fulfilment of these conditions increases the probability of exiting local minima.
Let E1 and E2 be the values of the loss function at two different local minima. Then the probability that the algorithm will leave a local minimum and converge to another local minimum will be proportional to the difference between the following values:
Thus, if the difference between the values of the loss function in different local minima is greater, then the probability of exiting the local minimum and converging to another minimum is higher.
Proof (27) indicates the feasibility of the proposed modification of the SCG algorithm by introducing a moment coefficient into it when estimating new model parameters, which will avoid local minima. □
3. Results
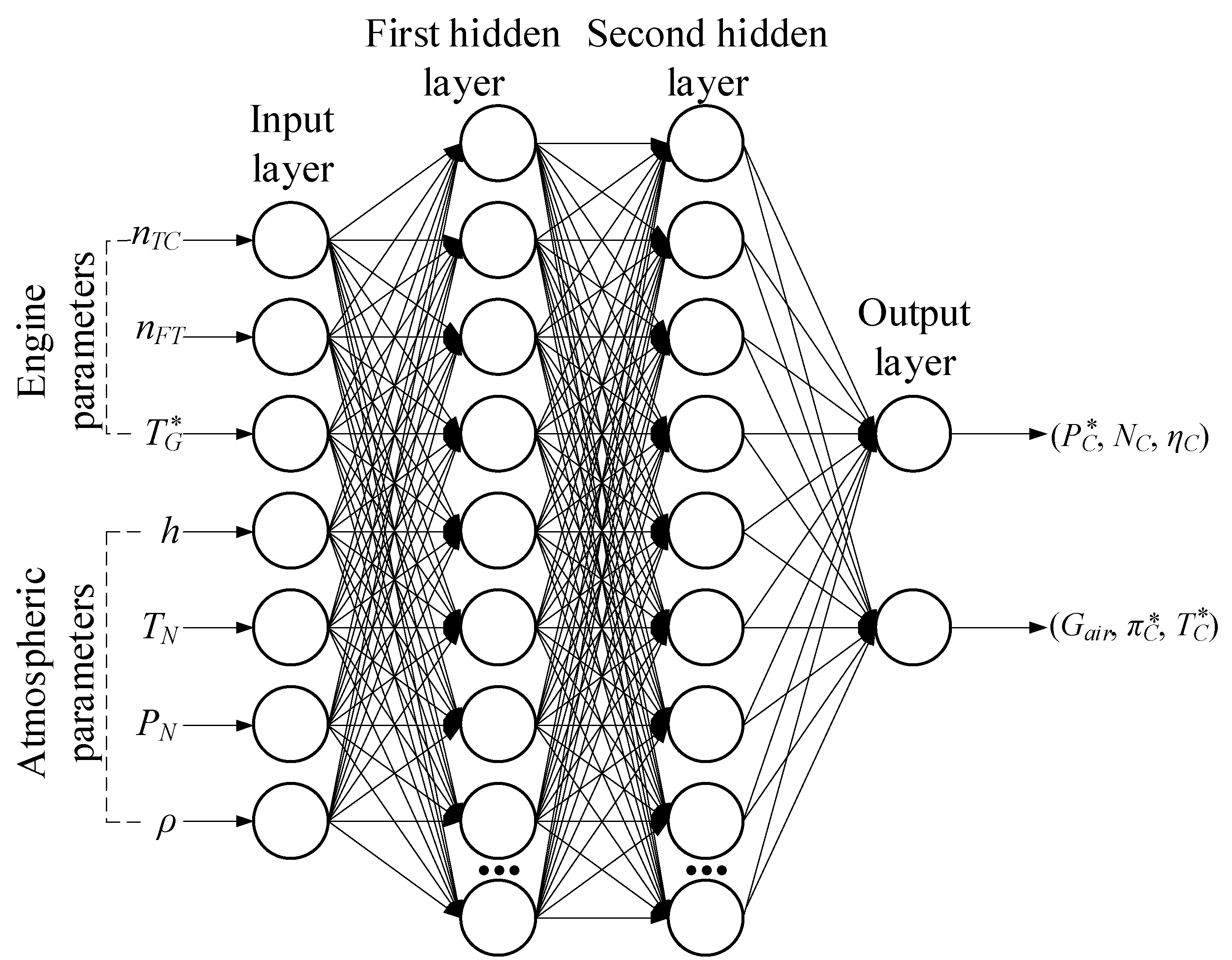
The computational experiment was carried out on a personal computer with an AMD Ryzen 5 5600 processor, 32 KB third-level cache, Zen 3 architecture, 6 cores, 12 threads, 3.5 GHz, RAM-32 GB DDR-4. A three-layer feed-forward neural network with linear neurons in the output layer is used (
Figure 1), and its training algorithm is a modified SCG algorithm.
The input data for neural network training are the helicopter turboshaft engine’s thermogas-dynamic parameters recorded during helicopter flight: gas-generator rotor r.p.m., free turbine rotor speed, and gas temperature in front of the compressor turbine. The results of experimental research on the TV3-117 engine (
Table 1) [
35,
36,
37] were used as initial data for identifying the helicopter TE mathematical model.
The detailed process of preprocessing elements of the training set is described in [
35,
36,
37]. This process begins with assessing the homogeneity of the sample, followed by dividing it into control and test samples and then analyzing their representativeness via cluster analysis.
To check the homogeneity of the training sample, the Fisher–Pearson test is used, based on observed frequencies and comparison with critical values of χ2 at given degrees of freedom and significance levels. The resulting value χ2 = 3.588 does not exceed the critical value of 22.362, which confirms the hypothesis of normal distribution of the parameters of the training sample and, therefore, its homogeneity. To further check homogeneity, the Fisher-Snedecor test is used, which shows the ratio of variance values. The resulting criterion value of 1.28 also does not exceed the critical value of 3.44, which further confirms the homogeneity of the training sample.
The representativeness of the training and test samples is assessed by cluster analysis, the results of which show the identification of eight classes (
Figure 2a). After randomization, training and test samples are formed in a ratio of 2:1 (67 and 33%, respectively). Cluster analysis of both samples also reveals eight classes (
Figure 2b), and the distances between clusters turn out to be almost identical, which indicates the representativeness of both samples.
Thus, the results of the process of preprocessing the elements of the training sample made it possible to form the optimal volume of training, control, test samples (
Table 2).
It is worth noting that the control sample was allocated only for training the neural network to determine the F1 mapping. To determine the F2 mapping, due to the lack of redundancy in the experimental data, from the point of view of describing complex surfaces of toxicity characteristics, a control sample of points was not selected. To prevent the effect of overtraining, a limit was applied to the duration of network training—1000 epochs.
The quality of approximation of helicopter TE characteristics by a neural network to determine the F1 mapping was assessed by the root mean square error value on the control sample:
Figure 3 shows the dependences of
(“□”),
(“×”) and
(“◯”) on the number of free parameters of the neural network to determine the mapping
F1, in
Figure 4—dependences of
(“□”),
(“×”) and
(“◯”) on the number of free parameters of the neural network to determine the mapping
F2. Each dependency data point was obtained by averaging the results of 8 experiments on training neural networks with random initial values of the elements of the weight coefficient matrices and neuron displacement vectors.
In this case, it is appropriate to express it as a percentage of the maximum values of the corresponding values of the root-mean-square error (RMSE) values:
Based on the RMSE values, the mean absolute errors (MAE) are calculated as:
The mean absolute percentage error (MAPE) is also calculated as:
Table 3 shows the results of calculating the maximum RMSE values, average absolute error values, and average absolute relative deviation.
Table 3 shows that the maximum root mean square error is 1.7%, the maximum MAE is 0.130, and the maximum MAPE is 1.8%. Thus, we can conclude that these values do not exceed 1.8%, which indicates the high accuracy of the neural network approximation of helicopter TE parameters.
The results of neural network training show that the quality of approximation of the helicopter’s TE parameters depends significantly on the total number of neurons and only slightly on their distribution among layers. Consequently, the structure of the neural network for implementing the mappings
F1 and
F2 can be characterized with sufficient accuracy by only one parameter—the number of synaptic weights (the number of free parameters of the neural network):
Analyzing the behaviour of the mean square error when changing the number of free parameters of the neural network
F1, the number of neurons in the first hidden layer
k11 = 8, and the number of neurons in the second hidden layer
k12 = 4. This structure corresponds to the number of free parameters
= 70. Such a neural network has the least complexity at which it is still possible to achieve the smallest approximation error. For the neural network
F2, we similarly obtain the values
k21 = 8, and
k22 = 8, which corresponds to the value
= 120. It is known that the research on the accuracy function (
Figure 5) and loss function (
Figure 6) of a neural network are important tools for assessing its performance and training. The accuracy function allows you to evaluate how well the model approximates the helicopter TE parameters, displaying the percentage of correctly approximated ones. On the other hand, the loss function shows how much the model’s predictions deviate from the actual values, helping to optimize the training process by minimizing this loss. By analyzing these graphs during training, conclusions are drawn about how effectively the model is training and measures can be taken to improve its performance.
The results obtained indicate the high efficiency and stability of the neural network during the training process. The accuracy of the model, assessed on the training and validation samples, tends to be unity, indicating its ability to well generalize and approximate the parameters of helicopter TE. In this case, the loss values in both samples do not exceed 0.025, which corresponds to 2.5%, and indicates a low level of errors in the approximation of helicopter TE parameters. Such results indicate that the neural network with the proposed training algorithm is successfully trained and is capable of providing high-quality helicopter TE parameters with a high degree of confidence.
Mathematically, “degree of confidence” can be defined as the probability of a correct approximation of helicopter TE parameters, expressed as a number between 0 and 1. This can be thought of as the probability that the model correctly classifies or predicts the data. In other words, this is the probability that the approximation of the helicopter’s TE parameters is correct. If the degree of confidence is close to 1, this means a high probability of a correct predict, and if it is close to 0, then the probability of an error is high. Thus, the “degree of confidence” is calculated as:
where
Ncor.app. is the number of correct approximations of the helicopter TE parameters,
Napp is the total number of approximations of the helicopter TE parameters made by the neural network.
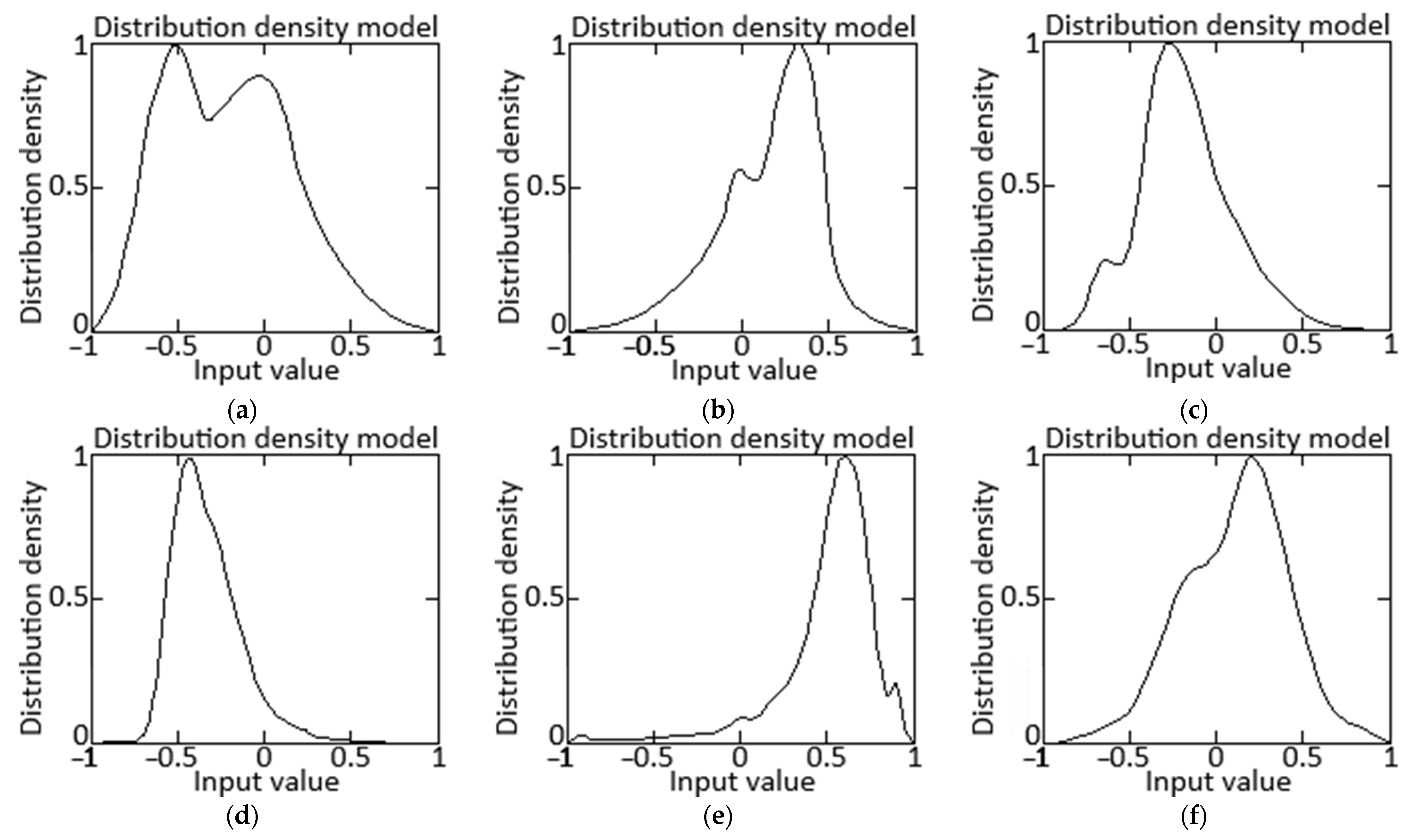
Figure 7 shows a distribution density diagram for the “degree of confidence” of the neural network, which shows how the confidence of the neural network is distributed in the approximation of helicopter TE parameters: a—
Gair, b—
, c—
, d—
, e—
NC, f—
ηC.
Figure 7 shows that most of the helicopter TE approximated parameters are concentrated near 1, which indicates the high confidence of the neural network in solving this task. In this case, the distribution density function is defined as:
where
is the estimate of the distribution density of the “degree of confidence” for the parameter
u,
n is the number of observations (
n = 256 is assumed to be the size of the training sample),
ui is the value of the “degree of confidence” for the
i-th observation, calculated according to (34),
K is the kernel function (Gaussian kernel is assumed),
h is the window width (kernel width,
h ≈ 0.0567 is assumed).
The kernel density estimator estimates the density distribution of the “degree of confidence” based on available observations. The choice of the optimal window width
h for kernel density estimation is important and may depend on the specific situation, including the amount of data, the distribution of “degree of confidence” and the required accuracy of the estimate. In general, the choice of
h affects the smoothing of the distribution density: the larger the value of
h, the smoother the density estimate will be, and vice versa. To select the optimal value of
h, Silverman’s rule of the form is applied:
where
IQR =
Q3 −
Q1 is the interquartile range—a measure of data dispersion that is not sensitive to outliers, that is, the difference between the 75th and 25th percentiles of the data,
Q1 is the 25th percentile (lower quartile),
Q3 is the 75th percentile (top quartile).
The choice of the optimal value of the window width h in kernel density estimation using Silverman’s rule takes into account both the characteristics of the data distribution and its volume. This rule allows you to tailor the window width to the characteristics of the data, taking into account both the magnitude of change (via standard deviation or interquartile range) and sample size. Thus, the optimal value of h is a balance between sufficient smoothing to reduce the influence of random noise and preserving distribution details to reveal structure in the data.
It is worth noting that using the interquartile range in (36) to determine the window width h allows for a measure of data dispersion that is not affected by outliers. This makes the method more robust to data anomalies while still being flexible enough to adapt to different distribution shapes. In this way, Silverman’s rule strikes a balance between smoothing and information preservation, making window-width choices more meaningful and efficient.
To experimentally confirm the feasibility of introducing the moment coefficient
β to avoid local minima when training a neural network.
Figure 8 shows a diagram of the cost function versus the torque coefficient. To construct this dependence diagram, a certain set of values for the moment coefficient
was selected, from which the following values of
β were selected: 0.1, 0.5, 0.9, 0.99. These values represent a range from small torque values to those close to unity, which will allow the impact of different inertia levels on the optimization process to be assessed. For each value of
β, several iterations of the neural network optimization algorithm are performed using this value.
Figure 8 shows that after optimizing the neural network for each value of
β, the following values of the cost function were obtained: for
β = 0.1: 94, for
β = 0.5: 80, for
β = 0.9: 75, for
β = 0.99: 72. From these results It can be seen that as the torque coefficient
β increases, the value of the cost function decreases. The optimal value for the torque coefficient
β in this case, may be 0.99, since it gives the smallest value of the cost function after optimization. Thus, with
β = 0.99, the possibility of falling into a local minimum is practically eliminated, which eliminates the likelihood of suboptimal setting of model parameters and, consequently, less efficient operation of the neural network on the test sample.
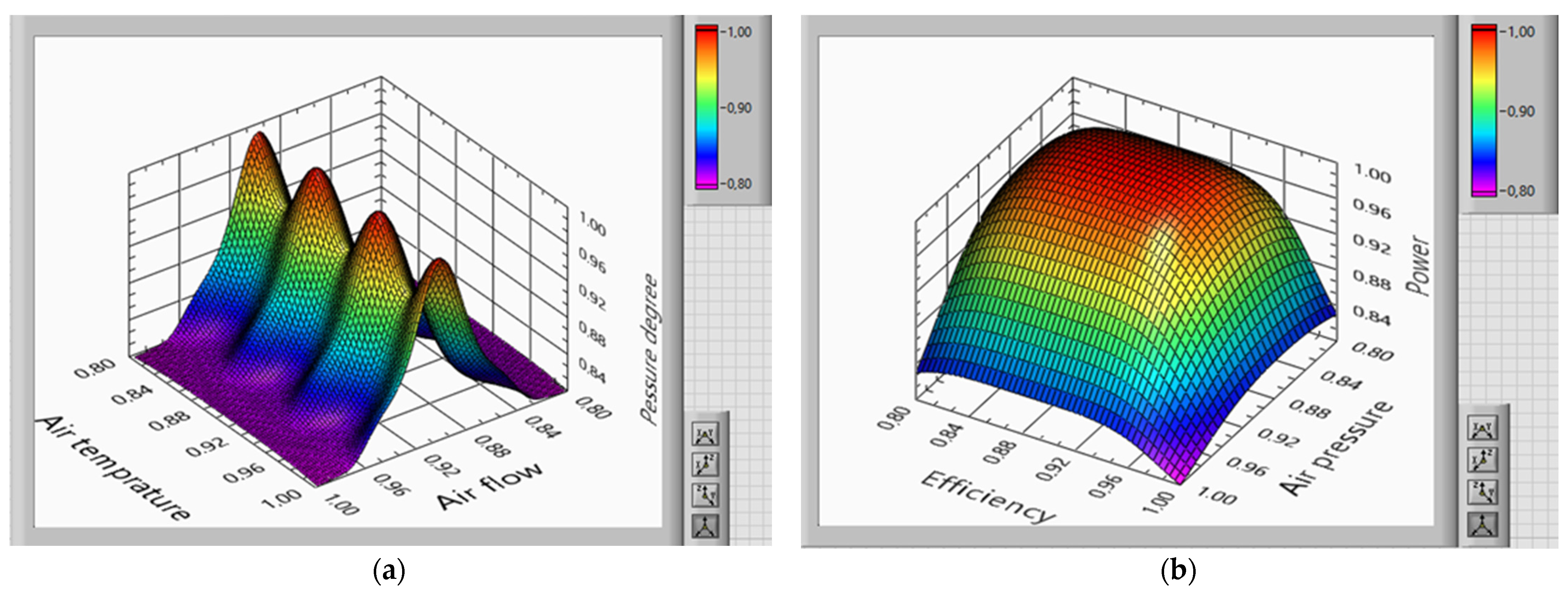
The obtained results of training the neural network made it possible to obtain approximate surfaces of dependencies
and
presented in
Figure 9, where (a) is the dependency surface
, (b) is the dependency surface
.
From the data obtained it follows that the neural network approximation made it possible to obtain dependency surfaces of the key parameters of helicopter TE within acceptable values. The first surface shows the dependence of the air pressure behind the compressor, the power of the compressor, and its efficiency (
Figure 9a), while the second represents the relations between the air flow through the compressor, the degree of increase in the total pressure in the compressor and the air temperature behind the compressor (
Figure 9b). This allows you to effectively control and optimize the operation of helicopter TE, helicopter ensuring stability and reliability in various operating conditions. In addition, this approach provides valuable information for further research and development in the field of improving the performance and helicopter TE efficiency.
In the next stage, research is carried out aimed at researching the helicopter TE characteristics (4), taking into account the limitation of engine power depending on the gas-generator rotor r.p.m. (5). Research includes the gas-generator operating parameters and its effect on the overall engine power. By analyzing data on the gas-generator rotor r.p.m. and the corresponding engine power, optimal operating modes are determined, as well as possible restrictions and limit values of engine parameters. Such studies make it possible for helicopter TE operation optimize, ensuring their efficiency and reliability in various operating conditions.
At the next stage, studies are carried out on helicopter TE characteristics (4), taking into account the limitation of engine power depending on the speed of the gas-generator rotor r.p.m. (5). By analyzing data on the gas-generator rotor r.p.m. and the corresponding engine power, optimal operating modes are determined, as well as possible restrictions and limit values of engine parameters. Such studies make it possible to optimize the helicopter TE operation, ensuring their efficiency and reliability in various operating conditions.
To model the helicopter TE power limitation depending on the gas-generator rotor r.p.m., it is proposed to use a differential equation of the form:
To find a solution to the differential Equation (37), it is necessary to divide it into two cases depending on whether the condition
is satisfied or not. If
, then:
If
, then:
where
C is a constant.
The solution to the differential Equation (38) will depend on the specific nTC function within the time being considered.
In general, the power required to rotate the compressor is described by the expression:
where
NC(
nTC) shows the power limitation at the gas-generator rotor r.p.m.
nTC,
NCmax is the maximum power,
k is the coefficient that characterizes the shape of the dependence,
nTCopt—is the optimal gas-generator rotor r.p.m.
In this context, the energy released during rotation of the helicopter TE compressor can be expressed as an integral of power over time, that is:
where
is the research time interval.
Also, according to (5), the helicopter TE characteristics (4), according to which the engine power is limited depending on the gas-generator rotor r.p.m., take the form:
Let us substitute
NC into (42) as
NC(
nTC) according to (40):
Thus, the
NC power limitation depends on the minimum value between the maximum engine power
and the calculated power
depending on the gas-generator rotor r.p.m.
nTC and other parameters. Also, taking into account (38), we can write:
Expression (44) describes the relations between the power required to rotate the helicopter’s TE compressor and the gas-generator rotor r.p.m., as well as its change over time. The term in (44) is the sum of the gas-generator rotor r.p.m. and the rate of its change over time, and takes into account both the current state and the dynamics of changes in the gas-generator rotor r.p.m. The presence of in (44) makes it possible to take into account not only static but also dynamic factors, such as acceleration or deceleration of gas-generator rotor r.p.m. Thus, plays a key role in adequately describing the energy requirements for rotating the helicopter’s TE compressor, taking into account both the current state and changes over time.
Thus, expression (43) is rewritten taking into account (44) in the form:
Consequently, the energy released during the rotation of the helicopter TE compressor is supplied in the form of a power integral over time (41) taking into account (45):
To integrate (46), it is necessary to consider two cases:
If
, then the minimum value will be
. Then:
If
, then the minimum value will be
. Then:
The total energy
E will be equal to the minimum of
E1 and
E2 since the minimum between two possible values is chosen:
Thus, by integrating the power limitation equation over time and taking into account the minimum condition between two possible expressions for energy, an analytical expression is obtained for the total energy expended on system operation for a given time interval. This expression takes into account the power limitations of helicopter TE, which depend on the gas-generator rotor r.p.m. and their changes over time, as well as the adjustment parameters kp1 and kp2. Such an analytical expression can be useful for assessing and analyzing the energy characteristics of the system under variable loads and operating conditions of helicopter TE.
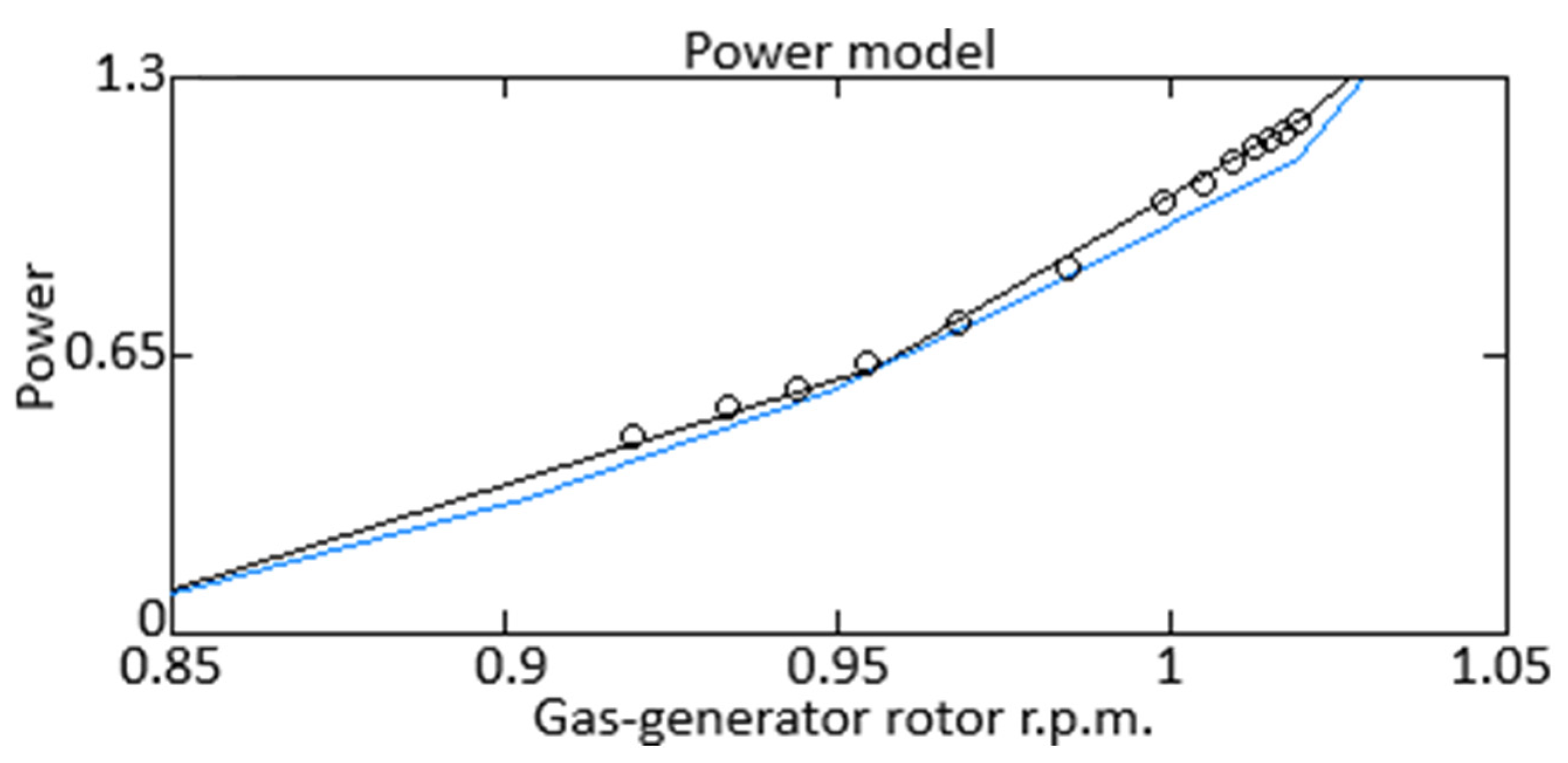
To research the energy characteristics of helicopter TE, diagrams of the changes in power (
Figure 10) and energy (
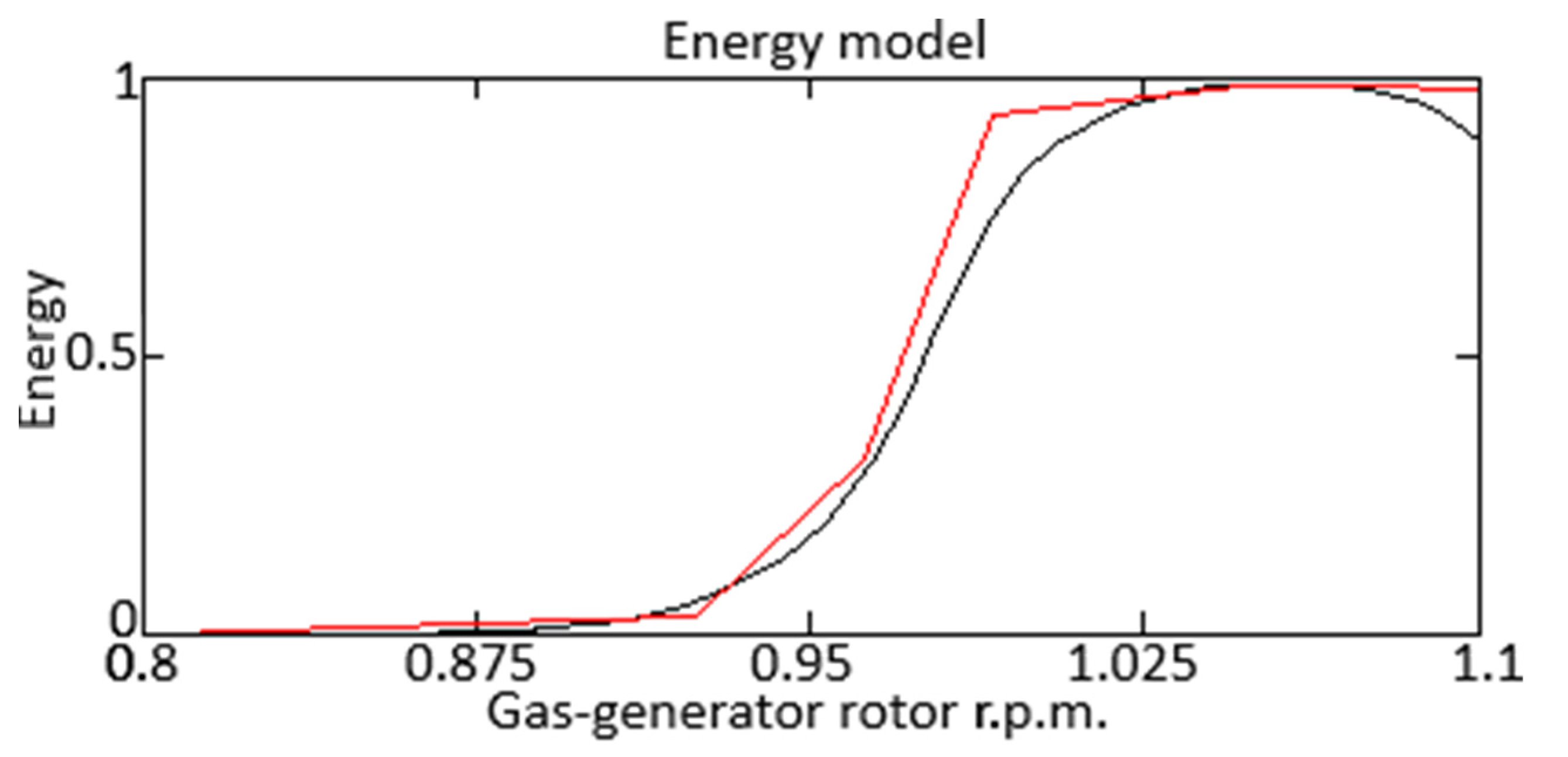
Figure 11) were presented as a function of the gas-generator rotor r.p.m., where “black curve” are the results obtained in this work using a neural network approximation of dependencies (44) and (49), “blue curve” are the results obtained using the helicopter TE mathematical model in [
38], “◯” are the results obtained using the full-scale experiment, which is described in [
38].
As can be seen from
Figure 10, the results obtained in this work using a neural network approximation of dependencies (44) and (29) practically coincide with the results obtained using a full-scale experiment, and most accurately show the dependence of power changes on the gas-generator rotor r.p.m. than the results obtained using helicopter TE mathematical model in [
38].
Table 4 shows the results of calculations of the main statistical accuracy criteria, the obtained dependences of the change in power on the helicopter TE gas-generator rotor r.p.m.: RMSE, MAE, and MAPE.
As can be seen from
Table 4, RMSE of the results obtained in this work using neural network approximation is 2.78 times less than the results obtained using the helicopter TE mathematical model in [
38], MAE of the results obtained in this work using neural network approximation is 1.68 times less than the results obtained using helicopter TE mathematical model in [
38], the MAPE results obtained in this work using neural network approximation are 2.89 times smaller than the results obtained using the helicopter TE mathematical model in [
38]. The results of statistical analysis show that the use of neural network approximation for modelling data on the helicopter’s TE operation in this work leads to a significant improvement in forecasting accuracy compared to the use of the helicopter TE mathematical model presented in [
38]. This indicates the high efficiency and promise of neural network methods in the field of modelling and approximation of helicopter TE parameters.
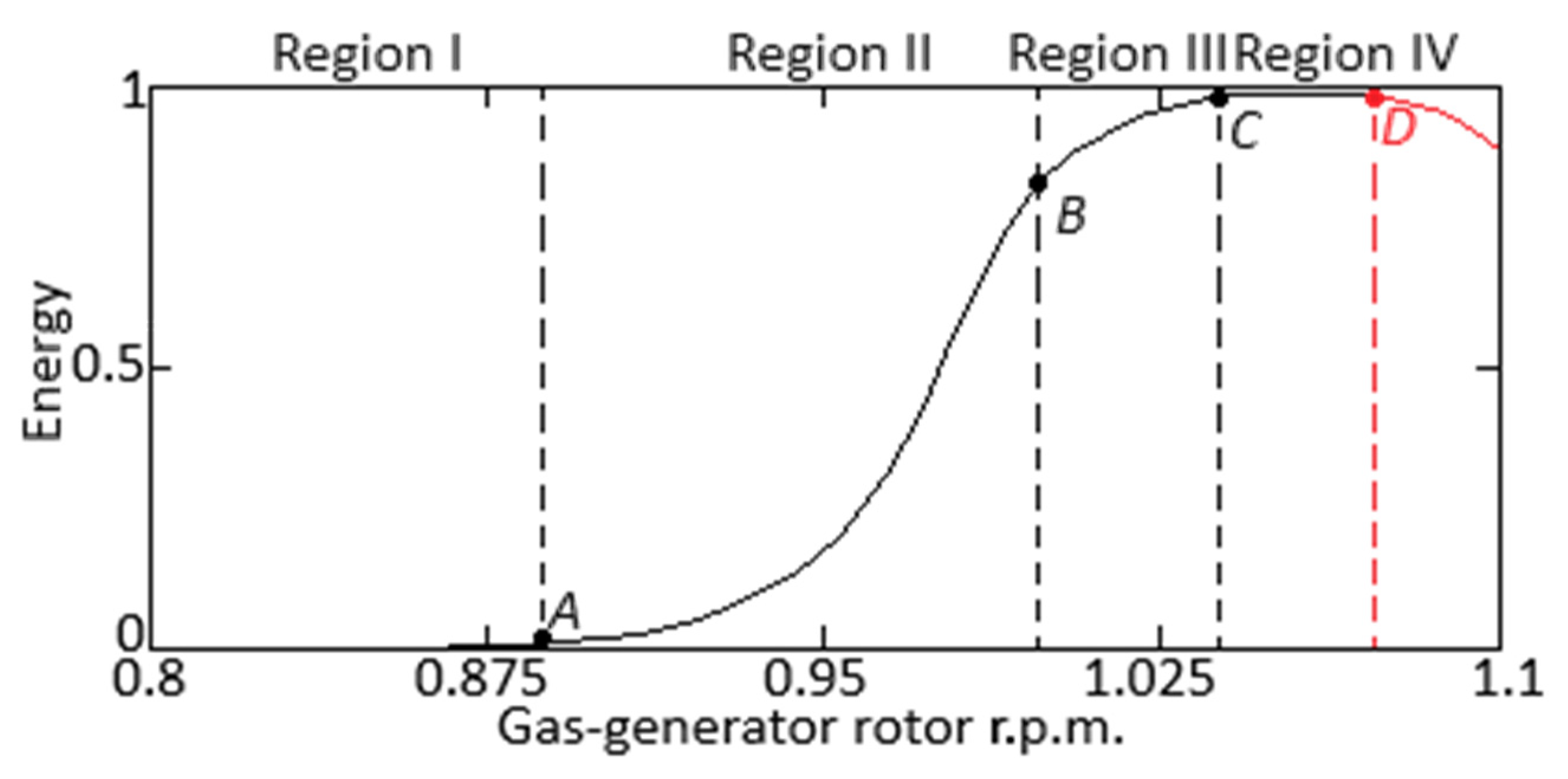
Figure 11, “region 1” shows to low gas-generator rotor r.p.m., in which the energy is low, “region 2”—to the average gas-generator rotor r.p.m., in which energy rapidly increases, “region 3”—to high gas-generator rotor r.p.m., while the efficiency of the compressor decreases and the energy grows more slowly, “region 4”—the maximum gas-generator rotor r.p.m., at which the energy reaches its maximum. Point “A” corresponds to the start of the compressor operation, “point B”—is the maximum efficiency of the compressor, “point C”—is the maximum gas-generator rotor r.p.m., “point D”—is the critical gas-generator rotor r.p.m.
The critical gas-generator rotor r.p.m. is determined by the highest frequency at which the maximum dynamic and thermal loads on engine structures and components remain within safety limits. This may be due to factors such as turbine speed limits, material temperature limits, compressor and turbine aerodynamic limitations, and engine stability.
According to the results obtained, it can be stated that at low rotor speeds, the energy is released when the compressor rotates at a lower speed since the compressor does not operate at full power. As the gas-generator rotor r.p.m. increases, the energy released when the compressor rotates also increases, as the need for air compression to provide the required level of compression increases. However, when a certain rotor speed is reached, the energy released when rotating the compressor may begin to decrease due to various factors (in
Figure 11, the energy decrease is depicted by the “red line” after “point D”), such as restrictions on the production of thermal energy or restrictions according to engine speed to avoid damage. Exceeding the critical compressor speed leads to various undesirable consequences, such as the following:
Engine overheating—when the gas-generator rotor r.p.m. exceeds a critical speed, the load on engine components increases, which can cause increased heat generation and overheating, especially in high-temperature areas such as the combustion chamber.
Loss of stability—going beyond the critical gas-generator rotor r.p.m. leads to a violation of the aerodynamic stability of the compressor and turbine, which can lead to a loss of efficiency and a drop in engine performance.
Mechanical loads—when the critical gas-generator rotor r.p.m. is exceeded, significant mechanical loads occur on engine components, which can lead to wear or even damage.
Thus, the results of the research on the dependence of the energy released during the helicopter’s TE compressor rotation on the gas-generator rotor r.p.m. of the helicopter’s TE are critical for further optimization of engine operation and ensuring its safe operation. The presented data indicate the complex nature of this relation: at low rotor frequencies, the energy may be low due to insufficient compressor operation, while as the frequency increases, the energy increases, providing the necessary air compression. However, exceeding a critical gas-generator rotor r.p.m. can lead to serious problems such as engine overheating, loss of stability and increased mechanical stress, which can lead to reduced performance and component damage. Thus, understanding and controlling gas-generator rotor r.p.m. are key aspects of helicopter TE ensuring efficient and safe operation.
The results of assessing the adequacy of the obtained dependence curve are given in
Table 5, where the following statistical criteria are applied: determination coefficient, standard error of estimation and Fisher’s F-test. In this case, a significance level of 0.01 was adopted, since the statistical analysis performed required a high degree of confidence in rejecting or accepting the null hypothesis in the statistical test. A significance level of 0.01 in the assessment of the adequacy of the results obtained means that the probability of making a type I error (rejecting the correct null hypothesis—there is no statistically significant relation between the energy released during the helicopter TE gas-generator operation and its gas-generator rotor r.p.m.) is only 1%, which provides high confidence in the correctness of the decision made.
In
Table 5 is the sum of squared residuals (the sum of squared differences between actual energy values and values predicted by the model),
is the total sum of squares (sum of squares of the difference between the actual energy values and their average value),
n = 256 is the training sample size,
p = 7 is the model parameters number (including free term),
Ei is the actual energy value,
is the predicted energy value from the model,
is the regression sum of squares (sum of squares of the difference between the values predicted by the model and the mean energy).
The obtained coefficient of determination value of 0.99126 indicates a high degree of fit of the model to the data. This means that more than 99% of the energy variation can be explained by the gas-generator rotor r.p.m. variation, indicating that the model describes the relations between these variables well.
The resulting standard error of estimation of 0.00974 indicates the high accuracy and reliability of the model. Given the low standard error, it can be concluded that the model fits the data well and produces energy predictions with high accuracy. This means that the predicted energy values differ from the actual values with little error, making the model useful and reliable for energy prediction at different gas-generator rotor r.p.m.
The obtained value of Fisher’s F-test is 4.782 (the critical value of Fisher’s test with 7 model parameters and 256 sample elements at a significance level of 0.01 is 3.97) indicating the statistically significant adequacy of the model. Considering that the obtained Fisher’s F-test value exceeds the critical value at the selected significance level, the null hypothesis that the model is not statistically significant is rejected. This suggests that the model explains data variation well and can be used to predict energy values based on gas-generator rotor r.p.m.
4. Discussion
The conducted researches indicate that helicopter TE parameters neural network approximation plays an important role at the stage of their operation, therefore it is important to have effective methods for training neural networks that ensure high accuracy and generalization ability of the model. Thus, an important task is to compare the proposed neural network training algorithm with already known methods. To do this, it is necessary to define key quality metrics that will help evaluate the performance of each method. Such metrics may include classification accuracy, root mean square error, convergence rate, and others. Each of these metrics plays its role in assessing the effectiveness of the training algorithm, based on the specifics of the task and the requirements for the model.
A comparative analysis of the main quality metrics will allow us to identify the advantages and disadvantages of each considered neural network training algorithm and make a reasonable conclusion about their comparative effectiveness.
Table 6 presents the results of calculating quality metrics for the proposed algorithm (modified SCG algorithm) for neural network training (Algorithm 1), the traditional SCG algorithm (Algorithm 2), the backpropagation algorithm (Algorithm 3), the quick propagation algorithm (Algorithm 4), the quasi-Newton (Algorithm 5), the Levenberg-Marquardt algorithm (Algorithm 6), according to the following quality metrics:
Efficiency coefficient—evaluates the efficiency of training a neural network, and is defined as the ratio of the change in the loss function at the current iteration to the change in the parameters of the neural network at the same iteration:
where
is the loss function value at the current iteration,
is the loss function value at the previous iteration, and
is the rate of change in the parameters of the neural network at the current iteration.
Quality coefficient—evaluates the accuracy of approximation of the neural network parameters, and is defined as the ratio of the reduction in the loss function at the current iteration to the total loss function at previous iterations:
where
E(
θ0) is the loss function initial value.
Determination coefficient—measures the proportion of variability in the de-pendent variable that is explained by the model:
where
yi is the actual value,
is the approximated value for the
i-th example,
is the average value of the actual values.
Correlation coefficient—measures the degree of linear dependence between actual and approximated values:
where
is the average value of the approximated values.
The accuracy of solving the task of helicopter TE parameters neural network approximation on a test data set is a measure of the correspondence of the out-put values of the neural network to the expected values of helicopter TE parameters based on the provided test data:
where
TP (True Positive) is the number of true positive results,
TN (True Negative) is the number of true negative results,
FP (False Positive) is the number of false positive results, and
FN (False Negative) is the number of false negative results.
Precision—is a metric used in assessing the quality of classification, which measures the proportion of objects that belong to the positive class among all objects that were predicted as positive:
The higher the Precision value, the fewer false positives the model produces, meaning that the model is less likely to misclassify negative class objects as positive. High accuracy is important when the cost of FP error (false positive) is high.
Recall (completeness, sensitivity)—is a metric used in assessing the quality of classification, which measures the proportion of objects of the positive class that the model correctly classified as positive:
F-score—is a metric used to measure the accuracy of the test, and is the harmonic mean between
Precision and
Recall:
Table 6.
Calculating results of the degree of improvement of the proposed neural network training algorithm compared to traditional ones (author’s research).
Table 6.
Calculating results of the degree of improvement of the proposed neural network training algorithm compared to traditional ones (author’s research).
| Quality Metric | Algorithm 1 | Algorithm 2 | Algorithm 3 | Algorithm 4 | Algorithm 5 | Algorithm 6 |
|---|
| Keff | 0.994 | 0.983 | 0.964 | 0.959 | 0.926 | 0.925 |
| Kquality | 0.993 | 0.980 | 0.952 | 0.948 | 0.912 | 0.915 |
| R2 | 0.997 | 0.981 | 0.953 | 0.950 | 0.917 | 0.920 |
| R | 0.992 | 0.977 | 0.943 | 0.935 | 0.908 | 0.911 |
| Accuracy | 0.993 | 0.985 | 0.960 | 0.949 | 0.910 | 0.916 |
| Precision | 0.987 | 0.969 | 0.945 | 0.937 | 0.913 | 0.910 |
| Recall | 1.0 | 1.0 | 1.0 | 0.950 | 0.922 | 0.903 |
| F-score | 0.988 | 0.962 | 0.951 | 0.938 | 0.908 | 0.846 |
Table 7 shows the results of improving the quality metrics of neural network training by the proposed modified SCG algorithm (Algorithm 1) in comparison with other algorithms (Algorithms 2–6).
As can be seen from
Table 7, the application of the proposed modified neural network training algorithm in the problem of neural network approximation of helicopter TE parameters improves the considered quality metrics from 1.008 to 1.168 times.
At the final stage of the computational experiment, errors of the first and second types are determined and analyzed, which in statistics play an important role in making statistical decisions. A first type error occurs when the null hypothesis is incorrectly rejected, suggesting the presence of an effect or difference where there is none. This is often related to the chosen significance level.
The paper uses a significance level of 0.01, which indicates that a decision on statistical significance is made only if the probability of obtaining these or more extreme results, provided that the null hypothesis is true, is less than 1%. A significance level of 0.01 was adopted because first type errors are undesirable and a very high level of confidence in statistical significance is required. In the approximation task, the null hypothesis is an incorrectly approximated value of the helicopter TE parameter, accepted as correct, and is calculated as:
A second type of error, on the other hand, occurs when the null hypothesis is not rejected even though it is false. This may be due to the insufficient power of the statistical test, which is unable to detect a true effect due to a small sample size or other factors. In the approximation task, the null hypothesis is the correctly approximated value of the helicopter’s TE parameter, accepted as incorrect. Both types of errors are important when assessing the reliability of the results of statistical analysis, and a decrease in one of them is often associated with an increase in the other and is calculated as:
where the concept of “power” of a test is defined as the probability of rejecting the null hypothesis when it is false.
Table 8 shows the results of calculating errors of the first and second kind both for the proposed modified SCG algorithm for training a neural network and for other algorithms discussed above:
The traditional SCG algorithm;
The backpropagation algorithm;
The quick propagation algorithm;
The quasi-Newton algorithm;
the Levenberg–Marquardt algorithm, in solving the task of neural network approximation of helicopter TE parameters–dependency surfaces.
Table 8.
Results of calculating the first and second types of errors (author’s research).
Table 8.
Results of calculating the first and second types of errors (author’s research).
Neural Network
Training Algorithm | Probability of Error in Neural Network Approximation of Helicopter TE Parameters |
|---|
| |
|---|
| First Kind Error | Second Kind Error | First Kind Error | Second Kind Error |
|---|
| Proposed modified SCG algorithm | 0.62 | 0.43 | 0.65 | 0.44 |
| Traditional SCG algorithm | 0.92 | 0.68 | 0.94 | 0.71 |
| Backpropagation algorithm | 1.25 | 1.07 | 1.28 | 1.09 |
| Quick propagation algorithm | 1.43 | 1.12 | 1.46 | 1.15 |
| Quasi-Newton algorithm | 1.68 | 1.34 | 1.72 | 1.37 |
| Levenberg-Marquardt algorithm | 1.55 | 1.41 | 1.58 | 1.42 |
A comparative analysis showed that the use of the proposed modified SCG algorithm for training a neural network reduces errors of the first and second types compared with the traditional SCG algorithm by 1.35…1.61 times, the backpropagation algorithm–by 1.97…2.49 times, the quick propagation algorithm–by 2.25…2.61 times, by the quasi-Newton algorithm–by 2.65…3.12 times, the Levenberg-Marquardt algorithm–by 2.43…3.28 times.
To compare the proposed helicopter TE parameters neural network approximation method based on a three-layer forward propagation neural network with linear neurons in the output layer, trained by a modified SCG algorithm, with the closest analogue [
28], which is based on hybrid fault detection and diagnosis, which consists of four main stages: data collection, data evaluation (analysis and normalization), data fusion (only for the supervised training method) and a neural network model—a three-layer perceptron trained by the classical backpropagation algorithm. Applying the training sample (
Table 1) to the model [
28], a diagram was constructed of the dependence of the energy change on the gas-generator rotor r.p.m. of the helicopter TE (
Figure 12, where the “black curve” is a diagram constructed using the helicopter TE parameters neural network approximation method proposed in the helicopters work, that is, similar to
Figure 11, the “red curve” is a diagram constructed using the model [
28]).
Research of the dependence of energy changes on the gas-generator rotor r.p.m. of a helicopter TE, carried out using the model [
28], demonstrates significant differences compared to the results obtained in this work. It should be noted that the results obtained in this work highlight the critical importance of the relations under research, emphasizing its importance for optimizing engine operation and helicopter TE ensuring safe operation, at a time when the results obtained using [
28] look less significant from a practical point of view applications. This is because the data presented in this work describes in detail the influence of the gas-generator rotor r.p.m. on the energy characteristics of the helicopter’s TE compressor and highlights critical moments that are important for ensuring optimal operation and safe operation of the engine. In contrast, the results obtained using the model [
28] may be less accurate or take into account fewer factors, making them less informative for engineering and practical purposes.
Table 9 shows the main advantages of the proposed method of neural network approximation of helicopter TE parameters over the closest approach [
28] according to the following parameters: neural network architecture, neural network training algorithm, neural network training time, efficiency coefficient, quality coefficient, determination coefficient, correlation coefficient, Accuracy, Precision, Recall, F-score.
Despite the three-layer perceptron model [
28] being trained 85 s faster than the one proposed in this work, the advantages of the modified SCG algorithm over the backpropagation algorithm offset the difference in training time, as evidenced by higher efficiency, quality, determination, correlation coefficients, accuracy, precision, recall, and F-score of the proposed method compared to the model [
28].
Thus, the results obtained during the comparative analysis (
Table 9) of the proposed method of helicopter TE parameters neural network approximation based on a 3LFNN with linear neurons in the output layer, trained by a modified SCG algorithm with the closest one to it, which is based using a three-layer perceptron trained with an error backpropagation algorithm [
28], indicate that the proposed method is more effective compared to [
28] in solving the task of helicopter TE parameters neural network approximation at helicopter flight mode.
5. Conclusions
For the first time, a helicopter turboshaft engine parameters neural network approximation method was developed, which, via the use of a three-layer neural network of direct propagation with linear neurons in the output layer, trained by a modified SCG algorithm, made it possible to obtain approximated surfaces of dependencies of helicopter TE parameters with an accuracy of at least 0.993 (99.3%).
The SCG algorithm, used in training feedforward neural networks, was further developed, which differs from the existing one in that by introducing the moment coefficient into the analytical expression for calculating new model parameters, the possibility of falling into a local minimum was eliminated, which eliminates the probability optimal setting of model parameters is not enough.
A mathematical model was created that determines the energy released during helicopter TE compressor rotation, taking into account the power limitations of helicopter TE, which depend on the gas-generator rotor r.p.m. and their changes over time. The adequacy of the created mathematical model was confirmed by calculating statistical quality metrics, such as RMSE, MAE, and MAPE, while the RMSE of the results obtained in this work using neural network approximation is 2.78 times less than the results obtained using the helicopter TE mathematical model in [
38], MAE of the results obtained in this work using neural network approximation is 1.68 times less than the results obtained using the helicopter TE mathematical model in [
38], and MAPE of the results obtained in this work using neural network approximation is 2.89 times less than the results obtained using the helicopter TE mathematical model in [
38].
The dependence of the energy released during the helicopter turboshaft engine compressor rotation on the gas-generator rotor r.p.m. was obtained, divided into the region of low gas-generator rotor r.p.m., in which the energy is low, the region of medium gas-generator rotor r.p.m., in which the energy rapidly increases, the region of high gas-generator rotor r.p.m., while the efficiency of the compressor decreases, and the energy grows more slowly, and the region of maximum gas-generator rotor r.p.m., in which the energy reaches its maximum. Application of the obtained dependence makes it possible to establish for a specific type of helicopter turboshaft engine the region of optimal gas-generator rotor r.p.m., where the optimal ratio of energy consumption and gas-generator operating efficiency is achieved, thereby ensuring optimal performance and reliability of the helicopter TE. The adequacy of the results obtained was confirmed by calculating the determination coefficient (its value is 0.99126), the standard error of estimation (its value is 0.00974), Fisher’s F-test (its value is 4.782, which is greater than the critical 3.97 at a significance level of 0.01), which indicates the possibility of accurately determining the optimal gas-generator rotor r.p.m. for a specific type of helicopter TE, where the best ratio of energy consumption and gas-generator operating efficiency is achieved, which ensures maximum performance and reliability of the helicopters TE.
It was experimentally confirmed that the obtained maximum root means square error values, the MAE value of the mean absolute relative deviation of the approximated parameters of helicopter TE are in the range from 1.1 to 1.8% and do not exceed 2%, which indicates their high approximation of a 3LFNN with linear neurons in the output layer trained by the proposed modified SCG algorithm.
It was experimentally proven that solving the task of neural network ap-proximation of helicopter TE parameters using a three-layer direct propagation neural network with linear neurons in the output layer, trained by the proposed modified SCG algorithm, reduces errors of the first and second kind compared to the traditional SCG algorithm by 1.35…1.61 times, to the backpropagation algorithm—by 1.97…2.49 times, to the quick propagation algorithm—by 2.25…2.61 times, to the quasi-Newton algorithm—by 2.65…3.12 times, to the Levenberg–Marquardt algorithm—by 2.43…3.28 times, which indicates a more accurate and efficient operation of the developed neural network approximation method.
It was experimentally confirmed that the use of the proposed modified SCG algorithm, used in training feedforward neural networks, in the task of neural network approximation of helicopter TE parameters, improves quality metrics, namely, efficiency coefficient, quality coefficient, determination coefficient, correlation coefficient, accuracy, precision, recall, F-score, compared to traditional SCG algorithm, backpropagation algorithm, fast error propagation algorithm, quasi-Newton algorithm, Levenberg-Marquardt algorithm, from 1.008 to 1.168 times.