Online Estimation of Three-Phase Induction Motor Parameters Using an Extended Kalman Filter for Energy Saving
Abstract
1. Introduction
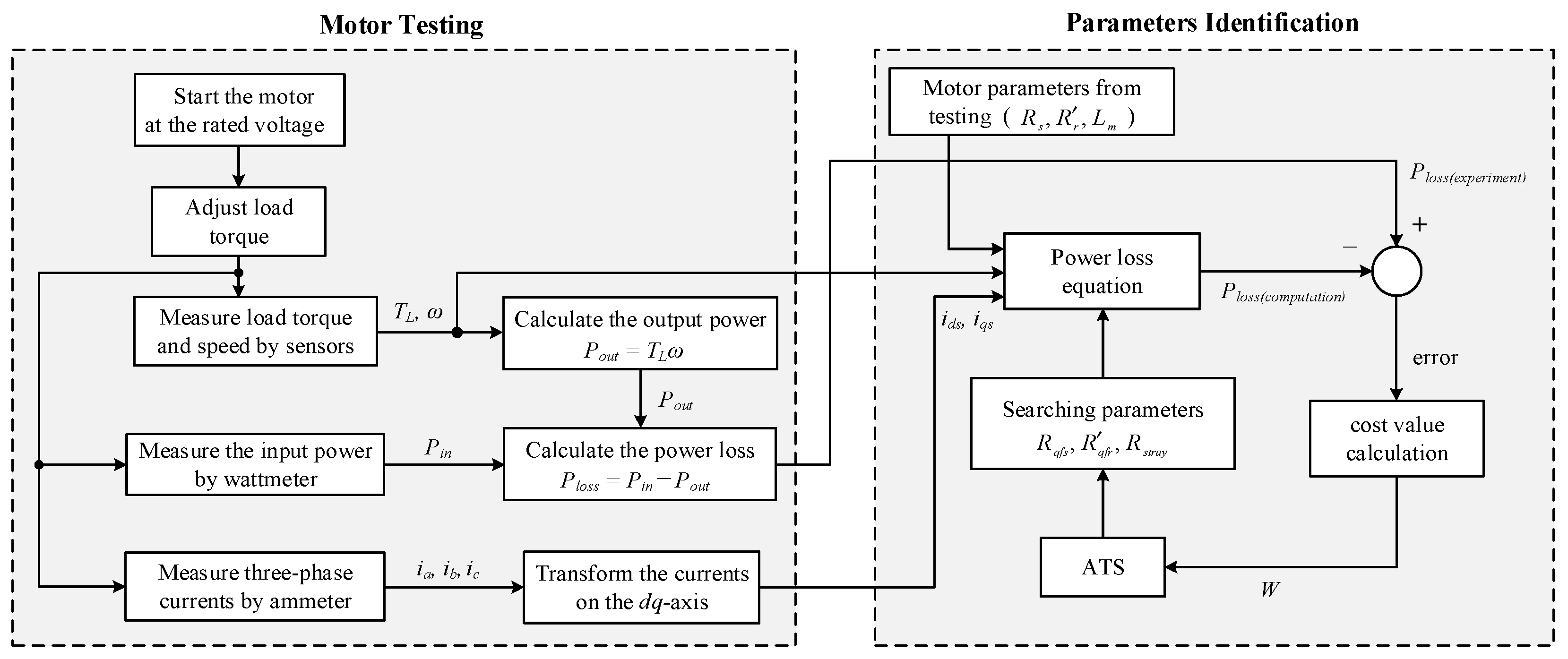
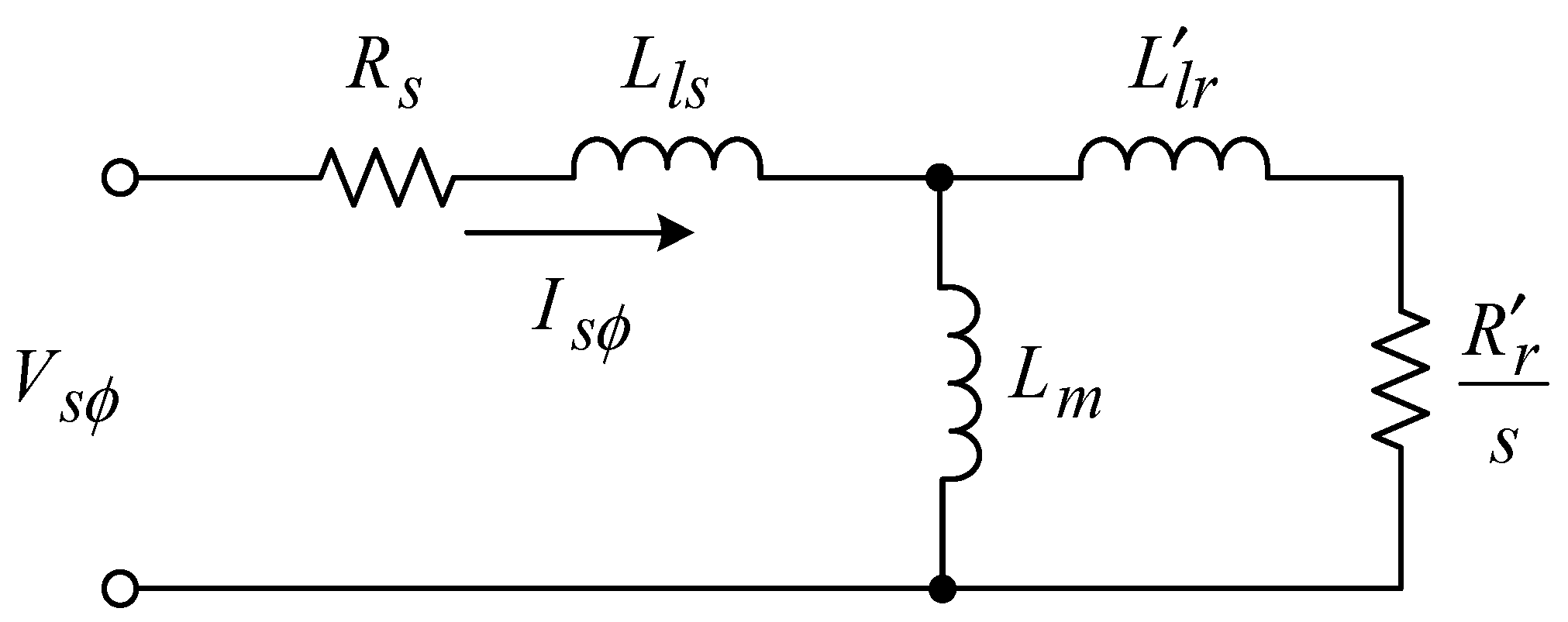
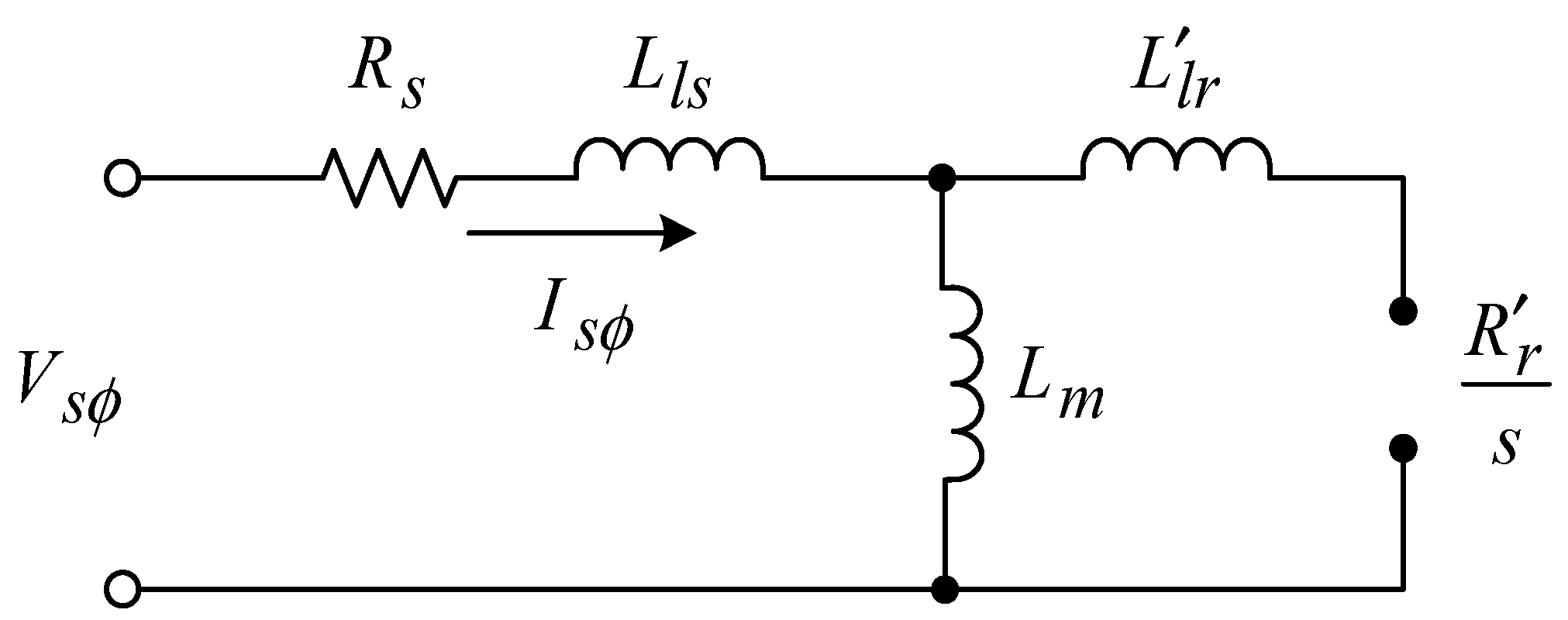
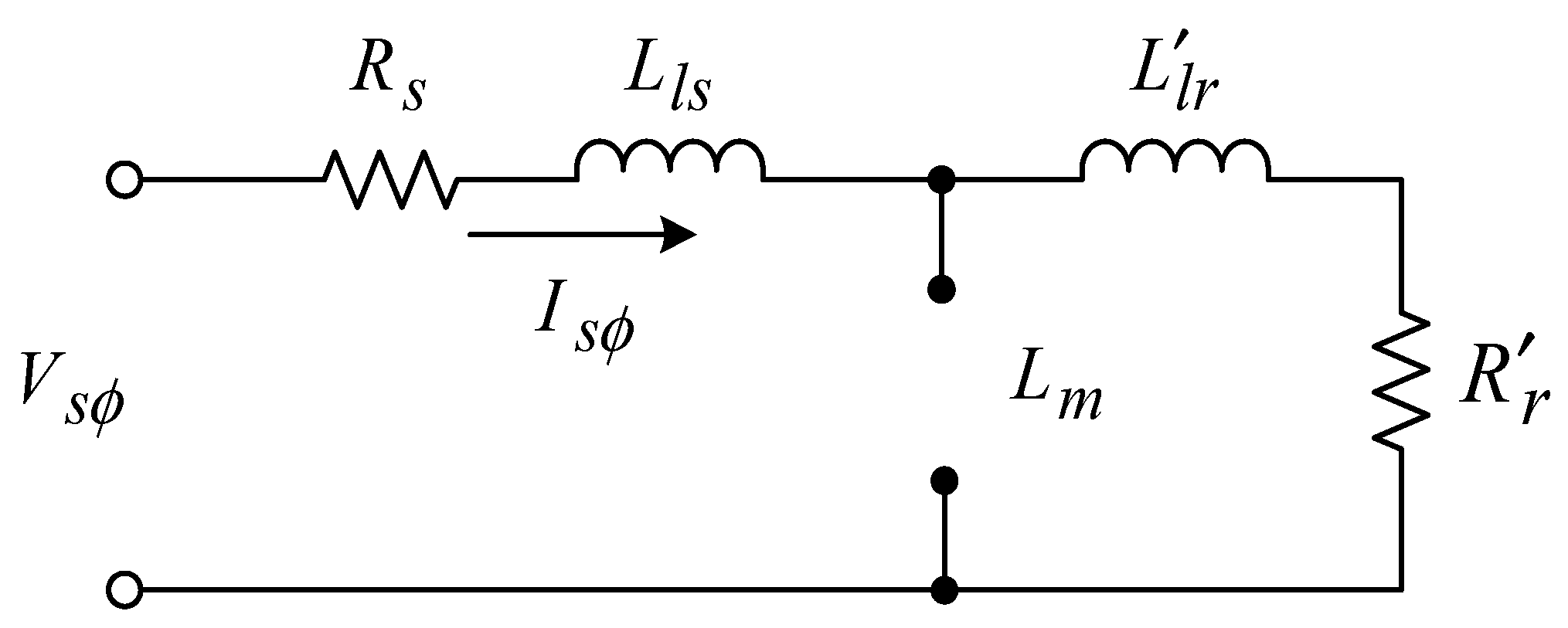
2. Power Loss Equation and Motor Testing
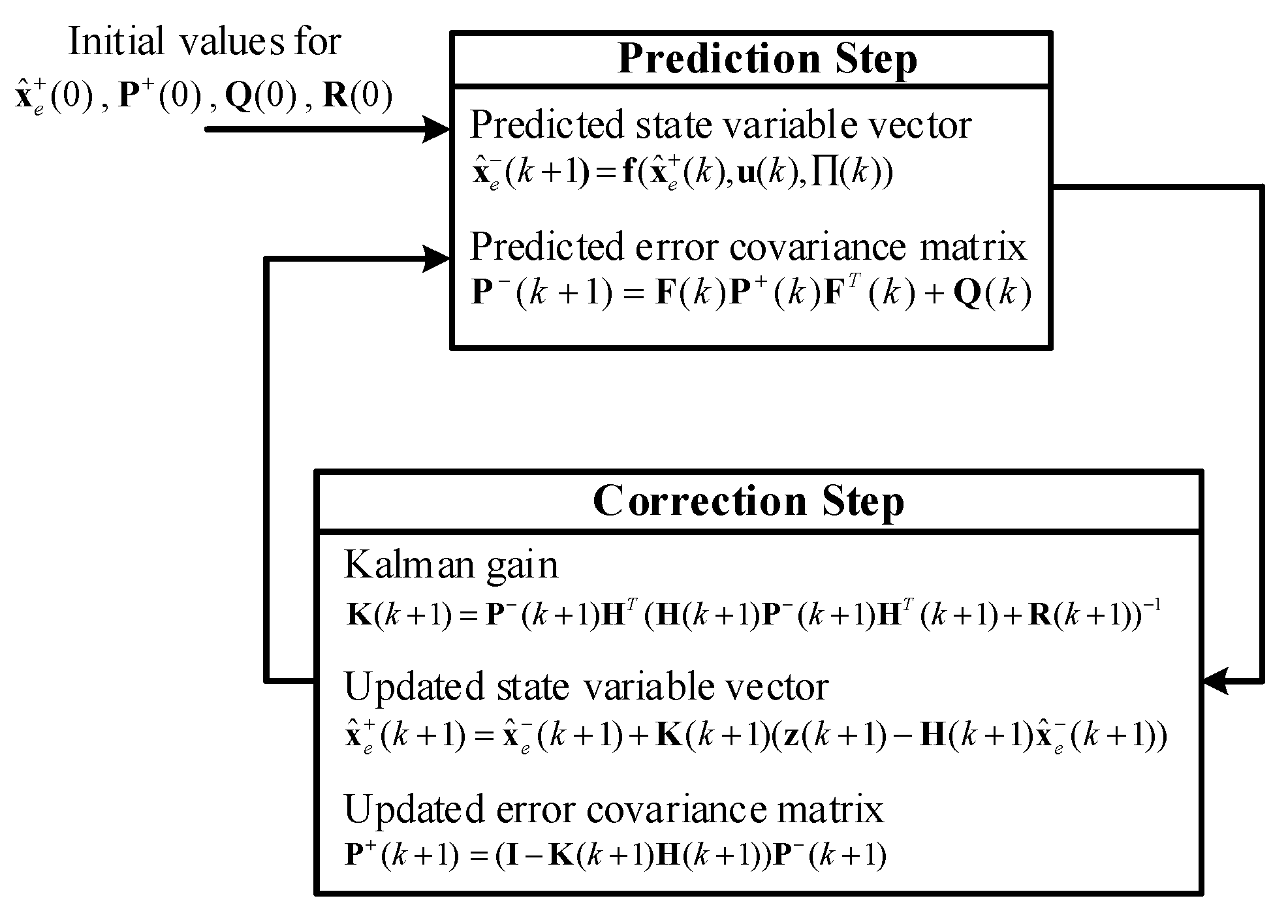
3. Extended Kalman Filter
3.1. Extended Kalman Filter Algorithm
3.2. Convergence Analysis of the Extended Kalman Filter
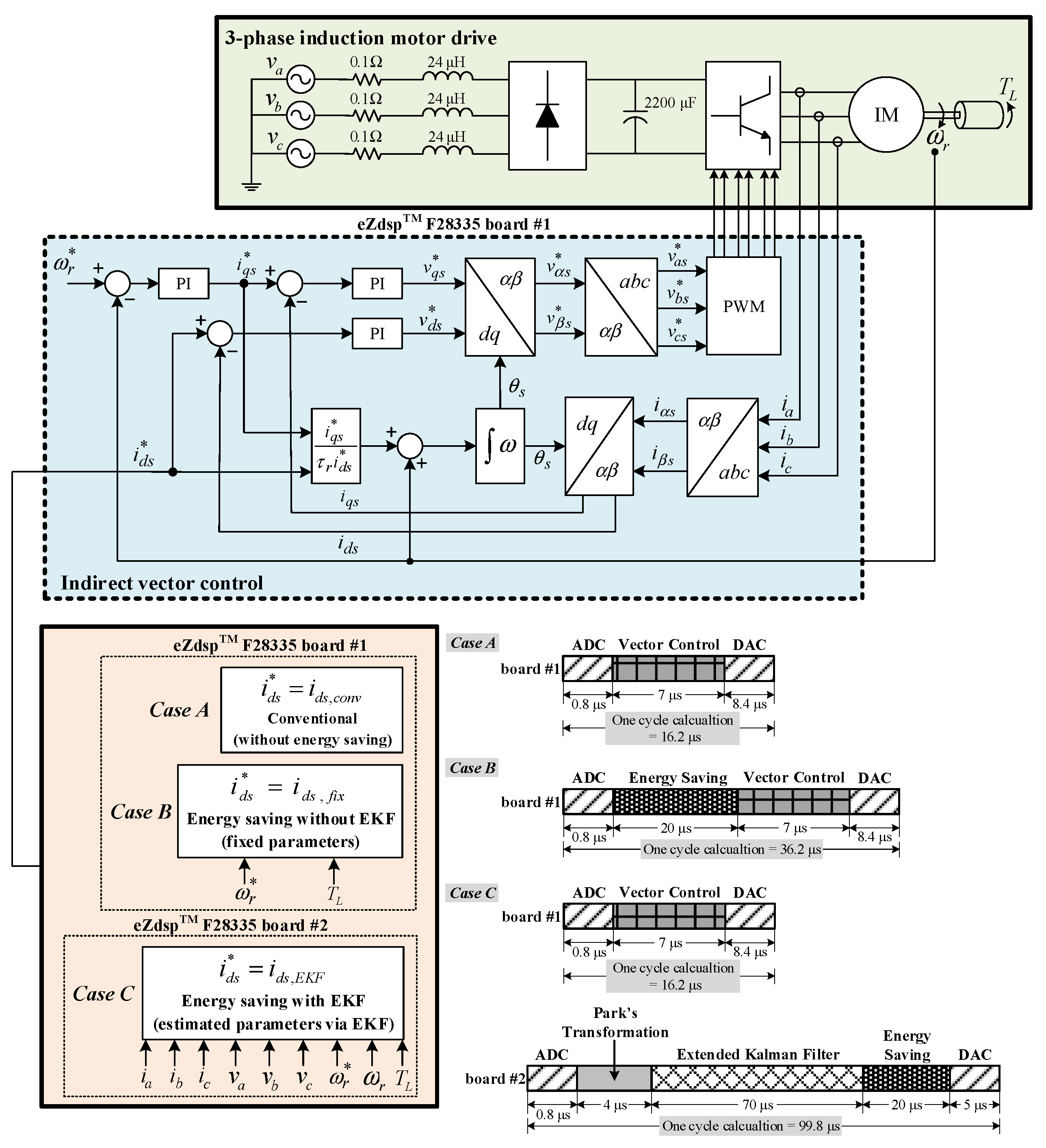
4. Experimental Results
4.1. Conventional Approach (Case A)
4.2. Energy-Saving Approach without EKF (Case B)
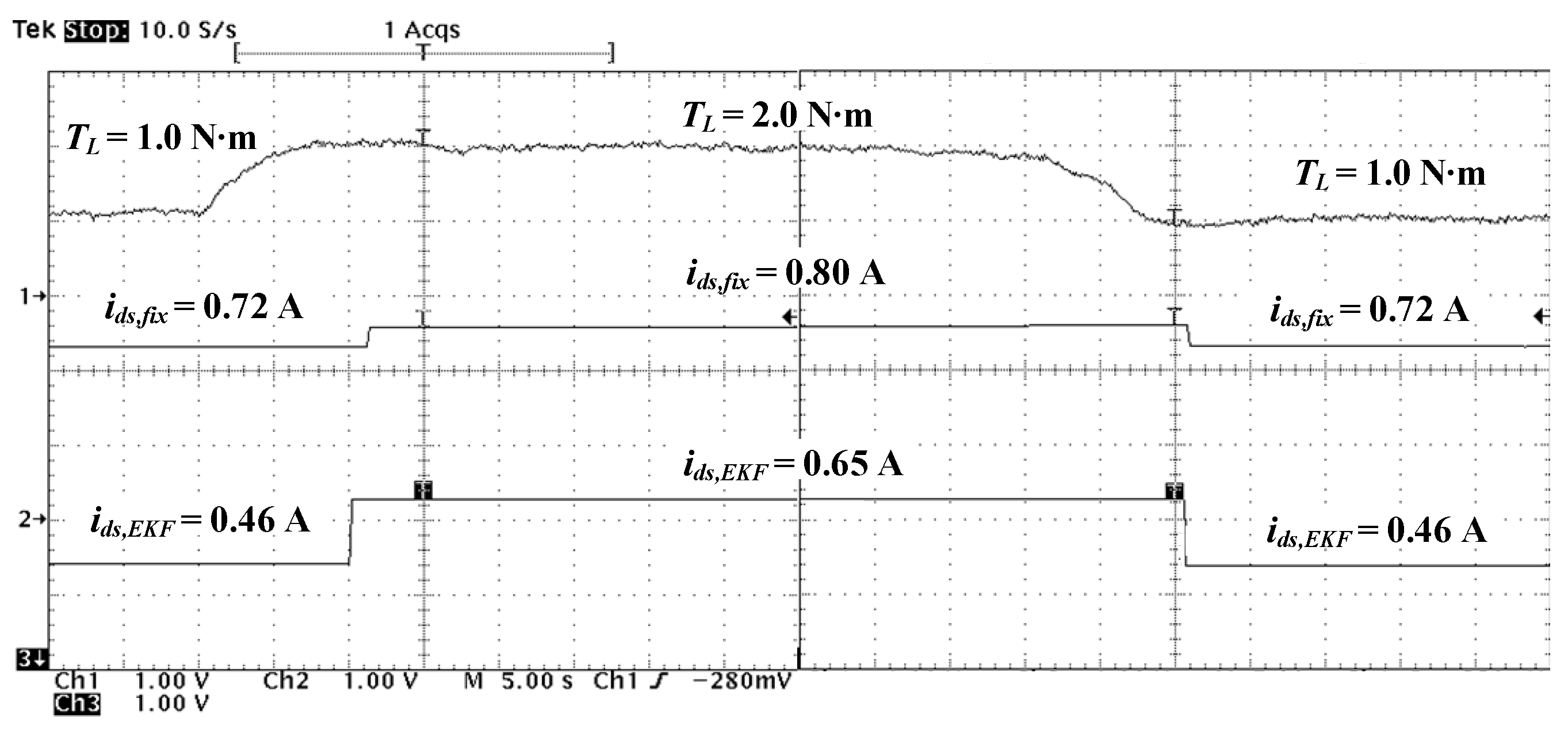
4.3. Energy-Saving Approach with EKF (Case C)
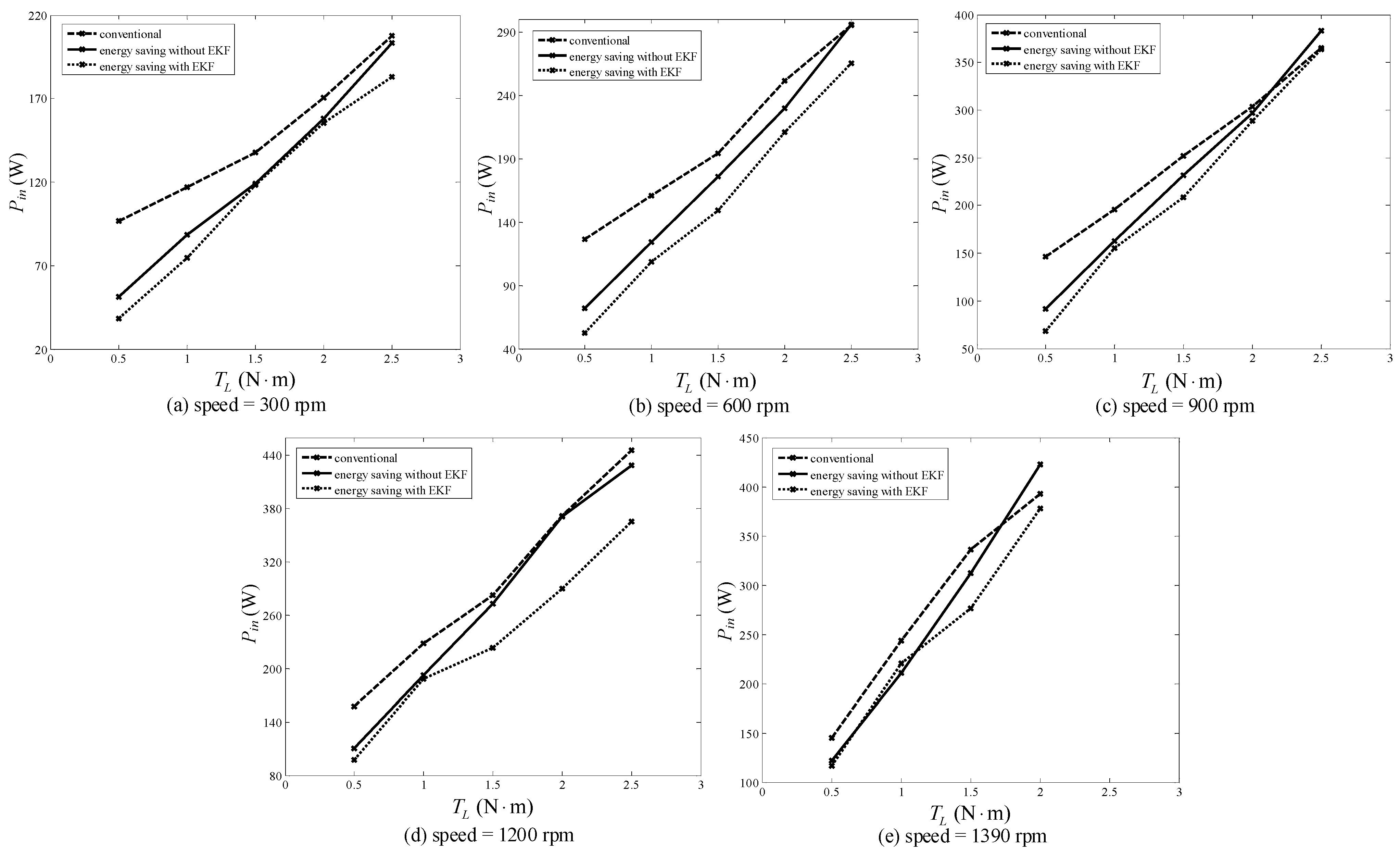
4.4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chapman, S.J. Electric Machinery Fundamentals, 5th ed.; McGraw-Hill: New York City, NY, USA, 2012. [Google Scholar]
- Un-Noor, F.; Padmanaban, S.; Mihet-Popa, L.; Mollah, N.M.; Hossain, E. A Comprehensive Study of Key Electric Vehicle (EV) Components, Technologies, Challenges, Impacts, and Future Direction of Development. Energies 2017, 10, 1217. [Google Scholar] [CrossRef]
- Yang, Z.; Shang, F.; Brown, I.P.; Krishnamurthy, M. Comparative study of interior permanent magnet, induction, and switched reluctance motor drives for EV and HEV applications. IEEE Trans. Transp. Electrif. 2015, 1, 245–254. [Google Scholar] [CrossRef]
- Kusko, A.; Galler, D. Control means for minimization of losses in AC and DC motor drives. IEEE Trans. Ind. Appl. 1983, IA-19, 561–570. [Google Scholar] [CrossRef]
- Famouri, F.; Cathev, J.J. Loss minimization control of an induction motor drives. IEEE Trans. Ind. Appl. 1991, 27, 32–37. [Google Scholar] [CrossRef]
- Zarchi, H.A.; Hesar, H.M.; Khoshhava, M.A. Online maximum torque per power losses strategy for indirect rotor flux-oriented control-based induction motor drives. IET Electr. Power Appl. 2019, 13, 267–273. [Google Scholar]
- Bruno, A.; Caruso, M.; Tommaso, A.O.D.; Miceli, R.; Nevoloso, C.; Viola, F. Simple and flexible power loss minimizer with low-cost MCU implementation for high-efficiency three-phase induction motor drives. IEEE Trans. Ind. Appl. 2021, 57, 1472–1481. [Google Scholar] [CrossRef]
- Hu, D.; Xu, W.; Dian, R.; Liu, Y.; Zhu, J. Dynamic loss minimization control of linear induction machine. In Proceeding of the IEEE Energy Conversion and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; pp. 3598–3603. [Google Scholar]
- Shi, Y.; Sarlioglu, B.; Lorenz, R.D. Real-time loss minimizing control of induction machines for dynamic load profiles under deadbeat-direct torque and flux control. In Proceeding of the IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 1641–1648. [Google Scholar]
- Li, J.; Xiao, F.; Zhang, S. Simplified loss model control efficiency optimization algorithm for vector control induction motor drives. In Proceedings of the 43rd Annual Conference of the Industrial Electronics Society (IECON), Beijing, China, 29 October–1 November 2017; pp. 5178–5183. [Google Scholar]
- Uddin, M.N.; Nam, S.W. New online loss-minimization based control of an induction motor drive. IEEE Trans. Ind. Appl. 2008, 23, 926–933. [Google Scholar] [CrossRef]
- Nobile, G.; Scelba, G.; Cacciato, M.; Scarcella, G. Loss minimization control for an integrated multidrive topology devoted to hybrid electric vehicles. IEEE Trans. Ind. Electron. 2019, 66, 8345–8360. [Google Scholar] [CrossRef]
- Yu, J.; Pei, W.; Zhang, C. A loss-minimization port-controlled Hamilton scheme of induction motor for electric vehicles. IEEE/ASME Trans. Mechatron. 2015, 20, 2645–2653. [Google Scholar]
- Rai, K.; Seksena, S.B.L.; Thakur, A.N. A comparative performance analysis for loss minimization of induction motor drive based on soft computing techniques. Int. J. Appl. Eng. Res. 2018, 13, 210–225. [Google Scholar]
- Rezk, H.; Elghany, A.A.; Al-Dhaifallah, M.; Sayed, A.H.M.; Ibrahim, M.N. Numerical estimation and experimental verification of optimal parameter identification based on modern optimization of a three phase induction motor. Mathematics 2019, 7, 1135. [Google Scholar] [CrossRef]
- Yin, Z.-G.; Zhao, C.; Zhong, Y.-R.; Liu, J. Research on robust performance of speed-sensorless vector control for the induction motor using an interfacing multiple-model extended Kalman filter. IEEE Trans. Power Electron. 2014, 29, 3011–3019. [Google Scholar] [CrossRef]
- Zerdali, E.; Barut, M. The comparison of optimized extended Kalman filters for speed-sensorless control of induction motors. IEEE Trans. Ind. Electron. 2017, 64, 4340–4351. [Google Scholar] [CrossRef]
- Cirrincione, M.; Pucci, M.; Cirrincione, G.; Capolino, G.-A. Constrained minimization for parameter estimation of induction motors in saturated and unsaturated conditions. IEEE Trans. Ind. Electron. 2005, 52, 1391–1402. [Google Scholar] [CrossRef]
- Tang, J.; Yang, Y.; Blaabjerg, F.; Chen, J.; Diao, L.; Lui, Z. Parameter identification of inverter-fed induction motor: A review. Energies 2018, 11, 2194. [Google Scholar] [CrossRef]
- Huynh, D.C.; Dunnigan, M.W.; Finney, S.J. On-line parameter estimation of an induction machine using a recursive least-squares algorithm with multiple time-varying forgetting factors. In Proceedings of the IEEE International Conference on Power and Energy (PECON2010), Kuala Lumpur, Malaysia, 29 November–1 December 2010. [Google Scholar]
- Popovic, V.; Oros, D.; Vasic, V. Tuning the rotor time constant parameter of IM using the minimum order recursive linear least square estimator. IET Electr. Power Appl. 2019, 13, 266–276. [Google Scholar] [CrossRef]
- Debbabi, F.; Nemmour, A.L.; Khezzar, A.; Chelli, S.E. An approved superiority of real-time induction machine parameter estimation operating in self-excited generating mode versus motoring mode using the linear RMS algorithm: Ideal & application. Int. J. Electr. Power Energy Syst. 2020, 118, 105725. [Google Scholar]
- Ozkurt, G.; Zerdali, E. Design and implementation of hybrid adaptive extended Kalman filter for state estimation of induction motor. IEEE Trans. Instrum. Meas. 2022, 71, 1–12. [Google Scholar] [CrossRef]
- Yang, S.; Ding, D.; Li, X.; Xie, Z.; Zhang, X.; Chang, L. A Novel Online Parameter Estimation Method for Indirect Field Oriented Induction Motor Drives. IEEE Trans. Energy Convers. 2017, 32, 1562–1573. [Google Scholar] [CrossRef]
- Yildiz, R.; Barut, M.; Demir, R. Extended Kalman filter based estimations for improving speed-sensored control performance of induction motors. IET Electr. Power Appl. 2020, 14, 2471–2479. [Google Scholar] [CrossRef]
- Demir, R.; Barut, M.; Yildiz, R. Reduced order extended Kalman filter based parameter estimations for speed-sensored induction motor drive. Pamukkale Univ. J. Eng. Sci. 2018, 24, 1464–1471. [Google Scholar] [CrossRef]
- Leite, V.; Araujo, R.; Freitas, D. A new online identification methodology for flux and parameters estimation of vector controlled induction motors. In Proceedings of the IEEE International Electric Machines and Driver Conference (IEMDC’03), Madison, WI, USA, 1–4 June 2003. [Google Scholar]
- Aksoy, S.; Muhurcu, A.; Kizmaz, H. State and parameter estimation in induction motor using the extended Kalman filtering algorithm. In Proceedings of the Modern Electric Power Systems (MEPS), International Symposium, Wroclaw, Poland, 20–22 September 2010. [Google Scholar]
- Horvath, K.; Kuslits, M. Dynamic performance of estimator-based speed sensorless control of induction machines using extended and unscented Kalman filters. Power Electron. Drives 2018, 3, 129–144. [Google Scholar] [CrossRef]
- Jirdehi, M.A.; Rezae, A. Parameters estimation of squirrel-cage induction motors using ANN and ANFIS. Alex. Eng. J. 2016, 55, 357–368. [Google Scholar] [CrossRef]
- Aminu, M. A parameter estimation algorithm for induction machines using artificial bee colony (ABC) optimization. Niger. J. Technol. 2019, 38, 193–201. [Google Scholar] [CrossRef]
- Bhowmick, D.; Manna, M.; Chowdhury, S.K. Estimation of equivalent circuit parameters of transformer and induction motor from load data. IEEE Trans. Ind. Appl. 2018, 54, 2784–2791. [Google Scholar] [CrossRef]
- Zaky, M.S.; Khater, M.; Yasin, H.; Shokralla, S.S. Review of different speed estimation schemes for sensorless induction motor drives. J. Electr. Eng. 2008, 8, 102–140. [Google Scholar]
- Elbuluk, M.E.; Kankam, M.D. Speed sensorless induction motor drives for electrical actuators: Schemes, trends and tradeoffs. In Proceedings of the IEEE National Aerospace and Electronics Conference, Dayton, OH, USA, 14–17 July 1997. [Google Scholar]
- Puangdownreong, D.; Areerak, K.-N.; Sri-kaew, A.; Sujijorn, S.; Totarong, P. System Identification via Adaptive Tabu Search. In Proceedings of the IEEE International Conference on Industrial Technology (ICIT’02), Bankok, Thailand, 11–14 December 2002; pp. 915–920. [Google Scholar]
- Onea, A.; Horga, V.; Ratoi, M. Indirect vector control of induction motor. In Proceedings of the 6th WSEAS International Conference on Simulation, Modelling and Optimization (SMO’06), Lisbon, Portugal, 22–24 September 2006; pp. 98–103. [Google Scholar]
- Prasad, S. Indirect field-oriented control of induction motor. In Proceedings of the Power Electronics Congress (CIEP) 12th International, San Luis Potosi, Mexico, 22–25 August 2010; pp. 102–105. [Google Scholar]
- Udomsuk, S.; Areerak, K.-L.; Areerak, T.; Areerak, K.-N. Power loss identification of three-phase induction motor using adaptive tabu search. In Proceedings of the 5th International Electrical Engineering Congress, Pattaya, Thailand, 8–10 March 2017. [Google Scholar]
- Yildiz, R.; Barut, M.; Zerdali, E. A comprehensive comparison of extended and unscented Kalman filters for speed-sensorless control applications of induction motors. IEEE Trans. Ind. Inform. 2020, 16, 6423–6432. [Google Scholar] [CrossRef]
- Zerdali, E. Adaptive extended Kalman filter for speed-sensorless control of induction motors. IEEE Trans. Energy Convers. 2019, 34, 798–800. [Google Scholar] [CrossRef]
- Kim, D.-W.; Park, C.-S. Application of Kalman filter for estimating a process disturbance in a building space. Sustainability 2017, 9, 1868. [Google Scholar] [CrossRef]
- Lewis, F.L. Applied Optimal Control and Estimation: Digital Design and Implementation; Prentice Hall: Upper Saddle River, NJ, USA, 1992. [Google Scholar]
- Lewis, P.H.; Yang, C. Basic Control Systems Engineering; Prentice Hall: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
- Gajic, Z.; Lelic, M. Modern Control Systems Engineering; Prentice Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Strang, G.; Borre, K. Linear Algebra, Geodesy, and GPS; Wellesley-Cambridge Press: Wellesley, MA, USA, 1997. [Google Scholar]
- Boutayeb, M.; Rafaralahy, H.; Darouach, M. Convergence analysis of the Extended Kalman filter used as an observer for nonlinear deterministic discrete-time systems. IEEE Trans. Autom. Control 1997, 42, 581–856. [Google Scholar] [CrossRef]
- Bose, B.K. Modern Power Electronics and AC Drives; Prentice Hall: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Ong, C.-M. Dynamic Simulation of Electric Machinery Using MATLAB/Simulink; Prentice Hall: Upper Saddle River, NJ, USA, 1998. [Google Scholar]


| Phase | Stator Resistance (Ω) |
|---|---|
| U | 24.80 |
| V | 25.10 |
| W | 25.50 |
| Average Value | 25.13 |
| Test Point | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | Average Values |
|---|---|---|---|---|---|---|---|---|---|
| 16.12 | 22.79 | 30.47 | 41.00 | 51.00 | 60.80 | 70.30 | 79.30 | ||
| 0.23 | 0.33 | 0.43 | 0.57 | 0.72 | 0.84 | 0.98 | 1.11 | ||
| 0.65 | 0.65 | 0.65 | 0.64 | 0.64 | 0.64 | 0.64 | 0.64 | ||
| 45.60 | 45.30 | 46.38 | 46.04 | 45.59 | 46.10 | 46.10 | 46.31 | 45.92 | |
| 53.26 | 52.69 | 54.23 | 55.27 | 54.73 | 52.69 | 55.35 | 54.14 | 54.41 |
| Symbol | Definition | Dimensions |
|---|---|---|
| state variable vector | ||
| system noise | ||
| measurement vector | ||
| measurement noise | ||
| state transition matrix | ||
| covariance matrix of | ||
| covariance matrix of | ||
| deterministic input vector | ||
| input matrix | ||
| measurement matrix |
| () | N (rpm) | Case A | Case B | Case C | |||
|---|---|---|---|---|---|---|---|
| Conventional Approach | Energy-Saving Approach without EKF | Energy-Saving Approach with EKF | |||||
| (A) | (W) | (A) | (W) | (A) | (W) | ||
| 0.5 | 300 | 0.94 | 96.58 | 0.59 | 51.48 | 0.46 | 38.46 |
| 600 | 126.18 | 0.57 | 72.17 | 0.41 | 52.23 | ||
| 900 | 146.55 | 0.54 | 91.97 | 0.36 | 68.27 | ||
| 1200 | 157.32 | 0.50 | 110.73 | 0.31 | 97.37 | ||
| 1390 | 145.09 | 0.48 | 122.17 | 0.26 | 117.14 | ||
| 1.0 | 300 | 117.06 | 0.74 | 88.65 | 0.53 | 74.44 | |
| 600 | 160.73 | 0.72 | 124.16 | 0.46 | 108.57 | ||
| 900 | 195.75 | 0.68 | 162.99 | 0.43 | 155.03 | ||
| 1200 | 228.01 | 0.65 | 192.24 | 0.41 | 188.68 | ||
| 1390 | 243.89 | 0.62 | 210.67 | 0.36 | 220.34 | ||
| 1.5 | 300 | 137.90 | 0.80 | 119.00 | 0.53 | 118.26 | |
| 600 | 194.09 | 0.77 | 176.00 | 0.55 | 149.27 | ||
| 900 | 251.96 | 0.73 | 231.46 | 0.53 | 208.70 | ||
| 1200 | 282.20 | 0.70 | 272.54 | 0.53 | 223.44 | ||
| 1390 | 335.89 | 0.67 | 312.25 | 0.58 | 276.71 | ||
| 2.0 | 300 | 170.55 | 0.82 | 158.12 | 0.67 | 155.25 | |
| 600 | 251.20 | 0.80 | 229.56 | 0.65 | 210.64 | ||
| 900 | 303.79 | 0.76 | 296.74 | 0.62 | 288.90 | ||
| 1200 | 371.92 | 0.72 | 370.92 | 0.60 | 289.83 | ||
| 1390 | 392.83 | 0.70 | 422.85 | 0.82 | 377.72 | ||
| 2.5 | 300 | 207.79 | 0.92 | 203.18 | 0.86 | 183.07 | |
| 600 | 295.19 | 0.90 | 295.59 | 0.84 | 265.09 | ||
| 900 | 364.88 | 0.86 | 382.90 | 0.74 | 363.99 | ||
| 1200 | 445.74 | 0.82 | 429.12 | 0.74 | 365.52 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Udomsuk, S.; Areerak, K.; Areerak, T.; Areerak, K. Online Estimation of Three-Phase Induction Motor Parameters Using an Extended Kalman Filter for Energy Saving. Energies 2024, 17, 2115. https://doi.org/10.3390/en17092115
Udomsuk S, Areerak K, Areerak T, Areerak K. Online Estimation of Three-Phase Induction Motor Parameters Using an Extended Kalman Filter for Energy Saving. Energies. 2024; 17(9):2115. https://doi.org/10.3390/en17092115
Chicago/Turabian StyleUdomsuk, Sasiya, Kongpol Areerak, Tidarut Areerak, and Kongpan Areerak. 2024. "Online Estimation of Three-Phase Induction Motor Parameters Using an Extended Kalman Filter for Energy Saving" Energies 17, no. 9: 2115. https://doi.org/10.3390/en17092115
APA StyleUdomsuk, S., Areerak, K., Areerak, T., & Areerak, K. (2024). Online Estimation of Three-Phase Induction Motor Parameters Using an Extended Kalman Filter for Energy Saving. Energies, 17(9), 2115. https://doi.org/10.3390/en17092115






