Research on Market Evaluation Model of Reserve Auxiliary Service Based on Two-Stage Optimization of New Power System
Abstract
1. Introduction
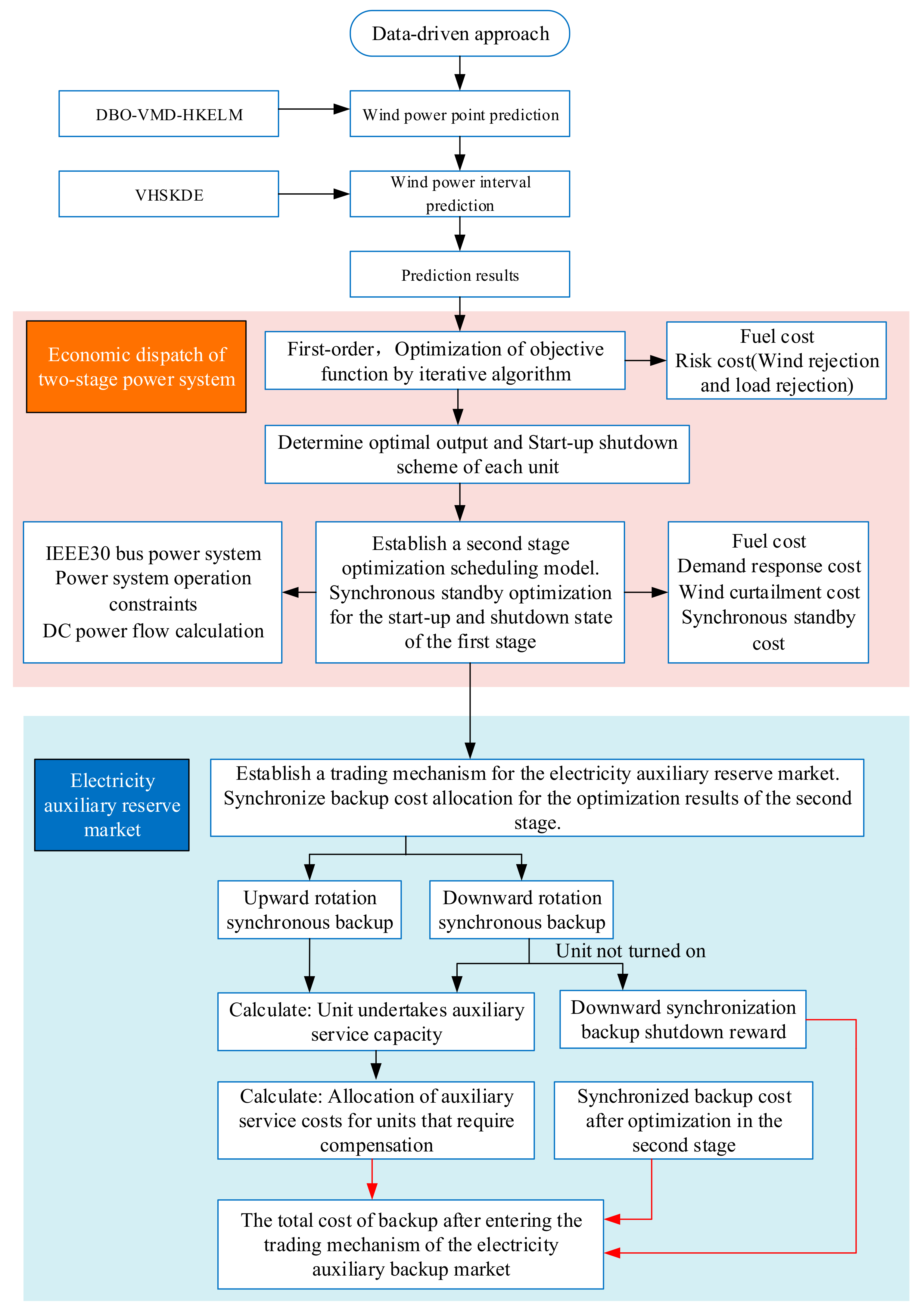
2. Research Theory
2.1. System Uncertainty Analysis
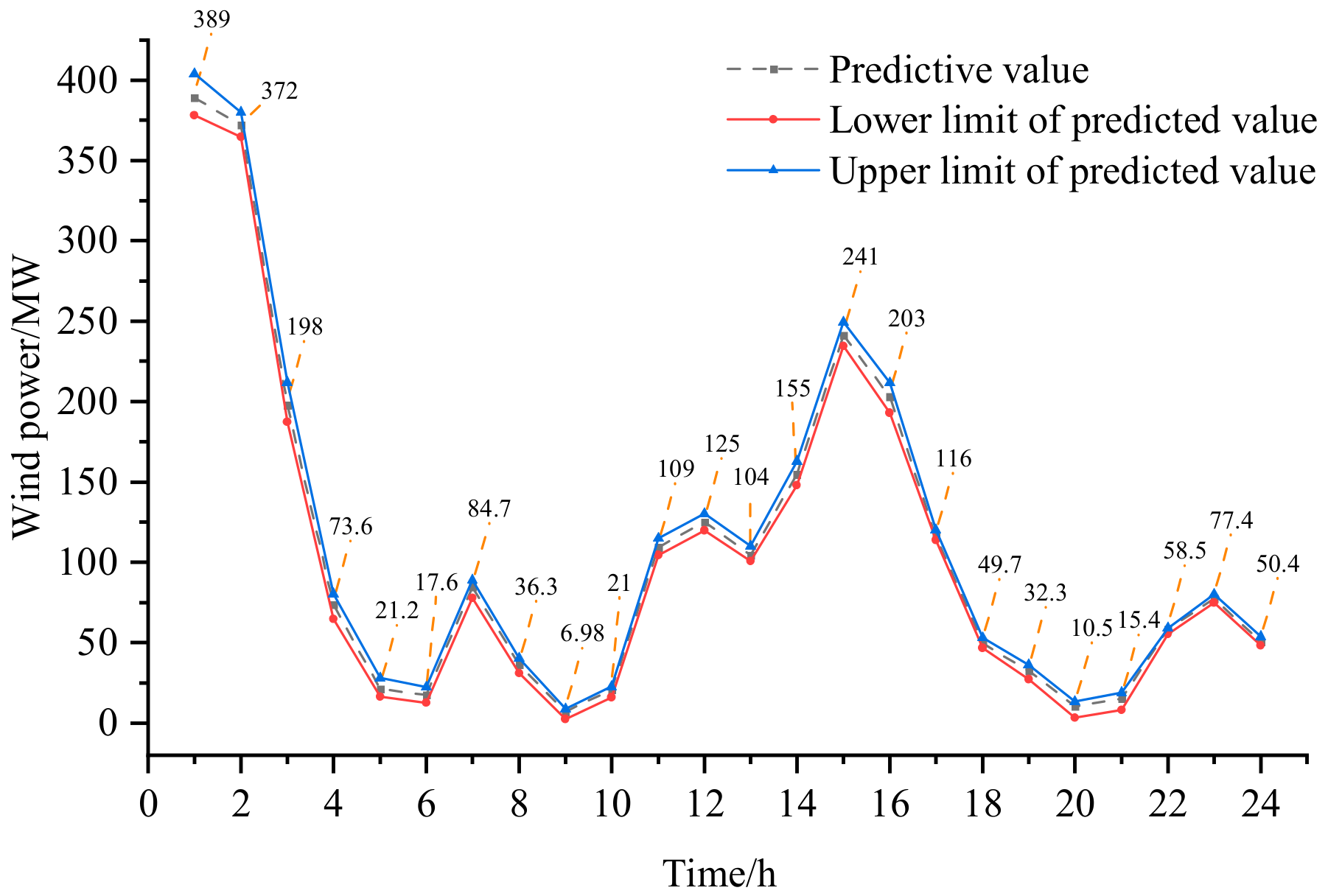
2.1.1. Data-Driven Wind Power Uncertainty Prediction
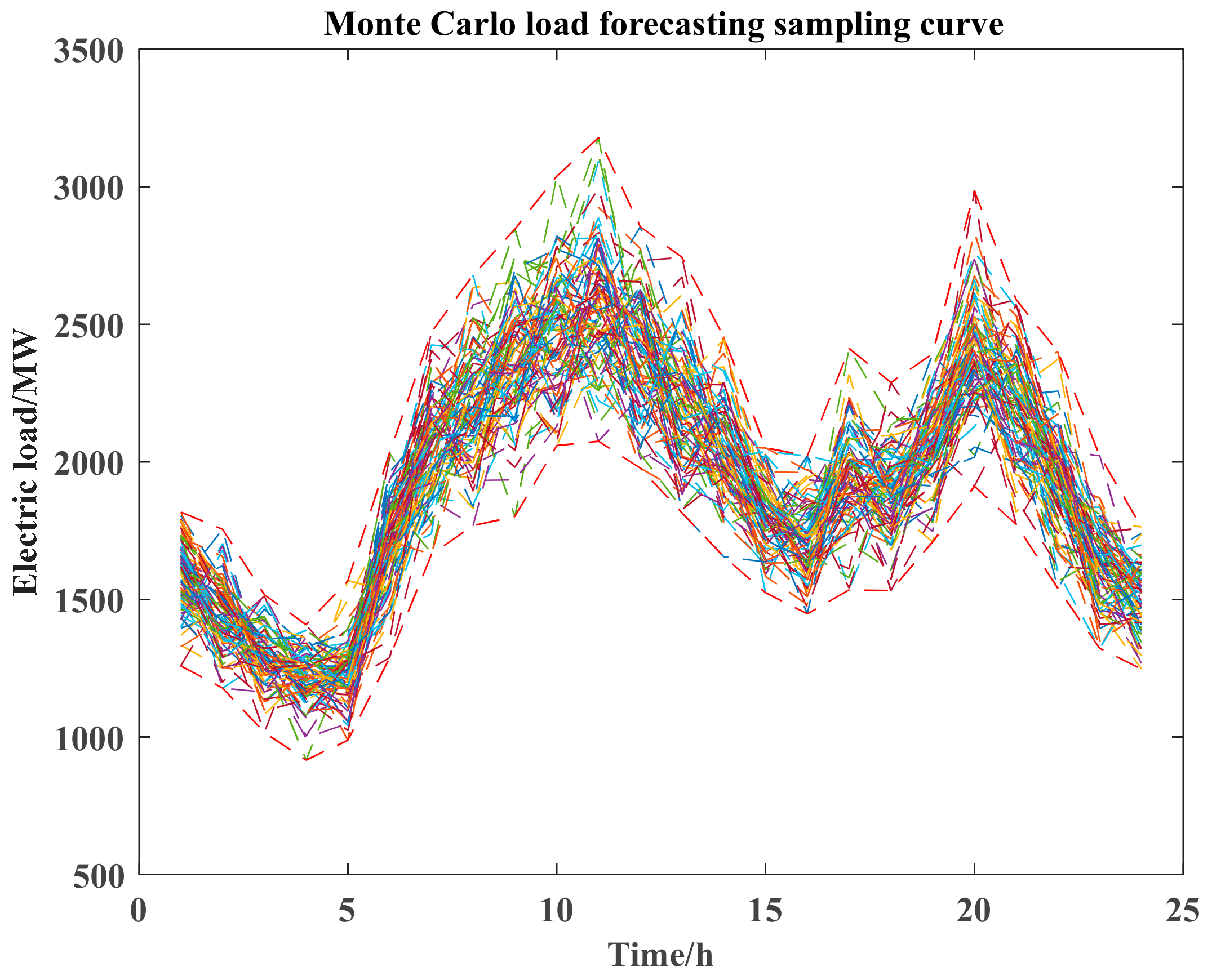
2.1.2. Load Uncertainty
2.2. Risk Assessment Based on CVaR
2.3. Two-Stage Optimization Scheduling Model for Day Ahead
2.3.1. Objective Function of the Two-Stage Optimization Model
2.3.2. Constraint Conditions
- (1)
- Constraint on the Start-Up and Shutdown of Thermal Power Units [22]
- (2)
- Constraint on the Ramping of Thermal Power Units [22]
- (3)
- Constraint on the Output Limits of Thermal Power Units
- (4)
- Wind Power Output Constraint
- (5)
- Load Balance Constraint
- (6)
- Synchronous Reserve Constraint
- (7)
- Line Flow Constraint [23]
2.3.3. Improved Binary Fish Swarm Optimization Algorithm
2.3.4. Seagull Optimization Algorithm (SOA)
- (1)
- Migration of seagulls (global search)
- (2)
- Seagull attack (localized search)
2.4. Assessment Mechanism for Power Auxiliary Reserve Market
3. Example Analysis
3.1. IEEE 30 Node System Example
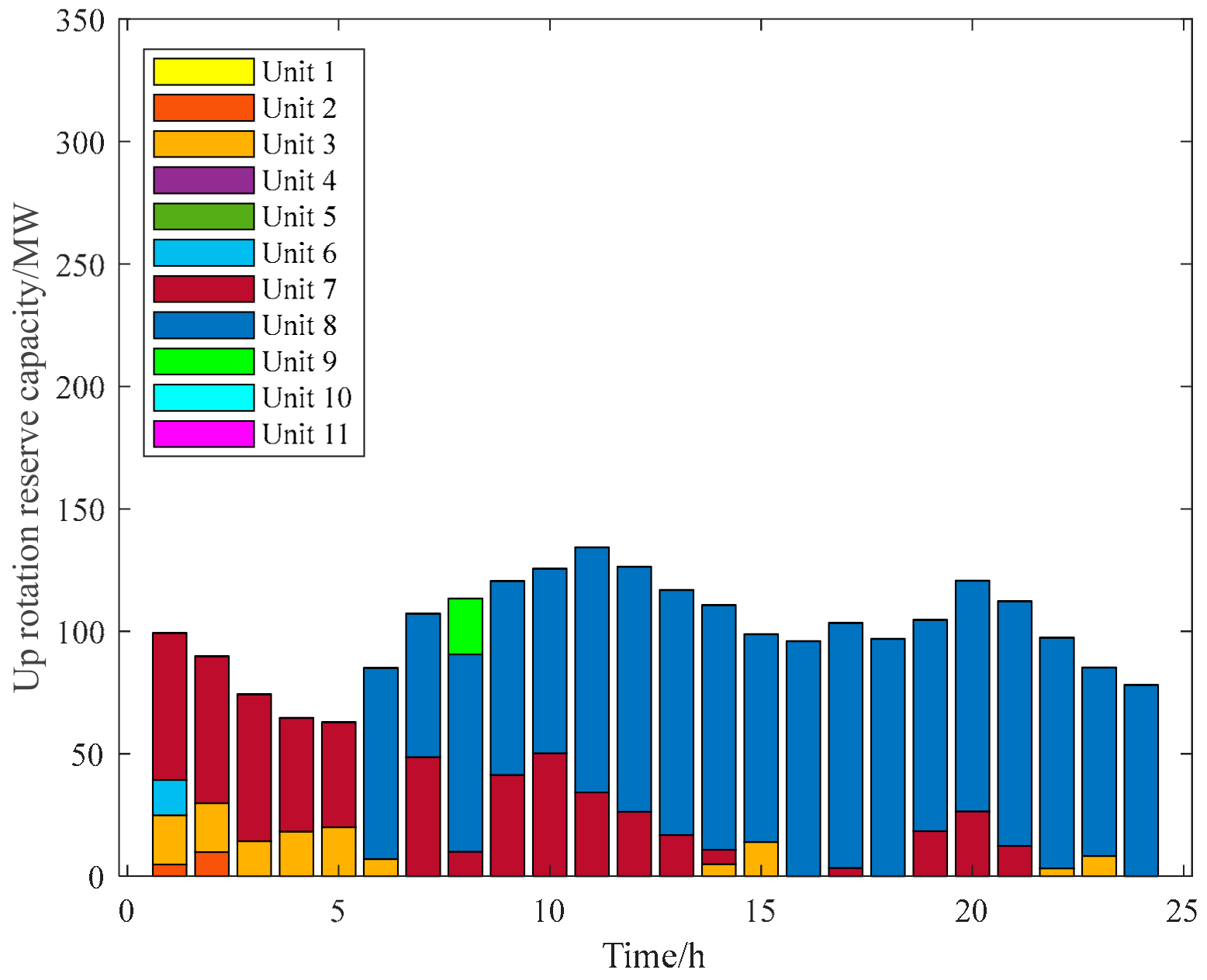
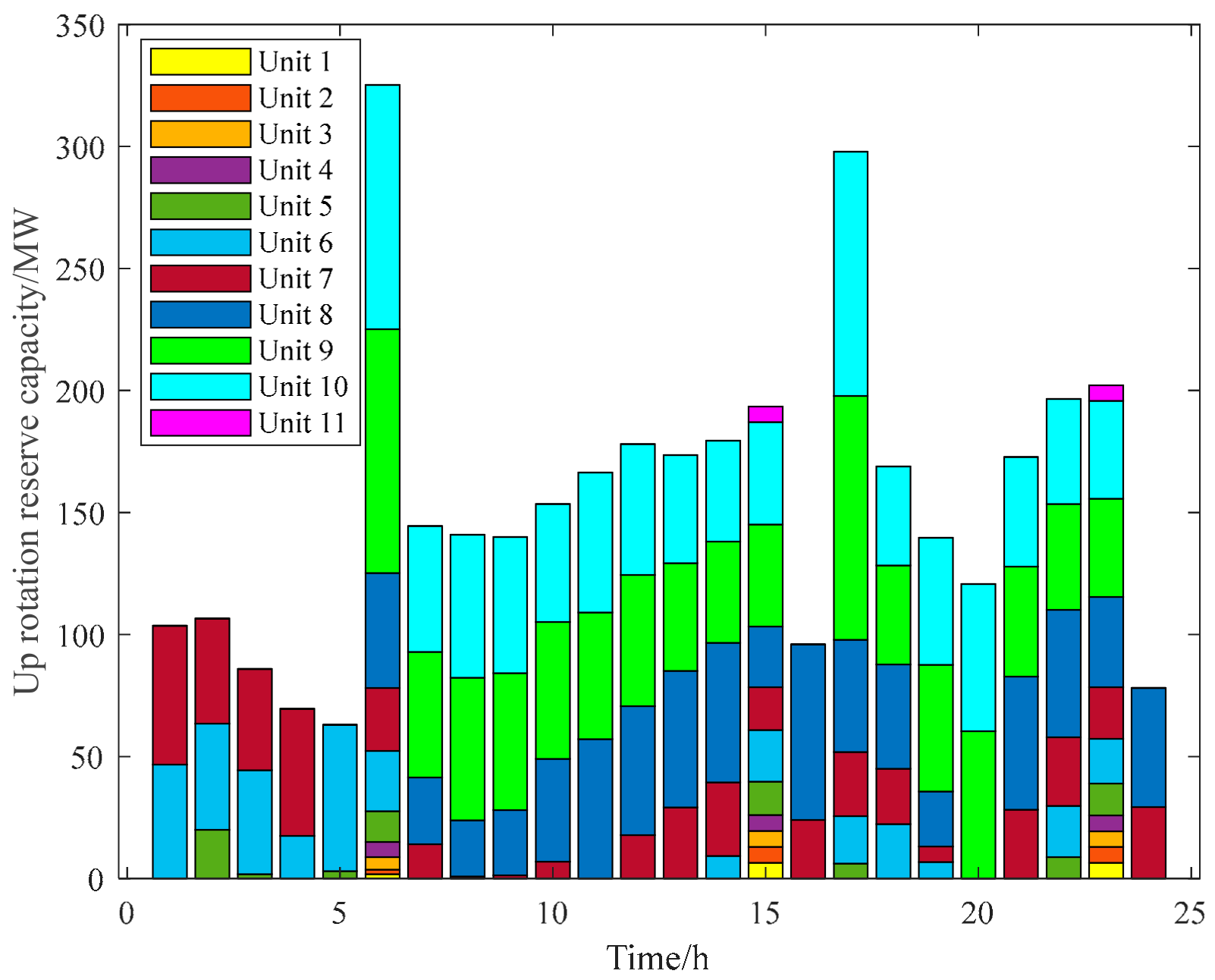
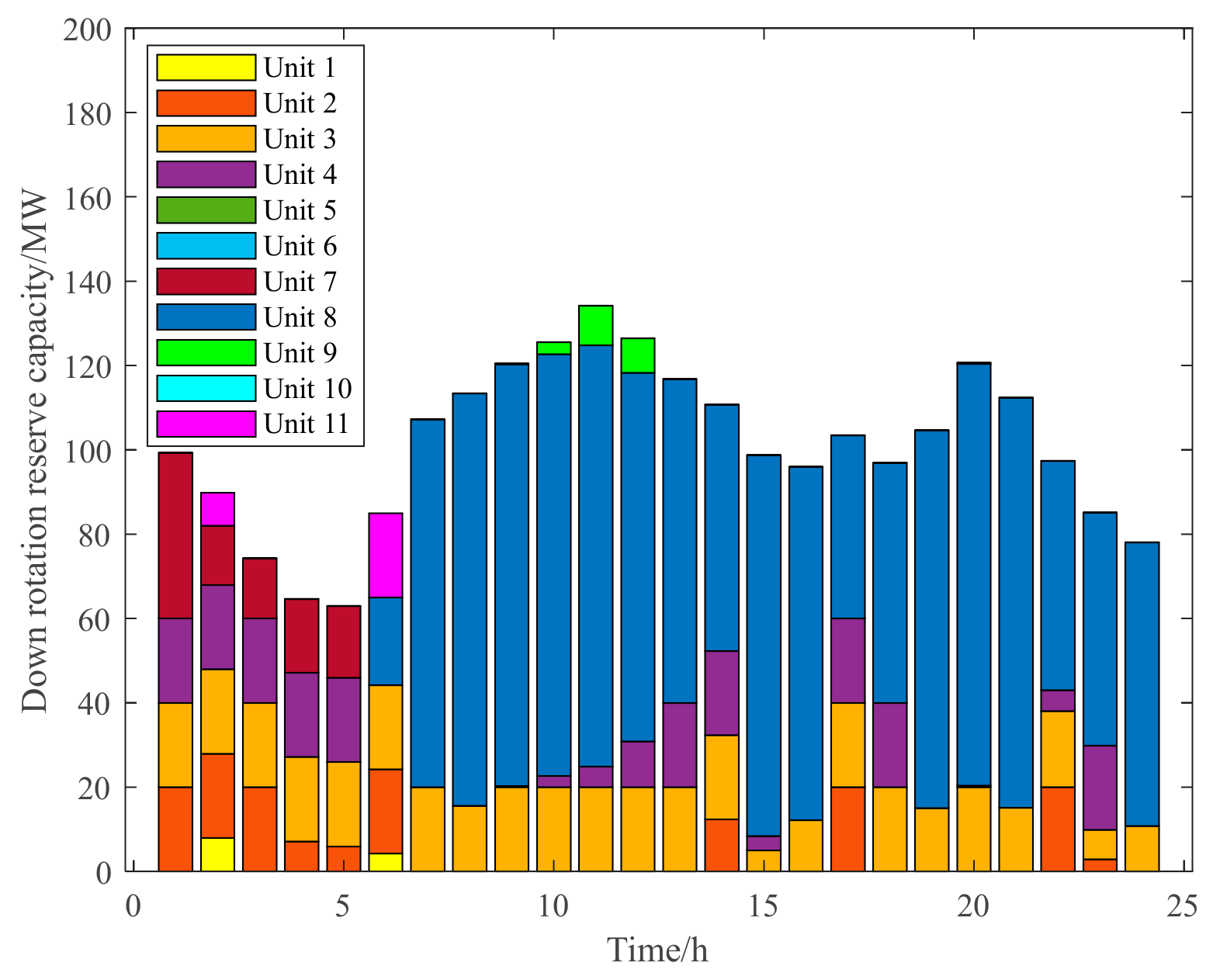
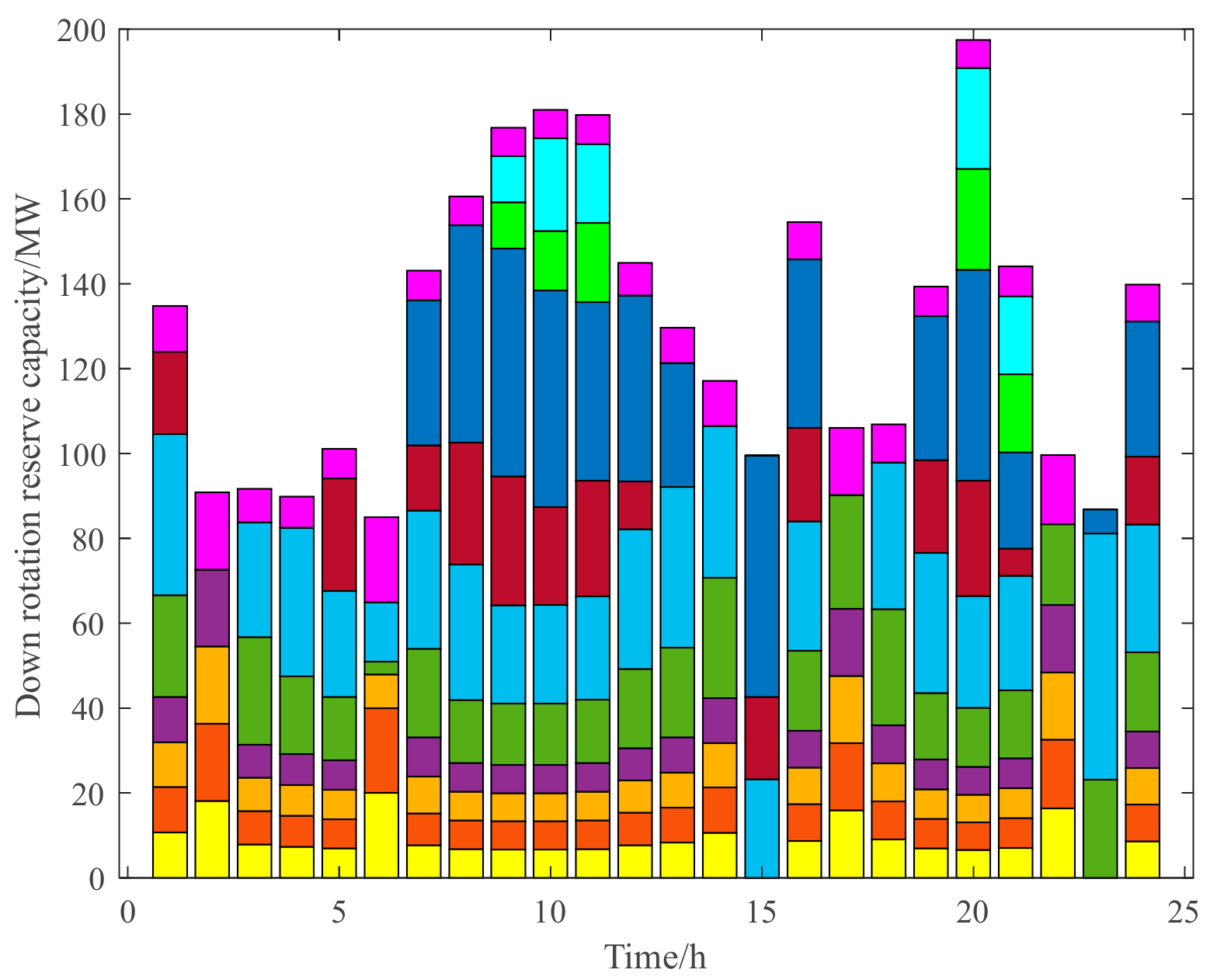
3.2. Analysis of Reserve Limits for Wind Power Systems Based on Uncertainty
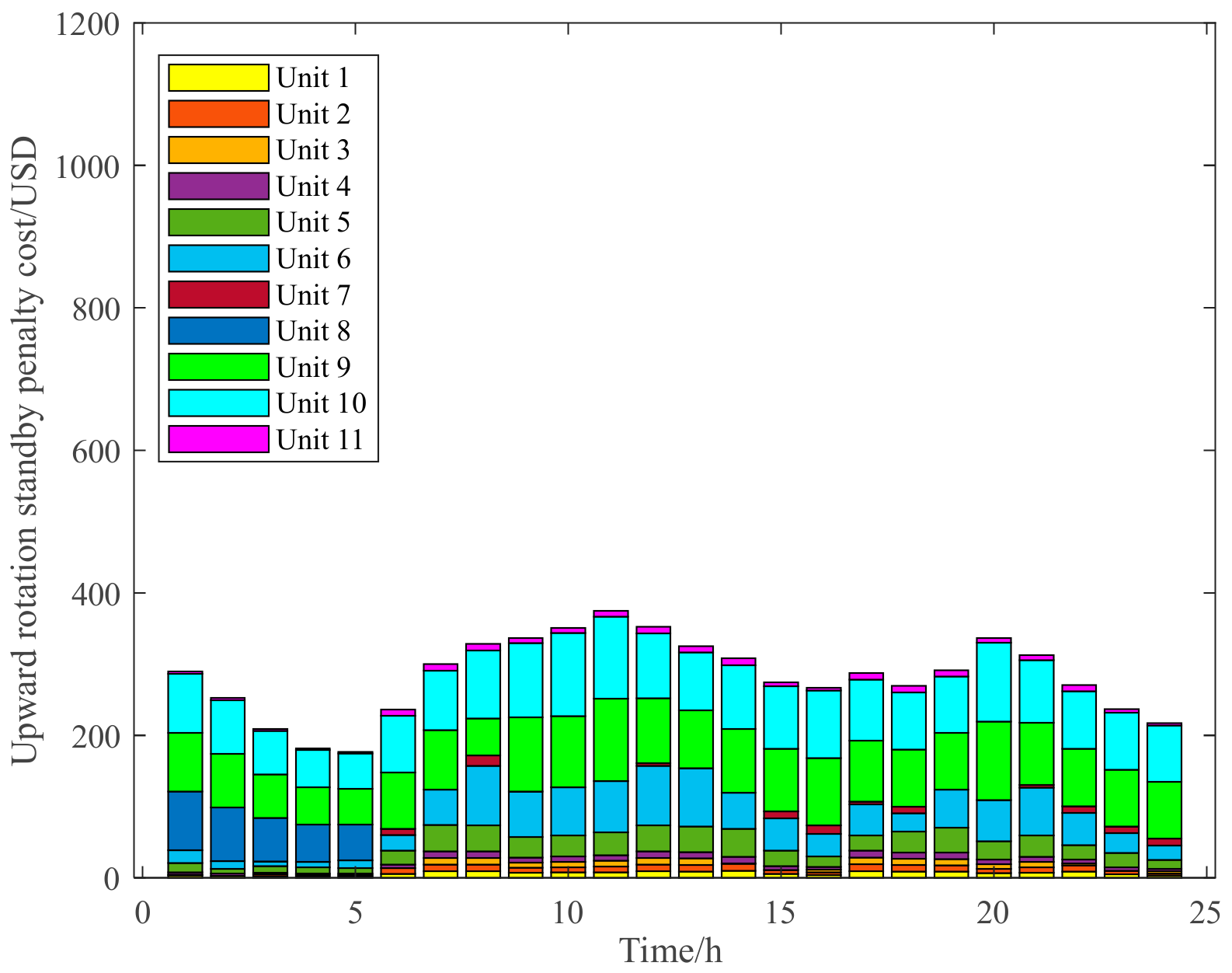
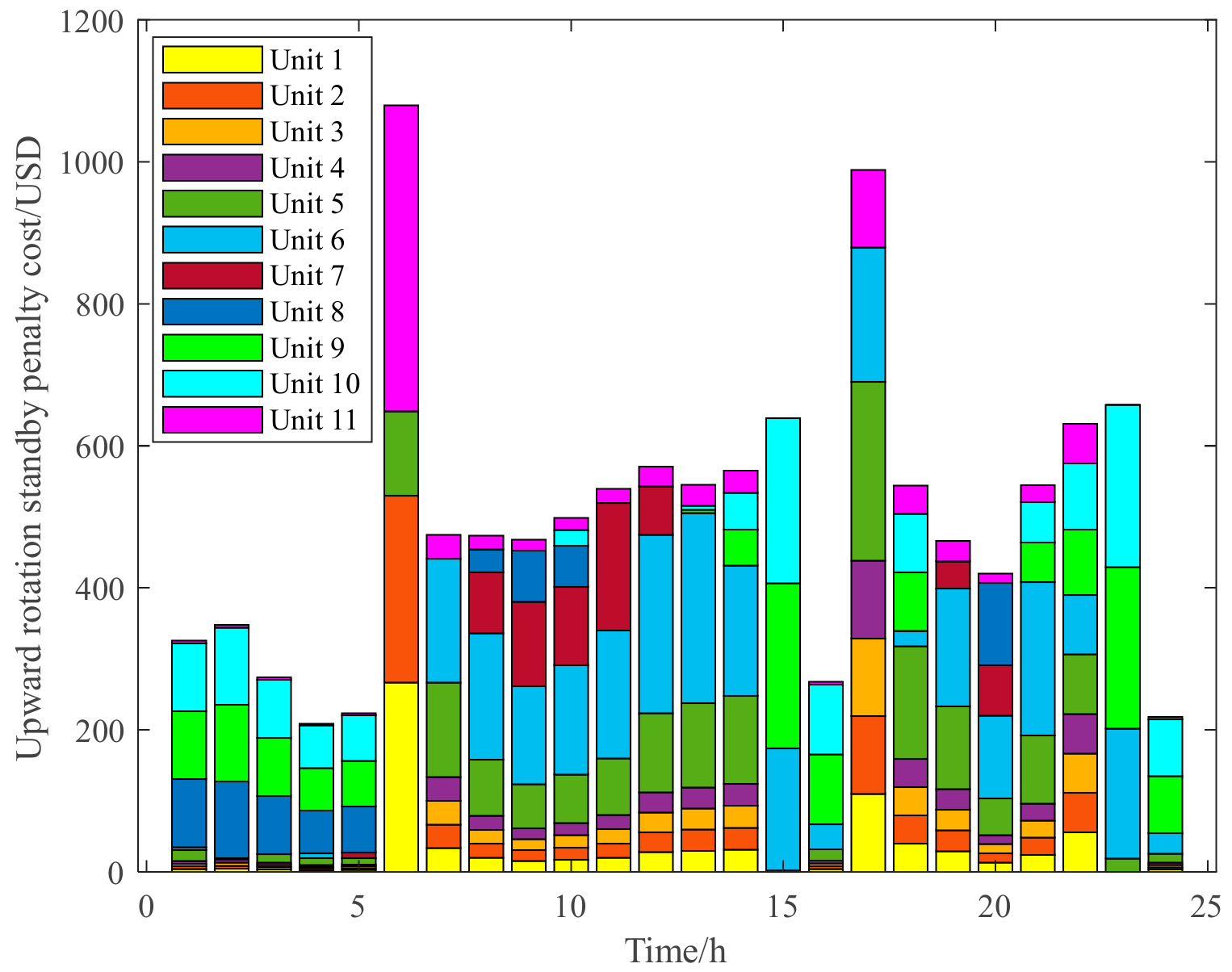
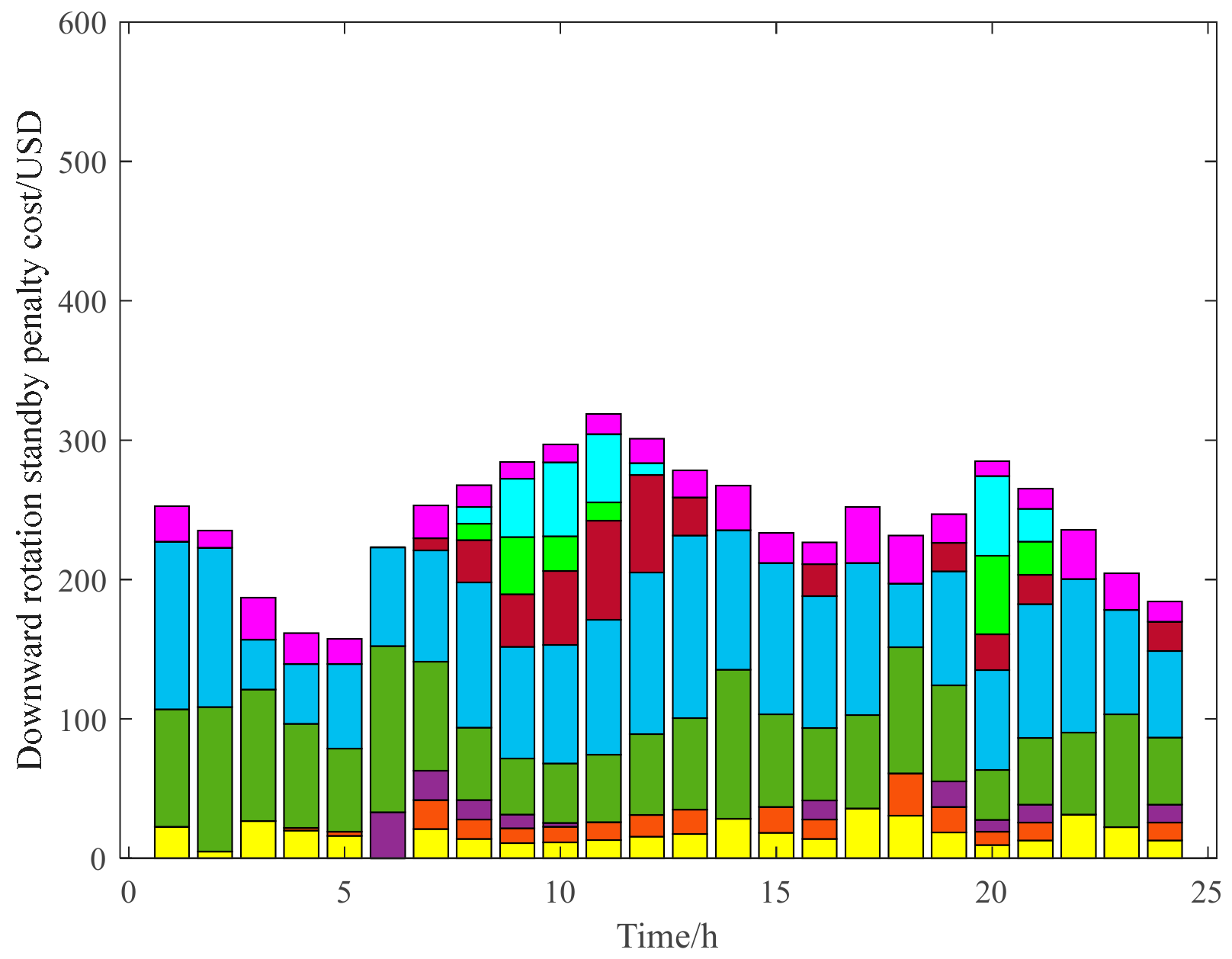
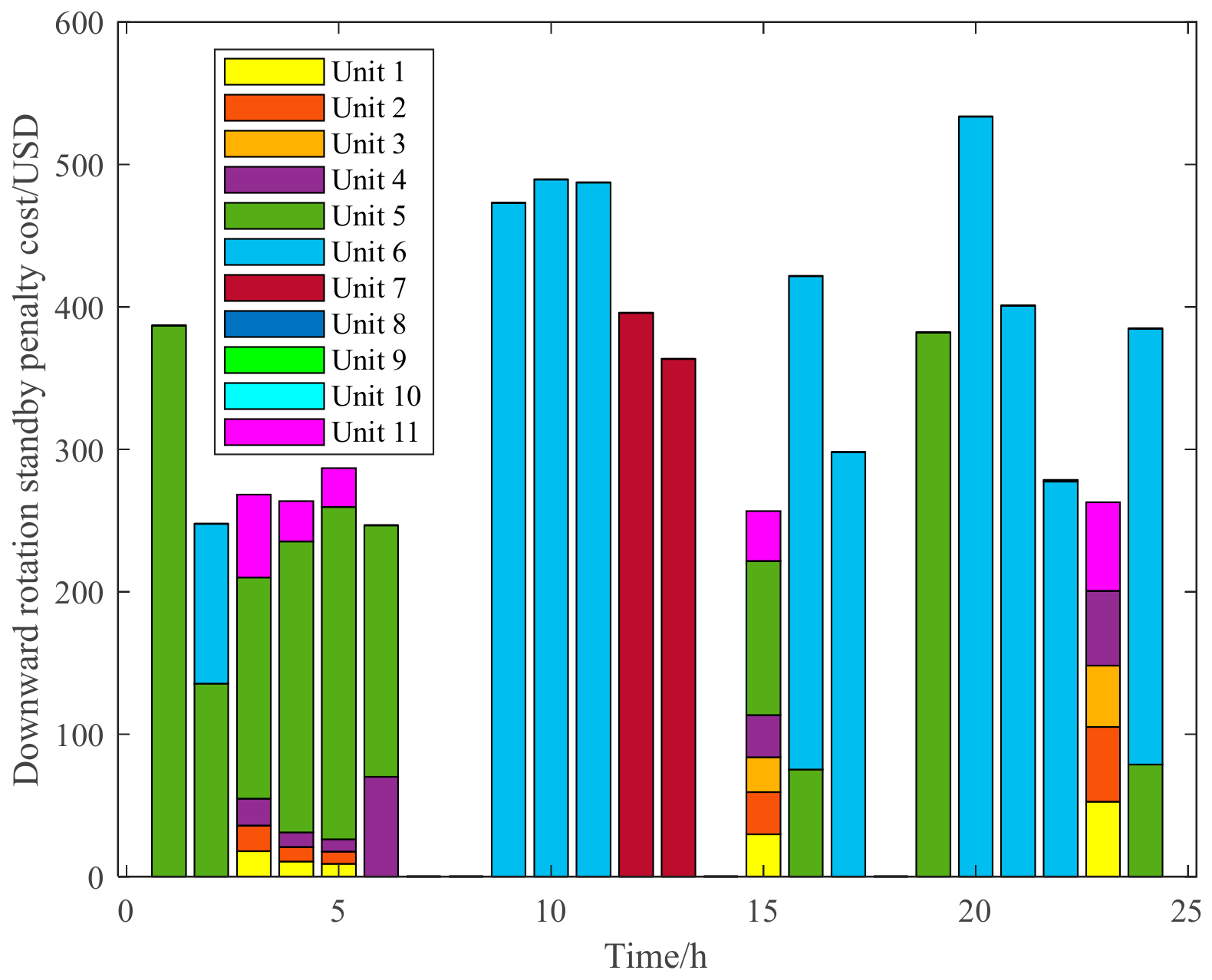
3.2.1. Analysis of the Effectiveness of the Evaluation Model of the Upper Limit Standby Auxiliary Service Market Based on Wind Power Forecasts
3.2.2. Analysis of the Effectiveness of the Evaluation Model of the Lower Limit Standby Auxiliary Service Market Based on Wind Power Forecasts
3.3. Analysis of Backup for Deterministic Wind Power
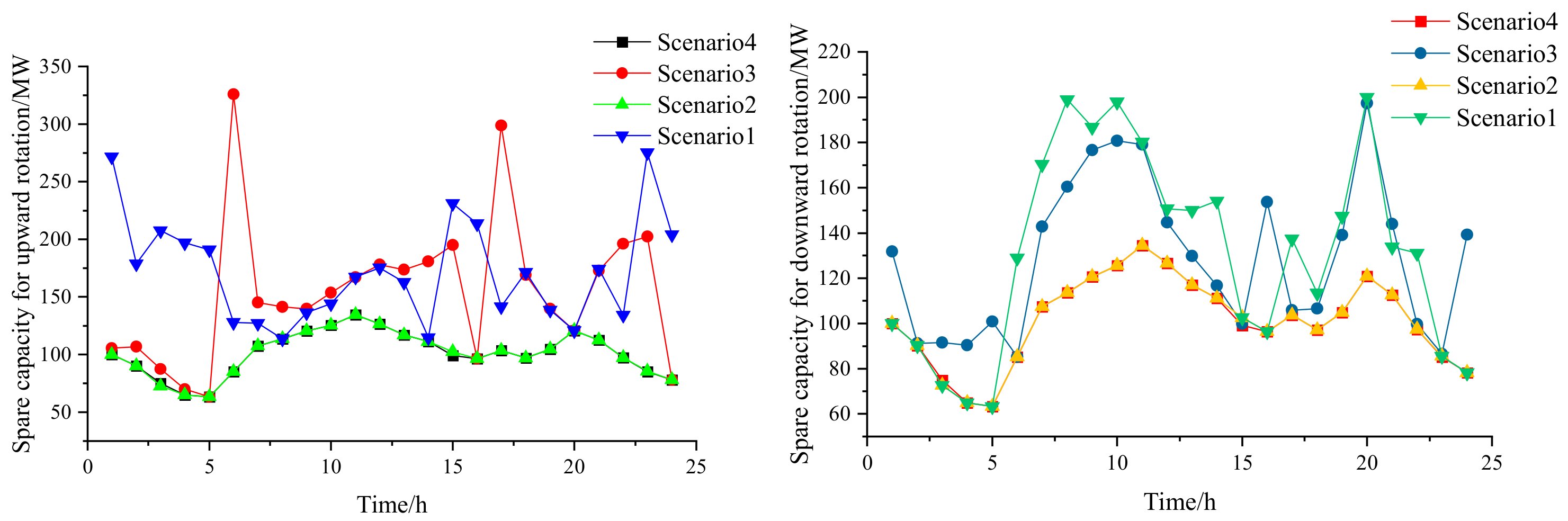
3.4. Operation Cost Analysis of Three Circumstances Based on Scenario 4
3.5. Analysis of the Running Results of Two Optimization Algorithms Based on the Optimal Scenario
4. Conclusions
- 1.
- The data-driven wind power prediction based on the upper bound circumstance (Circumstance 1) corresponding to the simultaneous consideration of start–stop optimization and standby optimization (Scenario 4) has the lowest total cost of operation and the best optimization results.
- 2.
- Based on the lowest optimization cost results (Circumstance 1, Scenario 4), DLBFSO is used to compare with SOA optimization algorithms, and it is found that SOA optimization methods have the lowest running cost and the best optimization results.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yun, Y.; Dong, H.; Chen, Z.; Huang, R.; Ding, K. A two-stage stochastic scheduling optimization for multi-source power system considering randomness and concentrating solar power plant participation. Power Syst. Prot. Control. 2020, 48, 30–38. [Google Scholar]
- Deng, T.; Lou, S.; Tian, X.; Wu, Y.; Li, N. Optimal dispatch of power system integrated with wind power considering demand response and deep peak regulation of thermal power units. Autom. Electr. Power Syst. 2019, 43, 34–41. [Google Scholar]
- Li, P.; Yu, D.; Yang, M.; Wang, J. Flexible look-ahead dispatch realized by robust optimization considering CVaR of wind power. IEEE Trans. Power Syst. 2018, 33, 5330–5340. [Google Scholar] [CrossRef]
- Jin, H.; Sun, H.; Niu, T.; Guo, Q.; Wang, B. Coordinated dispatch method of energy-extensive load and wind power considering risk constraints. Autom. Electr. Power Syst. 2019, 43, 9–16. [Google Scholar]
- Zhou, X.; Li, W.; Tang, J.; Wang, Q.; Yu, J.; Zhang, C. Coordinated allocation method of emergency reserve capacity based on risk Quantification. Power Syst. Technol. 2015, 39, 1927–1932. [Google Scholar]
- Ai, X.; Taierjiang, B.; Yang, L.; Yang, J.; Fang, J.K.; Wen, J. Spinning reserve optimization of wind power system based on Scenario set. Power Syst. Technol. 2018, 42, 835–841. [Google Scholar]
- Wang, J.; Xu, J.; Wang, J.; Ke, D.; Liao, S.; Sun, Y.; Wu, Y.; Bi-level Stochastic Optimization for A Virtual Power Plant Participating in Energy and Reserve Market Based on Conditional Value At Risk. Power System Technology, 2024, Web First Paper. Available online: https://kns.cnki.net/kcms2/article/abstract?v=wcPNn8Zia7NoLxS3GYI68UUmlF1-VOKNbfcttOWGuaZHtAYMFQhmPE9L_SuNFLk243PVObkGWwo6XtyCq0SmEDOjO0rxfRm57TSG0-xHzziIr-KQe_OPnm0pFTMkHEoIh8kihZIqlhs=&uniplatform=NZKPT&language=CHS (accessed on 11 January 2021).
- Yan, B.; Han, X.; Li, T.; Song, T.; Wu, Y. Operation Strategy for Active Distribution Networks with Energy Storage Considering. Autom. Electr. Power Syst. 2023, 47, 131–140. [Google Scholar]
- Yan, M. Electricity values equivalent pricing system and relevant systems design: Part four a probabilistic practical electricity values equivalent pricing method for operating reserve. Autom. Electr. Power Syst. 2023, 27, 1–6. [Google Scholar]
- ERCOT. Methodology for Implementing ORDC to Calculate Real Time Reserve Price Adder [EB/OL]. Available online: https://www.ercot.com/content/wcm/training_courses/107/ordc_workshop.pdf (accessed on 11 January 2021).
- Summary of 2019 MISO State of the Market Report; Potomac Economics: Fairfax, VA, USA, 2020.
- Hogan, W. Strengths and Weaknesses of the PJM Market Model [EB/OL]. Available online: https://scholar.harvard.edu/whogan/files/hogan_chapter_7_handbook_on_the_economics_of_electricity_112619r.pdf (accessed on 2 November 2019).
- Hogan, W. On an ‘Energy only’ Electricity Market Design for Resource Adequacy; Harvard University: Cambridge, MA, USA, 2005. [Google Scholar]
- ERCOT. ERCOT Market Training: Purpose of ORDC, Methodology for Implementing ORDC, Settlement Impacts for ORDC [EB/OL]. Available online: http://www.ercot.com/content/wcm/training_courses/107/ordc_workshop.pdf (accessed on 11 January 2021).
- Maggio, D.; Moorty, S.; Shaw, P. Scarcity Pricing Using ORDC for Reserves and Pricing Run for out of Market Actions [EB/OL]. Available online: https://cdn.misoenergy.org/20210513%20MSC%20Item%20XX%20Scarcity%20Pricing%20Evaluation%20Paper550162.pdf (accessed on 11 January 2021).
- Liu, R.; Jing, Z.; Liu, Y. Coupling clearing model of energy and reserve considering dynamic operation reserve demand curves. Autom. Electr. Power Syst. 2021, 45, 34–42. [Google Scholar]
- Harbord, D.; Pagnozzi, M. Britain’s electricity capacity auctions: Lessons from Colombia and New England. Electr. J. 2014, 27, 54–62. [Google Scholar] [CrossRef]
- Jing, R.; Zhou, Y.; Wu, J. Empowering zero carbon Future-experience and development trends of electric power system transition in the UK. Autom. Electr. Power Syst. 2021, 45, 87–98. [Google Scholar]
- ENTSO-E. Frequency Containment Reserve [EB/OL]. Available online: https://www.entsoe.eu/network_codes/eb/fcr/ (accessed on 11 January 2021).
- PJM. PJM Manual 11: Energy & Ancillary Services Market Operations [EB/OL]. Available online: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=200ce69f3ee2eea1f26897043555710ea30342cd (accessed on 11 January 2021).
- Zhu, J.; Ye, Q.; Zou, J.; Xie, P.; Xuan, P. Short-term operation service mechanism of ancillary service in the UK electricity market and its enlightenment. Autom. Electr. Power Syst. 2018, 42, 1–8. [Google Scholar]
- Zhang, G.; Li, F. Two-stage optimal dispatch for wind power integrated power system considering operational risk and reserve availability. Power Syst. Prot. Control. 2022, 50, 140–148. [Google Scholar]
- Kou, Y.; Wu, J.; Zhang, H.; Yang, J.; Jiang, H. Low carbon economic dispatch for a power system considering carbon capture and CVaR. Power Syst. Prot. Control. 2023, 51, 132–140. [Google Scholar]
- Liu, H.; Gao, X.; Liu, Y. Two-stage Day-ahead Optimal Dispatching of Active Distribution Network Based on Improved Artificial Fish Swarm Algorithm. Guangdong Electr. Power 2023, 36, 123–129. [Google Scholar]
- Zhang, S.; Zhang, J. Wind Power Load Combination Forecasting Based on Improved SOA and Ridge Regression Weighting. North China Electr. Power Univ. 2023, Web First Paper. Available online: https://kns.cnki.net/kcms2/article/abstract?v=wcPNn8Zia7P6dqHCTULDrCKVHV66YLQTTGJr8zUnFYKT4pFkiTxnBTct6g-cJPuY7SXwli8QMKHqv1-wezPH5JV9J3dnUPBlLSHWRZ7ySJZgGbZwi8JDGecQNXKkwvpeHUE3IYXXl68=&uniplatform=NZKPT&language=CHS (accessed on 11 January 2021).
- Sun, H.; Song, Y.; Chen, L.; Peng, C.; Jiang, Z. Source-grid coordination security and economic dispatching of new power system considering reserve risk. Electr. Power Autom. Equip. 2024, 44, 135–143. [Google Scholar] [CrossRef]
- Shui, Y.; Liu, J.; Gao, H.; Huang, S.; Jiang, Z. A Distributionally Robust Coordinated Dispatch Model for Integrated Electricity and Heating Systems Considering Uncertainty of Wind Power. Proc. CSEE 2018, 38, 7235–7247. [Google Scholar]

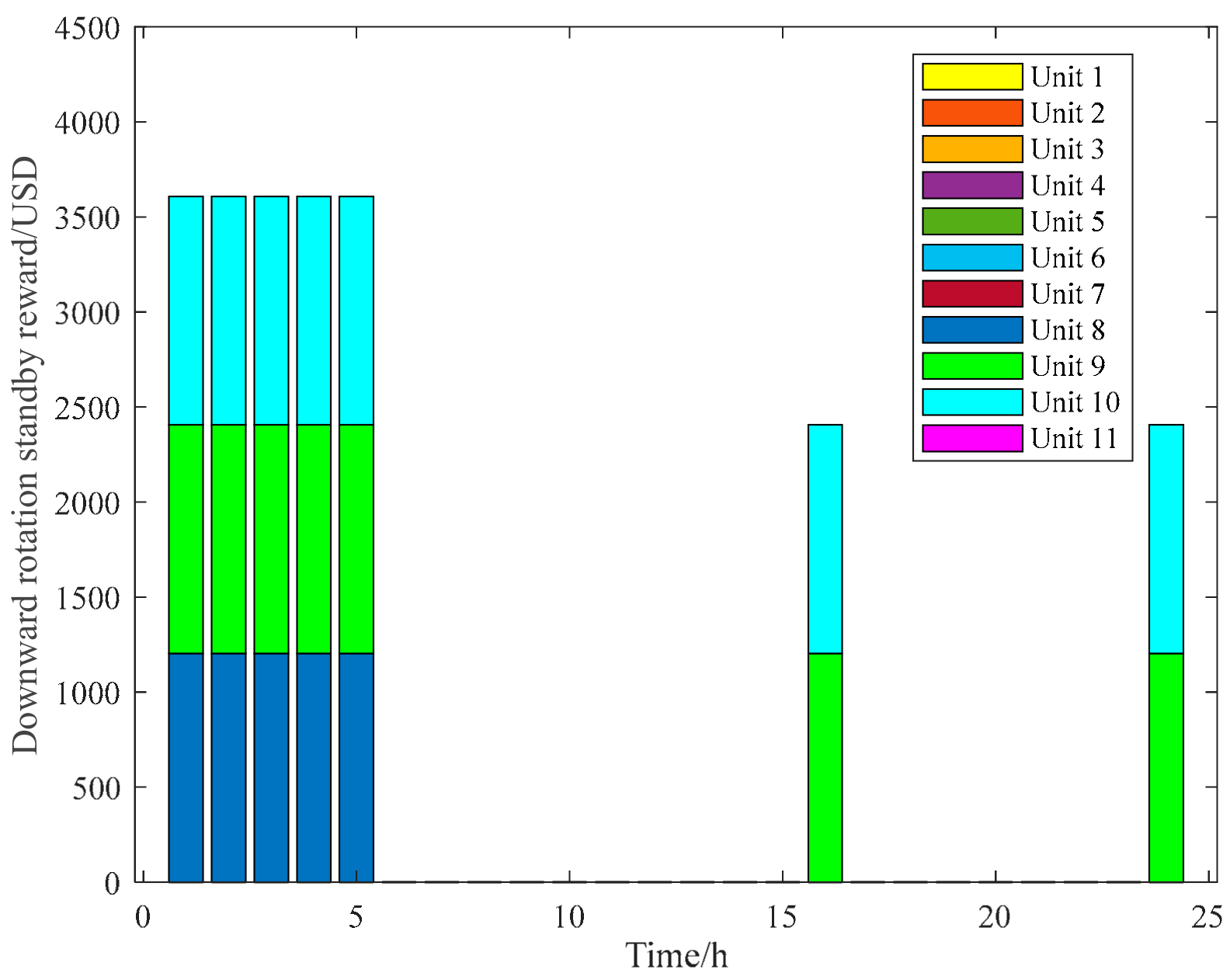

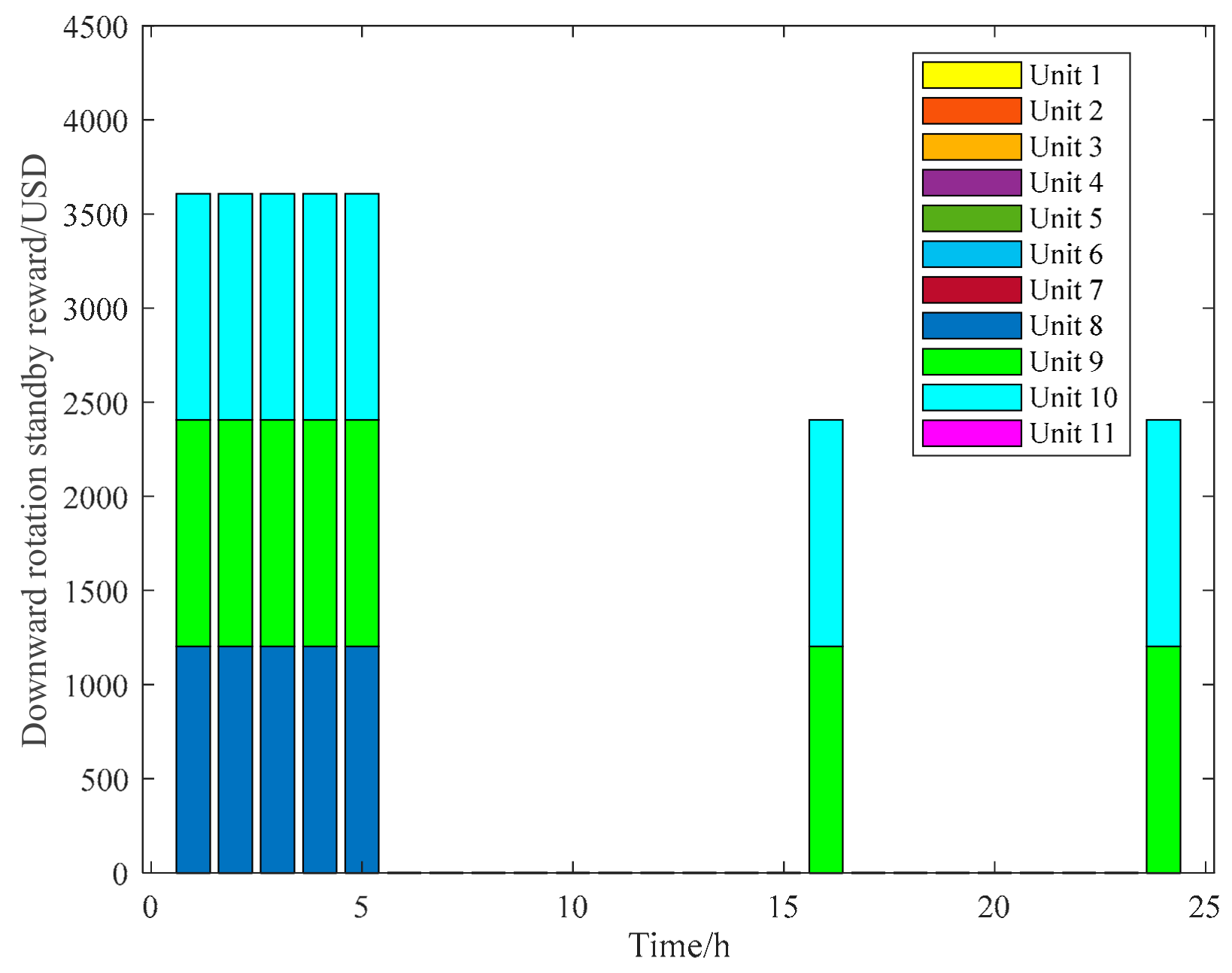
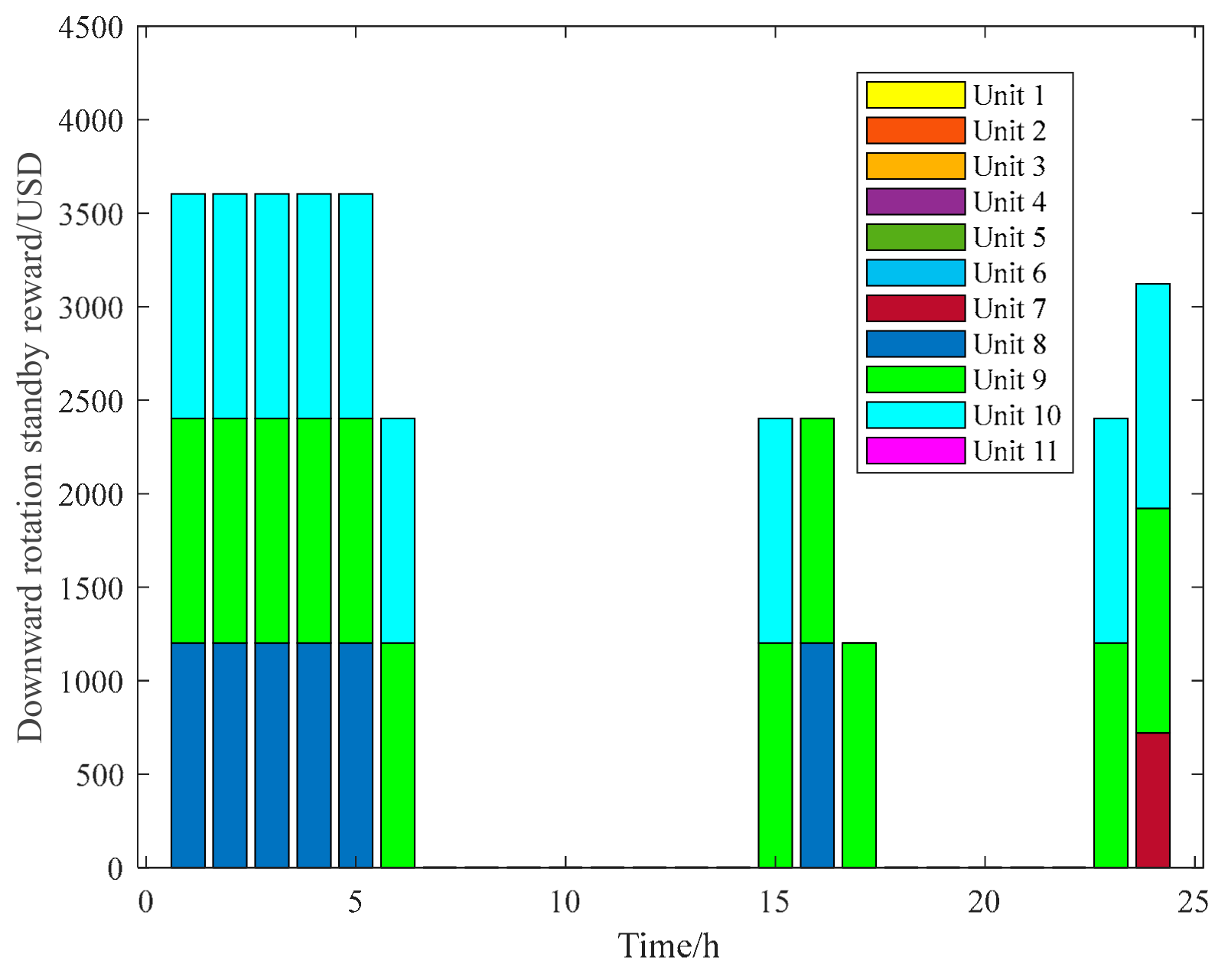

| Node Number | Maximum Output/MW | Minimum Output /MW | Climbing Rate | Start-Up Cost/USD | Downtime Costs/USD |
|---|---|---|---|---|---|
| 1 | 100 | 20 | 25 | 6 | 2 |
| 2 | 200 | 50 | 50 | 7 | 3 |
| 6 | 100 | 20 | 25 | 6 | 2 |
| 7 | 500 | 100 | 125 | 12 | 4 |
| 8 | 100 | 20 | 25 | 6 | 2 |
| 9 | 300 | 100 | 75 | 8 | 4 |
| 10 | 300 | 100 | 75 | 8 | 4 |
| 14 | 100 | 30 | 25 | 6 | 2 |
| 17 | 500 | 300 | 125 | 12 | 4 |
| 19 | 500 | 300 | 125 | 12 | 4 |
| 21 | 100 | 10 | 25 | 6 | 2 |
| Scheme | Phase 1 | Phase 2 |
|---|---|---|
| Scenario 1 | Start–stop optimization without considering operational risks | Disregard synchronous spare optimization |
| Scenario 2 | Start–stop optimization without considering operational risks | Consider synchronous spare optimization |
| Scenario 3 | Consider start–stop optimization of operating risks | Disregard synchronous spare optimization |
| Scenario 4 | Consider start–stop optimization of operating risks | Consider synchronous spare optimization |
| Cost/USD | Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 |
|---|---|---|---|---|
| Fuel | 156,600 | 156,723 | 150,482 | 150,736 |
| Abandoned wind | 4727 | 4727 | 7306 | 7306 |
| Reducible load | 3711 | 3711 | 4266 | 4266 |
| Start-up and shutdown | 2076 | 2076 | 1984 | 1984 |
| Synchronized reserve | 21,977 | 12,939 | 20,613 | 12,665 |
| Operating before assessment | 189,092 | 180,177 | 184,651 | 176,957 |
| Cost/USD | Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 |
|---|---|---|---|---|
| Upward synchronization backup penalty | 13,411 | 6893 | 12,012 | 6803 |
| Downward synchronization backup penalty | 5178 | 4979 | 7125 | 5863 |
| Downward synchronization standby reward | 8166 | 7396 | 26,256 | 22,846 |
| Backup after assessment | 32,310 | 17,415 | 13,494 | 2485 |
| Operation after assessment | 199,515 | 184,653 | 177,532 | 166,777 |
| Cost/USD | Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 |
|---|---|---|---|---|
| Fuel | 157,391 | 157,520 | 151,638 | 151,875 |
| Abandoned wind | 2233 | 2233 | 7552 | 7552 |
| Reducible load | 3818 | 3818 | 4264 | 4264 |
| Start-up and shutdown | 2076 | 2076 | 1984 | 1984 |
| Synchronized reserve | 21,841 | 12,875 | 20,538 | 12,596 |
| Operating before assessment | 187,359 | 178,522 | 185,976 | 178,271 |
| Upward synchronization backup penalty | 13,253 | 6863 | 11,927 | 6765 |
| Downward synchronization backup penalty | 5092 | 4955 | 7471 | 5831 |
| Downward synchronization standby reward | 8169.6 | 7391 | 26,219 | 22,849 |
| Backup after assessment | 32,016 | 17,302 | 13,716 | 2344 |
| Operation after assessment | 197,534 | 182,948 | 179,155 | 168,019 |
| Cost/USD | Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 |
|---|---|---|---|---|
| Fuel | 156,945 | 157,073 | 151,045 | 151,286 |
| Abandoned wind | 3290 | 3290 | 7328 | 7328 |
| Reducible load | 3768 | 3768 | 4264 | 4264 |
| Start-up and shutdown | 2076 | 2076 | 1984 | 1984 |
| Synchronized reserve | 21,932 | 12,908 | 20,580 | 12,635 |
| Operating before assessment | 188,011 | 179,115 | 185,201 | 177,497 |
| Upward synchronization backup penalty | 13,355 | 6878 | 11,971 | 6785 |
| Downward synchronization backup penalty | 5086 | 4968 | 7129 | 5849 |
| Downward synchronization standby reward | 8168 | 7394 | 26,236 | 22,853 |
| Backup after assessment | 32,204 | 17,360 | 13,443 | 2416 |
| Operation after assessment | 198,282 | 183,567 | 178,064 | 167,278 |
| Cost/USD | Predictive Values | Upper Limit of Wind Power Prediction Values | Lower Limit of Wind Power Prediction Values |
|---|---|---|---|
| Fuel | 151,286 | 150,736 | 151,875 |
| Abandoned wind | 7328 | 7306 | 7552 |
| Reducible load | 4264 | 4266 | 4264 |
| Start-up and shutdown | 1984 | 1984 | 1984 |
| Synchronized reserve | 12,635 | 12,665 | 12,596 |
| Operating before assessment | 177,497 | 176,957 | 178,271 |
| Upward synchronization backup penalty | 6785 | 6803 | 6765 |
| Downward synchronization backup penalty | 5849 | 5863 | 5831 |
| Downward synchronization standby reward | 22,853 | 22,846 | 22,849 |
| Backup after assessment | 2416 | 2485 | 2344 |
| Operation after assessment | 167,278 | 166,777 | 168,019 |
| Cost/USD | Scenario 4 (DLBFSO) | Scenario 4 (SOA) |
|---|---|---|
| Fuel | 150,736 | 146,935 |
| Abandoned wind | 7306 | 0 |
| Reducible load | 4266 | 5400 |
| Start-up and shutdown | 1948 | 1924 |
| Synchronized reserve | 12,665 | 12,702 |
| Operating before assessment | 176,957 | 166,961 |
| Upward synchronization backup penalty | 6803 | 6840 |
| Downward synchronization backup penalty | 5863 | 5862 |
| Downward synchronization standby reward | 22,846 | 31,949 |
| Backup after assessment | 2485 | −6545 |
| Operation after assessment | 166,777 | 147,714 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, B.; Fu, L. Research on Market Evaluation Model of Reserve Auxiliary Service Based on Two-Stage Optimization of New Power System. Energies 2024, 17, 1921. https://doi.org/10.3390/en17081921
Qu B, Fu L. Research on Market Evaluation Model of Reserve Auxiliary Service Based on Two-Stage Optimization of New Power System. Energies. 2024; 17(8):1921. https://doi.org/10.3390/en17081921
Chicago/Turabian StyleQu, Boyang, and Lisi Fu. 2024. "Research on Market Evaluation Model of Reserve Auxiliary Service Based on Two-Stage Optimization of New Power System" Energies 17, no. 8: 1921. https://doi.org/10.3390/en17081921
APA StyleQu, B., & Fu, L. (2024). Research on Market Evaluation Model of Reserve Auxiliary Service Based on Two-Stage Optimization of New Power System. Energies, 17(8), 1921. https://doi.org/10.3390/en17081921





