Breaking Borders with Joint Energy and Transmission Right Auctions—Assessing the Required Changes for Empowering Long-Term Markets in Europe †
Abstract
1. Introduction
1.1. Policy Context
1.2. Current Status of the Long-Term, Cross-Border Market in Europe
1.3. Literature Review and Research Gap
- The first criterion concerns the satisfaction of superposition and netting properties. Since these properties cannot always be guaranteed in the short-term market due to the non-linearity of GSKs, the authors infer that they would also fail in the long-term market.
- The second criterion focuses on the firmness of FTRs under FBMC. A critical challenge for achieving FTR firmness lies in the simultaneous feasibility test under FBMC, which would require the set of transmission rights allocated in the forward market to be feasible for the day-ahead zonal PTDF. This necessitates information about both grid topologies and generation demand shift keys (GDSK) in the day-ahead market. However, GDSKs are not available in the forward market, and acquiring this information is not the responsibility of TSOs, even if it exists.
1.4. Research Questions and Scope
- What could be an effective mechanism for developing long-term transmission rights and forward market coupling?
- Is the zonal pricing-based FBMC currently implemented in the European cross-border market conducive to establishing the proposed long-term market?
- Are current institutional settings fit for purpose?
1.5. Paper Organization
2. Joint Energy and Transmission Right Auction Model
2.1. JETRA: A Recipe for Long-Term Market Development
2.1.1. A Wide Range of Hedging Instruments
- FTRs are forward contracts that entitle their holders to the right to receive locational marginal price differences between the specified withdrawal and injection points during a specified time interval [20]. From a market player’s perspective, holding FTRs allows them to pay congestion charges based on nodal differences, regardless of the power flow distribution through the network. When coupled with long-term contracts, FTR can provide market players with a perfect hedge against spot price volatility. The allocation of FTRs requires a central view of network conditions from the SO.
- PTRs give their holders the right to collect the shadow price of the specified transmission element in accordance with the specified direction and time interval [21]. To hedge against locational price differences, a PTR portfolio must be composed and weighted for each transmission path associated with the underlying energy contract. Thus, it requires an accurate calculation by the user of the transmission path usage for the intended transaction. Market players can bid PTR for the most likely congested transmission network element to hedge a portion of the congestion risk or to collect congestion rent. PTRs alone can be allocated without a central auction, as the physical limits of certain transmission elements can be individually determined by the owners of network assets.
2.1.2. The Multi-Settlement Rules
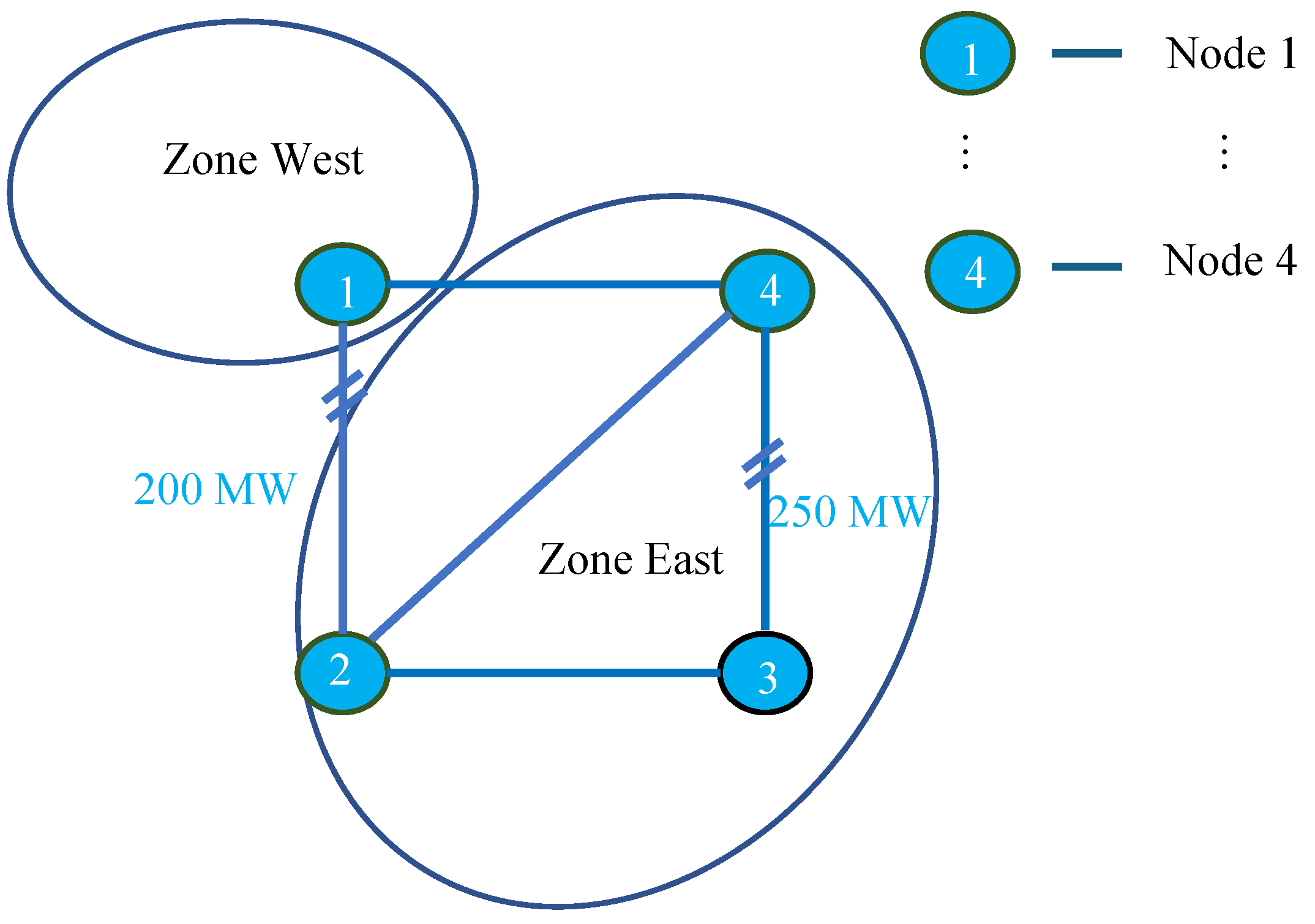
2.2. Case Study Network and Bids
3. Institutions, Spatial, and Temporal Dimensions of Nodal and Zonal Markets
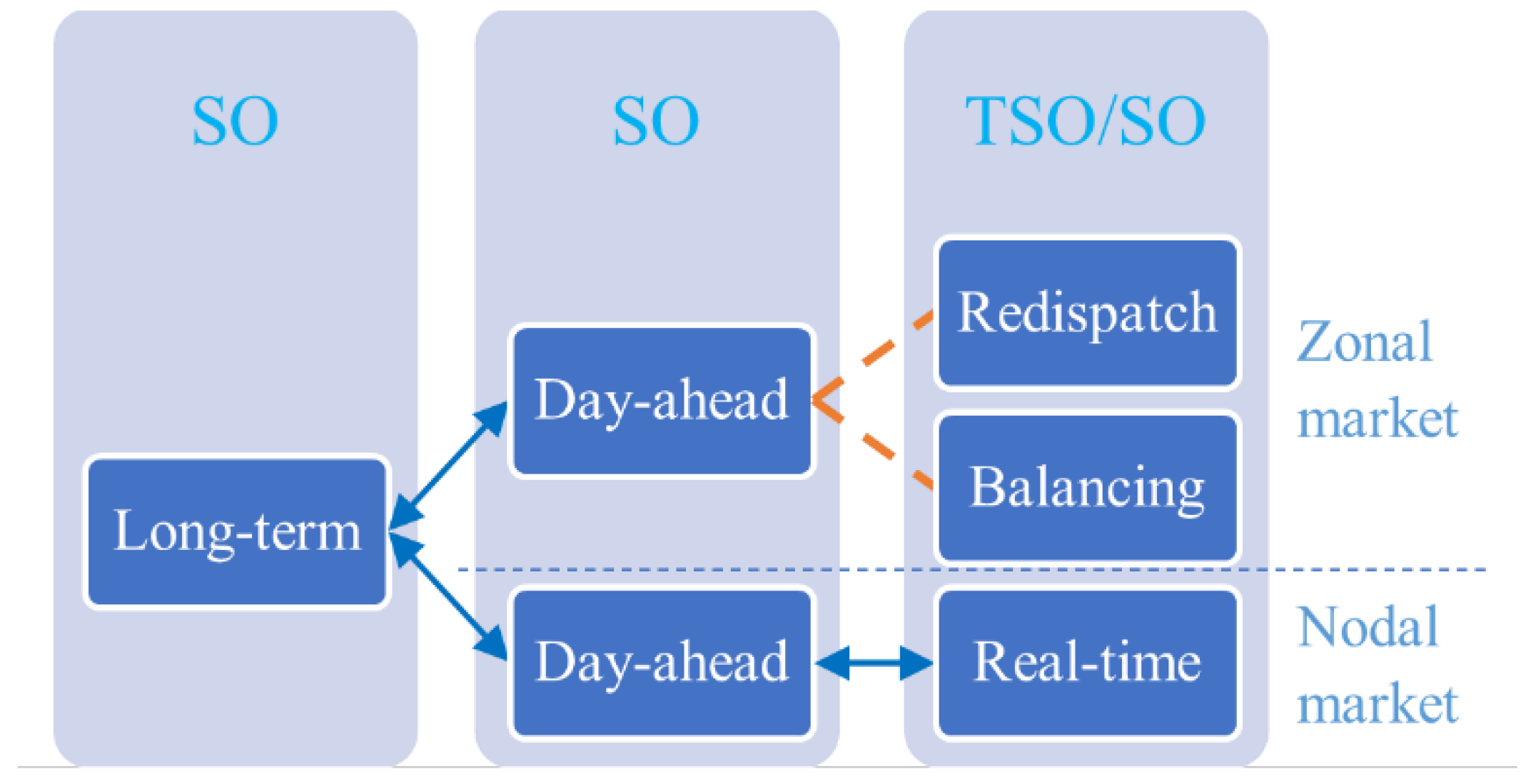
3.1. Institutional Design
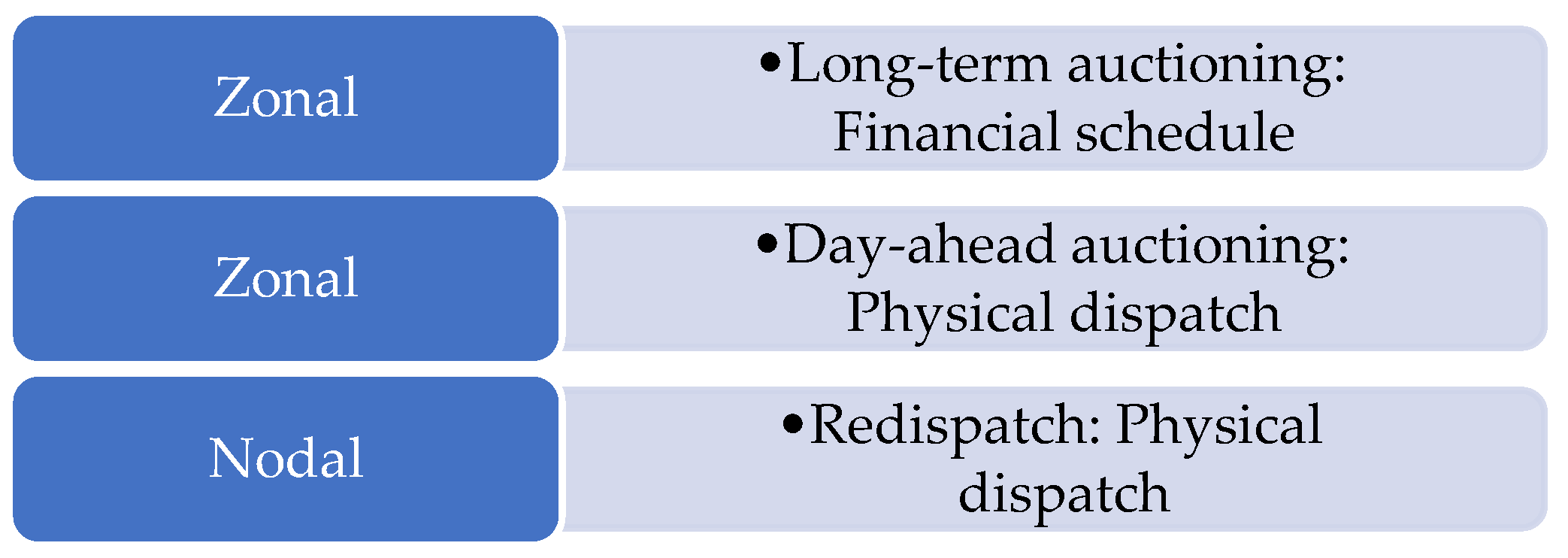
3.2. Financial Schedule and Physical Dispatch
4. Adapting JETRA to Flow-Based Market Coupling
4.1. Flow-Based Market Coupling
4.1.1. JETRA with Flow-Based Market Coupling
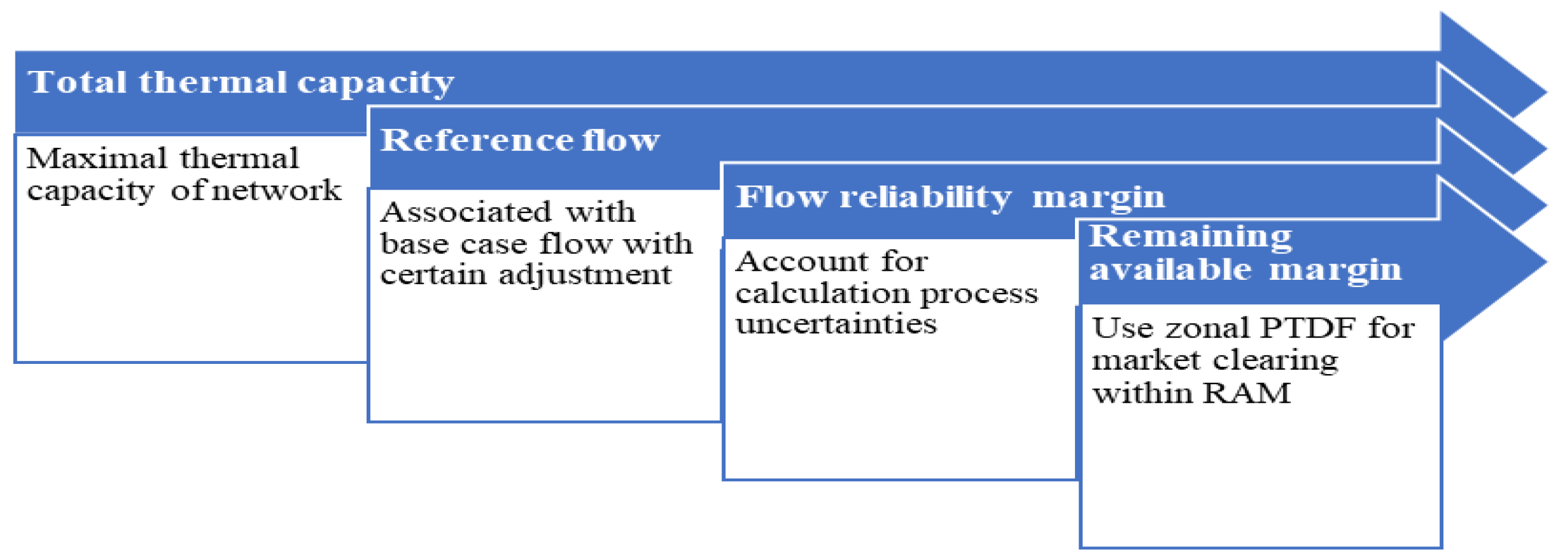
4.1.2. Base Case and Zonal PTDF
- The base case plays a crucial role in defining the feasible region for interzonal trade volume, and its construction provides another source of flow estimation error. As case A in Appendix B shows, neglecting intrazonal network constraints in the zonal market model can result in a much higher cleared volume of intrazonal transactions compared with nodal dispatch. This high intrazonal trade not only results in intrazonal congestion but also leads to an initial underestimation of the impact of intrazonal trade on interconnection capacity utilization in grid modeling. Consequently, it results in an overoptimistic, feasible flow region for potential interzonal trade at the grid modeling stage.
- An overly stringent zonal PTDF can lead to the overestimation of interconnection flow, and the zonal market clearing outcome can result in the underutilization of interconnection capacity, as in case study C. Meanwhile, overly loose assumptions with smaller than actual zonal PTDF values can lead to an underestimation of interconnection flow in the grid modeling process. As a result, zonal market clearing can result in interconnection congestion and require redispatch, as indicated in case B.
4.2. JETEA Adaptation to Flow-Based Market Coupling: Methodological Challenges
4.2.1. FTR Firmness under High Uncertainty
- Day-ahead FBMC: As the European day-ahead market reflects physical dispatch that corresponds to generation and load patterns, TSOs can leverage historical operating data to approximate the physical flow resulting from market clearing. Additionally, TSOs retain the option to utilize the redispatch mechanism to adjust the day-ahead market energy bids, ensuring grid feasibility.
- JETRA with FTRs: The financial forwards in JETRA long-term auctions may not correspond directly with the overall generation and load patterns within physical dispatch. For instance, FTRs are part of a bidding portfolio spanning long-term and short-term markets. Forecasting market participant bidding behavior and assessing their impact on interconnection flow is significantly more challenging compared to forecasting generation load patterns before the short-term market. Section 4.2.2 will illustrate with an example why the base case method used in day-ahead FBMC is not applicable when both the energy and FTR bids are involved in the long-term market. Additionally, to uphold the integrity of the long-term contracts supported by FTRs, redispatch cannot curtail the generation specified as energy injection within cross-border FTRs. To guarantee the physical feasibility of long-term JETRA bids, an additional GDSK rule is proposed in Section 4.2.3 proposes an additional GDSK rule, and a higher FRM is applied in the grid modeling of long-term auctions.
4.2.2. Base Case Effectiveness in a Long-Term Auction
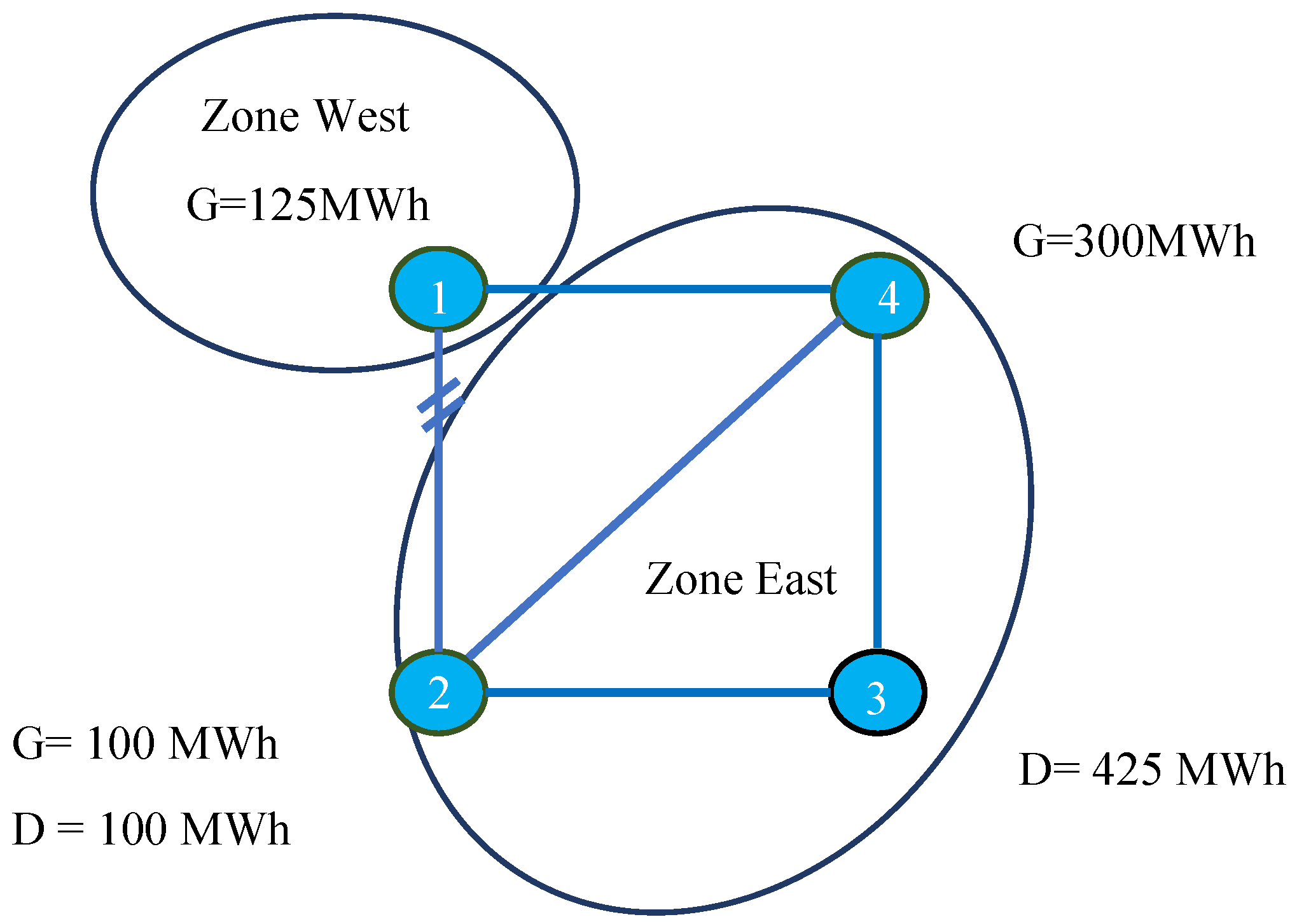
- Scenario 1: In a forward market auction, the energy purchase quantity solely represents the total amount of energy bid into hedging products from the demand side, which may not necessarily align with the expected real-time load. It is possible that the main demand at node 3 adopts a strategy of spreading out energy bids across different timeframes, resulting in a lower energy purchase bid in the long-term auction. In other words, the demand at node 3 may employ a bidding strategy to acquire a portion of its load in later market frames, anticipating a potential decrease in spot market prices.
- Scenario 2: Another possibility is that the demand at load 3 enters into a long-term, cross-border bilateral contract to fulfill a significant portion of its future energy demand, while the supplier in zone west submits FTR bids to support these long-term contracts. Considering the lead time in the long-term market, generation sources involved from zone west could potentially include new power plants that have not yet reached the operational phase. Consequently, the base case, which relies on historical data, may not accurately capture the transactions associated with these new investments. Moreover, in the joint auction, only injection/withdrawal zone information is available for the FTR bids, which limits the ability of TSOs to effectively forecast the demand pattern solely based on the observed results of the previous auction round. Scenarios 1 and 2 are illustrated in Figure 6 with textboxes S1 and S2:
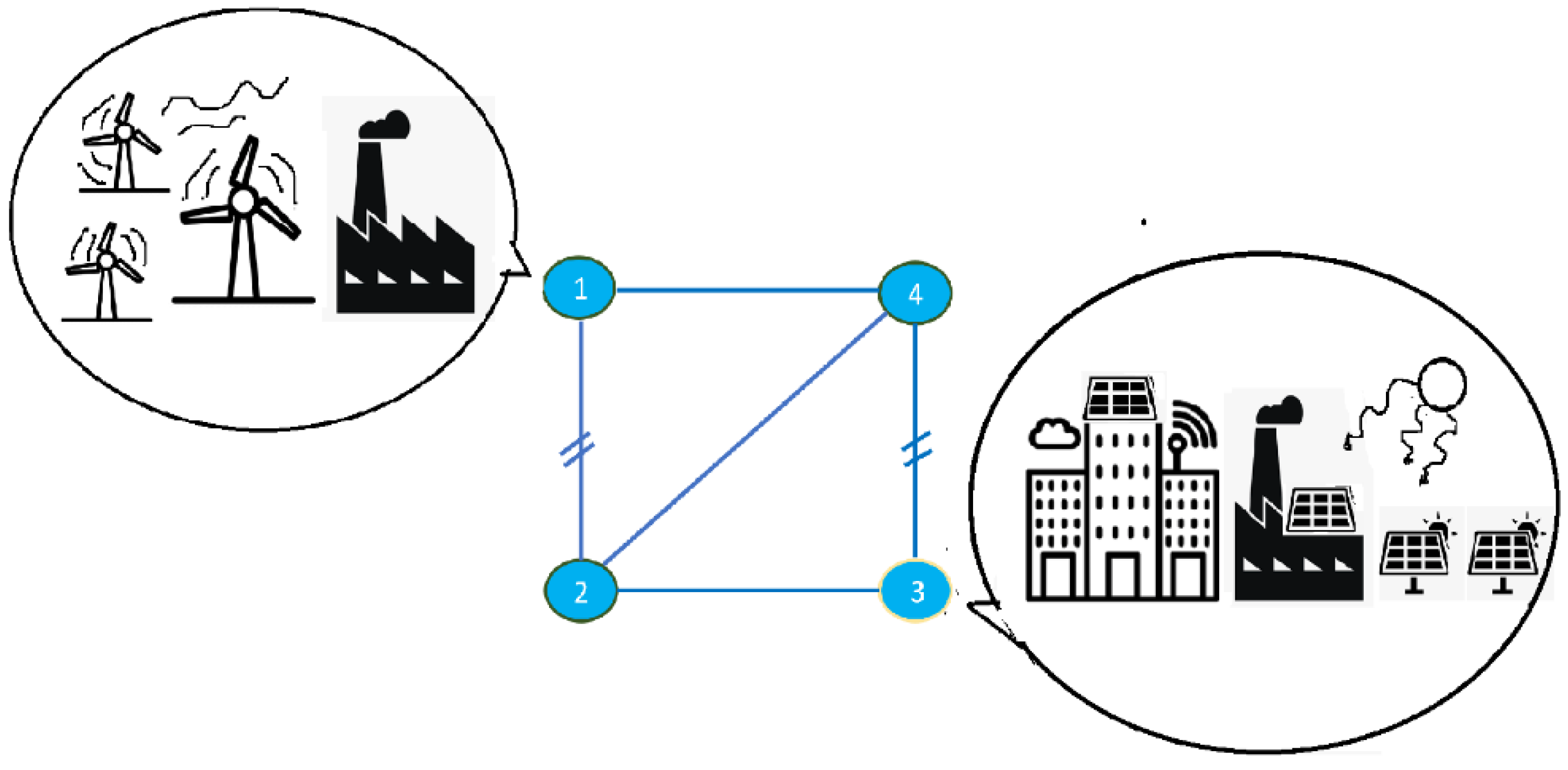
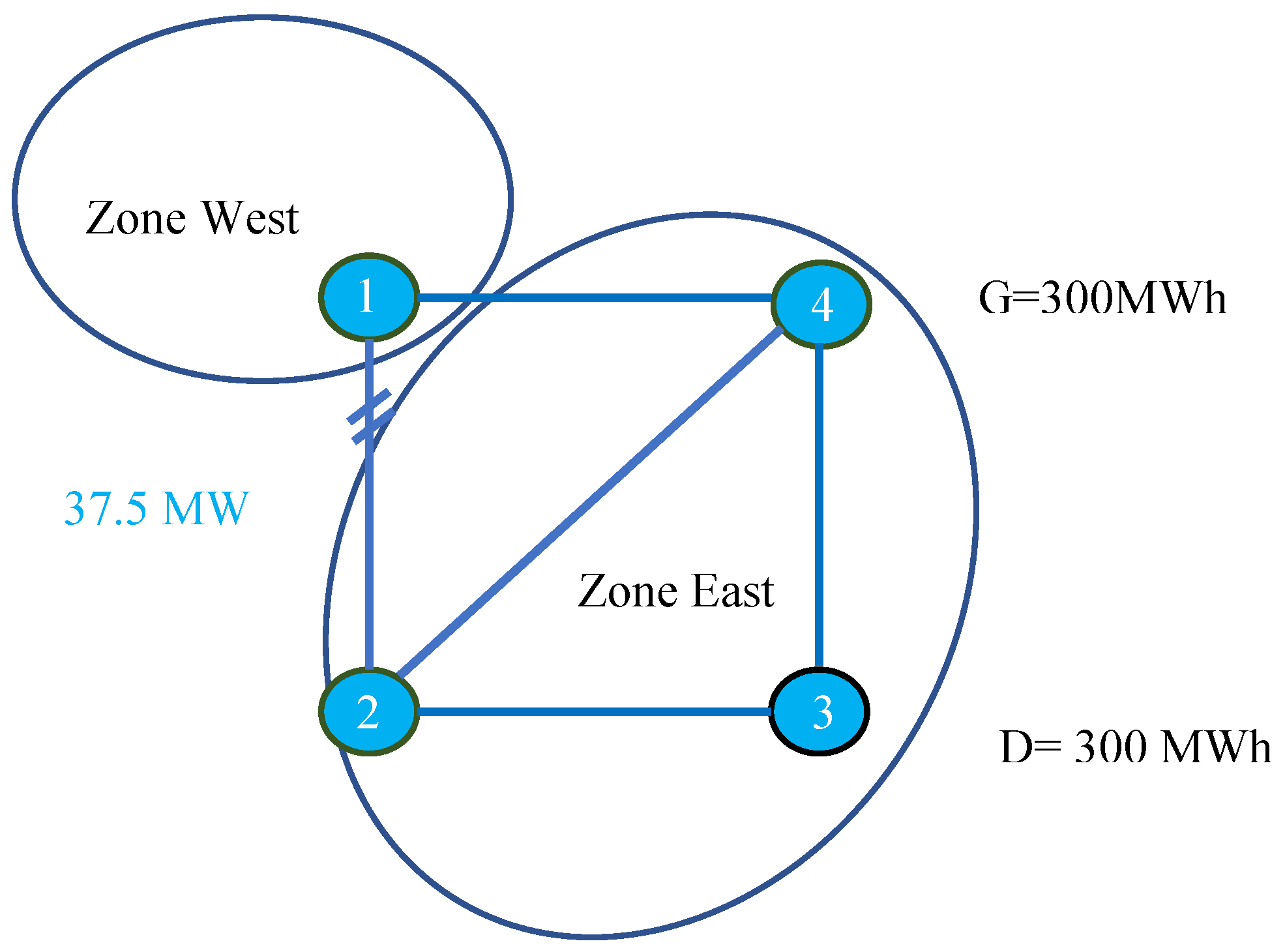
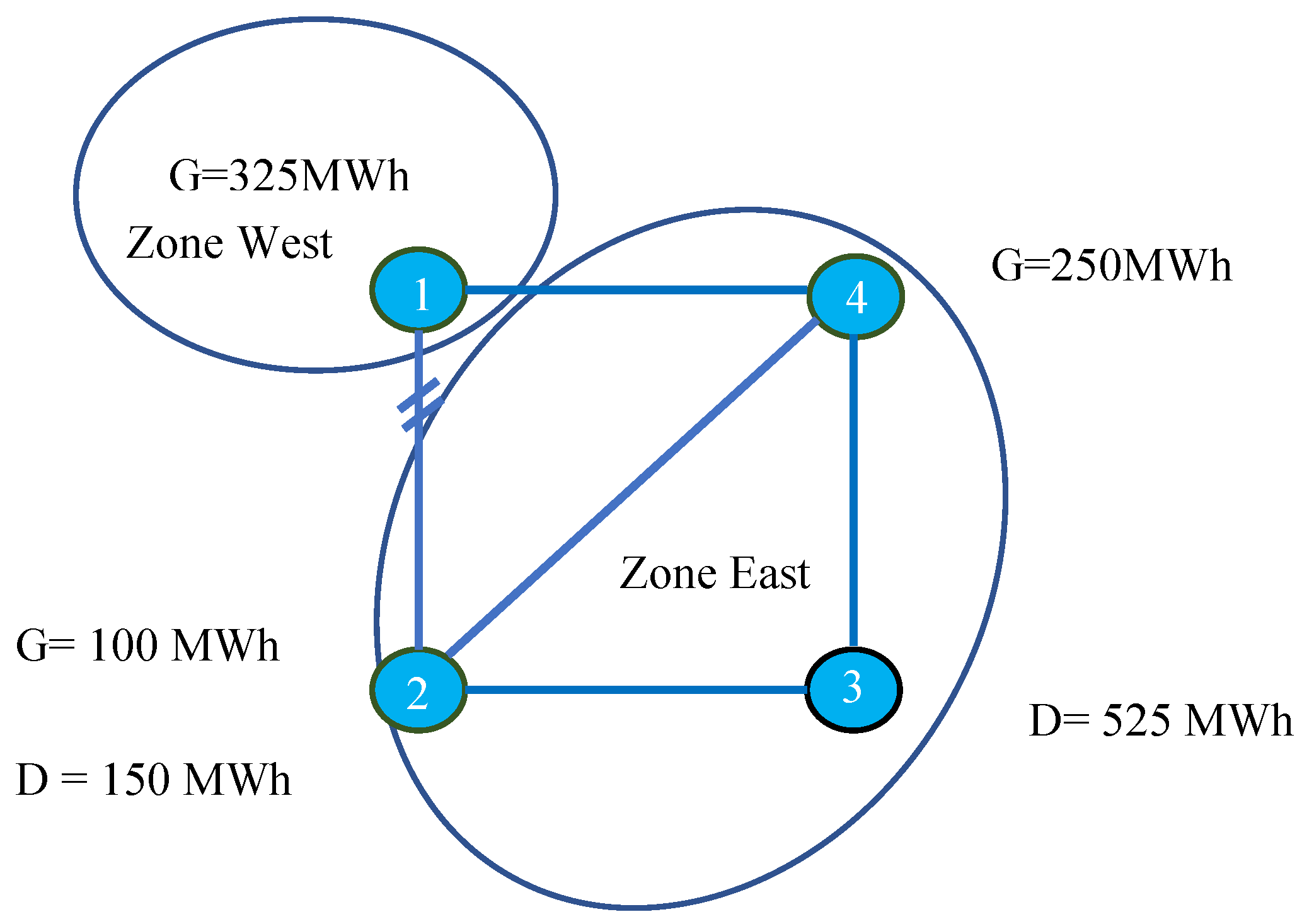
- Scenario 3: Considering the lead time before electricity delivery, whether the lower energy bid volume in zone east is the result of planned structural changes on the demand side is worth questioning. One possible explanation is that there is a planned demand shift at node 3, which is achieved by relocating industries closer to low-cost renewable energy sources at node 1 as illustrated in the left circle of Figure 7. This strategy could decrease energy purchase bids from the main load center during the long-term auction.
- Scenario 4: Another scenario to consider is a net reduction in demand resulting from investments in local generation, as illustrated in the right circle of Figure 7. This example highlights the limitations of relying on reference day generation and load bid profiles from historical data for long-term auctions.
4.2.3. GDSK Rule for Conservative Grid Modeling
- Using dispatchable generators,
- Assigning a higher weight to the generation decrease or demand increase at the node associated with the critical transaction from a congestion perspective for interconnection lines.
4.3. Grid Modeling for JETRA in the Day-Ahead Market and Redispatch
5. Case Study Results
5.1. Market Clearing and Settlements in the Case Study under Nodal Pricing
5.1.1. Long-Term Auction Outcome under Nodal Pricing
5.1.2. Day-Ahead and Real-Time Market Outcomes under Nodal Pricing
5.2. Base Cases, GDSK, and FRM in the Case Study
5.2.1. Base Case and Reference Flow in the Long-Term Auction
5.2.2. Base Case and Reference Flow in the Day-Ahead Market
5.2.3. GDSK and FRM in the Long-Term and Day-Ahead Markets
- Node 4 is characterized as an intermittent generator in zone east with a generation cost that marginally surpasses that of the generator at node 1.
- The generator at node 2 represents dispatchable generation with a flexible output.
- The transaction between nodes 1 and 2 exhibits the highest PTDF value on interconnection line 1–2.
5.3. Joint Auction under Zonal Pricing
5.3.1. Long-Term Market Clearing and Settlements under Zonal Pricing
5.3.2. Day-Ahead Market Clearing and Settlements under Zonal Pricing
5.3.3. Redispatch Outcomes
6. JETRA Performance Indices and Case Study Evaluation
6.1. JETRA Performance Indices
- The total net payment for demand over various timeframes is calculated to compare the dynamic economic efficiency of using congestion hedging instruments in nodal and zonal pricing markets. In this case study, we assume that the costs of FTR and energy purchases across different timeframes are ultimately borne by the user, who represents the demand at the primary load node.
- The GDSK metric, used as input for each round of zonal market clearing, is compared with the theoretically optimal GDSK calculated ex-post. The GDSK used for grid modeling in the auction presents predicted nodal net changes per unit of zonal net position change. Retrospectively, given the auction clearing outcome under nodal pricing, nodal dispatch is compared with the base case generation load pattern to derive the theoretically optimal GDSK. The realized GDSK metric calculates the realized net export at each node after market clearing and compares it with the base case to compute the GDSK ex-post market clearing. The formula for different GDSK metrics is presented in Appendix D.1. The GDSK metric reveals an important source of inefficiencies in system dispatch under FBMC.
- Cross-border trade potential: In the forward market, this index evaluates the cross-border trade volume and the potential for market players to use the market to procure hedging instruments across borders. In the market timeframe that has physical dispatch, this index indicates the physical cross-border trade volume enabled by the market design.
- Revenue adequacy for SO: In the literature, revenue adequacy is defined as the SO’s ability to compensate energy and transmission rights holders from the surplus accrued through energy and transmission rights auctions or generation and load payments. This research extends this concept to include the SO’s capability for cost recovery via market-based mechanisms. Revenue adequacy in JETRA in the day-ahead market under nodal pricing assesses whether energy and transmission right revenue from the day-ahead auction is sufficient for paying the rights holders from the long-term auction. For JETRA in the real-time market under nodal pricing or the day-ahead market under zonal pricing, revenue adequacy assesses whether generation and load net payments suffice to pay the right holders from the previous auction. In the redispatch under zonal pricing, this index measures whether the surplus from the day-ahead market, namely the amount left with the SO after the energy and transmission rights are paid, is enough to pay the redispatch costs.
6.2. Case Study Evaluation
6.2.1. Total Costs
6.2.2. GDSK in the Long-Term, Day-Ahead Markets, and Redispatch Phase
- The Euclidean distance between the ex-post GDSK derived from the national redispatch and the theoretically optimal GDSK for the day-ahead auction is 0.34. The ex-post GDSK value obtained through national redispatch also allows for consideration of grid congestion in generation load patterns. This reduces the Euclidean distance of the ex-ante GDSK metric from the theoretically optimal value, which is 0.725 in the day-ahead market.
- The cross-border redispatch in Figure 17 aligns with the real-time nodal pricing market outcome in Figure 9 in Section 5.1.2, signifying that the realized GDSK following the cross-border redispatch matches the theoretically optimal GDSK.
- When we view the GDSK distance together with total costs, the closer the realized redispatch GDSK is to the optimal value, the lower the total costs for the demand at node 3.
6.2.3. Cross-Border Trade in Long-Term and Day-Ahead Markets
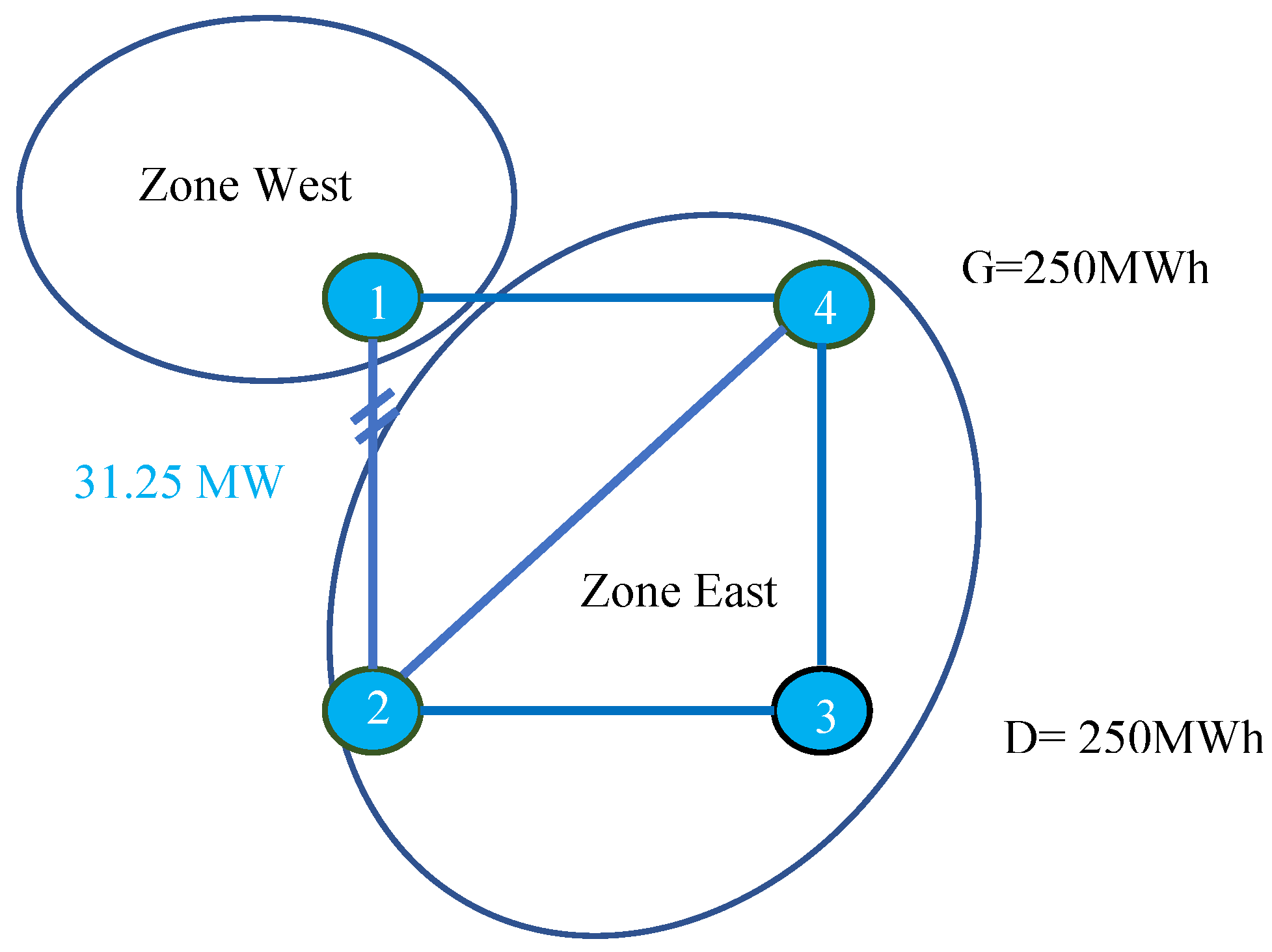
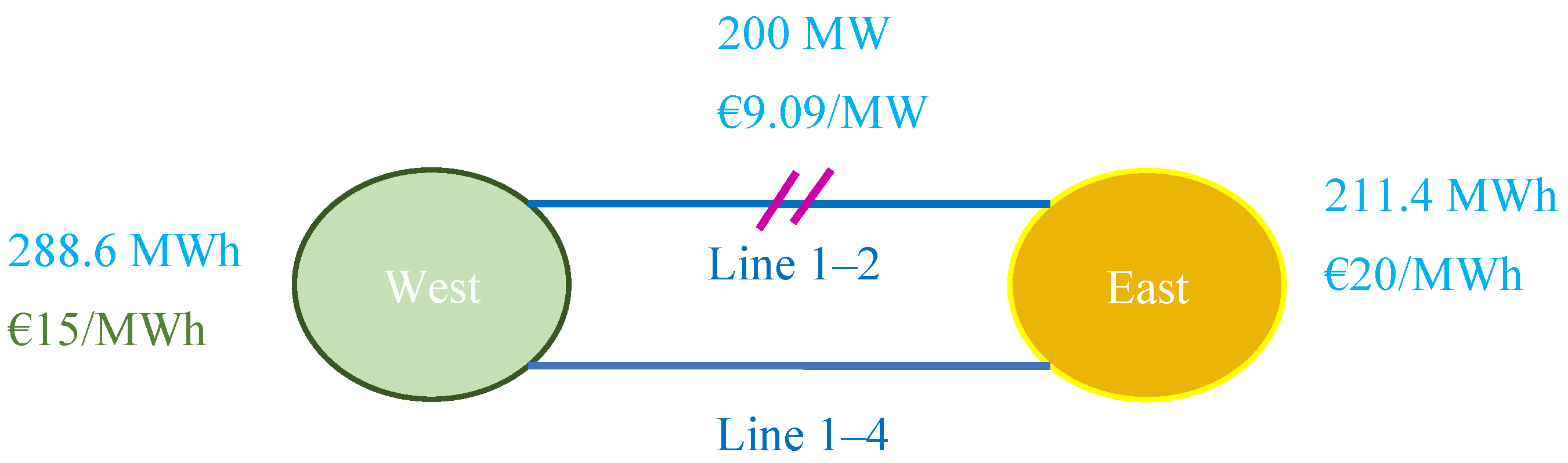
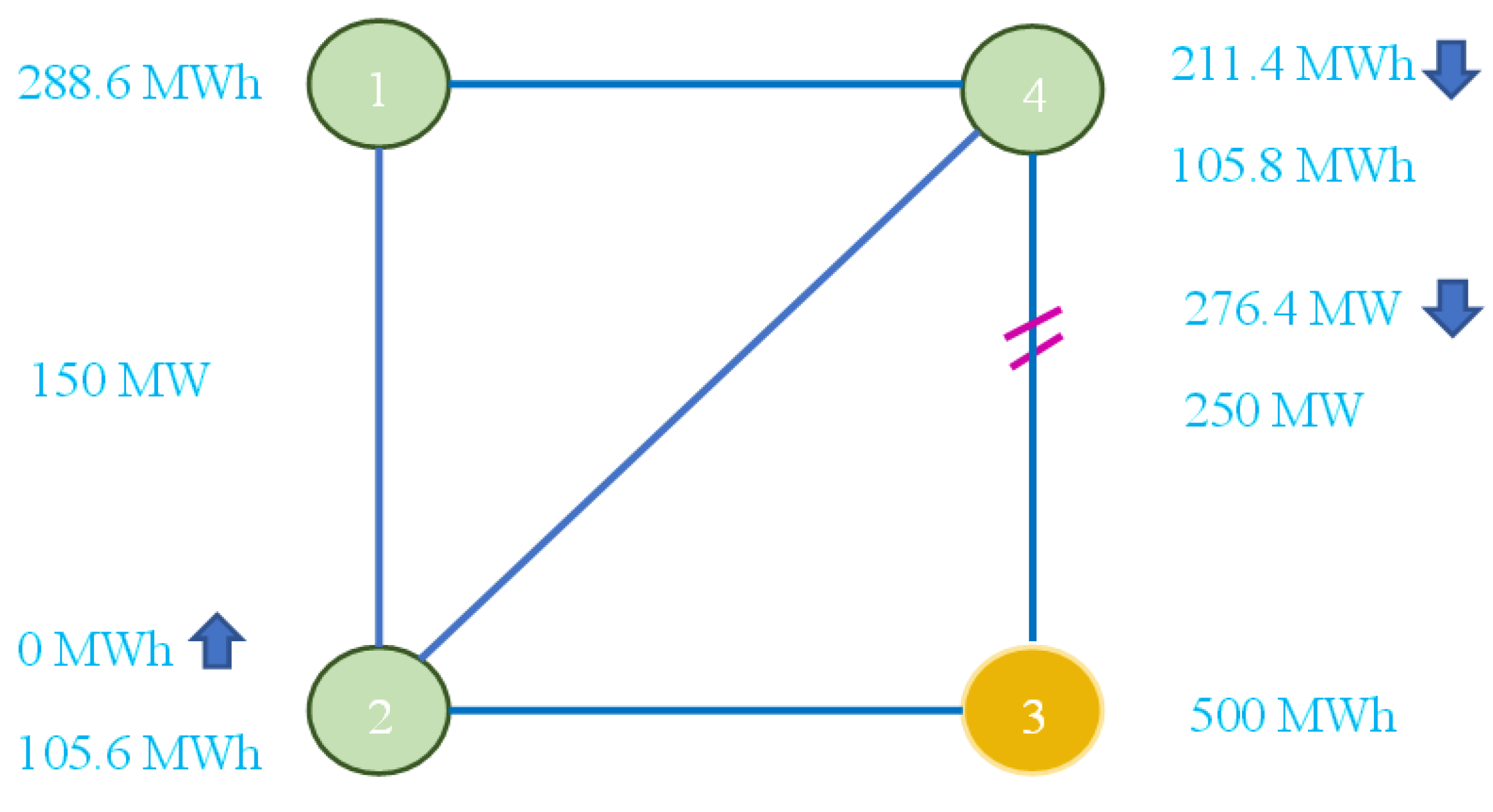
- The cross-border zonal trade with an accepted FTR bid of 217.8 MWh in the long-term auction falls significantly short of the 375 MWh FTR obtained under nodal pricing. This discrepancy arises because of two factors, namely: the larger volume of FRM applied and a more restrictive GDSK rule in the long-term auction, which factors in higher uncertainties in the timeframe. During the day-ahead timeframe, the cleared cross-border trade amounts to 288.6 MWh. This improvement is facilitated by the more relaxed GDSK rules and the reduced FRM value applied in the RAM calculation.
- The divergence between the cleared cross-border trade and the potential optimal interzonal transaction indicates the improvement of cross-border trade when the theoretical optimal GDSK is applied. The difference between potential optimal interzonal transactions and cross-border trade under nodal pricing demonstrates the influence of RAM calculation on the potential for cross-border trade.
6.2.4. Revenue Adequacy
6.3. Observations Regarding Zonal Market Outcomes
- From the SO’s standpoint, there is less interconnection capacity used for cross-border trade under zonal pricing than under nodal pricing. In addition, the case study reveals that intrazonal trade patterns and intrazonal networks that are not well represented in the zonal grid model necessitate redispatch. The redispatch costs challenge revenue adequacy, and the cost gap must be allocated across borders according to administratively negotiated rules.
- From the grid user’s perspective, the hedging function of long-term cross-border transmission rights and energy contracts is significantly weaker under zonal pricing compared with that under nodal pricing. The diminished potential for cross-border trade under zonal pricing is a crucial factor behind this difference. Another contributing factor is the varying levels of granularity of the network constraints used in the optimization process. Under the zonal model, the nodal grid view is solely implemented in the redispatch, where buyer bids are no longer accessible to market participants. Thus, transmission rights and energy contracts issued from joint auctioning, based on the zonal model in long-term auctions, cannot hedge against redispatch costs incurred post-market closure. This predicament raises the question of whether implementing auction energy contracts and transmission rights to link long-term and day-ahead markets alone can create effective hedging instruments under zonal pricing. For the hedging instruments to work more effectively, consistent grid modeling and market rules are required.
7. Conclusions and Policy Implications
- Increased uncertainties in JETRA grid modeling: The inherent methodological dilemma of FBMC lies in the information asymmetry between the TSO and market players for grid modeling. Our analysis of the challenges in computing key grid modeling parameters—base case and zonal PTDF—reveals that this information asymmetry becomes particularly critical for JETRA grid modeling in long-term auctions. Simultaneously, the obligation to ensure the firmness of cross-border FTRs auctioned in JETRA, acting as a prerequisite for safeguarding long-term contract integrity, poses substantial challenges for TSOs. The combined effect of these is conservative grid modeling, inefficient dispatch, and low interconnection utilization, as demonstrated by the case study.
- Limited applicability of multi-settlement rules: In the zonal pricing setting of the case study, which adheres to the current European market design, physical dispatch starting from the day-ahead market dictates that the multi-settlement rule can only link the forward markets with the day-ahead market. Furthermore, market participants who hold long-term hedging products cleared with a zonal grid model cannot effectively hedge against redispatch costs incurred using a nodal grid model, weakening the overall effectiveness of hedging strategies. The high redispatch costs also render the granular cost allocation across borders based on market price signals, a key advantage of multi-settlement rules under nodal pricing, impracticable in the current zonal pricing framework.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B. Base Case and Zonal PTDF Impact on Outcome
Appendix B.1. Case A: Nodal Dispatch Intrazonal Trade Pattern as a Base Case
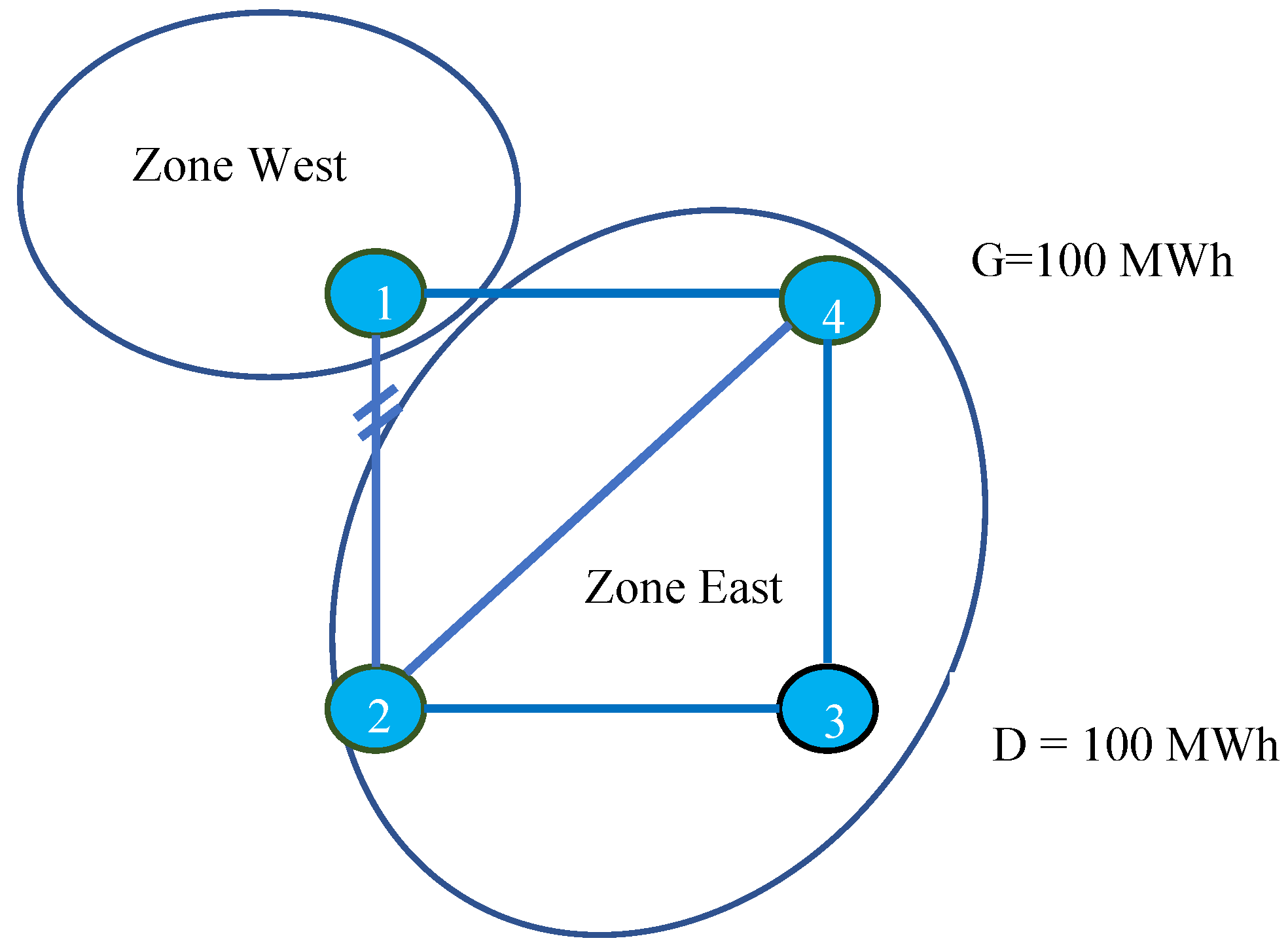
Appendix B.2. Case B: Overly Relaxed GDSK Assumption and Small Zonal PTDF
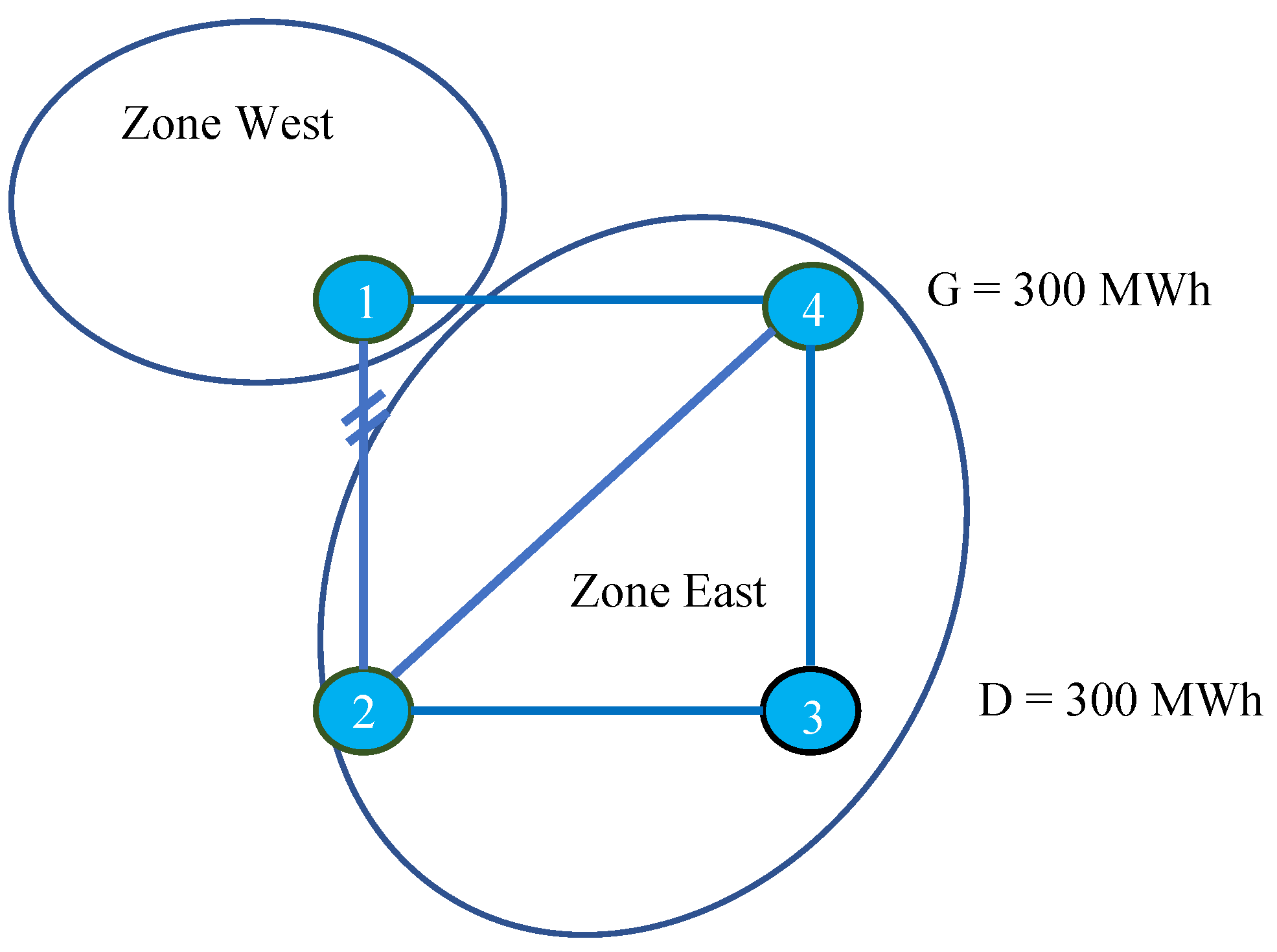
Appendix B.3. Case C: Overly Stringent GDSK Assumption and Large Zonal PTDF
Appendix C. Physical Feasibility of Energy and Transmission Rights in JETRA
Appendix D. GDSK Calculation and Total Cost Decomposition for JETRA Indices
Appendix D.1. GDSK Calculation
Appendix D.2. Total Cost Decomposition
References
- European Commission. Communication from the Commission to the European Parliament, the European Council, the Council, the European Economic and Social Committee and the Committee of the Regions: REPowerEU Plan. EC Website. 2022. Available online: https://commission.europa.eu/strategy-and-policy/priorities-2019-2024/european-green-deal/repowereu-affordable-secure-and-sustainable-energy-europe_en (accessed on 1 February 2024).
- Pexapark. European PPA Market Outlook 2023: Navigating the Energy Transition Peaks and Valleys: A Shock-Therapy for Renewables and a Lesson to Remember. Pexapark Website. 2023. Available online: https://pexapark.com/european-ppa-market/ (accessed on 23 March 2023).
- European Commission. Proposal for a Regulation of the European Parliament and of the Council amending Regulations (EU) 2019/943 and (EU) 2019/942 as well as Directives (EU) 2018/2001 and (EU) 2019/944 to Improve the Union’s Electricity Market Design. Strasburg. 2023. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:52023PC0148 (accessed on 15 March 2023).
- European Commission. Commission Regulation (EU) 2016/1719 of 26 September 2016 Establishing a Guideline on Forward Capacity Allocation. Brussels. 2016. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:32016R1719 (accessed on 1 February 2024).
- Meeus, L.; Schittekatte, T. Who gets the rights to trade across borders? In The Evolution of Electricity Markets in Europe, 1st ed.; Edward Elga: Cheltenham, UK, 2020; pp. 25–42. [Google Scholar] [CrossRef]
- ACER. ACER to Consult on the Harmonised Allocation Rules for Long-Term Electricity Transmission Rights. ACER Website. 2023. Available online: https://www.acer.europa.eu/news-and-events/news/acer-consult-harmonised-allocation-rules-long-term-electricity-transmission-rights (accessed on 1 February 2024).
- Hogan, W. Restructuring the Electricity Market: Institutions for Network Systems (Working paper, John F. Kennedy School of Government, 02138). Harvard University, Cambridge, MA, USA. 1999. Available online: https://scholar.harvard.edu/whogan/files/hjp0499.pdf (accessed on 1 February 2024).
- Jamasb, T.; Nepal, R.; Davi-Arderius, D. Electricity Markets in Transition and Crisis: Balancing Efficiency, Equity, and Security; Working Paper/Department of Economics, Copenhagen Business School No. 04-2023CSEI Working Paper No. 2023; Department of Economics, Copenhagen Business School: Frederiksberg, Denmark, 2023; Available online: https://research-api.cbs.dk/ws/portalfiles/portal/87935064/tooraj_jamasb_et_al_working_paper_04_2023.pdf (accessed on 1 February 2024).
- D’Aertrycke, G.; Smeers, Y. Transmission Rights in the European Market Coupling System: An Analysis of Current Proposals. In Financial Transmission Rights: Analysis, Experiences and Prospects (Lecture Notes in Energy, 7); Springer: London, UK, 2013; pp. 333–375. [Google Scholar] [CrossRef]
- Spodniak, P.; Collan, M.; Makkonen, M. On Long-Term transmission rights in the Nordic electricity markets. Energies 2017, 10, 295. [Google Scholar] [CrossRef]
- Beato, P. Long Term Interconnection, Transmission Rights and Renewable Deployment (RSC Working Paper 2021/57); Florence School of Regulation: Florence, Italy, 2021; Available online: https://hdl.handle.net/1814/71818 (accessed on 1 February 2024).
- Van Den Bergh, K.; Boury, J.; Delarue, E. The Flow-Based Market Coupling in Central Western Europe: Concepts and Definitions. Electr. J. 2016, 29, 24–29. [Google Scholar] [CrossRef]
- Schönheit, D.; Kenis, M.; Lorenz, L.; Möst, D.; Delarue, E.; Bruninx, K. Toward a Fundamental Understanding of Flow-Based Market Coupling for Cross-Border Electricity Trading. Adv. Appl. Energy 2021, 2, 100027. [Google Scholar] [CrossRef]
- Purchala, K. EU Electricity Market: The Good, the Bad and the Ugly. In PSE Website. 2018. Available online: https://www.pse.pl/documents/31287/20965583/PSE_16102018_The_good_the_bad_the_ugly.pdf (accessed on 1 February 2023).
- Eicke, A.; Schittekatte, T. Fighting the Wrong Battle? A Critical Assessment of Arguments against Nodal Electricity Prices in the European Debate. Energy Policy 2022, 170, 113220. [Google Scholar] [CrossRef]
- O’Neill, R.P.; Helman, U.; Hobbs, B.F.; Stewart, W.R.; Rothkopf, M.H. A Joint Energy and Transmission Rights Auction: Proposal and Properties. IEEE Trans. Power Syst. 2002, 17, 1058–1067. [Google Scholar] [CrossRef]
- Huang, D.; Deconinck, G. Coupling European Long-Term Electricity Market with Joint Energy and Transmission Right Auction—Institutional Setting, Market Mechanism and Grid Modelling Comparison between Nodal Pricing and Flow Based Zonal Pricing. In Proceedings of the 7th AIEE Energy Symposium: Current and Future Challenges to Energy Security—The Energy Crisis, the Impact on Transition Roadmap, Virtual Conference, 14–16 December 2022; Italian Association of Energy Economists (AIEE): Rome, Italy, 2022; pp. 136–168. Available online: https://www.aieesymposium.eu/wp-content/uploads/2023/01/BOOK-SYMPOSIUM_2022.pdf (accessed on 1 February 2024).
- Smeers, Y.; Study on the General Design of Electricity Market Mechanisms Close to Real Time. Creg Website. 2008. Available online: https://www.creg.be/sites/default/files/assets/Publications/Studies/F810UK.pdf (accessed on 1 February 2024).
- Oren, S.S. Point to Point and Flow-Based Financial Transmission Rights: Revenue Adequacy and Performance Incentives. In Financial Transmission Rights Analysis, Experiences and Prospects Lecture Notes in Energy; Springer: London, UK, 2012; pp. 77–94. [Google Scholar] [CrossRef]
- Hogan, W.W. Contract Networks for Electric Power Transmission. J. Regul. Econ. 1992, 4, 211–242. [Google Scholar] [CrossRef]
- Chao, H.P.; Peck, S.C. A Market Mechanism for Electric Power Transmission. J. Regul. Econ. 1996, 10, 25–59. [Google Scholar] [CrossRef]
- O’Neill, R.P.; Helman, U.; Hobbs, B.F.; Rothkopf, M.H.; Stewart, W.R. A Joint Energy and Transmission Rights Auction on a Network with Nonlinear Constraints: Design, Pricing and Revenue Adequacy. In Financial Transmission Rights Analysis, Experiences and Prospects Lecture Notes in Energy; Springer: London, UK, 2012; pp. 95–127. [Google Scholar] [CrossRef]
- De Hauteclocque, A. Long-term contracts across Member States: The problem of priority access to interconnectors. In Book Market Building through Antitrust; Edward Elgar: Cheltenham, UK, 2013. [Google Scholar] [CrossRef]
- Felten, B.; Osinski, P.; Felling, T.; Weber, C. The Flow-Based Market Coupling Domain—Why We Can’t Get It Right. Util. Policy 2021, 70, 101136. [Google Scholar] [CrossRef]
- O’Neill, R.P.; Helman, U.; Hobbs, B.F.; Baldick, R. Independent system operators in the USA: History, lessons learned, and prospects. In International Experience in Restructured Electricity Markets: What Works, What Does Not and Why? Elsevier: Amsterdam, The Netherlands, 2006; pp. 479–528. [Google Scholar]
- Glachant, J.; Ruester, S. The EU Internal Electricity Market: Done Forever? Util. Policy 2014, 31, 221–228. [Google Scholar] [CrossRef]
- Weinhold, R. Evaluating Policy Implications on the Restrictiveness of Flow-Based Market Coupling with High Shares of Intermittent Generation: A Case Study for Central Western Europe. arXiv 2021. [Google Scholar] [CrossRef]
- Alderete, G.B. FTRs and revenue adequacy. In Financial Transmission Rights Analysis, Experiences and Prospects Lecture Notes in Energy; Springer: London, UK, 2012; pp. 253–270. [Google Scholar] [CrossRef]
- Creos; TenneT; Amprion; Transnet BW; Elia; 50 Hertz; APG. Documentation of the CWE FB MC Solution. Creg Website. 2020. Available online: https://www.creg.be/sites/default/files/assets/Consult/2020/2106/PRD2106Annex1.pdf (accessed on 20 January 2023).
- Voswinkel, S.; Felten, B.; Felling, T.; Weber, C. Flow-Based Market Coupling—What Drives Welfare in Europe’s Electricity Market Design? Working Paper No. 08/2019; House of Energy Markets & Financing: Essen, Germany, 2019. [Google Scholar] [CrossRef]
- Rious, V.; Glachant, J.; Saguan, M.; Dessante, P.; Usaola, J. Assessing Available Transfer Capacity on a Realistic European Network: Impact of Assumptions on Cross-Border Exchanges and on Wind Power Generation. In Proceedings of the 1st International Scientific Conference “Building Networks for a Brighter Future”, Rotterdam, The Netherlands, 10–12 November 2008. [Google Scholar] [CrossRef]
- ACER. Annual Report on the Results of Monitoring the Internal Electricity and Natural Gas Markets in 2020 Electricity Wholesale Markets Volume. ACER Website. 2021. Available online: https://acer.europa.eu/Official_documents/Acts_of_the_Agency/Publication/ACER%20Market%20Monitoring%20Report%202020%20%E2%80%93%20Electricity%20Wholesale%20Market%20Volume.pdf (accessed on 1 February 2024).
- PSE. European Electricity Market—Diagnosis. PSE Website. 2018. Available online: https://www.pse.pl/documents/31287/20965583/PSE_Diagnosis_full_FINAL_EN.pdf (accessed on 1 February 2024).
- Case T-446/21: Action Brought on 28 July 2021—Commission de Régulation de L’énergie v ACER (OJC, C/368, 13.09.2021). CELEX. p. 32. Available online: https://eur-lex.europa.eu/LexUriServ/LexUriServ.do?uri=CELEX:62021TN0446:EN:PDF (accessed on 1 February 2024).
- Kunz, F.; Zerrahn, A. Coordinating Cross-Country Congestion Management: Evidence from Central Europe. Energy J. 2016, 37 (Suppl. 3), 81–100. [Google Scholar] [CrossRef]
- Oggioni, G.; Smeers, Y. Degrees of Coordination in Market Coupling and Counter-Trading. Energy J. 2012, 33, 39–90. [Google Scholar] [CrossRef]


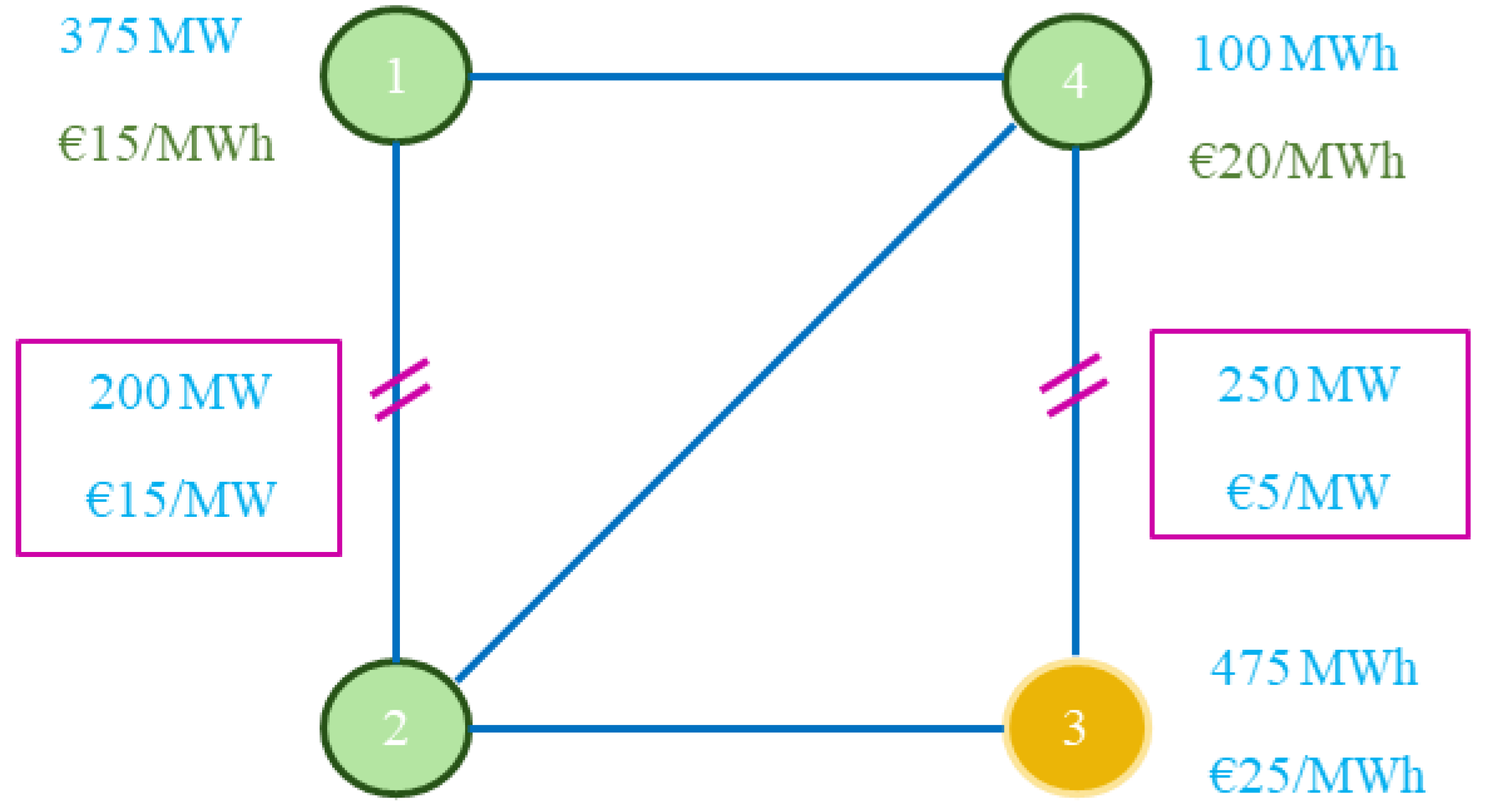
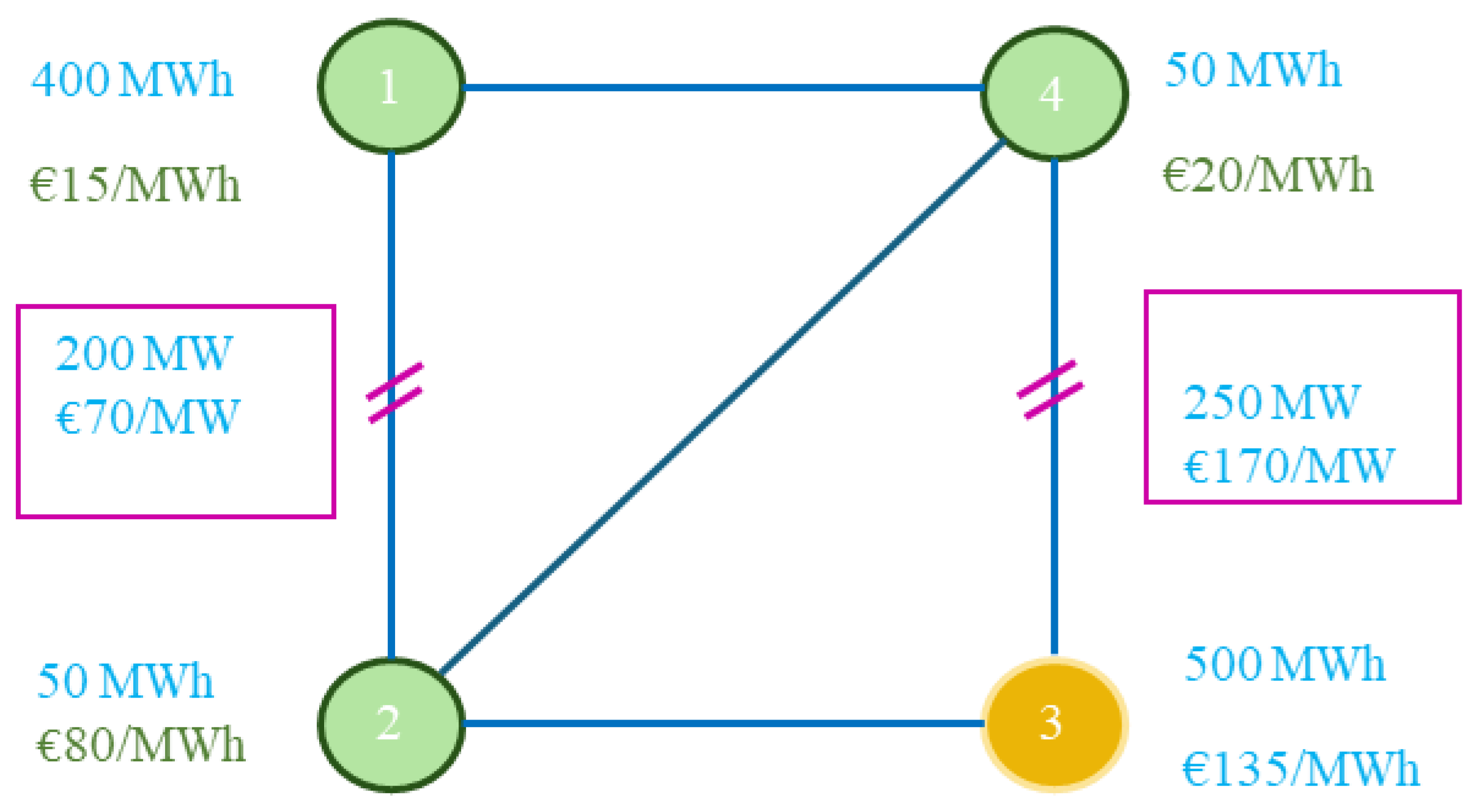



| Bid Products | Location | Price (€/MWh) | Volume Lower Boundary (MW) | Volume Higher Boundary (MW) | |
|---|---|---|---|---|---|
| Bid 1 | FTR | Injection at node 1 (zone west) and withdrawal at node 3 (zone east) | 10 | 200 | 500 |
| Bid 2 | Energy sale | Injection at node 2 | 80 | 0 | 150 |
| Bid 3 | Energy sale | Injection at node 4 | 20 | 0 | 300 |
| Bid 4 | PTR | Interconnection between node 1 and node 2 | 10 | 0 | 150 |
| Bid 5 | Energy purchase | Withdrawal at node 3 | 25 | 0 | 300 |
| Time Step | Real-World Process for TSOs and Power Exchange | Computation Process |
|---|---|---|
| Before the long-term auction |
|
|
| On the day of the long-term auction |
|
|
| D-2 |
|
|
| D-1 |
|
|
| D |
|
|
| Capacity (MW) | Bid 1 | Bid 2 | Bid 3 | Bid 4 | Bid 5 | Shadow Price (€/MW) | |
|---|---|---|---|---|---|---|---|
| Line 1–2 | 200 | 0.5 | −0.125 | 0.125 | 1 | 0 | 15 |
| Line 2–1 | 200 | −0.5 | 0.125 | −0.125 | −1 | 0 | 0 |
| Line 1–4 | 400 | 0.5 | 0.125 | −0.125 | 0 | 0 | 0 |
| Line 4–1 | 400 | −0.5 | −0.125 | 0.125 | 0 | 0 | 0 |
| Line 2–3 | 400 | 0.5 | 0.625 | 0.375 | 0 | 0 | 0 |
| Line 3–2 | 400 | −0.5 | −0.625 | −0.375 | 0 | 0 | 0 |
| Line 2–4 | 400 | 0 | 0.25 | −0.25 | 0 | 0 | 0 |
| Line 4–2 | 400 | 0 | −0.25 | 0.25 | 0 | 0 | 0 |
| Line 3–4 | 250 | −0.5 | −0.375 | −0.625 | 0 | 0 | 0 |
| Line 4–3 | 250 | 0.5 | 0.375 | 0.625 | 0 | 0 | 5 |
| Bidder 1 | Bidder 2 | Bidder 3 | Bidder 4 | Bidder 5 | |
|---|---|---|---|---|---|
| Type | Financial Transmission Rights | Energy Sale | Energy Sale | Physical Transmission Rights | Energy Purchase |
| Upper bound (MW) | 500 | 150 | 300 | 100 | 300 |
| Lower bound (MW) | 200 | 0 | 0 | 0 | 0 |
| Bid price (€/MWh) | 10 | 80 | 20 | 10 | 25 |
| Result quantity (MWh) | 375 | 0 | 100 | 0 | 100 |
| Result price (€/MW) | 10 | 0 | 20 | 0 | 25 |
| Payment to SO (€) | 3750 | 0 | −2000 | 0 | 2500 |
| Bidder 1 | Bidder 2 | Bidder 3 | Bidder 4 | Bidder 5 | |
|---|---|---|---|---|---|
| Type | Financial Transmission Rights | Energy Sale | Energy Sale | Physical Transmission Rights | Energy Purchase |
| Quantity (MW) | 375 | 0 | 100 | 0 | 100 |
| Price (€/MW) | 120 | 0 | 20 | 0 | 135 |
| Payment to SO (€) | 45,000 | 0 | −2000 | 0 | 13,500 |
| Capacity Limit (MW) | PTDF Bid 1 | PTDF Bid 2 | PTDF Bid 3 | PTDF Bid 4 | PTDF Bid 5 | |
|---|---|---|---|---|---|---|
| Line 1–2 | 122.5 | 0.5625 | 0 | 0 | 1 | 0 |
| Line 2–1 | 197.5 | −0.5625 | 0 | 0 | 0 | 0 |
| Line 1–4 | 400 | 0.4375 | 0 | 0 | 0 | 0 |
| Line 4–1 | 400 | −0.4375 | 0 | 0 | 0 | 0 |
| Bidder 1 | Bidder 2 | Bidder 3 | Bidder 4 | Bidder 5 | |
|---|---|---|---|---|---|
| Type | Financial Transmission Rights | Energy Sale | Energy Sale | Physical Transmission Rights | Energy Purchase |
| Upper bound (MW) | 500 | 150 | 300 | 100 | 300 |
| Lower bound (MW) | 200 | 0 | 0 | 0 | 0 |
| Bid price (€/MW) | 10 | 35 | 20 | 10 | 25 |
| Quantity | 217.77 | 0 | 300 | 0 | 300 |
| Price (€/MW) | 10 | 0 | 25 | 0 | 25 |
| Payment to SO (€) | 2178 | 0 | −7500 | 0 | 7500 |
| Capacity (MW) | PTDF Bid 1 | PTDF Bid 2 | PTDF Bid 3 | PTDF Bid 5 | Shadow Price (€/MW) | |
|---|---|---|---|---|---|---|
| Line 1–2 | 158.75 | 0.55 | 0 | 0 | 0 | 9.09 |
| Line 2–1 | 221.25 | −0.55 | 0 | 0 | 0 | 0 |
| Line 1–4 | 400 | 0.45 | 0 | 0 | 0 | 0 |
| Line 4–1 | 400 | −0.45 | 0 | 0 | 0 | 0 |
| Type | Generation | Generation | Generation | Load |
|---|---|---|---|---|
| Zone | Zone West | Zone East | Zone East | Zone East |
| Quantity (MW) | 288.6 | 0 | 211.4 | 500 |
| Price (€/MW) | 15 | 0 | 20 | 20 |
| Payment to SO (€) | 4329 | 0 | 4228 | 10,000 |
| Bidder 1 | Bidder 2 | Bidder 3 | Bidder 4 | Bidder 5 | |
|---|---|---|---|---|---|
| Type | Financial Transmission Rights | Energy Sale | Energy Sale | Physical Transmission Rights | Energy Purchase |
| Quantity (MW) | 217.8 | 0 | 300 | 0 | 300 |
| Price (€/MW) | 5 | 0 | 20 | 0 | 20 |
| Payment to SO (€) | 1089 | 0 | 6000 | 0 | 6000 |
| Generator 2 | Generator 4 | |
|---|---|---|
| Redispatch type | + (Generation increase) | − (Generation decrease) |
| Volume (MW) | 105.6 | 105.6 |
| Net payment from SO to generator (€) | 8448 | 0 |
| Generator 1 | Generator 2 | Generator 4 | |
|---|---|---|---|
| Redispatch type | + (Generation increase) | + (Generation increase) | − (Generation decrease) |
| Volume (MW) | 111.4 | 50 | 161.4 |
| Net payment from SO to generator (€) | 1671 | 4000 | 0 |
| Nodal Pricing (€) | Under National Redispatch (€) | Under Cross-Border Redispatch (€) |
|---|---|---|
| 15,250 | 21,037 | 18,260 |
| Optimal GDSK in Zone East among Nodes 2, 3, and 4 | Ex-Ante GDSK in Zone East among Nodes 2, 3, and 4 | Euclidean Distance between the Ex-Ante and Optimal Values | Realized GDSK in Zone East among Nodes 2, 3, and 4 | |
|---|---|---|---|---|
| Long-term auction | (0, 0.47, 0.53) | (0.5, 0.5, 0) | 0.729 | (0, 1, 0) |
| Day-ahead/Real-time market | (−0.125, 0.625, 0.5) | (0.4, 0.6, 0) | 0.725 | (0, 0.866, 0.134) |
| Ex-Post GDSK | Optimal GDSK for Day-Ahead Market | Euclidean Distance | |
|---|---|---|---|
| National redispatch | (−0.366, 0.866, 0.5) | (−0.125, 0.625, 0.5) | 0.34 |
| Cross-border redispatch | (−0.125, 0.625, 0.5) | (−0.125, 0.625, 0.5) | 0 |
| Cross-Border FTR Nodal Pricing (MWh) | Cross-Border Trade Zonal Pricing (MWh) | Potential Optimal Interzonal Transaction Zonal Pricing (MWh) | Interconnection Utilization Rate under Zonal Pricing (%) | |
|---|---|---|---|---|
| Long-term auction | 375 | 217.8 | 282.3 | 73.2 |
| Day-ahead/real-time market | 400 | 288.6 | 378 | 85.4 |
| SO Surplus from Generation Load Payment in Day-Ahead Market (€) | SO Payment to Long-Term Right Holders (€) | SO Balance after Day-Ahead Market (€) | National-Based Redispatch Costs (€) | Cross-Border Redispatch Costs (€) |
|---|---|---|---|---|
| 1443 | 1089 | 354 | 8448 | 5671 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, D.; Deconinck, G. Breaking Borders with Joint Energy and Transmission Right Auctions—Assessing the Required Changes for Empowering Long-Term Markets in Europe. Energies 2024, 17, 1923. https://doi.org/10.3390/en17081923
Huang D, Deconinck G. Breaking Borders with Joint Energy and Transmission Right Auctions—Assessing the Required Changes for Empowering Long-Term Markets in Europe. Energies. 2024; 17(8):1923. https://doi.org/10.3390/en17081923
Chicago/Turabian StyleHuang, Diyun, and Geert Deconinck. 2024. "Breaking Borders with Joint Energy and Transmission Right Auctions—Assessing the Required Changes for Empowering Long-Term Markets in Europe" Energies 17, no. 8: 1923. https://doi.org/10.3390/en17081923
APA StyleHuang, D., & Deconinck, G. (2024). Breaking Borders with Joint Energy and Transmission Right Auctions—Assessing the Required Changes for Empowering Long-Term Markets in Europe. Energies, 17(8), 1923. https://doi.org/10.3390/en17081923







