Influence of a Built-in Finned Trombe Wall on the Indoor Thermal Environment in Cold Regions
Abstract
1. Introduction
- (1)
- A three-dimensional numerical model of a coupled fin-type Trombe wall and a room under steady-state conditions was established;
- (2)
- By adding fins to the HAS, the air generates vortices and secondary flow during the flow process, which causes damage to the boundary layer, thereby exchanging the momentum and energy between the mainstream region and the boundary layer region, facilitating the enhancement of convective heat transfer;
- (3)
- Combined with floor heating, the influence of changing fin parameters on TW heat transfer and the indoor thermal environment under the combined action of solar radiation intensity and indoor floor heating is studied.
2. Numerical Approach
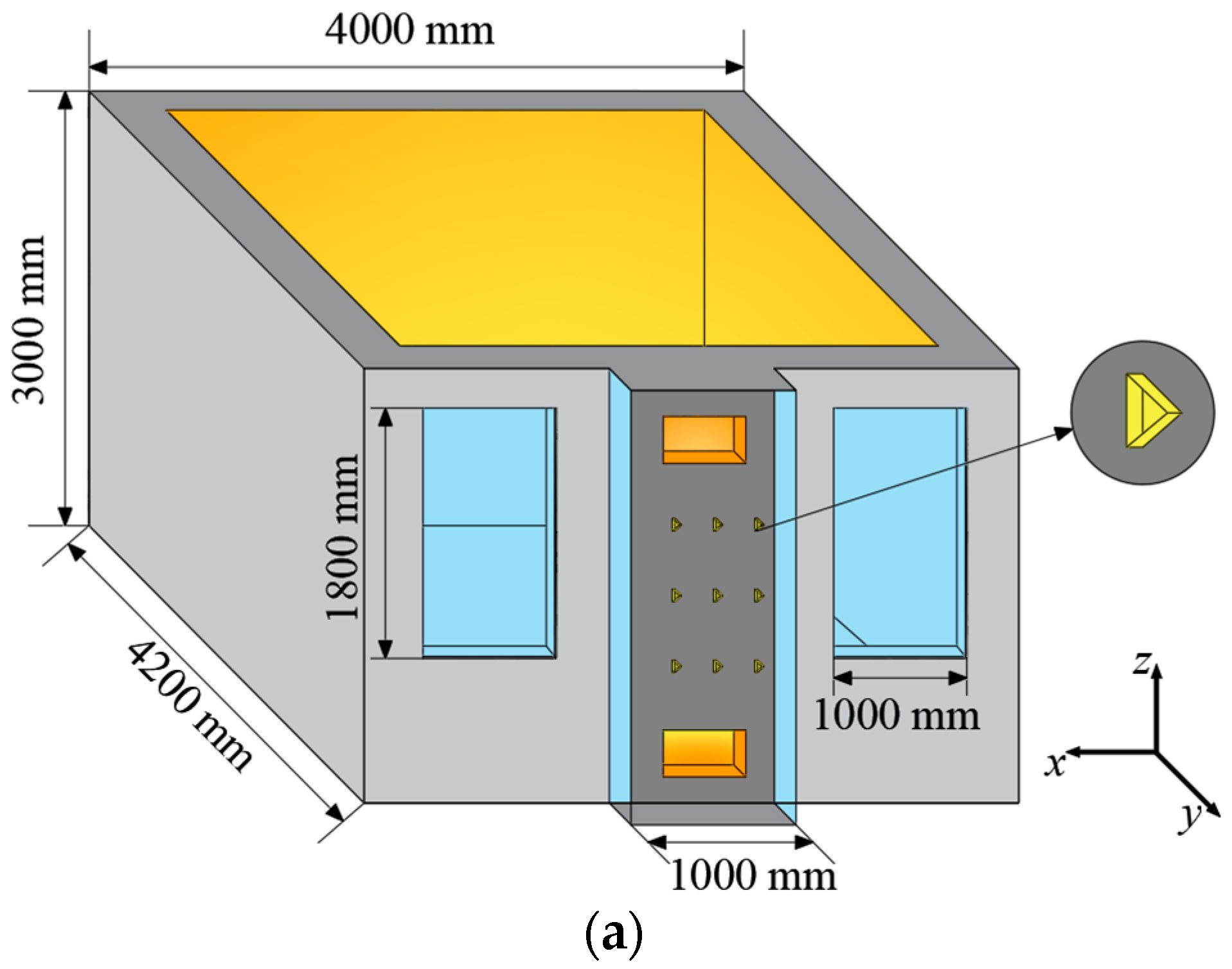
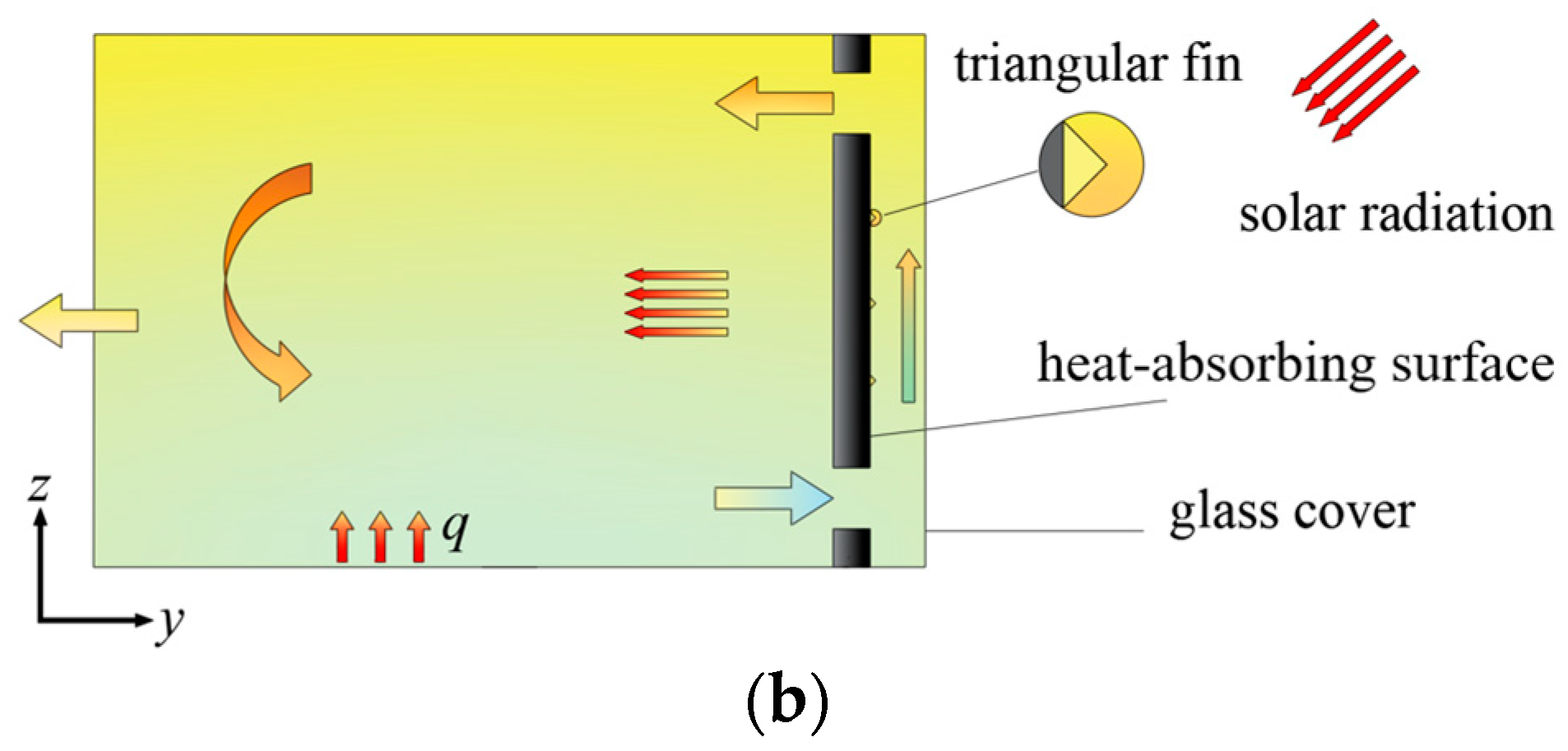
2.1. Physical Model
2.2. Mathematical Model
2.3. Related Assumptions and Boundary Conditions
2.3.1. Relevant Assumptions
- (1)
- Air is an incompressible fluid with constant fluid properties;
- (2)
- Air density corresponds to the Boussinesq hypothesis, and it is assumed to be a radiation-transparent medium, which does not engage in radiation heat transfer;
- (3)
- Each surface is a diffuse gray surface;
- (4)
- Heat transfer between the room and the upper room is ignored;
- (5)
- The glass cover’s heat transfer along the thickness direction is ignored.
2.3.2. Boundary Conditions
3. The Validation of the Numerical Approach
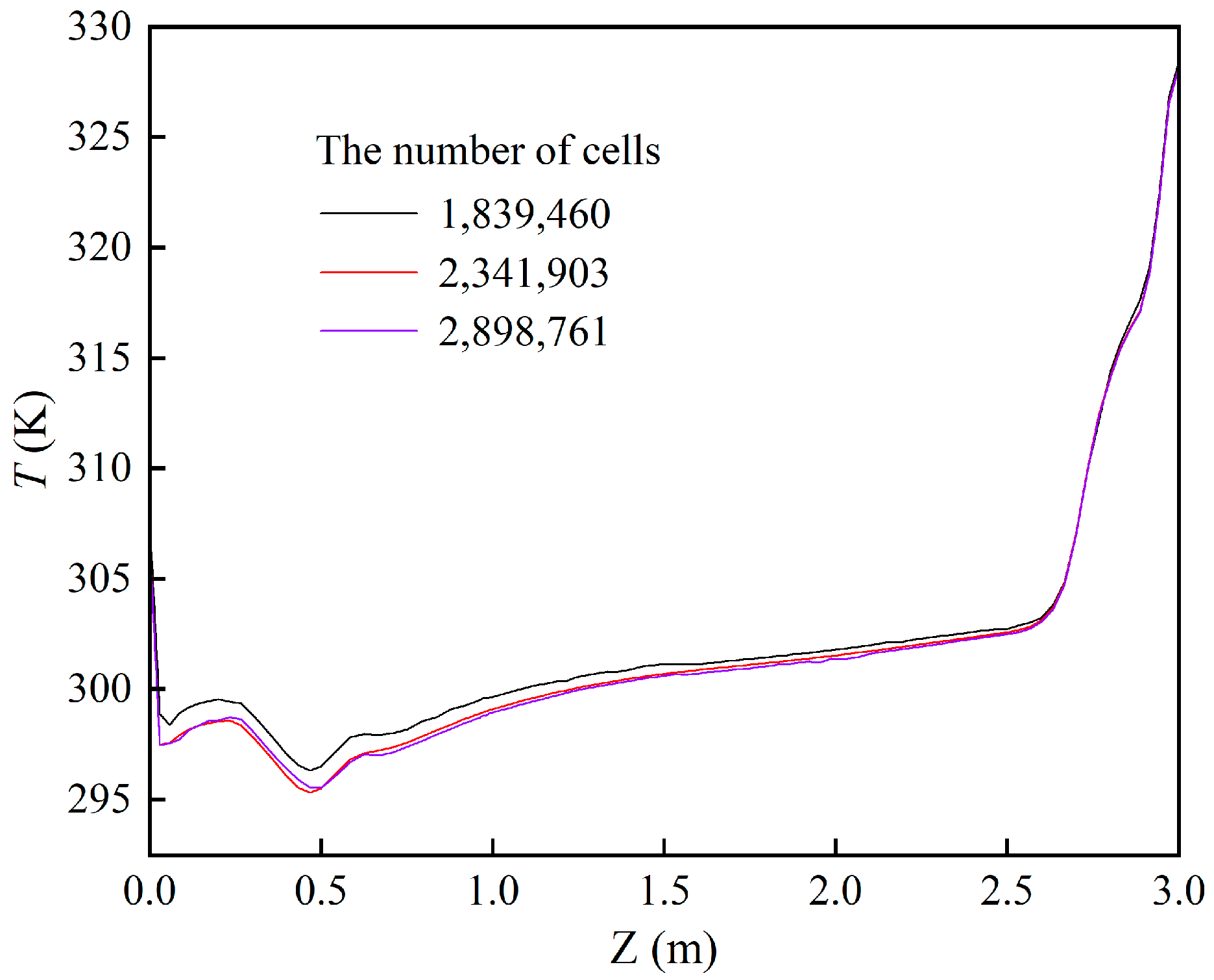
3.1. The Test for Grid Independence
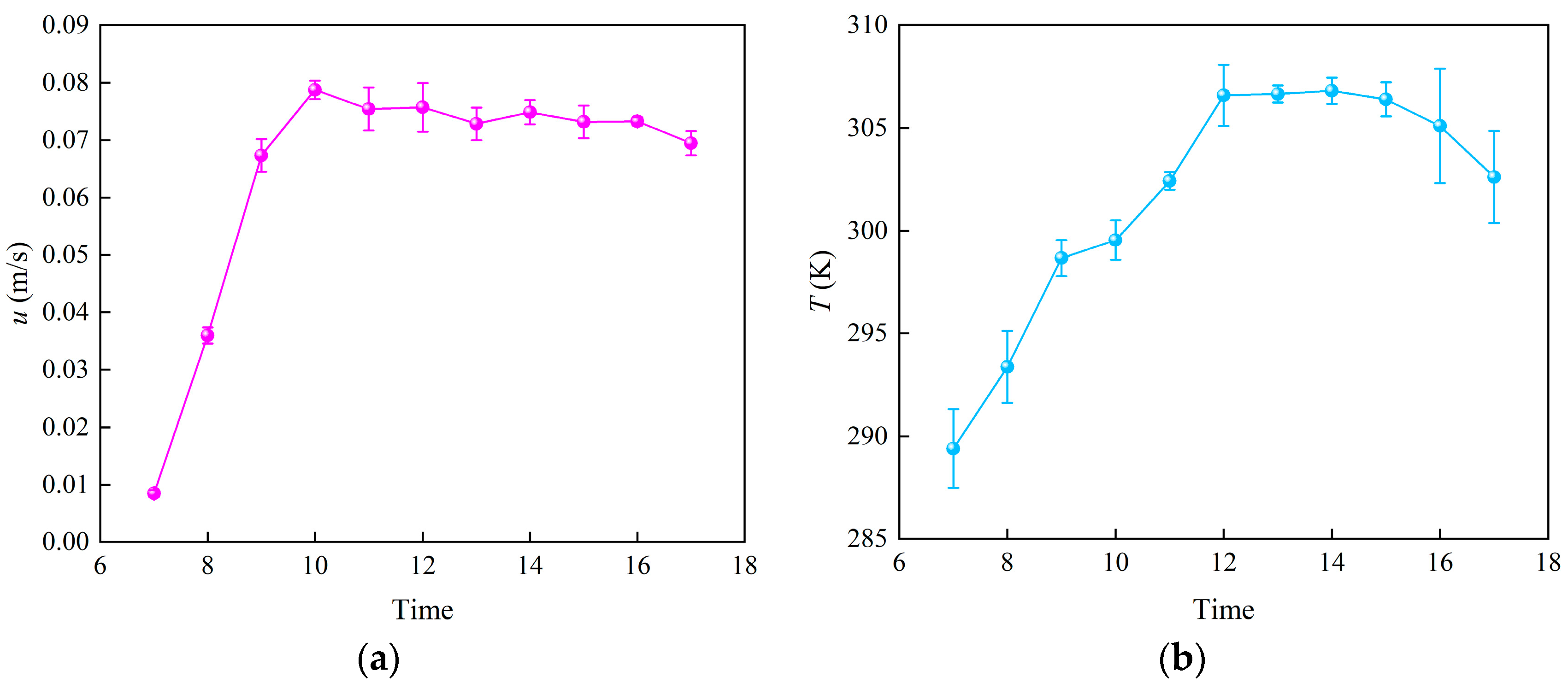
3.2. The Validation of the Model
4. Results and Discussion
4.1. Investigating the Fin Parameters’ Impact on the TW’s Thermal Performance
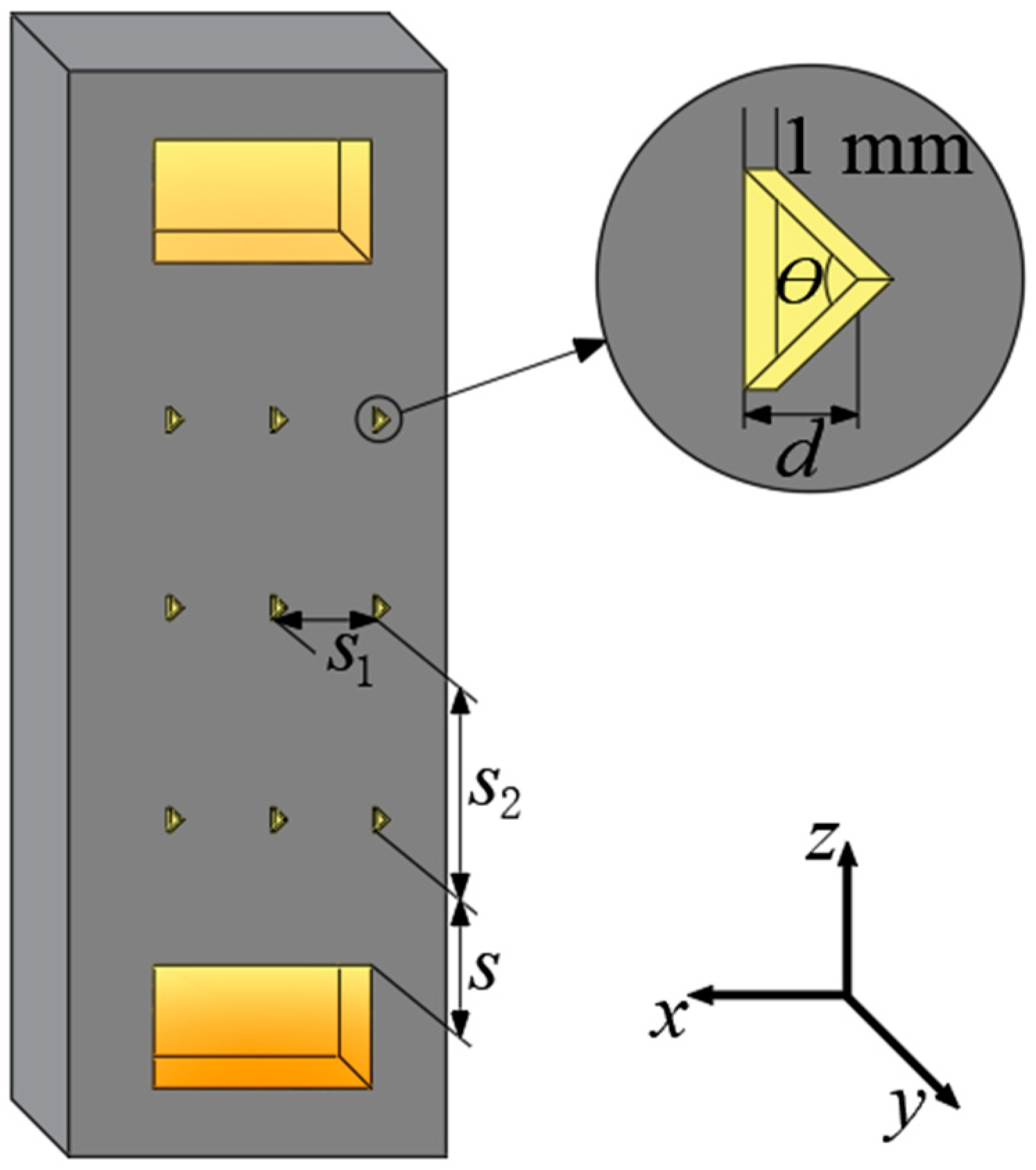
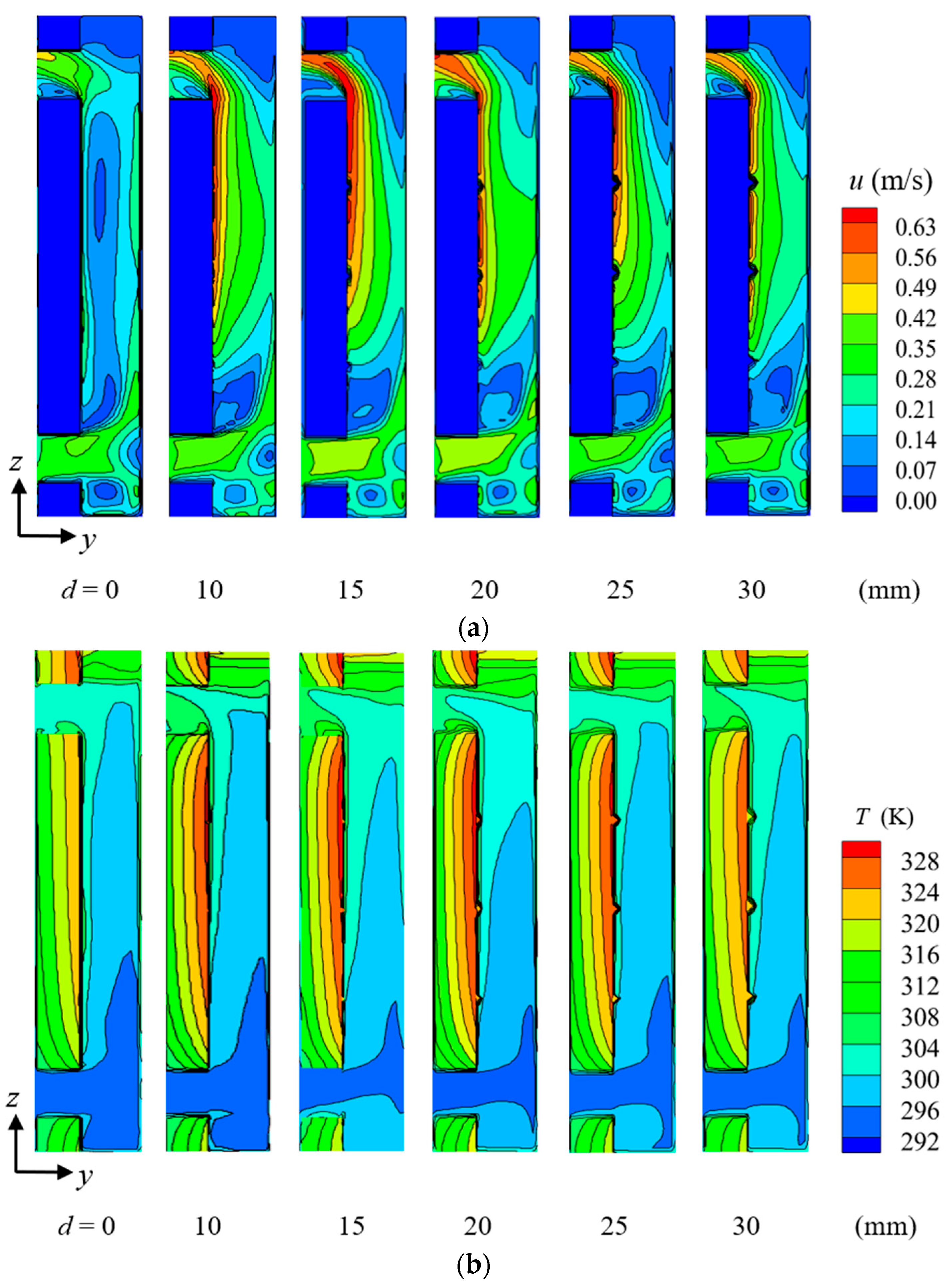
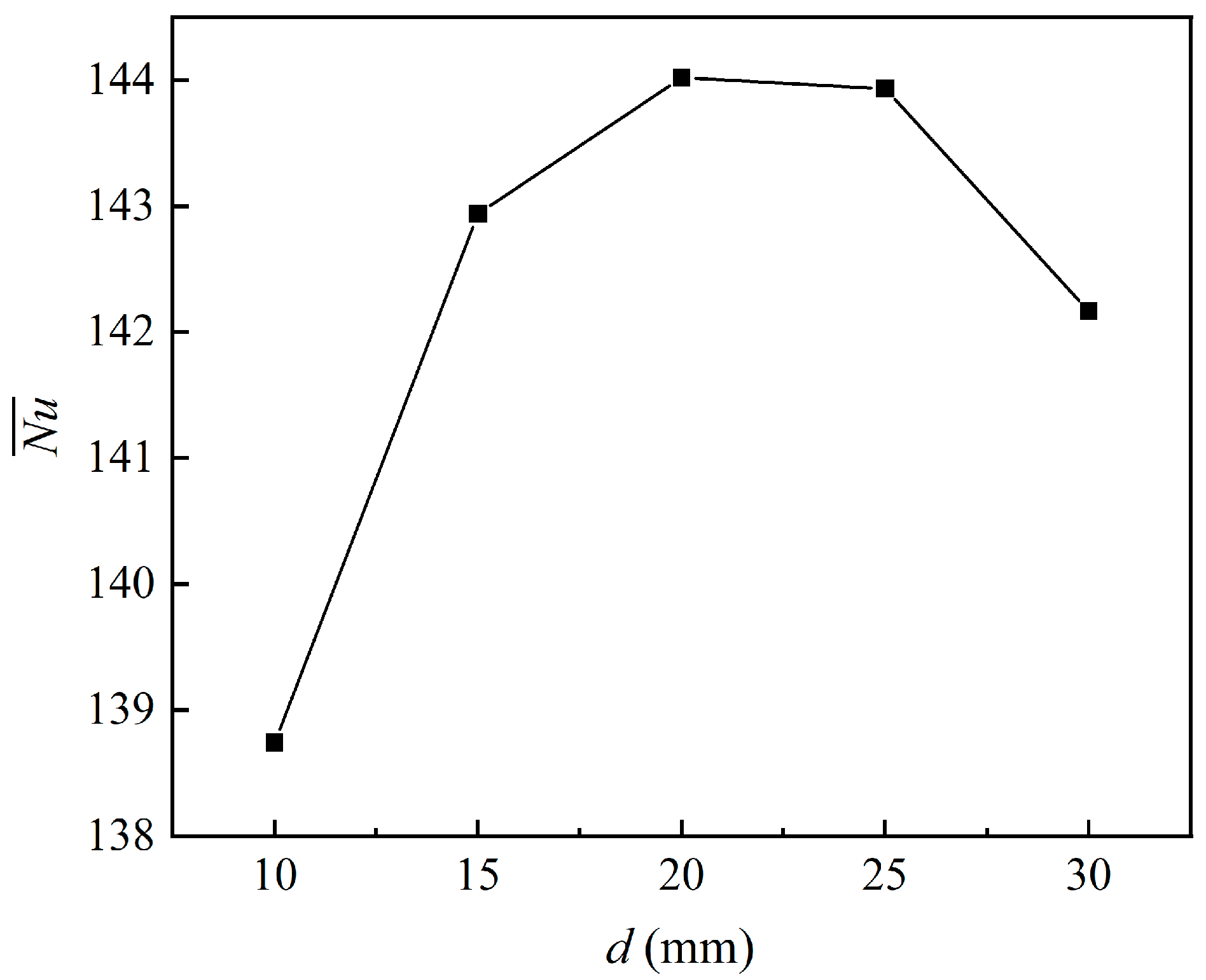
4.1.1. The Height of the Fin
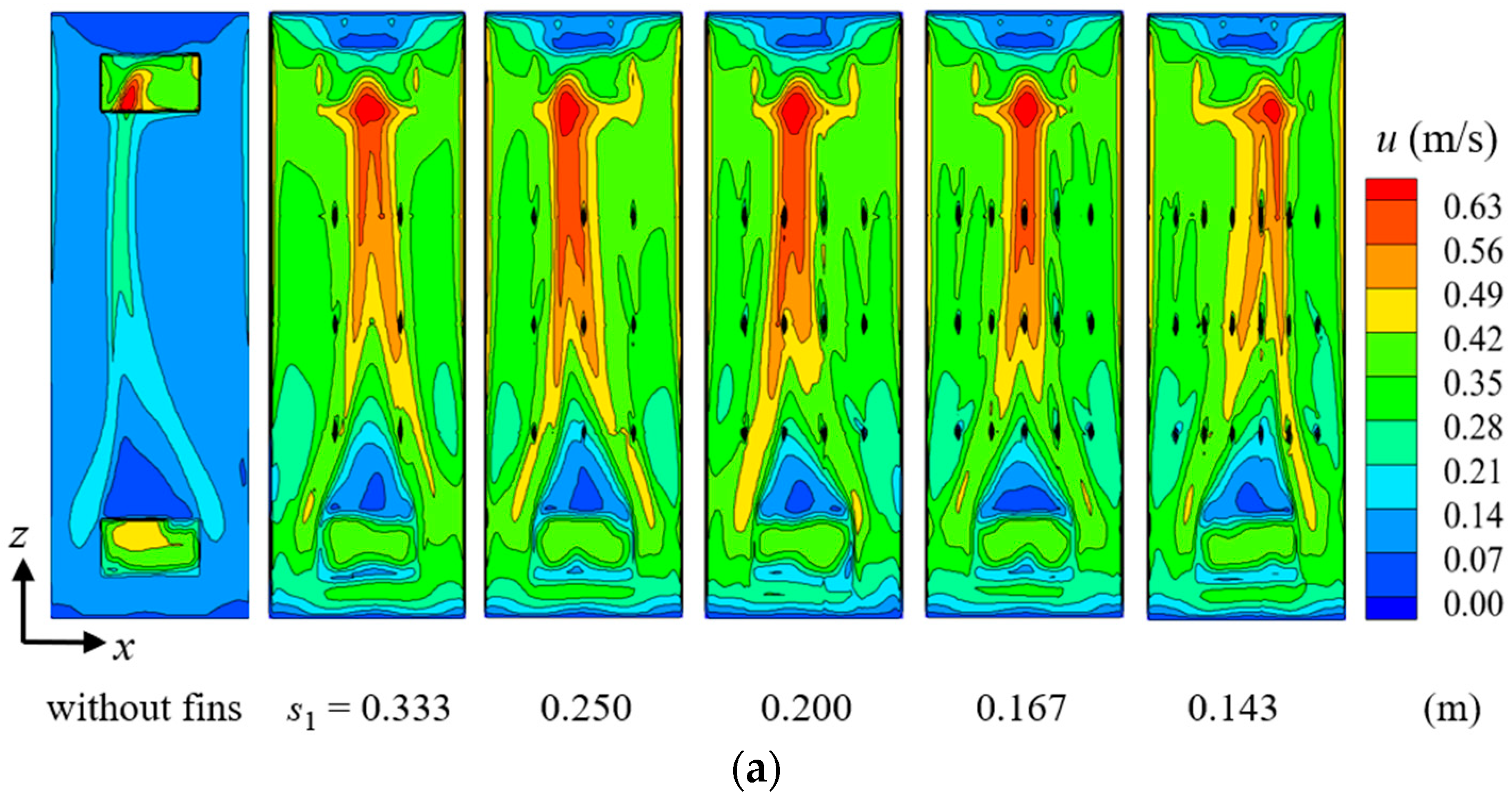
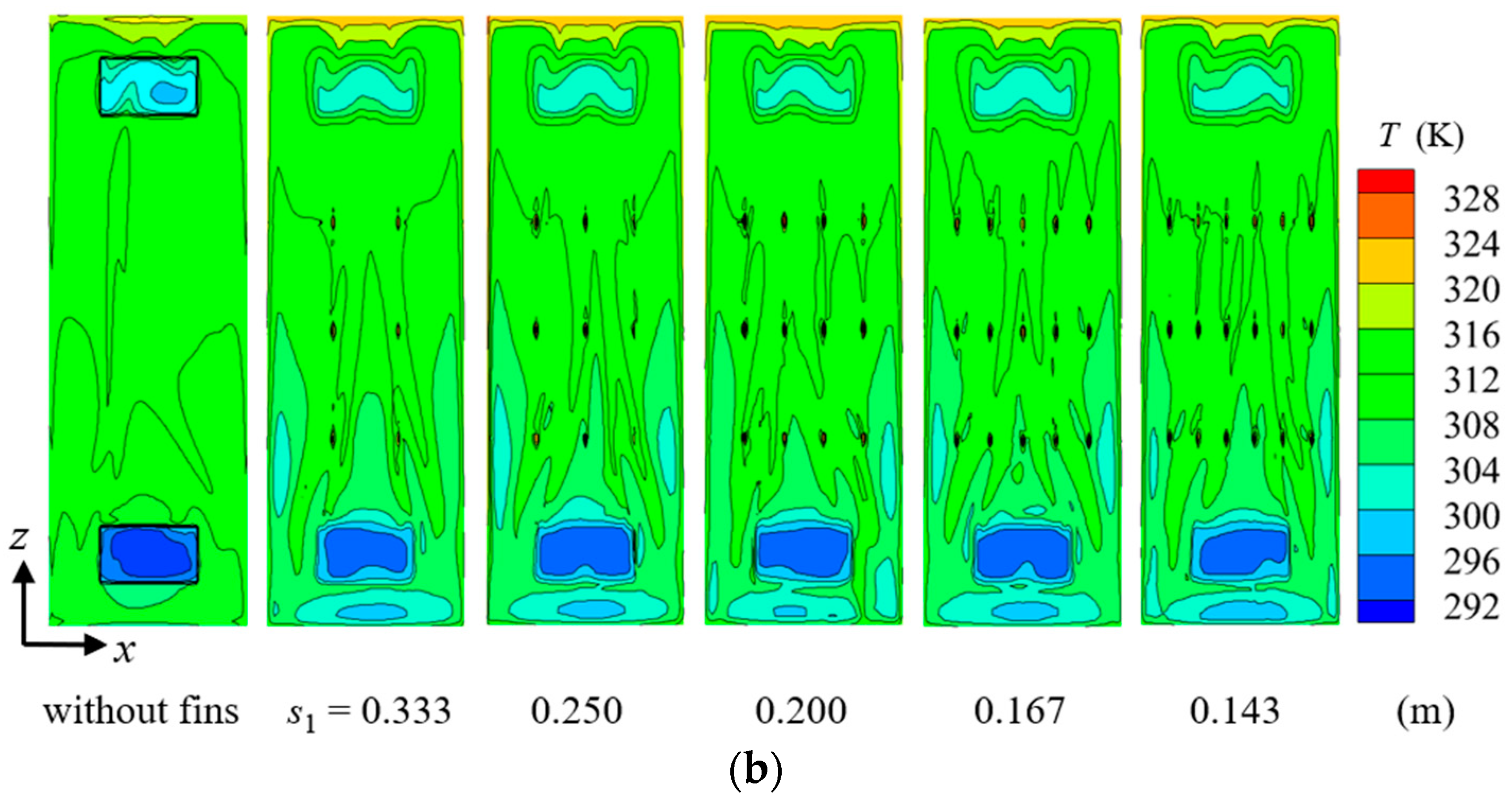
4.1.2. Fin Transverse Spacing
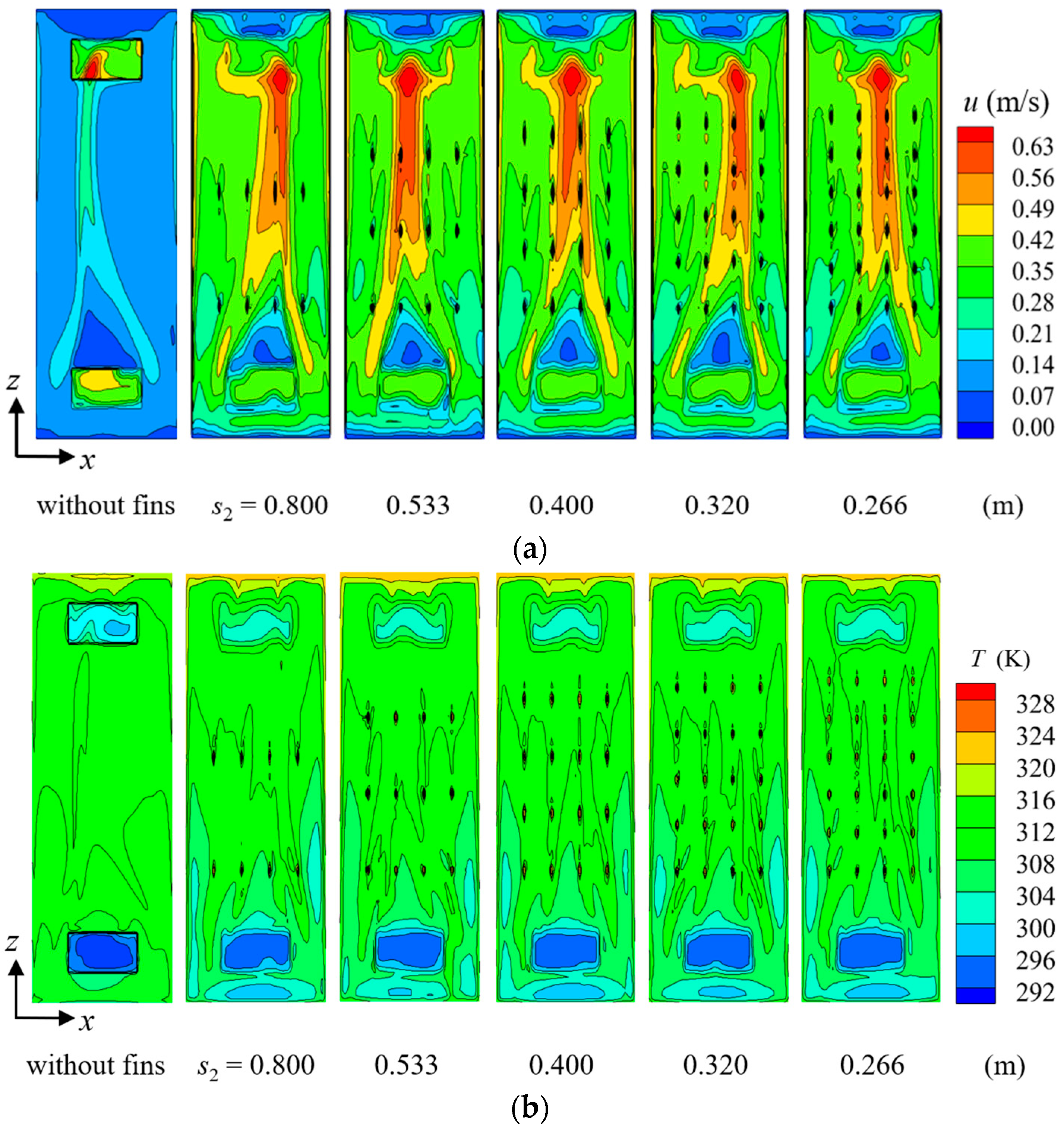
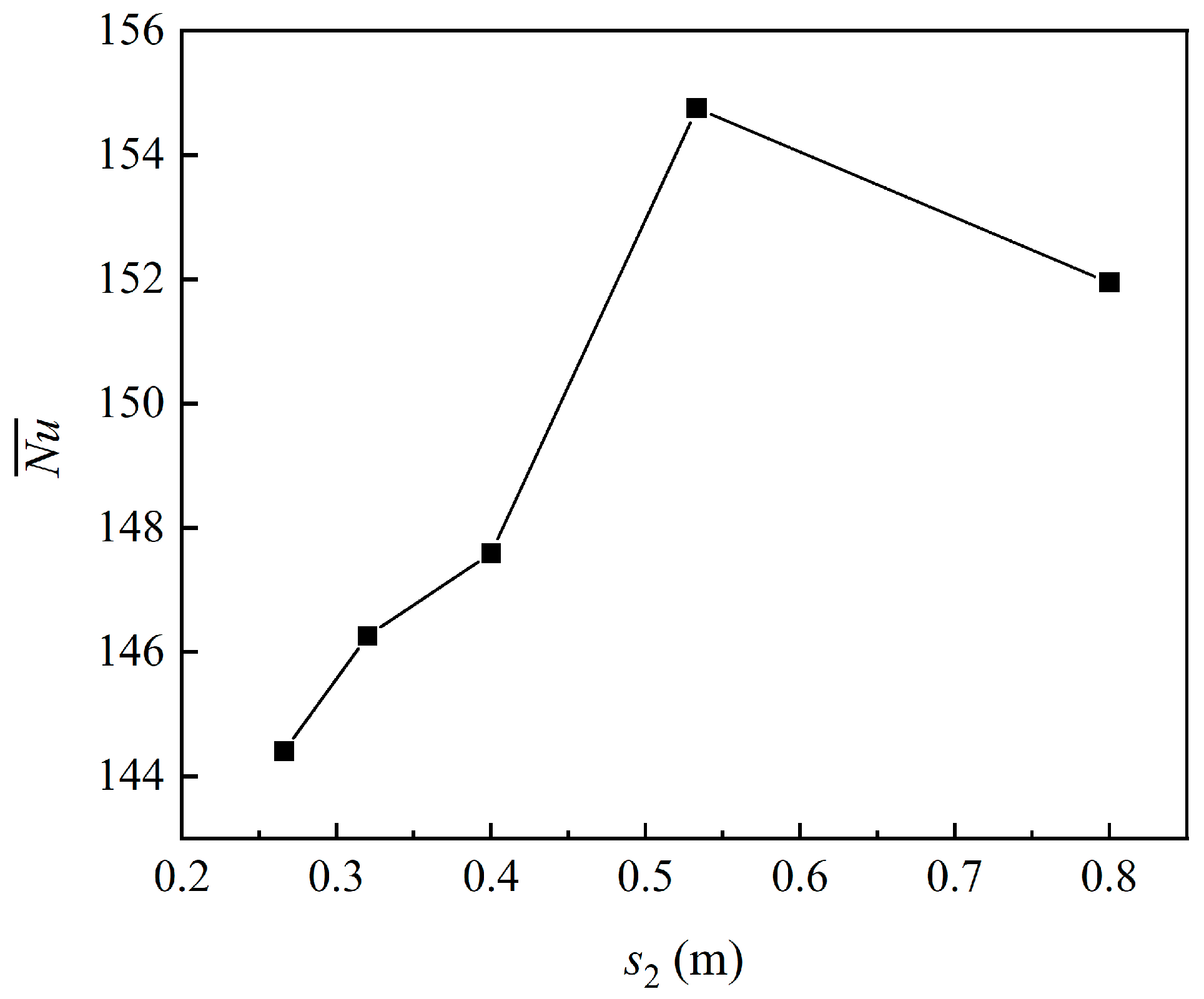
4.1.3. Longitudinal Spacing of Fins
4.1.4. Fin Arrangement
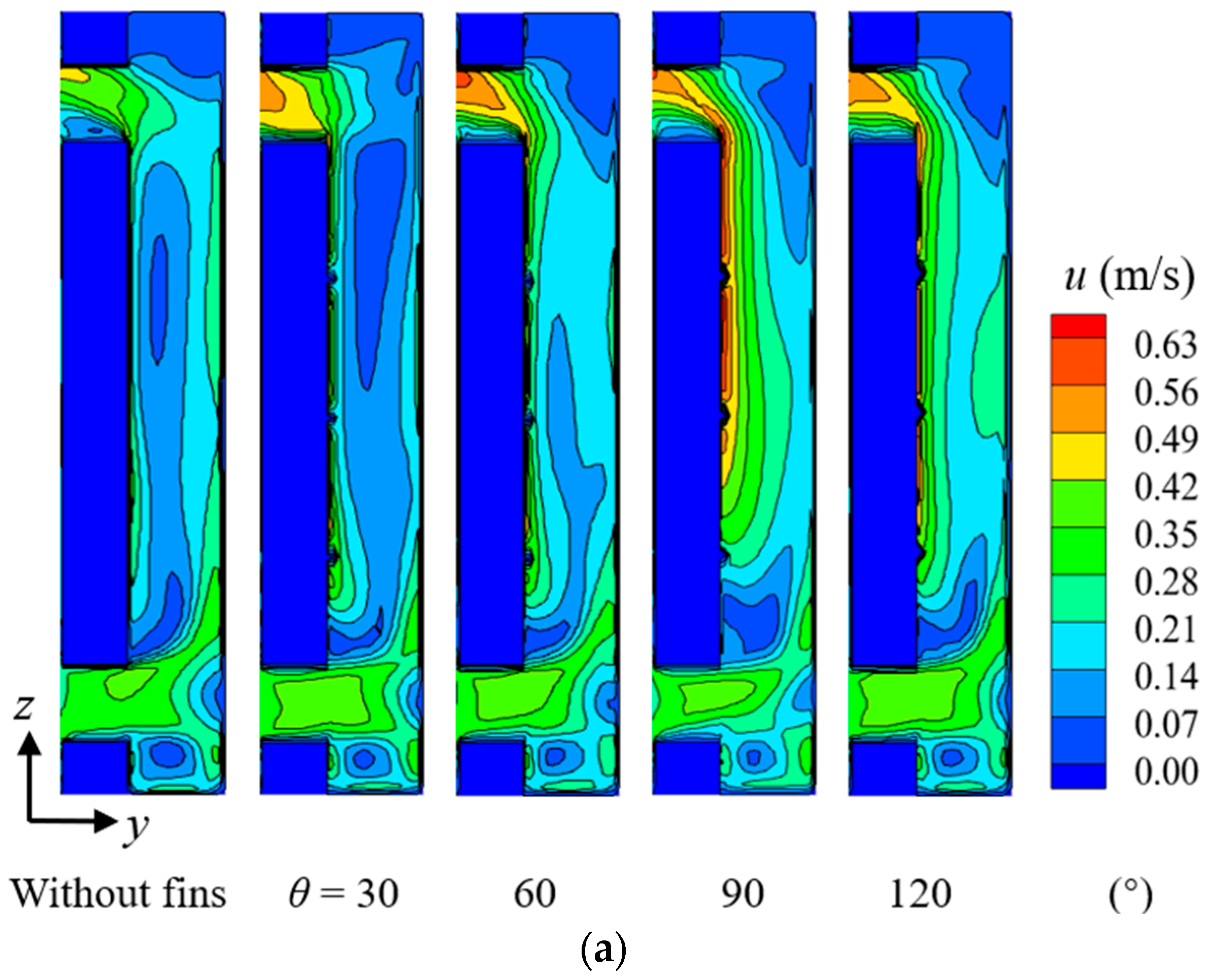
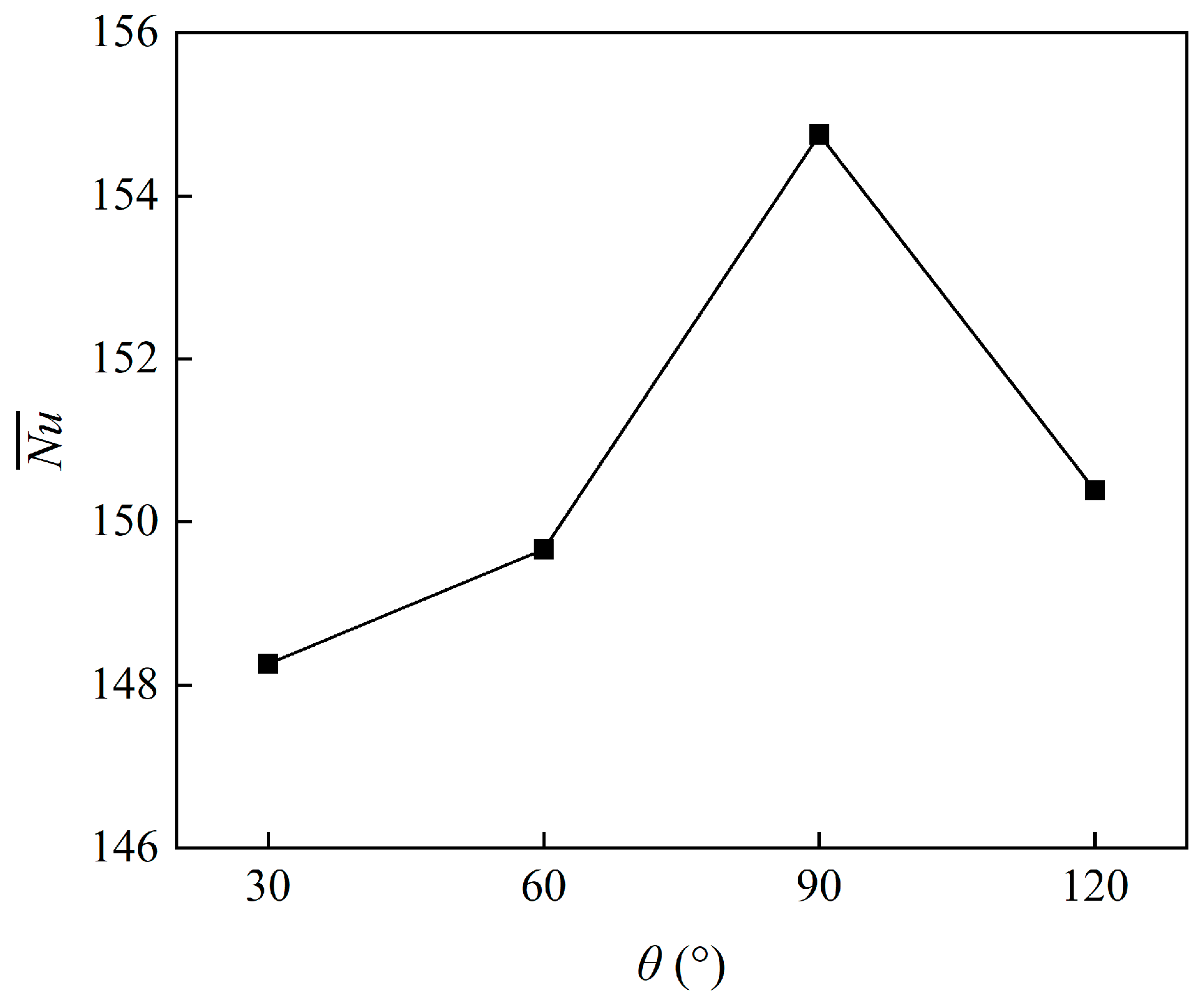
4.1.5. Different Types of Isosceles Triangle Fins
4.2. Thermal Environment Analysis of Fin-Type-Trombe-Wall-Containing Room
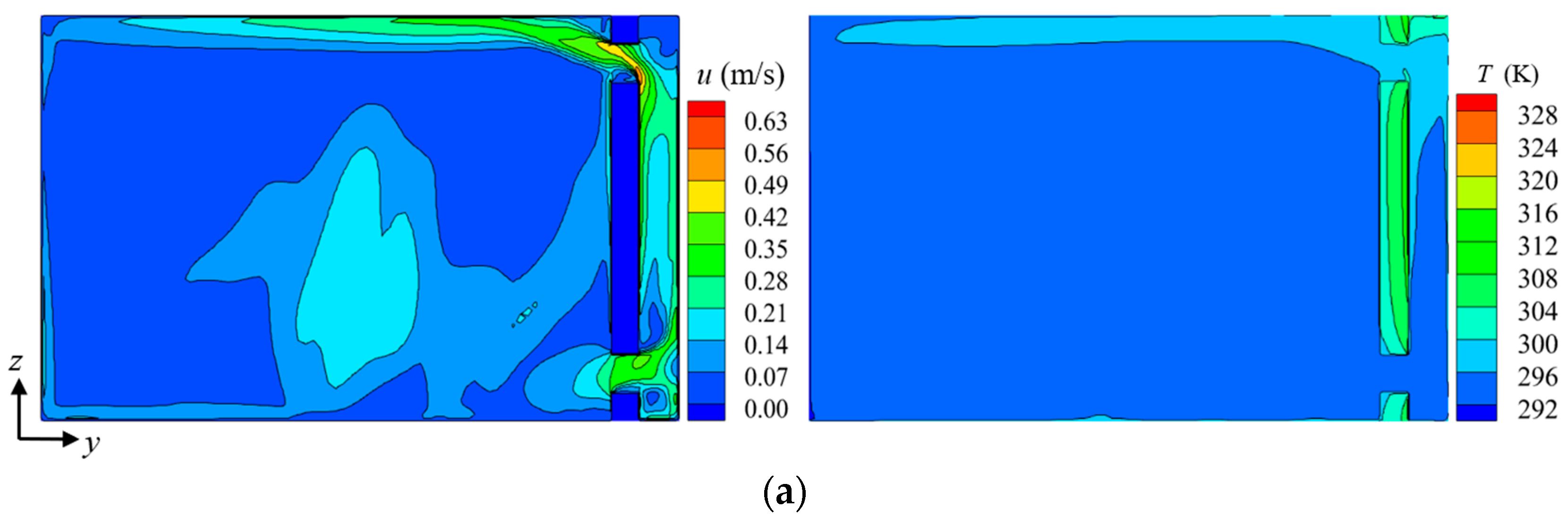
4.2.1. Thermal Performance Analysis
4.2.2. Thermal Comfort Analysis
4.2.3. Energy-Saving Effect Analysis
5. Conclusions
- (1)
- This study found that the optimal height of the fins is d = 20 mm, the lateral spacing is s1 = 0.200 m, the longitudinal spacing is s2 = 0.533 m, and the arrangement in line has the greatest impact on the heat transfer performance of the TW, and this effect is optimal. Under these conditions, the HAS reaches its maximum, which is 9.42% higher than that of the finless TW, and the convective heat transfer efficiency is increased by 7.70%.
- (2)
- Based on the simulation calculation of the above parameters, in order to study the influence of different shapes of isosceles triangle fins on the heat transfer performance of a TW, four working conditions with vertex angles of θ = 30°, 60°, 90°, and 120° were selected. It was found that when the HAS was modified with isosceles triangle fins with a vertex angle of 90°, the TW could obtain greater heat transfer capacity. The values of other triangular fin HASs with different vertex angles were 150.39, 148.26, and 148.46, respectively, while the of isosceles triangular fin HAS with vertex angle of 90° was 154.75.
- (3)
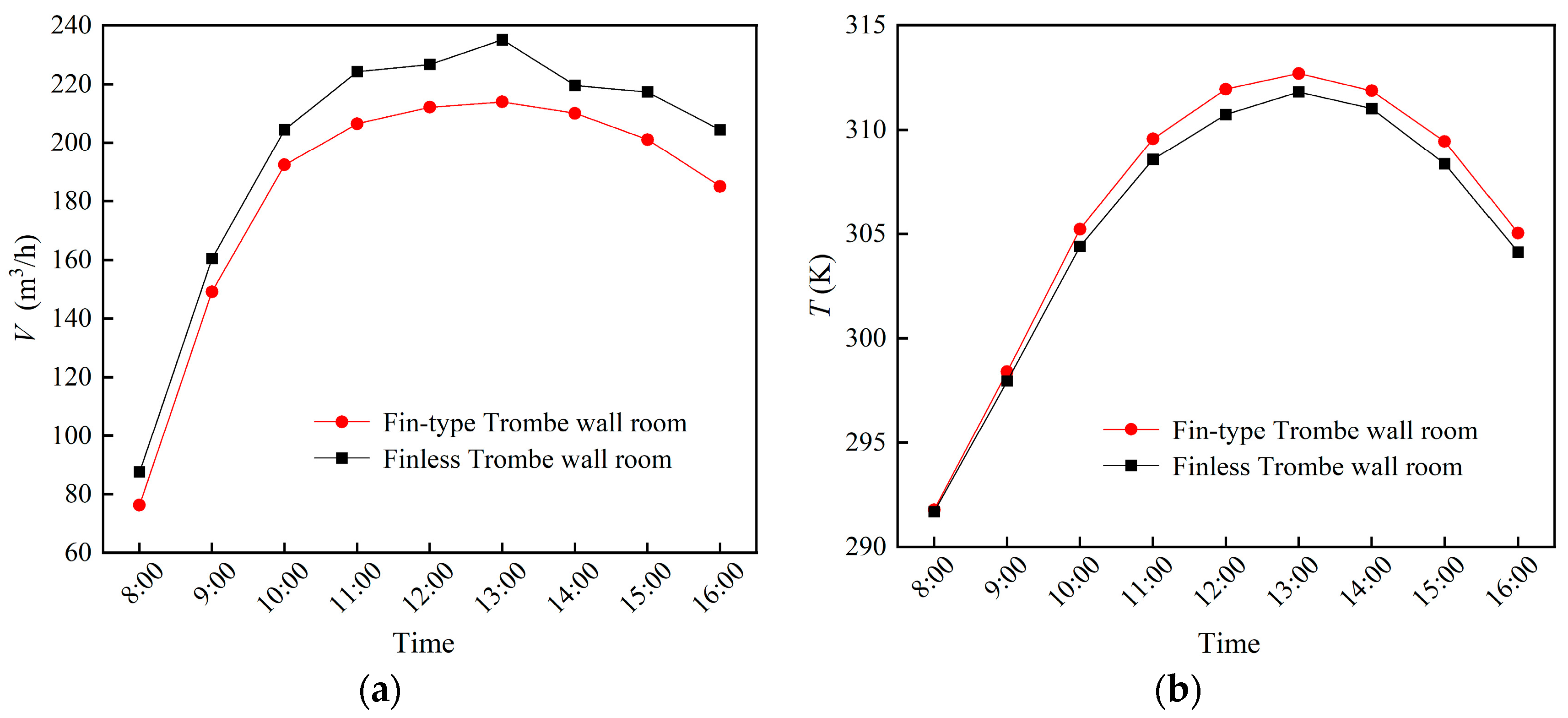
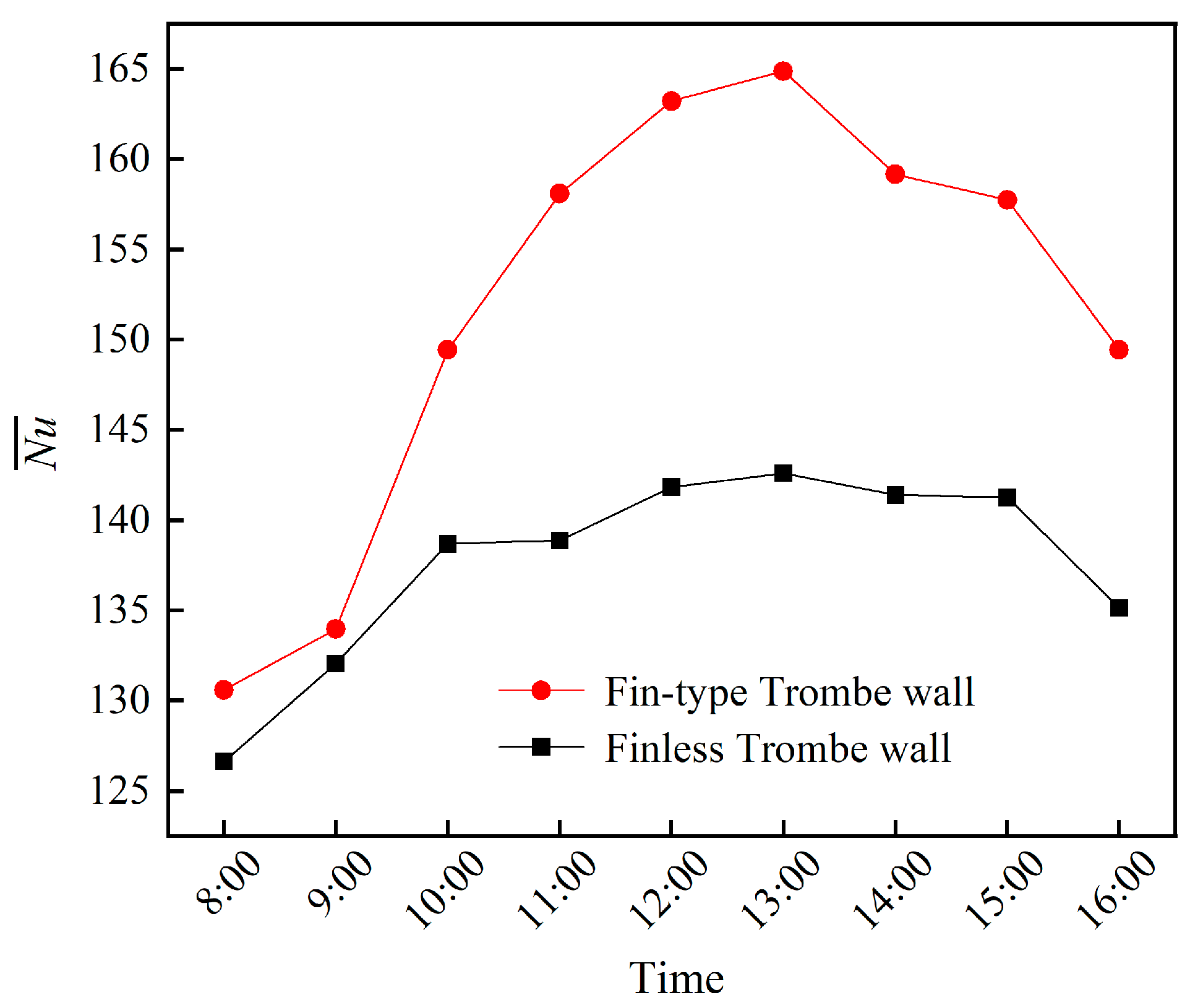
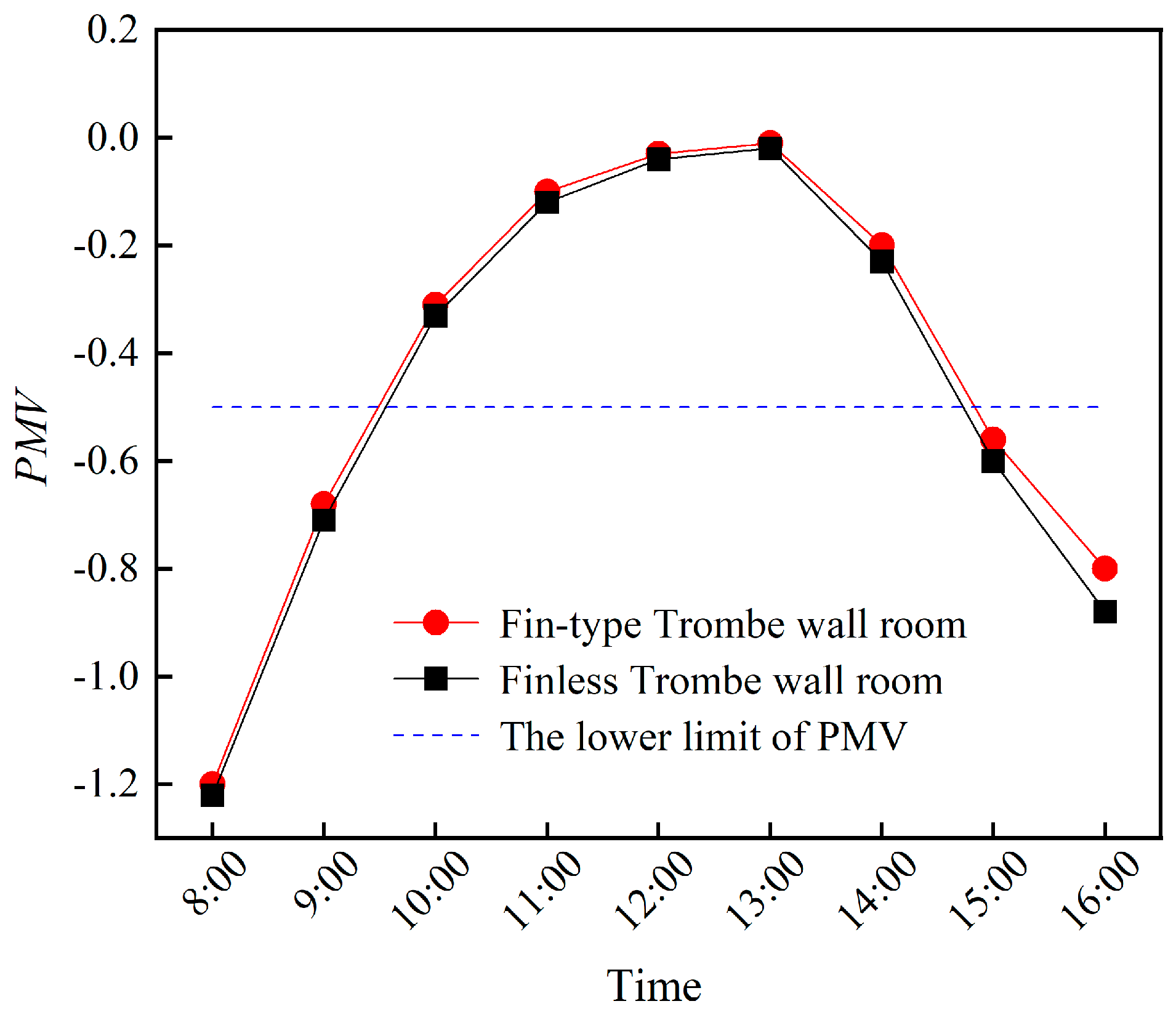
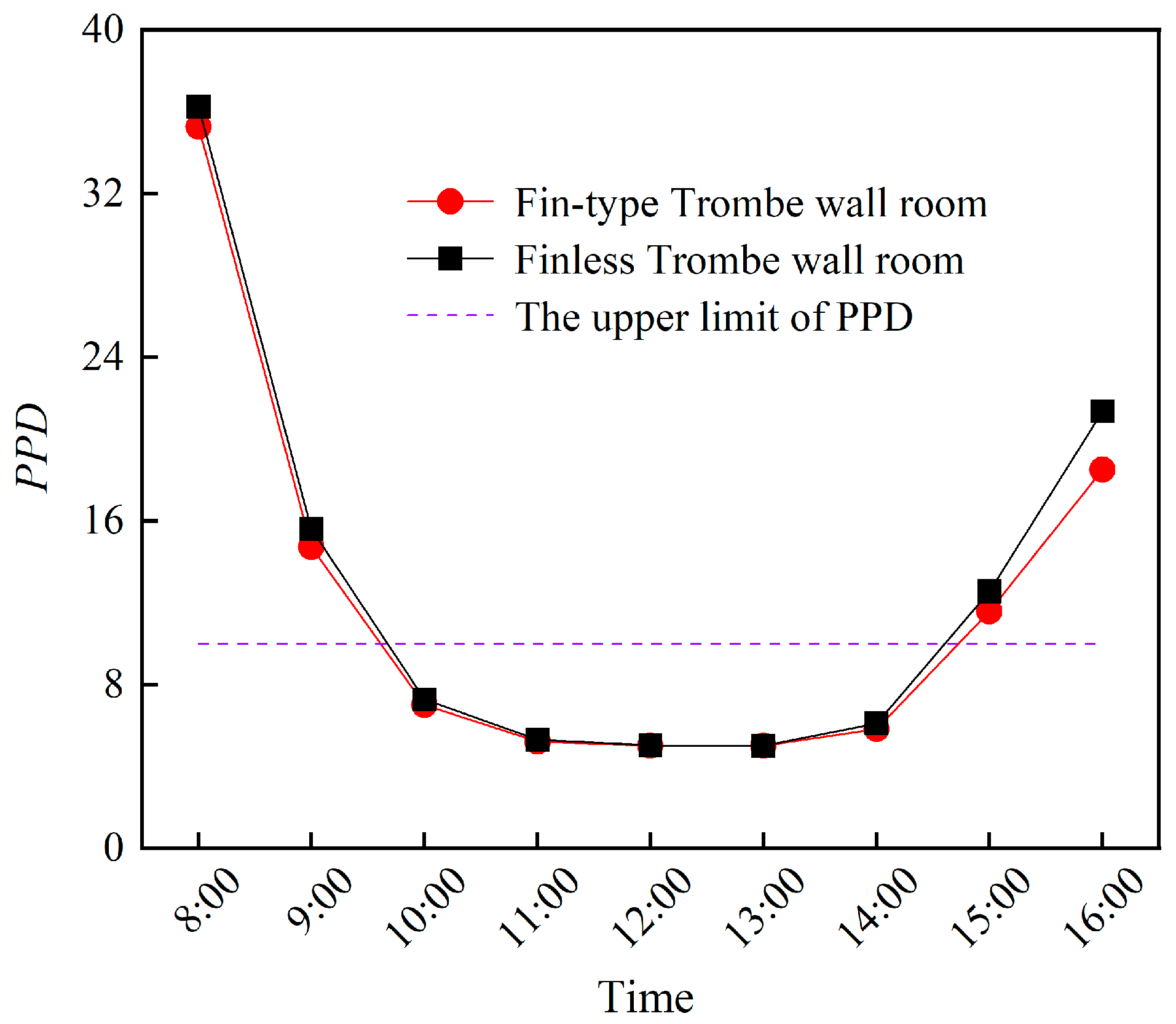
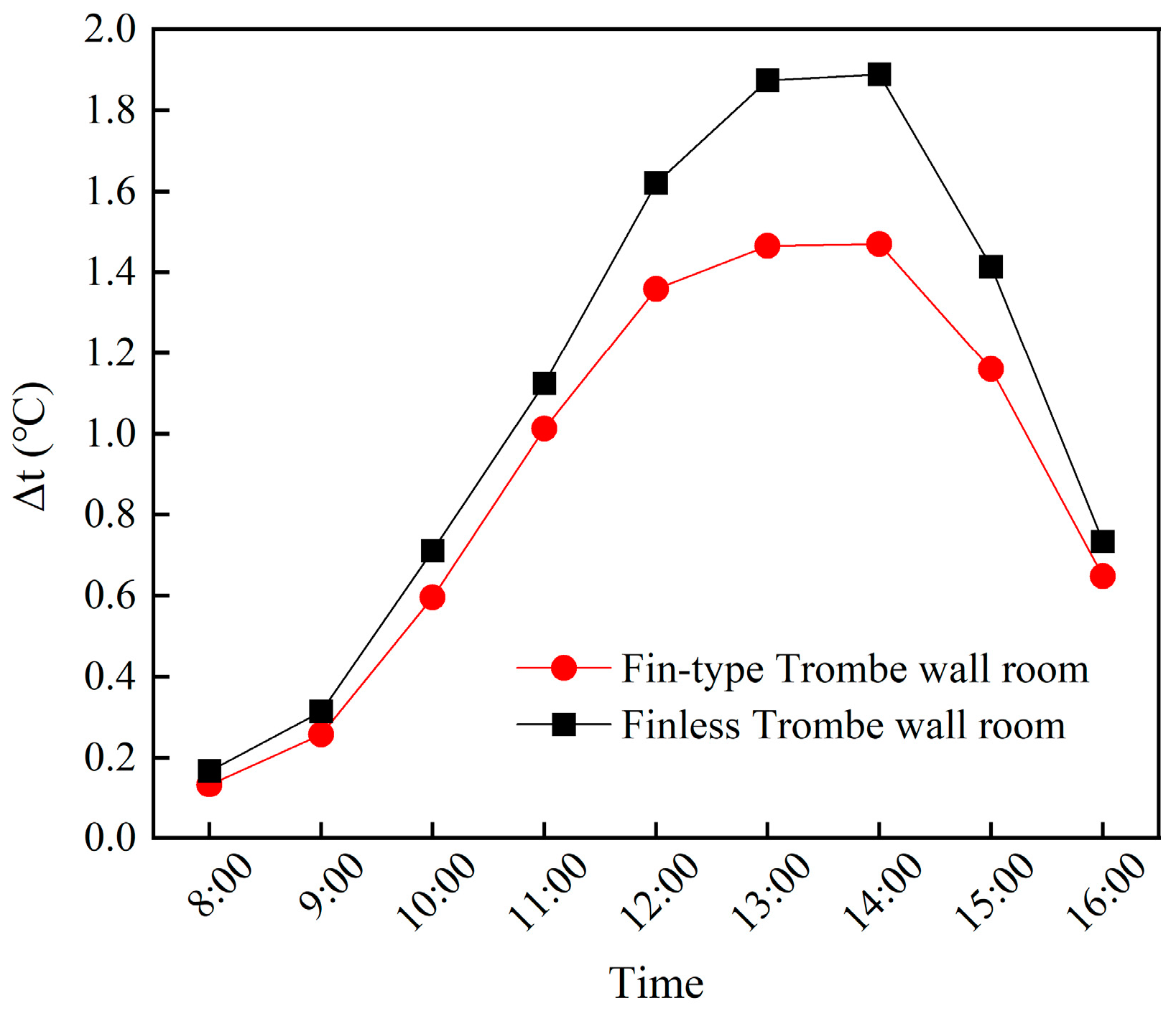
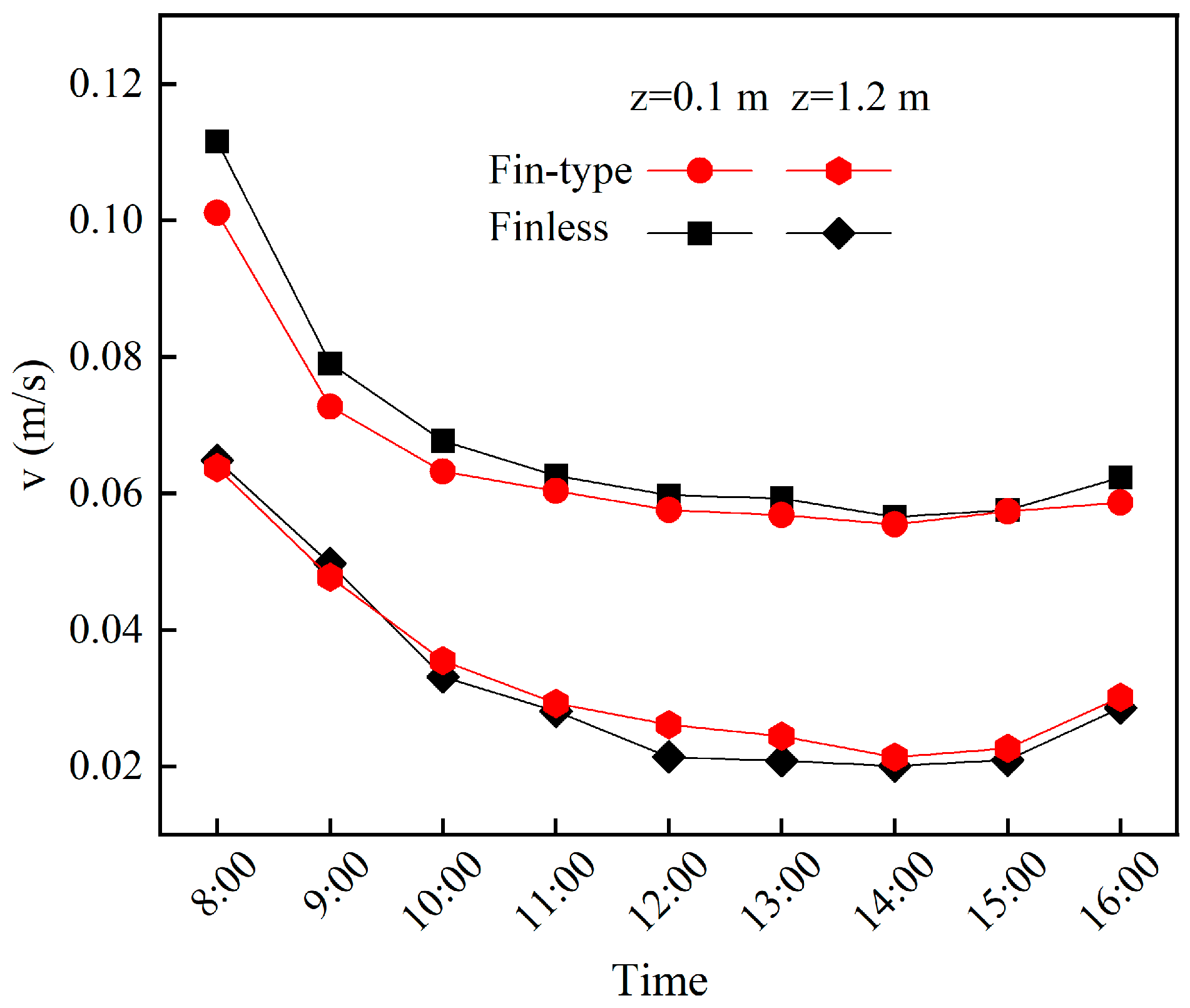
- Aiming at obtaining an optimized fin structure and arrangement, the heat transfer performance and room TE of finless and fin-type TWs were simulated from 8:00 to 16:00. It was found that the HAS for the Trombe wall with an isosceles right-angle triangular fin was 3.51% greater than that of the finless TW. Although the PMV-PPD of the fin-type TW room and the non-fin-type TW rooms are not very different, the comfort duration of the fin-type TW room is greater. For the whole period, the LPD3 of the finless TW room and the fin type TW was less than 10%, but the head–foot temperature difference of the fin type TW was less than that of the finless TW room. The wind speed at the head and ankle of the two different-TW-type rooms was less than 0.12 m/s, the air gust sensation was not strong, and the level of thermal comfort was good. This shows that adding fins is beneficial to the improvement of indoor thermal comfort.
- (4)
- Compared with the ordinary room, the TW room with fins and the TW room without fins had a better energy-saving impact, and the energy-saving rates were 44.63% and 36.38%, respectively. Compared with the energy-saving ratio of the room without a finned TW, the energy savings of the room with a finned TW increased by 8.25%. Adding certain fins can optimize a TW’s heat transfer capacity and improve the indoor TE.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | area, m2 |
| c | empirical coefficients |
| C0 | blackbody radiative coefficient, W/(m2⋅K4) |
| Cp | specific heat capacity, kJ/(kg·K) |
| d | fin height, mm |
| g | gravity acceleration, m2/s |
| H | vertical height, m |
| h | heat transfer coefficient, W/(m2·K) |
| I | solar radiation intensity, W/m2 |
| k | pulsation turbulent kinetic energy |
| mass flow rate, kg/s | |
| Nu | Nusselt number |
| Pr | Prandtl number |
| p | pressure, Pa |
| Q | convective heat supply, W |
| q | heat flux, W/m2 |
| s | front-end distance, m |
| s1 | transverse space, mm |
| s2 | longitudinal spacing, m |
| T | temperature, K |
| u | interlayer air velocity, m/s |
| V | ambient wind speed, m/s |
| Greeks | |
| α | absorptivity |
| β | coefficient of thermal expansion of air, 1/K |
| ε | dissipation rate of pulsating kinetic energy |
| τ | transmittance |
| η | efficiency |
| θ | apex angle of fins |
| λ | coefficient of heat conductivity, W/(m⋅K) |
| ν | viscosity coefficient, m2/s |
| ρ | density, kg/m3 |
| Г | generalized diffusion coefficient |
| Subscripts | |
| a | air |
| amb | ambient |
| b | bottom |
| d | down |
| f | floor |
| g | glass cover |
| th | thermal |
| x | endothermic surface |
References
- Dudley, B. BP Statistical Review of World Energy; BP p.l.c.: London, UK, 2022. [Google Scholar]
- Navakrishnan, S.; Sivakumar, B.; Senthil, R.; Kumar, R.S. Heating and Cooling Application in Energy Efficient Buildings using Trombe Wall: A Review. J. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1130, 012015. [Google Scholar] [CrossRef]
- Yu, B.; He, W.; Li, N.; Wang, L.; Cai, J.; Chen, H.; Ji, J.; Xu, G. Experimental and numerical performance analysis of a TC-Trombe wall. J. Appl. Energy 2017, 206, 70–82. [Google Scholar] [CrossRef]
- Yu, B.; Hou, J.; He, W.; Liu, S.; Hu, Z.; Ji, J.; Chen, H.; Xu, G. Study on a high-performance photocatalytic-Trombe wall system for space heating and air purification. J. Appl. Energy 2018, 226, 365–380. [Google Scholar] [CrossRef]
- Yu, B.; Yang, J.; He, W.; Qin, M.; Zhao, X.; Chen, H. The performance analysis of a novel hybrid solar gradient utilization photocatalytic-thermal-catalytic-Trombe wall system. J. Energy 2019, 174, 420–435. [Google Scholar] [CrossRef]
- Ji, J.; Yi, H.; Pei, G.; Lu, J. Study of PV-Trombe wall installed in a fenestrated room with heat storage. J. Appl. Therm. Eng. 2007, 27, 1507–1515. [Google Scholar] [CrossRef]
- Hu, Z.; He, W.; Hu, D.; Lv, S.; Wang, L.; Ji, J.; Chen, H.; Ma, J. Design, construction and performance testing of a PV blind-integrated Trombe wall module. J. Appl. Energy 2017, 203, 643–656. [Google Scholar] [CrossRef]
- Lin, Y.; Ji, J.; Zhou, F.; Ma, Y.; Luo, K.; Lu, X. Experimental and numerical study on the performance of a built-middle PV Trombe wall system. J. Build. Energy Effic. 2019, 200, 47–57. [Google Scholar] [CrossRef]
- Wu, S.; Xu, L.; Xiao, L. Performance study of a novel multi-functional Trombe wall with air purification, photovoltaic, heating and ventilation. J. Energy Convers. Manag. 2020, 203, 112229. [Google Scholar] [CrossRef]
- Long, J.; Yongga, A.; Sun, H. Thermal Insulation Performance of a Trombe Wall Combined with Collector and Reflection Layer in Hot Summer and Cold Winter Zone. J. Energy Build. 2018, 171, 144–154. [Google Scholar] [CrossRef]
- Long, J.; Jiang, M.; Lu, J.; Du, A. Vertical temperature distribution characteristics and adjustment methods of a Trombe wall. J. Build. Environ. 2019, 165, 106386. [Google Scholar] [CrossRef]
- Stazi, F.; Mastrucci, A.; Perna, C.D. The behaviour of solar walls in residential buildings with different insulation levels: An experimental and numerical study. J. Energy Build. 2012, 47, 217–229. [Google Scholar] [CrossRef]
- Kara, Y.A.; Kurnuc, A. Performance of coupled novel triple glass and phase change material wall in the heating season: An experimental study. J. Sol. Energy 2012, 86, 2432–2442. [Google Scholar] [CrossRef]
- Pittaluga, M. The electrochromic wall. J. Energy Build. 2013, 66, 49–56. [Google Scholar] [CrossRef]
- Zhou, L.; Huo, J.; Zhou, T.; Jin, S. Investigation on the thermal performance of a composite Trombe wall under steady state condition. J. Energy Build. 2020, 214, 109815. [Google Scholar] [CrossRef]
- Hu, Z.; Luo, B.; He, W. An experimental investigation of a novel trombe wall with venetian blind structure. J. Energy Procedia 2015, 70, 691–698. [Google Scholar] [CrossRef]
- Lei, Y.; Gu, Y.; Song, C.; Wang, F. Performance of solar ventilation wall with built-in grille induced channel. J. Tongji Univ. Nat. Sci. Ed. 2016, 44, 1938–1942+1968. [Google Scholar]
- Corasaniti, S.; Manni, L.; Russo, F.; Gori, F. Numerical simulation of modified Trombe-Michel Walls with exergy and energy analysis. J. Int. Commun. Heat Mass 2017, 88, 269–276. [Google Scholar] [CrossRef]
- Gracia, A.D.; Navarro, L.; Castell, A.; Pardo, A.R.; Alvarez, S.; Cabeza, L.F. Solar absorption in a ventilated facade with PCM. Experimental results. J. Energy Procedia 2012, 30, 986–994. [Google Scholar] [CrossRef]
- Leang, E.; Tittelein, P.; Zalewski, L.; Lassue, S. Numerical study of a composite Trombe solar wall integrating microencapsulated PCM. J. Energy Procedia 2017, 122, 1009–1014. [Google Scholar] [CrossRef]
- Duan, S.; Wang, L.; Zhao, Z.; Zhang, C. Experimental study on thermal performance of an integrated PCM Trombe wall. J. Renew. Energy 2021, 163, 1932–1941. [Google Scholar] [CrossRef]
- Benkaddour, A.; Faraji, M.; Faraji, H. Numerical study of the thermal energy storage behaviour of a novel composite PCM/Concrete wall integrated solar collector. J. Mater. Today Proc. 2020, 30, 905–908. [Google Scholar] [CrossRef]
- Faraji, H.; Yıldız, Ç.; Arshad, A.; Arıcı, M.; Choukairy, K.; El Alami, M. Passive thermal management strategy for cooling multiple portable electronic components: Hybrid nanoparticles enhanced phase change materials as an innovative solution. J. Energy Storage 2023, 70, 108087. [Google Scholar] [CrossRef]
- Consuegra, F.M.; Alonso, C.; Perez, G.; Frutos, B.; Guerrero, A.; Oteiza, I. Design, optimization and construction of a prototype for a thermochromic Trombe wall. J. Adv. Build. Energy Res. 2019, 15, 161–178. [Google Scholar] [CrossRef]
- Ahmadi, M.; Mostafavi, G.; Bahrami, M. Natural convection from rectangular interrupted fins. Int. J. Therm. Sci. 2014, 82, 62–71. [Google Scholar] [CrossRef]
- Hosseini, S.S.; Ramiar, A.; Ranjbar, A.A. Numerical investigation of rectangular fin geometry effect on solar chimney. J. Energy Build. 2017, 155, 296–307. [Google Scholar] [CrossRef]
- Rabani, M.; Rabani, M. Heating performance enhancement of a new design trombe wall using rectangular thermal fin arrays: An experimental approach. J. Energy Storage 2019, 24, 100796. [Google Scholar] [CrossRef]
- Wu, S.; Yan, R.; Xiao, L. Numerically predicting the effect of fin on solar Trombe wall performance. J. Sustain. Energy Technol. 2022, 52, 102012. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, X.; Qi, X.; Zhou, J. Numerical study on the effect of optimizing the Trombe wall structure with built-in fins on improving building energy efficiency in severe cold region. J. Renew. Energy 2024, 222, 119856. [Google Scholar] [CrossRef]
- DB62/T 3151-2018; Design Standard for Energy Efficiency (75%) of Residential Buildings in Severe Cold Regions. Local Standards of Gansu Province: Lanzhou, China, 2018.
- Liu, J. Building Physics, 4th ed.; China Architecture & Building Press: Beijing, China, 2009. [Google Scholar]
- Wang, Y.; He, T.; Hu, J.; Tian, H.; Zhao, X. Influence of built-in fin parameters on the flow and heat transfer performance in enclosed cavity. J. Sci. Technol. Eng. 2022, 22, 11911–11917. [Google Scholar]
- Rabani, M.; Vali, K.; Dehghan, A.A.; Faghih, A.K. Experimental study of the heating performance of a Trombe wall with a new design. J. Sol. Energy 2015, 118, 359–374. [Google Scholar] [CrossRef]
- CABR. Technical Specification for Floor Radiant Heating; China Architecture & Building Press: Beijing, China, 2004. [Google Scholar]
- Zhu, X. Built Environment, 4th ed.; China Architecture & Building Press: Beijing, China, 2016. [Google Scholar]
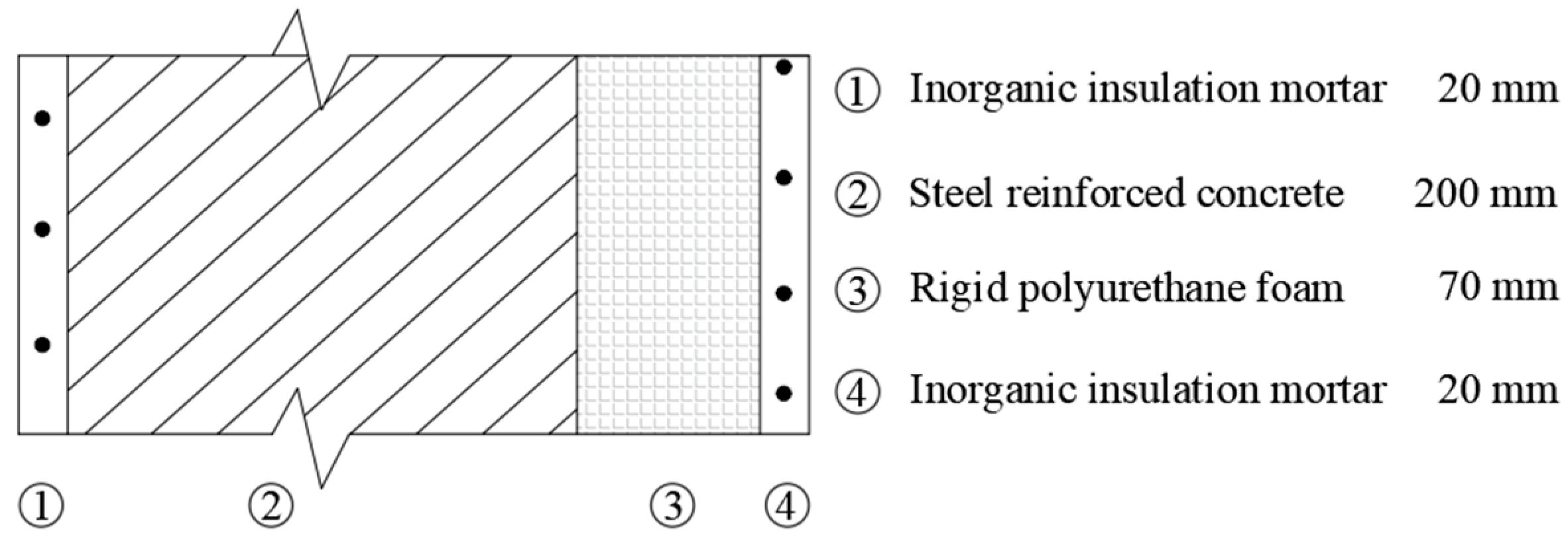


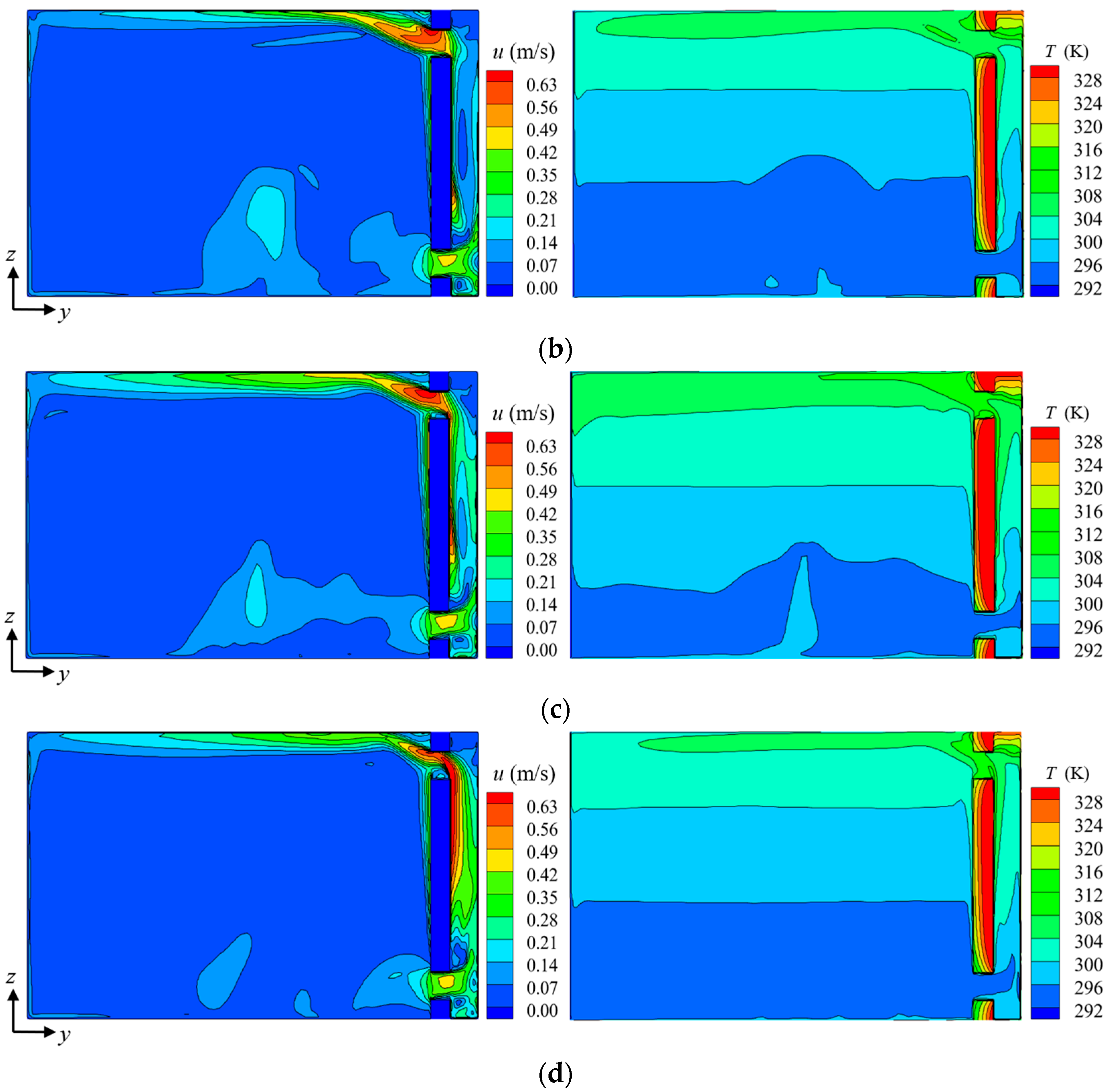
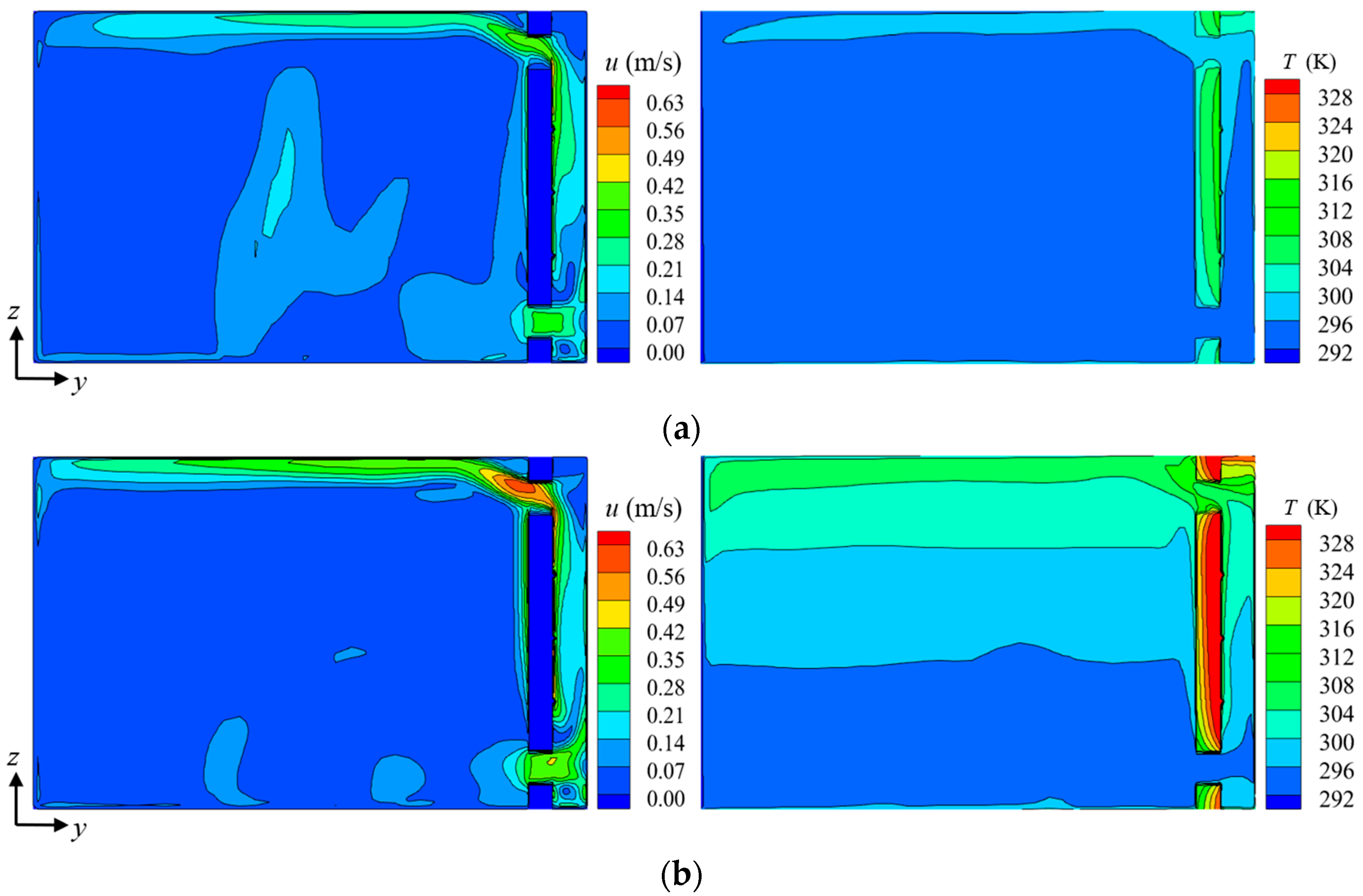
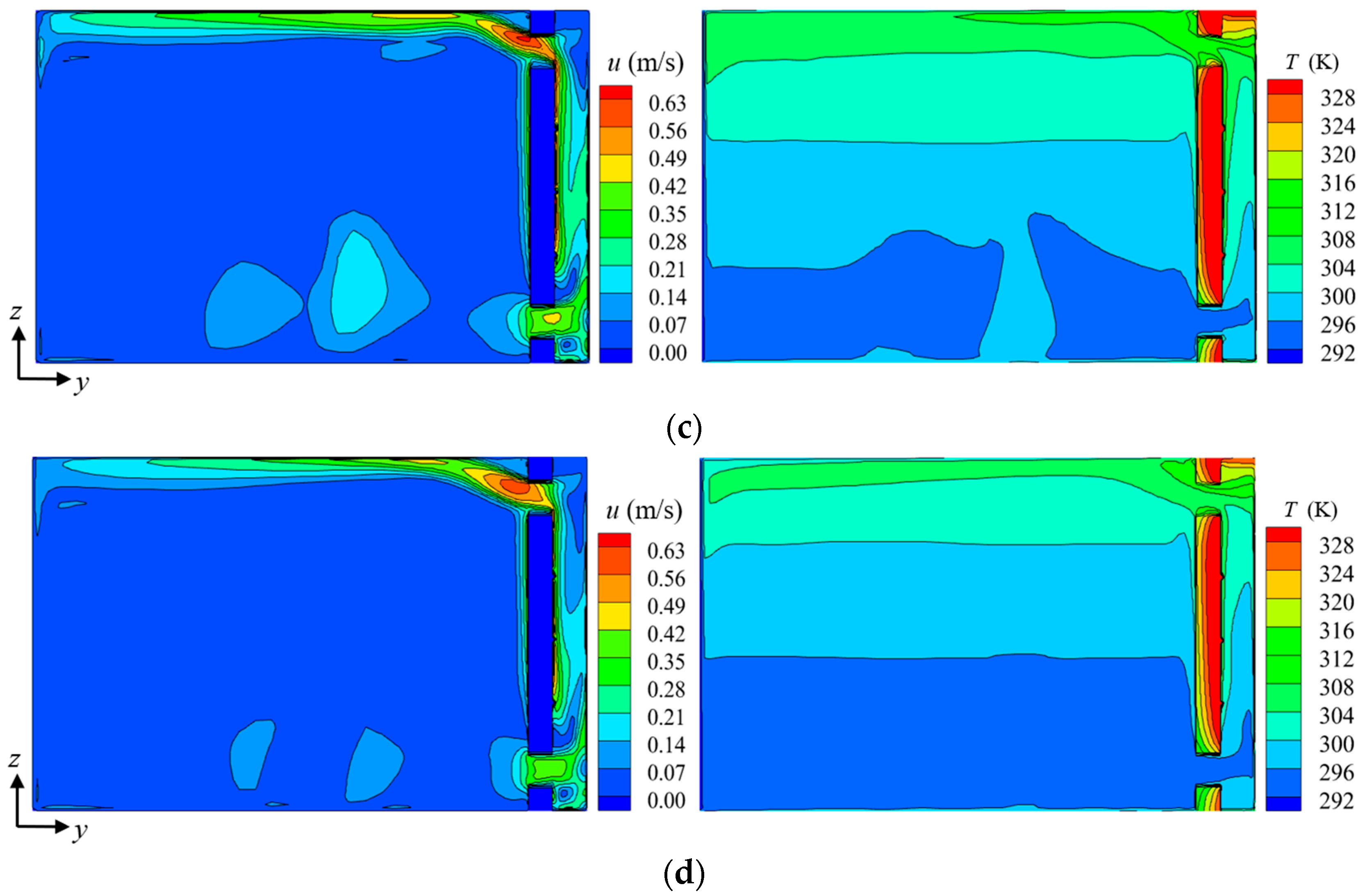



| Material Names | Density ρ (kg/m3) | Specific Heat Capacity c [kJ/(kg·K)] | Coefficient of Heat Conductivity λ [W/(m·K)] |
|---|---|---|---|
| Inorganic insulation mortar | 600 | 1.05 | 0.18 |
| Steel-reinforced concrete | 2400 | 0.84 | 1.54 |
| Rigid polyurethane foam | 45 | 1.72 | 0.025 |
| Glass | 2500 | 0.84 | 0.76 |
| Fin | 8954 | 0.384 | 398 |
| 8:00 | 9:00 | 10:00 | 11:00 | 12:00 | 13:00 | 14:00 | 15:00 | 16:00 | |
|---|---|---|---|---|---|---|---|---|---|
| East wall/(K) | 289.87 | 289.87 | 289.86 | 289.86 | 289.86 | 289.86 | 289.87 | 289.88 | 289.89 |
| South wall/(K) | 289.94 | 289.93 | 289.93 | 289.92 | 289.92 | 289.92 | 289.93 | 289.94 | 289.96 |
| West wall/(K) | 289.88 | 289.87 | 289.87 | 289.86 | 289.86 | 289.86 | 289.86 | 289.86 | 289.87 |
| North wall/(K) | 289.85 | 289.84 | 289.84 | 289.83 | 289.83 | 289.83 | 289.83 | 289.84 | 289.85 |
| Floor thermal density/(W/m2) | 39.52 | 37.30 | 32.11 | 26.75 | 23.68 | 24.46 | 23.27 | 22.86 | 23.79 |
| Research Object | Arrangement | Ventilation of the Upper Vent (m3/h) | Temperature of the Upper Vent (K) | |
|---|---|---|---|---|
| Fins on the HAS of Trombe wall | In-line | 201.33 | 305.87 | 154.75 |
| Staggered | 186.11 | 305.84 | 147.79 |
| Thermal Sensation | Very Hot | Hot | A Little Hot | Neutrality | A Little Cold | Cold | Very Cold |
|---|---|---|---|---|---|---|---|
| PMV | +3 | +2 | +1 | 0 | −1 | −2 | −3 |
| Room Type | Thermal Load (MJ) | South Window Heat (MJ) | Convective Heat Supply (MJ) | Floor Active Heat Supply (MJ) | ESF (%) |
|---|---|---|---|---|---|
| Ordinary room | 22.61 | 0.18 | / | 22.43 | / |
| Finless Trombe wall room | 22.61 | 0.18 | 8.16 | 14.27 | 36.38 |
| Fin-type Trombe wall room | 22.61 | 0.18 | 10.01 | 12.42 | 44.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, X.; Wang, J.; Wang, Y. Influence of a Built-in Finned Trombe Wall on the Indoor Thermal Environment in Cold Regions. Energies 2024, 17, 1874. https://doi.org/10.3390/en17081874
Qi X, Wang J, Wang Y. Influence of a Built-in Finned Trombe Wall on the Indoor Thermal Environment in Cold Regions. Energies. 2024; 17(8):1874. https://doi.org/10.3390/en17081874
Chicago/Turabian StyleQi, Xiaobing, Jialong Wang, and Ye Wang. 2024. "Influence of a Built-in Finned Trombe Wall on the Indoor Thermal Environment in Cold Regions" Energies 17, no. 8: 1874. https://doi.org/10.3390/en17081874
APA StyleQi, X., Wang, J., & Wang, Y. (2024). Influence of a Built-in Finned Trombe Wall on the Indoor Thermal Environment in Cold Regions. Energies, 17(8), 1874. https://doi.org/10.3390/en17081874




