Electromagnetic Design Optimization Integrated with Mechanical Stress Analysis of PM-Assisted Synchronous Reluctance Machine Topologies Enabled with a Blend of Magnets †
Abstract
1. Introduction
2. Machine Topology and Specifications
2.1. Baseline Design
2.2. Initial PMASynRM Topology
2.3. Modified PMASynRM Topology
3. Design Optimization
3.1. Design Constraints and Objectives
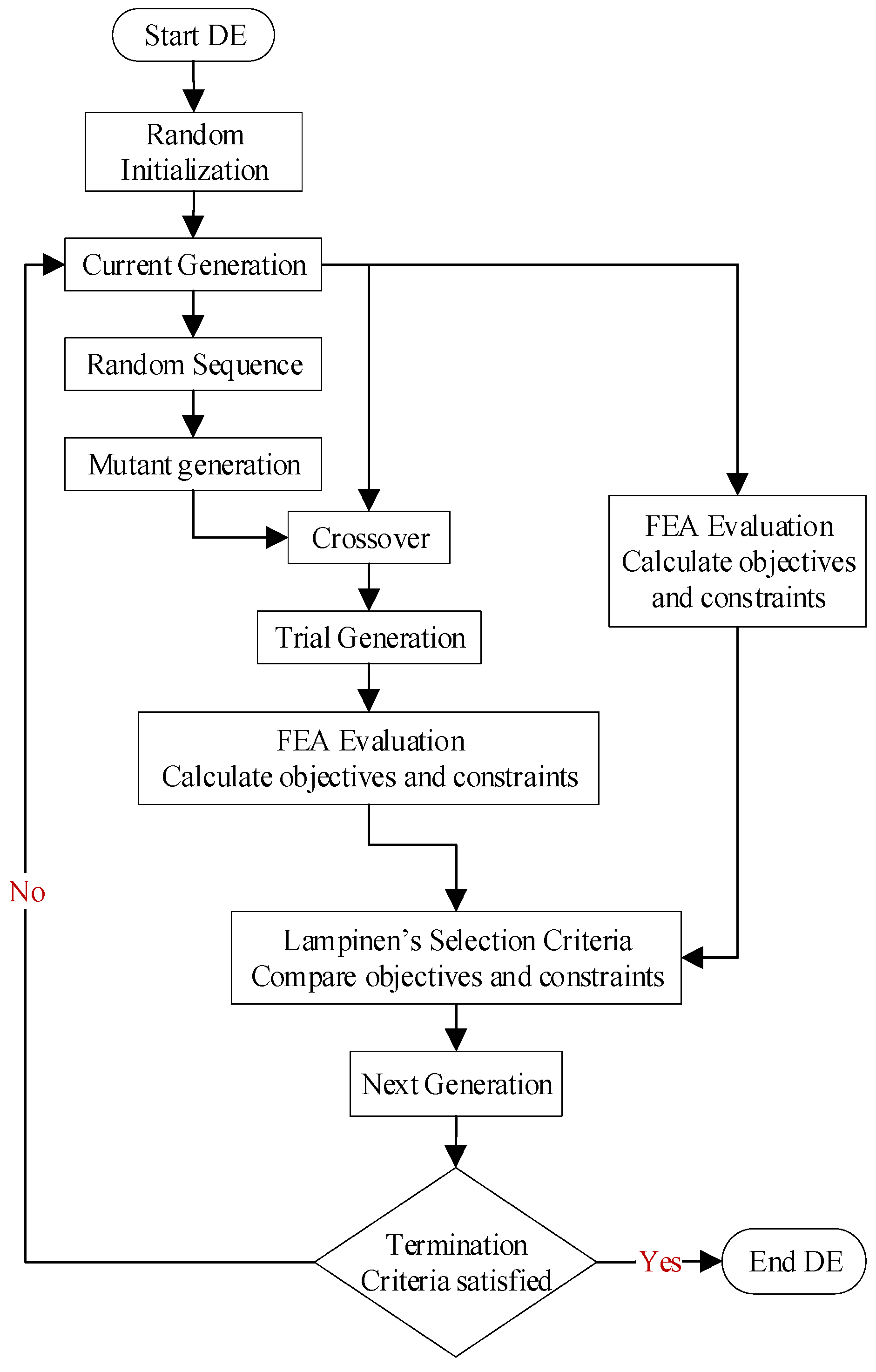
3.2. Optimization Algorithm and Procedure
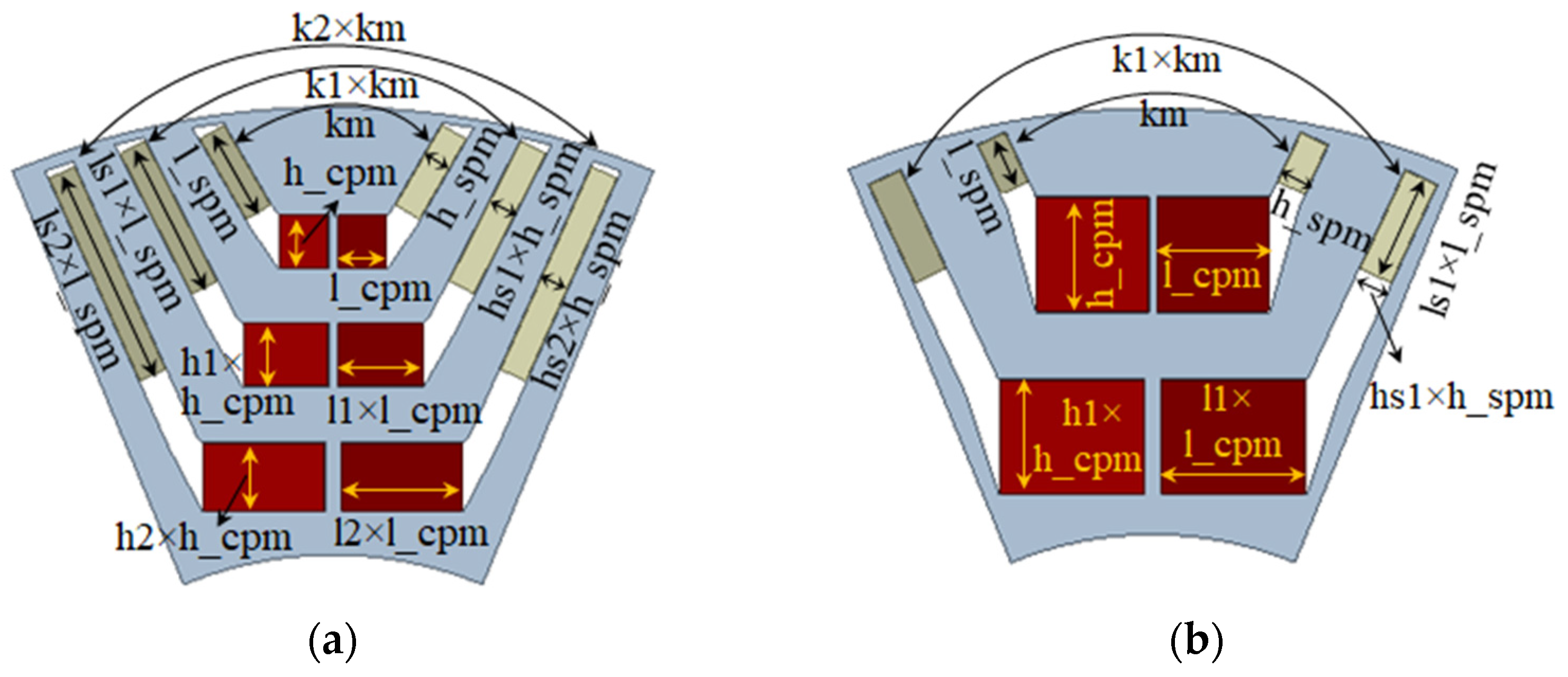
3.3. Optimization Parameters
3.4. Trade-Off Plots
3.4.1. Rare-Earth and Iron Nitride Magnet Combinations
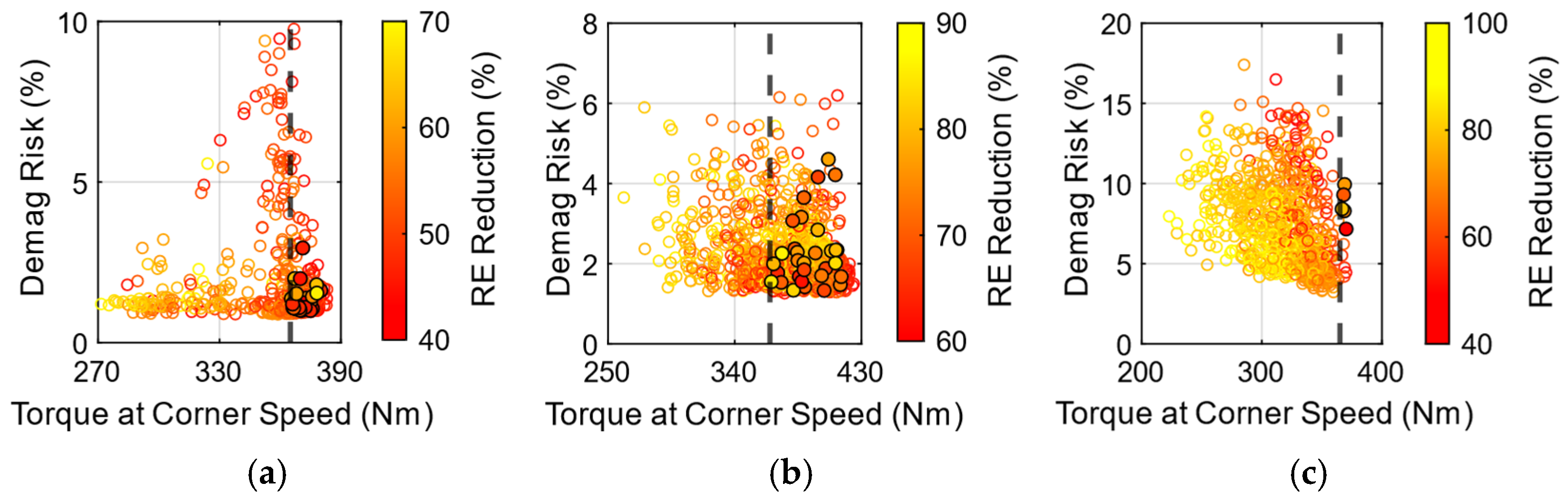

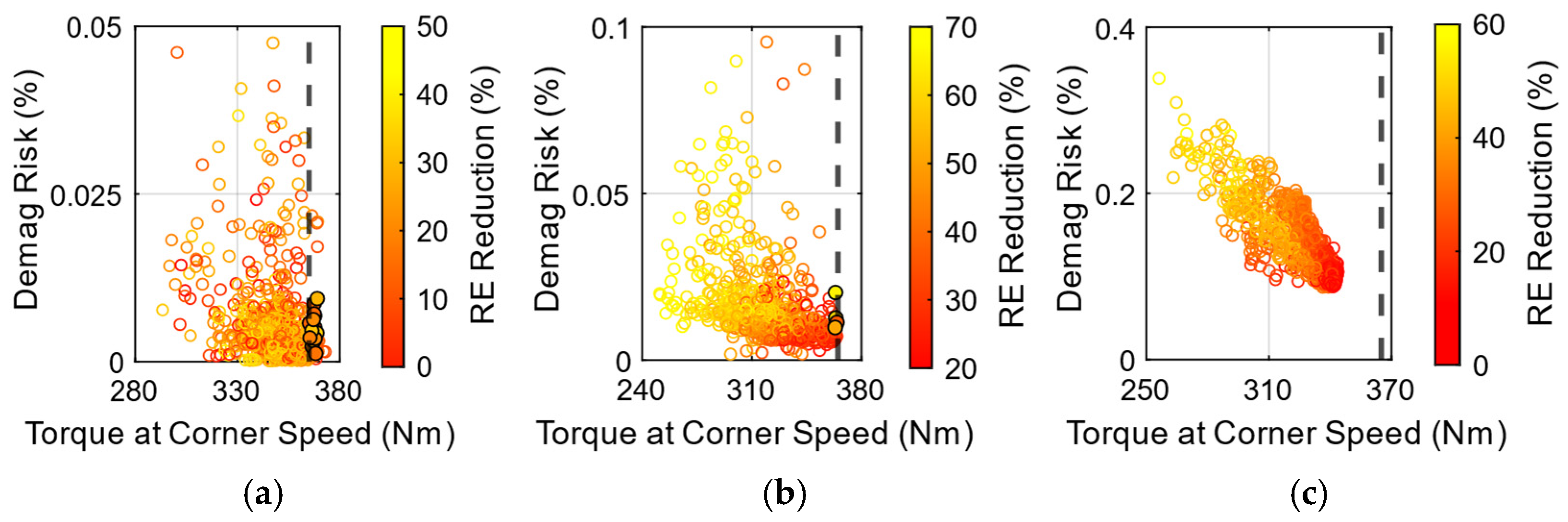
3.4.2. Rare-Earth and Ferrite Magnet Combinations
3.4.3. Rare-Earth-Free Magnet Combinations

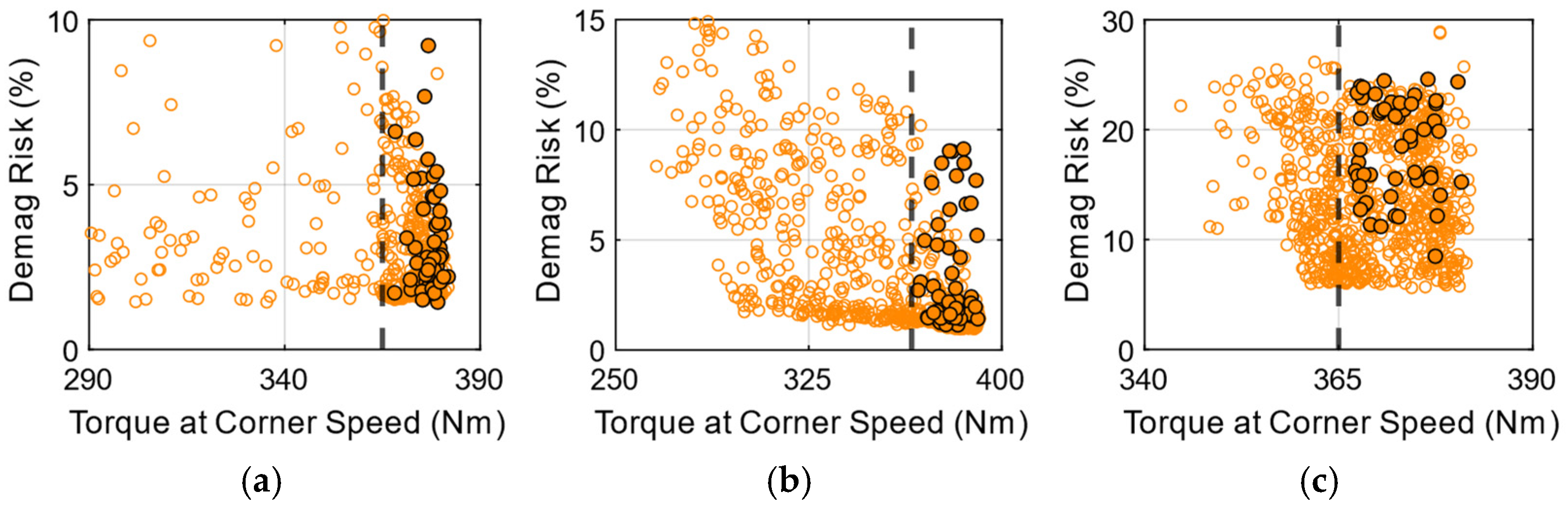

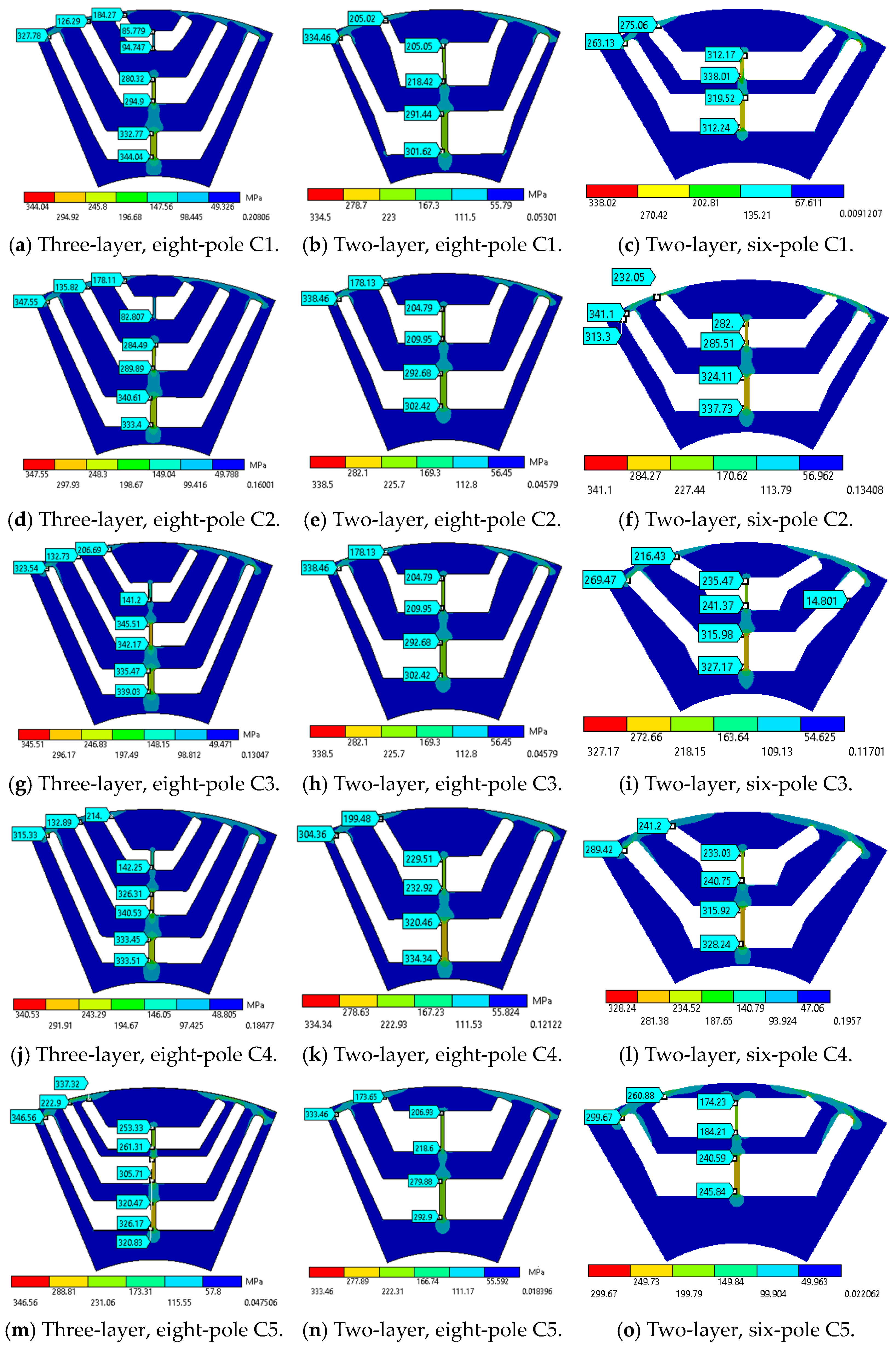
3.5. Mechanical Stress Analysis
3.6. Design Optimization Performance
4. Performance Analysis and Comparison
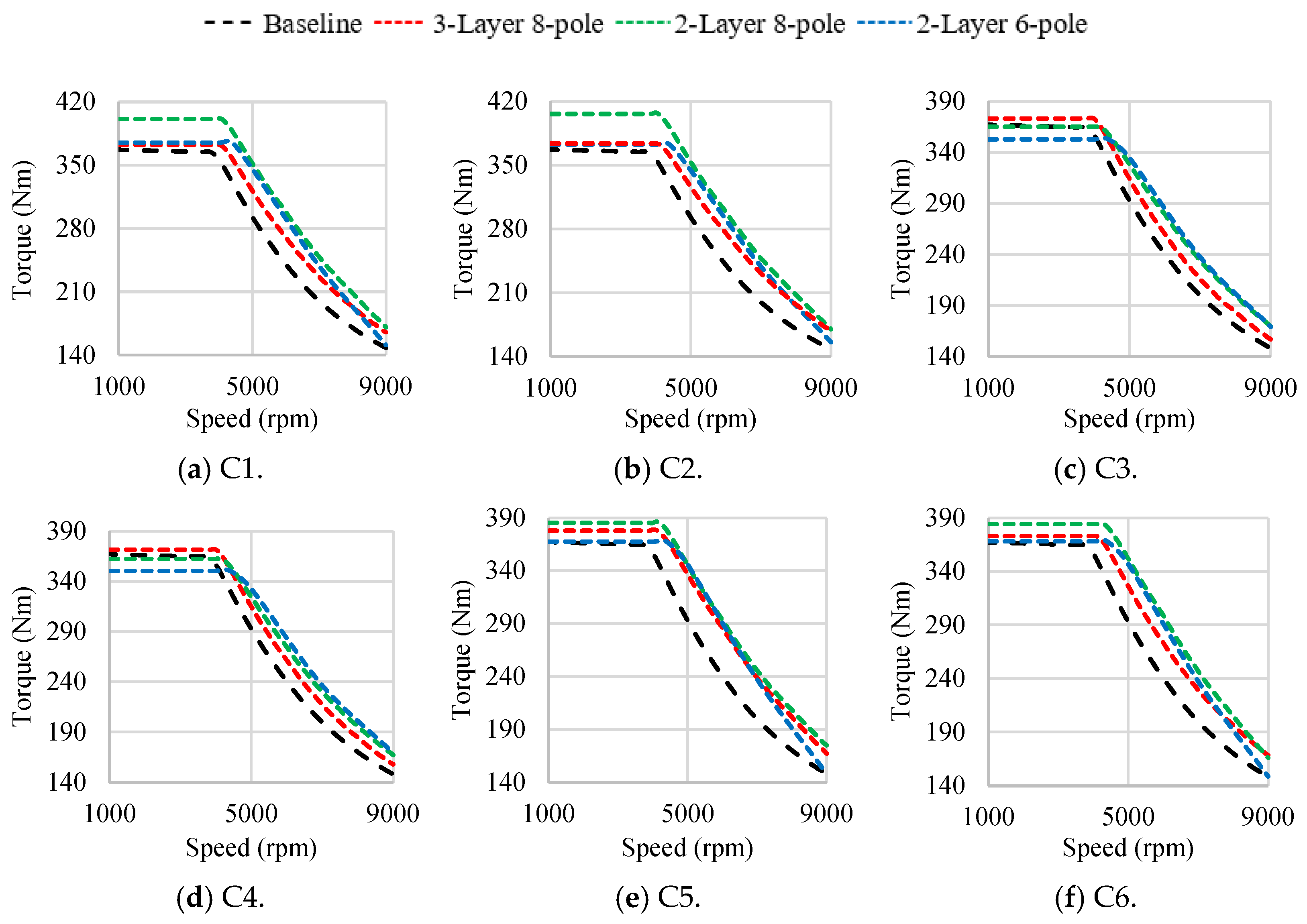
4.1. Torque–Speed Characteristics
4.2. Power–Speed Characteristics
4.3. Torque Ripple
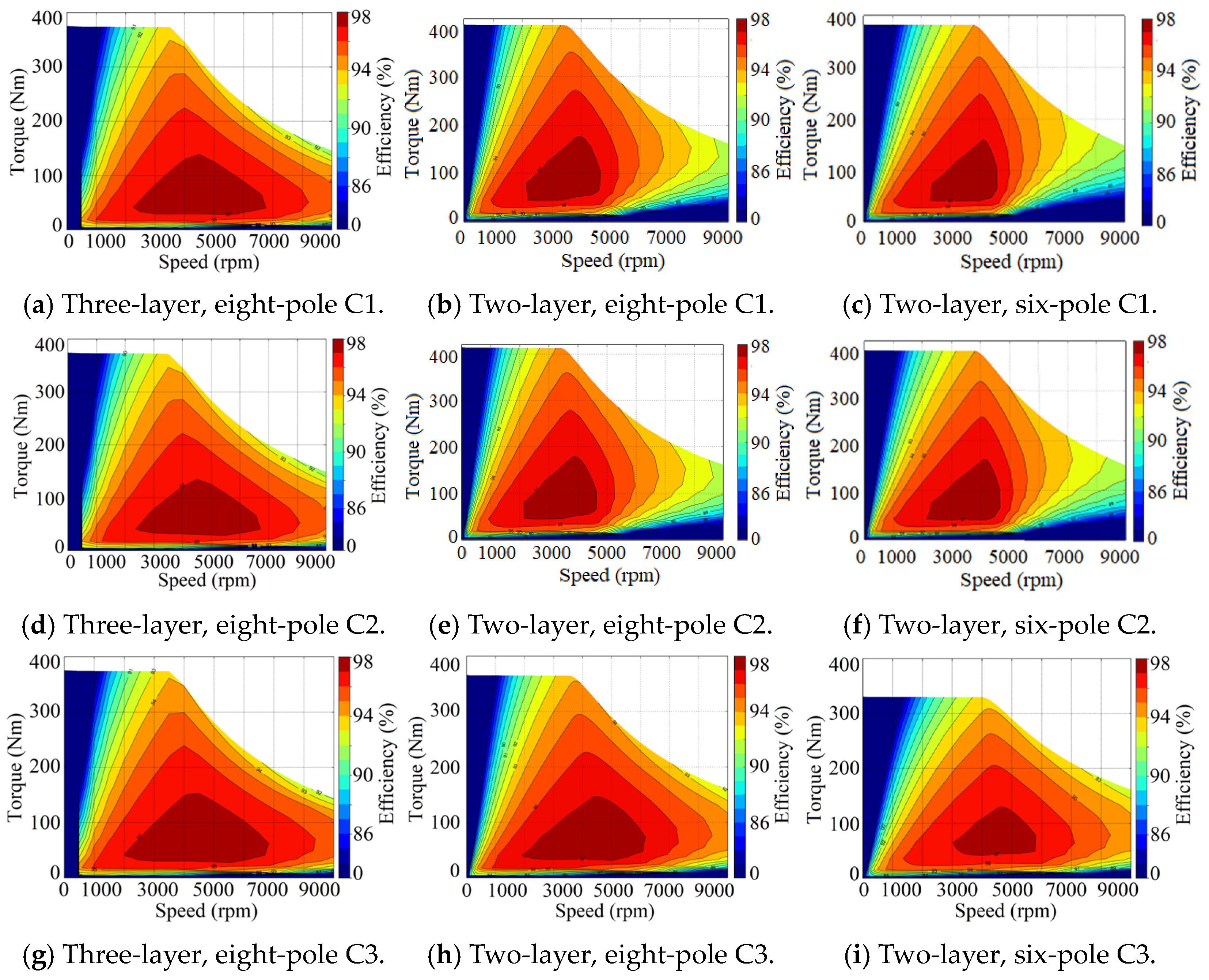
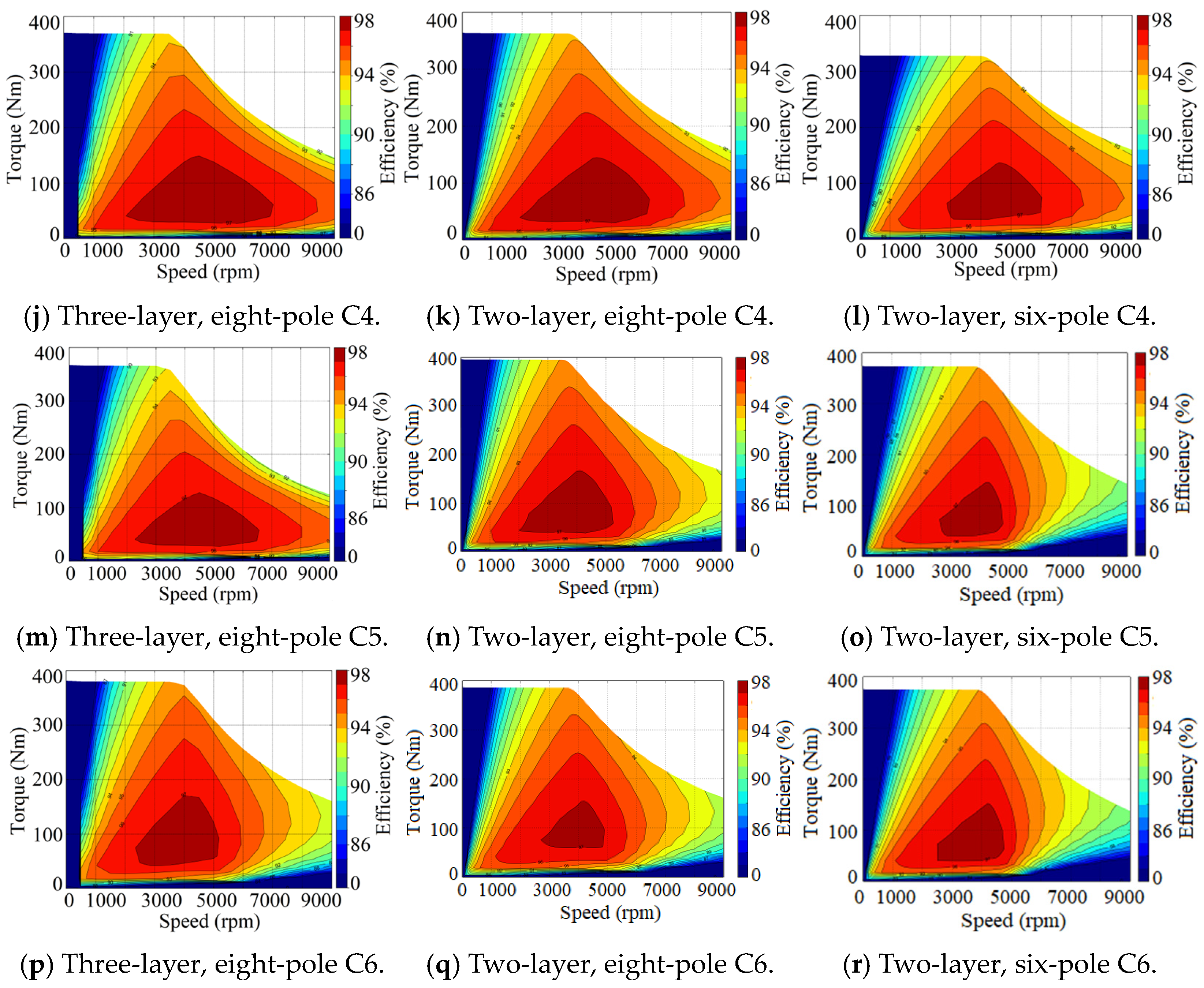
4.4. Efficiency Maps
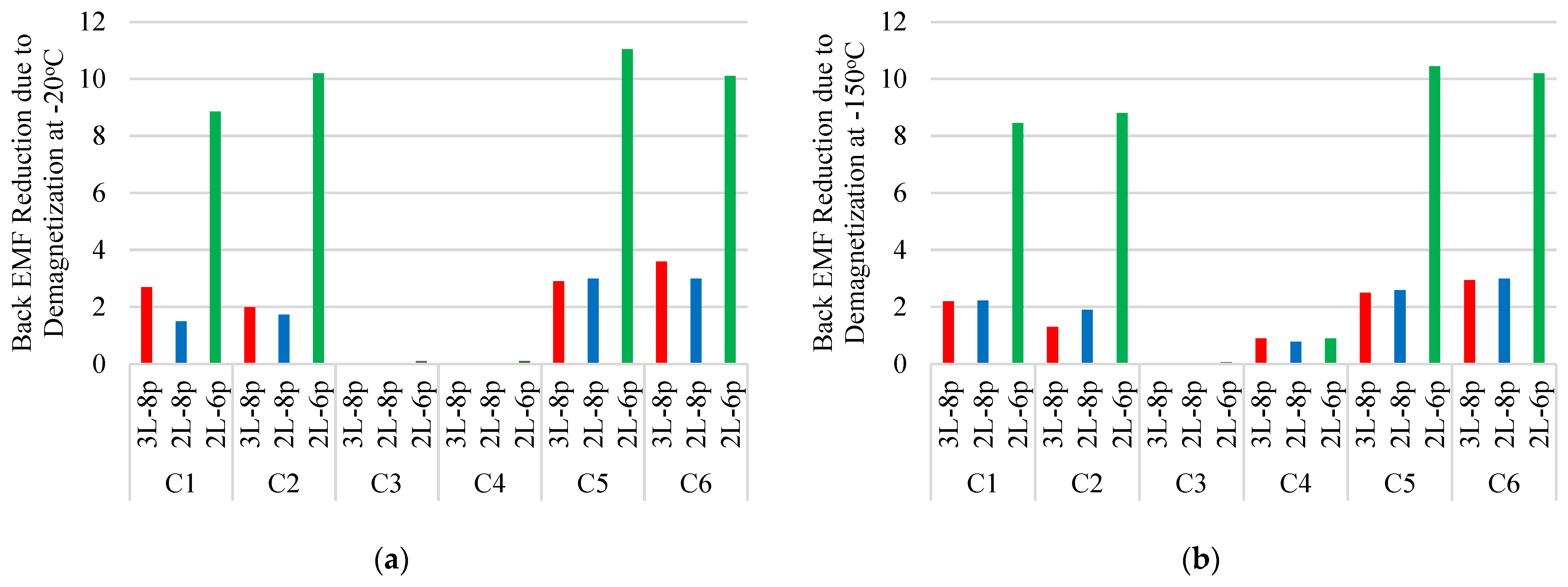
4.5. Demagnetization Analysis
4.6. Cost Assessment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guglielmi, P.; Boazzo, B.; Armando, E.; Pellegrino, G.; Vagati, A. Permanent-Magnet Minimization in PM-Assisted Synchronous Reluctance Motors for Wide Speed Range. IEEE Trans. Ind. Appl. 2013, 49, 31–41. [Google Scholar] [CrossRef]
- Ferrari, M.; Bianchi, N.; Fornasiero, E. Analysis of Rotor Saturation in Synchronous Reluctance and PM-Assisted Reluctance Motors. IEEE Trans. Ind. Appl. 2015, 51, 169–177. [Google Scholar] [CrossRef]
- Obata, B.M.; Morimoto, S.; Sanada, M.; Inoue, Y. Performance of PMASynRM with Ferrite Magnets for EV/HEV Applications Considering Productivity. IEEE Trans. Ind. Appl. 2014, 50, 2427–2435. [Google Scholar] [CrossRef]
- Hofer, M.; Schrödl, M. Investigation of Permanent Magnet assisted Synchronous Reluctance Machines for Traction Drives in High Power Flux Weakening Operation. In Proceedings of the 2020 IEEE Transportation Electrification Conference & Expo (ITEC), Chicago, IL, USA, 23–26 June 2020; pp. 335–339. [Google Scholar]
- Barcaro, M.; Bianchi, N. Interior PM Machines Using Ferrite to Replace Rare-Earth Surface PM Machines. IEEE Trans. Ind. Appl. 2014, 50, 979–985. [Google Scholar] [CrossRef]
- Cai, H.; Guan, B.; Xu, L. Low-Cost Ferrite PM-Assisted Synchronous Reluctance Machine for Electric Vehicles. IEEE Trans. Ind. Electron. 2014, 61, 5741–5748. [Google Scholar] [CrossRef]
- Du, Z.S.; Lipo, T.A. Cost-Effective High Torque Density Bi-Magnet Machines Utilizing Rare Earth and Ferrite Permanent Magnets. IEEE Trans. Energy Convers. 2020, 35, 1577–1584. [Google Scholar] [CrossRef]
- Du, Z.S.; Lipo, T.A. Interior permanent magnet machines with rare earth and ferrite permanent magnets. In Proceedings of the 2017 IEEE International Electric Machines and Drives Conference (IEMDC), Miami, FL, USA, 21–24 May 2017; pp. 1–8. [Google Scholar]
- Ma, Q.; El-Refaie, A.; Lequesne, B. Low-Cost Interior Permanent Magnet Machine with Multiple Magnet Types. IEEE Trans. Ind. Appl. 2020, 56, 1452–1463. [Google Scholar] [CrossRef]
- Won, H.; Hong, Y.-K.; Choi, M.; Bryant, B.; Platt, J.; Choi, S. Cost-Effective Hybrid Permanent Magnet Assisted Synchronous Reluctance Machine for Electric Vehicle. In Proceedings of the 2021 IEEE International Electric Machines & Drives Conference (IEMDC), Hartford, CT, USA, 17–20 May 2021; pp. 1–6. [Google Scholar]
- Wu, W.; Zhu, X.; Quan, L.; Du, Y.; Xiang, Z.; Zhu, X. Design and analysis of a hybrid permanent magnet assisted synchronous reluctance motor considering magnetic saliency and PM usage. IEEE Trans. Appl. Supercond. 2018, 28, 5200306. [Google Scholar] [CrossRef]
- Ma, Q.; EL-Refaie, A.; Fatemi, A.; Nehl, T. Comparative Analysis of Two Different Types of Blended Permanent Magnet Assisted Synchronous Reluctance Machine. In Proceedings of the 2021 IEEE Energy Conversion Congress and Exposition (ECCE), Vancouver, BC, Canada, 10–14 October 2021; pp. 4189–4196. [Google Scholar]
- Ma, Q.; Ayman, E.R.; Fatemi, A. Multi-objective Design Optimization of a Blended Permanent Magnet Assisted Synchronous Reluctance Machine. In Proceedings of the 2021 IEEE International Electric Machines & Drives Conference (IEMDC), Hartford, CT, USA, 17–20 May 2021. [Google Scholar]
- Kumar, P.; Ma, Q.; Al-Qarni, A.; Chowdhury, T.; EL-Refaie, A. Design Optimization and Comparison of PM-Assisted Synchronous Reluctance Machine using Different Magnet Combinations. In Proceedings of the 2022 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 9–13 October 2022; pp. 1–8. [Google Scholar]
- Vagati, A.; Boazzo, B.; Guglielmi, P.; Pellegrino, G. Design of ferrite-assisted synchronous reluctance machines robust toward demagnetization. IEEE Trans. Ind. Appl. 2014, 50, 1768–1779. [Google Scholar] [CrossRef]
- Li, S.; Li, Y.; Sarlioglu, B. Partial Irreversible Demagnetization Assessment of Flux-Switching Permanent Magnet Machine Using Ferrite Permanent Magnet Material. IEEE Trans. Magn. 2015, 51, 8106209. [Google Scholar]
- Wang, J.; Howe, D.; Jewell, G.W. Analysis and design optimization of an improved axially magnetized tubular permanent-magnet machine. IEEE Trans. Energy Convers. 2004, 19, 289–295. [Google Scholar] [CrossRef]
- Lei, G.; Liu, C.; Guo, Y.; Zhu, J. Multidisciplinary design analysis and optimization of a PM Transverse flux machine with soft magnetic composite Core. IEEE Trans. Magn. 2015, 51, 8109704. [Google Scholar] [CrossRef]
- Hemmati, R.; Rahideh, A. Optimal design of slot less tubular linear brushless PM machines using metaheuristic optimization techniques. J. Intell. Fuzzy Syst. 2017, 32, 351–361. [Google Scholar] [CrossRef]
- Qinghua, L.; Jabbar, M.A.; Khambadkone, A.M. Response surface methodology based optimization of interior permanent magnet synchronous motor for wide speed operation. PEMD Mach. Drives 2004, 2, 546–555. [Google Scholar]
- Kim, J.B.; Hwang, K.Y.; Kwon, B.I. Optimization of two phase in-wheel IPMSM for wide speed range by using the Kriging model based on Latin Hypercube sampling. IEEE Trans. Magn. 2011, 47, 1078–1081. [Google Scholar] [CrossRef]
- Ishikawa, T.; Yamada, M.; Kurita, N. Design of magnet arrangement in interior permanent magnet synchronous motor by response surface methodology in consideration of torque and vibration. IEEE Trans. Magn. 2011, 47, 1290–1293. [Google Scholar] [CrossRef]
- Seifert, R.; Bargalló Perpiñà, R. Multiobjective optimization of IPM synchronous motor using Response Surface Methodology and filtered Monte Carlo approach. In Proceedings of the 2014 International Conference on Electrical Machines (ICEM), Berlin, Germany, 2–5 September 2014; pp. 1307–1313. [Google Scholar]
- Sizov, G.Y.; Ionel, D.M.; Demerdash, N.A.O. Modeling and design optimization of PM AC machines using computationally efficient-finite element analysis. In Proceedings of the IEEE Energy Conversion Congress and Exposition ECCE, Atlanta, GA, USA, 12–16 September 2010; pp. 578–585. [Google Scholar]
- Popescu, M.; Ionel, D.; Boglietti, A.; Cavagnino, A.; Cossar, C.; McGilp, M. A general model for estimating the laminated steel losses under pwm voltage supply. IEEE Trans. Ind. Appl. 2010, 46, 1389–1396. [Google Scholar] [CrossRef]
- Ionel, D.M.; Popescu, M. Finite element surrogate model for electric machines with revolving field—Application to IPM motors. IEEE Trans. Ind. Apps. 2010, 46, 2424–2433. [Google Scholar] [CrossRef]
- Ionel, D.M.; Popescu, M. Ultra-fast finite element analysis of brushless PM machines based on space-time transformations. IEEE Trans. Ind. Appl. 2011, 47, 744–753. [Google Scholar] [CrossRef]
- Peng, Z.; Sizov Gennadi, Y.; Ionel Dan, M.; Nabeel Demerdash, A.O. Design optimization of spoke-type ferrite magnet machines by combined design of experiments and differential evolution algorithms. In Proceedings of the 2013 International Electric Machines & Drives Conference, Chicago, IL, USA, 12–15 May 2013; pp. 892–898. [Google Scholar]
- Peng, Z.; Ionel Dan, M.; Demerdash Nabeel, A.O. Morphing parametric modeling and design optimization of spoke and V-type permanent magnet machines by combined design of experiments and differential evolution algorithms. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15–19 September 2013; pp. 5056–5063. [Google Scholar]
- Fatemi, A.; Ionel, D.M.; Demerdash, N.A.; Nehl, T.W. Fast multi-objective CMODE-type optimization of electric machines for multicore desktop computers. IEEE Trans. Ind. Appl. 2016, 52, 2941–2950. [Google Scholar] [CrossRef]
- Fatemi, A.; Demerdash, N.A.; Ionel, D.M. Design optimization of IPM machines for efficient operation in extended speed range. In Proceedings of the 2015 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 14–17 June 2015. [Google Scholar]
- Jiang, W.; Jahns, T.M.; Lipo, T.A.; Taylor, W.; Suzuki, Y. Machine design ptimization based on finite element analysis in a high-throughput computing environment. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Raleigh, NC, USA, 15–20 September 2012; pp. 869–879. [Google Scholar]
- Bramerdorfer, G.; Tapia, J.A.; Pyrhönen, J.J.; Cavagnino, A. Modern electrical machine design optimization: Techniques trends and best practices. IEEE Trans. Ind. Electron. 2018, 65, 7672–7684. [Google Scholar] [CrossRef]
- Kumar, P.; Wilson, R.; Chowdhury, T.; EL-Refaie, A. Multi-Objective Design Optimization and Comparison of 2-layer versus 3-layer PM-Assisted Synchronous Reluctance Machines using a Blend of Rare-Earth and Rare-Earth-Free Magnets. In Proceedings of the 2023 IEEE Energy Conversion Congress and Exposition (ECCE), Nashville, TN, USA, 29 October–2 November 2023; pp. 3930–3937. [Google Scholar] [CrossRef]
- Kumar, P.; Wilson, R.; EL-Refaie, A. Optimization of the Magnetization Direction of Magnets in a Permanent Magnet Assisted Synchronous Reluctance Machine to Minimize Demagnetization. In Proceedings of the 2023 IEEE International Electric Machines & Drives Conference (IEMDC), San Francisco, CA, USA, 15–18 May 2023; pp. 1–7. [Google Scholar] [CrossRef]
- Wilson, R.; Kumar, P.; El-Refaie, A. Minimization of Rare-Earth Permanent Magnets and Demagnetization Risk in PM-assisted Synchronous Reluctance Motor with Blended Magnets. In Proceedings of the 2023 IEEE Energy Conversion Congress and Exposition (ECCE), Nashville, TN, USA, 29 October–2 November 2023; pp. 4257–4264. [Google Scholar] [CrossRef]
- Rahman, K.M.; Hiti, S. Identification of machine parameters of a synchronous motor. In Proceedings of the 38th IAS Annual Meeting on Conference Record of the Industry Applications Conference, Salt Lake City, UT, USA, 12–16 October 2003; Volume 1, pp. 409–415. [Google Scholar] [CrossRef]
- Zarko, D.; Stipetic, S.; Martinovic, M.; Kovacic, M.; Jercic, T.; Hanic, Z. Reduction of computational efforts in finite element-based permanent magnet traction motor optimization. IEEE Trans. Ind. Electron. 2018, 65, 1799–1807. [Google Scholar] [CrossRef]
- Ma, Q.; Chen, H.; El-Refaie, A.; Sun, Y. A Review of Electrical Machine Optimization Methods with Emphasis on Computational Time. In Proceedings of the 2019 IEEE International Electric Machines & Drives Conference (IEMDC), San Diego, CA, USA, 12–15 May 2019; pp. 1895–1902. [Google Scholar] [CrossRef]
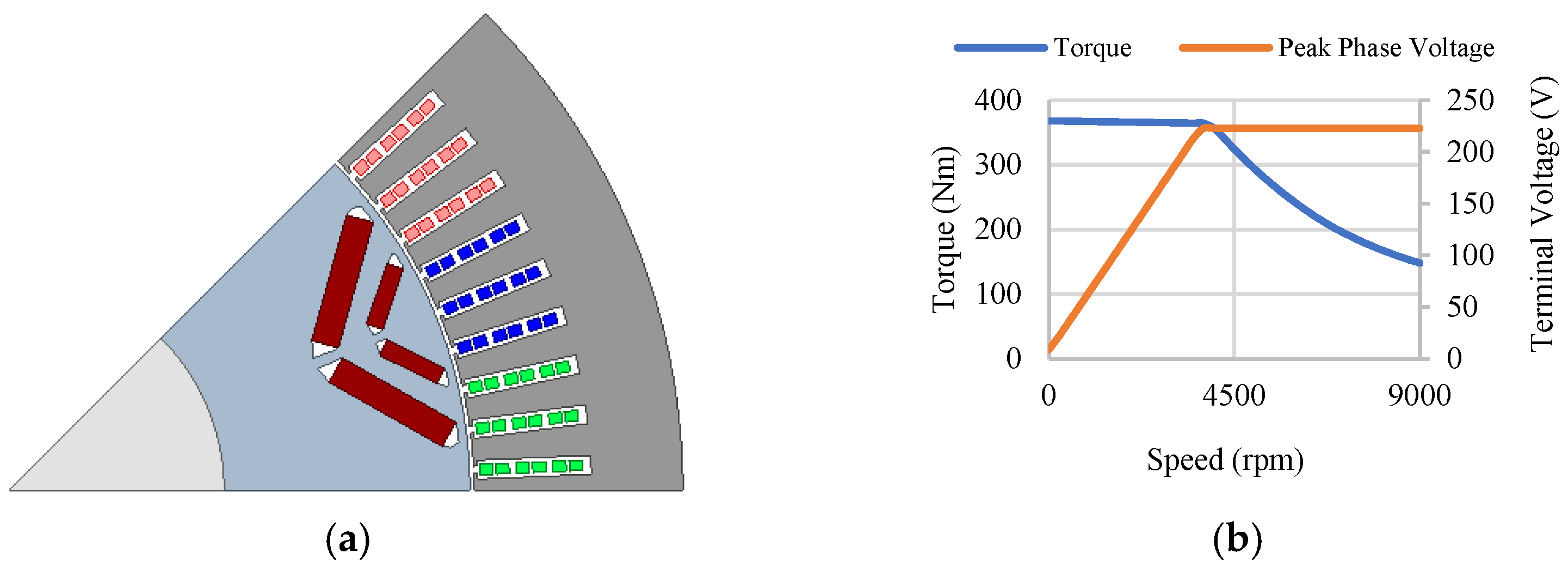

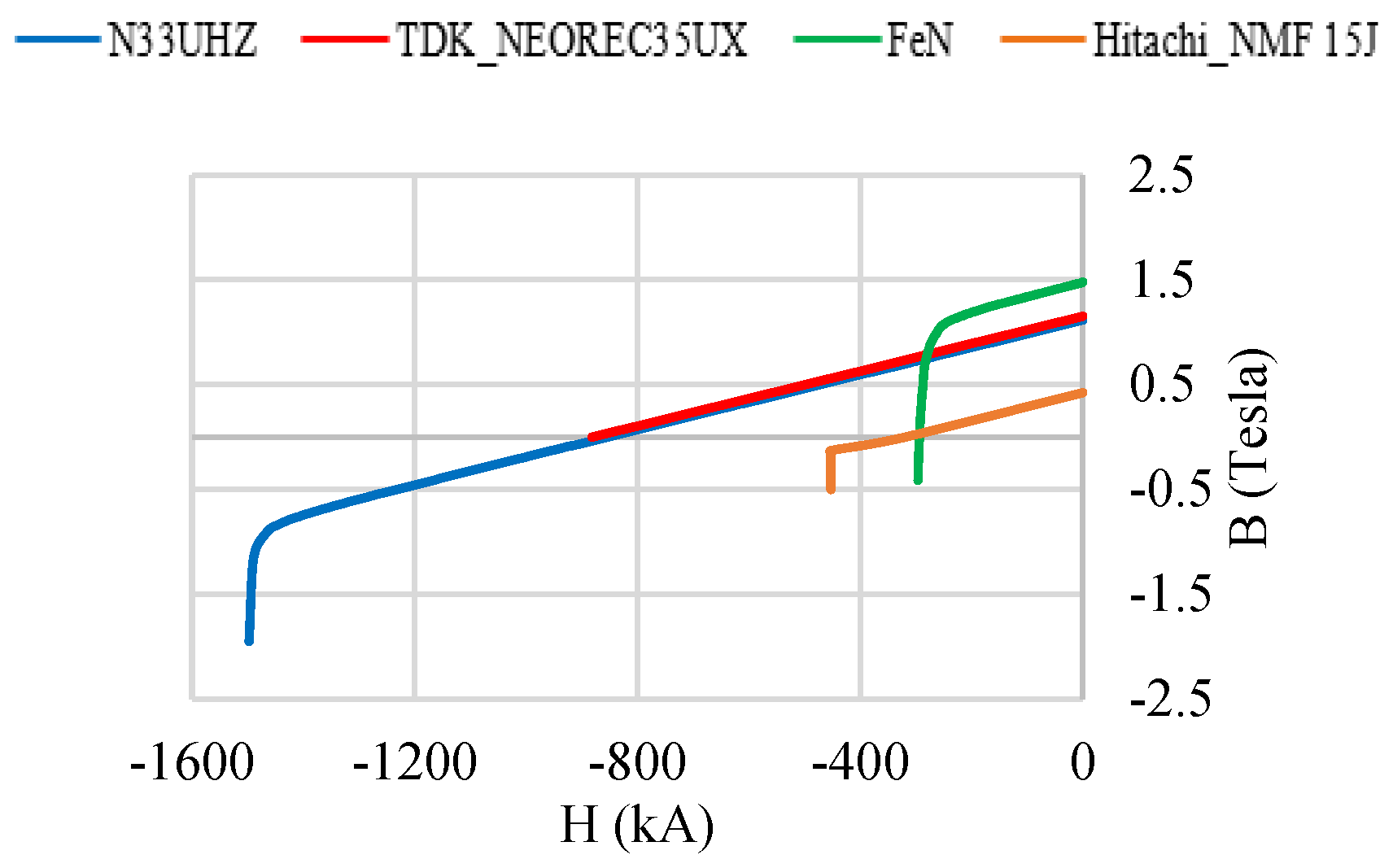
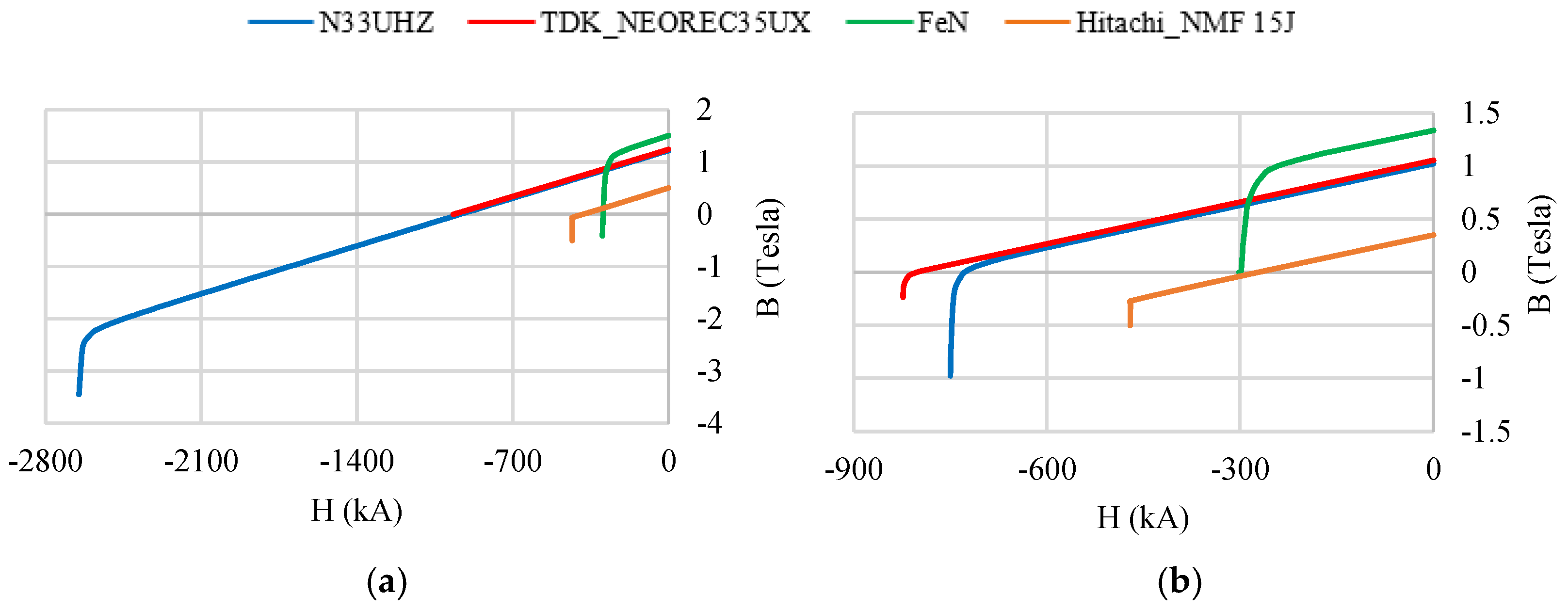
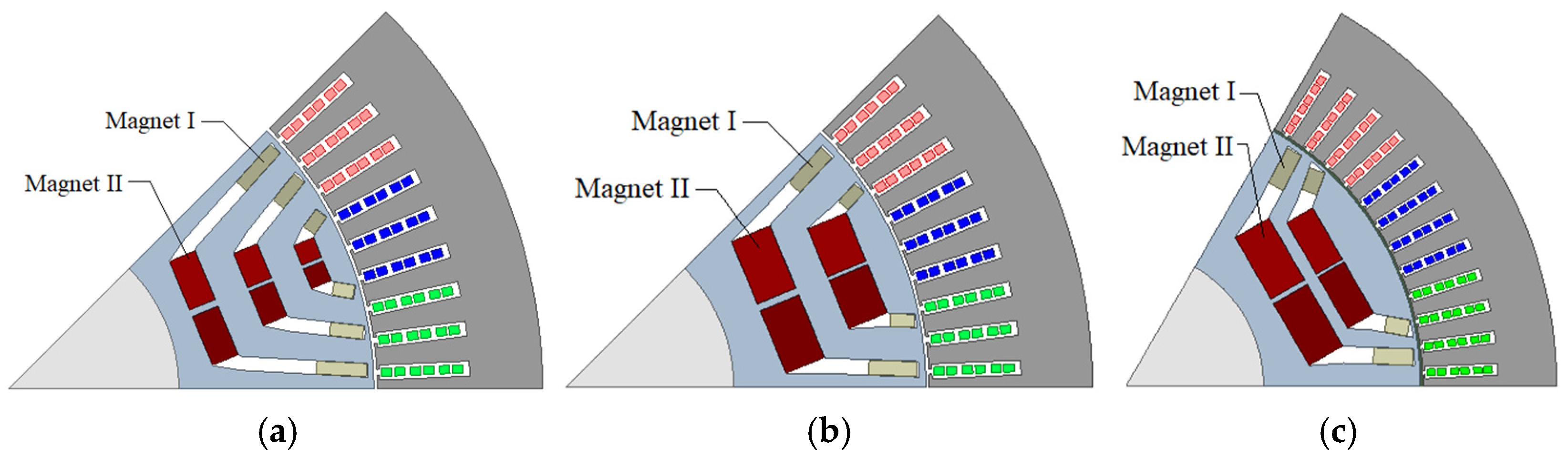



| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Slot/Pole Combination | 72s/8p | Peak Current (ARMS) | 400 |
| Stator OD (mm) | 204 | Peak Phase Voltage (V) | 223 |
| Rotor OD (mm) | 139.5 | Peak Power (kW) | 150 |
| Airgap Length (mm) | 0.625 | Corner Speed (rpm) | 3750 |
| Stack Length (mm) | 125 | Maximum Speed (rpm) | 9000 |
| Stacking Factor | 0.93 | Torque at 3750 rpm (Nm) | 365 |
| Series Turns per Phase | 24 | Torque at 5000 rpm (Nm) | 293 |
| Parallel Paths | 3 | Torque at 7000 rpm (Nm) | 200 |
| Conductors per Slot | 6 | Torque at 9000 rpm (Nm) | 148 |
| Combinations | Magnet I | Magnet II |
|---|---|---|
| C1 | NdFeB (Arnold Magnetics N33UHZ) | Iron Nitride (FeN-36MGOe) |
| C2 | Low-Dy NdFeB (TDK-NEOREC35UX) | Iron Nitride (FeN-36MGOe) |
| C3 | Low-Dy NdFeB (TDK-NEOREC35UX) | Ferrite (Hitachi_NMF-15J) |
| C4 | NdFeB (Arnold Magnetics N33UHZ) | Ferrite (Hitachi_NMF-15J) |
| C5 | Ferrite (Hitachi_NMF-15J) | Iron Nitride (FeN-36MGOe) |
| C6 | Air | Iron Nitride (FeN-36MGOe) |
| Optimization Parameters | Range | ||
|---|---|---|---|
| 2 Layers, 8 Poles | 2 Layers, 6 Poles | 3 Layers, 8 Poles | |
| Barrier angle, km (degrees) | 20–30 | 30–50 | 25–34 |
| Center magnet thickness, h_cpm (mm) | 6–11 | 6–9 | 3–6 |
| Side magnet thickness, h_spm (mm) | 2–3.5 | 3–4 | 2–3 |
| Center magnet length, l_cpm (mm) | 6–12.6 | 11–20 | 3–10 |
| Side magnet length, l_spm (mm) | 1–8.5 | 0.5–9 | 3–7.5 |
| Optimization Method | Complexity | Accuracy | Computational Time | Computational Cost |
|---|---|---|---|---|
| Analytical method | High | Low | Fast | Low |
| Response Surface Model-based methods | High | Fair | Fast | Low |
| Magnetostatic FE-based methods | High | Fair | Fast | Low |
| Time-stepped FE-based methods with parallel processing | Low | High | Fast | Moderate |
| Parameters | Baseline | C1 | C2 | C3 | C4 | C5 | C6 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3L-8p | 2L-8p | 2L-6p | 3L-8p | 2L-8p | 2L-6p | 3L-8p | 2L-8p | 2L-6p | 3L-8p | 2L-8p | 2L-6p | 3L-8p | 2L-8p | 2L-6p | 3L-8p | 2L-8p | 2L-6p | ||
| Rare-earth Reduction (%) | 0 | 53.8 | 63.7 | 61 | 55 | 68 | 62.3 | 21.7 | 22.6 | 6.3 | 16.9 | 21.2 | 5 | 100 | 100 | 100 | 100 | 100 | 100 |
| Torque at Corner Speed (Nm) | 365 | 370 | 399 | 375 | 373 | 405 | 373 | 368.5 | 367 | 353 | 367 | 364.5 | 351 | 378 | 382 | 367 | 374 | 381 | 368 |
| Torque at 5000 rpm (Nm) | 293 | 323 | 341 | 346 | 325 | 344 | 344 | 312 | 321 | 335 | 313 | 317.5 | 333 | 338 | 340 | 346 | 326 | 342 | 347 |
| Torque at 7000 rpm (Nm) | 200 | 225 | 239 | 239 | 229 | 240 | 239 | 213 | 227 | 237 | 216 | 224 | 237 | 239 | 239 | 237 | 229 | 239 | 237 |
| Torque at 9000 rpm (Nm) | 148 | 165 | 165 | 151 | 167 | 165 | 156 | 156 | 166 | 169 | 158 | 164 | 169 | 170 | 168 | 148 | 167 | 163 | 149 |
| Back EMF Reduction due to Demag at −20 °C (%) | 0 | 2.7 | 1.5 | 8.9 | 2 | 1.7 | 10.2 | 0.02 | 0.03 | 0.09 | 0 | 0.03 | 0.09 | 2.9 | 3 | 11.1 | 3.6 | 3 | 10 |
| Back EMF Reduction due to Demag at 150 °C (%) | 0 | 2.2 | 2.2 | 8.5 | 1.3 | 1.9 | 8.8 | 0.01 | 0.01 | 0.06 | 0.9 | 0.8 | 0.9 | 2.5 | 2.6 | 10.4 | 2.95 | 3 | 10.2 |
| Torque Ripple (%) | 7.1 | 8.7 | 4.7 | 17.8 | 9.2 | 5.4 | 15.1 | 11.2 | 5.5 | 12.6 | 12.7 | 5.8 | 12.9 | 7.5 | 3.4 | 19.4 | 14.6 | 11.5 | 13.1 |
| RE Magnet Mass (kg) | 1.62 | 0.75 | 0.59 | 0.64 | 0.73 | 0.5 | 0.61 | 1.27 | 1.25 | 1.52 | 1.35 | 1.28 | 1.55 | 0 | 0 | 0 | 0 | 0 | 0 |
| RE-Free Magnet Mass (kg) | 0 | 1.26 | 2.34 | 2 | 1.37 | 2.1 | 2.8 | 1.09 | 1.9 | 1.28 | 1.09 | 1.8 | 1.25 | 2.94 | 2.96 | 2.65 | 1.85 | 2.93 | 2.7 |
| Cost (USD) | 113.4 | 90.3 | 111.5 | 104.8 | 92.2 | 98 | 126.7 | 99.8 | 106.5 | 119.2 | 105.4 | 107.6 | 121 | 67.6 | 75.4 | 75.7 | 55.5 | 87.9 | 81 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, P.; Wilson, R.; EL-Refaie, A. Electromagnetic Design Optimization Integrated with Mechanical Stress Analysis of PM-Assisted Synchronous Reluctance Machine Topologies Enabled with a Blend of Magnets. Energies 2024, 17, 1873. https://doi.org/10.3390/en17081873
Kumar P, Wilson R, EL-Refaie A. Electromagnetic Design Optimization Integrated with Mechanical Stress Analysis of PM-Assisted Synchronous Reluctance Machine Topologies Enabled with a Blend of Magnets. Energies. 2024; 17(8):1873. https://doi.org/10.3390/en17081873
Chicago/Turabian StyleKumar, Praveen, Robin Wilson, and Ayman EL-Refaie. 2024. "Electromagnetic Design Optimization Integrated with Mechanical Stress Analysis of PM-Assisted Synchronous Reluctance Machine Topologies Enabled with a Blend of Magnets" Energies 17, no. 8: 1873. https://doi.org/10.3390/en17081873
APA StyleKumar, P., Wilson, R., & EL-Refaie, A. (2024). Electromagnetic Design Optimization Integrated with Mechanical Stress Analysis of PM-Assisted Synchronous Reluctance Machine Topologies Enabled with a Blend of Magnets. Energies, 17(8), 1873. https://doi.org/10.3390/en17081873






