Energy Harnessing Performance of Oscillating Foil Submerged in the Wake of a Fixed Cylinder

Abstract

The energy harnessing from flow-induced vibrations (FIV) by an oscillating foil placed tandemly behind a circular cylinder (which serves as a vortex generator) is investigated. The foil is submerged in the wake produced by the fixed cylinder and could oscillate in the direction perpendicular to the incoming flow with single-degree freedom. The spacing ratio ranges from 1.0 to 5.0. The oncoming fluid velocity is U = 1–10 m/s, corresponding to the reduced velocity U_r = 3.81–38.08 and the Reynolds number Re = 9.58 × 10³–9.58 × 10⁴. Four harnessing damping ratios (ζ_harness = 0.0054–0.0216) are used to simulate the energy conversion conditions. The main conclusions are: (1) The optimal oscillation pattern related to the highest harnessed energy emerges as the spacing ratio close to 1.0. (2) The airflow energy converted by the foil is positively correlated with the harnessing damping ratio because the amplitude responses are similar at various harnessing damping ratios. A high velocity yields the highest harnessed power. (3) The harnessing efficiency of the foil could reach 48.89%, which is much more than that of an isolated flapping foil.

1. Introduction

Flow-induced vibration (FIV) provides an alternative way to harness power from the flow. This phenomenon is observed in the flow field after a slender structure, with bluff sections such as circular or square sections. Alternating lift acts on the surfaces of these structures with vortex shedding from bodies that excited vortex-induced vibration (VIV) and galloping [1]. The energy exchanges from the flow and the slender body are typically suppressed in engineering applications [2,3]. Instead of suppressing FIV, Bernitsas et al. proposed the vortex-induced vibration aquatic clean energy (VIVACE) converter (Figure 1) for extracting ocean/river current hydrokinetic energy capable of high-efficiency energy at high-efficiency speeds as low as 0.5 knots by strengthening vortex shedding; the devices with three tandem cylinders are shown in [4].

Inspired by aquatic animals, insects, and birds that utilize oscillatory motions with wings or fins to achieve propelling, Wu et al. proposed a concept on which an oscillating wing could extract energy from a surrounding flow [5]. As a streamlined structure, von Karmen wake rarely occurs when fluid flows past the wing, which is fixed in a flow field with zero degrees of the angle-of-attack (AOA). McKinney and DeLaurier verified the concept by using a windmill to extract energy from the steady flow. A windmill experimental model which combined plunging and pitching motion was tested in the wind tunnel, and the highest efficiency was 28.3%, which could compare with that of traditional rotary turbines [6].

The research of the flapping foil energy converters can be classified into three types based on activating mechanisms: active, semi-active, and fully passive [7]. The active flapping foil energy converts the heaving and pitching motions, which are driven by the flow–structure coupling, and the parameters such as the top point of the heaving motion and the amplitude of the pitching motion are fixed. Jones et al. provided the plunge amplitude and pitch amplitude with their oscillating foil [8]. Dumas and Kinsey simulated NACA 0015 foil with a limitation of the angle of pitching in 0–90°, and the range of reduced frequency was 0–0.25; the efficiency finally reached as high as about 35% [9]. The pitching motion of semi-active foils is forced and induces plunging motion. Zhu and Peng studied the performance of the second type of foil under a low Reynolds number with an adjusted pitching axis and damping of the system [10]. The third type, a fully passive energy converter in which plunging and pitching motions are linked by mechanical structures such as phase gears, can achieve 26% efficiency. Young et al. raise the efficiency to 41% with the control of an effective AOA [11]. Extensive research on the flapping wing can be found in Bradley et al. [12], Zhu et al. [13], Teng et al. [14], Veilleux et al. [15,16], and so on.

VIV and galloping are the most common kinds of FIV for elastically supported structures. VIV has a limited amplitude and only occurs in the lock-in range [17,18,19]. On the contrary, the amplitude in galloping is larger than that in VIV and increases with the oncoming fluid velocity [20]. For imploring the performance of a multiple-bodies configuration consisting of cylinders in FIV, extensive research has been conducted. As we know, there are interactions between shear layers and vortexes when fluid flows past multiple body configurations that influence the vortex street downstream [21]. Zdravkovich [22] divided the flow regime of two stationary cylinders in a tandem arrangement into three parts based on the space between two bodies. The three flow regimes are a single slender body (1 < L/D < 1.2–1.8), reattachment (1.2–1.8 < L/D < 3.4–3.8), and a binary vortex street (L/D > 3.4–3.8), where L is the distance between the center of the two cylinders and D is the cylinder diameter. Qin et al. organized an experiment to investigate the flow-induced vibration of two circular cylinders in tandem at a spacing ratio L/D = 1.2–6.0 and a reduced velocity U_r = 3.8–47.8. The downstream cylinder underwent divergent violent galloping at L/D = 2.5 and U_r > 17.3, and the amplitude ratio was exceeding the value of the single cylinder and increased with velocity [23]. Assi et al. performed a study on the response of the downstream cylinder and found that wake unsteadiness plays a critical role in the wake-induced process [24]. Abundant studies have been conducted on energy conversion from the FIV. Sun et al. investigated the flow-induced motions of a single rough circular cylinder by changing the mass ratio, damping, and stiffness and found that the VIV regime narrowed with increasing harnessing damping ratios, which increased the onset of galloping [25]. Li et al. simulated a single cylinder with larger passive turbulence control (PTC) at an expanded Re range beyond MRELab and found that the curve of the amplitude ratio showed the back-to-back VIV and galloping at all tested damping ratios; more power could be extracted from the flow with increasing harnessing damping ratios [26]. Zhang et al. studied the impact of a downstream cylinder on harnessing energy from VIV, and the results revealed that the spacing ratio has an important influence on energy conversion [27].

Some scholars utilized the wake effect to enhance the performance of the energy converter. Alam et al. studied the aerodynamic characteristics of a cylinder submerged in the wake of another one; the lift force coefficient of the downstream cylinder was twice that of a single cylinder [28]. Chen et al. tested different diameter cylinders (d/D = 0.4; d is the diameter of the upstream cylinder which is fixed and D is the diameter of the other one) that were arranged in tandem in a wind tunnel. The amplitude response of the oscillators showed VIV, separated VIV and galloping, and combined VIV and galloping with various spacing ratios and damping ratios that were different from the response of the single cylinder, which only had a VIV phenomenon at the entire velocity regime [29]. Sun et al. investigated the effect of spacing on hydrokinetic energy conversion by two rough tandem cylinders and found the gap flow went to the bottom of the downstream cylinder and pushed its motion at the galloping regime, which meant more energy could be captured [30]. E. S. K. et al. conducted an experiment with two to four circular cylinders, and the amplitude of the first cylinder was 7.2% higher than that of a single cylinder [31]. Liao et al. studied the effects of vortex shedding from the upstream cylinder on the vorticity structure and lift force with flapping foil by changing the relative position between the cylinder and foil and the AOA of a foil [32]. Ma et al. researched a design of a dual flapping wings configuration in which the heaving and pitching motions are fully controlled by flow-induced flapping motions with NACA 0015 foil; the result revealed that a higher harnessing efficiency could reach smaller R and $\beta$ values [33]. Li et al. changed two parameters, the distance between the D-section cylinder and foil and the flapping frequency, to investigate the performance of flapping foils in the vortex street produced by the D-section cylinder [34]. The maximum efficiency is 39.81% when the flapping frequency is close to the frequency of wake. The influence of the wake produced by the cylinder is weaker as the distance increase. However, the type of foils in most wake effect studies is active or semi-active; fully passive research is rare. Referring to the above literature, the effect of the downstream vortex or shear layers produced by upstream bluff bodies has been verified. The bluff bodies arranged downstream could enhance its performance of energy conversion at certain conditions.

Although the flapping foil can harness energy from plunging and pitching motions, the plunging motion constitutes the main stimulus for power extraction [35]. In this paper, we prompt a design on which a fully passive NACA 0016 foil with a single degree of freedom is placed in the wake produced by a circular cylinder to study the performance of energy harnessing with the cylinder as a vortex generator. The direction of the single-degree-of-freedom motion is perpendicular to the oncoming flow. In order to convert kinetic energy to mechanical energy in foil, additional damping is introduced for simulating the generator. The distance between the circular cylinder and the foil and the different velocities of oncoming flow are researched. In Section 2, the simplified model of the system and the parameters are presented. In Section 3, the numerical method and mathematical modeling are provided. In Section 4, the amplitude and frequency response of the foil at different spacing ratios and the performance of energy conversion at S/L = 1.0 for various damping ratios are discussed. Section 5 is the conclusion of this research. The proposed application can be scaled up or down for commercial usage or for the micro sensor.

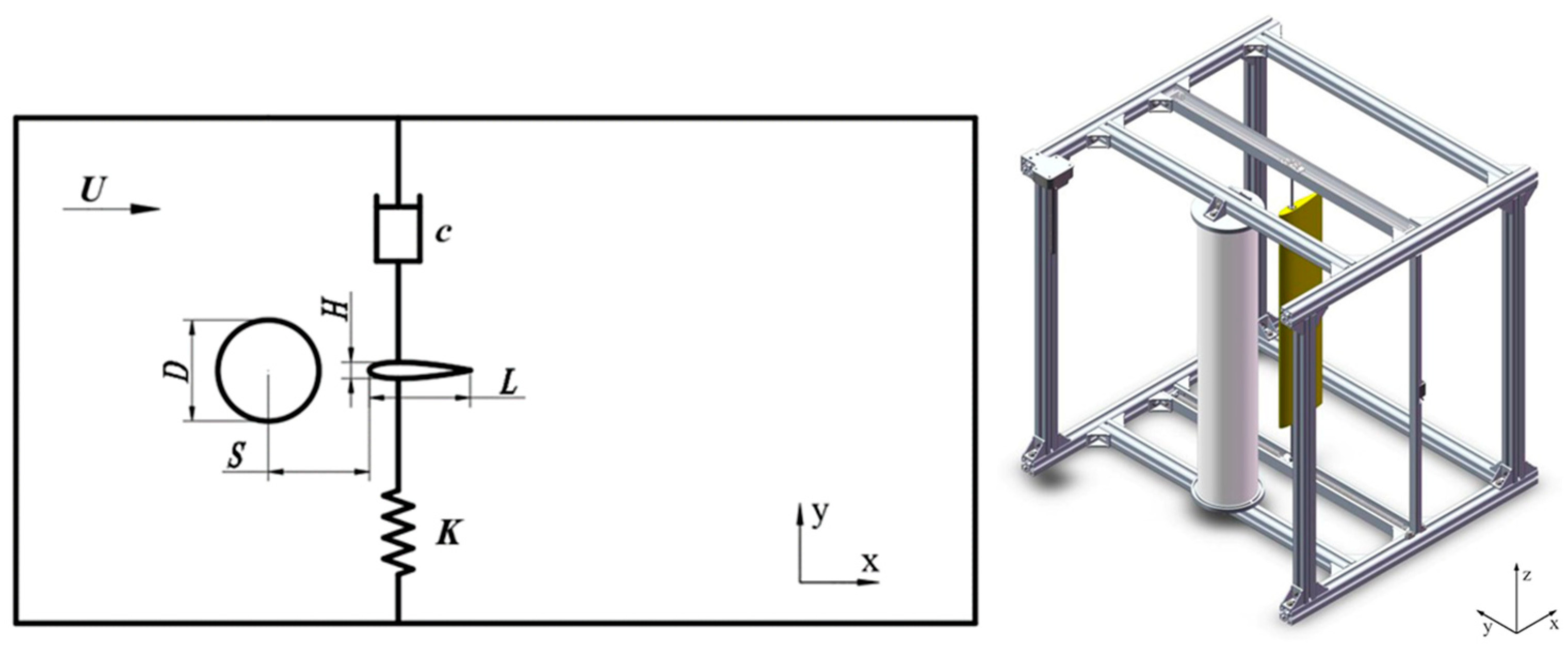
2. Physical Model

The physical model is simplified to a two-dimensional model. The physical model consists of a rigid circular cylinder, an oscillating foil, and a supporting linear spring, as shown in Figure 2. The diameter of the cylinder is $D$, and $L$ and $H$ are the chord length and the maximum thickness of the foil, respectively. $S$ is the distance from the cylinder’s center to the foil’s leading-edge point. $K$ is the stiffness of the spring, and $c$ is the damping of the system.

The cylinder and the foil are arranged in tandem, and the foil oscillates in the y-direction. The parameters of the system are listed in

Table 1. The parameters of the system.

Item	Symbol	Value
Diameter of the upstream cylinder	D [m]	0.14
Chord length of the wing	L [m]	0.14
The maximum thickness of the wing	H [m]	0.0227
Space	S [m]	0.14–0.7
Mass of the foil	mfoil [kg]	0.462
Spring constant	K [N/m]	64.14
The damping ratio of the structure	ζstructure [Ns/m]	0.0054
The damping ratio of harnessing	ζharness [Ns/m]	0.0054–0.0216
Natural frequency	fn [Hz]	1.8756

.

The damping ratio of the structure is 0.0054, which was used in an experiment conducted by Khalak et al. [36]. Four values from 0.0054 to 0.0216 are harnessing damping ratios that are adopted to simulate the condition of harvesting energy from flowing fluid.

3. Numerical Method and Mathematical Modeling

The numerical method of this simulation is introduced in this section. The mathematical modeling of the fluid dynamics and the oscillating foil, the computational domain, the grid generation, the grid sensitivity, and the validation are presented as well in this section.

3.1. Governing Equations

3.1.1. Fluid Dynamics

In the simulation, the air is employed as the medium of the flow field, and the velocity of incoming flow is much less than Ma 0.3, so we consider the flow incompressible in the flow field. The basic Reynolds-Averaged Navier–Stokes equations are:

$$\frac{\partial \rho u_i}{\partial x_i}=0$$

(1)

$$\frac{\partial (\rho u_i)}{\partial t}+\frac{\partial (\rho u_i{u}_j)}{\partial x_j}=-\frac{\partial p}{\partial x_i}+\frac{\partial (2\mu S_{ij}-\rho \overline{{u^{\prime }}_i{u^{\prime }}_j})}{\partial x_i}$$

(2)

where u is the time-average velocity of the fluid particle; p is the time-average pressure of the fluid particle; $\mu$ is the molecular viscosity; S_ij is the mean stress tensor; and $\overline{{u^{\prime }}_i{u^{\prime }}_j}$ is the Reynolds-stress tensor.

3.1.2. Turbulence Model and Numerical Schemes

The turbulence model employed in this simulation is the SST (Shear-Stress Transport) k-ω model, which is a two-equation model for solving the two transport equations of the kinematic eddy viscosity k and the specific dissipation rate ω. Detailed descriptions of this model can be found in Menter’s research [37]. For the problem of flow around the bluff body, the SST k-ω model shows good agreement with the initial VIV branch and lower branch [38] and can predict the separation phenomenon when undergoing adverse pressure gradient flows accurately. The SST k-ω model combines the k-ω model and the k-ε model with a mixed function, it applies k-ω the model in the boundary layer, and the k-ε model is used in the region out of the boundary layer. The transport equations of $k$ and ω are:

$$\frac{\partial (\rho k)}{\partial t}+\frac{\partial (\rho U_{j}k)}{\partial x_j}=\frac{\partial }{\partial x_j}·[(\mu +{\sigma }_k{\mu }_t)\frac{\partial k}{\partial x_j}]+{\tilde{P}}_k-{\beta }^{\ast }\rho \omega k$$

(3)

$$\frac{\partial (\rho \omega )}{\partial t}+\frac{\partial (\rho U_j\omega )}{\partial x_j}=\frac{\partial }{\partial x_j}[(\mu +{\sigma }_k{\mu }_t)\frac{\partial \omega }{\partial x_j}]+\frac{\alpha }{{\mu }_t}{\tilde{P}}_k-\beta \rho {\omega }^2+2(1-F_1)\frac{\rho {\sigma }_{\omega 2}}{\omega }\frac{\partial k}{\partial x_j}\frac{\partial \omega }{\partial x_j}$$

(4)

The equation ${\tilde{P}}_k$ is:

$${\tilde{P}}_k=\min (P_k,10{\beta }^{\ast }\rho k\omega )$$

(5)

$$P_k={\mu }_t\frac{\partial U_i}{\partial x_j}(\frac{\partial U_i}{\partial x_j}+\frac{\partial U_j}{\partial x_i})$$

(6)

where F₁ in Equation (4) is the first mix function, F₁ = 0, and the equations are the k-ε model. On the contrary, F₁ = 1, and the equations are the k-ω model. F₁ is:

$$F_1=\tanh ({\arg }_1^4)$$

(7)

where arg₁ is the function of the distance y from the node of the grid to the nearest wall:

$${\arg }_1=\min [\max (\frac{\sqrt{k}}{{\beta }^{\ast }\omega y},\frac{500\mu }{y^2\omega }),\frac{4\rho {\sigma }_{\omega 2}k}{C{D}_{k\omega }{y}^2}]$$

(8)

$$C{D}_{k\omega }=\max (2\frac{\rho {\sigma }_{\omega 2}}{\omega }\frac{\partial k}{\partial x_j}\frac{\partial \omega }{\partial x_j},{10}^{-10})$$

(9)

The viscosity of the turbulence eddy is defined as:

$${\nu }_t=\frac{{\mu }_t}{\rho }=\frac{a_{1}k}{\max (a_1\omega ,S{F}_2)}$$

(10)

where S is the invariant of the strain rate, and F₂ is the second mix function:

$$F_2=\tanh ({\arg }_2^2)$$

(11)

$${\arg }_2=\max (2\frac{\sqrt{k}}{0.09\omega y},\frac{500\mu }{y^2\omega })$$

(12)

Set ${\varphi }_1$ as the empirical parameters of the standard k-ω model (β₁, σ_k1, …, α₁) ${\varphi }_2$ as the empirical parameters of the k-ε model transformed into k-ω form (β₂, σ_k2, …, α₂), and $\varphi$ as the empirical parameters of the SST k-ω model. The relationship is:

$$\varphi =F_1{\varphi }_1+(1-F_1){\varphi }_2$$

(13)

The coefficients in the above equations are: β* = 0.09, β₁ = 0.075, β₂ = 0.0828, σ_k1 = 0.85, σ_k2 = 1.0, σ_ω1 = 0.5, σ_ω2 = 0.856, α₁ = 5/9, α₂ = 0.44, and a₁ = 0.31.

The dimensionless time step $\Delta t^{\ast }$ for each tested case is 0.005 ($\Delta t^{\ast }=\Delta tU/L$; $\Delta t$ is the time step of the actual calculation). In addition, a second-order upwind spatial discrete scheme and a second-order implicit time discretization are applied to discrete the governing equations, and the SIMPLEC (SIMPLE-Consistent [39]; SIMPLE is a Semi-Implicit Method for Pressure Linked Equations [40]) algorithm of pressure–velocity coupling is employed for the simulation. The ANSYS Fluent software (19.3) is adopted to realize the function. Because the oscillation foil is set in the wind tunnel in this research, the Reynolds number is set around 98,000; in higher Reynolds numbers, the mathematical model would not hold.

3.1.3. Motion Kinematics

As mentioned above, the model has been simplified to a mass-spring-damper oscillator model. The foil has a single degree of freedom and oscillates transversely to the free stream; the modeling equation is:

$$m\ddot{y}+c\dot{y}+Ky=F_y$$

(14)

where $\dot{y}$ is the velocity of the foil, $\ddot{y}$ is the acceleration of the foil, and F_y is the force applied on the foil by fluid in the y-direction.

The damping ratio ζ and natural frequency ω₀ are introduced into Equation (14):

$$\ddot{y}+2\zeta {\omega }_0\dot{y}+{\omega }_0^{2}y=F_y/m$$

(15)

Due to the medium of fluid being air, the added mass is relatively small compared with the mass of foil, so here, the added mass influence is ignored. A fourth-order Runge–Kutta algorithm is used to solve Equation (15) with a small-time step, and the y-direction motion of the foil and the fluid force are solved in a couple of ways.

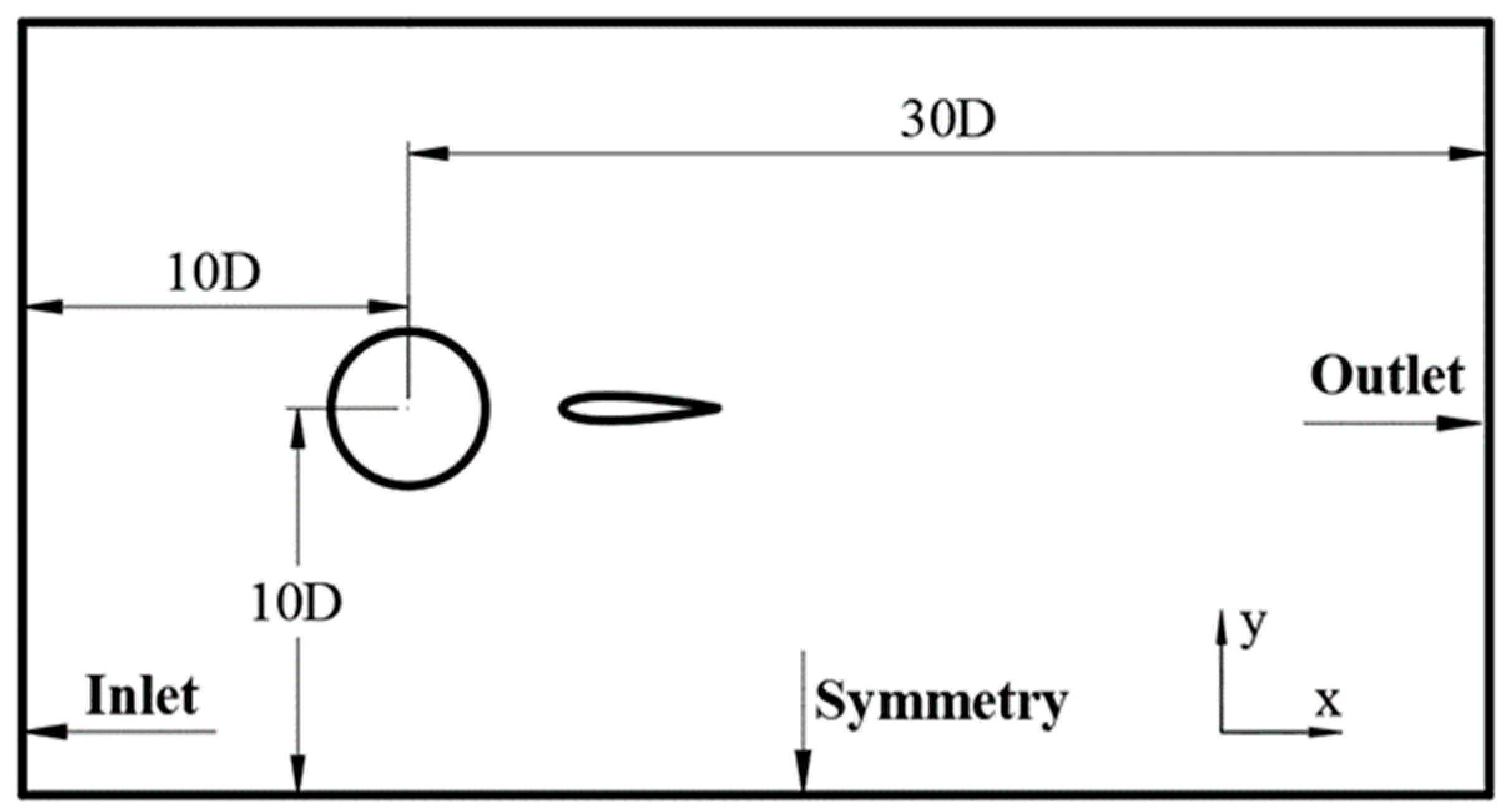
3.2. Computational Domain

The computational domain dimensions are 40D × 20D (Diameter), as shown in Figure 3. The inlet boundary is set 10D upstream from the center of the front cylinder and the velocity–inlet boundary condition is specified at the inlet boundary. 30D is the distance from the center of the cylinder to the outlet boundary whose boundary condition is the pressure outlet. The upper and lower boundaries are symmetry boundary conditions, and the distances are both 10D. The no-slip boundary condition is employed in the surfaces of the cylinder and the foil.

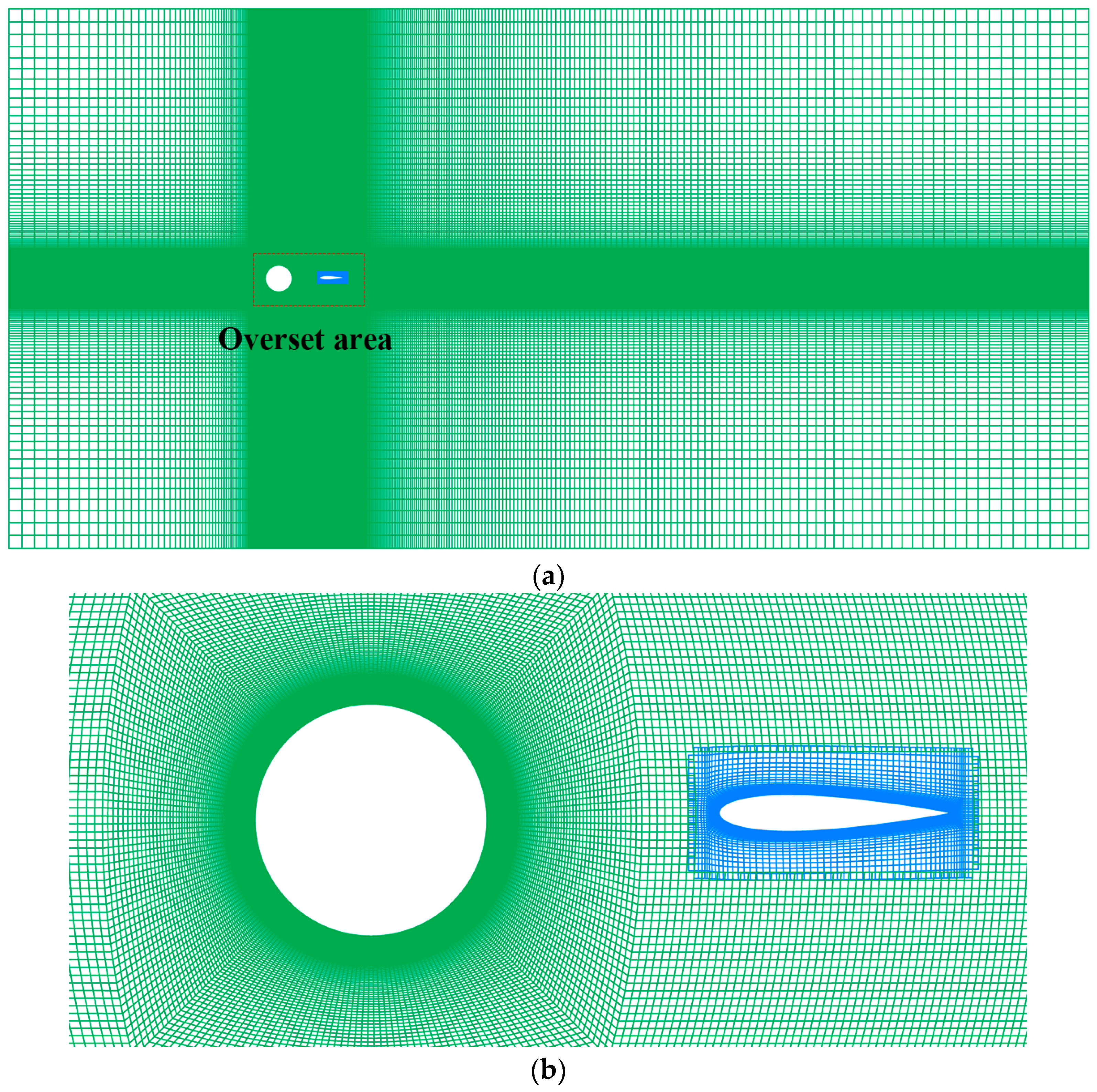
3.3. Grid Generation

The global grid generated mesh structured for each case in Figure 4a. To achieve the motion of the foil, the overset mesh and dynamic mesh technologies are applied. The overset grid method is dividing the complex area into sub-areas with simple geometric boundaries, and each sub-area generates an independent computational grid. The flow field information between different grids is transferred by interpolation at the overset domain boundaries. Figure 4b displays the close-up of the overset area; the overset boundary is the junction of the foil grid and the background grid. The background mesh of this numerical investigation includes the circular cylinder, and the foreground mesh is the grid around the foil. The moving velocity of the foil is calculated by the User-Defined Function (UDF) routine.

Due to the SST $k\text{-}\omega$ model being adopted, the first grid point away from the wall needs a viscous sublayer to solve the flow in the boundary layer. When <5, the first layer of the grid is located in the viscous sublayer; when 30 < y⁺ < 300, the first layer of the grid is located in the log-law layer. This article selects the SST k-w turbulence model for the simulation, which can be solved for the viscous bottom layer. So, the y⁺ (non-dimensional distance to the wall, Equation (16)) which is used to estimate the first grid spacing near the wall calculated is set in the order of one. If the y⁺ exceeds the range when we simulate in some cases, we adjust the spacing of the first grid near the wall and repeat the procedures until the y⁺ meets the requirement.

$$y^{+}=\frac{\Delta y\rho u_{\tau }}{\mu }$$

(16)

$${\mu }_{\tau }=\sqrt{\frac{{\tau }_w}{\rho }}$$

(17)

where $\Delta y$ is the grid distance to the wall; $u_{\tau }$ is the wall friction velocity; and ${\tau }_w$ is the wall shear stress.

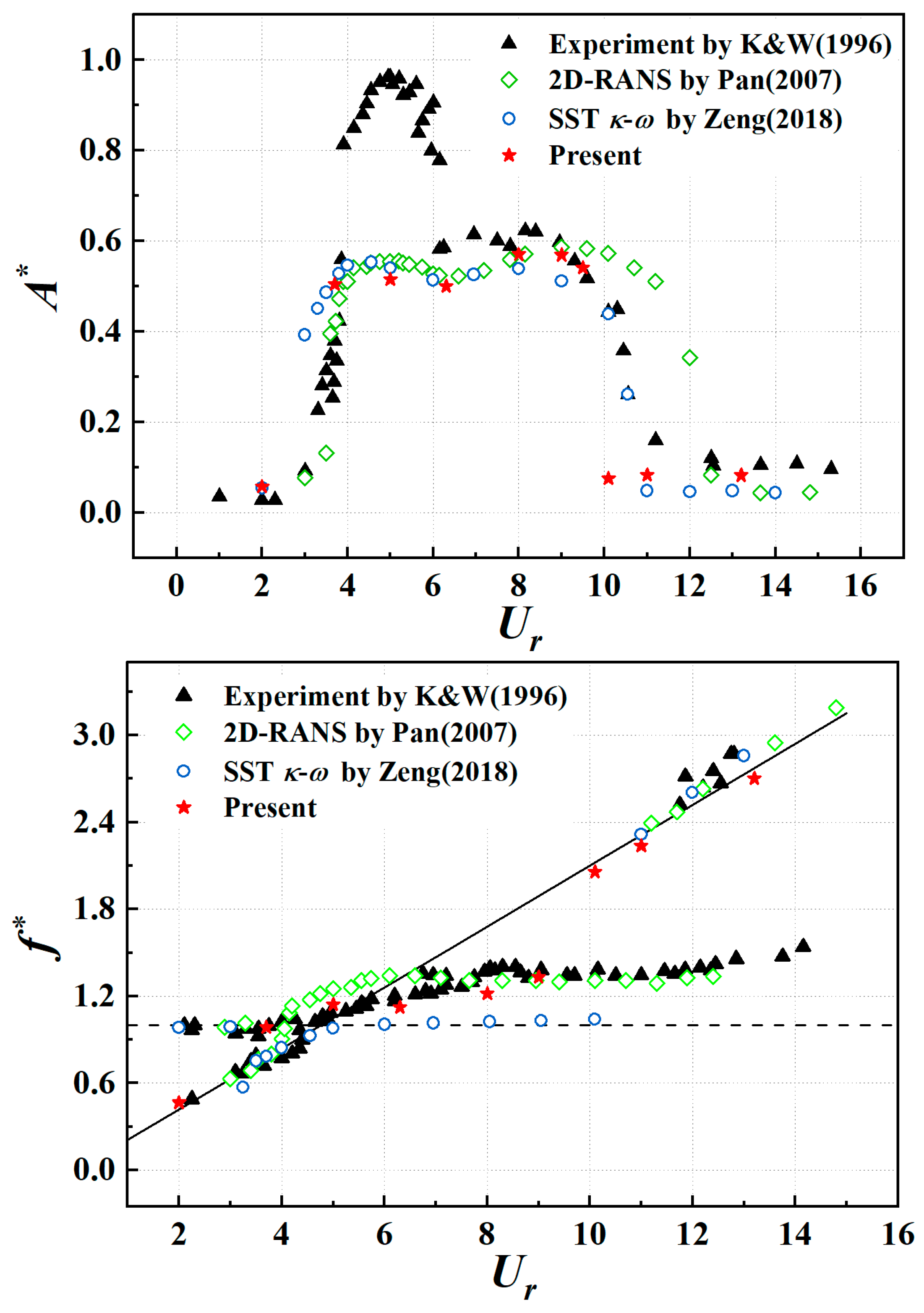
3.4. Validation of the Numerical Model

The grid sensitivity is discussed before the validation. A coarse mesh (circumferential × radial = 208 × 125), a medium mesh (248 × 145), and a high mesh (288 × 165) around the cylinder are studied first.

Three different grid levels are mentioned above a smooth stationary cylinder under the condition of Re = 3900, which is applied to verify the independence of the grid. The present results are compared with previous experimental and numerical results which employed different turbulence models. The time-averaged drag coefficient (C_d,ave) and Strouhal number (St) of each case are presented in

Table 2. Results compared with the experiment and simulations at Re = 3900.

Data Source	Dimension	Turbulence Model	Cd,ave (Drag Coefficient)	St
Parnaudeau [42] Exp.	3D	-	0.99	0.215
Franke J. and W. [43]	3D	LES	0.99	0.209
Lysenko [44]	3D	LES	1.18	0.190
Zhou [45]	2D	SST	1.5	0.215
Present (coarse)	2D	SST	1.534	0.221
Present (medium)	2D	SST	1.526	0.218
Present (high)	2D	SST	1.522	0.216

. There is a large deviation in results between the experiment and the simulations due to three-dimensional characters of vortex shedding from the spanwise direction of a circular cylinder [41]. As shown in Table 2, the deviation of C_d,ave and St for the medium-density grid is 0.26% and 0.92%, compared with that of the high-density grid, respectively. Three types of grids give close results; hence, the medium-density grid is selected for the following simulations.

C_d,ave is the fast Fourier transform (FFT) of the cylinder resistance coefficient time history curve after the vibration is stabilized. A user-defined function (UDF) is written to calculate the displacement of the foil forced by fluid force. For testing the accuracy of the code, a series of simulations regarding a single cylinder is performed, with the parameters setting referred to by Williamson et al. [36]. The amplitude ratios (A* = y(t)/D; D is the diameter of the single cylinder) and frequency ratios (f* = f_osc/f_n) variations with a reduced velocity (U_r = U/f_nD) of the present study are compared with experimental data by Williamson et al. [36] and simulation data by Pan [38] and Zeng [46]; the results are shown in [46]. Although the present amplitude decreases suddenly between U_r = 9 and 11, the trends are captured well with experiments and simulations. There is an upper branch in the experiment that cannot be reached by all simulations. For the numerical solutions with the SST $k\text{-}\omega$ model, the reason for not capturing the upper branch is that the random effect of turbulence is neglected with the introduction of the model. However, the overall trend aside from the upper branch is in good agreement with the numerical and experimental data found in the literature [46].

Figure 5, the U_r corresponds to two amplitude and frequency ratios. This phenomenon is caused by the alternation of the VIV branch. As U_r changes, the initial branch changes to the upper branch and the lower branch changes to the desynchronized branch; the same U_r will appear with two frequencies, one frequency ratio falling on the solid line (the solid line is based on the Strouhal number, the relationship between the estimated frequency ratio and U_r), and the other frequency ratio falling on the dotted line (f* = 1.0).

4. Results and Analysis

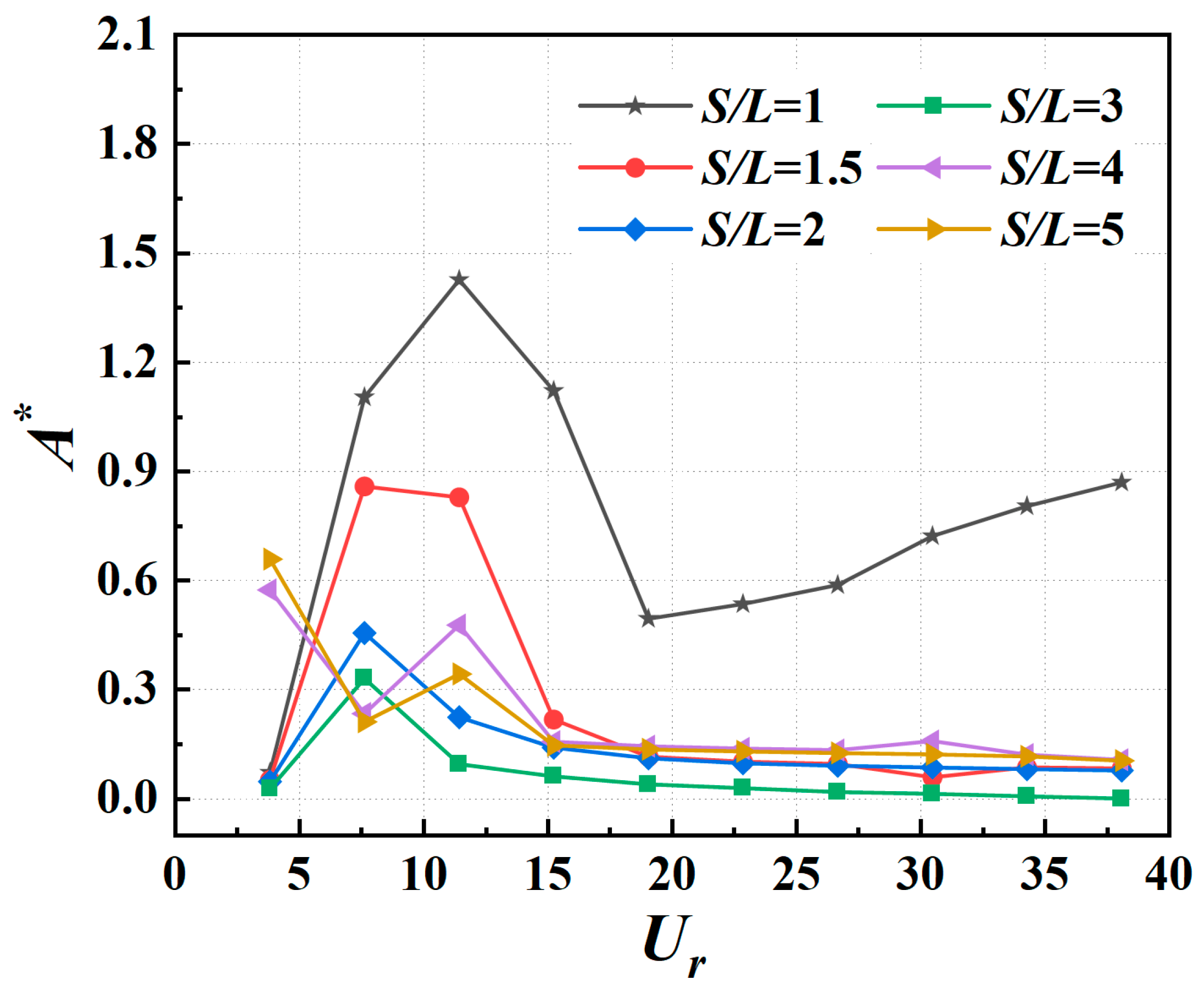
4.1. Amplitude Responses

A series of numerical tests are conducted at S/L = 1.0–5.0 and ζ_structure = 0.0054 for U = 1–10 m/s (corresponding to a reduced velocity U_r = 3.81–38.08 and Reynolds numbers Re = 9.58 × 10³–9.58 × 10⁴). The amplitude A is calculated by the displacement root-mean-square (RMS) value of the foil times $\sqrt{2}$. The variation in amplitude responses with a reduced velocity is shown in Figure 6.

• At S/L ≤ 3.0, the amplitude ratio first increases with an increasing reduced velocity and then drops suddenly to around 0.15 at S/L = 1.5–3.0. The A* drops earlier as the S/L increases because the effect of vortexes shedding from the cylinder is weaker when the gap is larger between the cylinder and the foil at the same U_r. Bokaian et al. investigated the behavior of an oscillating circular cylinder submerged in the wake of a stationary rigid body with various values of cylinder separation ranging from 0.59 to 3, and the system mass-damping ratio is 0.109 [47]. The cylinder exhibited four types of resonances, including vortex-resonance (S/L > 2.5), galloping (S/L = 0.59), combined vortex-resonance and galloping (S/L = 1.0), and separated vortex-resonance and galloping (1.5 < S/L < 2.5). In the present study, the amplitude ratio at S/L = 1.0 first increases until U_r = 11.43 and declines at U_r = 11.43–19.04; then, it rises at a smaller rate again as U_r grows. The trend at S/L = 1.0 can be divided into combined vortex-resonance and galloping, which is in good agreement with the previous conclusion. However, the amplitude resonances at the other space ratios in Figure 6 are different from Bokaian’s results, which can be attributed to the shape differences in oscillators between the two investigations.
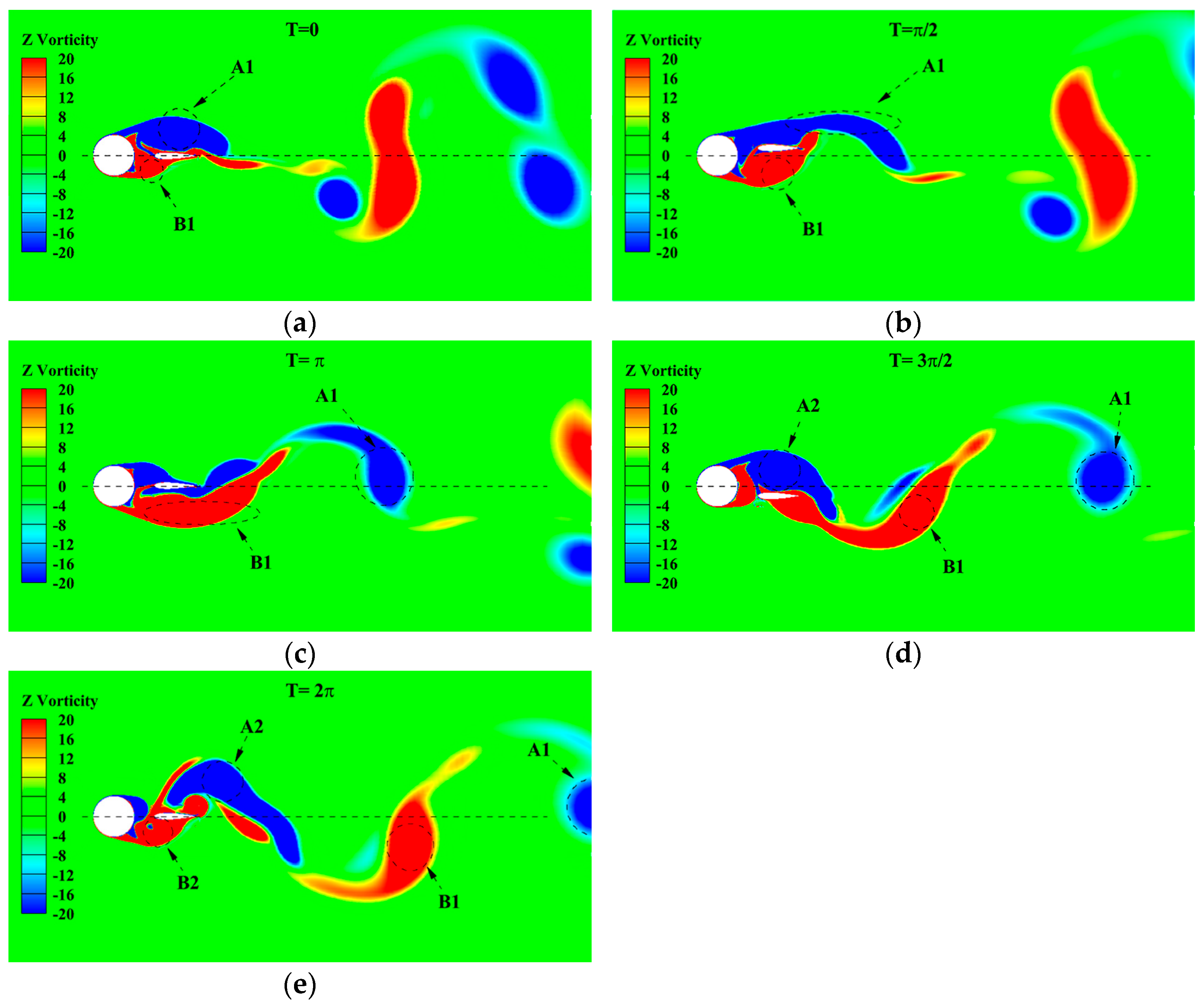
• The amplitude ratios of the foil reach about 0.6 when S/L = 4.0 and S/L = 5.0 at U_r = 3.81, which are obvious differences from the conditions on which S/L ≤ 3.0 corresponds to A* < 0.1. Figure 7 shows the vorticity contours at the moment, pointing at the maximum displacement of the foil at U_r = 3.81 and every space ratio, respectively. The dashed line in the picture is the initial position of the foil. Figure 7a–d shows that the vortex shedding position is located downstream of the foil, and the shear layer affected by the foil is prolonged by the present configuration, which is considered as a whole body consisting of the cylinder. As shown in Figure 7e,f, the vortexes shed in the gap between two rigid bodies and flow downstream along the direction of the incoming velocity, finally forcing the foil to oscillate in the y-direction with a higher amplitude than the former.
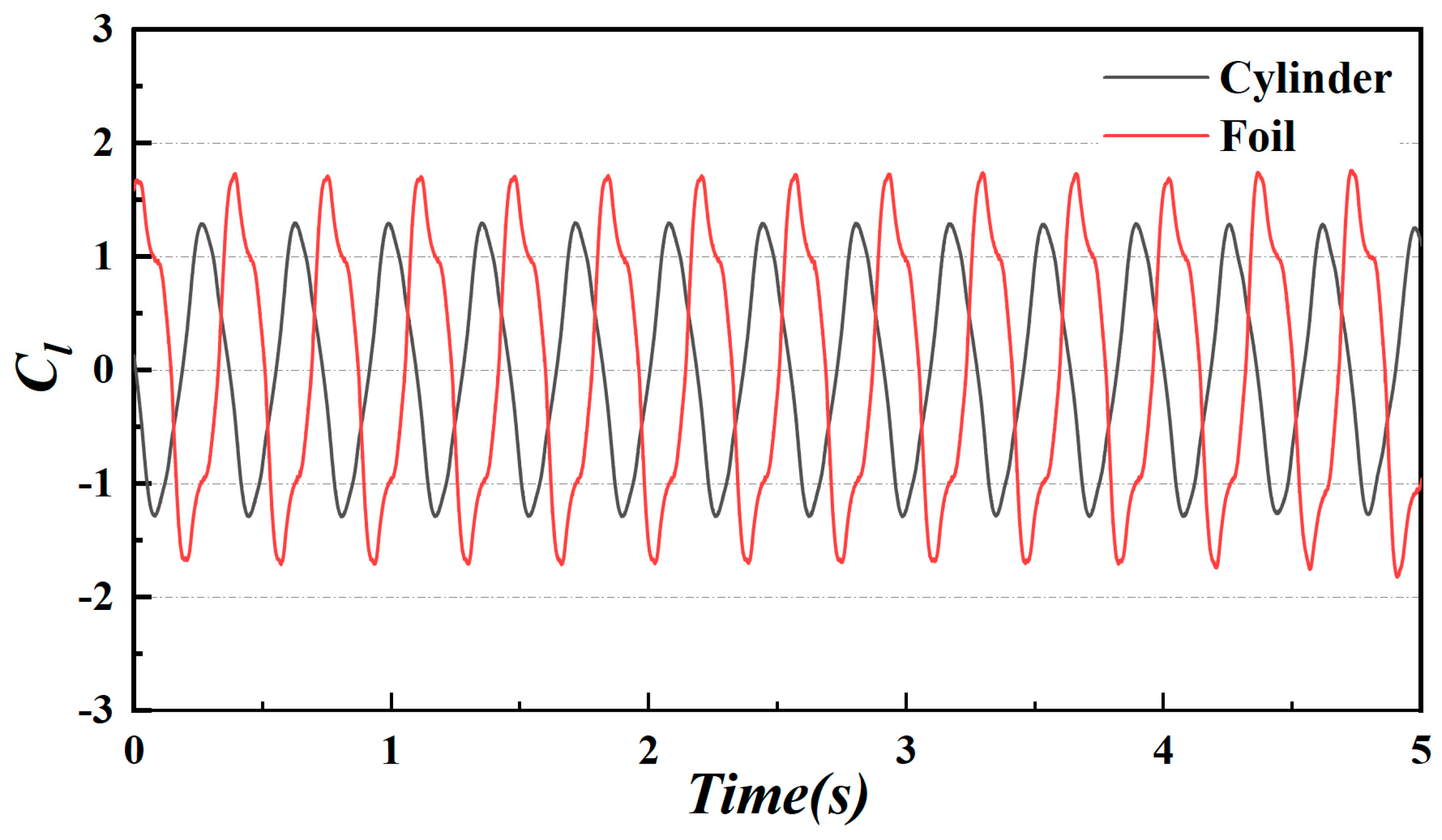
• With the changes in space ratios and reduced velocities, the maximum amplitude ratio (A* = 1.43) appears at U_r = 15.23 and S/L = 1.0. For exploring the phenomenon, the lift coefficient curves of the cylinder and the foil in 5 s at the present parameters are plotted in Figure 8 first, the phase difference is 131.77° between the two life coefficient curves. However, the phase difference is not the determinate factor of this result; the corresponding value is 140.73°, S/L = 1.5, which has a much smaller amplitude ratio (A* = 0.22).

Hence, the vorticity contours are plotted in an oscillating period at S/L = 1.0 and U_r = 15.23, which are shown in Figure 9 (which are at difference period within one cycle). During this period, the motion of the foil is completely affected by the vortex (A1, B1, A2, and B2) shedding from the cylinder. At the beginning (T = 0), A1 has been generated and moves downstream; the foil is close to the equilibrium position at this time. B1 is generated at the bottom cylinder and causes a trend of moving upward for the foil. When T = π/2, B1 reaches the bottom of the foil, which is pointing at the upward extreme position. As B1 extends and moves with the flow downstream, the foil turns the direction downward and reaches the extreme position of downward motion at T = 3π/2 under the joint action of B1 and A2. Finally, the foil returns to its initial position and completes the vibration process in a cycle under the effect of B2. It should be noted that a portion of B2 moves to the top of the foil through the gap between the two bodies, which makes the counterclockwise vortex flowing under the foil smaller than the time at T = π/2, which also causes the upward motion of the foil to be reduced by 27.94% compared with the previous period. It can be seen that the motion of the foil is completely affected by vortex shedding at the present parameters. The process of vortex generation and shedding affect the direction and trend of motion.

4.

The amplitude ratios A* are ≤ 0.2 at space ratios S/L > 1.0 and the reduced velocity is U_r ≥ 15.23; as the reduced velocity increases, the amplitude ratio tends to be stable. This is due to the vortex shedding frequency, which increases with the incoming flow velocity. It speeds up the flow field variation frequency around the foil but reduces the oscillating amplitude.

4.2. Frequency Responses

The frequency spectrums are obtained by the Fast Fourier Transform (FFT) of the amplitude responses of the foil at different spacing ratios and reduced velocities, as shown in Figure 10. The dashed line in every figure is the natural oscillating frequency, defined as

$$f_n=\frac{1}{2\pi }\sqrt{\frac{K}{m}}$$

(18)

(a)

At each spacing ratio, the oscillating frequency of the foil increases with the growth in the reduced velocity. The phenomenon can be attributed to the increasing vortex shedding frequency. As described in Section 4.1, the motion of the oscillator is completely affected by the vortex shedding, so its oscillating frequency shows a gradual increase trend with the incremental oncoming flow velocity.

(b)

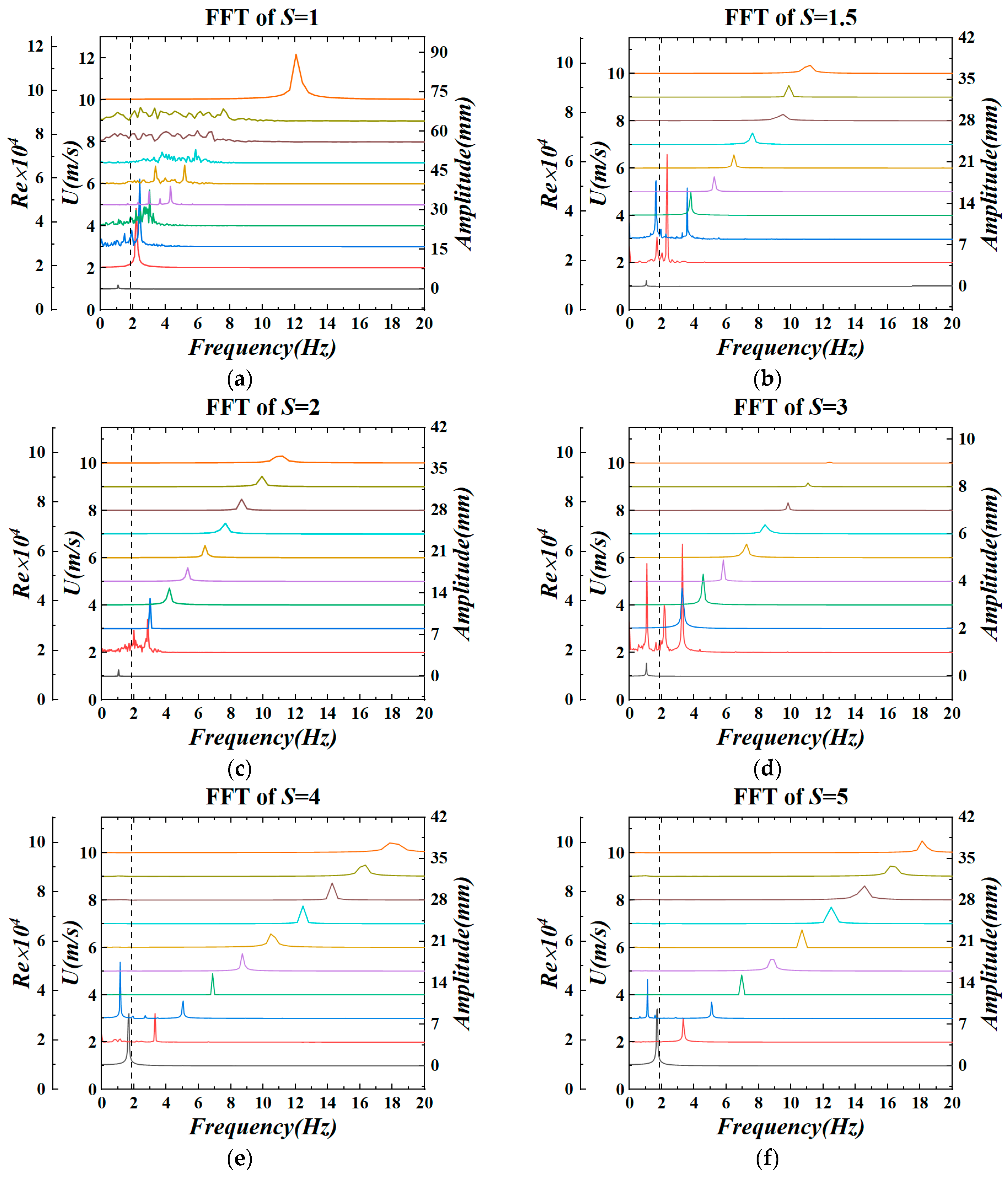
The increasing rate of oscillating frequency at S/L ≤ 3.0 is smaller than S/L ≥ 4.0 with the changes in reduced velocity, as shown in Figure 8. At the former spacing ratio (S/L ≤ 3.0), because of the influence of the position of the foil, the vortex shedding position located downstream of the foil and the shear layer is extended, which needs more time to isolate from the rigid body, so the vortex shedding frequency at the same reduced velocity is smaller than the latter space ratio (S/L ≥ 4.0). When S/L ≥ 4.0, the vortex shedding position is in the gap between the cylinder and the foil; the vortex sheds earlier and improves the vortex shedding frequency.

(c)

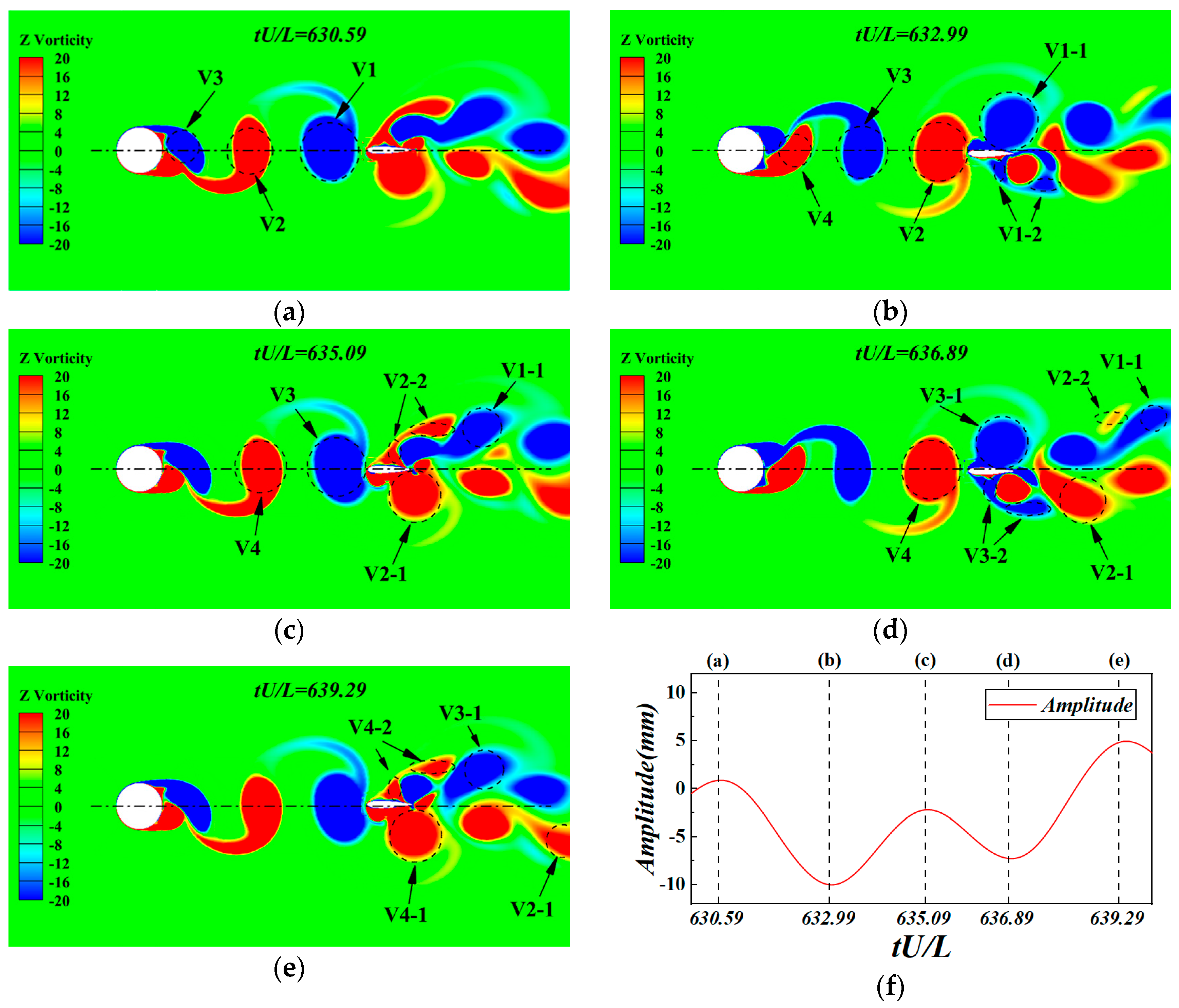
At the corresponding time of the maximum amplitude at each spacing ratio, the amplitude response has more than two oscillating frequencies. When the spacing ratio S/L = 5.0 and U_r = 11.43, the instantaneous vorticity contours of the two vortex-shedding cycles of the upstream cylinder and the corresponding foil displacement time history curve are shown in Figure 11. At the moment shown in Figure 11a, the foil is at the extreme value of upward movement under the effect of the previous vortex. When it comes to Figure 11b, vortex V1 is cut apart into two sub-vortexes by the foil. The upper sub-vortex V1-1 plays a key role in forcing the foil to gradually move downward and reach the extreme value. The lower vortex V1-2 is dissipated under the influence of surrounding vortices. In the same way, vortexes V2, V3, and V4 similarly displace the foil. It should be noted that after the vortex is split, the sub-vortex plays a role in the foil displacement, which is on the same side as the original vortex, and the sub-vortex on the other side is gradually dissipated under the influence of the residual part of the previous vortex. On the one hand, with the alternating influence of vortices, the foil oscillator makes a reciprocating motion, so one frequency of the displacement curve is equal to the vortex shedding frequency at this time. On the other hand, when a current vortex makes the foil move to the extreme value, as shown in Figure 11b, the subsequent vortex V2 has been affected by the foil, which leads to the sub vortex V2-1 of V2 being smaller than the sub vortex of V1-1. During the upward movement of the flapping wing caused by V2-1, V3 is cut off to make the foil move downward so that the displacement time history curve of the foil shows a rising trend of fluctuation, which also makes the displacement have multiple frequencies.

(d)

As shown in Figure 11e,f, when the spacing ratio is equal to 4.0 and 5.0, and the reduced velocity U_r = 11.43, a larger amplitude is less than the natural frequency and a smaller amplitude is equal to the upstream cylinder vortex shedding frequency, which appears on the FFT curve. This is due to the alternating rise and fall of the oscillator under the action of the vortex at this reduced velocity. In Figure 11b, the oscillator is at the limit value of the downward motion, and then the wave rises to the extreme value of the upward motion; this process is about three to four cylindrical vortex shedding cycles. In the vortex shedding period close to the initial position of the foil, the amplitude of the vibration is small, so there is a peak on the FFT curve on the right side close to the vortex shedding frequency, but the amplitude is relatively small.

4.3. Harnessed Energy and Efficiency

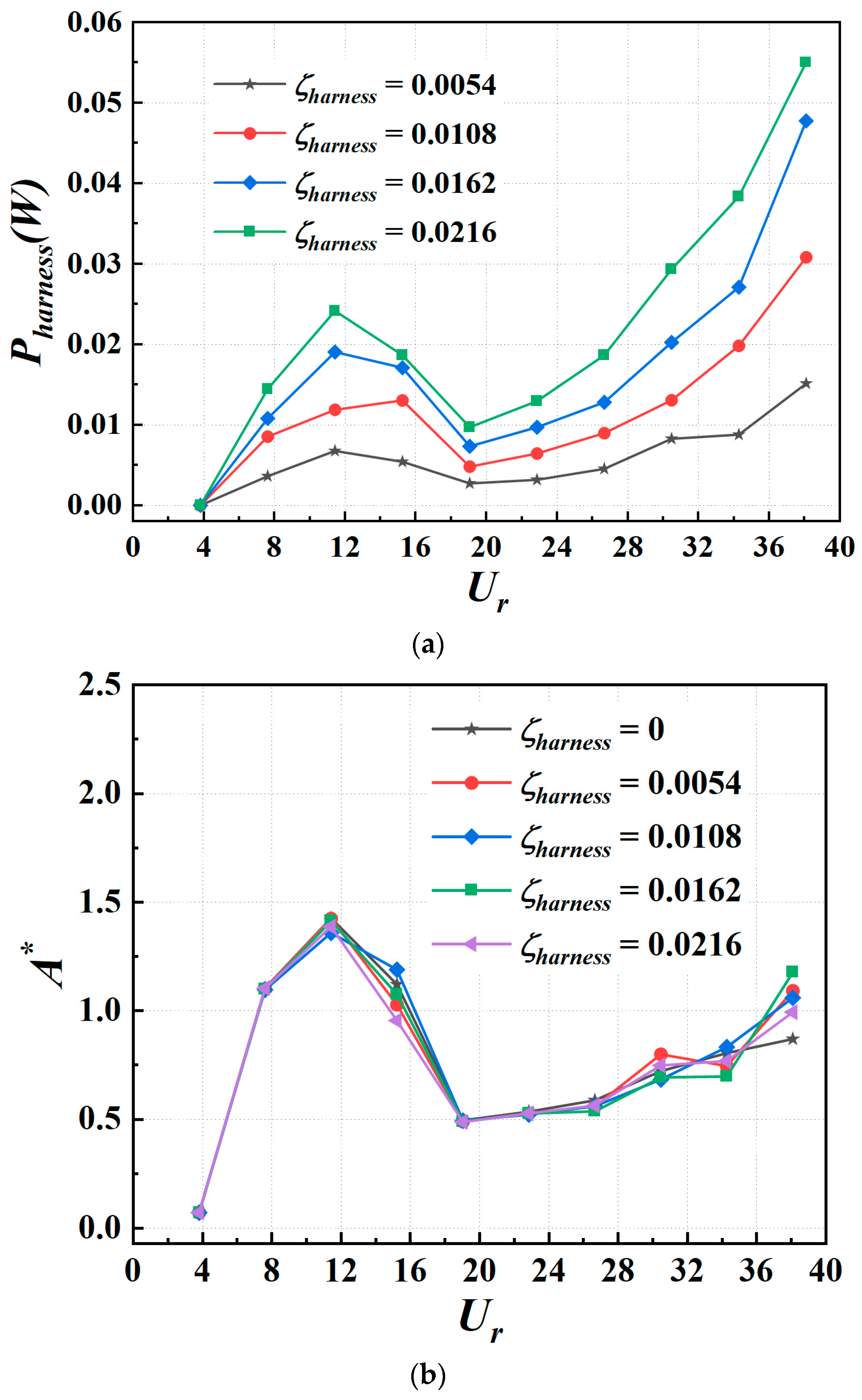
4.3.1. Harnessed Energy

Four harness damping ratios (ζ_harness) and S/L = 1.0, which has the maximum amplitude, are employed to simulate the energy harvesting conditions. With the periodic oscillating motions of the foil, the fluid kinematic energy is converted to the foil mechanical energy. The dynamics model in Equation (14) is employed to compute the converted power, as given by [17]; the equation of the total converted power is

$$P_{total}=\frac{1}{T_{osc}}{\displaystyle {\int }_0^{T_{osc}}(m\ddot{y}+C_{total}\dot{y}+Ky)\dot{y}dt}$$

(19)

The excitation and response are assumed as sinusoidal motion with a frequency $f_{osc}$, and the instantaneous transverse displacement of the foil is expressed as

$$y(t)=A\sin (2\pi f_{osc}t)$$

(20)

The total converted power obtained by introducing Equation (20) into Equation (19) is

$$P_{total}=\frac{1}{T_{osc}}{\displaystyle {\int }_0^{T_{osc}}(4\pi m{\zeta }_{total}\dot{y}{f}_n)\dot{y}dt}=8{\pi }^{3}m{\zeta }_{total}{(A{f}_{osc})}^2{f}_n$$

(21)

where ${\zeta }_{total}={\zeta }_{structure}+{\zeta }_{harness}$. Thus, the harnessing power is

$$P_{harness}=8{\pi }^{3}m{\zeta }_{harness}{(A{f}_{osc})}^2{f}_n$$

(22)

The curves of the harnessed energy at different damping ratios in the present simulations are shown in Figure 12a.

The highest energy harnessed by the foil reaches 0.055 W at ζ_harness = 0.0216 in the current tested condition. In Equation (22), the harnessed power is proportional to ζ_harness, A, and f_osc. For all three cases investigated, the P_harness is higher as the damping ratio increases at the entire reduced velocity range, which can be attributed to the amplitudes of three harnessed damping ratios which have few differences, which is shown in Figure 12. The trend of P_harness varies with U_r and is suited with the corresponding variation in the amplitude. At U_r = 3.81–11.43, the harnessed power increases at a smaller rate and then swerves downward and enhances at a greater rate again at U_r = 19.04; then, it finally reaches a much bigger value than the former extreme one. As seen in the frequency spectrums of amplitudes (Figure 13), the oscillating frequencies at U_r = 7.62–11.43 are nearly the same and are locked in around the natural frequency that indicated the flow pattern at this moment in the VIV regime. The lines of frequency fluctuate at U_r = 26.66–38.08, and no main frequency occurs at this range. Though the RMS values of amplitude at these flow speeds are relatively small compared to U_r = 11.43, the fluctuation is more intensive and violent at a higher damping ratio, which results in the rapid growth of P_harness.

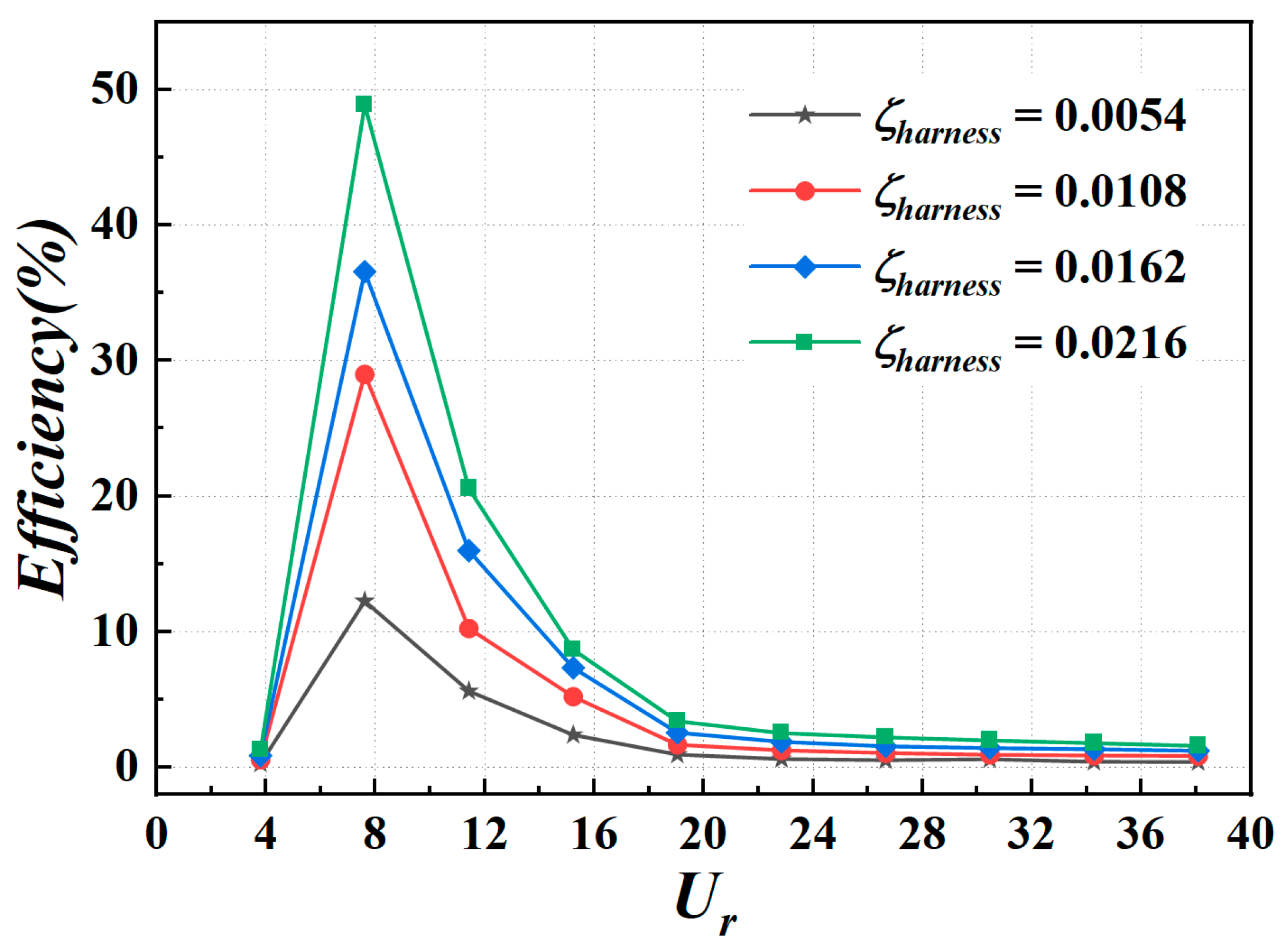
4.3.2. Harnessed Efficiency

The fluid kinematic energy through the area S_foil swept by the foil with oscillations is given.

$$P_{fluid}=\frac{1}{2}\rho U^3{S}_{foil}$$

(23)

For a consistent comparison with the area swept by a propeller or a cylinder in FIV [34], S_foil in the present work is expressed as (2A + H)L; hence, we have

$$P_{fluid}=\frac{1}{2}\rho U^3(2A+H)L$$

(24)

The swept area changes with the foil amplitude, which is different from turbines and propellers that have a fixed value of the area. There is a theoretical maximum efficiency that extracts energy from open flow, and the value is equal to 59.26%. Based on the Betz limit, the total energy-converted efficiency from the fluid η_total and the harnessing efficiency η_harness are calculated as

$${\eta }_{total}=\frac{P_{total}}{P_{fluid}\times BetzLimit}$$

(25)

$${\eta }_{harness}=\frac{P_{harness}}{P_{fluid}\times BetzLimit}$$

(26)

As described in the previous section, the harnessed energy is on the dependence of U_r and ζ_harness, and the available energy of the incoming flow is the function as the cube of the approaching velocity (Equation (24)) if the harnessed efficiency has the same trend as harnessed power. Figure 14 shows the curves of the harnessed efficiency changes with U_r for various ζ_harness values.

Similar to the harnessed energy curves, a higher damping ratio has a higher efficiency in the entire flow range. The efficiency increases first with U_r and then declines at a reduced velocity range from 7.62 to 19.04; finally, it remains at a weaker rate, descending until the last test speed. All the efficiency curves show a peak at U_r = 7.62; the corresponding frequency of the oscillating amplitude is closest to the natural frequency, which indicated that the optimal efficiency for harnessed energy occurs at this regime, and the maximum harnessed efficiency is equal to 48.89% at ζ_harness = 0.0216. The reduced velocity is close to the top of the upper branch (VIV); in other words, the vortex shedding frequency is close to the natural frequency of the oscillating foil. As a consequence, the harnessing efficiency tends to be higher here due to the denominator being relatively lower. In the numerical study conducted by Wang et al. [16], they studied the energy harvesting performance of a fully passive flapping foil, and the highest efficiency was observed to be 32%, which was slightly lower than that of 34% in Kinsey and Dumas [9]. The discrepancy in harnessed efficiency between the present study and that of Wang et al. could be due to the difference in the oscillating motions, Reynolds numbers, etc.

At U_r ≥ 19.04, the harnessed efficiencies have a smooth trend, and the values are small (around 1.2% at ζ_harness = 0.0162); η_harness is even smaller than 0.6% at ζ_harness = 0.0054 and $U_r\ge 26.66$. However, the harnessed energy in this regime of reduced velocity (U_r ≥ 26.66) is much greater due to the higher velocity of the free stream. This means the foil could convert more energy from the fluid as long as the incoming flow carries enough kinematic energy, even if the efficiency at U_r ≥ 26.66 is relatively low compared with the regime 7.62 ≤ U_r ≤ 19.04.

5. Conclusions

A series of simulations are conducted to investigate the FIVs for a foil that has a single degree of freedom and is submerged in the wake of a circular cylinder in this paper by changing system parameters such as the space between two rigid bodies. The amplitude and frequency responses are tested for S/L = 1.0–5.0 and U_r = 3.81–38.08. Four various harnessed energy damping ratios (ζ_harness = 0.0054–0.0216) are adopted to study the character of the configuration for harvesting energy from the free stream. Overall, the cylinder serves as the vortex generator and has a positive impact on the harnessing energy of the oscillating foil; by adjusting the spacing ratios, the efficiency is affected positively as well. The conclusions are:

(1)

High energy conversion occurred at a close spacing, which has a relatively higher amplitude response. At low spacing ratios, there is a dramatic disturbance in the area behind the cylinder because of the vortex shedding. Hence, the foil could utilize the effect and oscillates with a higher amplitude, which could harness more power from the fluid.

(2)

A critical spacing ratio for the vortex shedding position is between 3.0 and 4.0. Due to the change in the position, the oscillation of the foil is suppressed with an increasing velocity for S/L ≥ 4.0, which means less energy can be captured.

(3)

There are two local high values for harnessed power with an increasing velocity. One is around U_r = 11.43, which could be seen as the end of VIV. The other one occurs at U_r = 38.08 which is the upper limit of the tested velocity. According to the current trend, more power may be harnessed with the continuous increase in velocity.

(4)

A higher harnessing damping ratio converts more energy essentially. The highest harnessed power in the conducted simulations is 0.055 W at ζ_harness = 0.0216, which is about four times the value at ζ_harness = 0.0054.

(5)

The highest harnessed efficiencies reach the maximum of about 12.3–48.8% and occur at the oscillating frequency that is close to the natural frequency. The efficiency of the foil with a fixed cylinder is higher compared to that of the single isolated flapping foil, where the optimal efficiency is 34%.

Based on the current research, some interesting phenomena can be further investigated—for instance, more foil can be added either in tandem or parallel-placed, and the interaction can be beneficial for a higher harness energy. The practical application can be scaled up for higher consumer energy usage or scaled down for a micro sensor power supply, depending on the situation.