A Model Modification for a Microturbine Set with Partial Admission Stages
Abstract
1. Introduction
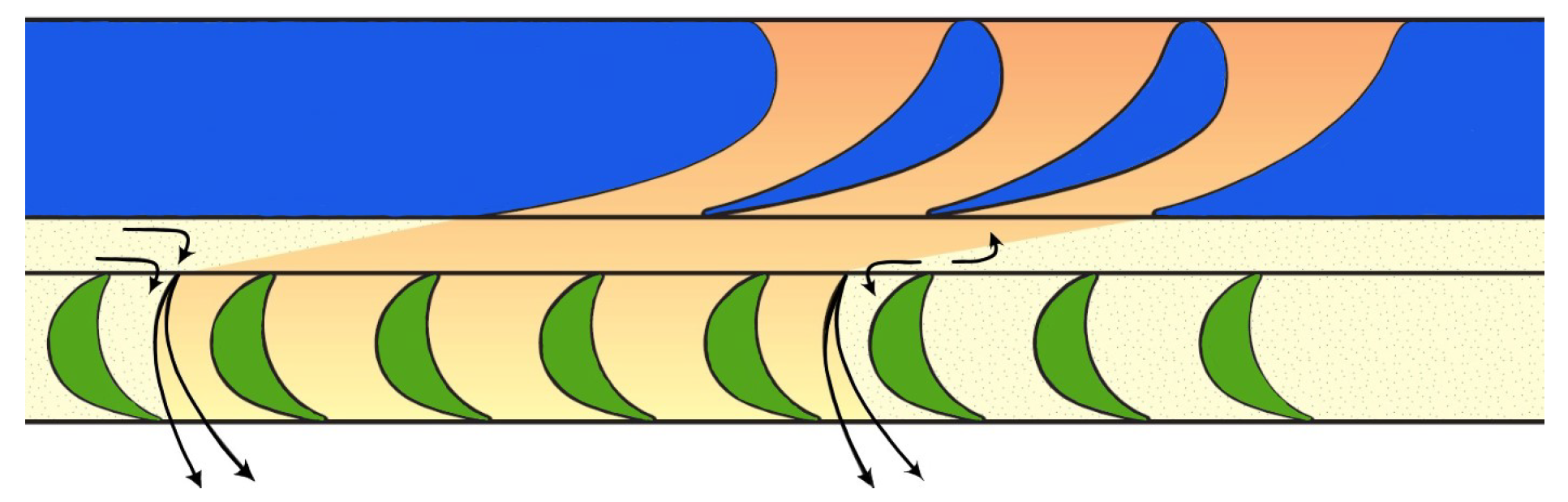
- The mathematical model of the microturbine set has been modified to take into account the partial admission of turbine stages.
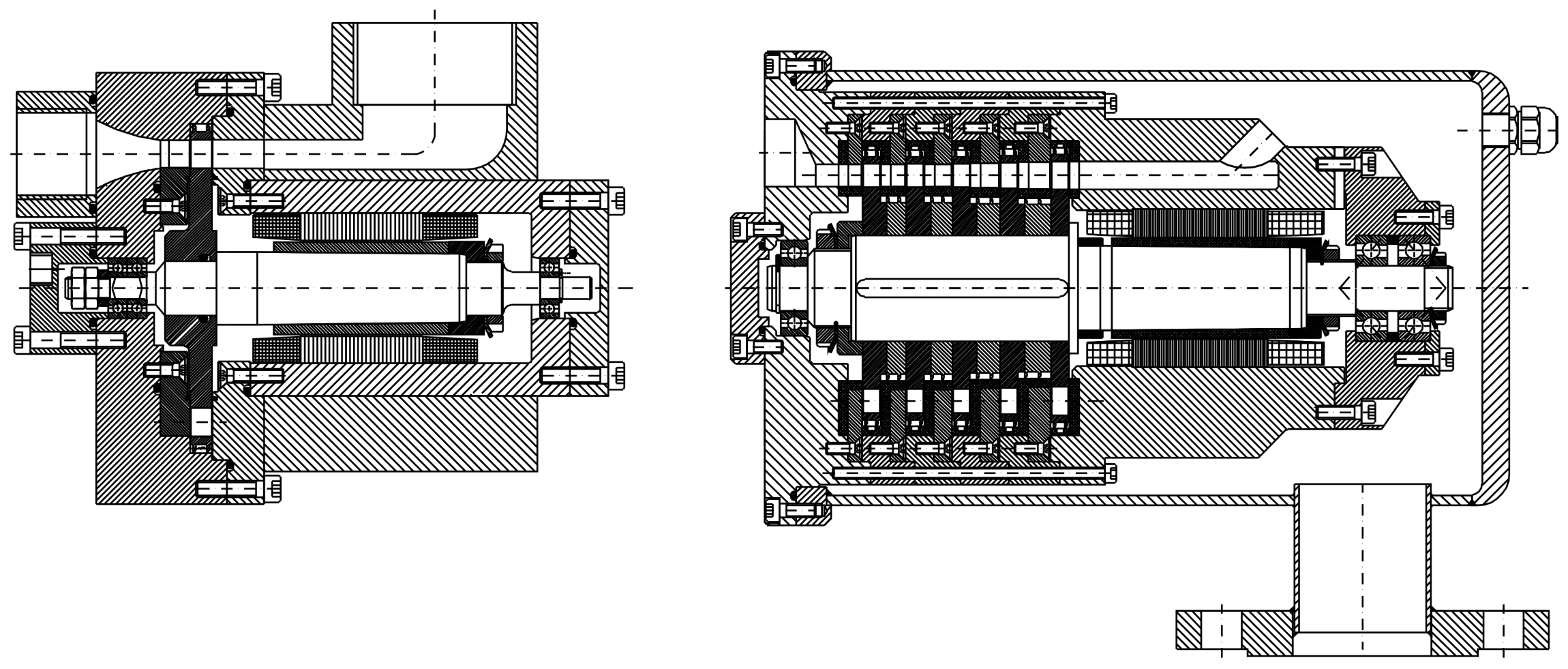
- The model has been verified through unique experimental research. The analysis covered two structurally comparable microturbine sets that differed in the number of turbine stages with partial admission. The findings of such studies have not yet been published.
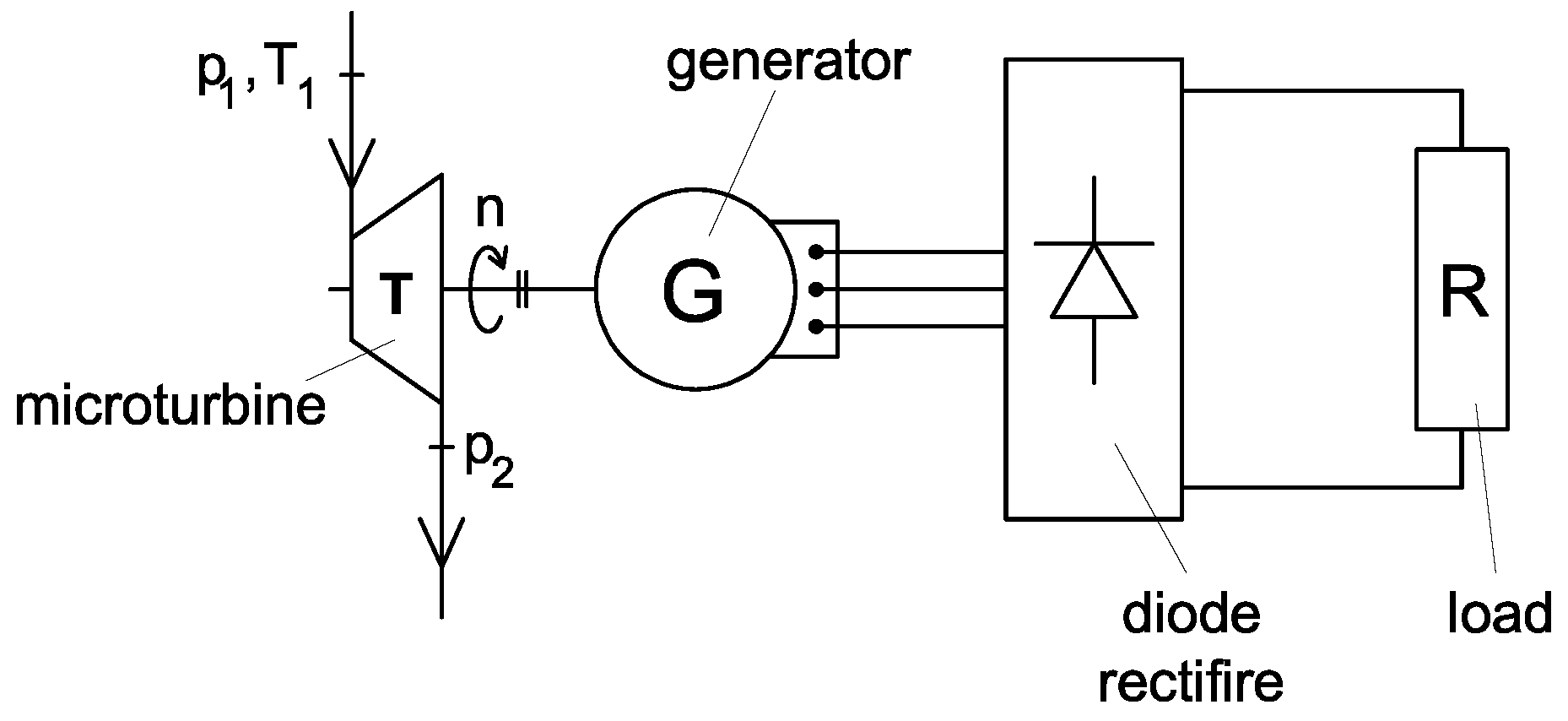
2. Mathematical Description of a Microturbine Set
2.1. Model without the Effect of a Partial Admission—Base Model
2.2. Model with the Effect of a Partial Admission—Developed Model
3. Models Validation
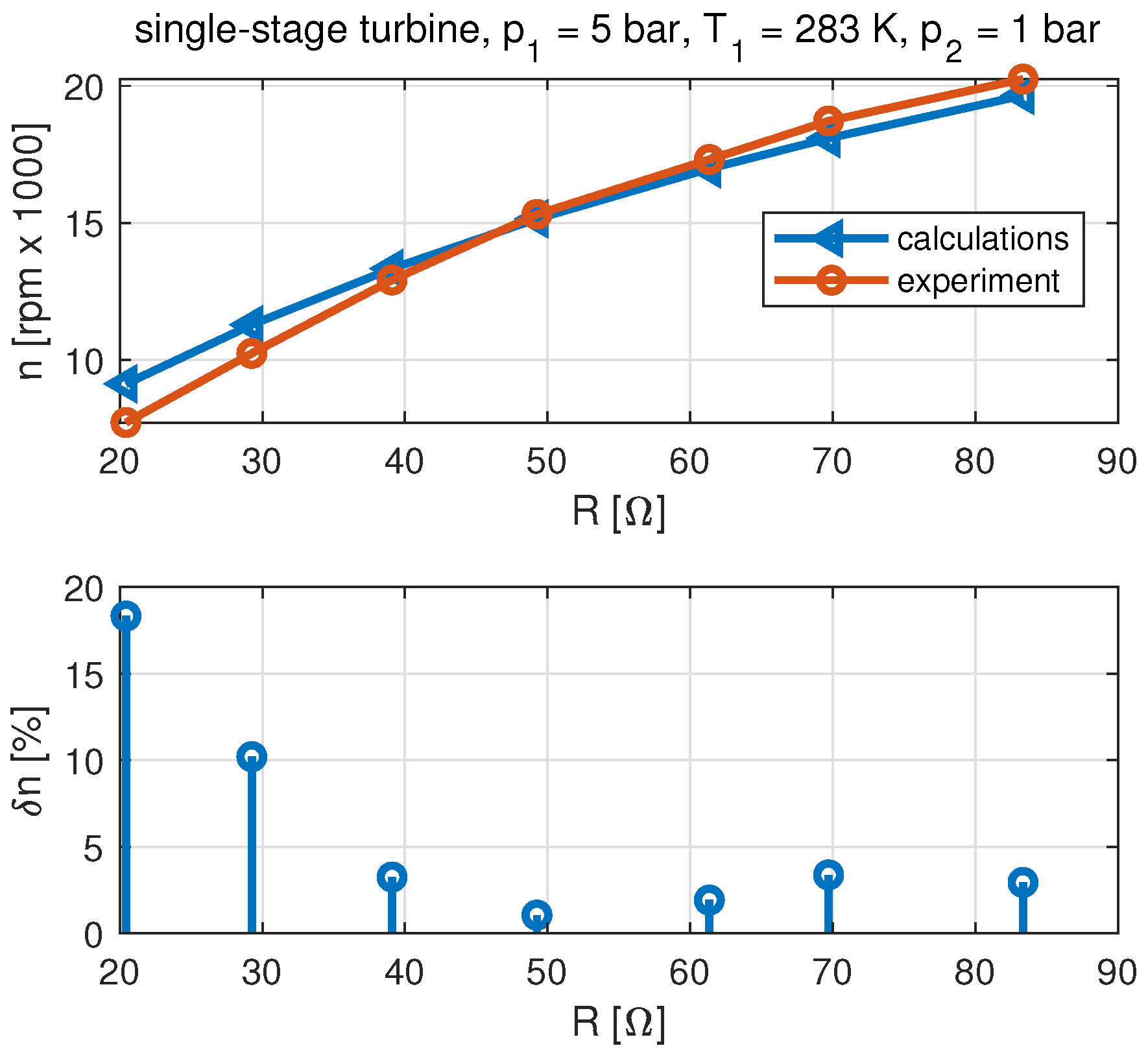
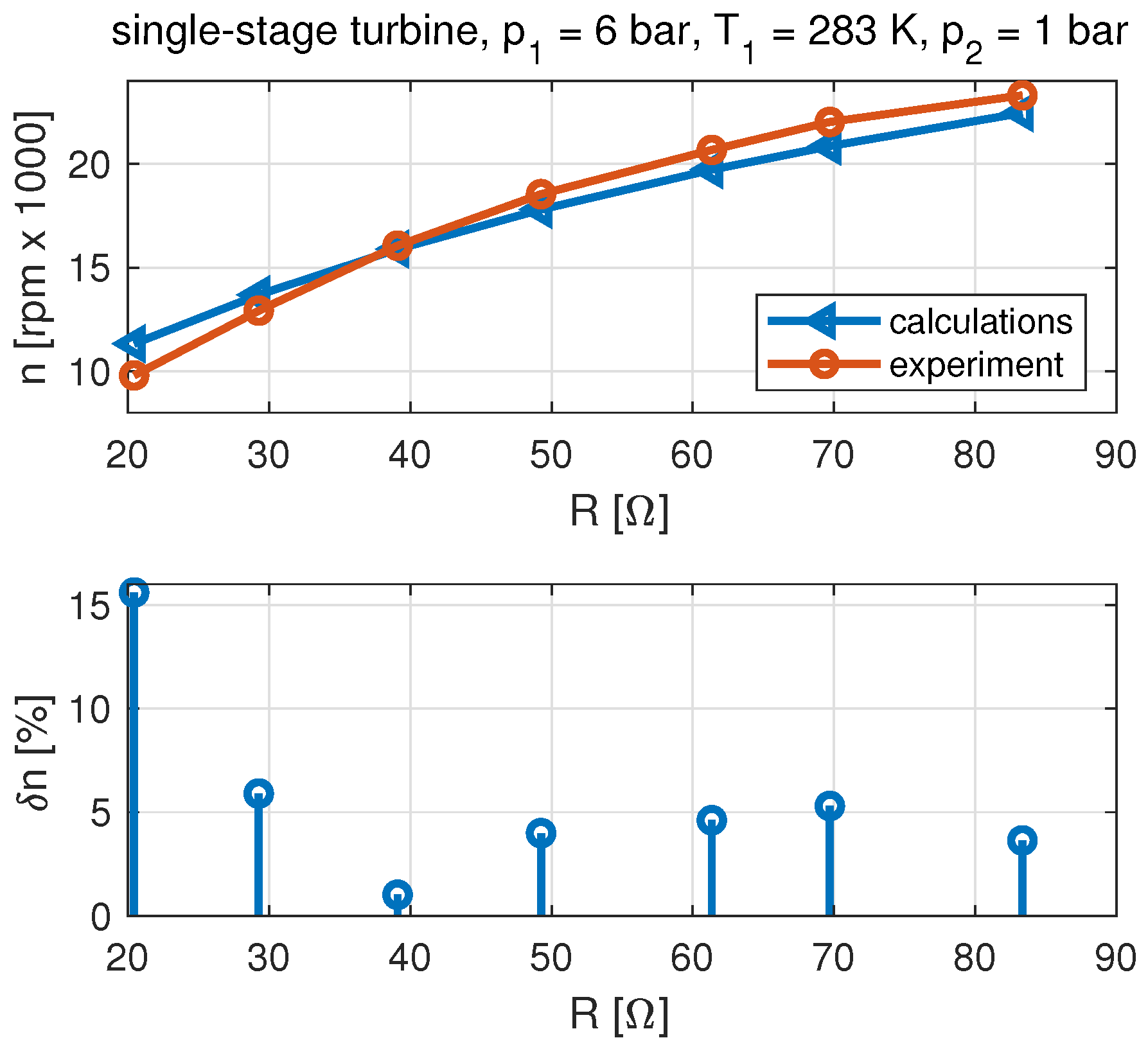
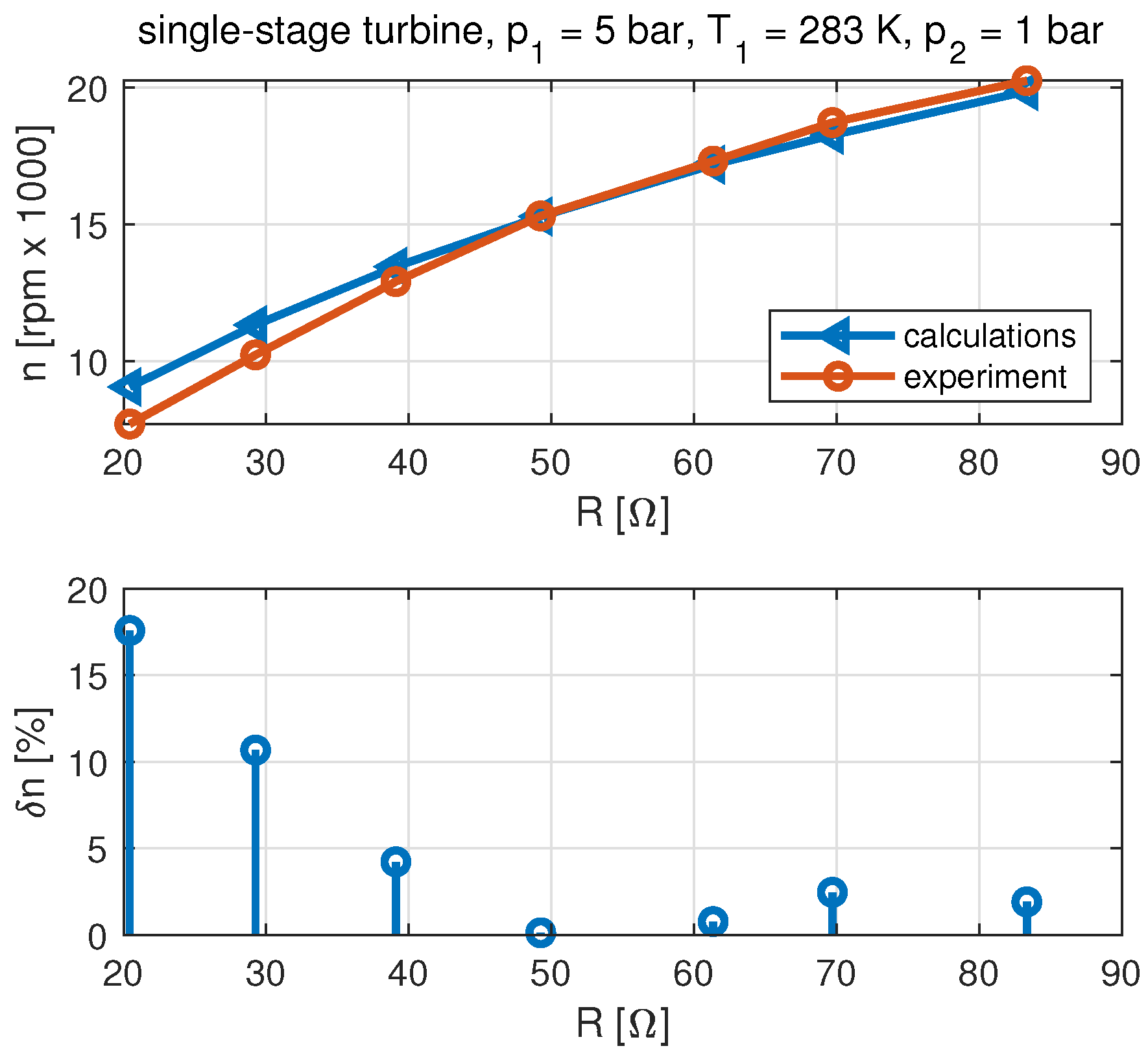
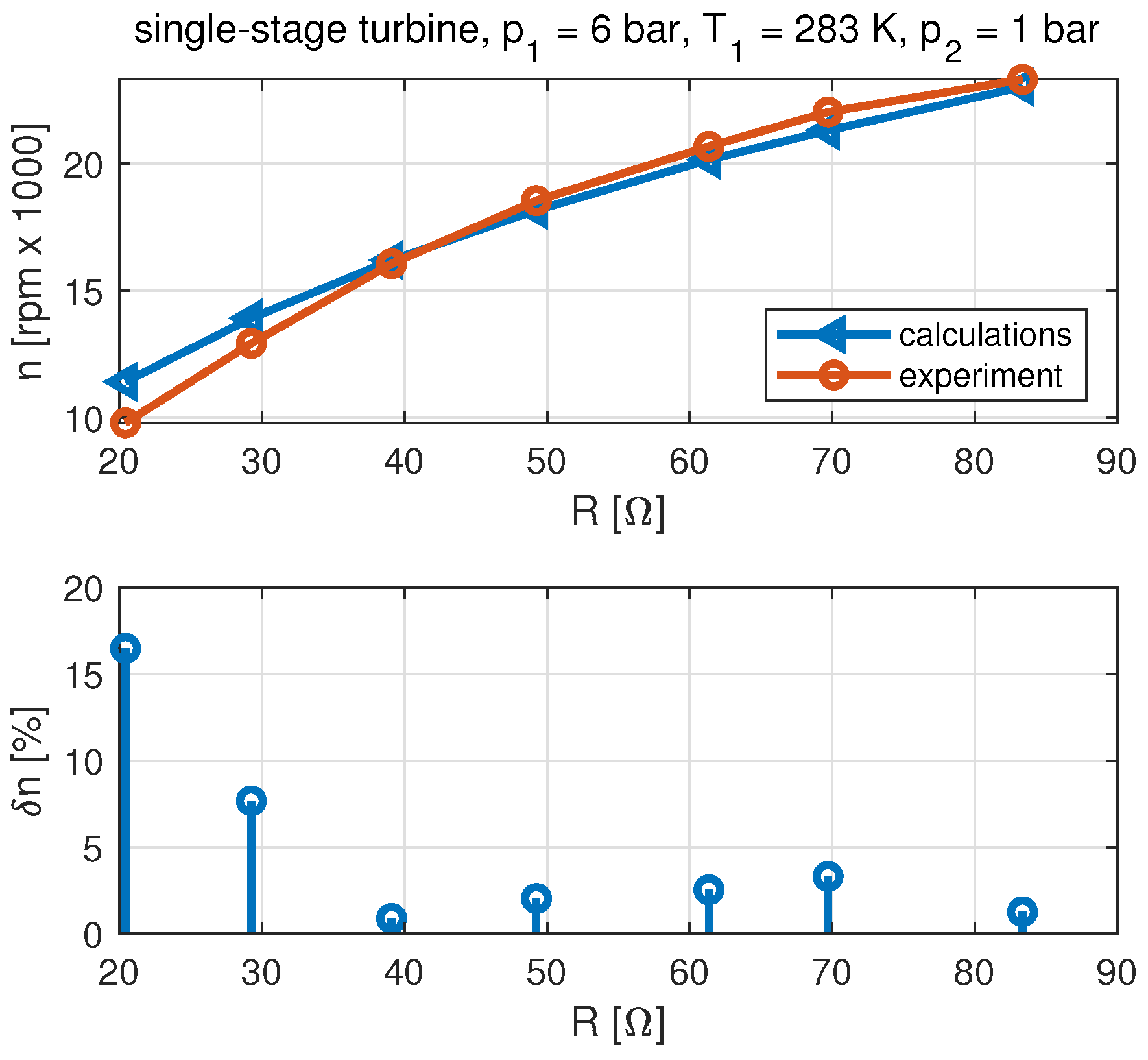
3.1. Base Model
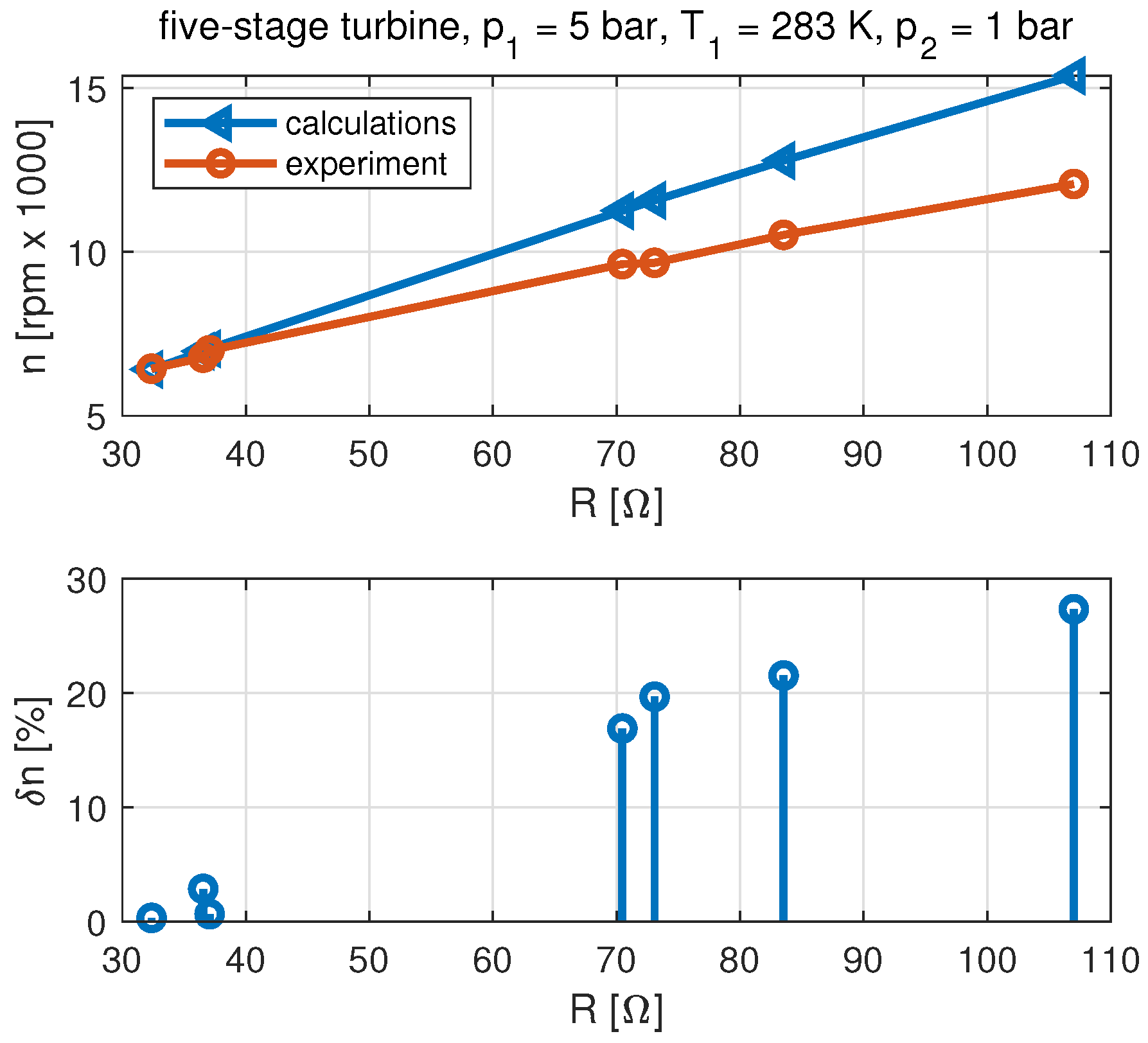
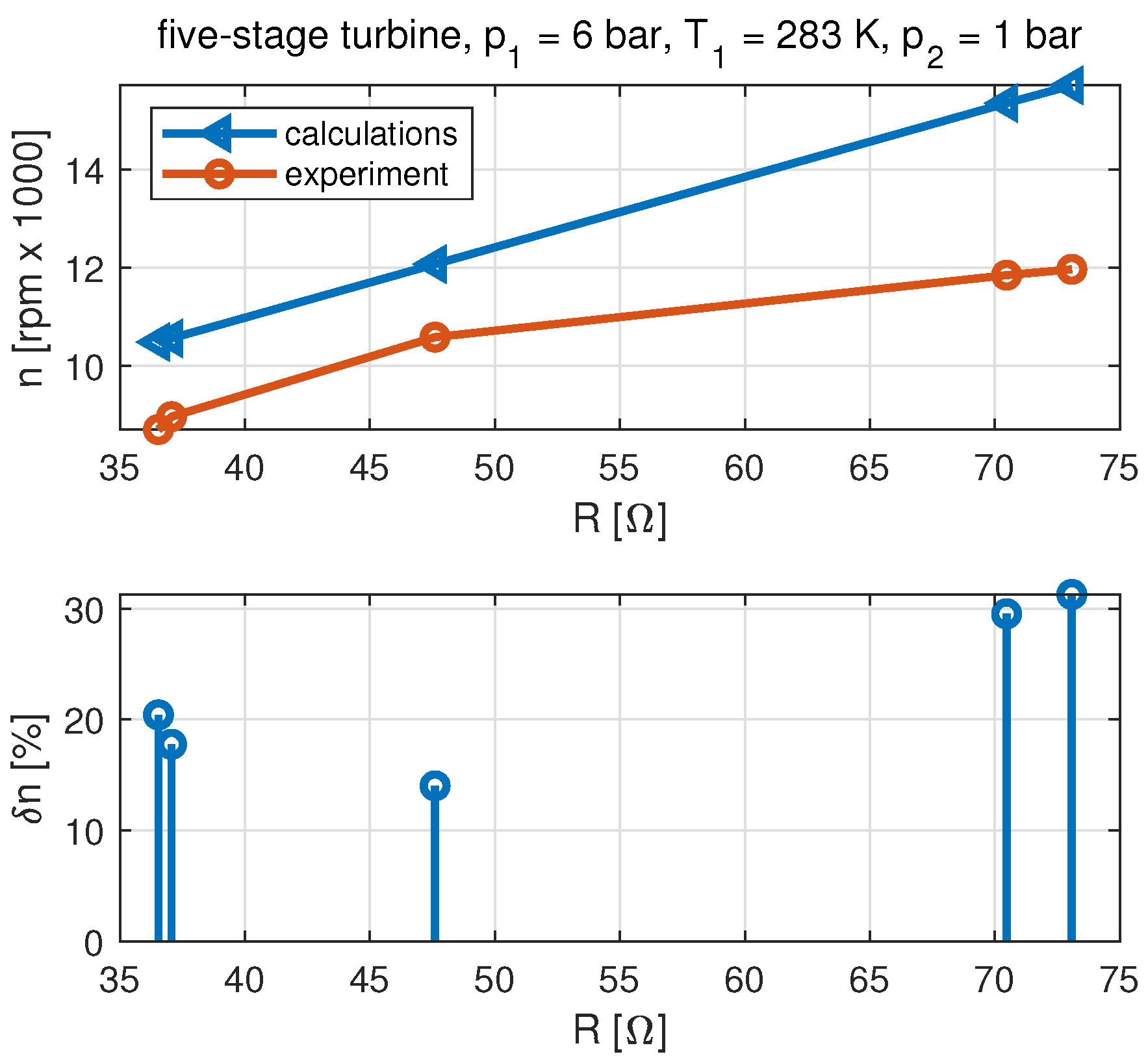
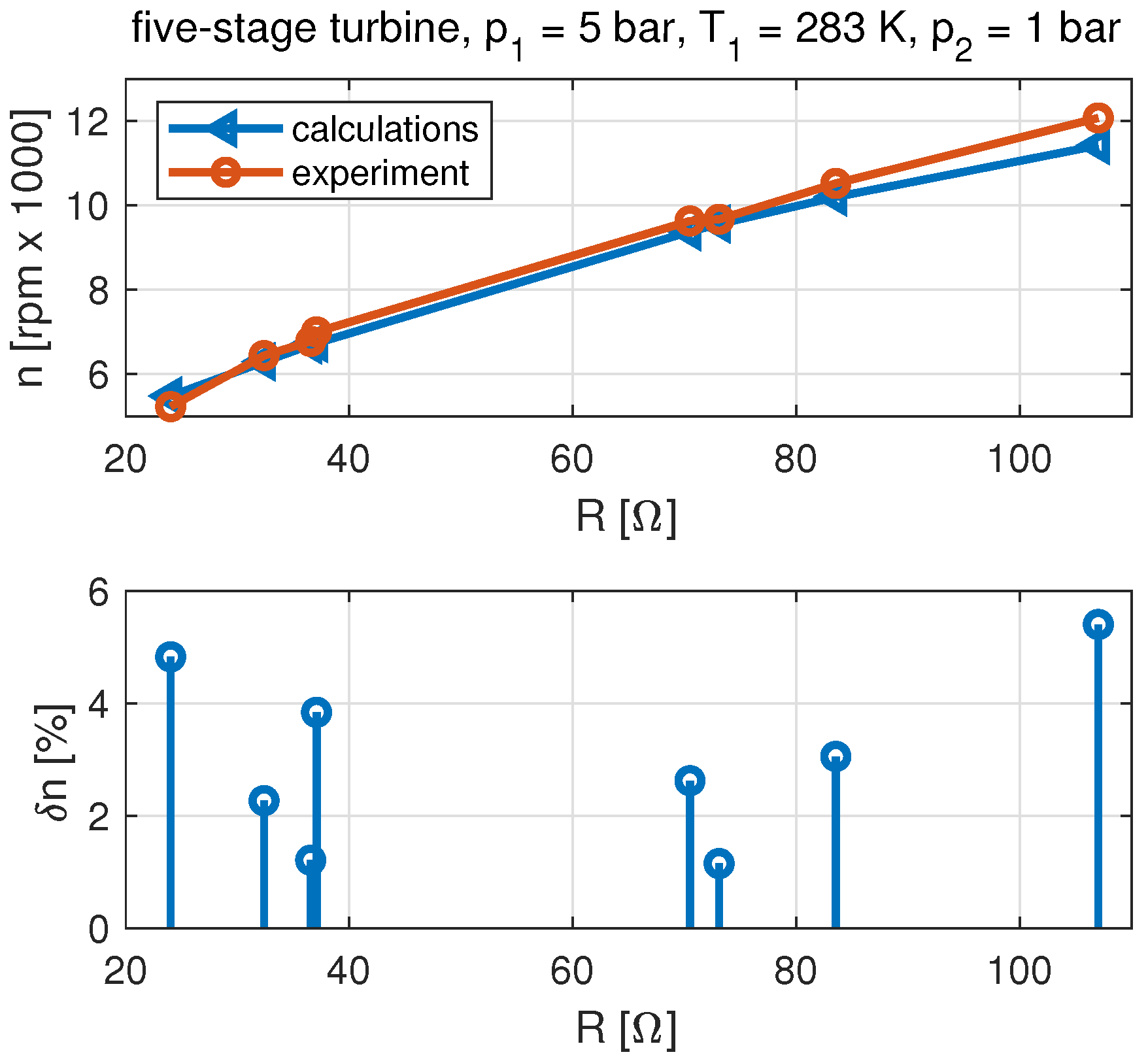
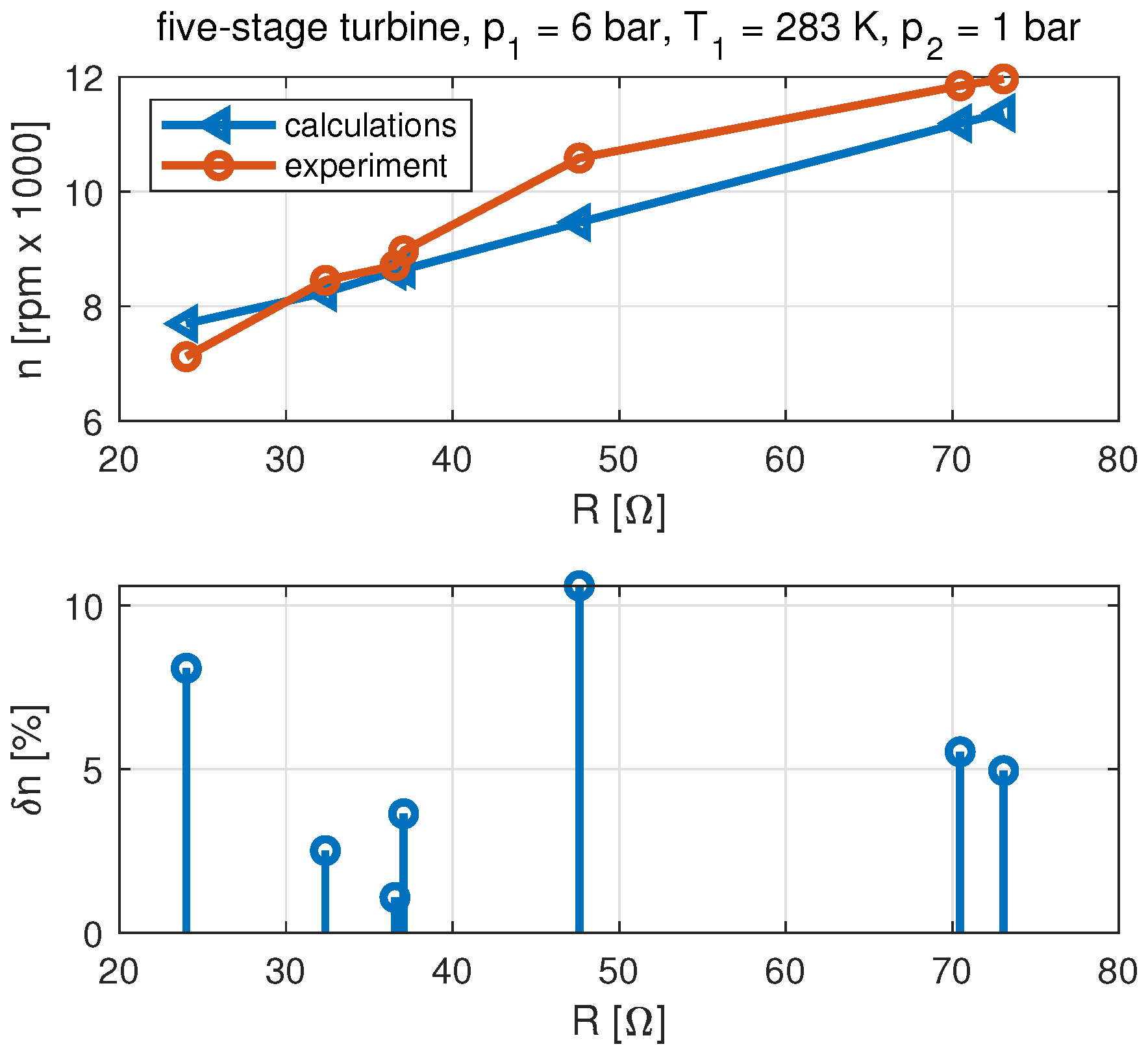
3.2. Developed Model
3.3. Discussion
4. Conclusions
- The experimental data were used to determine the model parameter values. The data from the two distinct microturbine sets were utilised. The microturbines were structurally comparable, however, they differed in the number of turbine stages with partial admission.
- Calculations were performed to simulate the performance of both microturbine sets. The simulation data were compared to the results of the experimental tests. Tests were performed within a large range of operational areas.
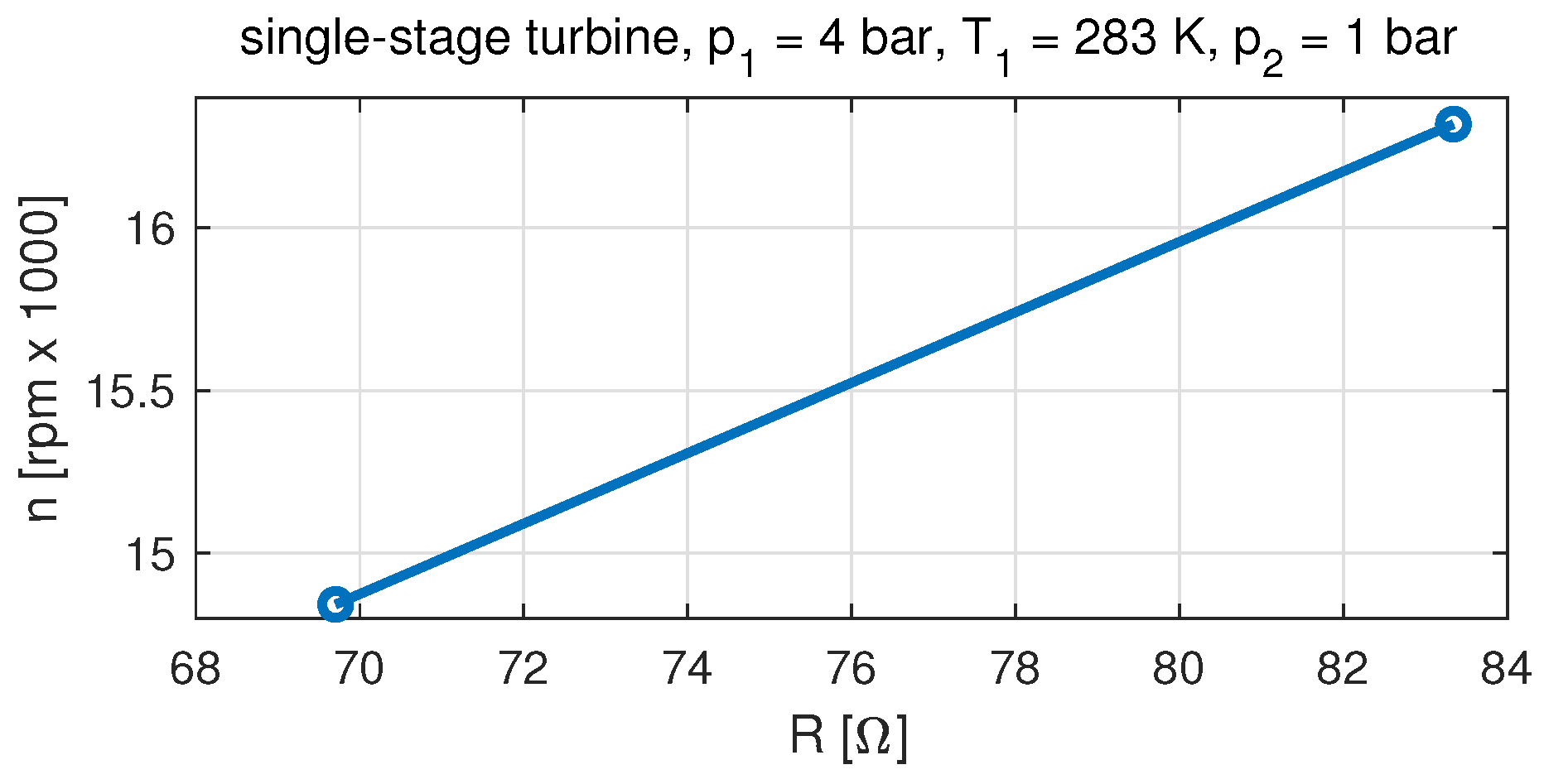
- The results of the single-stage microturbine set have indicated that the developed modification of the model did not increase the simulation accuracy.
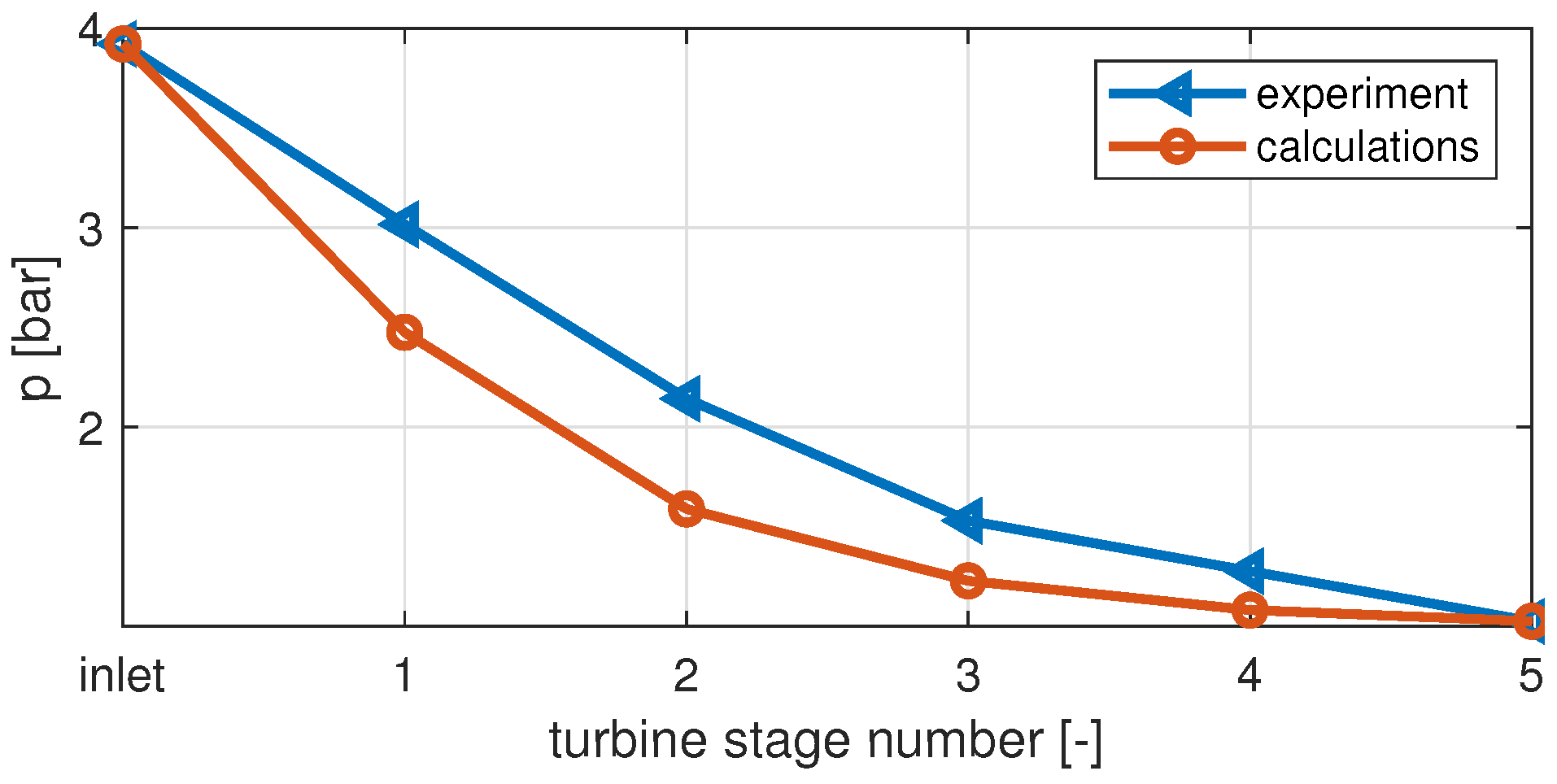
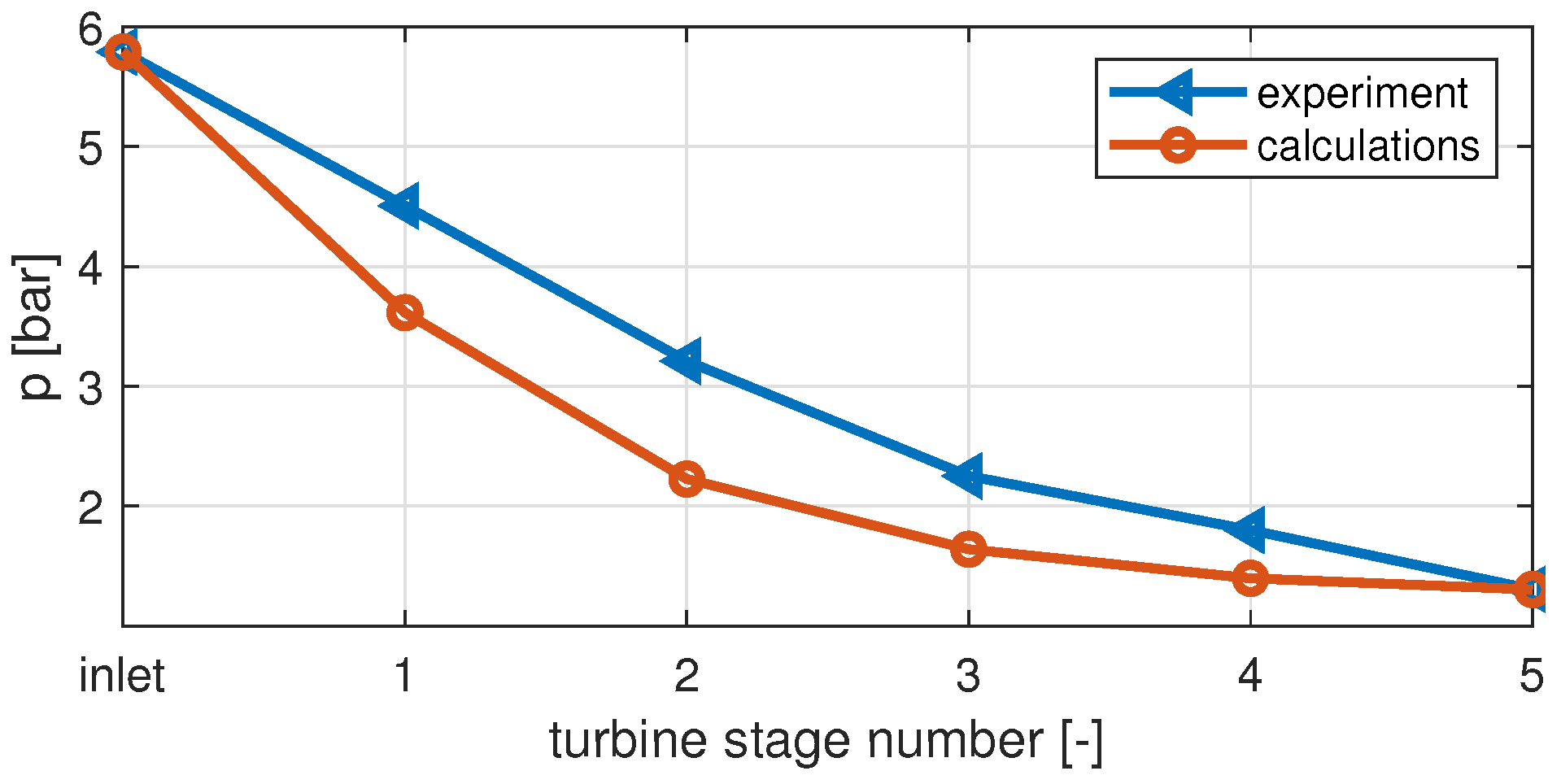
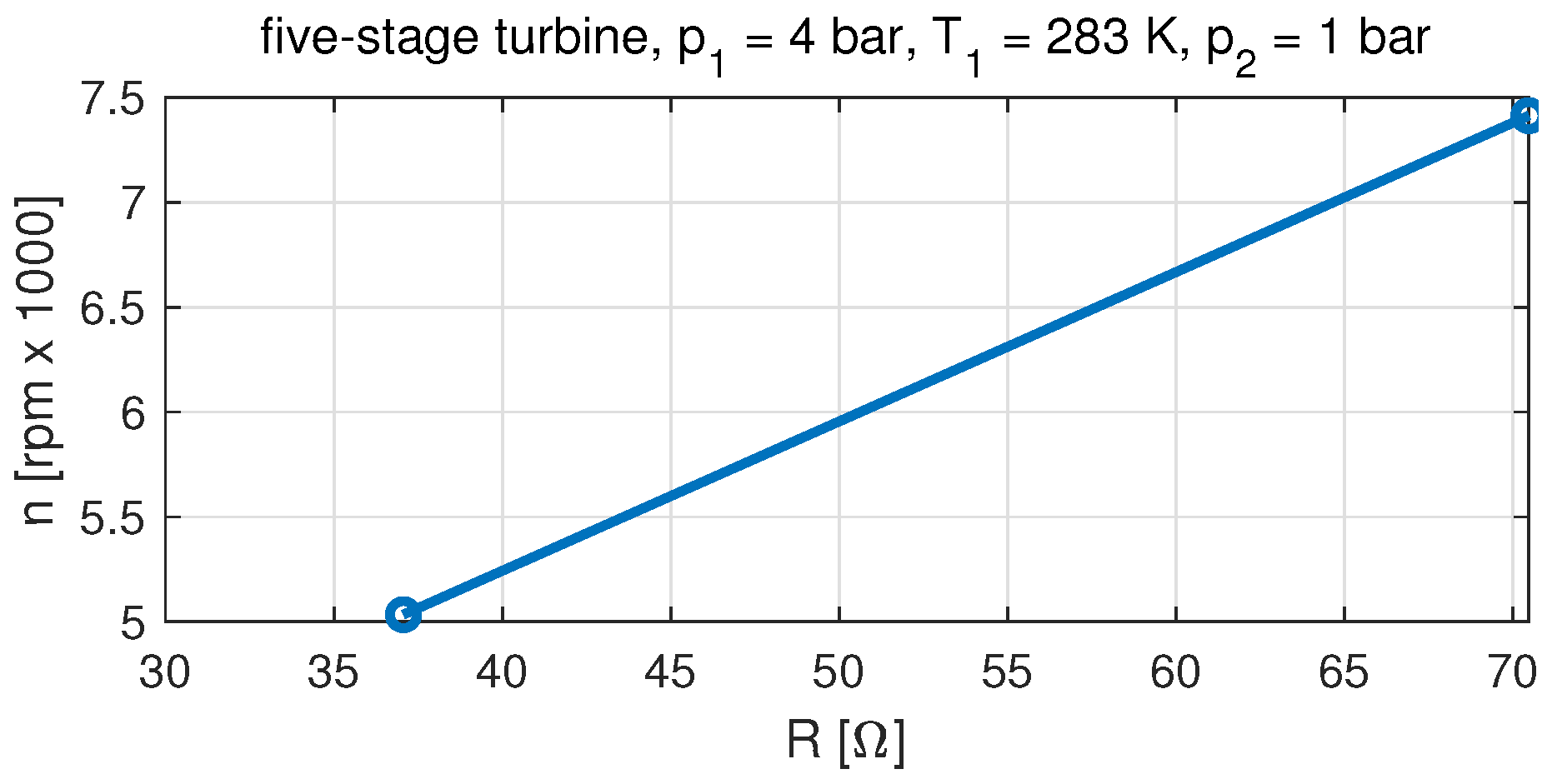
- The analysis of the tests of the five-stage microturbine leads to different conclusions. Simulating the operation of the five-stage microturbine set by the relation that does not include partial admission results in accuracy that can be unacceptable in practical applications. The developed model has significantly improved the accuracy of the simulation of the multi-stage microturbine.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Calculation Algorithm

Appendix A.2. Calculation Results vs. Experiment

References
- Dumont, O.; Dickes, R.; De Rosa, M.; Douglas, R.; Lemort, V. Technical and economic optimization of subcritical, wet expansion and transcritical Organic Rankine Cycle (ORC) systems coupled with a biogas power plant. Energy Convers. Manag. 2018, 157, 294–306. [Google Scholar] [CrossRef]
- Dutra, J.; Gonzalez-Carmona, M.; Lazaro-Alvarado, A.; Coronas, A. Modeling of a Cogeneration System with a Micro Gas Turbine Operating at Partial Load Conditions. J. Sustain. Dev. Energy Water Environ. Syst. 2017, 5, 139–150. [Google Scholar] [CrossRef]
- Massardo, A.; McDonald, C.; Korakianitis, T. Microturbine/Fuel-Cell Coupling for High-Efficiency Electrical Power Generation. J. Eng. Gas Turbines Power 2002, 124, 110–116. [Google Scholar] [CrossRef]
- Kaczmarczyk, T.; Żywica, G. Experimental study of a 1 kW high-speed ORC microturbogenerator under partial load. Energy Convers. Manag. 2022, 272, 116381. [Google Scholar] [CrossRef]
- Piwowarski, M.; Stepniak, D. Analyzing Selection of Low-Temperature Medium for Cogeneration Micro Power Plant. Pol. J. Environ. Stud. 2014, 23, 1417–1421. [Google Scholar]
- Bina, S.; Jalilinasrabady, H. Fujii, Energy, economic and environmental (3e) aspects of internal heat exchanger for orc geothermal power plants. Energy 2017, 140, 1096–1106. [Google Scholar] [CrossRef]
- Zanellato, L.; Astolfi, M.; Serafino, A.; Rizzi, D.; Macchi, E. Field Performance Evaluation of ORC Geothermal Power Plants Using Radial Outflow Turbines. Energy Procedia 2017, 129, 607–614. [Google Scholar] [CrossRef]
- Piwowarski, M. Design analysis of ORC micro-turbines making use of thermal energy of oceans. Pol. Marit. Res. 2013, 20, 48–60. [Google Scholar] [CrossRef][Green Version]
- Mikielewicz, D.; Wajs, J.; Ziolkowski, J.; Mikielewicz, J. Utilisation of waste heat from the power plant by use of the orc aided with bleed steam and extra source of heat. Energy 2016, 97, 11–19. [Google Scholar] [CrossRef]
- Dong, D.; Wang, Y.; Xu, G.; Wen, J.; Quan, Y. Design and analysis of an axial turbine for high-temperature organic Rankine cycle. Therm. Sci. Eng. Prog. 2023, 46, 2451–9049. [Google Scholar] [CrossRef]
- Mikielewicz, D.; Wajs, J.; Mikielewicz, J. Alternative cogeneration thermodynamic cycles for domestic orc. Chem. Process. Eng. 2018, 39, 75–84. [Google Scholar]
- Wood, G.; Newborough, M. Dynamic energy-consumption indicators for domestic appliances: Environment, behaviour and design. Energy Build. 2003, 35, 821–841. [Google Scholar] [CrossRef]
- Chen, C.; Liu, M.; Li, M.; Wang, Y.; Wang, C.; Yan, J. Digital twin modeling and operation optimization of the steam turbine system of thermal power plants. Energy 2024, 290, 129969. [Google Scholar] [CrossRef]
- Fethi, O.; Dessaint, L.; Al-Haddad, H. Modeling and simulation of the electric part of a grid connected microturbine. IEEE Power Eng. Soc. Gen. Meet. 2004, 2, 2212–2219. [Google Scholar]
- Gaonkar, D.; Patel, R. Modeling and simulation of microturbine based distributed generation system. In Proceedings of the 2006 IEEE Power India Conference, New Delhi, India, 10–12 April 2006. [Google Scholar]
- Nayak, S.; Gaonkar, D. Modeling and performance analysis of microturbine generation system in grid connected/islanding operation. Int. J. Renew. Energy Res. 2012, 2, 750–757. [Google Scholar]
- Torres, E.; Larragueta, J.; Eguia, P.; Mazon, J.; San, M.; Zamora, I. Dynamic performance of a microturbine connected to a low voltage network. Renew. Energy Power Qual. J. 2008, 1, 468–473. [Google Scholar] [CrossRef]
- Sun, H.; Qin, J.; Yan, P.; Huang, H.; Hung, T. Performance evaluation of a partially admitted axial turbine using R245fa, R123 and their mixtures as working fluid for small-scale organic Rankine cycle. Energy Convers. Manag. 2018, 171, 925–935. [Google Scholar] [CrossRef]
- Klonowicz, P.; Witanowski, L.; Suchocki, T.; Jedrzejewski, T.; Lampart, P. Selection of optimum degree of partial admission in a laboratory organic vapour microturbine. Energy Convers. Manag. 2019, 202, 112189. [Google Scholar] [CrossRef]
- Pini, M.; De Servi, C.; Burigana, M.; Bahamonde, S.; Rubino, A.; Vitale, S.; Colonna, P. Fluid-dynamic design and characterization of a mini-ORC turbine for laboratory experiments. Energy Procedia 2017, 129, 1141–1148. [Google Scholar] [CrossRef]
- Martins, G.; Braga, S.; Ferreira, S. Design optimization of partial admission axial turbine for ORC service. Appl. Therm. Eng. 2016, 96, 18–25. [Google Scholar] [CrossRef]
- Włodarsk, W. Experimental investigations and simulations of the microturbine unit with permanent magnet generator. Energy 2018, 158, 59–71. [Google Scholar] [CrossRef]
- Włodarsk, W. A model development and experimental verification for a vapour microturbine with a permanent magnet synchronous generator. Appl. Energy 2019, 252, 113430. [Google Scholar] [CrossRef]
- Traupel, W. Thermische Turbomaschinen; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Kosowski, K.; Piwowarski, M.; Stepien, R.; Włodarsk, W. Design and investigations of the ethanol microturbine. Arch. Thermodyn. 2018, 39, 41–54. [Google Scholar]
- Kosowski, K. Steam and Gas Turbines; Alstom: Saint-Ouen-sur-Seine, France, 2007. [Google Scholar]
- Kosowski, K.; Stepien, R.; Wlodarski, W.; Piwowarski, M.; Hirt, L. Partial Admission Stages of High Efficiency for a Microturbine. J. Vib. Eng. Technol. 2014, 2, 441–448. [Google Scholar]

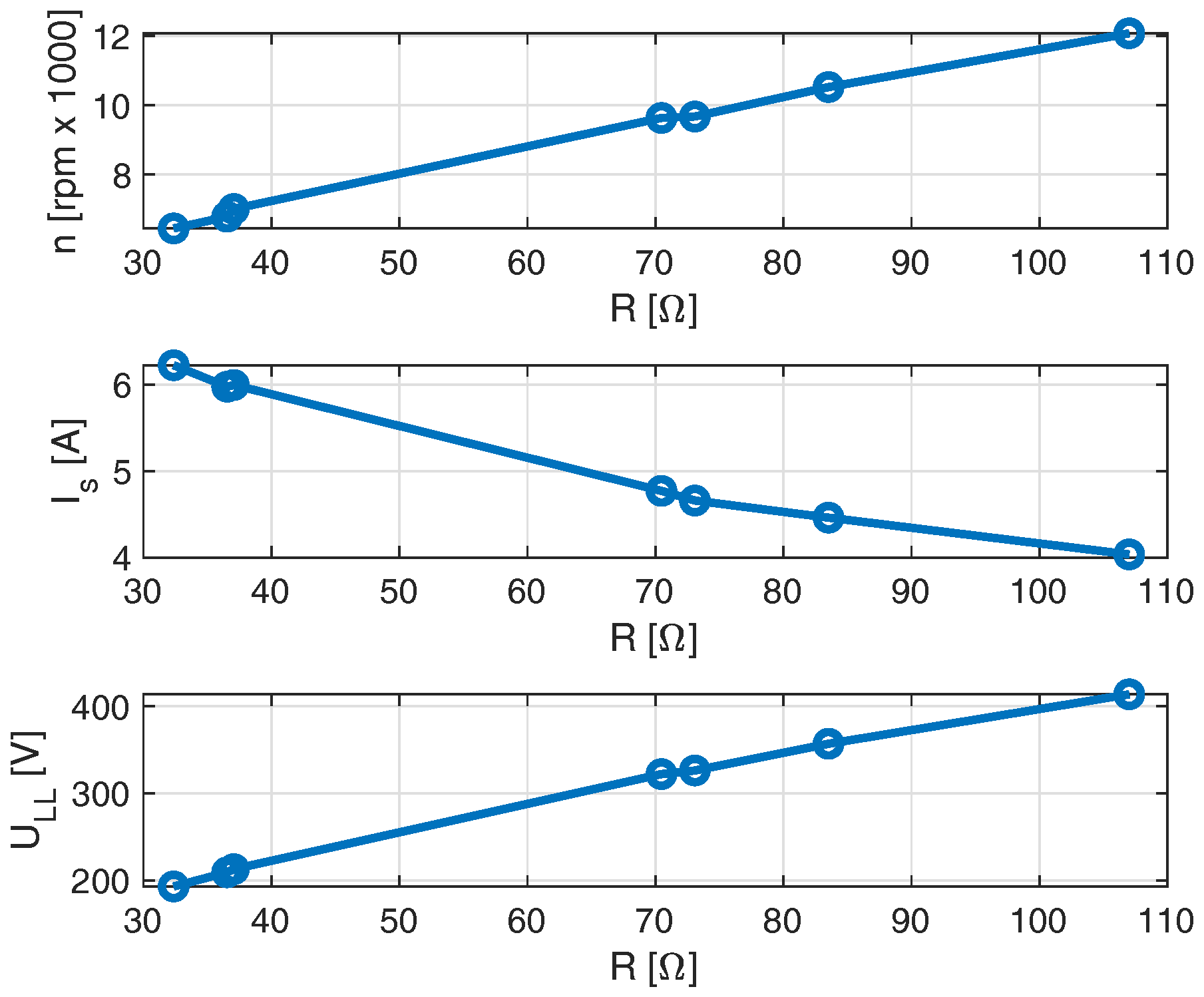
| Stage Number | Ratio of Admission |
|---|---|
| 1 | 0.067 |
| 2 | 0.109 |
| 3 | 0.171 |
| 4 | 0.236 |
| 5 | 0.323 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Włodarski, W.; Piwowarski, M. A Model Modification for a Microturbine Set with Partial Admission Stages. Energies 2024, 17, 1792. https://doi.org/10.3390/en17081792
Włodarski W, Piwowarski M. A Model Modification for a Microturbine Set with Partial Admission Stages. Energies. 2024; 17(8):1792. https://doi.org/10.3390/en17081792
Chicago/Turabian StyleWłodarski, Wojciech, and Marian Piwowarski. 2024. "A Model Modification for a Microturbine Set with Partial Admission Stages" Energies 17, no. 8: 1792. https://doi.org/10.3390/en17081792
APA StyleWłodarski, W., & Piwowarski, M. (2024). A Model Modification for a Microturbine Set with Partial Admission Stages. Energies, 17(8), 1792. https://doi.org/10.3390/en17081792








