Optimal Observer-Based Power Imbalance Allocation for Frequency Regulation in Shipboard Microgrids
Abstract
1. Introduction
1.1. Main Contribution
1.2. Notation and Power Sign Convention
1.3. Structure of the Paper
2. System Description
2.1. SMG Architecture
2.2. Modes of Operation
2.3. State-Space Representation
2.3.1. ESS Modelling
2.3.2. SMG Synchronous Machine Modelling
2.3.3. Compact Representation
- SMG Model:
3. Problem Formulation
- (A1)
- The first time derivative of is bounded with an a priori known bound, that is, .
- (A2)
- The signal remains constant where is an unknown positive constant. It is common practise to assume that the power load requirement remains constant when designing control strategies for power systems and microgrids [18]. This is required to guarantee the reach of the (optimal) equilibrium point.
- (A3)
- To ensure that the optimal power imbalance allocation is feasible, we assume thatwhere . Furthermore, there is always a sufficient level of energy storage given the initial condition, and a time horizon , such that
- (A4)
4. Problem Solution and Stability Analysis
- Low-Level STA Controller:
- Low-Level STA Observer
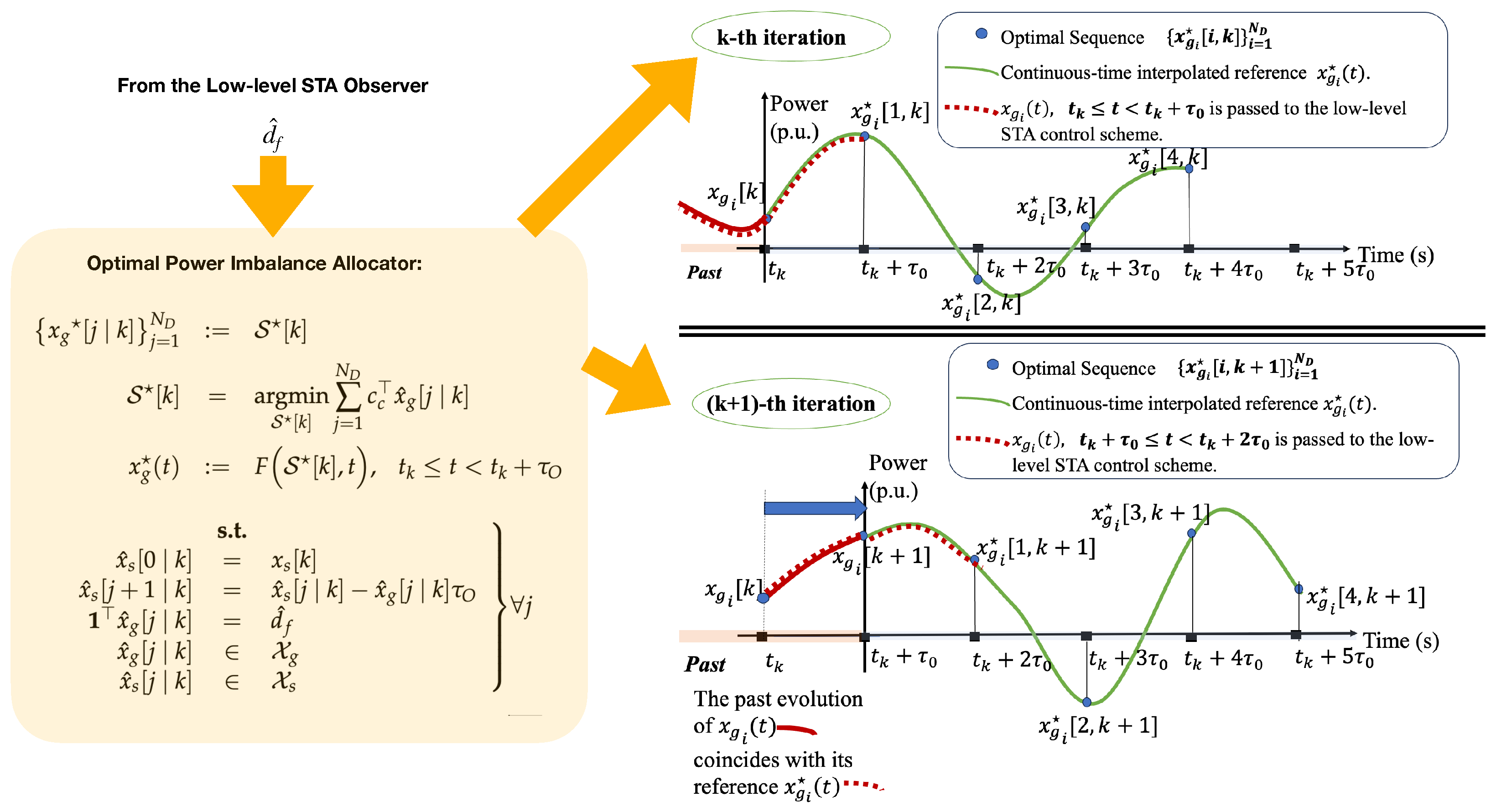
- High-Level Optimal Power Imbalance Allocator:
- (I)
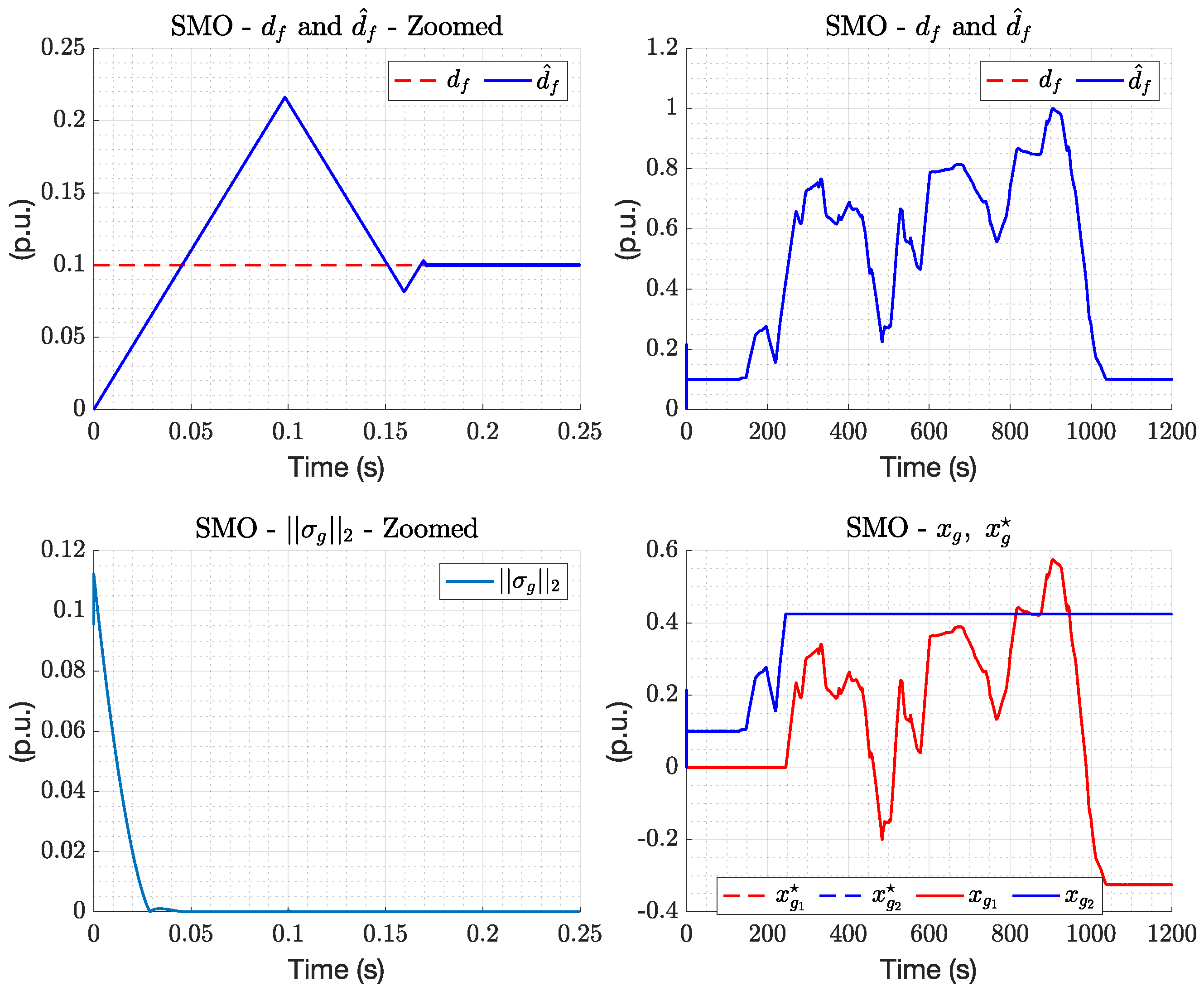
- The low-level STA observer is capable of estimating the unknown load power demand in a finite time .
- (II)
- (III)
- The low-level STA controllers are capable of driving to in a finite time and of dynamically tracking its smooth evolution over time.
- (a)
- If during the time horizon of seconds, the evolution of does not breach any of its associated constraints as per (19c), then the minimum for will also minimise the overall cost function (19b). A series composed of identical references will be generated and interpolated via the interpolator (19c).
- (b)
- If at a generic m-th step, the boundaries for the energy storage are reached, these can be reflected by constraining the associated output powers to be equal to zero, hence obtaining a different hyper-rectangle redefining the boundaries of and finding another single minimum for the cost function. A series composed of nonidentical references will be generated and interpolated via the interpolator (19c).
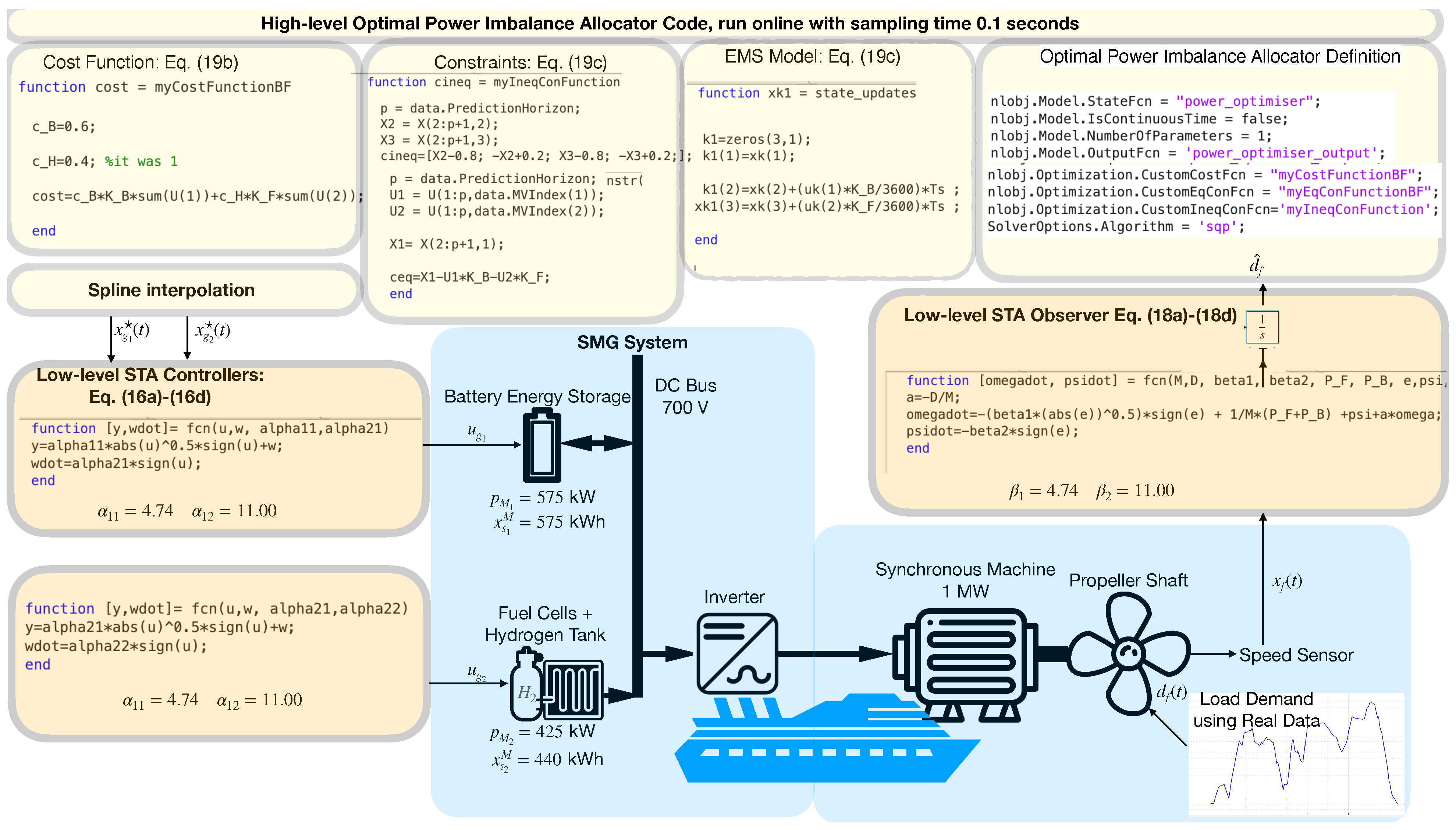
5. Simulation
- Scenario PI: an arbitrarily defined power imbalance allocator is imposed to determine the power reference for each ESS, i.e., Furthermore, during this scenario, each ESS is regulated via conventional PI controller.
- Scenario PIO: during which our optimal power imbalance allocator is utilised, and each ESS is regulated via PI controllers. The proportional and integral gains for the PI controllers are set equal to −1.
- Scenario SM: the arbitrary power allocator defined in the scenario PI is used and each ESS is regulated via STA controllers.
- Scenario SMO: the proposal of this paper, where the optimal power imbalance allocator is used in conjunction with STA controllers.
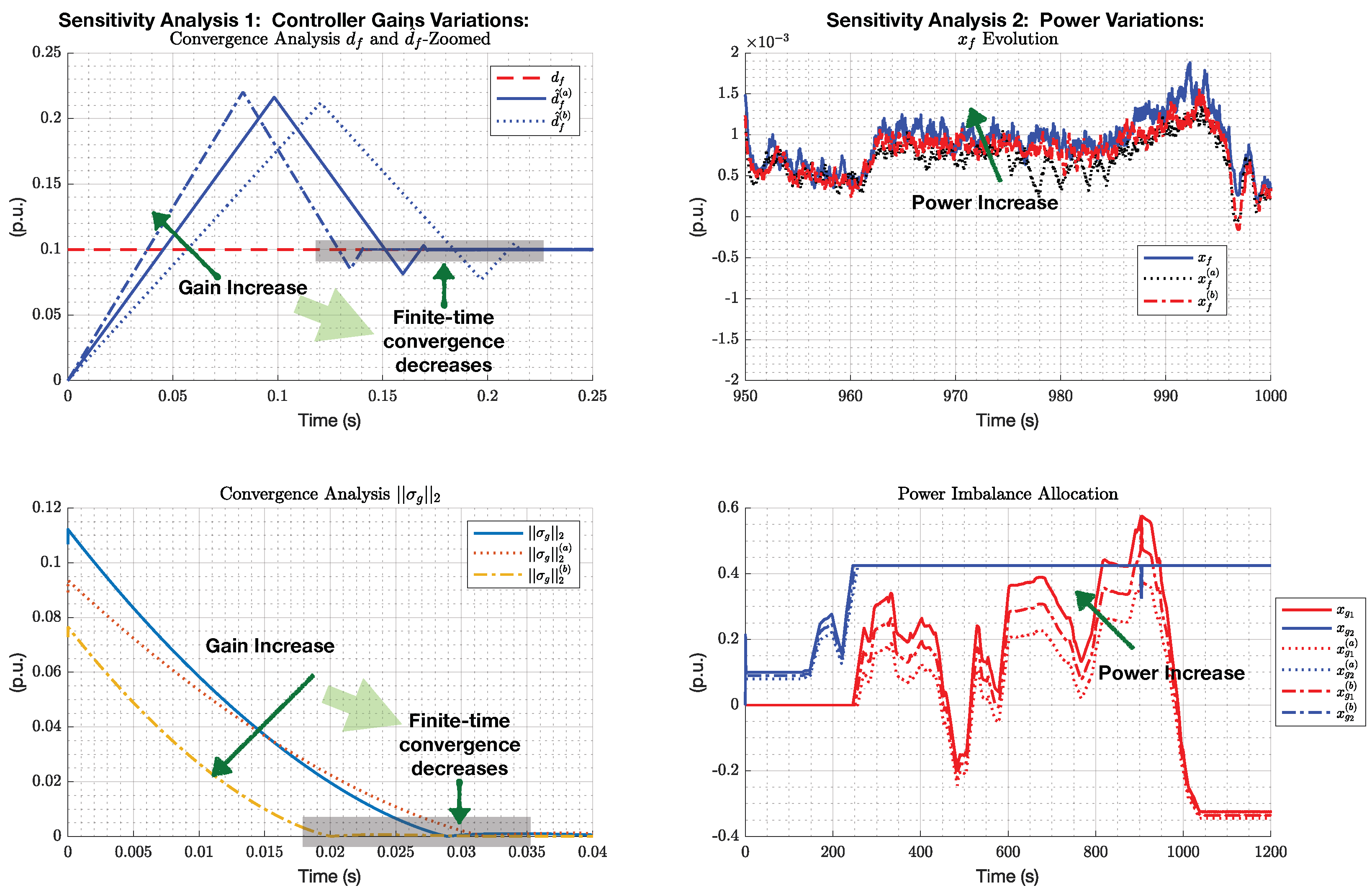
5.1. Sensitivity Analysis
5.1.1. Sensitivity Analysis 1
5.1.2. Sensitivity Analysis 2
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| STA | Super-Twisting Algorithm |
| ESS | Energy Storage System |
| SMG | Shipboard Microgrid |
| LFC | Load Frequency Control |
| BESS | Battery Energy Storage System |
| FC | Fuel Cell |
| EMS | Energy Management System |
References
- International Maritime Organization. Fourth Greenhouse Gas Study; International Maritime Organization: London, UK, 2020. [Google Scholar]
- Yildirim, B.; Gheisarnejad, M.; Khooban, M.H. Delay-dependent stability analysis of modern shipboard microgrids. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 1693–1705. [Google Scholar] [CrossRef]
- Xu, L.; Guerrero, J.M.; Lashab, A.; Wei, B.; Bazmohammadi, N.; Vasquez, J.C.; Abusorrah, A. A review of DC shipboard microgrids—Part I: Power architectures, energy storage, and power converters. IEEE Trans. Power Electron. 2021, 37, 5155–5172. [Google Scholar] [CrossRef]
- Feng, X.; Butler-Purry, K.L.; Zourntos, T. Real-time electric load management for DC zonal all-electric ship power systems. Electr. Power Syst. Res. 2018, 154, 503–514. [Google Scholar] [CrossRef]
- Aboelezz, A.M.; Sedhom, B.E.; El-Saadawi, M.M.; Eladl, A.A.; Siano, P. State-of-the-Art Review on Shipboard Microgrids: Architecture, Control, Management, Protection, and Future Perspectives. Smart Cities 2023, 6, 1435–1484. [Google Scholar] [CrossRef]
- Hassan, M.A.; Su, C.L.; Pou, J.; Sulligoi, G.; Almakhles, D.; Bosich, D.; Guerrero, J.M. Dc shipboard microgrids with constant power loads: A review of advanced nonlinear control strategies and stabilization techniques. IEEE Trans. Smart Grid 2022, 13, 3422–3438. [Google Scholar] [CrossRef]
- Vafamand, N.; Khooban, M.H.; Dragičević, T.; Boudjadar, J.; Asemani, M.H. Time-delayed stabilizing secondary load frequency control of shipboard microgrids. IEEE Syst. J. 2019, 13, 3233–3241. [Google Scholar] [CrossRef]
- Yuan, Z.L.; Zhang, C.K.; Shangguan, X.C.; Jin, L.; Xu, D.; He, Y. Stability analysis of load frequency control for shipboard microgrids with occasional large delays. IEEE Trans. Circuits Syst. II Express Briefs 2021, 69, 2161–2165. [Google Scholar] [CrossRef]
- Xi, K.; Dubbeldam, J.L.; Lin, H.X.; van Schuppen, J.H. Power-imbalance allocation control of power systems-secondary frequency control. Automatica 2018, 92, 72–85. [Google Scholar] [CrossRef]
- Rinaldi, G.; Menon, P.P.; Edwards, C.; Ferrara, A. Sliding mode observer-based finite time control scheme for frequency regulation and economic dispatch in power grids. IEEE Trans. Control Syst. Technol. 2021, 30, 1296–1303. [Google Scholar] [CrossRef]
- Zia, M.F.; Elbouchikhi, E.; Benbouzid, M. Microgrids energy management systems: A critical review on methods, solutions, and prospects. Appl. Energy 2018, 222, 1033–1055. [Google Scholar] [CrossRef]
- Zhao, C.; Mallada, E.; Dörfler, F. Distributed frequency control for stability and economic dispatch in power networks. In Proceedings of the 2015 American Control Conference (ACC), Chicago, IL, USA, 1–3 July 2015; pp. 2359–2364. [Google Scholar]
- Shankar, R.; Chatterjee, K.; Chatterjee, T. Coordination of economic load dispatch and load frequency control for interconnected power system. J. Inst. Eng. (India) Ser. B 2015, 96, 47–54. [Google Scholar] [CrossRef]
- Drakunov, S.V.; Utkin, V.I. Sliding mode control in dynamic systems. Int. J. Control 1992, 55, 1029–1037. [Google Scholar] [CrossRef]
- Castillo, I.; Fridman, L.; Moreno, J.A. Super-twisting algorithm in presence of time and state dependent perturbations. Int. J. Control 2018, 91, 2535–2548. [Google Scholar] [CrossRef]
- Nagesh, I.; Edwards, C. A multivariable super-twisting sliding mode approach. Automatica 2014, 50, 984–988. [Google Scholar] [CrossRef]
- Kali, Y.; Saad, M.; Benjelloun, K.; Khairallah, C. Super-twisting algorithm with time delay estimation for uncertain robot manipulators. Nonlinear Dyn. 2018, 93, 557–569. [Google Scholar] [CrossRef]
- Machado, J.E.; Rinaldi, G.; Cucuzzella, M.; Menon, P.P.; Scherpen, J.M.; Ferrara, A. Online Parameters Estimation Schemes to Enhance Control Performance in DC Microgrids. Eur. J. Control 2023, 74, 100860. [Google Scholar] [CrossRef]
- Incremona, G.P.; Ferrara, A.; Magni, L. Hierarchical model predictive/sliding mode control of nonlinear constrained uncertain systems. IFAC PapersOnLine 2015, 48, 102–109. [Google Scholar] [CrossRef]
- Incremona, G.P.; Cucuzzella, M.; Magni, L.; Ferrara, A. MPC with sliding mode control for the energy management system of microgrids. IFAC PapersOnLine 2017, 50, 7397–7402. [Google Scholar] [CrossRef]
- Palmieri, A.; Rosini, A.; Procopio, R.; Bonfiglio, A. An MPC-sliding mode cascaded control architecture for PV grid-feeding inverters. Energies 2020, 13, 2326. [Google Scholar] [CrossRef]
- Bahrampour, E.; Dehghani, M.; Asemani, M.H.; Abolpour, R. Load frequency fractional-order controller design for shipboard microgrids using direct search alghorithm. IET Renew. Power Gener. 2023, 17, 894–906. [Google Scholar] [CrossRef]
- Khooban, M.H.; Dragicevic, T.; Blaabjerg, F.; Delimar, M. Shipboard microgrids: A novel approach to load frequency control. IEEE Trans. Sustain. Energy 2017, 9, 843–852. [Google Scholar] [CrossRef]
- Liu, B.; Song, Z.; Yu, B.; Yang, G.; Liu, J. A Feedforward Control-Based Power Decoupling Strategy for Grid-Forming Grid-Connected Inverters. Energies 2024, 17, 424. [Google Scholar] [CrossRef]
- Magni, L.; Scattolini, R. Model predictive control of continuous-time nonlinear systems with piecewise constant control. IEEE Trans. Autom. Control 2004, 49, 900–906. [Google Scholar] [CrossRef]
- Bejestani, A.K.; Annaswamy, A.; Samad, T. A hierarchical transactive control architecture for renewables integration in smart grids: Analytical modeling and stability. IEEE Trans. Smart Grid 2014, 5, 2054–2065. [Google Scholar] [CrossRef]
- Moreno, J.A.; Osorio, M. Strict Lyapunov functions for the super-twisting algorithm. IEEE Trans. Autom. Control 2012, 57, 1035–1040. [Google Scholar] [CrossRef]
- Bertsimas, D.; Tsitsiklis, J.N. Introduction to Linear Optimization; Athena Scientific: Belmont, MA, USA, 1997; Volume 6. [Google Scholar]
- Chalanga, A.; Kamal, S.; Fridman, L.M.; Bandyopadhyay, B.; Moreno, J.A. Implementation of super-twisting control: Super-twisting and higher order sliding-mode observer-based approaches. IEEE Trans. Ind. Electron. 2016, 63, 3677–3685. [Google Scholar] [CrossRef]


| Symbol | Physical Meaning and Measurement Unit |
|---|---|
| ESS output power (p.u.) | |
| ESS output power optimal reference (p.u.) | |
| ESS energy storage level and its discrete time prediction (p.u. s) | |
| ESS low-level control (p.u.) | |
| Power load demand and its estimate (p.u.) | |
| Frequency deviation (p.u.) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rinaldi, G.; Baby, D.K.; Menon, P.P. Optimal Observer-Based Power Imbalance Allocation for Frequency Regulation in Shipboard Microgrids. Energies 2024, 17, 1703. https://doi.org/10.3390/en17071703
Rinaldi G, Baby DK, Menon PP. Optimal Observer-Based Power Imbalance Allocation for Frequency Regulation in Shipboard Microgrids. Energies. 2024; 17(7):1703. https://doi.org/10.3390/en17071703
Chicago/Turabian StyleRinaldi, Gianmario, Devika K. Baby, and Prathyush P. Menon. 2024. "Optimal Observer-Based Power Imbalance Allocation for Frequency Regulation in Shipboard Microgrids" Energies 17, no. 7: 1703. https://doi.org/10.3390/en17071703
APA StyleRinaldi, G., Baby, D. K., & Menon, P. P. (2024). Optimal Observer-Based Power Imbalance Allocation for Frequency Regulation in Shipboard Microgrids. Energies, 17(7), 1703. https://doi.org/10.3390/en17071703






