Next Article in Journal
Optimal Observer-Based Power Imbalance Allocation for Frequency Regulation in Shipboard Microgrids
Next Article in Special Issue
Value Evaluation Model of Multi-Temporal Energy Storage for Flexibility Provision in Microgrids
Previous Article in Journal
Principles for the Design of a Biomass-Fueled Internal Combustion Engine
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Energies
Volume 17
Issue 7
10.3390/en17071702
energies-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

A Review of Peer-to-Peer Energy Trading Markets: Enabling Models and Technologies

by
Shama Naz Islam
School of Engineering, Deakin University, Geelong, VIC 3216, Australia
Energies 2024, 17(7), 1702; https://doi.org/10.3390/en17071702
Submission received: 28 February 2024 / Revised: 27 March 2024 / Accepted: 30 March 2024 / Published: 2 April 2024
(This article belongs to the Special Issue Intelligent Operation and Management of Microgrids II)
Browse Figures
Versions Notes

Abstract

:
This paper presents a detailed review of the existing literature on peer-to-peer (P2P) energy trading considering market architectures, trading strategies, and enabling technologies. P2P energy trading enables individual users in the electricity network to act as sellers or buyers and trade energy among each other. To facilitate the discussion on different aspects of P2P energy trading, this paper focuses on P2P market mechanisms, relevant bidding strategies, and auction models. In addition, to solve the energy management problems associated with P2P energy trading, this paper investigates widely used solution methods such as game-theoretic models, mathematical optimisation, as well as more recent machine learning techniques and evaluates them in a critical manner. The outcomes of this investigation along with the identification of the challenges and limitations will allow researchers to find suitable P2P energy trading mechanisms based on different market contexts. Moreover, the discussions on potential future research directions are expected to improve the effectiveness of P2P energy trading technologies.

1. Introduction

The increasing adoption of distributed renewable energy sources such as rooftop solar in the electricity grid has enabled consumers to become prosumers, who can generate and sell energy to other users [1]. This leads to a new form of energy market acting in parallel with the traditional wholesale or retail energy market. In an electricity distribution network, if there are many users with distributed energy resources (DERs), there can be some users with an energy excess and other users with an energy deficit. If these users can share or trade energy among each other, they can balance their electricity supply/demand locally, thus forming a peer-to-peer (P2P) energy market [2]. Such energy transactions are often monitored by centralised platforms with mechanisms to settle market prices between prosumers ensuring fairness and end user engagement.
Government agencies and energy policy makers throughout the world aim to achieve ‘Net Zero by 2050’ target aligned with United Nation’s Sustainable Development Goals (SDG) on climate action and affordable clean energy [3]. To achieve this goal, they provide incentives for renewable energy integration and uptake of energy efficiency technologies [4]. P2P energy trading technologies can help achieve such goals by enhancing the adoption of renewable energy technologies and reducing carbon emissions [5,6,7]. The existing energy market mechanisms often fail to manage the new challenges arising with changes in the energy mix. In this regard, P2P energy trading mechanisms can offer innovative market solutions [8] to engage new participants in the market. With the increasing penetration of renewable energy sources, there can be adverse effects on electricity distribution networks such as reverse power flow and voltage rise issues. P2P energy trading can balance the energy excess/deficit locally and prevent the aforementioned issues. As a result, network operators can avoid the need for expensive upgrades of the electricity infrastructure, which would otherwise be required for maintaining the required network performance.
Existing research on P2P energy markets identified different categories based on connectivity among peers. These categories include full (one-to-one), community based (one-to-many) and hybrid (both one-to-one and one-to-many at different levels) P2P energy markets [9]. One of the very first contributions in P2P energy trading research has identified three different P2P energy trading strategies, namely bill sharing, mid-market rate and supply–demand ratio [10,11]. Bill sharing considers a community microgrid architecture where the overall electricity costs are shared by individual customers. The mid-market rate assigns the energy exchange price as the mid-point between energy buying and selling prices in the network. The supply–demand ratio considers the ratio of electricity supply and demand, based on which the electricity exchange price is determined [12]. These strategies were evaluated in [11], which implemented a multi-agent simulation framework to simulate prosumer behaviour for residential customers in Great Britain. The studies found that the mid-market ratio performs well when solar penetration is at moderate levels; whereas with increasing solar penetration, the supply–demand ratio outperforms other mechanisms. The P2P energy trading strategies can be further characterised as centralised (presence of a central coordinator) [13] and decentralised markets (decentralised bidding and market coordination) [14].
Apart from the aforementioned strategies, there can be other strategies based on game theory and optimisation models. Game-theoretic approaches formulate the competing interests of sellers and buyers as a game and aim to achieve an equilibrium point where both seller and buyer utilities are maximised [15]. A commonly used game-theoretic model is the Stackelberg game, where a prosumer acts like the leader and sets up the prices, while others become followers [16]. Since P2P energy trading problems are associated with maximising the utilities of the prosumers either in terms of profit or cost savings, different optimisation approaches have been undertaken in many existing research studies in P2P energy trading. These approaches include mixed integer linear programming (MILP) [17], convex [18] and non-convex programming [19]. Existing research on P2P energy trading has also emphasised the importance of auction mechanisms and bidding. In a P2P market, prosumers will submit bids to optimise their utilities based on maximising profits and savings. In addition, there can be different types of auction-based approaches, where an auctioneer determines which prosumers can participate in the trading and what is the market clearing price. With the advancement of big data, P2P energy trading problems are being integrated with machine learning (ML) algorithms such as reinforcement learning for managing P2P energy trading decisions [20,21]. Another important aspect of P2P energy trading integration in electricity networks is battery energy storage, which can add a new dimension to the energy/load combination. The authors in [22] considered a central energy storage for all participants in a P2P energy market to minimise the electricity costs for end users. A non-cooperative game theoretic model was implemented in [23] to obtain the market equilibrium for P2P market participants embedded with shared energy storage units. On the other hand, a strategic bidding model was adopted in [24] for individual energy storage units considering uncertainties in wind power generation.
There have been a number of review papers that outlined the P2P energy trading mechanisms, potential technologies, challenges and barriers towards the adoption of such technologies. Three different types of market architectures, namely, community self-consumption, transactive energy and P2P architectures, were discussed in [25]. Similarly, the authors in [26] described and compared P2P, community-based, and a group of community-based architectures. The authors in [27] described the categorisation of P2P energy trading mechanisms through a systematic framework. In particular, they defined market models in terms of market scope, assumptions, objectives, and market mechanisms with detailed discussions on corresponding allocation and payment rules. Different pricing strategies for P2P energy trading, such as synchronous, asynchronous, uniform, and negotiation-based strategies were discussed in [28]. The authors in [29] described a transactive energy framework with different approaches towards the integration of DERs, and highlighted P2P energy trading as an option for DER integration. The physical components that enable the P2P energy trading and the challenges associated with the physical network constraints were outlined in [30]. Different optimisation algorithms for solving the P2P energy trading problem were reviewed in [7] with a detailed discussion on game theory, operational research, machine learning models, and blockchain technologies. A number of P2P energy trading pilot projects were discussed in [31]. From the perspectives of developing countries, the authors in [32] discussed suitable business models for promoting P2P energy trading technologies. From the aforementioned discussion, it can be observed that the existing review papers have focused on a certain number of enabling technologies among game theory, optimisation, bidding, auction and ML models. However, a joint consideration of all these enabling technologies and comparative review of their suitability is missing in the existing review papers, which is important to investigate. Table 1 shows a comparative analysis of the existing review papers and the proposed work in terms of the key aspects elaborated in these papers.
Based on the research gap outlined in the previous discussion and tabulated in Table 1, this paper presents an in-depth review of the P2P market architecture, enabling technologies such as game theory, optimisation, and machine learning, as well as bidding and auction models. In particular, the comparison among different market mechanisms, strategies, and technologies is evaluated critically to identify the suitability of these solutions in different scenarios. The key contributions made in the proposed research are as follows:
  • A detailed analysis of different P2P market architectures as well as different market mechanisms is presented. In addition, different bidding strategies and auction models that enable effective P2P energy trading are compared and evaluated.
  • Different solution methods for P2P energy trading problems such as game theory, mathematical optimisation, and machine learning-based techniques are reviewed. The analysis helps evaluate the suitability of the aforementioned solution methods towards the P2P energy trading applications.
  • The challenges associated with the P2P energy trading implementation in real-life platforms are reviewed. Finally, a number of innovative solutions which can further enhance the effectiveness of P2P energy trading are proposed for future research.
The rest of the paper is organised as follows. The architecture of P2P energy markets and different market mechanisms are described in Section 2. A number of real-life P2P energy trading platforms and implementation projects are discussed in Section 3. The technological solutions that enable P2P energy trading, such as the game theoretic, optimisation-based, or auction models, are outlined in Section 4. The key challenges and barriers for different economies to adopt P2P energy trading are elaborated in Section 5. Potential future research directions to overcome these barriers are presented in Section 6. Finally, the concluding remarks are outlined in Section 7.

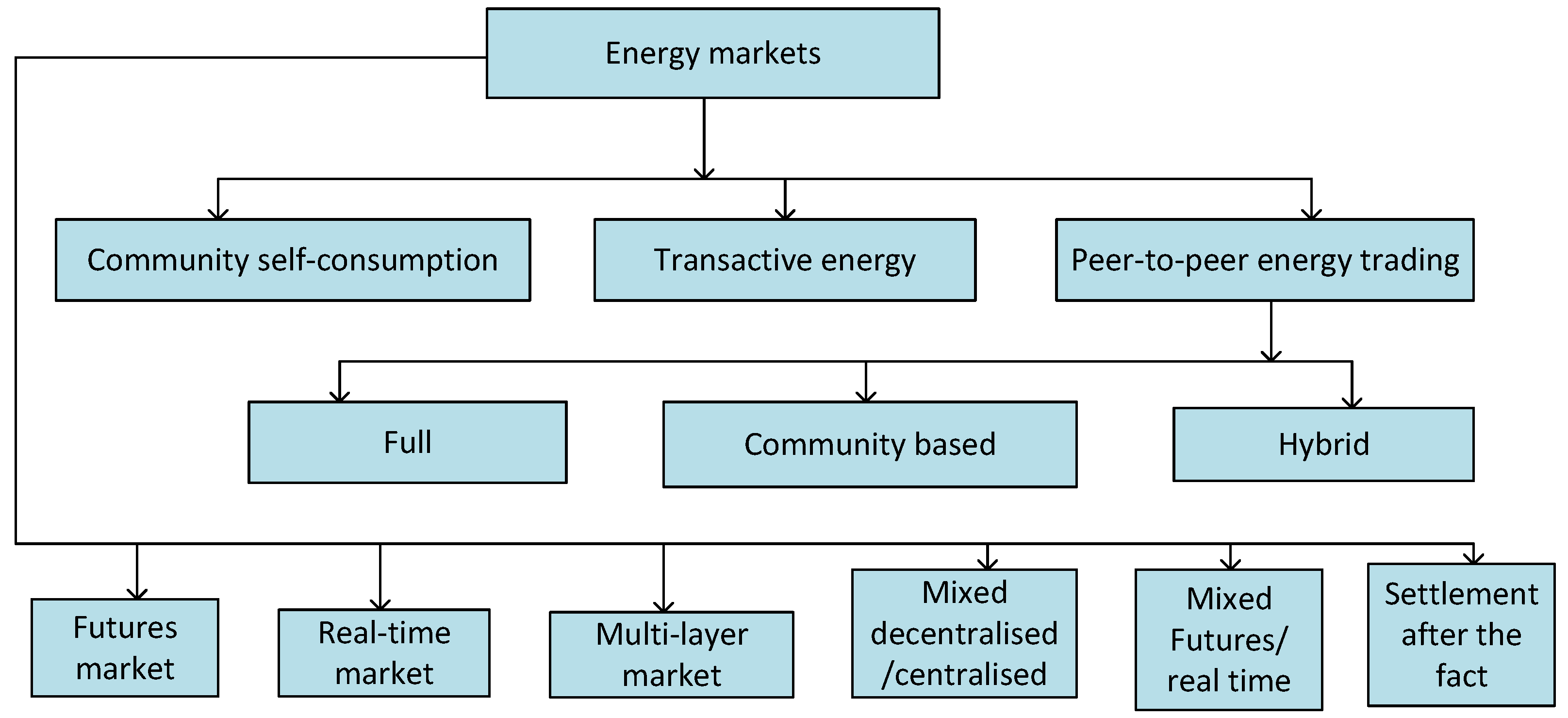
2. Overview of P2P Market Structure

The emergence of the P2P market needs to be viewed in relation to two other relevant market structure evolving from the introduction of the innovative demand response and renewable energy technologies. These market structures incorporate community self consumption (CSC) and transactive energy (TE) models [25]. Any user integrated with renewable energy generation can be part of the CSC market model, who is able to store or sell excess energy to other loads in close proximity [33]. On the other hand, TE models focus on balancing the supply and demand in a dynamic manner through appropriate control technologies, often enabled by real-time pricing mechanisms [34]. In contrast to CSC, TE models incorporate the entire electricity grid ranging from small-scale to large-scale networks [35]. P2P market models can be considered a special case of TE, where the key motivation is obtaining profits by selling energy to peers rather than dynamically changing load patterns for improved network reliability [1].
Based on the connectivity of the peers, a P2P market can be categorised into full, community-based, and hybrid P2P markets [9]. In a full P2P market, the participants engage directly with each other for energy transactions. There is no centralised controller to manage the energy sell/purchase activities. Thus, the market involves a number of bilateral trades among the peers [36]. In a community-based P2P market, a central energy management platform will be present to monitor and coordinate the energy transactions among the participants in the market [37]. This central manager can also coordinate with external markets such as the utility grid to negotiate financial incentives for the community for providing different market services [38]. The hybrid P2P market represents a combination of both full and community P2P markets [39]. In this market, the end users will be selling/purchasing energy through a central energy management system (EMS), and there will be clusters of central EMSs who will directly exchange market decisions as in a full P2P market [40].
Based on the interactions of the market participants with the market settlements, the market architectures are categorised into six classes. These designs include the futures market, real-time market, multi-layer market, mixed decentralised/centralised market, mixed futures/real-time market, and settlement-after-the-fact market [1]. The futures market is the most common type of market design observed in the real-life energy markets, which involve trading decisions made before the actual market settlement [2]. In contrast to the futures market, the real-time market allows participants to update their trading decisions during the settlement [19]. Though such markets offer more flexibility for renewable-based users, as their supply/demand balance can change during the settlement, achieving the overall balance in supply/demand in such markets can be challenging [1]. The typical market mechanisms associated with the aforementioned markets are the different types of auctions [41] and bilateral contracts [42]. The multi-layer market has settlements at multiple layers. For example, in the lower level, the individual communities can trade energy within the peers of the communities, and then the remaining supply/demand can be settled by an aggregator from each community with external markets [43]. The mixed decentralised/centralised market adopts a similar mechanism, but it involves bilateral negotiations at the lower level, and the residuals are then settled through a central auction [44]. In the mixed futures/real-time market, some energy trading occurs prior to the settlement and any remaining supply/demand is then traded during the settlement period [45]. Finally, the settlement-after-the-fact market involves any trading that happens after settlement, and a fixed price is charged to any participants who need to achieve supply/demand balance after the settlement [46]. The different types of market architectures are illustrated in Figure 1.
There are a number of price formation strategies for the P2P energy trading market as discussed by the authors in [1]. These strategies include auction-based, negotiation-based, system-determined and equilibrium-based mechanisms. Auction-based markets involve either one party (single auction) [47] or both parties (double auction) [48] to ask for specific prices or specific quantities of energy as bids. Negotiation-based mechanisms involve one-to-one bids rather than a centralised method like auctions to determine the market price [49]. System-determined mechanisms enable a system entity, such as the network operator or aggregator, to set the market prices [50]. On the other hand, equilibrium-based mechanisms are associated with reaching an equilibrium point between sellers’ and buyers’ utilities, for example, as in a game theoretic model [51].
It is essential to have the discussions on bidding mechanisms given their strong correlation with the market structure and operation. The authors in [32] identified three different types of bidding strategies for the P2P energy trading market, which involves zero intelligence, zero intelligence plus, and adaptive aggressiveness. Zero intelligence bidding involves randomly generated bids without any prior knowledge of the supply/demand conditions of the market [52]. On the other hand, zero intelligence plus involves prior knowledge of the bids from different buyers and sellers, which allows them to update their profit margin [53]. Zero intelligence plus algorithms can be more effective than zero intelligence algorithms if the bids are updated based on certain thresholds. Adaptive aggressiveness enables automatic updates of the bids by adapting with the changes in market clearing prices using a learning mechanism [54]. The authors in [54] found that such mechanisms can bring more profits in comparison to the two other mechanisms mentioned before. A similar approach was presented in [14], where prosumers obtain knowledge of each other’s bids through automatic learning based on the market prices without violating user privacy. It can be noted that the zero intelligence mechanism needs the least computational resources among the three bidding strategies. Thus, there is a trade-off between the benefits achieved from additional information and required memory resources. Zero intelligence plus and adaptive aggressiveness can be quite useful when users have specific bidding trends. On the other hand, if most of the users are bidding randomly, then it might be sufficient to adopt a simpler bidding strategy such as zero intelligence. Zero intelligence plus and adaptive aggressiveness strategies can help manipulate the outcomes of the P2P energy trading models, and hence, there should be appropriate limits designed for bids. The effectiveness of these bidding mechanisms can be further enhanced by the integration of machine learning algorithms such as reinforcement learning, which can assist with intelligent decision making [55].
The authors in [56] reviewed a number of bidding mechanisms based on how the payoff will be distributed among the participants. These include the best offer approach and market power approach. In the best offer approach, market participants aim for the best bids without consideration of the supply/demand scenario. On the other hand, the market power approach takes into account the imbalance between supply and demand, and based on this, determines how competitive the participants need to be. For example, when the market demand exceeds the market supply, all sellers may achieve some payoff, whereas only the buyer with the best bid can win.

3. P2P Energy Trading Platforms

To validate the theoretical and conceptual model of the P2P energy trading framework, a number of pilot projects have been implemented commercially throughout the world. The sustainability benefits integrated with the popular perception of energy independence as well as the inception of new business models have motivated many retailers and software developers to work together towards successful implementations of P2P energy trading platforms. It is essential to reflect on the findings from such projects to better understand the key design considerations of the P2P energy trading technologies.
The authors in [31] have outlined a number of pilot implementation projects undertaken by different countries. One of the very popular P2P energy trading pilot implementation projects is Piclo in the UK, where an online platform was developed for energy trading between prosumers [57]. Other similar projects include Vandebron in the Netherlands [58], Peer Energy Cloud [59], Pebbles [60], Sonnen Energy Community [9], Lichtblick Swarm Energy [61] and Smart Watts [58] in Germany, Brooklyn Microgrid [8] in the USA, City of Fremantle (Renew Nexus) [62] in Australia, Chiang Mai University in Thailand [63], Energy Collective in Denmark [64], EnerPort in Ireland [65], eRex peer-to-peer trial in Japan [66], NRGcoin in Belgium [67], SEDA peer-to-peer trial in Malaysia [68], and Prosumer Driven Integrated Smart Grid in India [31]. A detailed list of real-world P2P projects along with their scale and technological features is available in [69]. In the following part, a number of the aforementioned projects are briefly discussed to shed light on the real-world challenges and implementation issues in a pilot scale P2P energy trading project.
The Brooklyn microgrid involves a number of residential and commercial users integrated with solar energy and blockchain technologies [70]. To enable P2P energy trading, additional smart meters needed to be incorporated with existing utility meters along with the energy management system platform where users share the price limits and energy source preferences through a mobile application. On the other hand, the Pebbles project in Germany involves solar, wind, and battery energy storages as well as controllable loads, which allows prosumers to trade energy in a blockchain-enabled platform [60]. Piclo in the UK involves commercial users purchasing energy from renewable energy generators who have the ability to prioritise the generators from whom they want to purchase [57]. A similar platform is Vandebron, which involves farmers with wind turbines, allowing them to sell electricity to other consumers [58]. Sonnen Community, developed by sonnenBatterie energy storage manufacturers in Germany, involves users with battery storage who can share surplus energy through a virtual pool without involving the utility network [9].
Some of the pilot P2P energy trading projects have only been implemented through small-scale trials. For example, Uttar Pradesh in India hosted the P2P pilot trading project through blockchain technologies by including nine prosumers and three consumers [71]. The trial continued for three months through a simulated platform without involving direct financial transaction among the participants. Similarly, a testbed with three prosumers was developed in Indian Institute of Technology Gandhinagar (IITGN) [31]. These prosumers are set up at the laboratory scale, considering the different types of loads a residential user may have. There are blockchain-based platforms to coordinate the financial transactions and a microcomputer to aggregate the solar generation and load demand data for optimisation and forecasting applications. Another example is Enerport, which aims to develop a laboratory-scale prototype of smart homes enabled with P2P energy trading features in NUI Galway, Ireland [65]. A functional interface is being developed between the blockchain simulator and smart metering platforms for implementing different types of auction mechanisms.

4. P2P Energy Trading Techniques

Existing research has explored a number of techniques that enable P2P energy trading considering different aspects of energy system networks. It is important to investigate these techniques in terms of their unique features, challenges and complexities for practical implementation. Particularly, this section will highlight some insights on popular methods such as game theory, mathematical optimisation, and auction methods as well as machine learning-based approaches for P2P energy trading.

4.1. Game Theoretic Approaches

Game theory has been widely adopted for P2P energy trading techniques due to the fact that participants in P2P energy market compete against a common financial objective which can be modelled as a game to identify the market equilibrium [72]. Game theoretic models can be categorised as non-cooperative and cooperative games [51]. In the non-cooperative scenario, the participants act independently for achieving a common goal that can have conflicting interests [12]. The actions can take place once in the game for static non-cooperative games. On the other hand, dynamic non-cooperative games allow participants to take actions multiple times based on the decisions of other participants [15]. Non-cooperative games can be solved using the Nash equilibrium, which defines a stable point in the game where no participant can earn benefits by deviating from their action in the Nash equilibrium if other participants are following their equilibrium actions [73].
In a non-cooperative game, there is usually a leader (e.g., aggregator) who coordinates the participants’ actions while participants act like followers [74]. In such games, the leader can first publish the prices, and participants optimise their actions accordingly. The other option is that participants inform their prices and the leader optimises the market clearing [7]. Bilateral contracts can also be considered non-cooperative games given that they match participants’ actions and expectations through a set of interactions between two parties [75]. The authors in [74] evaluated optimal pricing strategies for prosumers in a Stackelberg game. On the other hand, the authors in [76] formulated a generalised Nash game to model distributed P2P energy trading.
Different from the non-cooperative games, cooperative games focus on providing incentives for a group of participants so that they can act together to achieve the common goal [77]. Cooperative games can include canonical coalition, coalition formation, and coalition graph games. Canonical coalition games investigate how to form a grand coalition and how the benefits can be fairly shared with the participants. Coalition formation games analyse how different participants interact with each other to form a coalition. Coalition graph games define a network graph to evaluate how participants are connected to each other in terms of communicating their actions [77].
Cooperative games involve the redistribution of incentives among the participants forming the coalition. Usually, the participants have an agreement on how the profit will be shared among each other prior to joining the games. The individual participant’s optimal actions should also converge with the group’s optimal strategies [78]. There are a number of profit redistribution strategies proposed in the literature, which include the Vickrey–Clarke–Groves (VCG) model, the Shapley value, and nucleus methods [7]. The VCG model aims for the maximisation of combined profit [79], whereas the Shapley-value method redistributes profit based on participants’ marginal contributions [80]. On the other hand, the nucleus method minimises costs or losses resulting from the non-optimal distribution of incentives [81].

4.2. Mathematical Optimisation

P2P energy trading often involves the maximisation of incentives or minimisation of costs, implying the necessity of optimisation-based approaches. Existing research has considered a significant number of optimisation-based approaches to obtain the most effective solutions for P2P energy trading. Some of these approaches are associated with centralised optimisation at the aggregator [43] or decentralised/distributed optimisation at the participants [82]. In terms of the goals of the optimisation, existing research has considered cost minimisation [83], the optimisation of power exchanges among peers [36], the maximisation of retailer welfare [84], the minimisation of battery depreciation [85] or the optimisation of participant profits for voltage management services [17]. A number of mathematical optimisation algorithms, including linear programming, mixed-integer linear programming, convex optimisation, second-order cone programming, quadratically constrained quadratic programming, and non-convex programming are widely used in the context of P2P energy trading optimisation based on the aforementioned objectives. These optimisation algorithms are explained in the following part of this subsection.
Linear programming problems are associated with the linear objective function and linear constraints. The variables involved in the optimisation problem can be integers or real numbers. Usually, these problems are solved using the simplex method and graphical method. The authors in [44] optimised battery flexibility through a multi-period linear programming problem in a pool-based P2P market considering grid consumption, battery charging, and discharging as linear variables over a number of time periods. On the other hand, the optimal capacity of different distributed energy resources was optimised in [40] to achieve the optimal supply–demand balance in a P2P market. Mixed integer linear programming (MILP) is a special subclass of linear programming, where the variables can be a mix of integer and floating point numbers. Typical solution algorithms include branch-and-bound, cutting plane and branch-and-cut methods. The authors in [17] utilised MILP to solve the social welfare maximisation of prosumers and consumers as well as the cost minimisation problem of consumers in a P2P energy market. The supply/demand balance problem from a household level was modelled as MILP in [53] while considering the selling and purchasing prices as well as the amount of energy sold/purchased.
Convex optimisation problems involve minimising convex objective functions or maximising concave objective functions over convex constraints. These functions can be linear or non-linear. Convex functions are characterised by those functions for which the line connecting two points in the graph of the function lies above the graph. Convex problems include linear programming, quadratic programming (with convex objectives and linear/convex quadratic constraints), and second-order cone programming [86]. There are a range of solution methods for convex problems, such as bundle methods, the subgradient method, the ellipsoid method and the Lagrange multiplier method [87]. The authors in [84] maximised prosumer profit and minimised consumer purchase costs by optimising energy sold and purchased through joint consideration of two convex optimisation problems. A quadratic utility function as well as a quadratic cost function were considered in [39] and modelled as convex optimisation problem to maximise the total welfare in the P2P market.
Second-order cone programming (SOCP) and quadratically constrained quadratic programming (QCQP) (with convex objective and constraints) are special subclasses of convex programming. SOCPs are non-linear convex problems, where a linear function is minimised over a second-order quadratic cone [88]. SOCPs are solved using the primal-dual interior point method [89]. The authors in [18] considered energy cooperation among multiple microgrids while applying convex relaxations to optimal power flow problem and transforming it into a SOCP to optimise the charging/discharging power of batteries as well as power drawn from the utility grid and other microgrids. QCQPs can be formulated as SOCPs if the objective function and constraints are convex. QCQPs are transformed to convex problems using semidefinite programming relaxation. The authors in [43] solved a QCQP using the branch and bound method to optimise the profit at the sellers considering that the prices are functions of energy sold. Non-convex programming defines a broad subclass of optimisation problems which do not satisfy the convexity conditions. Such problems are hard to solve due to the presence of local minima and widely changing curvatures. Such problems are solved using stochastic gradient descent, mini-batching, and alternating minimisation methods. The authors in [19] minimised the operating cost of community microgrids by solving a non-convex optimisation problem to optimise the energy purchased from utility, battery energy storages and other prosumers. Table 2 illustrates the state-of-the-art mathematical optimisation algorithms and what features make them distinct.

4.3. Auction Methods

Auction defines a mechanism where multiple parties can submit bids and negotiate with each other for trading a certain object [32]. Auctions can be categorised into single-round and multi-round auctions [90]. Single-round auctions involve a single bid for each trading interval, whereas multi-round auctions are associated with multiple bids submitted during the same interval. Single-round auctions can be further categorised into first-price and second-price sealed bid auctions, and descending and ascending bid auctions. In first-price sealed bid auctions, the seller will choose the buyer with highest bid, and the selected buyer will pay the highest bid price. The second-price sealed bid auction is similar except the fact that the selected buyer (with highest bid) now pays the second highest bid price [91]. The terminology ‘sealed’ occurs from the fact that historically, bids were submitted in auction through sealed envelopes. In the descending bid auction, the auctioneer sets the price at a higher level initially and then buyers submit lower bids that match their capacity until the winning bidder is found. The ascending bid auction starts at a lower price defined by the seller, which then gradually increases as buyers submit higher bids [90].
Auctions can be further categorised into single-sided and double-sided auctions. Single-sided auctions involve a single buyer and multiple sellers (reverse auction) or a single seller and multiple buyers (forward auction). On the other hand, double-sided auctions involve multiple sellers and multiple buyers, where both sellers and buyers submit bids [92]. Double auction mechanisms are widely used to model the P2P energy trading markets. Natural ordering is used to determine the buyers and sellers who will be participating in the trading process based on the breakeven index [93]. Then, the auctioneer determines the market clearing price using a number of mechanisms, including average, Vickrey–Clarke–Groves (VCG) mechanism, trade reduction or McAfee’s mechanism. In the average mechanism, the bid prices of buyers and sellers are averaged, while each buyer pays the lowest equilibrium price and each seller receives the highest equilibrium price in VCG mechanism [94]. The trade reduction mechanism allows buyers to pay the buyer bid at breakeven index, whereas sellers receive the seller bid at the breakeven index [95]. McAfee’s mechanism [96] can be considered a hybrid between the average and trade reduction mechanisms. If the buyer bid at breakeven is higher than the seller bid, then the market clearing is based on the average mechanism. Otherwise, market clearing follows the trade reduction mechanism.
Double-sided auctions can be of different types, such as continuous double auction, periodic double auction, k-double auction, and distributed double auction. Continuous double auction refers to the case when the participants can submit as many bids as they like during a certain trading period [97]. Such auctions are very popularly used in P2P energy trading applications. For example, the authors in [98] designed a continuous double auction market while considering utilisation fees as functions of electrical distances and trading losses for taking into account network constraints. Periodic double auction allows the bidding only during a specified market clearing period [99]. A periodic double auction-based bidding strategy was implemented in [100], which forecasts clearing prices for different time periods and perform Monte Carlo tree search to design the bids for multiple time periods. In k-double auction, the market clearing price is determined from the range between the highest seller bid and lowest buyer bid so that no seller/buyer will have to receive/pay less/more than their bids [101]. A multi-k double auction mechanism for P2P energy trading was designed in [102] and compared with benchmark auction mechanisms in terms of the flexibility of the participants. Distributed double auction allows any of the market participants to act as the auctioneer and manage the bidding mechanism in a distributed manner [103]. A decentralised double auction mechanism was designed in [104] that takes into account the flocking behaviour of the birds to decentralise the double auction process for improved convergence of P2P energy trading among neighbourhoods. The different types of auction mechanisms are illustrated in Figure 2.

4.4. Machine Learning Approaches

Very recently, machine learning (ML)-based approaches have been integrated for managing P2P energy trading [7]. One of the most popular choices for ML models in P2P energy trading involves reinforcement learning (RL). RL models are based on the concept of incentives and penalties so that certain actions are associated with incentives, whereas other actions cause penalties. The correlation of these actions is reinforced through the learning model, which aims to converge within a suitable time frame. In [105], the P2P energy trading is modelled as a partially observable Markov decision process (MDP), and reinforcement learning is applied in a decentralised manner for optimising trading strategies. A deep RL model integrating deep neural networks with RL was developed in [106], which considers separate RL models for individual household clusters and assigns incentives for P2P energy trading, whereas the households are penalised based on their contribution to the overall peak demand. The high-dimensionality problem that often arises from RL models is addressed with mean-field RL, which uses mean-field approximation to improve the training performance. The authors in [107] applied a decentralised MDP to model the randomness in user behaviour and solved the double auction-based P2P energy trading problem through mean-field RL. To ensure that private information of individual households is not shared with the central control or aggregator, distributed learning frameworks such as federated learning (FL) are introduced. In this essence, FL is integrated with RL as a federated reinforcement learning to optimise the energy and carbon trading jointly [108].
A prediction-integration strategy optimisation model was investigated in [52], which maps the correlation between prosumer bids and market clearing prices to predict the market behaviour. Apart from optimising the incentive or market models for P2P energy trading, the ML models are also widely used in predicting the behaviours of generation sources as well as the demand patterns. The authors in [109] considered a number of ML models such as support vector, regression trees, and neural networks to predict solar and wind generation while considering the variability in weather data for improved planning of the P2P energy trading. On the other hand, an uncertainty set was constructed for renewable generation sources in [110] by extracting probability distributions using a weighted kernel density estimation approach. Given that P2P energy trading decisions are strongly correlated with human behaviour attributes, it is important to predict the sentiment of the prosumers for improving the effectiveness of the overall system. To address this, the authors in [111] integrated the convolutional neural network to extract information from text for classifying the sentiment data and then implemented long short-term memory (LSTM) model to predict how much energy will be traded. Cyber attacks such as false data injection attacks can bring significant threats to the effectiveness of P2P energy trading models by enabling the attacker to obtain peer energy for free. To mitigate such issues, the ML-based classification model such as k-means clustering was adopted in [112] to separate out the attack data from legitimate data.

5. Challenges in P2P Energy Trading

Though P2P energy trading opens up new markets for prosumers and creates opportunities for new services in the electricity distribution network, there are certain challenges which hinder the uptake of such models in the electricity market. The following section elaborates some of these challenges:
Appropriate P2P energy trading platforms:
There are a number of existing P2P energy trading platforms such as Powerledger and Ethereum, based on blockchain technologies. However, the effectiveness of such platforms largely depends on the scale of the application, and they can have high computational complexity and costs associated with them [113]. Moreover, such platforms can be application specific and may not be easily transferred across different applications. The privacy and security of the participants will become the most crucial features of such platforms and need due consideration [9]. It will also be important to handle data quality issues such as missing data, resulting in incomplete information about the market.
Consideration of network constraints:
The existing research on P2P energy trading often assumes an ideal market and does not factor in the constraints imposed by the electricity utility networks. There will be certain limitations based on required voltage levels and power flow, which in turn will limit the possible energy trading. To satisfy these constraints, the market strategy needs to be designed in such a way that can prevent transactions which violate the constraints. These network constraints can also be integrated with pricing mechanisms to transform the P2P market models more organically [1]. Moreover, it will be important to understand how the P2P trading models interact with existing wholesale energy markets and how they can influence the physical network constraints [27].
Appropriate optimisation algorithms:
Though there has been significant research in various optimisation algorithms focusing on the application of P2P energy trading, the suitability of a certain algorithm for a specific energy trading optimisation problem is often not very clear. State-of-the-art optimisation methods assume that complete information is available for all market participants along with accurate forecasts of energy generation and demand [114]. However, this will not be feasible in a practical setting, and forecasting errors as well as imperfect prosumer behaviour can be reasonably expected. Though machine learning-based methods can be useful by enabling a large number of possible choices and rewards, the computation complexity will be quite high and appear as an expensive alternative. Thus, new methods that can leverage benefits from both approaches will be required and need to be adapted for the specific P2P energy trading problem requirements [7].
Appropriate market models:
Existing research has explored different market models for P2P energy trading, which include centralised as well as full P2P energy trading approaches. Though centralised approaches would be simpler to implement, they cannot ensure reliability and scalability. On the other hand, full P2P approaches will have higher reliability but will be expensive to implement. Distributed P2P energy trading can achieve a trade-off between the two, but such schemes need to be further investigated for different applications, such as the incorporation of ancillary services and demand response. To identify the suitability of different P2P market models, market stability under different price mechanisms should also be investigated [113].
Bid generation mechanisms:
Though there have been vast discussions on how prosumer bids are evaluated in the P2P market models under various auction mechanisms, the bid generation processes at the prosumer end are often neglected. This is a critical parameter that influences the effectiveness of P2P energy trading models and should be investigated in detail. The bids generated from prosumers should reflect the user preferences and factor in the generation and demand forecasts [37]. The generated bids may also depend on how users prioritise the peers involved in the trading model, such as preferred community groups. Moreover, the imperfections in the bidding mechanisms resulting from uncertainty in user behaviour need to be incorporated, given that users can change their mind and offer a smaller amount of energy for the P2P market [1].

6. Future Directions

Despite a number of challenges that can impede the integration of P2P energy trading technologies in power system networks, there are potential research directions that can strengthen the confidence of the utility operators to incorporate such disruptive technologies. The following discussion elaborates on some of the future research directions aligned with P2P energy trading mechanisms:
New optimisation models:
As outlined in the previous section, a suitable optimisation framework is essential for enhancing the effectiveness of P2P energy trading markets [7]. In this essence, optimisation models should explore the trade-off between sellers’ and buyers’ incentives as well as uncertainty in user behaviour to leave sufficient room for adjusting the day-ahead optimal solutions. To improve the scalability, efficient solution mechanisms need to be developed that cater to the specific needs of P2P energy trading applications. The integration of machine learning models and evolutionary algorithms with state-of-the-art mathematical optimisation frameworks can help overcome the aforementioned challenges by improving computational efficiency.
New policy development:
The existing energy market policies are developed for utility-scale electricity networks and need to undergo significant policy reforms before these can be applied to the P2P energy networks [113]. The tariff structure needs to be reformed to adapt with the unique features of P2P energy trading models, which can show high variability due to variations in renewable energy generation and diversity in electricity consumption patterns. There should be appropriate regulations to control prosumers’ behaviour so that they cannot manipulate the state of the P2P energy market by sudden changes in their energy trading decisions. It is also important to engage the electricity utilities in the market structure to incentivise their participation in the promotion and advancement of this new technology.
Enabling scalability and flexibility:
The existing P2P energy trading models have often been investigated in terms of fixed number of users and parameters [1]. Thus, the scalability of such models needs to be enhanced to cater to increasing number of users [42]. This will allow the existing models to transform from proof-of-concept to market-ready commercial prototypes. The existing P2P energy market models are often not flexible enough to adapt to changing market conditions, which can be quite common for a renewable-rich environment. Thus, new models need to be developed which take into account dynamic variations in market conditions. Moreover, the P2P energy trading evaluation prototypes need to be designed in such a way that these evaluations are repeatable and yield consistent outcomes.
Interaction between retail and P2P energy markets:
Given that P2P energy trading can result into the formation of new energy market, its interaction with existing retail market should be an important consideration [9]. P2P energy markets can act as a competitor of the retail market, enabling the development of competitive price models. Retailers may need to update their operational strategies with the evolution of P2P energy markets, which can enhance the value of energy services and products for end users. The fact that the presence of P2P energy markets can defer the requirements of new investments on energy network assets should be taken into account for developing a new tariff structure with a co-existing P2P energy market.
New business models for P2P energy markets:
Existing research on P2P energy markets often consider that such markets can benefit only the individual consumers/prosumers [9]. However, there is an opportunity for retailers and utilities to participate in the P2P markets by adopting the role of an intermediary or aggregator. This can help improve the scale of the P2P markets and motivate the formation of new business models for electricity retailers. There should be an appropriate consideration of user preferences, and users should have the ability to choose their preferred retailer.

7. Conclusions

A detailed review of different aspects associated with P2P energy trading has been explored throughout this paper. In particular, different P2P market architectures such as full, community-based, and hybrid P2P have been discussed along with relevant considerations of different market settlement mechanisms. Different price formation strategies such as auction-based, negotiation-based, system-determined, and equilibrium-based mechanisms have been discussed and compared. Moreover, different bidding strategies with and without prior knowledge of the market have been described. The paper also discussed a number of relevant P2P energy trading platforms and projects across different countries throughout the world, such as Brooklyn microgrid, Piclo, Pebbles, and Sonnen Community. These platforms mostly rely on blockchain technologies and may need further research for more computational efficient models to enable large-scale integration.
There has been a detailed discussion on different game theoretic models, mathematical optimisation algorithms, and machine learning-based solutions for managing P2P energy trading. The comparison between different types of games, such as cooperative and non-cooperative games, has been elaborated. Similarly, a number of optimisation models such as MILP, convex programming, SOCP and non-convex optimisation have been investigated and compared. Different types of auction models such as single-round, multiple round, and single and double auction methods have been discussed. In addition, different types of market clearing mechanisms such as average, trade reduction, VCG, and McAfee’s mechanisms have been critically reviewed. Moreover, the application of ML models such as different types of RL algorithms for setting up the reward mechanisms in P2P energy trading has been explored.
Despite the technological advances, the P2P energy trading model is still in its initial phases due to a number of challenges. This study elaborated a number of such key challenges, which include the lack of appropriate market models, implementation platforms, optimisation and bidding mechanisms, and the incorporation of network constraints. To address these challenges, future research should consider developing new technologies that can enable scalability and flexibility for P2P energy markets with enhanced participation of the retail utility sector. Similarly, there need to be policy reforms to accommodate the new business model associated with P2P energy trading.

Funding

This research received no external funding.

Data Availability Statement

Not applicable.

Conflicts of Interest

The author declares no conflicts of interest.

References

  1. Capper, T.; Gorbatcheva, A.; Mustafa, M.A.; Bahloul, M.; Schwidtal, J.M.; Chitchyan, R.; Andoni, M.; Robu, V.; Montakhabi, M.; Scott, I.J.; et al. Peer-to-peer, community self-consumption, and transactive energy: A systematic literature review of local energy market models. Renew. Sustain. Energy Rev. 2022, 162, 112403. [Google Scholar] [CrossRef]
  2. Zhang, C.; Wu, J.; Zhou, Y.; Cheng, M.; Long, C. Peer-to-Peer energy trading in a Microgrid. Appl. Energy 2018, 220, 1–12. [Google Scholar] [CrossRef]
  3. United Nations Department of Economic and Social Affairs. Sustainable Development. Available online: https://sdgs.un.org/goals (accessed on 2 February 2024).
  4. Shah, W.U.H.; Hao, G.; Yan, H.; Yasmeen, R.; Padda, I.U.H.; Ullah, A. The impact of trade, financial development and government integrity on energy efficiency: An analysis from G7-Countries. Energy 2022, 255, 124507. [Google Scholar] [CrossRef]
  5. Hvelplund, F. Renewable energy and the need for local energy markets. Energy 2006, 31, 2293–2302. [Google Scholar] [CrossRef]
  6. Faria, A.S.; Soares, T.; Orlandini, T.; Oliveira, C.; Sousa, T.; Pinson, P.; Matos, M. P2P market coordination methodologies with distribution grid management. Sustain. Energy Grids Netw. 2023, 34, 101075. [Google Scholar] [CrossRef]
  7. Xia, Y.; Xu, Q.; Li, S.; Tang, R.; Du, P. Reviewing the peer-to-peer transactive energy market: Trading environment, optimization methodology, and relevant resources. J. Clean. Prod. 2023, 383, 135441. [Google Scholar] [CrossRef]
  8. Mengelkamp, E.; Gärttner, J.; Rock, K.; Kessler, S.; Orsini, L.; Weinhardt, C. Designing microgrid energy markets: A case study: The Brooklyn Microgrid. Appl. Energy 2018, 210, 870–880. [Google Scholar] [CrossRef]
  9. Sousa, T.; Soares, T.; Pinson, P.; Moret, F.; Baroche, T.; Sorin, E. Peer-to-peer and community-based markets: A comprehensive review. Renew. Sustain. Energy Rev. 2019, 104, 367–378. [Google Scholar] [CrossRef]
  10. Long, C.; Wu, J.; Zhang, C.; Thomas, L.; Cheng, M.; Jenkins, N. Peer-to-peer energy trading in a community microgrid. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; pp. 1–5. [Google Scholar]
  11. Zhou, Y.; Wu, J.; Long, C. Evaluation of peer-to-peer energy sharing mechanisms based on a multiagent simulation framework. Appl. Energy 2018, 222, 993–1022. [Google Scholar] [CrossRef]
  12. Liu, N.; Yu, X.; Wang, C.; Li, C.; Ma, L.; Lei, J. Energy-sharing model with price-based demand response for microgrids of peer-to-peer prosumers. IEEE Trans. Power Syst. 2017, 32, 3569–3583. [Google Scholar] [CrossRef]
  13. Long, C.; Wu, J.; Zhou, Y.; Jenkins, N. Peer-to-peer energy sharing through a two-stage aggregated battery control in a community Microgrid. Appl. Energy 2018, 226, 261–276. [Google Scholar] [CrossRef]
  14. Zhou, W.; Dang, W.; Peng, F.; Mahesuti, R.; Zhang, L.; Sun, K. A decentralized peer-to-peer energy trading strategy considering flexible resource involvement and renewable energy uncertainty. Int. J. Electr. Power Energy Syst. 2023, 152, 109275. [Google Scholar] [CrossRef]
  15. Saad, W.; Han, Z.; Poor, H.V.; Basar, T. Game-theoretic methods for the smart grid: An overview of microgrid systems, demand-side management, and smart grid communications. IEEE Signal Process. Mag. 2012, 29, 86–105. [Google Scholar] [CrossRef]
  16. Dimitriadis, C.; Tsimopoulos, E.; Georgiadis, M. A Review on the Complementarity Modelling in Competitive Electricity Markets. Energies 2021, 14, 7133. [Google Scholar] [CrossRef]
  17. Park, S.W.; Cho, K.S.; Son, S.Y. Voltage Management Method of Distribution System in P2P Energy Transaction Environment. IFAC-PapersOnLine 2019, 52, 324–329. [Google Scholar] [CrossRef]
  18. Liu, T.; Tan, X.; Sun, B.; Wu, Y.; Tsang, D.H. Energy management of cooperative microgrids: A distributed optimization approach. Int. J. Electr. Power Energy Syst. 2018, 96, 335–346. [Google Scholar] [CrossRef]
  19. Meena, N.K.; Yang, J.; Zacharis, E. Optimisation framework for the design and operation of open-market urban and remote community microgrids. Appl. Energy 2019, 252, 113399. [Google Scholar] [CrossRef]
  20. Chen, T.; Su, W. Local Energy Trading Behavior Modeling With Deep Reinforcement Learning. IEEE Access 2018, 6, 62806–62814. [Google Scholar] [CrossRef]
  21. Kim, J.G.; Lee, B. Automatic P2P Energy Trading Model Based on Reinforcement Learning Using Long Short-Term Delayed Reward. Energies 2020, 13, 5359. [Google Scholar] [CrossRef]
  22. Sahebi, H.; Khodoomi, M.; Seif, M.; Pishvaee, M.; Hanne, T. The benefits of peer-to-peer renewable energy trading and battery storage backup for local grid. J. Energy Storage 2023, 63, 106970. [Google Scholar] [CrossRef]
  23. Zheng, B.; Wei, W.; Chen, Y.; Wu, Q.; Mei, S. A peer-to-peer energy trading market embedded with residential shared energy storage units. Appl. Energy 2022, 308, 118400. [Google Scholar] [CrossRef]
  24. Dimitriadis, C.N.; Tsimopoulos, E.G.; Georgiadis, M.C. Strategic bidding of an energy storage agent in a joint energy and reserve market under stochastic generation. Energy 2022, 242, 123026. [Google Scholar] [CrossRef]
  25. Schwidtal, J.; Piccini, P.; Troncia, M.; Chitchyan, R.; Montakhabi, M.; Francis, C.; Gorbatcheva, A.; Capper, T.; Mustafa, M.; Andoni, M.; et al. Emerging business models in local energy markets: A systematic review of peer-to-peer, community self-consumption, and transactive energy models. Renew. Sustain. Energy Rev. 2023, 179, 113273. [Google Scholar] [CrossRef]
  26. Faia, R.; Lezama, F.; Soares, J.; Pinto, T.; Vale, Z. Local electricity markets: A review on benefits, barriers, current trends and future perspectives. Renew. Sustain. Energy Rev. 2024, 190, 114006. [Google Scholar] [CrossRef]
  27. Tsaousoglou, G.; Giraldo, J.S.; Paterakis, N.G. Market Mechanisms for Local Electricity Markets: A review of models, solution concepts and algorithmic techniques. Renew. Sustain. Energy Rev. 2022, 156, 111890. [Google Scholar] [CrossRef]
  28. Kim, H.J.; Chung, Y.S.; Kim, S.J.; Kim, H.T.; Jin, Y.G.; Yoon, Y.T. Pricing mechanisms for peer-to-peer energy trading: Towards an integrated understanding of energy and network service pricing mechanisms. Renew. Sustain. Energy Rev. 2023, 183, 113435. [Google Scholar] [CrossRef]
  29. Guerrero, J.; Gebbran, D.; Mhanna, S.; Chapman, A.C.; Verbič, G. Towards a transactive energy system for integration of distributed energy resources: Home energy management, distributed optimal power flow, and peer-to-peer energy trading. Renew. Sustain. Energy Rev. 2020, 132, 110000. [Google Scholar] [CrossRef]
  30. Azim, M.I.; Tushar, W.; Saha, T.K.; Yuen, C.; Smith, D. Peer-to-peer kilowatt and negawatt trading: A review of challenges and recent advances in distribution networks. Renew. Sustain. Energy Rev. 2022, 169, 112908. [Google Scholar] [CrossRef]
  31. Suthar, S.; Cherukuri, S.H.C.; Pindoriya, N.M. Peer-to-peer energy trading in smart grid: Frameworks, implementation methodologies, and demonstration projects. Electr. Power Syst. Res. 2023, 214, 108907. [Google Scholar] [CrossRef]
  32. Muhsen, H.; Allahham, A.; Al-Halhouli, A.; Al-Mahmodi, M.; Alkhraibat, A.; Hamdan, M. Business Model of Peer-to-Peer Energy Trading: A Review of Literature. Sustainability 2022, 14, 1616. [Google Scholar] [CrossRef]
  33. Parliament, E. Council of the European Union Directive (EU) 2018/2001 of the European Parliament and of the Council of 11 December 2018 on the promotion of the use of energy from renewable sources. Off. J. Eur. Union 2018, 328, 1–128. [Google Scholar]
  34. NIST. Transactive Energy: An Overview. 2017. Available online: https://www.nist.gov/el/smart-grid-menu/hot-topics/transactive-energy-overview (accessed on 27 November 2023).
  35. Chen, S.; Liu, C. From demand response to transactive energy: State of the art. J. Mod. Power Syst. Clean Energy 2017, 5, 10–19. [Google Scholar] [CrossRef]
  36. Sorin, E.; Bobo, L.; Pinson, P. Consensus-Based Approach to Peer-to-Peer Electricity Markets with Product Differentiation. IEEE Trans. Power Syst. 2019, 34, 994–1004. [Google Scholar] [CrossRef]
  37. Moret, F.; Pinson, P. Energy Collectives: A Community and Fairness Based Approach to Future Electricity Markets. IEEE Trans. Power Syst. 2019, 34, 3994–4004. [Google Scholar] [CrossRef]
  38. Tushar, W.; Chai, B.; Yuen, C.; Huang, S.; Smith, D.B.; Poor, H.V.; Yang, Z. Energy Storage Sharing in Smart Grid: A Modified Auction-Based Approach. IEEE Trans. Smart Grid 2016, 7, 1462–1475. [Google Scholar] [CrossRef]
  39. Khorasany, M.; Mishra, Y.; Ledwich, G. A Decentralized Bilateral Energy Trading System for Peer-to-Peer Electricity Markets. IEEE Trans. Ind. Electron. 2020, 67, 4646–4657. [Google Scholar] [CrossRef]
  40. Long, C.; Wu, J.; Zhang, C.; Cheng, M.; Al-Wakeel, A. Feasibility of Peer-to-Peer Energy Trading in Low Voltage Electrical Distribution Networks. Energy Procedia 2017, 105, 2227–2232. [Google Scholar] [CrossRef]
  41. Zepter, J.M.; Lüth, A.; Crespo del Granado, P.; Egging, R. Prosumer integration in wholesale electricity markets: Synergies of peer-to-peer trade and residential storage. Energy Build. 2019, 184, 163–176. [Google Scholar] [CrossRef]
  42. Chakraborty, S.; Baarslag, T.; Kaisers, M. Automated peer-to-peer negotiation for energy contract settlements in residential cooperatives. Appl. Energy 2020, 259, 114173. [Google Scholar] [CrossRef]
  43. Islam, S.N. A New Pricing Scheme for Intra-Microgrid and Inter-Microgrid Local Energy Trading. Energies 2019, 8, 989. [Google Scholar] [CrossRef]
  44. Lüth, A.; Zepter, J.M.; Crespo del Granado, P.; Egging, R. Local electricity market designs for peer-to-peer trading: The role of battery flexibility. Appl. Energy 2018, 229, 1233–1243. [Google Scholar] [CrossRef]
  45. Wang, S.; Taha, A.F.; Wang, J.; Kvaternik, K.; Hahn, A. Energy Crowdsourcing and Peer-to-Peer Energy Trading in Blockchain-Enabled Smart Grids. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 1612–1623. [Google Scholar] [CrossRef]
  46. Cali, U.; Çakir, O. Energy Policy Instruments for Distributed Ledger Technology Empowered Peer-to-Peer Local Energy Markets. IEEE Access 2019, 7, 82888–82900. [Google Scholar] [CrossRef]
  47. Li, Z.; Shahidehpour, M.; Alabdulwahab, A.; Al-Turki, Y. Valuation of distributed energy resources in active distribution networks. Electr. J. 2019, 32, 27–36. [Google Scholar] [CrossRef]
  48. Behboodi, S.; Chassin, D.P.; Djilali, N.; Crawford, C. Transactive control of fast-acting demand response based on thermostatic loads in real-time retail electricity markets. Appl. Energy 2018, 210, 1310–1320. [Google Scholar] [CrossRef]
  49. Pinto, T.; Faia, R.; Ghazvini, M.A.F.; Soares, J.; Corchado, J.M.; Vale, Z. Decision Support for Small Players Negotiations Under a Transactive Energy Framework. IEEE Trans. Power Syst. 2019, 34, 4015–4023. [Google Scholar] [CrossRef]
  50. Pires Klein, L.; Krivoglazova, A.; Matos, L.; Landeck, J.; de Azevedo, M. A novel peer-to-peer energy sharing business model for the portuguese energy market. Energies 2019, 13, 125. [Google Scholar] [CrossRef]
  51. Tushar, W.; Saha, T.K.; Yuen, C.; Morstyn, T.; McCulloch, M.D.; Poor, H.V.; Wood, K.L. A motivational game-theoretic approach for peer-to-peer energy trading in the smart grid. Appl. Energy 2019, 243, 10–20. [Google Scholar] [CrossRef]
  52. Chen, K.; Lin, J.; Song, Y. Trading strategy optimization for a prosumer in continuous double auction-based peer-to-peer market: A prediction-integration model. Appl. Energy 2019, 242, 1121–1133. [Google Scholar] [CrossRef]
  53. Guerrero, J.; Chapman, A.C.; Verbič, G. Decentralized P2P Energy Trading Under Network Constraints in a Low-Voltage Network. IEEE Trans. Smart Grid 2019, 10, 5163–5173. [Google Scholar] [CrossRef]
  54. Wang, J.; Wang, Q.; Zhou, N.; Chi, Y. A novel electricity transaction mode of microgrids based on blockchain and continuous double auction. Energies 2017, 10, 1971. [Google Scholar] [CrossRef]
  55. Zang, H.; Kim, J. Reinforcement learning based peer-to-peer energy trade management using community energy storage in local energy market. Energies 2021, 14, 4131. [Google Scholar] [CrossRef]
  56. Lin, J.; Pipattanasomporn, M.; Rahman, S. Comparative analysis of auction mechanisms and bidding strategies for P2P solar transactive energy markets. Appl. Energy 2019, 255, 113687. [Google Scholar] [CrossRef]
  57. Piclo Flex. Piclo. Available online: https://picloflex.com/ (accessed on 27 November 2023).
  58. Zhang, C.; Wu, J.; Long, C.; Cheng, M. Review of Existing Peer-to-Peer Energy Trading Projects. Energy Procedia 2017, 105, 2563–2568. [Google Scholar] [CrossRef]
  59. Brandherm, B.; Baus, J.; Frey, J. Peer energy cloud–civil marketplace for trading renewable energies. In Proceedings of the 2012 Eighth International Conference on Intelligent Environments, Guanajuato, Mexico, 26–29 June 2012; pp. 375–378. [Google Scholar]
  60. Pebbles. Peer to Peer Energy Trading Based on Blockchain Infrastructure. Available online: https://pebbles-projekt.de/en/ (accessed on 27 November 2023).
  61. Lichtblick. Now for the Solar System with Storage for More Independence. Available online: https://www.lichtblick.de/zuhause/solar/ (accessed on 27 November 2023).
  62. Jemma Green, P.N.; Forse, N. RENeW Nexus: Enabling Resilient, Low Cost & Localised Electricity Markets through Blockchain P2P & VPP Trading. 2020. Available online: https://assets.website-files.com/5fc9b61246966c23f17d2601/607e724f8dfb1a2d5928bbc0_renew-nexus-project-report.pdf (accessed on 27 November 2023).
  63. Enapter. Solar-Battery-Hydrogen Microgrid. Available online: https://www.enapter.com/application/solar-battery-hydrogen-microgrid#21491 (accessed on 27 November 2023).
  64. Danmarks Tekniske Universitet (DTU). The Energy Collective. 2016. Available online: https://energiforskning.dk/en/node/15513 (accessed on 27 November 2023).
  65. Verma, P.; O’Regan, B.; Hayes, B.; Thakur, S.; Breslin, J.G. EnerPort: Irish Blockchain project for peer-to-peer energy trading. Energy Inform. 2018, 1, 14. [Google Scholar] [CrossRef]
  66. Partz, H. Japan’s Kanto Region to Track Surplus Solar Energy with Power Ledger. 2019. Available online: https://cointelegraph.com/news/japans-kanto-region-to-track-surplus-solar-energy-with-power-ledger (accessed on 27 November 2023).
  67. NRGcoin. What is NRGcoin? 2023. Available online: https://nrgcoin.org/about/ (accessed on 27 November 2023).
  68. SEDA. Malaysia’s 1st Pilot Run of Peer-to-Peer (P2P) Energy Trading. 2020. Available online: https://www.seda.gov.my/malaysias-1st-pilot-run-of-peer-to-peer-p2p-energy-trading/ (accessed on 27 November 2023).
  69. Gunarathna, C.L.; Yang, R.J.; Jayasuriya, S.; Wang, K. Reviewing global peer-to-peer distributed renewable energy trading projects. Energy Res. Soc. Sci. 2022, 89, 102655. [Google Scholar] [CrossRef]
  70. Brooklyn Microgrid. Available online: https://www.brooklyn.energy/about (accessed on 27 November 2023).
  71. Powerledger. Uttar Pradesh Power Corporation Limited Launches First P2P Solar Power Trading in South Asia. 2020. Available online: https://www.powerledger.io/media/uttar-pradesh-power-corporation-limited-launches-first-p2p-solar-power-trading-in-south-asia (accessed on 27 November 2023).
  72. Başar, T.; Olsder, G.J. Dynamic Noncooperative Game Theory; SIAM: Philadelphia, PA, USA, 1998. [Google Scholar]
  73. Soto, E.A.; Bosman, L.B.; Wollega, E.; Leon-Salas, W.D. Peer-to-peer energy trading: A review of the literature. Appl. Energy 2021, 283, 116268. [Google Scholar] [CrossRef]
  74. Cui, S.; Wang, Y.W.; Liu, N. Distributed game-based pricing strategy for energy sharing in microgrid with PV prosumers. IET Renew. Power Gener. 2018, 12, 380–388. [Google Scholar] [CrossRef]
  75. Ryu, Y.; Lee, H.W. A real-time framework for matching prosumers with minimum risk in the cluster of microgrids. IEEE Trans. Smart Grid 2020, 11, 2832–2844. [Google Scholar] [CrossRef]
  76. Le Cadre, H.; Jacquot, P.; Wan, C.; Alasseur, C. Peer-to-peer electricity market analysis: From variational to generalized Nash equilibrium. Eur. J. Oper. Res. 2020, 282, 753–771. [Google Scholar] [CrossRef]
  77. Tushar, W.; Yuen, C.; Mohsenian-Rad, H.; Saha, T.; Poor, H.V.; Wood, K.L. Transforming energy networks via peer-to-peer energy trading: The potential of game-theoretic approaches. IEEE Signal Process. Mag. 2018, 35, 90–111. [Google Scholar] [CrossRef]
  78. Han, L.; Morstyn, T.; McCulloch, M. Incentivizing prosumer coalitions with energy management using cooperative game theory. IEEE Trans. Power Syst. 2018, 34, 303–313. [Google Scholar] [CrossRef]
  79. Rosenschein, J.S. Understanding Mechanism Design—Part 2 of 3: The Vickrey-Clarke-Groves Mechanism. IEEE Intell. Syst. 2021, 36, 80–81. [Google Scholar] [CrossRef]
  80. Han, L.; Morstyn, T.; McCulloch, M. Estimation of the shapley value of a peer-to-peer energy sharing game using multi-step coalitional stratified sampling. Int. J. Control. Autom. Syst. 2021, 19, 1863–1872. [Google Scholar] [CrossRef]
  81. Han, L.; Morstyn, T.; McCulloch, M.D. Scaling up cooperative game theory-based energy management using prosumer clustering. IEEE Trans. Smart Grid 2020, 12, 289–300. [Google Scholar] [CrossRef]
  82. Wang, L.; Zhang, B.; Li, Q.; Song, W.; Li, G. Robust distributed optimization for energy dispatch of multi-stakeholder multiple microgrids under uncertainty. Appl. Energy 2019, 255, 113845. [Google Scholar] [CrossRef]
  83. Gregoratti, D.; Matamoros, J. Distributed Energy Trading: The Multiple-Microgrid Case. IEEE Trans. Ind. Electron. 2015, 62, 2551–2559. [Google Scholar] [CrossRef]
  84. Zhang, X.; Zhu, S.; He, J.; Yang, B.; Guan, X. Credit rating based real-time energy trading in microgrids. Appl. Energy 2019, 236, 985–996. [Google Scholar] [CrossRef]
  85. Morstyn, T.; McCulloch, M.D. Multiclass Energy Management for Peer-to-Peer Energy Trading Driven by Prosumer Preferences. IEEE Trans. Power Syst. 2019, 34, 4005–4014. [Google Scholar] [CrossRef]
  86. Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
  87. Hiriart-Urruty, J.B.; Lemaréchal, C. Fundamentals of Convex Analysis; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
  88. Lobo, M.S.; Vandenberghe, L.; Boyd, S.; Lebret, H. Applications of second-order cone programming. Linear Algebra Appl. 1998, 284, 193–228. [Google Scholar] [CrossRef]
  89. Nesterov, Y.; Nemirovskii, A. Interior-Point Polynomial Algorithms in Convex Programming; Studies in Applied and Numerical Mathematics; SIAM: Philadelphia, PA, USA, 1994. [Google Scholar]
  90. Chattopadhyay, S.; Chatterjee, R. Understanding Auctions; Routledge: London, UK, 2019. [Google Scholar]
  91. Dixit, A.K.; Nalebuff, B.J. The Art of Strategy: A Game Theorist’s Guide to Success in Business and Life; Norton: New York, NY, USA, 2008. [Google Scholar]
  92. Friedman, D. The Double Auction Market: Institutions, Theories, and Evidence; Routledge: London, UK, 1993. [Google Scholar]
  93. Zheng, X.; Shah, S.B.H.; Usman, S.; Mahfoudh, S.; KS, F.S.; Shukla, P.K. Resource allocation and network pricing based on double auction in mobile edge computing. J. Cloud Comput. 2023, 12, 56. [Google Scholar] [CrossRef]
  94. Roughgarden, T.; Nisan, N. Algorithmic Game Theory; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
  95. Zhang, J.; Wen, D.; Zeng, S. A Discounted Trade Reduction Mechanism for Dynamic Ridesharing Pricing. IEEE Trans. Intell. Transp. Syst. 2016, 17, 1586–1595. [Google Scholar] [CrossRef]
  96. McAfee, R. A dominant strategy double auction. J. Econ. Theory 1992, 56, 434–450. [Google Scholar] [CrossRef]
  97. Wellman, M.P. Continuous Double Auctions; Synthesis Lectures on Artificial Intelligence and Machine Learning; Springer: Cham, Switzerland; Berlin, Germany, 2011. [Google Scholar]
  98. Liaquat, S.; Hussain, T.; Celik, B.; Fourney, R.; Hansen, T.M. Day-ahead continuous double auction-based peer-to-peer energy trading platform incorporating trading losses and network utilisation fee. IET Smart Grid 2023, 6, 312–329. [Google Scholar] [CrossRef]
  99. Bokkisam, H.R.; Singh, S.; Acharya, R.M.; Selvan, M. Blockchain-based peer-to-peer transactive energy system for community microgrid with demand response management. CSEE J. Power Energy Syst. 2021, 8, 198–211. [Google Scholar]
  100. Chowdhury, M.M.P.; Kiekintveld, C.; Tran, S.; Yeoh, W. Bidding in Periodic Double Auctions Using Heuristics and Dynamic Monte Carlo Tree Search. In Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence, Stockholm, Sweden, 13–19 July 2018; pp. 166–172. [Google Scholar]
  101. Satterthwaite, M.A.; Williams, S.R. The Bayesian theory of the k-double auction. In The Double Auction Market; Routledge: London, UK, 2018; pp. 99–124. [Google Scholar]
  102. Angaphiwatchawal, P.; Sompoh, C.; Chaitusaney, S. A Multi-k Double Auction Pricing Mechanism for Peer-to-Peer Energy Trading Market of Prosumers. In Proceedings of the 2021 18th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Chiang Mai, Thailand, 19–22 May 2021; pp. 473–476. [Google Scholar]
  103. Thakur, S.; Hayes, B.P.; Breslin, J.G. Distributed double auction for peer to peer energy trade using blockchains. In Proceedings of the 2018 5th International Symposium on Environment-Friendly Energies and Applications (EFEA), Rome, Italy, 24–26 September 2018; pp. 1–8. [Google Scholar]
  104. Bandara, K.Y.; Thakur, S.; Breslin, J. Flocking-based decentralised double auction for P2P energy trading within neighbourhoods. Int. J. Electr. Power Energy Syst. 2021, 129, 106766. [Google Scholar] [CrossRef]
  105. Wang, J.; Li, L.; Zhang, J. Deep reinforcement learning for energy trading and load scheduling in residential peer-to-peer energy trading market. Int. J. Electr. Power Energy Syst. 2023, 147, 108885. [Google Scholar] [CrossRef]
  106. Qiu, D.; Ye, Y.; Papadaskalopoulos, D.; Strbac, G. Scalable coordinated management of peer-to-peer energy trading: A multi-cluster deep reinforcement learning approach. Appl. Energy 2021, 292, 116940. [Google Scholar] [CrossRef]
  107. Qiu, D.; Wang, J.; Dong, Z.; Wang, Y.; Strbac, G. Mean-Field Multi-Agent Reinforcement Learning for Peer-to-Peer Multi-Energy Trading. IEEE Trans. Power Syst. 2023, 38, 4853–4866. [Google Scholar] [CrossRef]
  108. Qiu, D.; Xue, J.; Zhang, T.; Wang, J.; Sun, M. Federated reinforcement learning for smart building joint peer-to-peer energy and carbon allowance trading. Appl. Energy 2023, 333, 120526. [Google Scholar] [CrossRef]
  109. Liu, J.; Zhou, Y.; Yang, H.; Wu, H. Uncertainty energy planning of net-zero energy communities with peer-to-peer energy trading and green vehicle storage considering climate changes by 2050 with machine learning methods. Appl. Energy 2022, 321, 119394. [Google Scholar] [CrossRef]
  110. Mohseni, S.; Pishvaee, M.S.; Dashti, R. Privacy-preserving energy trading management in networked microgrids via data-driven robust optimization assisted by machine learning. Sustain. Energy Grids Netw. 2023, 34, 101011. [Google Scholar] [CrossRef]
  111. Fu, X.; Zhang, S.; Chen, J.; Ouyang, T.; Wu, J. A Sentiment-Aware Trading Volume Prediction Model for P2P Market Using LSTM. IEEE Access 2019, 7, 81934–81944. [Google Scholar] [CrossRef]
  112. Mohammadi, S.; Eliassen, F.; Zhang, Y.; Jacobsen, H.A. Detecting False Data Injection Attacks in Peer to Peer Energy Trading Using Machine Learning. IEEE Trans. Dependable Secur. Comput. 2022, 19, 3417–3431. [Google Scholar] [CrossRef]
  113. Bukar, A.L.; Hamza, M.F.; Ayub, S.; Abobaker, A.K.; Modu, B.; Mohseni, S.; Brent, A.C.; Ogbonnaya, C.; Mustapha, K.; Idakwo, H.O. Peer-to-peer electricity trading: A systematic review on current developments and perspectives. Renew. Energy Focus 2023, 44, 317–333. [Google Scholar] [CrossRef]
  114. Kochupurackal, A.; Pancholi, K.P.; Islam, S.N.; Anwar, A.; Oo, A.M.T. Rolling horizon optimisation based peer-to-peer energy trading under real-time variations in demand and generation. Energy Syst. 2023, 14, 541–565. [Google Scholar] [CrossRef]
Energies 17 01702 g001
Figure 1. Different types of market architectures.
Figure 1. Different types of market architectures.
Energies 17 01702 g001
Energies 17 01702 g002
Figure 2. Different types of auction mechanisms.
Figure 2. Different types of auction mechanisms.
Energies 17 01702 g002
Table 1. Comparison table for existing review papers on P2P energy trading.
Table 1. Comparison table for existing review papers on P2P energy trading.
PaperMarket StructureGame TheoryOptimisation AlgorithmsMachine LearningBidding StrategiesAuction Models
[9]✓×××××
[25]✓×✓×✓×
[26]✓✓✓××✓
[27]×✓✓✓×✓
[28]✓✓✓××✓
[29]✓✓✓×✓✓
[30]✓✓✓×✓✓
[7]✓✓✓✓××
[31]✓✓✓×✓✓
[32]✓✓××✓✓
This paper✓✓✓✓✓✓
Table 2. Comparison table for state-of-the-art optimisation algorithms.
Table 2. Comparison table for state-of-the-art optimisation algorithms.
Optimisation AlgorithmDistinct Features
Linear programmingLinear objective function with linear constraints
Mixed integer linear programmingVariables can be a combination of integer and floating point numbers
Convex programmingObjective function and constraints should be convex
Second-order cone programmingLinear objective minimised over a second-order quadratic cone
Quadratically constrained quadratic programmingQuadratic objective function with quadratic constraints
Non-convex programmingNon-convex objective and/or non-convex constraints
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Islam, S.N. A Review of Peer-to-Peer Energy Trading Markets: Enabling Models and Technologies. Energies 2024, 17, 1702. https://doi.org/10.3390/en17071702

AMA Style

Islam SN. A Review of Peer-to-Peer Energy Trading Markets: Enabling Models and Technologies. Energies. 2024; 17(7):1702. https://doi.org/10.3390/en17071702

Chicago/Turabian Style

Islam, Shama Naz. 2024. "A Review of Peer-to-Peer Energy Trading Markets: Enabling Models and Technologies" Energies 17, no. 7: 1702. https://doi.org/10.3390/en17071702

APA Style

Islam, S. N. (2024). A Review of Peer-to-Peer Energy Trading Markets: Enabling Models and Technologies. Energies, 17(7), 1702. https://doi.org/10.3390/en17071702

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop