Small-Signal Stability of Hybrid Inverters with Grid-Following and Grid-Forming Controls
Abstract
1. Introduction
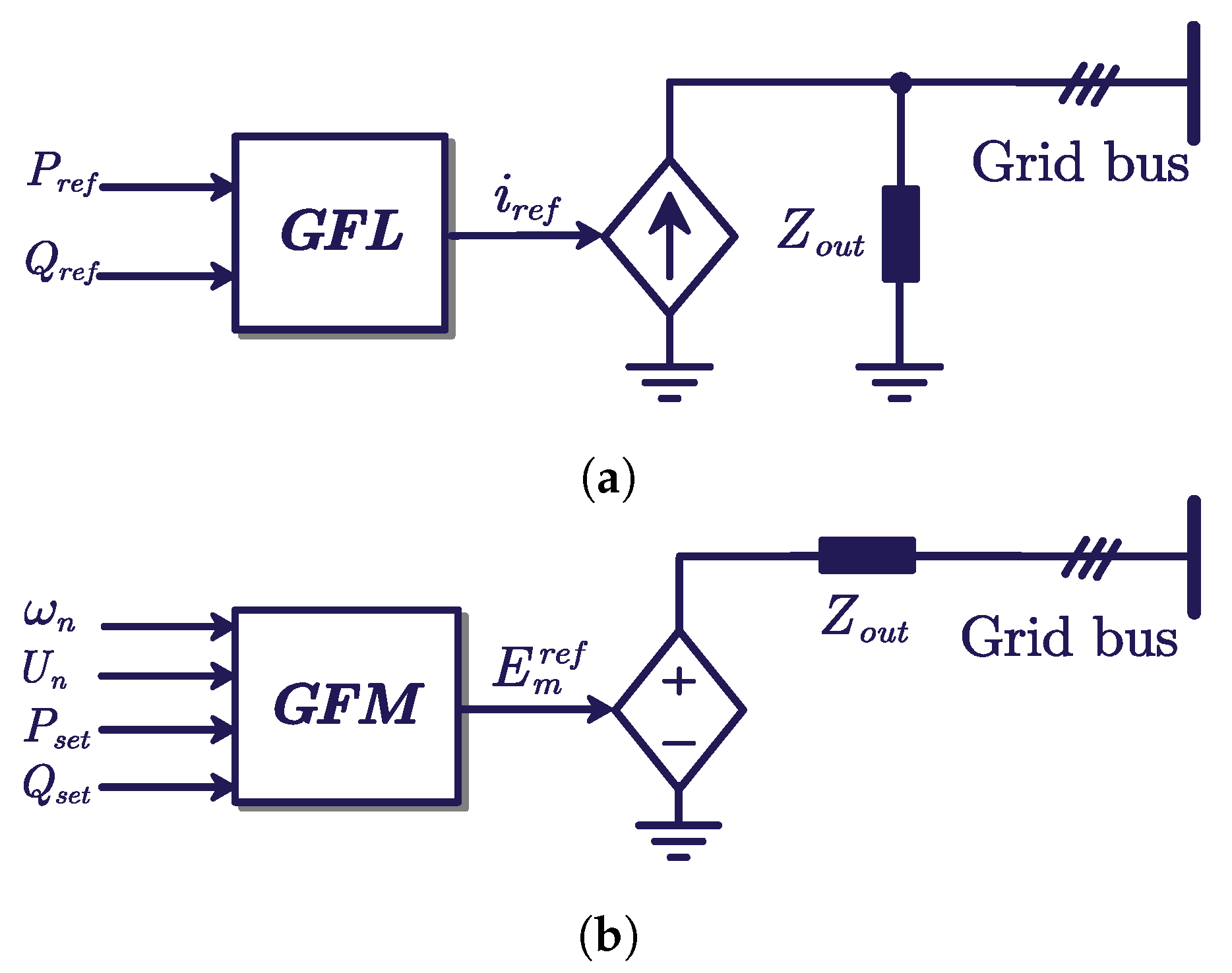
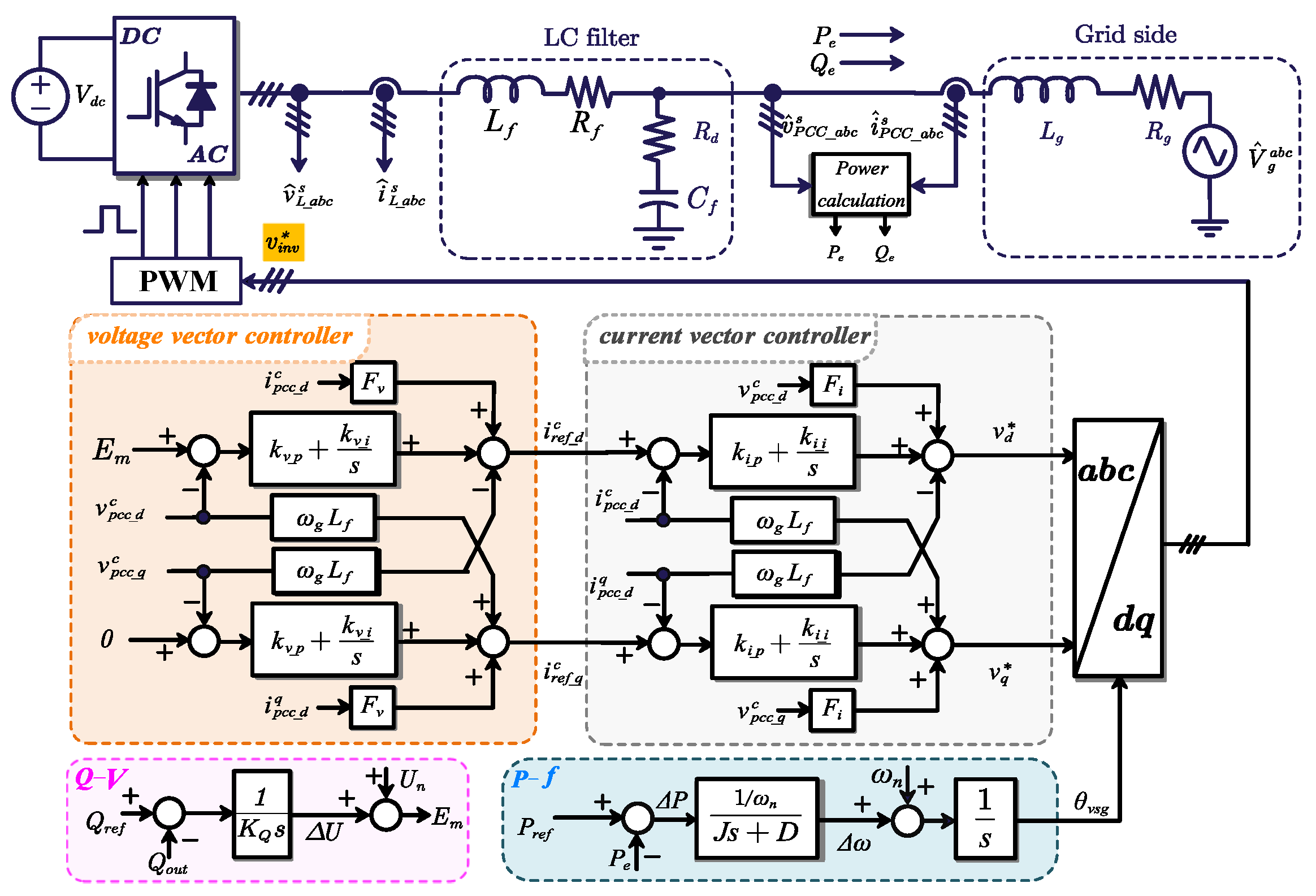
2. Control and Modeling of the Individual Inverter
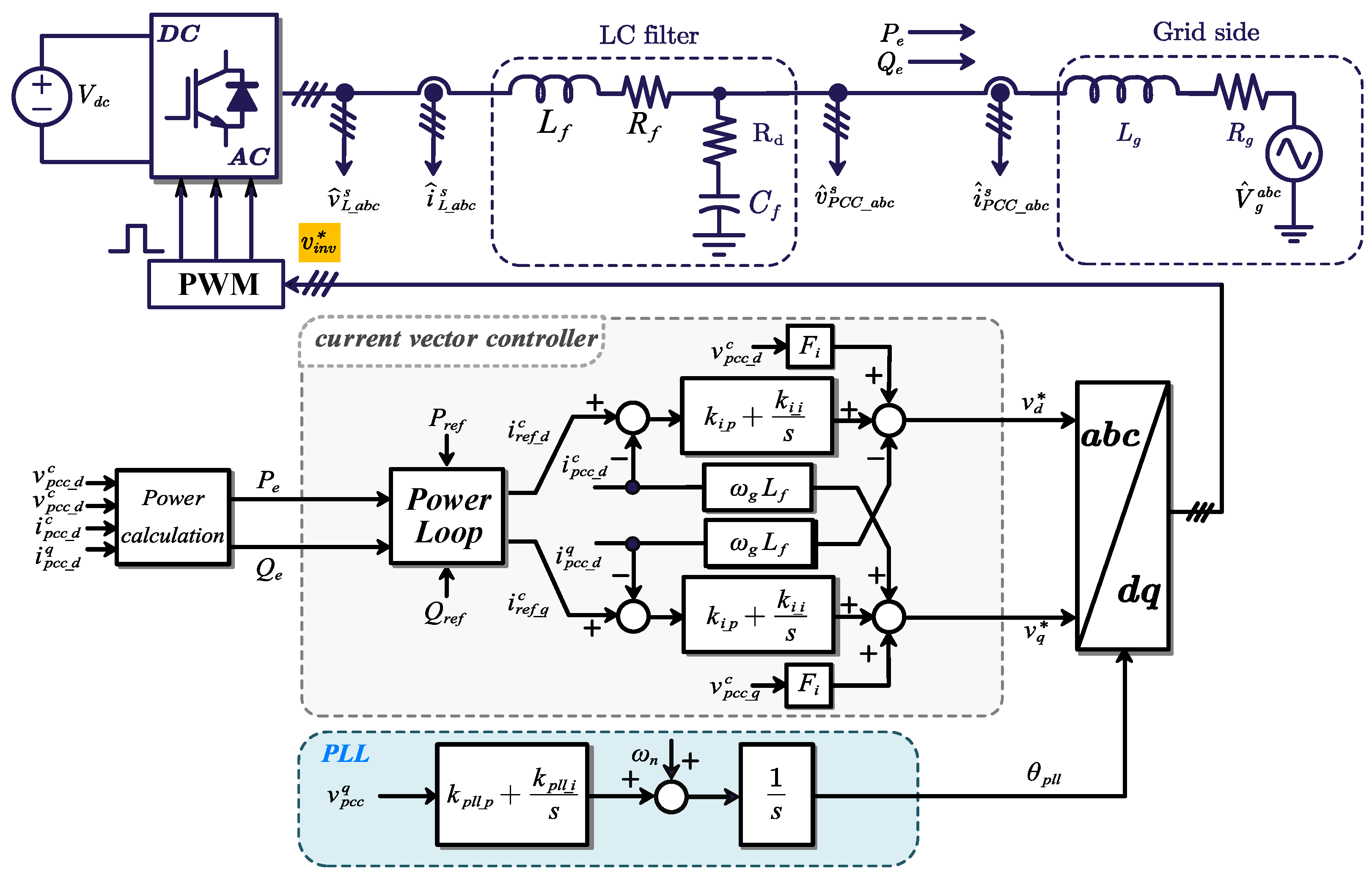
2.1. Grid-Following Control
2.1.1. Phase-Locked Loop
2.1.2. Power Control Loop
2.1.3. Current Controller Loop
2.1.4. Physical Circuit Model
2.1.5. Effect of Time Delay
2.1.6. State-Space Model of the GFL Inverter
2.2. Grid-Forming Control
2.2.1. Power Loop Control
2.2.2. Voltage Control Loop
2.2.3. State-Space Model of the GFM Inverter
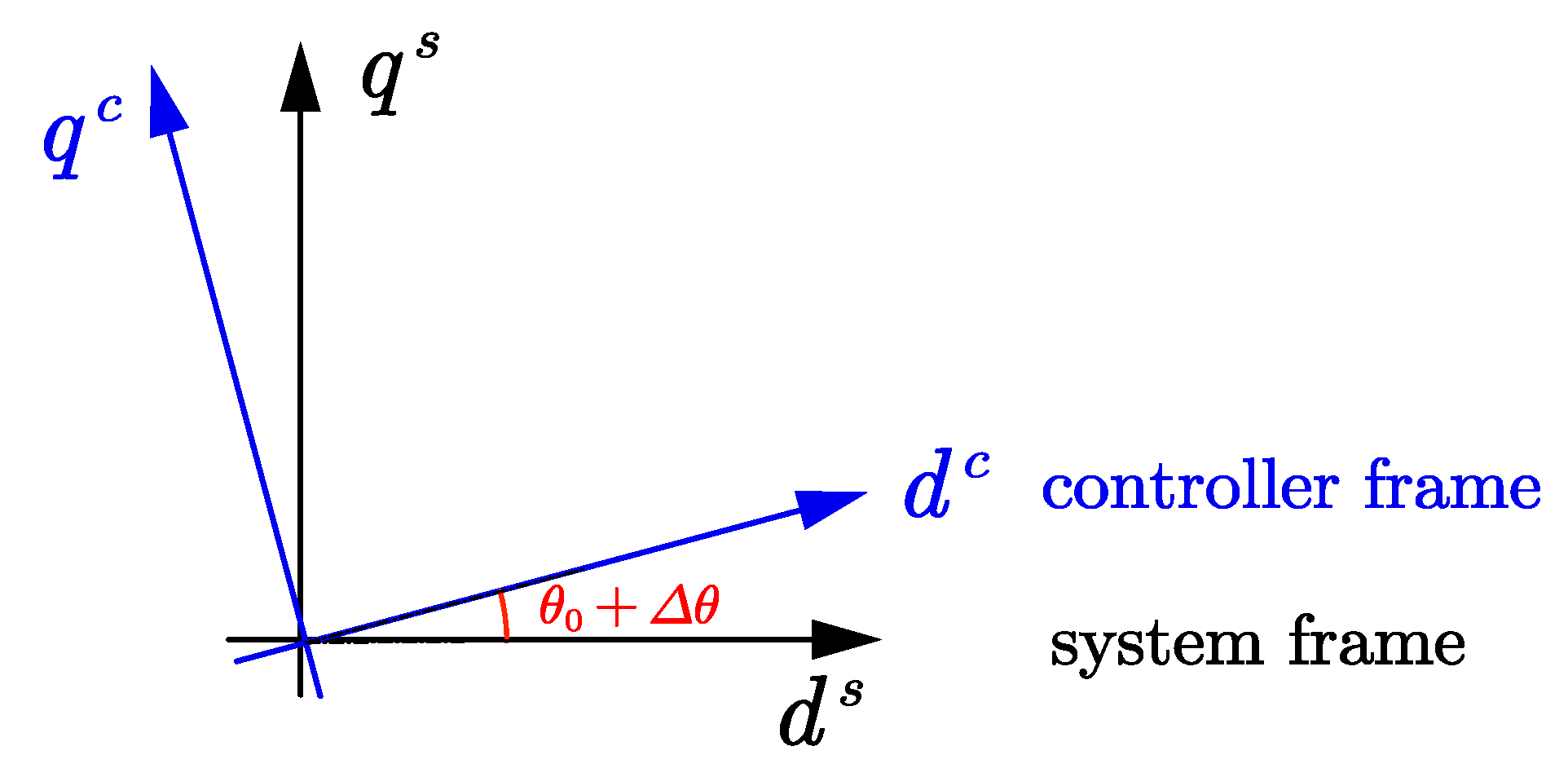
2.3. Small-Signal Modeling of the Power Plant
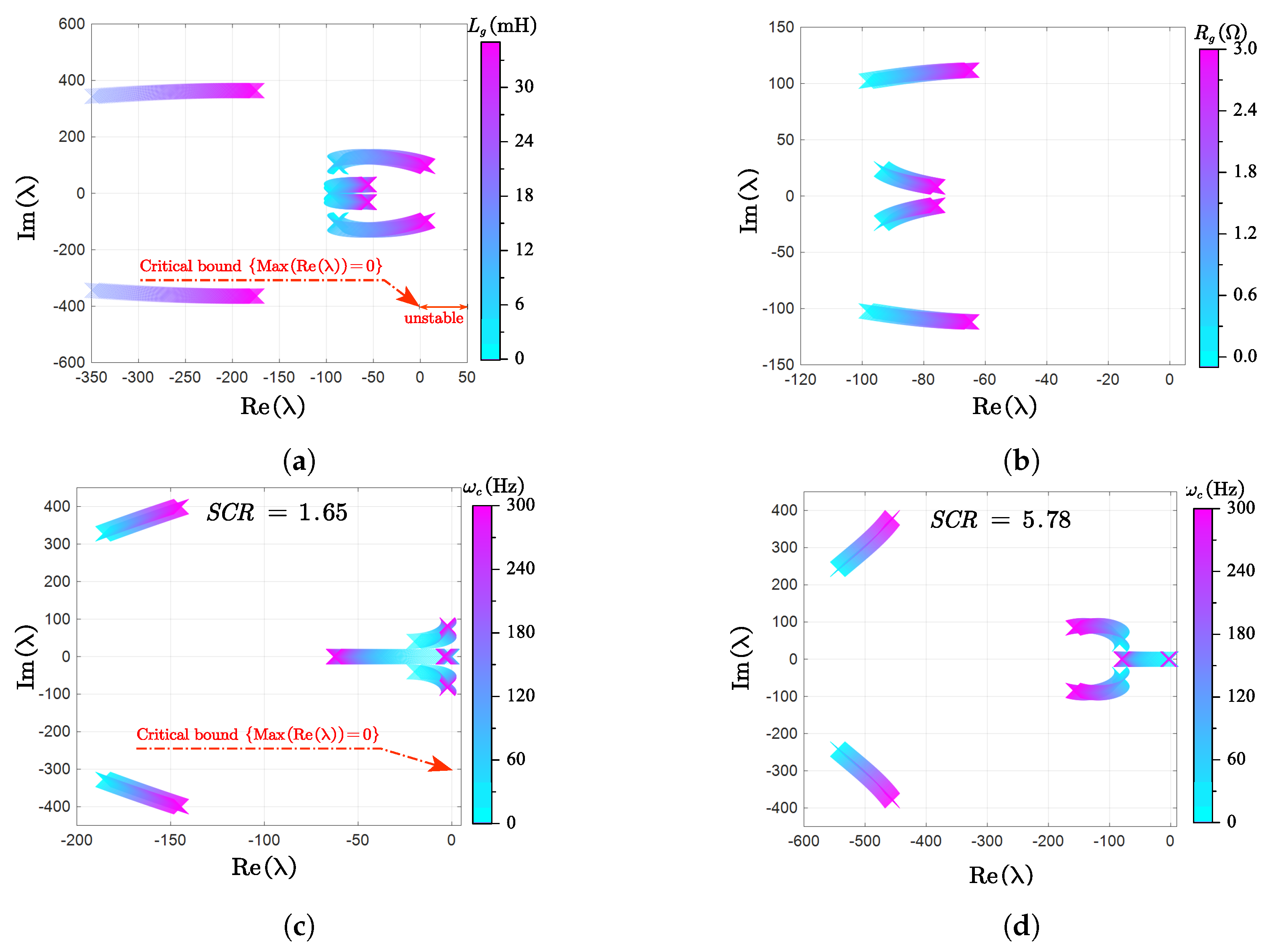
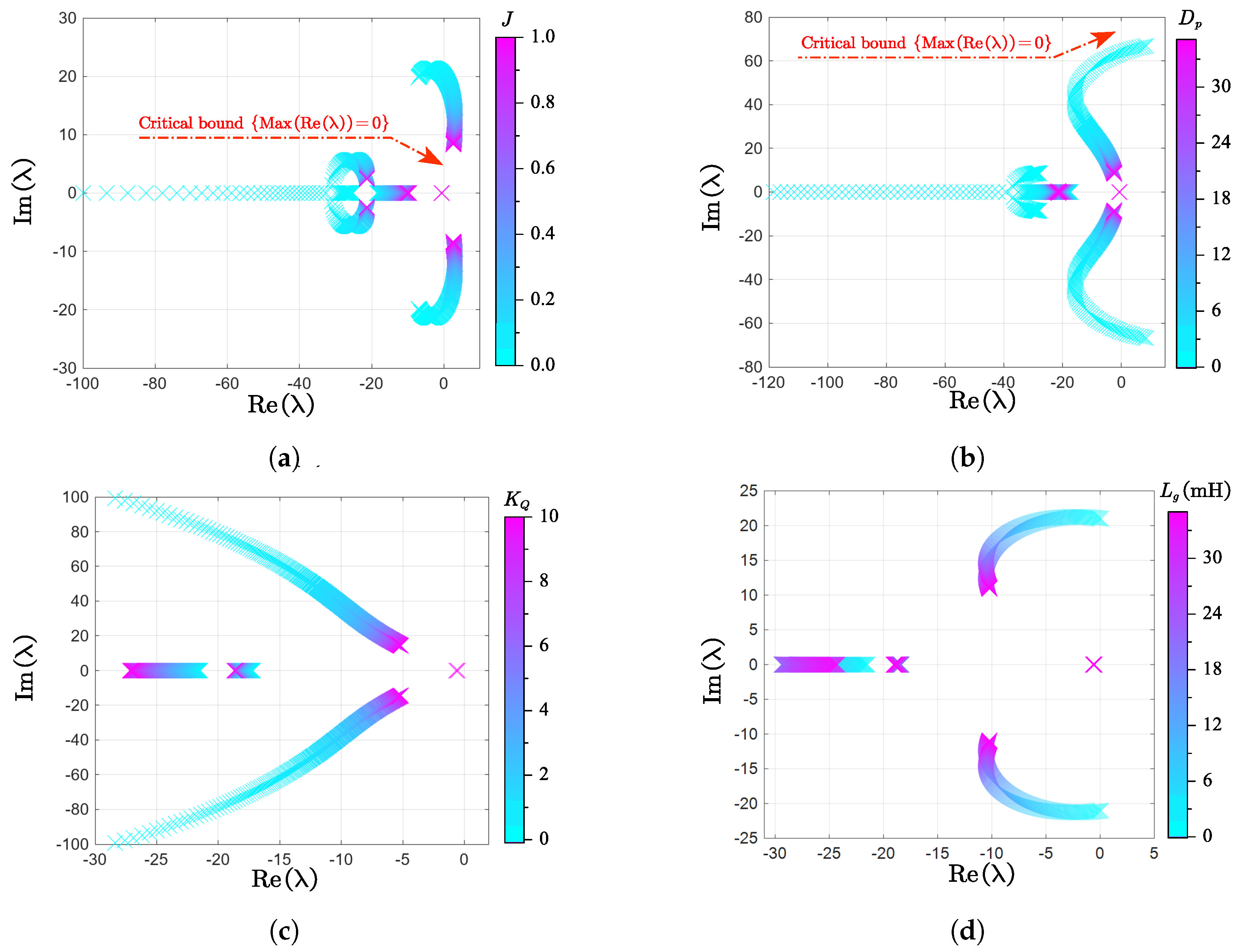
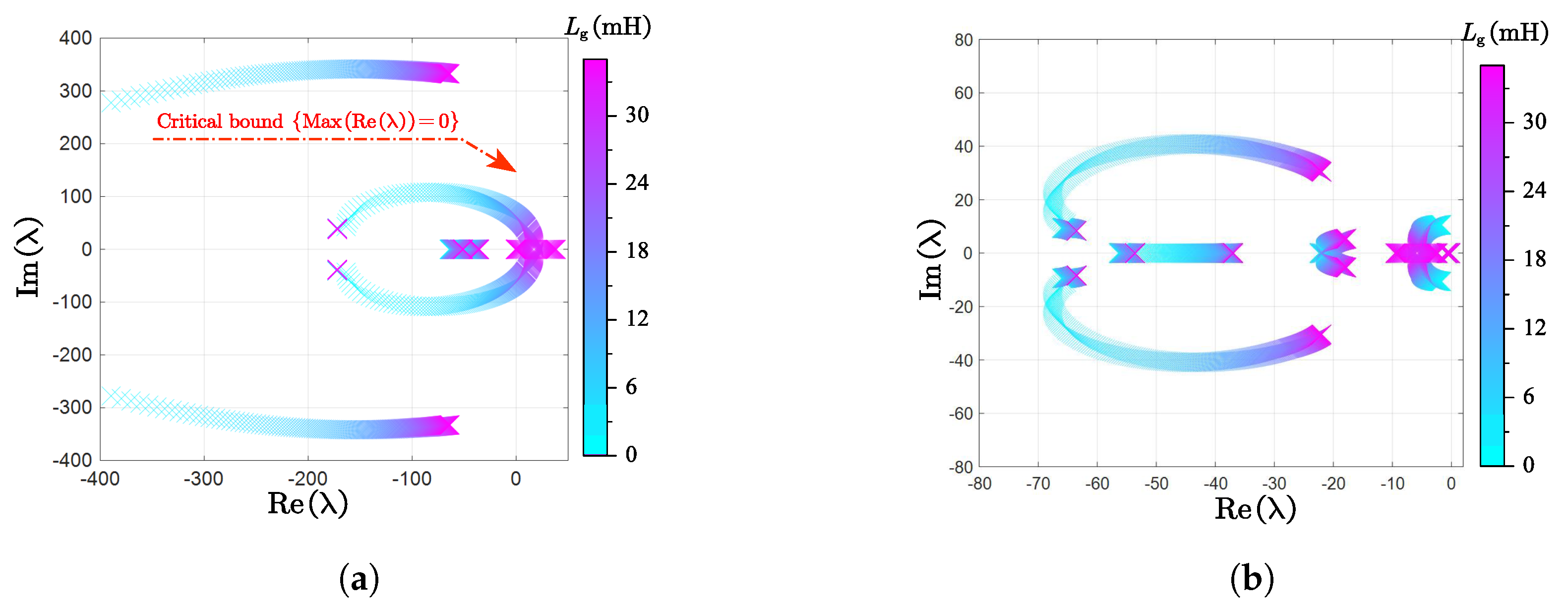
3. Small-Signal Stability Analysis of Parallel Inverters
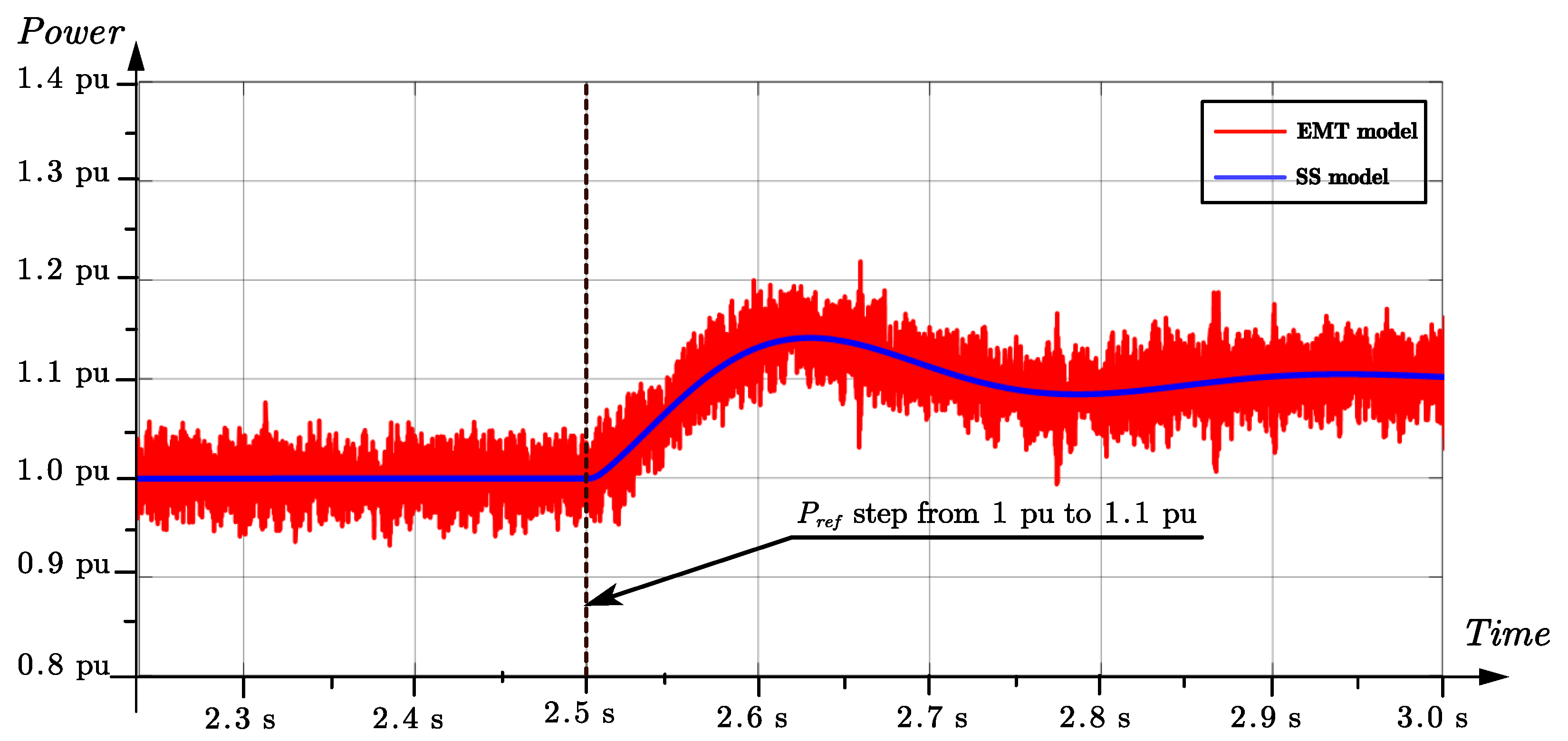
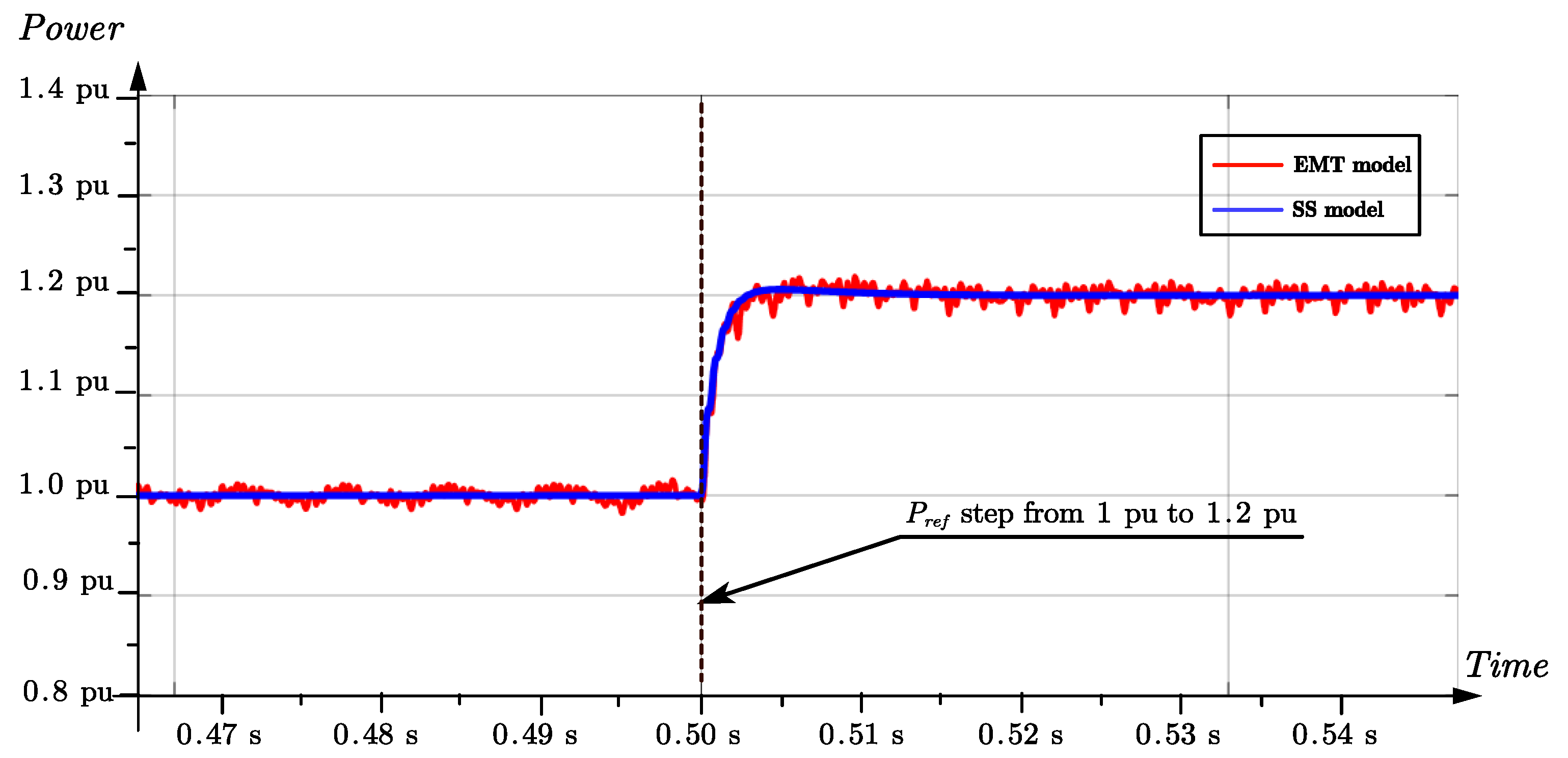
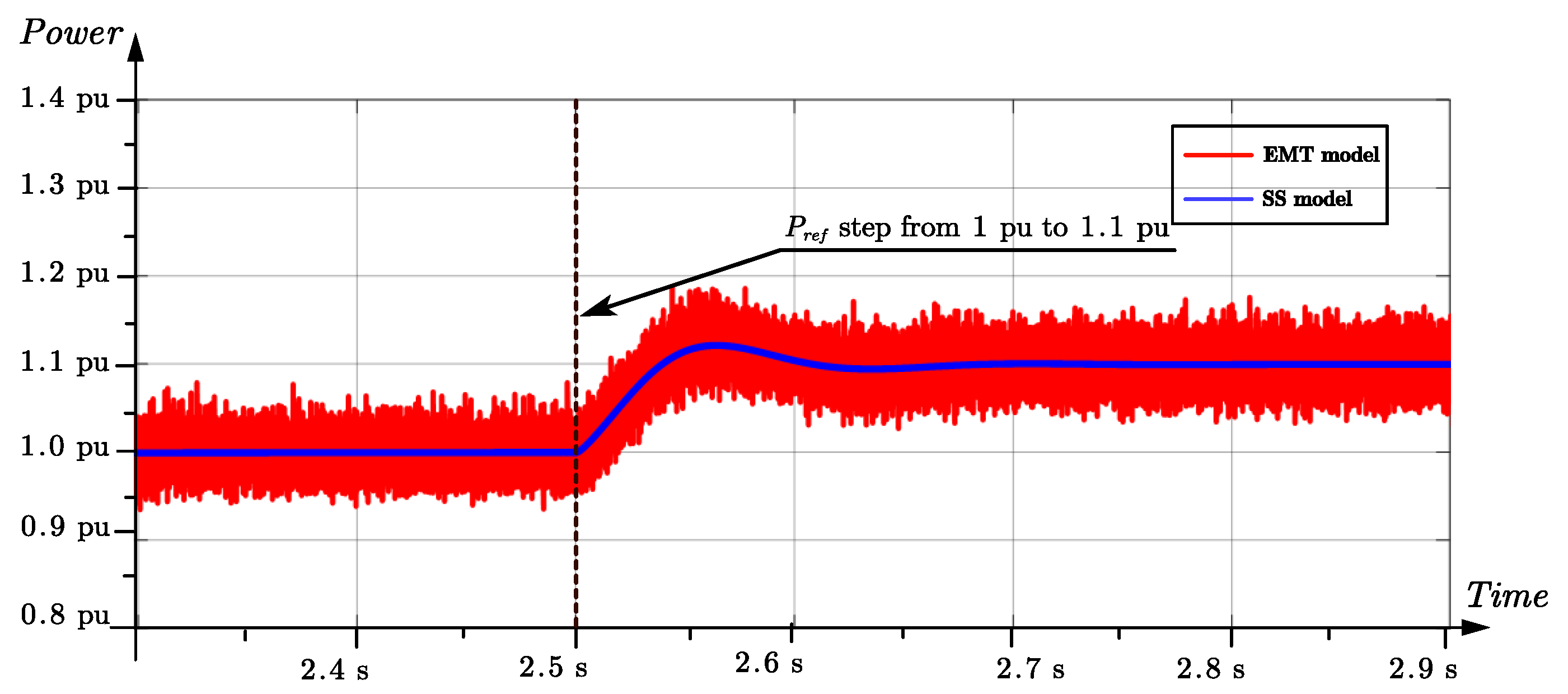
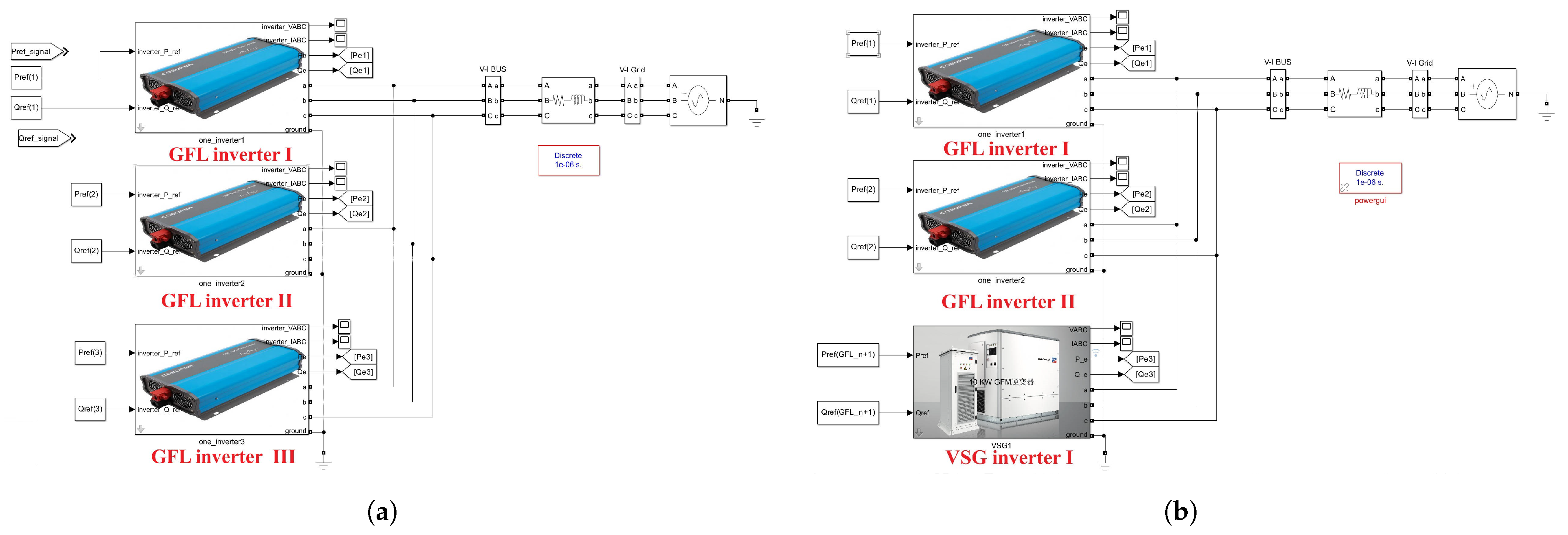
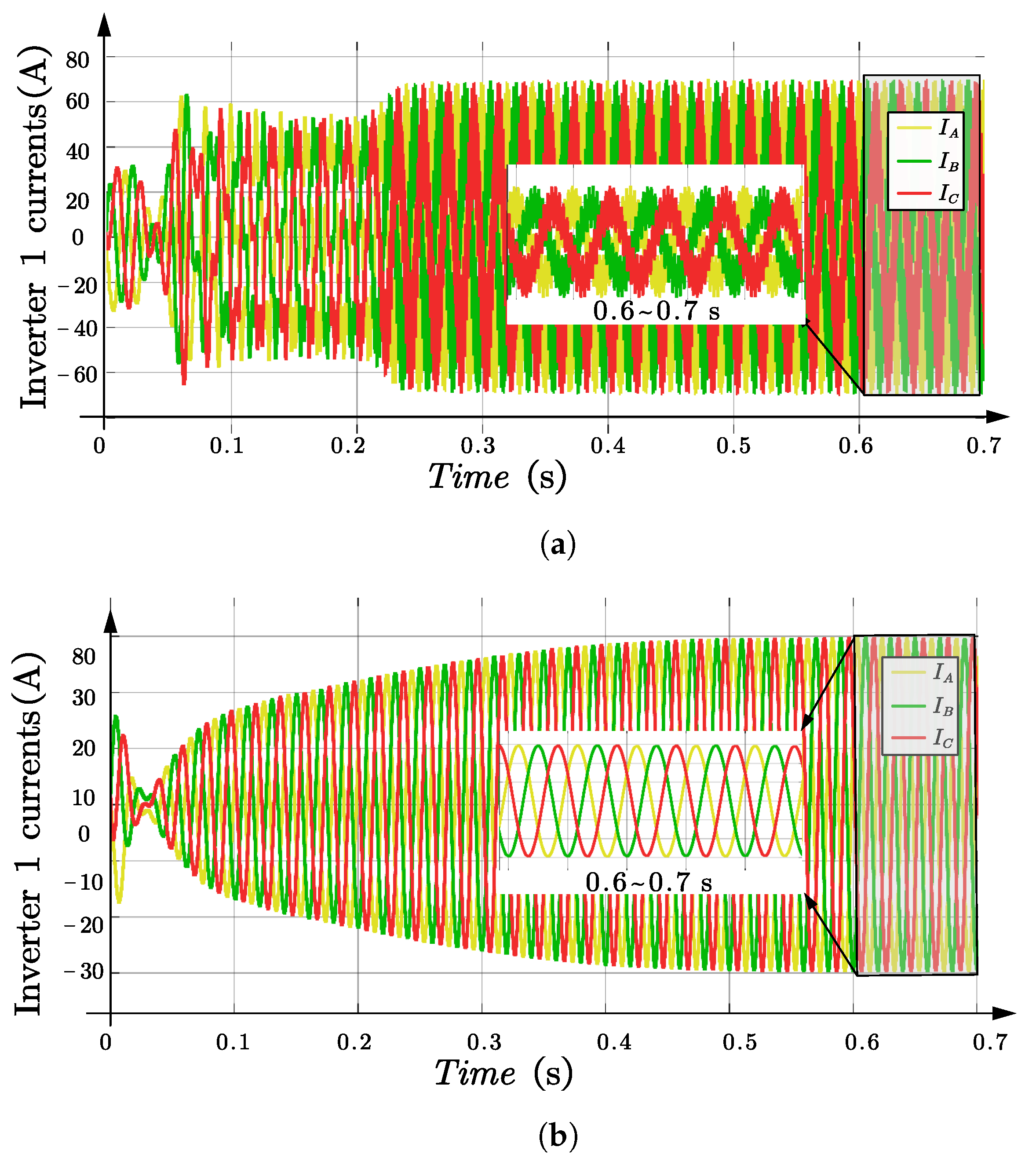
4. Simulation Validation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Rocabert, J.; Luna, A.; Blaabjerg, F.; Rodríguez, P. Control of Power Converters in AC Microgrids. IEEE Trans. Power Electron. 2012, 27, 4734–4749. [Google Scholar] [CrossRef]
- Ulbig, A.; Borsche, T.S.; Andersson, G. Impact of Low Rotational Inertia on Power System Stability and Operation. IFAC Proc. Vol. 2014, 47, 7290–7297. [Google Scholar] [CrossRef]
- Christensen, P.; Andersen, G.; Seidel, M.; Bolik, S.; Engelken, S.; Knueppel, T.; Krontiris, A.; Wuerflinger, K.; Bülo, T.; Jahn, J.; et al. High Penetration of Power Electronic Interfaced Power Sources and the Potential Contribution of Grid Forming Converters; University of Strathclyde Glasgow: Glasgow, UK, 2020. [Google Scholar]
- Blaabjerg, F.; Yang, Y.; Kim, K.A.; Rodriguez, J. Power Electronics Technology for Large-Scale Renewable Energy Generation. Proc. IEEE 2023, 111, 335–355. [Google Scholar] [CrossRef]
- Driesen, J.; Visscher, K. Virtual synchronous generators. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting–Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2018; IEEE: Piscataway, NJ, USA, 2008. [Google Scholar]
- Beck, H.P.; Hesse, R. Virtual synchronous machine. In Proceedings of the 2007 9th International Conference on Electrical Power Quality and Utilisation, Barcelona, Spain, 9–11 October 2007; IEEE: Piscataway, NJ, USA, 2007. [Google Scholar]
- Sano, K.; Horiuchi, S.; Noda, T. Comparison and Selection of Grid-Tied Inverter Models for Accurate and Efficient EMT Simulations. IEEE Trans. Power Electron. 2022, 37, 3462–3472. [Google Scholar] [CrossRef]
- Horiuchi, S.; Sano, K.; Noda, T. An Inverter Model Simulating Accurate Harmonics With Low Computational Burden for Electromagnetic Transient Simulations. IEEE Trans. Power Electron. 2021, 36, 5389–5397. [Google Scholar] [CrossRef]
- Harnefors, L.; Bongiorno, M.; Lundberg, S. Input-Admittance Calculation and Shaping for Controlled Voltage-Source Converters. IEEE Trans. Ind. Electron. 2007, 54, 3323–3334. [Google Scholar] [CrossRef]
- Wen, B.; Boroyevich, D.; Burgos, R.; Mattavelli, P.; Shen, Z. Analysis of D-Q Small-Signal Impedance of Grid-Tied Inverters. IEEE Trans. Power Electron. 2016, 31, 675–687. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhang, Z.; Luo, H.; Zhu, Y.; Yang, Y.; Molinas, M.; Xu, D. Stability Analysis of Grid-Forming Inverter Considering Different Operating Points. In Proceedings of the 2023 25th European Conference on Power Electronics and Applications (EPE’23 ECCE Europe), Aalborg, Denmark, 4–8 September 2023; IEEE: Piscataway, NJ, USA, 2023. [Google Scholar]
- Wen, B.; Boroyevich, D.; Burgos, R.; Mattavelli, P.; Shen, Z. Inverse Nyquist Stability Criterion for Grid-Tied Inverters. IEEE Trans. Power Electron. 2017, 32, 1548–1556. [Google Scholar] [CrossRef]
- Samanes, J.; Urtasun, A.; Barrios, E.L.; Lumbreras, D.; Lopez, J.; Gubia, E.; Sanchis, P. Control Design and Stability Analysis of Power Converters: The MIMO Generalized Bode Criterion. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1880–1893. [Google Scholar] [CrossRef]
- Qiao, L.; Xue, Y.; Kong, L.; Wang, F. A Potential Issue of Using the MIMO Nyquist Criterion in Impedance-Based Stability Analysis. IEEE Open J. Power Electron. 2022, 3, 899–904. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Blaabjerg, F.; Chen, Z. Harmonic Instability Assessment Using State-Space Modeling and Participation Analysis in Inverter-Fed Power Systems. IEEE Trans. Ind. Electron. 2017, 64, 806–816. [Google Scholar] [CrossRef]
- Yang, L.; Xu, Z.; Østergaard, J.; Dong, Z.Y.; Wong, K.P.; Ma, X. Oscillatory Stability and Eigenvalue Sensitivity Analysis of A DFIG Wind Turbine System. IEEE Trans. Energy Convers. 2011, 26, 328–339. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhu, Y.; Yang, Y.; Peng, Y.; Duan, Q.; Zhu, Z. Operational Flexibility of Grid-Connected Power Converters for Renewable Energy Integration. In Proceedings of the 2023 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Chiang Mai, Thailand, 28 November–1 December 2023; pp. 1–3. [Google Scholar]
- Zhou, Y.; Xin, H.; Wu, D.; Liu, F.; Li, Z.; Wang, G.; Yuan, H.; Ju, P. Small-Signal Stability Assessment of Heterogeneous Grid-Following Converter Power Systems Based on Grid Strength Analysis. IEEE Trans. Power Syst. 2023, 38, 2566–2579. [Google Scholar] [CrossRef]
- Schramm Dall’Asta, M.; Brunelli Lazzarin, T. Small-Signal Modeling and Stability Analysis of a Grid-Following Inverter with Inertia Emulation. Energies 2023, 16, 5894. [Google Scholar] [CrossRef]
- Pogaku, N.; Prodanovic, M.; Green, T.C. Modeling, Analysis and Testing of Autonomous Operation of an Inverter-Based Microgrid. IEEE Trans. Power Electron. 2007, 22, 613–625. [Google Scholar] [CrossRef]
- Khan, M.M.S.; Lin, Y.; Johnson, B.; Purba, V.; Sinha, M.; Dhople, S. A Reduced-order Aggregated Model for Parallel Inverter Systems with Virtual Oscillator Control. In Proceedings of the 2018 IEEE 19th Workshop on Control and Modeling for Power Electronics (COMPEL), Padova, Italy, 25–28 June 2018; IEEE: Piscataway, NJ, USA, 2018. [Google Scholar]
- Zhang, B.; Yan, X.; Li, D.; Zhang, X.; Han, J.; Xiao, X. Stable Operation and Small-Signal Analysis of Multiple Parallel DG Inverters Based on a Virtual Synchronous Generator Scheme. Energies 2018, 11, 203. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, Y. Control Flexibility of Power Converters for Seamless Transition between Grid-Following and Grid-Forming Modes. In Proceedings of the 2023 IEEE 2nd International Power Electronics and Application Symposium (PEAS), Guangzhou, China, 10–13 November 2023; pp. 1015–1020. [Google Scholar]
- Liu, P.; Xie, X.; Li, Y.; Yi, S.; Su, P.; Dai, X.; Ma, N. Mechanism and Characteristics of Grid-forming Control for Improving Sub/Super Synchronous Oscillation Stability of Grid-following-based Grid-connected Converter. Power Syst. Technol. 2023, 48, 990–997. [Google Scholar] [CrossRef]
- Song, Y.; Sahoo, S.; Yang, Y.; Blaabjerg, F. Probabilistic Risk Evaluation of Microgrids Considering Stability and Reliability. IEEE Trans. Power Electron. 2023, 38, 10302–10312. [Google Scholar] [CrossRef]
- Markovic, U.; Stanojev, O.; Aristidou, P.; Vrettos, E.; Callaway, D.; Hug, G. Understanding Small-Signal Stability of Low-Inertia Systems. IEEE Trans. Power Syst. 2021, 36, 3997–4017. [Google Scholar] [CrossRef]
- Zhao, L.; Jin, Z.; Wang, X. Analysis and Damping of Low-Frequency Oscillation for DC-Link Voltage-Synchronized VSCs. IEEE Trans. Power Electron. 2023, 38, 8177–8189. [Google Scholar] [CrossRef]
- Wang, X.; Ruan, X.; Liu, S.; Tse, C.K. Full Feedforward of Grid Voltage for Grid-Connected Inverter With LCL Filter to Suppress Current Distortion Due to Grid Voltage Harmonics. IEEE Trans. Power Electron. 2010, 25, 3119–3127. [Google Scholar] [CrossRef]
- Tu, Y.; Liu, J.; Liu, Z.; Xue, D.; Cheng, L. Impedance-Based Analysis of Digital Control Delay in Grid-Tied Voltage Source Inverters. IEEE Trans. Power Electron. 2020, 35, 11666–11681. [Google Scholar] [CrossRef]
- de Bosio, F.; de Souza Ribeiro, L.A.; Freijedo, F.D.; Pastorelli, M.; Guerrero, J.M. Effect of State Feedback Coupling and System Delays on the Transient Performance of Stand-Alone VSI With LC Output Filter. IEEE Trans. Ind. Electron. 2016, 63, 4909–4918. [Google Scholar] [CrossRef]



| Circuit Parameters | Symbol | Value |
|---|---|---|
| DC-side voltage | 700 V | |
| AC-side voltage (RMS) | 220 V | |
| Rated grid frequency | 50 Hz | |
| Switching frequency | 20 kHz | |
| Rated active power | 10 kW | |
| Rated reactive power | 0 kVar | |
| Grid inductance | 2 mH | |
| Grid resistance | 0.2 Ω | |
| Filter inductance | 5 mH | |
| Filter resistance | 0.5 Ω | |
| Filter capacitance | 500 μF | |
| Damping resistance | 3 Ω | |
| Sampling time | 50 μs |
| GFL Control Parameters | Symbol | Value |
|---|---|---|
| Proportional coefficient of the PLL | ||
| Integral coefficient of the PLL | ||
| Proportional coefficient of the current controller | ||
| Integral coefficient of the current controller | 800 | |
| Voltage-forward coefficient | 0 | |
| Active power reference | 4 kW | |
| Reactive power reference | 0 Var | |
| Delay time | 75 μs | |
| Delay orders | 3 |
| GFM Control Parameters | Symbol | Value |
|---|---|---|
| Inertia coefficient | J | |
| Damping coefficient | ||
| Integral coefficient of the Q-V loop | ||
| Proportional coefficient of the voltage controller | ||
| Integral coefficient of the voltage controller | ||
| Proportional coefficient of the current controller | 28 | |
| Integral coefficients of the current controller | 600 | |
| Current-forward coefficient | 0 | |
| Voltage-forward coefficient | 0 | |
| Active power reference | 4 kW | |
| Reactive power reference | 0 Var | |
| Delay time | 75 μs | |
| Delay orders | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, X.; Liu, D.; Jiang, K.; Zhang, Z.; Yang, Y. Small-Signal Stability of Hybrid Inverters with Grid-Following and Grid-Forming Controls. Energies 2024, 17, 1644. https://doi.org/10.3390/en17071644
Ji X, Liu D, Jiang K, Zhang Z, Yang Y. Small-Signal Stability of Hybrid Inverters with Grid-Following and Grid-Forming Controls. Energies. 2024; 17(7):1644. https://doi.org/10.3390/en17071644
Chicago/Turabian StyleJi, Xiaotong, Dan Liu, Kezheng Jiang, Zhe Zhang, and Yongheng Yang. 2024. "Small-Signal Stability of Hybrid Inverters with Grid-Following and Grid-Forming Controls" Energies 17, no. 7: 1644. https://doi.org/10.3390/en17071644
APA StyleJi, X., Liu, D., Jiang, K., Zhang, Z., & Yang, Y. (2024). Small-Signal Stability of Hybrid Inverters with Grid-Following and Grid-Forming Controls. Energies, 17(7), 1644. https://doi.org/10.3390/en17071644






