Advances in the Study of Techniques to Determine the Lithium-Ion Battery’s State of Charge
Abstract
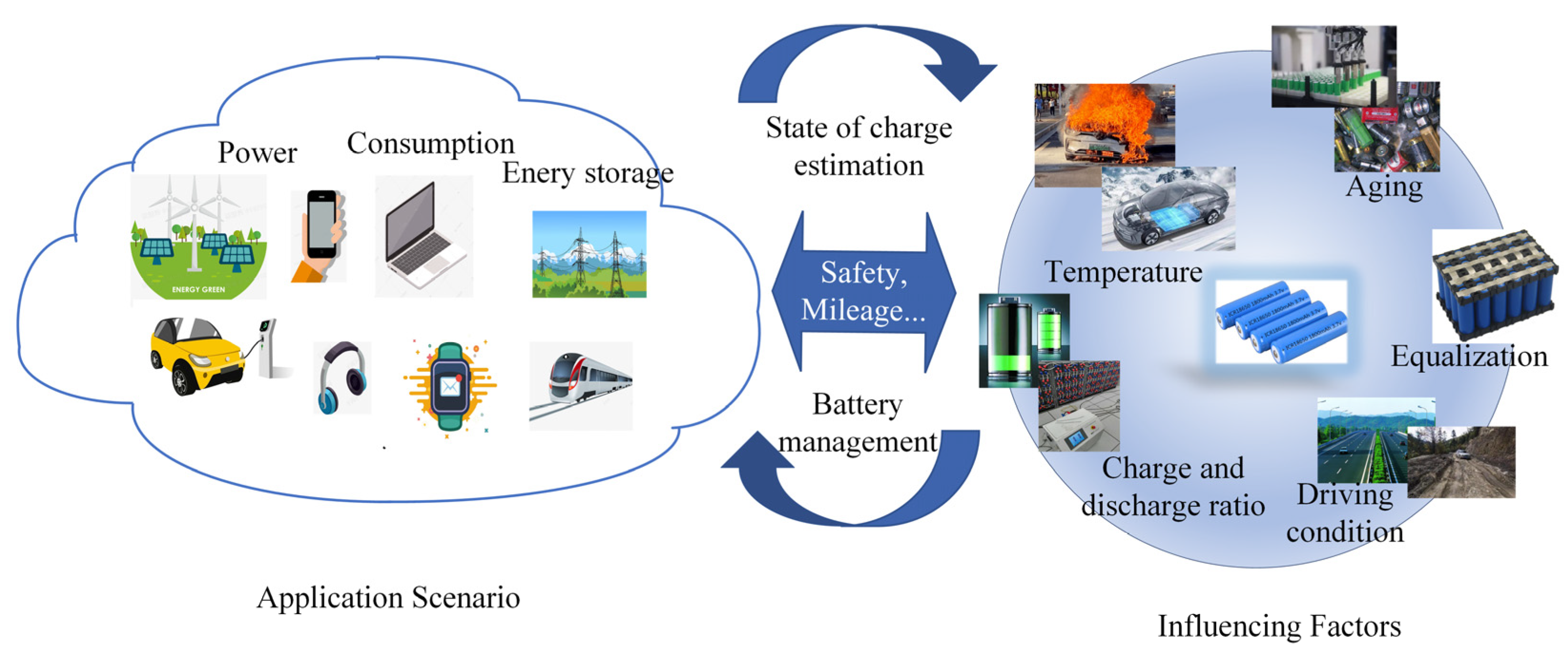
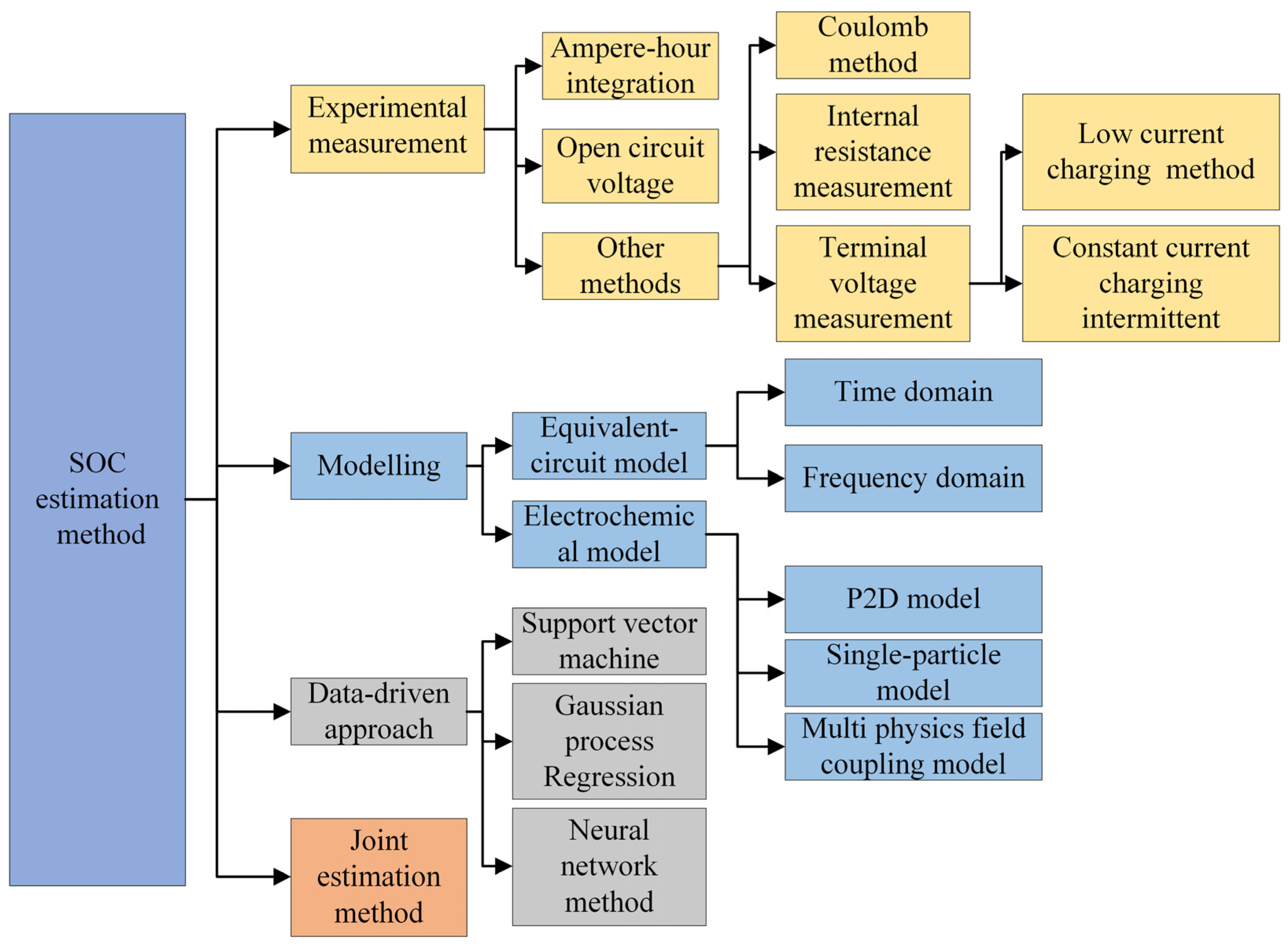
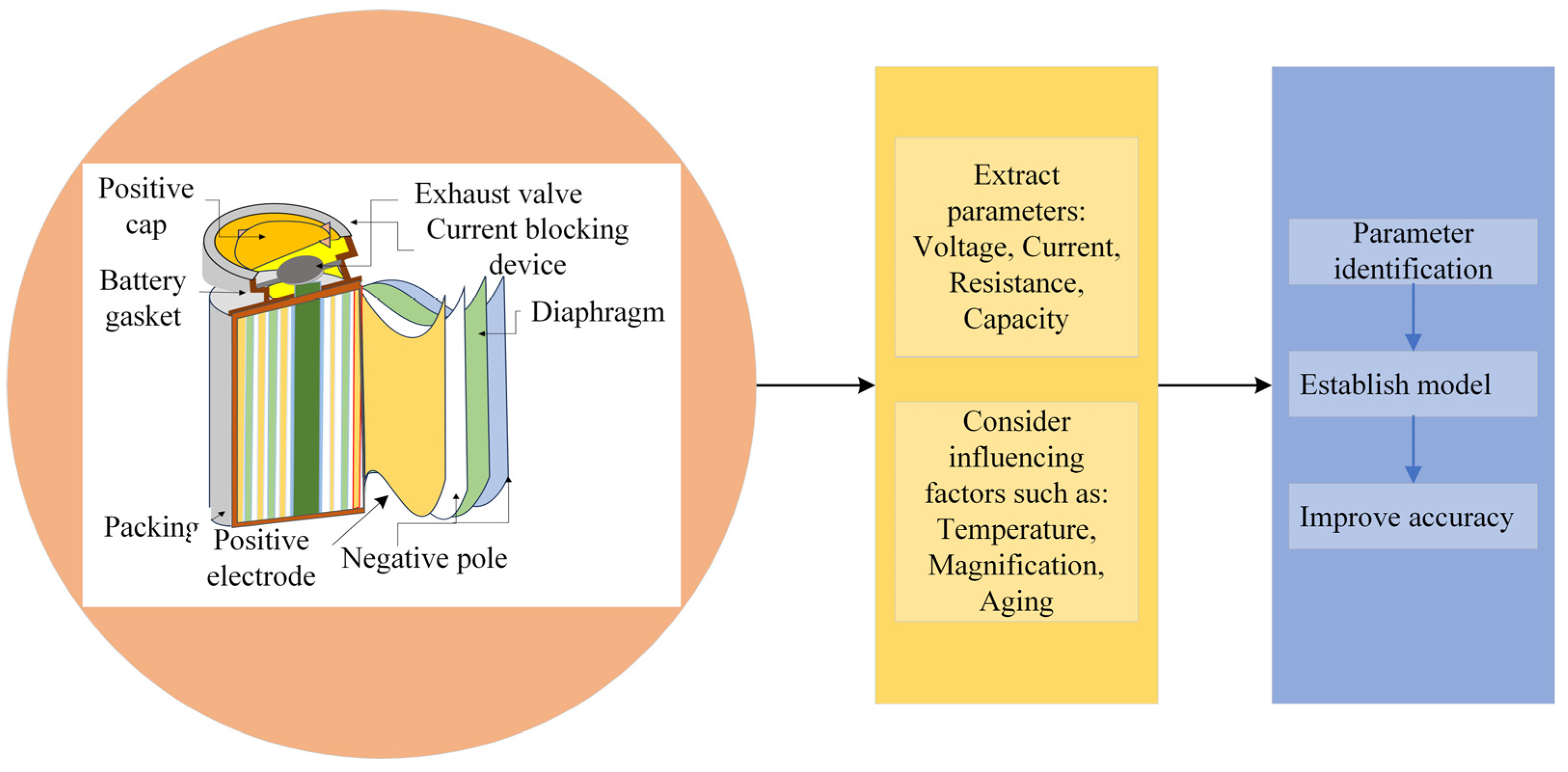
1. Introduction
2. Experimental Measurement Method
2.1. Ampere-Hour Integration Method
2.2. Open Circuit Voltage Method
2.3. Other Methods
3. Modeling Method
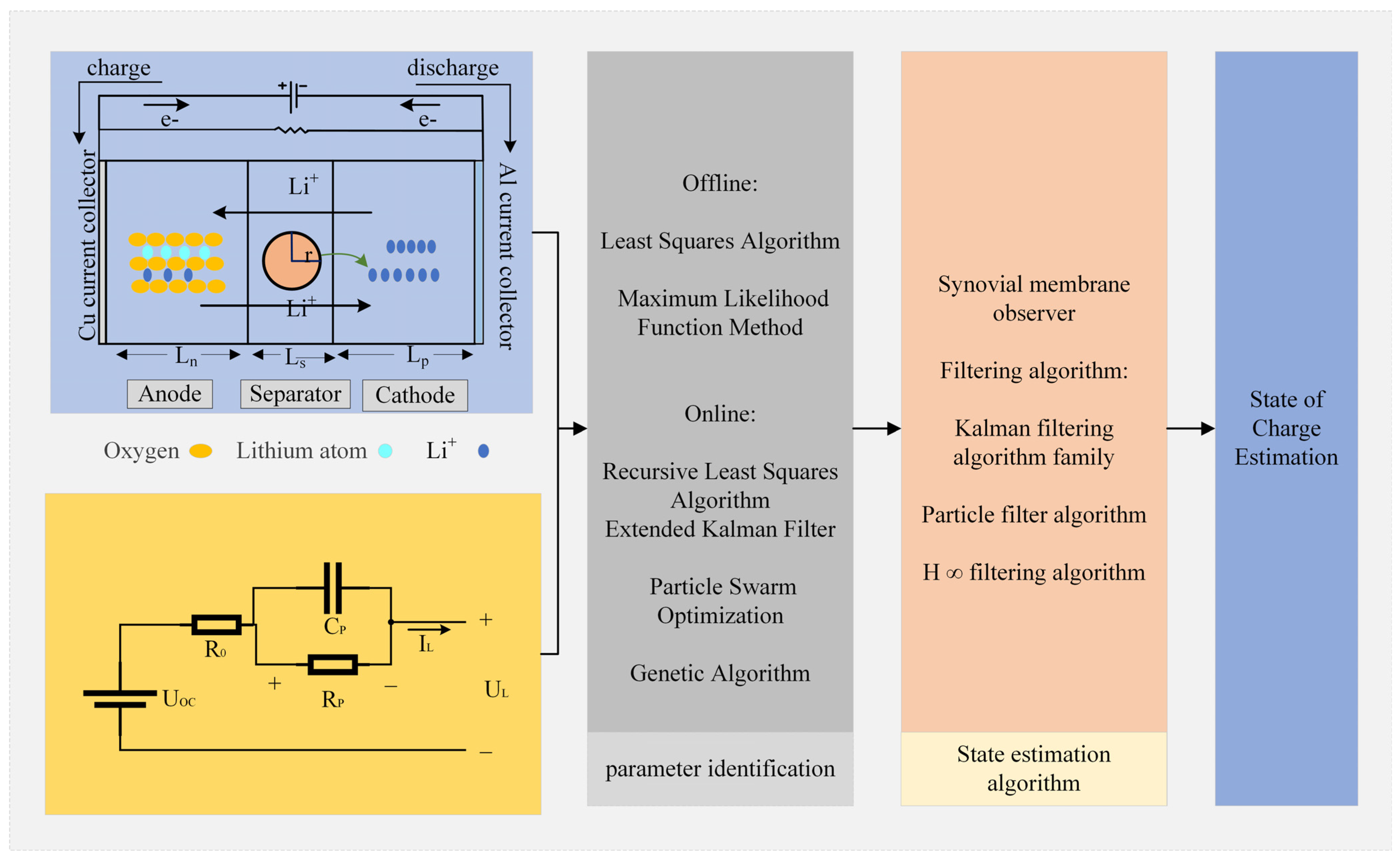
3.1. Electrochemical Modeling Method
3.2. Equivalent Circuit Modeling Method
4. Data-Driven Approach
5. Joint Estimation Method
5.1. SOC Estimate Approach Based on the Combination of a Model and Algorithm
5.1.1. Model Parameters’ Identification
5.1.2. State Estimation Algorithm
5.2. Combining Different Methods
6. Conclusions and Outlook
6.1. Conclusions
6.2. Outlook for Future Research on SOC
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tolomeo, R.; De Feo, G.; Adami, R.; Sesti Osséo, L. Application of Life Cycle Assessment to Lithium Ion Batteries in the Automotive Sector. Sustainability 2020, 12, 4628. [Google Scholar] [CrossRef]
- Masias, A.; Marcicki, J.; Paxton, W.A. Opportunities and Challenges of Lithium Ion Batteries in Automotive Applications. ACS Energy Lett. 2021, 6, 621–630. [Google Scholar] [CrossRef]
- Zhang, M.; Fan, X. Review on the State of Charge Estimation Methods for Electric Vehicle Battery. World Electr. Veh. J. 2020, 11, 23. [Google Scholar] [CrossRef]
- Kucinskis, G.; Bozorgchenani, M.; Feinauer, M.; Kasper, M.; Wohlfahrt-Mehrens, M.; Waldmann, T. Arrhenius plots for Li-ion battery ageing as a function of temperature, C-rate, and ageing state—An experimental study. J. Power Sources 2022, 549, 232129. [Google Scholar] [CrossRef]
- Krupp, A.; Beckmann, R.; Diekmann, T.; Ferg, E.; Schuldt, F.; Agert, C. Calendar aging model for lithium-ion batteries considering the influence of cell characterization. J. Energy Storage 2022, 45, 103506. [Google Scholar] [CrossRef]
- Xie, J.; Lu, Y.C. A retrospective on lithium-ion batteries. Nat. Commun. 2020, 11, 2499. [Google Scholar] [CrossRef]
- Feng, F.; Teng, S.; Liu, K.; Xie, J.; Xie, Y.; Liu, B.; Li, K. Co-estimation of lithium-ion battery state of charge and state of temperature based on a hybrid electrochemical-thermal-neural-network model. J. Power Sources 2020, 455, 227935. [Google Scholar] [CrossRef]
- Du, J.; Liu, Y.; Mo, X.; Li, Y.; Li, J.; Wu, X.; Ouyang, M. Impact of high-power charging on the durability and safety of lithium batteries used in long-range battery electric vehicles. Appl. Energy 2019, 255, 113793. [Google Scholar] [CrossRef]
- Attanayaka, S.; Karunadasa, J.P.; Hemapala, K.T.M.U. Estimation of state of charge for lithium-ion batteries—A Review. AIMS Energy 2019, 7, 186–210. [Google Scholar] [CrossRef]
- Li, W.; Fan, Y.; Ringbeck, F.; Jöst, D.; Han, X.; Ouyang, M.; Sauer, D.U. Electrochemical model-based state estimation for lithium-ion batteries with adaptive unscented Kalman filter. J. Power Sources 2020, 476, 228534. [Google Scholar] [CrossRef]
- Ghaeminezhad, N.; Ouyang, Q.; Wei, J.; Xue, Y.; Wang, Z. Review on state of charge estimation techniques of lithium-ion batteries: A control-oriented approach. J. Energy Storage 2023, 72, 108707. [Google Scholar] [CrossRef]
- Zhang, X.; Hou, J.; Wang, Z.; Jiang, Y. Study of SOC Estimation by the Ampere-Hour Integral Method with Capacity Correction Based on LSTM. Batteries 2022, 8, 170. [Google Scholar] [CrossRef]
- Deng, Z.; Yang, L.; Cai, Y.; Deng, H.; Sun, L. Online available capacity prediction and state of charge estimation based on advanced data-driven algorithms for lithium iron phosphate battery. Energy 2016, 112, 469–480. [Google Scholar] [CrossRef]
- Zhang, M.; Fan, X. Design of battery management system based on improved ampere-hour integration method. Electr. Hybrid. Veh. 2022, 14, 14. [Google Scholar] [CrossRef]
- Ahmed, M.S.; Balasingam, B. A Scaling Approach for Improved Open Circuit Voltage Modeling in Li-ion Batteries. In Proceedings of the 2019 IEEE Electrical Power and Energy Conference (EPEC), Montreal, QC, Canada, 16–18 October 2019; pp. 1–6. [Google Scholar]
- Xiao, L.; Li, X.; Jiang, Q.; Geng, G. Online state-of-charge estimation refining method for battery energy storage system using historical operating data. J. Energy Storage 2023, 57, 106262. [Google Scholar] [CrossRef]
- Xiong, R.; Yu, Q.; Wang, L.Y. Open circuit voltage and state of charge online estimation for lithium ion batteries. Energy Procedia 2017, 142, 1902–1907. [Google Scholar] [CrossRef]
- Saji, D.; Babu, P.S.; Ilango, K. SoC Estimation of Lithium Ion Battery Using Combined Coulomb Counting and Fuzzy Logic Method. In Proceedings of the 2019 4th International Conference on Recent Trends on Electronics, Information, Communication & Technology (RTEICT), Bangalore, India, 17–18 May 2019; pp. 948–952. [Google Scholar]
- Chen, L.; Zhang, M.; Ding, Y.; Wu, S.; Li, Y.; Liang, G.; Li, H.; Pan, H. Estimation the internal resistance of lithium-ion-battery using a multi-factor dynamic internal resistance model with an error compensation strategy. Energy Rep. 2021, 7, 3050–3059. [Google Scholar] [CrossRef]
- Liu, Y.; Ma, R.; Pang, S.; Xu, L.; Zhao, D.; Wei, J.; Huangfu, Y.; Gao, F. A Nonlinear Observer SOC Estimation Method Based on Electrochemical Model for Lithium-Ion Battery. IEEE Trans. Ind. Appl. 2021, 57, 1094–1104. [Google Scholar] [CrossRef]
- Dees, D.W.; Battaglia, V.S.; Bélanger, A. Electrochemical modeling of lithium polymer batteries. J. Power Sources 2002, 110, 310–320. [Google Scholar] [CrossRef]
- Doyle, M.; Fuller, T.F.; Newman, J. Modeling of galvanostatic charge and discharge of the lithium/polymer/insertion cell. J. Electrochem. Soc. 1993, 140, 1526, Erratum in: J. Electrochem. Soc. 2018, 165, X13. [Google Scholar] [CrossRef]
- Fuller, T.F.; Doyle, M.; Newman, J. Relaxation phenomena in lithium-ion-insertion cells. J. Electrochem. Soc. 1994, 141, 982–990. [Google Scholar] [CrossRef]
- Zhang, D.; Popov, B.N.; White, R.E. Modeling lithium intercalation of a single spinel particle under potentiodynamic control. J. Electrochem. Soc. 2000, 147, 831–838. [Google Scholar] [CrossRef]
- Zhao, L.; Liu, Z.; Ji, G. Lithium-ion battery state of charge estimation with model parameters adaptation using H∞ extended Kalman filter. Control Eng. Pract. 2018, 81, 114–128. [Google Scholar] [CrossRef]
- Chen, J.; Wang, R.; Li, Y.; Xu, M. A simplified extension of physics-based single particle model for dynamic discharge current. IEEE Access 2019, 7, 186217–186227. [Google Scholar] [CrossRef]
- Yang, S.; Yan, B.; Wu, J.; Lu, L.; Zeng, K. Temperature-Dependent Lithium-Ion Diffusion and Activation Energy of Li1.2Co0.13Ni0.13Mn0.54O2 Thin-Film Cathode at Nanoscale by Using Electrochemical Strain Microscopy. ACS Appl. Mater. Interfaces 2017, 9, 13999–14005. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Park, J.; Lin, X.; Sastry, A.M.; Lu, W. A thermal-electrochemical model that gives spatial-dependent growth of solid electrolyte interphase in a Li-ion battery. J. Power Sources 2014, 268, 482–490. [Google Scholar] [CrossRef]
- Liu, L.; Zhu, M. Modeling of SEI Layer Growth and Electrochemical Impedance Spectroscopy Response using a Thermal-Electrochemical Model of Li-ion Batteries. ECS Trans. 2014, 61, 43. [Google Scholar] [CrossRef]
- Guan, P.; Liu, L.; Lin, X. Simulation and Experiment on Solid Electrolyte Interphase (SEI) Morphology Evolution and Lithium-Ion Diffusion. J. Electrochem. Soc. 2015, 162, A1798. [Google Scholar] [CrossRef]
- Lin, X.; Park, J.; Liu, L.; Lee, Y.; Sastry, A.M.; Lu, W. A Comprehensive Capacity Fade Model and Analysis for Li-Ion Batteries. J. Electrochem. Soc. 2013, 160, A1701. [Google Scholar] [CrossRef]
- Liu, C.; Liu, L. Optimal Design of Li-Ion Batteries through Multi-Physics Modeling and Multi-Objective Optimization. J. Electrochem. Soc. 2017, 164, E3254. [Google Scholar] [CrossRef]
- Mu, W.; Liu, X.; Wen, Z.; Liu, L. Numerical simulation of the factors affecting the growth of lithium dendrites. J. Energy Storage 2019, 26, 100921. [Google Scholar] [CrossRef]
- Liu, S.; Liu, X.; Dou, R.; Zhou, W.; Wen, Z.; Liu, L. Experimental and simulation study on thermal characteristics of 18,650 lithium–iron–phosphate battery with and without spot–welding tabs. Appl. Therm. Eng. 2020, 166, 114648. [Google Scholar] [CrossRef]
- Gao, Y.; Liu, C.; Liang, Y.; Hamed, S.K.; Wang, F.; Bi, B. Minimizing Energy Consumption and Powertrain Cost of Fuel Cell Hybrid Vehicles with Consideration of Different Driving Cycles and SOC Ranges. Energies 2022, 15, 6167. [Google Scholar] [CrossRef]
- Wang, Y.; Ni, R.; Jiang, X.; Yin, M.; Zhang, D.; Xie, Z. An electrochemical-mechanical coupled multi-scale modeling method and full-field stress distribution of lithium-ion battery. Appl. Energy 2023, 347, 121444. [Google Scholar] [CrossRef]
- Li, M.; Lu, J.; Chen, Z.; Amine, K. 30 Years of Lithium-Ion Batteries. Adv. Mater. 2018, 30, e1800561. [Google Scholar] [CrossRef]
- Xu, J.; Cai, X.; Cai, S.; Shao, Y.; Hu, C.; Lu, S.; Ding, S. High-Energy Lithium-Ion Batteries: Recent Progress and a Promising Future in Applications. Energy Environ. Mater. 2023, 6, e12450. [Google Scholar] [CrossRef]
- Pals, C.R.; Newman, J. Thermal Modeling of the Lithium/Polymer Battery: I. Discharge Behavior of a Single Cell. J. Electrochem. Soc. 1995, 142, 3274. [Google Scholar] [CrossRef]
- Pals, C.R.; Newman, J. Thermal Modeling of the Lithium/Polymer Battery: II. Temperature Profiles in a Cell Stack. J. Electrochem. Soc. 1995, 142, 3282. [Google Scholar] [CrossRef]
- Kespe, M.; Cernak, S.; Gleic, M.; Hammerich, S.; Nirschl, H. Three-dimensional simulation of transport processes within blended electrodes on the particle scale. Int. J. Energy Res. 2019, 43, 6762–6778. [Google Scholar] [CrossRef]
- Li, Y.; Xi, K.; Ma, M.; Lu, S.; Wu, H.; Cao, X.; Zhang, X.; Ding, S. Interfacial chemistry and ion-transfer mechanism for a tailored poly(thioether)-enabled hybrid solid polymer electrolyte with electrochemical properties in all-solid-state lithium-sulfur batteries. J. Mater. Chem. A 2023, 11, 23405–23417. [Google Scholar] [CrossRef]
- Nejad, S.; Gladwin, D.T.; Stone, D.A. A systematic review of lumped-parameter equivalent circuit models for real-time estimation of lithium-ion battery states. J. Power Sources 2016, 316, 183–196. [Google Scholar] [CrossRef]
- Ramsey, D.; German, R.; Bouscayrol, A.; Boulon, L. Comparison of equivalent circuit battery models for energetic studies on electric vehicles. In Proceedings of the 17th IEEE Vehicle Power and Propulsion Conference, VPPC 2020, Gijon, Spain, 18 November–16 December 2020; Institute of Electrical and Electronics Engineers Inc.: Gijon, Spain, 2020. [Google Scholar]
- Hidalgo-Leon, R.; Urquizo, J.; Jacome-Ruiz, P.; Litardo, J.; Singh, P.; Wu, J.; Soriano, G. Modeling Battery under Discharge Using Improved Thevenin-Shepherd Electrical Battery Model. In Proceedings of the 2018 IEEE Vehicle Power and Propulsion Conference (VPPC), Chicago, IL, USA, 27–30 August 2018; pp. 1–5. [Google Scholar]
- Milishchuk, R.; Bogodorova, T. Thevenin-based Battery Model with Ageing Effects in Modelica. In Proceedings of the 2022 IEEE 21st Mediterranean Electrotechnical Conference (MELECON), Palermo, Italy, 14–16 June 2022; pp. 243–248. [Google Scholar]
- Nemes, R.; Ciornei, S.; Ruba, M.; Hedesiu, H.; Martis, C. Modeling and simulation of first-order Li-Ion battery cell with experimental validation. In Proceedings of the 2019 8th International Conference on Modern Power Systems (MPS), Cluj, Romania, 21–23 May 2019; pp. 1–6. [Google Scholar]
- Madani, S.S.; Schaltz, E.; Kaer, S.K. A review of different electric equivalent circuit models and parameter identification methods of lithium-ion batteries. ECS Trans. 2018, 87, 23. [Google Scholar] [CrossRef]
- Li, F.; Zuo, W.; Zhou, K.; Li, Q.; Huang, Y.; Zhang, G. State-of-charge estimation of lithium-ion battery based on second order resistor-capacitance circuit-PSO-TCN model. Energy 2024, 289, 130025. [Google Scholar] [CrossRef]
- Yan, X.-W.; Guo, Y.-W.; Cui, Y.; Wang, Y.-W.; Deng, H.-R. Electric Vehicle Battery SOC Estimation based on GNL Model Adaptive Kalman Filter. J. Phys. Conf. Ser. 2018, 1087, 052027. [Google Scholar] [CrossRef]
- Selvaraj, V.; Vairavasundaram, I. A comprehensive review of state of charge estimation in lithium-ion batteries used in electric vehicles. J. Energy Storage 2023, 72, 108777. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, X.; Deng, Z.; Yang, L. Application of electrochemical impedance spectroscopy in battery management system: State of charge estimation for aging batteries. J. Energy Storage 2023, 57, 106275. [Google Scholar] [CrossRef]
- Rodríguez-Iturriaga, P.; Anseán, D.; Rodríguez-Bolívar, S.; González, M.; Viera, J.C.; López-Villanueva, J.A. A physics-based fractional-order equivalent circuit model for time and frequency-domain applications in lithium-ion batteries. J. Energy Storage 2023, 64, 107150. [Google Scholar] [CrossRef]
- Chen, L.; Yu, W.; Cheng, G.; Wang, J. State-of-charge estimation of lithium-ion batteries based on fractional-order modeling and adaptive square-root cubature Kalman filter. Energy 2023, 271, 127007. [Google Scholar] [CrossRef]
- Barcellona, S.; Colnago, S.; Dotelli, G.; Latorrata, S.; Piegari, L. Aging effect on the variation of Li-ion battery resistance as function of temperature and state of charge. J. Energy Storage 2022, 50, 10465. [Google Scholar] [CrossRef]
- Lin, M.; Yan, C.; Wang, W.; Dong, G.; Meng, J.; Wu, J. A data-driven approach for estimating state-of-health of lithium-ion batteries considering internal resistance. Energy 2023, 277, 127675. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, S.; Xie, Y.; Zhu, T.; Fernandez, C. An improved particle swarm optimization-least squares support vector machine-unscented Kalman filtering algorithm on SOC estimation of lithium-ion battery. Int. J. Green. Energy 2024, 21, 376–386. [Google Scholar] [CrossRef]
- Zhang, L.; Li, K.; Du, D.; Zhu, C.; Zheng, M. A sparse least squares support vector machine used for SOC estimation of Li-ion Batteries. IFAC-PapersOnLine 2019, 52, 256–261. [Google Scholar] [CrossRef]
- Ali, O.; Ishak, M.K.; Ahmed, A.B.; Salleh, M.F.M.; Ooi, C.A.; Khan, M.F.A.J.; Khan, I. On-line WSN SoC estimation using Gaussian Process Regression: An Adaptive Machine Learning Approach. Alex. Eng. J. 2022, 61, 9831–9848. [Google Scholar] [CrossRef]
- Deng, Z.; Hu, X.; Lin, X.; Che, Y.; Xu, L.; Guo, W. Data-driven state of charge estimation for lithium-ion battery packs based on Gaussian process regression. Energy 2020, 205, 118000. [Google Scholar] [CrossRef]
- Chen, C.; Xiong, R.; Yang, R.; Shen, W.; Sun, F. State-of-charge estimation of lithium-ion battery using an improved neural network model and extended Kalman filter. J. Clean. Prod. 2019, 234, 1153–1164. [Google Scholar] [CrossRef]
- Shah, S.A.A.; Niazi, S.G.; Deng, S.; Hamza Azam, H.M.; Mian Muhammad Yasir, K.; Kumar, J.; Xu, Z.; Wu, M. A novel positional encoded attention-based Long short-term memory network for state of charge estimation of lithium-ion battery. J. Power Sources 2024, 590, 233788. [Google Scholar] [CrossRef]
- Liu, L.; Sadegh Kouhestani, H.; Chandra, A.J.E.M.A. Data-Driven Prognosis of the Failure of Lithium-Ion Batteries. In Electrochemical Society Meeting Abstracts 240; The Electrochemical Society, Inc.: Pennington, NJ, USA, 2021; p. 1864. [Google Scholar]
- Kouhestani, H.S.; Liu, L.; Wang, R.; Chandra, A. Data-driven prognosis of failure detection and prediction of lithium-ion batteries. J. Energy Storage 2023, 70, 108045. [Google Scholar] [CrossRef]
- Liu, L. Data-Driven Prognosis of Multiscale and Multiphysics Complex System Anomalies: Its Application to Lithium-ion Batteries Failure Detection. J. Electrochem. Soc. 2023, 170, 050525. [Google Scholar] [CrossRef]
- Zhang, C.; Allafi, W.; Dinh, Q.; Ascencio, P.; Marco, J. Online estimation of battery equivalent circuit model parameters and state of charge using decoupled least squares technique. Energy 2018, 142, 678–688. [Google Scholar] [CrossRef]
- Zheng, Y.; Ouyang, M.; Han, X.; Lu, L.; Li, J. Investigating the error sources of the online state of charge estimation methods for lithium-ion batteries in electric vehicles. J. Power Sources 2018, 377, 161–188. [Google Scholar] [CrossRef]
- Xing, J.; Wu, P. State of Charge Estimation of Lithium-Ion Battery Based on Improved Adaptive Unscented Kalman Filter. Sustainability 2021, 13, 5046. [Google Scholar] [CrossRef]
- Havangi, R. Adaptive robust unscented Kalman filter with recursive least square for state of charge estimation of batteries. Electr. Eng. 2022, 104, 1001–1017. [Google Scholar] [CrossRef]
- Miranda, M.H.R.; Silva, F.L.; Lourenco, M.A.M.; Eckert, J.J.; Silva, L.C.A. Particle swarm optimization of Elman neural network applied to battery state of charge and state of health estimation. Energy 2023, 285, 129503. [Google Scholar] [CrossRef]
- Manriquez-Padilla, C.G.; Cueva-Perez, I.; Dominguez-Gonzalez, A.; Elvira-Ortiz, D.A.; Perez-Cruz, A.; Saucedo-Dorantes, J.J. State of Charge Estimation Model Based on Genetic Algorithms and Multivariate Linear Regression with Applications in Electric Vehicles. Sensors 2023, 23, 2924. [Google Scholar] [CrossRef]
- Kwak, M.; Lkhagvasuren, B.; Jin, H.S.; Seo, G.; Bong, S.; Lee, J. A Variable-length scale Parameter Dependent State of Charge Estimation of Lithium Ion Batteries by Kalman Filters. Int. J. Electrochem. Sci. 2022, 17, 220218. [Google Scholar] [CrossRef]
- Gustafsson, F.; Hendeby, G. Some Relations Between Extended and Unscented Kalman Filters. IEEE Trans. Signal Process. 2012, 60, 545–555. [Google Scholar] [CrossRef]
- Cheng, Z.; Lv, J.; Liu, Y.; Yan, Z. Estimation of State of Charge for Lithium-Ion Battery Based on Finite Difference Extended Kalman Filter. J. Appl. Math. 2014, 2014, 348537. [Google Scholar] [CrossRef]
- Nguyen, T.-T.; Khan, A.B.; Ko, Y.; Choi, W. An Accurate State of Charge Estimation Method for Lithium Iron Phosphate Battery Using a Combination of an Unscented Kalman Filter and a Particle Filter. Energies 2020, 13, 4536. [Google Scholar] [CrossRef]
- Wadi, A.; Abdel-Hafez, M.; Hussein, A.A. Computationally Efficient State-of-Charge Estimation in Li-Ion Batteries Using Enhanced Dual-Kalman Filter. Energies 2022, 15, 3717. [Google Scholar] [CrossRef]
- Fereydooni, A.; Vafa, E.; Pishvaie, M.R.; Ghalami Choobar, B. Robust adaptive sliding mode observer for core temperature and state of charge monitoring of Li-ion battery: A simulation study. J. Energy Storage 2023, 70, 107960. [Google Scholar] [CrossRef]
- Buchicchio, E.; De Angelis, A.; Santoni, F.; Carbone, P.; Bianconi, F.; Smeraldi, F. Battery SOC estimation from EIS data based on machine learning and equivalent circuit model. Energy 2023, 283, 128461. [Google Scholar] [CrossRef]
- Sun, D.; Yu, X.; Wang, C.; Zhang, C.; Huang, R.; Zhou, Q.; Amietszajew, T.; Bhagat, R. State of charge estimation for lithium-ion battery based on an Intelligent Adaptive Extended Kalman Filter with improved noise estimator. Energy 2021, 214, 119025. [Google Scholar] [CrossRef]
- Yu, H.; Zhang, L.; Wang, W.; Li, S.; Chen, S.; Yang, S.; Li, J.; Liu, X. State of charge estimation method by using a simplified electrochemical model in deep learning framework for lithium-ion batteries. Energy 2023, 278, 127846. [Google Scholar] [CrossRef]
- Liu, L.C.; Dong, S.F.; Nan, B.; Lu, K.C. Construction and simulation analysis of lithium-ion batteries thermoelectric coupling model based on digital twin. IET Renew. Power Gener. 2023. [Google Scholar] [CrossRef]

| Model | Circuit | Advantage | Disadvantage | |
|---|---|---|---|---|
| Time domain | Rint | 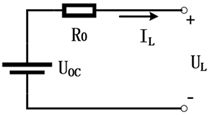 | Simple structure and calculation; easy to determine parameters | Only simulates ideal SOC, ignoring the internal battery reactions |
| Thevenin | 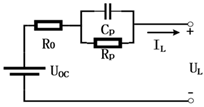 | Higher accuracy; simpler calculation; describes polarization reaction | Insufficient RC order; parameters are affected by aging and temperature | |
| PNGV | 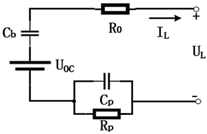 | Real-time estimation of open circuit voltage, capacity changes, and SOC | Difficulty in identifying cumulative errors in parameters | |
| DP |  | Higher simulation degree; strong real-time performance | More complex structure, without considering factors such as temperature; | |
| GNL | 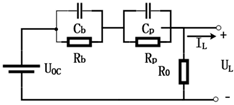 | High simulation accuracy; considers the effects of self-discharge and overcharging | complex model and calculations; difficult noise and parameter identification | |
| Frequency domain | Randles model | 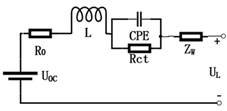 | High model accuracy, reflecting the internal chemical reactions from the frequency domain | Not necessarily consistent with time-domain characteristics |
| Improved Thevenin model | 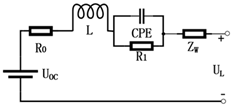 | Low calculation cost; the internal chemical reactions are analyzed from the frequency domain | Not necessarily consistent with time-domain characteristics | |
| Improved DP model | 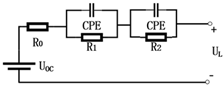 | High model accuracy, reflecting the internal chemical reactions from the frequency domain | Not necessarily consistent with time-domain characteristics |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Gao, Y.; Marma, K.; Miao, Y.; Liu, L. Advances in the Study of Techniques to Determine the Lithium-Ion Battery’s State of Charge. Energies 2024, 17, 1643. https://doi.org/10.3390/en17071643
Liu X, Gao Y, Marma K, Miao Y, Liu L. Advances in the Study of Techniques to Determine the Lithium-Ion Battery’s State of Charge. Energies. 2024; 17(7):1643. https://doi.org/10.3390/en17071643
Chicago/Turabian StyleLiu, Xinyue, Yang Gao, Kyamra Marma, Yu Miao, and Lin Liu. 2024. "Advances in the Study of Techniques to Determine the Lithium-Ion Battery’s State of Charge" Energies 17, no. 7: 1643. https://doi.org/10.3390/en17071643
APA StyleLiu, X., Gao, Y., Marma, K., Miao, Y., & Liu, L. (2024). Advances in the Study of Techniques to Determine the Lithium-Ion Battery’s State of Charge. Energies, 17(7), 1643. https://doi.org/10.3390/en17071643






