A Dependability Neural Network Approach for Short-Term Production Estimation of a Wind Power Plant
Abstract
1. Introduction
2. State of the Art
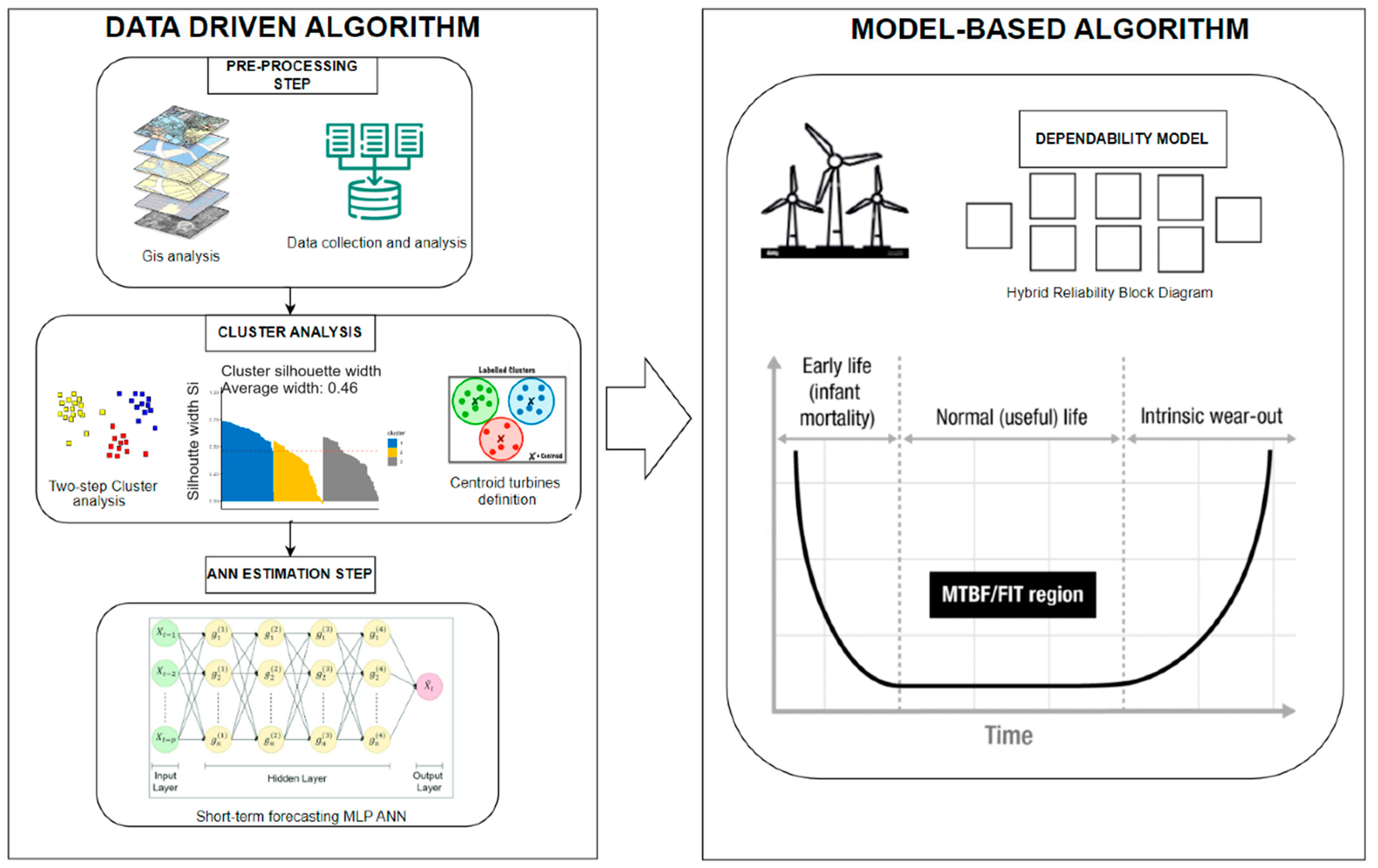
3. Methodology
- -
- Reduced Computational Effort: by focusing on key turbines, the approach lessens the computational load, enabling faster, more efficient processing.
- -
- High Precision: the combination of the dependability model with the data-driven module guarantees high accuracy in forecasting energy production, even with fewer data inputs.
3.1. Data-Driven Model
3.1.1. Pre-Processing Analysis
3.1.2. Cluster Analysis
- A pre-clustering that examines the data sample of each individual element (e.g., the wind turbine) to determine whether it can be integrated into an existing cluster or if it should serve as the centroid for a new cluster. This decision is based on a specific distance criterion. For the proposed model, the Euclidean distance was selected as the distance criterion, defined as follows:where is a tuple = (, , …, ) characterized by n variables. In these cases, represents the generic “k” wind turbine modeled by the 9 standardized variables (i.
- The clustering validity analysis is the step of the algorithm that determines the dimension and the number of elements of each cluster. This algorithm can iteratively perform a grouping with different sizes of elements. In order to select the most appropriate number of clusters, the silhouette (S) coefficient is used:
3.1.3. Artificial Neural Network Estimation Step
3.2. Model-Based Dependability
- -
- Early failures: where h(τ) decreases with time. This phase contributes to removing all the components which do not pass the trial stage, so that components are not placed on the market.
- -
- Random failures: where it is assumed that only random failures can occur. This is the phase that characterizes the useful life of a component, assuming that this failure rate is constant (this represents a general limitation of reliability models).
- -
- Deterioration: where h(τ) is increasing due to deterioration. This region corresponds to the phase where the component is old and should be replaced with a new component.

4. Case Study and Results
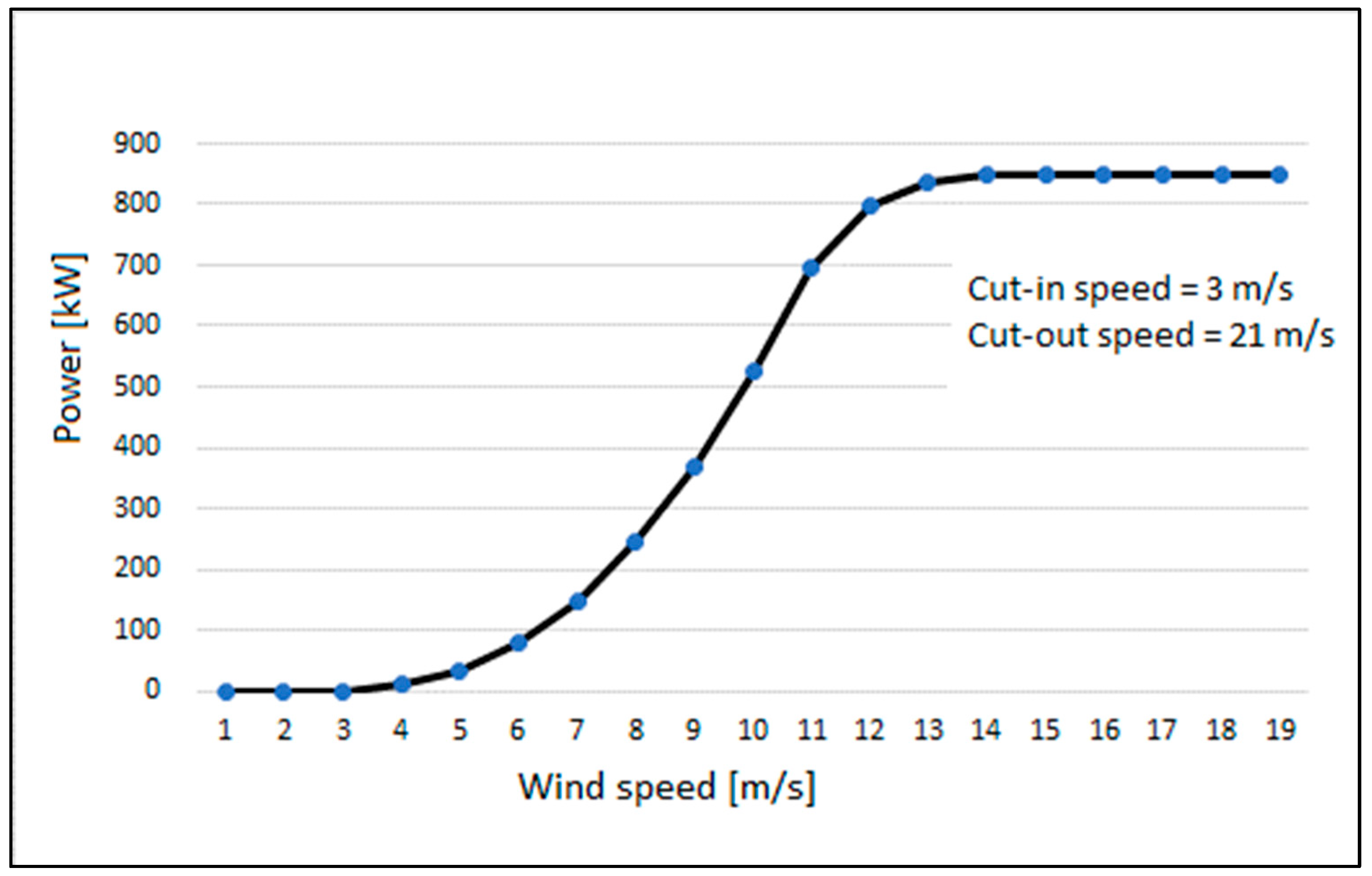
4.1. Wind Farm
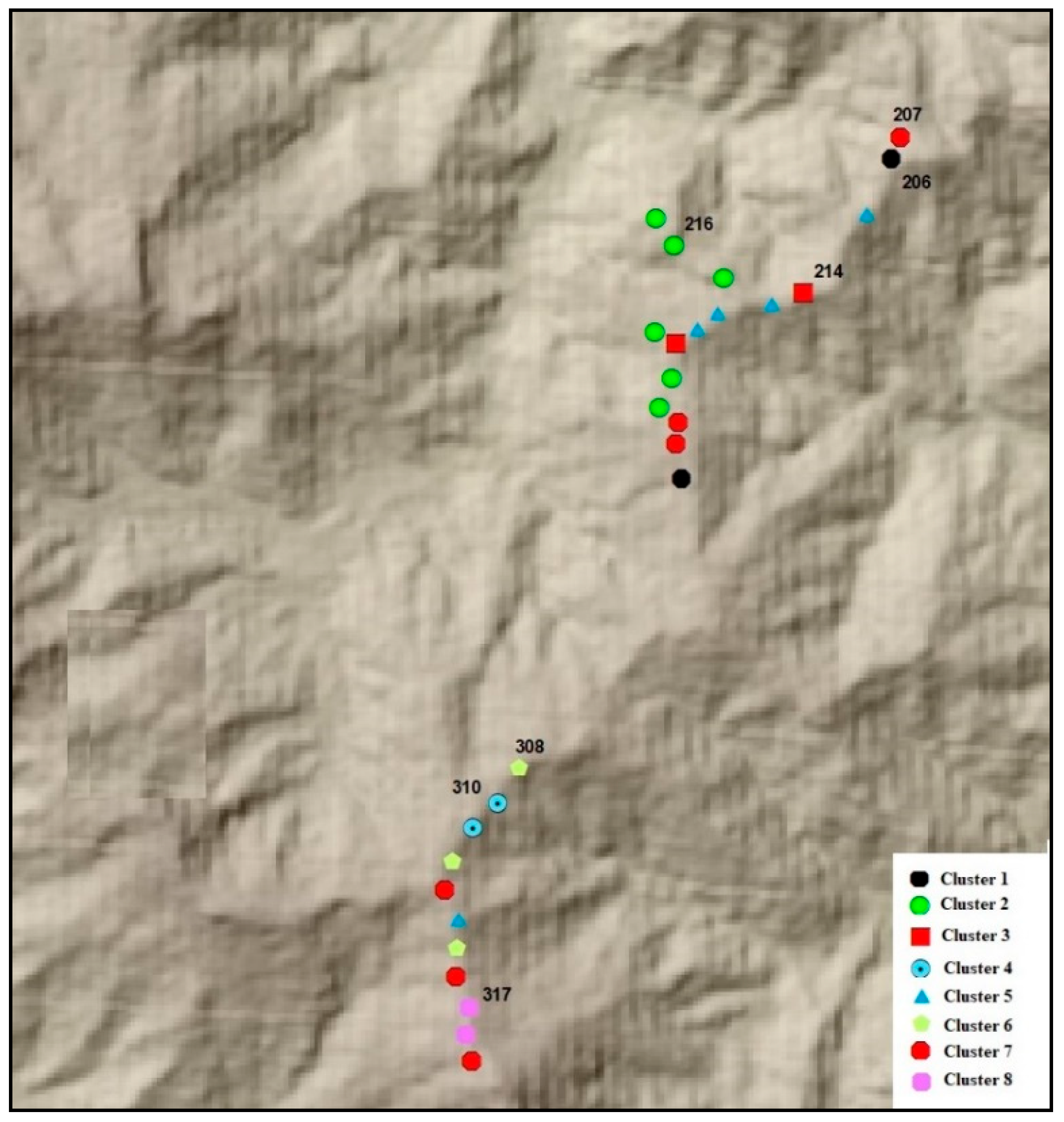
4.2. Cluster Analysis Results
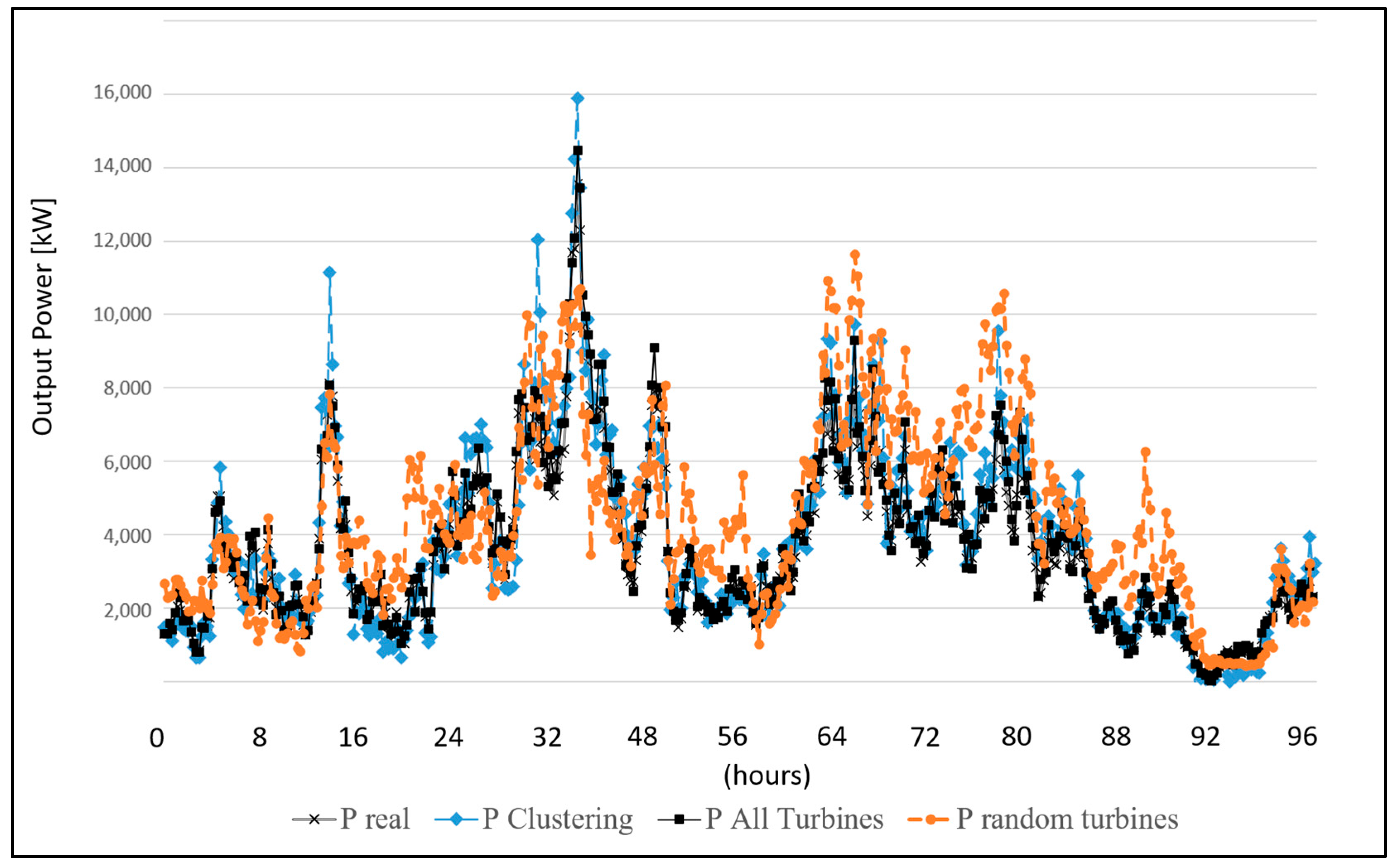
4.3. Neural Network Results
- -
- All turbines: the neural network is fed with the wind direction and wind speed of all the turbines of the wind farm (28 neurons in the input layer of the neural network).
- -
- Random turbine: the neural network is fed with the wind direction and wind speed of a random turbine (1 neuron in the input layer of the neural network).
- -
- Cluster centroid: the neural network is fed with the wind direction and wind speed of the centroid turbines of the clusters (8 neurons, depending on the cluster analysis, in the input layer of the neural network)
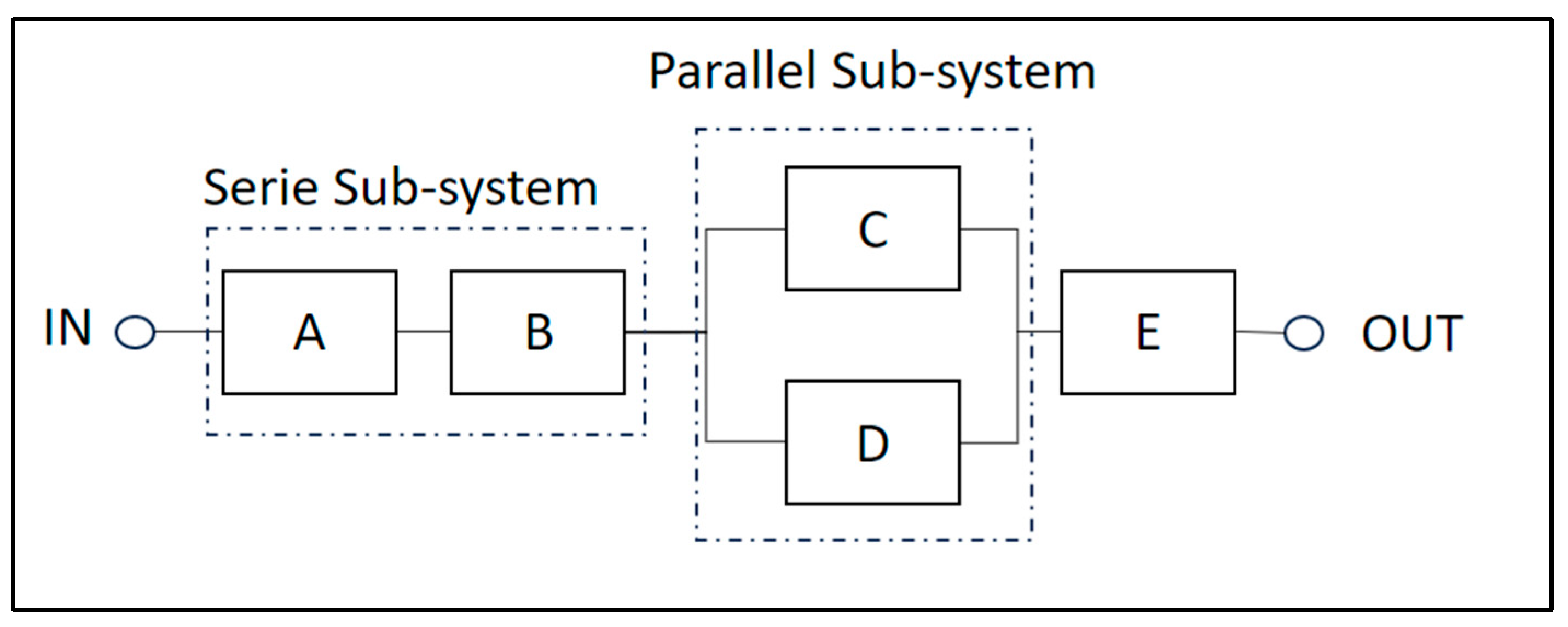
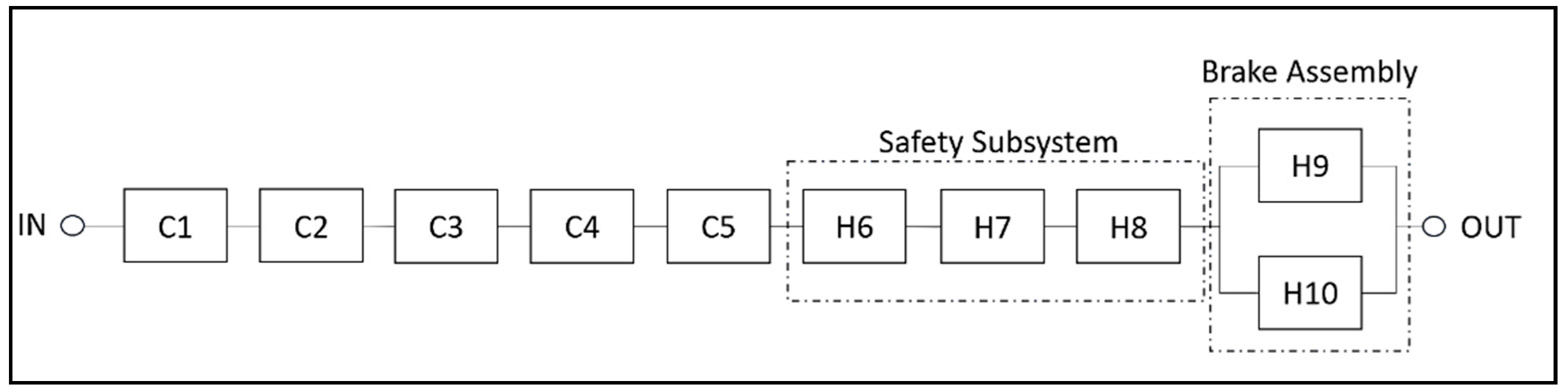
4.4. Hybrid Reliability Block-Diagram-Simulation Model of the Wind Turbine Generator
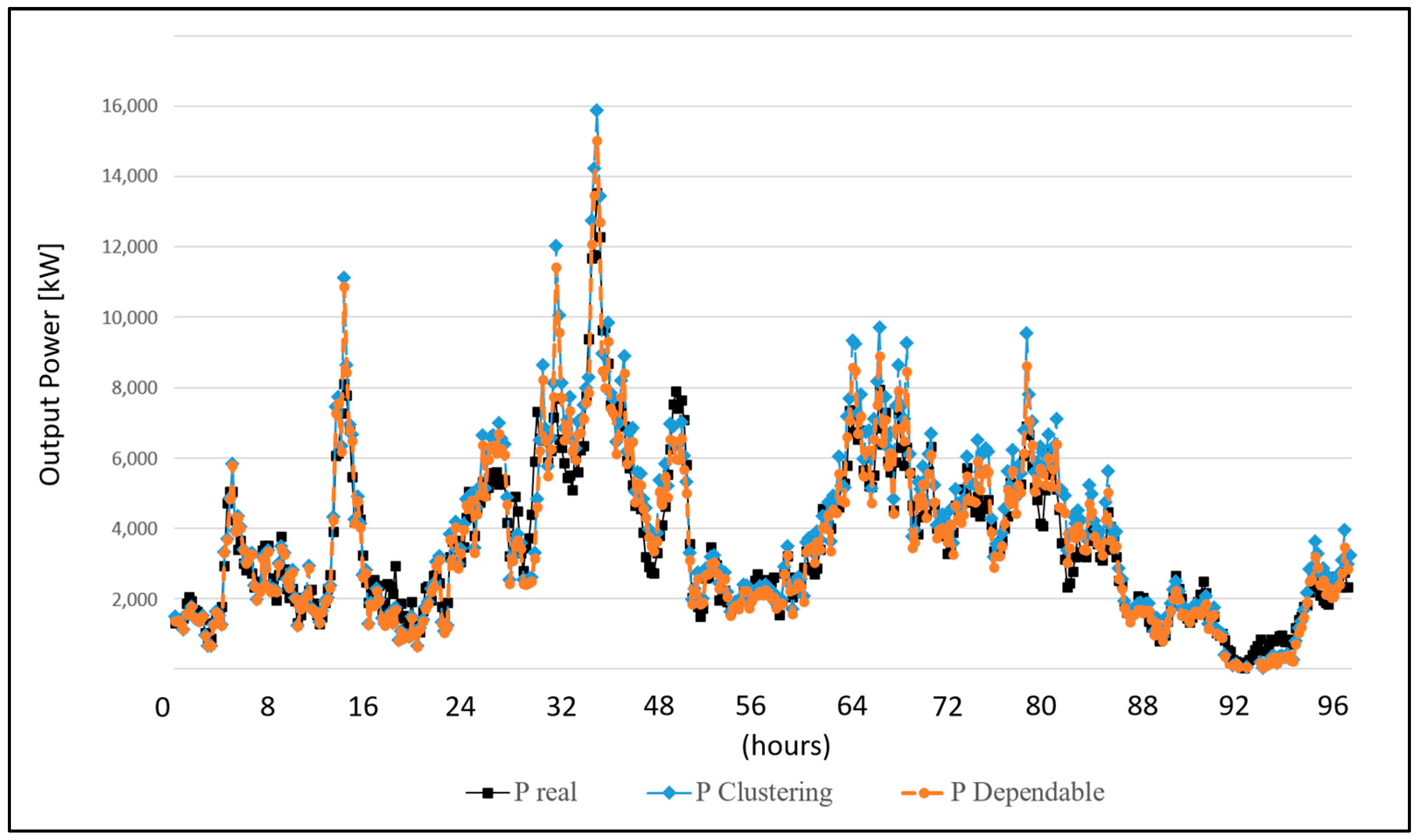
4.5. Results Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Acronym | Definition |
| ANN | Artificial Neural Network |
| IPCC | Intergovernmental Panel for Climate Change |
| GWEC | Global Wind Energy Council |
| MLP | Multilayer Perceptron |
| AI | Artificial Intelligence |
| ANNs | Artificial Neural Networks |
| SVMs | Support Vector Machines |
| SVR | Support Vector Regression |
| GPR | Gaussian Process Regression |
| BS | Bootstrap |
| PIs | Prediction Intervals |
| NWP | Numerical Weather Prediction |
| ARIMA | Autoregressive Integrated Moving Average |
| NARX | Non-Linear Autoregressive Network with exogenous inputs |
| VMD | Variational Mode Decomposition |
| MRMR | Maximum Relevance and Minimum Redundancy Algorithm |
| LSTM | Long Short-Term Memory Neural Network |
| FA | Firefly Algorithm |
| kNN | K-Nearest Neighbor |
| GP | Gaussian Process |
| VMD | Variational Mode Decomposition |
| TCN | Temporal Convolutional Network Model |
| SIA | Seasonal Index Adjustment |
| ERNN | Elman Recurrent Neural Network |
| FMOGMDRPs | Flexibility-based Multi-Objective Generation Maintenance scheduling associated with Demand Response Programs |
| PSO | Particle Swarm Optimization |
| GIS | Geographic Information System |
| SCADA | Supervisory Control And Data Acquisition |
| DCS | Distributed Control System |
| RBDs | Reliability Block Diagrams |
| HBRD | Hybrid Reliability Block Diagram |
| SHyFTOO | Stochastic Hybrid Fault Tree Object Oriented |
| NMSE | normalized mean squared error |
| Probability density function |
References
- Horowitz, C.A. Paris Agreement. Int. Leg. Mater. 2016, 55, 740–755. [Google Scholar] [CrossRef]
- EU Commission. Regulation (EU) 2021/1119 of the European Parliament and of the Council of 30 June 2021 Establishing the Framework for Achieving Climate Neutrality; The European Parliament and the Council of The European Union: Brussels, Belgium, 2021. [Google Scholar]
- European Commission. REPowerEU: Joint European Action for More Affordable, Secure and Sustainable Energy. Communication from the Commission to the European Parliament, the European Council, the Council, the European Economic and Social Committee and the Committee of the Regions. Strasbourg, 8 March 2022, COM (2022) 108 Final. 2022. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=celex:52022DC0108 (accessed on 11 December 2023).
- European Commission. Communication from the Commission to the European Parliament, the European Council, the European Economic and Social Committee and the Committee of the Regions. The European Green Deal. Brussels, 11 December 2019, COM (2019) 640 Final. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=COM%3A2019%3A640%3AFIN (accessed on 11 December 2023).
- GWEC–Global Wind Energy Council. GWEC–Global Wind Report 2023. Available online: https://gwec.net/globalwindreport2023/ (accessed on 19 March 2024).
- Cacciuttolo, C.; Cano, D.; Guardia, X.; Villicaña, E. Renewable Energy from Wind Farm Power Plants in Peru: Recent Advances, Challenges, and Future Perspectives. Sustainability 2024, 16, 1589. [Google Scholar] [CrossRef]
- Fan, Q.; Wang, X.; Yuan, J.; Liu, X.; Hu, H.; Lin, P. A Review of the Development of Key Technologies for Offshore Wind Power in China. J. Mar. Sci. Eng. 2022, 10, 929. [Google Scholar] [CrossRef]
- Yan, J.; Liu, Y.; Han, S.; Wang, Y.; Feng, S. Reviews on Uncertainty Analysis of Wind Power Forecasting. Renew. Sustain. Energy Rev. 2015, 52, 1322–1330. [Google Scholar] [CrossRef]
- Hodge, B.M.; Milligan, M. Wind Power Forecasting Error Distributions over Multiple Timescales. In Proceedings of the IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011. [Google Scholar]
- Chang, G.W.; Lu, H.J.; Chang, Y.R.; Lee, Y.D. An Improved Neural Network-Based Approach for Short-Term Wind Speed and Power Forecast. Renew. Energy 2017, 105, 301–311. [Google Scholar] [CrossRef]
- Wang, J.; Qin, S.; Zhou, Q.; Jiang, H. Medium-Term Wind Speeds Forecasting Utilizing Hybrid Models for Three Different Sites in Xinjiang, China. Renew. Energy 2015, 76, 91–101. [Google Scholar] [CrossRef]
- Kirchner-Bossi, N.; García-Herrera, R.; Prieto, L.; Trigo, R.M. A Long-Term Perspective of Wind Power Output Variability. Int. J. Climatol. 2015, 35, 2635–2646. [Google Scholar] [CrossRef]
- Landberg, L. A mathematical look at a physical power prediction model. Wind Energy Int. J. Prog. Appl. Wind Power Convers. Technol. 1998, 1, 23–28. [Google Scholar] [CrossRef]
- Landberg, L.; Myllerup, L.; Rathmann, O.; Petersen, E.L.; Jørgensen, B.H.; Badger, J.; Mortensen, N.G. Wind Resource Estimation–An Overview. Wind Energy 2003, 6, 261–271. [Google Scholar] [CrossRef]
- Kavasseri, R.G.; Seetharaman, K. Day-Ahead Wind Speed Forecasting Using f-ARIMA Models. Renew. Energy 2009, 34, 1388–1393. [Google Scholar] [CrossRef]
- Carolin Mabel, M.; Fernandez, E. Analysis of Wind Power Generation and Prediction Using ANN: A Case Study. Renew. Energy 2008, 33, 986–992. [Google Scholar] [CrossRef]
- Giebel, G.; Brownsword, R.; Kariniotakis, G.; Denhard, M.; Draxl, C. The State of the Art in Short-Term Prediction of Wind Power, A Literature Overview; ANEMOS.plus. 2011. Available online: https://orbit.dtu.dk/en/publications/the-state-of-the-art-in-short-term-prediction-of-wind-power-a-lit (accessed on 7 March 2024).
- Hao, Y.; Wang, Q.; Ma, T.; Du, J.; Cao, J. Energy Allocation and Task Scheduling in Edge Devices Based on Forecast Solar Energy with Meteorological Information. J. Parallel Distrib. Comput. 2023, 177, 171–181. [Google Scholar] [CrossRef]
- Sharifi, V.; Abdollahi, A.; Rashidinejad, M. Flexibility-Based Generation Maintenance Scheduling in Presence of Uncertain Wind Power Plants Forecasted by Deep Learning Considering Demand Response Programs Portfolio. Int. J. Electr. Power Energy Syst. 2022, 141, 108225. [Google Scholar] [CrossRef]
- Ying, C.; Wang, W.; Yu, J.; Li, Q.; Yu, D.; Liu, J. Deep Learning for Renewable Energy Forecasting: A Taxonomy, and Systematic Literature Review. J. Clean. Prod. 2023, 384, 135414. [Google Scholar] [CrossRef]
- Notton, G.; Nivet, M.L.; Voyant, C.; Paoli, C.; Darras, C.; Motte, F.; Fouilloy, A. Intermittent and Stochastic Character of Renewable Energy Sources: Consequences, Cost of Intermittence and Benefit of Forecasting. Renew. Sustain. Energy Rev. 2018, 87, 96–105. [Google Scholar] [CrossRef]
- Way, R.; Ives, M.C.; Mealy, P.; Farmer, J.D. Empirically Grounded Technology Forecasts and the Energy Transition. Joule 2022, 6, 2057–2082. [Google Scholar] [CrossRef]
- Lee, J.C.Y.; Jason Fields, M. An Overview of Wind-Energy-Production Prediction Bias, Losses, and Uncertainties. Wind Energy Sci. 2021, 6, 311–365. [Google Scholar] [CrossRef]
- Costa, A.; Crespo, A.; Navarro, J.; Lizcano, G.; Madsen, H.; Feitosa, E. A Review on the Young History of the Wind Power Short-Term Prediction. Renew. Sustain. Energy Rev. 2008, 12, 1725–1744. [Google Scholar] [CrossRef]
- Ernst, B.; Reyer, F.; Vanzetta, J. Wind Power and Photovoltaic Prediction Tools for Balancing and Grid Operation. In Proceedings of the 2009 CIGRE/IEEE PES Joint Symposium: Integration of Wide-Scale Renewable Resources into the Power Delivery System, Calgary, AB, Canada, 29–31 July 2009. [Google Scholar]
- Soman, S.S.; Zareipour, H.; Malik, O.; Mandal, P. A Review of Wind Power and Wind Speed Forecasting Methods with Different Time Horizons. In Proceedings of the North American Power Symposium 2010, NAPS 2010, Arlington, TX, USA, 26–28 September 2010. [Google Scholar]
- Li, C.; Lin, S.; Xu, F.; Liu, D.; Liu, J. Short-Term Wind Power Prediction Based on Data Mining Technology and Improved Support Vector Machine Method: A Case Study in Northwest China. J. Clean. Prod. 2018, 205, 909–922. [Google Scholar] [CrossRef]
- Lange, M.; Focken, U. Physical Approach to Short-Term Wind Power Prediction; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Najeebullah; Zameer, A.; Khan, A.; Javed, S.G. Machine Learning Based Short Term Wind Power Prediction Using a Hybrid Learning Model. Comput. Electr. Eng. 2015, 45, 122–133. [Google Scholar] [CrossRef]
- Li, H.; Jiang, Z.; Shi, Z.; Han, Y.; Yu, C.; Mi, X. Wind-Speed Prediction Model Based on Variational Mode Decomposition, Temporal Convolutional Network, and Sequential Triplet Loss. Sustain. Energy Technol. Assess. 2022, 52, 101980. [Google Scholar] [CrossRef]
- Famoso, F.; Brusca, S.; D’Urso, D.; Galvagno, A.; Chiacchio, F. A Novel Hybrid Model for the Estimation of Energy Conversion in a Wind Farm Combining Wake Effects and Stochastic Dependability. Appl. Energy 2020, 280, 115967. [Google Scholar] [CrossRef]
- Ioakimidis, C.S.; Genikomsakis, K.N.; Dallas, P.I.; Lopez, S. Short-Term Wind Speed Forecasting Model Based on ANN with Statistical Feature Parameters. In Proceedings of the IECON 2015–41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015. [Google Scholar]
- Rahman, M.M.; Shakeri, M.; Tiong, S.K.; Khatun, F.; Amin, N.; Pasupuleti, J.; Hasan, M.K. Prospective Methodologies in Hybrid Renewable Energy Systems for Energy Prediction Using Artificial Neural Networks. Sustainability 2021, 13, 2393. [Google Scholar] [CrossRef]
- Tascikaraoglu, A.; Uzunoglu, M. A Review of Combined Approaches for Prediction of Short-Term Wind Speed and Power. Renew. Sustain. Energy Rev. 2014, 34, 243–254. [Google Scholar] [CrossRef]
- Thordarson, F.Ö.; Madsen, H.; Nielsen, H.A.; Pinson, P. Conditional Weighted Combination of Wind Power Forecasts. Wind Energy 2010, 13, 751–763. [Google Scholar] [CrossRef]
- Foley, A.M.; Leahy, P.G.; Marvuglia, A.; McKeogh, E.J. Current Methods and Advances in Forecasting of Wind Power Generation. Renew. Energy 2012, 37, 1–8. [Google Scholar] [CrossRef]
- Ramasamy, P.; Chandel, S.S.; Yadav, A.K. Wind Speed Prediction in the Mountainous Region of India Using an Artificial Neural Network Model. Renew. Energy 2015, 80, 338–347. [Google Scholar] [CrossRef]
- Sharifzadeh, M.; Sikinioti-Lock, A.; Shah, N. Machine-Learning Methods for Integrated Renewable Power Generation: A Comparative Study of Artificial Neural Networks, Support Vector Regression, and Gaussian Process Regression. Renew. Sustain. Energy Rev. 2019, 108, 513–538. [Google Scholar] [CrossRef]
- Jursa, R.; Rohrig, K. Short-Term Wind Power Forecasting Using Evolutionary Algorithms for the Automated Specification of Artificial Intelligence Models. Int. J. Forecast. 2008, 24, 694–709. [Google Scholar] [CrossRef]
- Di Piazza, A.; Di Piazza, M.C.; La Tona, G.; Luna, M. An Artificial Neural Network-Based Forecasting Model of Energy-Related Time Series for Electrical Grid Management. Math. Comput. Simul. 2021, 184, 294–305. [Google Scholar] [CrossRef]
- Qin, G.; Yan, Q.; Zhu, J.; Xu, C.; Kammen, D.M. Day-Ahead Wind Power Forecasting Based on Wind Load Data Using Hybrid Optimization Algorithm. Sustainability 2021, 13, 1164. [Google Scholar] [CrossRef]
- Li, L.L.; Zhao, X.; Tseng, M.L.; Tan, R.R. Short-Term Wind Power Forecasting Based on Support Vector Machine with Improved Dragonfly Algorithm. J. Clean. Prod. 2020, 242, 118447. [Google Scholar] [CrossRef]
- Yesilbudak, M.; Sagiroglu, S.; Colak, I. A Novel Implementation of KNN Classifier Based on Multi-Tupled Meteorological Input Data for Wind Power Prediction. Energy Convers. Manag. 2017, 135, 434–444. [Google Scholar] [CrossRef]
- Treiber, N.A.; Kramer, O. Evolutionary Feature Weighting for Wind Power Prediction with Nearest Neighbor Regression. In Proceedings of the 2015 IEEE Congress on Evolutionary Computation, CEC 2015-Proceedings, Sendai, Japan, 25–28 May 2015. [Google Scholar]
- Kramer, O.; Gieseke, F. Short-Term Wind Energy Forecasting Using Support Vector Regression. In Proceedings of the Soft Computing Models in Industrial and Environmental Applications, 6th International Conference SOCO 2011, Salamanca, Spain, 6–8 April 2011; Advances in Intelligent and Soft Computing. Springer: Berlin/Heidelberg, Germany, 2011; Volume 87. [Google Scholar]
- Chen, N.; Qian, Z.; Nabney, I.T.; Meng, X. Wind Power Forecasts Using Gaussian Processes and Numerical Weather Prediction. IEEE Trans. Power Syst. 2014, 29, 656–665. [Google Scholar] [CrossRef]
- D’Urso, D.; Chiacchio, F.; Cavalieri, S.; Gambadoro, S.; Khodayee, S.M. Predictive Maintenance of Standalone Steel Industrial Components Powered by a Dynamic Reliability Digital Twin Model with Artificial Intelligence. Reliab. Eng. Syst. Saf. 2024, 243, 109859. [Google Scholar] [CrossRef]
- Sánchez, I. Short-Term Prediction of Wind Energy Production. Int. J. Forecast. 2006, 22, 43–56. [Google Scholar] [CrossRef]
- Al-Dahidi, S.; Baraldi, P.; Zio, E.; Lorenzo, M. Bootstrapped Ensemble of Artificial Neural Networks Technique for Quantifying Uncertainty in Prediction of Wind Energy Production. Sustainability 2021, 13, 6417. [Google Scholar] [CrossRef]
- Cassola, F.; Burlando, M. Wind Speed and Wind Energy Forecast through Kalman Filtering of Numerical Weather Prediction Model Output. Appl. Energy 2012, 99, 154–166. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, D.; Tang, Y. Clustered Hybrid Wind Power Prediction Model Based on ARMA, PSO-SVM, and Clustering Methods. IEEE Access 2020, 8, 17071–17079. [Google Scholar] [CrossRef]
- Cox, J. Impact of Intermittency: How Wind Variability Could Change the Shape of the British and Irish Electricity Markets; Poyry Energy (Oxford) Ltd.: Oxford, UK, 2009. [Google Scholar]
- Sinden, G. Characteristics of the UK Wind Resource: Long-Term Patterns and Relationship to Electricity Demand. Energy Policy 2007, 35, 112–127. [Google Scholar] [CrossRef]
- Kubik, M.L.; Coker, P.J.; Barlow, J.F.; Hunt, C. A Study into the Accuracy of Using Meteorological Wind Data to Estimate Turbine Generation Output. Renew. Energy 2013, 51, 153–158. [Google Scholar] [CrossRef]
- Wang, P.; Li, Y.; Zhang, G. Probabilistic Power Curve Estimation Based on Meteorological Factors and Density LSTM. Energy 2023, 269, 126768. [Google Scholar] [CrossRef]
- Berghout, T.; Benbouzid, M.; Amirat, Y. Interaction between Machine Learning and Maintenance Planning for Wind Energy Systems: A Theoretical Review and Analysis. In Proceedings of the 2023 IEEE 2nd Industrial Electronics Society Annual On-Line Conference (ONCON), Online Conference, 8–10 December 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar]
- Brusca, S.; Famoso, F.; Lanzafame, R.; Galvagno, A.; Mauro, S.; Messina, M. Wind Farm Power Forecasting: New Algorithms with Simplified Mathematical Structure. AIP Conf. Proc. 2019, 2191, 020028. [Google Scholar]
- Spinato, F.; Tavner, P.J.; Van Bussel, G.J.W.; Koutoulakos, E. Reliability of Wind Turbine Subassemblies. IET Renew. Power Gener. 2009, 3, 387–401. [Google Scholar] [CrossRef]
- Wang, S.; Tomovic, M.; Liu, H. Comprehensive Reliability Design of Aircraft Hydraulic System. In Commercial Aircraft Hydraulic Systems; Shanghai Jiao Tong University Press: Shanghai, China, 2016. [Google Scholar]
- Brusca, S.; Lanzafame, R.; Famoso, F.; Galvagno, A.; Messina, M.; Mauro, S.; Prestipino, M. On the Wind Turbine Wake Mathematical Modelling. Energy Procedia 2018, 148, 202–209. [Google Scholar] [CrossRef]
- Faulstich, S.; Hahn, B.; Tavner, P.J. Wind Turbine Downtime and Its Importance for Offshore Deployment. Wind Energy 2011, 14, 327–337. [Google Scholar] [CrossRef]
- Qiao, W.; Lu, D. A Survey on Wind Turbine Condition Monitoring and Fault Diagnosis—Part I: Components and Subsystems. IEEE Trans. Ind. Electron. 2015, 62, 6536–6545. [Google Scholar] [CrossRef]
- Pfaffel, S.; Faulstich, S.; Rohrig, K. Performance and Reliability of Wind Turbines: A Review. Energies 2017, 10, 1904. [Google Scholar] [CrossRef]
- Khodayee, S.M.; Oliveri, L.; Aizpurua, J.I.; D’Urso, D.; Chiacchio, F. Reliability Simulation of a Multi-State Wind Turbine Generator Using SHyFTOO. In Proceedings of the 21st International Conference on Modeling and Applied Simulation, MAS 2022, Rome, Italy, 19–21 September 2022. [Google Scholar]
- Su, C.; Fu, Y.Q. Reliability Assessment for Wind Turbines Considering the Influence of Wind Speed Using Bayesian Network. Eksploat. Niezawodn. 2014, 16, 1–8. [Google Scholar]
- Bilendo, F.; Meyer, A.; Badihi, H.; Lu, N.; Cambron, P.; Jiang, B. Applications and Modeling Techniques of Wind Turbine Power Curve for Wind Farms—A Review. Energies 2023, 16, 180. [Google Scholar] [CrossRef]
- Chiacchio, F.; Aizpurua, J.I.; Compagno, L.; D’Urso, D. SHyFTOO, an Object-Oriented Monte Carlo Simulation Library for the Modeling of Stochastic Hybrid Fault Tree Automaton. Expert Syst. Appl. 2020, 146, 113139. [Google Scholar] [CrossRef]




| Approach | Model Used | Reference Number |
|---|---|---|
| Data-Driven | Autoregressive Integrated Moving Mean Models (ARIMA) | [15] |
| Artificial neural networks (ANNs) | [32,34,37,49] | |
| Artificial neural networks (ANNs), Support Vector Regression (SVR), Gaussian Process Regression (GPR) | [38] | |
| Evolutionary Optimization Algorithms, Neural Networks, Nearest Neighbor Search | [39] | |
| Non-Linear Autoregressive Network with Exogenous Inputs (NARX) ANN | [40] | |
| Variational Mode Decomposition (VMD), Maximum Relevance and Minimum Redundancy Algorithm (MRMR), Long Short-Term Memory Neural Network (LSTM), Firefly Algorithm (FA) | [41] | |
| Support Vector Machines (SVMs) | [42] | |
| K-Nearest Neighbor Classifier (kNN) | [43,44] | |
| Support Vector Regression (SVR) | [45] | |
| Gaussian Process (GP), Numerical Weather Prediction Model (NWP) | [46] | |
| Statistical Forecasting System | [48] | |
| Kalman Filters | [50] | |
| Model-Based | Atmospheric Fluid Dynamics | [13,28] |
| Variational Mode Decomposition (VMD), Temporal Convolutional Network Model (TCN) | [30] | |
| Jensen wake mathematical theory | [31] | |
| Hybrid | Support Vector Regression (SVR), Seasonal Index Adjustment (SIA) and Elman Recurrent Neural Network (ERNN) | [11] |
| Non-dominated Sorting Genetic Algorithms | [18] | |
| Flexibility-based Multi-Objective Generation Maintenance scheduling associated with Demand Response Programs (FMOGMDRPs) | [19] | |
| Support Vector Machine (SVM) and Data Mining | [27] | |
| Machine-Learning based Short-Term Wind Power Prediction and Support Vector Regression | [29] | |
| Conditional Weighted Combination Method | [35] | |
| Dynamic Reliability Digital Twin | [47] | |
| AutoRegressive Moving Average (ARMA), Support Vector Machine (SVM), Particle Swarm Optimization (PSO) | [51] |
| Feature | Site |
|---|---|
| Position | 37°58′32″ N, 15°07′00″ E |
| N° Turbines | 28 |
| Turbine quote | 732–1149 m |
| Turbine Height | 52–58 m |
| N° Blades | 3 |
| Turbine Pout | 850 kW |
| Turbine ID | Mean Pout [kW] | Max Pout [kW] | Dev.std Pout [kW] | Mean Wind Speed [m/s] | Max Wind Speed [m/s] | Dev.std Wind Speed [m/s] |
|---|---|---|---|---|---|---|
| 206 | 163.75 | 850 | 199.61 | 5.67 | 23.71 | 3.27 |
| 216 | 75.89 | 828.73 | 146.39 | 4.07 | 16.21 | 2.38 |
| 214 | 351.51 | 843.11 | 194.18 | 7.71 | 21.45 | 3.48 |
| 309 | 144.21 | 848.55 | 198.83 | 5.85 | 20.35 | 3.53 |
| 213 | 170.69 | 849.81 | 206.23 | 5.57 | 27.76 | 3.30 |
| 308 | 216.21 | 849.99 | 229.90 | 6.51 | 25.17 | 3.59 |
| 207 | 163.88 | 848.45 | 204.53 | 5.21 | 33.81 | 3.47 |
| 317 | 111.42 | 849.41 | 165.92 | 4.85 | 17.86 | 2.54 |
| Cluster Silhouette Results | |||||||
|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| Coef. Silh. | 0.423 | 0.445 | 0.467 | 0.472 | 0.485 | 0.495 | 0.511 |
| Clusters | Turbine ID | Centroid Turbine ID |
|---|---|---|
| Cluster 1 | 206, 226 | 206 |
| Cluster 2 | 216, 217, 220, 222, 223 | 216 |
| Cluster 3 | 214, 221 | 214 |
| Cluster 4 | 309, 310 | 309 |
| Cluster 5 | 210, 213, 318, 219, 313 | 213 |
| Cluster 6 | 308, 311, 314, | 308 |
| Cluster 7 | 207, 224, 225, 312, 315,318 | 207 |
| Cluster 8 | 316, 317 | 317 |
| Month | NMSE_All Turbines | NMSE_Clustering | NMSE_Random Turbine |
|---|---|---|---|
| January | 0.01945 | 0.69648 | 6.81375 |
| February | 0.02126 | 0.65839 | 6.66039 |
| March | 0.01935 | 0.65967 | 6.49241 |
| April | 0.02075 | 0.76712 | 6.28689 |
| May | 0.02303 | 0.66172 | 6.82694 |
| June | 0.02171 | 0.75546 | 6.12375 |
| July | 0.02095 | 0.68517 | 6.64920 |
| August | 0.02017 | 0.76030 | 6.68725 |
| September | 0.02213 | 0.75023 | 6.45569 |
| October | 0.02265 | 0.71657 | 6.17180 |
| November | 0.02321 | 0.77436 | 6.37107 |
| December | 0.02223 | 0.72278 | 6.33632 |
| Component ID | Description | PDF (0 < wspd ≤ 20) | PDF (wspd > 20) |
|---|---|---|---|
| C1 | Generator | Weibull (76,000; 1.2) | Weibull (76,000; 1.2) |
| C2 | Gearbox | Weibull (123,000; 1.05) | Weibull (123,000; 1.05) |
| C3 | Blade | Normal (42,000; 663) | Normal (42,000; 663) |
| C4 | Electrical System | Weibull (35,000; 1.5) | Weibull (35,000; 1.5) |
| C5 | Converter System | Exponential (1/45,000) | Exponential (1/45,000) |
| H6 | Pitch Assembly | Normal (84,534; 506) | Normal (14,089; 506) |
| H7 | Yaw Assembly | Exponential (1/65,000) | Exponential (1/8125) |
| H8 | Hydraulic Assembly | Weibull (66,000; 1.3) | Weibull (33,000; 1.3) |
| H9 | Air Brake | Exponential (1/100,000) | Exponential (9/500,000) |
| H10 | Mechanical Brake | Exponential (1/120,000) | Exponential (1/30,000) |
| Component ID | Description | PDF (0 < wspd ≤ 20) |
|---|---|---|
| C1 | Generator | Exponential (1/120,000) |
| C2 | Gearbox | Exponential (1/120,000) |
| C3 | Blade | Exponential (1/120,000) |
| C4 | Electrical System | Exponential (1/120,000) |
| C5 | Converter System | Exponential (1/45,000) |
| H6 | Pitch Assembly | Exponential (1/120,000) |
| H7 | Yaw Assembly | Exponential (1/120,000) |
| H8 | Hydraulic Assembly | Exponential (1/120,000) |
| H9 | Air Brake | Exponential (1/100,000) |
| H10 | Mechanical Brake | Exponential (1/120,000) |
| Month | NMSE_Dependable | NMSE_Clustering |
|---|---|---|
| January | 0.53027 | 0.69648 |
| February | 0.54553 | 0.65839 |
| March | 0.51623 | 0.65967 |
| April | 0.53606 | 0.76712 |
| May | 0.51203 | 0.66172 |
| June | 0.53197 | 0.75546 |
| July | 0.53421 | 0.68517 |
| August | 0.54446 | 0.76030 |
| September | 0.53152 | 0.75023 |
| October | 0.52361 | 0.71657 |
| November | 0.53811 | 0.77436 |
| December | 0.53472 | 0.72278 |
| Month | NMSE_Dependable | NMSE_Clustering |
|---|---|---|
| January | 0.00075 | 0.00344 |
| February | 0.00078 | 0.00370 |
| March | 0.00071 | 0.00366 |
| April | 0.00074 | 0.00366 |
| May | 0.00077 | 0.00367 |
| June | 0.00077 | 0.00367 |
| July | 0.00077 | 0.00366 |
| August | 0.00071 | 0.00364 |
| September | 0.00075 | 0.00362 |
| October | 0.00074 | 0.00360 |
| November | 0.00078 | 0.00357 |
| December | 0.00078 | 0.00355 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Famoso, F.; Oliveri, L.M.; Brusca, S.; Chiacchio, F. A Dependability Neural Network Approach for Short-Term Production Estimation of a Wind Power Plant. Energies 2024, 17, 1627. https://doi.org/10.3390/en17071627
Famoso F, Oliveri LM, Brusca S, Chiacchio F. A Dependability Neural Network Approach for Short-Term Production Estimation of a Wind Power Plant. Energies. 2024; 17(7):1627. https://doi.org/10.3390/en17071627
Chicago/Turabian StyleFamoso, Fabio, Ludovica Maria Oliveri, Sebastian Brusca, and Ferdinando Chiacchio. 2024. "A Dependability Neural Network Approach for Short-Term Production Estimation of a Wind Power Plant" Energies 17, no. 7: 1627. https://doi.org/10.3390/en17071627
APA StyleFamoso, F., Oliveri, L. M., Brusca, S., & Chiacchio, F. (2024). A Dependability Neural Network Approach for Short-Term Production Estimation of a Wind Power Plant. Energies, 17(7), 1627. https://doi.org/10.3390/en17071627







