Fatigue Life Estimation of Critical Components in a Motor-Energized Spring Operating Mechanism Based on Theory of Reliability

Abstract

High-voltage switchgear is a key control and protection unit in power systems. The reliable operation of the operating mechanism is essential for the reliable opening and closing of the switchgear. This is a vital guarantee for the safety and stability of the power systems. The spring operating mechanism is a commonly used actuator for circuit breakers at 12–252 kV. However, a reliability estimation method that is convenient, practical and accurate is still lacking. The aim of this paper is to explore a reliability estimation method based on a stress–strength interference reliability theory and a fatigue life theory. The changing rules of the reliability of the main axis, and the closing pawl and opening pawl in the spring operating mechanism during operations, are achieved. The accuracy of the calculated reliability based on theories of stress–strength interference and fatigue life is verified by adopting a test data statistical reliability model based on Weibull distribution. The results show that the reliability estimation method based on stress–strength interference and fatigue life theories has a high degree of confidence. The maximum tolerance is 0.024. The study would help in providing a useful reference for the optimization and durability estimation of a spring operating mechanism and its key components in high-voltage circuit breakers.

1. Introduction

With the rapid development of new power systems under the double carbon target, and the large-scale development of new equipment of “high proportion of new energy” power generation and “high proportion of power electronics” energy consumption, how to deal with the relationship between clean energy development and system security, and guarantee the reliability of power supply and operation, is the key to the future development of power system and electrical equipment technological innovation. The key to the future development of power systems and electrical technology innovation is [1] to ensure the reliability of power supply and the safety and stability of operation. As one of the most important control and protection units of a power system, the reliable opening and closing of high-voltage switchgear directly determines the safe and stable operation of the system, while the operating mechanism is the core component of high-voltage switchgear designed to perform breaking and closing operations [2,3]. Improving the reliability and failure mechanisms is essential to ensure the safe and stable operation and reliable power supply of future power systems, mainly of new energy.

The improvement of the reliability of high-voltage circuit breakers and the in-depth analysis of failure mechanisms have been difficult issues for domestic and foreign power companies and users, switchgear-manufacturing companies, universities, and other research institutions [4,5]. The results of the three reliability surveys conducted by the SC A3 Working Group of the International Council on Large Electric Systems (CIGRE) on switchgear operating in the global grid show that circuit breaker failures caused by mechanical failures, such as the malfunction and refusal to operate of the operating mechanism, account for more than 70% of the total failure rate [6].

Table 1. Common failure modes and their probable reasons in the spring operating mechanism of a high-voltage circuit breaker.

Category		Anomalies	Possible Causes
Refuse to move	Refuse to cooperate	Iron core not activated	No voltage at coil terminals. (1) Poor contact of the three circuits, loose connection screws; (2) fuse; (3) auxiliary switch contact poor or not cut off. 2. There is voltage at the coil terminals. (1) Coil broken or burned; (2) core jammed.
		The iron core has been started, the four-link rod has no action	The coil terminal voltage is too low. The movement of the iron core is obstructed. Deformation of the iron core bumpers, insufficient travel. Four-link deformation, the force over the “dead” distance is too large. Closing latch snap into the traction bar depth is too large. The buckling surface is not hard enough to deform, friction, “bite”.
		Four-link action, traction bar not released	Traction bar over the “dead” distance is too small or not out of the “dead zone”. The mechanism or body has serious mechanical jamming. The four-link intermediate shaft over the “dead point” distance is too small. Torsional deformation of the four-link.
	Refusal of points	Iron core not activated	No voltage at coil terminals. (1) Fuse melted; (2) secondary circuit connection is loose, poor contact. 2. There is voltage at the coil terminals. (1) Coil burned or broken wire, especially if the lead is easy to break; (2) the core is stuck.
		The iron core has been started, the locking ditch or split gate of the four connecting rods is not released	The coil terminal voltage is too low. Small core clearance, insufficient impulse or core movement is blocked.
		Locking groove or four-link action, but the mechanism’s linked plate system does not move	Severe mechanical jamming of the mechanism or the body.
Misfiring	Automatic closing after energy storage		The four connecting rods are not reset, and the reversion spring is deformed The four connecting rods’ force over the “dead point” distance is too small Locking bracket support bolts are not tightened or are loose. Buckle to a lower depth or buckle surface deformation Motor power did not switch in time Traction bar over the “dead” distance is too large, resulting in too much impact force L-shaped latch deformation can not be locked
	Automatic separation without signal		The secondary circuit has a mixed line, two points of grounding in the branch circuit The minimum operating voltage of the breaking solenoid is too low The relay contact is closed for some reason The depth of the locking hook is too little or the middle shaft of the four connecting rods is too small, or the end of the locking hook is deformed and not securely fastened
	Divided when combined		The locking hooks or the four connecting rods are not reset The depth of the locking hook is too little, or the middle shaft of the four connecting rods of the locking gate is too small, or the end surface of the locking hook is seriously deformed, and the locking is not stable The reversion gap is adjusted too much when the locking hook is not under force Closing of the gate while the circuit has electricity, the secondary circuit has a mixed line

shows the results of the State Grid Corporation’s research on the failure modes of high-voltage circuit breakers in grid operation in China. It can be seen that the main relevant components causing circuit breaker failure are the operating mechanism part, the current-carrying part, the electrical control part and the auxiliary circuit part, and the operating mechanism plays a larger role in the whole mechanical system of the circuit breaker. Xi’an High Voltage Apparatus Research Institute Co., Ltd (Xi’an, China) has conducted a comprehensive study on the reliability evaluation index of power equipment, starting in 2012, and first developed a high-voltage switchgear reliability database system in 2014 [7,8]. In addition, Ref. [9] analyzed the reliability of vacuum circuit breakers under various failure modes. Ref. [10] proposed a fuzzy probabilistic hybrid reliability based on the operation of high-voltage circuit breaker maintenance technology. Ref. [11] discussed reliability prediction, determination and control methods of vacuum circuit breakers from the perspective of their manufacturers and users. Ref. [12] investigated the tolerance fit of the dimensional chain of the spring mechanism and closing release components from the perspective of reliable operation. Ref. [13] used the Fault Tree to analyze the basic components that caused the circuit breaker to fail, based on the topology of a hybrid DC circuit breaker, and the Markov model was here introduced into the reliability modeling of a hybrid DC circuit breaker to calculate the steady-state availability, failure rate and mean time between failures. Ref. [14] used the Weibull distribution to analyze the reliability test data of vacuum circuit breakers, obtained a reliability evaluation model of a vacuum circuit breaker, and analyzed the reliability of a vacuum circuit breaker with a permanent magnet actuator. Refs. [15,16] analyzed and discussed a reliability model of a high-voltage circuit breaker, and used stress–strength interferometry, the safety factor method, etc., to carry out the reliability design of key components. Ref. [17] analyzed the current status of reliability research on the spring actuator mechanism of high-voltage circuit breakers, and proposed the importance of reliability optimization and dynamic life assessment for high-voltage circuit breakers based on reliability physics and failure physics.

For high-voltage circuit breakers, when the circuit breaker is put into operation, with the increase in the number of openings, the strength of the mechanical parts in the operating mechanism will gradually reduce, and the mechanical reliability decreases. Then, the reliability of the circuit breaker will be a function of the number of operations, that is, the reliability function. Component failure is one of the main causes of failure of the entire mechanism, and includes broken springs, loose or worn connecting bolts, worn gears, etc., which can lead to a reduction in the performance of the entire mechanism or even complete failure. Therefore, studies of the reliability and failures of spring-operated mechanisms must focus on the reliability and failure mechanisms of each component. In engineering, if the approximate reliability of the main mechanical parts of the circuit breaker under different operation times can be easily and quickly given, this will impart important guidance for the prediction of the failure of the circuit breaker and state maintenance; further, by calculating the reliability of the mechanical parts under the actual load of the circuit breaker under different operation times, we can also provide a basis for the further selection or design of more reasonable structures and higher reliability in the parts. However, at present, studies of the reliability of high-voltage circuit breakers mainly focus on fault data collection and analysis, based on probability statistics. By seeking a certain probability distribution that can be used to analyze the reliability of a certain type of product, this method relies heavily on the accumulation of a large amount of data, and there is no complete theory that can be used as a guide. Thus, the reliability assessment of high-voltage circuit breaker operating mechanisms and the key components still lacks practical utility models.

The objective of this paper is to study the method of fatigue life assessment for key components of spring-operated mechanisms of high-voltage circuit breakers based on the stress–intensity distribution interference reliability theory. This paper takes the typical CT20 spring-operated 126 kV high-voltage circuit breaker as its research object; the installation and operating position of the circuit breaker are not considered in this article. The paper firstly introduces a reliability model based on stress–strength interference, a fatigue life reliability model and a statistical reliability model based on Weibull distribution; secondly, the fatigue reliability of the key components of the main shaft, the closing holding maker and the breaking maker in the operating mechanism are taken as examples, and the fatigue reliability of each component is obtained using the stress–strength interference reliability model and the fatigue life model, respectively; Finally, a statistical reliability model based on the Weibull distribution was used to compare and verify the above reliability results. The research results can provide a reference for the optimized design and life evaluation of the key components of the spring-operated mechanism of high-voltage circuit breakers.

2. Mathematic Model for Mechanical Reliability

2.1. Stress–Strength Interference Reliability Model

The term “reliability” first appeared in the “Electronic Reliability Design Handbook” and refers to the probability that a system will operate efficiently for a given period of time in a given environment [18]. Reliability is defined as the probability that a product or piece of equipment will perform a specified function under specified conditions and for a specified operating time. In mechanical products, whether parts are normal or effective depends on the relationship between strength (S) and stress (s); when the strength of the part is greater than the stress, it will work properly, but when the strength is less than the stress, ineffectiveness occurs. Therefore, parts are required to meet S > s or S − s > 0 under the specified conditions of use and within the specified time, and their reliability relates to the entire probability that the strength will be greater than the stress, that is:

$$R\left(t\right)=P\left(S>s\right)=P\left(S-s>0\right)=P\left(\frac{S}{s}>1\right)$$

(1)

The interference theory of stress–intensity distribution considers that stress and intensity, which affect the reliability of mechanical parts, are random variables, and these random variables show a certain distribution state. Whether the structure of a mechanical part fails or not depends not only on the mean values of stress and strength, but also on the degree of interference between the two distribution models. For mechanical parts in the early stage of work, the mean value of strength is greater than the mean value of stress, meaning there is no interference between the strength distribution and stress distribution and the parts will have high mechanical reliability; however, with the gradual increase in the number of working cycles over the part’s working time, the mean value of the strength of the parts will gradually decline. As such, the stress distribution that parts are subjected to does not in general undergo a large change, but this will gradually interfere with the stress distribution curve, making the part’s reliability gradually decrease, and with the growth of the interference area, this eventually leads to part failure. Stress–strength interference theory offers the reliability calculation method shown in Equation (2).

$$R\left(t\right)={\displaystyle \int dR}={\displaystyle {\int }_{-\infty }^{\infty }f\left(s\right)\left[{\displaystyle {\int }_S^{\infty }f\left(S\right)dS}\right]}ds$$

(2)

where R(t) is the reliability of the mechanical structure, S and s are the strength and stress random variables, and f(S) and f(s) are the probability density functions of the strength and stress distributions, respectively. When the strength and stress are random variables with different distribution types, their probability density functions are different, so the calculation results of reliability are also different.

Table 2. Reliability models for component design with different stress and strength distributions.

Stress Distribution	Intensity Distribution	Reliability Model
Normal distribution: $s ~ N\left({\mu }_s,{\sigma }_s^2\right)$	Normal distribution: $S ~ N\left({\mu }_S,{\sigma }_S^2\right)$	$R=\mathsf{\Phi }\left[\frac{{\mu }_S-{\mu }_s}{\sqrt{{\sigma }_S^2+{\sigma }_s^2}}\right]$
Log-normal distribution: $\ln s ~ N\left({\mu }_{\ln s},{\sigma }_{\ln s}^2\right)$	Log-normal distribution: $\ln S ~ N\left({\mu }_{\ln S},{\sigma }_{\ln S}^2\right)$	$R=\mathsf{\Phi }\left[\frac{{\mu }_{\ln S}-{\mu }_{\ln s}}{\sqrt{{\sigma }_{\ln S}^2+{\sigma }_{\ln s}^2}}\right]$
Index distribution: $s ~ e\left({\lambda }_s\right)$	Index distribution: $S ~ e\left({\lambda }_S\right)$	$R=\frac{{\lambda }_S}{{\lambda }_S+{\lambda }_s}$
Normal distribution: $s ~ N\left({\mu }_S,{\sigma }_S^2\right)$	Index distribution: $S ~ e\left({\lambda }_S\right)$	$R=\left[1-\mathsf{\Phi }\left(\frac{{\mu }_s-{\lambda }_S{\sigma }_s^2}{{\sigma }_S}\right)\right]\exp \left[-\frac{1}{2}\left(2{\mu }_s{\lambda }_S-{\sigma }_S^2{\sigma }_s^2\right)\right]$

shows the method for calculating the design reliability of parts with different distribution types of stress and strength based on stress–strength interference theory. μ_S and μ_s are the mean values of strength and stress in parts, respectively, σ_S and σ_s are the standard deviations of strength and stress in parts, respectively, μ_lnS and μ_lns are the mean values of the logarithm of strength and stress of parts, respectively, σ_lnS and σ_lns are the standard deviations of the logarithms of strength and stress of parts, respectively, and Φ is the probability of a standard normal distribution and can be obtained via a probability table query.

When the type of distribution of the stress and strength to which the mechanical part is subjected is determined, the mean and variance of the stress to which the part is subjected can be obtained through calculation or experimental testing, and the mean and variance of the tensile strength, torsional strength, yield limit, etc., of the strength of the part can be obtained according to the materials manual, then with reference to Table 2. This is the method used to assess the mechanical parts used in the circuit breaker and the design reliability under the actual load stress in the circuit breaker. The reliability refers to the static reliability of the component. However, as the part is put into operation for a longer period of time, its strength will show a different decline pattern. The key to calculating the reliability of the part under different working cycles through the reliability calculation model of stress–strength interference theory is to determine the offset of the mean strength value relative to the initial state. However, it is difficult to obtain this parameter accurately in practice, so the reliability approximation calculation method is generally used in engineering.

The method of determining the reliability of the calculation process and ideas is as follows: (1) Determine the distribution of the stress and strength of the part. This can be done by consulting the data or through actual tests of the hypothesis of the distribution type. (2) Determine the nature of the stress suffered by the part as the stress in the stress–strength reliability calculation model, and calculate the mean and variance of the stress suffered by the part. Approximate the mean and variance of the strength of the part for different numbers of cycles. The strength limit of the part is used as the mean value of the strength of the part at the beginning of its operation, and the mean value of the stress on the part is used as the mean value of the strength of the part at critical failure; then, the difference is divided by the working life of the part to obtain the decreasing mean value of the strength of the part over its life, thus approximating the mean value of the strength of the part in different working cycles.

2.2. Mechanical Fatigue Life Reliability Model

Fatigue life refers to the specific number of load cycles during the operation of a mechanical component or system that it can sustain until it is damaged. Due to the uncertainty and complexity seen in different materials in terms of their surface finish, internal structure and environment, this also includes various influencing factors related to residual stresses. The nominal stress method was the first fatigue life assessment method to emerge, and is the traditional method of safe life estimation, with the advantage that the nominal stress of a component can be calculated from external loads or obtained by measurement. This method considers that the main cause of fatigue in mechanical components is the cyclic stresses acting on the component. The assumption of the nominal stress method is that when parts composed of the same material have a consistent stress concentration system and a consistent load spectrum, the actual service lives of both will be consistent. The actual control parameters of this method include nominal stresses and stress concentration factors. The nominal stress is the actual calculated load level, i.e., the stress value under the area-averaged distribution behavior.

Under normal circumstances, when a part is damaged by fatigue, cracks initially appear from within or at the point of maximum stress, meaning that the fatigue life estimation process must start with finding this point of action. However, due to the variety of factors that actually influence the fatigue life of a part, such as size, surface roughness and residual stress–strain, which can make the calculation very complex, the application of the nominal stress method for life estimation effectively reduces the difficulty of the problem. The specific steps for fatigue life assessment using the nominal stress method are: (1) Assess the notch from a comprehensive viewpoint to find the location of the structural defect based on stress analysis or past operational experience. (2) Combine the actual stress measurements with the stress values at the defect site and derive the corresponding stress concentration coefficients according to the relevant standards. (3) Combine mathematical statistics and various counting methods to convert the measured fatigue stress spectrum into the nominal stress spectrum of the defective part. (4) Apply the interpolation method to derive the stress concentration coefficient and stress level curve (S–N curve) according to the derived stress spectrum. (5) Derive the fatigue life for different levels of stress, and use fatigue damage and other related theories to obtain the fatigue life of the defective part. Figure 1 shows the flow of the mechanical fatigue life reliability model.

Figure 1 shows the flow of the mechanical fatigue life reliability model. Both the stress–strength reliability calculation model and the fatigue life reliability calculation model are based on the stress–strength interference theory, but each of them has its own characteristics. The stress–strength reliability model is usually used to calculate the design reliability of mechanical parts, i.e., the maximum value of the reliability of the parts, and is a static reliability model. The fatigue life reliability model takes into account the cyclic and repeated effects of stress on each part of the system and the fatigue life of the stress, as well as other related factors, and can be used to determine the reliability of mechanical parts with different fatigue lives. The basic principle is: if the mechanical parts in the amplitude of a constant stress (s) cycle under the action of the fatigue life lead to damage for N, usually, the random variable N will be in line with the lognormal distribution, that is, ln N will be in line with the normal distribution. Thus, let the random variable ln N mean μ, and the standard deviation be σ. Then, the parts in a given number of cycles (fatigue life) will amount to N₁ with the reliability of:

$$R\left(N_1\right)=1-\mathsf{\Phi }\left[\frac{\ln N-\mu }{\sigma }\right]$$

(3)

where R(N₁) is the reliability of the part after cycling N₁ times, and Φ denotes the probability of standard normal distribution.

Most of the mechanical parts of the high-voltage circuit breaker are subjected to cyclic stresses of a constant magnitude during actual operation, so the reliability of the mechanical parts under different numbers of cycles can be calculated using the method given in the above equation. The stresses on the parts of the breaker spring-operated mechanism can be assumed to be cyclic stresses of a constant magnitude, so as long as the cyclic stresses can be determined, the reliability of each part can be obtained by looking up the mean and variance of the fatigue life lnN of the relevant metallic material and solving for it. For example,

Table 3. Fatigue life parameters of components made of carbon steel.

Cyclic Stress (MPa)	Number of Specimens	Fatigue Life Random Variable ln N Parameters
		μlnN	σlnN
159.8	50	9.12	1.02
455.0	50	5.59	0.11
514.0	32	5.14	0.09
592.8	27	4.72	0.07
661.8	18	4.40	0.05
730.9	11	4.10	0.07

gives the fatigue life parameters for carbon steel materials commonly used for spring-loaded actuators.

2.3. Statistical Reliability Model Based on Weibull Distribution

Weibull mathematical distribution has good adaptability and can simulate a variety of distribution forms, meaning it has wide applications in multidisciplinary fields such as electromechanical equipment, electronic devices, aerospace, the metallurgy and chemical industry, and biomedicine. The decreasing and increasing failure rates can be effectively modeled using the Weibull distribution, which is divided into two-parameter and three-parameter Weibull distributions. Considering the complex structure of the three-parameter Weibull distribution model, as well as the cumbersome calculations it involves and its lower applicability in actual engineering, the simplified two-parameter Weibull distribution model is used. Therefore, based on the theory of Weibull distribution, this paper verifies the correctness of the reliability analysis model of the key components of the operating mechanism proposed in this paper based on the reliability statistics of the manufacturers who design and manufacture the spring-loaded operating mechanism of high-voltage circuit breakers and their key components. This paper therefore adopts the simplified two-parameter Weibull distribution model, and uses the least squares method to statistically analyze the reliability test data of the key components of the circuit breaker operating mechanism, as well as giving the corresponding prediction model.

The reliability characteristic quantities used to describe the two-parameter Weibull distribution include: reliability, unreliability, failure probability, and failure rate.

• Reliability

Defined as the probability that a product or piece of equipment will perform a specified function under specified conditions and within a specified operating time, denoted as R(t):

$$R\left(t\right)=\exp \left[-{\left(\frac{t}{\eta }\right)}^{\beta }\right]$$

(4)

2.

Unreliability

Defined as the probability that a product or piece of equipment will lose its specified function (failures occur) under specified conditions and before a specified time t, expressed as F(t). F(t) is also known as the cumulative failure distribution function and is expressed as:

$$F\left(t\right)=1-R\left(t\right)=1-\exp \left[-{\left(\frac{t}{\eta }\right)}^{\beta }\right]$$

(5)

3.

Probability of failure

When the product life T is a continuous random variable, the unreliability function F(t) is derived, and the result is called the failure probability density function, or the failure probability.

The probability density function of the two-parameter Weibull distribution is thus obtained as:

$$f\left(t\right)=\frac{\beta t^{\beta -1}}{{\eta }^{\beta }}\exp \left[-{\left(\frac{t}{\eta }\right)}^{\beta }\right]$$

(6)

In the formula, η is the scale parameter, also known as the characteristic life. It is a life mean and gives the approximate location of the midpoint of the distribution; β is the shape parameter, and its size determines the shape of the density curve. β takes different values—the shape of the density curve is not always the same.

At present, the commonly used Weibull distribution parameter calculation method can be separated into the following types: the graph estimation method, the great likelihood estimation method and the least squares estimation method. The principle of the graph estimation method is relatively simple, but the subjective settings lead to results for accuracy that are not high. The great likelihood estimation method achieves better accuracy, but the calculation steps are cumbersome, making it unsuitable for engineering applications. The least squares estimation method is accurate and convenient, so it is currently the most commonly used method in engineering. After transforming both sides of Equation (5), we have

$$\ln \left[\ln \left(\frac{1}{1-F(t)}\right)\right]=\beta \ln t-\beta \ln \eta$$

(7)

Let $y=\ln \left[\ln \left(\frac{1}{1-F(t)}\right)\right]$, $x=\ln t$. Thus, Equation (7) can be changed to

$$y=\beta x-\beta \ln \eta$$

(8)

According to the principle of least squares, the estimation of the parameters in terms of the minimum horizontal residual sum of squares and the minimum vertical residual sum of squares, respectively, yields

$${\beta }_{xy}=\frac{{\displaystyle \sum _{i=1}^n{\left(y_i-\overline{y}\right)}^2}}{{\displaystyle \sum _{i=1}^n\left[\left(x_i-\overline{x}\right)\left(y_i-\overline{y}\right)\right]}}$$

(9)

$${\eta }_{xy}=\exp \left[-\left(\frac{\overline{y}}{{\beta }_{xy}}\right)-\overline{x}\right]$$

(10)

$${\beta }_{yx}=\frac{{\displaystyle \sum _{i=1}^n\left[\left(x_i-\overline{x}\right)\left(y_i-\overline{y}\right)\right]}}{{\displaystyle \sum _{i=1}^n{\left(x_i-\overline{x}\right)}^2}}$$

(11)

$${\eta }_{yx}=\exp \left[-\left(\frac{\overline{y}}{{\beta }_{yx}}\right)-\overline{x}\right]$$

(12)

where, β_xy, η_xy, β_yx and η_yx are the estimated parameters corresponding to the minimum horizontal residual sum of squares and the minimum vertical residual sum of squares, respectively, and $\overline{x}$ and $\overline{y}$ are the mean values of x and y, respectively. For the latter, the corresponding horizontal residual sum of squares and vertical residual sum of squares are:

$$R_{xy}={\displaystyle \sum _{i=1}^n{\left(x_i-\widehat{x}\right)}^2}$$

(13)

$$\widehat{x}=\frac{y-\beta \ln \beta }{\beta }$$

(14)

$$R_{yx}={\displaystyle \sum _{i=1}^n{\left(y_i-\widehat{y}\right)}^2}$$

(15)

$$\widehat{y}=\beta x-\beta \ln \eta$$

(16)

It thus follows that

$$\frac{R_{yx}}{R_{xy}}={\beta }^2$$

(17)

If the residual coefficient β > 1, then the residual calculation under the horizontal residual sum-of-squares model will be smaller than that under the vertical residual sum-of-squares model, meaning it will be better to use the horizontal residual sum-of-squares model for Weibull parameter calculation. If the opposite is true, then it will be better to choose the vertical residual sum-of-squares model for the calculation of the Weibull parameter, which further illustrates that the results derived when using this parameter for the circuit breaker failure rate analysis are better. The Weibull distribution function obtained by using median rank estimation in this paper is shown in Equation (18).

$$F=\frac{i-0.3}{k+0.4}$$

(18)

where F is the empirical value of the distribution function, and the specific choice of the value of F depends on the required accuracy; i is the serial number of the fault data; k is the number of fault data. Figure 2 shows the flow of the statistic reliability model based on Weibull distribution.

Figure 2 The specific steps of the reliability assessment method based on the Weibull distribution are: (1) ranking the fault maintenance data of the key components of the operating mechanism from shortest to longest failure time; (2) using the empirical formula of the distribution function to obtain F(t); (3) using the least squares method to estimate the parameters β and η of the Weibull distribution; (4) obtaining the reliability function of the key components of the operating mechanism.

3. Mechanical Reliability of Critical Components

3.1. Principle Axles

The spring-operated spindle mechanism is subjected to shear stress during the closing and breaking processes. In this paper, the maximum torque that the spindle can withstand is used as the strength parameter in the stress–strength reliability model, and the average value of the spindle strength is used at the beginning of the work. In general, due to the different safety factors in the design, the maximum torque that the spindle can withstand has specific upper and lower limits; if the spindle shows higher reliability when the maximum torque it can withstand is smaller, then it will show greater reliability when the maximum torque it can withstand is larger. Therefore, it is practical to calculate reliability when the maximum torque of the spindle is smaller. In this paper, the reliability of the spindle is calculated by taking the smaller value of 241 N-m as the maximum torque that the spindle can withstand. The average value of the stress on the spindle is used as the average value of the strength at critical failure of the spindle. Through research on the spring-operated mechanism, it is found that if the maximum torque that the spindle can withstand is small and the circuit breaker is operated frequently in a harsh environment, the spindle will fail when the circuit breaker opens around 20,000 times, so the life of the spindle is taken as 20,000 times; thus, the average value of the spindle’s strength under different working cycles can be obtained. The standard deviation of the spindle strength is taken as 3% of the mean value.

The reliability of the spindle of the actuator is calculated as follows:

• The mechanical parts of the shaft subjected to stress and their general strength agree with the normal distribution, so we must first determine the stress the spindle is subjected to and its strength in order to obey the normal distribution;
• The stress in the stress–strength reliability model is taken as the maximum torque to which the spindle is subjected during actual operation, and its mean value is determined by the following equation, i.e.,

$$\overline{S}=F_0{L}_0$$

(19)

where Equation (4), $\overline{s}$ is the average value of stress on the spindle (taking the maximum torque on the spindle during actual operation); F₀ is the spring force of the energy storage spring.

$$F_0=k_0{x}_0$$

(20)

$$k_0=\left(\frac{C-0.25}{C+1}+\frac{0.615}{C}\right)\times {10}^4$$

(21)

where $x_0$ is the extension of the energy storage spring in m, $k_0$ is the curvature coefficient, L₀ is the length dimension of the inflection arm connected to the energy storage spring in m; C is the spring winding ratio, C = D/d; D is the outer diameter of the spring and d is the inner diameter of the spring.

Although the standard deviation of the maximum torque to which the spindle is subjected is difficult to obtain, the standard deviation of the stress for the calculation can be taken as 3% of the mean value because the deviation of the maximum torque to which the spindle is subjected during each operation is small;

3.

Since the maximum torque applied to the spindle is used as the stress in the stress–strength reliability model, the same torque parameter should be used as the strength in the model;

4.

Apply the reliability calculation method given in Table 2 to approximate the mechanical reliability of the spindle at different numbers of working cycles.

Combined with the normal distribution reliability formula given in Table 1 and the engineering approximation calculation method, the reliability of the spindle after different numbers of openings is calculated, as shown in Figure 3. When the circuit breaker opens 10,000 times, the reliability of the operating mechanism spindle is 0.99858; after the number of openings is 25,000 times, the reliability of the spindle begins to decline significantly; when the number of openings is 30,000 times, its reliability drops to 0.6 or so. As such, in order to ensure the reliability of the operating mechanism before this reliability begins to drop rapidly, before the number of openings reaches 25,000 times, one should consider replacing the spindle.

3.2. Closing Latch

The spring-operated mechanism of the closing hold button is subjected to a constant force when the circuit breaker is in the closed position. Therefore, a fatigue life reliability calculation model is used to analyze its reliability. In order to determine the mean and standard deviation of the fatigue life corresponding to the stress s_a on the part, the magnitude of s_a must first be calculated.

$$s_a=\frac{F_1\cdot L_1}{d_{a0}\cdot S_1}$$

(22)

Here, s_a is the stress on the closing retainer in MPa; F₁ is the tension of the energy storage spring in N; L₁ is the length of the arm connected to the energy storage spring in m; d_a0 is the diameter of the spindle in m; $S_1$ is the cross-sectional area of the closing retainer in m².

As a result, the stresses on the closing latching pawl can be obtained, and the mean and standard deviation of the corresponding fatigue life can be further obtained. The reliability of the closing stopper can be obtained by substituting it into Equation (3). Figure 4 shows the reliability of the closing latching pawl in the spring operating mechanism after different opening and closing times. When the number of times the circuit breaker is opened reaches 10,000, its reliability remains at 0.99927; when the number of times it is opened reaches 25,000, the reliability of the switch rapidly decreases, and when the number of times it is opened reaches 30,000, its reliability will be less than 0.7. In order to protect the normal operation of the operating mechanism and the circuit breaker, before the number of times it is opened reaches 25,000, the switch should replaced.

3.3. Opening Latch

The stress on the splitter originates from the direct action of the output arm, and the force on the output arm is provided by the splitter spring, so the stress on the splitter is the same every time. The stresses applied to the splitter can be obtained using the following formula:

$$s_f=\frac{F_2\cdot L_2}{L_3\cdot S_2}$$

(23)

Here, $s_f$ is the cyclic stress in MPa; F₂ is the spring force in N; L₂ and L₃ are the lengths of the upper and right arms of the output inflection arm in m; S₂ is the cross-sectional area of the splitter in m².

Figure 5 shows the reliability of the opening pawl, which differs with different numbers of operation of the spring operating mechanism. It can be seen that when the number of openings of the circuit breaker operating mechanism reaches 10,000, the reliability of the divider is 0.99737, and when the number of openings reaches 20,000, the reliability of the divider decreases significantly. When the number of openings reaches 30,000, its reliability decreases to about 0.54767. Therefore, in order to ensure the reliable operation of the circuit breaker, the breaker should be replaced when it has completed the task of opening 20,000 times, and the design should be aimed at reducing the stress on the weak link of the breaker as much as possible to improve the mechanical reliability of the entire operating mechanism.

4. Discussion

In order to verify the accuracy of the results of the reliability calculation based on stress–strength theory and fatigue life theory, the reliability calculation results of the above spring-loaded actuator spindle, the closing holding maker and the breaking maker are verified separately in this paper using a statistical model based on the Weibull distribution test. The Weibull distribution-based reliability statistical model in this paper is based on the reliability test data of circuit breakers provided by the manufacturer of the circuit breaker operating mechanism.

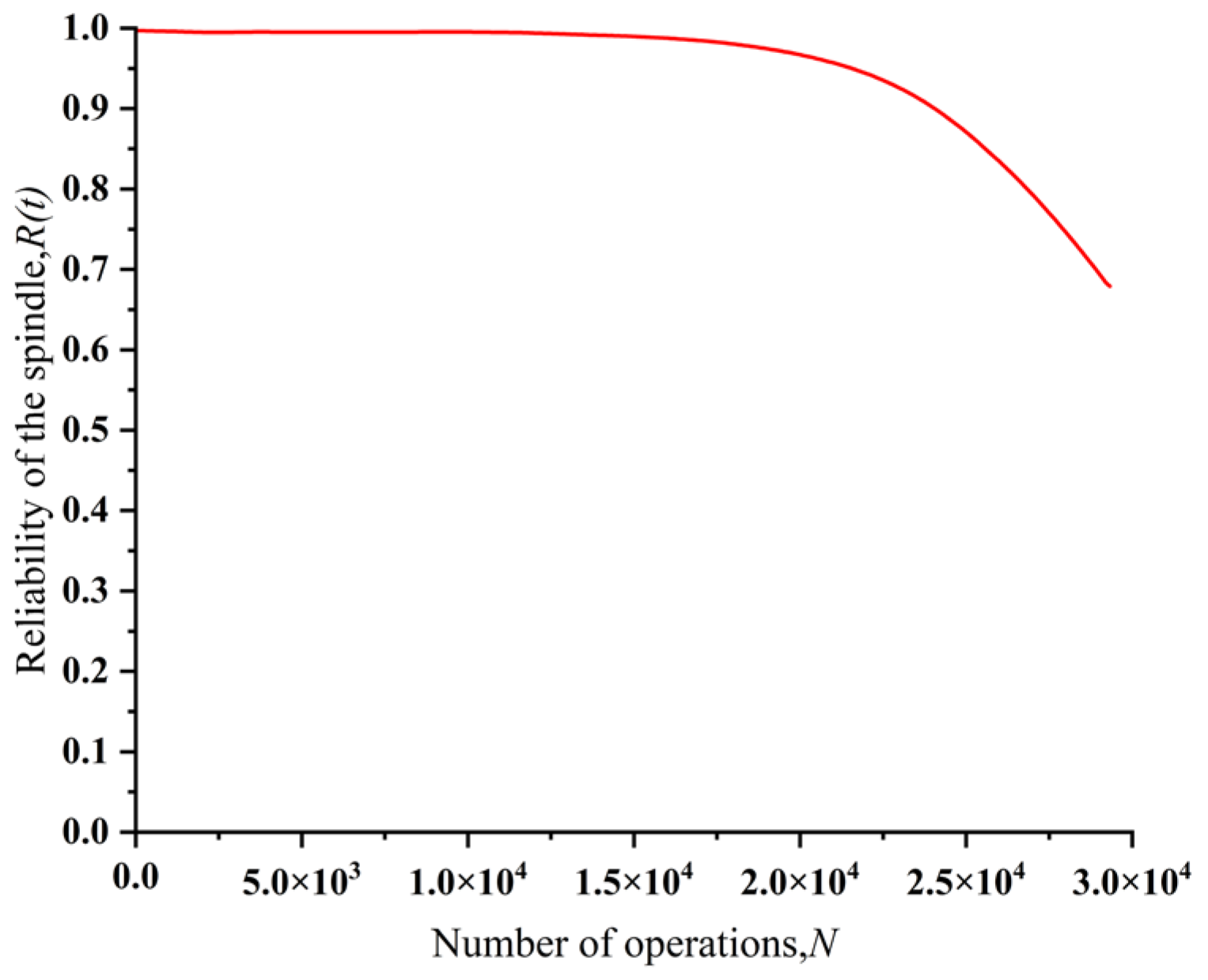
For the verification of the reliability of the actuator spindle, the manufacturer provided data on 16 breaker failures due to spindle failure. The numbers of circuit breaker operations at time of spindle failure are 18,621, 19,058, 19,463, 20,214, 20,633, 21,145, 21,876, 22,389, 22,953, 23,694, 23,912, 24,226, 24,934, 25,425, 26,327 and 27,355, listed in order, based on the reliability assessment steps described in Section 2.3—β_{Principle Axles}= 5.2687, η_{Principle Axles} = 34,721.5386. The reliability function of the principal axis based on the statistical data analysis in the reliability test is shown in Figure 6. From the figure, it can be seen that the results of the reliability analysis based on the stress–strength distribution interference model are very close to the results of the reliability calculation based on the reliability test statistics, and the maximum error of the reliability analysis is 0.024. The stress–strength reliability calculation model used in this paper is a static reliability model, and the source of error is, firstly, the approximate calculation of the mean value of the strength of the parts under different numbers of working cycles, and secondly, the mean values and variances of the stresses suffered by the key components are considered to undergo no significant changes during the reliability calculation.

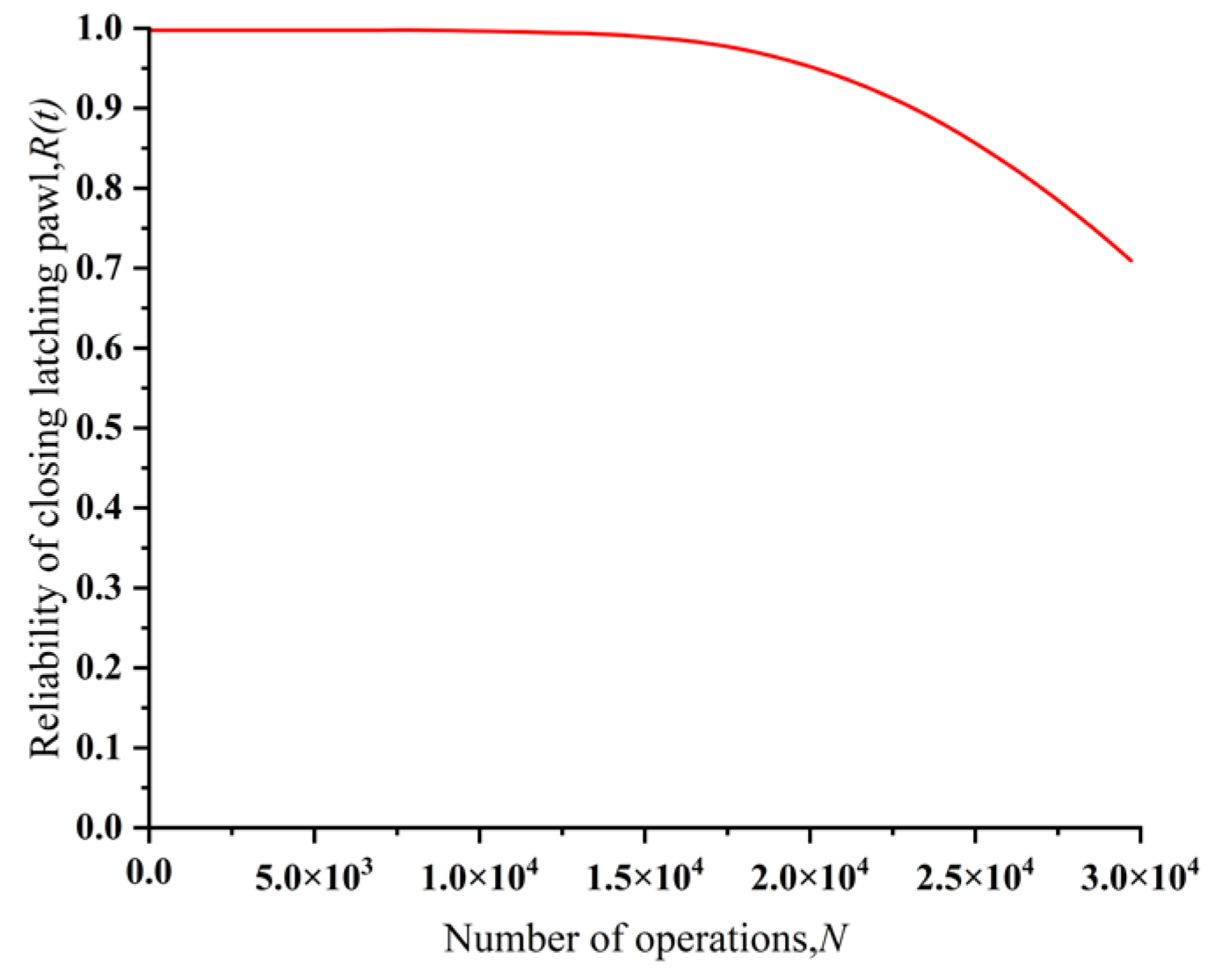
For the circuit breaker failures caused by the failure of the closing latching pawl and the opening pawl, the manufacturer provided 15 and 12, respectively. Similarly, the statis-tical data analysis of the failure statistics of the closing latching pawl and the opening pawl were calculated and analyzed, and we obtained β_{closing latching pawl} = 5.6434, η_{closing latching pawl} = 35867.4672; β_{opening pawl} = 4.9427 and η_{opening pawl} =33241.7214. 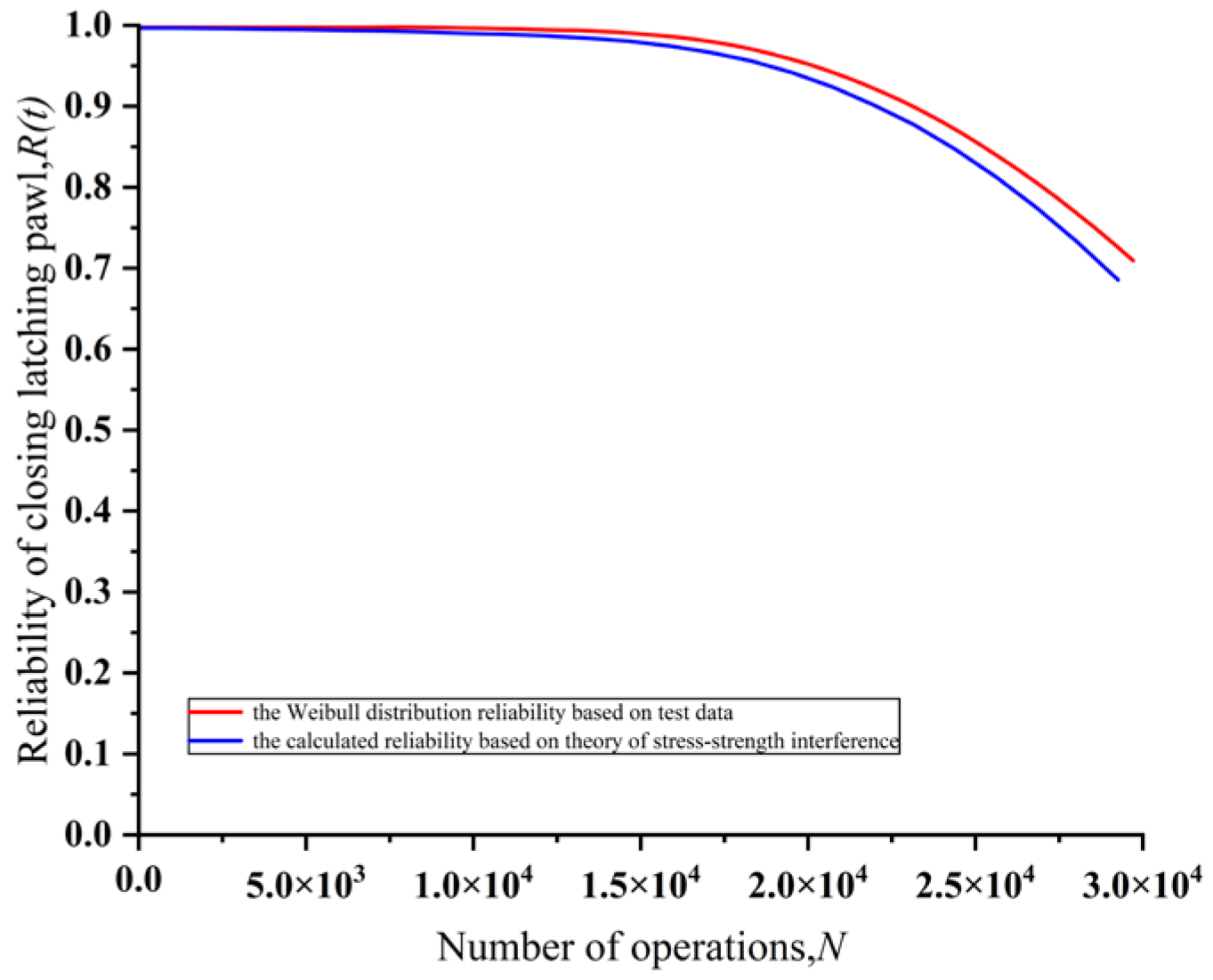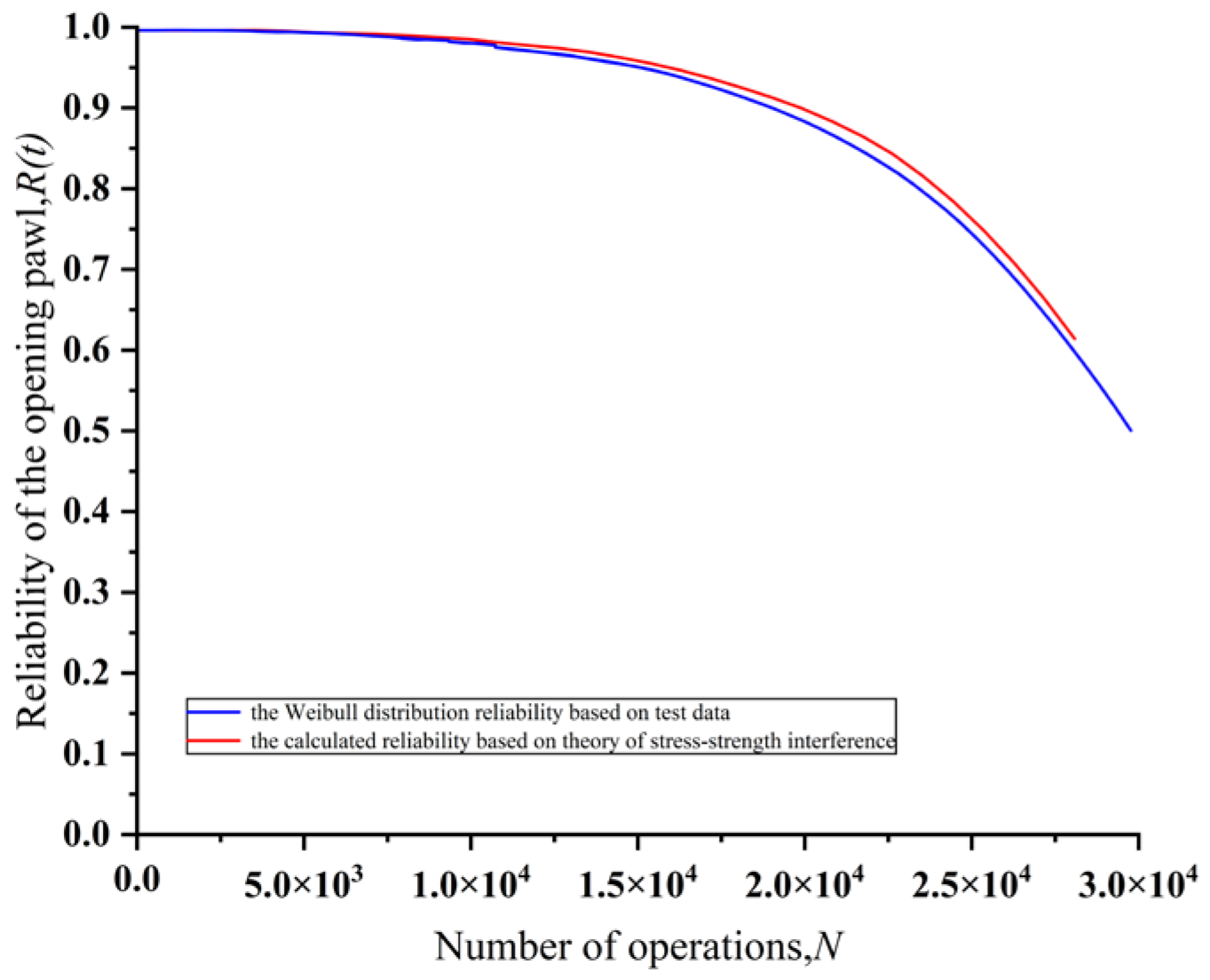Figure 7 and Figure 8 show the comparison of the reliability of the closing latching pawl and the opening pawl based on the statistical data analysis of reliability test and the reliability based on the calculation of stress intensity distribution interference model, respectively.

As can be seen from the figure, by analyzing the reliability test data of high-voltage circuit breaker manufacturers, the results of the stress intensity distribution interference reliability calculation model proposed in this paper are generally slightly higher than the reliability obtained based on the analysis of failure statistics, the reason is that the model in this paper is a more ideal case of reliability, which is in line with the actual situation than that based on the analysis of statistical data. Among them, the reliability analysis error of the opening pawl is the largest, 0.024.

5. Conclusions

At present, reliability studies of high-voltage circuit breakers mainly focus on fault data collection and analysis, based on probability statistics, and involve seeking a certain probability distribution to analyze the reliability of a certain type of product. This method relies heavily on the accumulation of a large amount of data, and there is no complete theory to act as a guide. This paper assessed methods of the reliability assessment of key components of spring-operated mechanisms in high-voltage circuit breakers based on the stress–intensity distribution interference reliability theory and fatigue life assessment theory, and applied the stress intensity distribution interference reliability model and fatigue life model, respectively, to the key components of the spring-operated mechanism, before analyzing the reliability of key components according to the number of closing and breaking operations of the circuit breaker. Based on the failure data provided by the manufacturer of the spring-operated mechanism, the accuracies of the stress intensity interference reliability assessment model and the fatigue life reliability assessment model were compared and analyzed using the test statistical reliability model based on Weibull distribution. The stress–strength reliability calculation model used in this paper is a form of static reliability model, and the source of error is, firstly, the approximate calculation of the mean values of the strengths of the parts with different numbers of working cycles. Secondly, the means and variances of the stresses suffered by the critical parts are considered to undergo no significant changes during the reliability calculation process. The research results can provide a reference for the optimization of the design and life evaluation of key components of high-voltage circuit breaker spring-operated mechanisms.