Data-Driven Techniques for Short-Term Electricity Price Forecasting through Novel Deep Learning Approaches with Attention Mechanisms

Abstract

The electricity market is constantly evolving, being driven by factors such as market liberalization, the increasing use of renewable energy sources (RESs), and various economic and political influences. These dynamics make it challenging to predict wholesale electricity prices. Accurate short-term forecasting is crucial to maintaining system balance and addressing anomalies such as negative prices and deviations from predictions. This paper investigates short-term electricity price forecasting using historical time series data and employs advanced deep learning algorithms. First, four deep learning models are implemented and proposed, which are a convolutional neural network (CNN) with an integrated attention mechanism, a hybrid CNN followed by a gated recurrent unit model (CNN-GRU) with an attention mechanism, and two ensemble learning models, which are a soft voting ensemble and a stacking ensemble model. Also, the optimized version of a transformer model, the Multi-Head Attention model, is introduced. Finally, the perceptron model is used as a benchmark for comparison. Our results show excellent prediction accuracy, particularly in the hybrid CNN-GRU model with attention, thereby achieving a mean absolute percentage error (MAPE) of 6.333%. The soft voting ensemble model and the Multi-Head Attention model also performed well, with MAPEs of 6.125% and 6.889%, respectively. These findings are significant, as previous studies have not shown high performance with transformer models and attention mechanisms. The presented results offer promising insights for future research in this field.

1. Introduction

In the current age characterized by our increasing dependence on electricity for various aspects of daily life, the precision of electricity price forecasting (EPF) has emerged as a matter of paramount importance. With the ever-growing demand for electricity spurred by factors such as population growth, industrial expansion, and the widespread adoption of electric vehicles, the need for precise and reliable electricity price predictions is more pronounced than ever. This research paper embarks on an exploration of the critical role that accurate electricity price forecasting plays, thereby delving into the multifaceted factors and methodologies that impact this pivotal aspect of the energy sector. A thorough understanding of electricity price trends is not only crucial for stakeholders within the energy market, but it also has significant relevance for policymakers, consumers, and advocates of environmental sustainability. This understanding directly influences financial decision making, cost management, sustainability initiatives, and the broader economic welfare of societies in today’s globally interconnected world. This paper seeks to illuminate the inherent challenges and the increasing significance of electricity price forecasting in the context of our contemporary energy landscape.

The significance and advancement of short-term electricity price prediction have garnered significant attention in recent years. The introduction of innovative market methodologies, including intraday timeframes, has further accentuated the demand for precise forecasts. This, in turn, enables market stakeholders to fine-tune their strategies and enhance the efficiency of their energy trading activities within shorter time intervals. These forecasts are of essential importance to market participants, thereby allowing them to competently oversee their assets, mitigate risks, and capitalize on opportunities arising from the dynamic nature of market conditions.

Also, accurate price predictions in the electricity sector are imperative for various critical facets. For utilities, these predictions are fundamental in resource planning, thereby allowing them to efficiently allocate resources to meet anticipated demand. Additionally, in energy trading, precise forecasts play a crucial role in guiding decisions to buy and sell electricity among market participants. The stability of the grid is crucially influenced by accurate predictions, thus helping operators anticipate and manage sudden fluctuations in demand or supply [1]. In addition, for the integration of renewable energy sources, such predictions aid in balancing electricity supply and demand, thereby ensuring grid stability in the face of intermittent energy generation [2]. Cost-saving measures for consumers, achieved by shifting usage to lower-priced periods, are facilitated by such forecasts.

Moreover, these forecasts are relevant for investment decisions, particularly for investors in energy projects who rely on price expectations to assess profitability. In particular, environmental impact is also influenced by accurate price predictions, thus prompting energy companies to opt for more ecofriendly energy generation methods during high-price periods. In conclusion, the precision of electricity price predictions profoundly shapes efficient and informed decision making across resource management, trading, grid stability, renewable energy integration, investment planning, and environmental considerations. Forecasts are integral in promoting effective electricity system management and influencing consumer behaviors. Several time series methods have been used to predict electricity prices, which will be presented below. In contrast to existing methods that aim to solve the electricity forecasting problem and that are presented in the literature review, the methods proposed in this paper employ complex attention mechanisms, thereby making the models proposed capable of assimilating extremely difficult fluctuations in price time series to capture both the positive and negative values of the data.

Regarding the contribution of this paper, the following key points are highlighted:

• Novel and advanced deep learning models are developed and proposed for electricity price forecasting approaches using time series data. The first is a convolutional neural network (CNN) with an integrated attention mechanism. The second is a hybrid CNN followed by a gated recurrent unit (CNN-GRU) with an integrated attention mechanism. The third is the soft voting ensemble model, which is an ensemble learning model that combines the predictions of the CNN-GRU with an attention mechanism model and a transformer model, the Multi-Head Attention model, thus creating a weighted output. The fourth is a stacking ensemble model, which combines the outputs of the CNN-GRU with attention and the transformer model in a dense layer, thus creating the final prediction. These architectures are robust in predicting data that do not follow specific patterns, such as those under study. More specifically, the proposed soft voting ensemble model exhibits optimal predictions. These four models that have not been previously utilized in electricity price prediction instill optimism for future studies based on their performance.
• Also, an enhanced and optimized version of the Multi-Head Attention model is introduced in such a way as to exhibit very satisfactory predictive accuracy compared to other works, where the transformers do not perform as well. This model demonstrates exceptionally high prediction accuracy within the electricity price framework.
• Explainability Process: The paper contributes to the field by employing an explainability process, thereby elucidating the impact of variables introduced into the models. This analysis provides insights into the factors that influence prediction outcomes, aids in understanding model behavior, and improves the interpretability of the results.
• Resolution of Sign Change Challenges: The paper addresses a common challenge in existing algorithms, namely their inability to capture abrupt sign changes in prediction time series. Considering the correct parameters and conducting thorough preprocessing analysis, the proposed models demonstrate improved performance in handling such variations.

In order to present a comprehensive view of the work carried out, this paper is structured as follows. Section 2 presents a general description of the mechanisms of the electricity market. In Section 3, a comprehensive review of the literature is presented, thus showcasing the most significant similar studies conducted. Subsequently, in Section 4, an in-depth analysis of all the data and correlations under examination is carried out. Section 5 clarifies the fundamental architectures of the models being developed. In Section 6, the results of the predictions are presented, and the respective metrics are compared with each other. Finally, in Section 7, the key conclusions arising from the study are outlined, along with notable suggestions for future research.

2. The Electricity Market

In order to make the electricity market more understandable, this section introduces both the mechanism and the three main markets that constitute the wholesale energy market: the day-ahead, intraday, and the balance market.

The electricity market [3] is a complex system that brings together electricity generators, distributors, retailers, and consumers to facilitate the production and consumption of electricity. The working mechanism of the electricity market can be broadly categorized into two parts: the wholesale market and the retail market.

In the wholesale market, electricity is traded between generators and retailers who submit bids and offers for the supply of electricity. The market clearing price is then determined by matching the bids and offers, and the generators that offer to supply electricity at or below the clearing price are dispatched to supply the required amount of electricity. The wholesale market operates in advance, which means that the market clearing price is set one day in advance.

In the retail market, retailers purchase electricity from the wholesale market and sell it to consumers at retail prices. Consumers can purchase electricity from their retailer or generate their own electricity through distributed generation technologies, such as rooftop solar panels. Retailers also provide various value-added services to consumers, such as billing, customer service, and energy efficiency advice. The electricity market is regulated by various government agencies to ensure that it operates fairly and efficiently. Regulatory bodies oversee the market design, market operations, and market participants to ensure that they comply with rules and regulations.

The electricity day-ahead market (DAM) is a crucial component of the electricity market structure, where electricity is bought and sold a day before actual delivery. It functions as a platform for electricity producers and consumers, thereby enabling them to trade electricity for delivery on the following day. Participants, including power generators, distributors, and large consumers, submit bids specifying the quantity of electricity they are willing to buy or sell at various price levels for each hour of the following day. The market operator then matches the bids to determine the clearing price for each hour, thereby considering the supply and demand conditions. This transparent and competitive market allows market participants to manage their electricity needs, balance supply and demand, and mitigate price volatility while ensuring efficient and reliable power delivery.

The intraday market (IDM) is like a special marketplace for electricity that operates during the day. It is where electricity is bought and sold for very short periods, like hours or even minutes, before it is actually used. This helps electricity companies and users adjust their plans and make sure that they have enough electricity to meet the needs of the moment. It is a bit like a last-minute electricity store, where you can quickly get what you need to keep the lights on and machines running smoothly during the day.

The balancing market involves the continuous matching of electricity supply with demand in real time to ensure grid stability. It is a crucial process that addresses inherent variability and unpredictability in power consumption and generation. Market operators use advanced technologies and forecasting tools to anticipate fluctuations in demand and supply, thus adjusting electricity generation or consumption accordingly. This involves dispatching additional power when demand exceeds forecasts or activating demand response mechanisms to curtail consumption during surplus periods. Balancing the electricity market is essential to maintain a reliable and resilient power system, to prevent overloads or blackouts, and to optimize the use of diverse energy sources in the most efficient manner.

3. Literature Review

Electricity price forecasting (EPF) plays a critical role in electricity markets, where the accuracy of these predictions is essential for stakeholders to make informed decisions about their electricity-related activities, be it production, consumption, or trading strategies. Over recent years, a variety of methodologies have emerged, which range from traditional statistical and econometric models to more advanced approaches based on machine learning and artificial intelligence.

To contribute to ongoing research in this field, this study offers an extensive review of the existing techniques and approaches used in electricity price forecasting. This review covers a wide range of studies, including both theoretical and empirical research, thereby providing a comprehensive assessment of the strengths and weaknesses of various forecasting methods. Particularly, this section focuses on the application of statistical models, as well as machine learning algorithms such as support vector regression, deep learning techniques, and ensemble models, in the context of electricity price forecasting.

The primary goal of this literature review is two-fold: firstly, to provide a thorough and current overview of the state of the art in electricity price forecasting and secondly, to outline the key challenges and potential directions for future research in this area. By synthesizing and critically analyzing the existing literature, this paper aims to offer insights and recommendations that can guide future research efforts in the field of electricity price forecasting.

In terms of statistical methods, the authors in [4] used ARIMA, SARIMA, SARIMAX, and multiple linear regression (MLR) forecasting methods to forecast day-ahead electricity prices for Germany based on a variation in input features. In the article of [5], a collaborative framework has been suggested between humans and machines to predict the day-ahead electricity price in wholesale markets. This framework combines numerous statistical and machine learning models, various exogenous features, a combination of several time series decomposition techniques, and a collection of time series characteristics derived from signal processing and time series analysis methods. The researchers in the work of [6] applied traditional inferential statistical methods, among others, for the prediction of electricity prices and proposed an innovative solution to forecast electricity spot prices. In the recent literature, statistical methods are mostly used as benchmark models to compare with machine, deep, and ensemble learning models, which are presented below.

Moreover, regarding machine learning (ML) applications, the authors in [7] presented a three-stage model for short-term electricity price forecasting using ensemble empirical mode decomposition (EEMD) and extreme learning machine (ELM). In [8], a probabilistic forecasting method for day-ahead electricity prices was proposed using SHapley Additive exPlanations (SHAP) feature selection, as well as long- and short-term time series network (LSTNet) quantile regression. The study in [9] discussed the use of artificial neural networks to predict the price and demand of the day of electricity, compared different neural network architectures, and found that methods that combine fully connected and recurrent or temporal convolutional layers present better performance. Following the previous study, a model for electricity price forecasting was proposed in [10], which improves precision by combining trend decomposition, a temporal convolutional network, and neural basis expansion analysis (STL-TCN-NBEATS). The authors in [11] proposed using the support vector machine (SVM) and k-nearest neighbor (KNN) classifiers for short-term electricity price and load forecasting. Their modified SVM achieved an accuracy of 88.2740% for price forecasting, while their modified KNN achieved an accuracy of 89.8605% for load forecasting. In [12], a novel hybrid machine learning algorithm was presented to predict the day-ahead EPF, thereby integrating linear regression with automatic relevance determination (ARD) and ensemble bagging extra tree regression (ETR) models. Recognizing that each model of EPF has its own strengths and weaknesses, the combination of several models presents more precise predictions and overcomes the constraints associated with any individual model. The researchers in [13] optimized an electricity price prediction model with inverted and discrete particle swarm optimization, which utilized variational mode decomposition and the k-means clustering algorithm. Additionally, the authors of [14] performed simulations for four primary regression techniques, including the support vector machine, Gaussian processes regression, regression trees, and multilayer perceptron. Based on the resulting performance, such as the MAE, RMSE, R, and the total number of percentage error anomalies, the support vector machine (SVM) stood out as the optimal selection for predicting the price of the electricity market. Finally, Mubarak et al. in [15] proposed a combination of single and hybrid machine learning models for predicting the short-term price of electricity. The hybrid models outperformed the single models, with the Logistic Regression–CatBoost model achieving the lowest MAE and RMSE values.

Furthermore, on the implementation of deep learning (DL) techniques in electricity forecasting tasks, Chatterjee et al. in [16] discussed electricity price forecasting using deep learning algorithms such as long short-term memory networks (LSTMs), deep neural networks (DNNs), convolutional neural networks (CNNs), CNN-LSTMs, and CNN-LSTM-DNNs. The accuracy of the models was evaluated using MAE and MAPE metrics. In addition, Krishna Prakash et al. in [17] presented a hybrid model that combines discrete wavelet transform (MODWT) denoising and empirical mode decomposition (EMD) with sequence-to-sequence LSTM neural networks for forecasting electricity prices. The proposed model outperformed other forecasting models such as LSTM and stacked LSTM. The authors in [18] presented a modular day-ahead electricity price forecasting approach that incorporates convolutional and recurrent neural networks to predict electricity prices. An optimized heterogeneous structure LSTM model was presented in [19] to forecast the electricity price, which improved the accuracy and stability compared to traditional models. The researchers in [20] proposed a hybrid neural network model for short-term load forecasting, thereby combining a temporal convolutional network (TCN) and a gated recurrent unit (GRU). The model was optimized using the AdaBelief optimizer. The authors in [21] investigated an efficient method for forecasting the daily electricity price using an LSTM neural network model. Daood et al. in [22] explored electricity price forecasting based on an enhanced convolutional neural network, while [23] proposed a novel methodology for probabilistic energy price forecast using Bayesian deep learning techniques. It focuses on providing prediction intervals and densities to enable enhanced bidding and planning strategies considering uncertainty explicitly. Following that work, in [24], a hybrid model was proposed for electricity price forecasting, which decomposes the price series, selects significant subseries, predicts each subseries using the GRU network, calculates the best weights using the particle swarm optimization algorithm (PSO), and combines the results to obtain the final price prediction. Furthermore, in [25], a short-term electricity price forecasting method based on data mining was introduced, thereby using a fuzzy classification miner and an LSTM model. In [26], a model was presented for the forecast of electricity prices based on gated recurrent units (GRUs). The model considers factors such as temperature, wind speed, and daily activities to increase the accuracy of the forecast. The authors in [27] proposed a feedforward deep neural network with the integration of an autoregression module to minimize errors on day-ahead price forecasting task.

Lastly, ensemble learning (EL) is gaining more and more interest in electricity price forecasting research. The authors of [28] proposed a hybrid decomposition approach that incorporates ensemble empirical modal decomposition (EEMD) and wavelet packet decomposition (WPD) within a quadratic framework coupled with a deep extreme learning machine (DELM) that is optimized using an improved hunter–prey optimization algorithm (TPHO). The combination of these techniques improves the precision of electricity price forecasting. The researchers in [29] proposed a short-term electricity price prediction methodology that utilizes days with similar load consumption among the historical data and the ensemble empirical mode decomposition (EEMD) technique. A gated recurrent unit neural network (GRU-NN) was used as the machine learning model and was combined with a feature selection model. The proposed method outperformed existing techniques in terms of accuracy.

4. Description of the Models

In this section, the architecture of the deep learning models developed and explored here is presented in detail. Initially, the four novel models proposed are analyzed, namely the CNN with an attention mechanism, the hybrid CNN-GRU with an attention mechanism, and the two ensemble learning models—the soft voting ensemble and the stacking ensemble model. Following that, the optimized version of the Multi-Head Attention model is presented, and finally, the benchmark perceptron model is analyzed.

4.1. CNN with Attention Mechanism Model

A CNN with an attention mechanism [30] synergistically integrates convolutional neural networks (CNNs) and attention mechanisms to improve the model’s proficiency in extracting crucial features from 2D images. In addition, the CNN with an attention mechanism model is designed to capture complex patterns in time series data, particularly focusing on electricity price prediction. The attention mechanism enhances the model’s ability to highlight relevant features. The key components of the model are described below.

Attention Mechanism

The attention mechanism computes attention weights ${\alpha }_i$, which are used to obtain the the final weighted value for each element in the input sequence, providing therefore, a weighted sum for context representation. For the input sequence X, the attention weights ${\alpha }_i$ and the context vector C are calculated as:

$${\alpha }_i=\frac{exp\left(e_i\right)}{{\sum }_{j=1}^{T}exp\left(e_j\right)}$$

(1)

$$C=\sum _{i=1}^T{\alpha }_i·X_i$$

(2)

where $e_i$ is the score computed for the i-th element in the input sequence X.

The model utilizes the context vector in conjunction with the output of a convolutional neural network (CNN). The attended feature map $\widehat{Z}$ is obtained by convolving the attention-weighted context vector with the CNN output, as:

$${\widehat{Z}}_{i,j}=\sum _{m=1}^H\sum _{n=1}^W{\alpha }_{m,n}·Z_{i+m,j+n}$$

(3)

where ${\widehat{Z}}_{i,j}$ represents the output at position $(i,j)$ in the output feature map, while ${\alpha }_{m,n}$ signifies the attention weights linked to each element in the input feature map. $Z_{i+m,j+n}$ refers to the elements in the input feature map, with indices $(i+m,j+n)$ indicating their position relative to the output position $(i,j)$. Additionally, H and W represent the height and width of the input feature map, respectively.

4.2. Hybrid CNN-GRU with Attention Mechanism Model

The hybrid CNN-GRU with an attention mechanism model represents an advanced and innovative approach for time series prediction, particularly in the context of electricity price forecasting. Combining the CNN, GRU, and attention mechanisms, this model exhibits a robust ability to capture intricate patterns in temporal data. Similarly to Section 4.1, the attention mechanism calculates attention weights ${\alpha }_i$, in order to emphasize relevant elements in the input sequence. For the input sequence X, the attention weights ${\alpha }_i$ and the context vector C are calculated based on Equations (1) and (2), respectively.

This novel model integrates the attention-weighted context vector with the output of both a CNN and a GRU network. Regarding the attended feature map $\widehat{Z}$, it is computed through the Equation (3). Through the integration of CNN and GRU with the attention, this algorithm excels at capturing intricate temporal patterns and extracting relevant features with very high accuracy.

4.3. Soft Voting Ensemble Model

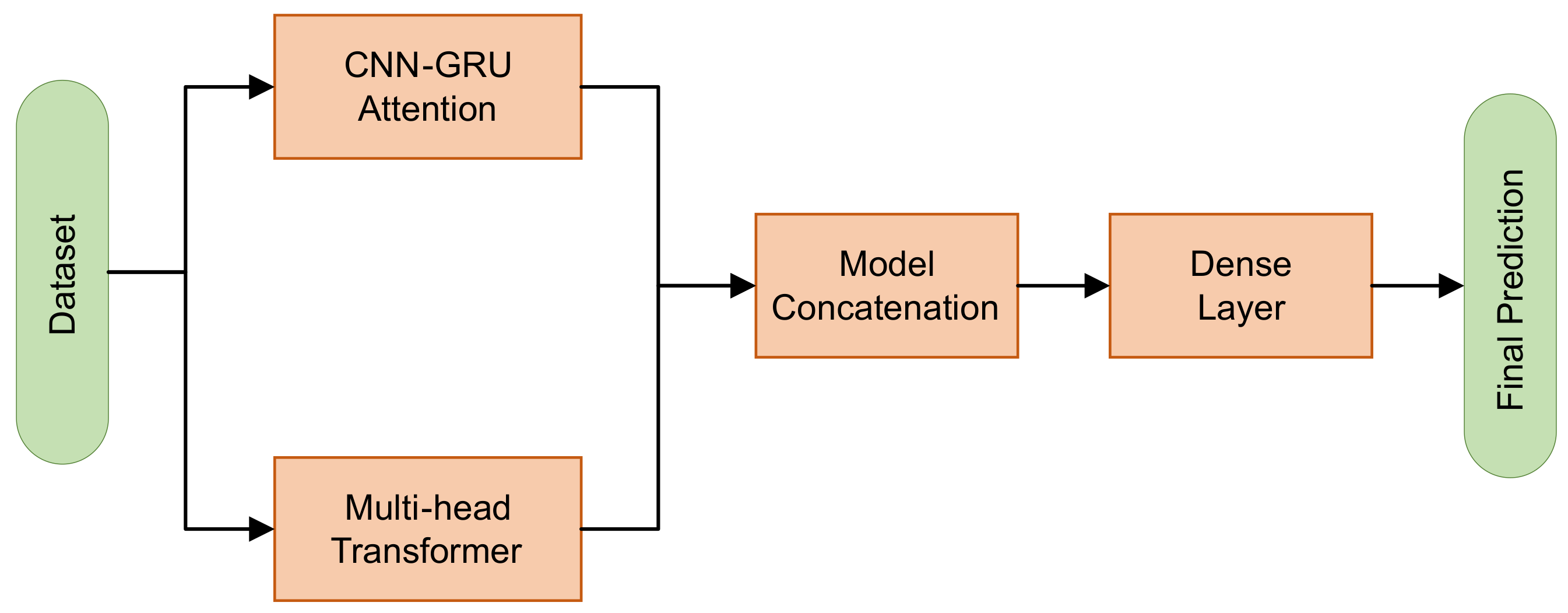
The soft voting ensemble Model, as shown in Figure 1, is a sophisticated ensemble learning approach that combines the predictive outputs of multiple base models, thereby aiming to enhance the overall predictive accuracy. In this context, it integrates the results of the Multi-Head Attention model and the hybrid CNN-GRU with attention model using a soft voting mechanism.

4.3.1. Multi-Head Attention Model

The Multi-Head Attention model is adept at capturing intricate patterns and dependencies within time series data. Utilizing parallel attention heads, each focused on different aspects of the input sequence, it produces diverse and informative representations of the data.

4.3.2. Hybrid CNN-GRU with Attention Model

The hybrid CNN-GRU with attention model seamlessly integrates the convolutional neural network (CNN), gated recurrent unit (GRU), and attention mechanisms. This combination allows for effective feature extraction and context-aware processing, thereby contributing to the model’s ability to capture both spatial and temporal dependencies.

4.3.3. Soft Voting Mechanism

The soft voting mechanism combines the outputs of the Multi-Head Attention and hybrid CNN-GRU with attention models by assigning weights (${\alpha }_i$) to each model’s output. The softmax function is then applied to the weighted sum to obtain the final ensemble prediction as presented in Equation (4).

$$\mathrm{Soft}\mathrm{Voting}\mathrm{Ensemble}\mathrm{Output}=\mathrm{Softmax}\left(\sum _{i=1}^N{\alpha }_i·{\mathrm{Output}}_i\right)$$

(4)

Here, N is the number of base models (two in this case), ${\alpha }_i$ represents the weight or confidence assigned to each base model’s output, and ${\mathrm{Output}}_i$ is the output of the ith base model.

4.4. Stacking Ensemble Model

The stacking ensemble model, which is presented in Figure 2, is an advanced ensemble learning technique designed to enhance the predictive performance by combining the outputs of multiple base models. In this configuration, it integrates the predictive capabilities of the Multi-Head Attention model and the hybrid CNN-GRU with attention model, thereby creating a powerful and accurate ensemble. It combines the predictions of the Multi-Head Attention and hybrid CNN-GRU with attention models in a final dense layer. The outputs of both models serve as input features for the dense layer, which learns to weigh and combine these features to produce the ensemble prediction.

$$\mathrm{Ensemble}\mathrm{Output}=\mathrm{Dense}\left([{\mathrm{Output}}_{\mathrm{Multi}-\mathrm{Head}\mathrm{Attention}},{\mathrm{Output}}_{\mathrm{Hybrid}\mathrm{CNN}-\mathrm{GRU}}]\right)$$

(5)

4.5. Optimized Multi-Head Attention Model

The optimized version of the Multi-Head Attention model [31] is an extension of the original transformer architecture using the Optuna optimization algorithm, thereby allowing the model to jointly attend to different positions or patterns in the input sequence effectively. Using multiple attention heads, it captures diverse information simultaneously. What follows are the key components and mathematical equations for a Multi-Head transformer: The advanced transformer model leverages the foundational architecture of the transformer while incorporating advanced parameterizations for enhanced adaptability. The scaled dot product attention mechanism is defined as follows:

$$\mathrm{Attention}(Q,K,V)=\mathrm{softmax}\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)·V$$

(6)

For Multi-Head Attention, the model concatenates individual attention heads, which are each computed as

$$\mathrm{Multi}-\mathrm{Head}(Q,K,V)=\mathrm{Concat}({\mathrm{head}}_1,\dots ,{\mathrm{head}}_h)W_O$$

(7)

$${\mathrm{head}}_i=\mathrm{Attention}(Q{W}_i^Q,K{W}_i^K,V{W}_i^V)$$

(8)

where Q, K and V are the Query, the Key, and the Value matrices, respectively, $W_i^Q$, $W_i^K$, and $W_i^V$ are learned weight matrices specific to each head, and $W^O$ is a learnable weight matrix for the output.

The positionwise feedforward (FFN) networks are given by

$$\mathrm{FFN}\left(x\right)=\mathrm{ReLU}(x{W}_1+b_1)W_2+b_2$$

(9)

where $W_1$, $W_2$, $b_1$, and $b_2$ are learnable weight matrices and biases, respectively.

Layer normalization and residual connections are applied through the following:

$$\mathrm{LayerNorm}(x+\mathrm{Sublayer}(x\left)\right)$$

(10)

As mentioned above, this model is introduced as optimized using the Optuna hyperparameter optimization framework, which is further elaborated in Section 4.7. The optimization parameters are the dimension of the model, the number of attention heads, and the number of transformer layers, and the goal is to find the appropriate combination of these parameters that can minimize the optimization function of the specific optimization algorithm, which is the validation loss of the mean squared error.

4.6. Benchmark Perceptron Model

The benchmark perceptron model constitutes a fundamental, yet powerful architecture commonly used as a baseline in various machine learning tasks. This model typically involves a single dense layer, also known as a fully connected layer, which serves as the primary component for learning and making predictions. The dense layer accepts input data, processes it through a set of interconnected neurons—with each connected to every neuron in the subsequent layer—and outputs the final predictions or classifications.

The perceptron model is a foundational neural network architecture, thereby forming the basis for more complex neural networks. It consists of a single layer with input nodes, with each associated with a weight and an activation function that determines the output. Mathematically, the output ($\widehat{y}$) of the perceptron for input features $x_1,x_2,\dots ,x_n$ and weights $w_1,w_2,\dots ,w_n$ is calculated as

$$\widehat{y}=\mathrm{activation}\left(\sum _{i=1}^n{x}_i·w_i+b\right)$$

(11)

where b is the bias term.

Completing the description of the architectures of all models, a brief review of both the explainability process technique and the Optuna optimization framework on which the optimization of each model was conducted is presented.

4.7. Explainability Process

In order to enhance interpretability, the paper introduces an explainability process, thereby shedding light on the impact of variables within the models. The specific equations for this process may vary based on the chosen explainability technique.

The integration of explainability in electricity price forecasting holds paramount significance, as it enhances the transparency and interpretability of predictive models. In an era dominated by complex machine learning algorithms and sophisticated models, understanding the rationale behind price predictions becomes imperative for stakeholders such as energy traders, grid operators, and policymakers. Explainability not only fosters trust in forecasting models but also facilitates the identification and mitigation of potential biases or inaccuracies. By shedding light on the intricate relationships between input variables and predicted outcomes, explainable models empower industry professionals to navigate the intricate terrain of electricity markets with greater confidence and precision, thereby ultimately contributing to more robust and reliable forecasts.

For this reason, SHAP (SHapley Additive exPlanations) [32] has been utilized. SHAP operates by decomposing the model output into sums of individual feature impacts. It computes values representing each feature’s contribution to the overall model outcome, thereby enabling a nuanced understanding of feature importance. However, time series data’s temporal dependencies necessitate additional preprocessing or the use of models that inherently capture sequential patterns. SHAP values, which indicate the impact of the features on predictions, can be interpreted through visualization, with positive and negative values denoting positive and negative contributions, respectively. It is crucial to consider dynamic features in the analysis.

4.8. Optimization Framework

Optuna [33] is a Python framework that automates hyperparameter optimization, thus making the task of finding optimal hyperparameter values to achieve superior model performance more convenient. It employs a trial-and-error methodology to autonomously explore and pinpoint the best hyperparameter configurations. This algorithm uses a historical record of previous trials to guide its decision making regarding which hyperparameter values to investigate next. These data inform its selection of promising areas within the hyperparameter search space, thereby guiding subsequent trials in those regions. As new results become available, Optuna refines its identification of even more promising regions. This iterative process is based on the knowledge accumulated from previous trials. At the core of this optimization process is the utilization of a Bayesian optimization algorithm called the tree-structured Parzen estimator.

5. Exploratory Data Analysis and Features Creation

In this section, the behavior of the time series of electricity prices over time is presented and analyzed in detail. Initially, reference is made to the selection of the data set, as well as the separation of the entire data set into training and test sets. Subsequently, the variability of the time series is extensively presented, including the seasonal patterns it exhibits and its overall behavior. This analysis initially includes the visualization and statistical features of the price timeseries, followed by the analysis of all variables under study and the correlations they exhibit with the price.

5.1. Data Set Selection

For this study, the German electricity market has been selected for three main reasons. Germany has more than 83 million residents and borders nine European countries: Denmark to the north; the Netherlands, Belgium, Luxembourg, and France to the west; Switzerland and Austria to the south; and the Czech Republic and Poland to the east. Additionally, Germany presents a diversity of energy sources used at the power plants for electricity production, from conventional energy sources like lignite, coal, gases, and nuclear power to renewable sources like wind turbines onshore and offshore, photovoltaics, and sewage gases. The selected period to retrieve these data was from 1 October 2018 to 30 August 2023.

The actual electricity consumption, electricity generation from all energy plants, and energy price data were retrieved from the Bundesnetzagentur’s electricity market information platform SMARD [34]. The resolution of the data is one time step per hour and does not contain missing values.

Furthermore, the climate condition for the period under investigation was retrieved from NASA’s Modern Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2) [35]. The parameters retrieved from the M2I1NXASM database are air temperature and air-specific humidity at 2 m in units of K and kg/kg, respectively. The resolution of the data is one time step per hour. The data set presents missing values that are filled with the mean value of the same timestep of other years in the data set.

The final data set is composed of the primary time series of sources mentioned above, which were processed and combined. Regarding data partitioning, the temporal period from October 2018 to February 2023 was selected as the training data set for the problem studied. The next six months of the data set were then designated as the testing set.

5.2. Electricity Price Variation

Initially, a crucial consideration involves evaluating the time series for stable seasonality. To achieve this, Figure 3 illustrates both the price variations from 2018 to 2023 and their corresponding weekly average prices. The figure depicted in the following chart confirms substantial fluctuations in electricity price volatility throughout the observed period.

More specifically, it can be observed that until November 2021, both the price and the average price exhibited stability, without extreme values. From November onward, a significant increase was observed in both time series, with the average hourly price reaching 600 €/MWh and the corresponding mean price reaching 40 €/MWh. Subsequently, from the beginning of 2023 onward, the price variation appeared to stabilize, and extreme values were eliminated. These extreme fluctuations create imbalances in the electricity market, thus making price prediction in wholesale trading an exceptionally challenging process. Political–economic factors caused imbalances in wholesaler transactions, thus resulting in the market losing its stability with respect to price fluctuations. Therefore, it becomes evident that the accurate prediction of the hourly price is a difficult task, but it is simultaneously a significant challenge for deep learning models.

In contrast,

Table 1. Descriptive statistics for electricity price.

Year	Number of Samples	Mean Value (€)	Standard Deviation (€)	Minimum Value (€)	Maximum Value (€)	Percentile 25% (€)	Percentile 50% (€)	Percentile 75% (€)
2018	2208	52.606	18.59	−19.43	128.26	44.305	51.83	64.207
2019	8760	37.674	15.468	−85.04	121.46	31.057	38.06	46.270
2020	8784	30.469	17.499	−83.94	200.04	21.750	30.99	40.242
2021	8760	96.855	73.676	−69.00	620.00	53.007	75.48	112.032
2022	8760	235.446	142.808	−19.04	871.00	134.197	208.34	310.080
2023	5832	99.705	44.918	−80.69	291.93	80.090	100.515	126.067

illustrates the annual electricity price statistics. The electricity price data spanning from 2018 to 2022 were utilized as training data, January and February 2023 served as validation data, and the final six months of our sample were designated for testing purposes. Upon examination of the data, notable patterns come to light. The standout year is 2022, which was marked by substantial shifts, particularly in maximum prices. A significant surge compared to the preceding years renders it the most volatile year within our dataset.

Therefore, from Table 1, it is evident that the maximum electricity price increased exponentially between 2020 and 2022. Specifically, there was a 335% increase between 2020 and 2022, thereby highlighting the exceptionally challenging nature of accurately predicting the electricity price. This fact gives special value to the problem, as it is a challenge.

5.3. Electricity Price Descriptive Analysis

In this subsection, a comprehensive analysis of the electricity price time series is presented, thereby starting from its fluctuation at the quarter and monthly levels and ending at the hour level for each average month.

5.3.1. Quarterly Density Variation

The regular hourly pattern persisted consistently throughout each month throughout the course of the study. In Figure 4, the quarterly analysis reveals that Q1 and Q4 notably displayed the highest occurrences of electricity price outliers, with June emerging as the month characterized by the highest frequency.

Furthermore, in all study years, July, August, September, and December consistently manifested the highest price levels. These observed trends can be attributed to diverse factors, including seasonal fluctuations in demand influenced by weather conditions and concurrent upswings in economic activity, among other contributing elements.

5.3.2. Monthly Price Variation

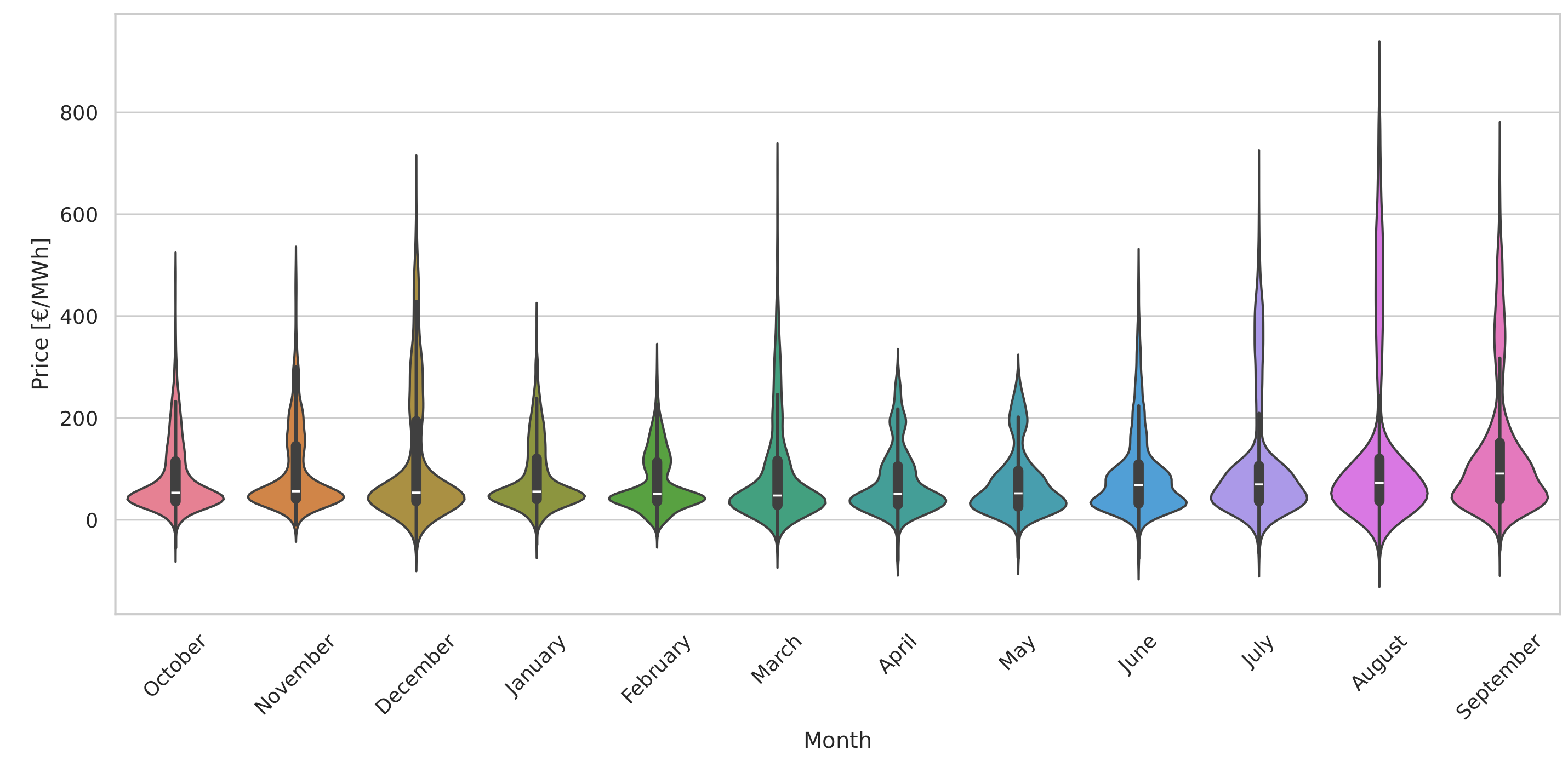
Figure 5 presents the violin plot of the average monthly price variation, thereby taking into account all the years from 2018 to 2023. We observe that all months showed negative electricity prices. While August and September had the highest prices compared to the other months, January, February, April, May, October, and November showed peaks, which represent high frequency and probability to exhibit values nearly the median.

5.3.3. Daily Price Variation

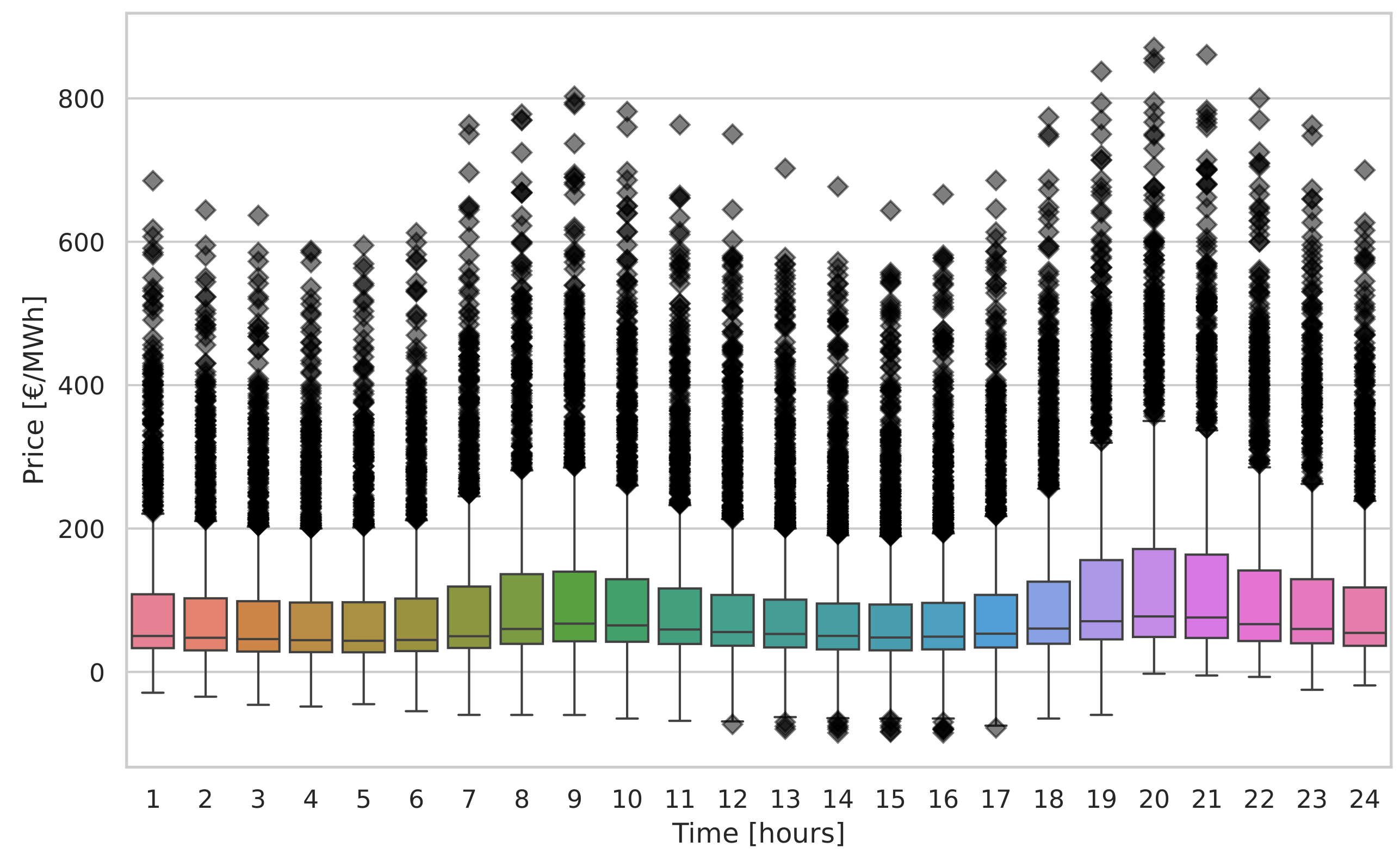
Figure 6 presents the volatility of the average price over a period of 24 h (1–24 h). It is noted that peak demand occurred during the hours of 09:00 and 20:00 throughout the day.

5.3.4. Daily per Month Price Variation

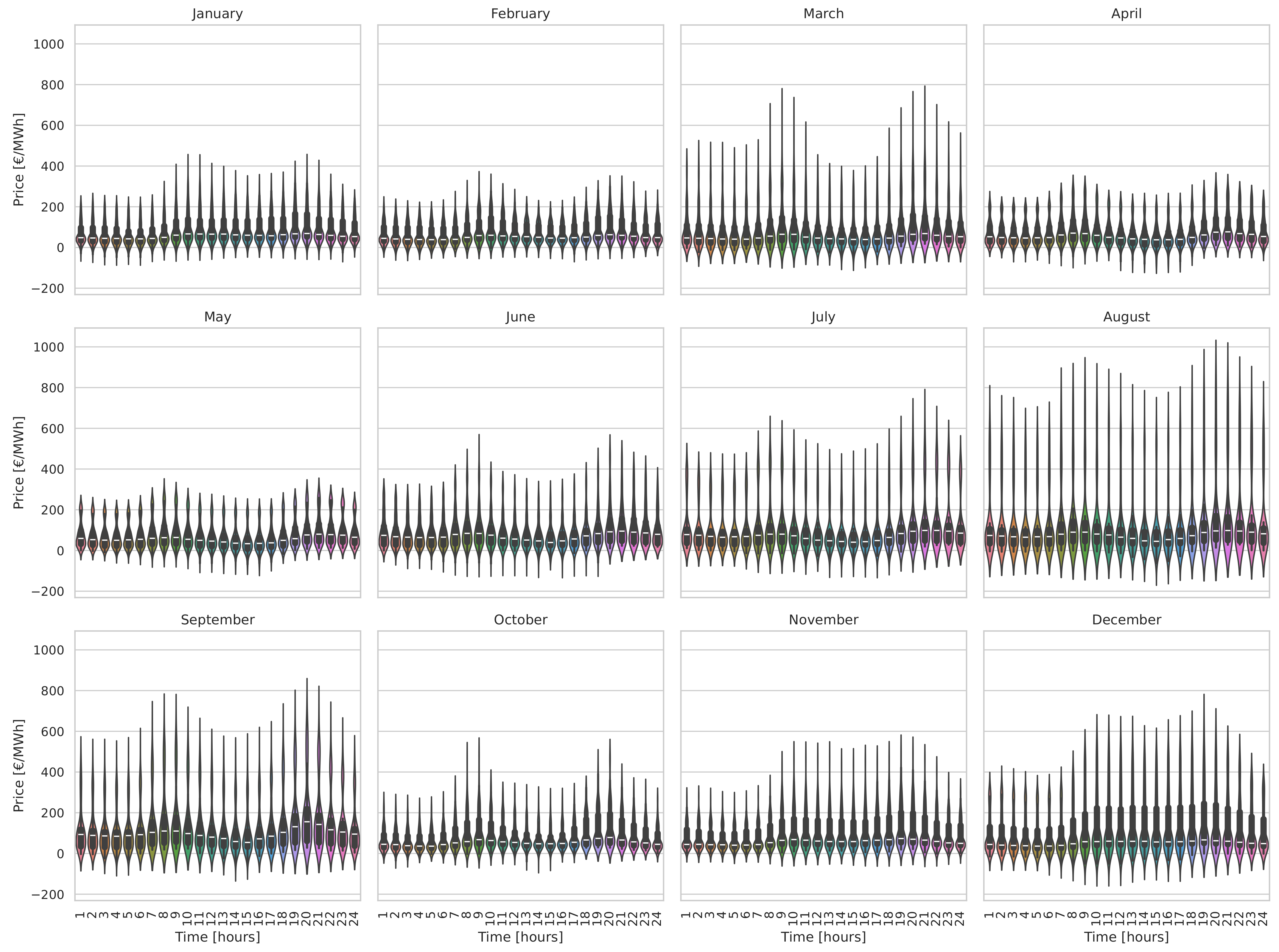
Figure 7 visualizes the average hourly price fluctuation of electrical energy for each of the months of the year. Specifically, during peak hours (specifically at 8 and 19 o’clock), the price rose during the daily peak. It should be noted that the fluctuation of the average hourly price exhibited common peak periods for each month of the year. Within the twenty-four-hour period, two peak intervals were observed. The first included the period between 7–9 h, and the second included hours 18–20. Therefore, it is evident that despite the time series exhibiting abrupt and irregular changes from hour to hour, the average fluctuation followed a more stable behavior. The presentation of exogenous variables follows, along with their correlations with the time series of prices, guide us in the final configuration of the input data for model training.

5.4. Feature Engineering and Variables Selection

The strategy followed in the paper in question regarding the data used as input variables in the created models initially included the collection of the relevant time series of data. Regarding the data collected, they included the following variables:

• Price [€/MWh];
• Actual Load;
• Fossil brown coal/lignite;
• Fossil gas;
• Fossil hard coal;
• Hydropumped storage;
• Hydro run-of-river and poundage;
• Hydro water reservoir;
• Nuclear;
• Solar;
• Wind onshore;
• Temperature;
• Humidity.

Then, we used the one-hot encoding technique [36] to create cyclical time variables, which can be used in short-term electricity price forecasting. This particular method enhances the ability of deep learning algorithms to capture the behavior of the time series at the weekly, daily, and hourly levels. Specifically, the following were detailed:

• day_of_week_sin;
• day_of_week_cos;
• Month of the Year Sin;
• Month of the Year Cos;
• IsWeekend;
• hour_sin;
• hour_cos;
• quarter.

Time series refer to systematically organized data sets arranged in chronological order and collected at regular intervals, such as hourly, daily, or weekly observations. The inherent structure of these sequential data sets introduces potential interconnections among response variables, which poses significant challenges for machine learning (ML) and deep learning (DL) algorithms, especially those commonly used in regression tasks. These challenges manifest mainly as issues of multicollinearity and nonstationarity. In addressing the prediction problem at hand, we had a total of 21 variables available for integration into our models. Generally, short-term forecasting of electricity prices is a complex, multidimensional problem that requires in-depth analyses of how each variable influences the final price prediction. Forecasting time series problems and tasks requiring the application of artificial intelligence models demand a comprehensive analysis of all correlations among variables to identify the most fitting ones for each specific problem.

To curate a data set suitable for the forecasting models employed, the time series undergoes transformation into a reshaped dataset featuring nontime-dependent input features (X) and output variables (Y). The input features take the form of [samples, lags, features], while the output variables maintain a structure of [samples, horizon], thus aligning with the model architecture outlined in this paper. This transformation involves implementing the sliding window technique, which is particularly advantageous for predicting time series data. In this context, a 24 h forecasting sliding window with electricity prices, as well as the exogenous variables, was selected for each forecasting hour. These choices resulted from a thorough analysis of time series tools and meticulous model tuning, thereby aligning with the model’s objective of providing short-term predictions for electricity prices. The application of this technique is visually represented.

5.5. Pearson’s and Spearman’s Correlation

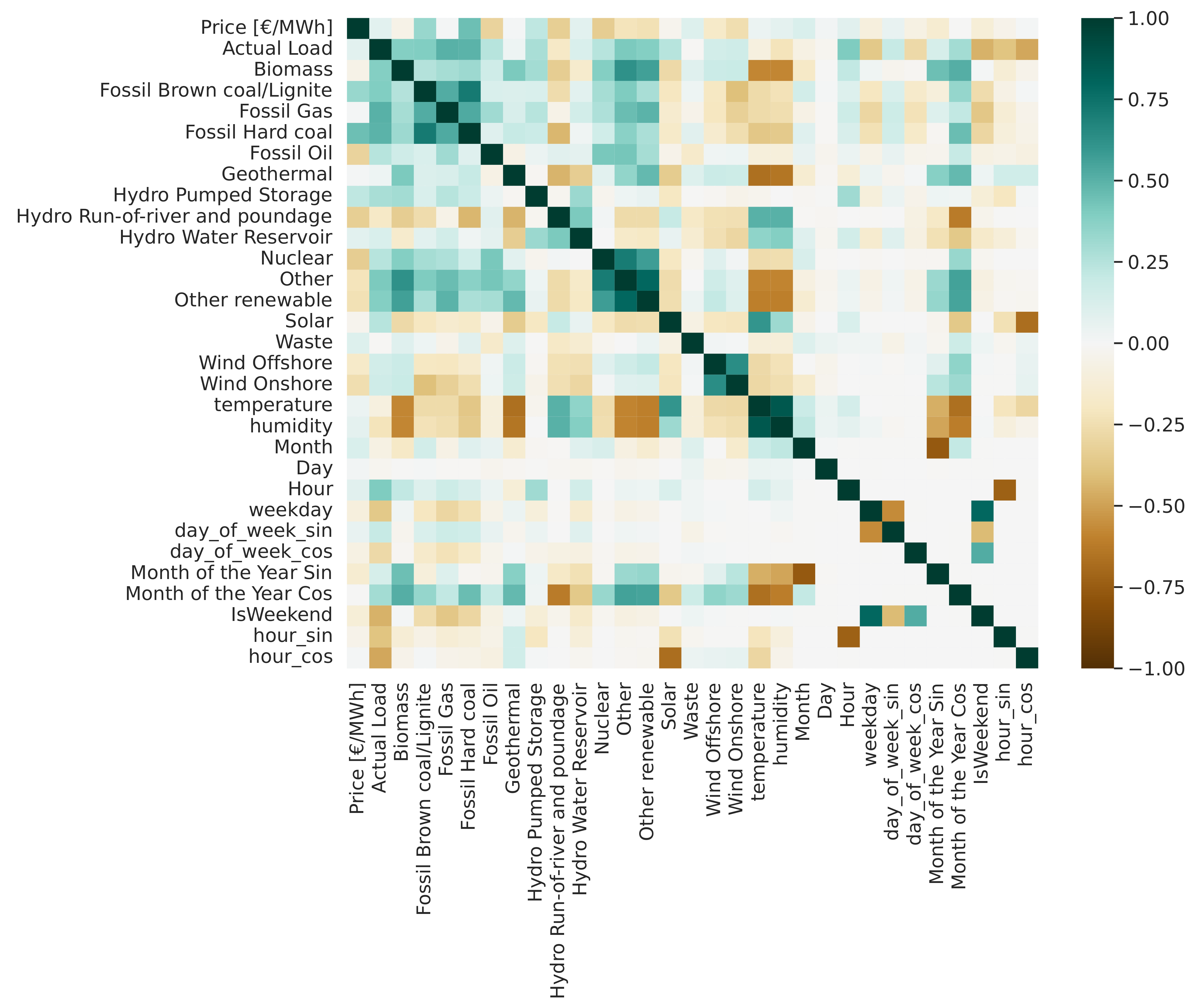
In this subsection, the correlations among all relevant time series are presented with the aim of arriving at the optimal combination of input parameters for the algorithms. For this purpose, the Pearson and Spearman correlations have been calculated and presented in Figure 8. In the realm of statistical analysis, the Pearson correlation constitutes a parametric metric utilized to evaluate the magnitude and direction of linear associations between two continuous variables. Based on the assumption of an approximate normal distribution of variables, Pearson’s (r) computes the correlation through normalization of covariance by the product of standard deviations. In contrast, the Spearman rank correlation, denoted as Spearman’s $\rho$, emerges as a nonparametric measure specifically designed to scrutinize the monotonic relationship between two variables. Not reliant on linearity assumptions, Spearman’s correlation is apt for ordinal or ranked data and crucially exhibits heightened resistance to outliers in comparison to the Pearson correlation. Both metrics assume pivotal roles in systematically examining and comprehending the interrelationships among variables within various research domains.

Based on the features that were studied and the correlations they exhibited, numerous experiments were conducted to identify the optimal variable combinations, thereby aiming to enhance the models’ performance in forecasting electricity prices. For this purpose, tests were performed with models that included both high-variability and single-variable models. Extensive experiments were carried out using historical data from the time series of prices in combination with cyclical temporal variables, as presented above. Concerning the high-variability scenario, tests were performed both with independent or exogenous variables in combination with the mentioned temporal variables and without them. On the basis of both the following diagrams and the experimental approaches conducted, we arrived at the optimal combination of input parameters for each of our models as follows. Based on experimental approaches, we arrived at the optimal combination of exogenous variables, from which the most accurate prediction results were derived. It was observed that our models performed better in understanding the patterns of the electricity price time series when the parameters were selected that not only exhibited high average correlation but also capture both negative and positive values of the price. Based on Figure 9, significant conclusions emerge regarding the formation of electricity prices in the Germany–Luxembourg interconnection and, more broadly, in the wholesale market.

The first reasonable conclusion drawn is that conventional energy sources exhibited a positive correlation, both in Pearson and Spearman analyses. Furthermore, renewable energy sources (RESs) showed negative correlations with price fluctuations. Remarkably, the variable ‘Hydro Run of River and Poundage’, despite accounting for only 14% of the average production compared to ‘Fossil Brown coal/Lignite’, demonstrated scientifically acceptable correlations of −0.33 and −0.35 with the price, respectively, thereby underscoring its consideration in price forecasting.

Therefore, upon a more comprehensive examination, it is discerned that the price time series manifests substantial fluctuations in polarity, thereby notably encompassing both negative and positive values. This intrinsic characteristic introduces complexity for a model to adapt to the time series, given the absence of stable patterns typically encountered in load forecasting. A thorough investigation into the origins of this phenomenon reveals that during periods characterized by extremely negative prices, there was a significant surge in renewable energy sources (RESs) production, particularly marked by a rapid increase in wind onshore generation. Simultaneously, conventional modes of production, such as ‘Fossil Brown coal/Lignite’ and ‘Fossil Hard coal’, witnessed substantial decreases in their output. Consequently, an excess of electrical energy occurred, thus surpassing demand during these intervals and leading to exceptionally negative price spikes. Figure 10 analyzes and confirms the above interactions between the examined features.

More generally in recent years, the phenomenon of zero or even negative electricity prices has been observed in the European energy market for some hours of the day. In particular, the combination of RESs and reduced demand seems to be shaking the European electricity market. The problem arises when the increase in RESs production, in periods of favorable weather conditions, is combined with a limited demand. Given that RESs are prioritized in the system, on days when there is excess production along with reduced demand, there is no room left in the system for thermal units. They do not function as reserves either, thus leaving the country’s system uncontrollable in the event of a sudden change in weather conditions, which will abruptly drop RESs production. Negative prices are an indication of what will happen to European electricity markets if the glut of planned renewable energy generation is not met by demand shifting. The hope is that eventually bigger fleets of electric cars, smarter grids, and better battery technology will fill the gap, but for now, the mismatch is causing concern for governments and companies.

5.6. Formation and Analysis of the Independent Variables

Based on the above analysis and after several trials conducted, which included both tests only with the price variable along with the cyclical temporal variables formed by one-hot encoding, as well as combinations of energy production variables with and without these cyclical variables, we have concluded that for an optimal model performance, a time series for each of the 24 preceding hours was to be used for the following six input variables: electricity price and the values of energy produced from the exogenous variables of ‘Fossil Brown coal/Lignite’, ‘Fossil Hard coal’, ‘Nuclear’, ‘Wind Onshore’, and ‘Hydro Run-of-river and poundage’.

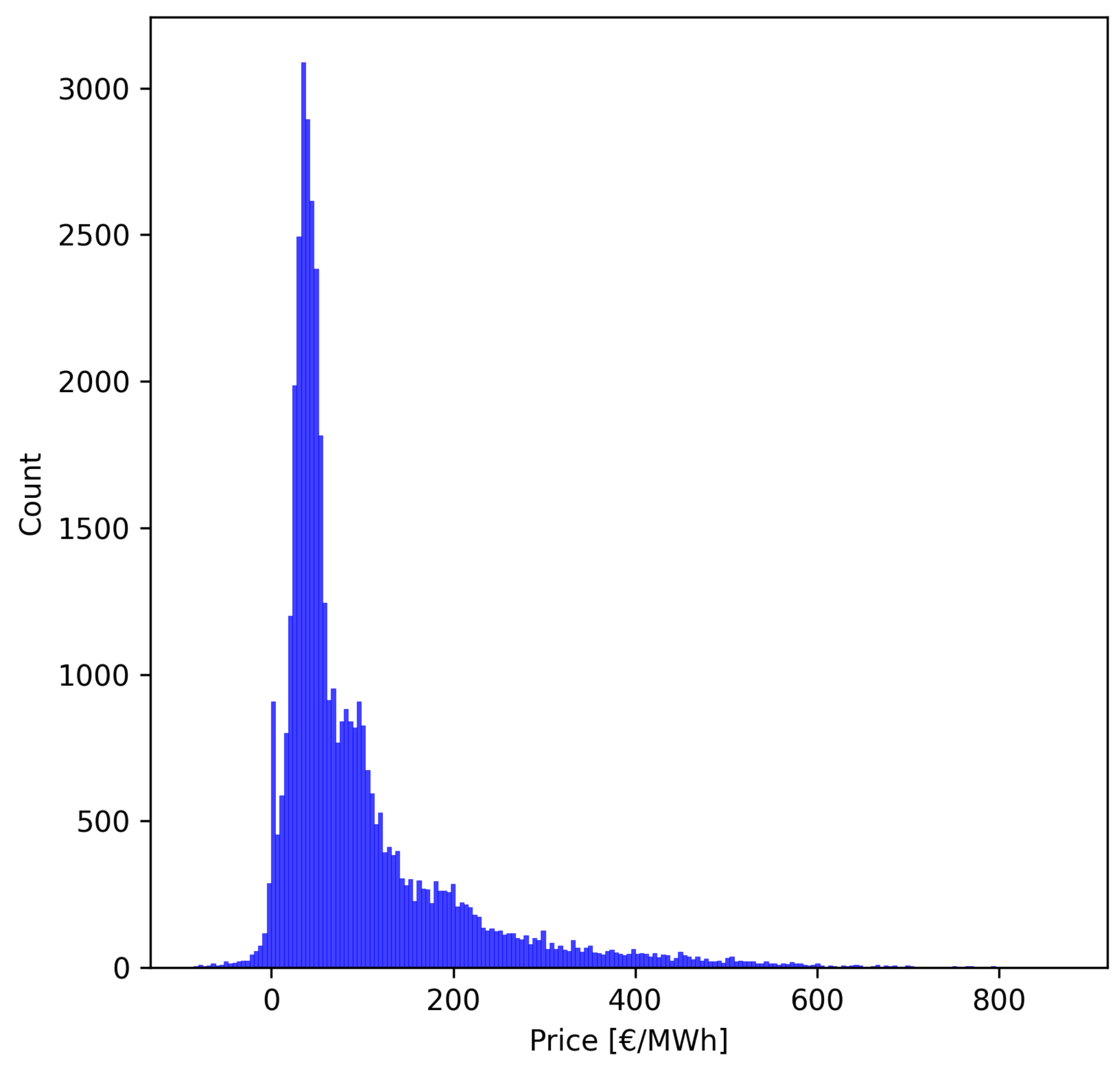
In Figure 11, the overall time series of values is presented, which represents the count of values for each hour. It appears that most of the values in the time series fell within the range of 50–100 €/MWh. However, simultaneously, the time series showed outliers, as a significant number of values exceeded 300 € and even reached 500 €. It is observed that the price distribution did not follow normality, with the majority of values being less than 100 €/MWh. Additionally, the combination of high values along with negative values created a time series that did not follow consistent patterns in hourly fluctuations, unlike load time series, which typically exhibit stable seasonality and variations.

Moving to the variables used as input to the models, Figure 12 illustrates the graphical representation of the distribution of the six input variables. Specifically, it is noteworthy that the time series of “Fossil Hard Coal” and “Wind Onshore” exhibited a uniform distribution, which a pattern that was also observed between the variables “Hydro Run-of-river and poundage” and “Fossil Brown coal/Lignite”. Notably, the distribution of “Nuclear” presented an intriguing pattern, thereby containing fluctuations and not adhering to a specific distribution approach, unlike the other forms of energy.

5.7. Graphical Illustration of Feature Relations

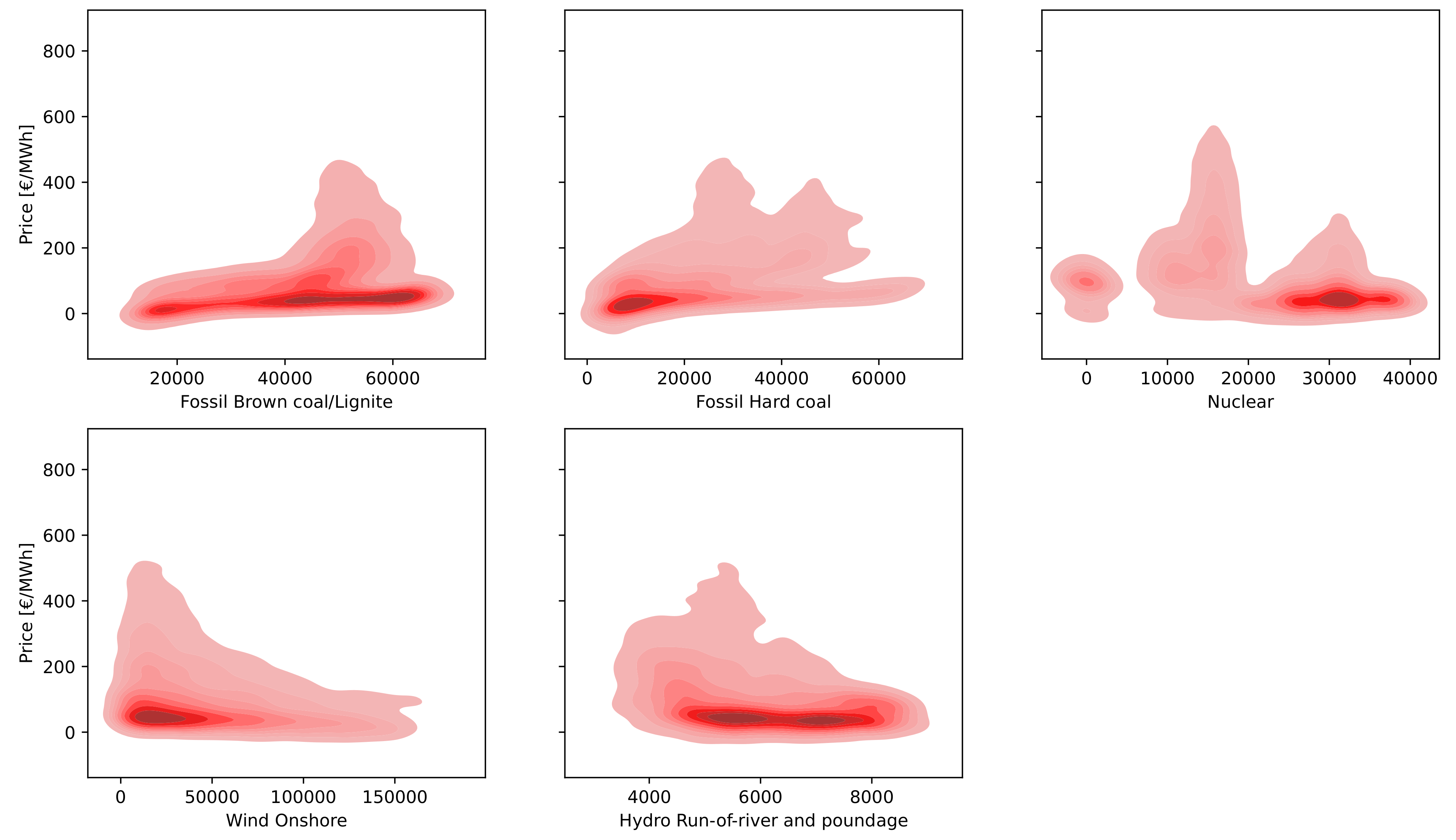
Figure 13 visualizes the relationship between each of the exogenous variables and the variable of electricity price. Contours and solid color map represent the estimated probability density function of the joint distribution.

Based on Figure 13, it is observed that the features “Fossil Brown coal/Lignite” and “Hydro Run-of-river and poundage” exhibited a smooth correlation with the price of electrical energy, a fact which is proved by the intense color that extends almost across their entire value range. Additionally, concerning the variables “Fossil Hard coal” and “Wind onshore”, a similar smoothness of prices was noted with a narrower range of price density concentration. Finally, regarding nuclear energy production, it is noted that the variable “Nuclear” demonstrated a higher density at higher values, which is a particularly interesting fact indicating its significant influence on shaping prices at higher nuclear energy production values.

5.8. Sliding Window Technique

For the training of our models and the formation of the 3D input, the sliding window technique was employed. For each forecasted hour, a 24 h sample of each of the six variables provided as inputs was utilized in order to make forecasts suitable for the intraday and balancing markets. In more detail, the methodology involves utilizing the preceding 24 values of electricity prices, the corresponding 24 historical values of conventional generation units—namely ‘Fossil Hard Coal’ and ‘Fossil Brown coal/Lignite’—and the historical 24 values of renewable energy sources such as ‘Wind Onshore’ and ‘Hydro Run-of-river and poundage’. Finally, the historical values of nuclear energy for the variable ‘Nuclear’ were incorporated.

5.9. Software Environment

The Python 3.9 programming language, along with the Tensorflow, sklearn, Keras, Pandas, and Numpy libraries, was used for the simulations in this study. All computational resources for these simulations were exclusively cloud-based, specifically utilizing Google’s Colab infrastructure. The daily forecasts for all models also differed depending on the size and complexity of each forecasting model. More intricate and computationally demanding models, such as deep learning structures, required extensive virtual GPU resources. The run times for these complex models ranged from several hours to several days, and they were executed in batches spanning three to five months. The adoption of cloud-based resources facilitated efficient and scalable computation of simulations, thereby enabling the concurrent execution of multiple models and datasets. The varying duration of each simulation run underscores the computational requirements of the forecasting models and emphasizes the importance of suitable resources to ensure accurate and timely results. These findings offer valuable information on the practical considerations when implementing energy demand forecasting models in real-world applications.

5.10. Evaluation Strategy

To evaluate the effectiveness of the various forecasting models and techniques used in this investigation, we assessed their results using a set of metrics. The following metrics were used for this purpose, thereby offering valuable insights into the precision and dependability of the forecasting models. Specifically, the mean square error (MSE) is given by Equation (12), where $y_i$ is the true value, and $\widehat{y_i}$ is the predicted value.

$$\mathrm{MSE}=\frac{1}{n}\sum _{i=1}^n{(y_i-\widehat{y_i})}^2$$

(12)

The root mean squared error (RMSE) is given by Equation (13), where $y_i$ is the true value, and $\widehat{y_i}$ is the predicted value.

$$\mathrm{RMSE}=\sqrt{\frac{1}{n}\sum _{i=1}^n{(y_i-\widehat{y_i})}^2}$$

(13)

The mean absolute percentage error (MAPE) is given by Equation (14), where $y_i$ is the true value, and $\widehat{y_i}$ is the predicted value.

$$\mathrm{MAPE}=\frac{1}{n}\sum _{i=1}^n\frac{|y_i-\widehat{y_i}|}{y_i}$$

(14)

6. Results Analysis and Discussion

In this section, the forecasting results of each model are presented. Based on the results of

Table 2. Performance comparison of each model.

Model	MSE (€/MWh)2	RMSE (€/MWh)	MAE (€/MWh)	MAPE (%)
CNN Attention	163.111	12.771	9.849	10.699
Multi-Head Attention	109.920	10.484	6.342	6.889
CNN-GRU Attention	110.738	10.523	5.832	6.333
Stacking Ensemble	128.389	11.330	8.377	9.100
Soft Voting Ensemble	108.185	10.401	5.639	6.125
Benchmark: Perceptron	229.706	15.156	12.240	13.296

, it is evident that, initially, the hybrid CNN-GRU with an attention mechanism and the Multi-Head Attention models achieved great prediction accuracy. Subsequently, the soft voting ensemble model achieved the highest performance in each of the four metrics, as shown in Table 2. These outcomes are quite satisfactory and encouraging, as in most previous studies on time series prediction, models incorporating attention mechanisms and transformers showed low performances.

6.1. Performance of the Models

The models’ performance outcomes were evaluated based on the mean absolute percentage error (MAPE) metric, thereby providing a clear and intuitive understanding of the prediction accuracy of the models. In particular, the novel CNN-GRU with an attention mechanism model demonstrated a high accuracy of prediction, with an MAPE of 6.333%. This is a notable achievement, especially considering the historical challenges associated with attention mechanisms in transformer models. Also, the Multi-Head Attention model achieved very high performance, thereby reaching an MAPE of 6.889%. The CNN attention model was observed to exhibit lower prediction results compared to the other deep learning models, thus indicating that convolutional mechanisms may not efficiently collaborate with the attention mechanism to achieve accurate prediction results.

The performance evaluation of the soft voting ensemble model showcases its efficacy in electricity price prediction. Metrics such as MAPE demonstrate the high accuracy of the model, with a notable value of 6.125%. Simultaneously, achieving an MSE of 108.185 €/MWh, an RMSE of 10.401 €/MWh, and an MAE of 5.639 €/MWh, this model leveraged the strengths of both the Multi-Head Attention and the hybrid CNN-GRU with attention models. The weighting mechanism allows the ensemble to adaptively give more influence to the model with higher confidence, thus resulting in improved predictive accuracy and robustness. Regarding the stacking ensemble model, this algorithm achieved an MAPE of 9.100%, which was higher than soft voting at 2.975%. This difference may be possibly attributed to the final dense layer, which introduces additional trainable parameters to the final model, thereby making it more challenging to converge to the optimal result during the training period.

Regarding the benchmark perceptron model, it is well suited for linearly separable problems and binary classification tasks. Its simplicity makes it computationally efficient and easy to interpret. However, its limitations include the inability to handle nonlinear relationships in data, which led it achieving the lowest performance compared to the other models, with an MAPE of 13.296%.

Additionally, concurrently with the performance of the models, a significant factor, especially for real-time conditions, is the training time of the models. As emphasized above, a virtual GPU was utilized for faster and more efficient training for all models. For the three deep learning models, CNN attention, CNN-GRU with attention, and Multi-Head Attention, the training time, once the optimal hyperparameters were found, did not exceed 20 min. In particular, the Multi-Head Attention model, due to the multiple number of heads, was the slowest compared to the other two. Regarding the stacking ensemble model, the training time exceeded that of the simple ones and was approximately 30 min. The soft voting ensemble model, due to initially relying on the training of two separate models, required approximately 20 min of training time. The perceptron model is considerably simpler than the others, with its training time estimated at 10 min.

The minimal disadvantages of modeling techniques are based on the fact that the proposed models, which all use attention mechanisms, are quite complex and have multiple trainable parameters, with the result that their training is quite difficult compared to simpler models, such as the benchmark perceptron model that is used.

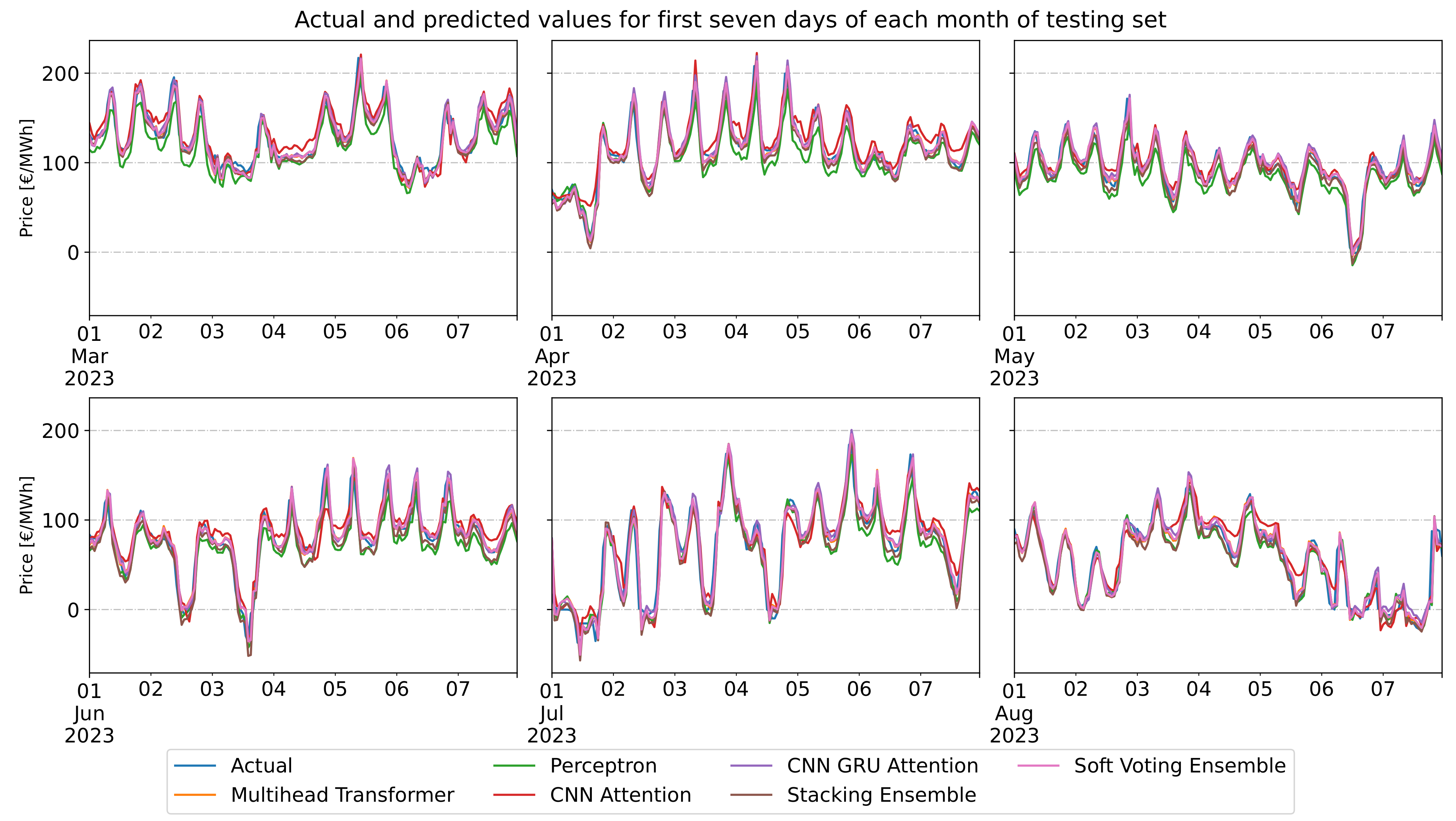
Finally, Figure 14 illustrates the plot diagram of the actual and predicted values for the first seven days of each month in the testing period. From the plots most of the models present exceptional predictability except for the base model and CNN with attention model, as described above. Additionally, in Figure 15, the residuals between actual and predicted values are plotted, so it clearly shows the performance of each model. The specific plot shows that all the models behaved approximately the same; they presented common prediction characteristics and prediction residual outliers.

6.2. Explainability Process

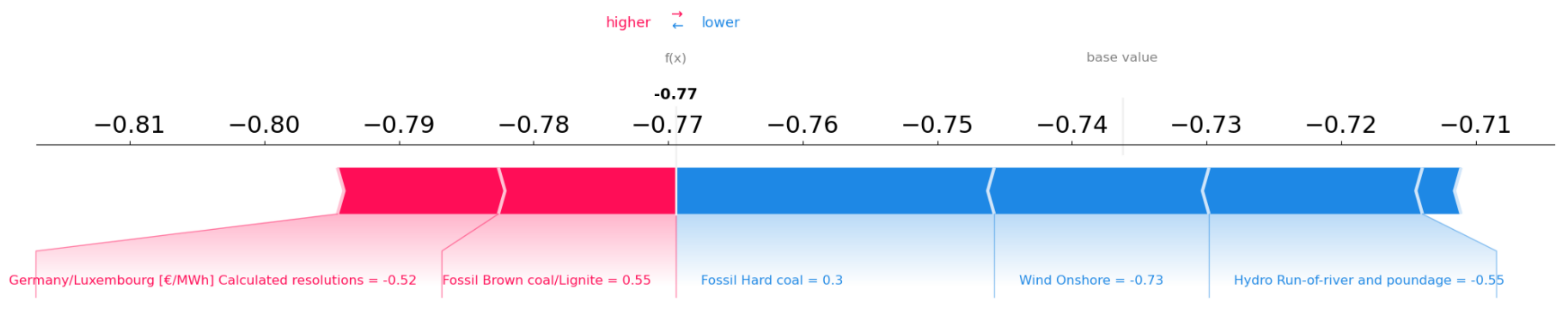
In this subsection, the explainability process is presented. We will try to interpret the impact of the independent exogenous variables used in our models as input parameters. For this purpose, we will use the benchmark model, and through the SHAP library, we will delve deeper into its functionality. According to Figure 16, it is observed that for the longest period of observations, the price, as well as the variable ‘Fossil Brown coal/Lignite’, had the highest effect on price prediction. More specifically, the price achieved a score of −0.52, the ‘Fossil Brown coal/Lignite’ achieved a score of 0.55, the ‘Fossil Hard coal’ achieved a score of 0.3, the ‘Wind onshore’ achieved a score of −0.73, and the variable ‘Hydro Run-of-river and poundage’ achieved a score of −0.55.

Following the explainability analysis, Figure 17 presents the effect of the input variables for a period in which negative electricity prices were observed. It is noteworthy that for the specific interval, the effect of the renewable energy sources was very high and presented negative values, a fact that shows a negative correlation between the RES variation and the price of electricity, as was analyzed above. Finally, it seems that the effect of conventional energy sources for these cases was quite small, with the variable ‘Fossil Hard coal’ showing a value of 0.3.

7. Conclusions and Future Work

In this study, a comprehensive and integrated investigation was conducted with the aim of developing novel high-accuracy deep learning algorithms to predict the price of electricity on a short-term basis. Its main objective is two-fold. Firstly, we looked to develop and propose two novel deep learning models: a hybrid CNN-GRU with an attention mechanism and an ensemble learning model that performs with the highest accuracy. Second, we explored the creation of advanced deep learning models with attention mechanisms and tested them on the electricity price data of the Germany–Luxembourg interconnection. For this purpose, an optimized Multi-Head transformer, a CNN attention model, and another ensemble learning category—a stacking ensemble—were investigated. A machine learning model, the perceptron, was selected as a benchmark reference. Among these models, the hybrid CNN-GRU with an attention mechanism stood out as a recommended model, as it has not been used in the literature for electricity price prediction problems until now, which is a fact that instills particular optimism for future studies and applications. Moreover, despite the general performance issues of most transformer algorithms in time series prediction problems, in our case, the Multi-Head transformer model predicted with exceptional accuracy on unknown data. Finally, the integration of two models from the ensemble learning domain and their successful results is both satisfying and challenging in terms of their selection.

A significant observation through the analysis is that the time series of electricity prices does not follow a specific pattern of formation, because their values are influenced by factors such as political conditions prevailing in neighboring countries. These factors are extremely difficult to simulate because of the uncertainty and reshuffling they cause in the wholesale energy market. Also, one more important observation is that the creation of advanced deep learning algorithms with integrated attention mechanisms could play a very important role in the field of wholesale electricity market. In combination with the use of the Optuna optimization algorithm, the hyperparameters of the models can be optimized, thereby acquiring the most suitable architecture and resulting in the achievement of the best results. Accurate price prediction could effectively contribute, in turn, to better production planning for producers, thus reducing deviations with undesirable consequences for system operation.

Regarding future work, the initial focus will be on delving into attention-based algorithms for tackling more intricate challenges in predicting electricity prices, which stands as a significant endeavor within the realm of artificial intelligence. Additionally, there is a prospect to assess the implementation of the algorithms elaborated in this study on short-term load prediction tasks for the flexibility market and day-ahead forecasting. Moreover, the soft voting ensemble Model underscores the potential of amalgamating diverse deep learning structures to enhance timeseries forecasting. Subsequent research could further investigate alternative model combinations, ensemble tactics, and optimization of weight assignments to push the boundaries of excellence in the field. It is worth noting that the models introduced, alongside their hyperparameter optimization techniques, could be explored in various other domains, including industrial, financial, and biomedical sectors for predictive purposes.

Finally, based on the explainability process presented above, future research could concentrate on uncertainty quantification, based on which methods to quantify and explain uncertainties associated with electricity price predictions could be explored. Understanding the level of confidence or uncertainty in forecasts is crucial for decision makers in the energy industry and allows them to make more informed choices regarding resource allocation, risk management, and strategic planning. Furthermore, by incorporating uncertainty quantification into decision processes, stakeholders can respond proactively to potential variations in electricity prices, thereby leading to more resilient and adaptive energy strategies.