Photovoltaic Solar Power Prediction Using iPSO-Based Data Clustering and AdaLSTM Network
Abstract
1. Introduction
1.1. Literature Review
1.2. Main Contributions of This Paper
1.3. Paper Organization
2. Methods
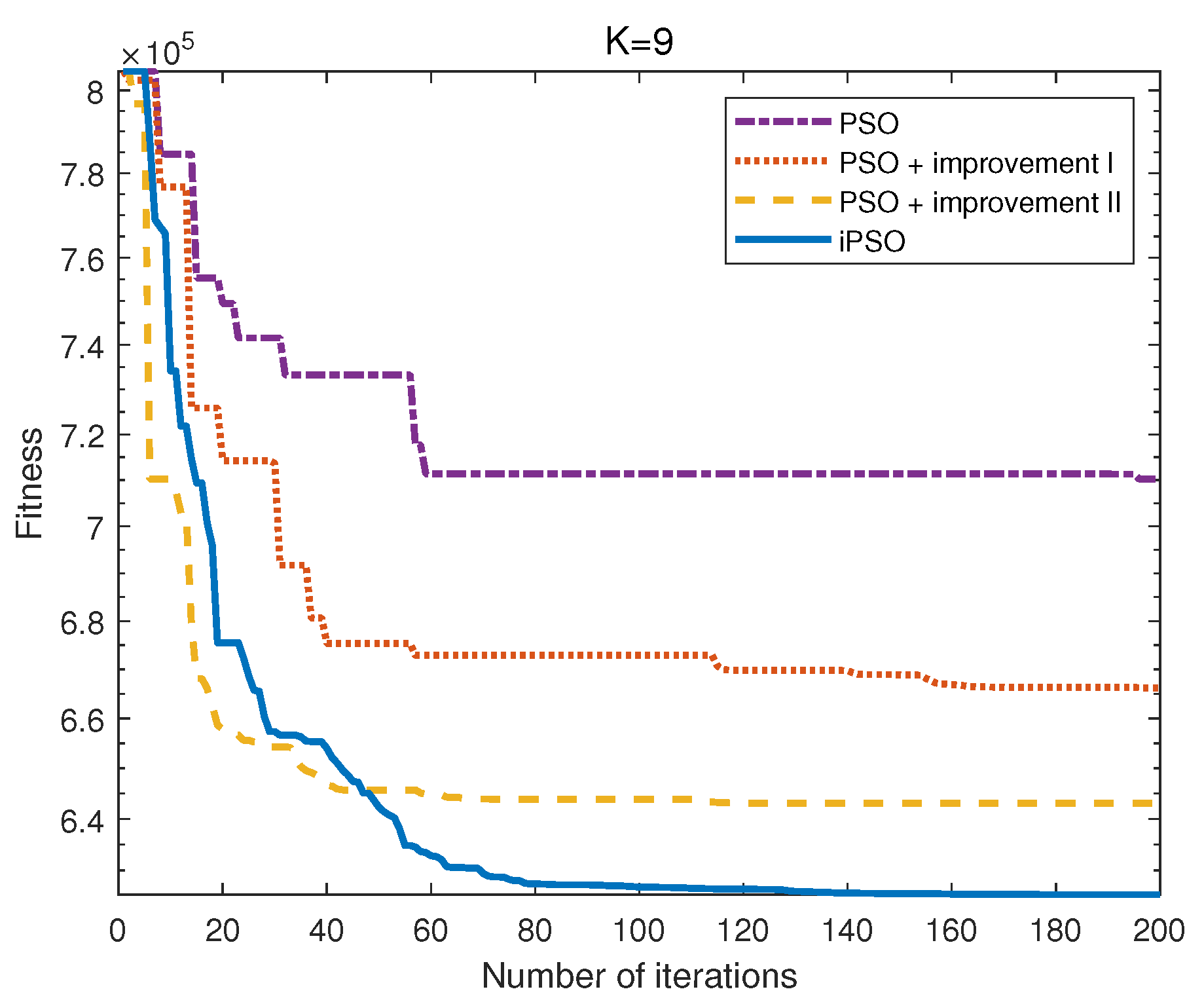
2.1. iPSO Based Data Clustering
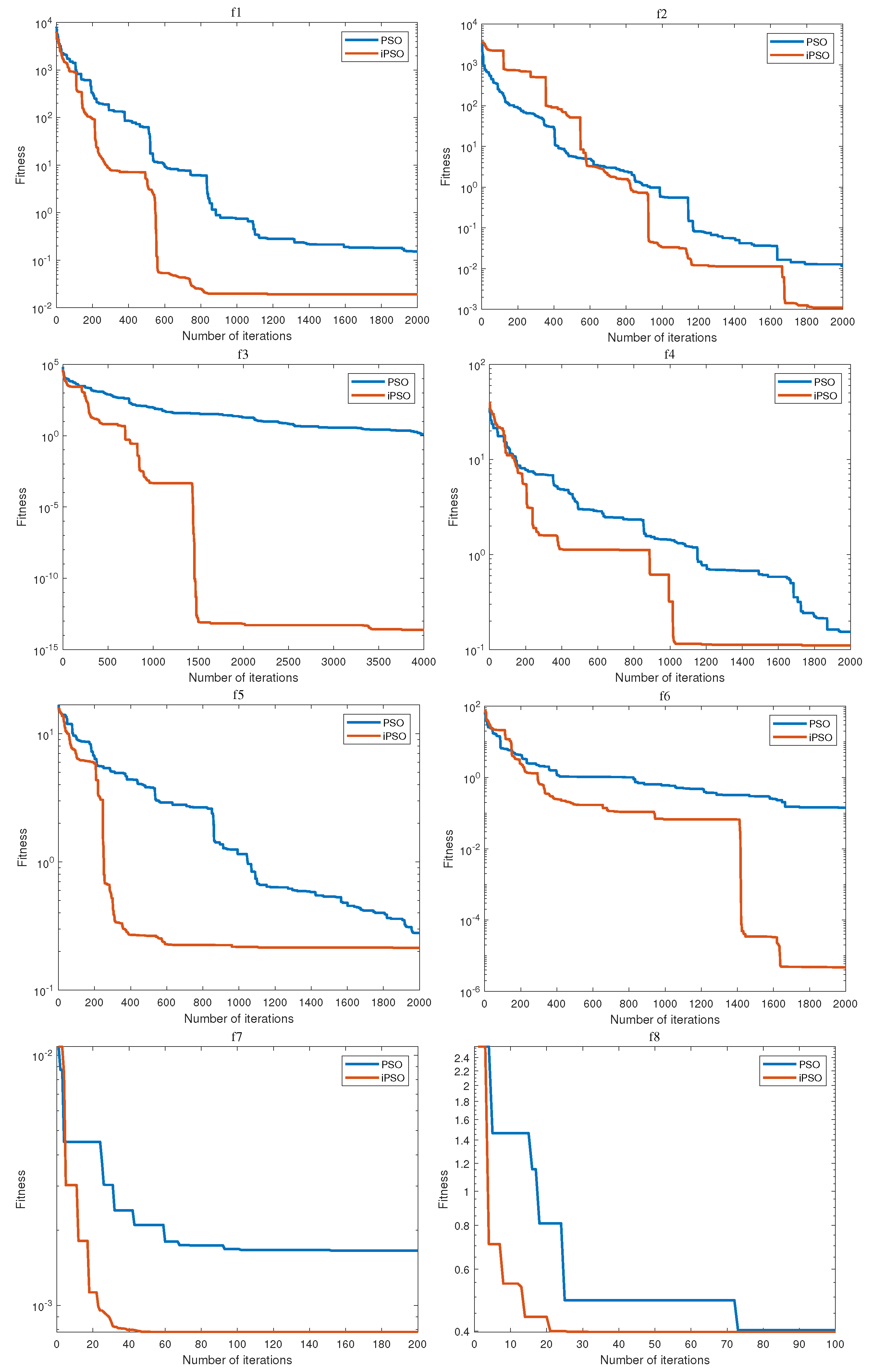
2.1.1. Improved PSO Algorithm
2.1.2. Process of iPSO-Based Clustering

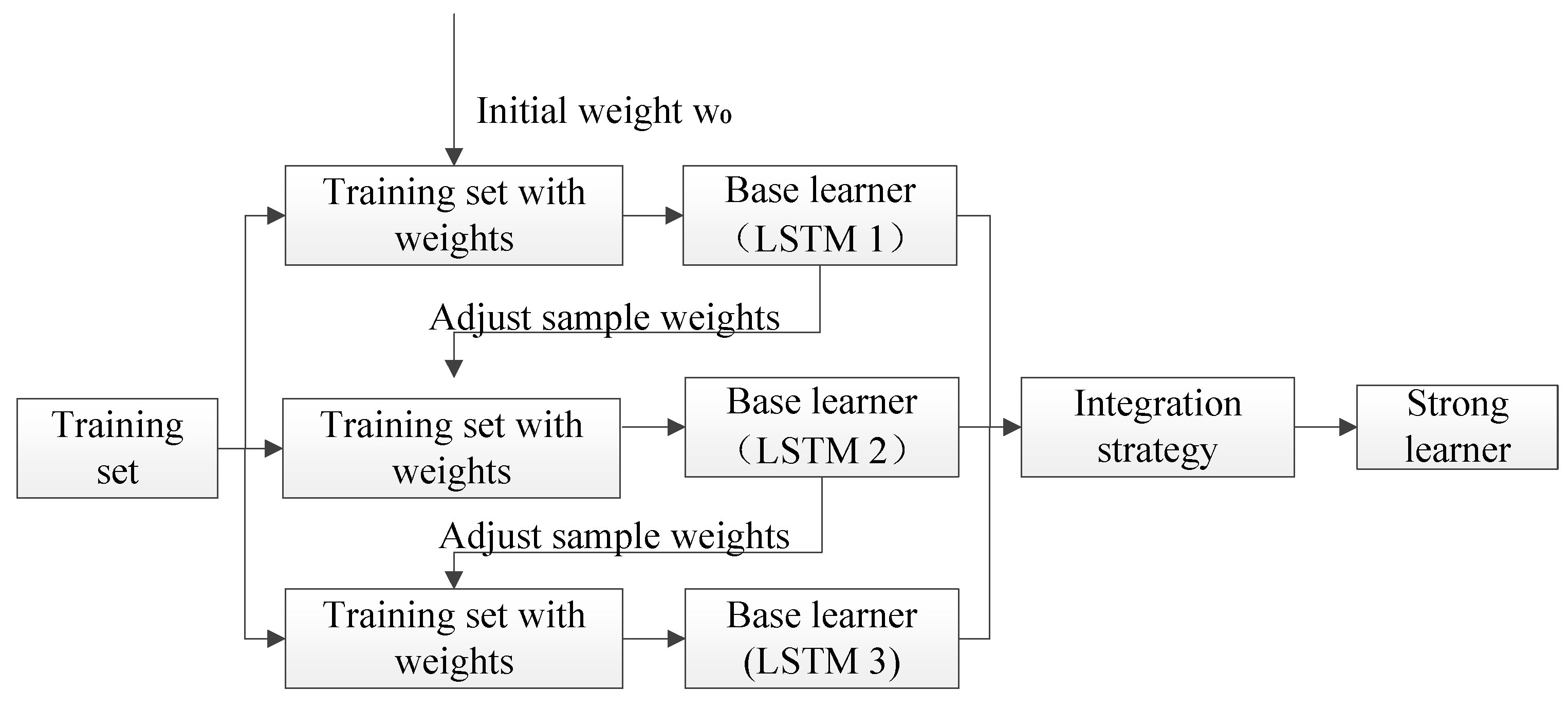
2.2. AdaLSTM
| Algorithm 1 AdaLSTM modeling |
Input Import training dataset (X, Y). X denotes feature input and Y denotes target output. Initialization Initialize the weight vector . N denotes the total number of samples. for i = 1 to P (number of base learners) Train the regression model . Calculate the error using testing set: e=. denotes the model output. for j = 1 to N Assign the weight vector according to the error.
end Set parameters of the ith base learner as: = 0.5 [36]. denotes the mean absolute error of the ith base learner. end Output Integrate the base learners into a strong learner: Y = . |
2.3. Overall Prediction Framework
3. Case Studies
3.1. Data Description
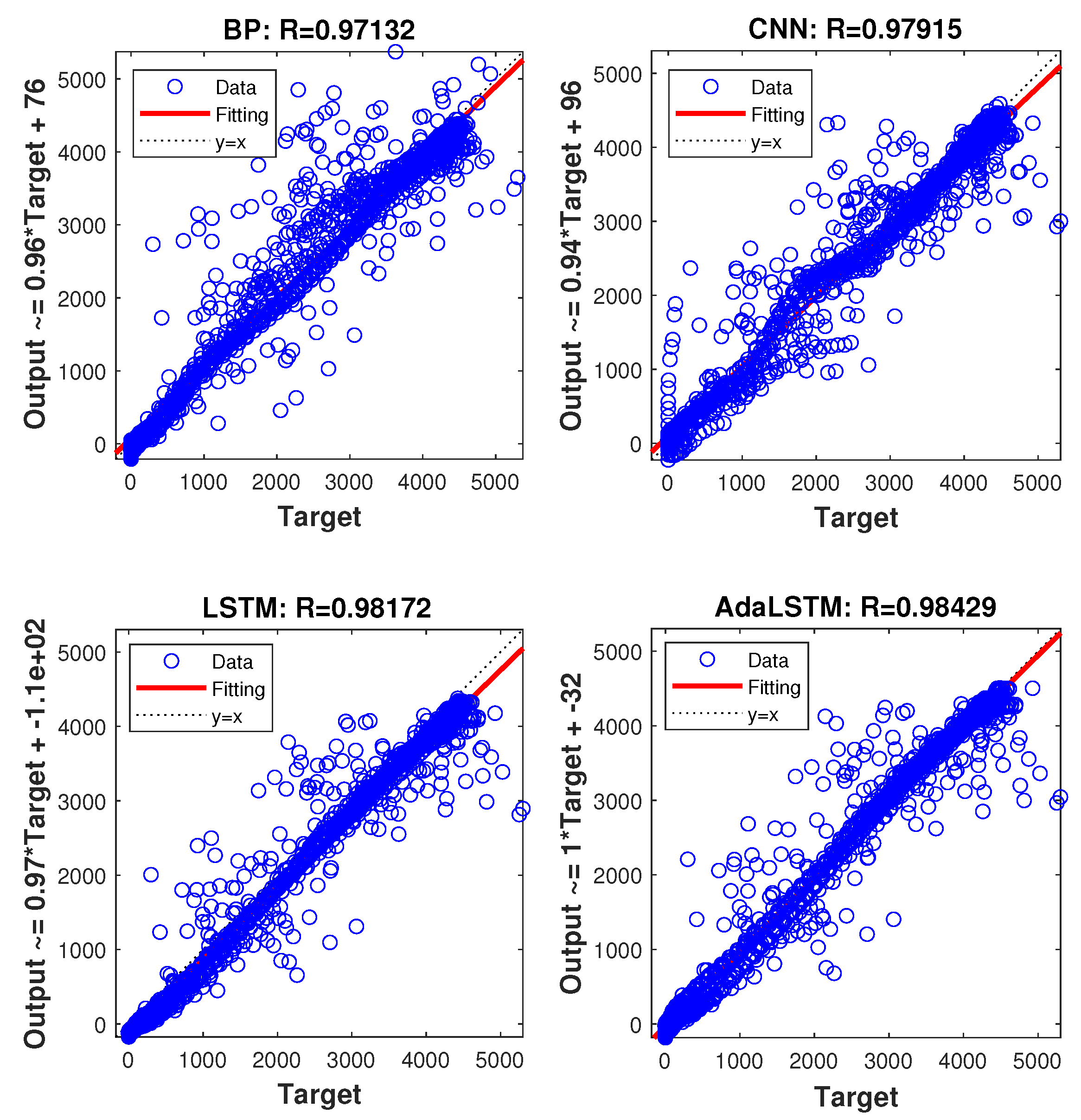
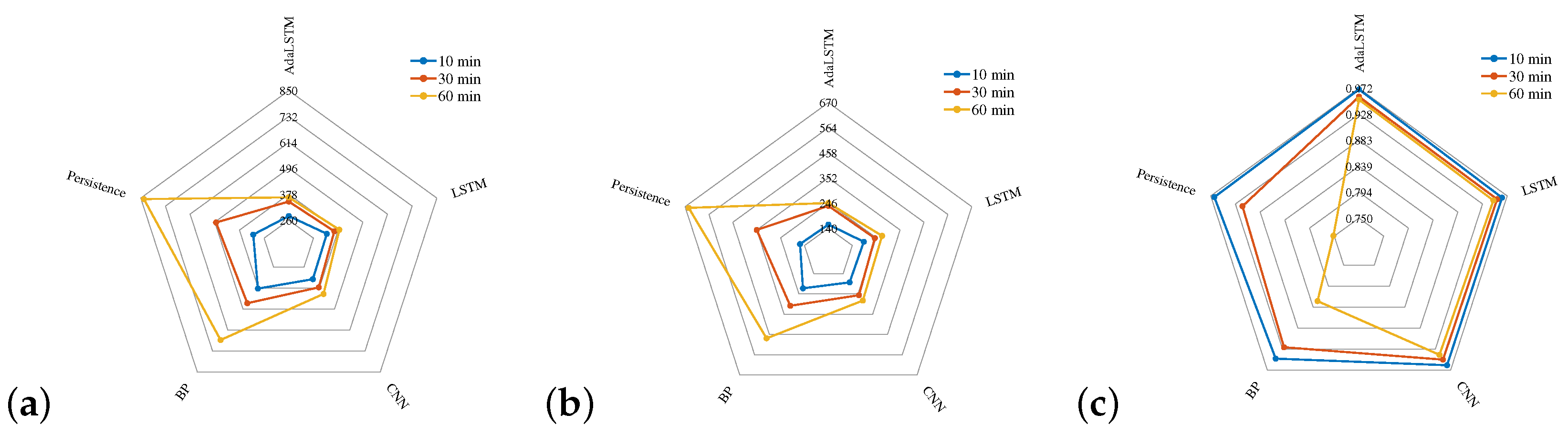
3.2. Validation of the AdaLSTM Model
3.3. Validation of iPSO Based Data Clustering
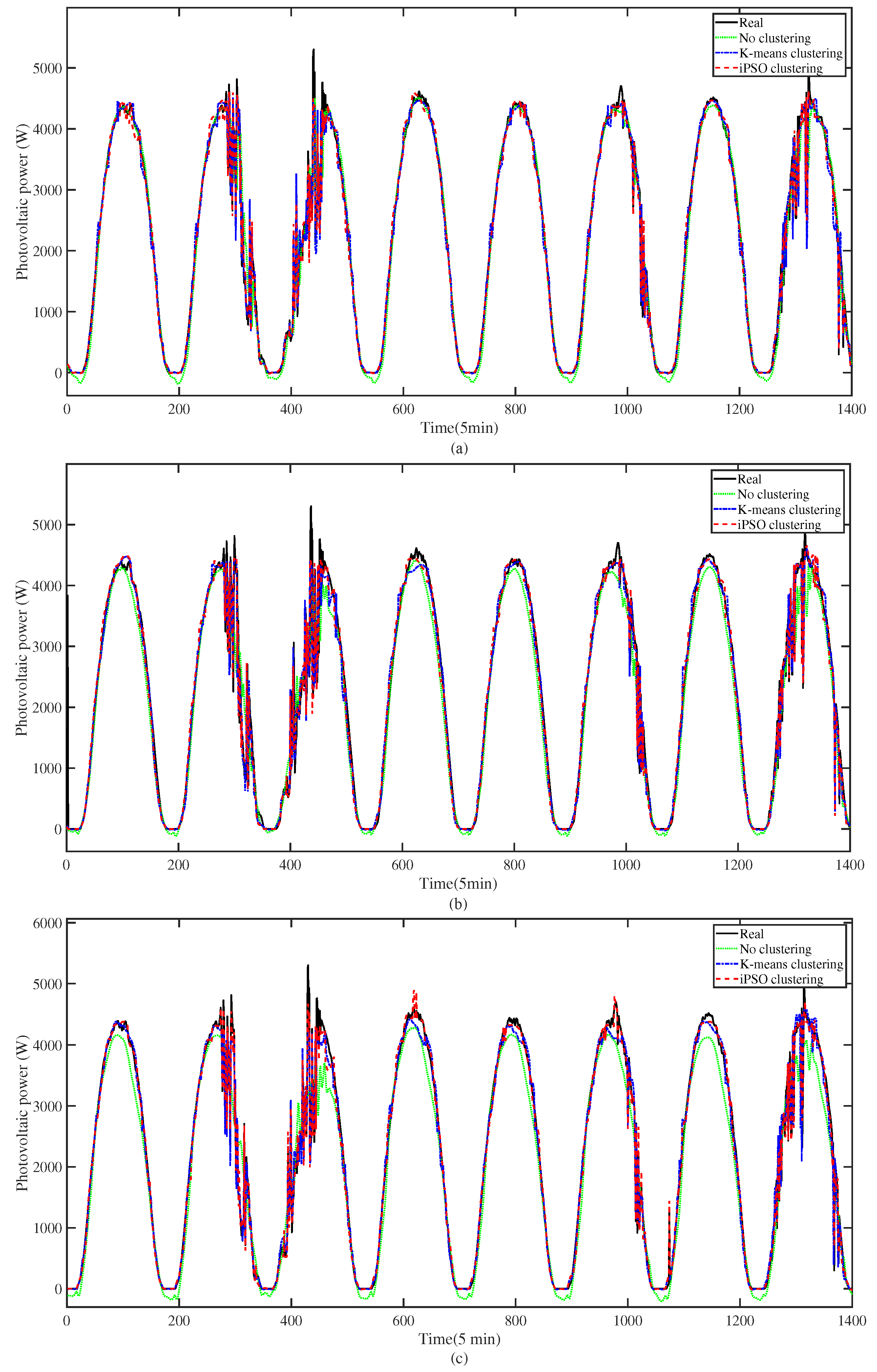
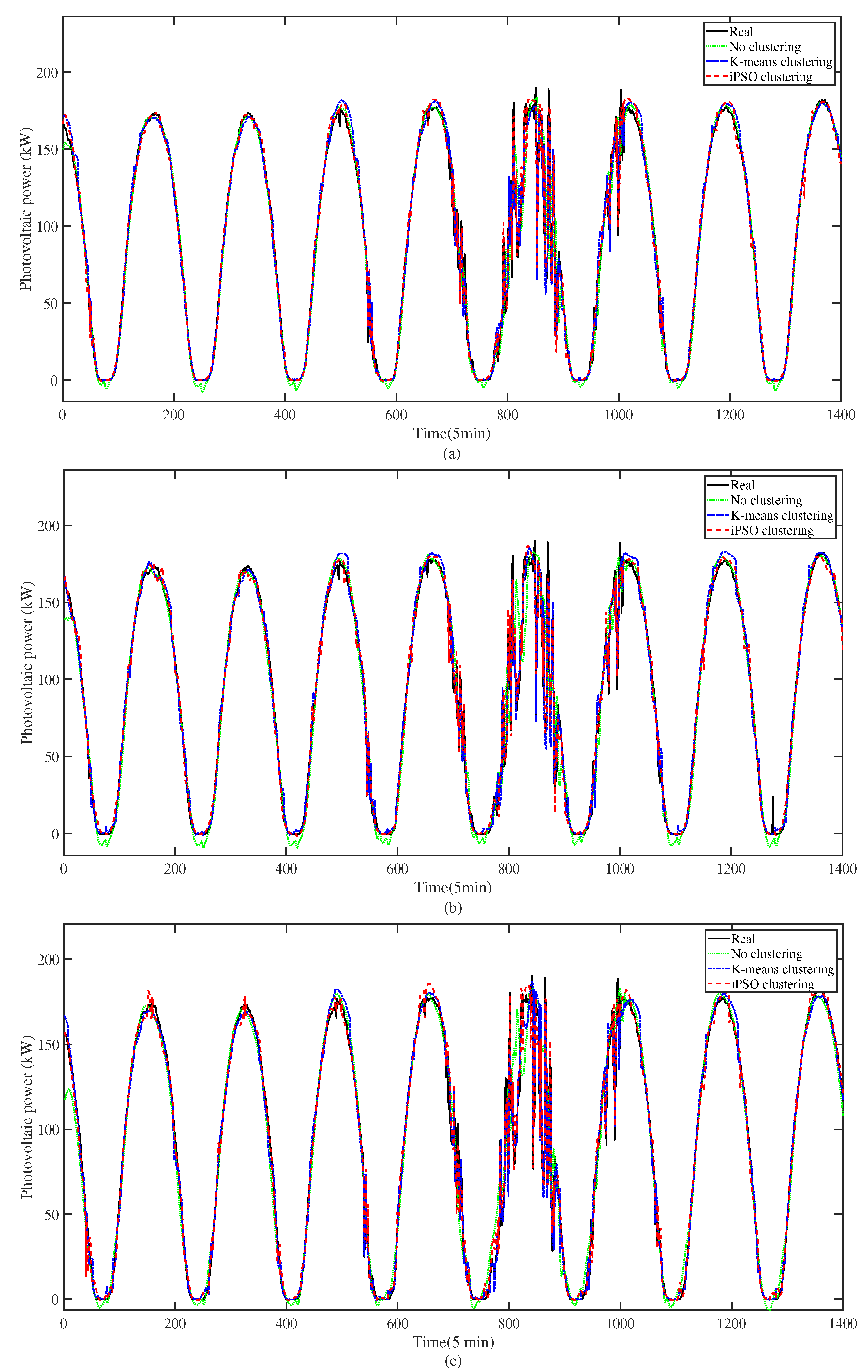
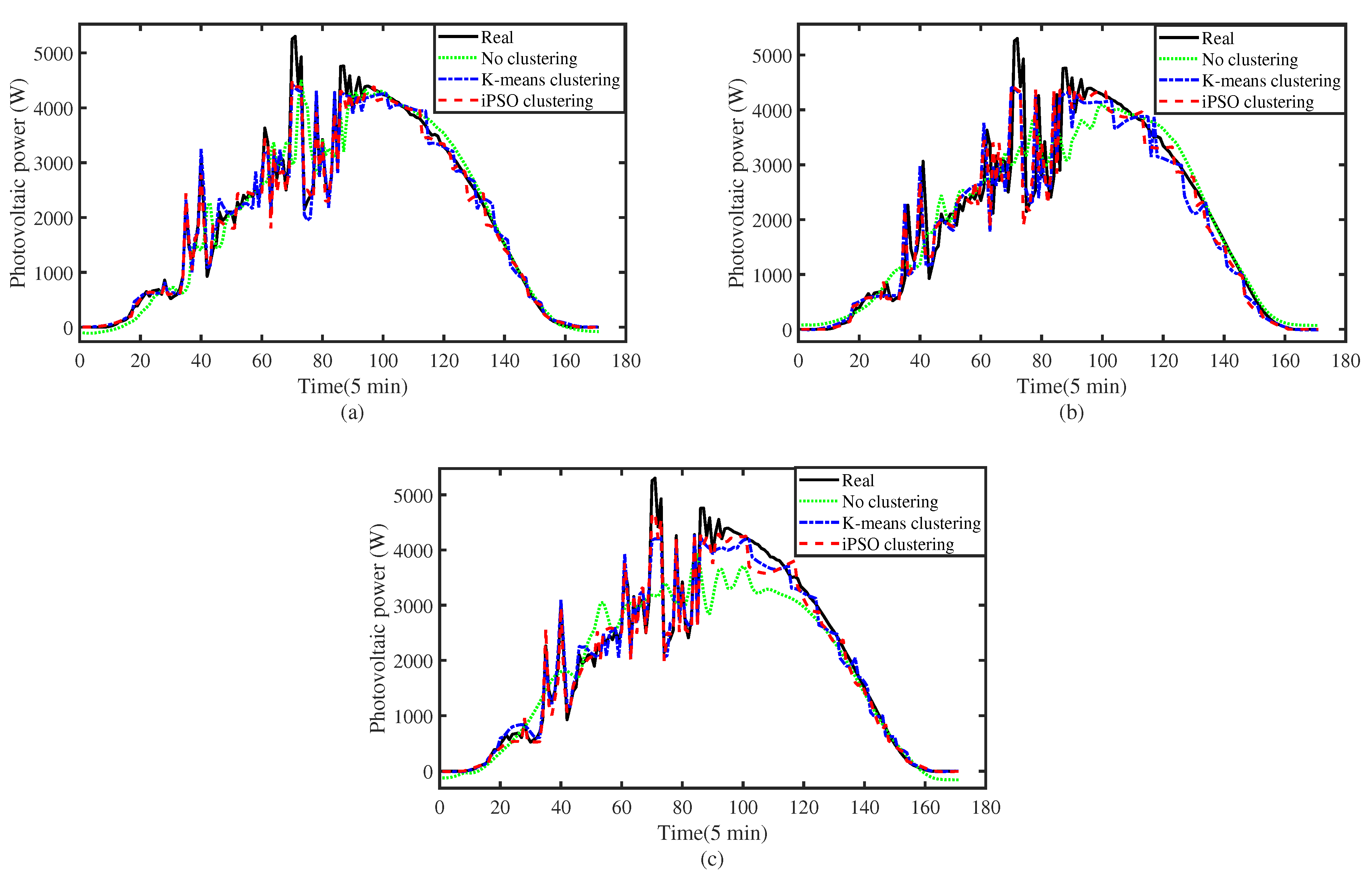
3.4. Influence of Clustering on Prediction Accuracy
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| AdaBoost | adaptive boosting |
| AdaLSTM | adaptive boosting LSTM |
| ANN | artificial neural network |
| ARMA | autoregressive moving average model |
| BPNN | back propagation neural network |
| CB | clustering-based |
| CHOA | chimp optimization algorithm |
| CNN | convolutional neural networks |
| DTCWT | dual tree complex wavelet transforms |
| EEMD | ensemble empirical mode decomposition |
| ELM | extreme learning machine |
| iPSO | improved particle swarm optimization |
| KNN | k-nearest neighbor |
| KSVD | k-singular value decomposition |
| LSSVM | least squares support vector machine |
| LSSVR | least square support vector regression |
| LSTM | long short-term memory |
| MAE | mean absolute error |
| MHFM | multiscale hybrid forecast model |
| MLP | multilayer perceptron |
| MLPNN | multilayer perceptron neural network |
| MTLBO | modified teaching learning based optimization |
| NAR | nonlinear autoregressive |
| NNE | neural network ensemble |
| PCA | principal components analysis |
| PSO | particle swarm optimization |
| PV | photovoltaic |
| R | multiple correlation coefficient |
| coefficient of determination | |
| RVFL | random vector functional link |
| RMSE | root mean square error |
| RNN | recurrent neural network |
| RVFLN | random vector functional link network |
| SCADA | supervisory control and data acquisition |
| STDI | standard deviation based index |
| SVM | support vector machine |
| VMD | variational mode decomposition |
| WRF | weather research and forecasting |
| WT | wavelet transform |
| best position of particle i | |
| position of the best particle | |
| learning probability of particle i | |
| population size | |
| m | refresh pointer |
| inertia weight | |
| minimum of inertia weight | |
| maximum of inertia weight | |
| minimum fitness of all particles | |
| average fitness of all particles | |
| K | number of clusters |
| prediction horizon |
Appendix A
| Function | Domain |
|---|---|
| [−100, 100] | |
| [−10, 10] | |
| [−100, 100] | |
| [−100, 100] | |
| [−32, 32] | |
| [−600, 600] | |
| = [0.1957, 0.1947, 0.1735, 0.16, 0.0844, 0.0627, 0.0456, 0.0342, 0.0323, 0.0235, 0.0246] | |
| [−5, 5] | |
| ∈ [−5, 10] ∈ [0, 15] |
References
- Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.-L.; Paoli, C.; Motte, F.; Fouilloy, A. Machine learning methods for solar radiation forecasting: A review. Renew. Energy 2017, 105, 569–582. [Google Scholar] [CrossRef]
- Tawn, R.; Browell, J. A review of very short-term wind and solar power forecasting. Renew. Sustain. Energy Rev. 2022, 153, 111758. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, C.; Li, Q.; Tai, Y.; Shi, J. A Comparison of Hour-Ahead Solar Irradiance Forecasting Models Based on LSTM Network. Math. Probl. Eng. 2020, 2020, 4251517. [Google Scholar] [CrossRef]
- Cao, J.; Cao, S. Study of forecasting solar irradiance using neural networks with preprocessing sample data by wavelet analysis. Energy 2006, 31, 3435–3445. [Google Scholar] [CrossRef]
- Voyant, C.; Muselli, M.; Paoli, C.; Nivet, M.-L. Numerical Weather Prediction (NWP) and hybrid ARMA/ANN model to predict global radiation. Energy 2012, 39, 341–355. [Google Scholar] [CrossRef]
- Monjoly, S.; André, M.; Calif, R.; Soubdhan, T. Forecast horizon and solar variability influences on the performances of multiscale hybrid forecast model. Energies 2019, 12, 2264. [Google Scholar] [CrossRef]
- Eseye, A.T.; Zhang, J.; Zheng, D. Short-term photovoltaic solar power forecasting using a hybrid Wavelet-PSO-SVM model based on SCADA and Meteorological information. Renew. Energy 2018, 118, 357–367. [Google Scholar] [CrossRef]
- Olatomiwa, L.; Mekhilef, S.; Shamshirband, S. Global Solar Radiation Forecasting Based on SVM-Wavelet Transform Algorithm. Int. J. Intell. Syst. Appl. (IJISA) 2016, 8, 19–26. [Google Scholar] [CrossRef]
- Sahu, R.K.; Shaw, B.; Nayak, J.R. Short/medium term solar power forecasting of Chhattisgarh state of India using modified TLBO optimized ELM. Eng. Sci. Technol. Int. J. 2021, 24, 1180–1200. [Google Scholar] [CrossRef]
- Wang, S.; Wang, Y.; Liu, Y.; Zhang, N. Hourly solar radiation forecasting based on EMD and ELM neural network. Electr. Power Autom. Equip. 2014, 34, 7–12. [Google Scholar]
- Zayed, M.E.; Zhao, J.; Li, W.; Elsheikh, A.H.; Abd Elaziz, M.; Yousri, D.; Zhong, S.; Mingxi, Z. Predicting the performance of solar dish Stirling power plant using a hybrid random vector functional link/chimp optimization model. Sol. Energy 2021, 222, 1–17. [Google Scholar] [CrossRef]
- Zayed, M.E.; Aboelmaaref, M.M.; Chazy, M. Design of solar air conditioning system integrated with photovoltaic panels and thermoelectric coolers: Experimental analysis and machine learning modeling by random vector functional link coupled with white whale optimization. Therm. Sci. Eng. Prog. 2023, 44, 102051. [Google Scholar] [CrossRef]
- De Araujo, J.M.S. Combination of WRF model and LSTM network for solar radiation forecasting—Timor leste case study. Comput. Water Energy Environ. Eng. 2020, 9, 108–144. [Google Scholar] [CrossRef]
- Hong, Y.-Y.; Martinez, J.J.F.; Fajardo, A.C. Day-ahead solar irradiation forecasting utilizing gramian angular field and convolutional long short-term memory. IEEE Access 2020, 8, 18741–18753. [Google Scholar] [CrossRef]
- Ren, Y.; Wang, J.; Yang, C.; Xiao, C.; Li, S. Wind and Solar Integrated Power Prediction Method Research Based on DT-CWT and LSTM. J. Phys. Conf. Ser. 2021, 1745, 012008. [Google Scholar] [CrossRef]
- Wang, J.; Li, J. Short-term Photovoltaic Power Forecasting Using the Combined KSVD and LSTM Method. In Proceedings of the 2022 International Conference on Machine Learning, Cloud Computing and Intelligent Mining (MLCCIM 2022), Xiamen, China, 5–7 August 2022; pp. 134–138. [Google Scholar]
- Elizabeth Michael, N.; Mishra, M.; Hasan, S.; Al-Durra, A. Short-term solar power predicting model based on multi-step CNN stacked LSTM technique. Energies 2022, 15, 2150. [Google Scholar] [CrossRef]
- Wang, K.; Qi, X.; Liu, H. Photovoltaic power forecasting based LSTM-Convolutional Network. Energy 2019, 189, 116225. [Google Scholar] [CrossRef]
- Zhang, C.; Yan, Z.; Ma, C.; Xu, X. Prediction of direct normal irradiation based on CNN-LSTM model. In Proceedings of the 2020 5th International Conference on Multimedia Systems and Signal Processing, Chengdu, China, 8–10 May 2020; pp. 74–80. [Google Scholar]
- Kumar, J.; Goomer, R.; Singh, A.K. Long short term memory recurrent neural network (LSTM-RNN) based workload forecasting model for cloud datacenters. Procedia Comput. Sci. 2018, 125, 676–682. [Google Scholar] [CrossRef]
- Chaouachi, A.; Kamel, R.M.; Nagasaka, K. Neural network ensemble-based solar power generation short-term forecasting. J. Adv. Comput. Intell. Intell. Inform. 2010, 14, 69–75. [Google Scholar] [CrossRef]
- Liu, J.; Huang, X.; Li, Q.; Chen, Z.; Liu, G.; Tai, Y. Hourly stepwise forecasting for solar irradiance using integrated hybrid models CNN-LSTM-MLP combined with error correction and VMD. Energy Convers. Manag. 2023, 280, 116804. [Google Scholar] [CrossRef]
- Zhou, Y.; Xue, W.; Liu, J.; Li, K. Photovoltaic power prediction based on SVMD-PCA-EL model. In Proceedings of the 2022 41st Chinese Control Conference (CCC), Hefei, China, 25–27 July 2022; pp. 5621–5626. [Google Scholar]
- Benmouiza, K.; Cheknane, A. Forecasting hourly global solar radiation using hybrid k-means and nonlinear autoregressive neural network models. Energy Convers. Manag. 2013, 75, 561–569. [Google Scholar] [CrossRef]
- Azimi, R.; Ghayekhloo, M.; Ghofrani, M. A hybrid method based on a new clustering technique and multilayer perceptron neural networks for hourly solar radiation forecasting. Energy Convers. Manag. 2016, 118, 331–344. [Google Scholar] [CrossRef]
- Malakar, S.; Goswami, S.; Ganguli, B.; Chakrabarti, A.; Roy, S.S.; Boopathi, K.; Rangaraj, A.G. Deep-learning-based adaptive model for solar forecasting using clustering. Energies 2022, 15, 3568. [Google Scholar] [CrossRef]
- Sun, S.; Wang, S.; Zhang, G.; Zheng, J. A decomposition-clustering-ensemble learning approach for solar radiation forecasting. Sol. Energy 2018, 163, 189–199. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. Int. Conf. Neural Netw. 1995, 4, 1942–1948. [Google Scholar]
- Bai, Q. Analysis of particle swarm optimization algorithm. Comput. Inf. Sci. 2010, 3, 180. [Google Scholar] [CrossRef]
- Cai, L.; Hou, Y.; Zhao, Y.; Wang, J. Application research and improvement of particle swarm optimization algorithm. In Proceedings of the 2020 IEEE International Conference on Power, Intelligent Computing and Systems (ICPICS), Shenyang, China, 28–30 July 2020; pp. 238–241. [Google Scholar]
- Liang, J.J.; Qin, A.K.; Suganthan, P.N.; Baskar, S. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions. IEEE Trans. Evol. Comput. 2006, 10, 281–295. [Google Scholar] [CrossRef]
- El-Zonkoly, A.; Saad, M.; Khalil, R. New algorithm based on CLPSO for controlled islanding of distribution systems. Int. J. Electr. Power Energy Syst. 2013, 45, 391–403. [Google Scholar] [CrossRef]
- Chen, X.; Wang, B.; Yu, M.; Jin, J.; Xu, W. The interpolation of missing wind speed data based on optimized LSSVM model. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016; pp. 1448–1451. [Google Scholar]
- Wang, W.; Cheng, J.; Gao, Y.; Yu, X. A scenario reduction method of PV output based on NBSO algorithm and STDI index. J. Phys. Conf. Ser. 2023, 2496, 012005. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Bai, Y.; Xie, J.; Wang, D.; Zhang, W.; Li, C. A manufacturing quality prediction model based on AdaBoost-LSTM with rough knowledge. Comput. Ind. Eng. 2021, 155, 107227. [Google Scholar] [CrossRef]
- Zhang, M.-L.; Zhou, Z.-H. ML-KNN: A lazy learning approach to multi-label learning. Pattern Recognit. 2007, 40, 7. [Google Scholar] [CrossRef]
- DKA Solar Centre. Available online: https://dkasolarcentre.com.au/download?location=alice-springs (accessed on 20 February 2024).
- DKA Solar Centre. Available online: https://dkasolarcentre.com.au/download?location=yulara (accessed on 20 February 2024).
- Pedro, H.T.C.; Coimbra, C.F.M. Assessment of forecasting techniques for solar power production with no exogenous inputs. Sol. Energy 2012, 86, 2017–2028. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, F.; Su, S. Solar irradiance short-term prediction model based on BP neural network. Energy Procedia 2011, 12, 488–494. [Google Scholar] [CrossRef]
- Agga, A.; Abbou, A.; Labbadi, M.; El Houm, Y.; Ali, I.H.O. CNN-LSTM: An efficient hybrid deep learning architecture for predicting short-term photovoltaic power production. Electr. Power Syst. Res. 2022, 208, 107908. [Google Scholar] [CrossRef]
- Abdel-Nasser, M.; Mahmoud, K. Accurate photovoltaic power forecasting models using deep LSTM-RNN. Neural Comput. Appl. 2019, 31, 2727–2740. [Google Scholar] [CrossRef]
- Wei, B.; Li, K.; Zhou, S.; Xue, W.; Tan, G. An instance based multi-source transfer learning strategy for building’s short-term electricity loads prediction under sparse data scenarios. J. Build. Eng. 2024, 85, 108713. [Google Scholar] [CrossRef]
- Asuero, A.G.; Sayago, A.; González, A.G. The correlation coefficient: An overview. Crit. Rev. Anal. Chem. 2006, 36, 41–59. [Google Scholar] [CrossRef]
- Lin, A.; Sun, W.; Yu, H.; Wu, G.; Tang, H. Adaptive comprehensive learning particle swarm optimization with cooperative archive. Appl. Soft Comput. 2019, 77, 533–546. [Google Scholar] [CrossRef]


| Ref | Location | Method | Dataset Covering Time | Performance Metrics | Characteristic |
|---|---|---|---|---|---|
| [3] | Colorado | LSTM-MLP | 1 January 2012 to 31 December 2016 | RMSE (62.1618 W/m2) | The role of lag time was significant when the input variables of the LSTM model were small. |
| [5] | Mediterranean area | ANN | October 2002 to December 2008 | nRMSE (14.9%) | A hybrid approach that utilized a coupled artificial neural network (ANN) and autoregressive moving average (ARMA) predictors could substantially decrease prediction errors. |
| [6] | Guadeloupe island | MHFM model | January 2012 to December 2012 | nRMSE (4.43–10.24%) | Four types of typical days were identified and datasets were established for each. |
| [7] | Beijing | Hybrid WT-PSO-SVM | one year with a time step of 10 min | MAPE (4.22%) | The PSO was used to optimize the parameters of the SVM in order to achieve a higher forecasting accuracy. |
| [9] | Chhattisgarh | MTLBO-ELM | February 2019 to December 2019 | MAPE (8.2091%) | ELM models based on MTLBO optimization outperformed ELM, ELM (randomly fixed weights and biases), and ANN models based on different optimizations. |
| [11] | Arizona | REVL-CHOA | March 2010 to June 2011 | RMSE (0.00047, 0.05995) | The RFVL-CHOA method was found to be superior and more effective than other optimization models studied for performance prediction. |
| [12] | Sohag | RVFLN-WWO | NA | The experimental results uniquely fitted with the predicted results of the proposed artificial intelligence model. | |
| [13] | Dili | WRF-LSTM | January to December 2014 | nRMSE (16.18%) | The combination of the WRF and LSTM methods had better performance and could be applied to simulate other locally relevant weather variables. |
| [14] | Taiwan | CNN-LSTN | 5 January 2017 to 4 January 2018 | RMSE (0.0472) | The network allowed for time series forecasting using a feature-rich approach, resulting in competitive forecasting performance even with small datasets. |
| [16] | Yulara soalr system | KSVD-LSTM | 7 March to 7 June 2021 | RMSE (0.3682) | The combined method of KSVD and LSTM achieved highly accurate prediction results. |
| [17] | Abu Dhabi | CNN-LSTM | July 2019 | RMSE (0.36) | The model predicts both solar irradiance and POA more accurately than what has been reported in the literature. |
| [18] | Alice Springs | LSTM-Convolutional Network | half year | RMSE (0.621) | The proposed hybrid model outperformed the convolutional LSTM network and had a better prediction effect than the single prediction model. |
| [20] | Alberta | LSTM-RNN | seven months | MSE (0.00317) | The hybrid model had higher accuracy. |
| [21] | TUAT | NNE | 2007 to 2008 | MAPE (3.6387) | Compared with traditional networks, neural network ensembles exhibited the highest level of prediction accuracy. |
| [22] | Folsom | CNN-LSTM-MLP | 1 January 2014 to 31 December 2016 | RMSE (12.53 W/m2) | The model was more accurate and robust than many traditional alternative methods. |
| [25] | Ames | Kmeans-mlpnn | 08/25–31/2013 | RMSE (32.01 W/m2) | The comparison with the benchmark solar radiation forecast model indicated that the model had superior forecasting capabilities. |
| [24] | Algeria | Kmeans-NAR | January 1994 to December 1996 | nRMSE (0.1985) | The obtained experimental results showed that the clustering of the input space was an important task to interpret the behavior of the series. |
| [26] | Begamganj | CB-LSTM | 2013 | nRMSE (19.74) | The performance was improved compared with a single site-specific model. |
| [27] | Beijing | EEMD-LSSVR-K-LSSVR | 1 January 2009 to 30 June 2017 | nRMSE (2.96%) | The DCE learning method showed promise for predicting solar radiation, with high levels of horizontal and directional accuracy, as well as robustness. |
| Parameter | Setting |
|---|---|
| MaxEpochs | 100 |
| Maximum number of iterations | 100 |
| Number of hidden neurons | 200 |
| Initial learn rate | 0.004 |
| Learn rate drop period | 90 |
| Learn rate drop factor | 0.2 |
| Prediction Horizon | Model | RMSE (W) | MAE (W) | |
|---|---|---|---|---|
| Persistence | 311.89 | 159.80 | 0.9655 | |
| BP | 381.46 | 216.80 | 0.9477 | |
| 10 min | CNN | 328.11 | 186.04 | 0.9616 |
| LSTM | 324.06 | 191.53 | 0.9626 | |
| AdaLSTM | 297.58 | 155.79 | 0.9685 | |
| Persistence | 489.55 | 352.64 | 0.9150 | |
| BP | 463.10 | 308.26 | 0.9236 | |
| 30 min | CNN | 374.39 | 253.01 | 0.9498 |
| LSTM | 360.05 | 240.33 | 0.9538 | |
| AdaLSTM | 345.12 | 234.57 | 0.9576 | |
| Persistence | 834.88 | 654.25 | 0.7516 | |
| BP | 698.60 | 477.88 | 0.8261 | |
| 60 min | CNN | 411.13 | 281.15 | 0.9396 |
| LSTM | 384.51 | 271.86 | 0.9471 | |
| AdaLSTM | 364.76 | 246.50 | 0.9526 |
| Prediction Horizon | Model | RMSE (kW) | MAE (kW) | |
|---|---|---|---|---|
| Persistence | 15.29 | 7.43 | 0.9462 | |
| BP | 12.65 | 6.28 | 0.9637 | |
| 10 min | CNN | 12.37 | 6.65 | 0.9652 |
| LSTM | 12.08 | 5.48 | 0.9669 | |
| AdaLSTM | 11.84 | 5.40 | 0.9684 | |
| Persistence | 22.50 | 15.13 | 0.8835 | |
| BP | 15.40 | 8.86 | 0.9461 | |
| 30 min | CNN | 14.12 | 8.14 | 0.9546 |
| LSTM | 12.39 | 7.01 | 0.9651 | |
| AdaLSTM | 12.14 | 5.99 | 0.9665 | |
| Persistence | 32.82 | 25.55 | 0.7562 | |
| BP | 20.97 | 14.17 | 0.8990 | |
| 60 min | CNN | 15.72 | 8.89 | 0.9437 |
| LSTM | 13.63 | 7.76 | 0.9577 | |
| AdaLSTM | 13.24 | 7.61 | 0.9601 |
| Parameter | Setting |
|---|---|
| Swarm size | 50 |
| 0.89 | |
| 0.7 | |
| M | 10 |
| 1.5 |
| K | STDI Value | RMSE (W) | MAE (W) | |
|---|---|---|---|---|
| 2 | 10 | 277.04 | 159.06 | 0.9727 |
| 3 | 25 | 258.84 | 154.01 | 0.9761 |
| 4 | 81 | 199.53 | 121.31 | 0.9858 |
| 5 | 229 | 201.37 | 131.16 | 0.9856 |
| 6 | 374 | 160.43 | 108.27 | 0.9901 |
| 7 | 529 | 169.44 | 112.96 | 0.9898 |
| 8 | 659 | 189.64 | 121.57 | 0.9911 |
| 9 | 1801 | 126.09 | 88.58 | 0.9943 |
| 10 | 1488 | 135.95 | 88.21 | 0.9934 |
| Prediction Horizon | Clustering Method | RMSE (W) | MAE (W) | |
|---|---|---|---|---|
| No clustering | 297.58 | 155.79 | 0.9685 | |
| 10 min | K-means clustering | 125.07 | 80.95 | 0.9944 |
| iPSO based clustering | 117.11 | 79.08 | 0.9951 | |
| No clustering | 345.12 | 234.57 | 0.9576 | |
| 30 min | K-means clustering | 135.94 | 91.20 | 0.9934 |
| iPSO based clustering | 121.32 | 82.17 | 0.9948 | |
| No clustering | 364.76 | 246.50 | 0.9526 | |
| 60 min | K-means clustering | 134.86 | 89.99 | 0.9935 |
| iPSO based clustering | 127.87 | 87.21 | 0.9941 |
| Prediction Horizon | Clustering Method | RMSE (kW) | MAE (kW) | |
|---|---|---|---|---|
| No clustering | 11.84 | 5.40 | 0.9684 | |
| 10 min | K-means clustering | 5.52 | 3.59 | 0.9930 |
| iPSO based clustering | 4.93 | 3.29 | 0.9945 | |
| No clustering | 12.14 | 5.99 | 0.9665 | |
| 30 min | K-means clustering | 5.53 | 3.93 | 0.9930 |
| iPSO based clustering | 5.16 | 3.62 | 0.9939 | |
| No clustering | 13.24 | 7.61 | 0.9601 | |
| 60 min | K-means clustering | 6.16 | 4.13 | 0.9913 |
| iPSO based clustering | 5.52 | 3.82 | 0.9936 |
| Model | Training Time (s) | Prediction Time (s) |
|---|---|---|
| LSTM | 70.40 | 4.29 |
| AdaLSTM | 223.68 | 13.15 |
| iPSO clustering + AdaLSTM | 105.70 | 10.74 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Li, K.; Xue, W. Photovoltaic Solar Power Prediction Using iPSO-Based Data Clustering and AdaLSTM Network. Energies 2024, 17, 1624. https://doi.org/10.3390/en17071624
Liu J, Li K, Xue W. Photovoltaic Solar Power Prediction Using iPSO-Based Data Clustering and AdaLSTM Network. Energies. 2024; 17(7):1624. https://doi.org/10.3390/en17071624
Chicago/Turabian StyleLiu, Jincun, Kangji Li, and Wenping Xue. 2024. "Photovoltaic Solar Power Prediction Using iPSO-Based Data Clustering and AdaLSTM Network" Energies 17, no. 7: 1624. https://doi.org/10.3390/en17071624
APA StyleLiu, J., Li, K., & Xue, W. (2024). Photovoltaic Solar Power Prediction Using iPSO-Based Data Clustering and AdaLSTM Network. Energies, 17(7), 1624. https://doi.org/10.3390/en17071624








