1. Introduction
As an amalgamation of several high-tech fields, multistage launch rocket technology reflects a country’s space exploration capabilities and national security. It also fosters innovation and promotes advancement in basic industries and frontier technologies. Interlevel separation, though brief, is a crucial aspect of the rocket launch process.
Research into the flow field and kinetic force during thermal separation has been ongoing since the 1960s. Wasko [
1] pioneered this in 1961 by experimenting with flow field characteristics in the interstage area of a two-stage jet engine. Similarly, Nave [
2] conducted ground tests on a J-2S engine for aerospace planes. Since then, studies into the mechanisms and engineering applications of the thermal separation process have gained importance. Zhu et al. [
3] proposed that ground joint tests could verify the feasibility of an interstage separation plan. Balesh et al. [
4] undertook experimental and numerical studies on the initial pressure boost of a multi-particle solid rocket motor, discovering the significance of the peripheral opening in reducing pressure increase in rocket motors.
However, wind tunnel or ground tests examining the flow field of a rocket body, its surroundings, and the first stage of separation oversimplify certain influencing factors, suggesting that the actual flow field deviates from the test conditions. Moreover, these tests are expensive and limited by various factors, such as the ground atmosphere, experimental plans, and tools.
Since the 1990s, growth in computational fluid dynamics (CFD) and computer processing power have facilitated studies on complex flow problems, such as thermal separation. Huseman et al. [
5] devised a method to analyze the stage separation of launch vehicles using CFD and rigid body dynamics. Shieh et al. [
6] applied an unsteady numerical modeling method to explore and predict the flow field amid the stages of thermal separation. Mirzaei et al. [
7] conducted a three-dimensional, non-steady numerical simulation of the interstage separation in a supersonic aircraft. Young Moo et al. [
8] evaluated the flow characteristics and rocket motion during the supersonic separation of an air-launching rocket from a mother plane. The three-dimensional Euler equations were numerically solved to analyze the steady and unsteady flow fields surrounding the rocket. The simulation results explicitly revealed the impact of the shock–expansion wave interaction between the rocket and its mother plane.
In the interstage thermal separation process, the key features of the flow field are the formation of unstable wave system structures in the interstage region by the upper-stage engine jet, the interference flow of the lateral jet in the interstage gap, the external supersonic incoming flow, and the severe aerothermal environment instigated by these elements. When separation occurs at a lower altitude, the interaction between the exhaust plume and free stream causes lateral interference, leading to potential aerodynamic issues, such as diminished stability, localized overheating, and reduced control effectiveness [
9,
10,
11,
12]. These circumstances trigger substantial shifts in the rocket’s attitude, impacting the safety and flight stability of the interstage separation.
In recent years, studying the flow field characteristics of plumes using the CFD method has gained significant importance. Ramirez et al. [
13] evaluated how different mesh types and scales influence the sorting process and provided guidance on selecting the appropriate mesh scale. Li et al. [
14] investigated staging dynamics and trajectories of a multistage rocket using the direct coupling of CFD and flight mechanics. They suggested potential harm to the upper stage’s thrust vector control (TVC) mechanisms from the plume reflected off the dropped stage and identified complexities in shock structures and cavity flows. The trajectories of the two stages proved challenging to predict, particularly the dropped stage, where motion was dominated by residual thrust, gravity, and exhaust gases of the upper stage. Kim et al. [
15] used the CFD method to understand how rocket exhaust plumes behave in varying flight situations and with different engine sizes, further validating their findings with scale models. Olcmen et al. [
16] explored the impact of varied flight altitudes and Mach numbers on a rocket plume, identifying conditions leading to induced flow separation on the rocket. Zhou et al. [
17] examined the flow field of a liquid rocket plume striking a deflector plate and noted the direct effect of the peak pressure area and exhaust plume. Li et al. [
18] simulated the high-pressure jet mixing process in a supersonic incoming flow using large-eddy simulation (LES), discovering two counter-rotating vortex pair (CVP) sets within the mixing region. Anandhanarayanan [
19] employed a method based on reverse particle tracking to predict plume paths. When applied to air-to-air missiles, the results indicated that this method could produce more accurate plume paths with fewer calculations. Li et al. [
20] used an annular lateral jet to model an exhaust plume at a separation gap, subsequently investigating the effects of the annular lateral jet on the interference of the preceding stage and the influencing factors.
In addition, despite its limitations in capturing complex flow phenomena such as separating flow regions, RANS (Reynolds-averaged Navier–Stokes) models remain a valuable method in computational fluid dynamics (CFD) simulations.
Alessia Fracassi et al. [
21,
22] highlight the importance of hybrid RANS-LES models, which aim to combine the advantages of RANS and Large Eddy Simulation (LES) techniques. They assess an improved Delayed X-LES (DDES) hybrid model for the investigation of off-design conditions in centrifugal pumps. They acknowledge that while RANS models fail to accurately predict separated flow regions, the DDES model can provide improved fidelity by resolving the relevant turbulent structures in these regions, using LES. These articles highlight the fact that while RANS models may have limitations in certain flow regimes, their continued use is justified by their computational efficiency and the availability of hybrid RANS-LES approaches that can mitigate their shortcomings in separated flow regions.
As highlighted above, the thermal separation flow field is intricate, experiencing abrupt changes and being subject to numerous influencing factors. The existing research insufficiently explains the internal flow field and unsteady separation process in the interstage region, thus necessitating further exploration. Therefore, this paper presents a numerical simulation of the interstage separation process of a two-stage rocket. The study aimed to explore the flow field structure of the interstage exhaust and the separation motion characteristics of two-stage rockets under different separation schemes. The first part of the paper provides a detailed analysis of the steady flow field at the separation moment and the aerodynamic motion characteristics of a two-stage rocket under design conditions. The latter part investigates the laws governing different separation timings in the initial stage of separation.
3. Aerodynamic Characteristics Analysis in Design Condition
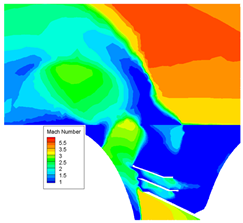
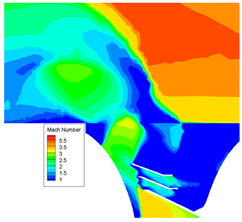
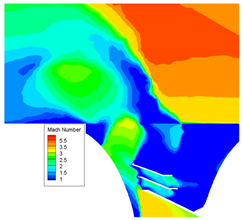
Figure 7 provides a schematic of the overall flow field structure of the center cross-section (
Φ = 22.5°) of the exhaust window when the two-stage rocket has not separated.
Figure 8 reveals the detailed structure of the interstage-induced separation flow field.
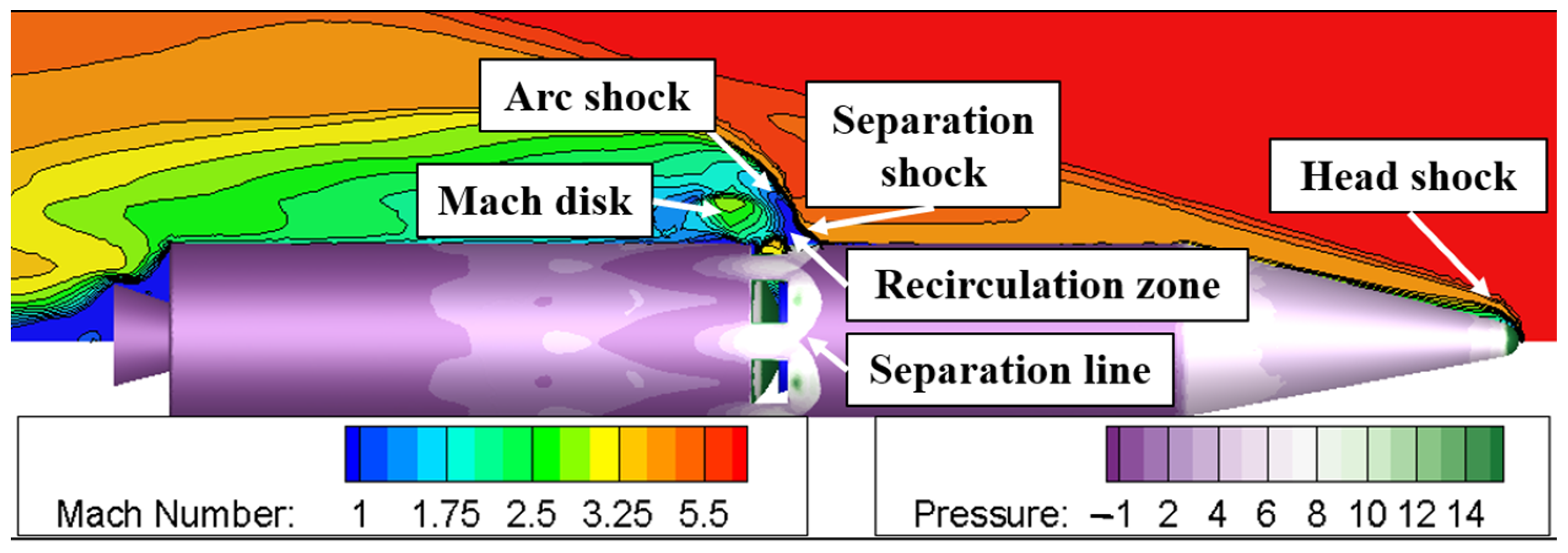
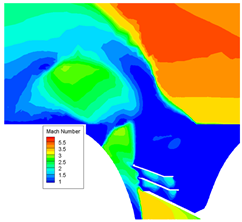
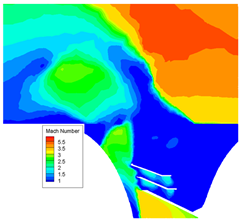
During the separation of the two stages, the ratio of the second-stage nozzle inlet pressure to the ambient pressure was high. The high-temperature, high-pressure combustion gas ejected from the nozzle first impacted the front head of the first stage, creating a series of complex vortices in the space between them. Subsequently, the gas was ejected from the exhaust window in a circular pattern. The under-expanded combustion gas formed a Mach disk that, interacting with the supersonic flow from the exterior, constructed a lateral jet flow structure. This structure slowed the free flow, creating a reverse pressure gradient near the tail of the second-stage rocket and forming a flow separation-recycling region. The expansion of the exhaust jet caused flow separation and a series of shock structures at the tail of the rocket, a phenomenon known as induced flow separation. This section examines the local flow field structure and aerodynamic properties of the region between the first and second stages at the moment of design condition separation, offering further insight into the aerodynamic properties of the first and second stages at this crucial juncture.
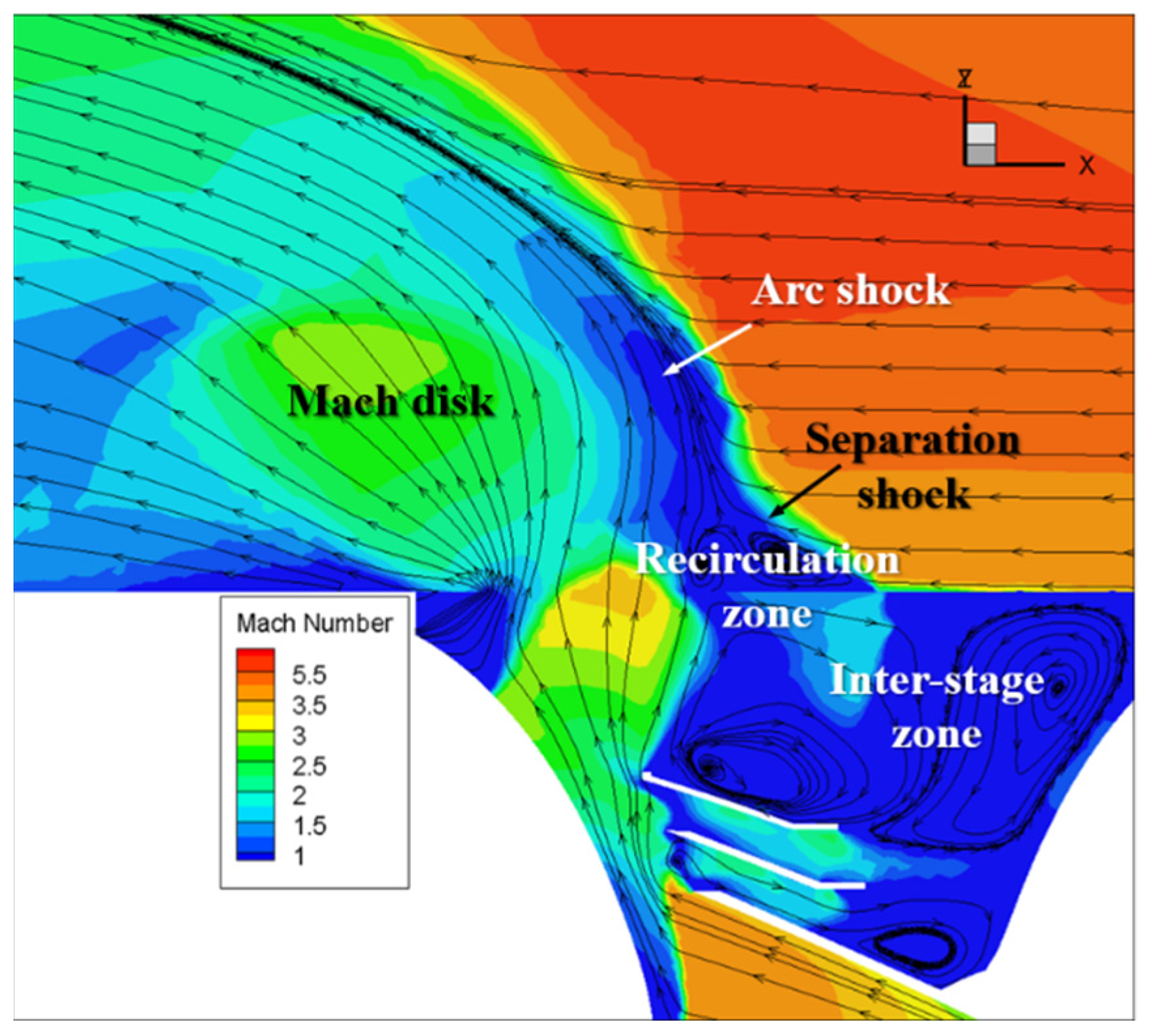
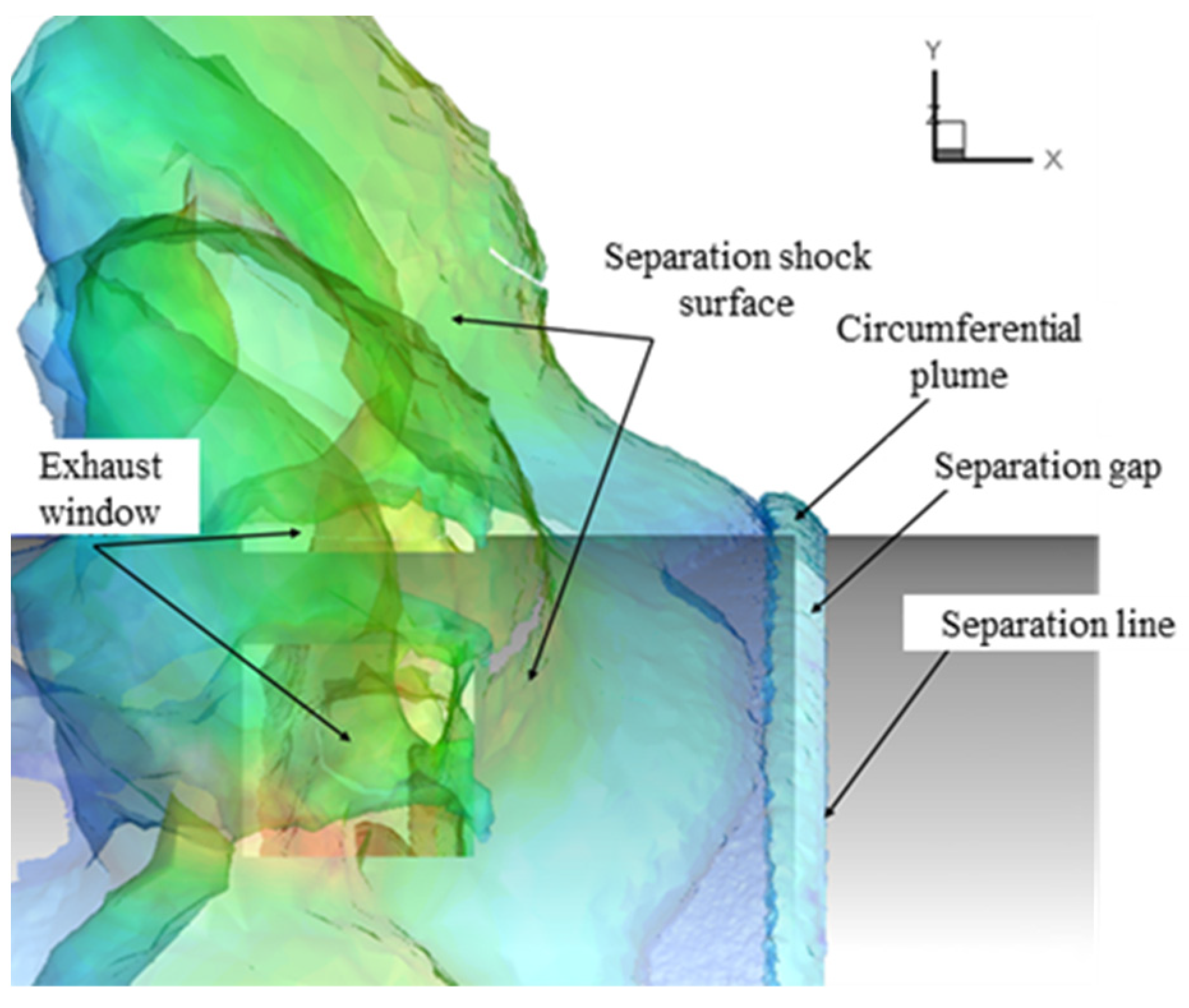
The interstage flow field, as depicted in
Figure 8, shows under-expanded gas being ejected from the two-stage nozzle, impacting the front cap of the first-stage rocket. The obstruction of the front cap’s wall forms a stagnant high-pressure zone near the nozzle outlet and flows out in four directions. Part of the gas is discharged through the exhaust port along the aft closure, expanding into the external environment to form a wake, while the remaining portion is blocked by the internal structure of the interstage region, creating a complex flow field consisting of a series of high-pressure zones and vortices within the interstage area. This dynamic acts similarly to an obstacle in the external flow, causing the incoming flow to bypass the jet expansion area and generate an arc shock due to the blocking effect. Upstream of the arc shock, a reverse pressure gradient causes the upstream boundary layer to separate from the wall, forming a separation shock at the point of separation. Downstream of this shock, a recirculation zone appears near the wall in which two vortices have opposite rotational directions: the primary upstream vortex (PUV) and the secondary upstream vortex (SUV). Due to the speed difference outside the recirculation zone, a shear layer is formed between the arc separation shock. Downstream of the arc shock, the high-temperature and high-pressure under-expanded gas discharged from the exhaust window expands into the main flow, forming a robust positive shock (Mach disk), balancing its momentum and pressure with the incoming external flow.
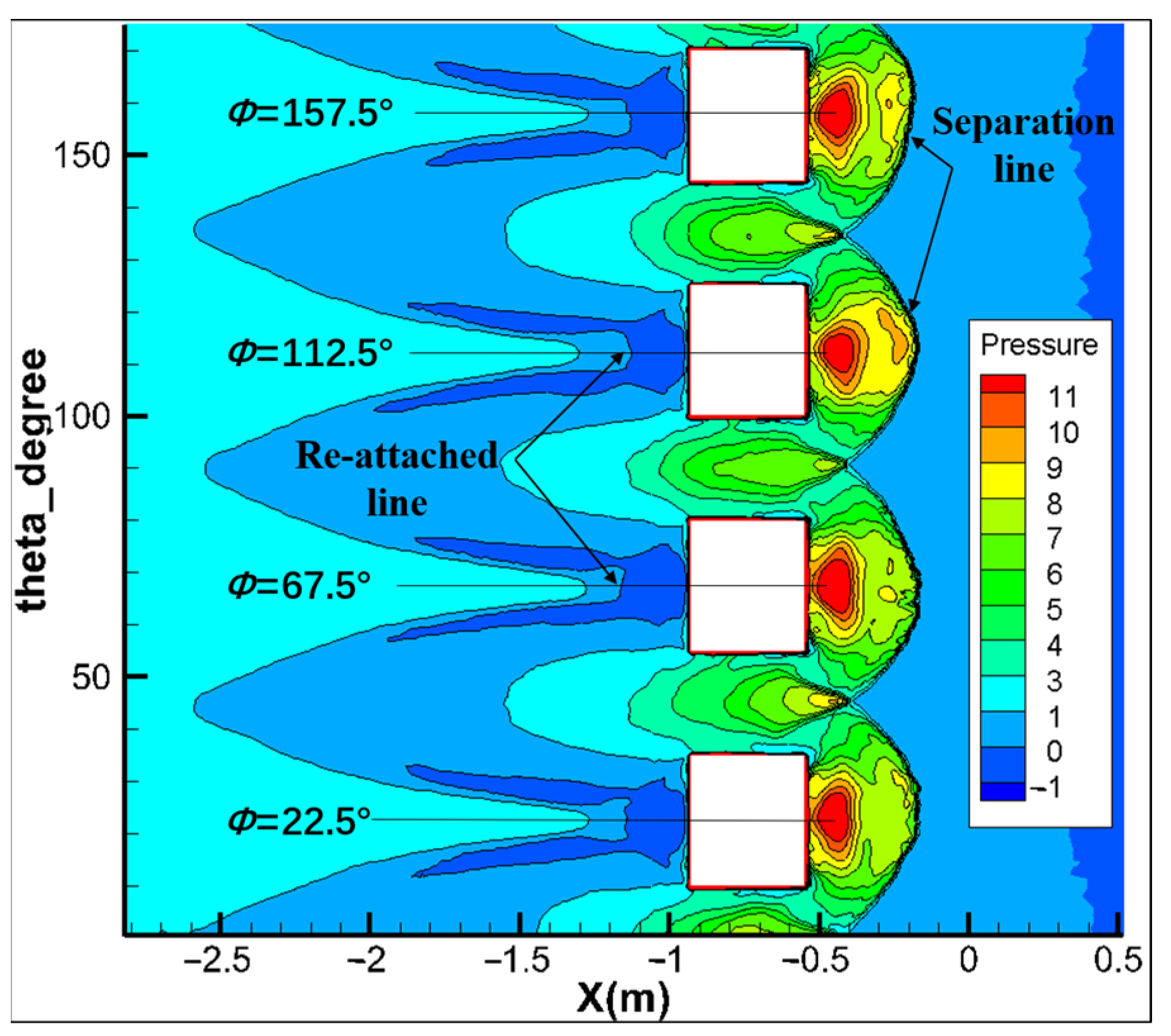
In the circumferential direction, the steady flow field of the jet stream is symmetrical.
Figure 9 presents the dimensionless wall pressure contour map after circumferential expansion. Due to the uniform distribution of the exhaust window, and in the absence of an attack angle and sideslip angle in the incoming flow, the wall pressure in the circumferential range of
Φ = 0~180° is periodically distributed, with a period of 45°.
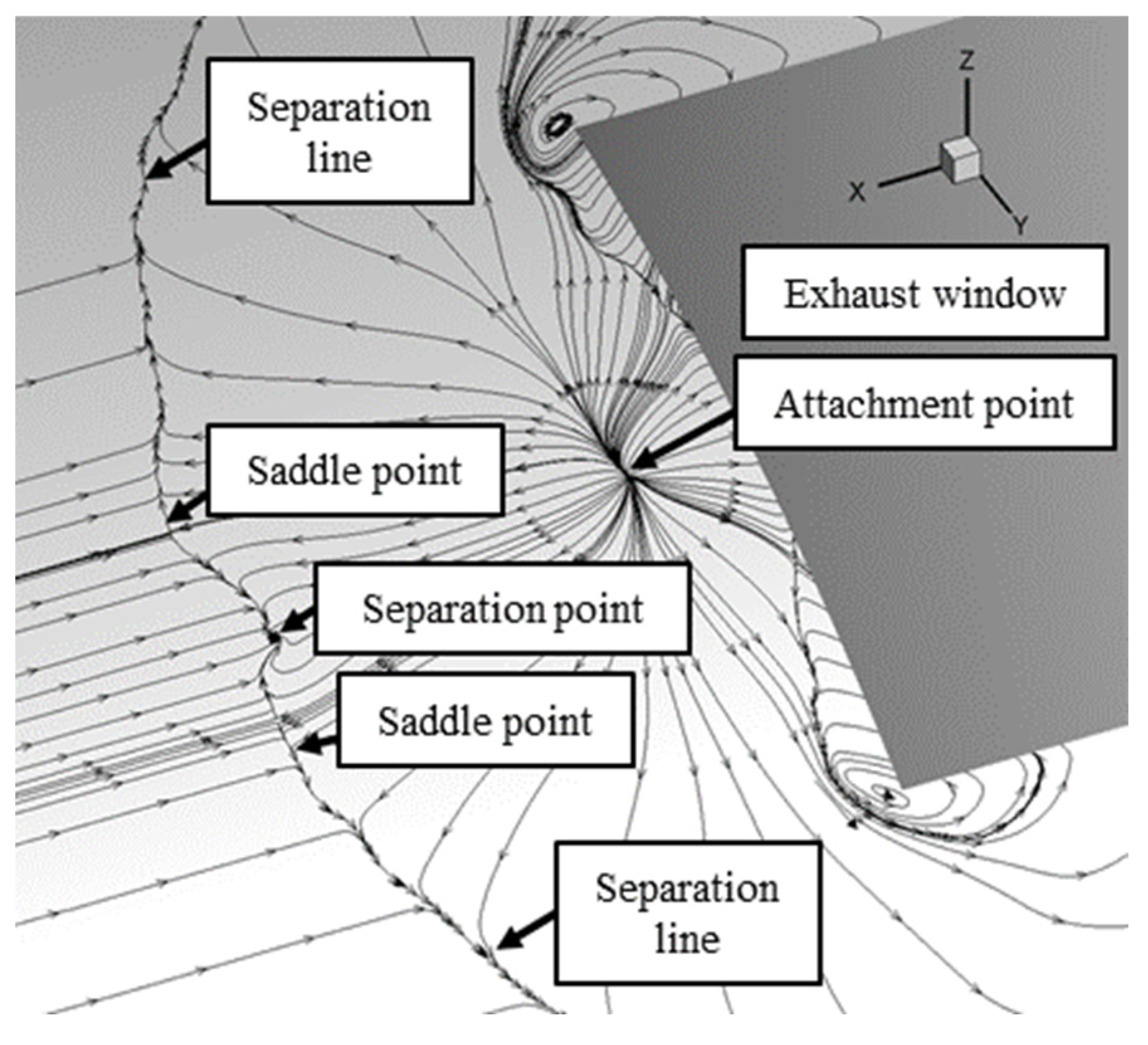
Figure 10 depicts the wall limit streamlines upstream of the exhaust window, which is also a friction line. According to Maskell’s separation model, the separation line is defined as follows: When flow separation occurs, there is a continuous three-dimensional separation line on the surface. The two families of limit streamlines on either side of the separation line gradually converge, eventually forming a single set of separation lines. Separation and attachment points are singular points (also known as attachment nodes) on the wall surface where the wall limit flows intersect or diverge. Furthermore, the flow separation induced by the jet stream significantly impacts the flow field structure and pressure distribution on the rocket surface near the exhaust window. However, this effect is regional and limited, and it has minimal influence on the flow field structure and the pressure distribution on the surface outside the separation point.
Figure 11 presents the dimensionless wall pressure distribution curves of the exhaust window centerline at
Φ = 22.5°, both with and without jet flow. These curves show that the wall pressure distributions under the same working conditions, with or without the wake, completely overlap. This implies that the wake’s influence was limited, only affecting the area downstream of the separation point.
Figure 12 illustrates the local flow field of the recirculation region. Upon passing through the separation shock, the incoming flow’s velocity decreases, and the pressure increases, diverging to the outside of the rocket and converging with the wake above the Mach disk. A triangular recirculation region forms between the separation shock and the Mach disk at the exhaust window.
The streamlines reveal CVP in the recirculation region, specifically the PUV and the SUV, both of which rotate inward. The wall pressure distribution in
Figure 12 indicates a pressure peak zone between these vortices, corresponding to the attachment point shown in
Figure 10. There are two extreme pressure points upstream of the exhaust window in
Figure 11, matching the separation and attachment points.
Figure 9 depicts a high-pressure zone on the body surface of the rocket, predominantly near each exhaust window’s centerline. The separation recirculation zones created by each exhaust window interfere with each other between the windows, resulting in increased pressure.
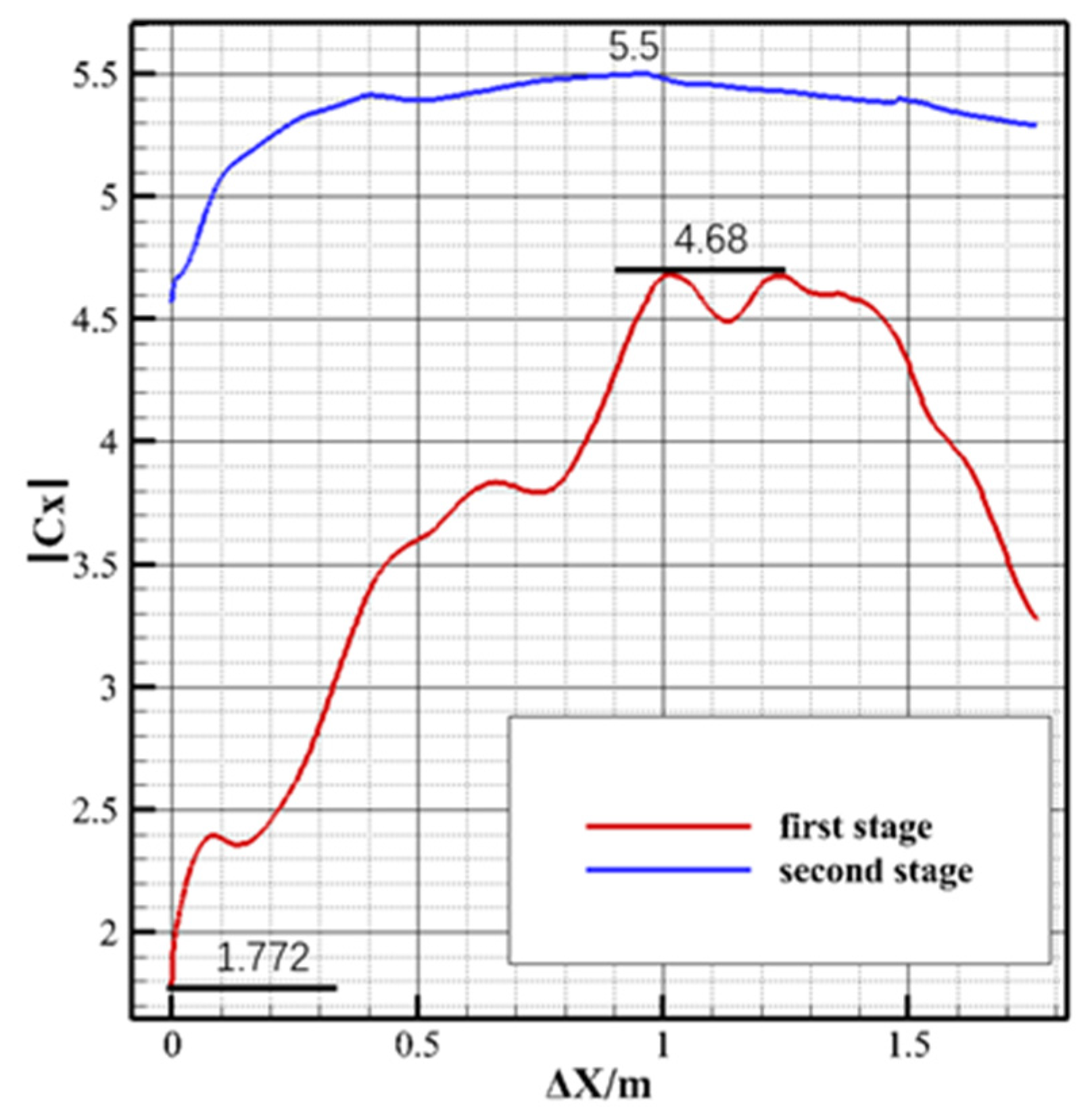
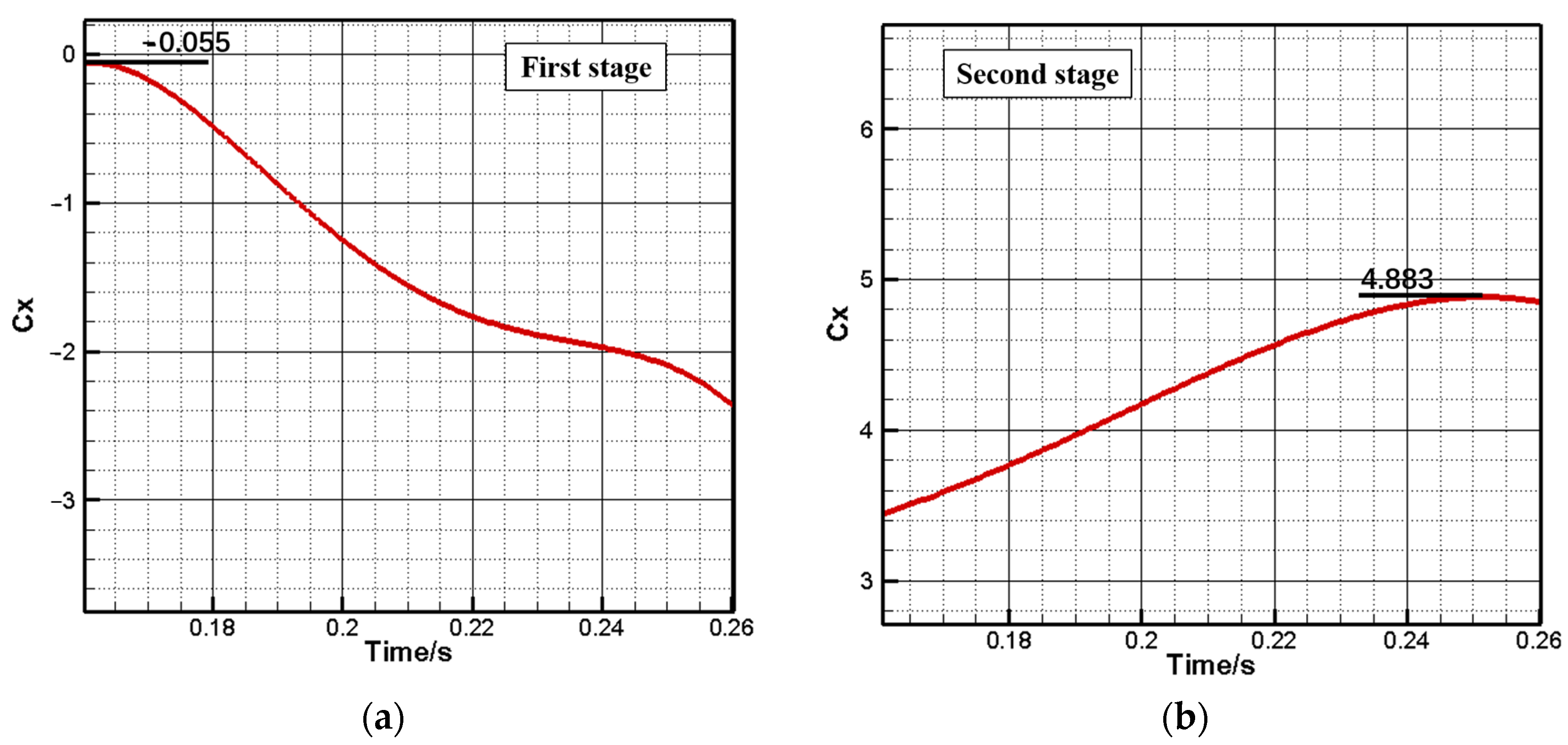
Figure 13 displays the axial displacement curves of the first and second stages during the separation process, with the separation time as the time zero point. Given the absence of the flight attack angle and sideslip angle in the design condition, the first and second stages did not move or rotate in other directions during the initial stage of separation. As the separation process progressed, the distance between the stages expanded, and the movements of the first and second stages decelerated. This trend is apparent in the axial force coefficient (
Figure 14). After 0.1525 s, the remaining thrust of the first stage led it to approach a uniform motion, while the speed of the second stage continued to rise.
Figure 14 presents the relationship between the axial force coefficient (
CX) and separation distance (Δ
X) during the first stage of separation under design conditions, where (
CX) is the absolute value.
Figure 15 shows that, during the initial stage of interstage separation motion (Δ
X < 1 m/Δ
X < 0.435 D), the axial force coefficient of the first and second stages increases rapidly as the high-temperature, high-pressure, under-expanded gas in the interstage area is released through the separation gap. The maximum values were obtained at Δ
X = 1.018 m and Δ
X = 0.962 m. This phase corresponds to the speed’s rapid increase before 0.15 s in
Figure 14; after 0.15 s of separation, when Δ
X > 0.435 D, the gas in the original interstage area is nearly fully expanded. As the wake flow phenomenon gradually fades, the axial force coefficient of the first-stage rocket drops rapidly, and the axial force coefficient of the second stage stabilizes under the maintenance of the engine thrust and ceases to increase.
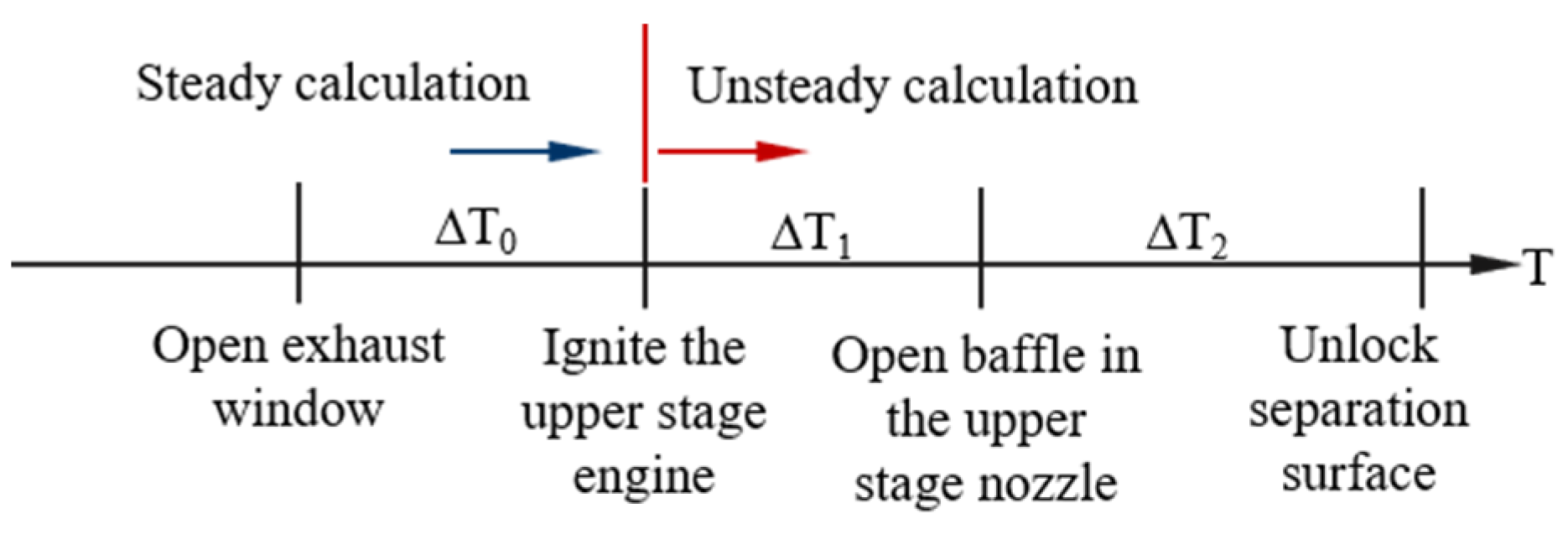
4. Effect of Separation Timing
Figure 16 illustrates that the timing of air separation in multistage rockets necessitates engine ignition, the opening of the nozzle baffle, and the unlocking of the first and second stages. These processes are represented in the timing diagram as two periods, ΔT
1 and ΔT
2, with the upper-stage engine ignition time set as time zero, and ΔT
1 = 60 ms and ΔT
2 = 160 ms in the design condition. Different methods of determining the separation timing will directly modify the flow field in the interstage area at the separation moment, which alters the force and motion of the rocket. Therefore, in this section, we examine the local flow field structure and aerodynamic properties under different ΔT
1 and ΔT
2 conditions to understand how separation timing impacts the motion of the first and second stages.
Figure 17 displays the exhaust window’s flow field at the time of separation for different baffle-opening times. By comparing and analyzing the flow fields of each condition with
Figure 15 (60 ms), it is observed that, before 75 ms, with the delay in the baffle-opening time, the range of the plume flow and the induced separation region continually expand. At 90 ms, the extent of the flow range is nearly the same as at 75 ms and ceases to increase. Only the separation point advances, and the recirculation area grows in the near-wall region in the inflow direction.
Furthermore, for the internal flow field structure of the recirculation area, it is clear that the previously mentioned CVP did not form under the conditions of the baffle opening at 30 ms. In other words, the flow separation induced by the wake flow was insignificant at this time; the intensity of the shockwave formed was weak, and the shear layer flow rate was low. For the 45~75 ms working conditions, the range of the CVP vortex pair did not change substantially. However, in the 90 ms working condition, the range of the CVP vortex pair increased considerably due to the volume flow rate through the exhaust window no longer increasing. However, the gas pressure continued to rise as the baffle-opening time extended.
Figure 18 illustrates the axial force coefficient curves of the first and second stages, where the abscissa represents the baffle-opening time for each working condition, and the curves are fitted using data points. As observed in
Figure 18a, for the first stage, the axial force coefficient,
CX, continuously increases and stabilizes with the delay in baffle-opening time. However, the separation time coefficient corresponding to the 30 ms working condition is small, indicating that the premature opening of the baffle inside the engine nozzle will not efficiently jettison the first stage. For the second stage, the axial force coefficient initially increases, then decreases, and reaches its highest point at approximately 75 ms because most of the thrust in the second stage originates from the gas combustion inside the engine and the interstage area.
If the baffle is opened too late, the interstage exhaust duration is reduced, leading to excess heat and pressure in the interstage area that does not receive sufficient exhaust. Simultaneously, the flow separation causes the recirculation area to expand rapidly, significantly enhancing the internal mixing in the interstage area (as shown in
Figure 17c,d), reducing the axial force coefficient when the second stage separates.
Moreover, the selection of the baffle-opening time must also consider that excessively harsh interstage conditions may result in the burning of instruments and structures in the interstage area.
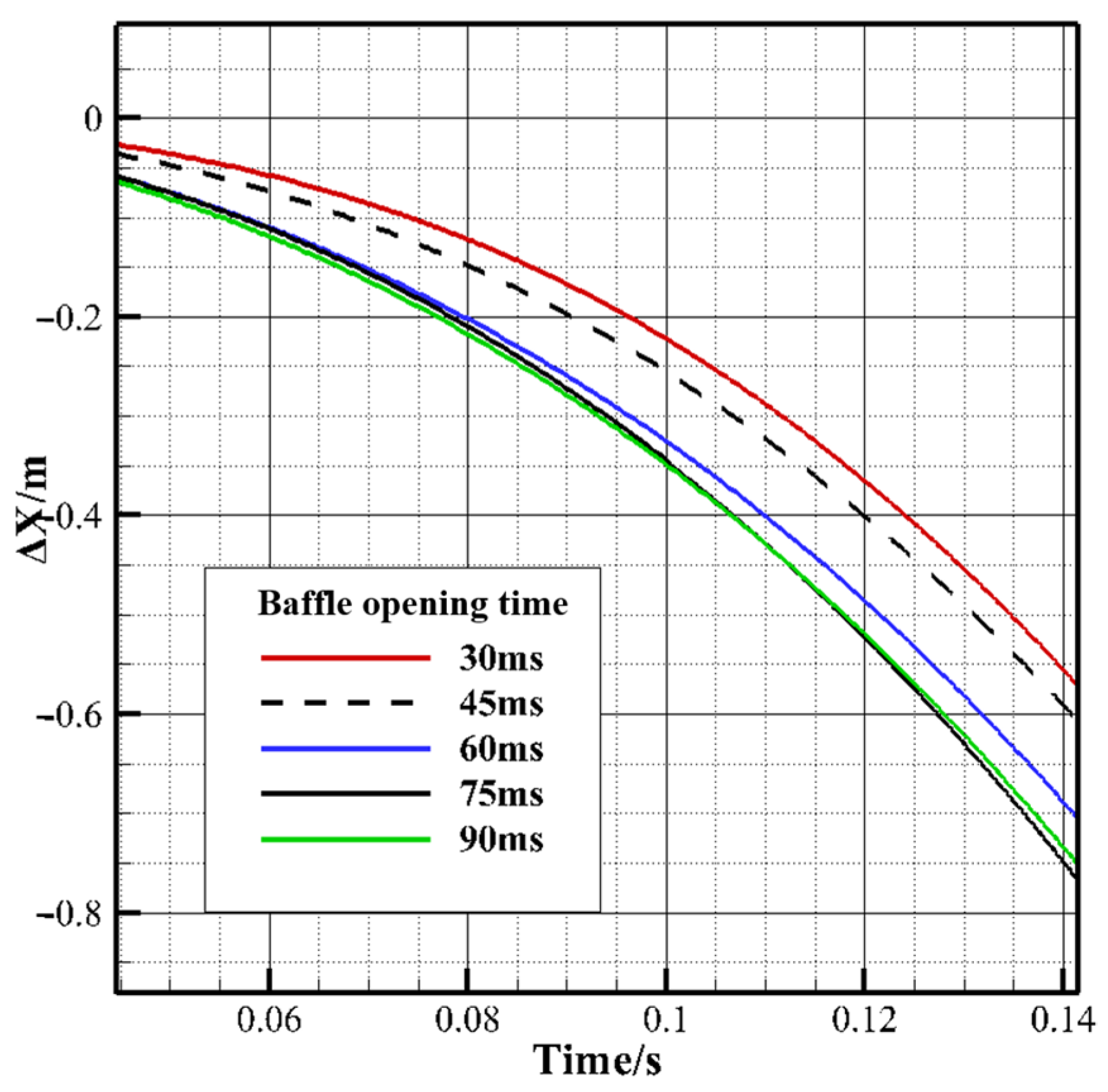
Figure 19 displays the relationship between the axial displacement of the first stage and different baffle-opening timings. It can be seen that, at the beginning of the motion, the motion trends of the curves corresponding to 30 and 45 ms are significantly different from those of 60 ms, with lower speeds. This trend aligns with the pattern observed in the axial force coefficient curve. The curves at 75 and 90 ms showed almost no difference at the beginning of the motion, and they did not produce a significant difference until 200 ms after separation, indicating that, for the motion characteristics of the first stage, a baffle-opening time of 75 ms or longer will not have a significant impact.
Similarly,
Figure 20 presents the flow field structure at different unlocking times between stages when the opening time of the interstage baffle is 60 ms (the design condition). At an unlocking time of 150 ms, the vortex structure in the recirculation zone had not yet formed, and only recirculation caused by the shear layer was observed. During the unlocking time of 185 ms, 220 ms (design condition) and 235 ms, the evolution of the flow field is noticeable. That is, as the separation and unlocking times progress, the total pressure at the engine’s outlet continues to increase; the extent of the Mach disc, return zone, and CVP gradually expands; the separation point moves forward; and the vortex structure in the interstage zone transforms into a pair of large vortices. The flow field structure at 235 ms is virtually identical to that at 250 ms, indicating that, at this point, the interstage flow field is fully developed, and the separation and unlocking times have little impact on the flow field, showing signs of stability.
This phenomenon is also reflected in the axial force coefficient curve in
Figure 21b, which demonstrates that, for the second stage, the aerodynamic coefficient stabilizes after 235 ms and no longer increases. Moreover, the relationship between the axial force coefficient and interstage separation time in
Figure 21 also reveals that, in terms of the overall aerodynamic characteristics, the influence of the separation time on the early aerodynamic characteristics before the design point (220 ms) is very smooth and nearly linear. However, this pattern differs beyond the design point. In the first stage, the axial force coefficient continues to increase with the delay in the separation time, but its variation curve has multiple points of curvature inflection. In the second stage, the axial force coefficient reaches its maximum at a separation time of 250 ms.
5. Conclusions
In this study, the initial stage of the thermal separation between two stages of a rocket was considered the research subject, with dynamic mesh technology employed to simulate the separation process of the two-stage rocket under different separation timings. By examining the influence of varying baffle opening times and first- and second-stage unlocking separation times on the initial flow field structure and aerodynamic characteristics of the separation, this study offers a reference point for the selection of the separation moment and aids in subsequent research and control system development. The following conclusions were drawn:
(1) For the design condition of the separation time flow field, the high-pressure combustion gas generated by the second-stage engine impacted the front of the first stage in the interstage region, forming a sequence of vortex structures, which were then discharged through the exhaust window. Outside the interstage region, the interaction between the exhaust window jet and supersonic boundary layer flow formed an interference flow field and a high-pressure separation zone. A pair of counter-rotating vortices were present in the separation zone, with a pressure peak line formed between the two vortices. In non-design conditions, the delay in the baffle opening time and separation time led to a continuous expansion of the wake and the induced separation region until it reached a particular range and achieved stability.
(2) The flow field structure and two-stage aerodynamic characteristics under different separation sequences demonstrated similar and unified trends. Under the design conditions, the axial force coefficients of the first and second stages initially increased and then decreased, increasing the separation distance. The baffle opening and separation times had different effects on the axial force coefficients of the first and second stages during the initial separation before and after the design point for non-design conditions. Variation curves were obtained to verify the rationality of the design condition.