Multi-Objective Optimization with Active–Passive Technology Synergy for Rural Residences in Northern China
Abstract
1. Introduction
2. Research Method
2.1. Research Object
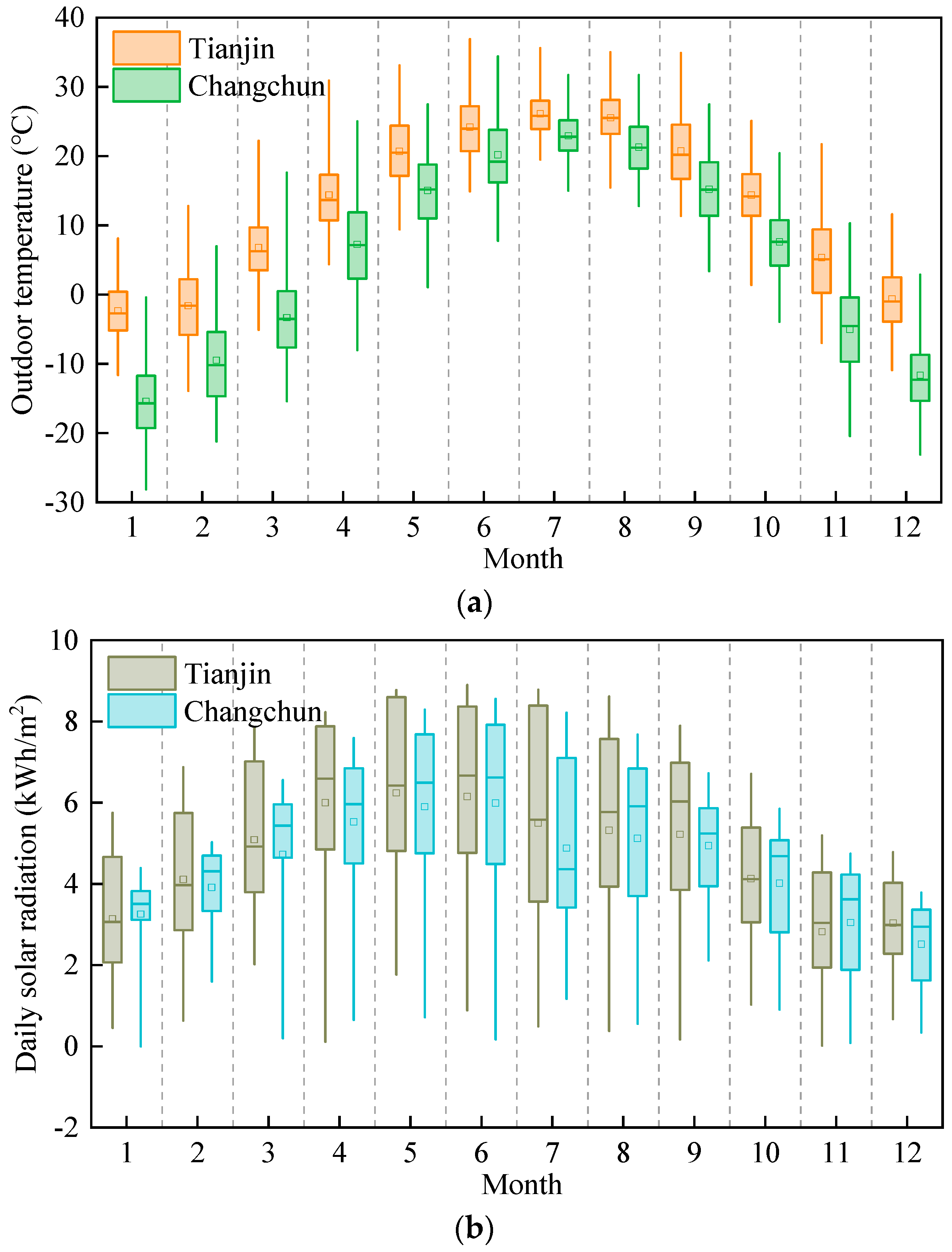
2.1.1. Typical City Meteorological Data
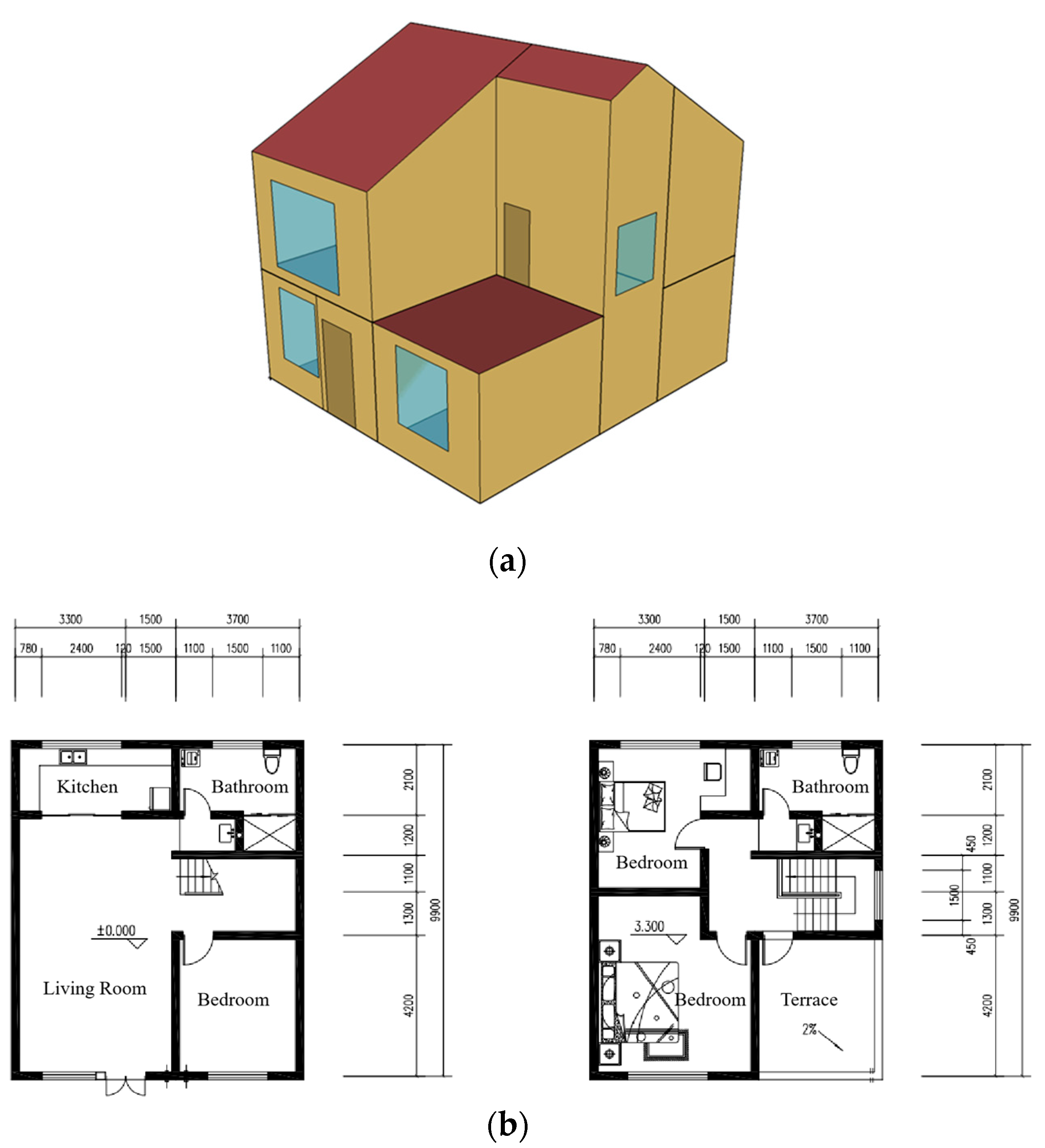
2.1.2. Residential Building Information
2.2. Multi-Objective Optimization Model with Active–Passive Technology Synergy
2.2.1. Optimization Objectives
- (1)
- Whole life cycle carbon emissions
- (2)
- The annual energy consumption of the HVAC system
- (3)
- The annual cost
- (4)
- Thermal comfort ranking value
2.2.2. Objective Function Calculation Parameters
2.2.3. Design Variables
- The parameters that can be adjusted at the design stage, such as the orientation and window–wall area ratio, which can affect the energy consumption of rural residences.
- The parameters that can be modified when rural residences are in use, such as the thickness of the envelope insulation layer, which can affect the heat transfer coefficient of the envelope.
- Passive energy-saving technology, such as the design of sunspace, which can play a role in reducing energy demand.
2.2.4. Multi-Objective Optimization Algorithm
3. Results and Discussion
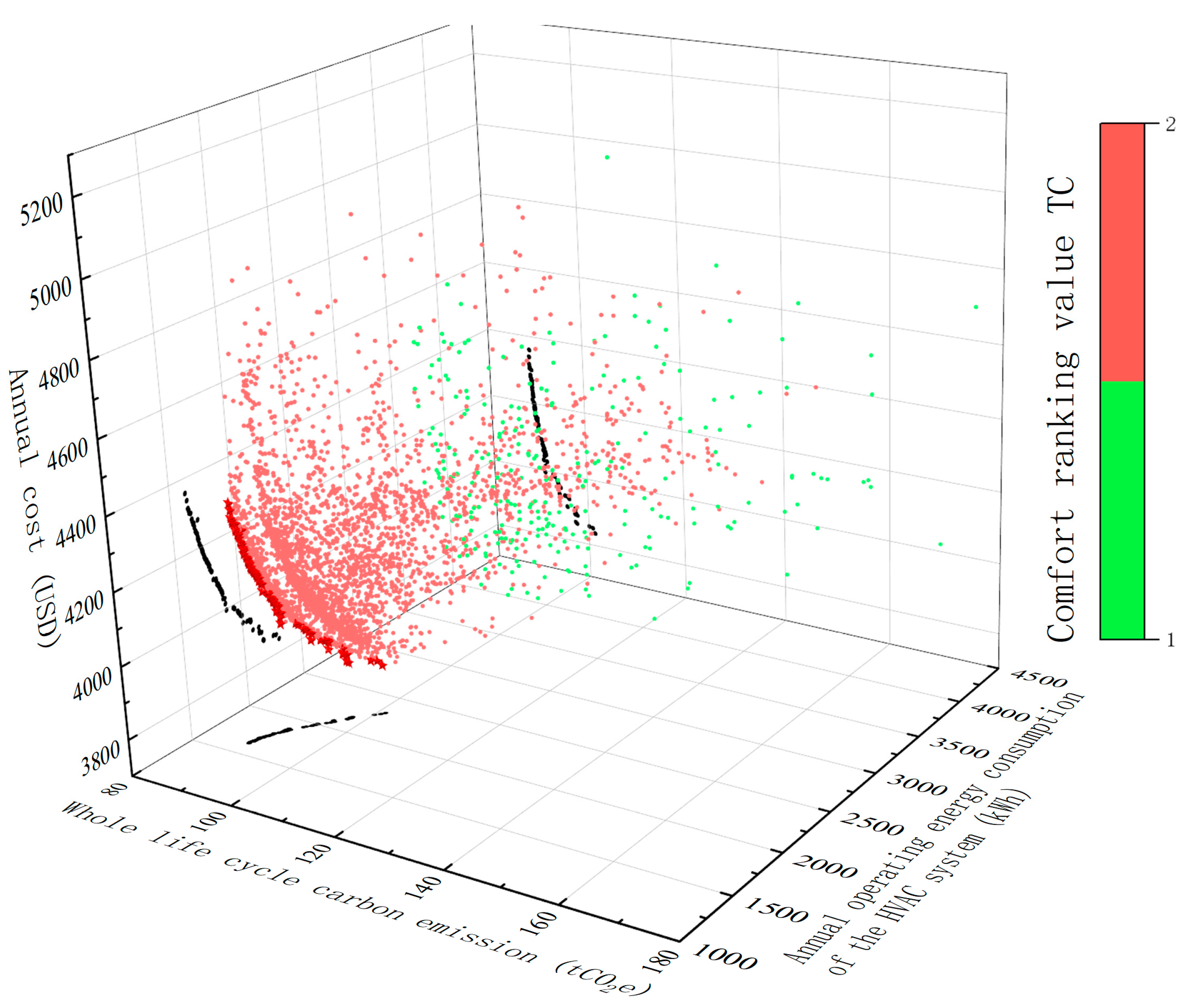
3.1. Multi-Objective Optimization Results Analysis in Changchun
3.2. Multi-Objective Optimization Results Analysis in Tianjin
3.3. Comparison of Optimization Results between Two Regions
3.4. Sensitivity Analysis
4. Conclusions
- From the standpoints of economy, energy efficiency, environmental friendliness, and thermal comfort, the optimal solution for rural residences derived from the ideal point method is preferred to the linear weighted sum method in severe cold and cold regions.
- In the Pareto-optimal solution set, the roof insulation thickness is the most sensitive design variable in the whole life cycle carbon emission, the annual energy consumption of the HVAC system, and the annual cost of rural residences. The objective function values decrease as the increase of roof insulation thickness.
- Compared with the prototype, the optimized carbon emissions of rural residences in severe cold and cold regions are decreased by 56.1% and 54.6%, respectively. The annual operating energy consumption is decreased by 59.7% and 62.2%. The optimized annual cost is decreased by 6.0% and 6.8%. Moreover, the thermal comfort is improved.
- Compared with the optimal solutions, the whole life cycle carbon emission, the annual energy consumption of the HVAC system, and the annual cost of rural residences in the cold region are 50.3%, 48.8%, and 90.9% of that in the severe cold region.
- Compared to the cold region, the orientation of the rural residence in the severe cold region is shifted eastward by 10°. The window-to-wall area ratio on the south elevation of the sunspace and the thickness of the envelope insulation are increased.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BIM | Building Information Modeling |
| ASHP | Air Source Heat Pump |
| DRHP | Direct-Condensation Radiant Heating Panel |
| HVAC | Heating, Ventilation and Air Conditioning |
| NSGA | Nondominated Sorting Genetic Algorithm |
| IMRFOA | Improved Manta-Ray Foraging Optimization Algorithm |
| SPEA | Strength Pareto Evolutionary Algorithm |
| GA | Genetic Algorithm |
| TAEA | Two-Archive Evolutionary Algorithm |
| TC | Thermal Comfort |
| LCA | Life Cycle Assessment |
| PMV | Predicted Mean Vote |
| PPD | Predicted Percentage Dissatisfied |
| SRC | Standardized Regression Coefficient |
| Symbols | |
| C | carbon emission, kgCO2e |
| E | energy consumption, kWh/a |
| M | annual cost, USD |
| G | consumption of building material, m3 |
| P | production carbon emission factor, kgCO2e/m3 |
| D | average transportation distance, km |
| Y | carbon emission factor per unit weight of transportation distance, kgCO2e/(t·km) |
| X | number of floors |
| A | area, m2 |
| y | building design life, a |
| EF | energy carbon emission factor, kgCO2e/kW·h |
| Z | inherent carbon emission conversion factor |
| capacity | |
| d | cost conversion factor |
| Superscripts | |
| nz | Whole life |
| sc | Building material production |
| ys | Building material transportation |
| yx | HVAC system operation |
| gy | HVAC system own |
| cc | Demolition phase |
| jz | Construction phase |
| i | Building material |
| b | Building |
| sys | System |
| A | Annual |
| ic | Initial investment |
| gz | Building materials |
| jcaz | Installation |
| qt | Other requirements |
| wh | HVAC maintenance |
References
- Chinese Association of Building Energy Efficiency. China Building Energy Consumption Research Report. 2022. Available online: https://carbon.landleaf-tech.com/report/4621/ (accessed on 20 July 2023).
- Wang, J.; Zhang, X. Study on the Current Situation of Rural Self-built Houses. Green Environ. Prot. Build. Mater. 2019, 2, 60–61. [Google Scholar] [CrossRef]
- Hao, X.; Sun, P.; Li, X.; Li, Y.; Li, C.; Zhang, T. Analysis on Current Situation of Rural Building Environment based on Field Investigation. Build. Energy Environ. 2021, 40, 31–34. [Google Scholar]
- Song, B.; Deng, Q. Technology for Present Situation and Prospect of Energy Rural Construction China Academy of Building Research. Dist. Heat. 2018, 5, 111–115. [Google Scholar] [CrossRef]
- Kistelegdi, I.; Horváth, K.R.; Storcz, T.; Ercsey, Z. Building Geometry as a Variable in Energy, Comfort, and Environmental Design Optimization—A Review from the Perspective of Architects. Buildings 2022, 12, 69. [Google Scholar] [CrossRef]
- Feng, J.; Luo, X.; Gao, M.; Abbas, A.; Xu, Y.-P.; Pouramini, S. Minimization of energy consumption by building shape optimization using an improved Manta-Ray Foraging Optimization algorithm. Energy Rep. 2021, 7, 1068–1078. [Google Scholar] [CrossRef]
- Abanda, F.H.; Byers, L. An investigation of the impact of building orientation on energy consumption in a domestic building using emerging BIM (Building Information Modelling). Energy 2016, 97, 517–527. [Google Scholar] [CrossRef]
- Xu, X.; Li, X. Construction of Building an Energy Saving Optimization Model Based on Genetic Algorithm. Int. J. Inf. Technol. Syst. Approach 2023, 16, 1–15. [Google Scholar] [CrossRef]
- Atashbar, H.; Noorzai, E. Optimization of Exterior Wall Cladding Materials for Residential Buildings Using the Non-Dominated Sorting Genetic Algorithm II (NSGAII) Based on the Integration of Building Information Modeling (BIM) and Life Cycle Assessment (LCA) for Energy Consumption: A Case Study. Sustainability 2023, 15, 15647. [Google Scholar] [CrossRef]
- Yao, S.; Jiang, Z.; Yuan, J.; Wang, Z.; Huang, L. Multi-objective optimization of transparent building envelope of rural residences in cold climate zone, China. Case Stud. Therm. Eng. 2022, 34, 102052. [Google Scholar] [CrossRef]
- Ruiz, M.C.; Romero, E. Energy saving in the conventional design of a Spanish house using thermal simulation. Energy Build. 2011, 43, 3226–3235. [Google Scholar] [CrossRef]
- Zhao, L.; Zhang, W.; Wang, W. BIM-Based Multi-Objective Optimization of Low-Carbon and Energy-Saving Buildings. Sustainability 2022, 14, 13064. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhou, Y.; Zhao, N.; Li, H.; Tohniyaz, B.; Mperejekumana, P.; Hong, Q.; Wu, R.; Li, G.; Sultan, M.; et al. Clean heating during winter season in Northern China: A review. Renew. Sustain. Energy Rev. 2021, 149, 111339. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, L.; Nie, J.; Li, Y. Techno-economic analysis of air source heat pump applied for space heating in northern China. Appl. Energy 2017, 207, 533–542. [Google Scholar] [CrossRef]
- Hu, B.; Wang, R.Z.; Xiao, B.; He, L.; Zhang, W.; Zhang, S. Performance evaluation of different heating terminals used in air source heat pump system. Int. J. Refrig. 2019, 98, 274–282. [Google Scholar] [CrossRef]
- Xiao, B.; He, L.; Zhang, S.; Kong, T.; Hu, B.; Wang, R.Z. Comparison and analysis on air-to-air and air-to-water heat pump heating systems. Renew. Energy 2020, 146, 1888–1896. [Google Scholar] [CrossRef]
- Huang, X.; Fang, H.; Zhang, L.; Liu, J.; Zhang, L. Preliminary Analysis on the Different Heating Technologies in a Rural Area of Shandong Province, China. In Proceedings of the 10th International Symposium on Heating, Ventilation and Air Conditioning (ISHVAC), Jinan, China, 22 October 2017; pp. 1461–1468. [Google Scholar]
- Fanger, P.O.; Christensen, N.K. Perception of draught in ventilated spaces. Ergonomics 1986, 29, 215–235. [Google Scholar] [CrossRef]
- Shao, S.; Zhang, H.; Fan, X.; You, S.; Wang, Y.; Wei, S. Thermodynamic and economic analysis of the air source heat pump system with direct-condensation radiant heating panel. Energy 2021, 225, 120195. [Google Scholar] [CrossRef]
- Shao, S.; Zhang, H.; Liu, Z.; You, S.; Wang, Y. Thermo-economic optimization of the direct-condensation radiant heating panel: A numerical-based approach. Energy Build. 2021, 240, 110908. [Google Scholar] [CrossRef]
- Wang, Y.; You, S.; Zhang, H.; Shao, S. Experimental Investigation of Air-Source Heat Pump Heating System With a Novel Thermal Storage Refrigerant-Heated Panel. J. Therm. Sci. Eng. Appl. 2021, 13, 011015. [Google Scholar] [CrossRef]
- Wu, H.; Deng, F.; Tan, H. Research on parametric design method of solar photovoltaic utilization potential of nearly zero-energy high-rise residential building based on genetic algorithm. J. Clean. Prod. 2022, 368, 133169. [Google Scholar] [CrossRef]
- Chen, R.; Tsay, Y.-S.; Zhang, T. A multi-objective optimization strategy for building carbon emission from the whole life cycle perspective. Energy 2023, 262, 125373. [Google Scholar] [CrossRef]
- Wang, W.; Yuan, M.; Li, Y.-Z.; Li, C. Numerical investigation on the impact of an on-top sunspace passive heating approach for typical rural buildings in northern China. Sol. Energy 2019, 186, 300–310. [Google Scholar] [CrossRef]
- Ciardiello, A.; Rosso, F.; Dell’Olmo, J.; Ciancio, V.; Ferrero, M.; Salata, F. Multi-objective approach to the optimization of shape and envelope in building energy design. Appl. Energy 2020, 280, 115984. [Google Scholar] [CrossRef]
- Wang, X.; Mai, X.; Lei, B.; Bi, H.; Zhao, B.; Mao, G. Collaborative optimization between passive design measures and active heating systems for building heating in Qinghai-Tibet plateau of China. Renew. Energy 2020, 147, 683–694. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, Z.; Wang, D.; Liu, Y.; Zhang, Y.; Liu, Y.; Zhao, Y.; Gao, M.; Fan, J. Co-optimization of passive building and active solar heating system based on the objective of minimum carbon emissions. Energy 2023, 275, 127401. [Google Scholar] [CrossRef]
- Xu, Y.; Yan, C.; Wang, D.; Li, J.; Shi, J.; Lu, Z.; Lu, Q.; Jiang, Y. Coordinated optimal design of school building envelope and energy system. Sol. Energy 2022, 244, 19–30. [Google Scholar] [CrossRef]
- García Kerdan, I.; Morillón Gálvez, D. Artificial neural network structure optimisation for accurately prediction of exergy, comfort and life cycle cost performance of a low energy building. Appl. Energy 2020, 280, 115862. [Google Scholar] [CrossRef]
- Zhan, J.; He, W.; Huang, J. Comfort, carbon emissions, and cost of building envelope and photovoltaic arrangement optimization through a two-stage model. Appl. Energy 2024, 356, 122423. [Google Scholar] [CrossRef]
- GB/T 50824-2013; Design Standard for Energy Efficiency of Rural Residential Buildings. China Architecture & Building Press: Beijing, China, 2013.
- Chen, Z. The collaborative optimization between active and passive heating technologies for residential building carbon emissions reduction in Tibet. Ph.D. Dissertation, Xi’an University of Architecture and Technology, Xi’an, China, 2020. [Google Scholar]
- Mao, X. Study on Building Life Cycle Carbon Emissions Prediction Model. Ph.D. Dissertation, Tianjin University, Tianjin, China, 2020. [Google Scholar]
- Zhao, X. The calculation of green building life cycle carbon emission and the evalutation of carbon reduction benefit. Ph.D. Dissertation, Dalian University of Technology, Dalian, China, 2018. [Google Scholar]
- GB 51366-2019; Standard for Building Carbon Emission Calculation. China Architecture & Building Press: Beijing, China, 2019.
- Gazis, E.; Harrison, G.P. Life Cycle Energy and Carbon Analysis of Domestic Combined Heat and Power Generators. In Proceedings of the 2011 IEEE Trondheim PowerTech, Trondheim, Norway, 19–23 June 2011; pp. 19–23. [Google Scholar]
- Shao, S.; Zhang, H.; Zheng, W.; You, S.; Wang, Y. Numerical and experimental investigations on heat transfer performance of the refrigerant-heated radiator. Appl. Therm. Eng. 2020, 179, 115748. [Google Scholar] [CrossRef]
- Shao, S. Investigation on Thermal Performance of a Novel Direct-Condensation Radiant Heating Panel for Air Source Heat Pump. Ph.D. Dissertation, Tianjin University, Tianjin, China, 2023. [Google Scholar]
- General Office of the Ministry of Ecology and Environment. Notice on the Work Related to the Management of Greenhouse Gas Emission Reports of Enterprises in the Power Generation Industry for 2023–2025. Available online: www.mee.gov.cn/xxgk2018/xxgk/xxgk06/202302/t20230207_1015569.html (accessed on 20 February 2023).
- Hamdy, M.; Nguyen, A.-T.; Hensen, J.L.M. A performance comparison of multi-objective optimization algorithms for solving nearly-zero-energy-building design problems. Energy Build. 2016, 121, 57–71. [Google Scholar] [CrossRef]
- Nguyen, A.-T.; Reiter, S.; Rigo, P. A review on simulation-based optimization methods applied to building performance analysis. Appl. Energy 2014, 113, 1043–1058. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Elshafei, G.; Vilčeková, S.; Zeleňáková, M.; Negm, A.M. An Extensive Study for a Wide Utilization of Green Architecture Parameters in Built Environment Based on Genetic Schemes. Buildings 2021, 11, 507. [Google Scholar] [CrossRef]
- Verma, S.; Pant, M.; Snasel, V. A Comprehensive Review on NSGA-II for Multi-Objective Combinatorial Optimization Problems. IEEE Access 2021, 9, 57757–57791. [Google Scholar] [CrossRef]
- WenBin, C.; YiJun, L.; Li, W.; XiaoLing, L. A Study of the Multi-objective Evolutionary Algorithm Based on Elitist Strategy. In Proceedings of the 2009 Asia-Pacific Conference on Information Processing, Shenzhen, China, 14–19 July 2009; pp. 136–139. [Google Scholar]
- Shao, Y.; Geyer, P.; Lang, W. Integrating requirement analysis and multi-objective optimization for office building energy retrofit strategies. Energy Build. 2014, 82, 356–368. [Google Scholar] [CrossRef]







| Year | Authors | Objectives | Optimization Variables | Optimization Algorithms |
|---|---|---|---|---|
| 2020 | Wang et al. [26] | Energy consumption Total cost | Building envelope Window-to-wall ratio Active heating system | NSGA-II |
| 2020 | Iván García Kerdan et al. [29] | Energy destructions Thermal comfort Life cycle cost | Building envelope HVAC system Photovoltaic arrangement Wind utilization | NSGA-II |
| 2020 | Adriana Ciardiello et al. [25] | Energy demand Energy cost Investment cost Carbon emissions | Geometry Building envelope | aNSGA-II |
| 2021 | Feng et al. [6] | Energy consumption Life cycle cost | Building shape Building envelope | IMRFOA |
| 2022 | Yao et al. [10] | Daylighting Energy efficiency Thermal comfort | Building envelope Sunspace | SPEA-II |
| 2022 | Zhao et al. [12] | Carbon emissions Energy consumption Daylighting | Orientation Window-to-wall ratio Window height Building materials | NSGA-II |
| 2022 | Wu et al. [22] | Annual energy demand Total power generation Investment cost | Orientation Window-to-wall ratio Heat transfer coefficient Photovoltaic system | NSGA-II |
| 2022 | Xu et al. [28] | Energy Thermal comfort Daylighting Life cycle cost | Building envelope Photovoltaic arrangement External window Shading | NSGA-II |
| 2023 | Xu et al. [8] | Thermal comfort Energy consumption | Heat transfer coefficient | GA |
| 2023 | Hossein Atashbar et al. [9] | Energy consumption Global warming potential | Building envelope materials | NSGA-II |
| 2023 | Chen et al. [23] | Life carbon emissions Life cycle costs Indoor discomfort hours | Building envelope HVAC system Internal gain | NSGA-II NSGA-III C-TAEA |
| 2024 | Zhan et al. [30] | Occupant comfort Life cycle carbon emissions Building cost | Building envelope Photovoltaic arrangement | NSGA-II NSGA-III C-TAEA |
| (a) Envelope Structure Parameters | ||||
| Type of Envelope | Envelope Structure (Outside to Inside) | |||
| External Wall | 20 mm composite mortar + 10 mm XPS (insulation layer) + 240 mm coal gangue porous brick + 20 mm composite mortar | |||
| Roof | 20 mm composite mortar + 10 mm XPS (insulation layer) + 50 mm expanded perlite + 120 mm reinforced concrete + 20 mm composite mortar | |||
| Floor | 20 mm composite mortar + 10 mm XPS (insulation layer) + 120 mm reinforced concrete + 20 mm composite mortar | |||
| Floorboard | 20 mm composite mortar + 50 mm XPS (insulation layer) + 120 mm reinforced concrete + 20 mm composite mortar | |||
| Interior Wall | 20 mm composite mortar + 240 mm coal gangue porous brick + 20 mm composite mortar | |||
| Door | 10 mm iron sheet + 30 mm wood chipboard + 10 mm iron sheet | |||
| Exterior Window | South | 6 mm single-layer plate glass (bridge-cutoff aluminum alloy), window–wall area ratio is 0.16 | ||
| North | 6 mm single-layer plate glass (bridge-cutoff aluminum alloy), window–wall area ratio is 0.23 | |||
| East | 6 mm single-layer plate glass (bridge-cutoff aluminum alloy), window–wall area ratio is 0.03 | |||
| (b) Envelope Structure Parameters | ||||
| Type of Envelope | Heat Transfer Coefficient W/(m2·K) | Solar Heat Gain Coefficient | Remarks | |
| External Wall | 0.117 | — | — | |
| Roof | 0.691 | — | ||
| Floor | 1.708 | — | ||
| Floorboard | 0.518 | — | ||
| Interior Wall | 0.122 | — | ||
| Door | 1.597 | — | ||
| Exterior Window | South | 5.778 | 0.862 | The area ratio of the window frame and hole is 0.15. |
| North | 5.778 | 0.862 | ||
| East | 5.778 | 0.862 | ||
| Room | Winter Room Temperature (°C) | Ventilation Times (h−1) | Number of People | Lighting Power Density (W/m2) | Equipment Power Density (W/m2) | Heating Period |
|---|---|---|---|---|---|---|
| Living room | 14 | 0.5 | 3 | 7 | 3.8 | Changchun: 20 October to 6 April Tianjin: 1 November to 31 March |
| Bedroom | 14 | 0.5 | 2 | 7 | 3.8 | |
| Kitchen | 14 | 0.5 | 1 | 7 | 3.8 | |
| Bathroom | 14 | 0.5 | 1 | 7 | 0 | |
| Stairwell | 14 | 0.5 | 1 | 7 | 0 |
| Envelope Material | Carbon Emission Factor (kgCO2e/Unit1) | Unit1 | Unit Price (USD/Unit2) | Unit2 | Density (kg/m3) |
|---|---|---|---|---|---|
| Composite mortar | 13 | m3 | 57.2 | t | 1700 |
| Coal gangue porous brick (240 × 115 × 53 mm) | 16 | m3 | 0.07 | block | 1400 |
| Reinforced concrete | 496 | m3 | 123 | m3 | 2500 |
| Iron sheet | 2400 | t | 1736 | t | 7250 |
| Wood chipboard | 336 | m3 | 833 | m3 | 200 |
| XPS | 3290 | t | 111 | m3 | 25 |
| EPS | 3130 | t | 55.6 | m3 | 18 |
| Expanded perlite | 1980 | t | 208 | t | 80 |
| 6 mm LowE glass | 0.88 | kg | 13.2 | m2 | 2500 |
| 6 mm plate glass | 0.76 | kg | 9.4 | m2 | 2500 |
| Bridge-cutoff aluminum alloy window | 194 | m2 | 2.6 | kg | 2690 |
| Equipment | Initial Investment (USD/kWh) | Maintenance Cost |
|---|---|---|
| ASHP with tuyere | 132 | 8% of initial investment |
| ASHP with DRHP | 139 |
| City | Time Frame | Electricity Price (USD/kWh) | Carbon Emission Factor (tCO2e/MWh) | |
|---|---|---|---|---|
| Changchun | Peak | 8:00–21:00 | 0.078 | 0.5703 |
| Valley | 21:00–8:00 next day | 0.046 | ||
| Tianjin | All day | 0.071 | ||
| Design Variable | Symbol | Value Range | |
|---|---|---|---|
| Main body | Orientation | −30–30°, step size 10° | |
| Window-to-wall area ratio on south elevation | 0.25–0.40, step size 0.05 (Changchun) | ||
| 0.25–0.45, step size 0.05 (Tianjin) | |||
| Window-to-wall area ratio on north elevation | 0.10–0.25, step size 0.05 (Changchun) | ||
| 0.10–0.30, step size 0.05 (Tianjin) | |||
| South wall insulation type | 1:XPS/2:EPS | ||
| South wall insulation thickness | 0.00–0.40 m, step size 0.01 m | ||
| North wall insulation type | 1:XPS/2:EPS | ||
| North wall insulation thickness | 0.00–0.40 m, step size 0.01 m | ||
| East wall insulation type | 1:XPS/2:EPS | ||
| East wall insulation thickness | 0.00–0.40 m, step size 0.01 m | ||
| West wall insulation type | 1:XPS/2:EPS | ||
| West wall insulation thickness | 0.00–0.40 m, step size 0.01 m | ||
| Roof insulation type | 1:XPS/2:EPS | ||
| Roof insulation thickness | 0.00–0.40 m, step size 0.01 m | ||
| Floor insulation type | 1:XPS/2:EPS | ||
| Floor insulation thickness | 0.00–0.40 m, step size 0.01 m | ||
| Glass type | 1: 6 mm Lowe glass/ 2: 6 mm plate glass | ||
| Number of glass layers | 1/2/3 | ||
| Sunspace | Depth | 0.6–1.5 m, step size 0.3 m | |
| Window-to-wall area ratio | 0.6–0.9, step size 0.1 | ||
| Glass lamination thickness | 0.003–0.024 m, step size 0.003 m | ||
| Parameter | Unit | Prototype | Ideal Point Method | Difference Percentage | |
|---|---|---|---|---|---|
| Economy | Passive Technology Initial Investment | USD | 44,914 | 49,460 | 10.1% |
| Active Technology Initial Investment | USD | 2379 | 1917 | −19.4% | |
| Total Initial Investment | USD | 47,293 | 51,378 | 8.6% | |
| Operation and Maintenance Cost | USD | 1067 | 501 | −53.1% | |
| Annual Cost | USD | 4494 | 4223 | −6.0% | |
| Environmental Protection | Passive Technology Carbon Emission | tCO2e | 45.0 | 34.7 | −22.9% |
| Active Technology Carbon Emission | tCO2e | 413.1 | 166.5 | −59.7% | |
| Total Carbon Emission | tCO2e | 458.2 | 201.2 | −56.1% | |
| Energy Efficiency | Annual Operating Energy Consumption | kWh | 14,128.4 | 5693.9 | −59.7% |
| Thermal Comfort | TC Ranking Value | — | 2 | 1 | — |
| Parameter | Unit | Prototype | Ideal Point Method | Difference Percentage | |
|---|---|---|---|---|---|
| Economy | Passive Technology Initial Investment | USD | 44,914 | 48,342 | 7.6% |
| Active Technology Initial Investment | USD | 1405 | 1138 | −19.0% | |
| Total Initial Investment | USD | 46,319 | 49,480 | 6.8% | |
| Operation and Maintenance Cost | USD | 542 | 252 | −53.4% | |
| Annual Cost | USD | 3898 | 3837 | −1.5% | |
| Environmental Protection | Passive Technology Carbon Emission | tCO2e | 45.0 | 33.9 | −24.7% |
| Active Technology Carbon Emission | tCO2e | 178.3 | 67.4 | −62.2% | |
| Total Carbon Emission | tCO2e | 223.3 | 101.3 | −54.6% | |
| Energy Efficiency | Annual Operating Energy Consumption | kWh | 6096.9 | 2304.7 | −62.2% |
| Thermal Comfort | TC Ranking Value | — | 2 | 1 | — |
| Parameter | Changchun | Tianjin | ||
|---|---|---|---|---|
| Sunspace Depth | m | 0.6 | 0.6 | |
| Orientation | ° | 20 | 10 | |
| Insulation Type | North Exterior Wall | EPS | EPS | |
| South Exterior Wall | EPS | EPS | ||
| East Exterior Wall | EPS | EPS | ||
| West Exterior Wall | EPS | EPS | ||
| Roof | EPS | EPS | ||
| Floor | EPS | EPS | ||
| Insulation Thickness | North Exterior Wall | m | 0.11 | 0.08 |
| South Exterior Wall | m | 0.06 | 0.01 | |
| East Exterior Wall | m | 0.05 | 0.04 | |
| West Exterior Wall | m | 0.06 | 0.01 | |
| Roof | m | 0.19 | 0.14 | |
| Floor | m | 0.13 | 0.01 | |
| Glass Type | 6 mm Plate Glass | 6 mm Plate Glass | ||
| Number of Glass Layers | 3 | 3 | ||
| Window-to-wall Area Ratio | North Elevation | 0.1 | 0.1 | |
| South Elevation | 0.4 | 0.45 | ||
| South Elevation of Sunspace | 0.7 | 0.6 | ||
| Glass Lamination Thickness of Sunspace | m | 0.015 | 0.015 | |
| ASHP Type | ASHP with DRHP | ASHP with DRHP | ||
| Whole Life Cycle Carbon Emission | tCO2e | 201.2 | 101.3 | |
| Annual Operating Energy Consumption of HVAC System | kWh | 4725.5 | 2304.7 | |
| Annual Cost | USD | 4223.4 | 3837.4 | |
| Comfort Ranking Value TC | 1 | 1 | ||
| Changchun | Tianjin | |
|---|---|---|
| Whole Life Cycle Carbon Emission | Glass lamination thickness of sunspace > Roof insulation thickness > Number of glass layers > Type of active heating system > Window-to-wall area ratio on north elevation | Roof insulation thickness > Type of active heating system > Number of glass layers |
| Annual Energy Consumption of HVAC System | Glass lamination thickness of sunspace > Roof insulation thickness > Number of glass layers > Type of active heating system > Window-to-wall area ratio on north elevation | Roof insulation thickness > Type of active heating system > Number of glass layers |
| Annual Cost | Glass lamination thickness of sunspace > Floor insulation thickness > West wall insulation thickness > East wall insulation thickness > Roof insulation type > Attached sunspace depth | East wall insulation thickness = Floor insulation thickness > West wall insulation thickness > Roof insulation type > Roof insulation thickness > North wall insulation thickness > Attached sunspace depth > East wall insulation thickness |
| TC Ranking Value | Type of active heating system | |
| Changchun | Tianjin | |
|---|---|---|
| Whole Life Cycle Carbon Emission | ||
| Annual Energy Consumption of HVAC System | ||
| Annual Cost |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Wang, Y.; Liu, X.; Wan, F.; Zheng, W. Multi-Objective Optimization with Active–Passive Technology Synergy for Rural Residences in Northern China. Energies 2024, 17, 1539. https://doi.org/10.3390/en17071539
Zhang H, Wang Y, Liu X, Wan F, Zheng W. Multi-Objective Optimization with Active–Passive Technology Synergy for Rural Residences in Northern China. Energies. 2024; 17(7):1539. https://doi.org/10.3390/en17071539
Chicago/Turabian StyleZhang, Huan, Yajie Wang, Xianze Liu, Fujing Wan, and Wandong Zheng. 2024. "Multi-Objective Optimization with Active–Passive Technology Synergy for Rural Residences in Northern China" Energies 17, no. 7: 1539. https://doi.org/10.3390/en17071539
APA StyleZhang, H., Wang, Y., Liu, X., Wan, F., & Zheng, W. (2024). Multi-Objective Optimization with Active–Passive Technology Synergy for Rural Residences in Northern China. Energies, 17(7), 1539. https://doi.org/10.3390/en17071539







