Development of Cycloid-Shaped Roll Charging Chute for Sintering Process for Energy Decarbonization and Productivity Improvement in Steel Plants
Abstract
1. Introduction
1.1. Background of Study
1.2. Problem Statement and Research Objectives
1.3. Literature Review
1.3.1. Reinforcing Sinter Charging Segregation
1.3.2. Sintering Productivity Improvement
1.3.3. Application of Cycloid Curve
1.3.4. Differences from Previous Studies
1.4. Research Framework and Development Process
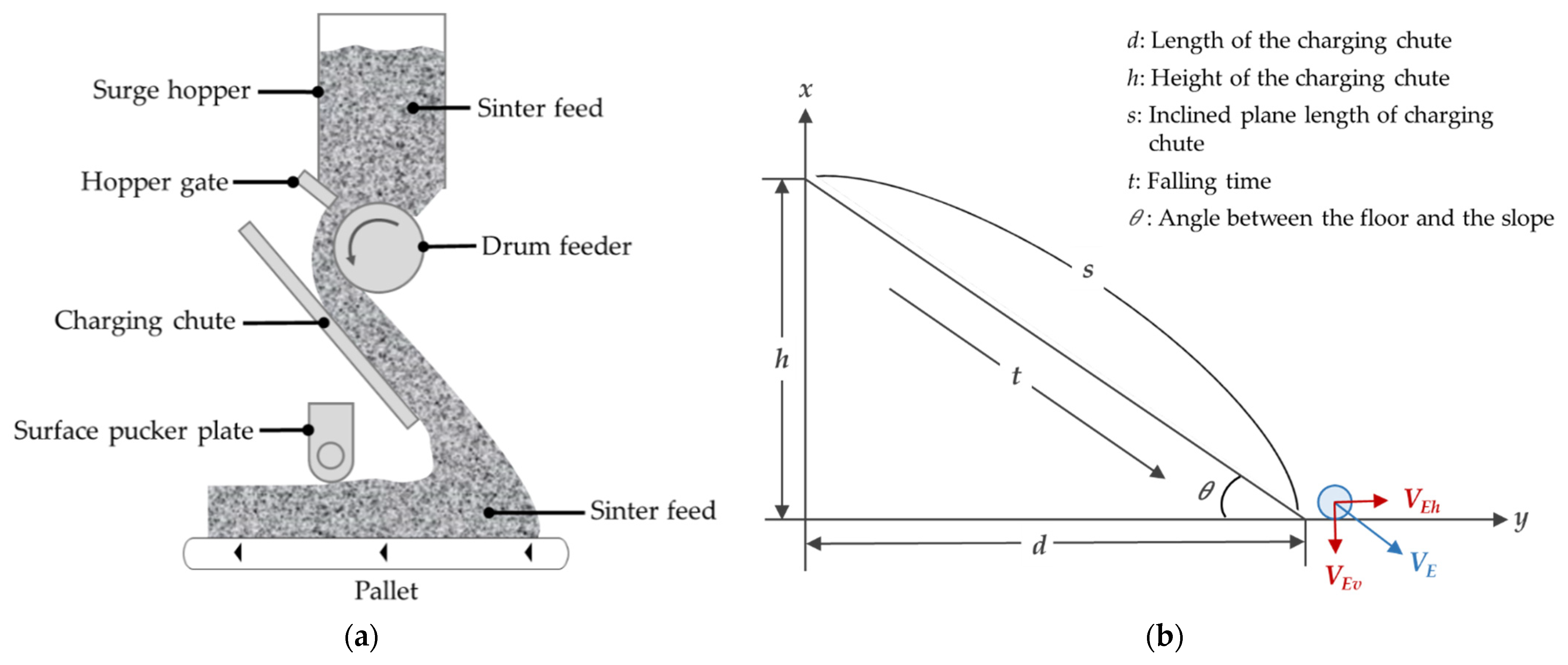
2. Cycloid-Shaped Charging Chute and Modelling
2.1. Particle Behavior on a Straight Inclined Plane and Its Simulation
2.1.1. Particle Behavior on a Straight Slope
- Differential equation for uniform acceleration motion on a straight slope (Equation (1)):where t represents the falling time, m is the slope of the charging chute, and g denotes the acceleration due to gravity, which is equal to 9.81 m/s2.
- Slope m of the straight slope (Equation (2)):where h is the vertical length (height) of the slope (charging chute), and d denotes the horizontal length of the slope (charging chute). The angle θ formed between the base and the slope on a straight slope is determined by the horizontal length (d) and vertical length (h) of the slope, and the length (s) of the slope is also determined.
- Falling time (t) on a straight slope (Equation (3)):
- The escape velocity (VE) of particles on a straight slope (Equation (4)):where a is the acceleration; VE is the particle’s escape velocity (drop speed at point E).
- Equation (5) represents the formula for calculating acceleration on a straight slope.where g is the acceleration of gravity, 9.81 m/s2; θ is the angle between the floor and the slope.
- The escape velocity can be decomposed into horizontal escape velocity (VEh) and vertical escape velocity (VEv), as shown in Equations (6) and (7):
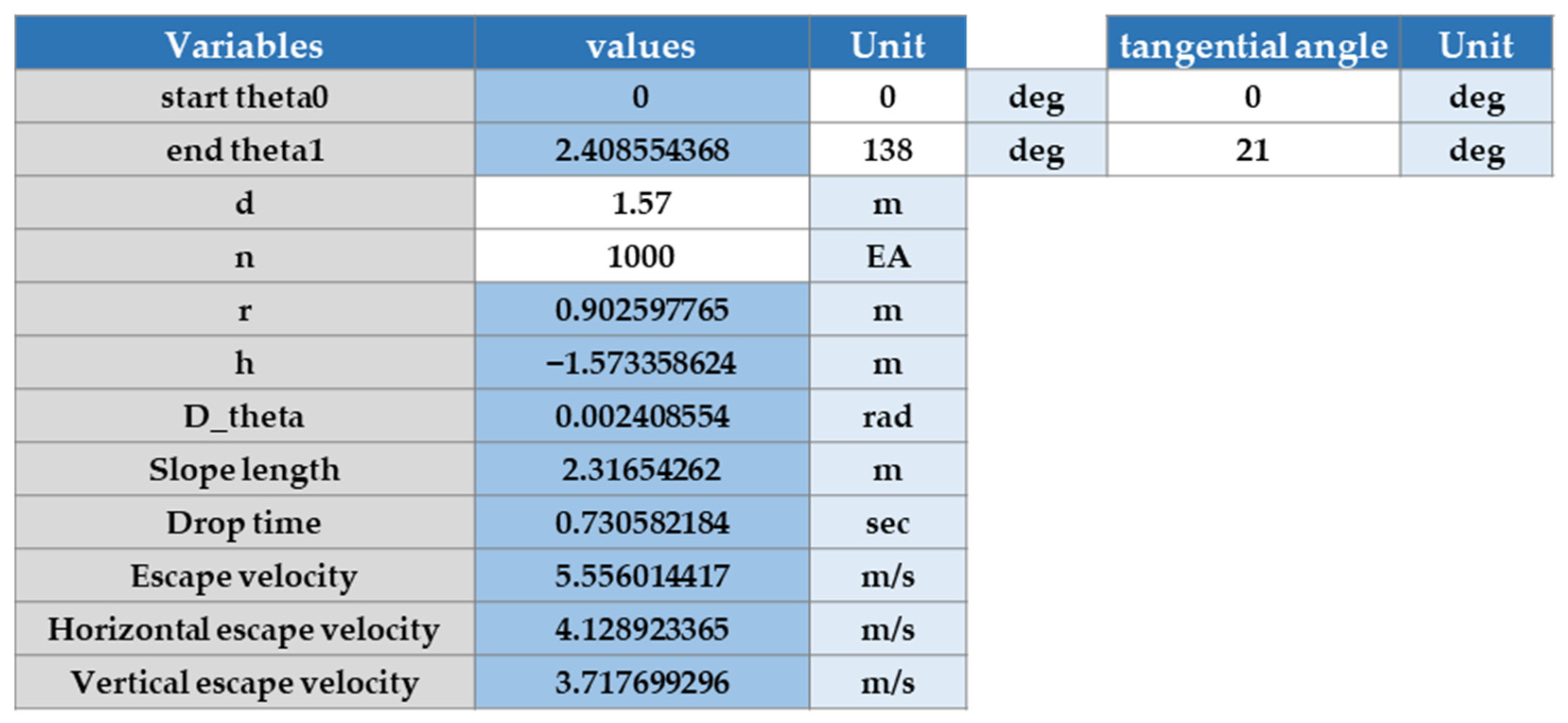
2.1.2. Simulation for the Particle Behavior Analysis on a Straight Incline
2.2. Particle Behavior on a Cycloid Shaped Charging Chute and Its Simulation
2.2.1. Particle Behavior on a Cycloid Curve
- The x and y coordinates of the cycloid curve (Equations (8) and (9)):where x represents the x-coordinate of the cycloid curve, y is the y-coordinate of the cycloid curve, θ is the parameter of the cycloidal curve, and r denotes the radius of the cycloid curve.
- The entry angle (φS) of the charging chute (Equation (10)):
- The exit angle (φE) of the charging chute (Equation (11)):where S represents the position where the sinter mix raw materials the charging chute from the drum feeder, E is the position where the raw material leaves the charging chute, φS is the entry angle at S, and φE represents the escape angle of the charging chute.
- Exit velocity (VE) at the point where the raw material leaves the charging chute (E) (Equation (12)).
- The horizontal exit velocity (VEh) is given by Equation (13):
- The vertical exit velocity (VEv) is given by Equation (14):
- And the travel time within the chute (t) are shown in Equation (15):
2.2.2. Simulation for the Particle Behavior Analysis on a Cycloid Curve
2.3. Comparison of Particle Behavior in Simulation between a Straight Incline and Cycloid Curve
3. Optimization of Roll-Type Charging Chute
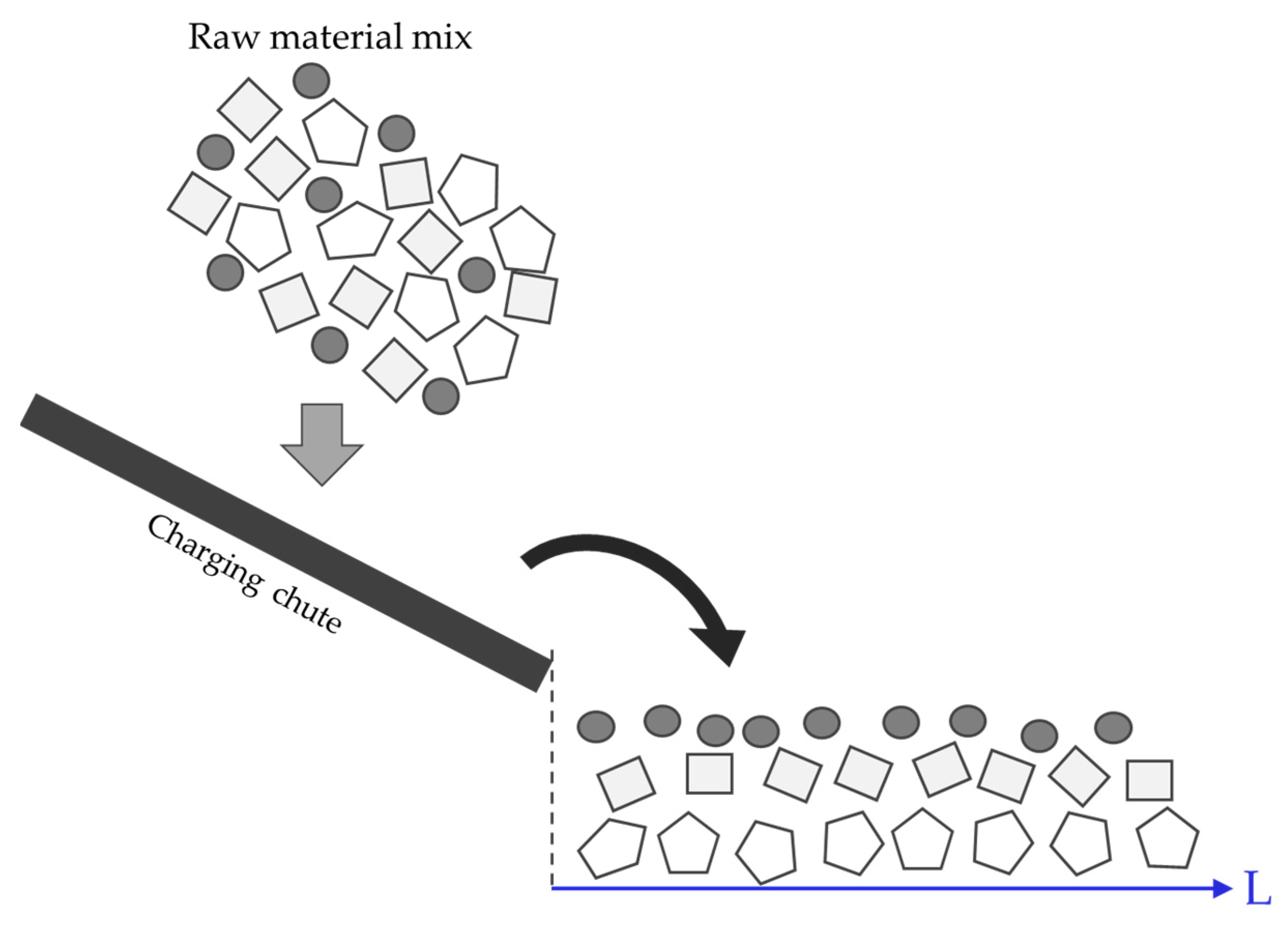
3.1. Trajectory Segregation
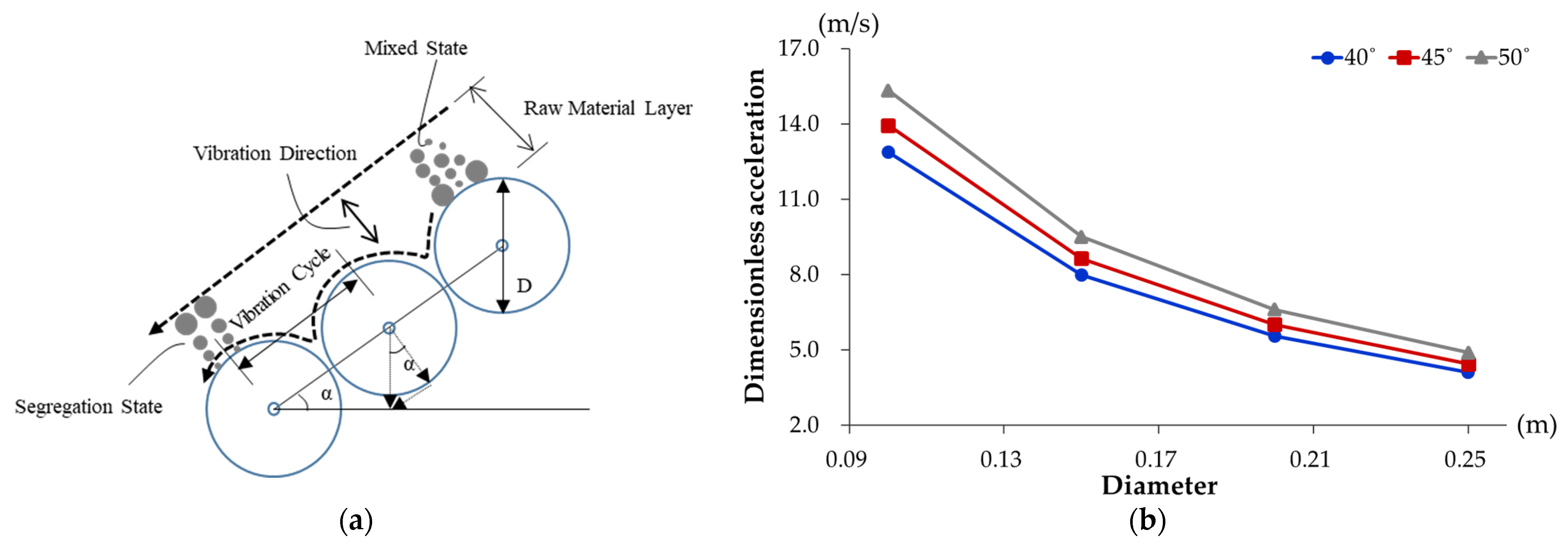
3.2. Rise of Coarse Particles by Vibration (Convection in Granular Media)
- Trajectory segregation: The horizontal movement distance of particles increases in proportion to horizontal velocity, size, and density [40].
- Percolation of fine particles: Small particles move down when a particulate material of different-sized particles moves [41].
- Rise of coarse particles on vibration: When the charged particles are vibrated, large particles rise, and small particles penetrate the generated void space [42].
3.3. Roll-Type Chute Optimization
3.3.1. Selecting the Roll Diameter
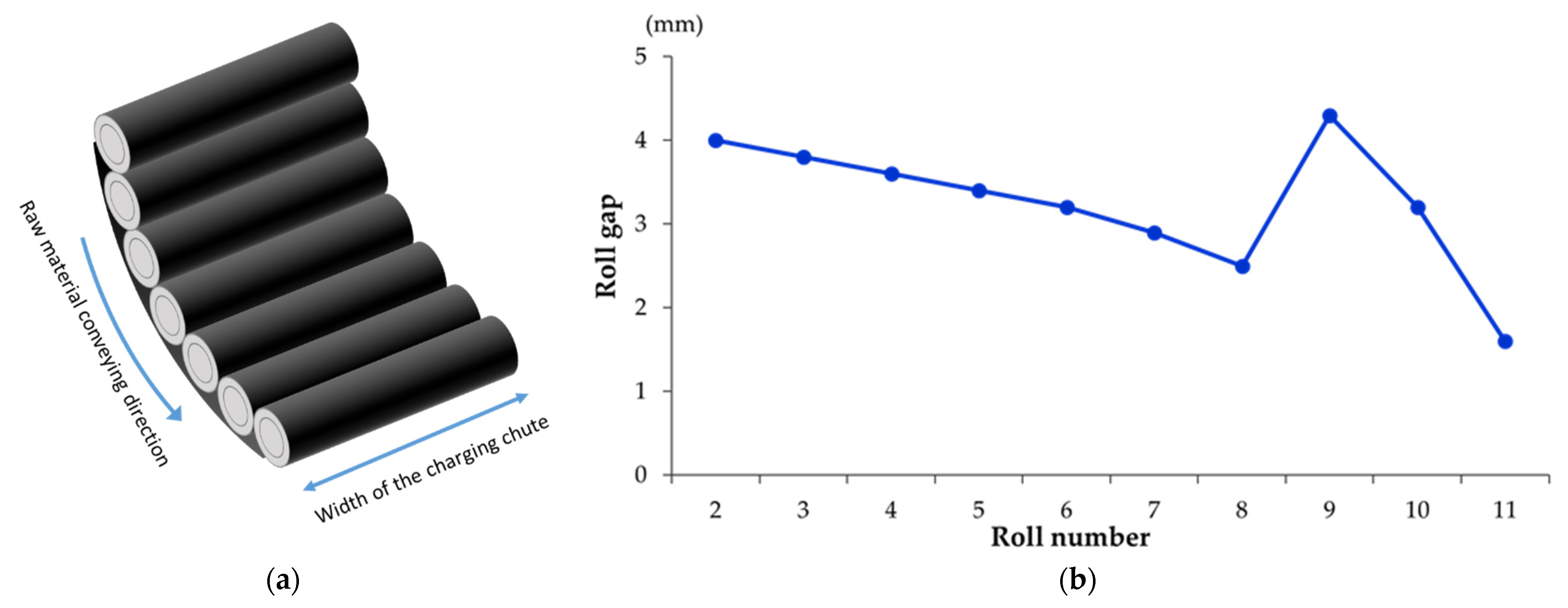
3.3.2. Selecting the Gap between the Rolls
4. Integrated Modeling of Cycloid Trajectory and Roll-Type Charging Chute
5. Pilot Test and Result
5.1. Dispersion Test and Result
5.2. Vertical Segregation Test and Result
6. Full-Scale Implementation
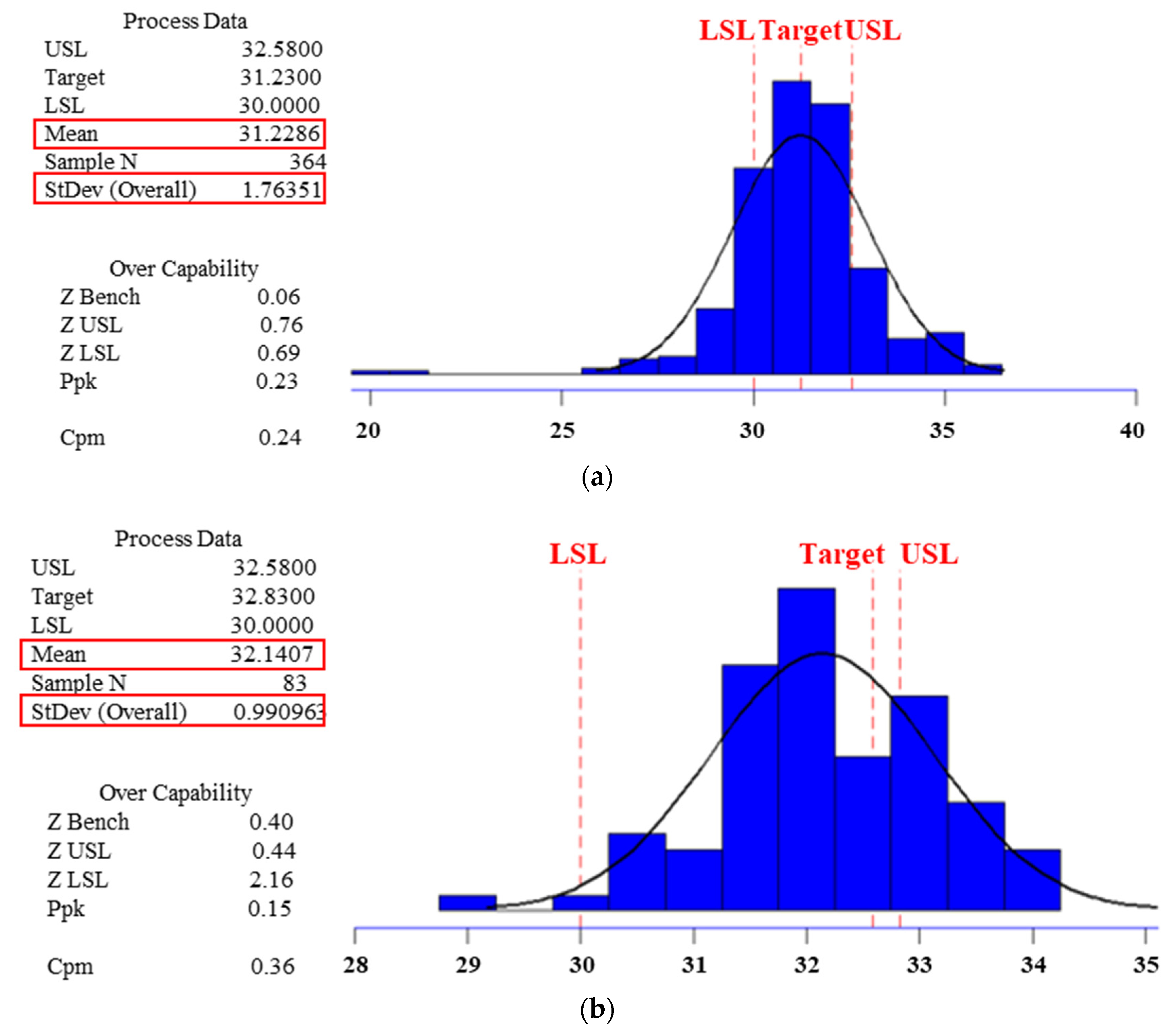
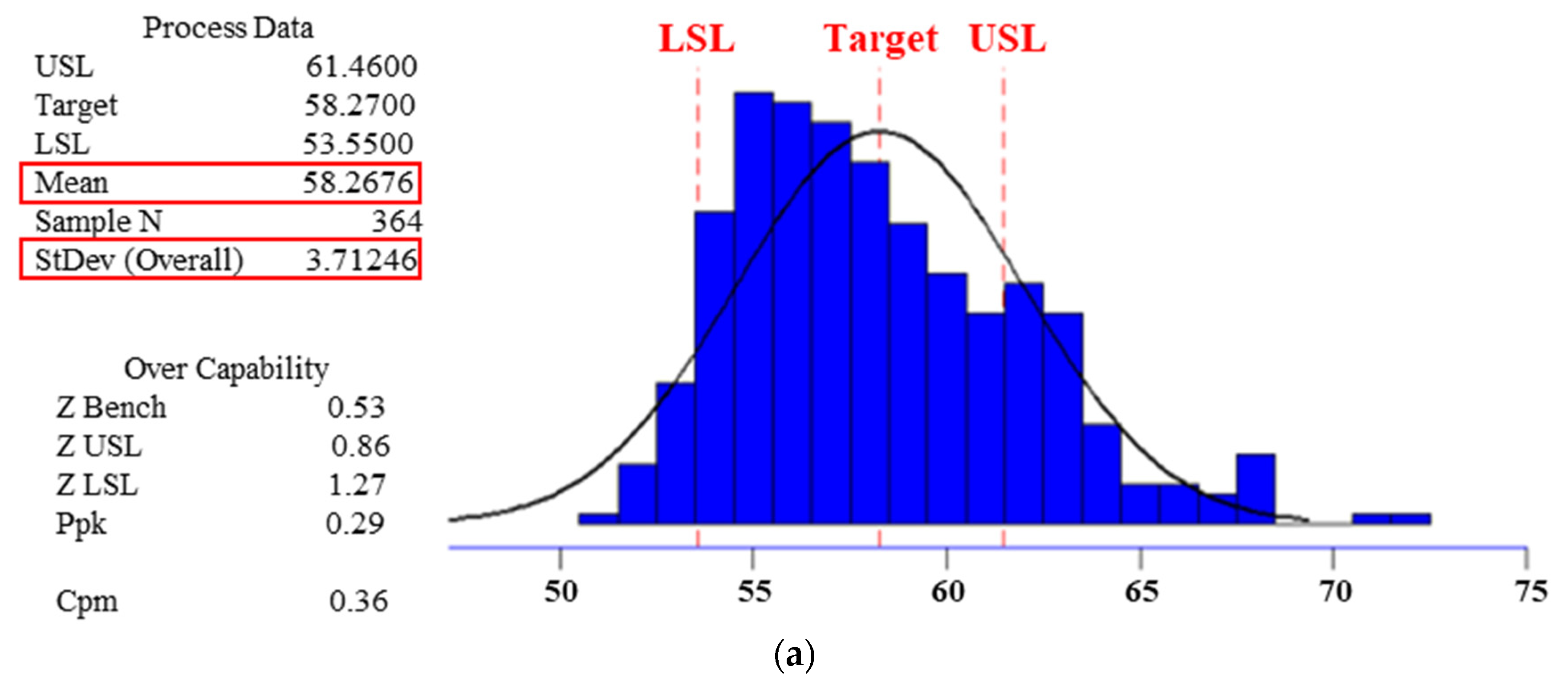
6.1. Comparison of Operational Productivity
6.2. Comparison of Fuel Consumption
6.3. Discussion
7. Economic Assessment of Improvement
7.1. Financial Effect
7.2. Operational and Environmental Effects
- Unlike the traditional blast furnace steelmaking process, which uses coal to extract iron, H-DRI utilizes hydrogen for reduction reactions, known for its environmentally friendly and energy-efficient iron production without CO2 emissions [53]. This method is emerging as a key technology in the future steel industry. However, it is still in its early stages of technological development and faces challenges such as high production costs. Thus, significant improvements are needed for economic feasibility, production demonstration, and commercialization.
- Currently, as a realistic alternative to H-DRI technology, which has limitations at the current technological level, the introduction of the EAF methods are being introduced for low-carbon steel production. The EAF involves refining molten iron from the blast furnace by inputting scrap steel into the furnace rather than iron ore, garnering attention as an environmentally friendly steel production method to achieve carbon neutrality [54]. However, the EAF method also has several drawbacks, including fluctuations in production costs due to changes in scrap iron prices, instability in scrap iron supply, and limited production scale.
- Finally, another technological development for carbon reduction involves optimizing equipment to decrease coal usage rates. This study demonstrates that after replacing the charging chute in the sintering machine, coal consumption decreased by 6% compared to before the replacement. This is attributed to both productivity improvements and a reduction in CO2 emissions. While the carbon reduction effect of such studies on individual equipment may be marginal, efforts to optimize operations and reduce fossil fuel usage through equipment optimization across numerous facilities within a steel plant can ultimately contribute to CO2 emission reduction and carbon neutrality.
8. Summary
8.1. Conclusions
8.2. Limitations and Further Study
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BAU | Business As Usual |
| CBAM | Carbon Border Adjustment Mechanism |
| DEM | Discrete Element Method |
| DL | Dwight-Lloyd |
| EAF | Electric Arc Furnace |
| ESG | Environment Society Governance |
| FGR | Flu Gas Recirculation |
| GI | Granulation Index |
| H-DRI | Hydrogen-based Direct Reduction Ironmaking |
| IRR | Internal Rate of Return |
| LOP | Local Operational Panel |
| MBF | Magnetic Braking Feeder |
| MCC | Motor Control Panel |
| MS | Mean Size |
| NPV | Net Present Value |
| RI | Reducibility Index |
| SSW | Segregated Slit Wire |
| STS | Stainless Steel |
| Sw | Strand-ward segregation index |
| VBA | Visual Basic for Applications |
Appendix A
| Category | Equations |
|---|---|
| Cycloid curve | , |
| Radius of a circle | |
| Height | |
| Drop speed at point E | |
| Horizontal/Vertical speed at point E | |
| Falling time |
References
- Fernández-González, D.; Ruiz-Bustinza, I.; Mochón, J.; González-Gasca, C.; Verdeja, L.F. Iron Ore Sintering: Process. Miner. Process. Extr. Metall. Rev. 2017, 38, 215–227. [Google Scholar] [CrossRef]
- Liu, Z.; Niu, L.; Zhang, S.; Dong, G.; Wang, Y.; Wang, G.; Kang, J.; Chen, L.; Zhang, J. Comprehensive Technologies for Iron Ore Sintering with a Bed Height of 1000 mm to Improve Sinter Quality, Enhance Productivity and Reduce Fuel Consumption. ISIJ Int. 2020, 60, 2400–2407. [Google Scholar] [CrossRef]
- Rajak, D.K.; Ballal, N.B.; Viswanathan, N.N.; Singhai, M. Effect of Oxygen Enrichment on Top Layer Sinter Properties. ISIJ Int. 2021, 61, 79–85. [Google Scholar] [CrossRef]
- Zhou, H.; Meng, H.; Ma, P.; Wang, J.; Cheng, F.; Fang, H. Experimental investigation on the effect of granulation moisture on the flame front propagation and pore structure in the high-temperature zone of the sinter bed. Powder Technol. 2022, 396, 663–672. [Google Scholar] [CrossRef]
- Thümmler, F.; Thomma, W. The sintering process. Metall. Rev. 1967, 12, 69–108. [Google Scholar] [CrossRef]
- Kim, K.-M.; Lee, K.-W.; Kwon, J.-H.; Jeong, H.-K.; Han, J.-W. Charging Behavior of Sinter Feed according to Types of Charging Chute. Korean J. Met. Mater. 2017, 55, 896–904. [Google Scholar] [CrossRef]
- Mosby, J.; de Silva, S.R.; Enstad, G.G. Segregation of particulate materials–mechanisms and testers. KONA Powder Part. J. 1996, 14, 31–43. [Google Scholar] [CrossRef]
- Nevraev, V.; Malygin, A.; Gurkin, M.; Detkova, T. Operation of sintering machines with a one-layer bed. Metallurgist 2006, 50, 291–297. [Google Scholar] [CrossRef]
- Nakano, M.; Abe, T.; Kano, J.; Kunitomo, K. DEM analysis on size segregation in feed bed of sintering machine. ISIJ Int. 2012, 52, 1559–1564. [Google Scholar] [CrossRef]
- Honorato, E.; Seshadri, V. Granulometric optimisation of raw materials for ISF continuous segregation system in Usiminas’ sintering plants. Ironmak. Steelmak. 2008, 35, 405–415. [Google Scholar] [CrossRef]
- Selvam, S.T.; Chaudhuri, S.; Das, A.; Singh, M.K.; Mahanta, H. An innovative magnetic charging chute to improve productivity of sinter machine at Rourkela Steel Plant. Phys. Procedia 2014, 54, 180–184. [Google Scholar] [CrossRef]
- Li, C.; Moreno-atanasio, R.; O’Dea, D.; Honeyands, T. DEM analysis of granule size segregation in iron ore sintering. In Proceedings of the 8th International Congress on Science and Technology of Ironmaking (ICSTI 2018), Vienna, Austria, 25–28 September 2018. [Google Scholar]
- Kim, K.-M.; Kim, J.-H.; Kwon, J.-H.; Lee, J.-A.; Han, J.-W. Effect of Deflector Plate for Particle Size Segregation Control. Arch. Metall. Mater. 2019, 64, 495–500. [Google Scholar] [CrossRef]
- Xu, Y.; Xu, J.; Liao, Z.; Pei, Y.; Gao, L.; Sun, C.; Kou, M.; Wen, L. DEM study on ternary-sized particle segregation during the sinter burden charging process. Powder Technol. 2019, 343, 422–435. [Google Scholar] [CrossRef]
- Terui, K.; Ichikawa, K.; Kashihara, Y. Estimation of Particle Segregation Behavior in Ore-coke Mixed Layer Using Screening Layer Model. ISIJ Int. 2020, 60, 463–469. [Google Scholar] [CrossRef]
- Ishihara, S.; Kushimoto, K.; Kano, J. Analysis of the Effect of Ventilation Bars on the Packing Structure of Sinter Bed by DEM Simulation. Energies 2020, 13, 3836. [Google Scholar] [CrossRef]
- Higuchi, K.-i.; Kawaguchi, T.; Kobayashi, M.; Hosotani, Y.; Nakamura, K.; Iwamoto, K.; Fujimoto, M. Improvement of productivity by stand-support sintering in commercial sintering machines. ISIJ Int. 2000, 40, 1188–1194. [Google Scholar] [CrossRef]
- Oyama, N.; Sato, H.; Takeda, K.; Ariyama, T.; Masumoto, S.; Jinno, T.; FUJII, N. Development of coating granulation process at commercial sintering plant for improving productivity and reducibility. ISIJ Int. 2005, 45, 817–826. [Google Scholar] [CrossRef]
- Ellis, B.; Loo, C.; Witchard, D. Effect of ore properties on sinter bed permeability and strength. Ironmak. Steelmak. 2007, 34, 99–108. [Google Scholar] [CrossRef]
- Ahn, H.-J.; Choi, S.-M.; Cho, B.-K. Process Modeling of an Iron Ore Sintering Bed for Flue Gas Recirculation. J. Korean Soc. Combust. 2011, 16, 23–30. [Google Scholar]
- El-Hussiny, N.; Mohamed, F.; Shalabi, M. Recycling of mill scale in sintering process. Sci. Sinter. 2011, 43, 21–31. [Google Scholar] [CrossRef]
- Cores, A.; Muñiz, M.; Ferreira, S.; Robla, J.; Mochón, J. Relationship between sinter properties and iron ore granulation index. Ironmak. Steelmak. 2013, 39, 85–94. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Kamijo, C.; Matsumura, M.; Kawaguchi, T. Improvement of permeability of sintering bed by adding dry particles to granulated raw materials. ISIJ Int. 2013, 53, 1538–1544. [Google Scholar] [CrossRef]
- Fan, X.-h.; Yu, Z.-y.; Gan, M.; Li, W.-q.; Ji, Z.-y. Influence of O2 content in circulating flue gas on iron ore sintering. J. Iron Steel Res. Int. 2013, 20, 1–6. [Google Scholar] [CrossRef]
- Zhou, M.; Zhou, H. Flame front propagation and sinter strength properties of permeable sintering bed prepared via enhanced granulation with hydrated lime. Asia-Pac. J. Chem. Eng. 2021, 16, e2592. [Google Scholar] [CrossRef]
- Malhotra, S.; Parameswaran, M. Analysis of a cycloid speed reducer. Mech. Mach. Theory 1983, 18, 491–499. [Google Scholar] [CrossRef]
- Blanche, J.G.; Yang, D.C.H. Cycloid Drives With Machining Tolerances. J. Mech. Transm. Autom. Des. 1989, 111, 337–344. [Google Scholar] [CrossRef]
- Hoffman, D.T. A cycloid race. Phys. Teach. 1991, 29, 395–397. [Google Scholar]
- Vecchiato, D.; Demenego, A.; Argyris, J.; Litvin, F.L. Geometry of a cycloidal pump. Comput. Methods Appl. Mech. Eng. 2001, 190, 2309–2330. [Google Scholar] [CrossRef]
- Jørgensen, F.T.; Andersen, T.O.; Rasmussen, P.O. The cycloid permanent magnetic gear. In Proceedings of the Conference Record of the 2006 IEEE Industry Applications Conference Forty-First IAS Annual Meeting, Tampa, FL, USA, 8–12 October 2006; pp. 373–378. [Google Scholar]
- Yong, Y.; Moheimani, S.; Petersen, I. High-speed cycloid-scan atomic force microscopy. Nanotechnology 2010, 21, 365503. [Google Scholar] [CrossRef]
- Chen, B.; Zhong, H.; Liu, J.; Li, C.; Fang, T. Generation and investigation of a new cycloid drive with double contact. Mech. Mach. Theory 2012, 49, 270–283. [Google Scholar] [CrossRef]
- Liu, S.; Ding, F.; Ding, C.; Man, Z. A high-pressure bi-directional cycloid rotor flowmeter. Sensors 2014, 14, 15480–15495. [Google Scholar] [CrossRef]
- Wang, G.; Liu, X.; Gao, W.; Yan, B.; Chen, T. Study on the design and cutting performance of a revolving cycloid milling cutter. Appl. Sci. 2019, 9, 2915. [Google Scholar] [CrossRef]
- Maharjan, P.; Bhatta, T.; Rasel, M.S.; Salauddin, M.; Rahman, M.T.; Park, J.Y. High-performance cycloid inspired wearable electromagnetic energy harvester for scavenging human motion energy. Appl. Energy 2019, 256, 113987. [Google Scholar] [CrossRef]
- Serway, R.A.; Jewett, J.W. Physics for Scientists and Engineers; Cengage Learning: Boston, MA, USA, 2018. [Google Scholar]
- Brandelik, A. CALCMIN—An EXCEL™ Visual Basic application for calculating mineral structural formulae from electron microprobe analyses. Comput. Geosci. 2009, 35, 1540–1551. [Google Scholar] [CrossRef]
- Barra, M. The cycloid. Educ. Stud. Math. 1975, 6, 93–98. Available online: https://www.jstor.org/stable/3482162 (accessed on 27 November 2023).
- Schelling, T.C. Models of Segregation. Am. Econ. Rev. 1969, 59, 488–493. Available online: https://www.jstor.org/stable/1823701 (accessed on 30 November 2023).
- Zhang, T.F.; Gan, J.Q.; Yu, A.B.; Pinson, D.; Zhou, Z.Y. Size segregation of granular materials during Paul-Wurth hopper charging and discharging process. Powder Technol. 2021, 378, 497–509. [Google Scholar] [CrossRef]
- Hashim, M.H.M.; Sharrock, G.B.; Saydam, S. A Review of Particle Percolation in Mining. In Proceedings of the SHIRMS 2008: Proceedings of the First Southern Hemisphere International Rock Mechanics Symposium, Perth, Australia, 16–19 September 2008; pp. 273–284. [Google Scholar]
- Xu, D.; Ametov, I.; Grano, S.R. Detachment of coarse particles from oscillating bubbles—The effect of particle contact angle, shape and medium viscosity. Int. J. Miner. Process. 2011, 101, 50–57. [Google Scholar] [CrossRef]
- Avila-Acevedo, J.G.; Tsotsas, E. Transient natural convection and heat transfer during the storage of granular media. Int. J. Heat Mass Transf. 2008, 51, 3468–3477. [Google Scholar] [CrossRef]
- Viridi, S.; Wahjoedi, S.A.; Satira, S.; Zen, F.P. Rise or sink: Spherical intruder in density frequency dependence static granular fluid. arXiv 2011, arXiv:1106.5285. [Google Scholar] [CrossRef]
- Rayat, C.S. Measures of Dispersion. In Statistical Methods in Medical Research; Springer: Singapore, 2018; pp. 47–60. [Google Scholar]
- Minitab Statistical Software, Minitab. Available online: https://www.minitab.com/products/minitab (accessed on 30 October 2023).
- Bracke, S. Reliability Engineering: Data Analytics, Modeling, Risk Prediction; Springer: Berlin/Heidelberg, Germany, 2024; pp. 403–448. [Google Scholar]
- Weber, T.A. On the (non-) equivalence of IRR and NPV. J. Math. Econ. 2014, 52, 25–39. [Google Scholar] [CrossRef]
- Balen, R.M.; Mens, H.; Economides, M.J. Applications of the net present value (NPV) in the optimization of hydraulic fractures. In Proceedings of the SPE Eastern Regional Meeting, Charleston, WV, USA, 1–4 November 1988; p. 181. [Google Scholar]
- Jursova, S.; Pustejovska, P.; Brozova, S. Study on reducibility and porosity of metallurgical sinter. Alex. Eng. J. 2018, 57, 1657–1664. [Google Scholar] [CrossRef]
- ISO 4695; Iron Ores for Blast Furnace Feedstocks Determination of the reducibility by the Rate of Reduction Index. International Organization for Standardization (ISO): Geneva, Switzerland, 2021.
- Long, H.-M.; Shi, Q.; Zhang, H.-L.; Wei, R.-F.; Chun, T.-J.; Li, J.-X. Application status and comparison of dioxin removal technologies for iron ore sintering process. J. Iron Steel Res. Int. 2018, 25, 357–365. [Google Scholar] [CrossRef]
- Rosner, F.; Papadias, D.; Brooks, K.; Yoro, K.; Ahluwalia, R.; Autrey, T.; Breunig, H. Green steel: Design and cost analysis of hydrogen-based direct iron reduction. Energy Environ. Sci. 2023, 16, 4121–4134. [Google Scholar] [CrossRef]
- Choi, S.-W.; Seo, B.-G.; Lee, E.-B. Machine Learning-Based Tap Temperature Prediction and Control for Optimized Power Consumption in Stainless Electric Arc Furnaces (EAF) of Steel Plants. Sustainability 2023, 15, 6393. [Google Scholar] [CrossRef]





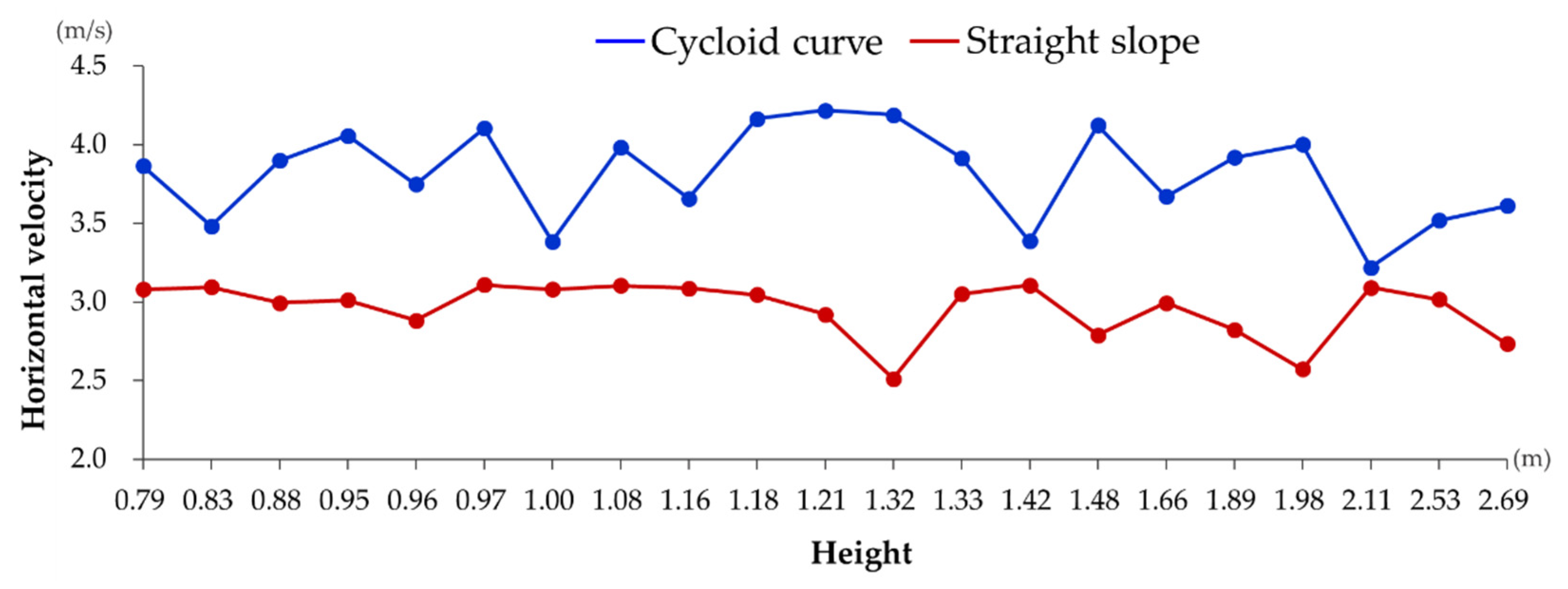



| Height (m) | Horizontal Velocity (m/s) | Difference on Cycloid Curves and Straight Slopes (%) | |
|---|---|---|---|
| Cycloid Curve | Straight Slope | ||
| 0.787 | 3.866 | 3.081 | 25% |
| 0.825 | 3.483 | 3.096 | 13% |
| 0.878 | 3.900 | 2.996 | 30% |
| 0.951 | 4.059 | 3.012 | 35% |
| 0.955 | 3.749 | 2.884 | 30% |
| 0.973 | 4.105 | 3.109 | 32% |
| 0.995 | 3.385 | 3.081 | 10% |
| 1.079 | 3.985 | 3.105 | 28% |
| 1.163 | 3.659 | 3.088 | 18% |
| 1.179 | 4.165 | 3.047 | 37% |
| 1.210 | 4.219 | 2.922 | 44% |
| 1.316 | 4.190 | 2.513 | 67% |
| 1.333 | 3.917 | 3.052 | 28% |
| 1.417 | 3.389 | 3.108 | 9% |
| 1.478 | 4.125 | 2.791 | 48% |
| 1.664 | 3.672 | 2.996 | 23% |
| 1.894 | 3.919 | 2.825 | 39% |
| 1.976 | 4.002 | 2.573 | 56% |
| 2.114 | 3.220 | 3.092 | 4% |
| 2.525 | 3.519 | 3.018 | 17% |
| 2.689 | 3.613 | 2.734 | 32% |
| Roll Number | Gap between Rolls (mm, Setting) | Angle (Deg) | Actual Gap (Projection, mm) |
|---|---|---|---|
| 1 | - | - | - |
| 2 | 5 | 36.6 | 4.0 |
| 3 | 5 | 39.8 | 3.8 |
| 4 | 5 | 43.1 | 3.6 |
| 5 | 5 | 46.7 | 3.4 |
| 6 | 5 | 50.5 | 3.2 |
| 7 | 5 | 54.7 | 2.9 |
| 8 | 5 | 59.4 | 2.5 |
| 9 | 10 | 64.8 | 4.3 |
| 10 | 10 | 71.6 | 3.2 |
| 11 | 10 | 80.7 | 1.6 |
| Roll Number | Gap between Rolls (mm) | Angle (Deg) | Actual Gap (Projection, mm) | Roll Center (X Coordinate) | Roll Center (Y Coordinate) |
|---|---|---|---|---|---|
| 1 | - | - | - | 0.000 | 0.000 |
| 2 | 5 | 36.6 | 4.0 | 0.145 | 0.107 |
| 3 | 5 | 39.8 | 3.8 | 0.283 | 0.222 |
| 4 | 5 | 43.1 | 3.6 | 0.414 | 0.345 |
| 5 | 5 | 46.7 | 3.4 | 0.538 | 0.477 |
| 6 | 5 | 50.5 | 3.2 | 0.652 | 0.615 |
| 7 | 5 | 54.7 | 2.9 | 0.756 | 0.762 |
| 8 | 5 | 59.4 | 2.5 | 0.848 | 0.917 |
| 9 | 10 | 64.8 | 4.3 | 0.925 | 1.080 |
| 10 | 10 | 71.6 | 3.2 | 0.981 | 1.251 |
| 11 | 10 | 80.7 | 1.6 | 1.001 | 1.370 |
| L* | S* | h* | |
|---|---|---|---|
| Straight shaped chute | 0.93 | 0.19 | 0.21 |
| Cycloid shaped chute | 1.08 | 0.56 | 0.27 |
| Difference | +0.15 | +0.37 | +0.06 |
| Growth rate | 16.13% | 194.74% | 28.57% |
| Productivity (t/d/m2) | Fuel Consumption (kg/t-sinter) | |||||
|---|---|---|---|---|---|---|
| Mean | StDev | Sigma | Mean | StDev | Sigma | |
| Before cycloid | 31.23 | 1.782 | 1.58 | 58.27 | 3.712 | 2.03 |
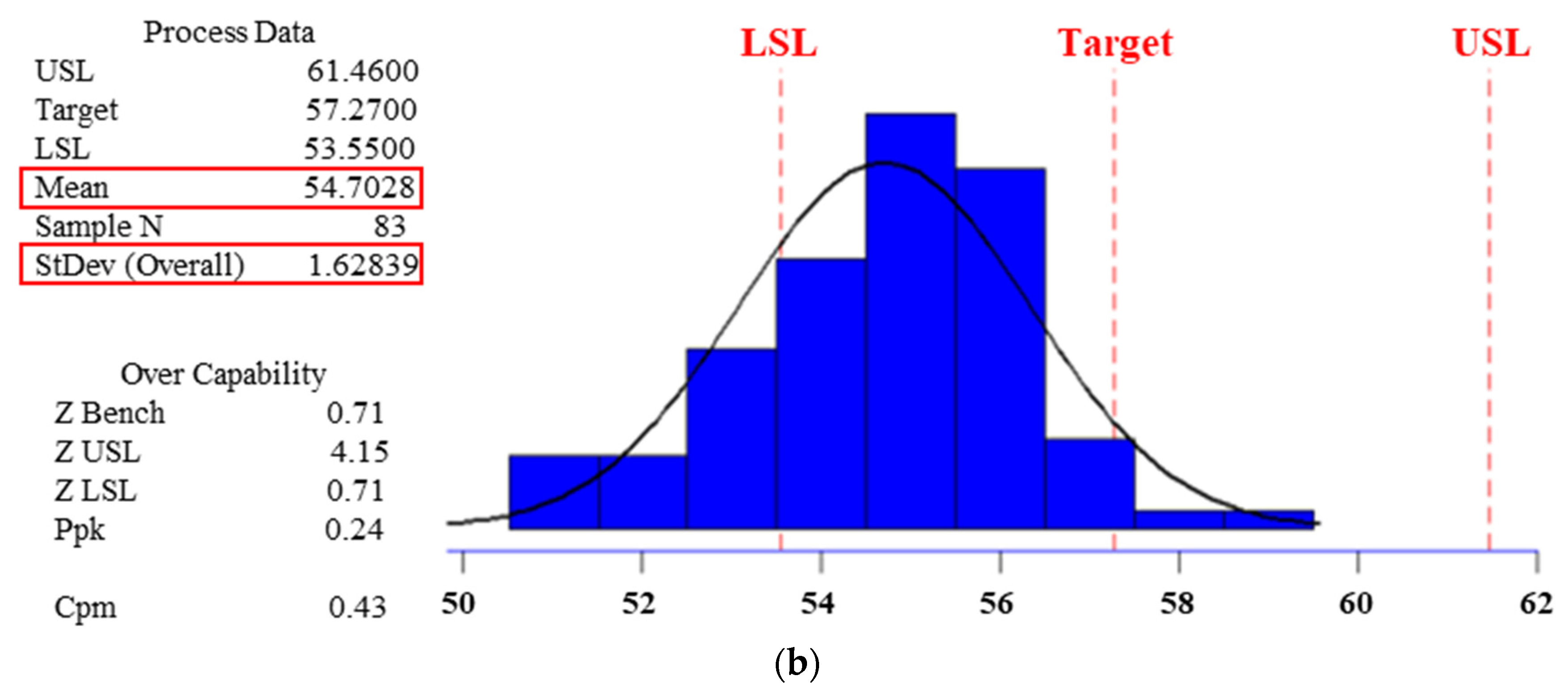
| After cycloid | 32.14 | 0.990 | 1.90 | 54.70 | 1.628 | 2.21 |
| Difference | 0.91 | −0.792 | 0.32 | −3.57 | −2.084 | 0.18 |
| Growth rate | 2.91% | −44.44% | 20.25% | −6.13% | −56.14% | 8.87% |
| Category | Value | Unit |
|---|---|---|
| Fixed cost | 7.9 | USD 1/ton-sinter |
| Unit cost of Fuel consumption | 138 | USD/ton |
| Unit cost of CO2 | 8.7 | USD/ton-CO2 |
| Total production per year | 5,538,658 | ton-sinter/year |
| Operating rate | 98 | % |
| Generating unit of CO2 | 3.402 | ton-CO2/ton-Coal |
| Investment cost | 14.9 K | USD |
| Corporate tax | 24.2 | % |
| Discount rate | 8.8 | % |
| Rate of cycloid chute contribution | 10 | % of total savings |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kwon, W.-H.; Choi, S.-W.; Lee, E.-B. Development of Cycloid-Shaped Roll Charging Chute for Sintering Process for Energy Decarbonization and Productivity Improvement in Steel Plants. Energies 2024, 17, 1536. https://doi.org/10.3390/en17071536
Kwon W-H, Choi S-W, Lee E-B. Development of Cycloid-Shaped Roll Charging Chute for Sintering Process for Energy Decarbonization and Productivity Improvement in Steel Plants. Energies. 2024; 17(7):1536. https://doi.org/10.3390/en17071536
Chicago/Turabian StyleKwon, Woo-Hyeon, So-Won Choi, and Eul-Bum Lee. 2024. "Development of Cycloid-Shaped Roll Charging Chute for Sintering Process for Energy Decarbonization and Productivity Improvement in Steel Plants" Energies 17, no. 7: 1536. https://doi.org/10.3390/en17071536
APA StyleKwon, W.-H., Choi, S.-W., & Lee, E.-B. (2024). Development of Cycloid-Shaped Roll Charging Chute for Sintering Process for Energy Decarbonization and Productivity Improvement in Steel Plants. Energies, 17(7), 1536. https://doi.org/10.3390/en17071536








