A Comprehensive Review of the Thermohydraulic Improvement Potentials in Solar Air Heaters through an Energy and Exergy Analysis
Abstract
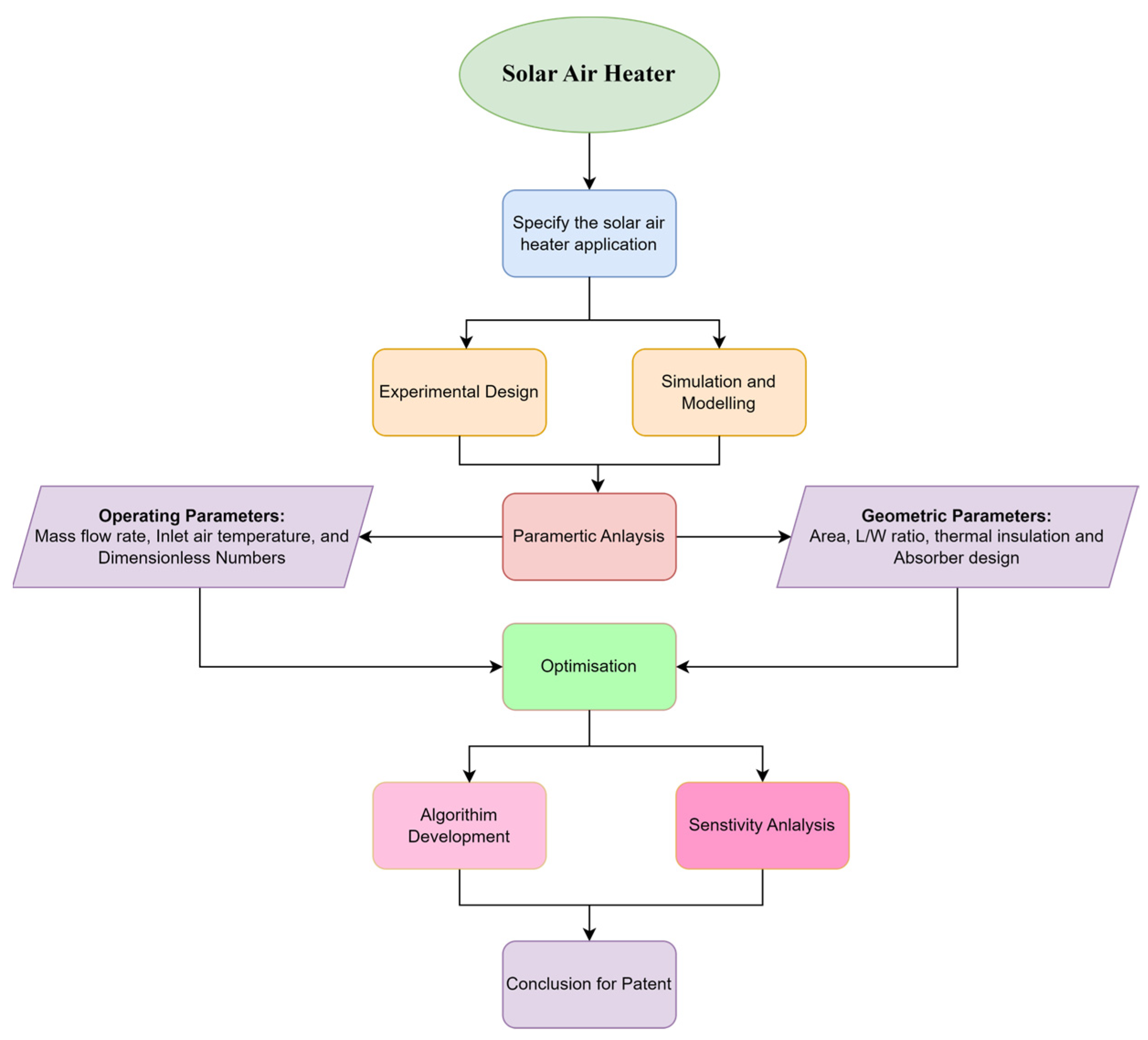
1. Introduction
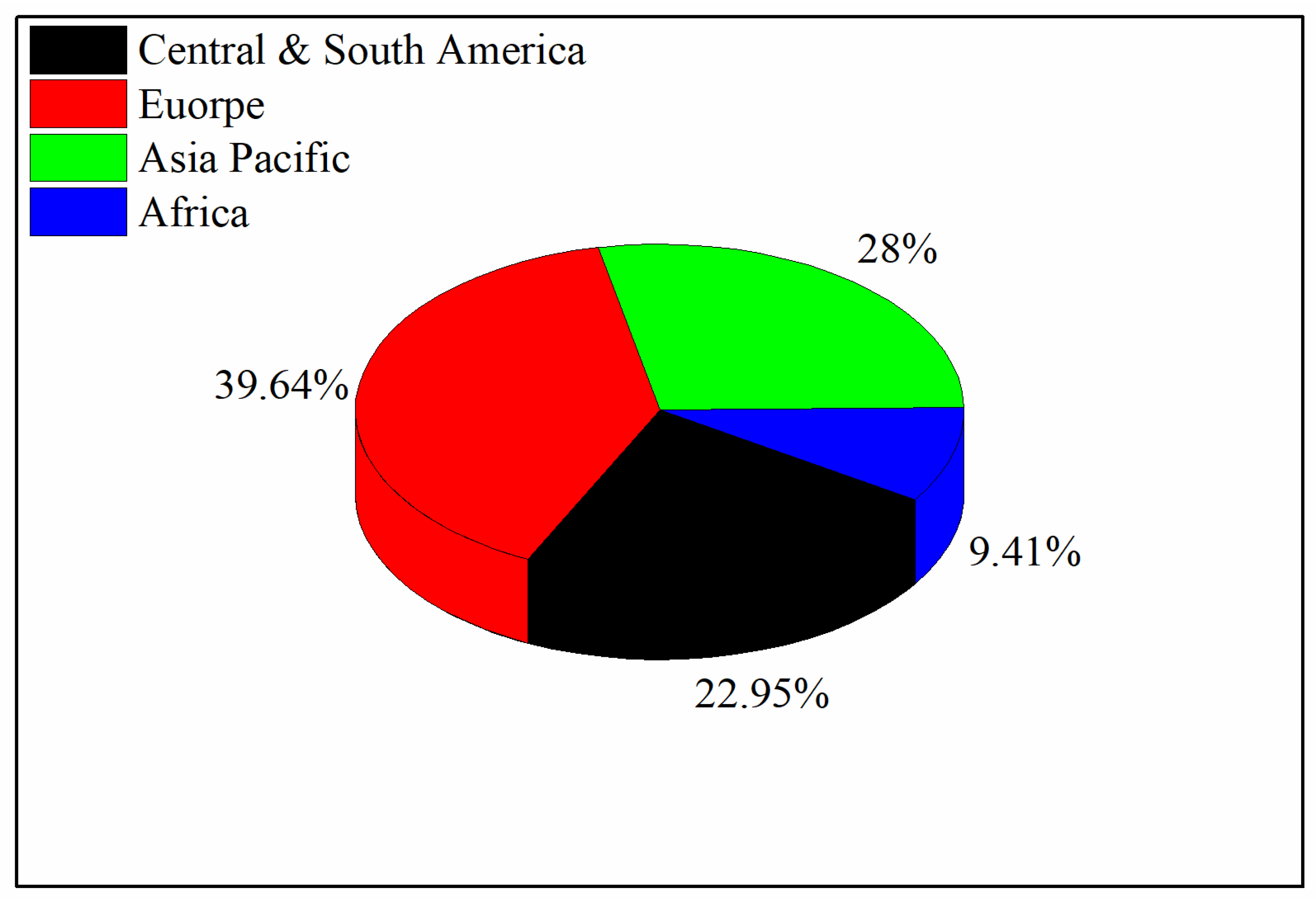
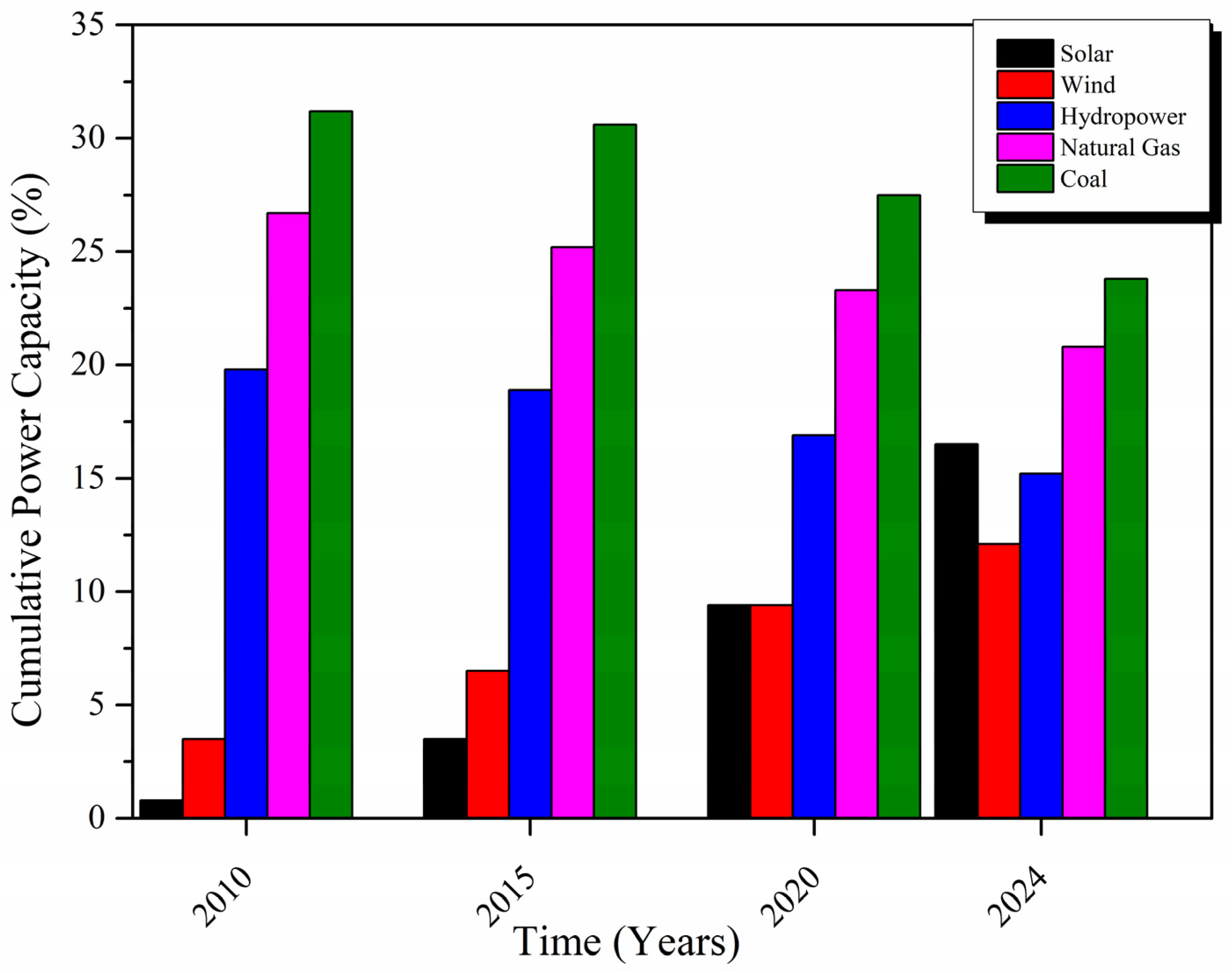
2. Global Energy Trend
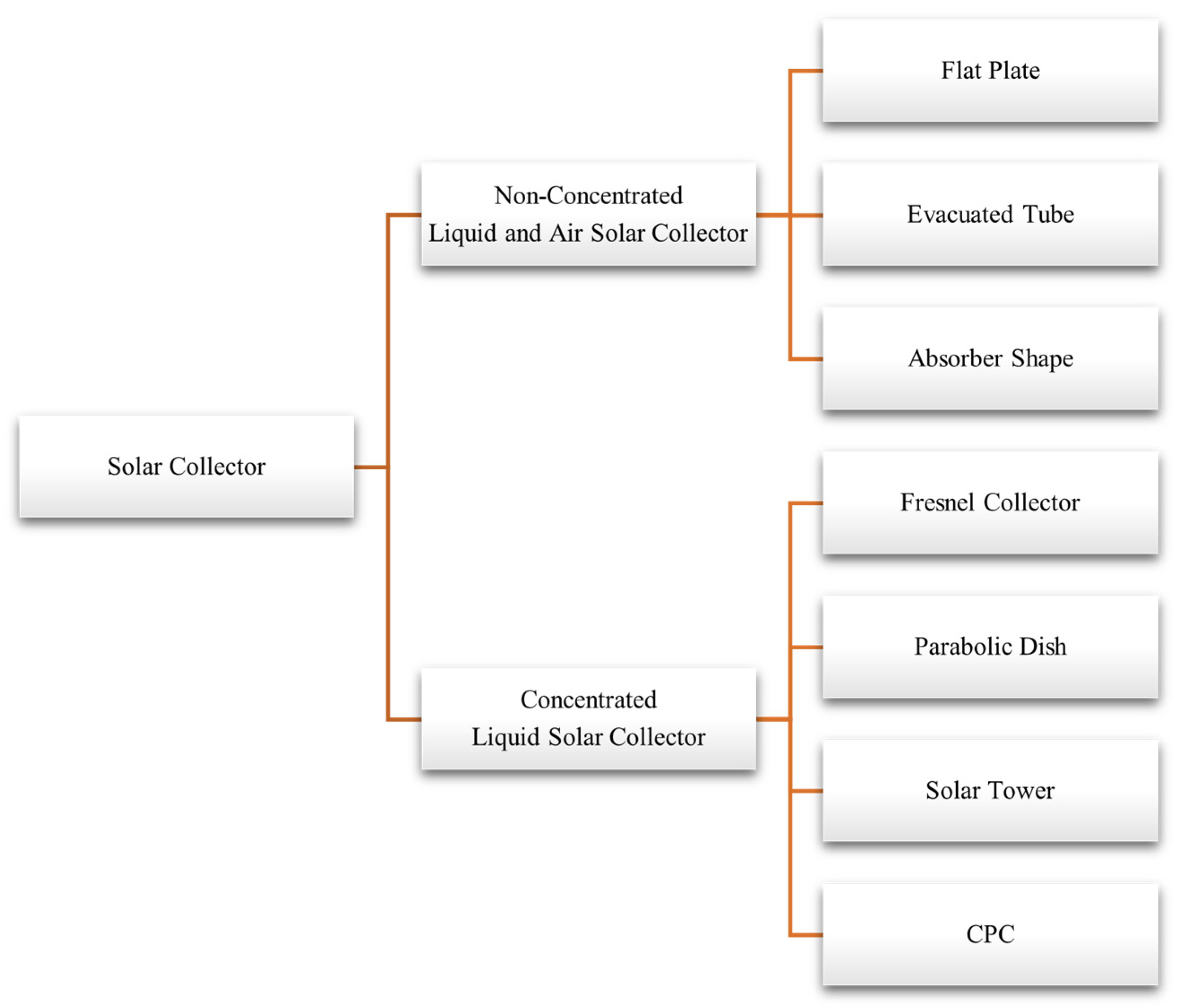
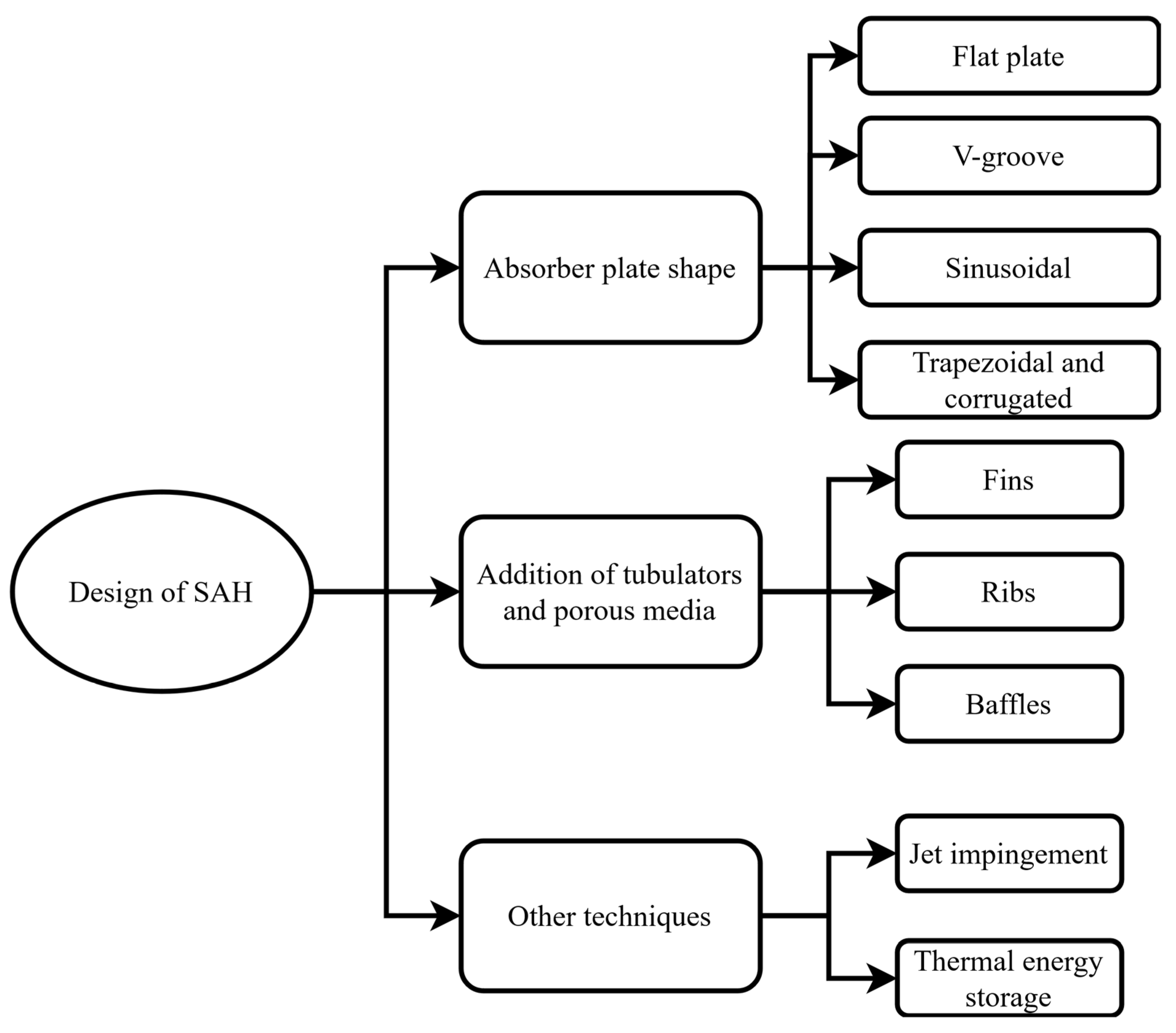
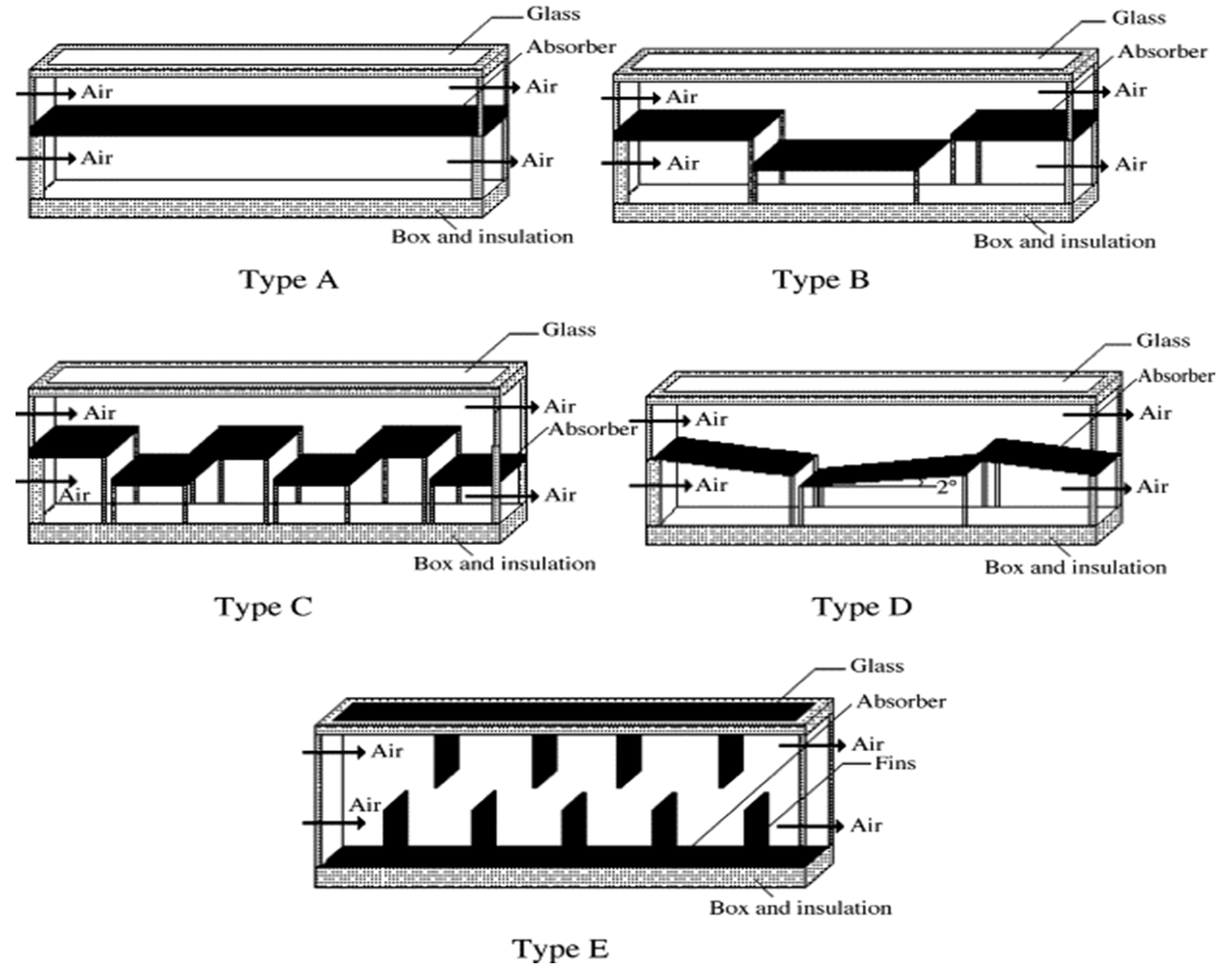
3. Classification of Solar Air Collectors
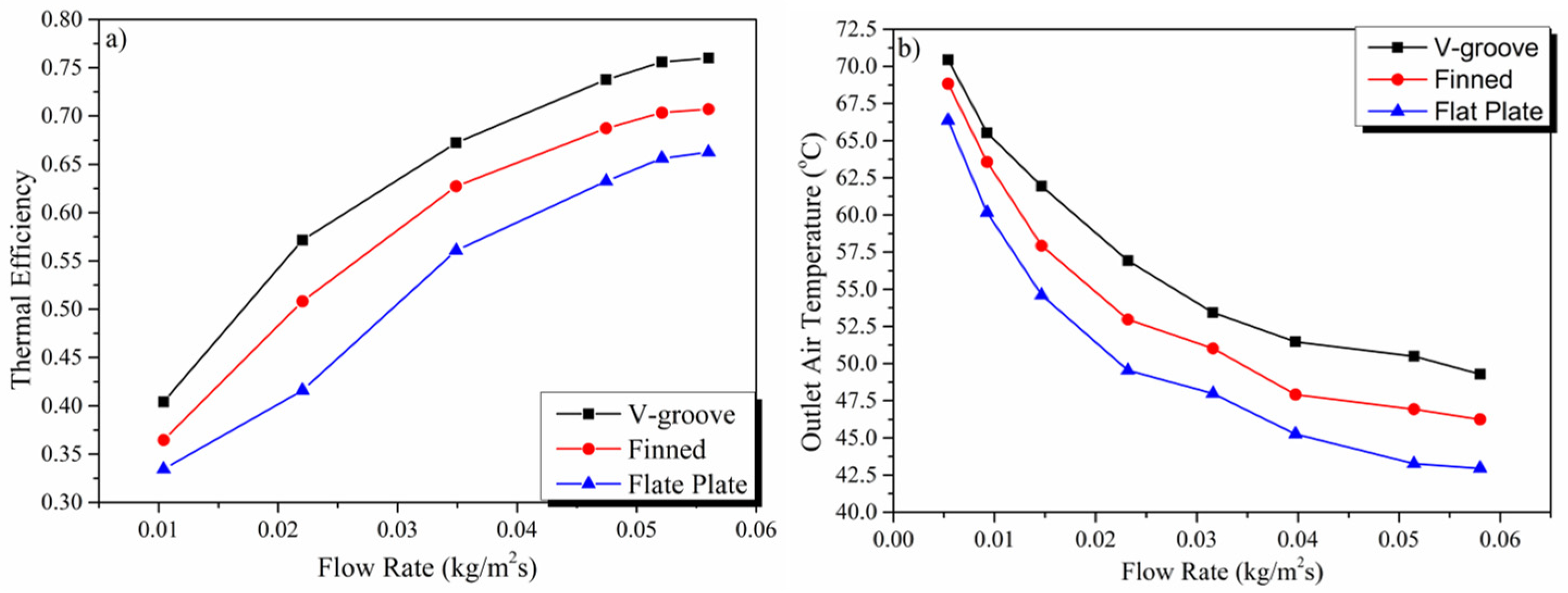
3.1. Effect of Flow Rate
3.2. Effect of Temperature Rise Parameters
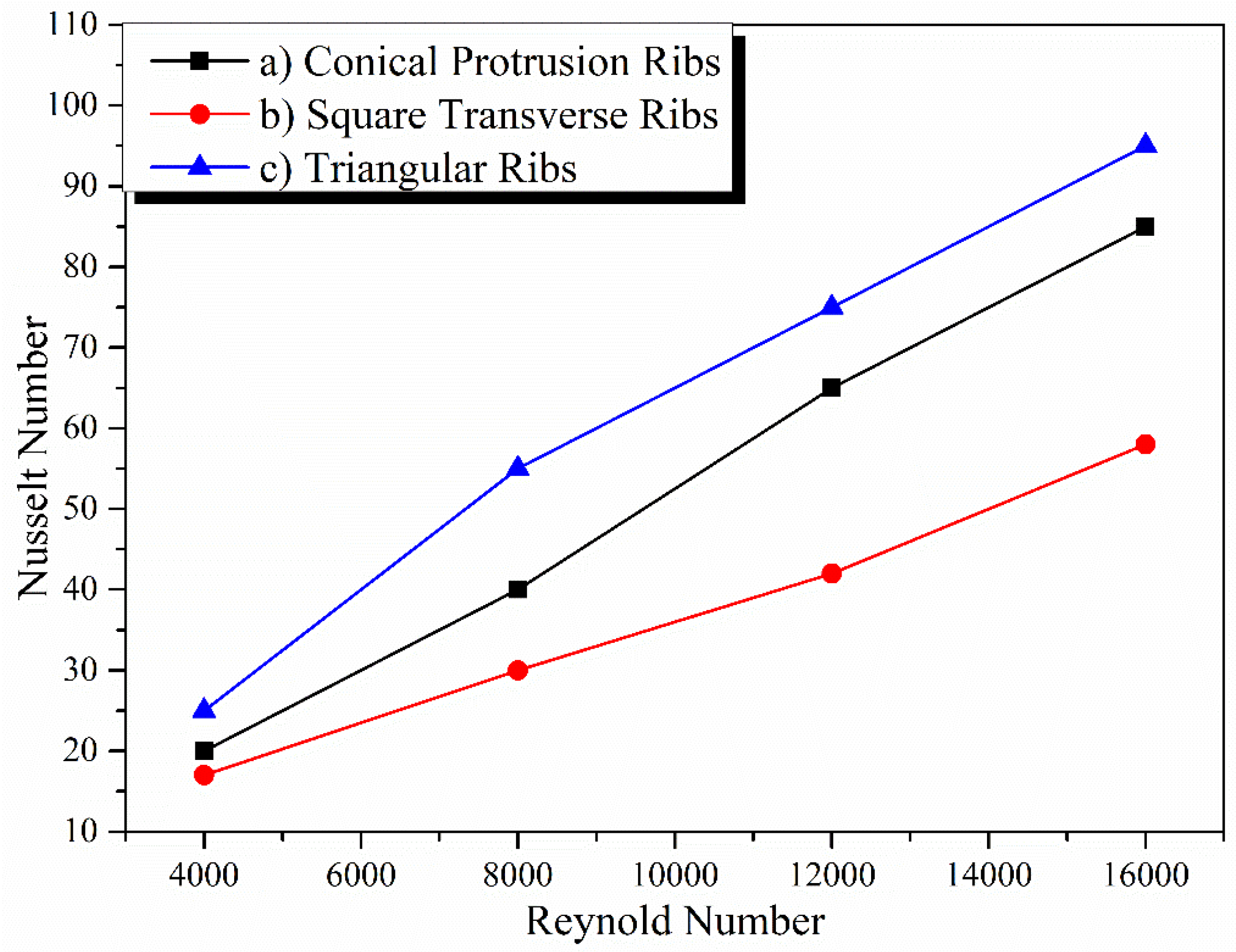
3.3. Effect of the Flow Rate and Re Number on Nusselt Number
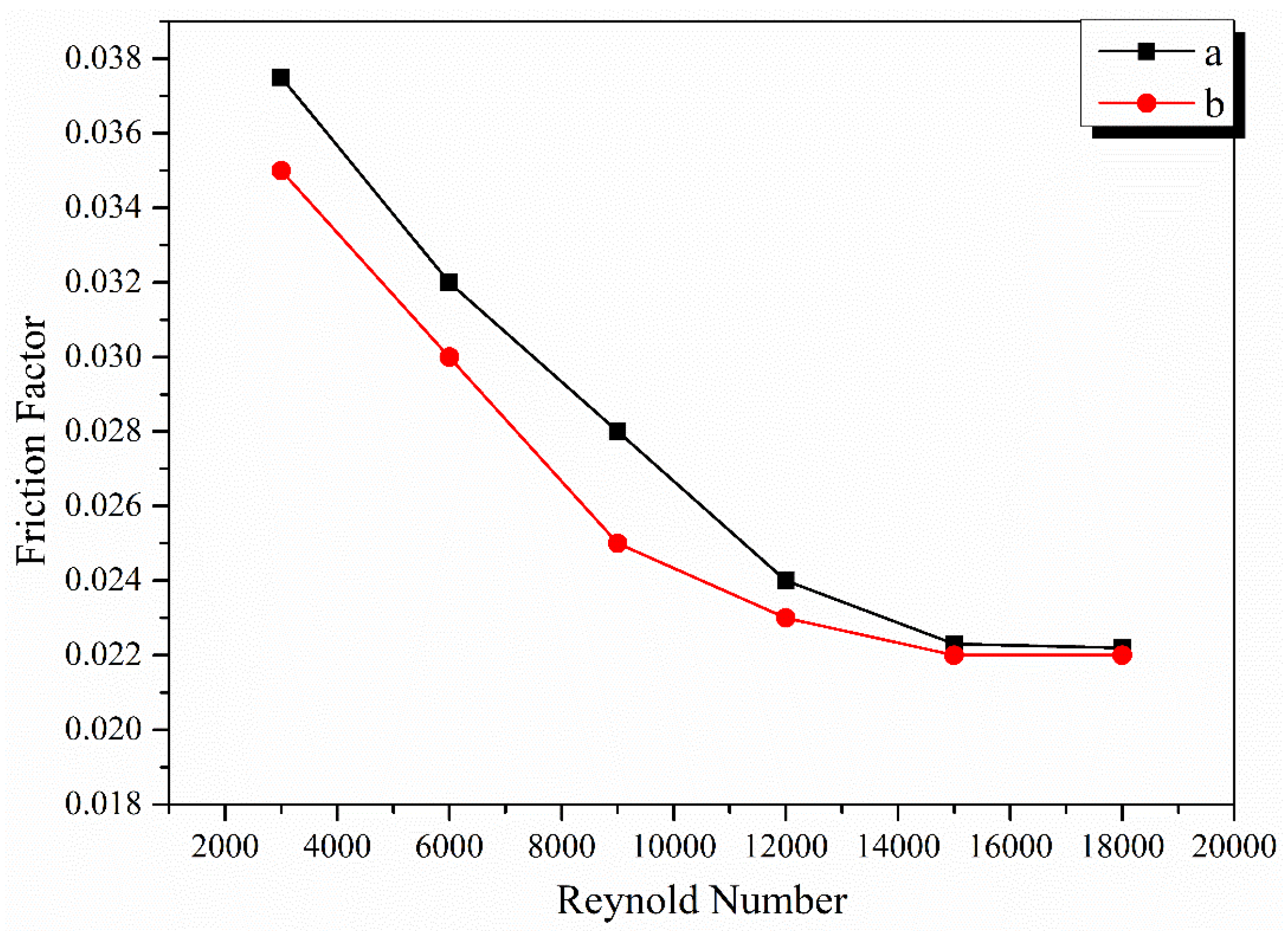
3.4. Effect of Reynold Number on Friction Factor
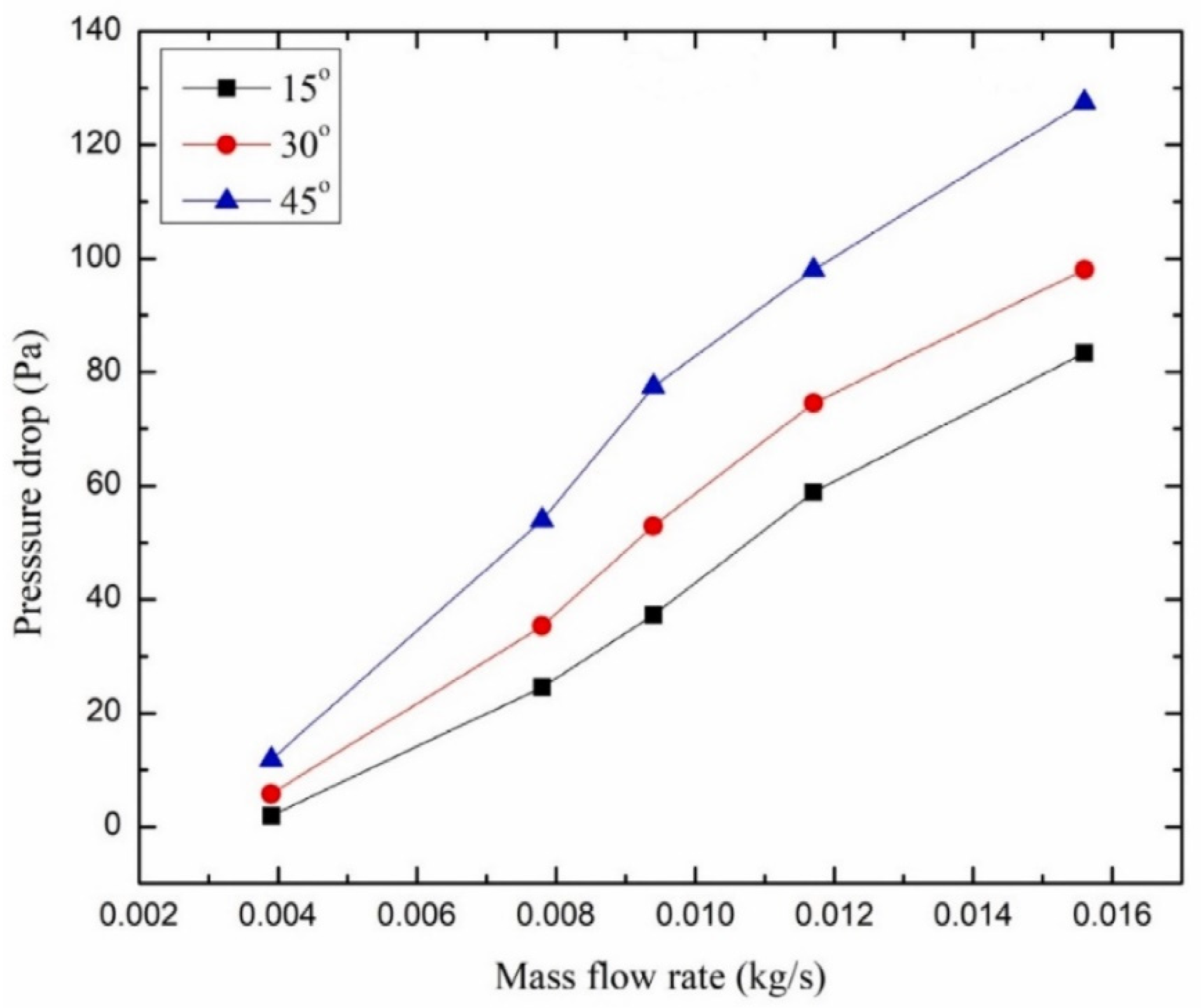
3.5. Impact of Geometry/Shape of SACs
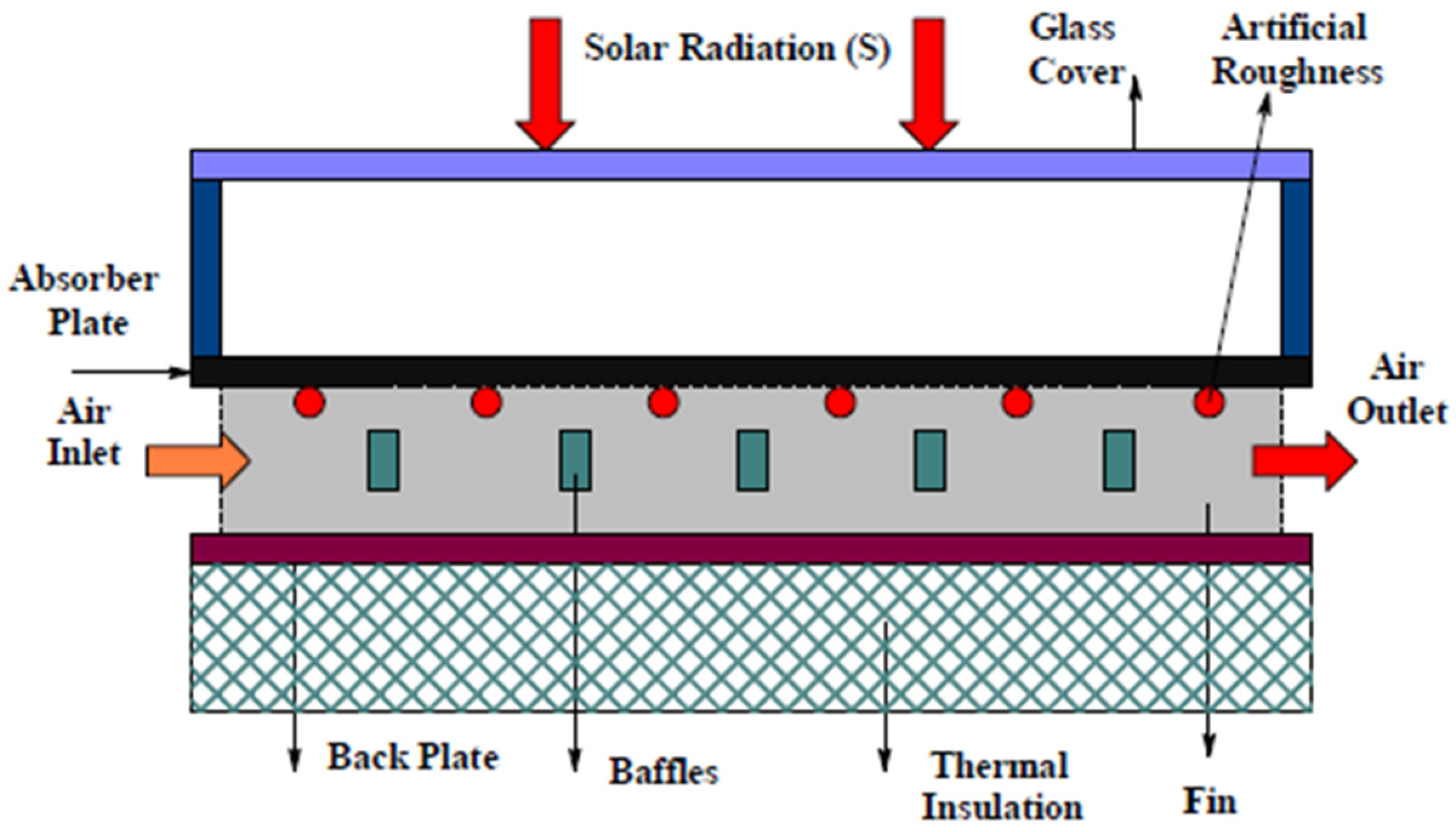
3.6. Absorber with Fins/Ribs
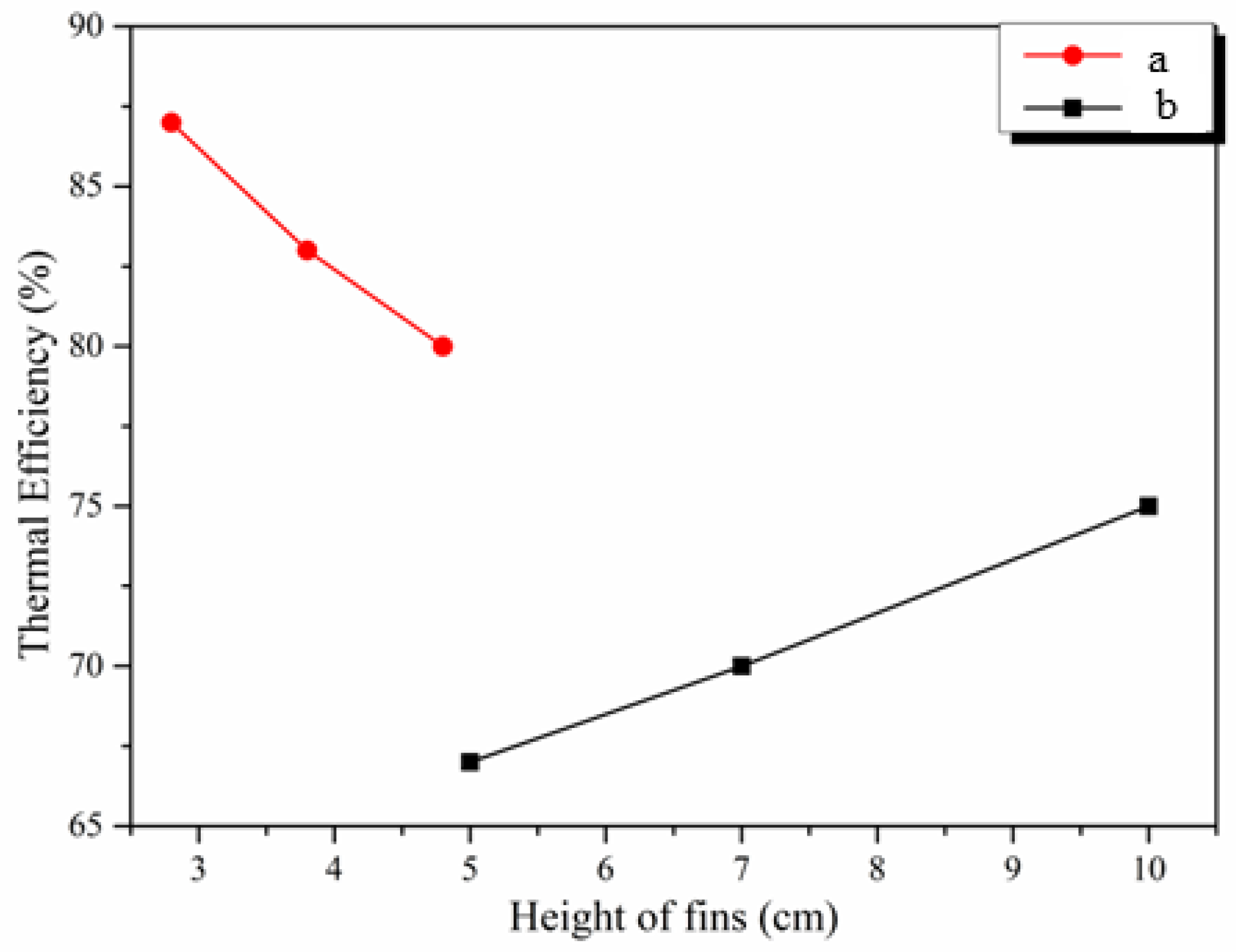
3.6.1. Fin/Ribs Spacing
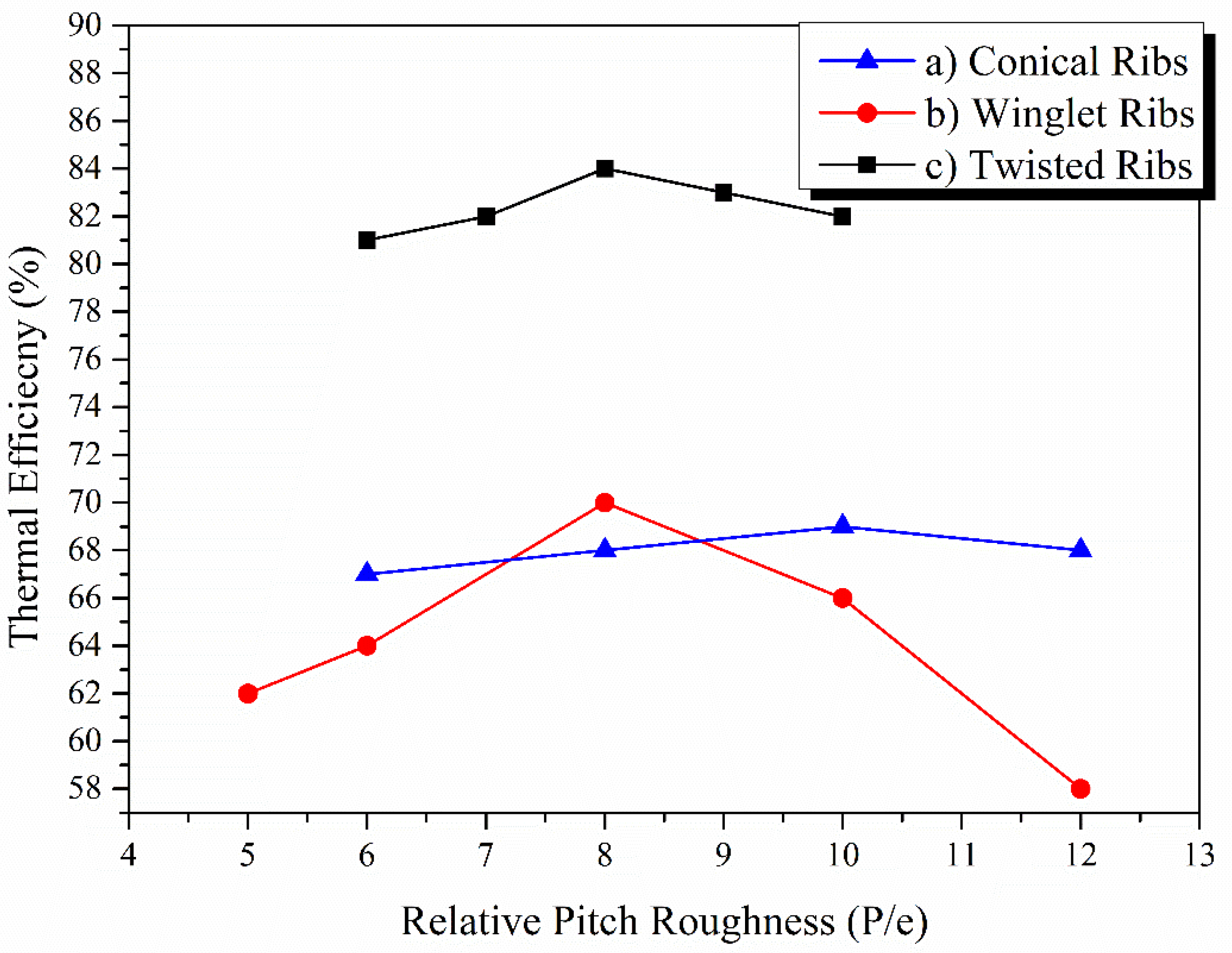
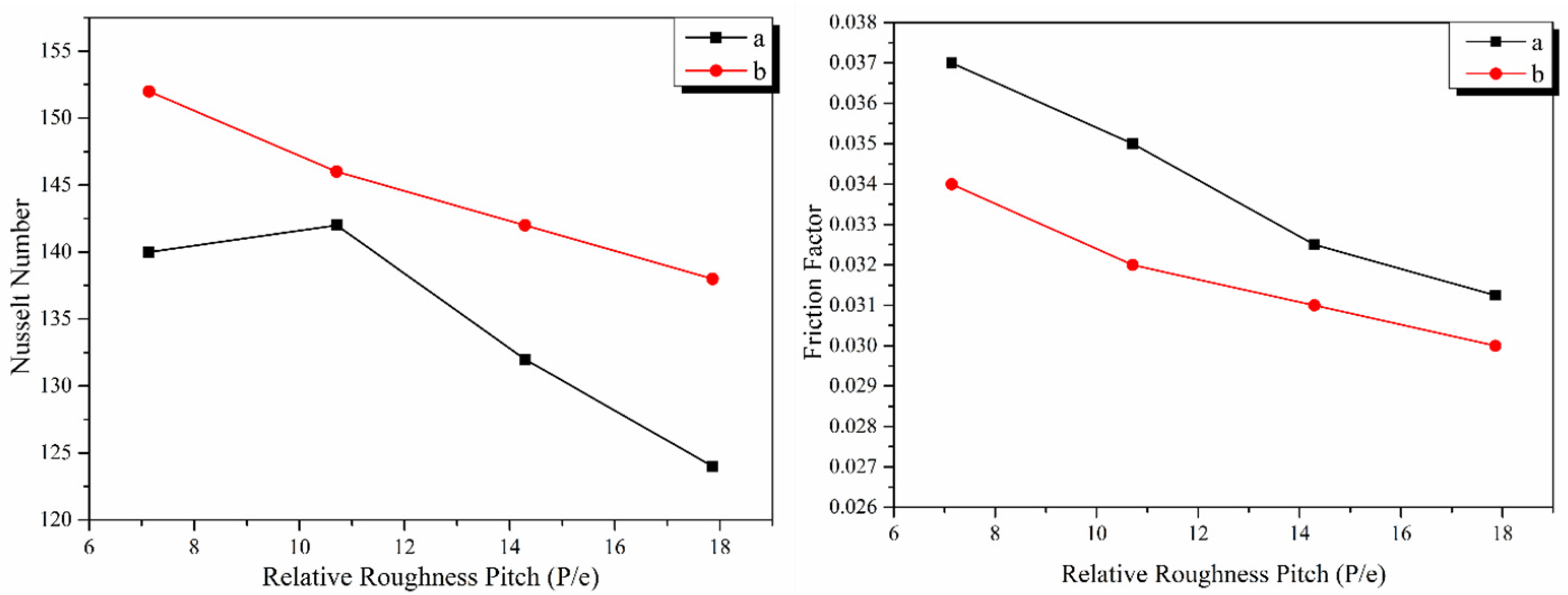
3.6.2. Relative Pitch Ratio
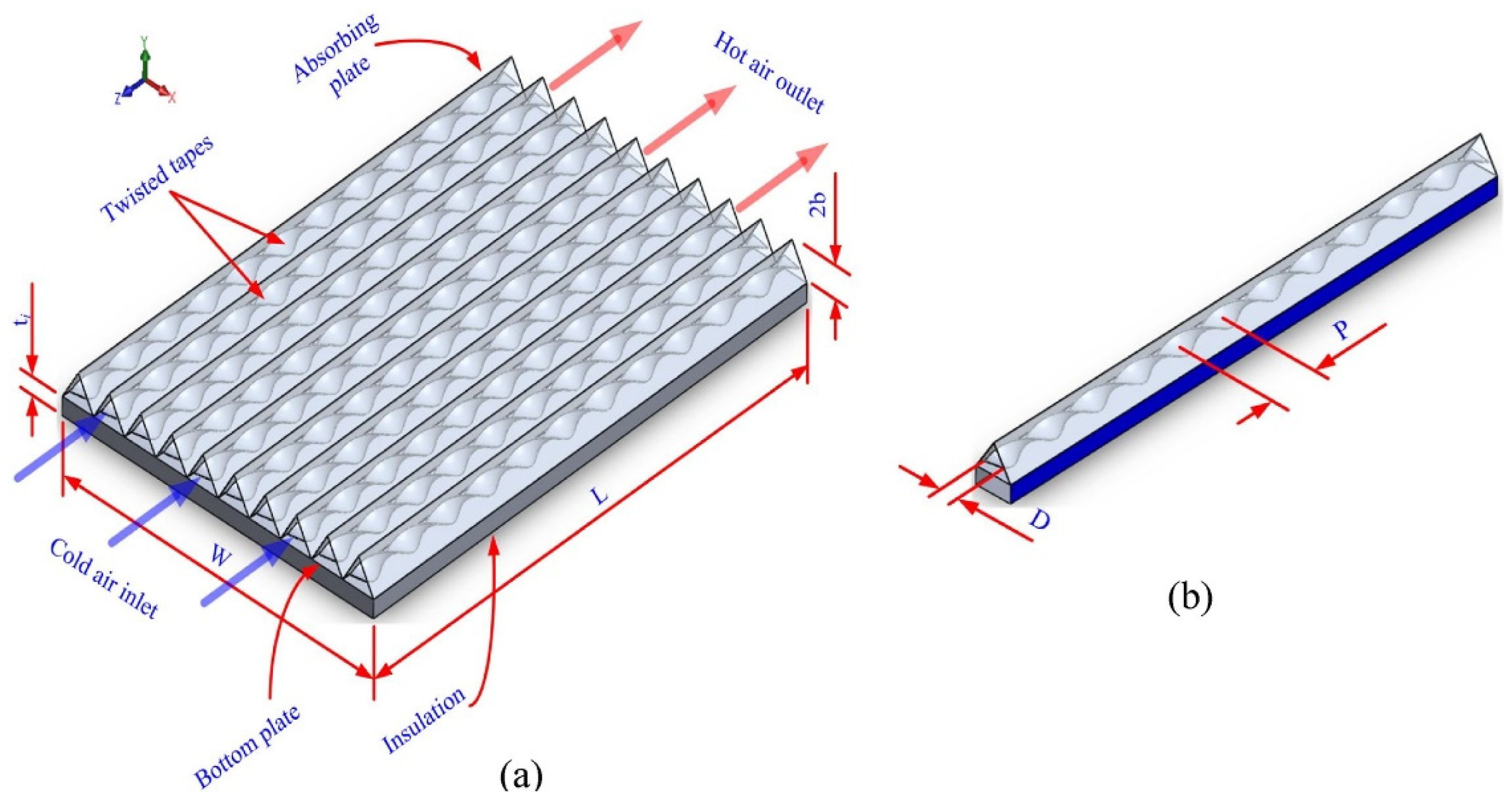
3.6.3. Geometry of Fins/Ribs
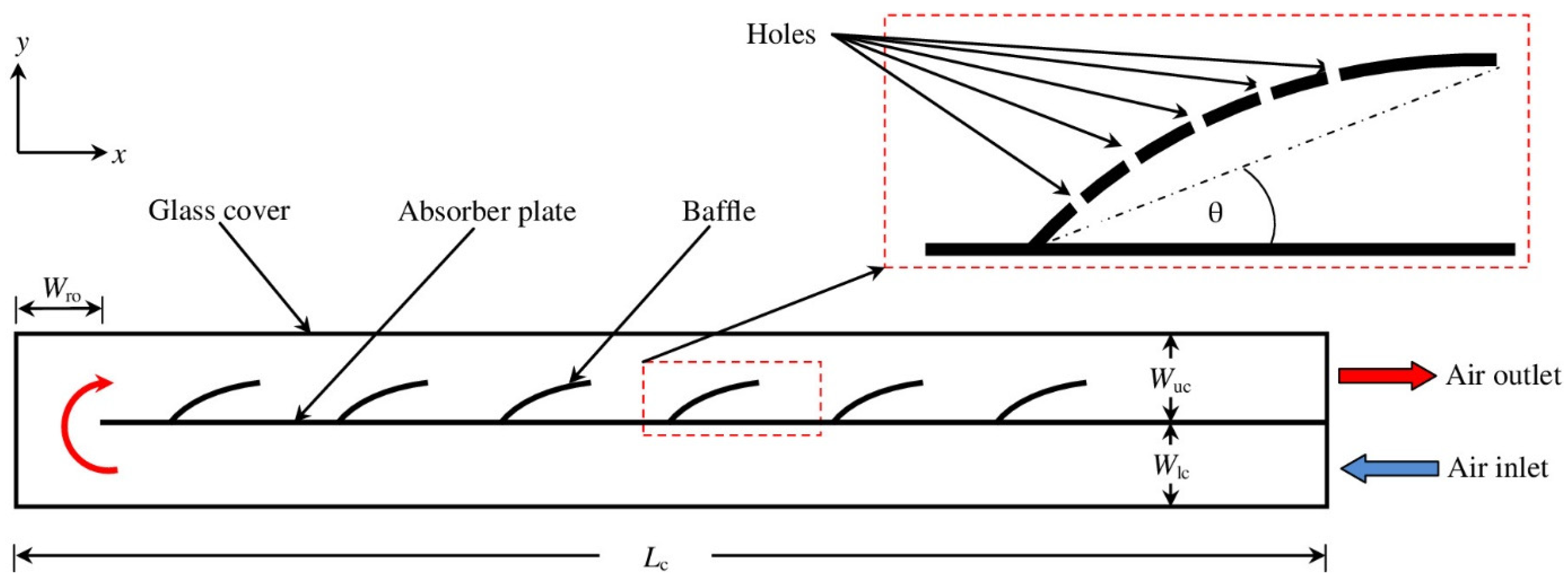
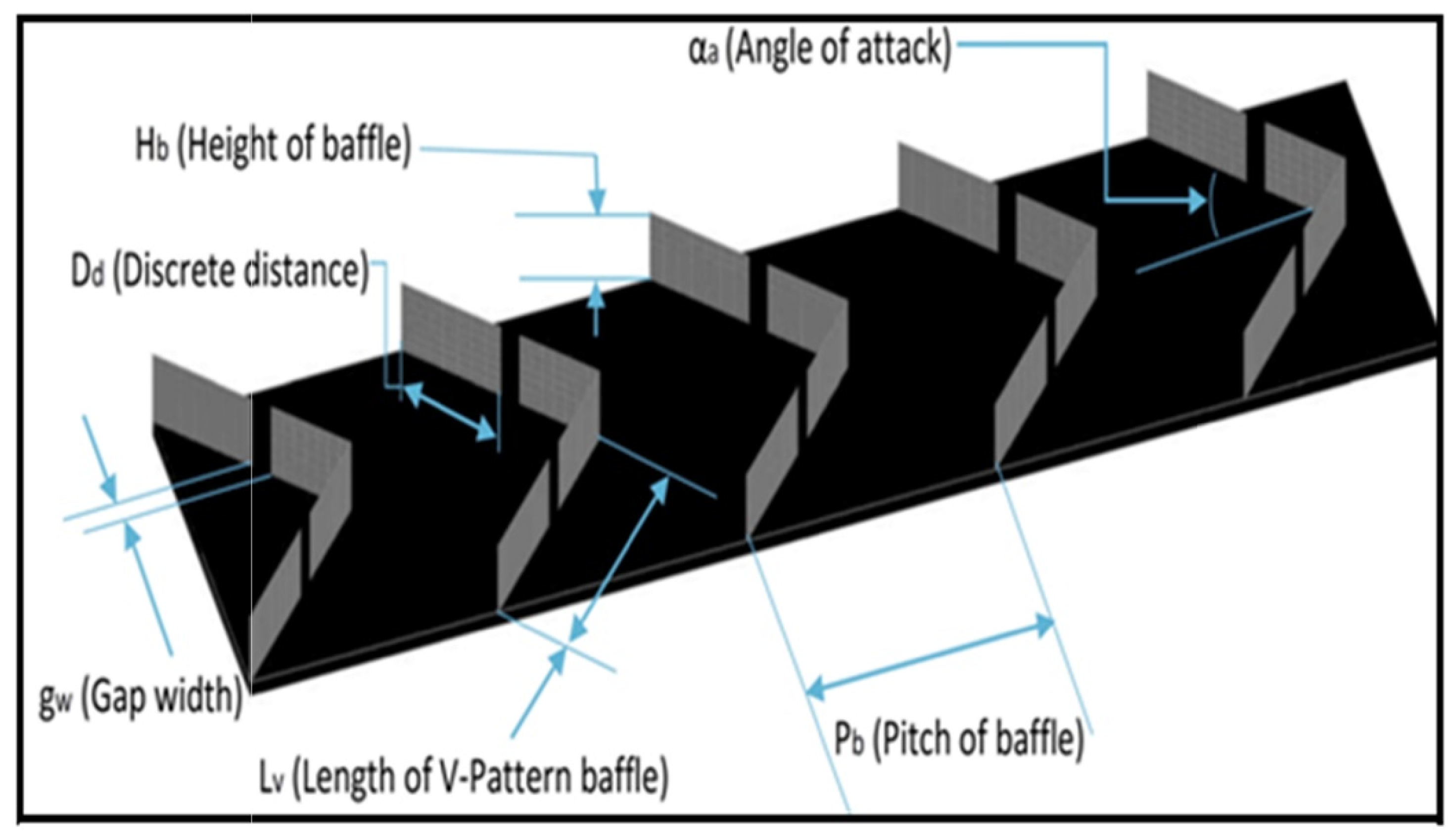
3.6.4. Absorber with Baffles
Baffle Width and Height
Baffle Position
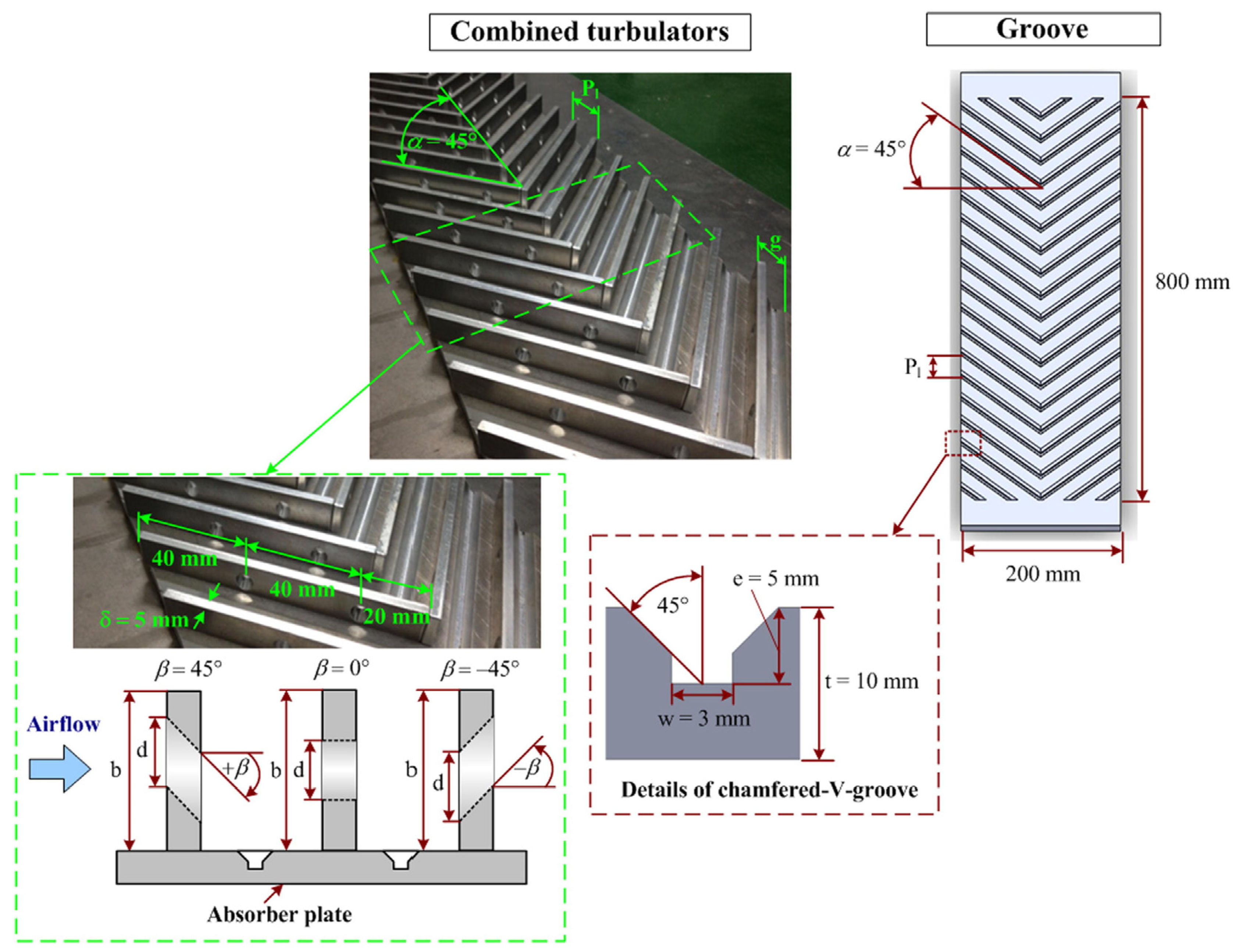
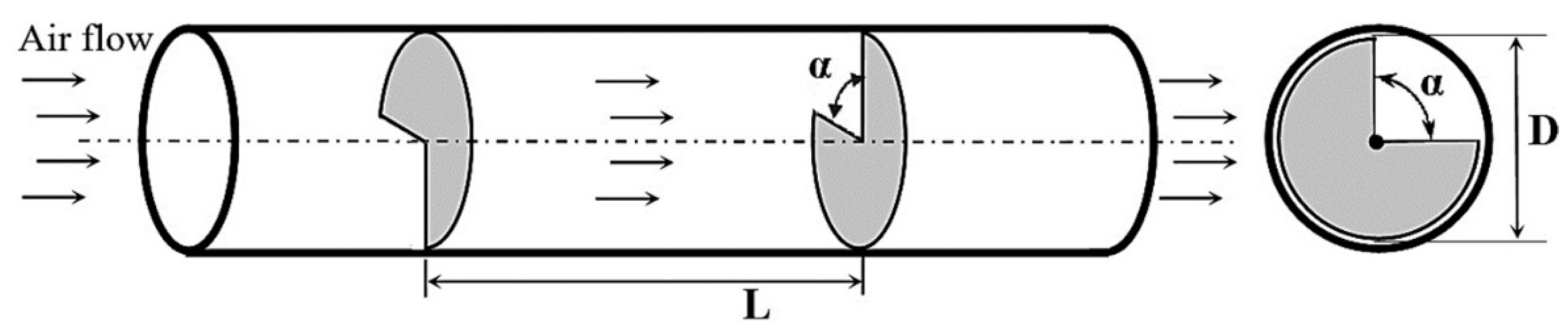
Baffle Shapes
3.6.5. V-Groove/Corrugated/Sinusoidal Absorber
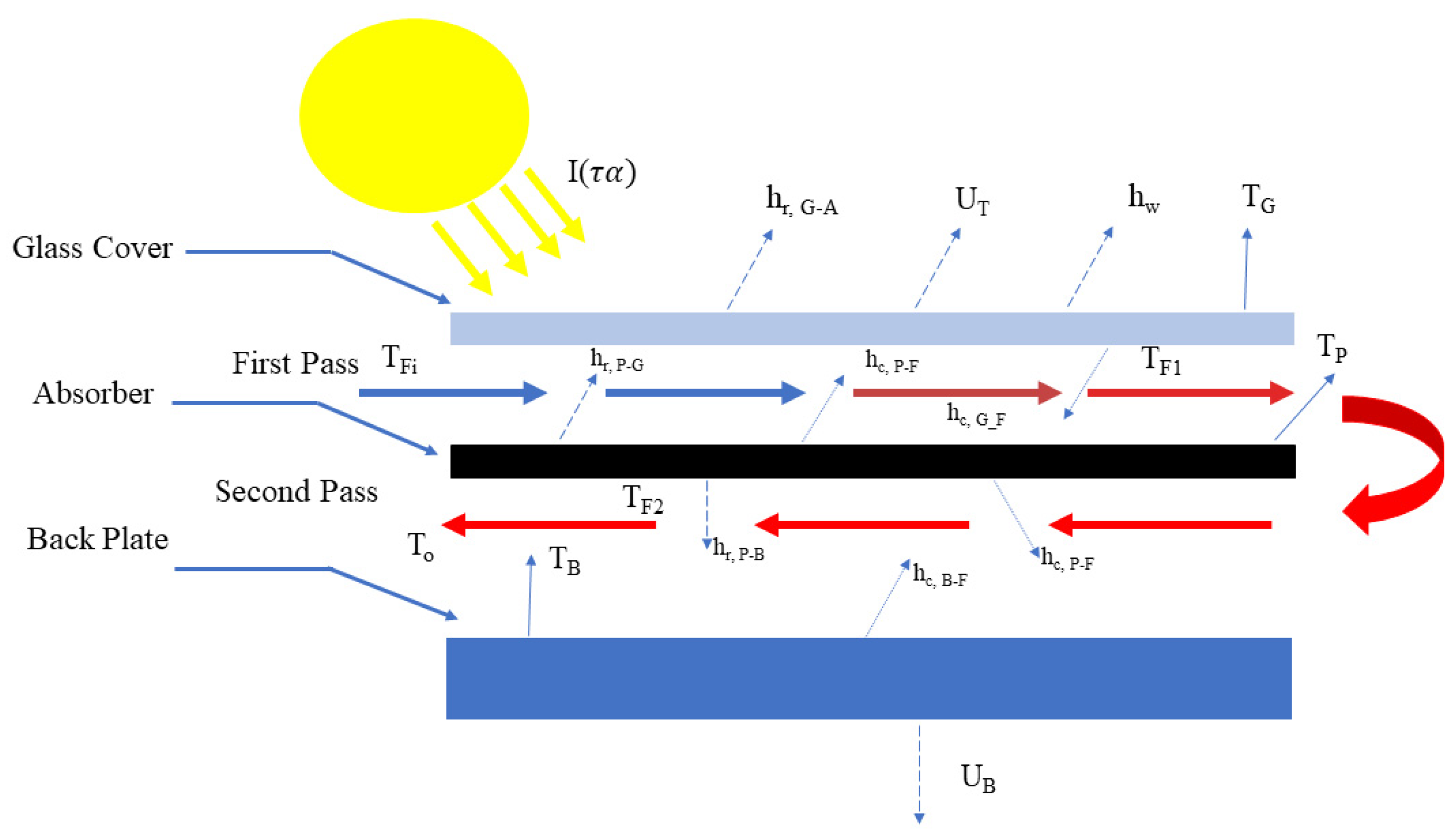
3.6.6. Single- and Multi-Pass Collectors
4. Exergy Analysis
Entropy Generation and Exergy Destruction
5. Outlook of Application of Solar Air Collectors in Industry
5.1. Space Heating and Cooling
5.2. Drying
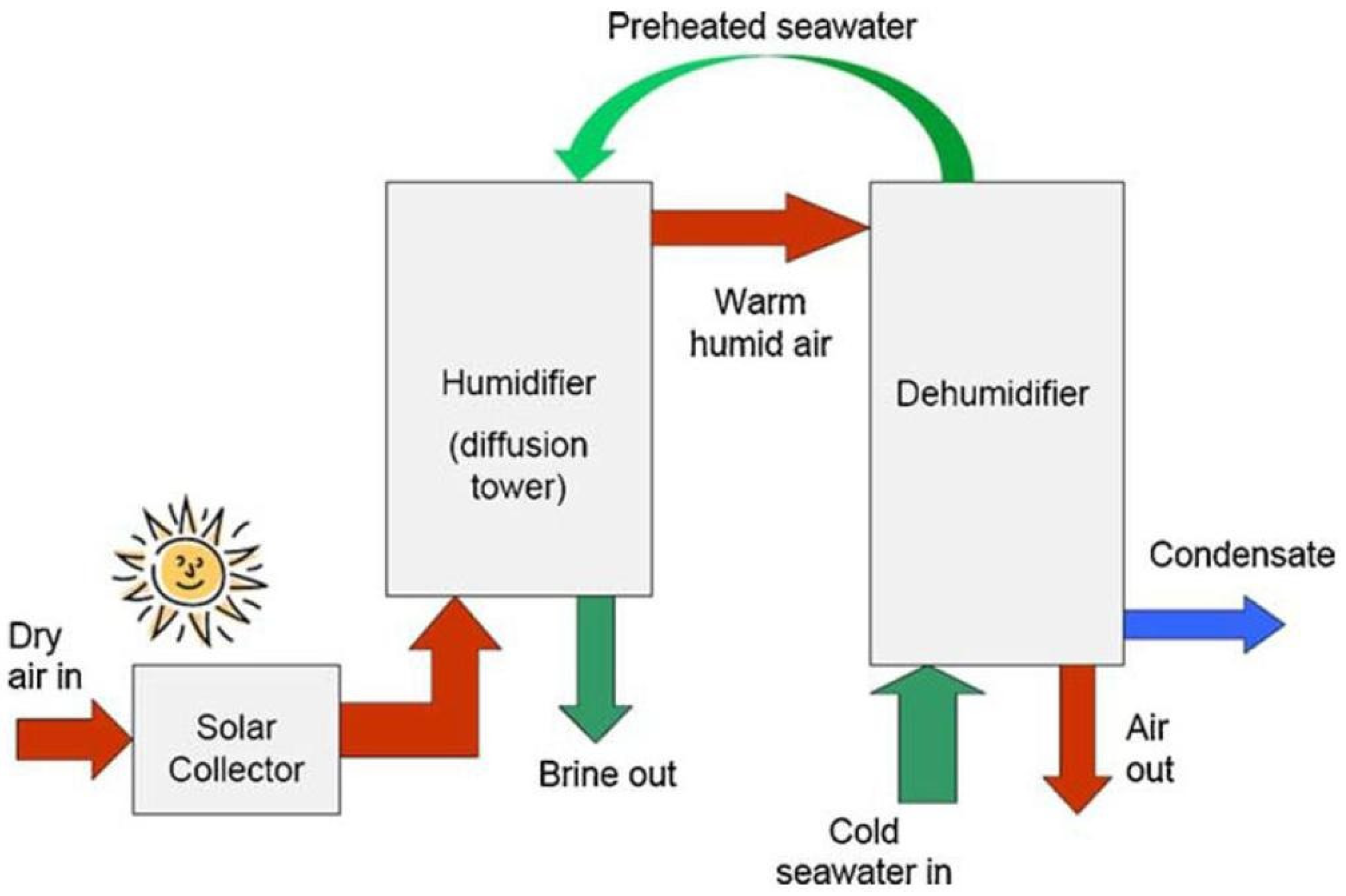
5.3. Water Desalination Using Humidification–Dehumidification
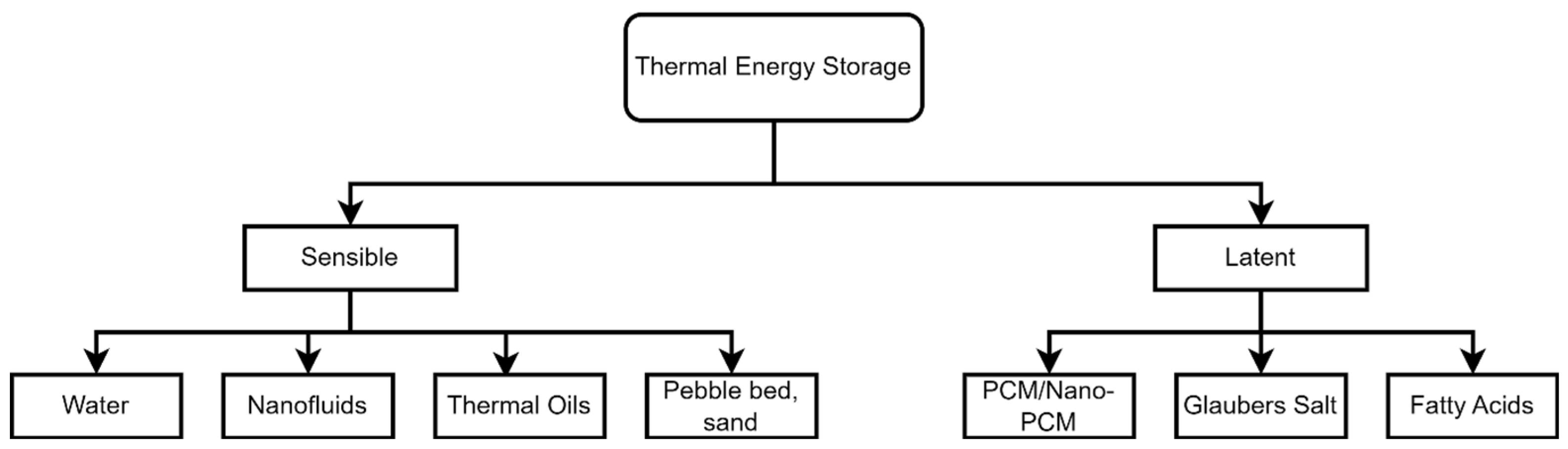
5.4. Thermal Energy Storage
6. Conclusions
- The thermal efficiency of SasC increases with an increase in the mass flow rate, though the increase rate stops at a higher flow rate due to the increased pumping power demand and decreased outlet temperature with an increase in the flow rate. From the literature review, it is recommended to maintain mass flow rates between 0.01 and 0.05 kg/s to achieve the desired thermal performance. Above 0.05 kg/s, a very small enhancement in thermal efficiency is expected with a low outlet air temperature. By changing the shape/Design of the absorber, thermal efficiency and outlet temperature can be increased from 40% to 90% and 35 to 83 °C, respectively.
- Conical fins provide higher thermal efficiency at around 83.6% compared to herringbone, longitudinal, and rectangular fins.
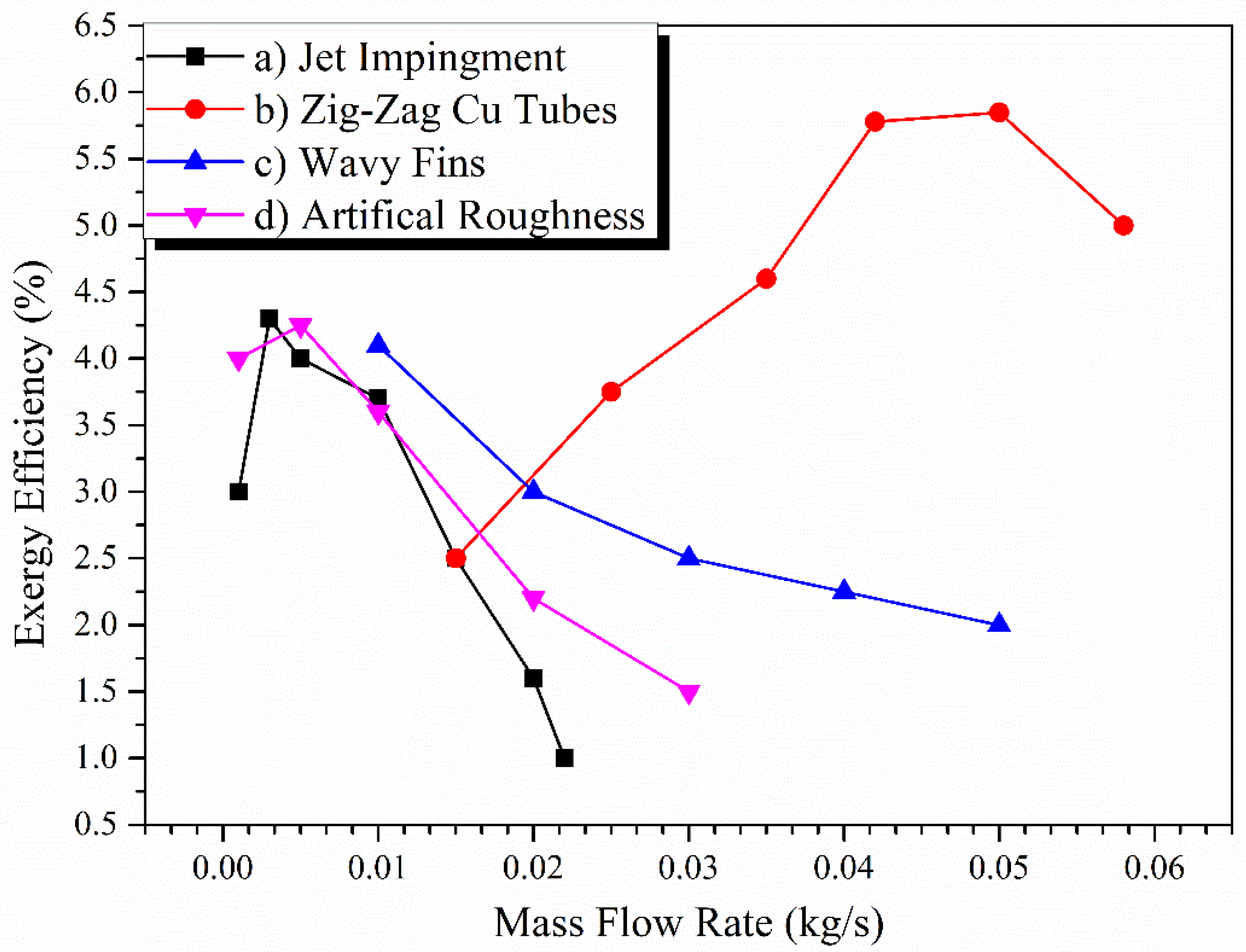
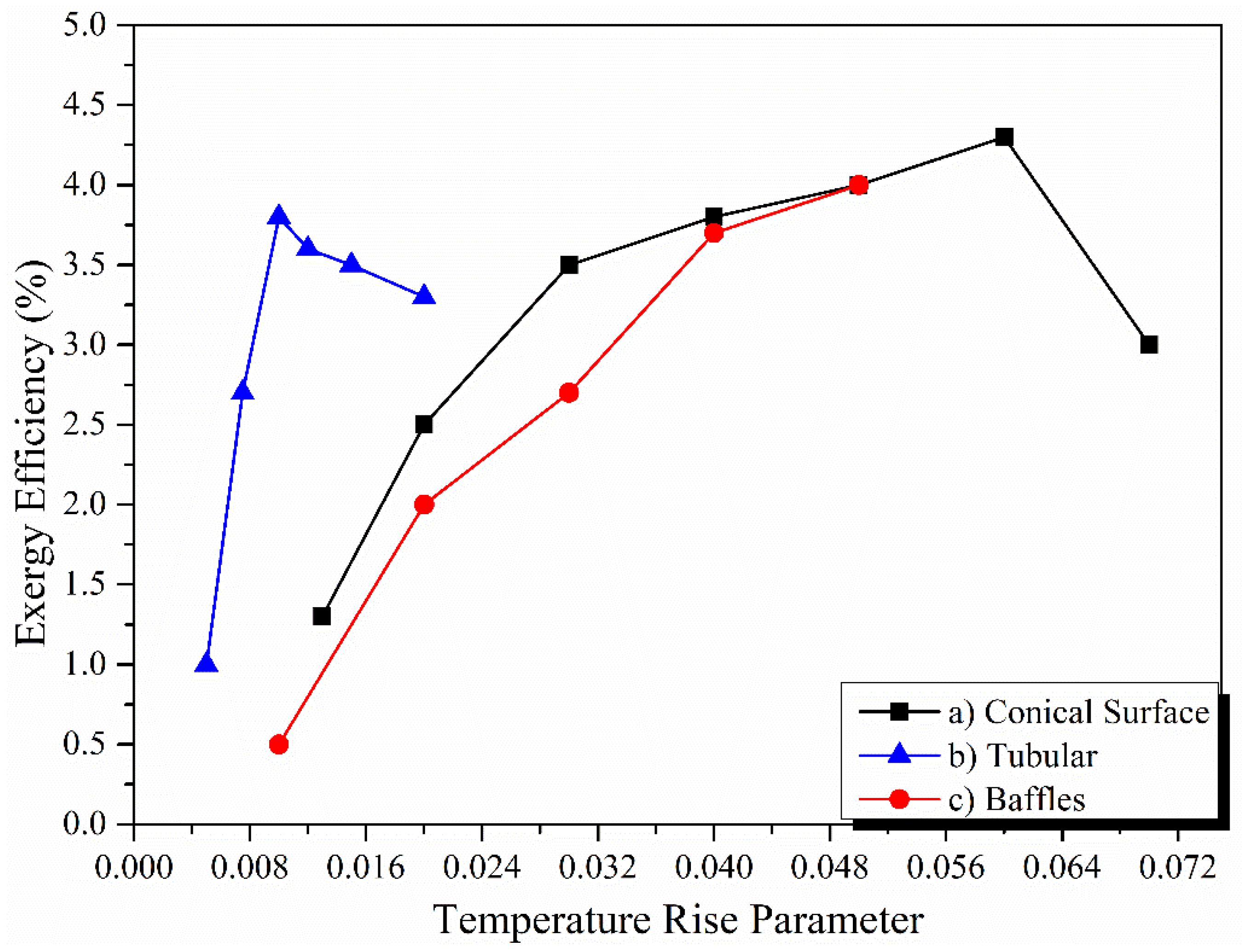
- Exergy efficiency of the system increases with increases in the mass flow rate, within a range of 0.005 to 0.01 kg/s in numerical perditions and between 0.04 and 0.05 kg/s in experimental reports. Numerical studies have shown the optimum mass flow rate for maximum exergy efficiency to be 0.005 to 0.01 kg/s, while experimental results have shown the optimum flow rate to be between 0.04 and 0.05 kg/s for maximum exergy efficiency.
- Dimensionless exergy loss has a negative trend with the Reynold number. Also, flat-plates have more dimensionless exergy losses, followed by reverse trapezoidal, reverse corrugated, trapeze, and corrugated absorbers.
- The sustainability index (SI) is a good indicator for the commercial use of solar air collectors. The sustainability index of solar air collectors is found to be around 2% in the literature. SI has a positive trend with the mass flow rate and a negative trend with the dead state temperature. This can be increased by minimizing the exergy losses in the system.
- The relative pitch roughness has a positive impact on the thermal efficiency of SACs up to an optimum point. Experiments and numerical investigations have slightly different findings on the optimum value of p/e. The optimum value of p/e also depends on the design of the fins, ribs, baffles, and artificial roughness.
- The optimum values of the span pitch wise ratio, stream-wise pitch ratio, and jet diameter ratio were recommended to be 0.869, 1.739, and 0.065, respectively, to achieve the maximum thermal output in single-pass double jet plates.
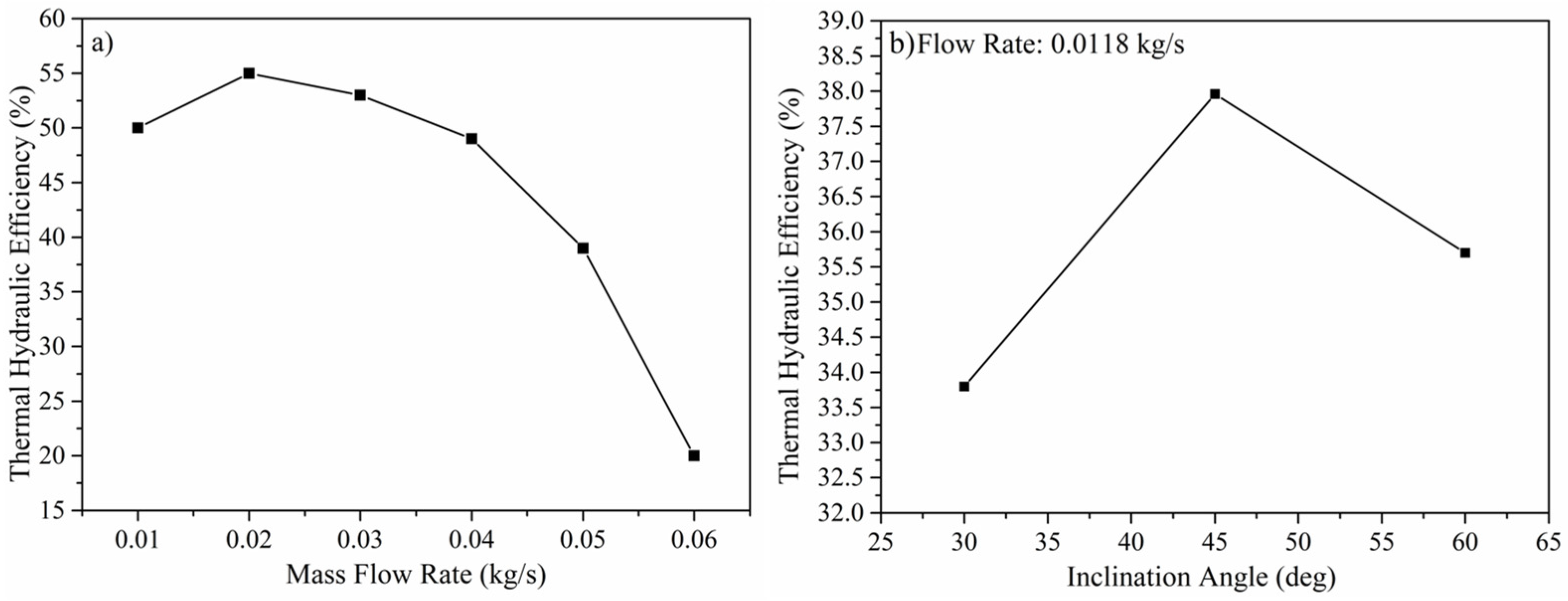
- The thermal hydraulic performance decreases with an increase in the Reynold number due to increments in the pumping power. THP increases with increases in the mass flow rate up to an optimum point.
7. Recommendations and Future Scope
- As the main drawback of SACs is the low heat transfer rate between air and the absorber, it is essential to implement new techniques to enhance the heat transfer rate. In recent years, the effect of jet impingement has been introduced in the SAC for enhanced heat transfer. More research studies are required to optimize the SAC jet impingement performance with different configurations such as fins, ribs, baffles, and artificial roughness with jet impingement, V-groove with jet impingement, or a combination of all these.
- A lot of research has been conducted on the thermal performance of solar air collectors in terms of energy efficiency. However, there is not enough literature available for the second law efficiency of solar air collectors for different absorbers, which is a key criterion for implementation in commercial applications. More research is required in exergy efficiency, exergy losses, improvement potential, and its sustainability index.
- Numerical studies need to be verified with experimental studies. In the case of an exergy analysis, numerical results have significant differences compared to experimental results, as mentioned in the conclusion.
- Research on using reflectors with SAHs may be conducted, as the efficiency of the system can be improved the using the effective sun tracking system.
- To minimize the power consumption in cooling systems, it is essential to conduct more research on desiccant cooling systems integrated with solar air heaters. Different types of absorbers should be used to find the optimum and suitable solar air heater for solar-assisted desiccant cooling systems.
- The productivity of water through water desalination using humidification–dehumidification depends on the humidification ability of air, which in turn depends on its high temperature. More research is required to find an optimum solar air heater with a high temperature output for water desalination.
- Research on solar air heaters integrated with thermal energy storage is limited. More research may be conducted using different absorbers and various types of thermal energy storage systems.
- From the literature, flat-plate, corrugated, V-groove, and trapezoidal solar air collectors with single-pass have been used for drying application. To the best of the authors’ knowledge, solar air heaters with fins, baffles, and ribs has not been studied yet for drying applications.
- The optimization of solar air heaters in different applications can be achieved by integrating machine learning approaches such as ANN. Dakovic et al. [196] discussed the different machine learning techniques to optimize the energy efficiency in the solar air drying field.
- An economic analysis needs to be performed for each type of solar air collector to determine whether it is economically and environmentally feasible for commercial use or not.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Number of fins in first row | Thermal conductivity of air (W/mK) | ||
| Louvered pitch (m) | Length of V-type baffle (m) | ||
| Louvered length (m) | Mean plate temperature (°C) | ||
| Fin thickness (m) | Ambient temperature (°C) | ||
| Length of collector (m) | Sun temperature (°C) | ||
| Width of collector (m) | Area of collector (m2) | ||
| Number of fins | Entropy generation (W/K) | ||
| Flow duct height (m) | Solar radiation (W/m2) | ||
| Profile distance of the offset strip fin (m) | s | Second | |
| Width of offset strip fin (m) | Turbulator tip height (m) | ||
| Length of offset strip fin (m) | Jet hole diameter (m) | ||
| Height of baffle (m) | Wind heat transfer coefficient (W/m2K) | ||
| Gap or discrete width (m) | Pitch of the turbulator (m) | ||
| Louvered angle | Span wise pitch | ||
| Width of fins (m) | Stefan–Boltzmann constant | ||
| Relative gap width | Relative roughness pitch | ||
| Relative baffle height | Relative roughness height | ||
| Relative pitch ratio | SPDDJP | Single-pass double-duct jet plate | |
| Pitch of baffle (m) | SAH | Solar air collector | |
| Height of fins (m) | Hydraulic diameter | ||
| Width of air channel (m) | HTF | Heat transfer fluid | |
| Depth of air channel (m) | SPSDJP | Single-pass single duct jet plate | |
| Angle of attack | |||
| Overall heat loss coefficient (W/m2K) | |||
| Relative baffle gap distance | |||
| Specific heat constant (J/kgK) | |||
| Gap or broken distance (m) |
References
- Prakash, S. Impact of Climate change on Aquatic Ecosystem and its Biodiversity: An overview. Int. J. Biol. Innov. 2021, 3, 312–317. [Google Scholar] [CrossRef]
- Abram, N.J.; Henley, B.J.; Gupta, A.S.; Lippmann, T.J.R.; Clarke, H.; Dowdy, A.J.; Sharples, J.J.; Nolan, R.H.; Zhang, T.; Wooster, M.J.; et al. Connections of climate change and variability to large and extreme forest fires in southeast Australia. Commun. Earth Environ. 2021, 2, 8. [Google Scholar] [CrossRef]
- Kemp, J.; McCowage, M.; Wang, F. Towards Net Zero: Implications for Australia of Energy Policies in East Asia; RBA Bulletin, 16 September 2021; Academic Press: Cambridge, MA, USA, 2021. [Google Scholar]
- Salameh, Z. Chapter 2-Photovoltaic. Renewable Energy System Design; Elsevier BV: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Kumar, A.; Saini, R.; Saini, J. A review of thermohydraulic performance of artificially roughened solar air heaters. Renew. Sustain. Energy Rev. 2014, 37, 100–122. [Google Scholar] [CrossRef]
- Han, Y.; Sun, Y.; Wu, J. A novel solar-driven waste heat recovery system in solar-fuel hybrid power plants. Energy 2023, 285, 129396. [Google Scholar] [CrossRef]
- Wahab, A.; Khan, M.A.Z.; Hassan, A. Impact of graphene nanofluid and phase change material on hybrid photovoltaic thermal system: Exergy analysis. J. Clean. Prod. 2020, 277, 123370. [Google Scholar] [CrossRef]
- Hassan, A.; Wahab, A.; Qasim, M.A.; Janjua, M.M.; Ali, M.A.; Ali, H.M.; Jadoon, T.R.; Ali, E.; Raza, A.; Javaid, N. Thermal management and uniform temperature regulation of photovoltaic modules using hybrid phase change materials-nanofluids system. Renew. Energy 2020, 145, 282–293. [Google Scholar] [CrossRef]
- Arthur, O.; Karim, M. An investigation into the thermophysical and rheological properties of nanofluids for solar thermal applications. Renew. Sustain. Energy Rev. 2016, 55, 739–755. [Google Scholar] [CrossRef]
- Sobri, S.; Koohi-Kamali, S.; Rahim, N.A. Solar photovoltaic generation forecasting methods: A review. Energy Convers. Manag. 2018, 156, 459–497. [Google Scholar] [CrossRef]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1980. [Google Scholar]
- Karim, M.A.; Hawlader, M. Mathematical modelling and experimental investigation of tropical fruits drying. Int. J. Heat Mass Transf. 2005, 48, 4914–4925. [Google Scholar] [CrossRef]
- Karim, M.A.; Arthur, O.; Yarlagadda, P.K.; Islam, M. Mahiuddin performance investigation of high temperature application of molten solar salt nanofluid in a direct absorption solar collector. Molecules 2019, 24, 285. [Google Scholar] [CrossRef] [PubMed]
- Close, D. Solar air heaters for low and moderate temperature applications. Sol. Energy 1963, 7, 117–124. [Google Scholar] [CrossRef]
- Alta, D.; Bilgili, E.; Ertekin, C.; Yaldiz, O. Experimental investigation of three different solar air heaters: Energy and exergy analyses. Appl. Energy 2010, 87, 2953–2973. [Google Scholar] [CrossRef]
- Stanciu, C.; Stanciu, D. Optimum tilt angle for flat plate collectors all over the World—A declination dependence formula and comparisons of three solar radiation models. Energy Convers. Manag. 2014, 81, 133–143. [Google Scholar] [CrossRef]
- Maia, C.B.; Ferreira, A.G.; Hanriot, S.M. Evaluation of a tracking flat-plate solar collector in Brazil. Appl. Therm. Eng. 2014, 73, 953–962. [Google Scholar] [CrossRef]
- Kalogirou, S.A.; Karellas, S.; Braimakis, K.; Stanciu, C.; Badescu, V. Exergy analysis of solar thermal collectors and processes. Prog. Energy Combust. Sci. 2016, 56, 106–137. [Google Scholar] [CrossRef]
- Moran, M.J.; Shapiro, H.N.; Boettner, D.D.; Bailey, M.B. Fundamentals of Engineering Thermodynamics; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2010. [Google Scholar]
- IEA. Renewables 2022; IEA: Paris, France, 2022. Available online: https://www.iea.org/reports/renewables-2022 (accessed on 10 February 2024).
- Karim, A.; Burnett, A.; Fawzia, S. Investigation of stratified thermal storage tank performance for heating and cooling applications. Energies 2018, 11, 1049. [Google Scholar] [CrossRef]
- Wahab, A.; Hassan, A.; Qasim, M.A.; Ali, H.M.; Babar, H.; Sajid, M.U. Solar energy systems–potential of nanofluids. J. Mol. Liq. 2019, 289, 111049. [Google Scholar] [CrossRef]
- Ali, H.M. Recent advancements in PV cooling and efficiency enhancement integrating phase change materials based systems—A comprehensive review. Sol. Energy 2020, 197, 163–198. [Google Scholar] [CrossRef]
- Sun, C.; Liu, Y.; Duan, C.; Zheng, Y.; Chang, H.; Shu, S. A mathematical model to investigate on the thermal performance of a flat plate solar air collector and its experimental verification. Energy Convers. Manag. 2016, 115, 43–51. [Google Scholar] [CrossRef]
- Abo-Elfadl, S.; Yousef, M.S.; Hassan, H. Energy, exergy, and enviroeconomic assessment of double and single pass solar air heaters having a new design absorber. Process. Saf. Environ. Prot. 2021, 149, 451–464. [Google Scholar] [CrossRef]
- Ho, C.-D.; Chang, H.; Hong, Z.-S.; Huang, C.-C.; Chen, Y.-H. Increasing the Device Performance of Recycling Double-Pass W-Ribs Solar Air Heaters. Energies 2020, 13, 2133. [Google Scholar] [CrossRef]
- Mahmood, A.; Aldabbagh, L.; Egelioglu, F. Investigation of single and double pass solar air heater with transverse fins and a package wire mesh layer. Energy Convers. Manag. 2015, 89, 599–607. [Google Scholar] [CrossRef]
- Chabane, F.; Moummi, N.; Benramache, S.; Bensahal, D.; Belahssen, O. collector efficiency by single pass of solar air heaters with and without using fins. Eng. J. 2013, 17, 43–55. [Google Scholar] [CrossRef]
- Labed, A.; Moummi, N.; Benchabane, A.; Aoues, K.; Moummi, A. Performance investigation of single- and double-pass solar air heaters through the use of various fin geometries. Int. J. Sustain. Energy 2012, 31, 423–434. [Google Scholar] [CrossRef]
- Fudholi, A.H.M.A.D.; Ruslan, M.H.; Haw, S.; Mat, M.; Othman, A.; Zaharim, K.S.; Sopian, K. Mathematical model of double-pass solar air collector with longitudinal fins. In Proceedings of the 9th WSEAS International Conference on Heat and Mass Transfer (HMT’12), Cambridge, MA, USA, 26–28 January 2012; pp. 114–120. [Google Scholar]
- Kumar, R.; Chand, P. Performance enhancement of solar air heater using herringbone corrugated fins. Energy 2017, 127, 271–279. [Google Scholar] [CrossRef]
- Yang, M.; Yang, X.; Li, X.; Wang, Z.; Wang, P. Design and optimization of a solar air heater with offset strip fin absorber plate. Appl. Energy 2013, 113, 1349–1362. [Google Scholar] [CrossRef]
- Hassan, A.; Nikbahkt, A.M.; Welsh, Z.; Yarlagadda, P.; Fawzia, S.; Karim, A. Experimental and thermodynamic analysis of solar air dryer equipped with V-groove double pass collector: Techno-economic and exergetic measures. Energy Convers. Manag. X 2022, 16, 100296. [Google Scholar] [CrossRef]
- Pfister, H.; Ralston, T.; Kim, S.W. A novel gridded solar air heater and an investigation of its conversion efficiency. Sol. Energy 2016, 136, 560–570. [Google Scholar] [CrossRef]
- Reddy, J.; Das, B.; Jagadish; Negi, S. Energy, exergy, and environmental (3E) analyses of reverse and cross-corrugated trapezoidal solar air collectors: An experimental study. J. Build. Eng. 2021, 41, 102434. [Google Scholar] [CrossRef]
- Debnath, S.; Das, B.; Randive, P.; Pandey, K. Performance analysis of solar air collector in the climatic condition of North Eastern India. Energy 2018, 165, 281–298. [Google Scholar] [CrossRef]
- El-Sebaii, A.; Aboul-Enein, S.; Ramadan, M.; Shalaby, S.; Moharram, B. Investigation of thermal performance of-double pass-flat and v-corrugated plate solar air heaters. Energy 2011, 36, 1076–1086. [Google Scholar] [CrossRef]
- Priyam, A.; Chand, P. Thermal and thermohydraulic performance of wavy finned absorber solar air heater. Sol. Energy 2016, 130, 250–259. [Google Scholar] [CrossRef]
- Bhushan, B.; Singh, R. Thermal and thermohydraulic performance of roughened solar air heater having protruded absorber plate. Sol. Energy 2012, 86, 3388–3396. [Google Scholar] [CrossRef]
- Deng, J.; Yang, X.; Yang, M.; Wang, Z. Experimental study of a single-pass flat plate solar air collector with severe dust deposition on the transparent glass cover. Energy Procedia 2015, 70, 32–40. [Google Scholar] [CrossRef][Green Version]
- Akpinar, E.K.; Koçyiğit, F. Energy and exergy analysis of a new flat-plate solar air heater having different obstacles on absorber plates. Appl. Energy 2010, 87, 3438–3450. [Google Scholar] [CrossRef]
- Chabane, F.; Hatraf, N.; Moummi, N. Experimental study of heat transfer coefficient with rectangular baffle fin of solar air heater. Front. Energy 2014, 8, 160–172. [Google Scholar] [CrossRef]
- Vaziri, R.; Ilkan, M.; Egelioglu, F. Experimental performance of perforated glazed solar air heaters and unglazed transpired solar air heater. Sol. Energy 2015, 119, 251–260. [Google Scholar] [CrossRef]
- Alam, T.; Kim, M.-H. Heat transfer enhancement in solar air heater duct with conical protrusion roughness ribs. Appl. Therm. Eng. 2017, 126, 458–469. [Google Scholar] [CrossRef]
- Yadav, A.S.; Bhagoria, J. A numerical investigation of square sectioned transverse rib roughened solar air heater. Int. J. Therm. Sci. 2014, 79, 111–131. [Google Scholar] [CrossRef]
- Yadav, A.S.; Bhagoria, J. A CFD based thermo-hydraulic performance analysis of an artificially roughened solar air heater having equilateral triangular sectioned rib roughness on the absorber plate. Int. J. Heat Mass Transf. 2014, 70, 1016–1039. [Google Scholar] [CrossRef]
- Kumar, A.; Layek, A. Nusselt number and friction factor correlation of solar air heater having winglet type vortex generator over absorber plate. Sol. Energy 2020, 205, 334–348. [Google Scholar] [CrossRef]
- Bekele, A.; Mishra, M.; Dutta, S. Effects of delta-shaped obstacles on the thermal performance of solar air heater. Adv. Mech. Eng. 2011, 3, 103502. [Google Scholar] [CrossRef]
- Prajapati, S.; Naik, N.; Chandramohan, V.P. Numerical solution of solar air heater with triangular corrugations for indirect solar dryer: Influence of pitch and an optimized pitch of corrugation for enhanced performance. Sol. Energy 2022, 243, 1–12. [Google Scholar] [CrossRef]
- Moummi, N.; Youcef-Ali, S.; Moummi, A.; Desmons, J.Y. Energy analysis of a solar air collector with rows of fins. Renew. Energy 2004, 29, 2053–2064. [Google Scholar] [CrossRef]
- Hachemi, A. Thermal performance enhancement of solar air heaters, by a fan-blown absorber plate with rectangular fins. Int. J. Energy Res. 1995, 19, 567–577. [Google Scholar] [CrossRef]
- Chand, S.; Chand, P. Performance evaluation of solar air heater equipped with louvered fins. Int. J. Heat Technol. 2018, 36, 741–751. [Google Scholar] [CrossRef]
- Priyam, A.; Chand, P. Thermal performance of wavy finned absorber solar air heater. Int. J. Heat Technol. 2018, 36, 1393–1403. [Google Scholar] [CrossRef]
- Rai, S.; Chand, P.; Sharma, S. Evaluation of thermo hydraulic effect on offset finned absorber solar air heater. Renew. Energy 2018, 125, 39–54. [Google Scholar] [CrossRef]
- Bahrehmand, D.; Ameri, M. Energy and exergy analysis of different solar air collector systems with natural convection. Renew. Energy 2015, 74, 357–368. [Google Scholar] [CrossRef]
- Naphon, P. On the performance and entropy generation of the double-pass solar air heater with longitudinal fins. Renew. Energy 2005, 30, 1345–1357. [Google Scholar] [CrossRef]
- Wang, D.; Liu, J.; Liu, Y.; Wang, Y.; Li, B.; Liu, J. Evaluation of the performance of an improved solar air heater with “S” shaped ribs with gap. Sol. Energy 2020, 195, 89–101. [Google Scholar] [CrossRef]
- Kabeel, A.; Hamed, M.H.; Omara, Z.; Kandeal, A. Influence of fin height on the performance of a glazed and bladed entrance single-pass solar air heater. Sol. Energy 2018, 162, 410–419. [Google Scholar] [CrossRef]
- Priyam, A.; Chand, P. Effect of wavelength and amplitude on the performance of wavy finned absorber solar air heater. Renew. Energy 2018, 119, 690–702. [Google Scholar] [CrossRef]
- Rai, S.; Chand, P.; Sharma, S. An analytical investigations on thermal and thermohydraulic performance of offset finned absorber solar air heater. Sol. Energy 2017, 153, 25–40. [Google Scholar] [CrossRef]
- Rahmani, E.; Moradi, T.; Fattahi, A.; Delpisheh, M.; Karimi, N.; Ommi, F.; Saboohi, Z. Numerical simulation of a solar air heater equipped with wavy and raccoon-shaped fins: The effect of fins’ height. Sustain. Energy Technol. Assess. 2021, 45, 101227. [Google Scholar] [CrossRef]
- Saboohi, Z.; Ommi, F.; Rahmani, E.; Moradi, T.; Fattahi, A.; Delpisheh, M.; Karimi, N. The effect of sinusoidal fins’ amplitude on the thermo-hydraulic performance of a solar air heater. Chem. Eng. Commun. 2022, 210, 773–787. [Google Scholar] [CrossRef]
- Singh, I.; Singh, S.; Vardhan, S. Heat transfer and fluid flow characteristics of solar air heater duct with non-uniform ribs. J. Mech. Sci. Technol. 2021, 35, 343–350. [Google Scholar] [CrossRef]
- Kumar, A.; Layek, A. Evaluation of the performance analysis of an improved solar air heater with Winglet shaped ribs. Exp. Heat Transf. 2020, 35, 239–257. [Google Scholar] [CrossRef]
- Kumar, A.; Layek, A. Energetic and exergetic performance evaluation of solar air heater with twisted rib roughness on absorber plate. J. Clean. Prod. 2019, 232, 617–628. [Google Scholar] [CrossRef]
- Saini, R.; Verma, J. Heat transfer and friction factor correlations for a duct having dimple-shape artificial roughness for solar air heaters. Energy 2008, 33, 1277–1287. [Google Scholar] [CrossRef]
- Hosseini, S.S.; Ramiar, A.; Ranjbar, A.A. Numerical investigation of natural convection solar air heater with different fins shape. Renew. Energy 2018, 117, 488–500. [Google Scholar] [CrossRef]
- Saravanan, A.; Murugan, M.; Reddy, M.S.; Ranjit, P.; Elumalai, P.; Kumar, P.; Sree, S.R. Thermo-hydraulic performance of a solar air heater with staggered C-shape finned absorber plate. Int. J. Therm. Sci. 2021, 168, 107068. [Google Scholar] [CrossRef]
- Saravanakumar, P.; Somasundaram, D.; Matheswaran, M. Exergetic investigation and optimization of arc shaped rib roughened solar air heater integrated with fins and baffles. Appl. Therm. Eng. 2020, 175, 115316. [Google Scholar] [CrossRef]
- Benhamza, A.; Boubekri, A.; Atia, A.; El Ferouali, H.; Hadibi, T.; Arıcı, M.; Abdenouri, N. Multi-objective design optimization of solar air heater for food drying based on energy, exergy and improvement potential. Renew. Energy 2021, 169, 1190–1209. [Google Scholar] [CrossRef]
- Webb, R.; Eckert, E.; Goldstein, R. Heat transfer and friction in tubes with repeated-rib roughness. Int. J. Heat Mass Transf. 1971, 14, 601–617. [Google Scholar] [CrossRef]
- Patel, S.S.; Lanjewar, A. Performance study of solar air heater duct with gap in V-rib with symmetrical gap and staggered ribs. Heat Mass Transf. 2019, 55, 2517–2532. [Google Scholar] [CrossRef]
- Deo, N.S.; Chander, S.; Saini, J. Performance analysis of solar air heater duct roughened with multigap V-down ribs combined with staggered ribs. Renew. Energy 2016, 91, 484–500. [Google Scholar] [CrossRef]
- Yadav, A.S.; Bhagoria, J. A CFD (computational fluid dynamics) based heat transfer and fluid flow analysis of a solar air heater provided with circular transverse wire rib roughness on the absorber plate. Energy 2013, 55, 1127–1142. [Google Scholar] [CrossRef]
- Prasad, B.; Saini, J. Effect of artificial roughness on heat transfer and friction factor in a solar air heater. Sol. Energy 1988, 41, 555–560. [Google Scholar] [CrossRef]
- Kumar, R.; Kumar, A.; Goel, V. A parametric analysis of rectangular rib roughened triangular duct solar air heater using computational fluid dynamics. Sol. Energy 2017, 157, 1095–1107. [Google Scholar] [CrossRef]
- Kumar, R.; Kumar, A.; Goel, V. Performance improvement and development of correlation for friction factor and heat transfer using computational fluid dynamics for ribbed triangular duct solar air heater. Renew. Energy 2018, 131, 788–799. [Google Scholar] [CrossRef]
- Jain, S.K.; Das Agrawal, G.; Misra, R.; Verma, P.; Rathore, S.; Jamuwa, D.K. Performance investigation of a triangular solar air heater duct having broken inclined roughness using computational fluid dynamics. J. Sol. Energy Eng. 2019, 141, 061008. [Google Scholar] [CrossRef]
- Nidhul, K.; Kumar, S.; Yadav, A.K.; Anish, S. Enhanced thermo-hydraulic performance in a V-ribbed triangular duct solar air heater: CFD and exergy analysis. Energy 2020, 200, 117448. [Google Scholar] [CrossRef]
- Kumar, A.; Kim, M.-H. Thermal hydraulic performance in a solar air heater channel with multi V-type perforated baffles. Energies 2016, 9, 564. [Google Scholar] [CrossRef]
- Mousavi, S.; Hooman, K. Heat and fluid flow in entrance region of a channel with staggered baffles. Energy Convers. Manag. 2006, 47, 2011–2019. [Google Scholar] [CrossRef]
- Yeh, H.-M.; Lin, T.-T. Efficiency improvement of flat-plate solar air heaters. Energy 1996, 21, 435–443. [Google Scholar] [CrossRef]
- Bensaci, C.-E.; Moummi, A.; de la Flor, F.J.S.; Jara, E.A.R.; Rincon-Casado, A.; Ruiz-Pardo, A. Numerical and experimental study of the heat transfer and hydraulic performance of solar air heaters with different baffle positions. Renew. Energy 2020, 155, 1231–1244. [Google Scholar] [CrossRef]
- Hu, J.; Liu, K.; Guo, M.; Zhang, G.; Chu, Z.; Wang, M. Performance improvement of baffle-type solar air collector based on first chamber narrowing. Renew. Energy 2019, 135, 701–710. [Google Scholar] [CrossRef]
- Bayrak, F.; Oztop, H.F.; Hepbasli, A. Energy and exergy analyses of porous baffles inserted solar air heaters for building applications. Energy Build. 2013, 57, 338–345. [Google Scholar] [CrossRef]
- Promvonge, P.; Sripattanapipat, S.; Kwankaomeng, S. Laminar periodic flow and heat transfer in square channel with 45° inline baffles on two opposite walls. Int. J. Therm. Sci. 2010, 49, 963–975. [Google Scholar] [CrossRef]
- Promvonge, P.; Kwankaomeng, S. Periodic laminar flow and heat transfer in a channel with 45° staggered V-baffles. Int. Commun. Heat Mass Transf. 2010, 37, 841–849. [Google Scholar] [CrossRef]
- Promvonge, P.; Sripattanapipat, S.; Tamna, S.; Kwankaomeng, S.; Thianpong, C. Numerical investigation of laminar heat transfer in a square channel with 45° inclined baffles. Int. Commun. Heat Mass Transf. 2010, 37, 170–177. [Google Scholar] [CrossRef]
- El-Said, E.M. Numerical investigations of fluid flow and heat transfer characteristics in solar air collector with curved perforated baffles. Eng. Rep. 2020, 2, e12142. [Google Scholar] [CrossRef]
- Fiuk, J.J.; Dutkowski, K. Experimental investigations on thermal efficiency of a prototype passive solar air collector with wavelike baffles. Sol. Energy 2019, 188, 495–506. [Google Scholar] [CrossRef]
- Khanlari, A.; Güler, H.; Tuncer, A.D.; Şirin, C.; Bilge, Y.C.; Yılmaz, Y.; Güngör, A. Experimental and numerical study of the effect of integrating plus-shaped perforated baffles to solar air collector in drying application. Renew. Energy 2020, 145, 1677–1692. [Google Scholar] [CrossRef]
- Kumar, R.; Sethi, M.; Chauhan, R.; Kumar, A. Experimental study of enhancement of heat transfer and pressure drop in a solar air channel with discretized broken V-pattern baffle. Renew. Energy 2017, 101, 856–872. [Google Scholar] [CrossRef]
- Chamoli, S.; Thakur, N. Correlations for solar air heater duct with V-shaped perforated baffles as roughness elements on absorber plate. Int. J. Sustain. Energy 2016, 35, 1–20. [Google Scholar] [CrossRef]
- Bopche, S.B.; Tandale, M.S. Experimental investigations on heat transfer and frictional characteristics of a turbulator roughened solar air heater duct. Int. J. Heat Mass Transf. 2009, 52, 2834–2848. [Google Scholar] [CrossRef]
- Karwa, R.; Maheshwari, B. Heat transfer and friction in an asymmetrically heated rectangular duct with half and fully perforated baffles at different pitches. Int. Commun. Heat Mass Transf. 2009, 36, 264–268. [Google Scholar] [CrossRef]
- Won, S.Y.; Burgess, N.K.; Peddicord, S.; Ligrani, P.M. Spatially resolved surface heat transfer for parallel rib turbulators with 45 deg orientations including test surface conduction analysis. J. Heat Transf. 2004, 126, 193–201. [Google Scholar] [CrossRef]
- Promvonge, P.; Jedsadaratanachai, W.; Kwankaomeng, S. Numerical study of laminar flow and heat transfer in square channel with 30° inline angled baffle turbulators. Appl. Therm. Eng. 2010, 30, 1292–1303. [Google Scholar] [CrossRef]
- Khanoknaiyakarn, C.; Kwankaomeng, S.; Promvonge, P. Thermal performance enhancement in solar air heater channel with periodically V-shaped baffles. In Proceedings of the 2011 International Conference & Utility Exhibition on Power and Energy Systems: Issues and Prospects for Asia (ICUE), Pattaya, Thailand, 28–30 September 2011. [Google Scholar]
- Shin, S.; Kwak, J.S. Effect of hole shape on the heat transfer in a rectangular duct with perforated blockage walls. J. Mech. Sci. Technol. 2008, 22, 1945–1951. [Google Scholar] [CrossRef]
- Gawande, V.B.; Dhoble, A.S.; Zodpe, D.B. CFD Analysis to study effect of circular vortex generator placed in inlet section to investigate heat transfer aspects of solar air heater. Sci. World J. 2014, 2014, 567257. [Google Scholar] [CrossRef] [PubMed]
- Alam, T.; Saini, R.P.; Saini, J.S. Experimental investigation of thermohydraulic performance of a rectangular solar air heater duct equipped with V-shaped perforated blocks. Adv. Mech. Eng. 2014, 6, 948313. [Google Scholar] [CrossRef]
- Tamna, S.; Skullong, S.; Thianpong, C.; Promvonge, P. Heat transfer behaviors in a solar air heater channel with multiple V-baffle vortex generators. Sol. Energy 2014, 110, 720–735. [Google Scholar] [CrossRef]
- Jedsadaratanachai, W.; Boonloi, A. Effects of blockage ratio and pitch ratio on thermal performance in a square channel with 30° double V-baffles. Case Stud. Therm. Eng. 2014, 4, 118–128. [Google Scholar] [CrossRef]
- Yadav, A.S.; Samant, T.S.; Varshney, L. A CFD based analysis of solar air heater having V-shaped perforated blocks on absorber plate. Int. Res. J. Eng. Tech. 2015, 2, 822–829. [Google Scholar]
- Garg, A.; Dhingra, S.; Singh, G. CFD analysis of laminar heat transfer in a channel provided with baffles: Comparative study between two models of baffles: Diamond-shaped baffles of different angle and rectangle. Int. J. Enhanc. Res. Sci. Technol. Eng. 2014, 3. [Google Scholar]
- Sparrow, E.; Lin, S. Absorption of thermal radiation in a V-groove cavity. Int. J. Heat Mass Transf. 1962, 5, 1111–1115. [Google Scholar] [CrossRef]
- Hollands, K. Directional selectivity, emittance, and absorptance properties of vee corrugated specular surfaces. Sol. Energy 1963, 7, 108–116. [Google Scholar] [CrossRef]
- Goldstein, L., Jr.; Sparrow, E. Experiments on the transfer characteristics of a corrugated fin and tube heat exchanger configuration. J. Heat Transfer. 1976, 98, 26–34. [Google Scholar] [CrossRef]
- Parker, B.; Lindley, M.; Colliver, D.; Murphy, W. Thermal performance of three solar air heaters. Sol. Energy 1993, 51, 467–479. [Google Scholar] [CrossRef]
- Hawlader, M.N.; Ho, J.C.A.; Karim, M.A.; Keat, W.M. Performance Evaluation of Solar Air Collectors for Drying Purposes. In Proceedings of the Second ASEAN Renewable Energy Conference, Phuket, Thailand, 5–9 November 1997. [Google Scholar]
- Karim, M.; Perez, E.; Amin, Z. Mathematical modelling of counter flow v-grove solar air collector. Renew. Energy 2014, 67, 192–201. [Google Scholar] [CrossRef]
- Desisa, D.G.; Shekata, G.D. Performance Analysis of Flat-Plate and V-groove Solar Air Heater Through CFD Simulation. Int. J. Renew. Energy Dev. 2020, 9, 369–381. [Google Scholar] [CrossRef]
- Karim, M.; Hawlader, M. Development of solar air collectors for drying applications. Energy Convers. Manag. 2004, 45, 329–344. [Google Scholar] [CrossRef]
- Karim, M.; Hawlader, M. Performance investigation of flat plate, v-corrugated and finned air collectors. Energy 2006, 31, 452–470. [Google Scholar] [CrossRef]
- Karim, M.A.; Hawlader, M. Performance evaluation of a v-groove solar air collector for drying applications. Appl. Therm. Eng. 2006, 26, 121–130. [Google Scholar] [CrossRef]
- Zulkifle, I.; Alwaeli, A.H.; Ruslan, M.H.; Ibarahim, Z.; Othman, M.Y.H.; Sopian, K. Numerical investigation of V-groove air-collector performance with changing cover in Bangi, Malaysia. Case Stud. Therm. Eng. 2018, 12, 587–599. [Google Scholar] [CrossRef]
- Ho, C.-D.; Hsiao, C.-F.; Chang, H.; Tien, Y.-E.; Hong, Z.-S. Efficiency of recycling double-pass V-corrugated solar air collectors. Energies 2017, 10, 875. [Google Scholar] [CrossRef]
- Sudhakar, P.; Cheralathan, M. Thermal performance enhancement of solar air collector using a novel V-groove absorber plate with pin-fins for drying agricultural products: An experimental study. J. Therm. Anal. Calorim. 2019, 140, 2397–2408. [Google Scholar] [CrossRef]
- Eswaramoorthy, M. A Comparative experimental study on flat and V groove receiver plates of a solar air heater for drying applications. Energy Sources Part A Recover. Util. Environ. Eff. 2015, 37, 68–75. [Google Scholar] [CrossRef]
- Liu, T.; Lin, W.; Gao, W.; Xia, C. A Comparative study of the thermal performances of cross-corrugated and v-groove solar air collectors. Int. J. Green Energy 2007, 4, 427–451. [Google Scholar] [CrossRef]
- Promvonge, P.; Skullong, S. Heat transfer in solar receiver heat exchanger with combined punched-V-ribs and chamfer-V-grooves. Int. J. Heat Mass Transf. 2019, 143, 118486. [Google Scholar] [CrossRef]
- Lakshmi, D.; Layek, A.; Kumar, P.M. Performance analysis of trapezoidal corrugated solar air heater with sensible heat storage material. Energy Procedia 2017, 109, 463–470. [Google Scholar] [CrossRef]
- Salih, M.M.M.; Alomar, O.R.; Yassien, H.N.S. Impacts of adding porous media on performance of double-pass solar air heater under natural and forced air circulation processes. Int. J. Mech. Sci. 2021, 210, 106738. [Google Scholar] [CrossRef]
- Farhan, A.A.; M.Ali, A.I.; Ahmed, H.E. Energetic and exergetic efficiency analysis of a v-corrugated solar air heater integrated with twisted tape inserts. Renew. Energy 2021, 169, 1373–1385. [Google Scholar] [CrossRef]
- Hassan, H.; Yousef, M.S.; Abo-Elfadl, S. Energy, exergy, economic and environmental assessment of double pass V-corrugated-perforated finned solar air heater at different air mass ratios. Sustain. Energy Technol. Assess. 2021, 43, 100936. [Google Scholar] [CrossRef]
- Pathak, P.K.; Chandra, P.; Raj, G. Comparative analysis of modified and convectional dual purpose solar collector: Energy and exergy analysis. Energy Sources Part A Recover. Util. Environ. Eff. 2019, 1–17. [Google Scholar] [CrossRef]
- Manjunath, M.; Karanth, K.V.; Sharma, N.Y. Numerical investigation on heat transfer enhancement of solar air heater using sinusoidal corrugations on absorber plate. Int. J. Mech. Sci. 2018, 138, 219–228. [Google Scholar] [CrossRef]
- Lingayat, A.; Chandramohan, V. Numerical investigation on solar air collector and its practical application in the indirect solar dryer for banana chips drying with energy and exergy analysis. Therm. Sci. Eng. Prog. 2021, 26, 101077. [Google Scholar] [CrossRef]
- Chandra, R.; Singh, N.; Sodha, M. Thermal performance of a triple-pass solar air collector. Energy Convers. Manag. 1990, 30, 41–48. [Google Scholar] [CrossRef]
- Prakash, J.; Garg, H.; Verma, R. Study of the thermal performance of a multiple pass solar collector. Energy Convers. Manag. 1992, 33, 965–970. [Google Scholar] [CrossRef]
- Mohamad, A. High efficiency solar air heater. Sol. Energy 1997, 60, 71–76. [Google Scholar] [CrossRef]
- Ramani, B.; Gupta, A.; Kumar, R. Performance of a double pass solar air collector. Sol. Energy 2010, 84, 1929–1937. [Google Scholar] [CrossRef]
- Razak, A.; Majid, Z.; Basrawi, F.; Sharol, A.; Ruslan, M.; Sopian, K. A performance and technoeconomic study of different geometrical designs of compact single-pass cross-matrix solar air collector with square-tube absorbers. Sol. Energy 2019, 178, 314–330. [Google Scholar] [CrossRef]
- Yang, M.; Wang, P.; Yang, X.; Shan, M. Experimental analysis on thermal performance of a solar air collector with a single pass. Build. Environ. 2012, 56, 361–369. [Google Scholar] [CrossRef]
- Tuncer, A.D.; Sözen, A.; Khanlari, A.; Amini, A.; Şirin, C. Thermal performance analysis of a quadruple-pass solar air collector assisted pilot-scale greenhouse dryer. Sol. Energy 2020, 203, 304–316. [Google Scholar] [CrossRef]
- Ho, C.-D.; Chang, H.; Hsiao, C.-F.; Huang, C.-C. Device performance improvement of recycling double-pass cross-corrugated solar air collectors. Energies 2018, 11, 338. [Google Scholar] [CrossRef]
- MesgarPour, M.; Heydari, A.; Wongwises, S. Geometry optimization of double pass solar air heater with helical flow path. Sol. Energy 2021, 213, 67–80. [Google Scholar] [CrossRef]
- Alic, E.; Das, M.; Akpinar, E.K. Design, manufacturing, numerical analysis and environmental effects of single-pass forced convection solar air collector. J. Clean. Prod. 2021, 311, 127518. [Google Scholar] [CrossRef]
- Nowzari, R.; Aldabbagh, L.; Egelioglu, F. Single and double pass solar air heaters with partially perforated cover and packed mesh. Energy 2014, 73, 694–702. [Google Scholar] [CrossRef]
- Fudholi, A.; Rusla, M.H.; Haw, L.C.; Fauzi, M.; Othman, M.Y.; Zaharim, A.; Sopian, K.B. Mathematical model of double-pass solar air collector. Sol. Energy Res. Inst. 2014, 2, 79–83. [Google Scholar]
- Dinçer, İ.; Zamfirescu, C. Drying Phenomena: Theory and Applications; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2016. [Google Scholar]
- Bejan, A. Advanced Engineering Thermodynamics, 3rd ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
- Mortazavi, A.; Ameri, M. Conventional and advanced exergy analysis of solar flat plate air collectors. Energy 2018, 142, 277–288. [Google Scholar] [CrossRef]
- Matheswaran, M.; Arjunan, T.; Somasundaram, D. Analytical investigation of solar air heater with jet impingement using energy and exergy analysis. Sol. Energy 2018, 161, 25–37. [Google Scholar] [CrossRef]
- Priyam, A.; Chand, P.; Sharma, S.P. Energy and exergy analysis of wavy finned absorber solar air heater. Int. Energy J. 2016, 16, 119–130. [Google Scholar]
- Matheswaran, M.M.; Arjunan, T.V.; Somasundaram, D. Energetic, exergetic and enviro-economic analysis of parallel pass jet plate solar air heater with artificial roughness. J. Therm. Anal. Calorim. 2019, 136, 5–19. [Google Scholar] [CrossRef]
- Kumar, D.; Mahanta, P.; Kalita, P. Performance analysis of a solar air heater modified with zig-zag shaped copper tubes using energy-exergy methodology. Sustain. Energy Technol. Assess. 2021, 46, 101222. [Google Scholar] [CrossRef]
- Abuşka, M. Energy and exergy analysis of solar air heater having new design absorber plate with conical surface. Appl. Therm. Eng. 2018, 131, 115–124. [Google Scholar] [CrossRef]
- Ucar, A.; Inallı, M. Thermal and exergy analysis of solar air collectors with passive augmentation techniques. Int. Commun. Heat Mass Transf. 2006, 33, 1281–1290. [Google Scholar] [CrossRef]
- Acır, A.; Canlı, M.E.; Ata, I.; Çakıroğlu, R. Parametric optimization of energy and exergy analyses of a novel solar air heater with grey relational analysis. Appl. Therm. Eng. 2017, 122, 330–338. [Google Scholar] [CrossRef]
- Luan, N.T.; Phu, N.M. Thermohydraulic correlations and exergy analysis of a solar air heater duct with inclined baffles. Case Stud. Therm. Eng. 2020, 21, 100672. [Google Scholar] [CrossRef]
- Gupta, M.; Kaushik, S. Exergetic performance evaluation and parametric studies of solar air heater. Energy 2008, 33, 1691–1702. [Google Scholar] [CrossRef]
- Debnath, S.; Das, B.; Randive, P. Energy and exergy analysis of plain and corrugated solar air collector: Effect of seasonal variation. Int. J. Ambient. Energy 2020, 43, 2796–2807. [Google Scholar] [CrossRef]
- Sahu, M.K.; Prasad, R.K. Exergy based performance evaluation of solar air heater with arc-shaped wire roughened absorber plate. Renew. Energy 2016, 96, 233–243. [Google Scholar] [CrossRef]
- Aktaş, M.; Sözen, A.; Tuncer, A.D.; Arslan, E.; Koşan, M.; Çürük, O. Energy-exergy analysis of a novel multi-pass solar air collector with perforated fins. Int. J. Renew. Energy Dev. 2019, 8, 47–55. [Google Scholar] [CrossRef]
- Dheep, G.R.; Sreekumar, A. Experimental studies on energy and exergy analysis of a single-pass parallel flow solar air heater. J. Sol. Energy Eng. 2020, 142, 011003. [Google Scholar] [CrossRef]
- Velmurugan, P.; Kalaivanan, R. Energy and exergy analysis in double-pass solar air heater. Sadhana 2016, 41, 369–376. [Google Scholar] [CrossRef]
- Sahoo, A.; Nandkeolyar, R. Entropy generation and dissipative heat transfer analysis of mixed convective hydromagnetic flow of a Casson nanofluid with thermal radiation and Hall current. Sci. Rep. 2021, 11, 3926. [Google Scholar] [CrossRef]
- Bejan, A. Entropy generation minimization: The new thermodynamics of finite-size devices and finite-time processes. J. Appl. Phys. 1996, 79, 1191–1218. [Google Scholar] [CrossRef]
- Chu, S.; Liu, L. Entropy generation analysis of two-dimensional high-temperature confined jet. Int. J. Therm. Sci. 2009, 48, 998–1006. [Google Scholar] [CrossRef]
- Phu, N.M.; Van Hap, N. Performance evaluation of a solar air heater roughened with conic-curve profile ribs based on efficiencies and entropy generation. Arab. J. Sci. Eng. 2020, 45, 9023–9035. [Google Scholar] [CrossRef]
- Sahu, M.K.; Prasad, R.K. Second law optimization and parametric study of a solar air heater having artificially roughened absorber plate. Arch. Thermodyn. 2019, 40, 107–135. [Google Scholar] [CrossRef]
- Layek, A.; Saini, J.; Solanki, S. Second law optimization of a solar air heater having chamfered rib–groove roughness on absorber plate. Renew. Energy 2007, 32, 1967–1980. [Google Scholar] [CrossRef]
- Benli, H. Experimentally derived efficiency and exergy analysis of a new solar air heater having different surface shapes. Renew. Energy 2013, 50, 58–67. [Google Scholar] [CrossRef]
- Daliran, A.; Ajabshirchi, Y. Theoretical and experimental research on effect of fins attachment on operating parameters and thermal efficiency of solar air collector. Inf. Process. Agric. 2018, 5, 411–421. [Google Scholar] [CrossRef]
- Biçer, A.; Devecioğlu, A.G.; Oruç, V.; Tuncer, Z. Experimental investigation of a solar air heater with copper wool on the absorber plate. Int. J. Green Energy 2020, 17, 979–989. [Google Scholar] [CrossRef]
- Kalaiarasi, G.; Velraj, R.; Swami, M.V. Experimental energy and exergy analysis of a flat plate solar air heater with a new design of integrated sensible heat storage. Energy 2016, 111, 609–619. [Google Scholar] [CrossRef]
- Chabane, F.; Moummi, N.; Benramache, S. Experimental study of heat transfer and thermal performance with longitudinal fins of solar air heater. J. Adv. Res. 2014, 5, 183–192. [Google Scholar] [CrossRef]
- Tuncer, A.D.; Khanlari, A.; Sözen, A.; Gürbüz, E.Y.; Şirin, C.; Gungor, A. Energy-exergy and enviro-economic survey of solar air heaters with various air channel modifications. Renew. Energy 2020, 160, 67–85. [Google Scholar] [CrossRef]
- Yilmaz, A.; Er, A. Thermal analysis of solar air collectors designed in different types with different flow rates using aluminum cans. Energy Sources Part A Recover. Util. Environ. Eff. 2022, 44, 5545–5561. [Google Scholar] [CrossRef]
- Darici, S.; Kilic, A. Comparative study on the performances of solar air collectors with trapezoidal corrugated and flat absorber plates. Heat Mass Transf. 2020, 56, 1833–1843. [Google Scholar] [CrossRef]
- Choudhury, P.K.; Baruah, D.C. Solar air heater for residential space heating. Energy Ecol. Environ. 2017, 2, 387–403. [Google Scholar] [CrossRef]
- Ismail, A.; Jusoh, N.; Makhtar, N.; Daraham, M.; Parimun, M.; Husin, M. Assessment of environmental factors and thermal comfort at Automotive Paint Shop. J. Appl. Sci. 2010, 10, 1300–1306. [Google Scholar] [CrossRef]
- Bianco, V.; Scarpa, F.; Tagliafico, L.A. Estimation of primary energy savings by using heat pumps for heating purposes in the residential sector. Appl. Therm. Eng. 2017, 114, 938–947. [Google Scholar] [CrossRef]
- Fan, W.; Kokogiannakis, G.; Ma, Z. Integrative modelling and optimisation of a desiccant cooling system coupled with a photovoltaic thermal-solar air heater. Sol. Energy 2019, 193, 929–947. [Google Scholar] [CrossRef]
- Kabeel, A.; Abdelgaied, M. Solar energy assisted desiccant air conditioning system with PCM as a thermal storage medium. Renew. Energy 2018, 122, 632–642. [Google Scholar] [CrossRef]
- Farooq, A.S.; Badar, A.W.; Sajid, M.B.; Fatima, M.; Zahra, A.; Siddiqui, M.S. Dynamic simulation and parametric analysis of solar assisted desiccant cooling system with three configuration schemes. Sol. Energy 2020, 197, 22–37. [Google Scholar] [CrossRef]
- Hussain, S.; Kalendar, A.; Rafique, M.Z.; Oosthuizen, P. Numerical investigations of solar-assisted hybrid desiccant evaporative cooling system for hot and humid climate. Adv. Mech. Eng. 2020, 12, 1687814020934999. [Google Scholar] [CrossRef]
- Li, H.; Dai, Y.; Li, Y.; La, D.; Wang, R. Experimental investigation on a one-rotor two-stage desiccant cooling/heating system driven by solar air collectors. Appl. Therm. Eng. 2011, 31, 3677–3683. [Google Scholar] [CrossRef]
- Eicker, U.; Schneider, D.; Schumacher, J.; Ge, T.; Dai, Y. Operational experiences with solar air collector driven desiccant cooling systems. Appl. Energy 2010, 87, 3735–3747. [Google Scholar] [CrossRef]
- Ahmad, A.; Prakash, O.; Kumar, A. Drying kinetics and economic analysis of bitter gourd flakes drying inside hybrid greenhouse dryer. Environ. Sci. Pollut. Res. 2021, 30, 72026–72040. [Google Scholar] [CrossRef]
- Vijayan, S.; Arjunan, T.; Kumar, A. Mathematical modeling and performance analysis of thin layer drying of bitter gourd in sensible storage based indirect solar dryer. Innov. Food Sci. Emerg. Technol. 2016, 36, 59–67. [Google Scholar] [CrossRef]
- Fudholi, A.; Sopian, K.; Yazdi, M.H.; Ruslan, M.H.; Gabbasa, M.; Kazem, H.A. Performance analysis of solar drying system for red chili. Sol. Energy 2014, 99, 47–54. [Google Scholar] [CrossRef]
- Hegde, V.N.; Hosur, V.S.; Rathod, S.K.; Harsoor, P.A.; Narayana, K.B. Design, fabrication and performance evaluation of solar dryer for banana. Energy, Sustain. Soc. 2015, 5, 23. [Google Scholar] [CrossRef]
- Mugi, V.R.; Chandramohan, V. Energy, exergy and economic analysis of an indirect type solar dryer using green chilli: A comparative assessment of forced and natural convection. Therm. Sci. Eng. Prog. 2021, 24, 100950. [Google Scholar] [CrossRef]
- Rabha, D.; Muthukumar, P.; Somayaji, C. Energy and exergy analyses of the solar drying processes of ghost chilli pepper and ginger. Renew. Energy 2017, 105, 764–773. [Google Scholar] [CrossRef]
- Khanlari, A.; Tuncer, A.D.; Sözen, A.; Şirin, C.; Gungor, A. Energetic, environmental and economic analysis of drying municipal sewage sludge with a modified sustainable solar drying system. Sol. Energy 2020, 208, 787–799. [Google Scholar] [CrossRef]
- Kishk, S.S.; ElGamal, R.A.; ElMasry, G.M. Effectiveness of recyclable aluminum cans in fabricating an efficient solar collector for drying agricultural products. Renew. Energy 2019, 133, 307–316. [Google Scholar] [CrossRef]
- Téllez, M.C.; Figueroa, I.P.; Téllez, B.C.; Vidaña, E.C.L.; Ortiz, A.L. Solar drying of Stevia (Rebaudiana Bertoni) leaves using direct and indirect technologies. Sol. Energy 2018, 159, 898–907. [Google Scholar] [CrossRef]
- Simo-Tagne, M.; Etala, H.D.T.; Tagne, A.T.; Ndukwu, M.C.; El Marouani, M. Energy, environmental and economic analyses of an indirect cocoa bean solar dryer: A comparison between natural and forced convections. Renew. Energy 2022, 187, 1154–1172. [Google Scholar] [CrossRef]
- Sethi, C.K.; Acharya, S.K.; Ghanem, S.R.; Behera, A.; Patnaik, P.P. Exergy, energy and economic analysis of a V-groove assist rotating tray type solar cabinet dryer for drying potato chips. J. Stored Prod. Res. 2021, 93, 101861. [Google Scholar] [CrossRef]
- Mugi, V.R.; Chandramohan, V. Comparison of drying kinetics, thermal and performance parameters during drying guava slices in natural and forced convection indirect solar dryers. Sol. Energy 2022, 234, 319–329. [Google Scholar] [CrossRef]
- Gilago, M.C.; Chandramohan, V. Performance evaluation of natural and forced convection indirect type solar dryers during drying ivy gourd: An experimental study. Renew. Energy 2022, 182, 934–945. [Google Scholar] [CrossRef]
- Kabeel, A.E.; Hamed, M.H.; Omara, Z.M.; Kandeal, A.W. Solar air heaters: Design configurations, improvement methods and applications–A detailed review. Renew. Sustain. Energy Rev. 2017, 70, 1189–1206. [Google Scholar] [CrossRef]
- Kasaeian, A.; Babaei, S.; Jahanpanah, M.; Sarrafha, H.; Alsagri, A.S.; Ghaffarian, S.; Yan, W.-M. Solar humidification-dehumidification desalination systems: A critical review. Energy Convers. Manag. 2019, 201, 112129. [Google Scholar] [CrossRef]
- Đaković, D.; Kljajić, M.; Milivojević, N.; Doder, Đ.; Anđelković, A.S. Review of Energy-Related Machine Learning Applications in Drying Processes. Energies 2023, 17, 224. [Google Scholar] [CrossRef]






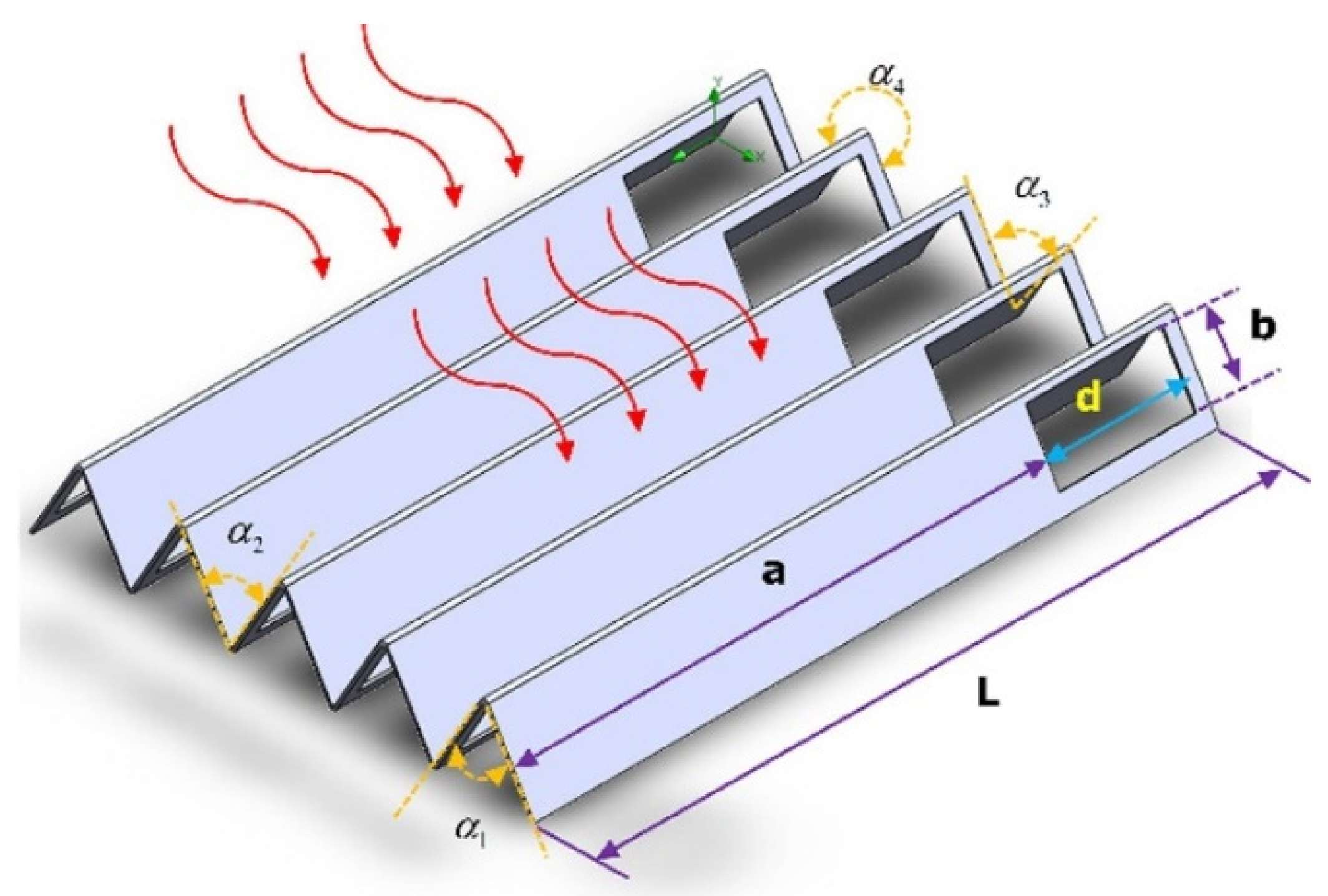
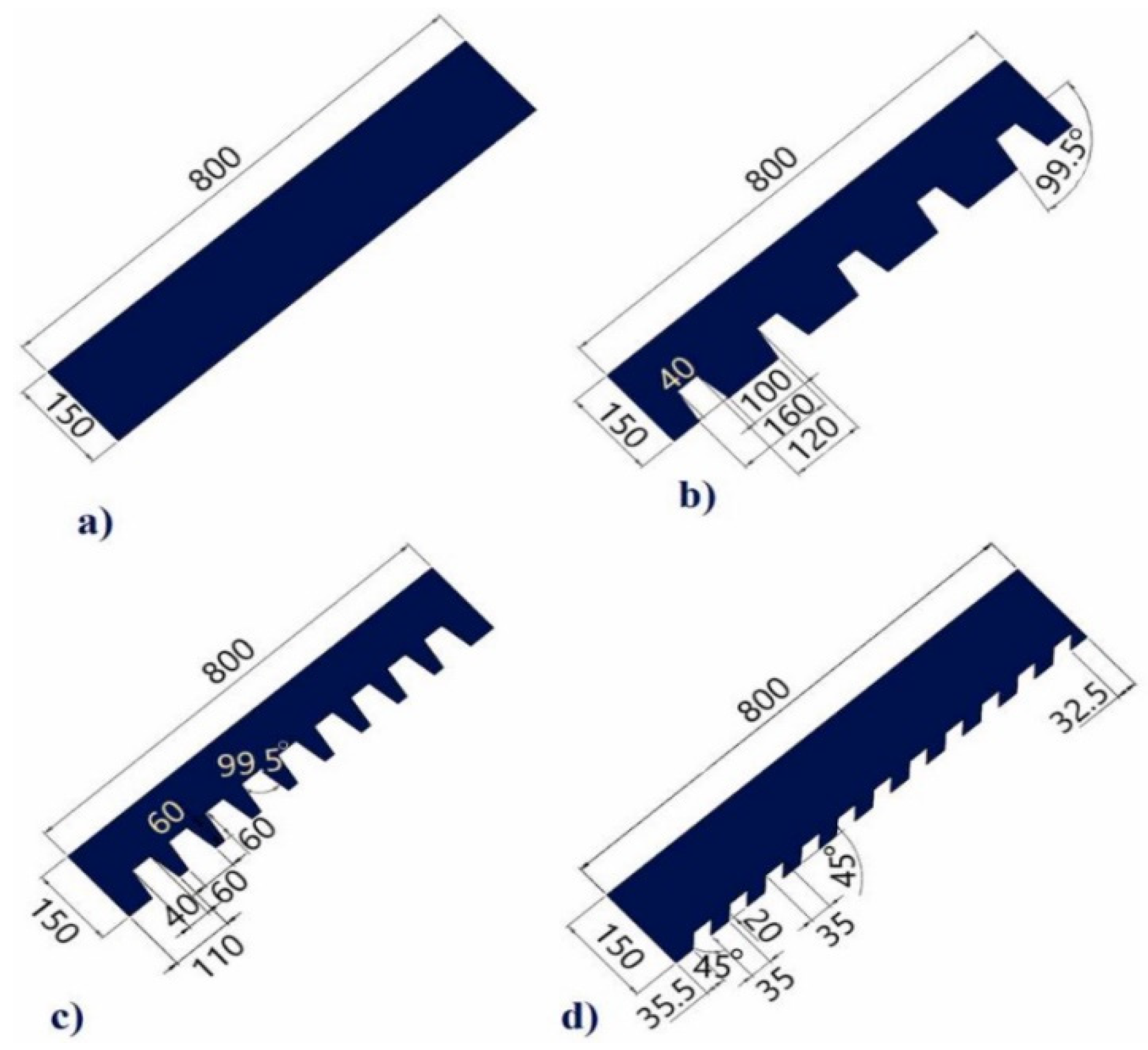




| Ref. | Ribs Design | THPP |
|---|---|---|
| [72] | V-rib | 1.46 |
| [73] | V-down ribs | 1.44 |
| [74] | Transverse wire ribs | 1.65 |
| [75] | Circular wire ribs | 1.66 |
| [76] | Transverse square rib | 1.89 |
| [77] | Transverse rectangular ribs | 1.44 |
| [78] | Discrete square rib | 1.98 |
| [79] | V-rib | 2.01 |
| Ref. | Baffle Shape | Operating Parameters Range | Remarks Compared to Flat Channel |
|---|---|---|---|
| [96] | Angled | Nuave = 3.16 and fave = 3.56 greater than the flat-plate | |
| [97] | Angled | Nuave = 3.45 and fave = 3.67 greater than the flat-plate | |
| [98] | V-shaped | Nuave = 4.05 and fave = 4.32 greater than the flat-plate | |
| [95] | Perforated | Nuave = 3.87 and fave = 4.12 greater than the flat-plate | |
| [99] | Transverse perforated | Nuave = 3.98 and fave = 4.2 greater than the flat-plate | |
| [100] | Transverse | Nuave = 3.45 and fave = 3.67 greater than the flat-plate | |
| [48] | Delta | Nuave = 3.67 and fave = 3.89 greater than the flat-plate | |
| [93] | V-Shape perforated | Nuave = 4.78 and fave = 5.12 greater than the flat-plate | |
| [101] | V-perforated-shaped block | Nuave = 4.98 and fave = 5.09 greater than the flat-plate | |
| [102] | Multi-V-shaped | Nuave = 6.28 and fave = 6.55 greater than the flat-plate | |
| [103] | V-Shaped | Nuave = 4.11 and fave = 4.39 greater than the flat-plate | |
| [104] | V-down perforated | Nuave = 4.62 and fave = 4.84 greater than the flat-plate | |
| [105] | Diamond-shaped | Nuave = 3.45 and fave = 3.59 greater than the flat-plate |
| Ref. | Method | Absorber | Operating Parameters | Thermal Efficiency | Exergy Efficiency | Outlet Air Temperature °C | Pressure Drop |
|---|---|---|---|---|---|---|---|
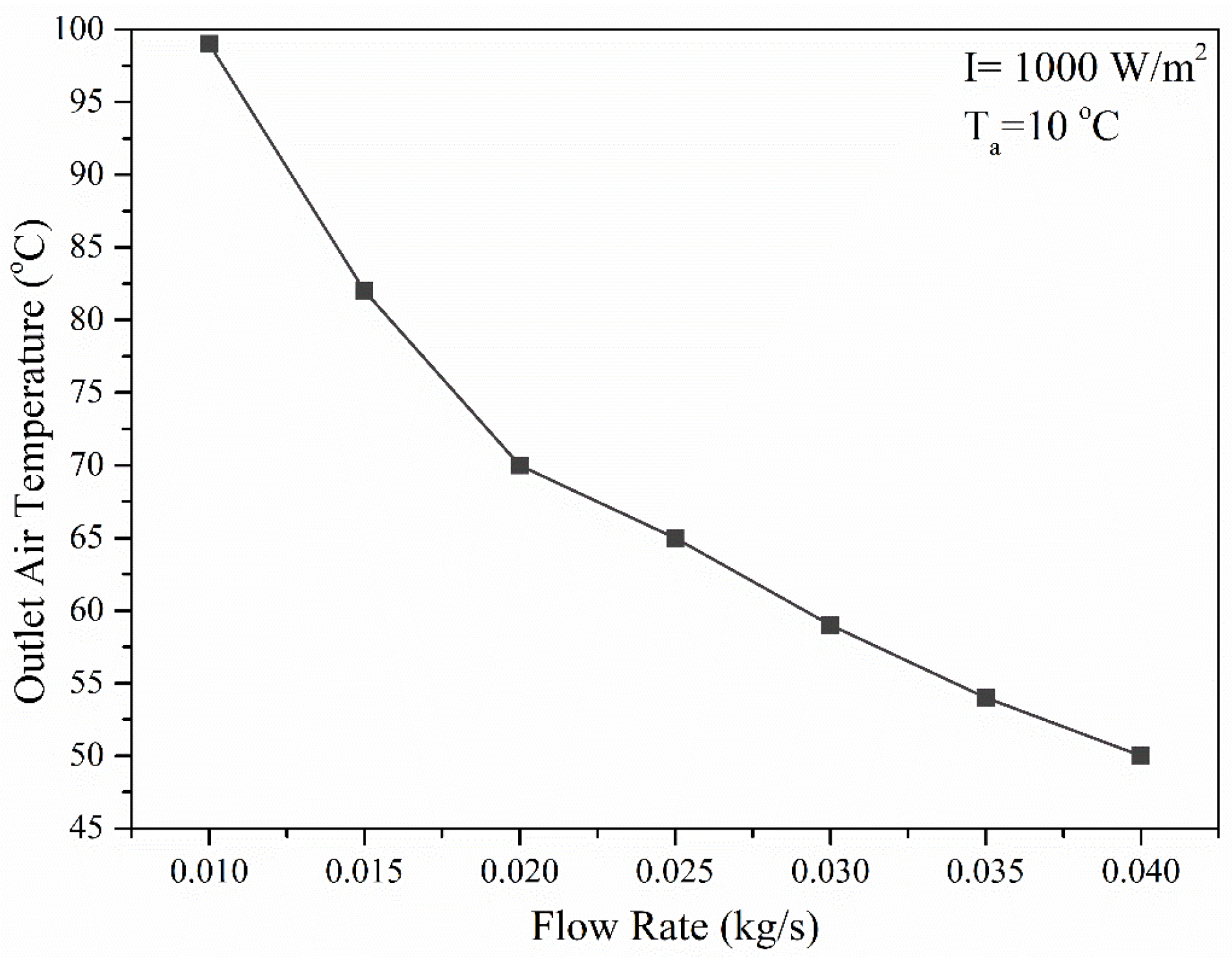
| [24] | Numerical | Aluminum | 0.010–0.050 kg/s | 55% at I = 1000 W/m2K Tin = 10 °C and 0.050 kg/s | Tout = 99 at I = 1000 W/m2 Tin = 10 °C and 0.010 kg/s | ||
| [25] | Experimental | Tubular aluminum | 0.025–0.075 kg/s | 86% at 0.075 kg/s | 2.57% at 0.025 kg/s | = 28 °C at 0.025 kg/s | 295 Pa at 0.075 kg/s, |
| [27] | Experimental | 16 steel wire mesh painted black | 0.011–0.032 kg/s | 65.8% at 3 cm height and 0.032 kg/s | = 45.3 K at 0.011 kg/s | 66 Pa at 3 cm height, and 0.032 kg/s | |
| [34] | Experimental | Triangular-shaped | 0.026–0.095 kg/s | 80% at 0.06 kg/s | 70 at 0.026 | 104 Pa at 0.095 kg/s | |
| [41] | Experimental | stainless steel with black chrome (obstacles) and black-painted cooper plate | 0.0052 and 0.0074 kg/s | 82% at 0.0074 kg/s for leaf-shaped obstacles | 0.44% at 0.0074 kg/s | = 55.2 °C at 0.0052 kg/s for leaf-shaped baffles | |
| [44] | Numerical | Conical ribs | Re = 4000–16,000 | 69.8% at e/D = 0.044 and p/e = 10 | |||
| [30] | Numerical | Longitudinal fins | 0.02–0.12 kg/s | 73% at N = 20 and H = 10 cm and 0.12 kg/s | 70 at 0.02 kg/s, N = 20, and H = 10 cm | ||
| [64] | Experimental | Winglets ribs | 0.004–0.039 kg/s | 69% | |||
| [65] | Experimental | Twisted ribs | 0.001–0.013 m2K/W | , and y/e = 3 | , and y/e = 3 | ||
| [69] | Numerical | Arc-shaped ribs | 0.01–0.08 kg/s | 5.2% at 0.012 kg/s | = 60 °C at 0.01 kg/s | ||
| [89] | Numerical | Perforated baffle | 0.03–0.07 kg/s | 77% at 3 mm diameter, 7° angle, and 0.07 kg/s flow rate. | 48 °C | 15.05 N/m2 | |
| [90] | Experimental | Aluminum wave-shaped baffles | 10–50 m3/h | 73.8% at I = 756 W/m2 | = 69 °C | ||
| [91] | Numerical and Experimental | Copper plate with plus-shaped baffles | 0.009 to 0.011 kg/s | 84.30% | = 25 °C | ||
| [124] | Numerical | V-corrugated with twisted tapes | Re = 3000–21,000 | 74.42% at Re = 12,000; Y = 1 | 10% at Re = 3000 | 85 at Y = 1, N = 14, and Re = 3000 | 750 Pa at Y = 1, N = 14 and Re = 20,000 |
| [125] | Experimental | Perforated V-corrugated | 71.85% maximum daily average | 0.975% maximum daily average | |||
| [165] | Numerical and experimental | Rectangular fins | 0.033 kg/s | 51% at 0.033 kg/s | 75 °C at 0.033 kg/s | ||
| [166] | Experimental | Copper wool | 0.034–0.044 kg/s | 83% at 0.044 kg/s | 60 °C at 0.035 kg/s | 26 Pa at 0.044 kg/s | |
| [167] | Experimental | Copper tube with fins | 0.018 and 0.026 kg/s | 59.02% at 0.026 kg/s | 37.53% at 0.026 kg/s | 82.43 °C at 0.026 kg/s | |
| [168] | Experimental | Galvanized iron sheet coated with longitudinal fins | 0.012–0.016 kg/s | 51.50% at 0.016 kg/s and number of fins = 5 | 68.10 °C at 0.016 kg/s and number of fins = 5 | ||
| [169] | Numerical and Experimental | V-corrugated with triple pass | 0.011–0.015 kg/s | 76.39 at 0.015 kg/s | 18.95% 0.015 kg/s | at 0.011 kg/s | |
| [170] | Experimental | Aluminum cans arranged in series and parallel connections | 3–6.5 m/s | 79% for series connection at 6.5 m/s | at 3 m/s for parallel SAC | ||
| [171] | Experimental | Trapezoidal | 0.02–0.044 kg/s | 74% at 0.044 kg/s | 65 °C at 0.033 kg/s | ||
| [33] | Numerical and Experimental | V-groove double-pass | 0.021–0.061 kg/s | 88.50% at 0.061 kg/s | 5.18 average exergy efficiency at 0.041 kg/s | 84.95 °C at 0.021 kg/s |
| Ref. | System | Results | Study |
|---|---|---|---|
| [175] | PVT-SAH | Maximum COP achieved was 19.8%. | Numerical |
| [176] | SAH with PCM | A total of 75.82% electrical energy was saved using solar energy with PCM compared to an electric heater for desiccant cooling applications. | Numerical |
| [177] | PV/T | Primary energy saved by 90% using the PV/T system in desiccant cooling systems. | Numerical (TRANSYS) |
| [178] | PV/T | COP achieved was 0.85 by integrating PV/T into the conventional desiccant cooling system. | TRANSYS |
| [179] | SAH | A total of 0.95 maximum COP was achieved for cooling purposes. | Experimental |
| [180] | SAH | A total of 50% efficiency was achieved during the full regeneration mode. | Numerical |
| Ref. | Product | Collector Type | Mass (kg) | Temperature (°C) | Time (hr.) | (%) | (%) | SEC kWh/kg | Moisture Variation |
|---|---|---|---|---|---|---|---|---|---|
| [128] | Banana | Corrugated single-pass | 4 | 41–73 | 10 | 64.40 | 55.30 | 3.566 to 0.2604 dry basis | |
| [33] | Pink lady Apple | V-groove double-pass | 1 | 40–85.4 | 7 | 88.5 | 3.01 kWh/kg | 82–15.85% wet basis | |
| [181] | Bitter gourd | Single-pass | 6 | 42.27 | 7.8% final M.C | ||||
| [182] | Bitter gourd | corrugated with sensible storage | 4 | 40–51 | 7 | 22.2 | 19.4 | 4.44 kWh/kg | 925 to 9% wet basis |
| [183] | Red chili | Double-pass with fins | 40 | 32–67 | 33 | 28 | 13 | 5.26 kWh/kg | 80% to 10% wet basis |
| [184] | Banana | Flat-plate | 1.5 | 33.5–45.5 | 16 | 38.3 | 5.8 | Final 3.1% wet basis | |
| [185] | Green chili | Single-pass trapezoidal | 0.8 | 32–72 | 18 | 53.84 | 8.9 | 1.532 kWh/kg | 0.714 kg water removed |
| [186] | Ghost chili pepper | 9 | 37–57 | 42 | 22.95 | 4.05 | 18.72 kWh/kg | 85.50 to 9.7% wet basis | |
| [187] | Sewage Sludge | 45 | 2.25–2.75 | 60 | 14 kWh/kg | ||||
| [188] | Tomato | Aluminum cans absorber | 50 | 30 h | 70 | 19 to less than 1 d.b | |||
| [189] | Stevia leaves | Flat-plate | 58 | 5.83 | 83.40–8.71% | ||||
| [190] | Cocoa bean | Single-pass Flat-plate | 8.934 | 50 | 32 | Above 30% | 9–14 | 15 kWh/kg | 0.08 kg/kg db |
| [191] | Potato chips | V-groove | 1.04 | 60 | 5 h. 40 min | 1.567 kWh/kg | 72 to 12% | ||
| [192] | Guava | Single-pass corrugated | 0.8 | 73 | 14 | 65.37 | 6.84 | 1.675 kWh/kg | 0.4574 kg/kg d.b |
| [193] | Ivy gourd | Single-pass corrugated | 0.8 | 66 | 16 | 94.5 | 17.45 | 5.96 kWh/kg | 15 to 0.036 kg/kg d.b |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hassan, A.; Nikbakht, A.M.; Fawzia, S.; Yarlagadda, P.; Karim, A. A Comprehensive Review of the Thermohydraulic Improvement Potentials in Solar Air Heaters through an Energy and Exergy Analysis. Energies 2024, 17, 1526. https://doi.org/10.3390/en17071526
Hassan A, Nikbakht AM, Fawzia S, Yarlagadda P, Karim A. A Comprehensive Review of the Thermohydraulic Improvement Potentials in Solar Air Heaters through an Energy and Exergy Analysis. Energies. 2024; 17(7):1526. https://doi.org/10.3390/en17071526
Chicago/Turabian StyleHassan, Ali, Ali M. Nikbakht, Sabrina Fawzia, Prasad Yarlagadda, and Azharul Karim. 2024. "A Comprehensive Review of the Thermohydraulic Improvement Potentials in Solar Air Heaters through an Energy and Exergy Analysis" Energies 17, no. 7: 1526. https://doi.org/10.3390/en17071526
APA StyleHassan, A., Nikbakht, A. M., Fawzia, S., Yarlagadda, P., & Karim, A. (2024). A Comprehensive Review of the Thermohydraulic Improvement Potentials in Solar Air Heaters through an Energy and Exergy Analysis. Energies, 17(7), 1526. https://doi.org/10.3390/en17071526