Research on Digital Twin Dynamic Modeling Method for Transmission Line Deicing System
Abstract
1. Introduction
2. Research on Modeling Methods for Digital Models of Deicing Oscillation
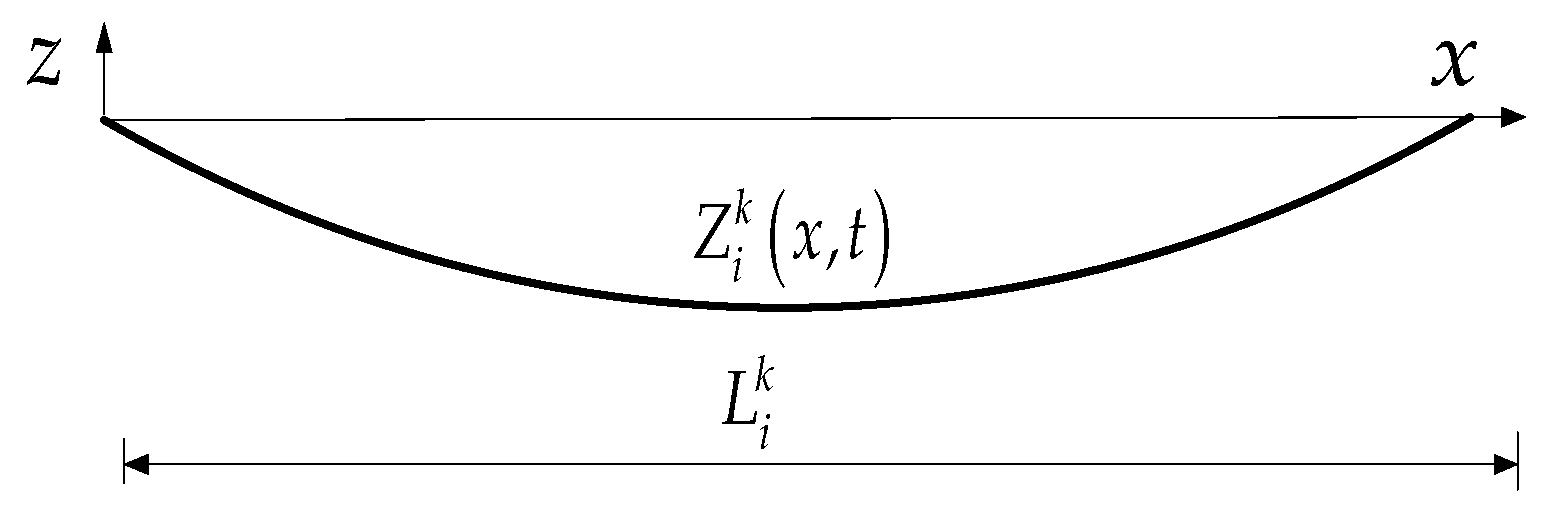
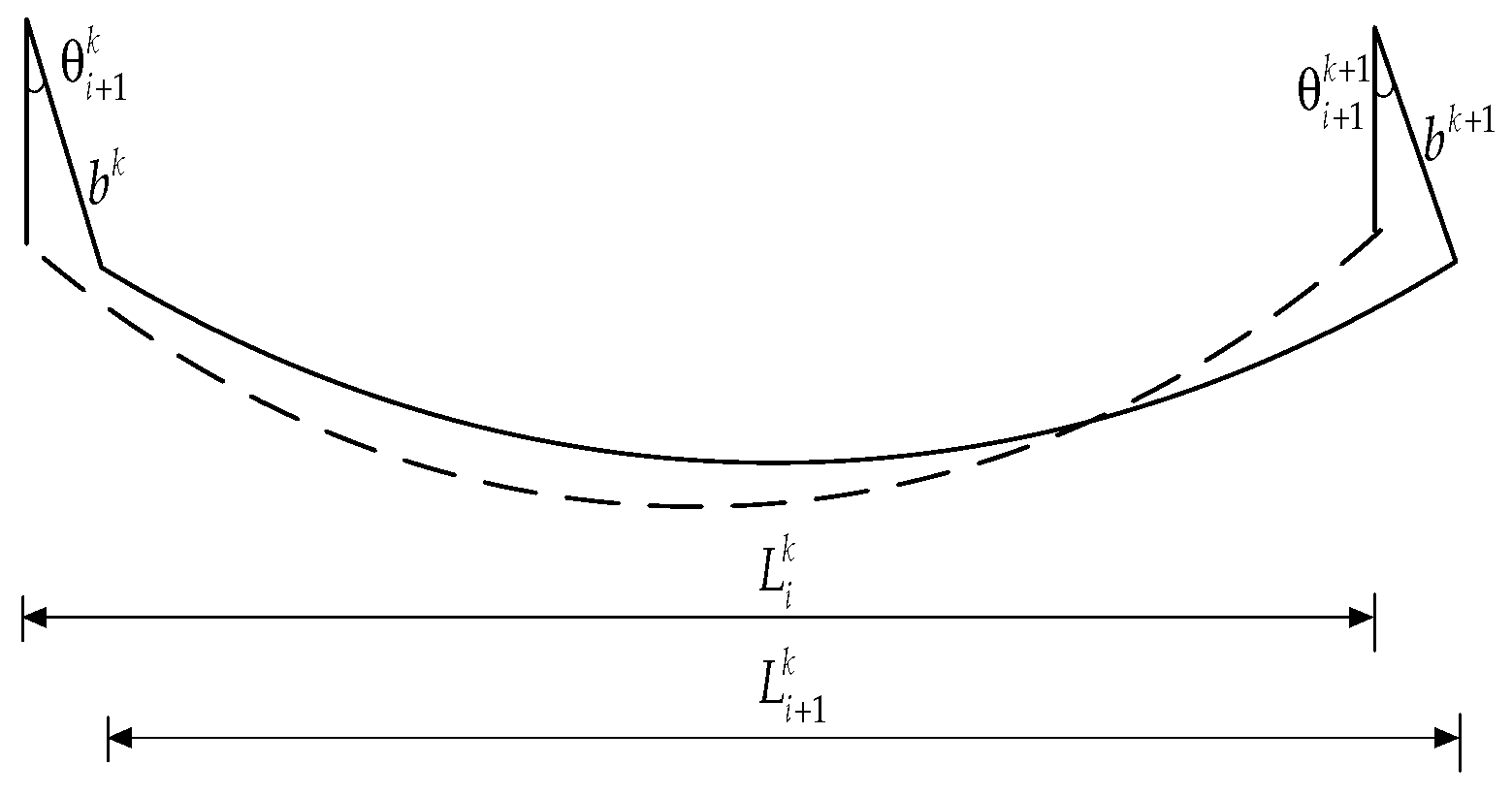
2.1. Theoretical Analysis of de Icing Oscillation
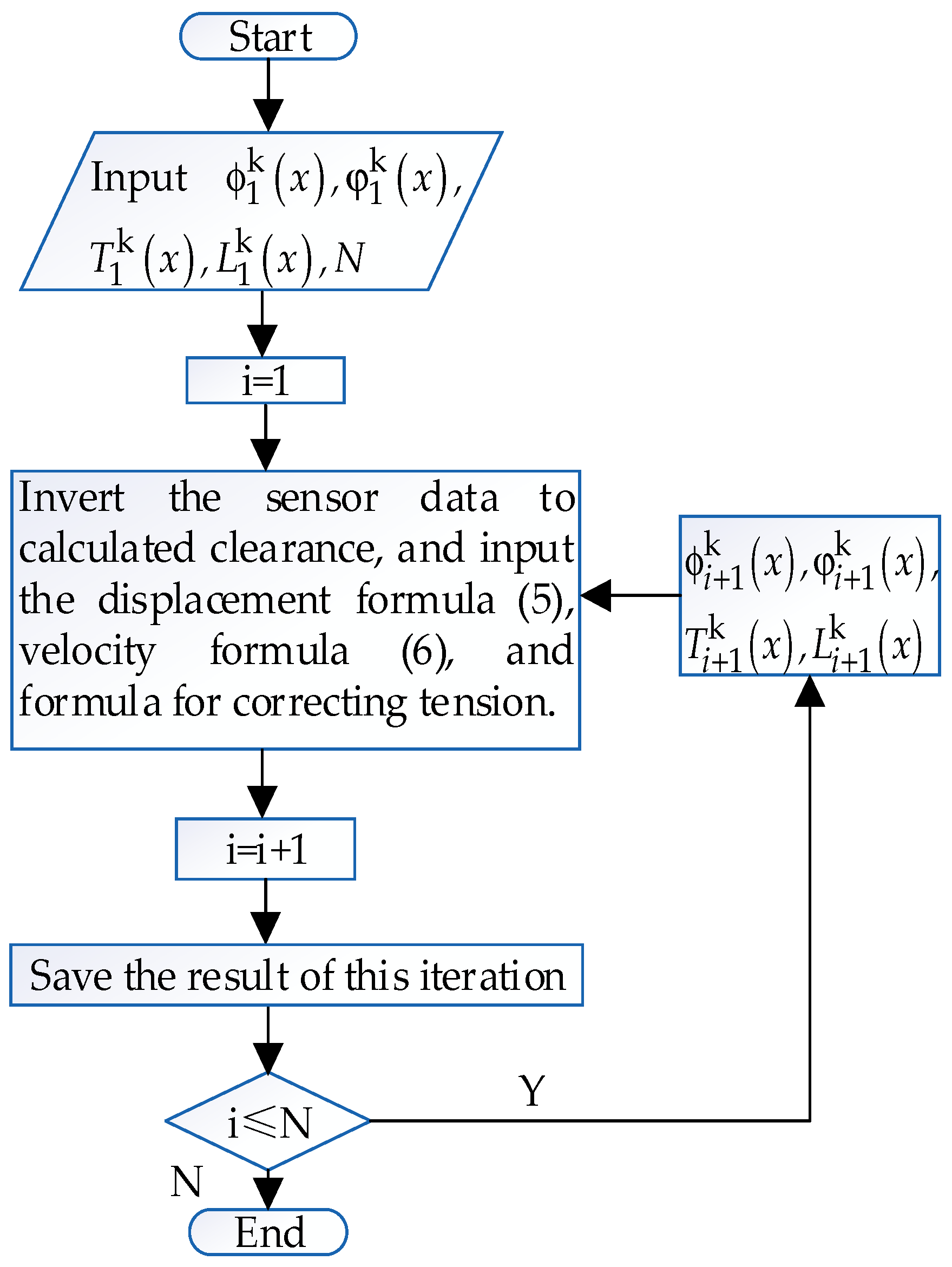
2.2. Analysis of the Modeling Process of Digital Models
- (1)
- Input Time-Varying Parameters:
- (2)
- Determine Initial Conditions for Iterative Model Updates
- (3)
- Storage
- (4)
- End
3. Research on Modeling Methods for Dynamic Geometric Models of Transmission Lines
3.1. Functional Analysis of Digital Twin Dynamic Geometric Models
- (1)
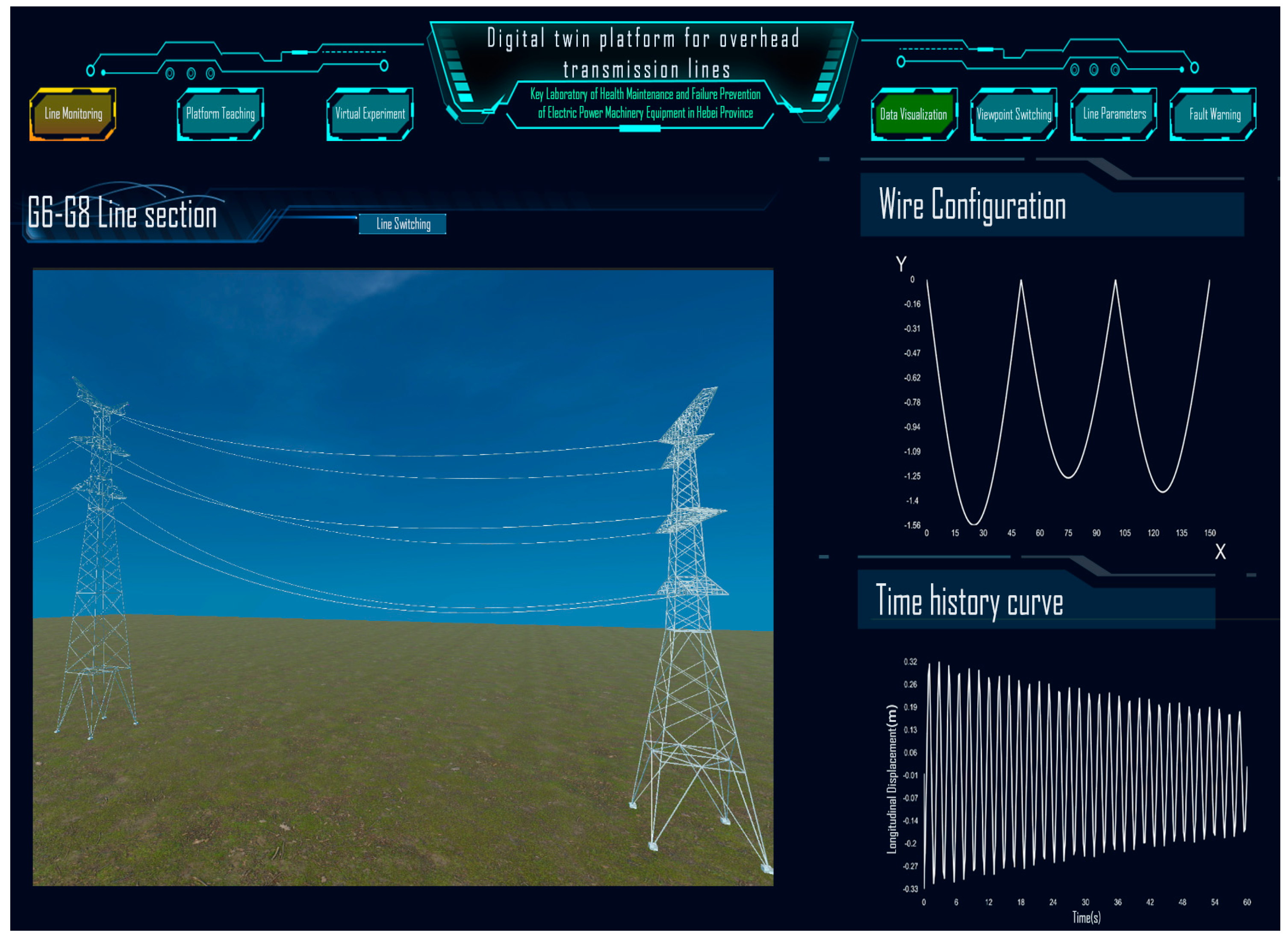
- Visualization of Line Status: Initially, a digital twin geometric model of the transmission line is created by replicating the physical spatial arrangement of the power transmission lines in a virtual space. Subsequently, a digital twin numerical model of the line is established, using twin data to govern the virtual line’s operation. This facilitates the real-time visualization of the actual line’s operational status, mapped onto the virtual representation within the twin platform. Enabling interactive communication between the physical and virtual lines ensures real-time synchronization of the operational status.
- (2)
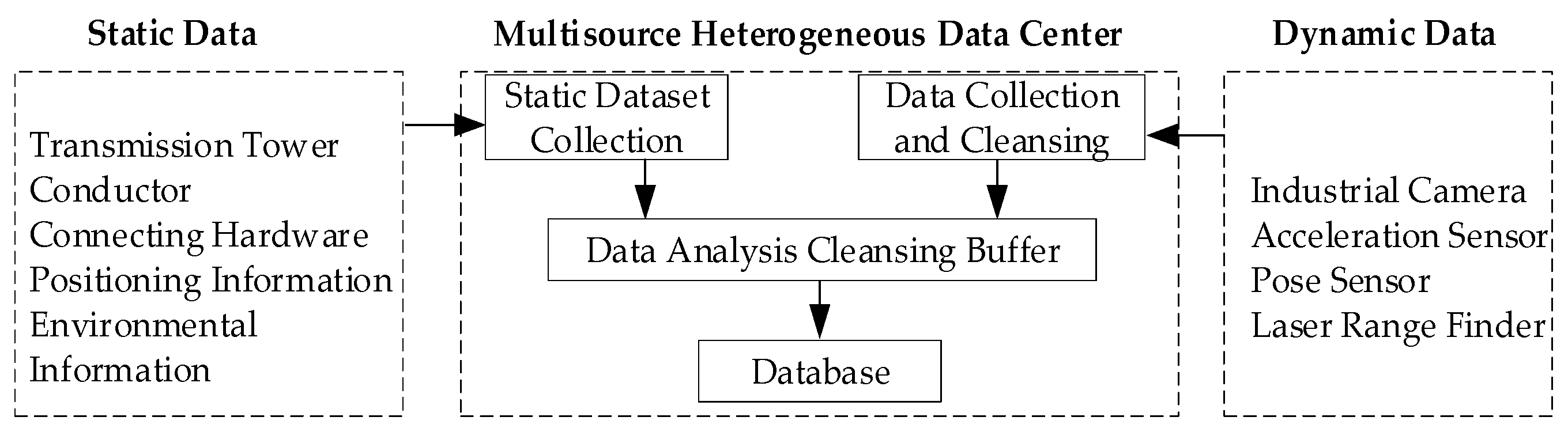
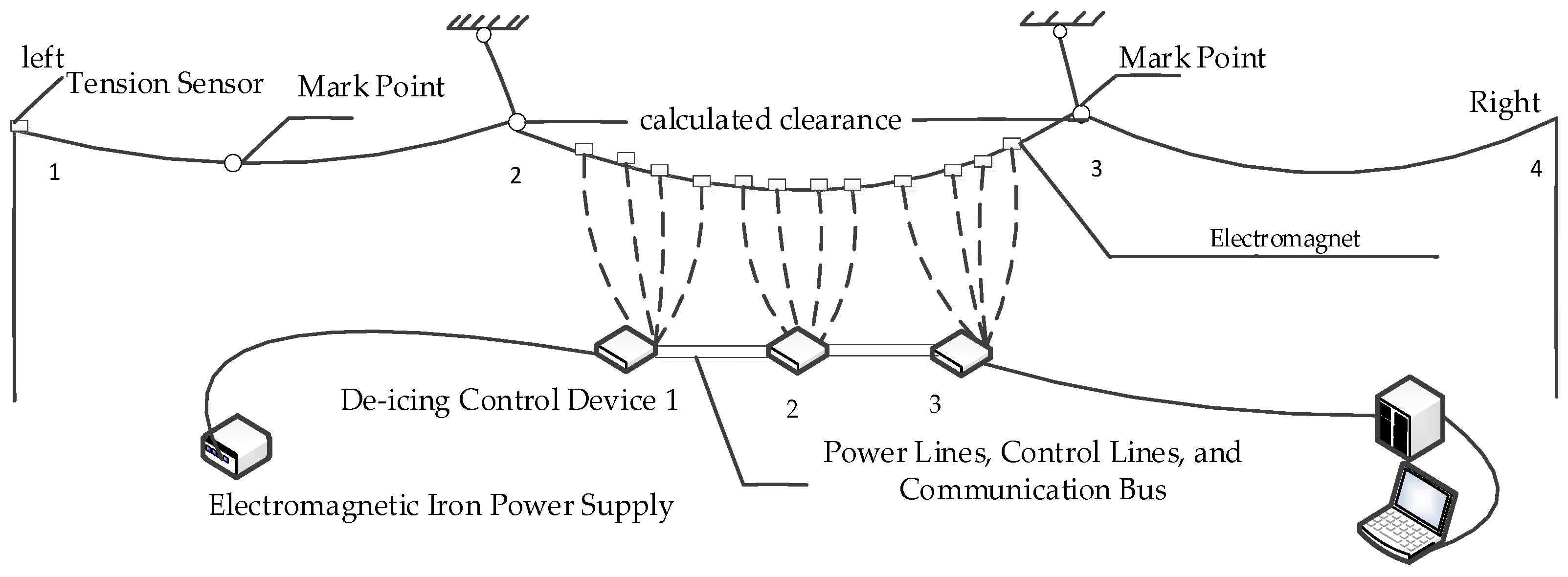
- Integration of Multi-Source Heterogeneous Data: The data sources utilized in visualization demonstrate both diversity and heterogeneity. Concerning diversity, this platform classifies data sources into static and dynamic categories. Static data include specific types, such as line towers, phases, ground wires, and insulator strings. Dynamic data, on the other hand, refer to real-time data, including noncontact machine vision recognition technology based on monocular or binocular methods and contact-based speed and acceleration sensors to obtain real-time dynamic data of the transmission line. In accordance with the requirements of digital twin visualization and actual line conditions, this platform introduces a digital twin visualization multi-source heterogeneous data collection architecture, as illustrated in Figure 4. The architecture divides the data in the digital twin visualization platform into two major components: static data collection and dynamic data collection. Both components involve multiple-source heterogeneous data processing centers for collection, processing, and storage, facilitating the integration of various data types and addressing the issue of visualization information isolation.
- (3)
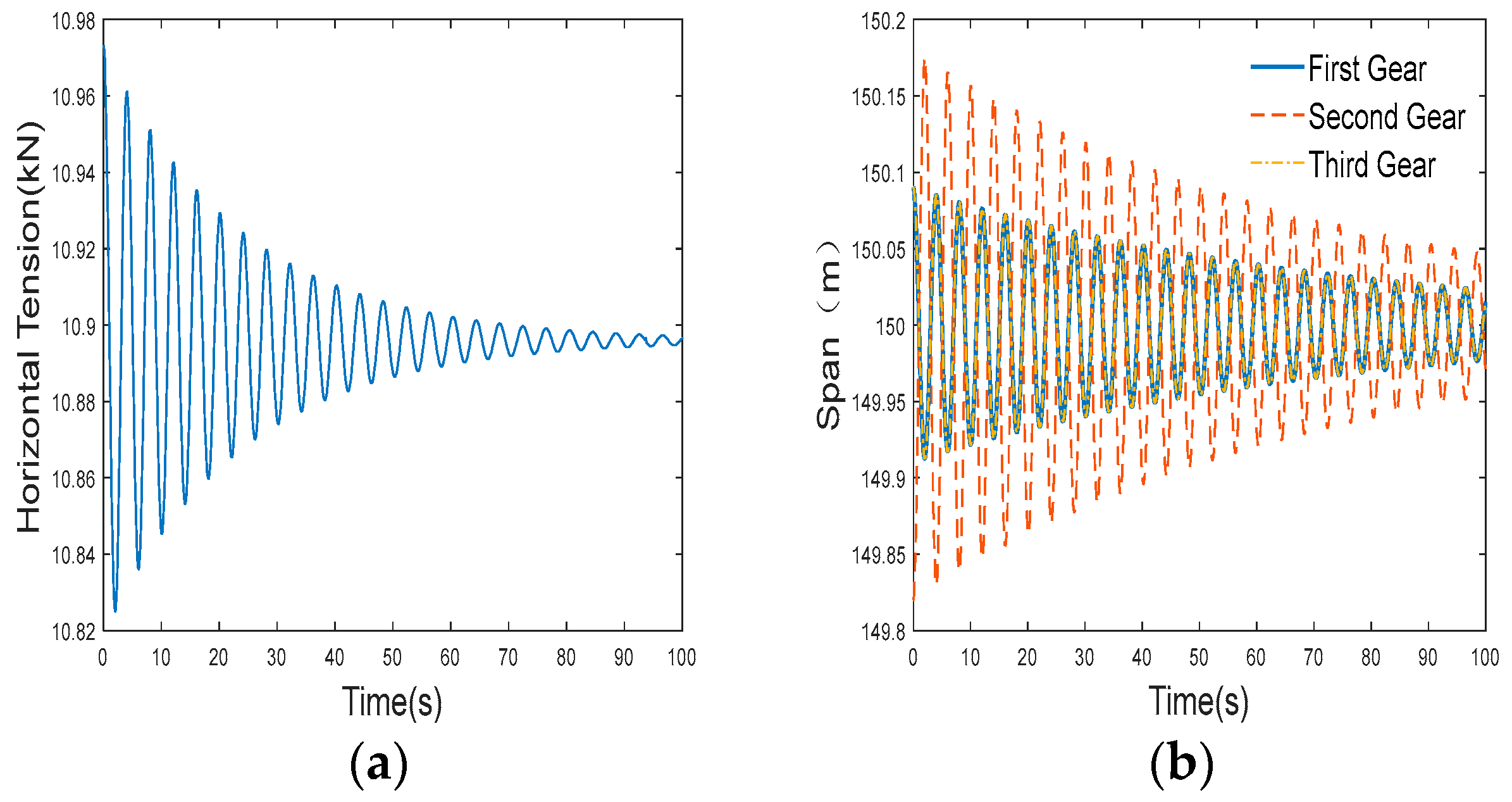
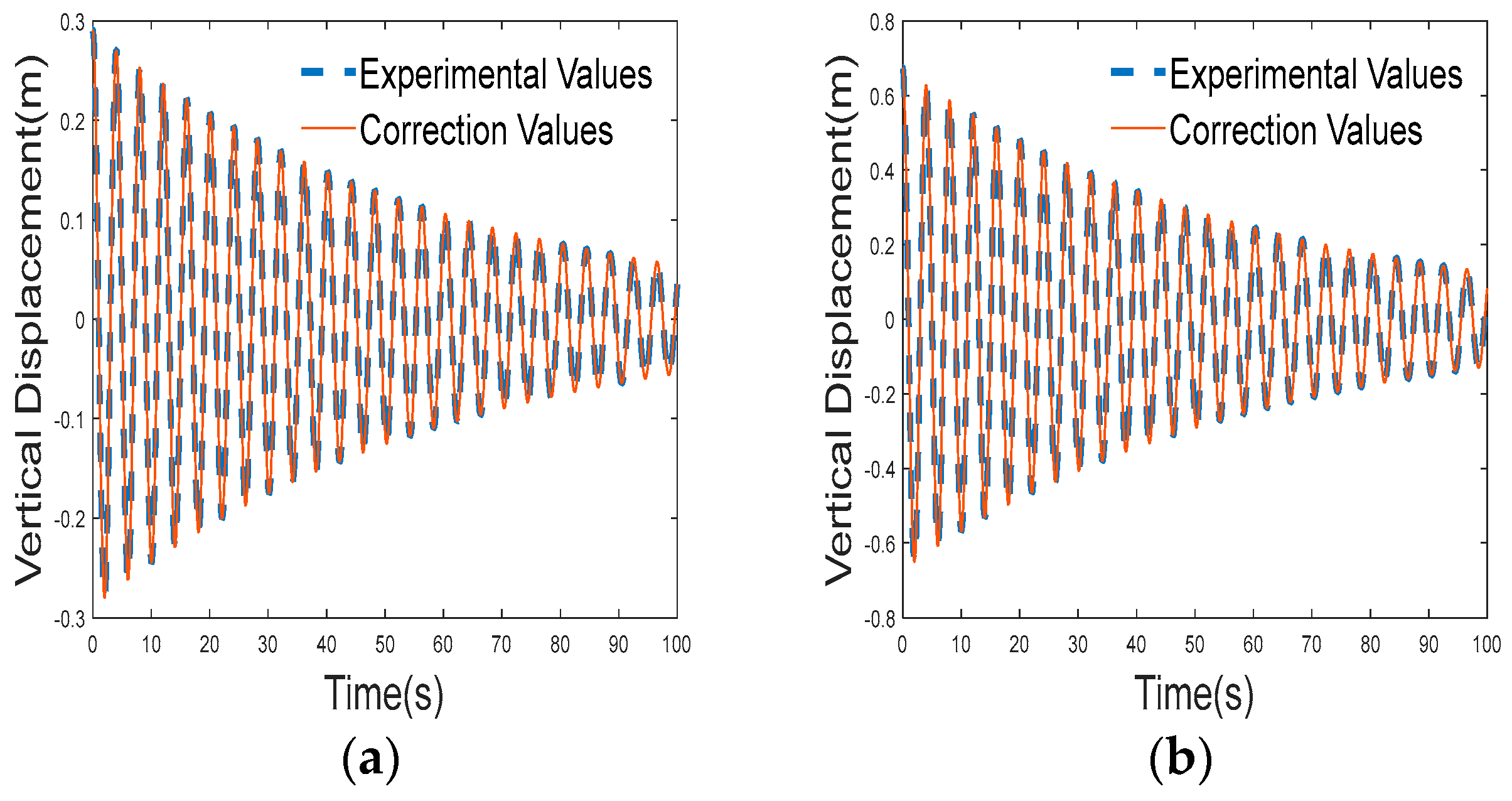
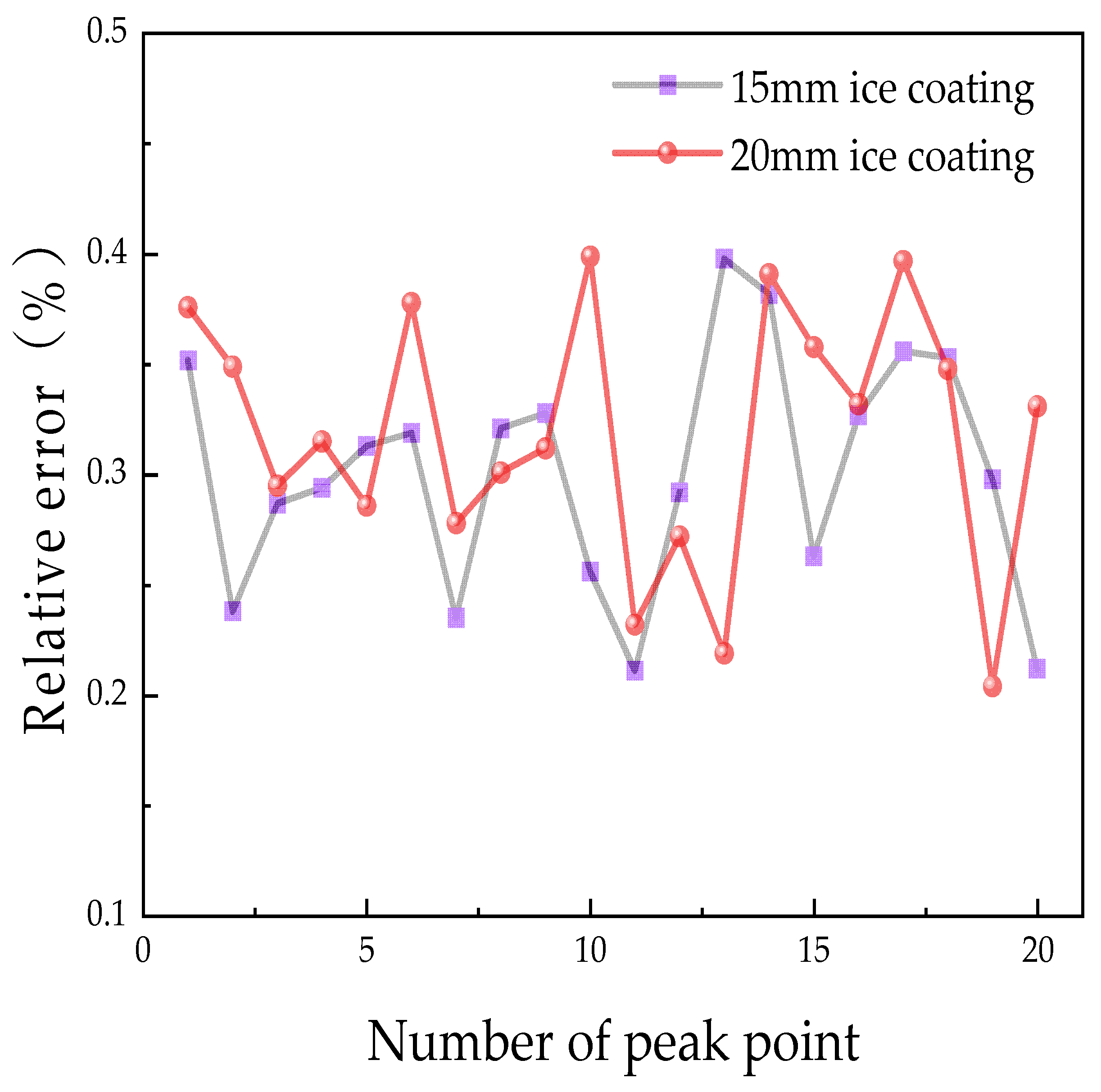
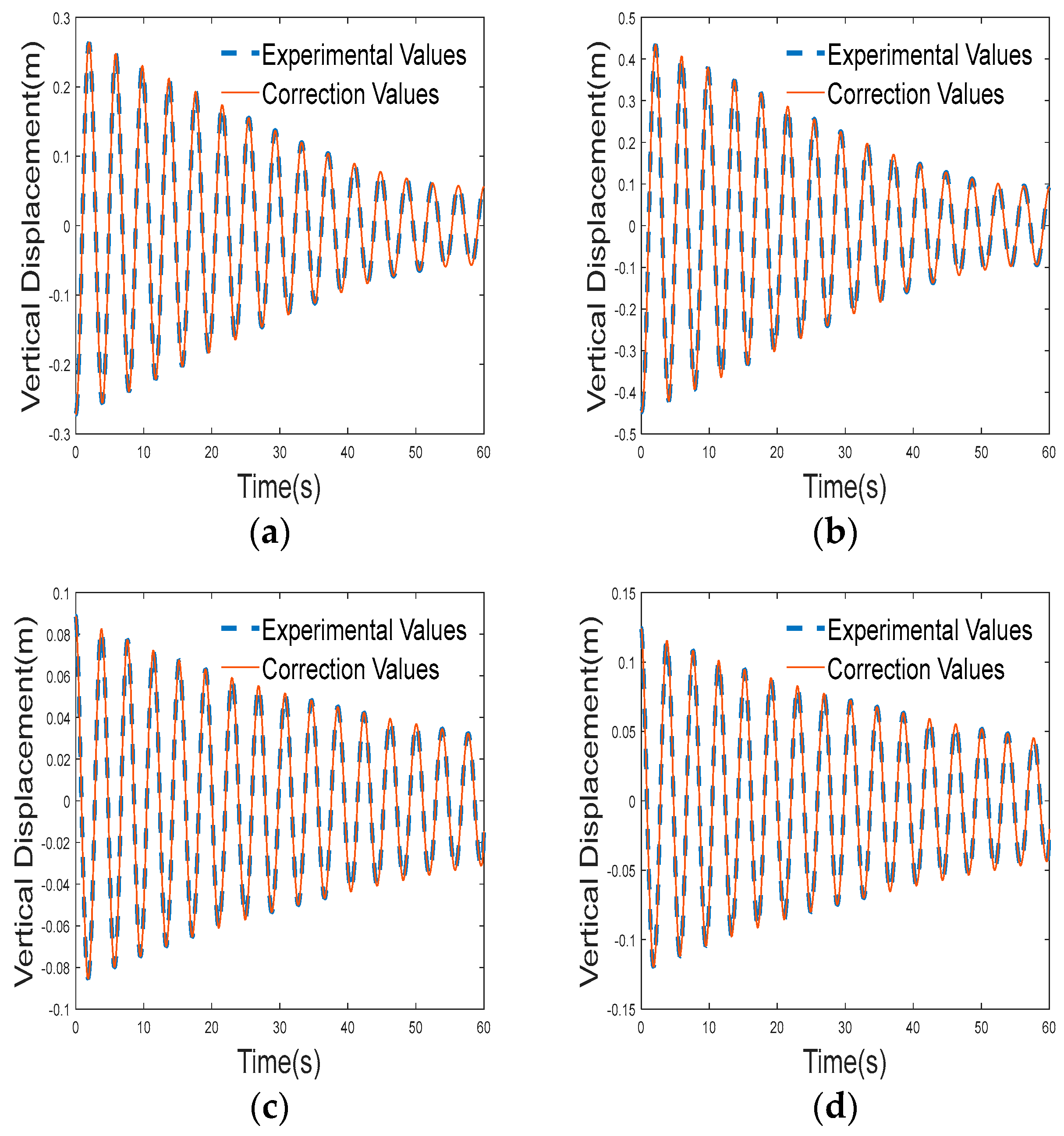
- Fusion Modeling of Analytical Solutions and Data: Owing to unpredictable time-varying factors like tension, calculated spacing, and ice shedding during conductor oscillation, the entire system demonstrates non-smooth dynamic characteristics with continuous displacement and discontinuous velocity and acceleration throughout the oscillation process. Sensors connected to the computer via a USB serial port transmit data to a database. Subsequently, Unity scripts within the digital twin environment access database information, establishing communication between the sensors and the Unity3D platform. This enables real-time data transmission from sensors to scripts and real-time data requests from scripts to sensors. A segmented smoothing algorithm is utilized to manage the system through segmentation in the time series. This involves combining real-time data obtained from measurements with analytical solutions for ice-shedding oscillations. The integration of analytical solutions and data forms the basis for constructing a digital twin model that incorporates both analytical solutions and measured data.
- (4)
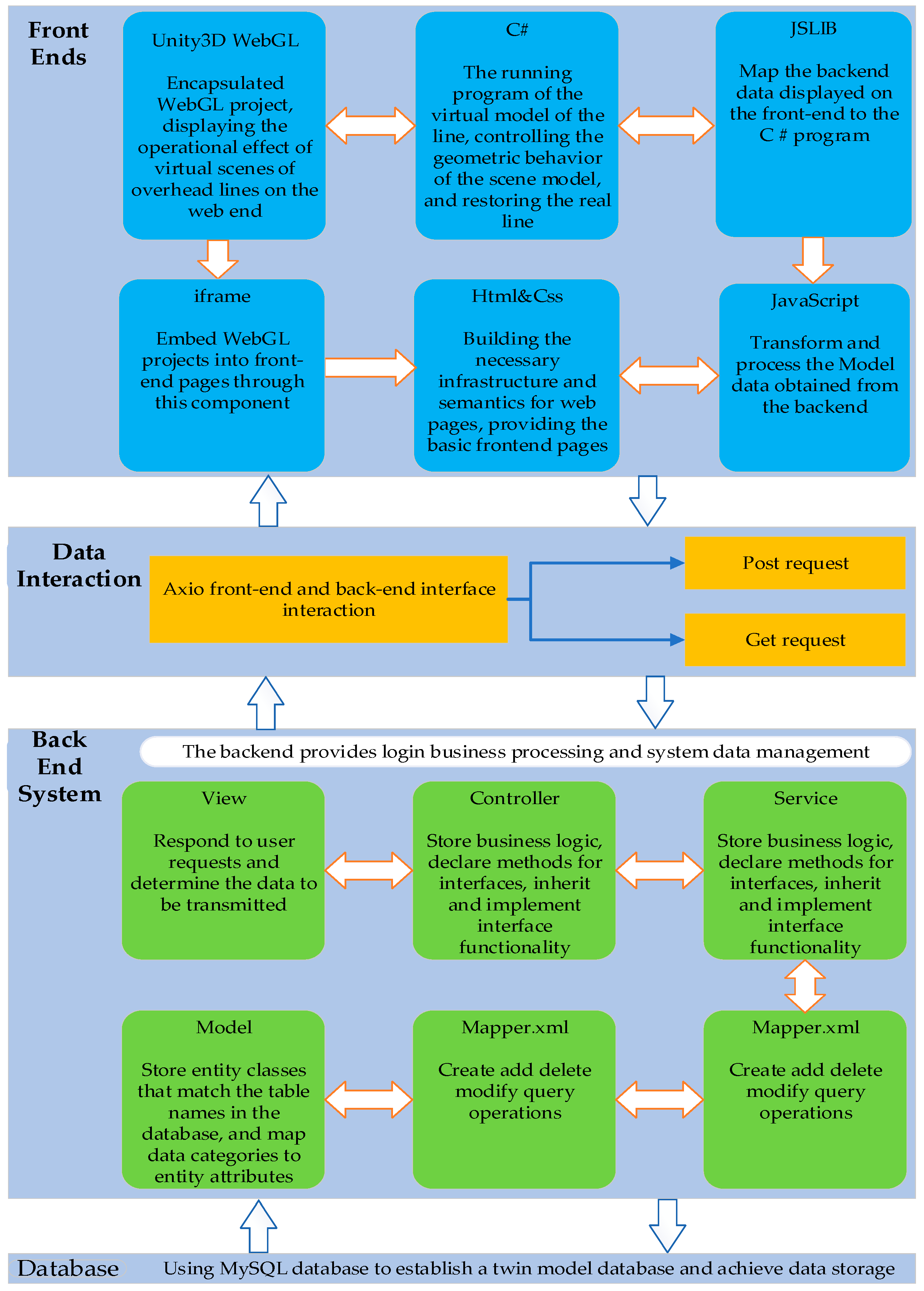
- Cross-Platform Device Access: Given that many digital twin visualization scenarios demand high-performance hardware and intricate software environments, this imposes considerable limitations on the presentation of digital twin visualizations. This paper suggests a web-based architecture for a digital twin-model information management system, employing a B/S (browser/server) model. The system can collect and process data through multiple interfaces and formats, enabling real-time transmission and operation of digital twin models and charts after unified processing. This design enables operators to access the system remotely using any mainstream browser via the HTTP protocol.
3.2. Analysis of Modeling Methods for Dynamic Geometric Models
- (1)
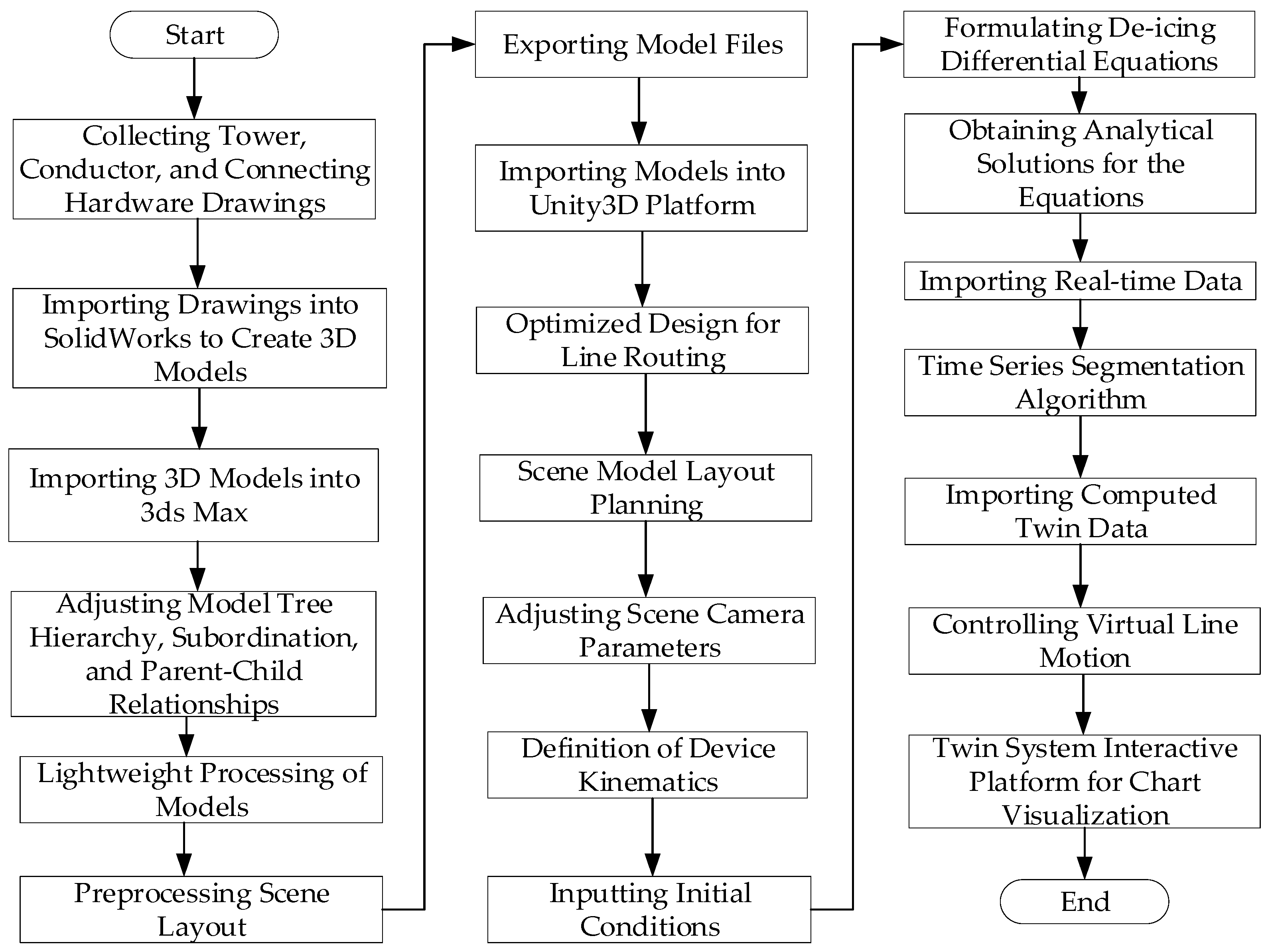
- Twin Three-Dimensional Geometric Model Construction: Examine the voltage level of the target power line and procure detailed drawings encompassing towers, conductors, ground wires, and connecting fittings. In the SolidWorks2016 software, initiate the creation of two-dimensional sketches for the line components. Utilize feature tools to meticulously refine the part sketches through operations such as stretching, rotating, filleting, and other relevant processes. Assemble and finalize the modeling, subsequently exporting the file in OBJ format. Following this, import the file into the 3Dmax platform for additional refinement. Within the material editor, carefully select suitable materials and apply them to each component of the power line by dragging and dropping. Proceed to configure rendering parameters, making meticulous adjustments to resolution, rendering quality, ray tracing, global illumination, shadows, depth of field, and other effects to heighten the realism of the equipment display. Last, impose constraints in accordance with the actual requirements of the power line.
- (2)
- Line Layout Planning: Import the processed model files into the Unity3D platform for the virtual engine, establishing a corresponding virtual scene for the transmission line and conducting layout planning. This process unfolds in three main steps:
- Step 1:
- Determine the coordinates of the towers in the virtual scene by analyzing micro-terrain features of the line section. Consider the impact of wind speed, ice thickness, and atmospheric conditions on the horizontal and vertical loads of conductors. Analyze the mechanical and physical characteristics of overhead lines, including elastic modulus, linear expansion coefficient, and tensile strength, influencing the positioning of the line. Calculate the safe distances of conductors to the ground and objects being crossed. Optimize under various conditions, adjusting positions and heights of towers in the crossing sections to achieve tower layout design for the virtual scene, providing positioning information for the towers.
- Step 2:
- Adjust the scene parameters of the virtual line to present the digital twin scene optimally. Modify scene camera parameters to capture the actions of the entire line scene effectively. Save multiple camera parameters, if necessary, for camera angle transitions, showcasing line positions and fitting details.
- Step 3:
- Add light sources, such as ambient light, directional light, and point light, to the virtual scene to enhance equipment visibility, improve material texture, and increase the realism of the digital twin line. Finally, save the created line to the model for later use on the digital twin interaction platform.
3.3. Analysis of Interaction Platform Design Methods
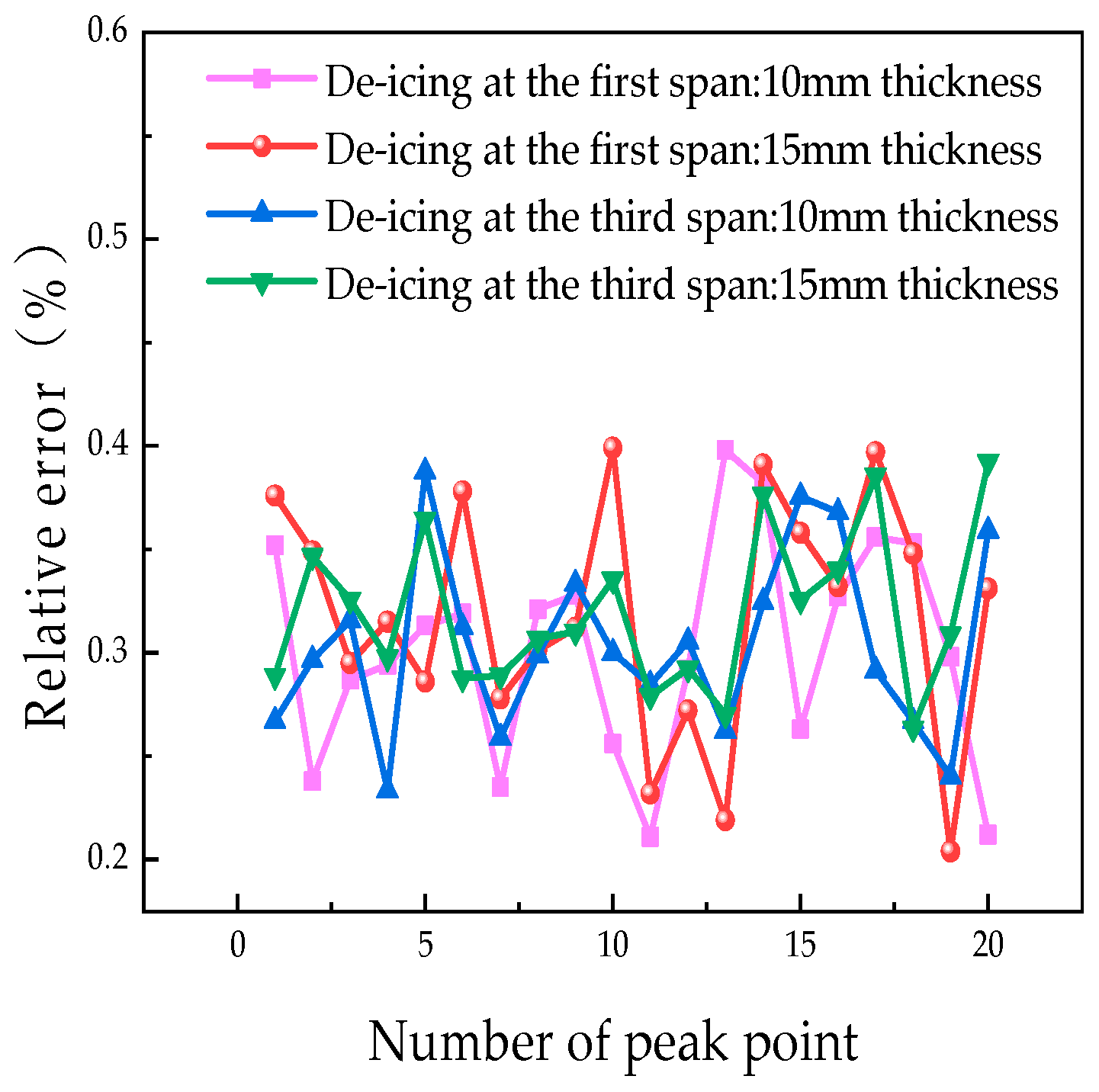
4. Comparisons and Discussion
5. Conclusions
5.1. Theoretical Contributions
5.2. Future Perspectives
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ru, L.; Yu, H.; Xiang, W.; Bo, Z.; Hao, C. Estimating the Impacts of a New Power System on Electricity Prices under dual Carbon Targets. J. Clean. Prod. 2024, 438, 140583. [Google Scholar] [CrossRef]
- Jing, H.; Feng, M.; Bi, R.; Zhou, T.; Ju, H.; Qiang, L. Minimum Inertial Demand Estimation of Renewable Energy Considering New Power System Frequency Constraints Using Sparrow Search Algorithm. Energy Rep. 2023, 9, 476–482. [Google Scholar] [CrossRef]
- Xiang, C.; Guang, T.; Yan, H.; Yang, Y.; Jia, L.; Yu, W.; Yuan, C. New Power System Development Path Mechanism Design. Glob. Energy Interconnect. 2023, 6, 166–174. [Google Scholar] [CrossRef]
- Jun, Z.; Chi, W.; Gong, W.; Du, J.; Yong, Y. Research on Investment-return Model of New power System Considering Financial Pressure. Energy Rep. 2023, 9, 540–546. [Google Scholar] [CrossRef]
- Viana, M.S.; Ramos, D.S.; Manas Junior, G.; Udaeta, M.E.M. Analysis of the Implementation of Virtual Power Plants and Their Impacts on Electrical Systems. Energies 2023, 16, 7682. [Google Scholar] [CrossRef]
- Chen, L.; Shi, X.; Peng, B.; Sun, J. Dynamic Simulation of Power Systems Considering Transmission Lines Icing and Insulators Flashover in Extreme Weather. IEEE Access 2022, 10, 39656–39664. [Google Scholar] [CrossRef]
- Liu, Y. Dynamic Interactive Characteristics Between Icicle Growth and Corona Discharge on HVDC Outdoor Insulator During Icing Accretion. High Volt. 2023, 8, 570–582. [Google Scholar] [CrossRef]
- Weng, B. Newly designed identifying method for ice thickness on high-voltage transmission lines via machine vision. High Volt. 2021, 6, 904–922. [Google Scholar] [CrossRef]
- Shu, L.; Liu, Y.; Jiang, X.; Hu, Q.; He, G.; Yu, Z.; Xiao, L. Three-dimensional electric field simulation and flashover path analysis of ice-covered suspension insulators. High Volt. 2020, 5, 327–333. [Google Scholar] [CrossRef]
- Huang, Y.; Jiang, X.; Virk, M.S. Ice Accretion Study of FXBW4-220 Transmission Line Composite Insulators and Anti-icing Geometry Optimization. Electr. Power Syst. Res. 2021, 194, 107089. [Google Scholar] [CrossRef]
- Hu, Q.; Li, T.; Shu, L. Dynamic Characteristics of the Corona Discharge during the Energised Icing Process of Conductors. IET Gener. Transm. Distrib. 2013, 7, 366–373. [Google Scholar] [CrossRef]
- Dong, B.; Jiang, X.; Yin, F. Development and Prospect of Monitoring and Prevention Methods of Icing Disaster in China Power Grid. IET Gener. Transm. Distrib. 2022, 16, 4480–4493. [Google Scholar] [CrossRef]
- Jamaleddine, A.; McClure, J. Simulation of Ice-shedding on Electrical Transmission Lines Using Adina. Comput. Struct. 1993, 47, 523–536. [Google Scholar] [CrossRef]
- Yan, B.; Chen, K.; Guo, Y. Numerical Simulation Study on Jump Height of Iced Transmission Lines after Ice Shedding. IEEE Trans. Power Deliv. 2013, 28, 216–225. [Google Scholar] [CrossRef]
- Huang, G. Experimental Study on Dynamic Response Characteristics of Isolated-span Transmission Lines after Ice-shedding. High Volt. 2023, 8, 196–208. [Google Scholar] [CrossRef]
- Chen, C.; Ming, L.; Li, M. Digital Twin Modeling and Operation Optimization of The Steam Turbine System of Thermal Power Plants. Energy 2024, 290, 129969. [Google Scholar] [CrossRef]
- Concetta, S.; Haya, A.; Dassisti, G. Guidelines for Designing a Digital Twin for Li-ion Battery: A Reference Methodology. Energy 2023, 284, 128699. [Google Scholar] [CrossRef]
- Shu, L.; Jian, T.; Zheng, J.; Yuan, D. Research on Multi-digital Twin and Its Application in Wind Power Forecasting. Energy 2024, 292, 130269. [Google Scholar] [CrossRef]
- Lei, Z.; Zhou, H.; Dai, X.; Hu, W.; Liu, G.-P. Digital Twin based Monitoring and Control for DC-DC Converters. Nat. Commun. 2023, 14, 5604. [Google Scholar] [CrossRef]
- Kobayashi, K.; Alam, S. Deep neural operator-driven real-time inference to enable digital twin solutions for nuclear energy systems. Sci. Rep. 2024, 14, 2101. [Google Scholar] [CrossRef]
- Fushimi, T.; Tagami, D.; Yamamoto, K.; Ochiai, Y. A digital twin approach for experimental acoustic hologram optimization. Commun. Eng. 2024, 3, 12. [Google Scholar] [CrossRef]
- Jiang, J.; Li, H.; Mao, Z.; Liu, F.; Zhang, J.; Jiang, Z.; Li, H. A Digital Twin Auxiliary Approach Based on adaptive sparse attention network for diesel engine fault diagnosis. Sci. Rep. 2022, 12, 675. [Google Scholar] [CrossRef]
- Isolan, L.; Malinconico, M.; Tieu, W.; Hollis, C.; Testa, M.; Melandri, M.; Brunetti, A.; Sumini, M. A Digital Twin for 64Cu Production with Cyclotron and Solid Target System. Sci. Rep. 2022, 12, 19379. [Google Scholar] [CrossRef]
- Wolf, K.; Dawson, R.; Mills, J.P.; Blythe, P.; Morley, J. Towards a Digital Twin for Supporting Multi-agency Incident Management in a Smart City. Sci. Rep. 2022, 12, 16221. [Google Scholar] [CrossRef]
- Jin, T.; Sun, Z.; Li, L.; Zhang, Q.; Zhu, M.; Zhang, Z.; Yuan, G.; Chen, T.; Tian, Y.; Hou, X.; et al. Triboelectric Nanogenerator Sensors for Soft Robotics Aiming at Digital Twin Applications. Nat. Commun. 2020, 11, 5381. [Google Scholar] [CrossRef]
- Min, W.; Wen, Y. Research on digital twin modeling and monitoring technology for smoke alarm calibration system. Sci. Rep. 2023, 13, 19239. [Google Scholar] [CrossRef]
- Huang, Y.; Tao, J.; Gang, S. A Novel Digital Twin Approach based on Deep Multimodal Information Fusion for Aero-engine Fault Diagnosis. Energy 2023, 270, 126894. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Q.; Liu, T.; Wang, Z.; Miao, R. Research on Digital Twin Dynamic Modeling Method for Transmission Line Deicing System. Energies 2024, 17, 1424. https://doi.org/10.3390/en17061424
Chen Q, Liu T, Wang Z, Miao R. Research on Digital Twin Dynamic Modeling Method for Transmission Line Deicing System. Energies. 2024; 17(6):1424. https://doi.org/10.3390/en17061424
Chicago/Turabian StyleChen, Qinghao, Tianyu Liu, Zhangqi Wang, and Rui Miao. 2024. "Research on Digital Twin Dynamic Modeling Method for Transmission Line Deicing System" Energies 17, no. 6: 1424. https://doi.org/10.3390/en17061424
APA StyleChen, Q., Liu, T., Wang, Z., & Miao, R. (2024). Research on Digital Twin Dynamic Modeling Method for Transmission Line Deicing System. Energies, 17(6), 1424. https://doi.org/10.3390/en17061424




