Topological Structure and Control Strategy of E-UPFC

Abstract

This article proposes a unified power flow controller with energy (E-UPFC) installed at the renewable energy grid connection node of the transmission network. Compared with other unified power flow controllers (UPFCs), the proposed E-UPFC can not only regulate the power flow on its connected transmission lines, but also suppress the power fluctuations of grid-connected nodes injected with large-scale renewable energy. At the same time, with the installation position of E-UPFC transferred from the transmission line to the node, the original stiff node can be transformed into a flexible node that can regulate the injected power flexibly. First, the PV grid-connected system with E-UPFC is introduced, and its principle of power flow regulation is detailed. In addition, the topology, mathematical modeling, and control strategies of E-UPFC are discussed. Finally, the E-UPFC is applied to the IEEE 3-generator 9-bus system with large-scale renewable energy integration in Matlab/Simulink in order to verify the correctness and feasibility of E-UPFC and its control strategies.

1. Introduction

In recent years, large-scale renewable energy, mainly composed of PV and wind power, has been continuously integrated into the transmission network. Due to the randomness and volatility of renewable energy, and the limited transmission capacity of power lines in the transmission network, the problems of insufficient absorption of renewable energy and the low power flow adjustability of lines have become increasingly serious, and have threatened the stable operation of the power system [1,2,3,4]. Therefore, flexible AC transmission systems (FACTS) have gradually become the focus of many scholars’ research in order to improve the operation capacity of the transmission network. And as an effective method of flexible regulation of power flow, it can significantly improve the transmission congestion and voltage regulation difficulties of the power grid so as to improve the reliability and operation flexibility of the transmission network [5,6].

Among various FACTS converters, there are static synchronous compensator (STATCOM), static synchronous series compensator (SSSC), UPFC, and other transformation devices [7,8]. The parallel FACTS devices can compensate reactive power, stabilize bus voltage, and improve system operation stability; for example, STATCOM can adjust its output reactive power through reactance, but it cannot effectively regulate the active power [9,10]. At the same time, the series FACTS devices can adjust line voltage, reduce line loss, and improve line transmission capacity; for example, SSSC can realize the functions of active power flow regulation, three-phase asymmetric compensation, harmonic suppression, etc. [11].

Therefore, series parallel hybrid FACTS devices such as UPFC were proposed in [6,12] in order to have the functions of parallel and series FACTS devices at the same time. The main function of the UPFC is to control the flow of real and reactive power by injecting a voltage in series with the transmission line. Both the magnitude and the phase angle of the voltage can vary independently. The UPFC combines a DC link capacitor with the series converter and the parallel converter. And the basic control for the UPFC is such that the series converter controls the transmission line’s real/reactive power flow and the shunt converter controls the bus voltage/parallel reactive power and the DC link capacitor [13]. The UPFC composed of a modular multilevel converter (MMC) was proposed in [14], which adopted a nonlinear strategy based on passive sliding mode variable structure control. A UPFC control strategy based on d-q axis theory was proposed in [15], which exhibited fast response performance in power flow control.

Due to the limited capacity of the DC link capacitor in UPFC, it is not possible to supply controllable active power for an extensive duration [16]. A new approach was proposed to enhance the regulation effect of the device in FACTS by integrating an energy storage system (ESS) in [17,18]. A UPFC with superconducting magnetic energy storage was proposed to regulate the power flow of the transmission line and improve the power transfer capability of the UPFC in [19]. And [20] proposed a static synchronous compensation device with ESS, which could effectively suppress the output fluctuations of renewable energy, expand the operation range of FACTS, and make the transmission more flexible, but it did not have the ability to regulate the power flow on the transmission line effectively. However, the above studies with ESS only achieved power flow regulation, and the utilization rate of ESS was not high.

At present, with the increasing proportion of renewable energy in the transmission network year by year, the power fluctuations caused by renewable energy injected into the grid cannot be ignored. And it has been proposed to connect the UPFC between the grid-connected renewable energy system and the main grid so as to realize the smooth integration of renewable energy into the grid in [21]. As the traditional UPFC is often installed in the transmission line of the distribution network, as shown in Figure 1, it is limited by the installation location and cannot regulate the injection power of renewable energy at the grid-connected node. In this paper, E-UPFC is installed at the renewable energy grid connection node of the transmission network, as shown in Figure 2. And the original stiff node is transformed into the flexible node through transformation, while the ESS is used to suppress the power fluctuations of renewable energy at the node and regulate the power flow on its connected transmission lines.

This article proposes an E-UPFC installed at the renewable energy grid connection node of the transmission network, which can suppress the power fluctuations of large-scale renewable energy and regulate the power flow on transmission lines flexibly. The rest of this article is organized as follows. In Section 2, the PV grid-connected system with E-UPFC is introduced, and the principles of power flow regulation are analyzed in detail. In Section 3, the topology and mathematical modeling of E-UPFC are presented. Then, the control strategy of E-UPFC is designed in Section 4. And the simulation results verify the correctness and feasibility of the proposed E-UPFC topology in Section 5. Finally, Section 6 concludes this article.

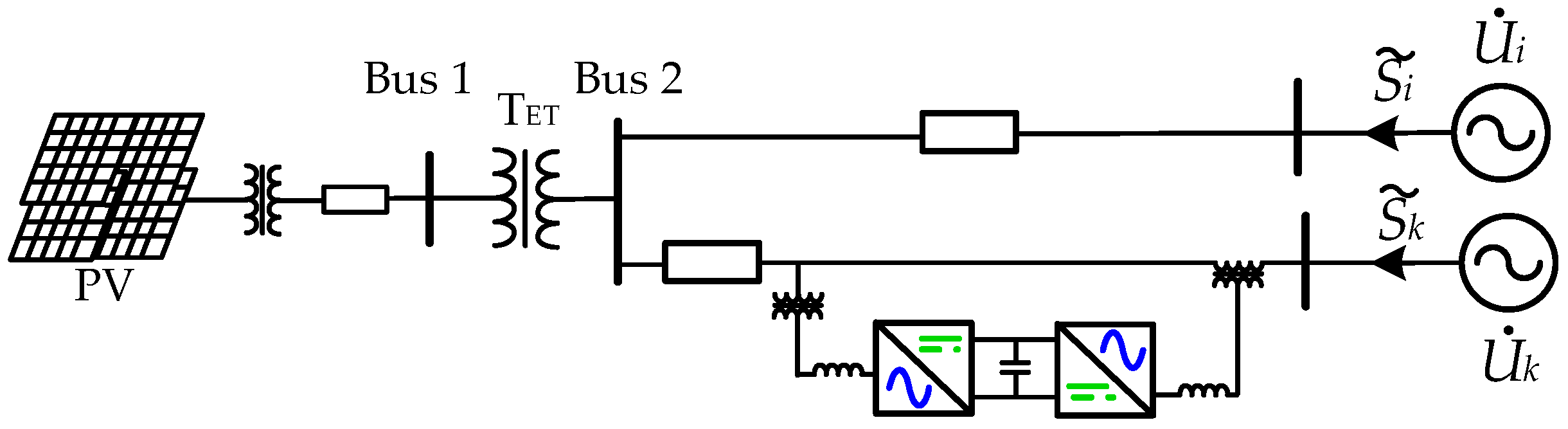
2. PV Grid-Connected System with E-UPFC

The schematic diagram of the PV grid-connected system with E-UPFC is shown in Figure 2. E-UPFC consists of double-winding power transformer T_ET, FE-MMC, and BE-MMC. FE-MMC is connected to the line in parallel through transformer T_ET1 and connected to Bus 1, which can suppress the power fluctuations of large-scale PV grid-connected system connected to Bus 1. And BE-MMC is connected to the transmission network through transformer T_ET2 in series and connected to bus 2, which can regulate the power flow on the transmission lines connected to bus 2. On this basis, FE-MMC and BE-MMC are connected back-to-back and share the same DC bus, and the ESS is connected in parallel with the DC side capacitor through the bidirectional DC-DC converter in order to provide an energy buffer for FE-MMC and BE-MMC.

When there is an excess of generated PV power after the photovoltaic output power meets the load demand of the grid, it is necessary to control the ESS to absorb the redundant power, and the power flows from the AC bus to the ESS through FE-MMC at this time. When the PV output power is not enough to meet the load demand of the grid, it is necessary to control the discharge of the ESS to compensate for the lack of power, and the power flows from the ESS to the AC bus through FE-MMC. Hence, the fluctuation components in the PV output power can be suppressed while the ESS is charged and discharged.

Specifically, with the large-scale renewable energy connected to the power grid, FE-MMC is equivalent to a controllable current source, which can effectively suppress the power fluctuations caused by intermittent and uncertain output of renewable energy. FE-MMC is equivalent to a controllable voltage source, which is equivalent to inserting an adjustable voltage in series in the line to actively support the voltage and regulate the power flow. At the same time, the ESS can control the DC side capacitor voltage stability through the power throughput, ensure the decoupling of the FE-MMC and BE-MMC, and enable them to exchange line power independently.

As the main part of the power suppression function, FE-MMC combines the basic idea of suppressing power fluctuations with the ESS to absorb and compensate for the fluctuation components of the renewable energy output through charge and discharge, which is expressed as:

$$P_{\mathrm{s}}=P_{\mathrm{w}}-P_{\mathrm{o}}$$

(1)

where P_w is the output power of the PV grid-connected system with fluctuation components, P_o is the reference value of the PV grid-connected power, and P_s is the power provided by the ESS to suppress power fluctuations.

FE-MMC is equivalent to a controllable voltage source, and the schematic diagram for realizing power flow regulation is shown in Figure 3. In Figure 3, U_M and U_N represent the voltages at sides M and N, respectively; I_M and I_N represent the currents of sides M and N, respectively; U_SC represents the equivalent series compensation voltage of BE-MMC; S_i is the equivalent load of the branch line I; and Z_j is the line impedance of the ring network j. If the influence of U_SC is not considered, the output power of side M can be calculated as follows:

$${\tilde{S}}_{\mathrm{M}}=\frac{{\displaystyle \sum _{i=1}^n({\tilde{S}}_i{\displaystyle \sum _{j=i+1}^{n+1}{Z}_j^{*}})}}{Z_{\Sigma }^{\ast }}+\frac{{\dot{U}}_{\mathrm{M}}({\dot{U}}_{\mathrm{M}}^{\ast }-{\dot{U}}_{\mathrm{N}}^{\ast })}{Z_{\Sigma }^{\ast }}$$

(2)

where Z_Σ is the total impedance of the loop network, Z_Σ = R_Σ + jX_Σ.

After using the controllable voltage U_SC generated by BE-MMC in series into the line at side M, the composite power output at side M can be expressed as:

$${\tilde{S}}_{\mathrm{M}}^{\prime }=\frac{{\displaystyle \sum _{i=1}^n({\tilde{S}}_i{\displaystyle \sum _{j=i+1}^{n+1}{Z}_j^{*}})}}{Z_{\Sigma }^{\ast }}+\frac{{\dot{U}}_{\mathrm{M}}({\dot{U}}_{\mathrm{M}}^{\ast }+{\dot{U}}_{\mathrm{SC}}^{\ast }-{\dot{U}}_{\mathrm{N}}^{\ast })}{Z_{\Sigma }^{\ast }}$$

(3)

It is assumed that the bus voltages at both sides are constant and the load is a constant power load. The series compensation voltage at side M can directly control the output power of this side, and its relationship can be expressed as:

$$\Delta {\tilde{S}}_{\mathrm{M}}={\tilde{S}}_{\mathrm{M}}^{\prime }-{\tilde{S}}_{\mathrm{M}}=\frac{{\dot{U}}_{\mathrm{M}}{\dot{U}}_{\mathrm{SC}}^{\ast }}{Z_{\Sigma }^{\ast }}$$

(4)

The relationship between the variation in active power ΔP_M at side M and the series compensation voltage U_SC (U_SC = U_SCx + jU_SCy) can be expressed as:

$$\Delta P_{\mathrm{M}}=\frac{U_{\mathrm{M}}}{R_{\Sigma }^2+X_{\Sigma }^2}(R_{\mathsf{\Sigma }}{U}_{\mathrm{SCx}}+X_{\mathsf{\Sigma }}{U}_{\mathrm{SCy}})$$

(5)

where ΔP_M is the adjustment amount of active power at side M. Moreover, the relationship between reactive power variation ΔQ_M and series compensation voltage U_SC can be expressed as:

$$\Delta Q_{\mathrm{M}}=\frac{U_{\mathrm{M}}}{R_{\mathsf{\Sigma }}^2+X_{\mathsf{\Sigma }}^2}(X_{\mathsf{\Sigma }}{U}_{\mathrm{SCx}}-R_{\mathsf{\Sigma }}{U}_{\mathrm{SCy}})$$

(6)

where ΔQ_M is the reactive power adjustment amount at side M, so BE-MMC changes the amount of power adjustment by c changing the compensation voltage connected in series in the transmission line so as to regulate the power flow.

3. Topology and Mathematical Modeling of E-UPFC

The power electronic converters in E-UPFC include FE-MMC, BE-MMC, and bidirectional DC/DC converters connected to the ESS. The FE-MMC is used to suppress fluctuations in renewable energy, BE-MMC is used to regulate power flow on transmission lines, and both FE-MMC and BE-MMC adopt MMC topology structures. Meanwhile, the bidirectional DC/DC converter for the ESS mainly provides power buffering for FE-MMC and BE-MMC, and it adopts a DC transformer (DCT) topology structure. Therefore, the topology design methods of FE-MMC, BE-MMC, and DCT for ESS are introduced in this section, which include the topology structure and the equivalent averaging model.

3.1. Topology and Equivalent Average Model of FE-MMC and BE-MMC

The MMC topology is adopted by both FE-MMC and BE-MMC, and a topology diagram of MMC and its half bridge (HB) submodule is shown in Figure 4. MMC has basic double ports of medium-voltage AC (MVAC) and medium-voltage DC (MVDC). In Figure 4, it is assumed that there are 2n submodules (SMs) in each phase, with an average of n SMs distributed in the upper or lower bridge. R_o and L_o are the resistance and inductance of each phase bridge arm, respectively, while L_ac is the filtering inductance. v_sj is the AC side voltage of phase j, v_pj and v_nj are the j phase voltages of the upper and lower bridge arms; U_dc is the MVDC side output voltage; i_pj and i_nj are the j phase voltages of the upper and lower bridge arms; i_vj is the j phase output current of the MVAC side; and i_cirj is the internal circulating current of each phase (j = a, b, c).

According to Kirchhoff’s Voltage Law (KVL), the equation for the upper and lower bridge arm circuits of each phase of MMC can be expressed as:

$$\left\{\begin{array}{l}{u}_{sj}+L_{ac}\frac{d{i}_{vj}}{dt}+u_{pj}+R_0{i}_{pj}=U_{\mathrm{dc}}/2\\ u_{sj}+L_{ac}\frac{d{i}_{vj}}{dt}-u_{\mathrm{n}j}-R_0{i}_{pj}=-U_{\mathrm{dc}}/2\end{array}\right.(j=\mathrm{a},\mathrm{b},\mathrm{c})$$

(7)

To further simplify the analysis, according to [22,23], the following three variables can be expressed as:

$$\left\{\begin{array}{l}{u}_{diffj}=\frac{1}{2}(u_{nj}-u_{pj})\\ u_{comj}=\frac{1}{2}(u_{pj}+u_{nj})\\ i_{cirj}=\frac{1}{2}(u_{pj}+u_{nj})\end{array}\right.(j=\mathrm{a},\mathrm{b},\mathrm{c})$$

(8)

where u_diffj represents the differential-mode voltage in phase j of MMC, and u_comj represents the common-mode voltage in phase j of MMC.

According to Equation (7), the AC side average model and DC side average model of MMC can be calculated as follows:

$$\left\{\begin{array}{l}(L_{ac}+L_o/2)\frac{d{i}_{vj}}{dt}+\frac{R_o}{2}{i}_{vj}=-u_{sj}+u_{diffj})\\ L_o\frac{d{i}_{cirj}}{dt}+R_o{i}_{cirj}=U_{dc}/2-u_{comj}\end{array}\right.$$

(9)

where L_ac is the equivalent line inductance and L_o is filter inductance.

The average models of equivalent circuits on both the AC and DC sides of MMC are shown in Figure 5.

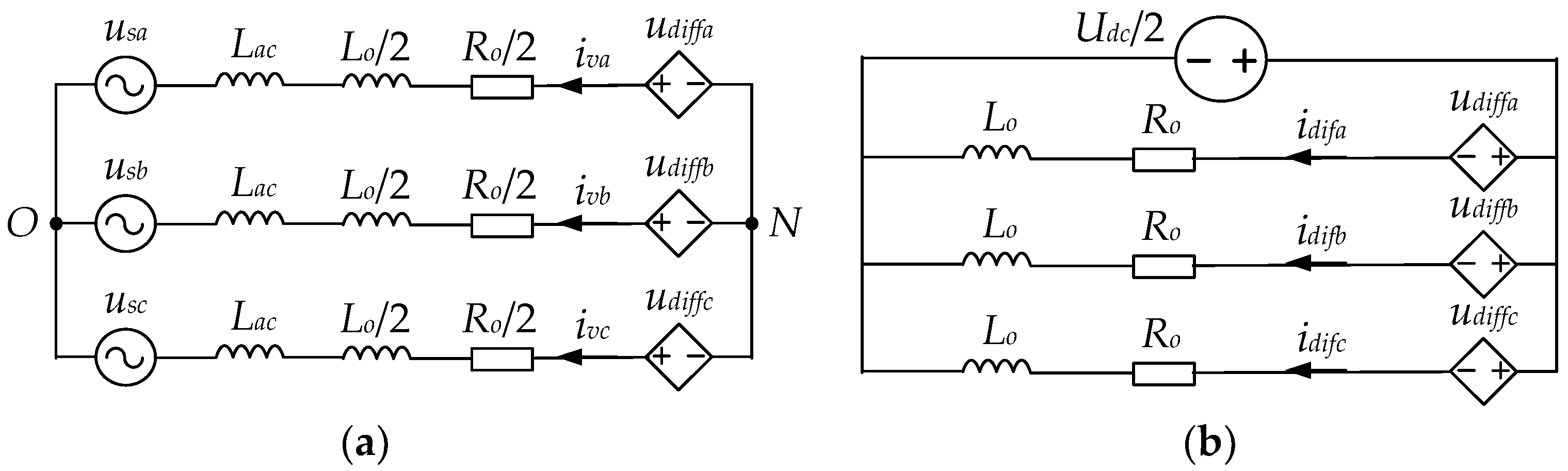
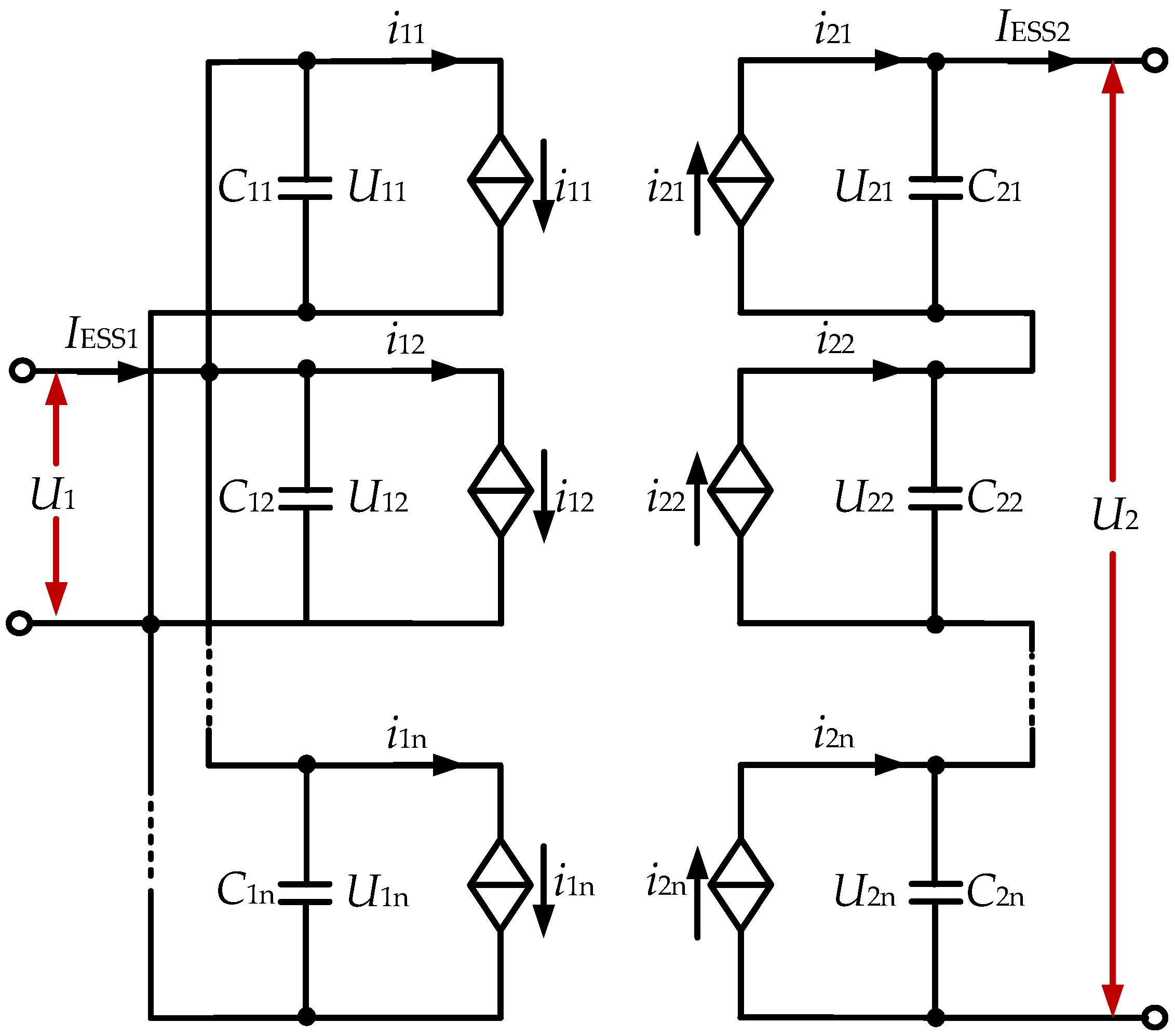
3.2. Topology and Equivalent Average Model of DCT

The DCT consists of dual-active bridge (DAB) converters, with its low-voltage side connected to the ESS and its medium-voltage side connected parallel to the DC capacitor between the FE-MMC and the BE-MMC. The topology of the DCT is shown in Figure 6, and each DAB converter is connected in parallel on the low-voltage side and in series on the medium-voltage side of the DCT.

In Figure 6, a DAB converter consists of a low-voltage H-bridge (LV-HB) converter, a medium-voltage H-bridge (MV-HB) converter, and a high-frequency transformer (HFT). U₁ and U₂ are the voltages of the LV side and MV side; u₁ and u₂ are the square wave output voltage of the LV-HB converter and MV-HB converter when the duty cycle is 50%; i₁ and i₂ are the LV side and MV side currents of HFT; C₁ and C₂ are the regulated capacitors at the low-voltage side and high-voltage side of the DAB; k is the HFT transformation ratio; and L is the leakage inductance of HFT. Meanwhile, the LV-HB converter and MV-HB converter output square wave voltages with different phases and a duty cycle of 50% according to the phase shift control in each DAB, and the leakage inductance of the HFT is excited by the voltage difference to generate a high-frequency current.

It is assumed that the DCT includes n DABs. According to [24], the output power P_DABx of the x-th DAB unit (x = 1, 2, …, n) in a single switching cycle can be expressed as:

$$P_{DABx}=\frac{k_x{U}_1{U}_{2x}{D}_x(1-D_x)}{2f_s{L}_x}$$

(10)

where U_2x is the output voltage of the x-th DAB, D_x is the phase-shift duty cycle of the x-th DAB, f_s is the operating frequency of the x-th DAB, and L_x is the equivalent leakage inductance of the x-th DAB unit converted to the MV side.

According to [25], the equivalent average-value model of DCT with n DABs is established, as shown in Figure 7.

As shown in Figure 7, according to [26], in a single switching cycle, i_1x is the average value of the LV side and MV side currents of the HFT in the x-th DAB, and I_ESS is the output current of the ESS. And according to Equation (10), i_1x and i_2x can be expressed as follows:

$$\left\{\begin{array}{l}{i}_{1x}=\frac{k_x{U}_{2x}{D}_x(1-D_x)}{2f_s{L}_x}\\ i_{2x}=\frac{k_x{U}_1{D}_x(1-D_x)}{2f_s{L}_x}\end{array}\right.(x=1,2,\dots ,n)$$

(11)

According to the equivalent average-value model in Figure 7, using KVL and Kirchhoff’s current law, the relationship between i_1x and I_ESS is as follows:

$${\displaystyle \sum _{x=1}^n{C}_{1n}\frac{d{U}_1}{dt}={\displaystyle \sum _{x=1}^n{i}_{1n}-I_{ESS}=\frac{k_x}{2f_s}{\displaystyle \sum _{x=1}^n\frac{U_{2x}{D}_x(1-D_x)}{L_x}}-}}{I}_{ESS}$$

(12)

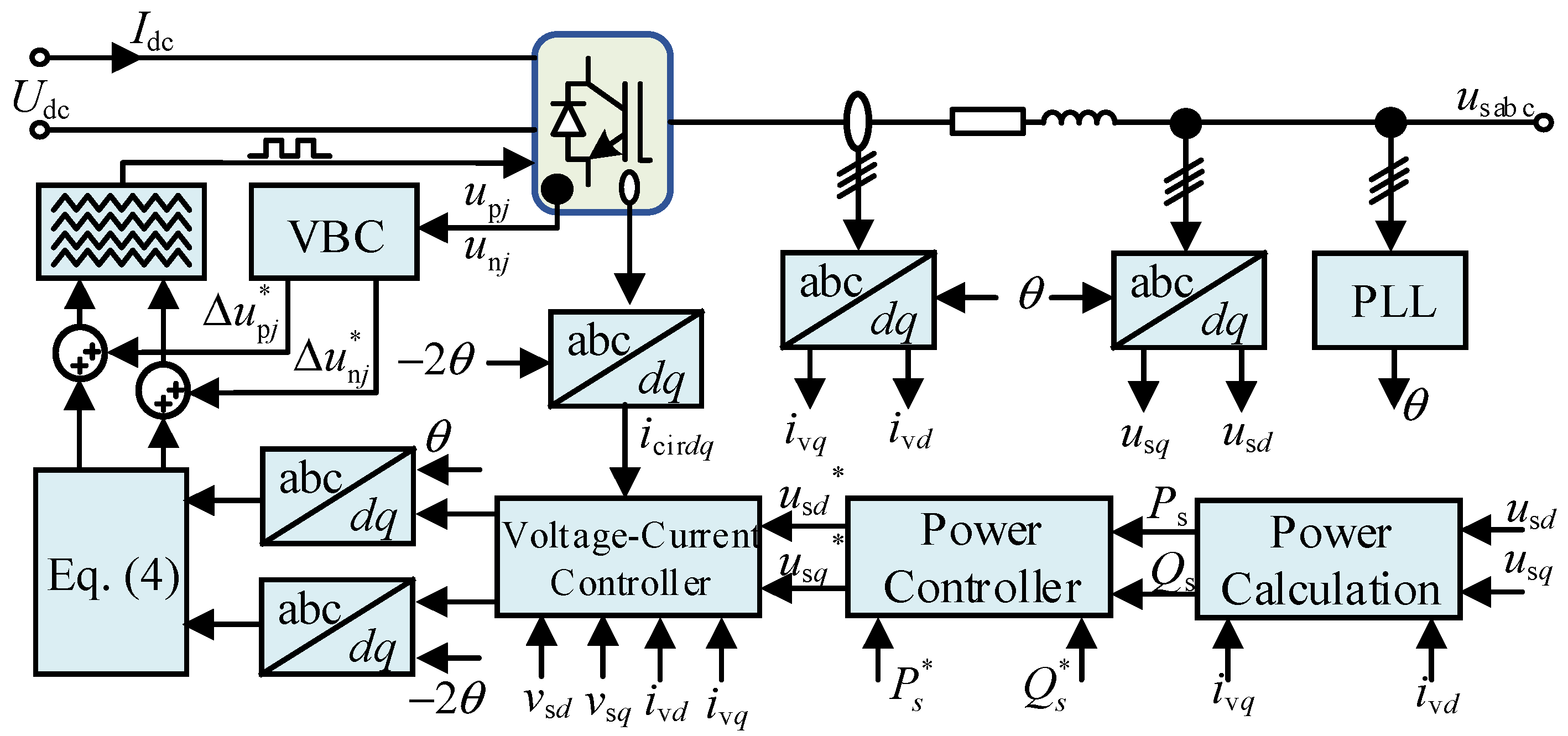
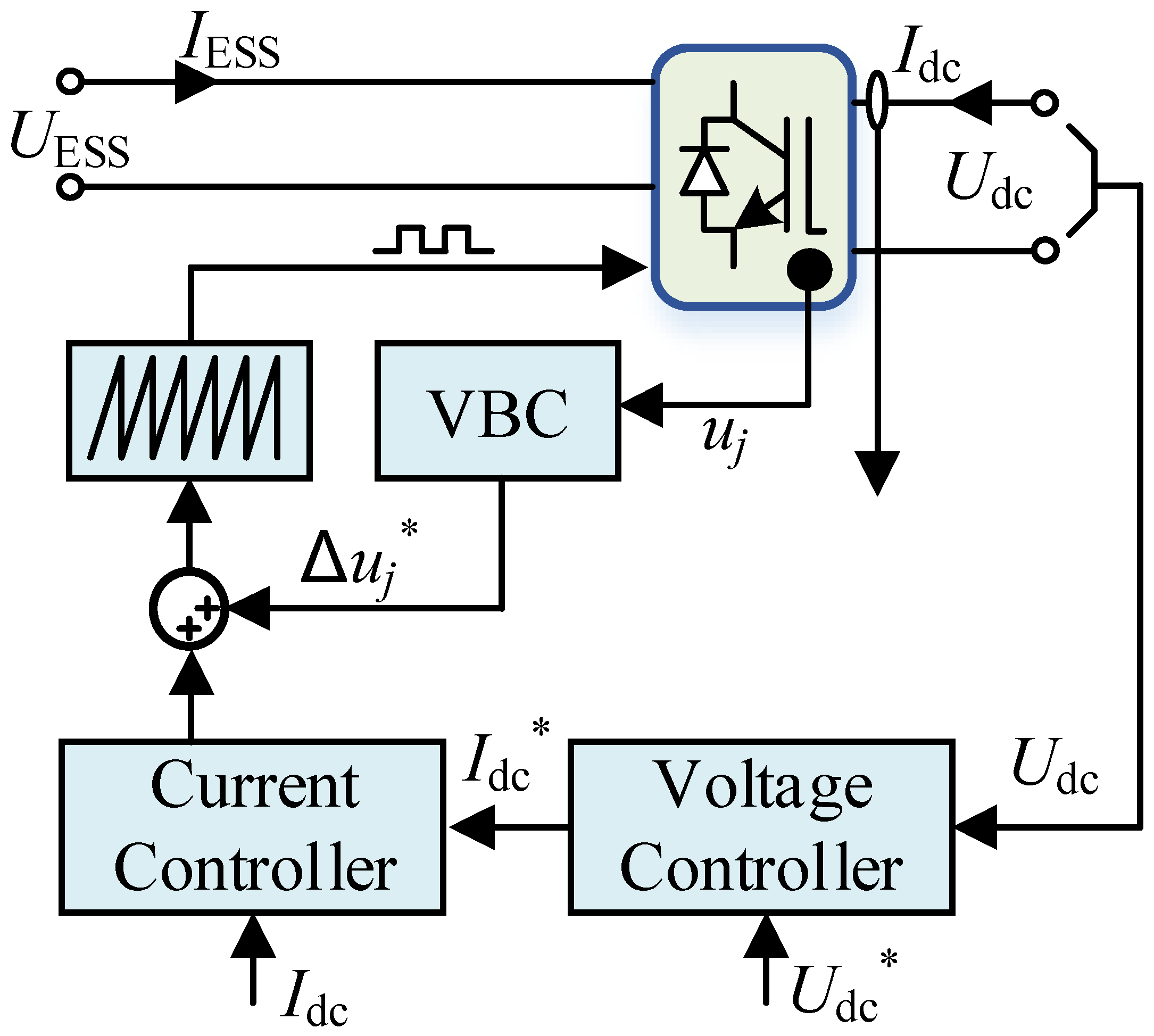
4. Control Strategy of E-UPFC

In this section, the control strategies of FE-MMC, BE-MMC, and DCT are designed to ensure the safe and stable operation of E-UPFC. FE-MMC achieves power control by controlling the current, BE-MMC achieves power control by controlling the voltage, and DCT stabilizes the voltage of the MVDC bus. The detailed control strategy is introduced as follows.

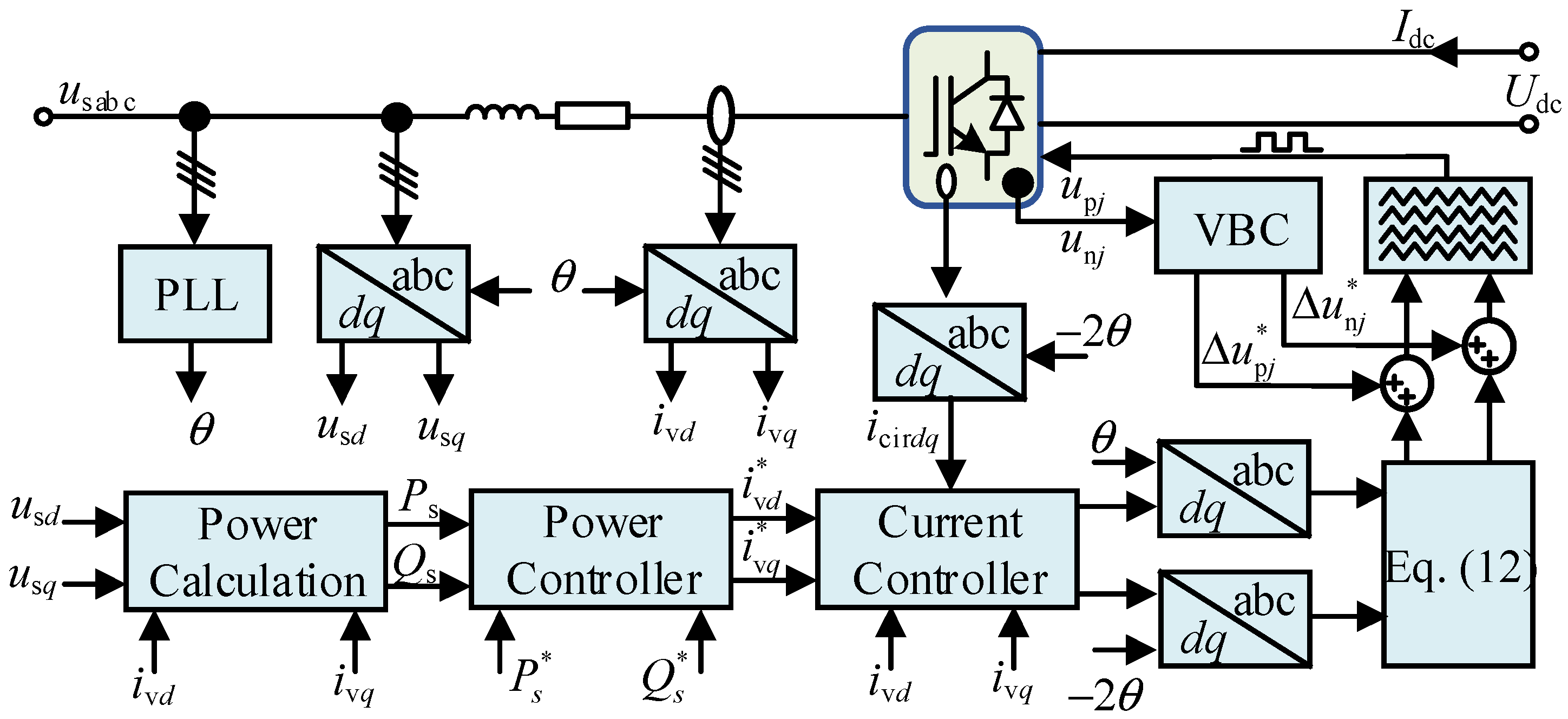
4.1. Control Strategy of FE-MMC

The MVAC port of FE-MMC is connected in parallel to the 35 kV bus through the step-up transformer, and its main function is to suppress the power fluctuations of new energy generation. The control target is the power of the MVAC port. The specific control strategy is shown in Figure 8, which mainly includes dq transformation, power calculation, an outer loop power controller, an inner loop current controller (including circulating current suppression) and a capacitor voltage balance controller (VBC). In Figure 8, u_sd is the d-axis voltage of u_sj after dq transformation. u_sq is the q-axis voltage of u_sj after dq transformation. i_vd is the d-axis current of i_vj after dq transformation. i_vq is the q-axis current of i_vj after dq transformation. P_s and Q_s are the three-phase active power and reactive power, respectively. P_s^* and Q_s^* are the reference values of three-phase active power and reactive power, respectively. i_vd^* and i_vq^* are the current reference values of the d-axis and q-axis, respectively. i_cirdq is the d-axis and q-axis circulating current i_cirj after dq transformation. ∆u_pj and ∆u_nj are the capacitance voltage correction of each SM, respectively.

The expressions for u_pj and u_nj can be obtained from Equation (7), as shown in Equation (12).

$$\begin{array}{l}{u}_{\mathrm{p}j}^{*}=u_{\mathrm{com}j}^{*}-u_{\mathrm{diff}j}^{*}\\ u_{\mathrm{n}j}^{*}=u_{\mathrm{com}j}^{*}+u_{\mathrm{diff}j}^{*}\end{array}$$

(13)

4.2. Control Strategy of BE-MMC

The MVAC port of BE-MMC is connected in series to the 220 kV bus through a step-up transformer, and its main function is power flow regulation. Its control target is the voltage of MVAC port. The specific control strategy is shown in Figure 9, mainly including dq conversion, power calculation, an outer loop voltage controller, an inner loop current controller (including circulating current suppression), and capacitor VBC. The difference from FE-MMC control is that the BE-MMC power control loop obtains a voltage reference value, while the FE-MMC inner loop current controller is replaced by a voltage current dual loop controller.

4.3. Control Strategy of DCT

The low-voltage side of DCT is connected with energy storage, and the high-voltage side is connected with the DC bus of BTB-MMC. Its main function is to stabilize the DC bus voltage, so its control goal is DC bus voltage. The energy storage realizes adaptive charge and discharge through the power control of FE-MMC and BE-MMC. The specific control strategy is shown in Figure 6, which mainly includes the MVDC voltage controller, MVDC current controller, and capacitor VBC at the series side of the DAB module. In Figure 10, U_dc is the MVDC voltage, I_dc is the MVDC current, U_ESS is the energy storage voltage, and I_ESS is the energy storage current.

5. Simulation Verification

In this article, the simulation of the E-UPFC applied to the IEEE 3-generator 9-bus system with large-scale renewable energy integration is established in MATLAB/Simulink. This section verifies the effectiveness of the proposed E-UPFC topology and control strategy. As shown in Figure 11, the large-scale PV grid-connected system is boosted by 35 kV through T_G, and then connected to the transmission network at bus 5 through E-UPFC. It is assumed that the transformation ratio of T_ET is 35/220 kV, the transformation ratio of T_ET1 is 10/35 kV, and the transformation ratio of T_ET2 is 10/10 kV. S is a bypass switch that can control whether the power electronic converters of E-UPFC are connected to the system. When the S is closed, E-UPFC works in power suppression mode to stabilize the fluctuations of renewable energy power. And when the S is off, E-UPFC works in power regulation mode to regulate the power flow of the transmission network.

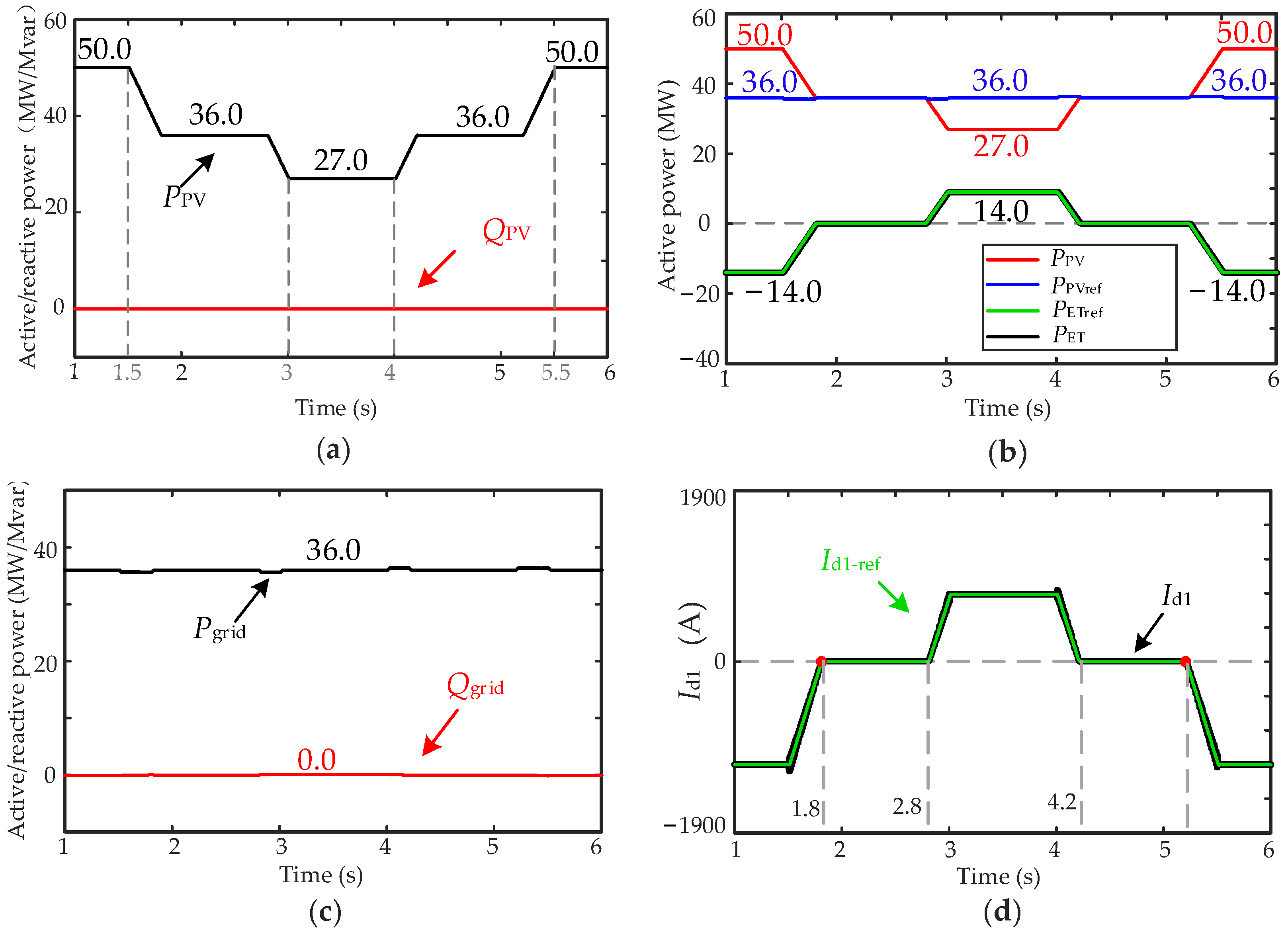
5.1. Power Suppression Mode

When the bypass switch S is closed, E-UPFC works in power suppression mode. In this paper, the rated capacity of PV power generation system is set as 50 MW. When t = 1.5 s~5.5 s, the output power of the PV power generation system simulates intermittent fluctuations. At 1.5 s, the output power of PV system gradually decreases from 50 MW to 27 MW, and then gradually increases to 50 MW, as shown in Figure 12a. At the same time, it is assumed that the reference value of the PV grid-connected power is 36 MW.

Figure 12b shows the actual power output of the PV power generation system and E-UPFC. As the output power of the PV grid-connected system begins to fluctuate within 0.5 s, E-UPFC dynamically compensates according to the calculated compensation power reference value, so as to ensure that the PV power generation system transmits constant power to the grid. Figure 12c shows that between 1.5 s and 5.5 s, the exchange power between the PV power generation system and the grid is a constant value of 36 MW, which means that the PV power fluctuation has no impact on the generation load balance of the transmission network.

Figure 12d shows the output current of FE-MMC of E-UPFC. At 0~2.2 s, when the output power P_W of the PV grid-connected system is greater than the reference value of the PV grid-connected power P_o, the inductance current I_d1 flows from the grid side to the DC side, and the ESS absorbs power and gradually decreases. At 2.2 s, when the current I_d1 is 0, the ESS neither absorbs nor releases power. When P_PV is less than P_o after 2.2 s, the current I_d1 flows from the DC side to the grid, and the ESS releases power. Similarly, after 4.09 s, the ESS absorbs and releases power according to Equation (1). Therefore, the ESS of E-UPFC can suppress the power fluctuation caused by the PV grid-connected system and ensure the stable operation of the transmission network.

5.2. Power Regulation Mode

It has been verified that T can suppress power fluctuations in the PV power generation system at the grid-connected node in Section 5.1. At the same time, the power flow regulation ability of E-UPFC on the transmission network is verified in this section. When the bypass switch S is disconnected, the BE-MMC in E-UPFC can be connected to Line 1 on the transmission network through the series winding of transformer T.

According to the diagram of the IEEE 3-generator 9-bus system in Figure 11, the following simulation verification of E-UPFC for power flow regulation is carried out. It is assumed that the load power (P_L + jQ_L = 125 + j50MVA) at bus 5 remains unchanged and the ratio of active and reactive power on line 1 and line 5 is constantly changed by E-UPFC. The simulation can be divided into the following three working conditions:

(a)

Condition 1: line power P1: P2 = 2:3, Q1: Q2 = 2: 3.

(b)

Condition 2: line power P1: P2 = 1:1, Q1: Q2 = 1: 1.

(c)

Condition 3: line power P1: P2 = 3:2, Q1: Q2 = 3: 2.

Figure 13 shows the simulation waveforms of the power on line 1 and line 2 regulated by E-UPFC. When the ratio of line 1 power P₁ + jQ₁ and line 2 power P₂ + jQ₂ is changed by E-UPFC, it can be seen that active power and reactive power on the two lines change with the output voltage of BE-MMC. The simulation values of E-UPFC power flow regulation under the three working conditions are given in

Table 1. The simulation values of E-UPFC power flow regulation under the three working conditions of power ratio change.

Condition	PL + jQL/MVA	P1 + jQ1/MVA	P2 + jQ2/MVA
1	125 + j50	50 + j20	75 + j30
2	125 + j50	62.5 + j25	62.5 + j25
3	125 + j50	75 + j30	50 + j20

. It can be seen from Figure 13 and Table 1 that E-UPFC can effectively regulate the power flow on the line, and it is verified that E-UPFC has high regulation accuracy.

According to the diagram of the IEEE 3-generator 9-bus system in Figure 11, it is assumed that the power of line 1 is set at the constant value P_L + jQ_L = 125 + j50MVA, and the simulation can be divided into the following three working conditions:

(a)

Condition 1: P_L + jQ_L = 125 + j50 MVA.

(b)

Condition 2: P_L + jQ_L = 100 + j30 MVA.

(c)

Condition 3: P_L + jQ_L = 160 + j65 MVA.

Figure 14 shows the simulation waveforms of the power flow regulation under load power change by E-UPFC. And the simulation values of E-UPFC power flow regulation under load power change are given in

Table 2. The simulation values of E-UPFC power flow regulation under load power change.

Condition	PL + jQL/MVA	P1 + jQ1/MVA	P2 + jQ2/MVA
1	125 + j50	50 + j20	75 + j30
2	110 + j40	50 + j20	60 + j20
3	150 + j65	50 + j20	100 + j45

. Therefore, it can be seen from Figure 14 and Table 2 that when the load power P_L + jQ_L at bus 5 changes, the power P₁ + jQ₁ on line 1 can remain unchanged under the regulation of E-UPFC, while the power P₂ + jQ₂ on line 2 changes due to load changes. At the same time, when the load increases or decreases suddenly, E-UPFC can control the output voltage of BE-MMC to adjust in time, and can control the current of line 1 to remain almost unchanged, that is, the power P₁ + jQ₁ on line 1 is always kept in a stable range.

6. Conclusions

This article proposes an E-UPFC installed at the renewable energy grid connection node of the transmission network, which can suppress the power fluctuations of grid-connected node injected by large-scale renewable energy and regulate the power flow on its connected transmission lines. In the above sections, the principle of power flow regulation and the topology and control strategies of E-UPFC are illustrated. The simulation results in power suppression mode and power regulation mode validate the correctness of the proposed E-UPFC. And the proposed E-UPFC has the following advantages.

• Through the buffering effect of ESS, the proposed E-UPFC can suppress the power fluctuations of large-scale renewable energy at the grid-connected node so as to ensure the friendly and smooth integration of renewable energy into the power grid;
• By transferring the installation position of E-UPFC from the transmission line to the node, the power transformer can be better protected, so as to extend the service life of the power transformer;
• The proposed E-UPFC can dynamically control the amplitude and phase of the output voltage and realize the decoupling control of the active power and reactive power of the transmission lines, so as to improve the dynamic regulation ability of the power flow of the transmission network.