A Compound Control Strategy for an Ultralight Power Generation System
Abstract
1. Introduction
2. Engine Control Strategy Design
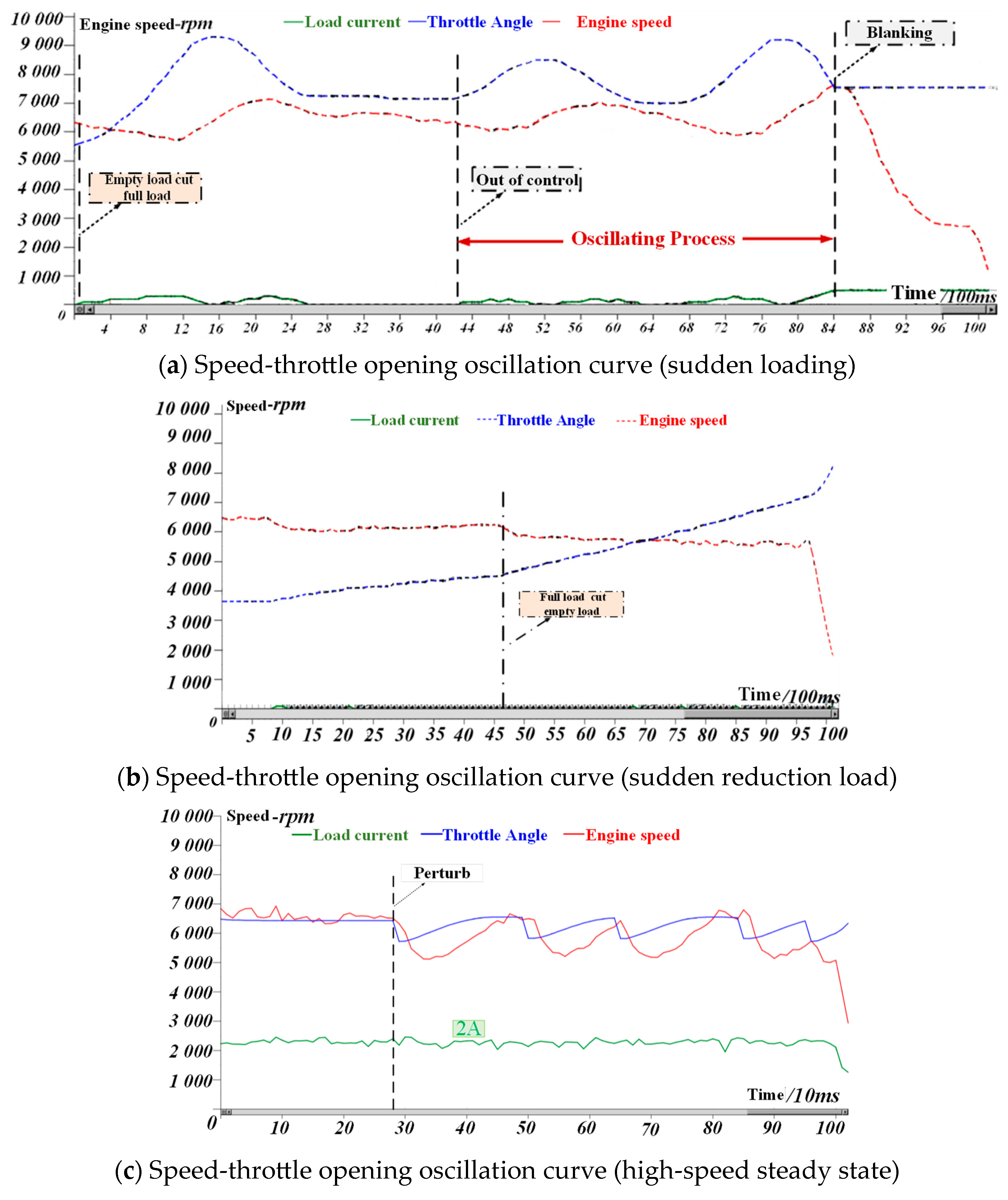
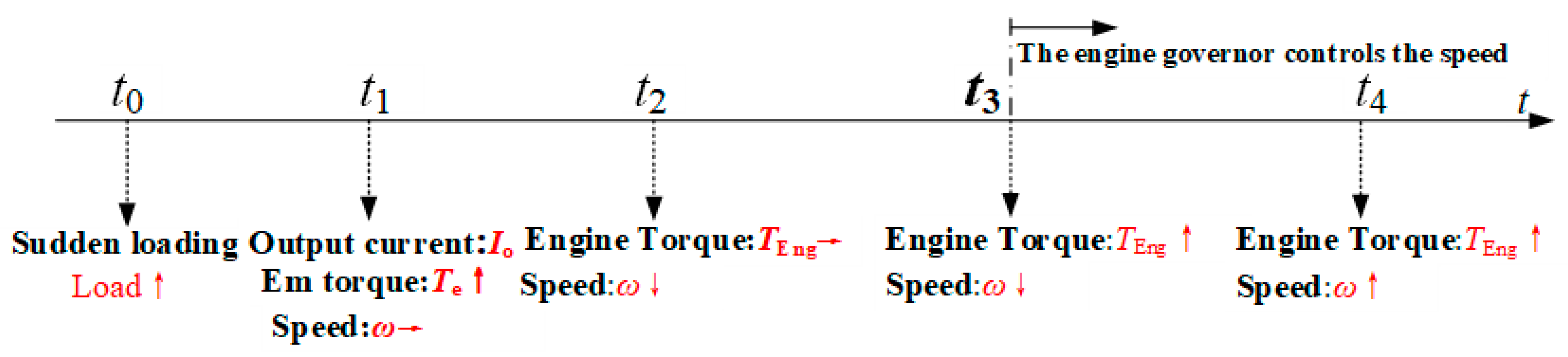
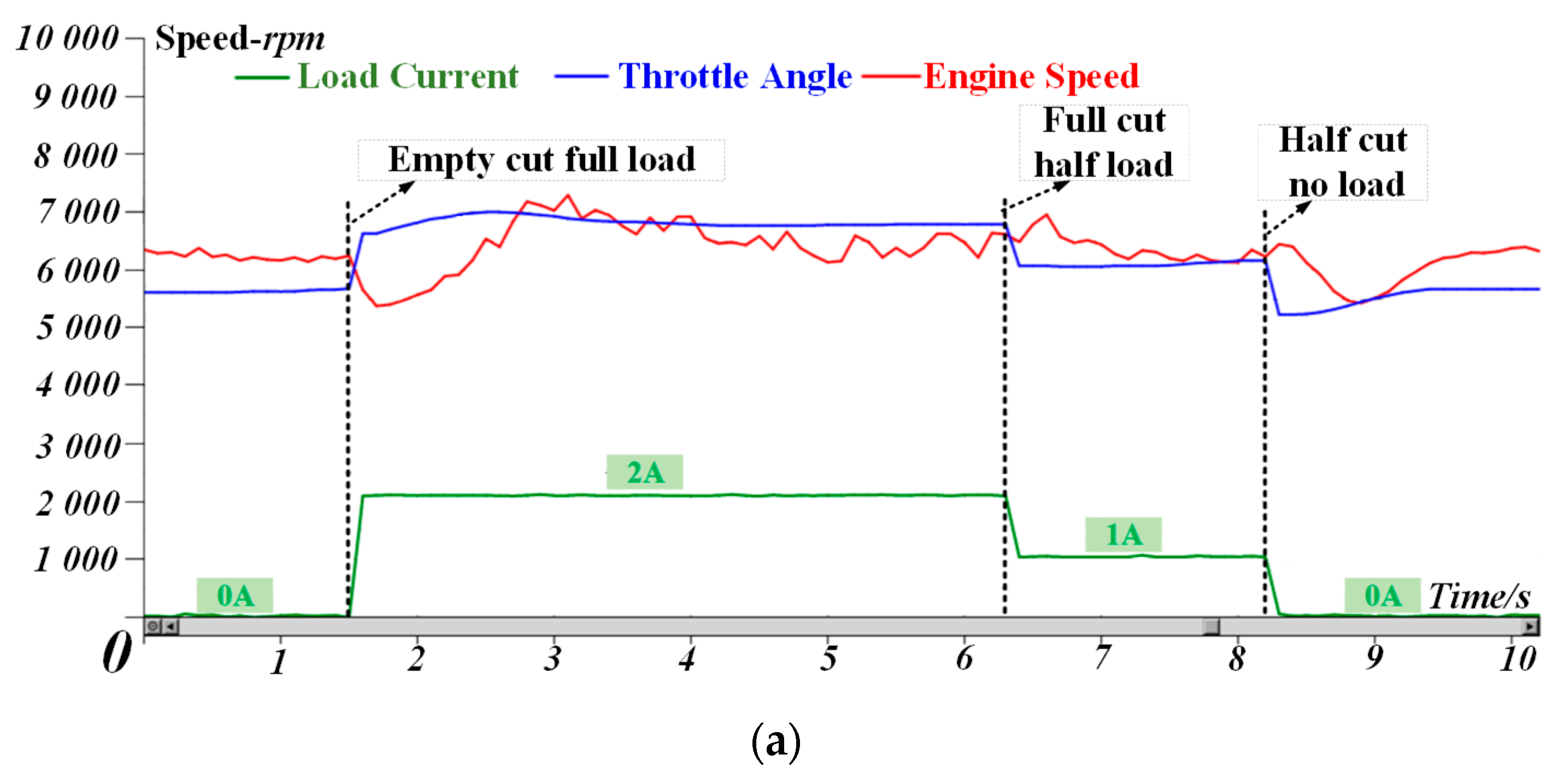
2.1. Engine Instability Principle and Control Task Analysis
- (1)
- Shaft speed oscillation and shutdown caused by a sudden load;
- (2)
- Speed and shutdown caused by a sudden load reduction;
- (3)
- Vibration of the shaft speed and fracture of connecting the shaft between the engine and generator caused by a minor disturbance during high-speed operation and stable conditions are shown in Figure 1, separately.
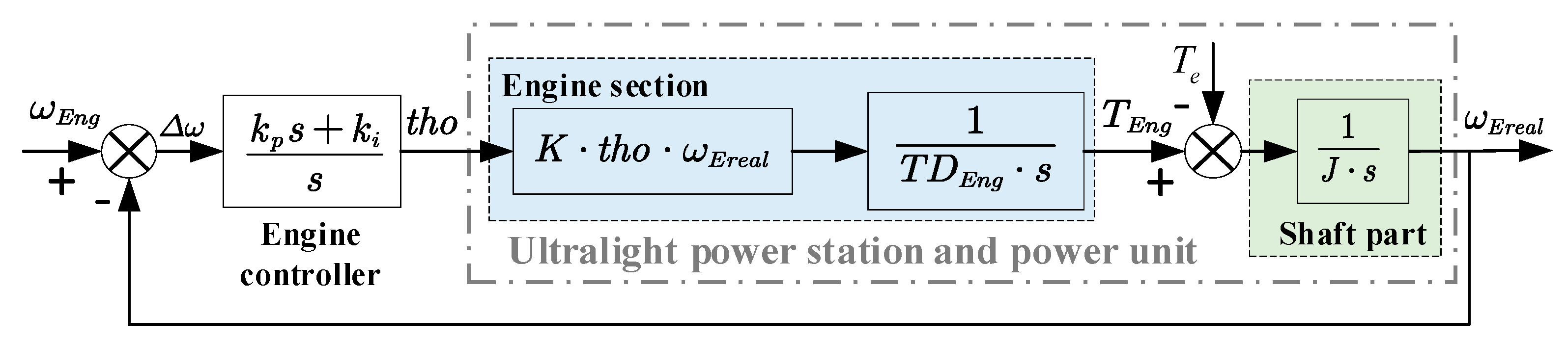
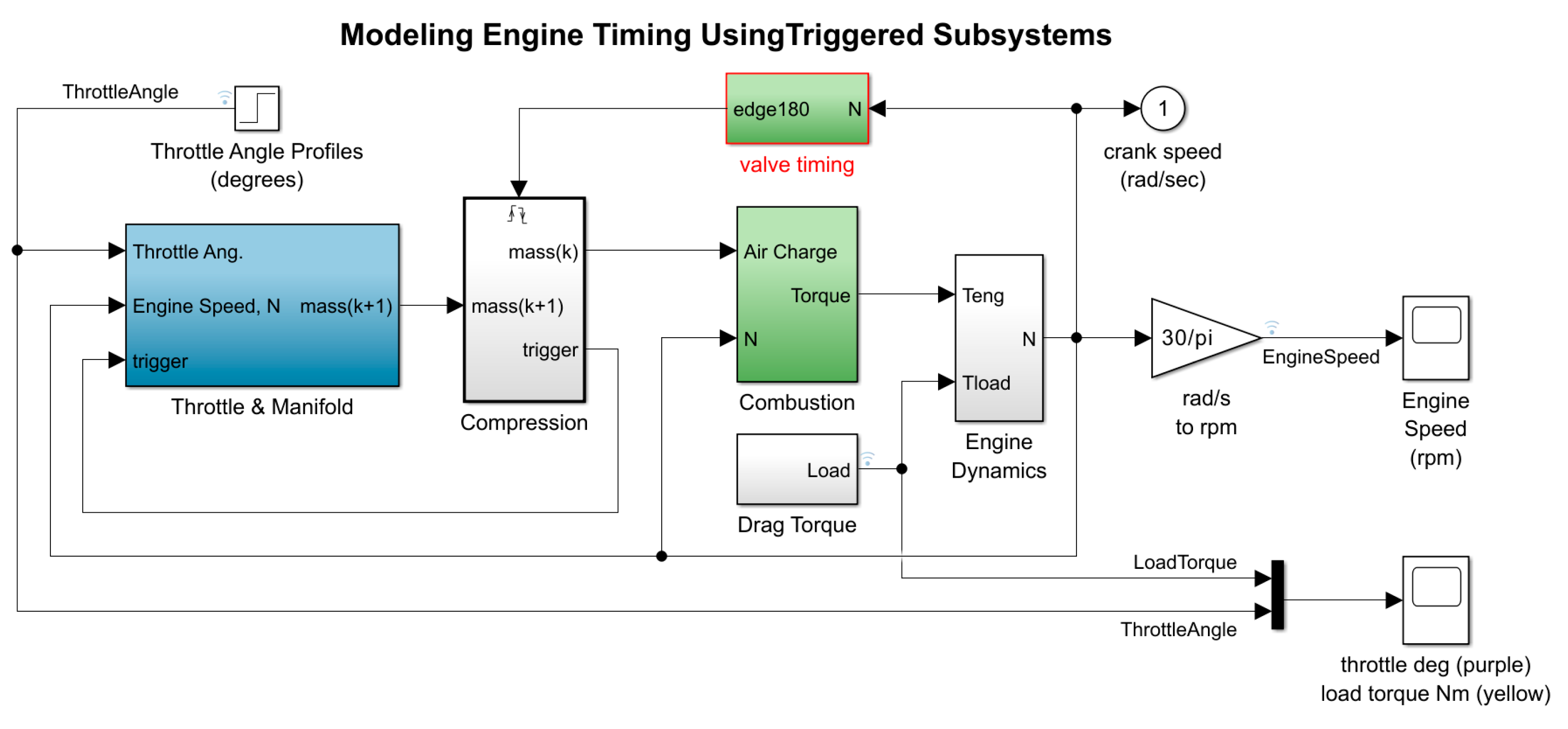
2.2. Design of the Engine Current Feedforward Control Strategy
3. Generator Control Strategy Design
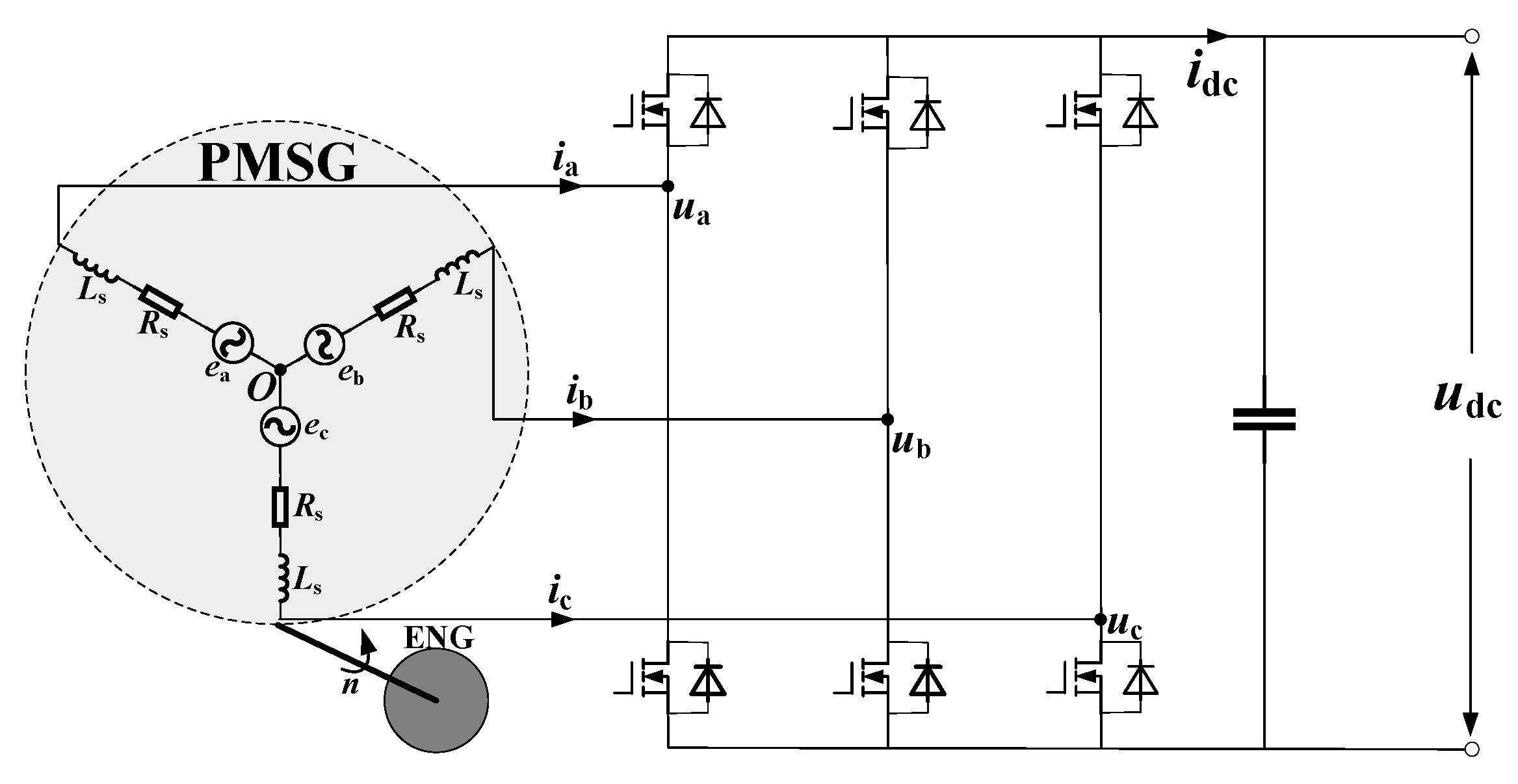
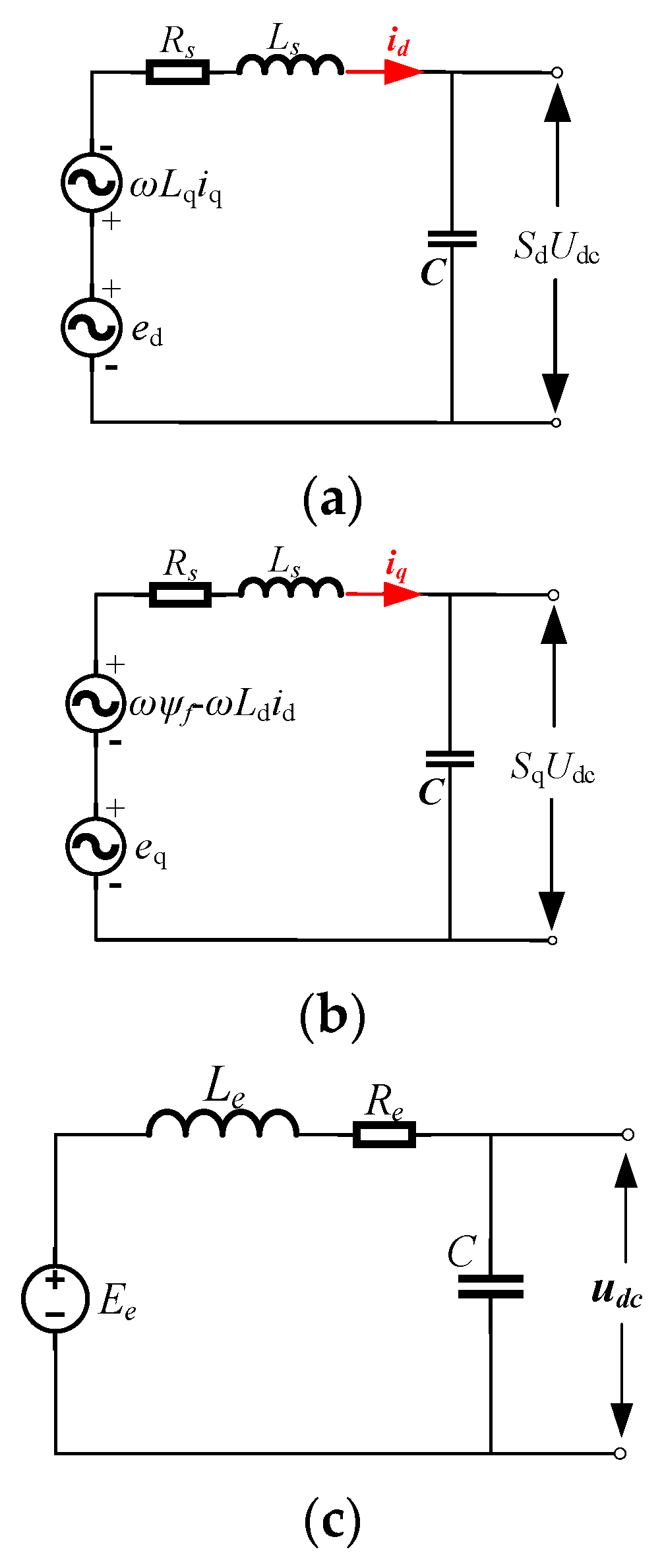
3.1. Analysis of the Equivalent Model of the Generator and PWM Rectifier
3.2. Instability Analysis of Generator and Engine
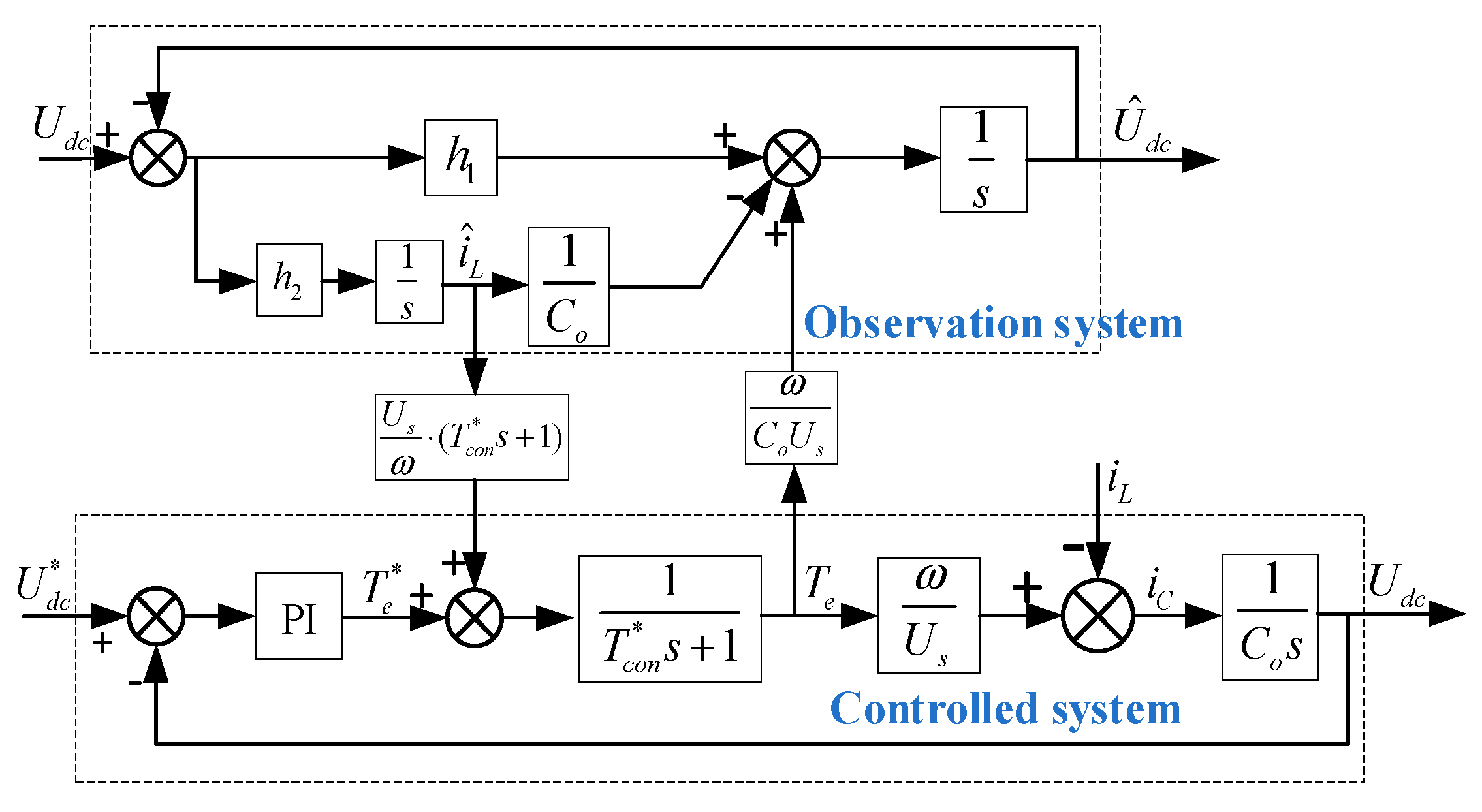
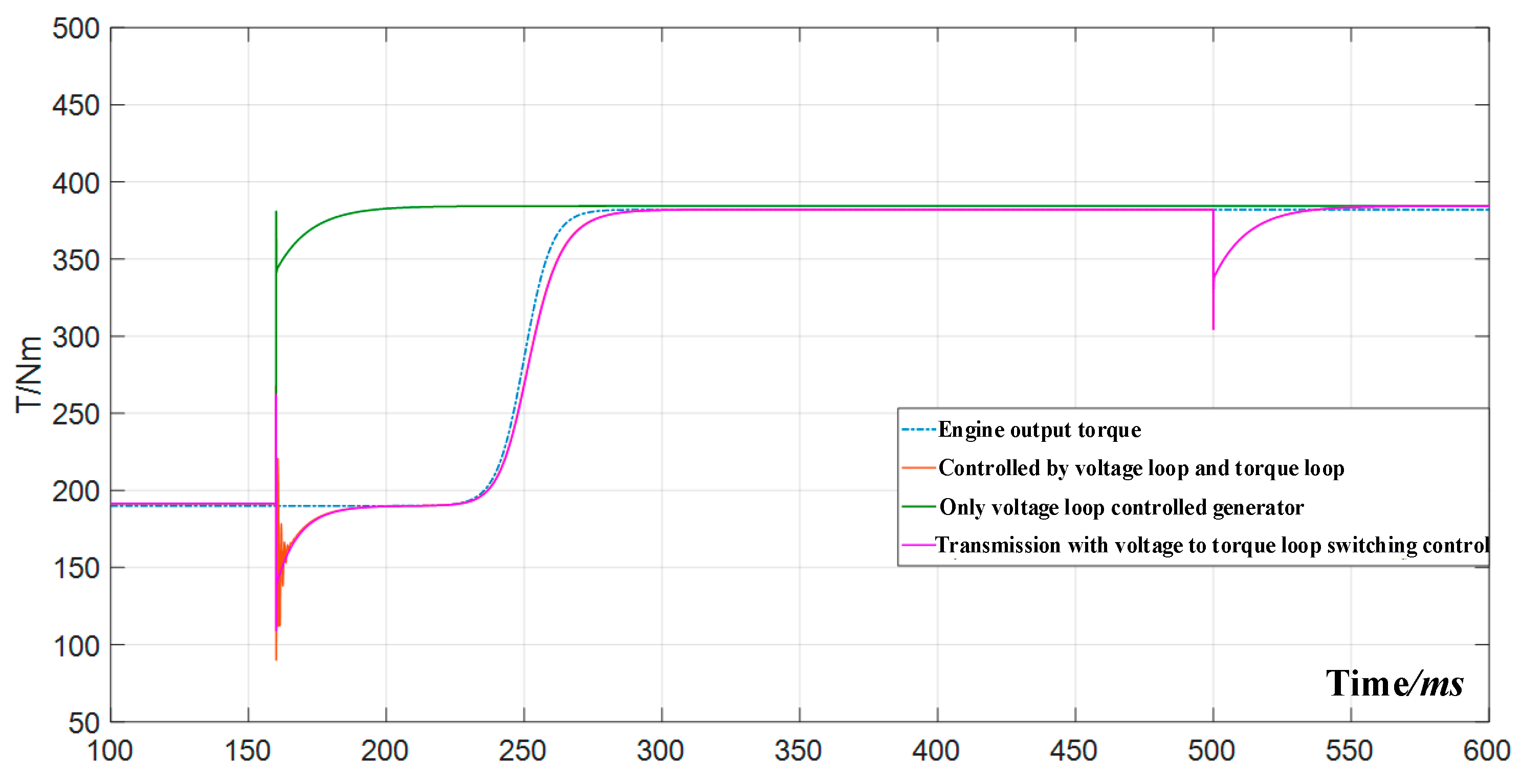
3.3. Generator Electromagnetic Torque following Strategy Design
4. Inverter Control Strategy Design
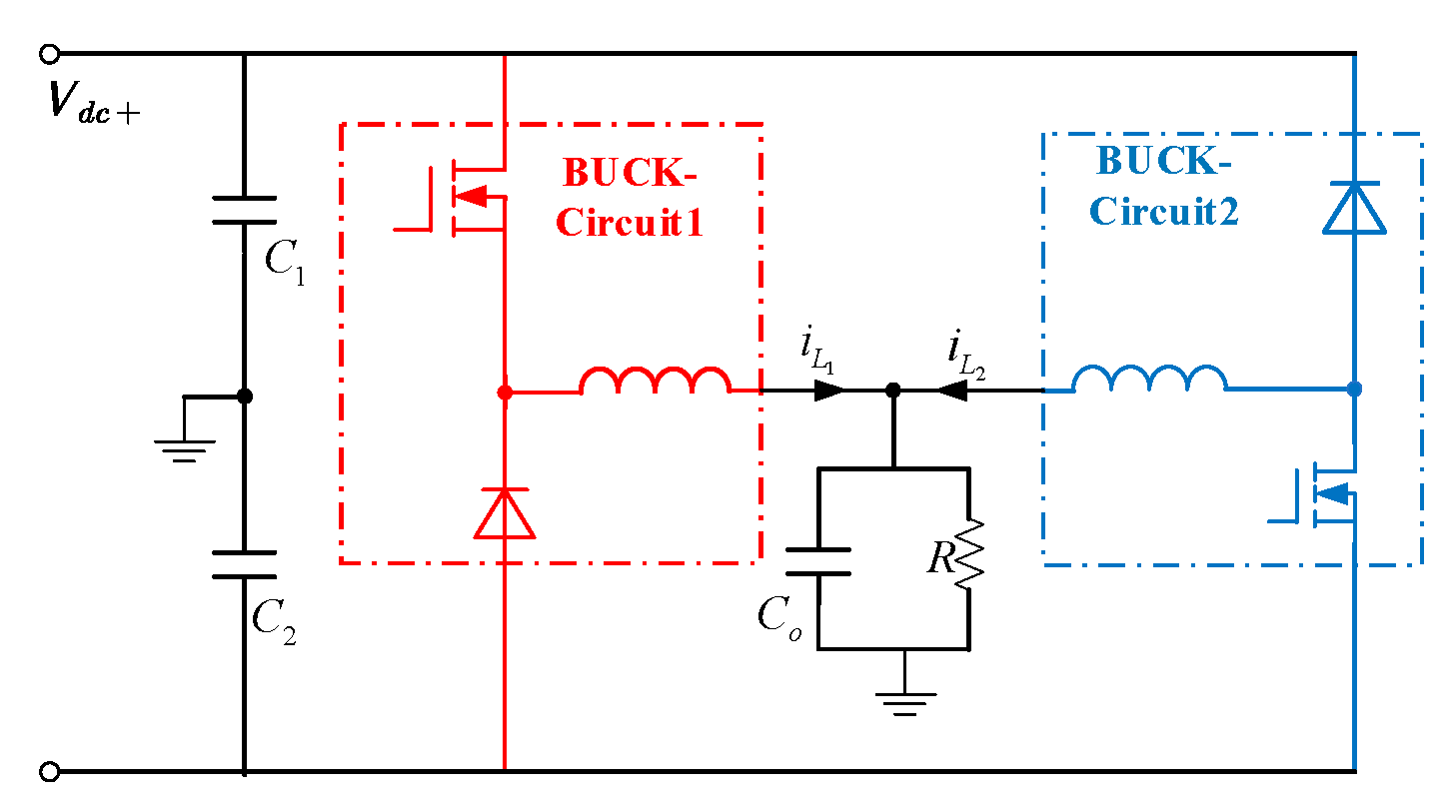
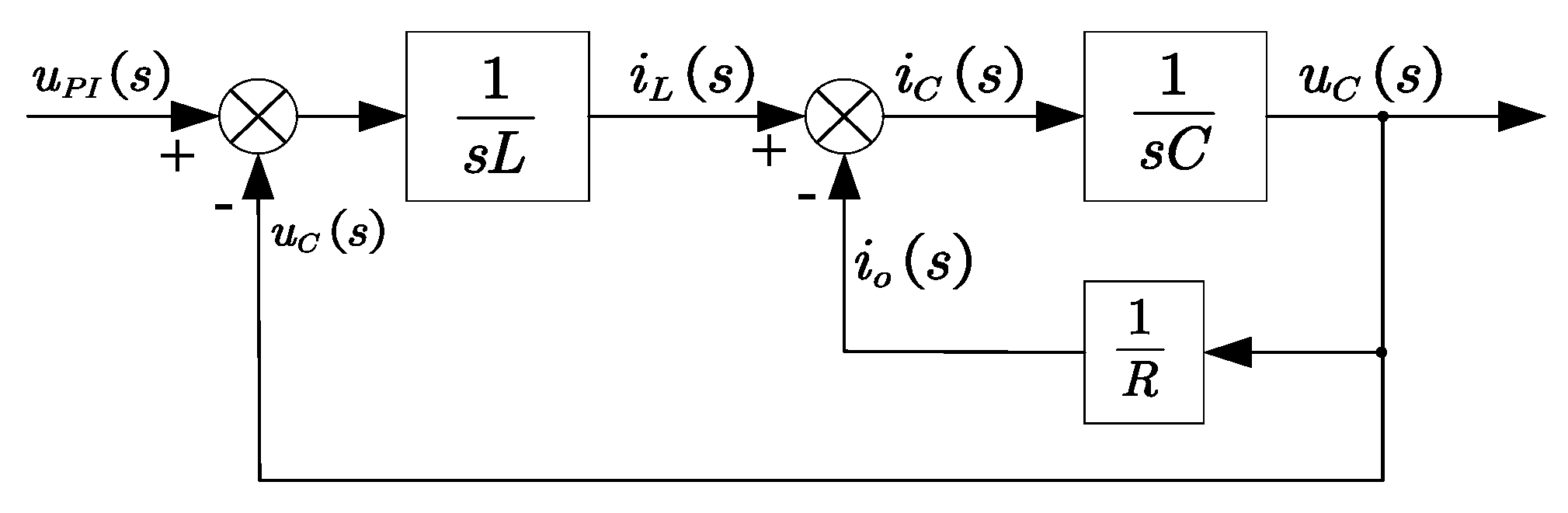
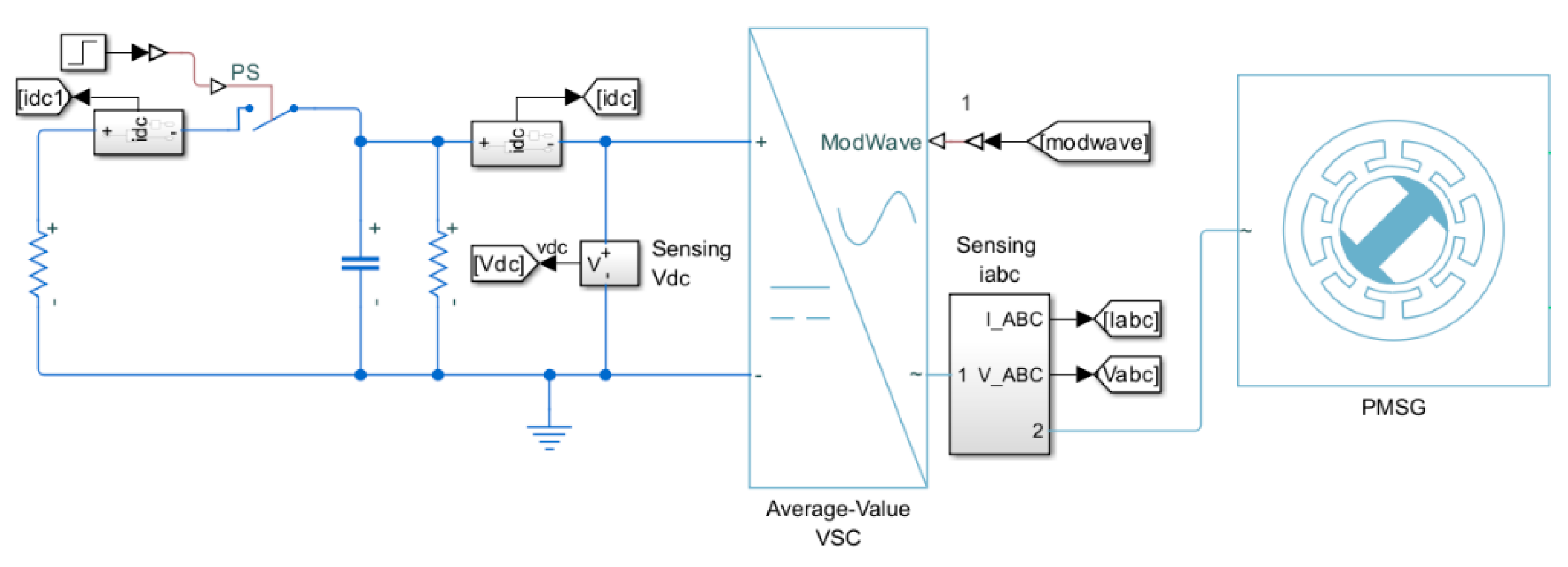
4.1. Inverter Topology and Working Principle Analysis
4.2. Design of Control Strategy Based on Feedback Linearization for the Inverter
- (1)
- {g, adfg,…, adfn−2g} is involutive at Ω;
- (2)
- {g, adfg,…, adfn−1g} is linearly independent on Ω;
5. Simulation and Experimental Results
5.1. Engine Control Strategy Simulation and Experimental Analysis
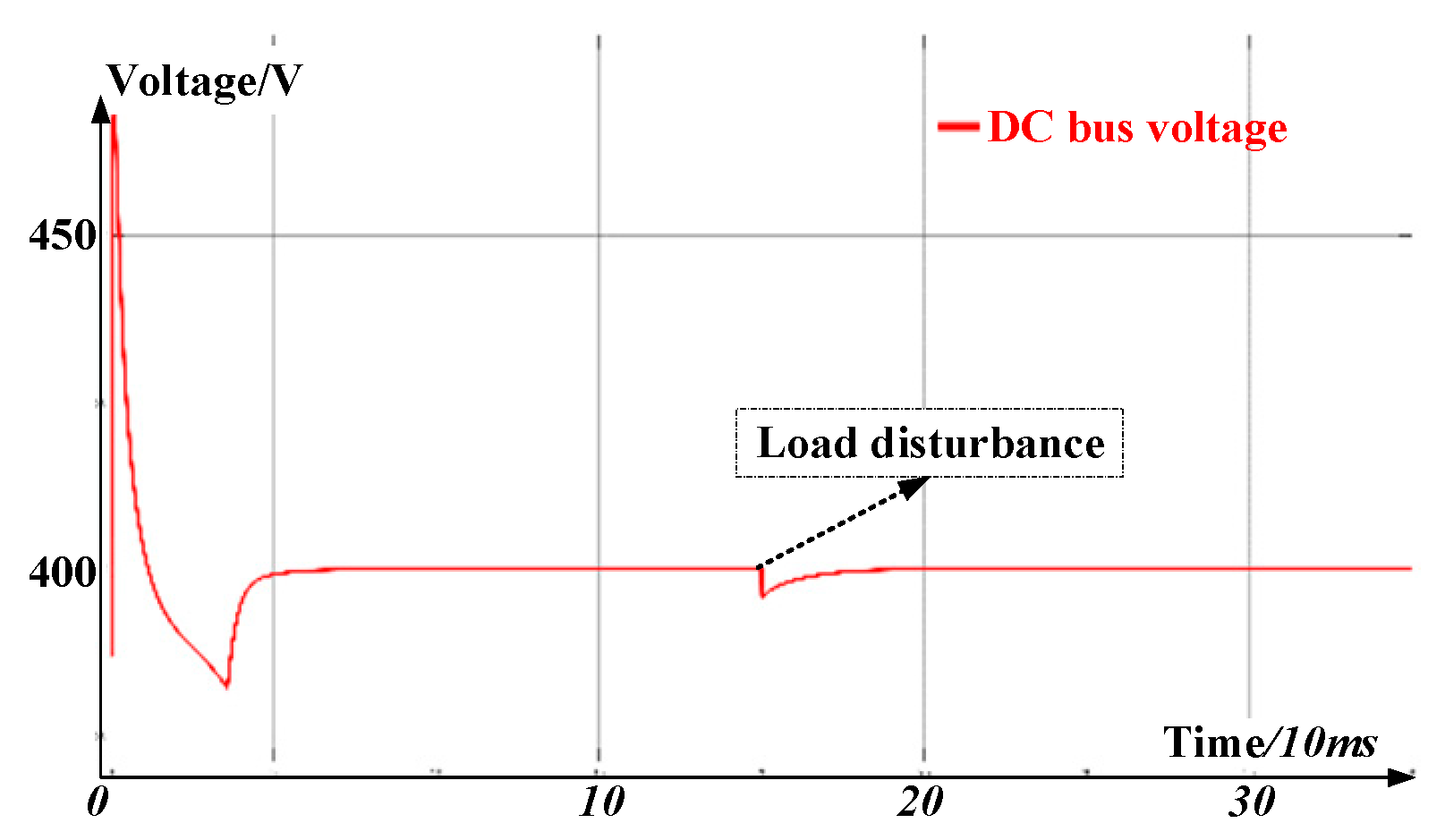
5.2. Simulation Analysis of the Generator Control Strategy
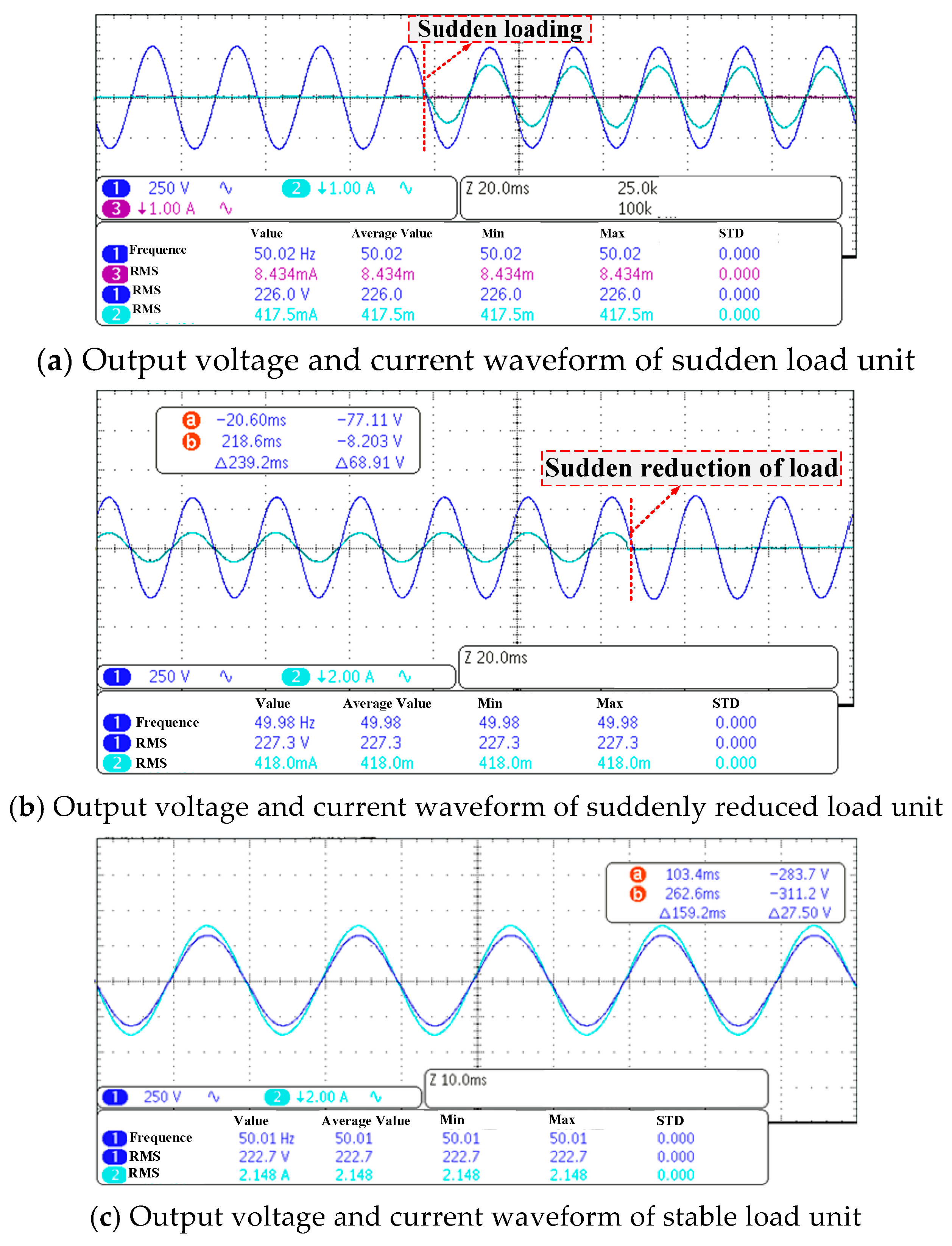
5.3. Experimental Analysis of the Inverter Control Strategy
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chinchilla, M.; Arnaltes, S.; Burgos, J.C. Control of permanent-magnet generators applied to variablespeed wind-energy systems connected to the grid. IEEE Trans. Energy Convers. 2006, 21, 130–135. [Google Scholar] [CrossRef]
- Kendouli, F.; Abed, K.; Nabti, K.; Benalla, H.; Azoui, B. High performance PWM converter control based PMSG for variable speed wind turbine. In Proceedings of the 2012 First International Conference on Renewable Energies and Vehicular Technology, Nabeul, Tunisia, 26–28 March 2012; pp. 502–507. [Google Scholar]
- Ovacik, L.; Bilgin, B. Developments in voltage regulation of variable-speed PM synchronous alternators in automotive electric systems. In Proceedings of the 2011 International Conference on Applied Electronics, Pilsen, Czech Republic, 7–8 September 2011; pp. 1–6. [Google Scholar]
- Burrow, S.G.; Mellor, P.H.; Churn, P.; Sawata, T.; Holme, M. Sensorless operation of a permanent-magnet generator for aircraft. IEEE Trans. Ind. Appl. 2008, 44, 101–107. [Google Scholar] [CrossRef]
- Ge, X.; Shi, Y.; Yan, F.; Zhu, X.; Liu, C. Research on Control Inertia and Stability of PMSG. Electronics 2022, 11, 1583. [Google Scholar] [CrossRef]
- Miao, L.; Lin, F.; Jiang, Y.; Li, Q.; Sun, W. Dynamic Operation Loss Minimization for Permanent Magnet Synchronous Generator Based on Improved Model Predictive Direct Torque Control. Electronics 2022, 11, 1406. [Google Scholar] [CrossRef]
- Lee, J.-H.; Lee, H.-K.; Lee, Y.-G.; Lee, J.-I.; Jo, S.-T.; Kim, K.-H.; Park, J.-Y.; Choi, J.-Y. Design and Analysis Considering Magnet Usage of Permanent Magnet Synchronous Generator Using Analytical Method. Electronics 2022, 11, 205. [Google Scholar]
- Shen, J.; Miao, D.M. Machine design and control strategy for wide-speed-range PMSG systems. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2015, 34, 92–109. [Google Scholar] [CrossRef]
- Miao, D.M.; Shen, J.X. Simulation and analysis of a variable speed permanent magnet synchronous generator with flux weakening control. In Proceedings of the 2012 International Conference on Renewable Energy Research and Applications (ICRERA), Nagasaki, Japan, 11–14 November 2012; pp. 1–6. [Google Scholar]
- Malinowski, M.; Kazmierkowski, M.P.; Trzynadlowski, A.M. A comparative study of control techniques for PWM rectifiers in AC adjustable speed drives. IEEE Trans. Power Electron. 2003, 18, 1390–1396. [Google Scholar] [CrossRef]
- Malinowski, M.; Kazmierkowski, M.P.; Hansen, S.; Blaabjerg, F.; Marques, G.D. Virtual-flux-based direct power control of three-phase PWM rectifiers. IEEE Trans. Ind. Appl. 2001, 37, 1019–1027. [Google Scholar] [CrossRef]
- Zhi, D.; Xu, L.; Williams, B.W. Improved direct power control of grid-connected DC-AC converters. IEEE Trans. Power Electron. 2009, 24, 1280–1292. [Google Scholar] [CrossRef]
- Liu, J.; He, J.; Iu, H.H.-C. Realization of Low-Voltage and High-Current Rectifier Module Control System Based on Nonlinear Feed-Forward PID Control. Electronics 2021, 10, 2138. [Google Scholar] [CrossRef]
- Liu, J.; Qu, X.; Iu, H.H.-C. Synchronous Generator Rectification System Based on Double Closed-Loop Control of Backstepping and Sliding Mode Variable Structure. Electronics 2021, 10, 1832. [Google Scholar] [CrossRef]
- Amin, M.M.N.; Mohammed, O.A. DC-bus voltage control technique for parallel-integrated permanent magnet wind generation systems. IEEE Trans. Energy Convers. 2011, 26, 1140–1150. [Google Scholar] [CrossRef]
- Wang, Y.; Deng, Z.; Wang, X. A parallel hybrid excitation flux-switching generator dc power system based on direct torque linear control. IEEE Trans. Energy Convers. 2012, 27, 308–317. [Google Scholar] [CrossRef]
- Miao, D.M.; Mollet, Y.; Gyselinck, J.; Shen, J.X. DC voltage control of a wide-speed-range permanentmagnet synchronous generator system for more electric aircraft applications. In Proceedings of the 2016 IEEE Vehicle Power and Propulsion Conference (VPPC), Hangzhou, China, 17–20 October 2016. [Google Scholar]
- Miao, D.M.; Mollet, Y.; Shen, J.X.; Gyselinck, J. Direct voltage field-oriented control for permanent-magnet synchronous generator systems with an active rectifier. In Proceedings of the 2016 IEEE International Energy Conference (ENERGYCON), Leuven, Belgium, 4–8 April 2016; pp. 1–6. [Google Scholar]
- Miao, D.M.; Shen, J.X. Direct voltage control strategies for variable-speed permanent magnet synchronous generator system. In Proceedings of the 10th International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte Carlo, Monaco, 31 March–2 April 2015; pp. 1–6. [Google Scholar]
- Thayumanavan, P.; Kaliyaperumal, D.; Subramaniam, U.; Bhaskar, M.S.; Padmanaban, S.; Leonowicz, Z.; Mitolo, M. Combined Harmonic Reduction and DC Voltage Regulation of a Single DC Source Five-Level Multilevel Inverter for Wind Electric System. Electronics 2020, 9, 979. [Google Scholar] [CrossRef]
- Loncarski, J.; Hussain, H.A.; Bellini, A. Efficiency, Cost, and Volume Comparison of SiC-Based and IGBT-Based Full-Scale Converter in PMSG Wind Turbine. Electronics 2023, 12, 385. [Google Scholar] [CrossRef]










| Symbol | Significance | Symbol | Significance |
|---|---|---|---|
| tho | Engine throttle angle | Te | Electromagnetic torque of generator |
| TEng | Engine torque | TDEng | Time constant of the engine inertia link |
| ωEreal | Actual speed of power unit | ωEng | Target speed of the power unit |
| Po | Target loading power | J | Inertia of the output shaft |
| Argument | Numerical Value | Argument | Numerical Value |
|---|---|---|---|
| Power unit output shaft moment of inertia J | 1.82 × 10−3 (kg·m2) | Torque–speed ratio K | 7.6 × 10−4 |
| Delay factor TDEng | 0.4 | Steady speed value | 7000 |
| Proportional coefficient kp | 0.2 | Integral coefficient ki | 0.008 |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Stator equivalent inductance Ld/(mH) | 7.79 | Number of poles | 5.0 |
| Stator equivalent resistance/(Ω) | 5.84 | Rotor equivalent resistance/(Ω) | 3.89 |
| Rated speed/(rpm) | 7000 | Rated torque/(N·m) | 0.5 |
| Rotor equivalent inductance Ld/(mH) | 7.79 | Mutual inductance/mH | 0.39 |
| Permanent magnet flux linkage ψf/(Wb) | 0.59 | Moment of inertia/(kg·m2) | 0.008 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, P.; Yuan, Z.; Yuan, Z.; Xu, H. A Compound Control Strategy for an Ultralight Power Generation System. Energies 2024, 17, 1402. https://doi.org/10.3390/en17061402
Wen P, Yuan Z, Yuan Z, Xu H. A Compound Control Strategy for an Ultralight Power Generation System. Energies. 2024; 17(6):1402. https://doi.org/10.3390/en17061402
Chicago/Turabian StyleWen, Pingping, Zhibao Yuan, Zengquan Yuan, and Haiping Xu. 2024. "A Compound Control Strategy for an Ultralight Power Generation System" Energies 17, no. 6: 1402. https://doi.org/10.3390/en17061402
APA StyleWen, P., Yuan, Z., Yuan, Z., & Xu, H. (2024). A Compound Control Strategy for an Ultralight Power Generation System. Energies, 17(6), 1402. https://doi.org/10.3390/en17061402





