Abstract
Renewable energy sources provide an environmentally sustainable solution to meet growing energy demands. Consequently, photovoltaics (PV) is regarded as a promising form of green distributed generation (GDG). The penetration of PV-GDG into distribution networks (DNs) is crucial, presenting a significant opportunity to improve power grid quality and reduce power losses. In this study, a comprehensive investigation was conducted to determine the optimal location, number, and capacity of PV-GDG penetrations with DN to achieve these objectives. Therefore, employing the Newton–Raphson (NR) technique and particle swarm optimization (PSO) approach for case studies, the analysis focused on the IEEE 33 bus test system as a benchmark test and the Iraq–Baghdad DN at 11 kV and 0.416 kV as a real case study. The outcomes revealed that integrating 4 × 1 MW PV-GDG units in a centralized configuration at bus 13 of the 11 kV Rusafa DN in the first scenario significantly reduced power losses and alleviated voltage drops across the network. In contrast, the second scenario entailed the utilization of dispersed PV panels with a capacity of 10 kW installed on rooftops at all 400 consumer load points with a cumulative capacity of 4 MW. This approach exemplified the enhancement of DN performance by significantly maximizing the power loss reduction and minimizing the voltage drops across the buses, exceeding the results achieved in the first scenario. The software applications employed in the practical implementation of this study included the CYMDist 9.0 Rev 04 program, PVsyst 7.2.20 software, and MATLAB R2022b.
1. Introduction
Considering the continuous expansion of global energy demand, the utilization of renewable energy sources serves as a primary motivator for the establishment of sustainable power grids in the forthcoming era [1]. Green distributed generation (GDG) refers to an energy infrastructure in which small units are installed close to the consumption point in centralized or diffusion forms with a power rating of 10 MW or less. Although it is a well-established concept, GDG is gaining momentum owing to a combination of factors, including increased customer demand, technological advances, favorable economic conditions, and growing environmental awareness [2]. Photovoltaic (PV) is considered to be one of the most significant uses of renewable energy worldwide, such as PV-GDG.
In particular, the design of the traditional radial configuration in the distribution system means that the existing renewable power generation facilities are not integrated into the system. Currently, the integration of PV-GDG has emerged as a key priority for countries worldwide [3]. This is evidenced by the proliferation of diverse types and large capacities of solar panels being produced to meet growing demand.
Hence, designers of distribution networks (DNs) must consider incorporating this vital technological necessity. Improper location, excessive quantity, or inadequate sizing of GDG installations may lead to an increase in power loss, voltage drop, and an overall unstable power system [4]. Although there are many optimization techniques, the choice between them depends on the specific requirements, objectives, and characteristics of the problem, as well as considerations such as optimization complexity, decision criteria of quantifiability, computational resources, and user expertise [5,6]. Therefore, to attain the maximum benefits from a long-term planning perspective, it is crucial to optimize the placement of GDGs and carefully select their size and quantity. Numerous objectives have been identified for the GDG allocation problem in the existing literature.
The application of the Ant Lion Optimization Algorithm (ALOA) for identifying the optimal placement of a hybrid combination of PV solar- and wind-turbine-based GDG within the DN holds significant promise, as discussed in [7]. Although this method can address many different optimization problems, it needs several important features, such as the necessity for parameter change, processing requirements, convergence barriers, and reduced clarity, making it more complicated. Moreover, Ali et al. [8] adopted an analytical method in their research. They proposed the ALOA to enhance the placement and sizing of GDG in radial distribution networks (RDNs). This study found that using PV-GDG embedded at bus 61 of IEEE 69 bus with an optimal capacity of 1800 kW and unity power factor led to a 63% decrease in power losses compared to preintegration. This study presents a comparison table with previous results obtained using PSO, which indicated a reduction in losses at the same location with a lower capacity of 1337.8 kW, approximately 25% less than using the ALOA. On the other hand, Bujal et al. [9] attempted to address the optimization challenges associated with RDNs by evaluating and comparing the efficacy of two distinct algorithms: the Gravitational Search Algorithm (GSA) and enhanced iteration (IGSA). These approaches effectively find the best solutions by concentrating on areas with potential, but how quickly they converge can change, depending on factors like settings and the nature of the problem. Also, the complexity stems from the use of a gravitational model unlike PSO, which is effective in exploring various solutions quickly, especially in straightforward optimization tasks. It is easy to implement and adjust, making it widely used for optimization.
Pandey et al. [10] presented a comprehensive analysis of the optimal placement of distributed generation (DG) within distribution systems. This is achieved by utilizing a novel algorithm known as JAYA, which is characterized by the absence of control parameters, thereby rendering it simpler than the other conventional algorithms. JAYA’s quicker convergence may be advantageous in specific cases, but its focus on exploitation and limited exploration makes it less resilient in noisy environments. On the other hand, PSO is a more dependable optimization option due to its capacity to tackle a variety of problems and explore intricate spaces.
Furthermore, in a separate study, Coelho et al. [11] proposed a hybrid optimization algorithm that addresses the challenges of the location and capacity of distributed generation (DG) units. Specifically, the authors developed a metaheuristic algorithm called the Empirical Discrete Metaheuristic (EDM) to tackle the siting problem. It achieved significant power loss reduction results, showing over a 12% difference compared to PSO results in the same IEEE 123 bus test system. However, because the combined capacity of the three DGs increased by a similar percentage compared to the total capacity used in the PSO analysis, this difference also suggests that the PSO method could achieve better loss reduction if applied with the same capacity that is used in the EDM.
According to the results presented in [12], satisfactory simulation outcomes were achieved, indicating that the PSO technique exhibited superior performance compared to the Genetic Algorithm (GA), which encompasses both the rate of convergence towards the optimum solution and the mitigation of power losses. Numerous other research works have been dedicated to the development and application of methods geared towards the estimation and mitigation of power losses within active distribution systems, with the assistance of smart grid technologies [13].
In addition, a novel technique for designing microgrids, comprising a dual-phase structure, was developed. In the first stage, an energy-based approach is utilized for dimensioning the DERs, and this stage involves an optimization problem expressed in the form of a mixed-integer linear programming model. Moreover, in the second phase, an optimized AC power flow framework is employed to establish a mixed-integer nonlinear programming model in which the DERs are allocated and the best conductor for each circuit is chosen. Therefore, this approach not only ensures the optimal allocation of DERs but also considers the choice of conductor, thereby increasing the efficiency and reliability of microgrids [14].
The contributions of this study are as follows:
- (1)
- This study suggests a strategy that uses PSO techniques to maximize PV-GDG system allocation. Finding the optimal size, number, and location of the embedded PV-GDG in the same algorithm process is determined using the PSO by considering particular limitations and requirements.
- (2)
- The method used in this study can be used for any DN, depending on the data and technical specifications of the electrical equipment operating in the network. The IEEE 33 bus test system was an important standard used to make sure the algorithm and analysis were accurate and useful for different Electrical Distribution Networks (EDNs). Choosing Baghdad’s networks as a case study aims to improve the reliability of the methodology. This helps it work better for networks facing operational issues, aged equipment, and shortages in power generation, along with rising annual demands exceeding power production capacity.
- (3)
- An evaluation of this approach involves comparing PSO results with those obtained from the analysis by the CYMEDist program, which represents both the IEEE 33 bus test system and a real case of studies. Additionally, this study assesses PV-GDG parameters using PVsyst 7.2.20 designing software tailored to this network and conducts power flow analysis using the Newton–Raphson (NR) numerical technique.
2. Power Flow Calculation [15,16,17,18,19]
Accurately assessing the dependability and efficiency of electric power networks requires the crucial task of calculating power flow. The Newton–Raphson method, a prevalent electrical engineering technique aimed at determining the power distribution in a given power system, is frequently employed in conjunction with load flow analysis.
To conduct a power flow analysis of the distribution system and implement the NR method, a complex power supply must be designated for each bus within the bus system model, as shown in Figure 1.
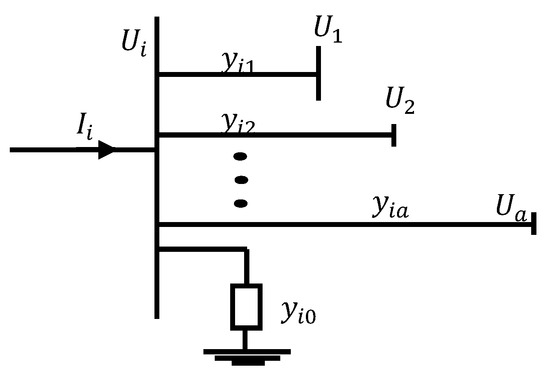
Figure 1.
Bus system model. Where the input current, , , are feeder impedances, the earth imedance.
In instances where swift load flow resolutions are required for automated power system control schemes, the present magnitude of electric current flowing into the bus is designated as follows:
where is the voltage at bus j, and with equivalent form, it can be represented as
The expressions and denote the power residuals representing the discrepancies between the scheduled and computed power values. The power residuals are denoted as follows:
The updated solution for the bus voltages is given by
The procedural framework of the Newton–Raphson method employed to obtain the power flow solution is systematically structured as follows:
- (1)
- For load buses, where and are specific voltage magnitudes and phase angle are set as the values of slack bus, or 1.0 and 0.0, ( and ) for voltage regulated buses, where and are specified, phase angles are set equal to the slack bus angle ().
- (2)
- The active power and reactive power for the load and buses.
- (3)
- and for the voltage-controlled buses.
- (4)
- The components of the Jacobian matrix (, , , and ) are computed.
- (5)
- The linearly synchronized Equation (2) is solved through a computational method.
- (6)
- In Equations (5) and (6), we computed the new voltage values with phase angles.
- (7)
- The procedure is persistent until the specified precision is more than the residuals and .
Figure 2 illustrates a flowchart depicting the Newton–Raphson load flow method.
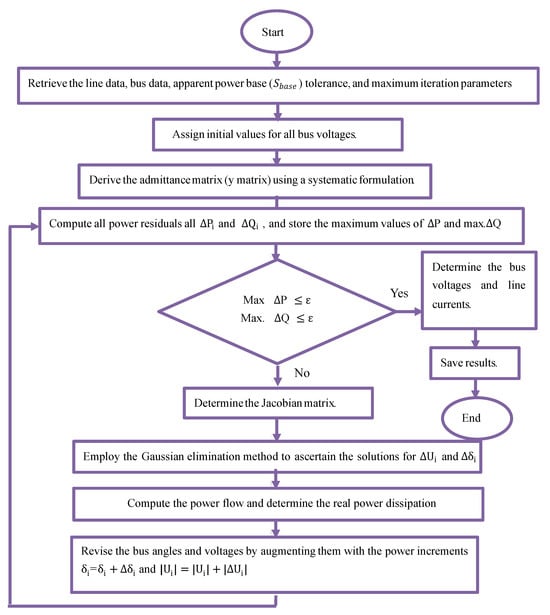
Figure 2.
Flowchart depicting the Newton–Raphson load flow method.
3. PSO Technique for Optimal GDG Integration in DNs
The PSO technique is frequently employed to determine the most favorable positioning and size of the GDG units within a power system. This heuristic optimization algorithm is inspired by the movement patterns of bird flocks and fish schools, with each particle (i.e., bird or fish) exploring the search space to locate the optimal solution informed by its individual experience and collective knowledge of neighboring particles [20].
The GDG optimization problem can be addressed using the PSO method by defining a function that must either be reduced to its minimum value or elevated to its maximum value, which may involve a total power loss or voltage deviation. The location, number, and capacity of the GDG units play critical roles in resolving this problem. This process continues until a termination criterion, such as the prescribed number of iterations or convergence criteria, is satisfied [21].
GDG planning challenge consists of two stages: selecting the appropriate bus position in the network and determining the optimal GDG size. Figure 3 shows the concept of a searching point by PSO [22,23,24]. The position of each particle can be determined by integrating its current velocity with its previous velocity and position, which is described as follows:
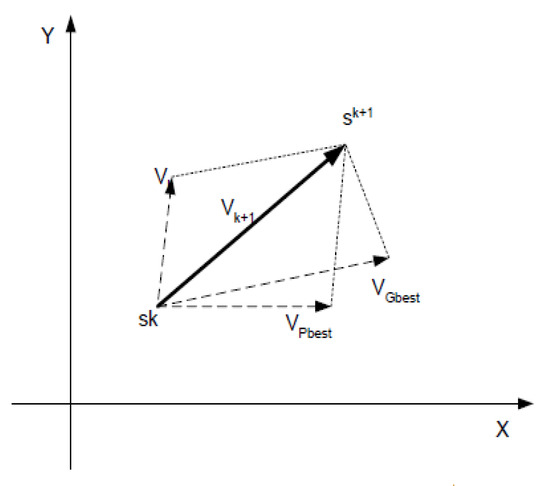
Figure 3.
Concept of a searching point by PSO.
The following parameters are defined:
: denotes the number of particles in a swarm or group;
: represents the number of particle dimensions, which may vary depending on the specific problem under consideration;
: signifies the iteration count, that is, the iteration;
: denotes the inertia weight factor used to control the balance between exploration and exploitation during the optimization;
are the acceleration constants that influence the cognitive and social components of the particle movement, respectively;
: a function that generates a uniform random value within the range [0, 1].
corresponds to the velocity of particle i at iteration k, which determines the movement of the particle in the search space;
represents the position of particle i at iteration k and indicates the location of the particle in the search space. The particle swarm optimization (PSO) methodology is applied to identify the optimal dimensions, and the placement of distributed generation units to minimize active power losses encompasses the ensuing procedural chart within the PSO schematic, as illustrated in Figure 4 [25,26].
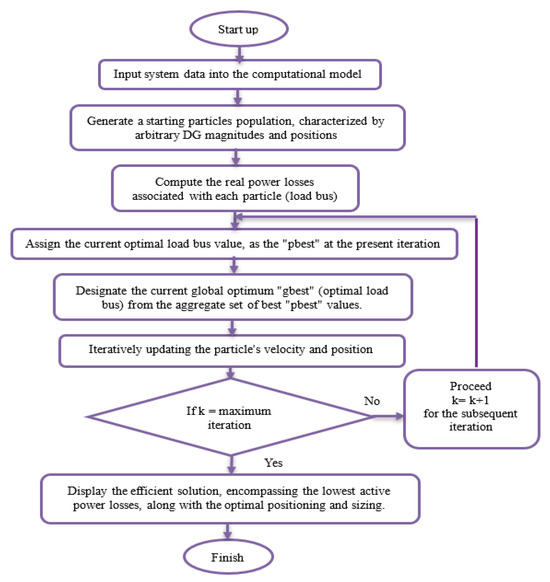
Figure 4.
Flowchart using the PSO algorithm.
4. CYMDist Background
CYMDist 9.0 Rev 04 by CYME Inc. is advanced distribution analysis software for the EDNs. It facilitates research, planning, and modeling, supporting diverse simulations and visual representations of network elements in both schematic and geographical formats. Appendix A will explain the load flow feature in this program.
4.1. Databases Employed in CYMDist
CYMDist employs a customizable database for network and device data storage, distinct from study files (.xst). Users can create and manage multiple iterations for different projects, with studies optionally saved alongside the database (.sxst).
4.1.1. Equipment Database
The electrical parameters of every piece of available equipment and machinery for the network connection are included in the equipment database. The only time this data must be updated is when new equipment becomes available because it is static.
4.1.2. Network Database
The network database contains information on each segment’s connectivity, including the utilized conductors and equipment types, equipment settings, connected loads, and GDG units in each section, along with the interconnections between the networks.
5. Practical Implementation and Comparative Study
The objective function of the methodology proposed in this study is to ascertain the optimal number, size, and placement of PV-DG units using the PSO algorithm to minimize active power losses and mitigate voltage drops. The proposed technique was assessed through an empirical investigation of the IEEE 33 bus system, as well as in the Al-Rusafa 11 kV and 0.416 kV distribution feeders in Baghdad City, which is represented by the geographical area confined by the military Tigris River and the army channel throughout the region extending from the northern to the southern boundaries of the city, including its outskirts.
5.1. IEEE 33 Bus Distribution Test System Analysis
The mathematical methods for the NR technique, PSO methodology, and CYMDist analysis are verified. In the IEEE 33 bus distribution test system, illustrated in Figure 5 [27], the PSO approach was utilized to ascertain the ideal number, size, and location of PV-GDG units, and the data related to the system load and line characteristics are included in the additional resources, specifically Appendix B [28].
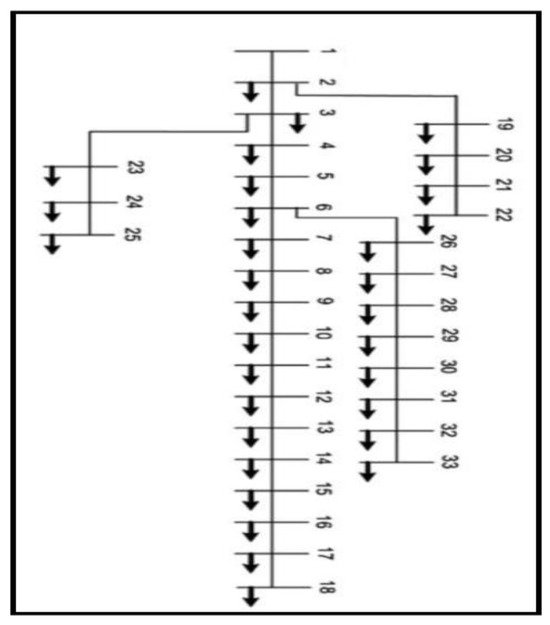
Figure 5.
Schematic representation of the IEEE 33 bus distribution test system.
We implemented the technique in MATLAB R2022b by representing bus 1 as the test system’s “slack bus”, while the other buses are “load buses”, carrying combined PQ buses with a total test system load of 3715 kW and 2300 KVar. Moreover, the voltage magnitude in the test system was 12.66 kV, with a system base of 100 MVA.
The initial stage of the PSO algorithm for PV-GDG involves generating a random distribution of particle positions and sizes, as discussed previously. To facilitate comparison with other techniques, the sizes were obtained from the sources cited in references [29,30,31] to assess the outcomes of including a single PV-GDG. In addition, references [27,28] were used to evaluate the optimization results when incorporating two and three units.
Furthermore, the positioning and velocities of the particles within the solution space exhibit inherent unpredictability [32]. Subsequently, the NR method of load flow is employed to determine the actual aggregate power loss. This task involves identifying the optimal number, capacity, and placement of the units of PV-GDG, which are subsequently interconnected with the load buses in the network. This process is guided by an algorithm that aims at the primary objective function to optimize system performance, with a central focus on diminishing power losses and establishing an optimal voltage profile.
- (1)
- Using CYMEDist software, a simulation of the IEEE 33 bus test system was conducted to perform load flow analysis in the absence of any PV-GDG units. Subsequently, based on the results obtained from the PSO algorithm, the generation units were connected at identified locations with suitable sizes. PV-GDG units are allowed to be installed between bus 2 and bus 33, with a rated power range of 1.0 MW 4.0 MW. Subsequent load flow analyses were repeated for configurations involving one, two, and three PV-GDG units, enabling the evaluation of active power losses and the identification of the bus with the lowest voltage level. Finally, a comparison was made between the outcomes obtained from CYMEDist and those obtained using MATLAB. Table 1 presents a comprehensive analysis of the results obtained when incorporating PV-GDG units into the test system of the IEEE 33 bus system using PSO methodology and CYMEDist software. The observations reported in [27,28,29,30,31] are consistent with the outcomes of this study. Importantly, it is worth highlighting that a comparison of these findings demonstrates a conspicuous level of similarity, as illustrated in Appendix C. The compelling results that demonstrate the effectiveness of PV-GDG units are shown in Figure 6.
 Table 1. The optimum number, locations, and capacities of PV-GDGs for the IEEE 33 bus system computed using MATLAB R2022b and CYME 9.04.
Table 1. The optimum number, locations, and capacities of PV-GDGs for the IEEE 33 bus system computed using MATLAB R2022b and CYME 9.04. Figure 6. Aggregate active power losses in the IEEE 33 bus distribution. system.
Figure 6. Aggregate active power losses in the IEEE 33 bus distribution. system.
- (2)
- This study evaluated the impact of integrating PV-GDG on the voltage drop in a power system, specifically focusing on bus 18. Initially, bus 18 experienced a voltage reduction of approximately 0.904 per unit before incorporating PV-GDG units. The voltage characteristics (profiles) of the IEEE 33 bus distribution system are shown in Figure 7. The figure shows the voltage scenarios when PV-GDG units are removed and added.
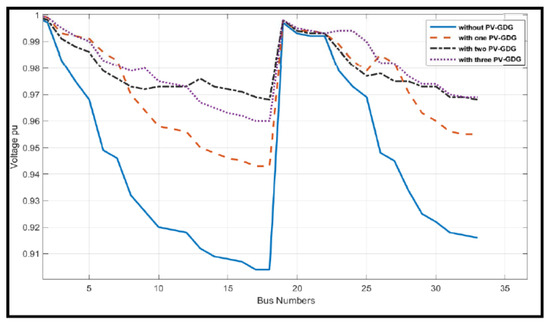 Figure 7. The voltage characteristics (profile) of the IEEE 33 bus system before and after the installation of PV-GDG units.
Figure 7. The voltage characteristics (profile) of the IEEE 33 bus system before and after the installation of PV-GDG units.
Discussion of the IEEE 33 Test System Results
Based on the findings of this study, it can be concluded that when PV-GDG units are absent, the distribution test system exhibits a maximum total power loss of 211 kW. However, with the integration of optimally sized PV-GDG units strategically placed within the system, the cumulative active power losses attained or reached their maximum values at the highest average values of 111 kW, 87 kW, and 76 kW for configurations involving one, two, and three PV-GDG units, respectively.
Consequently, significant reductions of approximately 47.4%, 58.8%, and 64% were achieved in the total active power loss of the system. This reduction can be attributed to the additional power supplied by the renewable energy system (RES) units connected close to the load. The analysis demonstrated that adding a constant integer size of 1 MW to each of the three ideally located PV-GDG units at buses 12, 24, and 30 would substantially reduce power losses by 73.8 kW, representing 65% of the overall losses before PV-GDG implementation.
Additionally, the minimum voltage dips at bus 18 were slightly reduced from 0.960 p.u. to 0.968 p.u. However, inefficient management of PV-GDG location, number, or capacity may exacerbate voltage and power quality issues. Local electricity generation through PV-GDG units can alleviate voltage drops, with the optimal addition of units leading to a significant reduction in voltage reduction.
This contributes to achieving a minimum voltage improvement of 4% to 7%, thereby bringing critical voltage levels within an acceptable range. Integration of PV-GDG stands as a crucial advancement in renewable energy systems development. For instance, integrating two PV-GDG systems totaling 2001 kW improved the minimum voltage drop at bus 18 due to their ideal location, despite the benefits of increasing the number and total capacity of the three embedded units (3059 kW) and subsequent loss reduction.
5.2. North of Al-Rusafa 11 kV Distribution Network
This section, as depicted in Figure 8, concentrates on identifying the optimal quantity, placement, capacity of PV-GDG integrated within one of the 11 kV feeders (Afaq-11). This feeder is supplied by transformer number two at the Afaq substation. Compared to other neighboring feeders supplied by the same substation, this feeder is longer and has a greater demand.
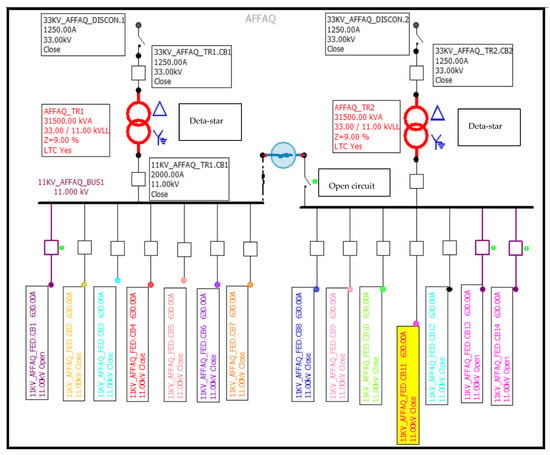
Figure 8.
The Afaq 33/11 kV substation.
5.2.1. Feeder Description (Afaq-11)
Following the 11 kV power distribution network comprising 20 distribution transformers, each rated at 250 kVA capacity, this feeder has residential distribution functions. These transformers are shown as spot loads in Figure 9. As the worst-case scenario for this study, the moment of the feeder’s maximum load during the summer was approximately 360 A. However, this feeder, along with four other 11 kV feeders, receives electricity from power transformer number two at the Afaq 33/11 kV substation.
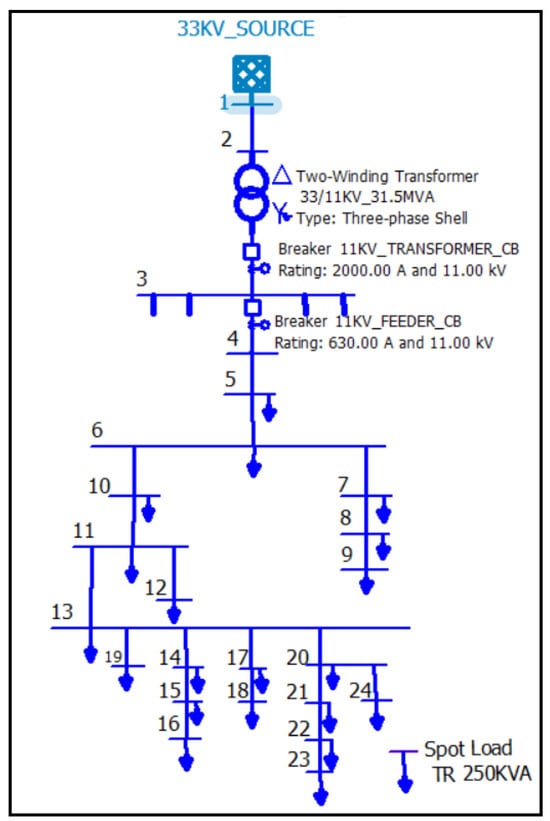
Figure 9.
Single-line diagram of the 11 kV feeder (Afaq-11).
Additionally, a 33 kV underground three-phase cable with a single core size of 1 × 400 mm2 and length of 2100 m supplied this power transformer. From the New-Adhamiya 132/33 kV substation, this 33 kV feeder carries electricity to the Afaq 33/11 kV substation, which is connected to power transformer number two. Data on the buses and lines of the 11 kV feeders, specifically the Afaq-11 feeder, can be found in Table 2, estimating the maximum load for all distribution transformers using a load power factor () of 0.85 as the worst operation case of this feeder.

Table 2.
The bus and line data for the 11 kV feeder (Afaq-11) with TR 2 and 33 kV source.
5.2.2. Low-Voltage Model
Low-voltage distribution networks (LVDNs) in Iraq have a system voltage of 0.416 kV. Consequently, in the single-line schematic of the 11 kV feeder (Afaq-11), bus 23 represents an actual LVDN linked to a 250 kVA distribution transformer. The LVDN model, which represents a real network with a peak load throughout summer, is shown in Figure 10. The materials of this simulation model were all constructed to meet the MOE requirements, which follow IEC standards.
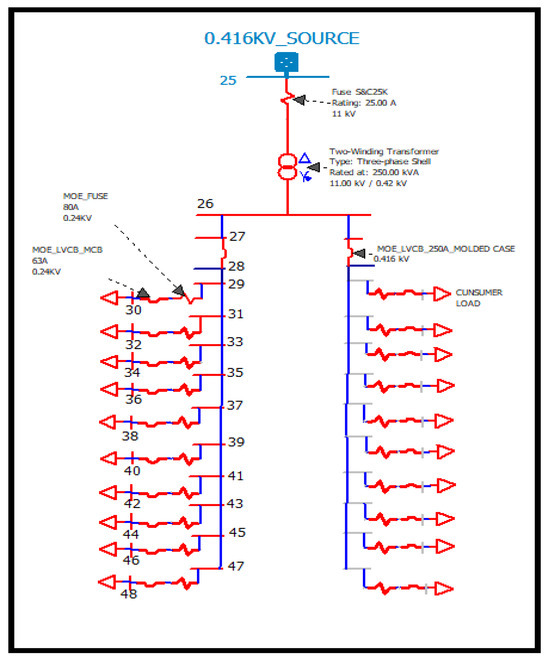
Figure 10.
A schematic diagram for the LVDN configuration of the distribution transformer connected to bus 23.
5.2.3. Grid-Connected PV-GDG Design
Derived from the electrical load-bearing capacity of the associated DN equipment, a total capacity of 4 MW was selected for PV-GDG. This was accomplished by strategically linking four units with a combined capacity of 1 MW.
In accordance with the inverter power factors utilized in this investigation with unity and 0.91, respectively, PV-GDG peak nominal power during daylight hours was calculated to be between 70.8% and 83.3% of the Afaq-11 kV feeder’s maximum residential load of 4800 kW.
Moreover, the region’s solar resource availability, PV panel size and orientation, location of the PV station building site, and the electrical load requirements of the distribution system are variables that require careful consideration. The feeder load was measured in August using a SCADA system.
Additionally, the peak sun hour (PSH) based on this study is 5 h, following other research employing weather performance in Baghdad City under clear-sky conditions [33,34]. Using PVsyst software, the tilt angle and azimuth angle, which were determined to be the best orientation parameters for the PV-GDG simulation, were 30° for the tilt angle and 0°, respectively.
Similarly, Table 3 lists the design parameters for the various PV units employed in this simulation to satisfy the flawless design of the PV-GDG station. Furthermore, photovoltaic (PV) panels should be oriented towards the south to increase the absorbed amount of solar energy they capture during the daytime depending on the city of Baghdad’s geographic coordinates, which are 33.40 N–44.34 E and 34 m altitude at the north of the equator with time zone 3.

Table 3.
The design parameters for different capacities of PV units.
According to the high-capacity factor and performance ratio (PR) with a lower , which reflects the ratio of the input DC power to the output AC () power, choosing 1 MW per PV-GDG unit capacity would be the best. It is essential to observe that the maximum short-circuit current value changes as PV-GDG size increases, which affects the rated capacity and cost of the protection systems for PV stations. In addition, the need for a clear space to guarantee that the panels receive full exposure to sunshine throughout the day is one of the main restrictions when choosing a PV-GDG array. Therefore, it was discovered that there was sufficient space adjacent to the feeder case study, Afaq-11 in this study, including real distribution networks, as shown in the aerial photograph in Figure 11.
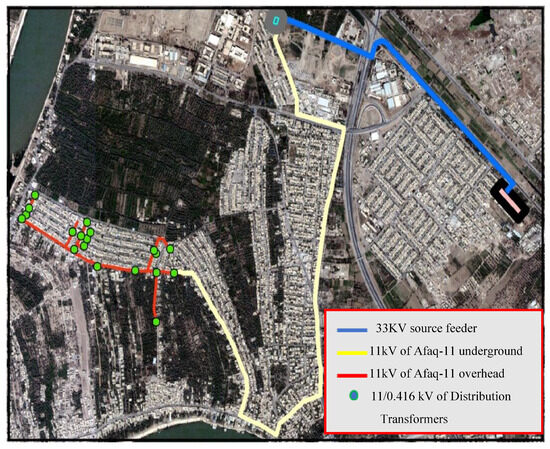
Figure 11.
Aerial photograph map from the GIS program showed the 4 MW PV-GDG location near the 11 kV feeder of Afaq-11.
5.2.4. Consideration of LF and PSO Results and Discussion
The optimal locations for PV-GDGs of various sizes and numbers were determined using the PSO approach, which has proven effective with the IEEE 33 bus test system. The results of integrating one, two, three, four, and five units are shown in Figure 12. In addition, to establish the best and worst cases in this study, two power factor values were investigated, unity and 0.91, for the smart control inverter used in the PV-GDG station.
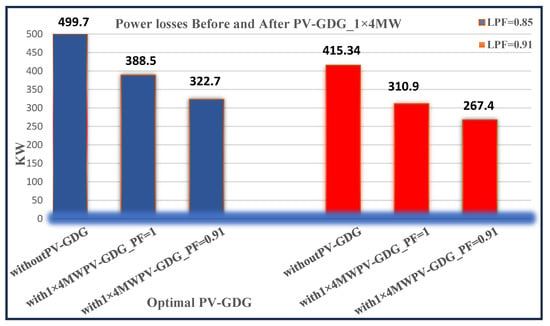
Figure 12.
Power losses for the 11 kV feeder Afaq-11 with LV in Rusafa north DN before and after 1 × 4 MW PV-GDG integration with the 11 kV network.
The following are the findings of an investigation of the NR load flow before and after PV-GDG penetration with two PV-GDG-connected arrangements.
- (1)
- Concentrated PV station at the 11 kV level feeder
In this method of investigation, the optimization process is focused on five different scenarios, each containing optimal PV-GDG unit configurations, especially those with optimum numbers 1, 2, 3, and 4, each having a total capacity of 4 MW. The minimization of active power losses acting as one of the primary objective functions is listed in Table 4, along with the results of the PSO and NR load flow methods. The worst-case scenario for the study’s analysis of the power losses of the optimal PV-GDG allocation is the penetration of a single 4 MW PV-GDG unit that consists of four parallel 1 MW subunits to bus number 13 when there is a heavy load, with an LPF of 0.85. After the introduction of PV-GDG penetration, there will be a notable maximum reduction in power losses, falling from 499.7 kW to 388.5 kW and then to 322.7 kW.

Table 4.
Optimal number, location, and capacity for a part of Rusafa north DN with power losses and voltage drop before and after PV-GDG penetration at the 11 kV feeder.
Using a smart control technique for inverter power factor values of 1 and 0.91, respectively, indicated a significant reduction in power losses to 22.3% and 35.4% during the peak PV generation during the daylight period. In situations when active power losses are already 17%, they are reduced to 415.34 kW at a light or normal load profile with an LPF of 0.91. When compared to all other situations investigated in this research case study, the prior integration of PV-GDG with optimum allocation recorded the largest percentage of power loss reduction, totaling 25.2% and 35.6%, respectively. Also, it is noted that the maximum real power losses are significantly minimized to 310.9 kW and 267.4 kW, with the amount of the decrease depending on the power factor management technique used for the inverter, which may be either 1 or 0.91.
As shown in Figure 13, the voltage profile is the second objective function under these conditions. After PV-GDG is linked to an appropriate allocation, the voltage drop improves.

Figure 13.
Voltage profile for the 11 kV feeder Afaq-11 with LV in Rusafa north DN with an LPF of 0.85 before and after 1 × 4 MW PV-GDG integration with the 11 kV network.
After connecting PV-GDG, there is a noticeable increase in the voltage of all buses in the DN compared with the situation without PV-GDG. According to the penetration with the network operating at an LPF of 0.85, the improvement percentages for PV-GDG inverter power factors 1 and 0.91 are 3.1% and 5.7%, respectively. Nevertheless, Figure 14 shows a percentage increase of 3% and 5.4% in the voltage level for all buses after adding PV-GDG with the prior two power factors of 1 and 0.91 integrating at the ideal number, size, and position of the 11 kV feeder Afaq-11 running with an LPF of 0.91. Moreover, a slight change was observed in the voltage drop profiles of the five cases listed in Table 3.
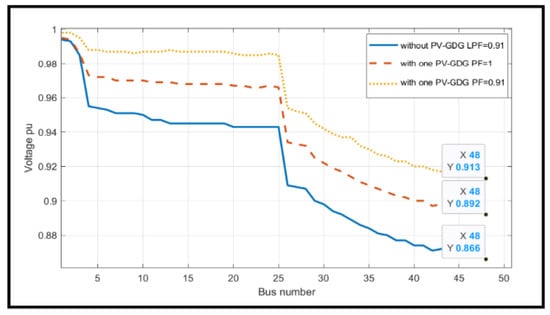
Figure 14.
Voltage profile for the 11 kV feeder Afaq-11 with LV in Rusafa north DN with an LPF of 0.91 before and after 1 × 4 MW PV-GDG integration with the 11 kV network.
- (2)
- Dispersed residential PV panels.
The distribution of photovoltaic (PV) panels among residential customers, with roofs serving as their principal installation site, is a more common layout. The highest predicted load recorded in August through the SCADA system served as the basis for the study’s assessment of each PV consumer’s capacity, which was 10 kW and was designed using PVsyst. software.
After the site survey was updated, it was found that the feeder Afaq-11 had 20 distribution transformers serving a total of 400 customers. Each transformer served twenty consumers split into two groups of ten, as shown in Figure 10. Thus, the total PV-GDG capacity was 4 MW at the location closest to the load. A load flow study was performed using the NR technique before and after the integration of PV-GDG, and the results showed two recorded load power factors (LPFs) of 0.85 and 0.91 for the worst and typical DN operations, respectively. The variations in active power losses and voltage dips during peak PV-GDG generation, which occur during daylight hours with clear sky and maximum efficiency, are detailed in Table 5.

Table 5.
Optimal number, location, and capacity for a part of Rusafa north DN with power losses and voltage drop before and after PV-GDG penetration with the the LVDN network.
Furthermore, the smart-control inverter power factor is predicted in this case study to be between unity and 0.91. The overall power losses for the Afaq-11 feeder, which include 11 kV and low-voltage DN cables, overhead lines, and transformers, are shown in Figure 15. In addition, the penetration of PV-GDG in the current study significantly reduced power losses. For the two distinct power factors of the PV-GDG inverter, the power loss reduction increased by approximately 72% and 95% for a low-voltage distribution network (LVDN) running at an LPF of 0.85.
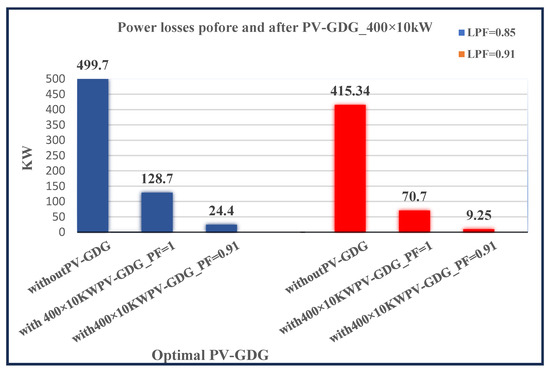
Figure 15.
Power losses for the 11 kV feeder Afaq-11 with LV in Rusafa north DN before and after 400 × 10 kW PV-GDG integration with the LVDN network.
The decrease in power loss reached 83% and was more than 97.8% for the two PV-GDG inverter power factors of unity and 0.91, respectively, when using an LPF of 0.91, which constituted the optimum scenario for power loss reduction. It is interesting that for a given capacity, the integration of PV-GDG with an LVDN close to consumers led to a larger percentage of maximum power loss reduction than integration with 11 kV buses.
Additionally, Table 4 outlines the findings for the second objective function of this study, which revealed that the voltage drops at the farthest bus 48 in the LVDN operating at 0.8 LPF, which will decrease by approximately 8.5% and 14%, respectively, after PV-GDG penetration with an inverter power factor of unity and 0.91, as shown in Figure 16. Because the voltage profile inside the system would reach its highest value at this specific site, one of the load points furthest away from the distribution transformer was selected for the load flow study.
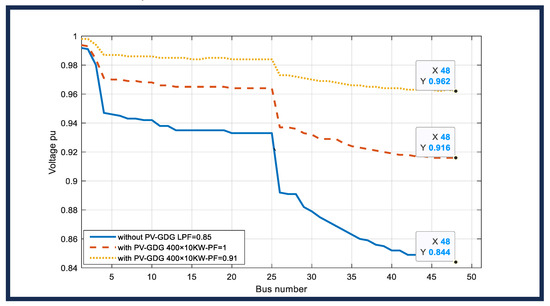
Figure 16.
Voltage profile for the 11 kV feeder Afaq-11 with LV in Rusafa north DN with an LPF of 0.85 before and after 400 × 10 kW PV-GDG integration with the LVDN network.
In addition, in Figure 17, for the same bus with 0.91 LPF, the reduction in voltage drop is slightly less significant because it was already enhanced early on with the addition of PV-GDG owing to a typical LPF of 0.91. It should be noted that the voltage at the source bus must reach an ideal value of unity.
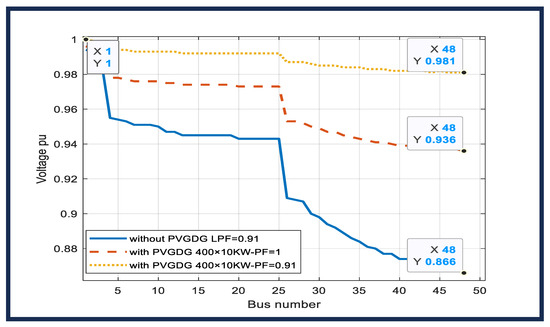
Figure 17.
Voltage profile for 11 kV feeder Afaq-11 with LV in Rusafa north DN with an LPF of 0.91 before and after 400 × 10 kW PV-GDG integration with the LVDN network.
6. Conclusions
This study confirmed that PV-GDG embedded in DNs at both low voltage (0.416 kV) and medium voltage (11 kV) increased the electrical network quality and operational performance. The active power loss magnitude and voltage drop profile were used as objective functions to evaluate the system before and after PV-GDG integration. In addition, the IEEE 33 bus test system was used as an RDN to verify the accuracy of the NR load flow and PSO algorithm.
Moreover, we simulated the test system using the CYMEDist program, repeated these analyses, and compared the results to guarantee the dependability of the software. This investigation procedure was applied to a real DN in Baghdad City to determine the influence of PV-GDG. However, the methodology used in this study can be applied to every distribution network according to the data and specifications set.
Therefore, the analysis results confirmed the selection of PV-GDG with an optimal number and capacity of 1 × 4 MW located at bus 13 of the 11 kV Afaq-11 feeder, resulting in a noteworthy decrease in energy losses and the minimization of voltage drop for all buses. The reduction in energy losses ranged from 9.3% to 14.8% for LPF values of 0.85 and 0.91, as well as for inverter power factor variations of unity and 0.91, respectively.
Notably, this scenario offers a highly reliable network owing to the presence of four parallel 1 MW subunits and a suitable geographical location for central PV station construction, as ample space is available near the optimal bus location. In contrast, the investigation ratified the embedded PV-GDG on a small scale of 10 kW on the rooftops of consumers. This deployment confers superior quality to the grid, as it reduces power losses and enhances the reduction in the minimum voltage drop across all network buses compared with the centralized arrangement. Furthermore, the consumer’s PV yielded a much higher reduction in energy losses between 30.9% and 40.7% for both the previous cases of LPF and smart-control inverter power factor. Additionally, the optimal grid-connected PV-GDG size can provide additional power generation to other neighboring feeders during periods of high reverse power generated from the PV during a light grid load. Future work will investigate the effect of PV-GDG on the thermal limits of DN equipment and short-circuit calculations for different types of faults. In addition, we determined the influence of PV-GDG on the protection scheme performance.
Author Contributions
Conceptualization, A.A.M. and M.A.; Methodology, A.A.M.; Validation, M.A.; Formal analysis, A.A.M.; Investigation, A.A.M.; Resources, A.A.M.; Data curation, A.A.M.; Writing—original draft, A.A.M.; Writing—review & editing, M.A.; Visualization, A.A.M.; Supervision, M.A. and A.A.; Project administration, M.A. All authors have read and agreed to the published version of the manuscript.
Funding
The first authors, A.A. Majeed, have received a Ph.D. scholarship from the Iraqi Ministry of Electricity. M. Abderrahim receives funding for his research activities from RoboCity2030-DIH-CM, Madrid Robotics Digital Innovation Hub, S2018/NMT-4331, funded by “The Community of Madrid and the European Social Funds”, and through the Strategic Action on Intelligent Robotic Systems and Automation 2012/00605/003 funded by the University Carlos III of Madrid.
Data Availability Statement
The data are not publicly available due to the fact that they are property of Iraqi Ministry of Electricity.
Conflicts of Interest
The authors declare that there is no conflict of interest.
Appendix A
The following computation techniques are available to users in the context of balanced networks:
- Voltage drops (requires CYMDist);
- Gauss–Seidel (requires CYMFLOW).
- Newton–Raphson (requires CYMFLOW).
- Fast decoupled (requires CYMFLOW).
The utilization of the Newton–Raphson method is contingent on the network model and its associated potential.
Appendix B

Table A1.
The input branch data for the radial distribution test system (IEEE 33 bus).
Table A1.
The input branch data for the radial distribution test system (IEEE 33 bus).
| Origin Bus | Receiving Bus | R p.u. | X p.u. | PL kW | QL kVAR | Origin Bus | Receiving Bus | R p.u. | X p.u. | PL kW | QL kVAR |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 0.0575 | 0.029 | 100 | 60 | 14 | 15 | 0.37 | 0.329 | 60 | 10 |
| 2 | 3 | 0.3076 | 0.157 | 90 | 40 | 15 | 16 | 0.466 | 0.341 | 60 | 20 |
| 2 | 19 | 0.1023 | 0.098 | 90 | 40 | 16 | 17 | 0.806 | 1.076 | 60 | 20 |
| 3 | 4 | 0.228 | 0.116 | 120 | 80 | 17 | 18 | 0.456 | 0.359 | 90 | 40 |
| 3 | 23 | 0.116 | 0.192 | 90 | 50 | 19 | 20 | 0.94 | 0.847 | 90 | 40 |
| 4 | 5 | 0.238 | 0.121 | 60 | 30 | 20 | 21 | 0.256 | 0.299 | 90 | 40 |
| 5 | 6 | 0.511 | 0.441 | 60 | 20 | 21 | 22 | 0.443 | 0.586 | 90 | 40 |
| 6 | 7 | 0.117 | 0.386 | 200 | 100 | 23 | 24 | 0.561 | 0.443 | 420 | 200 |
| 6 | 26 | 0.127 | 0.065 | 60 | 25 | 24 | 25 | 0.56 | 0.438 | 420 | 200 |
| 7 | 8 | 1.068 | 0.771 | 200 | 100 | 26 | 27 | 0.178 | 0.09 | 60 | 25 |
| 8 | 9 | 0.642 | 0.462 | 60 | 20 | 27 | 28 | 0.662 | 0.584 | 60 | 20 |
| 9 | 10 | 0.633 | 0.462 | 60 | 20 | 28 | 29 | 0.503 | 0.438 | 120 | 70 |
| 10 | 11 | 0.123 | 0.041 | 45 | 30 | 29 | 30 | 0.317 | 0.162 | 200 | 600 |
| 11 | 12 | 0.234 | 0.077 | 60 | 35 | 30 | 31 | 0.609 | 0.602 | 150 | 70 |
| 12 | 13 | 0.918 | 0.722 | 60 | 35 | 31 | 32 | 0.194 | 0.226 | 210 | 100 |
| 13 | 14 | 0.339 | 0.446 | 120 | 80 | 32 | 33 | 0.213 | 0.331 | 60 | 40 |
Appendix C

Table A2.
Results from references [27,28,29,30,31].
Table A2.
Results from references [27,28,29,30,31].
| Number of PV-GDG | Locations (Bus No.) | Size (kW) | Loss (kW) | Min. Voltage Drops at Bus 18 (p.u.) |
|---|---|---|---|---|
| Without PV-GDG | -------- | -------- | 211 | [29] 0.9037 |
| [30] 0.91 | ||||
| [31] 0.9038 | ||||
| [27] 0.91 | ||||
| [28] <0.92 | ||||
| 1 | 6 | [29] 2600 | 111 | 0.9665 |
| [30] 2590 | 111 | 0.942 | ||
| [31] 2492 | 111.24 | 0.941 | ||
| [27] 2 | 13 | 849 | 87.18 | 0.97 |
| 30 | 1152 | |||
| [28] 3 | 9 | 1062 | 74.4 | 0.969 |
| 24 | 1045 | |||
| 30 | 952 |
References
- Shawon, S.M.R.H.; Liang, X.; Janbakhsh, M. Optimal Placement of Distributed Generation Units for Microgrid Planning in Distribution Networks. IEEE Trans. Ind. Appl. 2023, 59, 2785–2795. [Google Scholar] [CrossRef]
- Kamel, S.; Khasanov, M.; Jurado, F.; Kurbanov, A.; Zawbaa, H.M.; Alathbah, M.A. Simultaneously Distributed Generation Allocation and Network Reconfiguration in Distribution Network Considering Different Loading Levels. IEEE Access 2023, 11, 105916–105934. [Google Scholar] [CrossRef]
- Palanisamy, R.; Muthusamy, S.K. Optimal Siting and Sizing of Multiple Distributed Generation Units in Radial Distribution System Using Ant Lion Optimization Algorithm. J. Electr. Eng. Technol. 2021, 16, 79–89. [Google Scholar] [CrossRef]
- Chang, G.W.; Chinh, N.C.; Sinatra, C. Equilibrium Optimizer-Based Approach of PV Generation Planning in a Distribution System for Maximizing Hosting Capacity. IEEE Access 2022, 10, 118108–118122. [Google Scholar] [CrossRef]
- Dai, H.; Huang, G.; Zeng, H. Multi-Objective Optimal Dispatch Strategy for Power Systems with Spatio-Temporal Distribution of Air Pollutants. Sustain. Cities Soc. 2023, 98, 104801. [Google Scholar] [CrossRef]
- Dai, H.; Huang, G.; Wang, J.; Zeng, H. VAR-Tree Model Based Spatio-Temporal Characterization and Prediction of O3 Concentration in China. Ecotoxicol. Environ. Saf. 2023, 257, 114960. [Google Scholar] [CrossRef]
- Samala, R.K.; Mercy Rosalina, K. Optimal Allocation of Multiple Photo-Voltaic and/or Wind-Turbine Based Distributed Generations in Radial Distribution System Using Hybrid Technique with Fuzzy Logic Controller. J. Electr. Eng. Technol. 2021, 16, 101–113. [Google Scholar] [CrossRef]
- Ali, E.S.; Abd Elazim, S.M.; Abdelaziz, A.Y. Optimal Allocation and Sizing of Renewable Distributed Generation Using Ant Lion Optimization Algorithm. Electr. Eng. 2018, 100, 99–109. [Google Scholar] [CrossRef]
- Bujal, N.R.; Sulaiman, M.; Abd Kadir, A.F.; Khatib, T.; Eltawil, N. A Comparison Between GSA and IGSA for Optimal Allocation and Sizing of DG and Impact to Voltage Stability Margin in Electrical Distribution System. J. Electr. Eng. Technol. 2021, 16, 2949–2966. [Google Scholar] [CrossRef]
- Pandey, A.K.; Kirmani, S.; Kumar, A.; Akhtar, I. Allocation of DG in Distribution Network Using Parameter Independent JAYA Algorithm. J. Electr. Eng. Technol. 2022, 18, 1675–1692. [Google Scholar] [CrossRef]
- Coelho, F.C.R.; da Silva Junior, I.C.; Dias, B.H.; Peres, W.; Ferreira, V.H.; Marcato, A.L.M. Optimal Distributed Generation Allocation in Unbalanced Radial Distribution Networks via Empirical Discrete Metaheuristic and Steepest Descent Method. Electr. Eng. 2021, 103, 633–646. [Google Scholar] [CrossRef]
- Khenissi, I.; Sellami, R.; Fakhfakh, M.A.; Neji, R. Power Loss Minimization Using Optimal Placement and Sizing of Photovoltaic Distributed Generation Under Daily Load Consumption Profile with PSO and GA Algorithms. J. Control Autom. Electr. Syst. 2021, 32, 1317–1331. [Google Scholar] [CrossRef]
- Biazzi, R.R.; Bernardon, D.P.; Becker, E.; de Chiara, L.M.; Silva, J.A. Technical and Nontechnical Energy Loss Estimation Including Volt/Var Control for Active Distribution Systems. J. Control Autom. Electr. Syst. 2022, 33, 255–267. [Google Scholar] [CrossRef]
- dos Santos, K.V.; Higino Silva Santos, L.; Bañol Arias, N.; López, J.C.; Rider, M.J.; da Silva, L.C.P. Optimal Sizing and Allocation of Distributed Energy Resources in Microgrids Considering Internal Network Reinforcements. J. Control Autom. Electr. Syst. 2023, 34, 106–119. [Google Scholar] [CrossRef]
- Glover, J.D.; Overbye, T.J.; Sarma, M.S. Power System Analysis & Design; Cengage Learning: Chicago, IL, USA, 2017; ISBN 9781305632134. [Google Scholar]
- Weedy, B.M.; Cory, B.J.; Jenkins, N.; Ekanayake, J.B.; Strbac, G. Electric Power Systems, 5th ed.; Wiley: Chichester, UK, 2012; ISBN 9780128044483. [Google Scholar]
- Bayat, M.; Koushki, M.M.; Ghadimi, A.A.; Tostado-Véliz, M.; Jurado, F. Comprehensive Enhanced Newton Raphson Approach for Power Flow Analysis in Droop-Controlled Islanded AC Microgrids. Int. J. Electr. Power Energy Syst. 2022, 143, 108493. [Google Scholar] [CrossRef]
- Al-Roomi, A.R. Optimal Coordination of Power Protective Devices with Illustrative Examples, 1st ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2022; ISBN 9781119794905. [Google Scholar]
- Jang, J.; Kim, D.; Kim, I. Singularity Handling for Unbalanced Three-Phase Transformers in Newton-Raphson Power Flow Analyses Using Moore-Penrose Pseudo-Inverse. IEEE Access 2023, 11, 40657–40674. [Google Scholar] [CrossRef]
- Manditereza, P.T.; Bansal, R. Manditereza, Patrick Tendayi Bansal, Ramesh. Renew. Sustain. Energy Rev. 2016, 58, 1457–1465. [Google Scholar] [CrossRef]
- Fayazi, H.; Fani, B.; Moazzami, M.; Shahgholian, G. An Offline Three-Level Protection Coordination Scheme for Distribution Systems Considering Transient Stability of Synchronous Distributed Generation. Int. J. Electr. Power Energy Syst. 2021, 131, 107069. [Google Scholar] [CrossRef]
- Radzi, M.Z.B.M. Optimal Allocation and Sizing of Distributed Generation Using Particle Swarm Optimization in Distribution System. Ph.D. Thesis, Universiti Tun Hussein Malaysia, Parit Raja, Malaysia, 2013. [Google Scholar]
- Bouzguenda, M.; Samadi, A.; Rajamohamed, S. Optimal Placement of Distributed Generation in Electric Distribution Networks. In Proceedings of the 2017 IEEE International Conference on Intelligent Techniques in Control, Optimization and Signal Processing (INCOS), Srivilliputtur, India, 23–25 March 2017; pp. 1–5. [Google Scholar] [CrossRef]
- El Haj Assad, M.; Rosen, M.A. Design and Performance Optimization of Renewable Energy Systems; Academic Press: Cambridge, MA, USA, 2021; ISBN 9780128216026. [Google Scholar]
- Zain, Z.M.; Sulaiman, M.H.; Mohamed, A.I.; Bakar, M.S.; Ramli, M.S. Proceedings of the 6th International Conference on Software and Computer Applications; Association for Computing Machinery: New York, NY, USA, 2021; ISBN 9789811686894. [Google Scholar]
- Baniodeh, H.M.; Zeid, S.M.; Eajal, A. The Pest Location and Size of Distributed Generation (DG) in A Radial Distribution Systems. Int. J. Adv. Res. Electr. Electron. Instrum. Eng. 2013, 2, 5160–5172. [Google Scholar]
- Santoso, D.B.; Sarjiya, S.; Sakti, F.P. Optimal Sizing and Placement of Wind-Based Distributed Generation to Minimize Losses Using Flower Pollination Algorithm. JTERA J. Teknol. Rekayasa 2018, 3, 167. [Google Scholar] [CrossRef]
- Duong, M.Q.; Pham, T.D.; Nguyen, T.T.; Doan, A.T.; Van Tran, H. Determination of Optimal Location and Sizing of Solar Photovoltaic Distribution Generation Units in Radial Distribution Systems. Energies 2019, 12, 174. [Google Scholar] [CrossRef]
- Nallagownden, P.; Mahesh, K.; Elamvazuthi, I. A Combined-Model for Uncertain Load and Optimal Configuration of Distributed Generation in Power Distribution System. Int. J. Simul. Syst. Sci. Technol. 2017, 17, 11.1–11.7. [Google Scholar] [CrossRef]
- Karimyan, P.; Vahidi, B.; Abedi, M.; Ahadi, S.M. Optimal Dispatchable DG Allocation in a Distribution Network Considering Load Growth with a Mixed-PSO Algorithm. Turk. J. Electr. Eng. Comput. Sci. 2016, 24, 3049–3065. [Google Scholar] [CrossRef]
- Nallagownden, P.; Mahesh, K.; Elamvazuthi, I. Optimal Placement and Sizing of Distributed Generation in Distribution System Using Analytical Method. Int. J. Recent Technol. Eng. 2019, 8, 6357–6363. [Google Scholar] [CrossRef]
- Guven, A.F.; Yorukeren, N.; Tag-Eldin, E.; Samy, M.M. Multi-Objective Optimization of an Islanded Green Energy System Utilizing Sophisticated Hybrid Metaheuristic Approach. IEEE Access 2023, 11, 103044–103068. [Google Scholar] [CrossRef]
- Sami, S.M.; Mahmood, A.L. Design and Simulation of Stand-Alone Photovoltaic System Supplying Bts in Iraq. Int. J. Power Electron. Drive Syst. 2021, 12, 463–473. [Google Scholar] [CrossRef]
- Atwan, A.F.; Kasim, N.K.; Jasim, N.A.; Hameed, J.S. Improvement the PV Solar Module Cooling Systems by Using Shallow Geothermal. AIP Conf. Proc. 2020, 2290, 050028. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).