A Soft-Switching Proportional Dimming LED Driver Based on Switched Capacitor
Abstract
1. Introduction
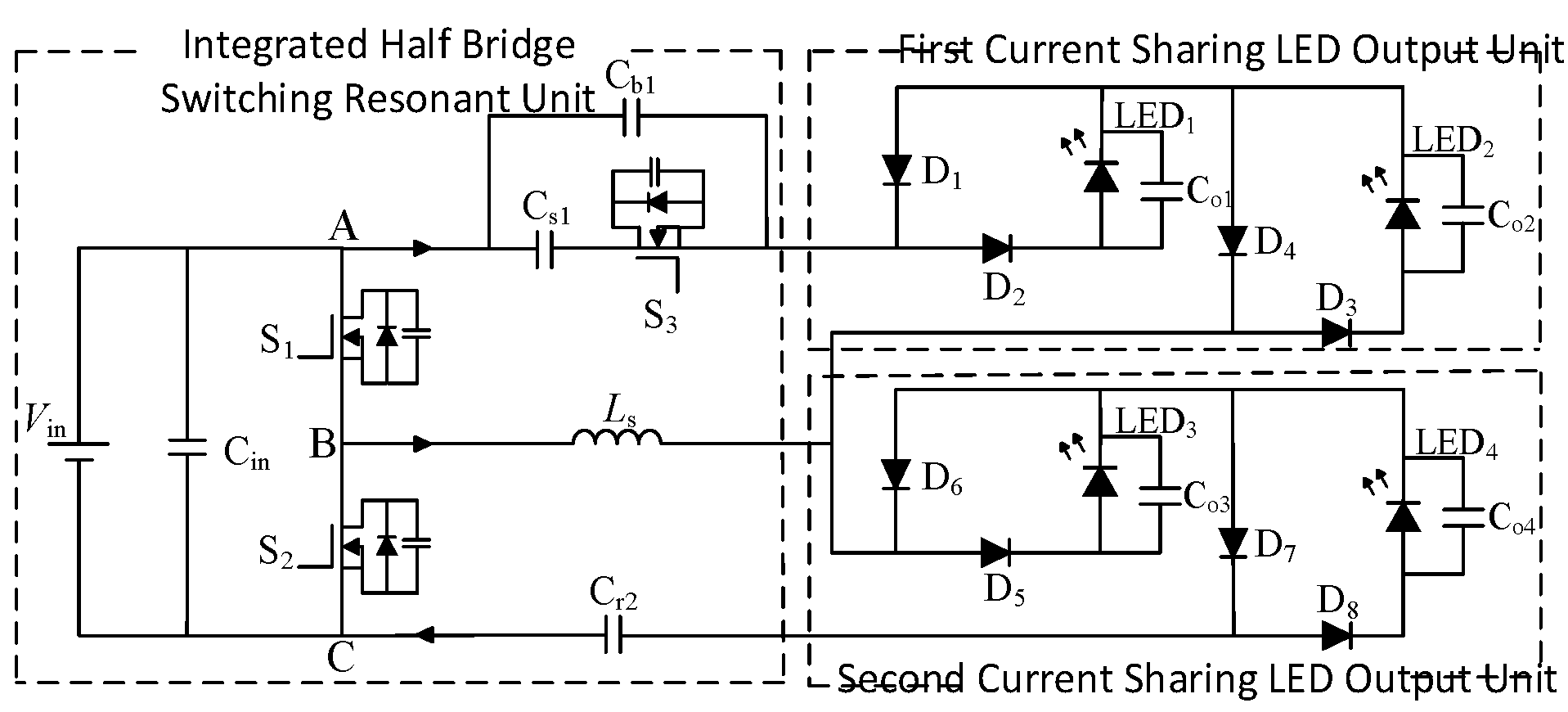
2. Analysis of Circuit Structure and Working Principle
2.1. Topology
2.2. Operational Modal Analysis
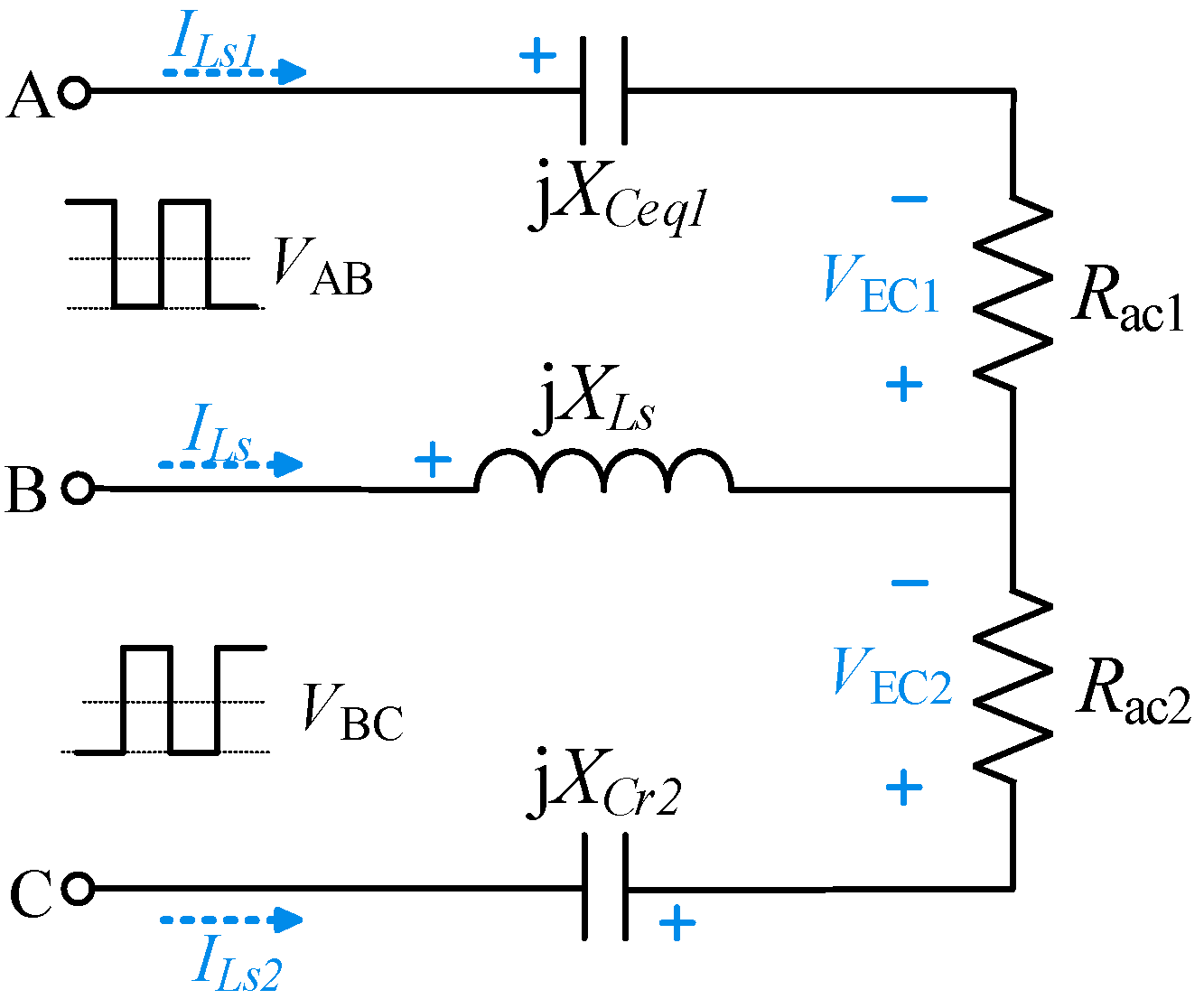
3. Gain Analysis and Dimming Control Strategy
3.1. Circuit Gain Analysis
3.2. Constant-Frequency PWM Dimming
4. Performance Analysis of LED Driver
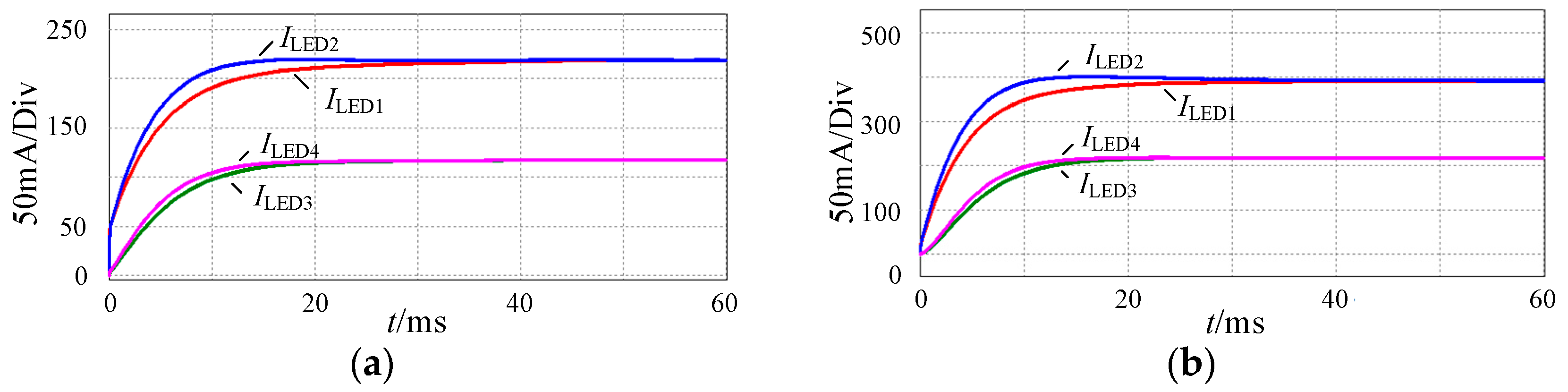
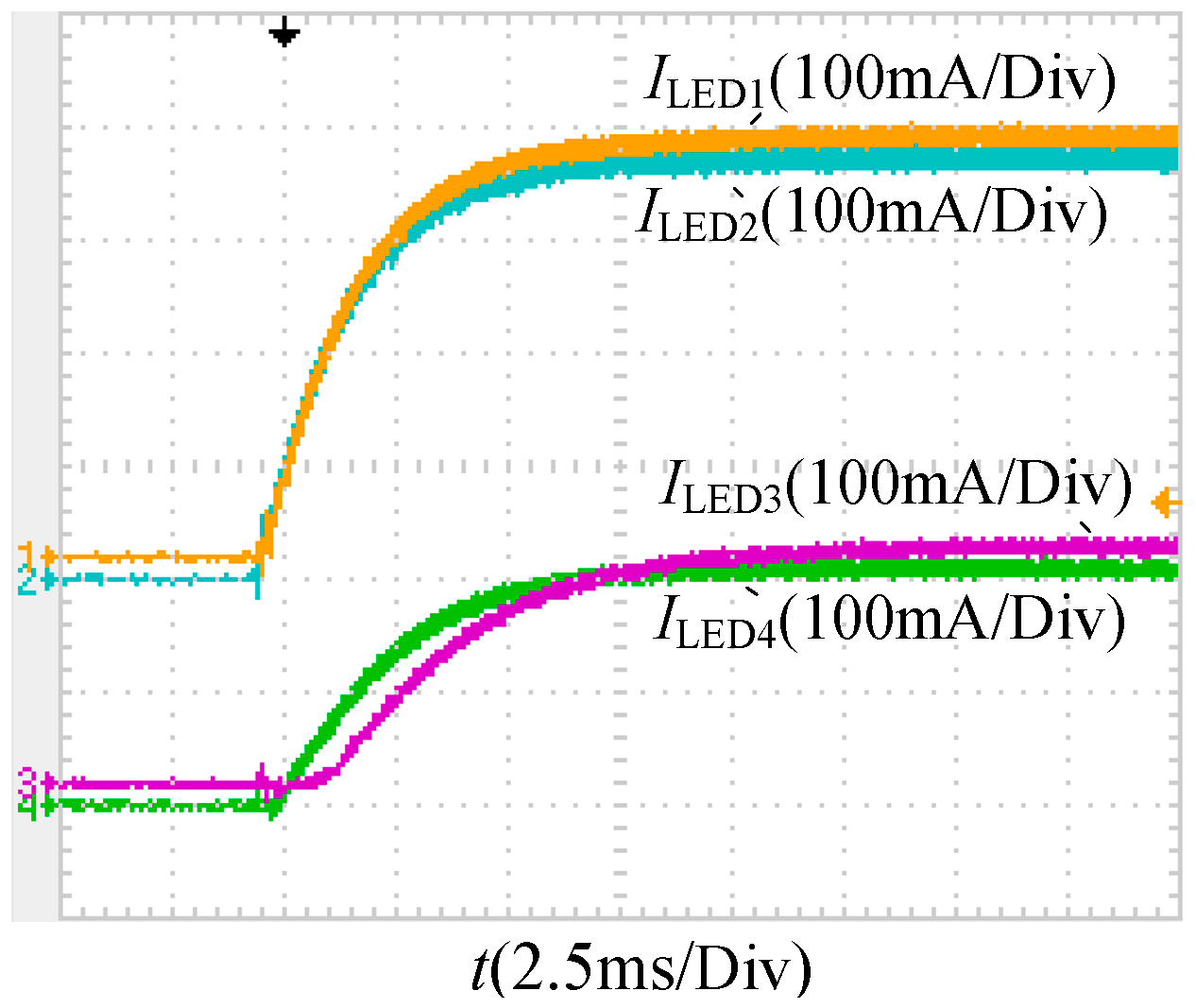
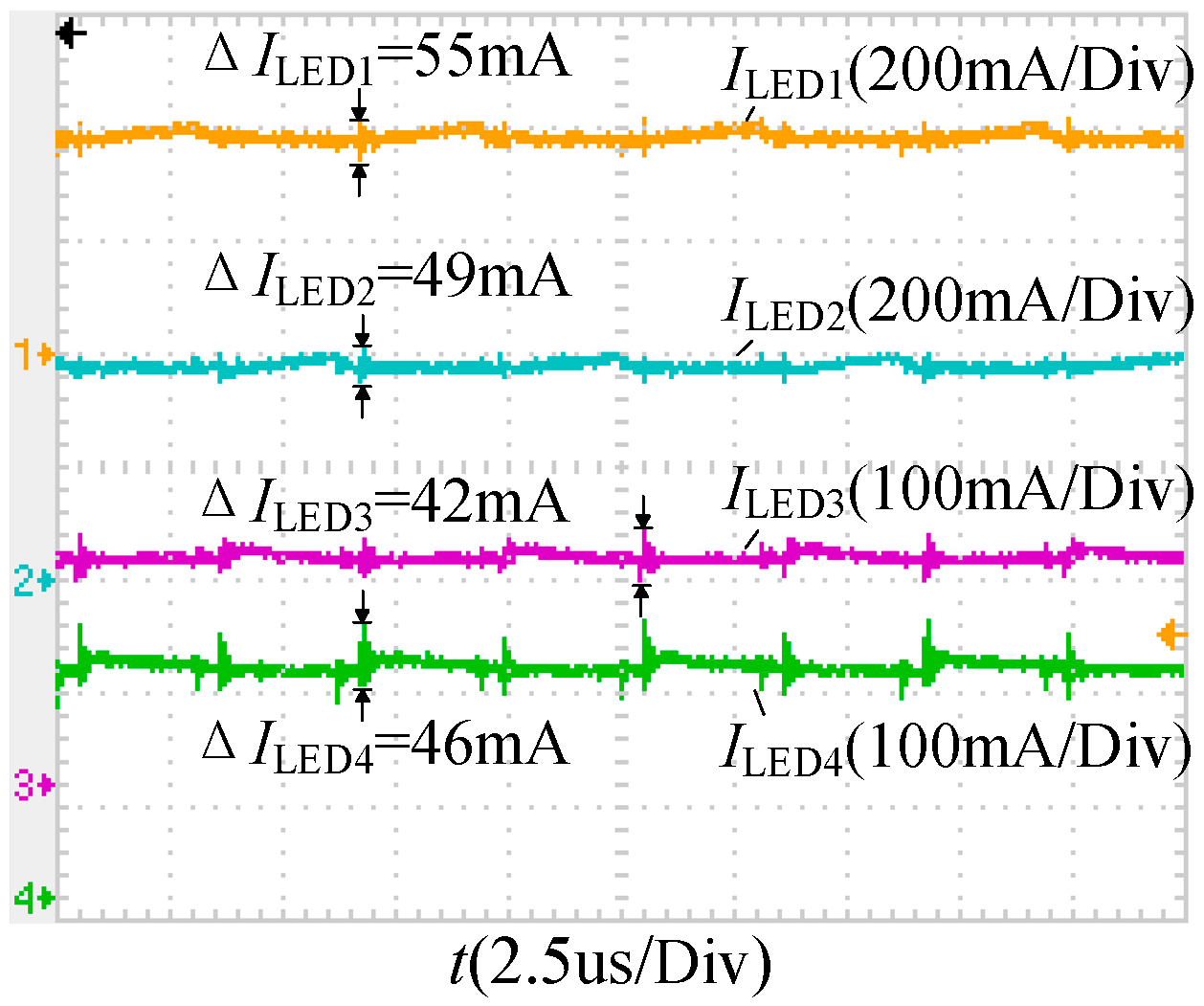
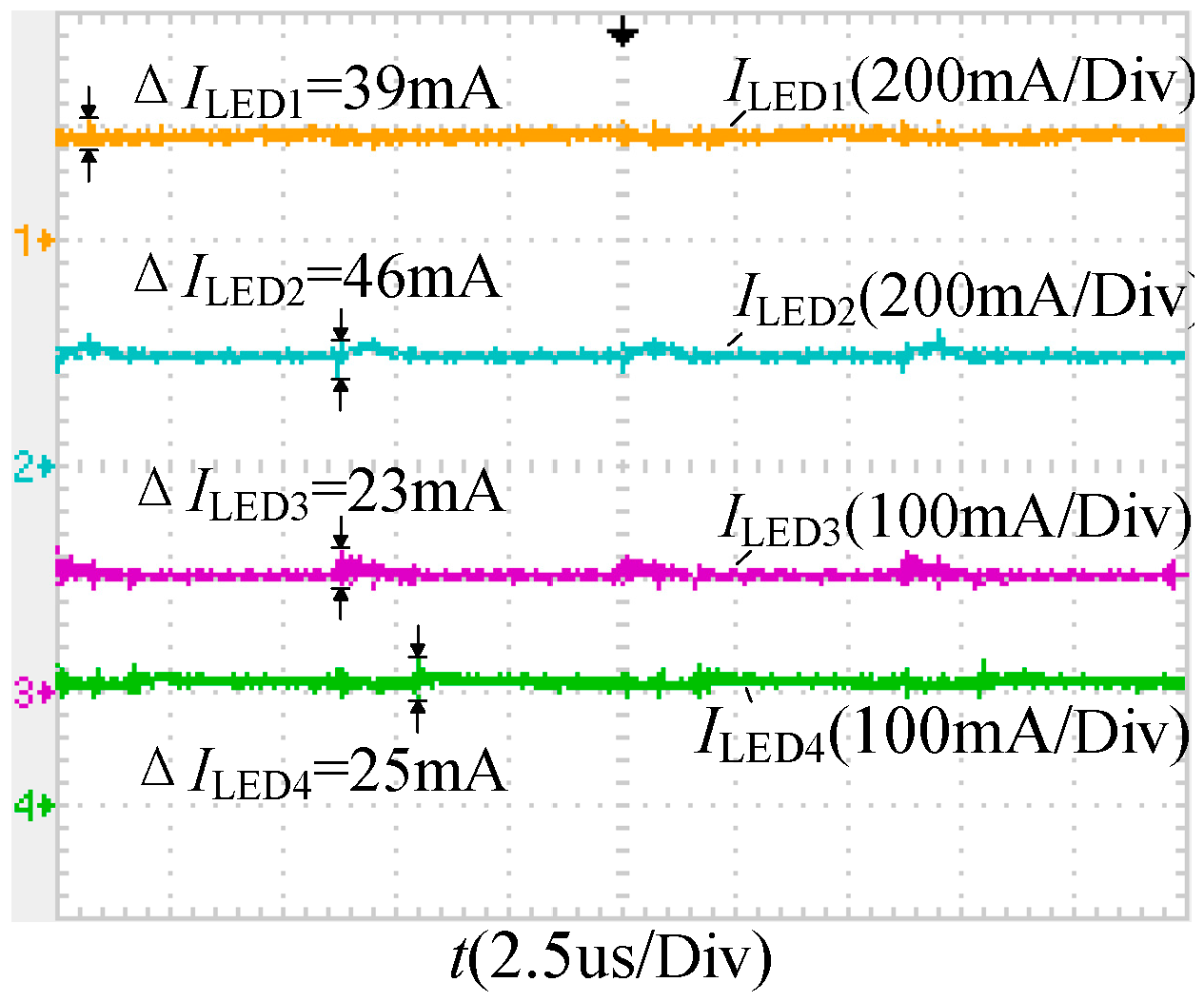
4.1. Current-Sharing Characteristics among Output Branches
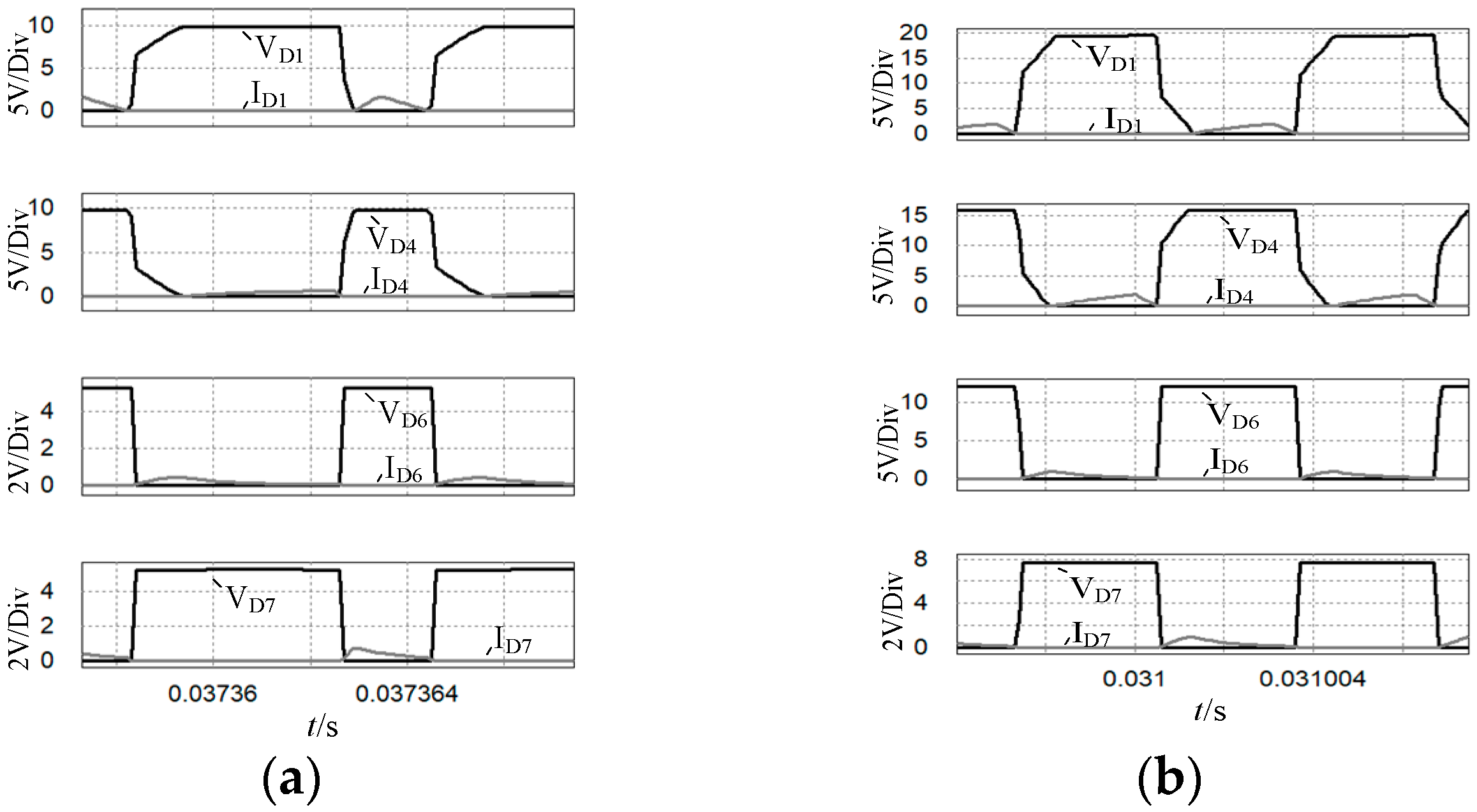
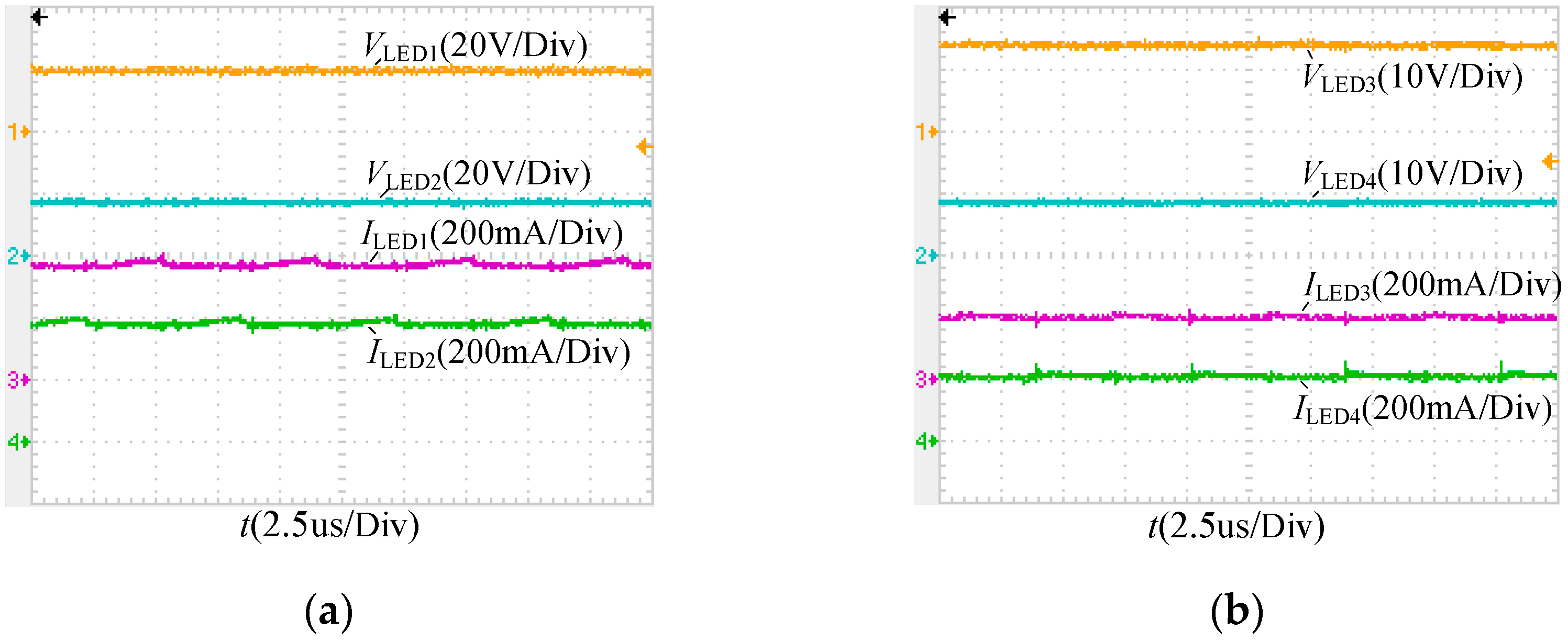
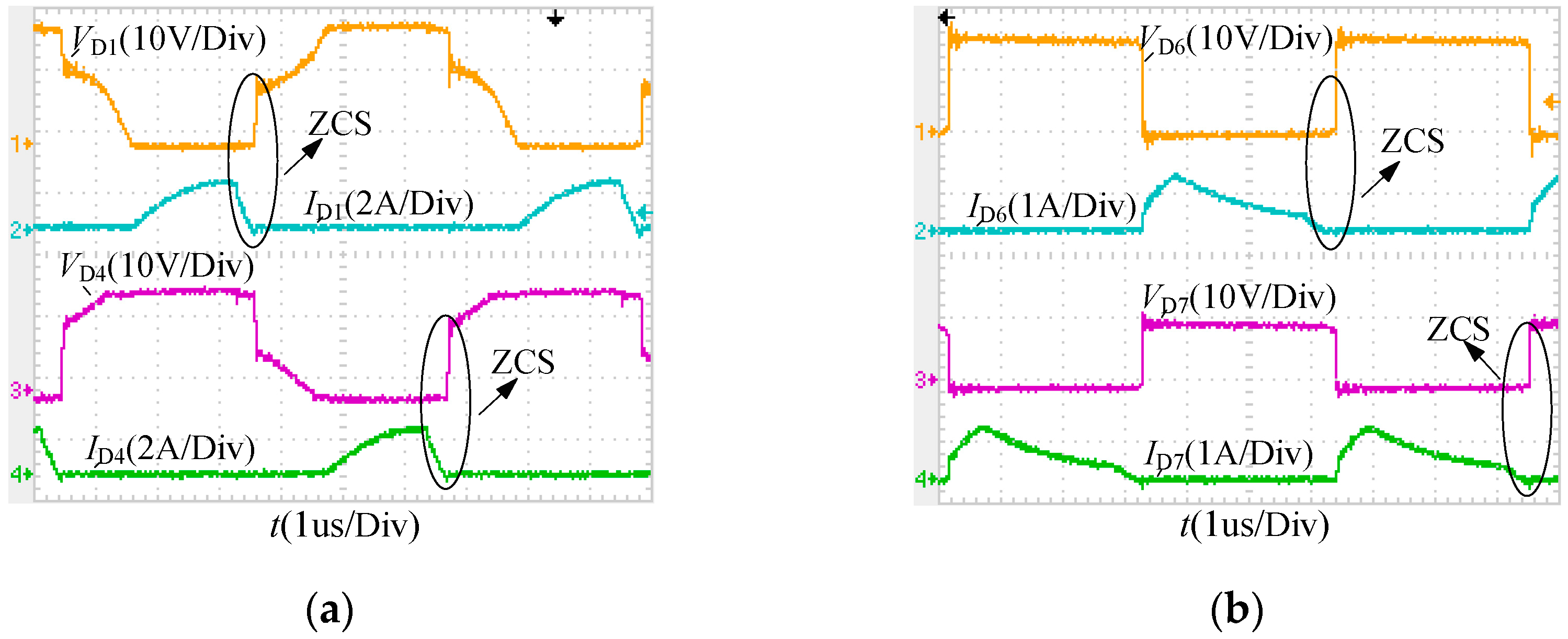
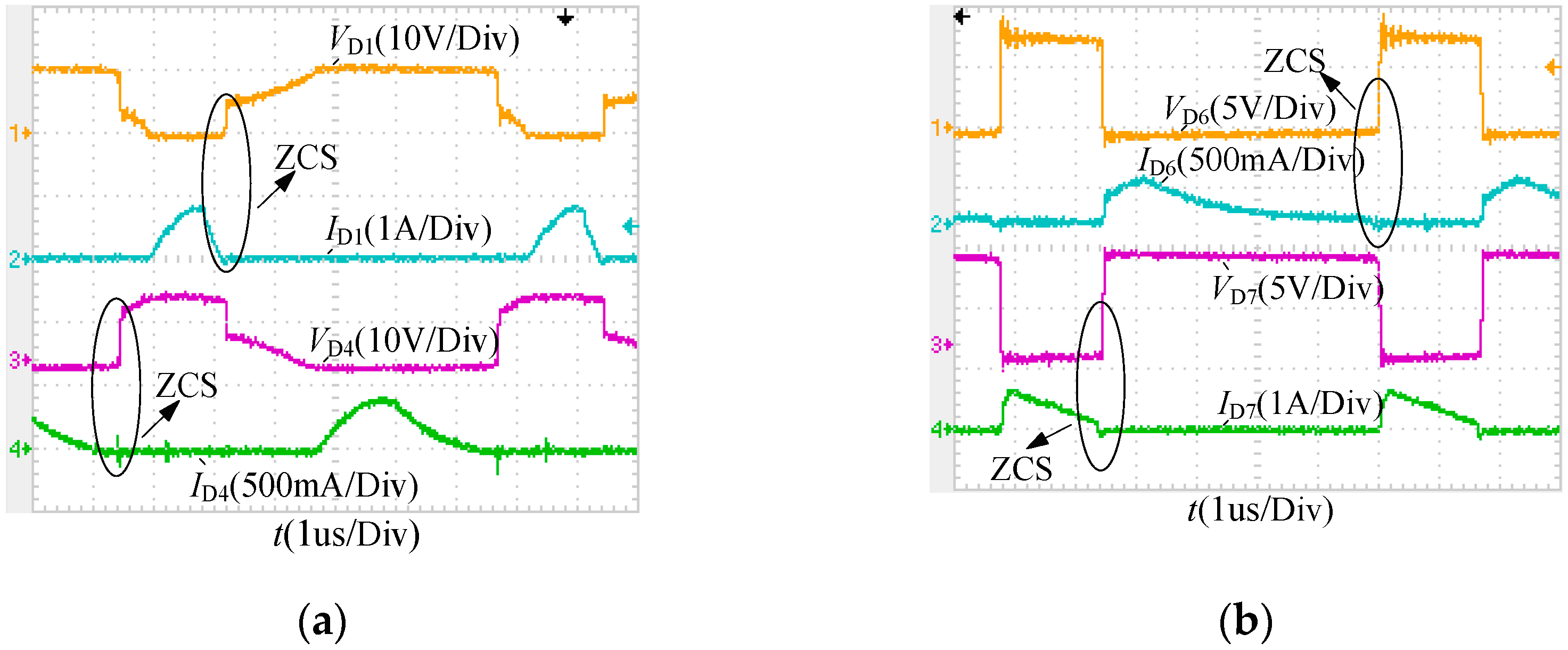
4.2. Realization of Soft-Switching Conditions
5. Simulation Analysis and Experimental Verification
5.1. Simulation Analysis
5.2. Experimental Verification
6. Discussion
7. Conclusions
- Energy efficiency: The driver’s ability to achieve soft switching reduces switching losses, leading to higher efficiency. This is especially valuable in a global context, where energy conservation is a major concern.
- Versatile lighting options: The multi-color lighting application of this driver allows for greater flexibility in creating diverse lighting effects and moods, catering to different global design and aesthetic preferences.
- Cost savings: The use of only three switches and one inductor in the design simplifies the circuit and potentially reduces manufacturing costs. This can have a positive impact on the global market, making the technology more accessible and cost-effective.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Castro, I.; Vazquez, A.; Lamar, D.G.; Arias, M.; Hernando, M.M.; Sebastian, J. An electrolytic capacitorless modular three-phase AC-DC LED driver based on summing the light output of each phase. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 2255–2270. [Google Scholar] [CrossRef]
- Wu, B.-S.; Mansoori, M.; Trumpler, K.; Addo, P.W.; MacPherson, S.; Lefsrud, M. Effect of Amber (595 nm) Light Supplemented with Narrow Blue (430 nm) Light on Tomato Biomass. Plants 2023, 12, 2457. [Google Scholar] [CrossRef] [PubMed]
- Guan, H.; Ji, Q.; Han, T.; Cheng, M. Research on DC distribution mode of LED lighting system in plant factory. Electron. World 2022, 25–27. [Google Scholar] [CrossRef]
- Nacheva, L.; Dimitrova, N.; Koleva-Valkova, L.; Stefanova, M.; Ganeva, T.; Nesheva, M.; Tarakanov, I.; Vassilev, A. In Vitro Multiplication and Rooting of Plum Rootstock ‘Saint Julien’ (Prunus domestica subsp. insititia) under Fluorescent Light and Different LED Spectra. Plants 2023, 12, 2125. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Zhang, Y.; Ma, D. A SIMO Parallel-String Driver IC for Dimmable LED Backlighting with Local Bus Voltage Optimization and Single Time-Shared Regulation Loop. IEEE Trans. Power Electron. 2012, 27, 452–462. [Google Scholar] [CrossRef]
- Dong, Z.; Chi, K.T.; Hui, S.R. Current-Source-Mode Single-Inductor Multiple-Output LED Driver with Single Closed-Loop Control Achieving Independent Dimming Function. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 1198–1209. [Google Scholar] [CrossRef]
- Reddy, U.R.; Narasimharaju, B.L. Cost-Effective Zero-Voltage Switching Dual-Output LED Driver. IEEE Trans. Power Electron. 2017, 32, 7941–7953. [Google Scholar] [CrossRef]
- Veeramallu, V.K.S.; Porpandiselvi, S.; Narasimharaju, B.L. A buck-boost integrated high gain non-isolated half-bridge seriesresonant converter for solar PV/battery fed multiple load LED lighting applications. Int. J. Circuit Theory Appl. 2020, 48, 266–285. [Google Scholar] [CrossRef]
- Veeramallu, V.K.S.; Porpandiselvi, S.; Narasimharaju, B.L. A Nonisolated Wide Input Series Resonant Converter for Automotive LED Lighting System. IEEE Trans. Power Electron. 2021, 36, 5686–5699. [Google Scholar] [CrossRef]
- Molavi, N.; Farzanehfard, H. Load-Independent Hybrid Resonant Converter for Automotive LED Driver Applications. IEEE Trans. Power Electron. 2022, 37, 8199–8206. [Google Scholar] [CrossRef]
- Molavi, N.; Farzanehfard, H. A Nonisolated Wide-Range Resonant Converter for LED Driver Applications. IEEE Trans. Ind. Electron. 2023, 70, 8939–8946. [Google Scholar] [CrossRef]
- Tian, H.; Liu, J.; Zeng, J. Constant frequency resonant multi-channel LED current sharing driver based on controllable switched capacitor. Acta Electrotech. Sin. 2019, 34, 286–295. [Google Scholar]
- Liang, G.; Tian, H.; An, Z.; Zhang, T.; Zhang, X. A new multi-channel independent dimming LED driver. New Technol. Electr. Energy 2020, 39, 72–80. [Google Scholar]
- Yada, T.; Katamoto, Y.; Yamada, H.; Tanaka, T.; Okamoto, M.; Hanamoto, T. Design and Experimental Verification of 400-W Class LED Driver with Cooperative Control Method for Two-Parallel Connected DC/DC Converters. Energies 2018, 11, 2237. [Google Scholar] [CrossRef]
- Kolla, H.R.; Vishwanathan, N.; Murthy, B.K. Independently Controllable Dual-Output Half-Bridge Series Resonant Converter for LED Driver Application. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 2178–2189. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Y.; Liu, Y.F.; Yang, Z.A.; Afsharian, J.; Gong, B. LLC resonant converter with shared power switches and dual coupled resonant tanks to achieve automatic current sharing. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; pp. 5712–5719. [Google Scholar]
- Martins, M.; Perdigao, M.S.; Mendes, A.M.; Pinto, R.A.; Alonso, J.M. Analysis, Design, and Experimentation of a Dimmable Resonant-Switched-Capacitor LED Driver With Variable Inductor Control. IEEE Trans. Power Electron. 2017, 32, 3051–3062. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, F.; Ni, J. Symmetrical jumper capacitor LED current sharing circuit. J. Electrotech. 2014, 29, 196–203. [Google Scholar]





| Name | Value or Model |
|---|---|
| Input voltage (Vin) | 48 V |
| Common inductance (Ls) | 10 uH |
| Resonant capacitance (Cs1/Cr2/Cb1) | 100 nF/68 nF/68 nF |
| Switching frequency (fs) | 112 kHz |
| Filter capacitor (Co1~Co4) | 10 uF |
| Load | 10 Ω |
| Switching (S1,S2,S3) | NCE0224K |
| Diode (D1~D8) | ES5DB |
| Number of Switch Tubes | Number of Inductance | Number of Capacitance | Number of Load | ZVS | ZCS | Maximum Efficiency | |
|---|---|---|---|---|---|---|---|
| Literature [4] | 3 | 1 | 2 | 2 | no | no | 88% |
| Literature [5] | 2 | 1 | 3 | 2 | yes | no | 95.5% |
| Literature [7] | 4 | 2 | 3 | 1 | yes | no | 94.19% |
| Literature [9] | 3 | 2 | 3 | 1 | yes | yes | 97.8% |
| Literature [10] | 3 | 1 | 10 | 4 | yes | no | 94.1% |
| Literature [12] | 3 | 2 | 6 | 2 | yes | no | 91.5% |
| this paper | 3 | 1 | 7 | 4 | yes | yes | 96.56% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Jiang, L.; Xie, W. A Soft-Switching Proportional Dimming LED Driver Based on Switched Capacitor. Energies 2024, 17, 1368. https://doi.org/10.3390/en17061368
Zhang J, Jiang L, Xie W. A Soft-Switching Proportional Dimming LED Driver Based on Switched Capacitor. Energies. 2024; 17(6):1368. https://doi.org/10.3390/en17061368
Chicago/Turabian StyleZhang, Jie, Lu Jiang, and Weichong Xie. 2024. "A Soft-Switching Proportional Dimming LED Driver Based on Switched Capacitor" Energies 17, no. 6: 1368. https://doi.org/10.3390/en17061368
APA StyleZhang, J., Jiang, L., & Xie, W. (2024). A Soft-Switching Proportional Dimming LED Driver Based on Switched Capacitor. Energies, 17(6), 1368. https://doi.org/10.3390/en17061368





