Equilibrium between Environmental and Economic Objectives: An Activity-Based Costing Approach Application for Carbon Emissions Management in the Aluminum Alloy Wheel Industry
Abstract
1. Introduction
2. Background and Literature
2.1. Research Background
2.2. Literature Review
3. Materials and Methods
3.1. The Assumptions of This Paper
- The ABC production process segregates activities into individual units and batch operations;
- The period under consideration maintains a constant unit selling price;
- Utilization of all machinery and labor is at a full 100%, with no expected failures or mishaps during this timeframe;
- Utilization of all materials is efficient, ensuring no damage or waste occurs;
- Material costs remain stable throughout this period, yet the company benefits from negotiated discounts with suppliers, directly influencing its profit margins. This discount agreement is in effect for the entire duration of this period;
- Municipal laws permit the extension of work hours, encompassing additional shifts that incur overtime, compensated at rates of 133% and 166% of the standard pay for the second and third tiers of overtime, respectively;
- The company incurs a carbon tax for each product, with the tax amount being proportional to the production volume;
- The extent of carbon rights is subject to various government policies, but the company is free to engage in unrestricted carbon rights trading within the carbon market.
- In this ABC model, outsourcing is not considered; all products, barring raw materials, are required to be manufactured in-house;
- Trading of carbon rights is initiated only when the company’s total emissions surpass the emission thresholds established by the government.
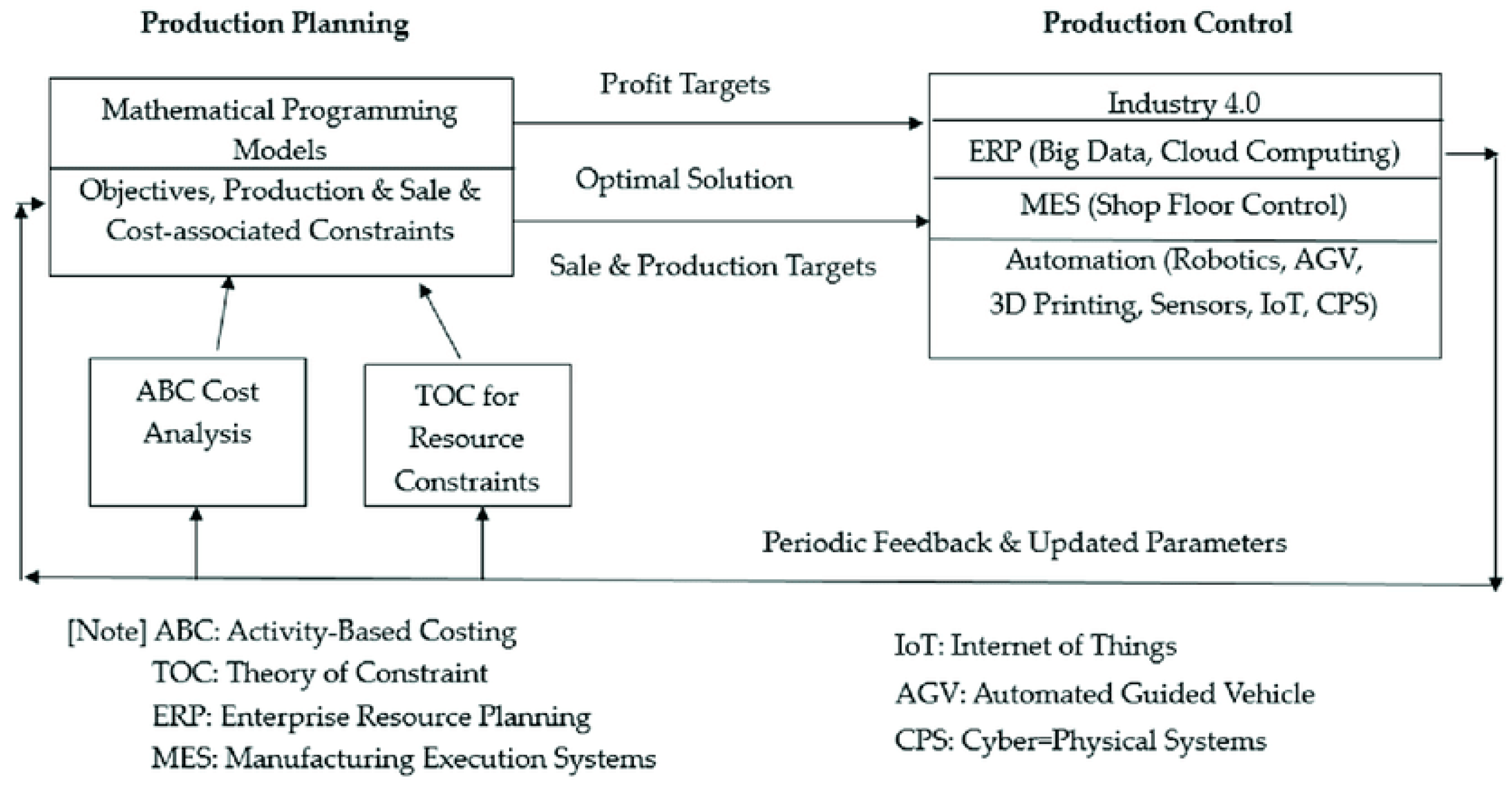
3.2. Basic Production Planning Model
| π | The maximum profit achievable by the company. |
| Si | The per-unit selling price of the ith product. |
| Pi | The production output of the ith product. |
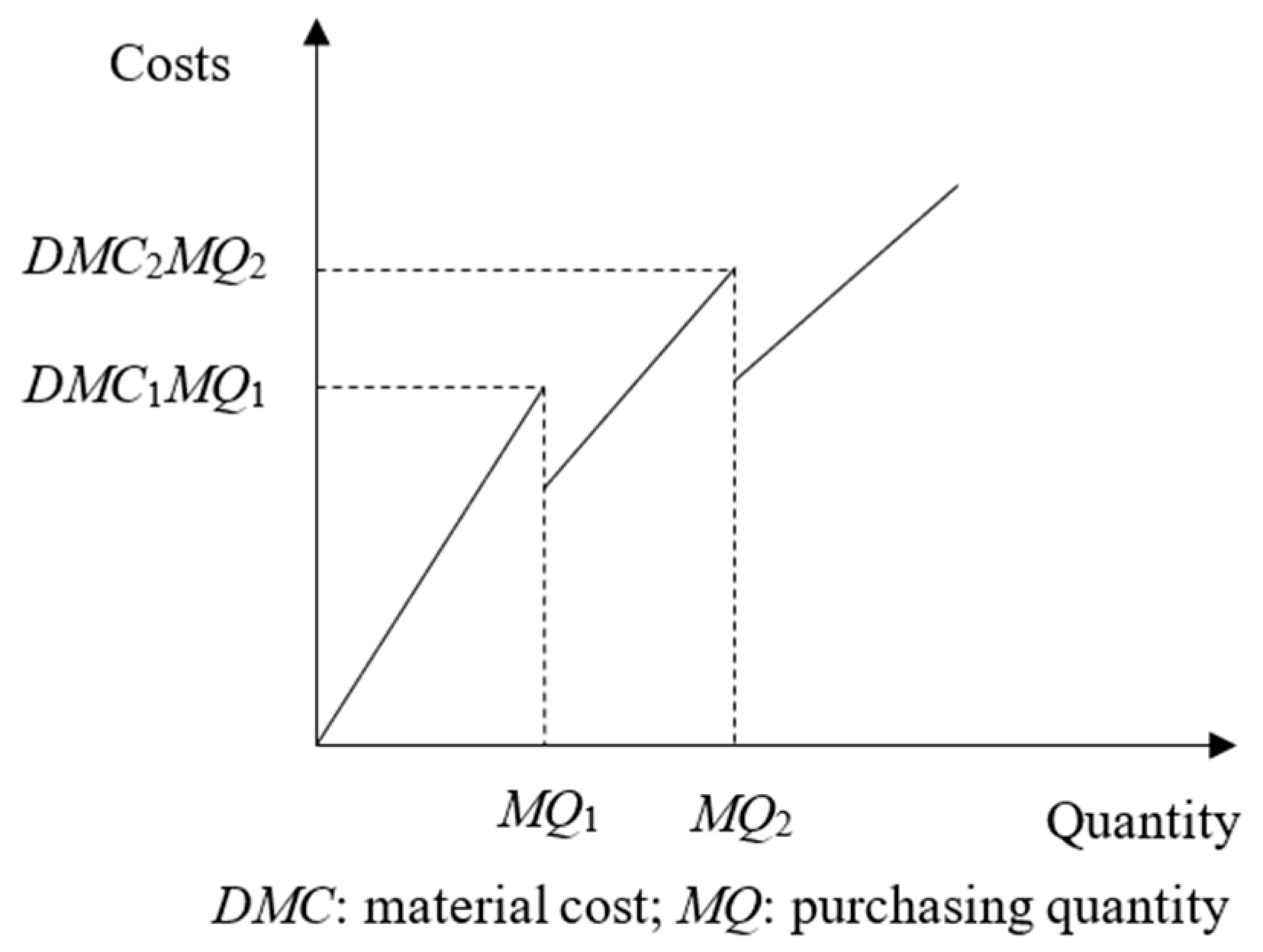
| DMC1, DMC2, DMC3 | The per-unit expense of materials (DMC1), the first-stage discounted cost (DMC2), the second-stage discounted cost (DMC3) |
| DQ1, DQ2, DQ3 | The amount used under standard operating conditions (DQ1), the amount of the initial segment in the discounted area (DQ2), and the amount for the second portion of the discount. (DQ3) |
| MCj | The cost per unit of the material. j. |
| qij | The amount of material j consumed when producing one unit of product i. |
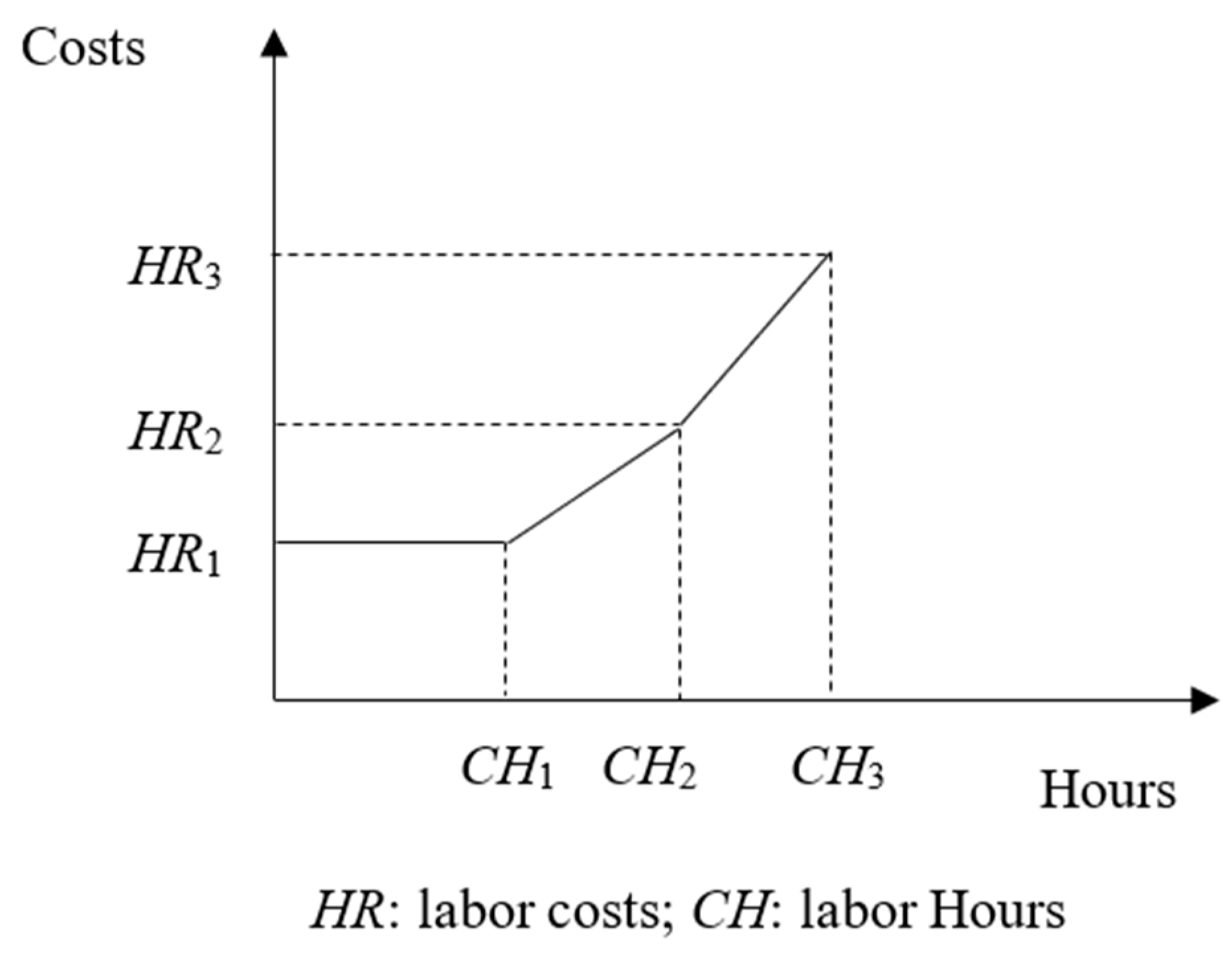
| HR1, HR2, HR3 | Direct labor costs under normal circumstances (HR1), overtime costs in the first period (HR2), and overtime costs in the second period (HR3). |
| ω0, ω1, ω2 | SOS2 variables refer to a group of variables that must have positive values, with the condition that no more than two variables in this group can have values greater than zero. |
| do | The cost incurred for performing one unit of operation ‘o’. |
| Ho | Batch operation (o ∈ B) demand under material handling operation. |
| Bo | The count of batch processes within the scope of material handling operations. (o ∈ B). |
| Sio | This refers to the market demand for product i when it is in the setting operation phase. (o ∈ B). |
| Bio | The quantity of batch production for product i during the setup operation. (o ∈ B). |
| F | The additional expenses that the company in the example incurs and remains constant. |
| MQ1, MQ2, MQ3 | The maximum purchase quantity under normal circumstances (MQ1), the first-tier discount (MQ2), and the second-tier discount situation (MQ3). |
| α0, α1, α2 | SOS1 variable: if one variable is assigned a value of 1, then all other variables must be set to zero precisely. |
| uio | This is the amount of labor time needed to produce one unit of product i during operation o. |
| CH1, CH2, CH3 | This refers to the highest number of direct labor hours available under typical working conditions (CH1), the first period of overtime (CH2), and the second period of overtime (CH3). |
| β1, β2 | SOS1 variable: when one of the variables is set to 1, the other variables must be exactly zero. |
| ρo | In simpler terms, this refers to the specific amount of materials needed for each set of operations in the material handling process (o ∈ B). |
| Ao | Capacity of batch-level operations (o ∈ B). |
| τio | The required quantity of each batch of batch-level operations for the production of i products under the setting work (o ∈ B). |
| rhio | The machine-hour demand for producing a unit of product i under o operation. |
| CPo | Machine capacity for operation o (o = 1, 2, 5). |
| CPCNC | CNC machine tool capacity. |
3.3. Objective Function for Producing Maximum Profit
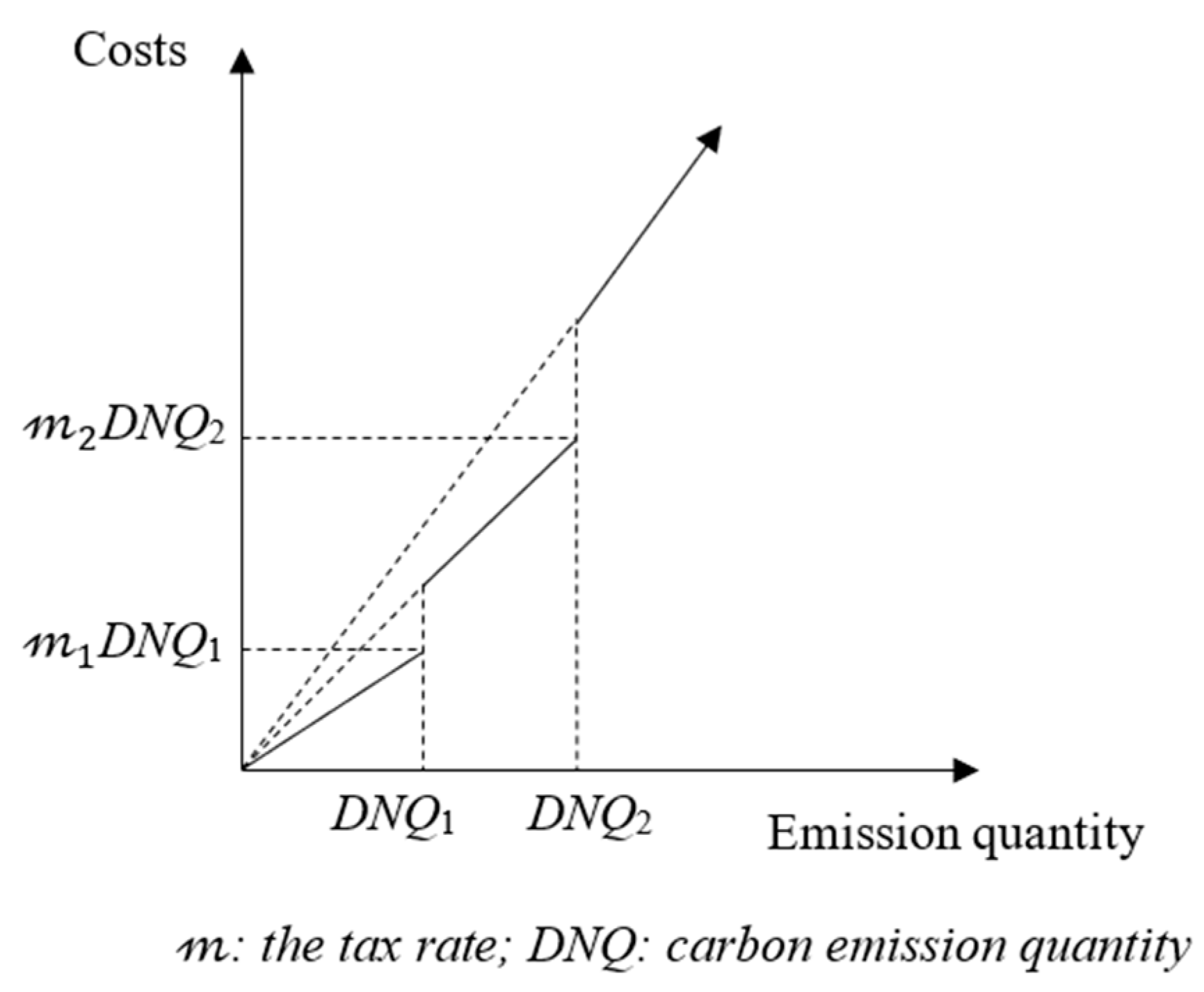
| 1,2,3 | Carbon tax rate for the first stage of carbon tax cost (1), carbon tax rate for the second stage of carbon tax cost (2), carbon tax rate for the third stage of carbon tax cost (3). |
| ,, | The carbon emission quantity of the first segment (), the carbon emission quantity of the second segment () and the carbon emission quantity of the third segment (). |
| DNQ1, DNQ2, DNQ3 | Maximum ceiling for carbon emissions in the first segment (DNQ1), carbon emissions in the second segment (DNQ2), and in the third segment (DNQ3) |
| 0, 1, 2 | SOS1 variables: when one of the variables is set to 1, the others must be exactly zero |
3.3.1. Carbon Tax Function with Full Progressive Tax Rates without Allowances (with Carbon Trading)
| 1, 2, 3 | The tax rate applied to carbon emissions for the initial phase of the carbon tax expense (1), the tax rate assigned to carbon emissions in the second phase of the carbon tax expenditure (2), the tax rate applied to carbon emissions during the third phase of calculating carbon tax costs (3). |
| , , | The carbon emission quantity of the first segment (), the carbon emission quantity of the second segment () and the carbon emission quantity of the third segment (). |
| Ø1, Ø2 | SOS1 variables: when one of the variables is set to 1, the others must be exactly zero. |
| r | unit carbon cost. |
| CCE | The aggregate amount of carbon dioxide released by the company. |
| GCE | Maximum carbon emissions cap set by the government. |
| CQ1, CQ2 | Determine if the business should acquire carbon credits, if CQ1 > 0, the company does not need to purchase carbon rights; conversely, if CQ2 > 0, the company must purchase carbon rights. |
| MBR | Maximum number of carbon rights purchased. |
3.3.2. Model C: Carbon Tax Function with Full Progressive Tax Rate with Allowances
| 1,2,3 | The initial price set for the carbon tax (1), the second carbon tax price (2), and the third carbon tax price (3). |
| SOS2 variable refers to a group of variables that are positive, and within this set, no more than two variables can have values greater than zero. | |
| The amount of carbon emissions from the tax-free allowance . | |
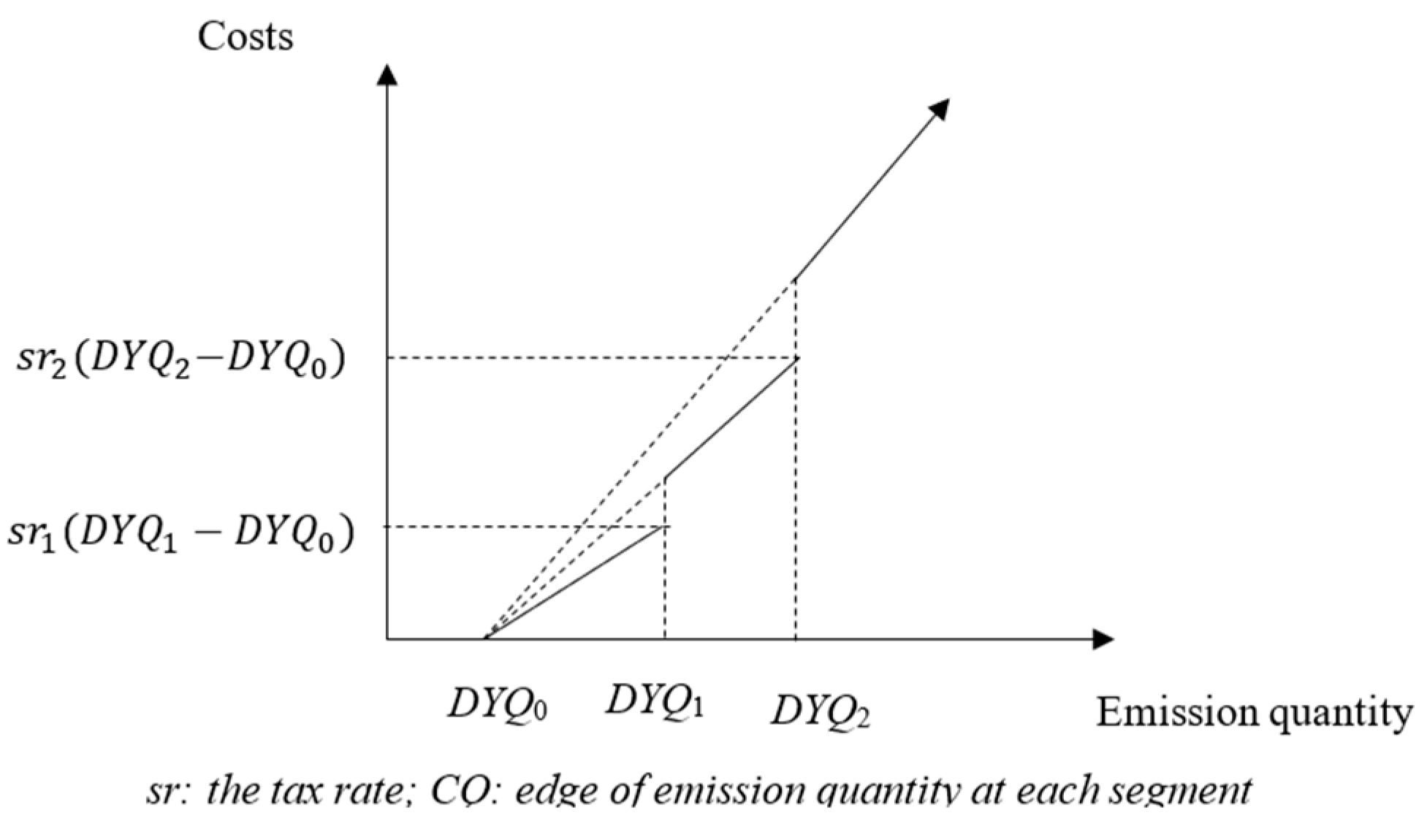
| ,, | The amount of carbon emissions occurring in the initial segment (), carbon emissions in the second segment (), and the carbon emissions in the third segment (). |
| DYQ0, DYQ1, DYQ2, DYQ3 | Carbon emissions of exemptions (DYQ0), carbon emissions of the first stage (DYQ1), the second stage (DYQ2), and carbon emissions of the third stage (DYQ3). |
| 0, 1,23 | SOS1 variables: when one of the variables is set to 1, the others must be exactly zero. |
3.3.3. Carbon Tax Function with Full Progressive Tax Rates with Allowances (with Carbon Trading)
| 1,2,3 | The first carbon tax price (1), the second carbon tax price (2), and the third carbon tax price (3). |
| The SOS2 variable refers to a group of variables that are all positive, and within this set, no more than two variables can have values other than zero. | |
| The quantity of carbon emissions that falls within the limit allowed without incurring tax . | |
| ,, | Carbon emissions in the first segment (), carbon emissions in the second segment (), and the carbon emissions in the third segment (). |
| Ø1, Ø2 | SOS1 variables: when one of the variables is set to 1, the others must be exactly zero. |
| r | unit carbon cost. |
| CCE | The company’s total carbon emissions. |
| GCE | Maximum carbon emissions cap set by the government. |
| CQ1, CQ2 | Decide whether the company wants to purchase carbon rights; if CQ1 > 0, the company does not need to purchase carbon rights; conversely, if CQ2 > 0, the company must purchase carbon rights. |
| MBR | Maximum number of carbon rights purchased. |
3.4. Methods and Material: Multi-Period Production Decision-Making Model
3.4.1. Objective Function
3.4.2. Direct Material Discount Function
3.4.3. Unit-Level Operations: Direct Labor Cost Function
3.4.4. Batch-Level Operations: Material Handling and Setting Cost Functions
3.4.5. Constraints of Machine Hours
3.5. Multi-Phase Model of Model 1
3.5.1. Carbon Tax Function with Full Progressive Tax Rates without Allowances
3.5.2. Carbon Tax Function with Full Progressive Tax Rates without Allowances (with Carbon Trading)
| ACQ1, ACQ2 | In the multi-period model, the enterprise evaluates the option of purchasing carbon credits. IF ACQ1 > 0, the company does not need to purchase carbon rights; on the contrary, if ACQ2 > 0, the company must purchase carbon rights. |
| MQ | Equivalent to the sum of GCE1 + GCE2 + …GCEt. |
| TMBR | The highest quantity of carbon credits a firm can buy over multiple planning periods. |
| λ1, λ2, | In an SOS1 variable set, if any single variable is assigned the value 1, all remaining variables in the set are constrained to be precisely zero. |
3.6. Multi-Phase Model of Model 2
3.6.1. Carbon Tax Function with Full Progressive Tax Rates with Allowances
3.6.2. Carbon Tax Function with Full Progressive Tax Rates with Allowances (with Carbon Trading)
| ACQ1, ACQ2 | In the multi-period framework, the decision to buy carbon credits hinges on specific conditions. Should be greater than zero, the company is exempt from the need to acquire carbon credits; however, if exceeds zero, the firm is obligated to purchase carbon rights. |
| MQ | Equivalent to the sum of GCE1 + GCE2 + …GCEt. |
| TMBR | Maximum number of carbon rights purchased in multi-period model |
| λ1, λ2, | SOS1 variables: when one of the variables is set to 1, the others must be exactly zero. |
4. Results and Discussion
4.1. Results
4.1.1. Sample Data
4.1.2. Data Analysis
4.1.3. Carbon Tax Function with Full Progressive Tax Rate without Allowance (Model 1)
4.1.4. Carbon Tax Function with Full Progressive Tax Rate with Allowances (Model 2)
4.1.5. Model Comparison
4.1.6. Review
4.2. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Metz, B.; Davidson, O.; Bosch, P.; Dave, R.; Meyer, L. Climate Change 2007: Mitigation of Climate Change; Cambridge University Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Chen, L.; He, F. Efficiency Analysis of Carbon Emission Quotas. J. Sci. Ind. Res. 2017, 76, 461–464. [Google Scholar]
- Ellerman, A.D.; Convery, F.J.; De Perthuis, C. Pricing Carbon: The European Union Emissions Trading Scheme; Cambridge University Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Kunsch, P.; Springael, J. Simulation with system dynamics and fuzzy reasoning of a tax policy to reduce CO2 emissions in the residential sector. Eur. J. Oper. Res. 2008, 185, 1285–1299. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, W.; Yuan, Y.; Zhou, R. An integrated carbon policy-based interactive strategy for carbon reduction and economic development in a construction material supply chain. Sustainability 2017, 9, 2107. [Google Scholar] [CrossRef]
- Liu, W.; Xie, W.; Qiu, P. The impact of carbon emission cap and carbon trade mechanism on the order decision with stochastic demand. Int. J. Shipp. Transp. Logist. 2015, 7, 347–376. [Google Scholar] [CrossRef]
- Daga, A. New Global Carbon Exchange to Launch in Singapore by Year-End. Reuters. Available online: https://www.reuters.com/business/sustainable-business/singapores-dbs-stanchart-team-up-global-carbon-credit-exchange-2021-05-20/ (accessed on 20 May 2021).
- Du, S.; Qian, J.; Liu, T.; Hu, L. Emission allowance allocation mechanism design: A low-carbon operations perspective. Ann. Oper. Res. 2020, 291, 247–280. [Google Scholar] [CrossRef]
- Fang, C.; Ma, T. Technology adoption with carbon emission trading mechanism: Modeling with heterogeneous agents and uncertain carbon price. Ann. Oper. Res. 2021, 300, 577–600. [Google Scholar] [CrossRef]
- Environmental Protection Administration, Executive Yuan. 2018 Republic of China National Greenhouse Gas Inventory Report; Environmental Protection Administration, Executive Yuan: Taipei, Taiwan, 2018. [Google Scholar]
- United Nations Framework Convention on Climate Change (UNFCCC). Adoption of the Paris Agreement. I: Proposal by the President (Draft Decision); United Nations Office: Geneva, Switzerland, 2015. [Google Scholar]
- Tsai, W.H.; Chu, P.Y.; Lee, H.L. Green activity-based costing production planning and scenario analysis for the aluminum-alloy wheel industry under industry 4.0. Sustainability 2019, 11, 756. [Google Scholar] [CrossRef]
- World Bank. State and Trends of Carbon Pricing. 2023. Available online: https://www.worldbank.org/en/research (accessed on 1 January 2024).
- Parry, I.W.H.; Black, S.; Zhunussova, K. Carbon Taxes or Emissions Trading Systems? Instrument Choice and Design; International Monetary Fund: Washington, DC, USA, 2022; 25p. [Google Scholar]
- Jonsson, S.; Ydstedt, A.; Asen, E. Looking Back on 30 Years of Carbon Taxes in Sweden; Fiscal Fact No. 727; The Tax Foundation: Washington, DC, USA, 2020. [Google Scholar]
- World Economic Forum. Global Carbon Pricing Can Reduce Emissions and Pay for Itself. Available online: https://www.weforum.org/press/2021/11/global-carbon-pricing-can-reduce-emissions-and-pay-for-itself/ (accessed on 1 January 2024).
- Hick, S. Morals Maketh the money. Aust. CPA 2000, 70, 72–73. [Google Scholar]
- Shapiro, J. Modeling the Supply Chain; Nelson Education: Toronto, ON, Canada, 2006. [Google Scholar]
- Das, S.K.; Green, J.A.S.; Kaufman, J.G. The development of recycle-friendly automotive aluminum alloys. JOM 2007, 59, 47–51. [Google Scholar] [CrossRef]
- Ascione, A. What is the Difference between Hastelloy® and Incoloy®? Continental Steel & Tube Company: Fort Lauderdale, FL, USA, 2015. [Google Scholar]
- Dwivedi, S.P.; Sharma, S.; Mishra, R.K. Characterization of waste eggshells and CaCO3 reinforced AA2014 green metal matrix composites: A green approach in the synthesis of composites. Int. J. Precis. Eng. Manuf. 2016, 17, 1383–1393. [Google Scholar] [CrossRef]
- The Aluminum Association. Aluminum: The element of sustainability. In A North American Aluminum Industry Sustainability Report; The Aluminum Association: Arlington, VA, USA, 2011; p. 33. [Google Scholar]
- Kaplan, R.S. Management accounting for advanced technological environments. Science 1989, 245, 819–823. [Google Scholar] [CrossRef]
- Malmi, T. Activity-based costing diffusion across organizations: An exploratory empirical analysis of Finnish firms. Account. Organ. Soc. 1999, 24, 649–672. [Google Scholar] [CrossRef]
- Cao, P.; Toyabe, S.; Kurashima, S.; Okada, M.; Akazawa, K. A modified method of activity-based costing for objectively reducing cost drivers in hospitals. Methods Inf. Med. 2006, 45, 462–469. [Google Scholar] [PubMed]
- Lin, B.Y.J.; Chao, T.H.; Yao, Y.; Tu, S.M.; Wu, C.C.; Chern, J.Y.; Chao, S.H.; Shaw, K.Y. How can activity-based costing methodology be performed as a powerful tool to calculate costs and secure appropriate patient care? J. Med. Syst. 2007, 31, 85–90. [Google Scholar] [PubMed]
- Kee, R.; Schmidt, C. A comparative analysis of utilizing activity-based costing and the theory of constraints for making product-mix decisions. Int. J. Prod. Econ. 2000, 63, 1–17. [Google Scholar] [CrossRef]
- Holmen, J.S. ABC vs. TOC: It’s a matter of time. Strateg. Financ. 1995, 76, 37. [Google Scholar]
- Kim, Y.-W.; Ballard, G. Activity-Based Costing and Its Application to Lean Construction. In Proceedings of the 9th Annual Conference of the International Group for Lean Construction, Singapore, 6–8 August 2001. [Google Scholar]
- Tsai, W.H.; Hsu, J.L.; Chen, C.H.; Chou, Y.W.; Lin, S.J.; Lin, W.R. Application of ABC in hot spring country inn. Int. J. Manag. Enterp. Dev. 2010, 8, 152–174. [Google Scholar] [CrossRef]
- Tsai, W.-H. Activity-based costing model for joint products. Comput. Ind. Eng. 1996, 31, 725–729. [Google Scholar] [CrossRef]
- Tsai, W.H.; Yang, C.H.; Chang, J.C.; Lee, H.L. An activity-based costing decision model for life cycle assessment in green building projects. Eur. J. Oper. Res. 2014, 238, 607–619. [Google Scholar] [CrossRef]
- Fichman, R.G.; Kemerer, C.F. Activity-Based Costing for Component-Based Software Development. Inf. Technol. Manag. 2002, 3, 137–160. [Google Scholar] [CrossRef]
- Roztocki, N. Using the Integrated Activity-Based Costing and Economic Value Added Information System for Project Management. In Proceedings of the 7th Americas Conference on Information Systems, Boston, MA, USA, 3–5 August 2001. [Google Scholar]
- AlMaryani, M.A.H.; Sadik, H.H. Strategic management accounting techniques in Romanian companies: Some survey evidence. Procedia Econ. Financ. 2012, 3, 387–396. [Google Scholar] [CrossRef]
- Almeida, A.; Cunha, J. The implementation of an activity-based costing (ABC) system in a manufacturing company. Procedia Manuf. 2017, 13, 932–939. [Google Scholar] [CrossRef]
- Goldratt, E.M.; Cox, J. The Goal: Excellence in Manufacturing; North River Press: Great Barrington, MA, USA, 1984. [Google Scholar]
- Radovilsky, Z.D. A quantitative approach to estimate the size of the time buffer in the theory of constraints. Int. J. Prod. Econ. 1998, 55, 113–119. [Google Scholar] [CrossRef]
- Pember, A.; Lemon, M. Measuring and Managing Environmental Sustainability: Using Activity-Based Costing/Management (ABC/M); The Consortium for Advanced Management—International (CAM—I): Austin, TX, USA, 2012. [Google Scholar]
- Cooper, R.; Kaplan, R.S. Measure costs right: Make the right decision. CPA J. 1988, 60, 38. [Google Scholar]
- Wesumperuma, A.; Ginige, A.; Ginige, A.; Hol, A. Green Activity Based Management (ABM) for Organisations. In Proceedings of the Australasian Conference on Information Systems, ACIS 2013, Melbourne, Australia, 4–6 December 2013. [Google Scholar]
- Jaedicke, R.K. Improving breakeven analysis by linear programming techniques. NAA Bull. 1961, 42, 5–12. [Google Scholar]
- Balakrishnan, J.; Cheng, C.H. Discussion: Theory of constraints and linear programming: A re-examination. Int. J. Prod. Res. 2010, 38, 1459–1463. [Google Scholar] [CrossRef]
- Fahimnia, B.; Sarkis, J.; Choudhary, A.; Eshragh, A. Tactical supply chain planning under a carbon tax policy scheme: A case study. Int. J. Prod. Econ. 2015, 164, 206–215. [Google Scholar] [CrossRef]
- Demeere, N.; Stouthuysen, K.; Roodhooft, F. Time-driven activity-based costing in an outpatient clinic environment: Development, relevance and managerial impact. Health Policy 2009, 92, 296–304. [Google Scholar] [CrossRef]
- Hsieh, C.L.; Tsai, W.H.; Chang, Y.C. Green activity-based costing production decision model for recycled paper. Energies 2020, 13, 2413. [Google Scholar] [CrossRef]
- Schulze, M.; Seuring, S.; Ewering, C. Applying activity-based costing in a supply chain environment. Int. J. Prod. Econ. 2012, 135, 716–725. [Google Scholar] [CrossRef]
- Tsai, W.H.; Lin, W.R.; Fan, Y.W.; Lee, P.L.; Lin, S.J.; Hsu, J.L. Applying a mathematical programming approach for a green product mix decision. Int. J. Prod. Res. 2012, 50, 1171–1184. [Google Scholar] [CrossRef]
- Zheng, C.W.; Abu, M.Y. Application of activity based costing for palm oil plantation. J. Mod. Manuf. Syst. Technol. 2019, 2, 1–14. [Google Scholar] [CrossRef]
- Kee, R. The sufficiency of product and variable costs for production-related decisions when economies of scope are present. Int. J. Prod. Econ 2008, 114, 682–696. [Google Scholar] [CrossRef]
- Dekker, R.; Bloemhof, J.; Mallidis, I. Operations research for green logistics—An overview of aspects, issues, contributions, and challenges. Eur. J. Oper. Res. 2012, 219, 671–679. [Google Scholar] [CrossRef]
- Qian, L.; David, B.A. Parametric cost estimation based on activity-based costing: A case study for design and development of rotational parts. Int. J. Prod. Econ. 2008, 113, 805–818. [Google Scholar] [CrossRef]
- Plenert, G. Optimizing theory of constraints when multiple constrained resources exist. Eur. J. Oper. Res. 1993, 70, 126–133. [Google Scholar] [CrossRef]

| Merchandise SKU | Accessible | |||||||
|---|---|---|---|---|---|---|---|---|
| o | Car rim | Truck Rim | Custom Rims | Capacity | ||||
| Max/min production volume | Pi | >2000 | >1000 | >2000, 6000 | ||||
| Selling price | Si | 4000 | 6000 | <8000 | ||||
| Direct materials at the unit level | ||||||||
| Aluminum ingot (m = 1) | Refer to the “Discounted material costs” section for the unit price. | qi1 | 10 | 20 | 10 | |||
| Coating (m = 2) | MC2 = $50/unit | qi2 | 2 | 3 | 4 | |||
| Discounted material cost | ||||||||
| Quantity | MQ1 = 80,000 | MQ2 = 250,000 | >250,000 | |||||
| Cost | DMC1 = $70 | DMC2 = $69 | DMC3 = $67 | |||||
| Unit level work | ||||||||
| machine hours | Casting | 1 | rhi1 | 2 | 3 | 2 | CP1 = 46,200 | |
| Heat treatment | 2 | rhi2 | 3 | 4 | 3 | CP2 = 50,400 | ||
| CNC | 3 | rhi3 | 1 | 1 | 1 | CPCNC = 18,900 | ||
| CNC 2nd | 4 | rhi4 | 0 | 0 | 0.9 | |||
| Painting | 5 | rhi5 | 0.1 | 0.1 | 0.2 | CP5 = 2070 | ||
| Labor hours | Casting | 1 | ui1 | 1.2 | 1.7 | 1.2 | ||
| Heat treatment | 2 | ui2 | 1.5 | 2 | 1.5 | |||
| CNC | 3 | ui3 | 1 | 1 | 1.6 | |||
| CNC 2nd | 4 | ui4 | 0 | 0 | 1 | |||
| Painting | 5 | ui5 | 0.3 | 0.3 | 0.7 | |||
| Product Item | Available Capacity | |||||||
|---|---|---|---|---|---|---|---|---|
| o | Car Rim | Truck Rim | Custom Rims | |||||
| Batch level operation | ||||||||
| Material handling | d6 = $2500/batch | 6 | H6 | 1 | A6 = 8800 | |||
| ρ6 | 70 | |||||||
| Setting | d7 = $200/batch | 7 | Si7 | 1 | 1 | 2.5 | A7 = 17,600 | |
| τi7 | 2 | 2 | 1 | |||||
| Direct labor cost | ||||||||
| Cost | HR1 = $7,022,400 | HR2 = $14,018,400 | HR3 = $23,337,600 | |||||
| Labor hours | CH1 = 52,800 | CH2 = 79,200 | CH3 = 105,600 | |||||
| Salary rate | $133/h | $177/h | $ 221/h | |||||
| Carbon tax with full progressive tax rate without allowance (Model 1) | ei | 1.5 | 2 | 3 | ||||
| Cost | 1 DNQ1 | 2 DNQ2 | 3DNQ3 | |||||
| Quantity | DNQ1 = 10,000 | DNQ2 = 20,000 | DNQ3 > 20,000 | |||||
| Tax rate | 1 = $250/unit | 2 = $300/unit | 3 = $350/unit | |||||
| Carbon tax with full progressive tax rate with allowance (Model 2) | ei | 1.5 | 2 | 3 | ||||
| Cost | sr1(DYQ1–DYQ0) | sr2(DYQ1–DYQ0) | sr3(DYQ3–DYQ0) | |||||
| Quantity | DYQ0 = 5000 | DYQ1 = 15,000 | DYQ2 = 25,000 | DYQ3 > 25,000 | ||||
| Tax rate | sr1 = $250/unit | sr2 = $300/unit | sr3 = $350/unit | |||||
| Product Item | Available | |||||||
|---|---|---|---|---|---|---|---|---|
| o | Car Rim | Truck Rim | Custom Rims | Truck Rim | ||||
| Linear carbon right cost | ||||||||
| Carbon right cost | r = $250/unit | Maximum carbon emissions cap set by the government | GCE = 28,000 | |||||
| Quantity | MBR = 100,000 | |||||||
| Other fixed costs | F = 10,000,000 | |||||||
| The approach or method used for decision-making in multi-stage production processes. | ||||||||
| The upper limit of three-phase carbon emission | GCE1 = 28,000 | GCE2 = 25,200 | GCE3 = 22,400 | |||||
| The upper limit of three-phase materials | UDQ = 39,000 | |||||||
| [Ideal result] | |
| π = 26,588,110; P1 = 2006; P2 = 3624; P3 = 5914; DQ1 = 0; DQ2 = 151,680; DQ3 = 0; ω0 = 0.6656061; ω1 = 0.3343939; ω2 = 0; B6 = 2167; B17 = 1003; B27 = 1812; B37 = 5914; ν1 = 0; ν2 = 0; ν3 = 1; α1 = 0; α2 = 1; α3 = 0; β1 = 1; β2 = 0; CCE = 27,999 | |
| [Object function] | |
| Maximum π = 4000*P1 + 6000*P2 + 8000*P3 − (70*DQ1 + 69*DQ2 + 67*DQ3 − 100*P1 + 150*P2 + 200*P3) − [7,022,400 + ω1*6,996,000 + ω2*16,315,200] − 2500*B6 − 200*B17 − 200*B27 − 500*B37 − (250*1 + 300*2 + 350*3) – 10,000,000 | |
| [Constraints] | |
| Direct material discount: | Direct labor: |
| 10*P1 + 20*P2 + 10*P3 = DQ1 + DQ2 + DQ3 | 4*P1 + 5*P2 + 6*P3 = 52,800 − ω1*26,400 − ω2*52,800 |
| 0 ≤ DQ1 ≤ α0*200,000 | ω0 − β1 ≤ 0 |
| α1*200,000 < DQ2 ≤ α1*500,000 | ω1 − β1 − β2 ≤ 0 |
| α2*500,000 < DQ3 | ω2 − β2 ≤ 0 |
| α0 + α1 + α2 = 1 | ω0 + ω1 + ω2 = 1 |
| β1 + β2 = 1 | |
| Batch Level: Material Handling | |
| 10*P1 + 20*P2 + 10*P3 ≤ 70*B6 | Batch Level: Settings |
| 1*B6 ≤ 8800 | P1 ≤ 2*B17 |
| P2 ≤ 2*B27 | |
| Machine hours: | P3 ≤ 1*B37 |
| o = 1: 2*P1 + 3*P2 + 2*P3 ≤ 46,200 | 1*B17 + 1*B27 + 2.5*B37 ≤ 17,600 |
| o = 2: 3*P1 + 4*P2 + 3*P3 ≤ 50,400 | |
| o = 3, 4: 1*P1 + 1*P2 + 1.9*P3 ≤ 18,900 | Min/Max demand: |
| o = 5: 0.1*P1 + 0.1*P2 + 0.2*P3 ≤ 2070 | P1 > 2000; P2 > 1000; 6000 > P3 > 2000 |
| A carbon levy employing a fully graduated rate system inclusive of exemptions: | |
| 1.5*P1 + 2*P2 + 3*P3 = NQ1 + NQ2 + NQ3 | |
| 1.5*P1 + 2*P2 + 3*P3 ≤ 28,000 0 ≤ NQ1 ≤ 10,000*ν1 | |
| 10,000*ν2 ≤ NQ2 ≤ 20,000*ν2 | |
| 20,000*ν3 ≤ NQ3 | |
| ν1 + ν2 + ν3 = 1 | |
| [Ideal result] | |
| π = 28,418,590; P1 = 2000; P2 = 6910; P3 = 5257; DQ1 = 0; DQ2 = 210,770; DQ3 = 0; ω0 = 0.1934848; ω1 = 0.8065152; ω2 = 0; B6 = 3011; B17 = 1000; B27 = 3455; B37 = 5257; ν1 = 0; ν2 = 0; ν3 = 1; α1 = 0; α2 = 1; α3 = 0; β1 = 1; β2 = 0; GCE = 28,000; Ø1 = 0; Ø2 = 1; CQ1 = 0; CQ2 = 32,591 | |
| [Object function] | |
| Maximum π = 4000*P1 + 6000*P2 + 8000*P3 − (70*DQ1 + 69*DQ2 + 67*DQ3 − 100*P1 + 150*P2 + 200*P3) − [7,022,400 + ω1*6,996,000 + ω2*16,315,200] − 2500*B6 − 200*B17 − 200*B27 − 500*B37 − (250*1 + 300*2 + 350*3) − 250*(GCE − CCE))* Ø1 − (250*1 + 300*2 + 350*3 + 250*(CCE − GCE))* Ø2 – 10,000,000 | |
| [Constraints] | |
| Direct material discount: | Direct labor: |
| 10*P1 + 20*P2 + 10*P3 = DQ1 + DQ2 + DQ3 | 4*P1 + 5*P2 + 6*P3 = 52,800 − ω1*26,400 − ω2*52,800 |
| 0 ≤ DQ1 ≤ α0*200,000 | ω0 − β1 ≤ 0 |
| α1*200,000 < DQ2 ≤ α1*500,000 | ω1 − β1 − β2 ≤ 0 |
| α2*500,000 < DQ3 | ω2 − β2 ≤ 0 |
| α0 + α1 + α2 = 1 | ω0 + ω1 + ω2 = 1 |
| β1 + β2 = 1 | |
| Batch Level: Material Handling | |
| 10*P1 + 20*P2 + 10*P3 ≤ 70*B6 | Batch Level: Settings |
| 1*B6 ≤ 8800 | P1 ≤ 2*B17 |
| P2 ≤ 2*B27 | |
| Machine hours: | P3 ≤ 1*B37 |
| o = 1: 2*P1 + 3*P2 + 2*P3 ≤ 46,200 | 1*B17 + 1*B27 + 2.5*B37 ≤ 17,600 |
| o = 2: 3*P1 + 4*P2 + 3*P3 ≤ 50,400 | |
| o = 3, 4: 1*P1 + 1*P2 + 1.9*P3 ≤ 18,900 | Min/Max demand: |
| o = 5: 0.1*P1 + 0.1*P2 + 0.2*P3 ≤ 2070 | P1 > 2000; P2 > 1000; 6000 > P3 > 2000 |
| Linear carbon rights: | A carbon levy employing a fully graduated rate system inclusive of exemptions: |
| 1.5*P1 + 2*P2 + 3*P3 = CQ1 + CQ2 = CCE | 1.5*P1 + 2*P2 + 3*P3 = NQ1+ NQ2 + NQ3 |
| 0 ≤ CQ1 ≤ 28,000*Ø1 | 1.5*P1 + 2*P2 + 3*P3 ≤ 28,000 |
| 28,000*Ø1 < CQ2 ≤ 128,000*Ø2 | 0 ≤ NQ1 ≤ 10,000*ν1 |
| Ø1 + Ø2 = 1 | 10,000*ν2 ≤ NQ2 ≤ 20,000*ν2 |
| 20,000*ν3 ≤ NQ3 | |
| ν1 + ν2 + ν3 = 1 | |
| [Ideal result] | |
| π = 28,338,110; P1 = 2006; P2 = 3624; P3 = 5914; DQ1 = 0; DQ2 = 151,680; DQ3 = 0; ω0 = 0.6656061; ω1 = 0.3343939; ω2 = 0; B6 = 2167; B17 = 1003; B27 = 1812; B37 = 5914; δ0 = 0; δ1 = 0; δ2 = 0; δ3 = 1; α1 = 0; α2 = 1; α3 = 0; β1 = 1; β2 = 0; CCE = 27,999 | |
| [Object function] | |
| Maximum π = 4000*P1 + 6000*P2 + 8000*P3 − (70*DQ1 + 69*DQ2 + 67*DQ3 − 100*P1 + 150*P2 + 200*P3) − [7,022,400 + ω1*6,996,000 + ω2*16,315,200] − 2500*B6 − 200*B17 − 200*B27 − 500*B37 − (δ1*250*(w1 − 5000) +δ2*300*(w2 − 5000) + δ3 *350*(w3 − 5000)) − 10,000,000 | |
| [Constraints] | |
| Direct material discount: | Direct labor: |
| 10*P1 + 20*P2 + 10*P3 = DQ1 + DQ2 + DQ3 | 4*P1 + 5*P2 + 6*P3 = 52,800 − ω1*26,400 − ω2*52,800 |
| 0 ≤ DQ1 ≤ α0*200,000 | ω0 − β1 ≤ 0 |
| α1*200,000 < DQ2 ≤ α1*500,000 | ω1 − β1 − β2 ≤ 0 |
| α2*500,000 < DQ3 | ω2 − β2 ≤ 0 |
| α0 + α1 + α2 = 1 | ω0 + ω1 + ω2 = 1 |
| β1 + β2 = 1 | |
| Batch Level: Material Handling | |
| 10*P1 + 20*P2 + 10*P3 ≤ 70*B6 | Batch Level: Settings |
| 1*B6 ≤ 8800 | P1 ≤ 2*B17 |
| P2 ≤ 2*B27 | |
| Machine hours: | P3 ≤ 1*B37 |
| o = 1: 2*P1 + 3*P2 + 2*P3 ≤ 46,200 | 1*B17 + 1*B27 + 2.5*B37 ≤ 17,600 |
| o = 2: 3*P1 + 4*P2 + 3*P3 ≤ 50,400 | |
| o = 3, 4: 1*P1 + 1*P2 + 1.9*P3 ≤ 18,900 | Min/Max demand: |
| o = 5: 0.1*P1 + 0.1*P2 + 0.2*P3 ≤ 2070 | P1 > 2000; P2 > 1000; 6000 > P3 > 2000 |
| A carbon levy employing a fully graduated rate system inclusive of exemptions: | |
| 1.5*P1 + 2*P2 + 3*P3 = w0 + w1 + w2 + w3 | |
| 1.5*P1 + 2*P2 + 3*P3 ≤ 28,000 | |
| 0 ≤ w0 ≤ 5000*δ1 | |
| 5000*δ1 ≤ w1 ≤ 15,000*δ1 15,000*δ1 ≤ w2 ≤ 25,000*δ1 | |
| 25,000*δ1 ≤ w3 | |
| δ0 + δ1 + δ2 + δ3 = 1 | |
| [Ideal result] | |
| π = 30,168,590; P1 = 2000; P2 = 6910; P3 = 5257; DQ1 = 0; DQ2 = 210,770; DQ3 = 0; ω0 = 0.1934848; ω1 = 0.8065152; ω2 = 0; B6 = 3011; B17 = 1000; B27 = 3455; B37 = 5257; δ0 = 0; δ1 = 0; δ2 = 0; δ3 = 1; α1 = 0; α2 = 1; α3 = 0; β1 = 1; β2 = 0; GCE = 28,000; Ø1 = 0; Ø2 = 1; CQ1 = 0; CQ2 = 32,591 | |
| [Goal function] | |
| Maximum π = 4000*P1 + 6000*P2 + 8000*P3 − (70*DQ1 + 69*DQ2 + 67*DQ3 − 100*P1 + 150*P2 + 200*P3) − [7,022,400 + ω1*6,996,000 + ω2*16,315,200] − 2500*B6 − 200*B17 − 200*B27 − 500*B37 − (δ1*250*(w1 − 5000) + δ2*300*(w2 − 5000) + δ3 *350*(w3 − 5000) − 250*(GCE − CCE))* Ø1 − (δ1*250*(w1 − 5000) + δ2*300*(w2 − 5000) + δ3*350*(w3 − 5000) + 250*(CCE − GCE))*Ø2 − 10,000,000 | |
| [Constraints] | |
| Direct material discount: | Direct labor: |
| 10*P1 + 20*P2 + 10*P3 = DQ1 + DQ2 + DQ3 | 4*P1 + 5*P2 + 6*P3 = 52,800 − ω1*26,400 − ω2*52,800 |
| 0 ≤ DQ1 ≤ α0*200,000 | ω0 − β1 ≤ 0 |
| α1*200,000 < DQ2 ≤ α1*500,000 | ω1 − β1 − β2 ≤ 0 |
| α2*500,000 < DQ3 | ω2 − β2 ≤ 0 |
| α0 + α1 + α2 = 1 | ω0 + ω1 + ω2 = 1 |
| β1 + β2 = 1 | |
| Batch Level: Material Handling | |
| 10*P1 + 20*P2 + 10*P3 ≤ 70*B6 | Batch Level: Settings |
| 1*B6 ≤ 8800 | P1 ≤ 2*B17 |
| P2 ≤ 2*B27 | |
| Machine hours: | P3 ≤ 1*B37 |
| o = 1: 2*P1 + 3*P2 + 2*P3≤ 46,200 | 1*B17 + 1*B27 + 2.5*B37 ≤ 17,600 |
| o = 2: 3*P1 + 4*P2 + 3*P3 ≤ 50,400 | |
| o = 3, 4: 1*P1 + 1*P2 + 1.9*P3 ≤ 18,900 | Min/Max demand: |
| o = 5: 0.1*P1 + 0.1*P2 + 0.2*P3 ≤ 2070 | P1 > 2000; P2 > 1000; 6000 > P3 > 2000 |
| Linear carbon rights: | A carbon levy employing a fully graduated rate system inclusive of exemptions: |
| 1.5*P1 + 2*P2 + 3*P3 = CQ1 + CQ2 = CCE | 1.5*P1 + 2*P2 + 3*P3 = w0 + w1 + w2 + w3 |
| 0 ≤ CQ1 ≤ 28,000*Ø1 | 1.5*P1 + 2*P2 + 3*P3 ≤ 28,000 |
| 28,000*Ø1 < CQ2 ≤ 128,000*Ø2 | 0 ≤ w0 ≤ 5000*δ1 |
| Ø1 + Ø2 = 1 | 5000*δ1 ≤ w1 ≤ 15,000*δ1 15,000*δ1 ≤ w2 ≤ 25,000*δ1 |
| 25,000*δ1 ≤ w; | |
| δ0 + δ1 + δ2 + δ3 = 1 | |
| Model | Gain | Volume of Merchandise | CO2 Discharge | Emissions Tax | Emission Credits | Price of Emission Permits | Amount of Supplies Bought | Workforce Expenditure | Working Hours |
|---|---|---|---|---|---|---|---|---|---|
| 1-1 | 26,588,110 | P1 = 2006; P2 = 3624; P3 = 5914 | 27,999 | 9,799,650 | 0 | 0 | 151,680 | 9,361,820 | 61,628 |
| 1-2 | 28,418,590 | P1 = 2000; P2 = 6910; P3 = 5257 | 32,591 | 11,406,850 | 4591 | 1,147,750 | 210,770 | 12,664,780 | 74,092 |
| 2-1 | 28,338,110 | P1 = 2006; P2 = 3624; P3 = 5914 | 27,999 | 8,049,650 | 0 | 0 | 151,680 | 9,361,820 | 61,628 |
| 2-2 | 30,168,590 | P1 = 2000; P2 = 6910; P3 = 5257 | 32,591 | 9,656,850 | 4591 | 1,147,750 | 210,770 | 12,664,780 | 74,092 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsai, W.-H.; Chang, S.-C.; Teng, Y. Equilibrium between Environmental and Economic Objectives: An Activity-Based Costing Approach Application for Carbon Emissions Management in the Aluminum Alloy Wheel Industry. Energies 2024, 17, 1331. https://doi.org/10.3390/en17061331
Tsai W-H, Chang S-C, Teng Y. Equilibrium between Environmental and Economic Objectives: An Activity-Based Costing Approach Application for Carbon Emissions Management in the Aluminum Alloy Wheel Industry. Energies. 2024; 17(6):1331. https://doi.org/10.3390/en17061331
Chicago/Turabian StyleTsai, Wen-Hsien, Shuo-Chieh Chang, and Yuchun Teng. 2024. "Equilibrium between Environmental and Economic Objectives: An Activity-Based Costing Approach Application for Carbon Emissions Management in the Aluminum Alloy Wheel Industry" Energies 17, no. 6: 1331. https://doi.org/10.3390/en17061331
APA StyleTsai, W.-H., Chang, S.-C., & Teng, Y. (2024). Equilibrium between Environmental and Economic Objectives: An Activity-Based Costing Approach Application for Carbon Emissions Management in the Aluminum Alloy Wheel Industry. Energies, 17(6), 1331. https://doi.org/10.3390/en17061331





