BLDC Motor Speed Control with Digital Adaptive PID-Fuzzy Controller and Reduced Harmonic Content

Abstract

Low power brushless direct current (BLDC) motors are used in many consumer appliances. These motors have a relatively high winding resistance and therefore current control loop can be avoided in some cases, but fast and accurate speed regulation can be still needed. To minimize harmonics and generated sound noise, improved sinusoidal pulse width modulation (PWM) has been tested in the paper. As the most suitable commutation type, the sine wave with the third harmonic component has been selected. This type of communication reduced the torque ripple of the motor. This paper analyses the possibility to improve traditional proportional-integral-derivative (PID) speed regulator with Fuzzy logic block. A simulation model of BLDC motor, inverter, speed detection circuit and controller have been created. Simulation results showed that by applying the Fuzzy-based PID controller, the transient time can be reduced from 0.2 s to 0.05 s and overshoot can be avoided in comparison with traditional PID controller. Experimental results show a significant improvement in the motor dynamics—the overshoot and transient time were reduced twice. The difference with simulation results and experimental ones can be explained by delays introduced by the microcontroller.

1. Introduction

In the recent years, the use of brushless DC motors (BLDC) with permanent magnets has drastically increased. This is due to the discovery of new stronger magnets, higher efficiency, and the better performance of this motor type [1]. In the work presented in [2] it is mentioned that the BLDC motor-based electric drives have limited fault tolerance capability, increased electromagnetic interference, increased acoustic noise, and increased torque ripple. All these challenges can be addressed by the control system. Fault-tolerant control, electromagnetic interference control (EMI), and acoustic noise control improve the feasibility of the motor [2]. Torque ripples in BLDC motors are reduced by the improved design of the motor, but the control algorithm contributes to the torque ripple significantly as well.

BLDC motors have high power density and therefore, this type of motor often is used in devices that are required to be energy efficient, lightweight, and powerful. BLDC are more reliable than traditional brushed DC motors as this type of motors eliminate the need for brushes, which are prone to wear and tear over time due to friction and sparking. This absence of brushes reduces mechanical failure points and enhances reliability. With no brushes to replace or maintain, BLDC motors require less frequent servicing, resulting in lower maintenance costs and downtime. BLDC motors allow smoother operation, precise speed control, and reduced electrical noise, resulting in improved reliability and performance. BLDC motors are mostly preferred for dynamic applications where speed response is important. Nowadays various types of robots and automated systems are increasingly growing, and they require rapid and accurate speed change [3]. In low-power applications, the motor winding resistance is relatively high and therefore, the current peak is not critical in the transition processes, meaning only speed control can be used, which allows to reduce the number of sensors, thus, reducing the price of the inverter. In that case, the issues of reducing harmonics and noise of the motor by choosing the most appropriate pulse width modulation method (PWM) as well as the development of a high-response speed regulator remain relevant. The goal of this paper is to design a fast speed controller for low inertia, low power BLDC motor with 60 degree Hall-effect sensors by extracting the speed of these sensors and implementing controller into inexpensive microcontroller.

The most widely used type of speed controller today remains the proportionally integral (PI) regulator [4]. Considering that microcontroller performance is increasing today, it is possible to create more sophisticated control algorithms, potentially improving motor reaction speeds. A comparison of the different regulators is provided in [4,5,6]. The results show that adaptive controllers, such as neuron networks, genetic algorithms, Fuzzy logic regulator and others, allow improve the dynamics of the motor even they do not require a precise motor model to create such a controller. Sliding mode control for BLDC motor control has been used in the works referenced in [7,8], model-based adaptive control in the scientific works presented in [9,10], genetic algorithm based control in the works presented in [11,12], neural network control algorithm in the works presented in [13,14], swarm optimization algorithm in the works presented in [15,16], robust control was proposed in the works presented in [17,18]. Although these methods showed good performance at least in simulation, for implementation there is a need for a high-performance controller and the model of the motor should be known in some cases. Fuzzy control was applied in the research papers [19,20,21]. The Fuzzy logic-based control algorithm has the advantage that there is no need for mathematical model of the motor and inverter. The main disadvantage of Fuzzy control is that the definition of intervals of fuzzy subsets is subjective, and this can lead to a poor performance of the controller. To mitigate this problem, the Fuzzy controller is combined with a traditional proportionally integrally differential (PID) control algorithm. A similar idea has been analyzed in the scientific works presented in [6,21] with an additional current control loop. In this case, additional control method will be implemented to face the electromagnetic interference which is challenging when six step control method with Hall-effect-based rotor position sensors [22].

The goal of the paper is investigating of improved control algorithms to optimize the speed performance of the motor. This includes the development of an algorithm for rotor position detection from Hall-effect sensors, and an investigation of different switching techniques to reduce electromagnetic noise. The paper includes validation of developed control methods through simulation and experiments. Implementation of control method into inexpensive microcontroller and comparison of speed performance of the BLDC motor with a traditional PID control will be given.

2. Simulation Based Study of BLDC Motor Control Method

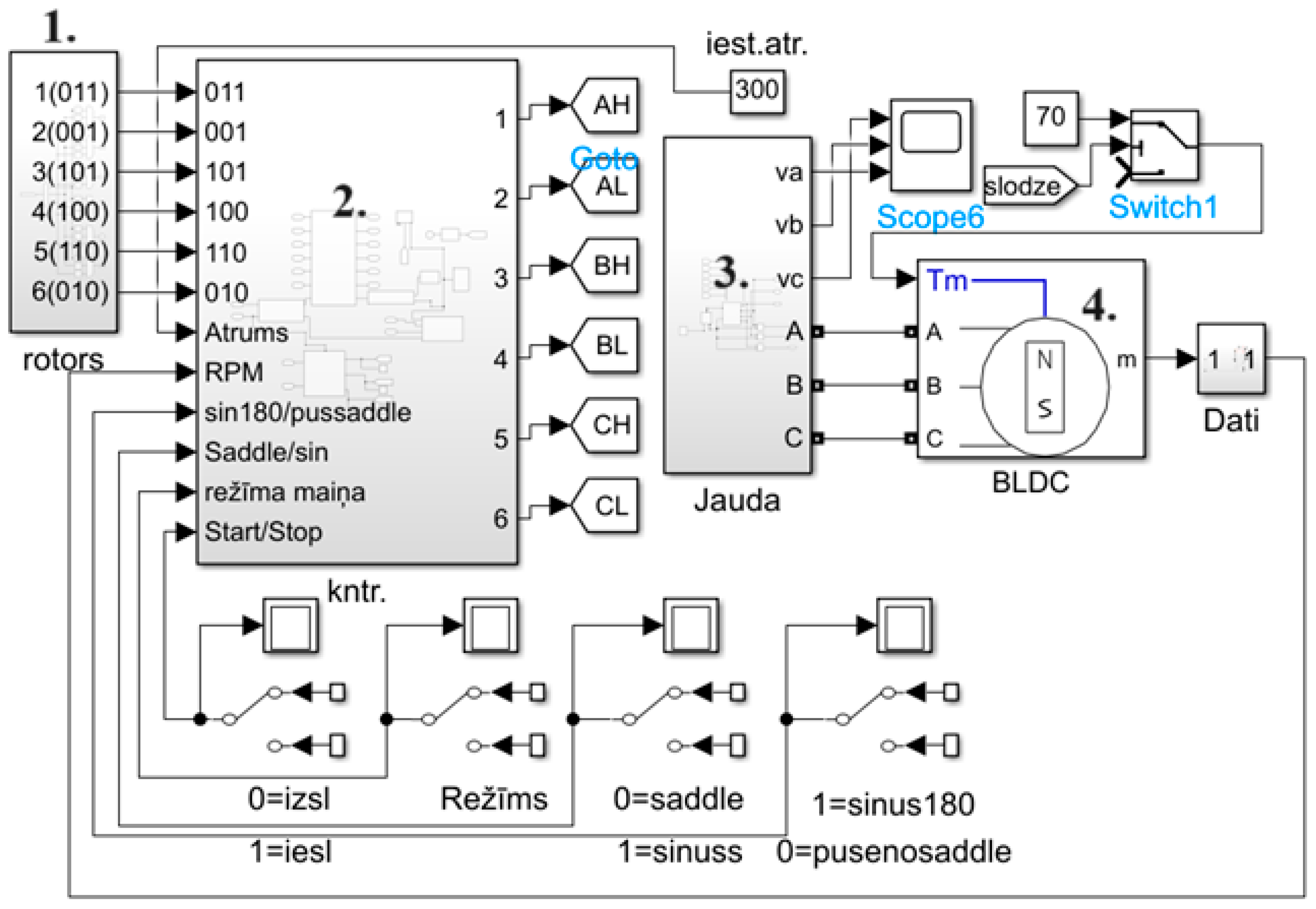
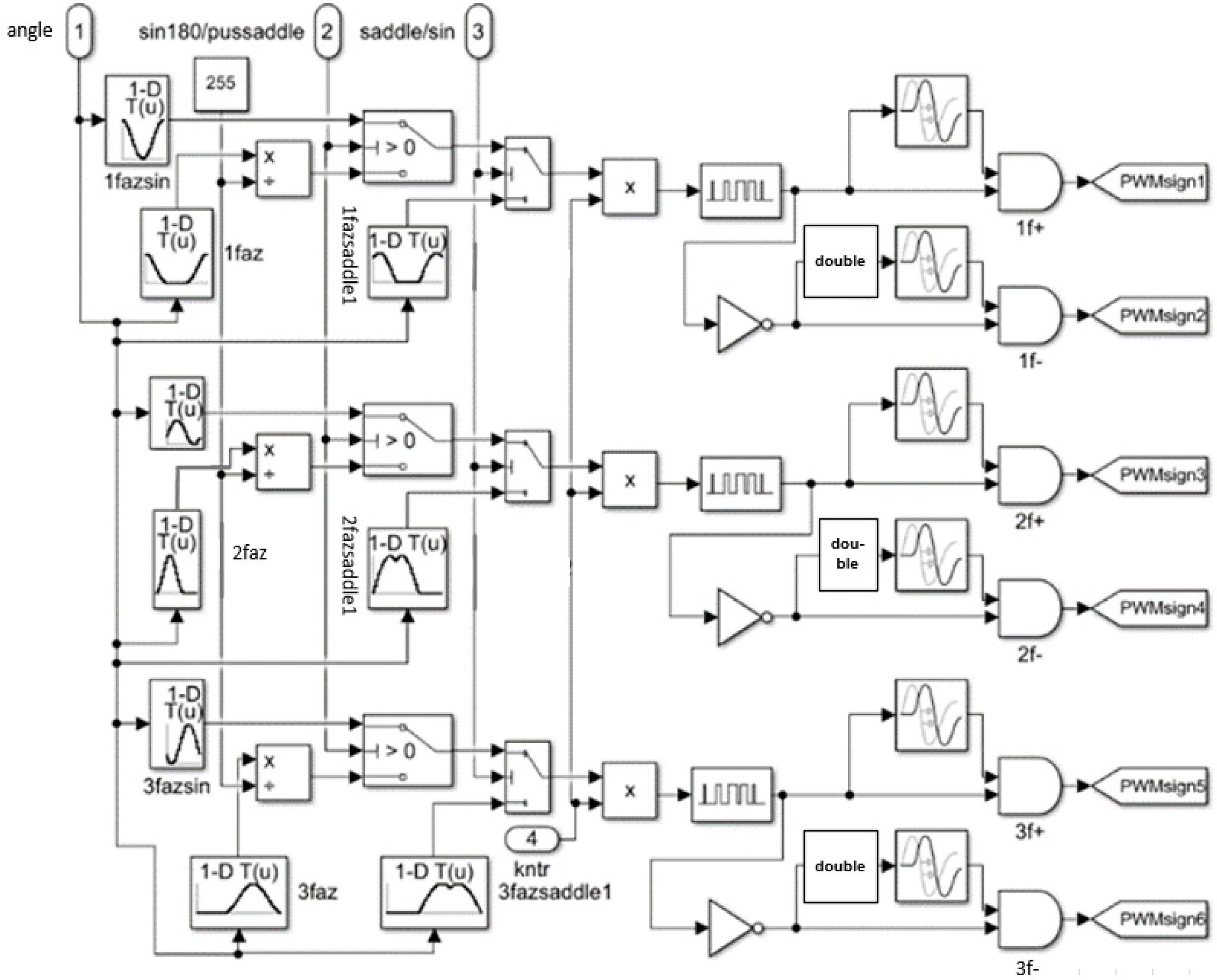
The control system of BLDC motor was first simulated in Matlab R2023b using Simulink blocks as can be seen in Figure 1. Block 1 corresponds to a signal from a Hall-effect-based position sensor that describes rotor position with a unique 3-bit code. Block 2 is a control system which controls the speed and provides six-pulse with modulated (PWM) signals to the three-phase inverter with six transistors. These control signals are labeled as AH, AL, BH, BL, CH, and CL and are connected with “goto” function internally to corresponding transistor of the Block 3. In the labels, the first letter A, B, or C corresponds to phase of the inverter. The second letter H clarifies that this is high-side transistor, but the letter L indicates that this is low-side transistor. Block 3 represents the inverter of BLDC motor. Block 4 is built in the BLDC motor simulation block using Matlab Simulink and is used to simulate the motor.

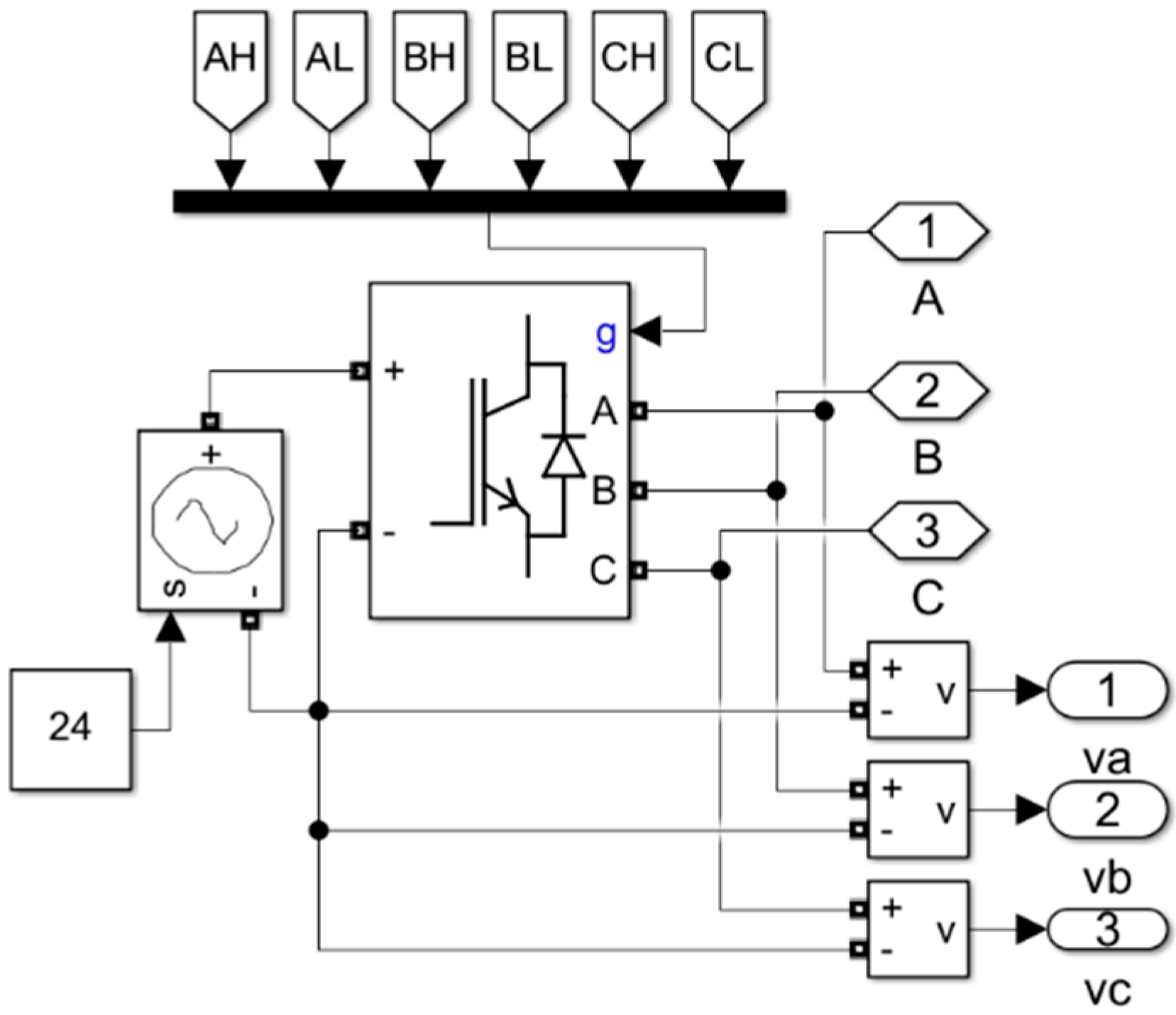
As shown in Figure 1, the simulation model consists of power and control parts, where you can select the control mode of the BLDC motor. In the simulations three phase inverter with IGBT (isolated gate bipolar transistors) were used. The model of the inverter can be seen in Figure 2. The inverter is connected to an ideal DC source with a nominal voltage of 24 V DC that also corresponds to the voltage to be used in the prototype. The three-phase inverter is not ideal, meaning it has electric losses, so the simulation is closer to the real-world results. Output signals A, B and C are connected to the motor as it can be seen in Figure 1.

The sinusoidal control requires knowledge of the precise angular state of the BLDC rotor. With Hall-effect sensors for rotor position detection, it is possible to obtain an angular rotor position with accuracy equal to 60 electrical degrees. Furthermore, it is possible to process the signals of the Hall-effect sensors and get the exact rotator angle. The simulation model that can be used to detect speed and angle of the rotor can be seen in Figure 3.

Before the angular position can be determined, it is necessary to calculate the rotational speed of the rotor. For that purpose, signals that are obtained from the Hall-effect-based sensors can be used and they change the state in the moment when the rotor reaches the next sector. One sector is equal to 60 electrical degrees. State change of the sensors can be detected by capturing rising edge. The time at which the rotor makes 60 electrical degree rotation of the motor (t_s) can be measured by using timers and after that the rotational speed of the motor can be calculated by Equation (1).

$$RPM=\frac{\frac{1}{t_s}\times 60}{pp}\times 6,$$

(1)

where

• RPM—rotor revolutions per minute;
• t_s—the time period during which the rotor rotates by 60 electrical degrees, s;
• pp—number of pole pairs of the BLDC motor.

BLDC motor rotor speed and angle calculation block system shown in Figure 3 uses the signal obtained from the rotors Hall-effect sensors. Rising fronts of this signal are chaotic in the beginning of the simulation. This is why signal delay is used once, thus, improving stability of the Matlab Simulink simulation. After removing this first chaotic rising front, this signal is fed to the developed custom memory logic. This memory consists of interlocking controlled switches, multiplication operation and Simulink cyclical memories. Simulink cyclic memory records the value of the signal connected to it and stores its value when disconnected from it. On this principle, the two mutually connected counters have been created that are cyclically able to determine the time (t_s) between two following rising fronts of the signal from Hall-effect sensors. Since it is known that this time corresponds to 60 electrical degrees, the rotational speed of the motor can be calculated by using Equation (1).

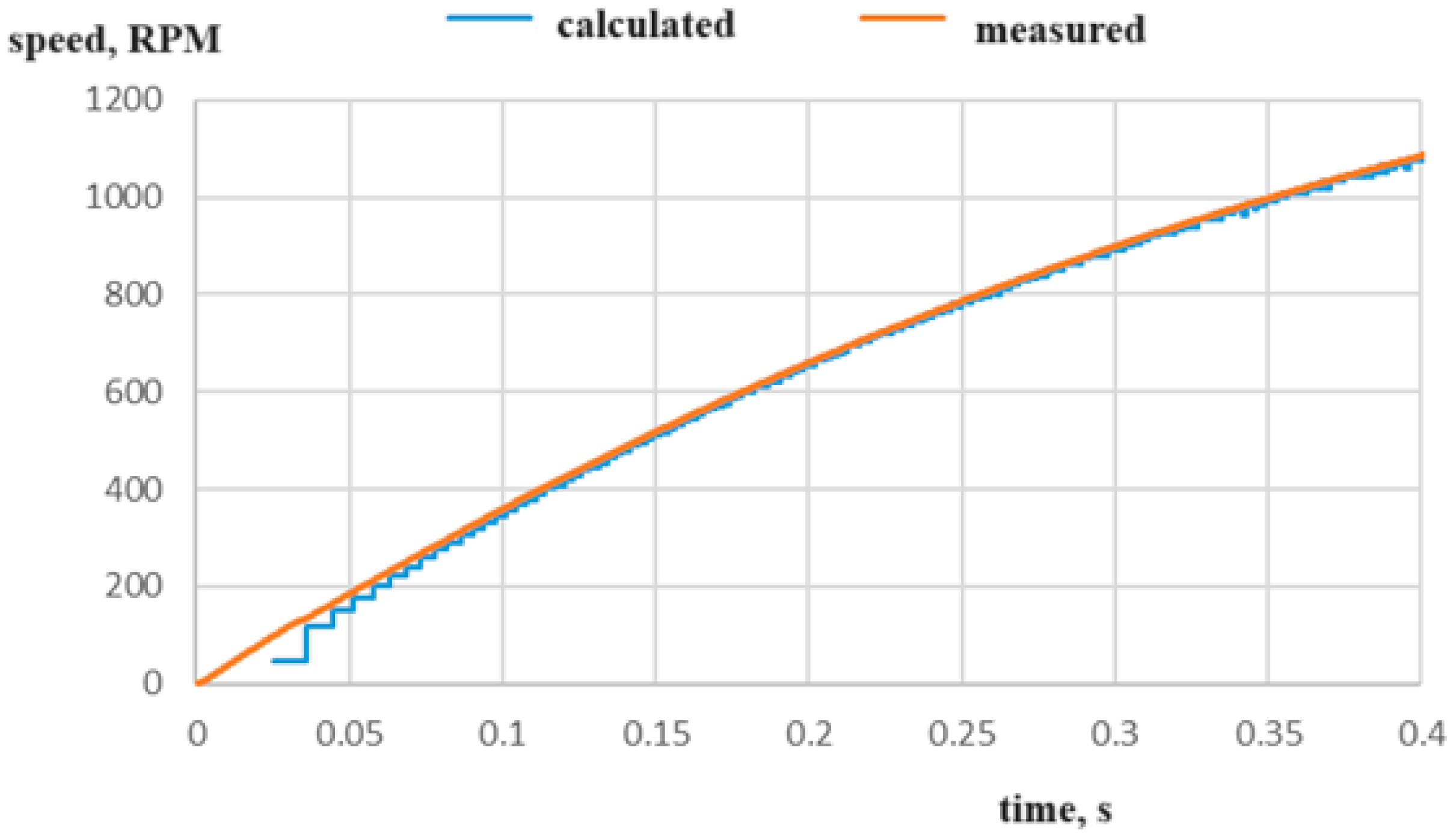
When the rising front pulse is detected, the counter starts to count at a certain frequency. The falling front in the counter control memory stops the counter and updates it to the initial state. At this point, this number of counter counts is also stored in the memory and is further used for rotor speed calculations. Because the counter starts and stops counting with the rising front, it skips one period. Therefore, two counters are used synchronously. The second counter operates with an inverted input signal. It makes the counters work cyclically, that is, when one period counter completes the count, then at that point the other period counter starts to count. An optional switch is used which at the right times passes both period counters data for further operations. This improves the speed and accuracy of the period counter system. Data obtained through simulation calculations is compared with real speed signal (measured) that is determined directly from the BLDC motor block in Matlab Simulink and this can be seen in Figure 4.

As can be seen in Figure 4 the accuracy of the system depends directly on the speed of the BLDC motor. That means that a higher rotor speed increases the accuracy of the resulting RPM signal. As has already been mentioned above, it is necessary to obtain the precise angle position of the rotor. The rotor angle can be obtained using Equation (2):

$${deg}_{rot}=∆t\times (RPM\times K_1)+K_2\times K_3,$$

(2)

where

• deg_rot—BLDC rotor angular position;
• K₁—coefficient;
• K₂—number of rotor sectors;
• K₃—angle of one rotor sector;
• $∆t$—lenght of one period, s;
• RPM—BLDC motor revolutions per one minute.

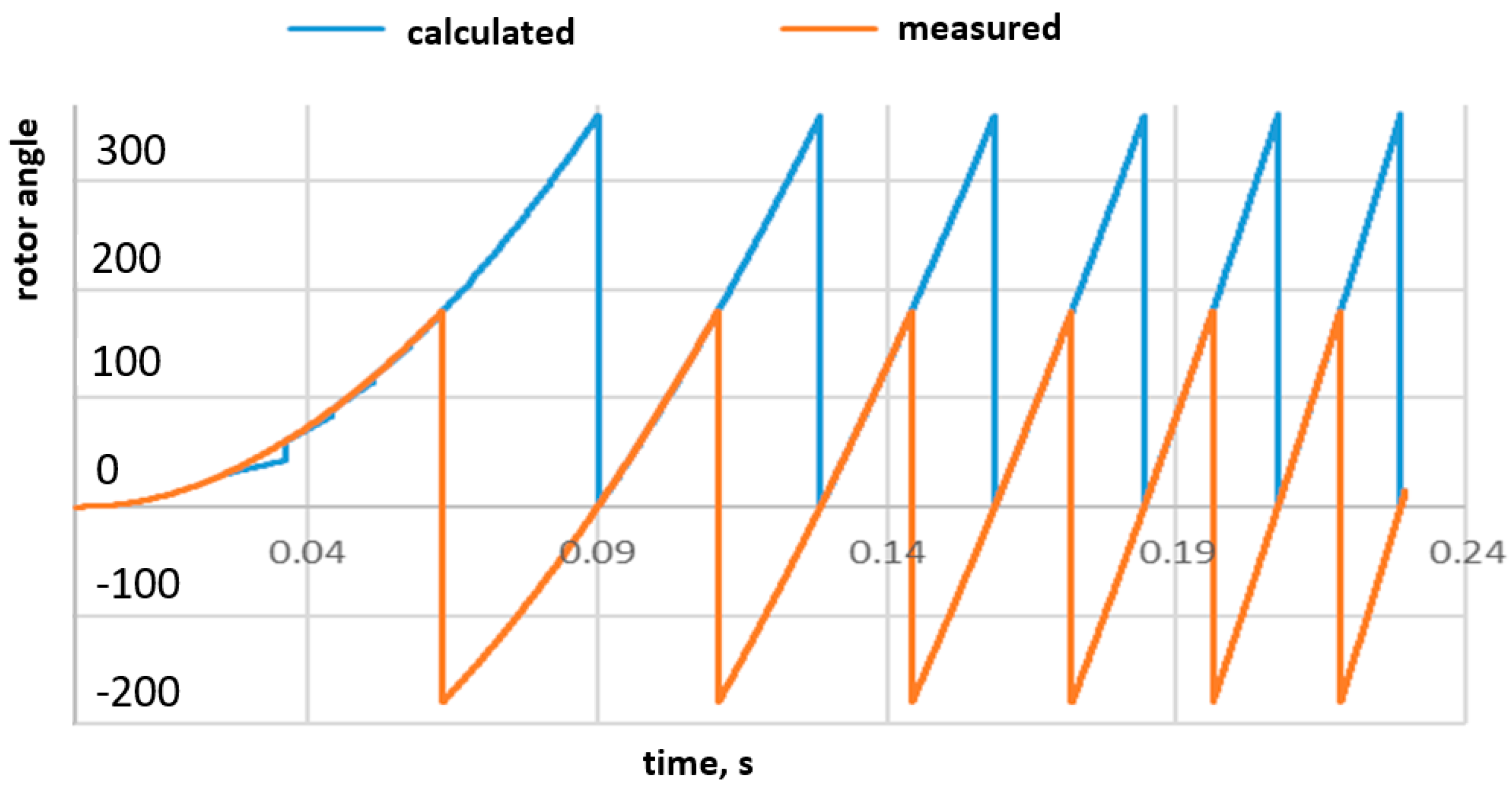
The period interval ∆t was obtained using the period counter control signals mentioned above, which are fed to the interval counter. The number of counts is summed and multiplied by the duration of one pulse. This pulse duration is further multiplied by the angular velocity obtained by multiplying the revolutions per minute by the constant. The result is then summed up at the angular position of the last known rotor position obtained from the Hall-effect sensor signals. The mechanical angle calculated in the simulation was compared with the BLDC motor block angular signal, which is referred in the figure as measured. These signals can be seen in Figure 5.

As can be seen in Figure 5, a similar relationship can be observed to the rotor speed graph in Figure 4—more accurate data is obtained as the rotor speed increases. It is also observed that the data have sufficient precision to allow the implementation of sinusoidal pulse width modulation (SPWM) and all the other commutation methods observed in these experiments. The MATLAB/Simulink block that allows for the implementation of sinusoidal PWM with or without third harmonic injection can be seen in Figure 6. In the sinusoidal control unit, it is possible to choose between three types of control methods—full sine wave modulation, sine wave modulation with a third harmonic component, and half-period sine with a third harmonic component. Corresponding duty cycles are stored into memory in the form of a data table. The necessary duty cycle is generated at each BLDC rotor mechanical angle. Regardless of a control method, BLDC motor speed is controlled with the same controller that will be analyzed further. With the multiplication block, the maximum value of the duty cycle is kept below 100 percent.

3. Fuzzy Logic Based Adaptive PID Controller of a BLDC Motor Speed

PID controllers are used primarily in scientific papers and practice as the design of PID controllers for many applications is well known. From the other side, the proper tuning of such a controller is challenging and can be difficult in a practice [23]. This promotes researchers and engineers to develop more advanced tuning methods and approaches for PID controller improvement. As it has been shown in the literature [24], adaptive controllers allow for the increase in the dynamics of the BLDC motor. PID controller improvement with Fuzzy logic makes PID control tuning simpler if the proper model of motor is not known [25]. Fuzzy control has recently found wider application within the motion control industry due to the model free concept [26]. Many scientific papers lack experimental and practical implementation. This paper proposes a Fuzzy-based adaptive PID controller for speed response improvement of small power BLDC motor with simultaneous harmonic content reduction. This paper describes the practical implementation of a Fuzzy-based PID controller with non-expensive microcontroller and verification in the MATLAB/Simulink environment. The goal of such controller selection is not only the simplified tuning of the controller, but also the improved speed response.

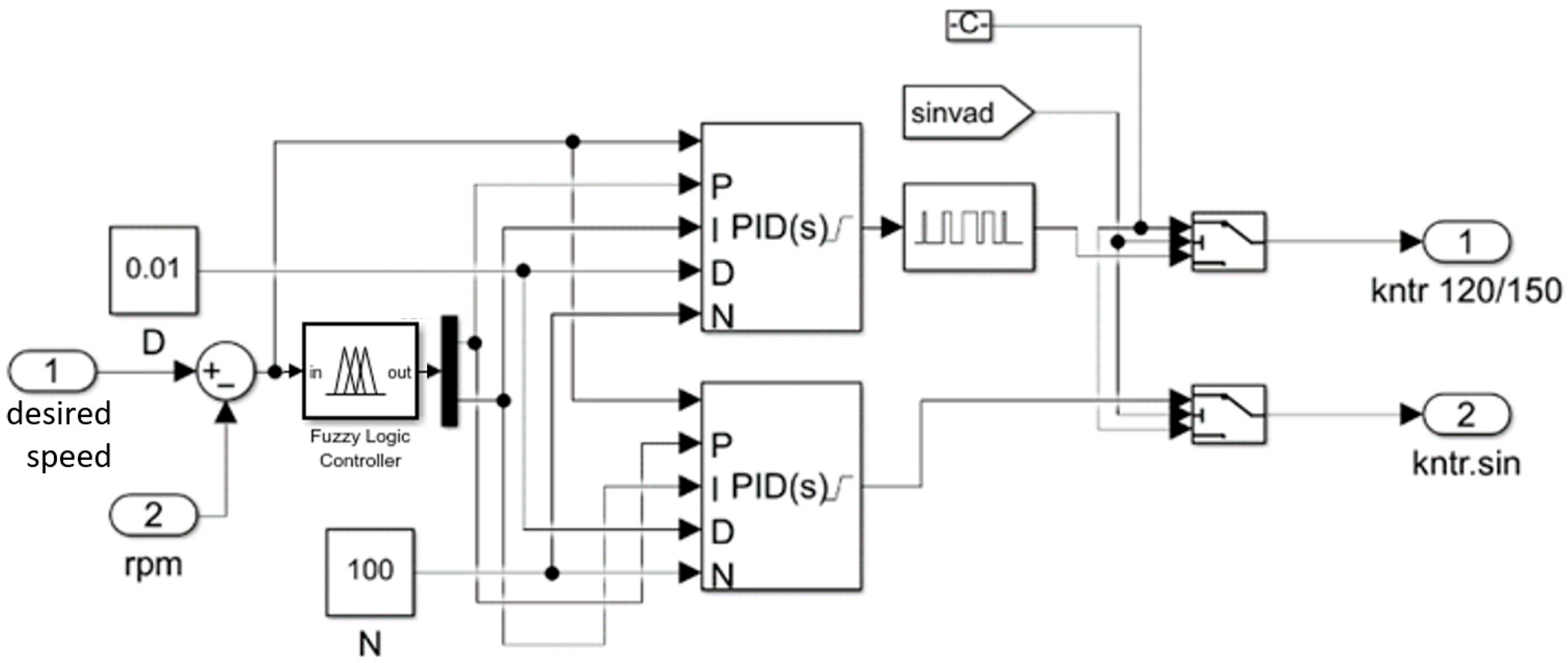
At first the controller was verified in MATLAB/Simulink software R2023b. The simulation model of Fuzzy-based PID controller (FUZZY + PID) can be seen in in Figure 7. Trapezoidal and sinusoidal commutation methods have their own PID controllers. The output of the controller is connected to the PWM forming block shown in Figure 6. Both of PID controllers are connected to one FUZZY logic block that adapts PID controller coefficients. The Fuzzy logic block controls the P and I coefficients, while the D coefficient stays constant.

As can be seen in

Table 1. Definition of Fuzzy rules for PID coefficient adaption.

Speed Error (Fuzzy Input)	Kp (Fuzzy Output)	Ki (Fuzzy Output)	Priority (0–1)
Very slow	Very slow	Very slow	0.5
Too slow	Very slow	Very slow	0.5
Set speed	Correct	Correct	1
Too fast	Very slow	Very slow	0.01
Fast	Slow	Very slow	0.5
Very fast	Very slow	Very slow	0.5
Almost slow	Almost slow	Correct	0.5
Almost fast	Almost slow	Correct	0.5

, specific output values are shown for each speed range and each condition. There is an additional coefficient that determines input impact. With this rank, the behavior of the controller can be used to prioritize a particular relationship between the Fuzzy logic input and outputs.

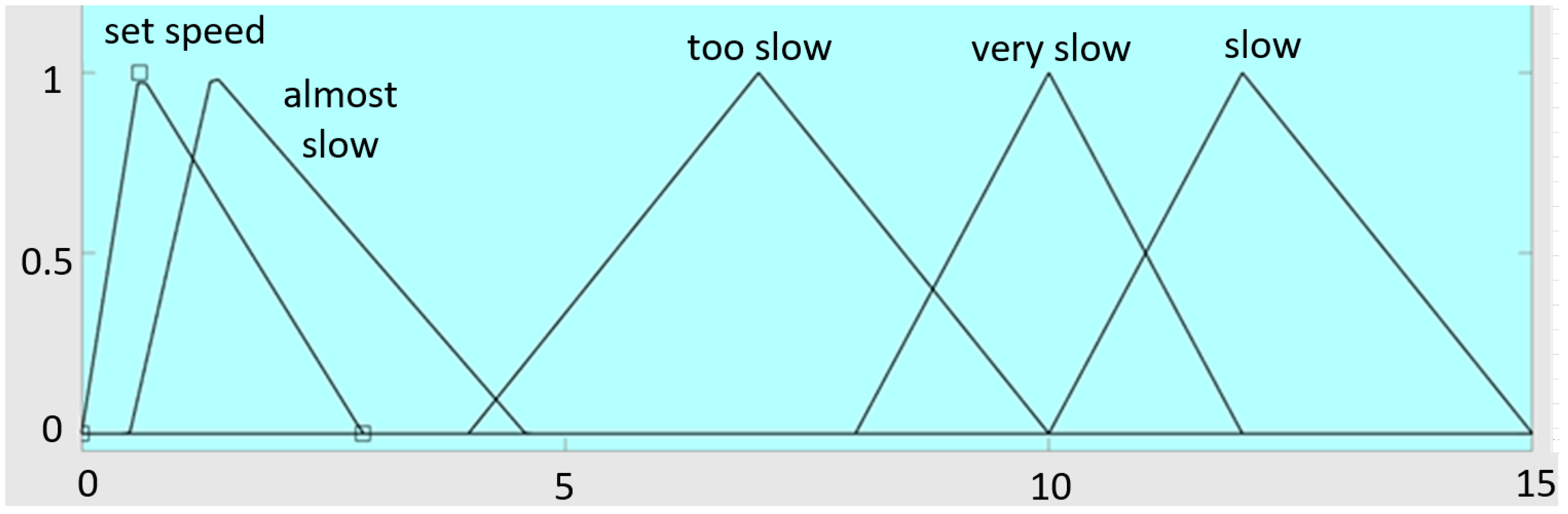
As can be seen in Table 1, Fuzzy controller error is divided into 9 parts—from very slow to very fast. If the error is positive, then the BLDC motor is rotating too slow, segments are allocated there accordingly—“very slow”, “too slow”, “slow”, “almost slow”. Otherwise, when the error is negative, then the BLDC motor rotates too fast, segments are allocated accordingly in that range—“very fast’’, “too fast”, “fast’’, and “almost fast’’. The range “set speed” has been defined in the case when the error is close to zero. All the defined ranges overlap with adjacent conditions, thus achieving smooth transition from one segment to the other. Input configuration can be seen in Figure 8, and the rules are shown in Table 1. The proportional and integral gain factor definition as an output can be seen in Figure 9 and Figure 10. The fuzzy logic was built in such a way that the P and I coefficients increase the speed of the control system, in case the control error deviates more from the desired value. Such control system also contributes to a decrease in overshoot.

4. Simulation Results

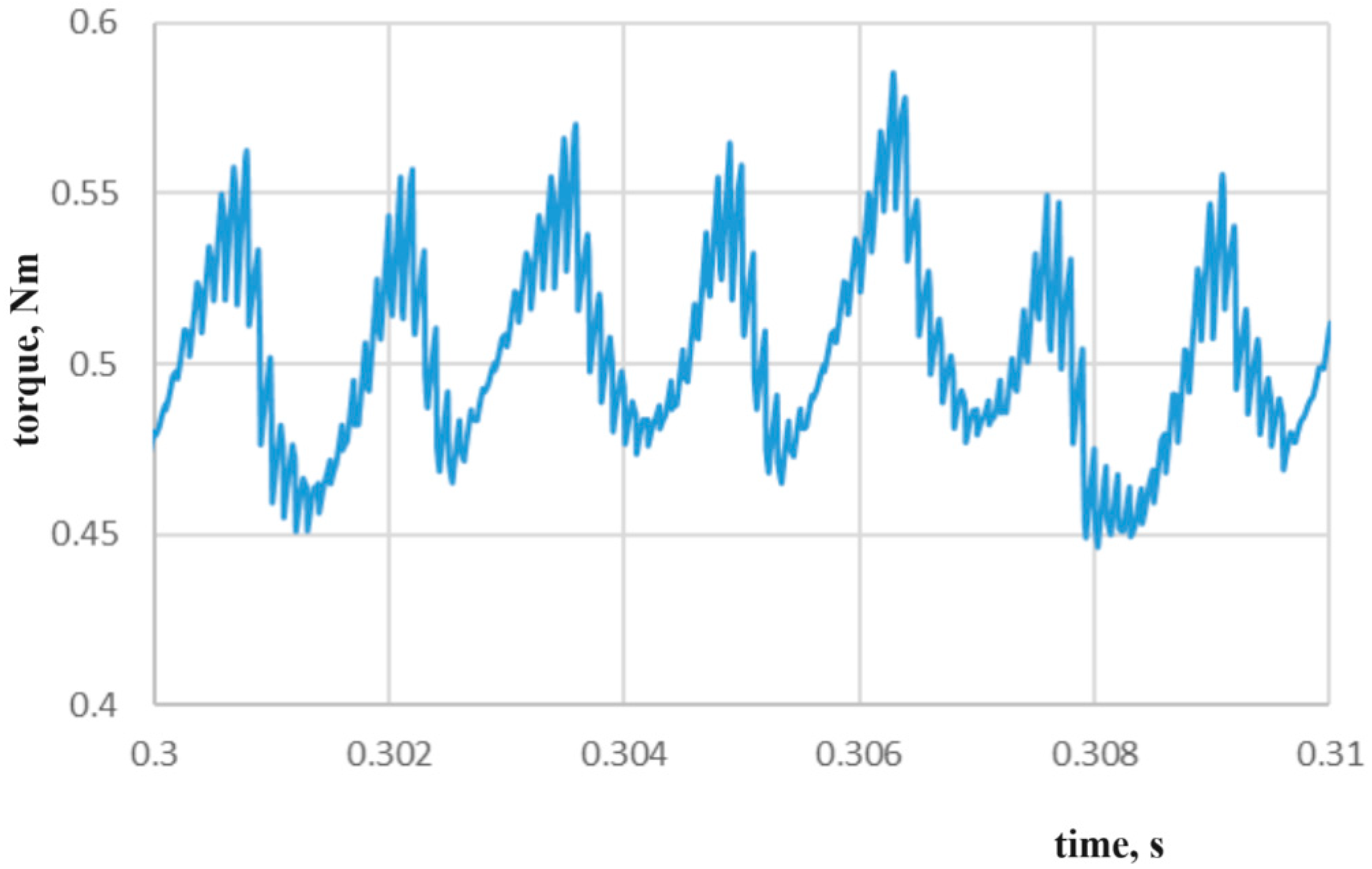
Previously described simulation models were used to tune the controller and compare different control methods. Figure 11 shows current waveforms in case of sinusoidal modulation with third harmonic injection. As can be seen, the current is close to sinusoidal, and therefore, the content of harmonics is much less than in the case of other modulation methods. Figure 12 shows the torque ripple. As the current is not controlled, the torque ripple level is acceptable. The motor was operated at 1500 RPM and loaded with 0.5 Nm.

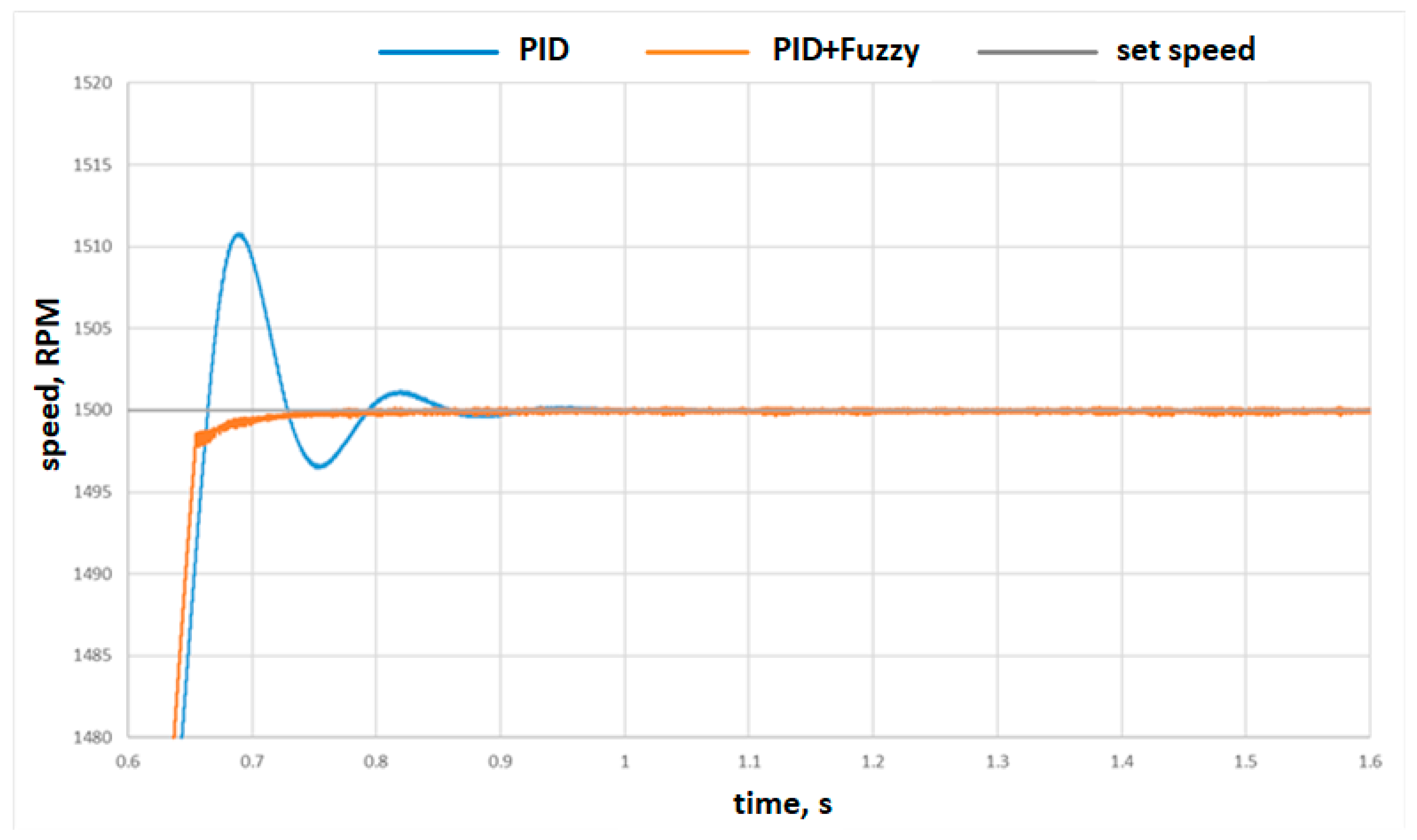
In Figure 13, a comparison between a PID controller and a FUZZY + PID controller was presented during the start-up of the motor. It can be clearly seen that the PID controller with constant proportional and integral coefficients is unable to stably ensure the desired speed and Fuzzy logic re-adjustment helps significantly in speed response improvement and overshoot reduction. It was observed that, with such control, the electromagnetic torque developed by the BLDC motor has some fluctuations in the rotor rotation speed as well. However, for the control where FUZZY changed the proportional and integral coefficients of the PID controller, smaller electromagnetic torque fluctuations were observed. This is due to the fact that FUZZY logic dynamically changes the PID coefficients depending on the error, thus providing faster settling time and more precise speed control.

5. Experimental Results

An experimental setup has been developed to implement the developed control algorithm in Matlab Simulink simulation environment as microcontroller program and create a real test bench. The operator will run the test bench operation and the test data will be obtained through the STM32 processor programming environment on the personal computer (PC). The STM32 microcontroller and gate drivers are supplied from USB connection with PC.

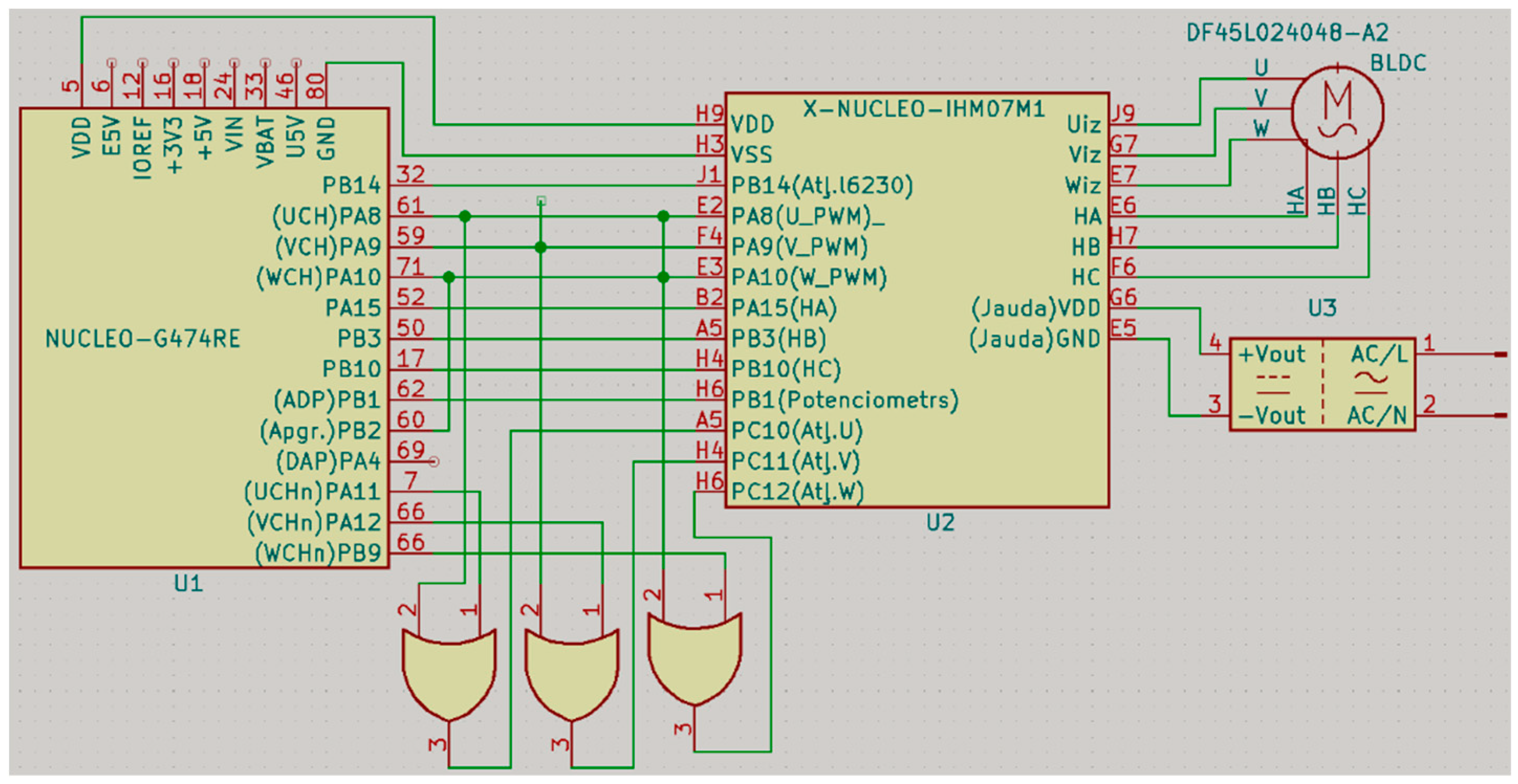
The STM32-NUCLEO prototype board has been used for the tests, and it is connected with the XNUCLEO-IHM07M1 expansion board. The expansion board handles BLDC motor Hall sensor signals and provides motor phase voltage commutation with transistors being placed on this board. The NUCLEO-G747RE prototyping board is connected to the inverter board, which can be seen in Figure 14. The control boards are based on the STM43G747RE microcontroller.

The X-NUCLEO-IHM07M1X (U2 in Figure 14) expansion board is based on the L6230PD integrated chip. The L6230 is a fully integrated three-phase motor inverter with integrated drivers and overcurrent protection. An uncommitted comparator with open-drain output is available. The expansion board provides Hall sensor signal processing, phase current and voltage readings, and other important functions for BLDC motor control. The L6230PD chip uses metal oxide field effect transistors (MOSFET) in the three-phase bridge configuration, which are controlled using the enable and pulse with modulated (PWM) signals.

An experimental setup can be seen in Figure 15. The BLDC motor (2) has been attached to the platform with four screws in a horizontal orientation. A rotating cylindrical mass (1) with a constant weight of 120 g and a diameter of 37 mm have been used as a load. Board with logic (5) has been used to enable inverter switching action. A DF45L024048-A2 BLDC motor was used in the experimental setup. The flywheel has been selected as a load since inertia is main parameter that influences speed transient process. Similar setups also have been used in many scientific papers where the speed loop was investigated, for example, in the work presented in [27].

Figure 16 shows the result of calculating the electric angle of the rotor of the BLDC motor from the Hall sensor signals. Digitally calculated rotor position is marked with a blue color. It can be observed that the shape of the signal is “stepped”. This can be explained by the fact that Hall sensors provide information about the angular position of the rotor at the specified reference points. To obtain more precise rotor angle between these reference points mentioned above, it is necessary to know how many degrees the rotor makes per second. The microcontroller program determines the speed of rotation of the rotor, from which further information about the instantaneous angular position of the rotor can be obtained. In Figure 16, the orange curve represents the data where the instantaneous rotor angle has been obtained. As can be seen, this obtained curve complements the information gaps of the previous method of determining the rotor angle and provides more detailed information about the instantaneous angular position of the rotor. However, there are some inaccuracies in determining the rotor angle. These inaccuracies arise from program execution time lags.

The PID and Adaptive PID control algorithms were implemented into microcontroller. Each test was first performed with PID control, and then with PID control, and the coefficients have been updated based on Fuzzy control logic. The high-speed test of the BLDC motor was performed at a starting speed of 200 rpm. Further, in the testing process, the desired speed value was set to 800 and then 500 revolutions per minute. Thus, the speed of the created control system was studied. 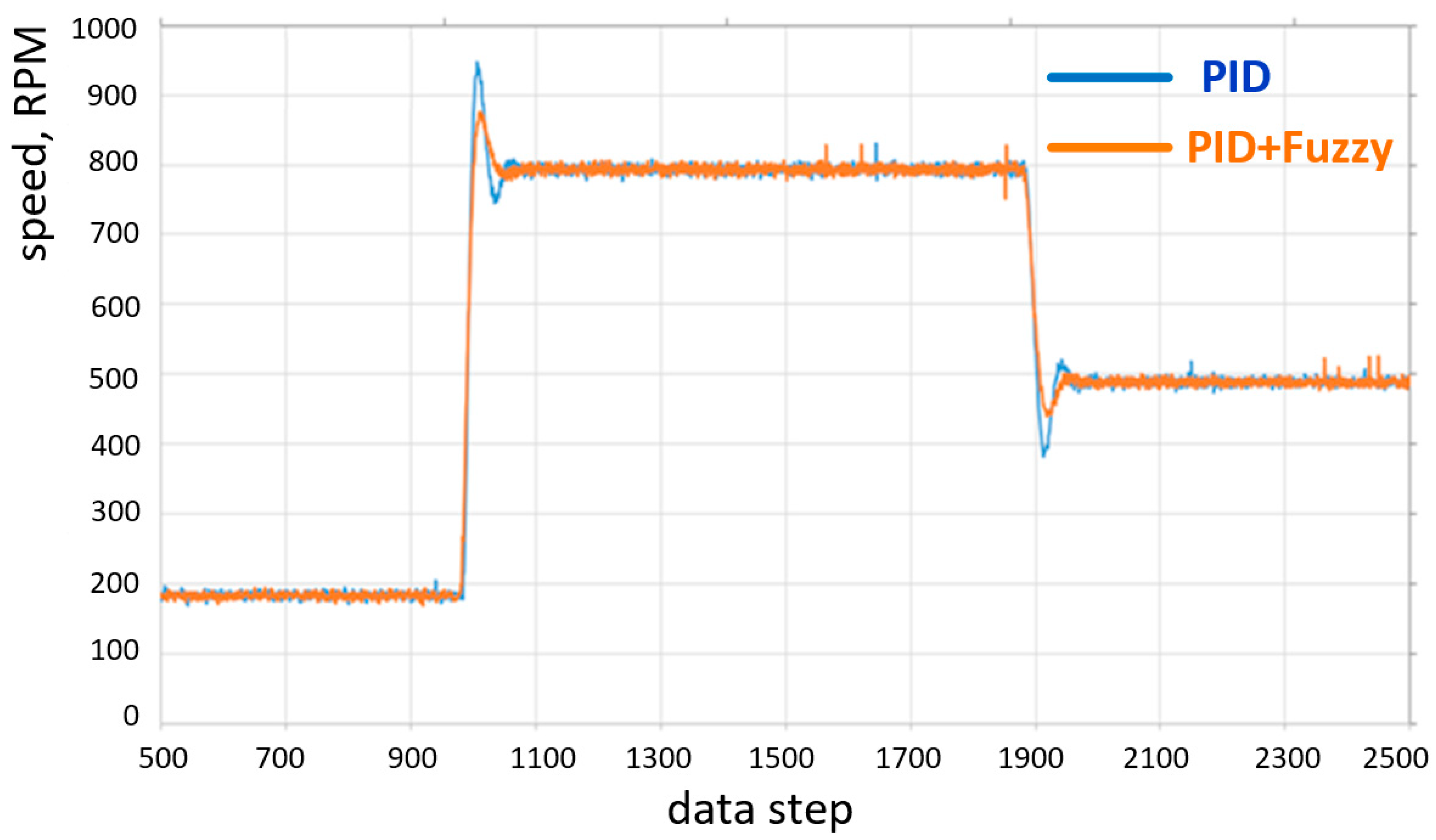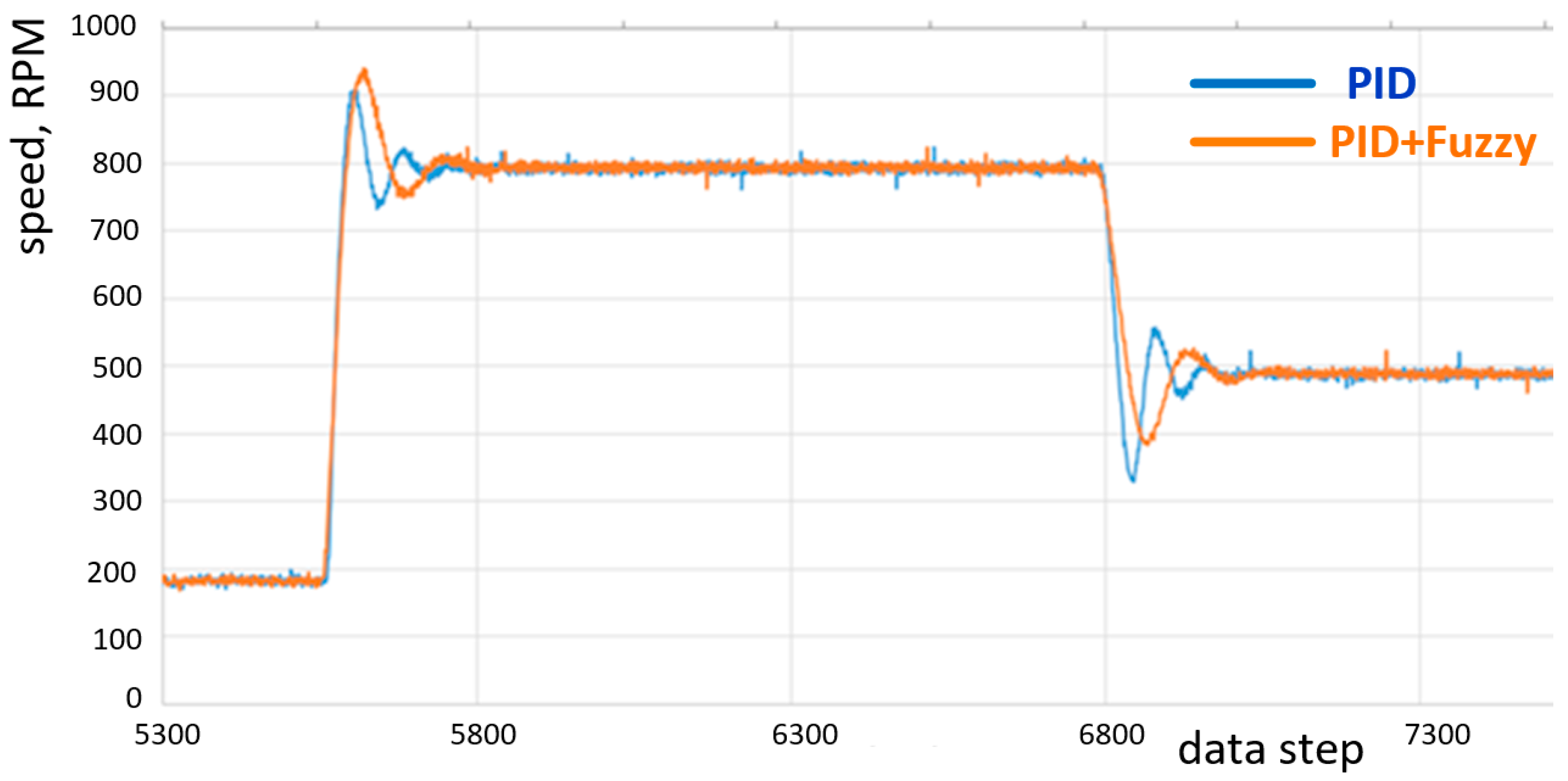Figure 17 and Figure 18 show experimental results. In Figure 17, no load was applied to the axis of the BLDC motor. The orange curve shows the test result with Fuzzy + PID and the blue curve shows the speed of the PID control. As can be seen in the figures, adaptive Fuzzy-based control allows for the improvement of the speed response of the motor.

It was observed that, in Figure 16, as the BLDC motor accelerates at no load, the overshoot of the PID control logic peaks at approximately 950 of the set 800 rpm. However, PID + Fuzzy control reduced this overshoot to 870 rpm. As the BLDC motor decelerated, the PID + Fuzzy logic was also able to perform better than the PID controller, where the deceleration overshoot peak was reduced from 390 to 450 rpm. Experimental results with a load connected are shown in Figure 17. As the BLDC motor accelerated with the load, the overshoot peak of the PID control logic reached a smaller value than the PID + Fuzzy control, i.e., PID override is equal to 901 and PID + Fuzzy override is equal to 939 rpm. However, when the BLDC motor was decelerating, the PID + Fuzzy logic was able to perform better than the PID controller. The deceleration undershoot peak was reduced from 330 to 387 rpm. It was observed that under the load, PID + Fuzzy controller prevented the motor from reducing the rotor RPM too rapidly, thus, reducing overshoot. When comparing both cases with and without an inertia wheel, it can be concluded that, with an inertia transient, the process is longer, but the overshoot is lower. In other papers [9,28], it is suggested to use an adaptive Fuzzy-based PID controller. Many other adaptive controllers for motor control can be found in the literature. Although in a simulation they show fast speed response, like the proposed controller in the simulations, they require a high componential power of the digital controller and therefore, cannot be implemented by using conventional microcontroller as in this case. An expensive high-performance controller, in most cases, is not a good solution for low power inexpensive BLDC motor control.

6. Conclusions

The paper analyses different modulation methods. At first, a Matlab Simulink simulation model has been created and used for several different types of BLDC motor commutation testing. As a most suitable commutation type, the sine with the third harmonic component has been selected. This type of communication also improves the torque of the motor as traditional six-step method has torque drops that negatively affects the speed and speed stability of the BLDC motor.

A simulation model has been created with a traditional PID speed controller. It was observed that the PID controller has a limited speed response. To improve the speed response proportional (P) and integral (I) coefficients of PID controller were adapted by using Fuzzy logic block. In the simulations, the proposed adaptive solution, where the PID and Fuzzy logic-based controllers are combined, completely canceled the overshoot, thus ensuring the speed accuracy and high-speed response operation of the BLDC motor.

A BLDC motor test bench has been practically created, which was used for testing the control algorithms. During the testing process, it was established that the control algorithm based on the STM32 microprocessor can determine the instantaneous angular position of the BLDC motor rotor and its rotation speed with some delay.

The Fuzzy logic-based adaptable PID algorithm has been implemented into the microcontroller and tested on an experimental test bench. The experiment shows only slightly better performance than traditional PID controller. It can be explained by significant delays introduced by digital algorithm implementation. The still adaptive PID controller improved the speed response, reduced the overshoot, and improved the torque of the motor. The more advanced microcontroller could improve the performance of the adaptive controller.