Research on Coordinated Optimization of Source-Load-Storage Considering Renewable Energy and Load Similarity
Abstract
1. Introduction
2. Renewable Energy and Load Similarity Measure
2.1. Renewable Energy and Load Data Normalization
2.2. Euclidean Distance
2.3. Load Tracking Factor
2.4. Net Load Smoothness Measure Function
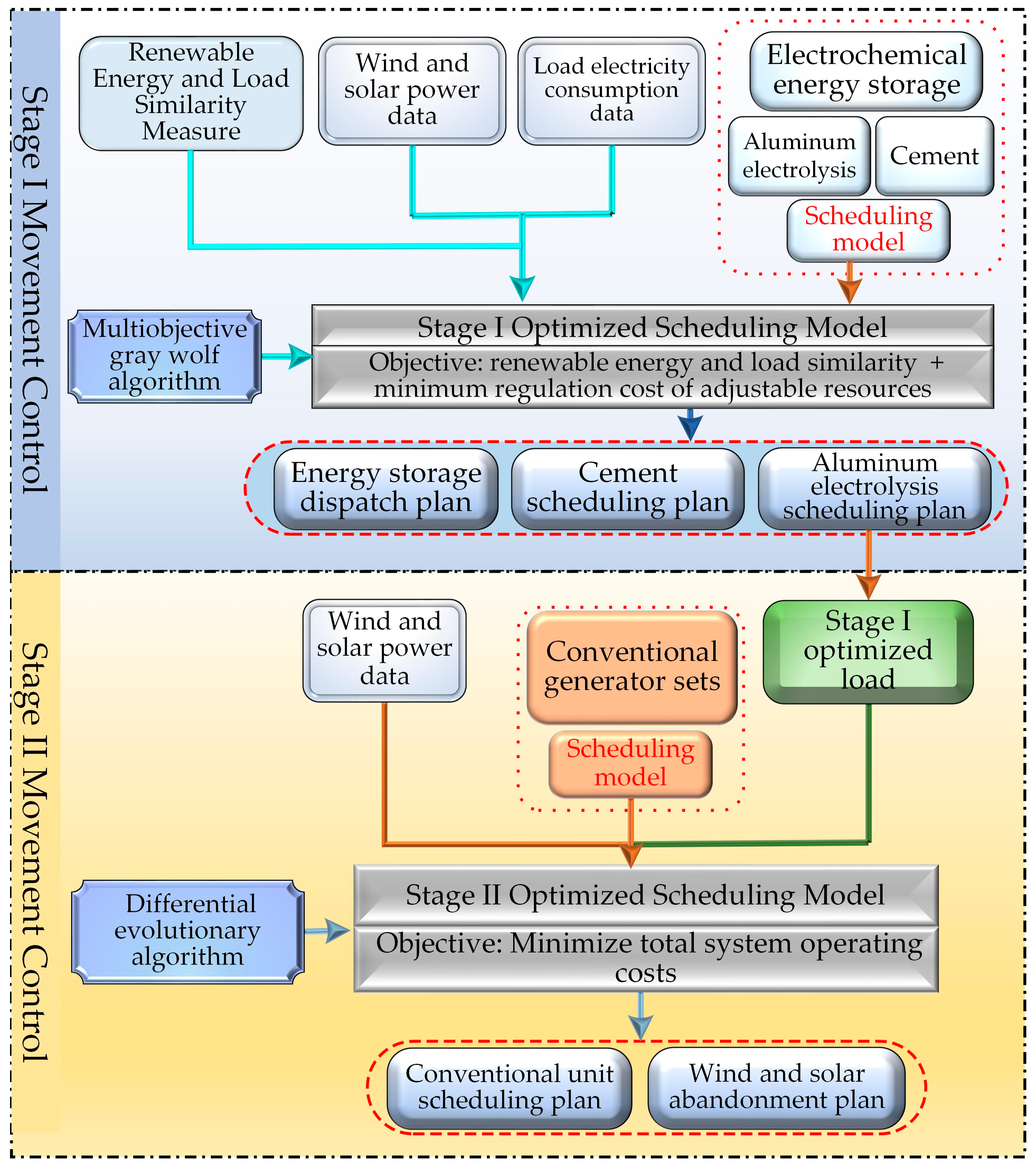
3. A Two-Phase Scheduling Framework for Energy Storage and Industrial Load Participation Considering Renewable Energy and Load Similarity
4. Modeling of Two-Stage Scheduling Considering Renewable Energy and Load Similarity
4.1. Phase I Scheduling Model
4.1.1. Objective Function
- (1)
- Objective 1: The renewable energy and load similarity metric function is given by (5).
- (2)
- Objective 2: The cost of adjustable resources is given by (6).where represents the power of ith energy storage power station at time t; denotes the cost of charging and discharging battery energy storage. In addition, and are the number of cement and aluminum enterprises, respectively. Moreover, indicates the per unit power compensation price of ith cement enterprise, signifies the power of each crusher of the ith cement enterprise, symbolizes the number of regulating crushers of the ith cement enterprise at time t, defines the per unit power compensation price of regulating load of the ith aluminum electrolysis enterprise, represents the power of regulating load of the ith aluminum electrolysis enterprise at time t, and denotes the running state of the ith aluminum electrolysis load at time t.
4.1.2. Optimization Constraints
- (1)
- Cement load constraints:
- ①
- Regulating crusher quantity constraints:where and are the maximum and minimum number of crushers that can be selected in the ith cement company, respectively.
- ②
- Cement company storage constraints:
- (2)
- Electrolytic aluminum load constraints:
- ①
- Upper and lower power constraints:where and are the maximum increase and decrease values of load power of the ith electrolytic aluminum enterprise participating in the dispatch, respectively.
- ②
- Electrolytic aluminum load regulation time constraints:where represents the operating state of the ith electrolytic aluminum load at time t, indicates the minimum continuous response time of the ith electrolytic aluminum load, and denotes the response time of the ith electrolytic aluminum load at time t.
- (3)
- Electrochemical energy storage plant constraints:
- ①
- Energy storage charge/discharge power:where and are the maximum output and input powers of the ith energy storage device, respectively.
- ②
- Energy storage state of charge:where represents the state of charge of ith energy storage device at time t, and denotes the loss coefficient of the storage plant. Moreover, and are the energy input and output conversion efficiency of the storage plant. signifies the ith energy storage device. and indicate the maximum and minimum state of charges of the storage plant, respectively.
4.2. Phase II Scheduling Model
4.2.1. Objective Function
4.2.2. Restrictive Condition
- (1)
- Power balance constraints:
- (2)
- Conventional generator set constraints:
- ①
- Upper and lower power limits for conventional generator sets:where and are the maximum and minimum values of the power of the ith conventional generator set, respectively. In addition, indicates the start and stop states of the ith conventional generator set at time t, and its value 1 means start, and 0 means stop.
- ②
- Conventional generator set climbing constraints:where denotes the ramp rate of the ith conventional generator set.
- ③
- Minimum start-up and shutdown times of conventional generator sets:
- (3)
- Wind abandonment, solar abandonment, and lost load constraints:where , , and are the predicted values of wind, solar, and load power at time t, respectively.
- (4)
- Power constraints of transmission lines:where represents the maximum power delivered by the transmission line between nodes i and j, denotes the susceptance between nodes i and j, and indicates the phase angle at node i at time t.
5. Net Load Smoothness Evaluation Index
5.1. Indicators of the Volatility of the Curve
5.2. Indicators of Peak-to-Valley Differences in Curves
6. Case Study
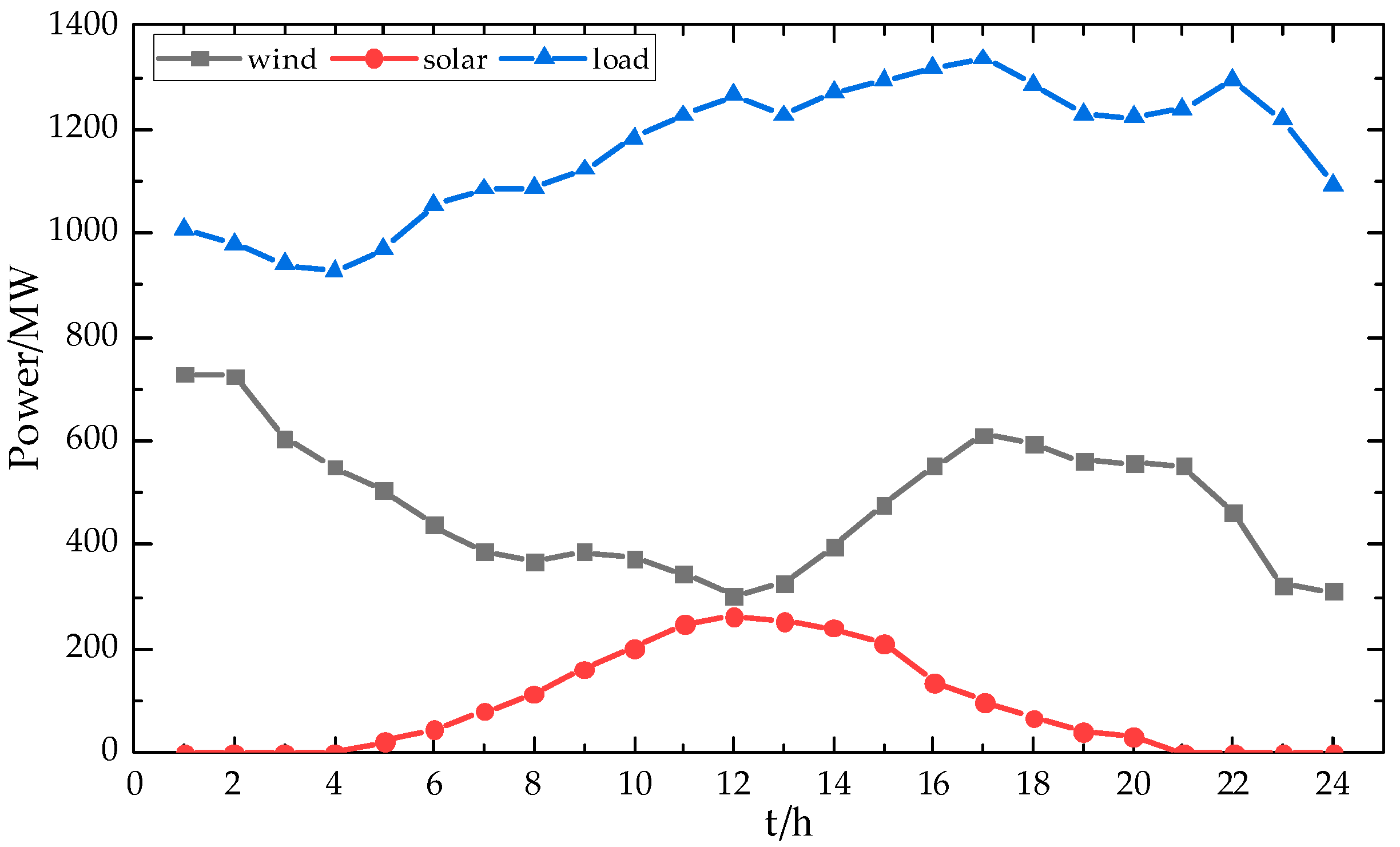
6.1. Description
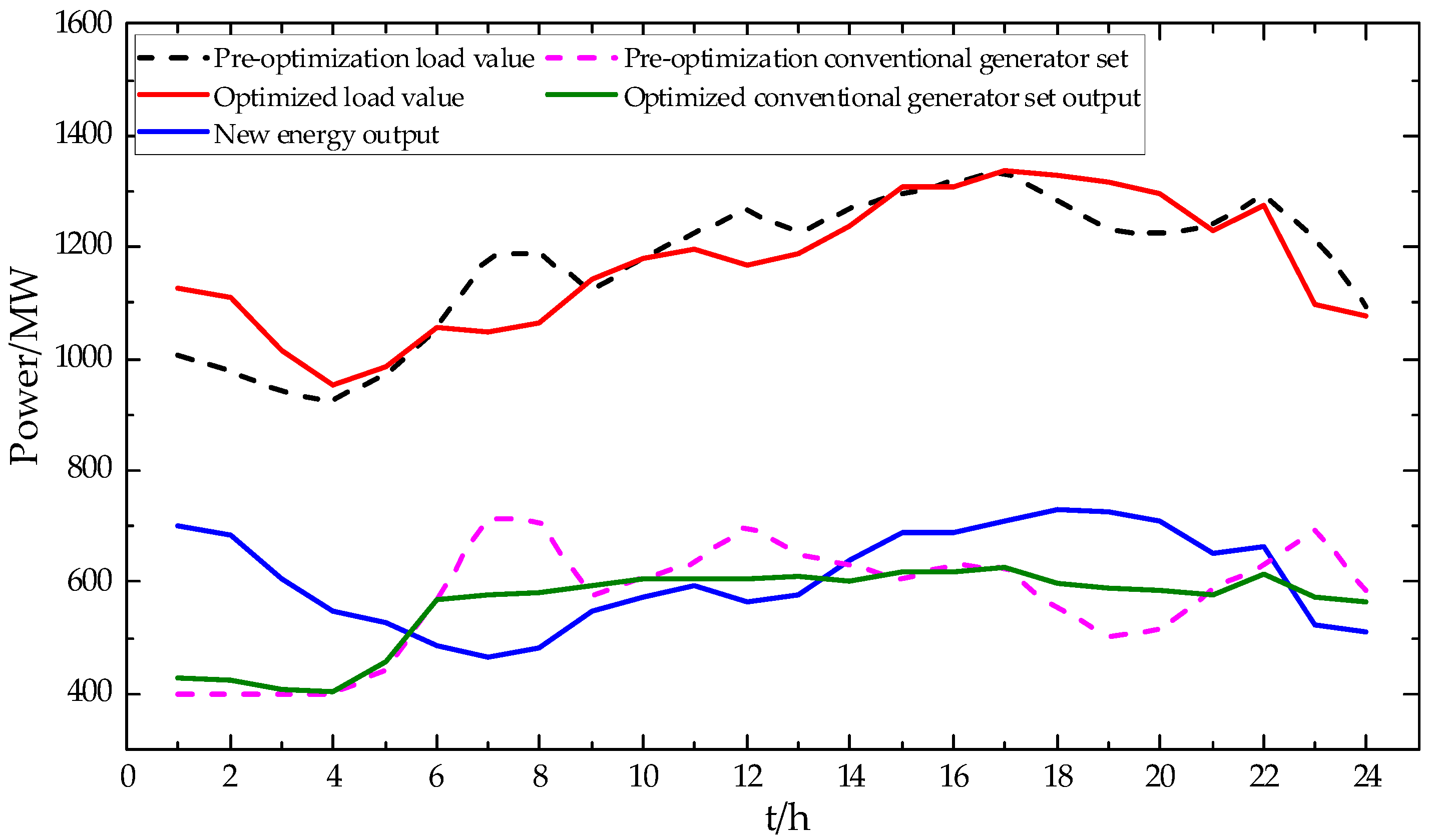
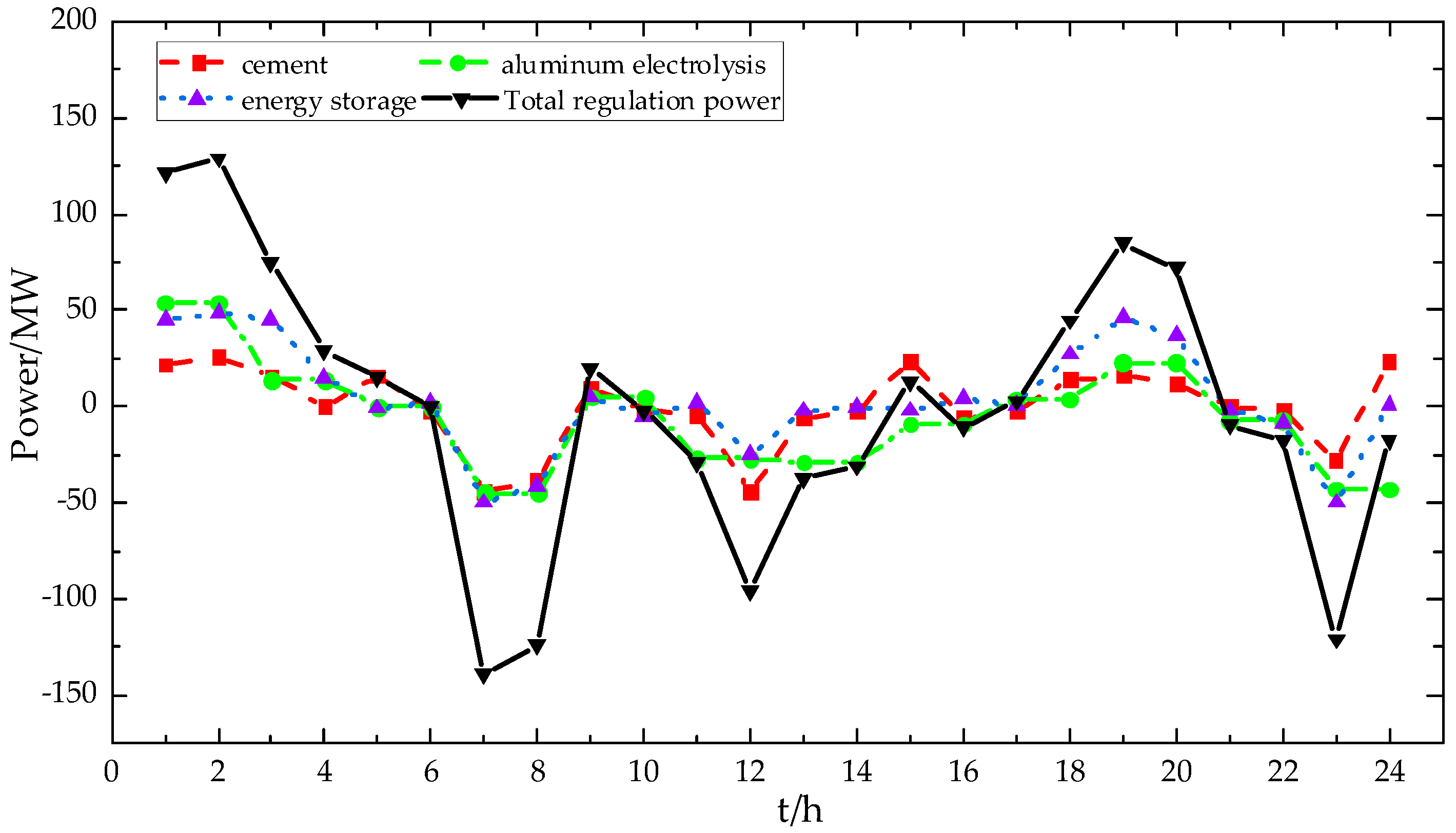
6.2. Analysis of Optimized Scheduling Results
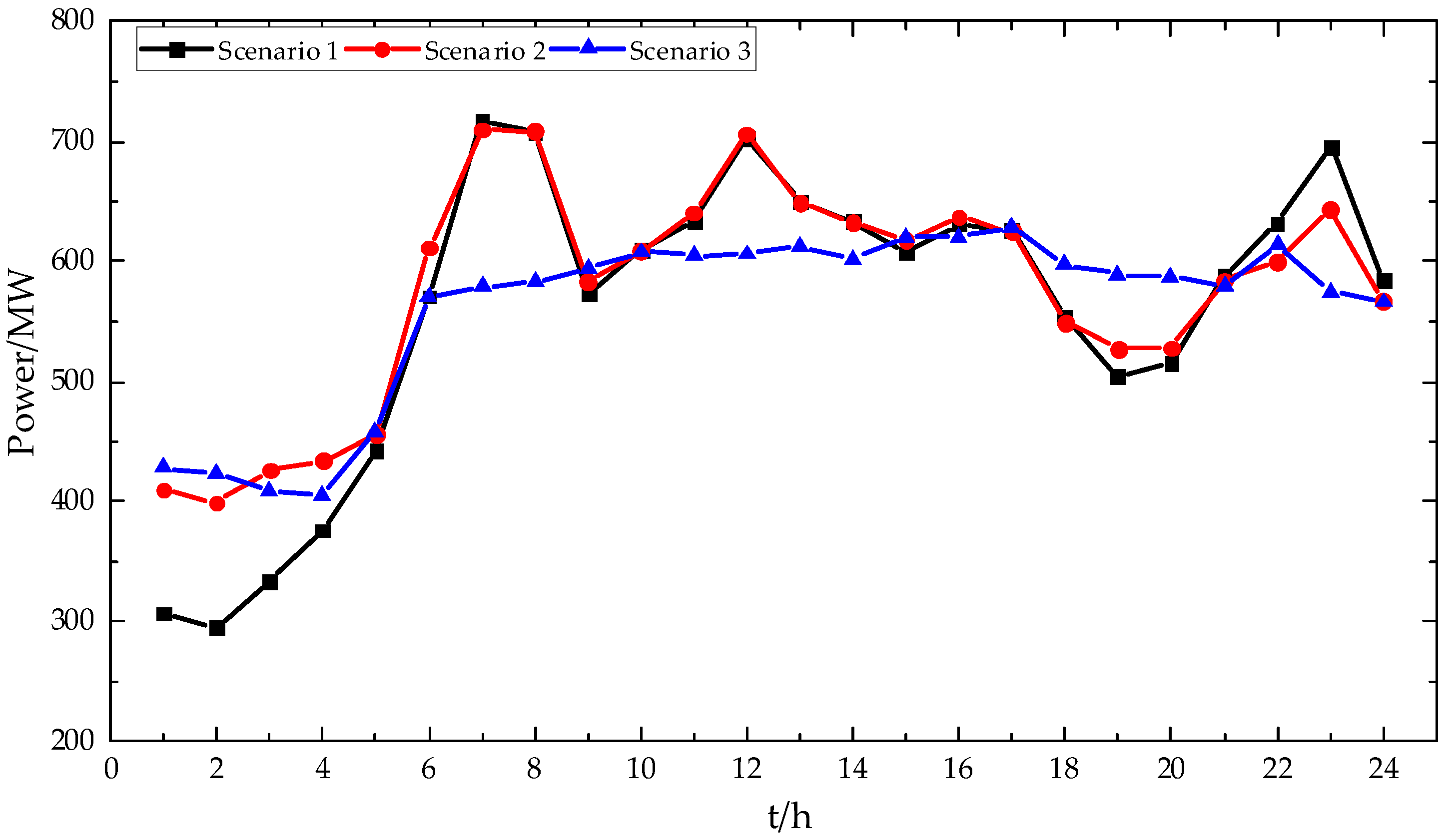
6.3. Comparative Analysis of Different Scheduling Strategies
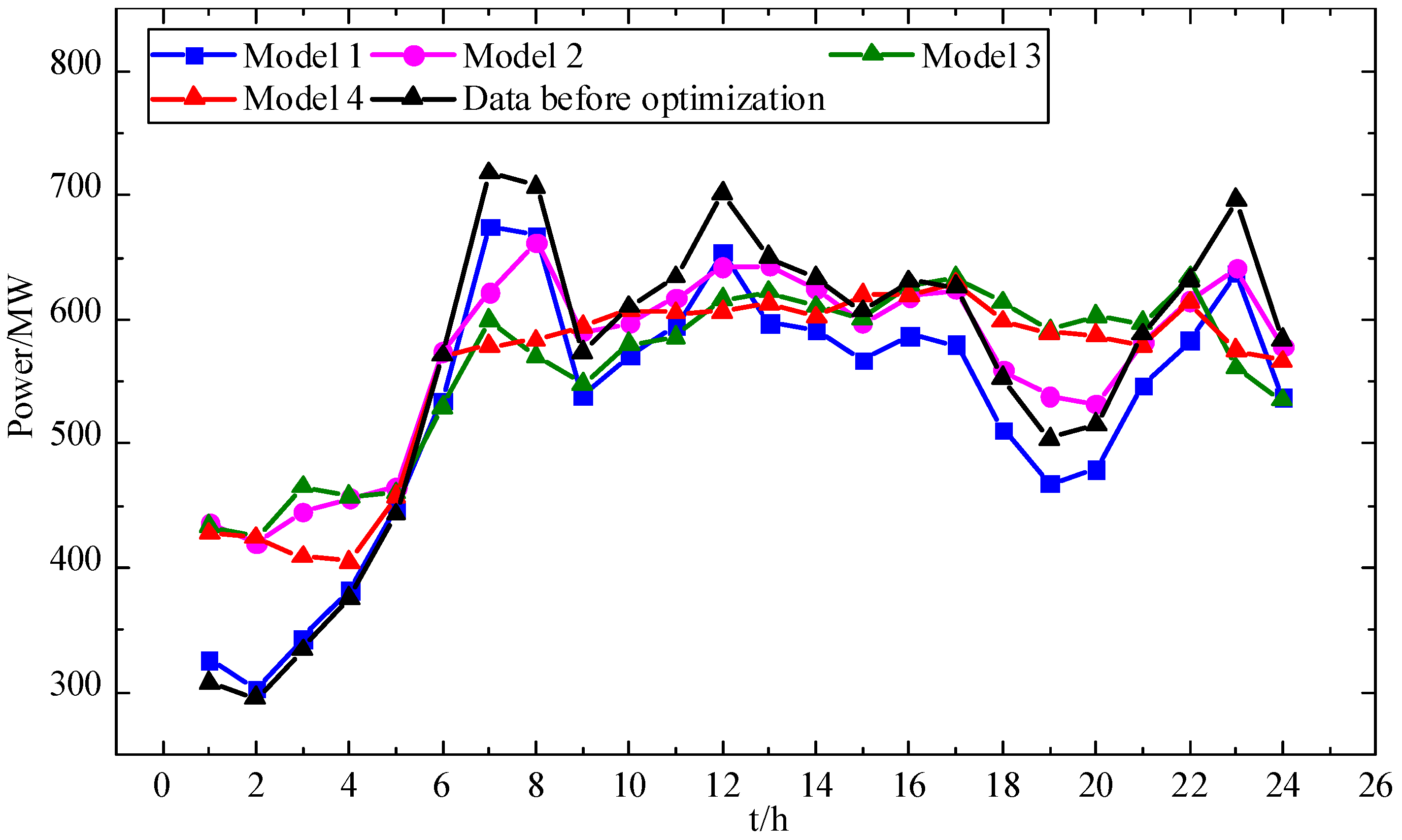
6.4. Comparative Analysis of Different Renewable Energy and Load Similarity Measures
7. Conclusions
- (1)
- Compared to traditional methods such as the Euclidean distance, net load variance, and correlation coefficient, the proposed similarity measurement method for renewable energy load can more effectively depict the matching degree of load to the output of renewable energy. Using the renewable energy and load similarity measure function to establish the adjustable resource response target can effectively reduce the peak-to-valley difference of the net load and smooth out the net load curve to stabilize the output of the conventional unit.
- (2)
- The two-stage scheduling model of source-load-storage coordination and optimization built in this paper aims to maximize the renewable energy and load similarity and minimize the regulation cost of adjustable resources in the upper layer and the overall operation cost in the lower layer. From an economic perspective, it can significantly reduce the cost of curtailed renewable energy and lower the overall operating cost of the system by 4.19%, thereby enhancing the overall economic efficiency of the system. From the peak regulation effect perspective, the net load peak–valley difference is reduced by 212 MW due to the participation of industrial load and energy storage in system dispatching. Moreover, the net load fluctuation is reduced by 67.54%, effectively alleviating the peak regulation pressure on conventional units and improving the level of renewable energy consumption.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
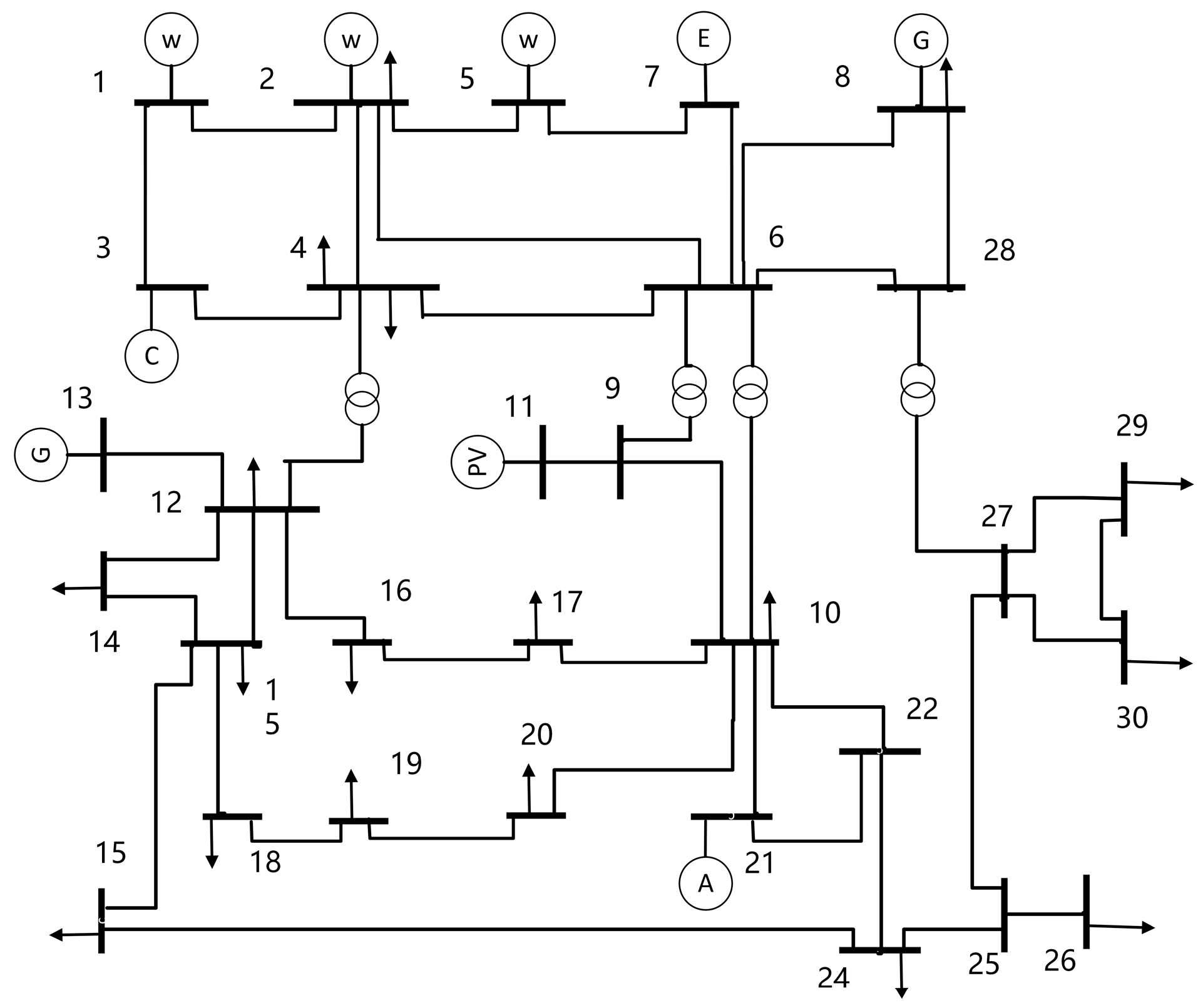
| Parameters | Rated Power/MW | Minimum Power/MW | Climb Rate Range/(MW·h−1) | Minimum Start/Stop Time/h | Start-Up Costs/CNY | Downtime Costs/CNY | Cost Factor a/b/c |
|---|---|---|---|---|---|---|---|
| Unit 1 | 800 | 250 | −250~250 | 5\4 | 900,000 | 400,000 | 0.00173/20.26/244.2 |
| Unit 2 | 500 | 150 | −150~150 | 5\4 | 900,000 | 400,000 | 0.0021/24.68/176.8 |
| Parameters | Cement | Parameters | Aluminum Electrolysis |
|---|---|---|---|
| Maximum number of pulverizers’ increase/decrease | 13/24 | Regulate the upper and lower power limits/MW | 56/−45 |
| Power per pulverizer/MW | 2 | Minimum continuous running time/h | 2 |
| Compensatory price in CNY/(MW·h) | 60 | Compensatory price in CNY/(MW·h) | 60 |
| Maximum storage capacity/(MW·h) | 250 | \ | \ |
| initial capacity/(MW·h) | 110 | \ | \ |
References
- Islam, F.; Moni, N.; Akhter, S. Feasibility Analysis of a 100MW Photovoltaic Solar Power Plant at Rajshahi, Bangladesh Using RETScreen Software. Int. J. Eng. Manuf. 2023, 13, 1–10. [Google Scholar] [CrossRef]
- Islam, M.d.S.; Islam, F.; Habib, M.d.A. Feasibility Analysis and Simulation of the Solar Photovoltaic Rooftop System Using PVsyst Software. Int. J. Educ. Manag. Eng. 2022, 12, 21–32. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, Y.; Chen, J.; Xu, B. Pricing Mechanism and Trading Strategy Optimization for Microgrid Cluster Based on CVaR Theory. Electronics 2023, 12, 4327. [Google Scholar] [CrossRef]
- National Energy Board 2023 Q1 Press Conference Transcript—National Energy Board. Available online: http://www.nea.gov.cn/2023-02/13/c_1310697149.htm (accessed on 26 April 2023).
- Liu, S.; Yang, Y.; Yang, Z.; Chen, Q. Determination of Reserve Capacity Considering Random Characteristics of New Energy and Its Cost Allocation. Autom. Electr. Power Syst. 2023, 47, 10–18. [Google Scholar]
- Hu, J.; Ma, R.; Qin, K.; Liu, W.; Li, W.; Deng, H. A Demand Side Response Optimization Model Considering the Output Characteristics of New Energy. In Proceedings of the 2023 6th International Conference on Energy, Electrical and Power Engineering (CEEPE), Guangzhou, China, 12–14 May 2023; pp. 1412–1417. [Google Scholar]
- Yang, W.; Zhu, X.; Nie, F.; Jiao, H.; Xiao, Q.; Yang, Z. Chaos Moth Flame Algorithm for Multi-Objective Dynamic Economic Dispatch Integrating with Plug-In Electric Vehicles. Electronics 2023, 12, 2742. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, Y.; Bo, W.; Wang, D.; Zhang, D.; Shi, J. Optimal Scheduling of Virtual Power Plant Considering Revenue Risk with High-Proportion Renewable Energy Penetration. Electronics 2023, 12, 4387. [Google Scholar] [CrossRef]
- Wynn, S.L.L.; Boonraksa, T.; Boonraksa, P.; Pinthurat, W.; Marungsri, B. Decentralized Energy Management System in Microgrid Considering Uncertainty and Demand Response. Electronics 2023, 12, 237. [Google Scholar] [CrossRef]
- Li, Y.; Li, R.; Shi, L.; Wu, F.; Zhou, J.; Liu, J.; Lin, K. Adjustable Capability Evaluation of Integrated Energy Systems Considering Demand Response and Economic Constraints. Energies 2023, 16, 8048. [Google Scholar] [CrossRef]
- Chang, G.; Yang, X.; Jiang, H.; Cui, Y.; Zhang, Y.; Hao, S.; Zhang, Y. Rolling flexible regulation strategy for multi-stage demand response of power grid with high proportion of new energy access considering industrial load characteristics. Electr. Power Autom. Equip. 2023, 43, 1–14. [Google Scholar] [CrossRef]
- Shu, J.; Guan, R.; Han, B. Industrial large customer time-of-use electricity price optimization method. Proc. CSEE 2018, 33, 1552–1559. [Google Scholar] [CrossRef]
- Yu, Q.; Yang, H.; Liu, J.; Liao, S.; Meng, K. Optimal allocation of wind and solar capacity based on the active response capability of cascaded hydropower and high-load energy demand power variations. Power Syst. Autom. Equip. 2020, 40, 71–78. [Google Scholar] [CrossRef]
- Oskouei, M.Z.; Zeinal-Kheiri, S.; Mohammadi-Ivatloo, B.; Abapour, M.; Mehrjerdi, H. Optimal Scheduling of Demand Response Aggregators in Industrial Parks Based on Load Disaggregation Algorithm. IEEE Syst. J. 2022, 16, 945–953. [Google Scholar] [CrossRef]
- Golmohamadi, H.; Keypour, R.; Bak-Jensen, B.; Pillai, J.R. A Multi-Agent Based Optimization of Residential and Industrial Demand Response Aggregators. Int. J. Electr. Power Energy Syst. 2019, 107, 472–485. [Google Scholar] [CrossRef]
- Hu, X.; Xu, G.; Shang, C.; Wang, L.; Weng, W.; Cheng, H. Joint planning of Battery Energy Storage and Demand Response for industrial park participating in Peak Shaving. Autom. Electr. Power Syst. 2019, 43, 116–123. [Google Scholar]
- Liu, C.; Sun, A.; Wang, Y.; He, H.; Zhang, H.; Ning, L. Day-ahead and intra-day joint economic dispatching method of electric power system considering combined peak-shaving of fused magnesium load and energy storage. Electr. Power Autom. Equip. 2022, 42, 8–15. [Google Scholar] [CrossRef]
- Hao, C.; Wang, Y.; Liu, C.; Zhang, G.; Yu, H.; Wang, D.; Shang, J. Research on Two-Stage Regulation Method for Source–Load Flexibility Transformation in Power Systems. Sustainability 2023, 15, 13918. [Google Scholar] [CrossRef]
- Xu, J.; Chen, Y.; Liao, S.; Sun, Y.; Yao, L.; Fu, H.; Jiang, X.; Ke, D.; Li, X.; Yang, J.; et al. Demand Side Industrial Load Control for Local Utilization of Wind Power in Isolated Grids. Appl. Energy 2019, 243, 47–56. [Google Scholar] [CrossRef]
- Shi, L.; Zhou, R.; Li, J.; Wang, Y.; Xu, F.; Wang, Y. New energy-load characteristic index based on time series similarity measurement. Power Syst. Autom. Equip. 2019, 39, 75–81. [Google Scholar] [CrossRef]
- Zhou, R.; Li, B.; Huang, Q.; Tang, X.; Peng, Y.; Fang, S.; Shi, L. Source-Load-Storage Coordinated Optimization Model with Source-Load Similarity and Curve Volatility Constraints. Proc. CSEE 2020, 40, 4092–4102. [Google Scholar] [CrossRef]
- Wang, T.; Li, F.; Zhou, Y.; Cui, W. Source-load-energy storage coordinated optimal scheduling for peak regulation based on new energy resource-load similarity. Electr. Power Autom. Equip. 2023, 1–10. [Google Scholar] [CrossRef]
- Ye, L.; Qu, X.; Mo, Y.; Zhang, J.; Wang, Y.; Huang, Y.; Wang, W. Analysis on intraday operation characteristics of hybrid wind-solar-hydro power generation system. Autom. Electr. Power Syst. 2018, 42, 158–164. [Google Scholar]
- Sun, C. Multiple Load Coordination Optimization Scheduling Strategy of Active Distribution Network to Improve New Energy Consumption Capacity. Master’s Thesis, North China Electric Power University, Beijing, China, 2022. [Google Scholar]
- Vujanic, R.; Mariéthoz, S.; Goulart, P.; Morari, M. Robust Integer Optimization and Scheduling Problems for Large Electricity Consumers. In Proceedings of the 2012 American Control Conference (ACC), San Diego, CA, USA, 27–29 June 2012; pp. 3108–3113. [Google Scholar]
- Golmohamadi, H.; Keypour, R.; Bak-Jensen, B.; Pillai, J.R.; Khooban, M.H. Robust Self-Scheduling of Operational Processes for Industrial Demand Response Aggregators. IEEE Trans. Ind. Electron. 2020, 67, 1387–1395. [Google Scholar] [CrossRef]
- Jin, H.; Sun, H.; Guo, Q.; Wang, B.; Cheng, R.; Wang, W. Dispatch Strategy Based on Energy Internet Customer-Centered Concept for Energy Intensive Enterprise and Renewable Generation to Improve Renewable Integration. Power Syst. Technol. 2016, 40, 139–145. [Google Scholar] [CrossRef]
- Qi, Y.; Shang, X.; Nie, J.; Huo, X.; Wu, B.; Su, W. Optimization of CCHP micro-grid operation based on improved multi-objective grey wolf algorithm. Electr. Meas. Instrum. 2022, 59, 12–19+52. [Google Scholar] [CrossRef]
- Feleke, S.; Pydi, B.; Satish, R.; Kotb, H.; Alenezi, M.; Shouran, M. Frequency Stability Enhancement Using Differential-Evolution- and Genetic-Algorithm-Optimized Intelligent Controllers in Multiple Virtual Synchronous Machine Systems. Sustainability 2023, 15, 13892. [Google Scholar] [CrossRef]
- Kannan, S.; Baskar, S.; McCalley, J.D.; Murugan, P. Application of NSGA-II Algorithm to Generation Expansion Planning. IEEE Trans. Power Syst. 2009, 24, 454–461. [Google Scholar] [CrossRef]
| Evaluation Indicators | Peak-to-Valley Difference | Volatility |
|---|---|---|
| Scenario 1 | 436 | 54.65 |
| Scenario 2 | 312 | 42.67 |
| Scenario 3 | 224 | 17.74 |
| Cost Item/CNY | Conventional Generator Set | Abandonment of Renewable Energy Sources | Loss of Load | Regulatable Resources | Total Cost |
|---|---|---|---|---|---|
| Scenario 1 | 304,181 | 85,205 | 16 | \ | 389,402 |
| Scenario 2 | 313,251 | 16,897 | 849 | 44,016 | 375,013 |
| Scenario 3 | 296,972 | 0 | 0 | 76,100 | 373,072 |
| Evaluation Indicators | Peak-to-Valley Difference | Volatility |
|---|---|---|
| Data before optimization | 436 | 54.65 |
| Model 1 | 373 | 49.70 |
| Model 2 | 263 | 31.30 |
| Model 3 | 231 | 24.91 |
| Model 4 | 224 | 17.74 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Du, X.; Wang, H.; Yan, S.; Fan, T. Research on Coordinated Optimization of Source-Load-Storage Considering Renewable Energy and Load Similarity. Energies 2024, 17, 1301. https://doi.org/10.3390/en17061301
Wang X, Du X, Wang H, Yan S, Fan T. Research on Coordinated Optimization of Source-Load-Storage Considering Renewable Energy and Load Similarity. Energies. 2024; 17(6):1301. https://doi.org/10.3390/en17061301
Chicago/Turabian StyleWang, Xiaoqing, Xin Du, Haiyun Wang, Sizhe Yan, and Tianyuan Fan. 2024. "Research on Coordinated Optimization of Source-Load-Storage Considering Renewable Energy and Load Similarity" Energies 17, no. 6: 1301. https://doi.org/10.3390/en17061301
APA StyleWang, X., Du, X., Wang, H., Yan, S., & Fan, T. (2024). Research on Coordinated Optimization of Source-Load-Storage Considering Renewable Energy and Load Similarity. Energies, 17(6), 1301. https://doi.org/10.3390/en17061301






