FLC-Based Ultra-Low-Frequency Oscillation Suppression Scheme for Interconnected Power Grids

Abstract

The appearance of ultra-low-frequency oscillations in the grid at the sending end, after asynchronous grid interconnection, poses a significant threat to the stable operation of the system. For post-asynchronous interconnection in a multi-DC transmission system, an investigation is conducted to analyze the causes of ultra-low-frequency oscillations and the utilization of a Frequency Limit Controller (FLC) which aims to suppress these oscillations. Furthermore, a method is developed to rank DC sensitivity, considering the hydroelectric distribution in the sending-end grid, by combining the DC FLC impact factor and DC control sensitivity. Subsequently, a novel approach for ultra-low-frequency oscillation suppression is proposed. This approach employs the stochastic subspace method for parameter estimation and the NSGA-II optimization algorithm to convert the multi-DC optimization challenge into multiple sequential cyclic optimization problems, each focusing on a single DC, ensuring a more effective suppression of ultra-low-frequency oscillations. The proposed scheme’s effectiveness is validated through simulations using a specific locations’ interconnected power grid.

1. Introduction

In the context of the rapid development of new energy sources [1,2,3,4], direct current (DC) transmission technology offers advantages of lower power losses compared to alternating current (AC) transmission [5,6]. Moreover, it presents broader prospects for application in long-distance power transmission and asynchronous grid interconnection [7,8].

Internationally, there are numerous demonstration projects for DC transmission systems. For instance, the Yubei-Ezhou Flexible DC Back-to-Back Transmission Project [9] (referred to as the “Yubei-Ezhou Project”) stands as the pioneering flexible DC transmission endeavor with the highest voltage level and maximum transmission capacity, rated at 5000 MW, with a nominal voltage of ±420 kV.

The widespread implementation of DC transmission projects has led to the occurrence of some ultra-low-frequency oscillations in practical power grids in recent years [10] (oscillations with frequencies lower than 0.1 Hz). Based on these occurrences, researchers [11] conducted an analysis focusing on the frequency, damping, and manifestations of ultra-low-frequency oscillations within the context of single-machine and single-load systems. The findings highlighted significant distinctions between ultra-low-frequency oscillations and conventional frequency stability issues. The manifestations of these frequency oscillations do not exhibit relative oscillations between generator rotors; instead, they represent oscillations in the overall network frequency. Therefore, they differ from traditional low-frequency oscillations in power systems.

Presently, scholars have introduced several studies; for instance, the literature [12] has proposed a DC frequency control system, employing multivariable control in the frequency regulation of DC systems. This allows for a better adjustment of the frequency of AC systems while ensuring the stability of both AC systems. Additionally, some researchers have conducted an analysis of the speed governor models of hydroelectric units, identifying them as the primary factors contributing to the occurrence of ultra-low-frequency oscillations [13]. The literature [14] has presented a method applicable for ultra-low-frequency oscillation analysis in multi-machine systems through single-machine equivalencing. In another context, researchers [15] elucidated the impact of DC frequency regulation on enhancing the frequency stability in the Yunnan power grid after asynchronous operation, analyzing factors such as the adjustment range and dead-band setting of DC frequency regulation on AC system frequency stability. Furthermore, based on the ChuSui and PuQiao Ultra High Voltage Direct Current (UHVDC) island operation test, researchers [16] analyzed the ultra-low-frequency oscillation mechanism under isolated island condition based on the operation test of Chusui and Puqiao UHVDC islands, and proposed frequency stabilization measures for hydropower units to coordinate DC frequency modulation.

Regarding measures to suppress ultra-low-frequency oscillations, the literature [17] analyzes this and proposes that coordinating the deadband settings of hydro and thermal power unit governors can effectively suppress ultra-low-frequency oscillations. However, increasing the primary frequency control deadband means abandoning the governor’s adjustment to minor load fluctuations, which reduces the system’s frequency quality; setting the FLC deadband smaller than the governor deadband also implies a reduction in the unit’s primary frequency control performance. On the other hand, due to negative damping, the system outside the deadband may still oscillate near the deadband [18]. And, governors frequently set PID control parameters too sensitively in order to meet frequency control performance indicators. This results in negative damping being provided by the hydro turbine governor to the system, which triggers ultra-low-frequency oscillation incidents. The governor’s PID parameters are optimized using the critical parameter method [19] based on a linearized model. This improves system damping and suppresses ultra-low-frequency oscillations. The focus of PID parameter optimization is on enhancing the algorithm’s global optimization capability by improving the solution algorithm, which includes using methods with random dynamic inertia weight coefficients [20].

This paper presents a set of ultra-low-frequency oscillation suppression strategies based on FLC by analyzing the mechanisms behind such oscillations. Initially, a direct current sensitivity sorting method considering the hydro distribution of the sending-end power grid is introduced. Subsequently, optimization of the parameters within the direct current FLC is achieved using a combination of Stochastic Subspace Identification and Non-Dominated Sorting Genetic Algorithm-II (NSGA-II), aiming to attain a more effective suppression of ultra-low-frequency oscillations.

2. Analysis of Ultra-Low-Frequency Oscillations and Mechanisms for FLC Suppression

For the hydroelectric generator units in the sending-end power grid, the equations governing their rotor motion can be derived as follows [20]:

$$M\frac{d\Delta \omega }{dt}=\Delta T_{\mathrm{M}}-(\Delta T_{\mathrm{E}}+\Delta T_{\mathrm{dc}})-D\Delta \omega ,$$

(1)

where M represents the rotational inertia of the generator rotor, ΔT_M denotes the change in mechanical torque, ΔT_E signifies the change in electromagnetic torque, ΔT_dc represents the variation in additional DC torque, D stands for the damping coefficient, and Δω indicates the change in angular velocity.

When ultra-low-frequency oscillations occur, the most significant variations primarily occur in the mechanical torque. The mechanical torque is predominantly determined by the governing system of the prime mover, represented by GGOV(s), which denotes the transfer function of the prime mover governing system. Therefore, the change in mechanical torque can be expressed as [20]

$$\Delta T_{\mathrm{M}}=-G_{\mathrm{GOV}}(s)\Delta \omega ,$$

(2)

where s = jω_d, and assuming K_GOV, represents the amplitude of the transfer function of the prime mover governing system in polar coordinates, and φ_GOV represents the phase of the transfer function of the prime mover governing system.

Therefore, Equation (2) can be transformed into [20]

$$\begin{array}{ll}\Delta T_{\mathrm{M}}& =-K_{\mathrm{GOV}} {\mathrm{e}}^{\mathrm{j}{\phi }_{\mathrm{GOV}}} \Delta \omega \\ & =-K_{\mathrm{GOV}}\cos {\phi }_{\mathrm{GOV}}\Delta \omega +K_{\mathrm{GOV}}\sin {\phi }_{\mathrm{GOV}}\Delta \omega \\ & =-K_{\mathrm{GOV}}\cos {\phi }_{\mathrm{GOV}}\Delta \omega +K_{\mathrm{GOV}}\sin {\phi }_{\mathrm{GOV}}\frac{{\omega }_d}{{\omega }_0}\Delta \delta \end{array}.$$

(3)

Hence, ΔT_M can be divided into two parts:

$$\begin{array}{l} \Delta T_{\mathrm{M}}=\Delta T_{\mathrm{S}}+\Delta T_{\mathrm{D}}\\ \left\{\begin{array}{l}\Delta T_{\mathrm{D}}=-K_{\mathrm{GOV}}\cos {\phi }_{\mathrm{GOV}}\Delta \omega \\ \Delta T_{\mathrm{S}}=K_{\mathrm{GOV}}\sin {\phi }_{\mathrm{GOV}}\omega \Delta \delta \end{array}\right.\end{array}.$$

(4)

where ΔT_S denotes the synchronous torque variation, and ΔT_D represents the damping torque variation.

The term D_GOV defines the prime mover damping coefficient [20]:

$$D_{\mathrm{GOV}}=K_{\mathrm{GOV}}\cos {\phi }_{\mathrm{GOV}}=-\frac{\Delta T_{\mathrm{D}}}{\Delta \omega }.$$

(5)

Thus, Equation (1) can be transformed into [20]

$$M\frac{d\Delta \omega }{dt}=\Delta T_{\mathrm{S}}-\Delta T_{\mathrm{E}}-\Delta T_{\mathrm{dc}}-(D_{\mathrm{GOV}}+D)\Delta \omega .$$

(6)

Figure 1 shows the damping coefficient decomposition coordinate system. The projection of ΔT_M on the abscissa represents ΔT_S, while the projection of ΔT_M on the vertical axis signifies ΔT_D. The projection of ΔT_M on the vertical axis represents the effect on dynamic stability. When D_GOV is greater than 0 and ΔT_D, which is equal to D_GOV multiplied by Δω, and is less than 0, the projection of ΔT_M on the ordinate axis is positioned on the negative half-axis. This indicates that the speed control system provides positive damping torque. Conversely, when D_GOV is less than 0, the projection of ΔT_M on the ordinate axis is situated on the positive half-axis, indicating that the speed control system generates negative damping torque. The length of ΔT_D reflects the strength of damping. In the positive damping region, the length of the projection is directly proportional to the positive damping intensity provided by the control system. A larger absolute value of ΔT_D implies stronger positive damping, which is highly advantageous for system stability. However, in the negative damping region, the length of the projection is directly proportional to the negative damping intensity generated by the control system. A larger absolute value of ΔT_D implies stronger negative damping, which can be detrimental to system stability.

Within the range of 0 < f < 0.1 Hz, the negative damping coefficient provided by D_GOV increases as T_w increases. For systems that contain large-capacity hydro-generating units, the damping coefficient D_GOVwater of the water turbine governing system differs in some way from the system damping coefficient D when the direct current input of FLC is disregarded (i.e., ΔT_dc = 0). If D_GOVwater + D < 0, the system exhibits overall negative damping in the ultra-low-frequency range, which ultimately results in the generation of ultra-low-frequency oscillations.

Based on the equivalent method for the generator’s ΔT_M, the formula for calculating the additional direct current torque ΔT_dc is the sum of the additional synchronous torque ΔT_sdc and the additional damping torque ΔT_Ddc, that is

$$\Delta T_{\mathrm{dc}}=\Delta T_{\mathrm{Sdc}}+\Delta T_{\mathrm{Ddc}}=\Delta T_{\mathrm{Sdc}}+D_{\mathrm{dc}}\Delta \omega ,$$

(7)

where D_dc represents the additional direct current damping coefficient.

Substituting Equation (7) into Equation (6), we can obtain [20]

$$M\frac{d\Delta \omega }{dt}=\Delta T_{\mathrm{S}}-\Delta T_{\mathrm{E}}-\Delta T_{\mathrm{Sdc}}-(D_{\mathrm{GOVwater}}+D_{\mathrm{dc}}+D)\Delta \omega .$$

(8)

Therefore, by appropriately configuring the parameters of FLC, it is possible to provide positive damping to the system, countering the negative damping introduced by the hydro-generating units within the system (i.e., D_GOVwater + D + D_dc > 0), ultimately achieving suppression of ultra-low-frequency oscillations.

3. Suppression Strategy for Ultra-Low-Frequency Oscillations

Figure 2 shows the Steps of Ultra-Low-Frequency Oscillation Suppression Scheme based on FLC.

Firstly, power disturbances applied to each DC output channel undergo system identification using the stochastic subspace method. This step aims to determine the primary ultra-low-frequency oscillation modes within the system and the corresponding oscillation amplitudes at this frequency. The magnitude of the DC power disturbance is calculated based on equivalent frequency oscillation deviations. The impact factor of the DC FLC is also computed, which subsequently yields the sorting factor for the DC signals that are eligible for FLC attachment. Based on the sorting factor of the DC signals and the practical system scenario, the number ‘l’ of additional DC signals controlled by FLC is determined, and the installation locations for the DC FLC are established. Finally, a Non-Dominated Sorting Genetic Algorithm-II (NSGA-II) optimization model is developed to sequentially optimize each DC signal, with the aim of suppressing ultra-low-frequency oscillations.

4. System Identification Based on the Stochastic Subspace Method and Sensitivity Ranking of DC Signals

4.1. System Parameter Identification

Assuming that the sending-end system has m direct current output channels available for additional FLC control, the system’s state–space model can be transformed into a discrete state–space equation [19] using the stochastic subspace method. The equation is expressed as follows when the k-th direct current imposes a disturbance [21]:

$$\left\{\begin{array}{l}{x}_{k+1}=\mathit{A}{x}_k+{\mathit{w}}_k\hfill \\ y_k=\mathit{C}{x}_k+{\mathit{v}}_k\hfill \end{array}\right..$$

(9)

where A represents the state matrix governing the internal dynamics of the system, and C represents the matrix representing the connection between the output and the system’s internal dynamics. The terms w_k ∈ Rⁿ and v_k ∈ R^l are both assumed to be white noise, where E(w_k) = E(v_k) = 0.

To perform data acquisition for Equation (9) and to construct the Hankel matrix, follow these steps [21]:

$$\left[\frac{\begin{array}{cccc}{y}_0& y_1& \cdots & y_{j-1}\\ y_1& y_2& \cdots & y_j\\ \cdots & \cdots & \cdots & \cdots \\ y_{i-1}& y_i& \cdots & y_{i+j-2}\end{array}}{\begin{array}{cccc}{y}_i& y_{i+1}& \cdots & y_{i+j-1}\\ y_{i+1}& y_{i+2}& \cdots & y_{i+j}\\ \cdots & \cdots & \cdots & \cdots \\ y_{2i-1}& y_{2i}& \cdots & y_{2i+j-2}\end{array}}\right]=\left[\frac{{\mathit{Y}}_{0,i-1}}{{\mathit{Y}}_{i,2i-1}}\right]=\frac{{\mathit{Y}}_{\mathrm{p}}}{{\mathit{Y}}_{\mathrm{f}}},$$

(10)

where i = 2n, n represents the system order, and j denotes the number of measurement samples.

To solve Equation (10), perform QR decomposition [21].

$$\frac{{\mathit{Y}}_p}{{\mathit{Y}}_f}=\left[\begin{array}{cc}{\mathit{R}}_{11}& 0\\ {\mathit{R}}_{21}& {\mathit{R}}_{22}\end{array}\right]\left[\begin{array}{c}{\mathit{Q}}_{\mathrm{l}}^{\mathrm{T}}\\ {\mathit{Q}}_2^{\mathrm{T}}\end{array}\right].$$

(11)

The matrix obtained from orthogonal projection is as follows:

$${\mathit{R}}_i={\mathit{Y}}_{\mathrm{f}}/{\mathit{Y}}_{\mathrm{p}}={\mathit{R}}_{21}{\mathit{Q}}_1^{\mathrm{T}}.$$

(12)

The projection involves reducing the data while preserving the original information of the signal. After the QR decomposition, the data, which were originally a 2i × j-dimensional Hankel matrix, transforms into an i × j-dimensional matrix.

Singular Value Decomposition (SVD) is then performed on the projection matrix.

$${\mathit{R}}_i=\left[\begin{array}{cc}{U}_1& U_2\end{array}\right]\left[\begin{array}{cc}{S}_1& 0\\ 0& 0\end{array}\right]\left[\begin{array}{c}{V}_1^{\mathbf{T}}\\ V_2^{\mathbf{T}}\end{array}\right]={\mathit{U}}_1{\mathit{S}}_1{\mathit{V}}_1^{\mathrm{T}},$$

(13)

where U₁ ∈ R^li×n, S₁ ∈ R^n×n, V₁ ∈ R^li×n

The observability matrix Γi and the Kalman filter state can be multiplied to decompose the projection matrix.

$${\mathit{R}}_i={\mathit{\Gamma }}_i{\hat{\mathit{X}}}_i,$$

(14)

where

$${\mathit{\Gamma }}_i=\left[\begin{array}{c}C\\ CA\\ C{A}^2\\ ⋮\\ C{A}^{i-1}\end{array}\right], {\hat{\mathit{X}}}_i=[\begin{array}{ccc}{\hat{\mathit{x}}}_i& \cdots & {\hat{x}}_{i+j-1}\end{array}]$$

Substitute Equation (14) into the system’s state–space equation [21].

$$\left[\begin{array}{c}{\hat{\mathit{X}}}_{i+1}\\ {\mathit{Y}}_{i,i}\end{array}\right]=\left[\begin{array}{c}\mathit{A}\\ \mathit{C}\end{array}\right]{\hat{\mathit{X}}}_i+\left[\begin{array}{c}{\mathit{w}}_i\\ {\mathit{v}}_i\end{array}\right].$$

(15)

The computation of A and C using the method of least squares results in [21]

$$\left[\begin{array}{c}\mathit{A}\\ \mathit{C}\end{array}\right]=\left[\begin{array}{c}{\hat{\mathit{X}}}_{i+1}\\ {\mathit{Y}}_{i,i}\end{array}\right]{\left[{\hat{\mathit{X}}}_i\right]}^{+},$$

(16)

where [ ]⁺ represents the pseudo-inverse of the matrix. Once we have obtained the system’s state matrix A, we use the method of least squares to determine the amplitude and phase angle of each oscillatory mode [21].

$$\mathit{Y}=\mathit{\lambda }\mathit{C},$$

(17)

where

$$\begin{gathered} \mathit{C}={[c_1,c_2,\cdots ,c_{N-1}]}^T \\ {\mathit{Y}}_{\beta }={[y(0),y(1),\cdots ,y(N-1)]}^T \\ \mathit{\lambda }=\left[\begin{array}{cccc}1& 1& \cdots & 1\\ {\lambda }_1& {\lambda }_1& \cdots & {\lambda }_1\\ ⋮& ⋮& & ⋮\\ {\lambda }_1^{N-1}& {\lambda }_1^{N-1}& \cdots & {\lambda }_1^{N-1}\end{array}\right] \end{gathered}$$

The Equation (17) can be solved to obtain [21]:

$$\mathit{C}={({\mathit{\lambda }}^H\mathit{\lambda })}^{-1}{\lambda }^H\mathit{Y}.$$

(18)

Therefore, the amplitudes and phases of individual components are

$$a_i=2\left|c_i\right|.$$

(19)

$${\theta }_i=\arg c_i.$$

(20)

In this case, we can find the time–domain expression of the system’s step response with a direct current input k as G_k(s).

4.2. Definition of Direct Current Sensitivity

The Section 1 analysis shows that ultra-low-frequency oscillations are mainly caused by the negative damping torque of hydro-generating units. To suppress these oscillations, additional DC FLC control can track the frequency variations and adjust the power inversely. However, in practical systems, the distribution of hydro-generating units is linked to the watershed. The impact of additional FLC on DC power can cause changes in hydroelectric channel power, which may have a minor effect on the remaining AC channels, according to power flow distribution. To assess the extent of the DC FLC’s influence on the AC system, the DC FLC impact factor is defined. The calculation formula for this factor is as follows:

$${\xi }_k=\frac{\Delta P_k-{\displaystyle \sum _{b=1}^b\Delta P_{Hydroelectric}}}{\Delta P_k}\times 100\%,$$

(21)

where ΔP_k denotes the power variation of direct current k (100 MW), ΔP_{Hydroelectric} represents the power variations from hydroelectric channels, ξ_k signifies the DC FLC impact factor, which represents the percentage of power variation in the remaining AC channels caused by the variation in direct current k power, excluding the hydroelectric channels.

Given the known required direct current modulation power for each direct current when causing the same frequency deviation in the system, as well as the DC FLC impact factor ξ_k, the further definition of the direct current sensitivity factor is as follows:

$$S_k={\tau }_k\times {\xi }_k.$$

(22)

The Equation (22) uses S_k to represent the direct current sensitivity factor. This factor describes the sensitivity of direct current k to ultra-low-frequency oscillation modes and its impact on the AC system.

Assuming the direct current sensitivity factor corresponding to the j-th direct current is represented as S_j, with the maximum value denoted as S_max corresponding to direct current number 1, and the minimum value as S_min corresponding to direct current number m, arranging these factors in descending order creates the sequence table of DC with FLC, as depicted in

Table 1. The sequence table of DC with FLC.

The Sequence Table	1	2	…	4	…	m
Name	DC 1	DC 2	…	DC k	…	DC m
The direct current sensitivity factor	S1	S2	…	Sk	…	Sm

.

The number of DCs controlled by additional FLC is denoted as l (l ≤ m). Based on practical considerations, such as the direct current equipment, rated capacity of the DC system, and strength of the AC grid at the DC receiving end, the actual attached DCs in a practical project can be determined.

5. Parameter Optimization of Additional FLC

5.1. Selection of Objective Function

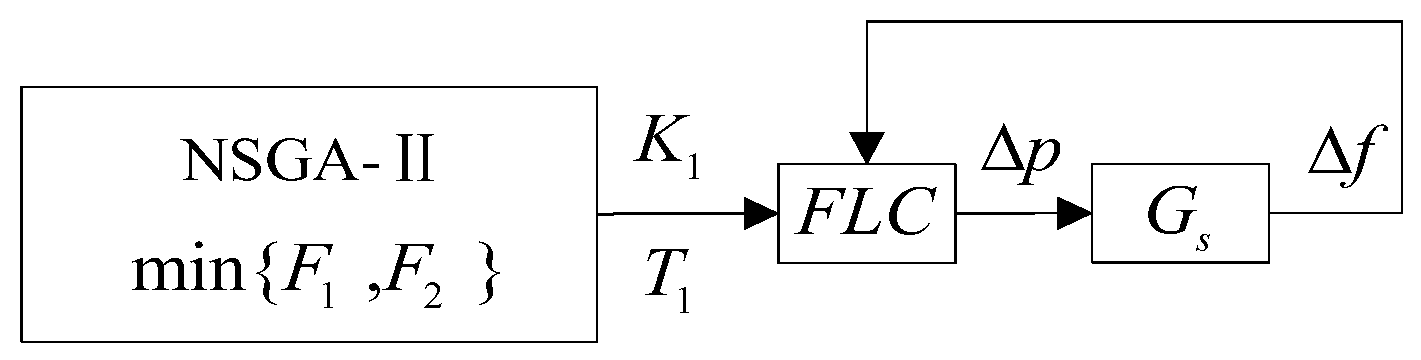
After obtaining the low-order linear model G_k(s) of the system, this paper uses the Non-Dominated Sorting Genetic Algorithm-II (NSGA-II) with an elite strategy to optimize the Proportional–Integral (PI) parameters of the FLC for direct current k [22]. The FLC parameter optimization model is shown in Figure 3.

The first optimization objective is to improve the system’s transient frequency response. After the direct current FLC participates in regulating the system’s frequency, it results in a superior effect, characterized by reduced peak frequency deviation, fewer oscillations in frequency under step disturbances, and a shorter recovery time for stability. Therefore, the effectiveness of the direct current FLC in enhancing the system’s transient frequency response can be measured by utilizing the standard deviation of the frequency. The objective function for optimization using the NSGA-II is expressed as the integral of the absolute value of the system frequency deviation Δf over time.

$$\min F_1={\displaystyle {\int }_0^{T}t}\left|\Delta f\right|dt.$$

(23)

where t is the simulation time; T is the upper limit of the integration time; and Δf is the frequency deviation of the system.

Furthermore, during the participation of the DC FLC in the grid frequency regulation, the DC power varies with frequency changes. In this process, deviations from the rated operation of the DC transmission power will have certain effects on the DC system itself, and excessive deviations may adversely affect the converter station equipment. Therefore, in this paper, the integrated value of the total DC power deviation during the multi-DC FLC control process is taken as the objective function F₂ to measure the overall effect of multi-DC FLC on the DC system under different control parameters.

$$\min F_2={\displaystyle {\int }_0^{T}t\left|\Delta P_{\mathrm{FLC}}\right|} \mathrm{d}t.$$

(24)

where t is the simulation time; T is the upper limit of the integration time; and ΔP_FLC is the deviation of the DC transmission power of the system.

This paper examines the dead-zone parameter of the direct current FLC as the decision variable for optimization. Therefore, it is crucial to ensure that the dead-zone of the direct current FLC remains greater than ±0.05 Hz during the optimization process. Increasing the dead-zone of the direct current FLC also increases the risk of instability in the system’s transient frequency stability. To ensure the safety and stability of the system, the upper limit for the dead-zone of the direct current FLC has been set to 0.1 Hz. In summary, the size of the dead-zone for the direct current FLC must meet the following criterion [23]:

$$0.05\le f_{db}\le 0.1,$$

(25)

where f_db represents the dead-zone parameter of the direct current FLC.

The direct current FLC output’s power regulation capacity is limited by the power transmission constraints within the DC system. To ensure the safe and stable operation of the DC system, the upper limit for the direct current FLC output power is approximately 1.1 times the rated power, while the lower limit is around 0.9 times the rated power. Based on the power–frequency characteristics of the system, it has been observed that a higher adjustable power capacity of the direct current FLC leads to a better frequency response of the disturbed system. However, larger variations in direct current power have a greater impact on both the transmitting and receiving ends of the DC system. Therefore, this paper sets the constraints for the power adjustment of the direct current FLC as follows [23]:

$$-10\%P_{DC}\le \Delta P_{FLC}\le 5\%P_{DC},$$

(26)

where P_DC represents the rated power of the direct current system, and ΔP_FLC represents the adjustment active power of the direct current.

The multi-objective optimization model for the dead-zone parameters of the direct current FLC constructed in this paper can be described as follows:

$$\begin{array}{ll}& \min \{F_1, F_2\}\\ \mathrm{s}.\mathrm{t}.& \left\{\begin{array}{l}0.05\le f_{db}\le 0.1\\ -10\%P_{DC}\le \Delta P_{FLC}\le 5\%P_{DC}\end{array}\right.\end{array}.$$

(27)

5.2. Optimization Process of NSGA-II Algorithm

Figure 4 shows the flowchart of the NSGA-II algorithm.

Step 1: Initialization of the algorithm involves defining the objective functions and configuring algorithm parameters based on the practical aspects of problem-solving. Key parameters include population size, iteration count, crossover rate, mutation rate, among others. Initialize the population P_t, and set t = 0.

Step 2: Compute the fitness of each individual within the population.

Step 3: Select N individuals from set P_t using a chosen mechanism and perform crossover and mutation operations on them to generate offspring population Q_t.

Step 4: Merge P_t and Q_t to form a new population R_t, where R_t = P_t ∪ Q_t.

Step 5: Conduct fast non-dominated sorting on the combined parent and offspring population R_t to create a new non-dominated layer set. Then, compute the crowding distance for each individual within the population.

Step 6: Use R_t to generate a new population, P_t+1.

Step 7: Check if the algorithm’s termination condition is met. If it is, terminate the algorithm. If not, repeat steps 3 to 6 until the termination conditions are satisfied, resulting in the optimal outcome.

6. Case Studies

The effectiveness of the ultra-low-frequency oscillation suppression scheme based on FLC is validated using an example of an interconnected power grid in a certain regional area, as shown in Figure 5.

Area 1′s power grid is interconnected through several DC projects, including a ±800 kV line (6400 MW), a ±800 kV line (7200 MW), a ±800 kV line (8000 MW), a ±500 kV line (3000 MW), and a back-to-back ±420 kV line (5000 MW), connecting with the external power grid. The grid in Area 1 consists of six major hydropower channels, and this study focuses on it. The impact of frequency variations on DC transmission power at the receiving end is disregarded. The DC project d and three major UHVDC transmission lines are operating at full capacity. This is achieved using constant current control on the rectifier side and constant voltage control on the inverter side. The back-to-back DC project exports 2000 MW of power.

6.1. Additional FLC DC Sensitivity Ranking

The stochastic subspace method steps are used to identify data and showcase varying power changes in different DC projects under the same frequency deviation, as shown in

Table 2. Area 1′s grid-attached FLC power change table.

DC Project Name	a	b	c	d	Back-to-Back
The power variation (pu)	0.11	0.09	0.89	0.3	0.5

.

The power variations are as follows: a back-to-back DC project with a power change of 0.5 pu, DC project d with a power change of 0.3 pu, DC project a with a power change of 0.11 pu, DC project b with a power change of 0.09 pu, and DC project c with a power change of 0.089 pu. Applying a power disturbance of 100 MW to each DC project individually using a comprehensive program, we determined the FLC impact factors for the back-to-back DC project, DC project a, DC project b, DC project c, and DC project d. The impact factors were calculated as 65%, 50%, 12%, 48%, and 58%, respectively. The DC sensitivity ranking for the additional FLC in the Area 1′s power grid is presented in

Table 3. The DC sensitivity ranking table for the additional FLC in Area 1′s power grid.

The Sequence Table	1	2	3	4	5
Name	b	c	a	d	Back-to-Back
The DC sensitivity factor (%)	1.08	4.27	5.5	17.4	32.5

.

Table 3 shows that DC project b is the most effective in suppressing ultra-low-frequency oscillations, considering both sensitivity to these oscillations and the impact of DC FLC on the AC system. DC projects c and a demonstrate similar suppression effects, which are very close to the suppression effect of DC project b. DC project d is connected to the three major UHVDC lines, while the back-to-back DC project has the lowest suppression effect.

6.2. Verification of a Scheme for Suppressing Ultra-Low-Frequency Oscillations

To enhance the practical guidance of the ultra-low-frequency oscillation suppression scheme, the effectiveness of the proposed approaches will be validated using single DC and multiple DC schemes as examples.

6.2.1. Suppression Scheme of Single Direct Current Ultra-Low-Frequency Oscillation

Using the installation site of FLC as an example in DC project b, a single direct current scheme for suppressing ultra-low-frequency oscillations is illustrated, combined with a NSGA-II. The system’s frequency is perturbed by applying it to DC project b. The system’s low–order linearized model is then identified using the Random Subspace Method. When the order of the system is 8, Equation (28) represents the open-loop transfer function of the system. Figure 6 illustrates the comparison between the actual system and the output signal of the transfer function.

$$\begin{array}{cc}G{\left(s\right)}_1=& (-0.142s^8-0.2801s^7-0.5813s^6-0.5489s^5-\\ & 0.3869s^4-0.3004s^3-0.0734s^2-0.04927s)/\\ & (s^8+0.5928s^7+1.4865s^6+0.7633s^5+0.569s^4\\ & +0.2481s^3+0.0655s^2+0.0224s-7.483\times {10}^{-6})\end{array}$$

(28)

Using the installation site of FLC as an example in DC project b, a single direct current scheme for suppressing ultra-low-frequency oscillations is illustrated, combined with a Non-Dominated Sorting Genetic Algorithm-II. The system’s frequency is perturbed by applying it to DC project b. The system’s low–order linearized model is then identified using the stochastic subspace method. When the order of the system is 8, Equation (28) represents the open-loop transfer function of the system. Figure 7 illustrates the comparison between the actual system and the output signal of the transfer function.

An optimization model was developed using the NSGA-II algorithm in MATLAB, based on the low–order linear model obtained through system identification. The dead-zone for the FLC is set at 0.05 Hz, which exceeds the dead-zone of the hydroelectric unit governor at 0.048 Hz. The initial population size is set to 200, with a maximum iteration count of 500. The recommended values of 20 were used for both the crossover distribution parameter and mutation distribution parameter. The crossover probability was set to 0.9, and the mutation probability is set to 0.1. Iterations continued until the maximum iteration count was reached. The optimized FLC parameters for DC engineering B were determined to be K₁ = 1.4910 and T₁ = 0.5436.

To validate the effectiveness of the proposed approach, an N−1 fault is induced in the critical AC2 transmission line. Three simulation scenarios were conducted to observe the system frequency variation curves. The scenarios included without FLC in the DC system, with FLC implemented in DC project d, and with FLC implemented in DC project b. The results are illustrated in Figure 7.

The implementation of DC project b’s DC FLC successfully suppressed the system’s ultra-low-frequency oscillations. Moreover, it is worth noting that when FLC is added to DC project b, the system frequency deviation stabilizes within 2.4 s, which is faster than the 7.6 s required for DC project d, assuming equal DC modulation power between the two projects. Furthermore, DC project b exhibits a maximum frequency deviation of only 0.3 Hz during the recovery process, compared to 0.6 Hz for DC project d. These results confirm the effectiveness of the DC ranking factor in favor of adding FLC to DC project b over DC project d.

6.2.2. Multiple DC Scheme for Suppressing Ultra-Low-Frequency Oscillations

Following the deployment of the planned back-to-back DC projects, it is expected that all three ultra-high-voltage grids in Area 1 may use FLC. To mitigate impacts on the receiving-end system, multiple DC lines will concurrently modulate and suppress ultra-low-frequency oscillations, thereby collectively sharing the DC power adjustment. Therefore, it may be considered to implement DC projects a, b, and c simultaneously to effectively suppress ultra-low-frequency oscillations (l = 3).

In Section 6.2.1, the optimization outcomes of the FLC in DC project a were detailed. After integrating the FLC of DC project a, perturbations were imposed on DC project c to observe the system’s frequency variations. The stochastic subspace method was used to identify the system model, and the NSGA-II algorithm was used to determine the optimized parameters for DC project b, resulting in K₂ = 12.848 and T₂ = 0.2592. The optimized FLCs of DC projects a and c were then implemented, and the system model was identified again using the Random Subspace Method and the NSGA-II algorithm. This yielded the optimized parameters for DC project c as K₃ = 3.6785 and T₃ = 0.3296.

Figure 8 illustrates the system frequency variation curve used to validate the effectiveness of the multi-DC approach in the event of an N−1 fault occurring in the critical AC2 interconnection line.

Simulations were conducted for two scenarios: one where only DC project a engages FLC, and another where all three DC projects (a, b, and c) engage FLC simultaneously. According to the figure, the system frequency deviation reaches stability within 1.2 s when all three DC projects engage FLC simultaneously, with a maximum frequency deviation of 0.4 Hz during the recovery process. The proposed approach appears to suppress ultra-low-frequency oscillations more effectively than the single DC engagement scheme, as the latter takes 12.3 s to stabilize with a maximum deviation of 0.6 Hz. This suggests that the proposed approach may be more effective overall.

Furthermore, a comparison was carried out between the simulation results obtained using the PSO algorithm and the method described in this paper. The comparison was performed for the scenario in which all three DC projects (DC projects a, b, and c) simultaneously engage FLC. It was noted that the maximum frequency deviation during the recovery process with the PSO algorithm was approximately 0.5 Hz. In comparison to the PSO algorithm, the method proposed in this paper aims to achieve a smoother process for recovering system frequency, with smaller fluctuation amplitudes. Meanwhile, according to the literature [23], multi-objective optimization algorithms have been shown to outperform single-objective optimization algorithms.

7. Conclusions

(1) The use of DC FLC as a suppression measure has effectively mitigated the occurrence of ultra-low-frequency oscillations in multi-DC transmission systems following asynchronous interconnection.

(2) Addressing the phenomenon of ultra-low-frequency oscillations in the sending-end system, a direct current ordering method based on the hydroelectric distribution at the sending end has been used to provide a more comprehensive approach to sorting multiple DC systems.

(3) Transforming the optimization problem of multiple DC FLC parameters into several individual DC FLC parameter optimization problems has reduced the complexity of the optimization problem. This enables better application in engineering practices. And, the proposed method has a significant advantage in suppressing ultra-low-frequency oscillations in multiple DCs. It reduces the suppression time by ninety per cent compared to a single DC. Additionally, the designed method reduces the oscillation amplitude and improves the frequency stability of the system compared to other methods.