Abstract
The cylinder linear induction motor (CLIM) is a variation of the rotary induction motor. Its structure is simple, it has a low manufacturing cost, and it can generate linear thrust without the need for a conversion mechanism. It is particularly suitable for electromagnetic catapults, magnetic levitation transport, and industrial production fields, due to its strong environmental adaptability. Designing a high-thrust and high-efficiency CLIM is a great challenge due to its inherent drawbacks, such as the low thrust density and power density of induction motors. In this article, two CLIMs with different topologies are proposed to meet the demand for control-rod drives in high-temperature and high-pressure environments. The article elucidates the topologies of the two CLIMs and proposes an analytical computational approach for the CLIM. Modern optimization algorithms were utilized to optimize the design of the structural parameters of both CLIMs. A 3D-FEA simulation was used to compare and analyze the air-gap magnetism and thrust characteristics of two CLIMs. The results indicate that the copper-ring secondary CLIM has a higher thrust density and is more suitable for use in control-rod drive mechanism (CRDM) systems.
1. Introduction
The linear induction motor (LIM), due to its high-temperature resistance, simple structure, and strong environmental adaptability in electromagnetic ejection, maglev trains, industrial production, and other fields, has a wide range of applications [1,2]. The CLIM is a deformation of a rotary induction motor, with the motor primary side slotted in the circular direction and the moving motion into a linear motion along the axis. The LIM technology is a new research direction in the field of CRDM for nuclear reactors, due to its stepless speed regulation and direct linear motion without any intermediate conversion device [3,4]. CRDM is the primary equipment in a nuclear reactor that controls the normal operation and shuts by driving the control rod, as per the system instructions. A large number of research studies on linear induction motors in the fields of electromagnetic ejection [5] and maglev trains are of great reference value for the research on CLIM. In [6], the authors present an efficient multi-objective optimization model for LIM, which employs a novel approximation and prediction strategy. The model uses a 3D approach to obtain the sample data, considering the skin effect and edge effect, and a multi-analytical model is established using the Latin Hypercube Sampling (LHS) method and the Extreme Gradient Boost (XGBoost) method. The model is used to optimize the design of the motor structural parameters, which can be realized more quickly and accurately, and it reduces the computational complexity of eddy current analysis. In [7], a novel analytical equivalent circuit for a Single-sided Linear Induction Motor (SLIM) is proposed, which considers the secondary reactance for both edge effects, i.e., entry and exit sides. In [8], mathematical analysis was conducted for each factor that mutually affects the control of the train. The magnitude of the normal force related to the safety of the train is limited, and operating efficiency was improved by varying the slip frequency according to the operating conditions of the train. One of the main limitations to the large-scale application of the LIM is its low thrust density and power factor.
Improving the secondary structure of motors is a feasible approach and has been extensively researched in this direction [9]. To enhance the thrust and power factor of the LIM, flat-solid secondary structures, and ladder-slit secondary structures have been used to improve secondary conductivity or to standardize secondary eddy current circuits [10]. However, when it comes to CLIM-related research and application, this has received comparatively less attention. Furthermore, the parameter design method for composite secondary structures has not received sufficient attention.
The article compares the effect of two different secondary structures, the copper ring and copper shell, of CLIM on the electromagnetic thrust characteristics. In [11], the air-gap flux density, eddy currents, and forces of the linear induction motor with the ladder-slit secondary structure are calculated and compared with the linear induction motor with the flat-solid secondary structure.
To enable the LIM to output stable levitation and thrust, the electromagnetic relationship and force characteristics of the device must be accurately analyzed. Due to the special characteristics of the CLIM structure, a new set of analytical methods must be established to calculate the force characteristics to guide the design of the CLIM structural parameters. In [12], starting from the electromagnetic field analysis, the electromagnetic field analytical calculation, the secondary equivalent air-gap and equivalent radius are corrected, and the thrust characteristics can be calculated directly.
To compare the impact of two different secondary structures on the thrust characteristics of a motor objectively, a multi-objective design optimization strategy has been used to improve the thrust, thrust ripple, and consumed magnet volume for a linear motor [6,13,14]. According to the optimization results, the best parameter combination is selected for 3D-FEA modeling and simulation calculation. In [15,16], a design method for non-integer pole segmented linear motors with low thrust fluctuation and high thrust density and researched the thrust fluctuation and positioning-force problems of linear motors. Methods such as the use of magnetic isolation materials, special winding settings, and the setting of auxiliary teeth are proposed to suppress the third harmonic of the motor, improve the winding coefficient of the motor, and increase the thrust of the motor. This article proposes two different types of CLIMs with varying secondary structures—the copper-shell secondary CLIM and the copper-ring secondary CLIM. For each structure, we have designed various combinations of structural parameters for the motors and compared the radial air-gap magnetic-field characteristics and axial-thrust characteristics of the two motors.
The article compares the structures of transformers and CLIM to explain how the induced currents of CLIM are generated and how they are distributed. It analyzes the eddy current distributions of SLIM and CLIM and introduces the advantages of CLIM, particularly in improving motor thrust density and power factor. The CLIM analytical calculation model is established, laying the foundation for thrust calculation. Modern optimization algorithms were used to optimize the structural parameters of CLIM with different structures, and a 3D-FEA calculation model was established to compare the effects of the two secondary structures on the motor air-gap flux density and thrust characteristics.
2. Topology and Structural Parameters
The topology of a CLIM mainly consists of a primary core, a ring winding, and a secondary core. The secondary core of a motor is the core component that induces eddy current and generates thrust force. Usually, the secondary core of a CLIM is a conductive metal bar. From the structure of CLIM, the primary and secondary structures of CLIM are similar to the high-voltage and low-voltage windings of a transformer, as shown in Figure 1. When the primary winding is fed with an AC power supply, alternating flux is generated to establish the motor electromagnetic field, and the alternating flux passes through the primary, air-gap, and secondary structure to form the main flux. With the change in, alternating current in the CLIM winding, the air-gap electromagnetic field rotates symmetrically in the radius direction. It moves along the axial direction, thus making the motor secondary for generating induced electromotive force and induced current. The induced current in the secondary structure of the motor interacts with the magnetic field to produce a force that causes the motor to move in the axial direction.
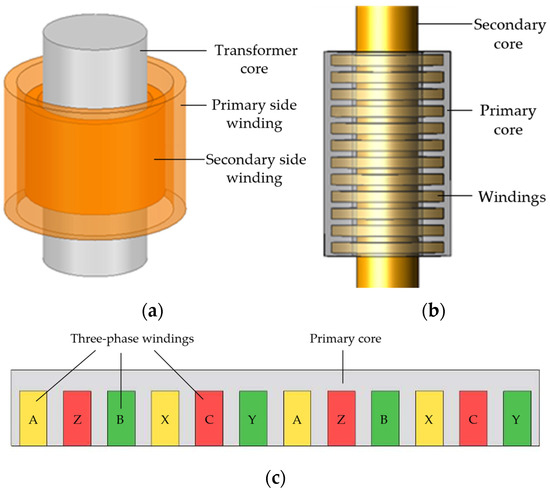
Figure 1.
Comparison of transformer and CLIM structure. (a) Transformer, (b) CLIM, (c) winding distribution.
2.1. Secondary Structural Analysis
Different secondary structures will affect the current distribution and current density of the secondary structure. The secondary iron bar is coated with a layer of copper shell, which reduces material resistance and increases current density in comparison to the pure iron secondary structure, as shown in Figure 2b. The copper-ring secondary structure is embedded in the secondary iron bar at certain intervals in a group of copper rings, so that the motor secondary induced current is concentrated in the strong conductivity of the copper ring; at the same time, the iron teeth between the copper rings play a role in reducing the secondary magnetoresistance, and, compared with the copper-shell secondary structure, can reduce the equivalent electromagnetic air-gap and improve the air-gap magnetic density of the motor, as shown in Figure 2c.

Figure 2.
Comparison of different secondary structures. (a) Copper-shell secondary structure, (b) copper-ring secondar structure, (c) CLIM axial section diagram.
2.2. The Design of the Structural Parameter
The article describes a CLIM design that is primarily used in environments with high temperature and pressure. To provide thermal protection, a layer of insulation is incorporated inside the primary and outside the secondary structure of the motor, creating a significant electromagnetic air gap between them. To evaluate the impact of various secondary constructions on the thrust characteristics of the motor, we kept the primary construction parameters and winding parameters the same. This allowed us to compare the performance of two motor schemes by changing only the motor secondary structure. This approach reduces processing costs and saves research and development time.
Referring to the design of squirrel-cage rotary motors, when designing the number of secondary slots, there must be a proper fit with the number of primary slots. If the match is not correct, the performance of the motor will deteriorate; for example, it may lead to additional losses, vibration, and noise increase, which will lead to lower efficiency, higher temperature rise, worse starting performance, and even serious failure to start. The design parameters of the CLIM investigated in this article are listed in Table 1.

Table 1.
Design Parameters of the CLIM.
3. Characteristics of Eddy Current Distribution
When the primary winding of the motor is energized with three-phase AC power, the three-phase AC will form a cross-linked magnetic circuit between the primary and secondary structure of the motor, generate an induced current in the secondary one, and different topologies will affect the distribution of the induced current.
3.1. Comparison of Eddy Current Distribution between Flat-Plate Secondary and Cylinder Secondary Structures
SLIM has a longitudinal component in the secondary current due to the transverse opening, and the longitudinal component is parallel to the direction of magnetic-field motion, which does not contribute to the motor thrust, but rather increases the resistance and generates additional useless power and loss, as shown in Figure 2a. In contrast, the CLIM has only a toroidal induction current perpendicular to the direction of magnetic-field motion in the secondary structure of the motor, due to the characteristics of the cylindrical structure, which reduces the useless power and losses of the motor, as shown in Figure 3b.

Figure 3.
Eddy current distribution of LIMs. (a) Secondary eddy-current distribution of SLIM, (b) secondary eddy-current distribution of CLIM.
3.2. Characteristics of Eddy Current Distribution in Copper-Shell Secondary and Copper-Ring Secondary Structures
In this simulation model, symmetric boundary conditions were used in the axial cross-section of the model to calculate on half of the model, and default boundary conditions were used on other surfaces; a 2 mm element size was applied to the conductive layer, the inner-wall protective shell of the stator, and the outer-wall protective shell of the actuator, and a 5 mm element size were applied to the stator, the actuator, and the winding, with 237,903 grid cells; the mesh type was generated mesh at each step, the mesh generation method was semi auto mesh, due to the structural characteristics of CLIM, and the solver type was 3D magnetic field transient analysis. The subsequent simulation calculations are based on the above simulation conditions.
Compared with the copper-shell secondary structure, the copper-ring secondary structure means that the secondary induced current is concentrated in the copper ring; the secondary iron teeth have only a weak induced current, as shown in Figure 4. As the primary winding is powered by a three-phase AC, the density distribution of the induced current on the secondary structure also presents sinusoidal distribution characteristics. Due to the high current density at the peak moment of the induced current, it is necessary to increase the thickness of the copper shell or ring to reduce the secondary resistance, increase the induced current, and increase the motor thrust density.

Figure 4.
Eddy current distributions. (a) Eddy current distribution of copper-shell secondary structure. (b) Eddy current distribution of copper-ring secondary structure.
4. Electromagnetic Analysis Model of CLIM
Through a series of reasonable assumptions, the 2D electromagnetic analysis model of CLIM is established in the cylindrical coordinate system, as shown in Figure 5. According to the principle of equality of traveling-wave potential, the current layer is used instead of the actual winding current:
where is the amplitude of winding currents.
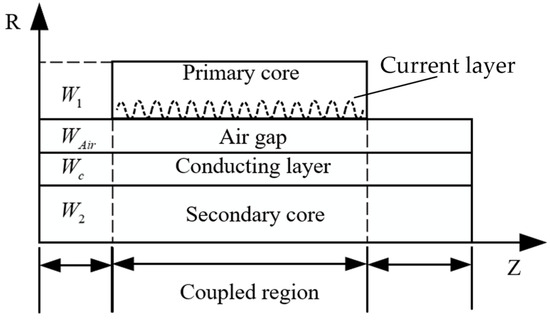
Figure 5.
Electromagnetic analysis model of CLIM.
The relationship between the secondary velocity and the primary traveling-wave magnetic-field synchronization velocity is as follows:
where is the slip rate.
According to Ampere’s law, in the coupling region in Figure 5
The secondary current density can be expressed as
The expression of air-gap flux density in the coupling region can be expressed as
where , .
In the coupling region, the inner diameter of the primary core is and the secondary thrust is directly calculated from the secondary electric density and the air-gap flux density, which can be expressed as
where is the correction factor of the effective radius of CLIM.
Inside the coupled region, the primary-core inner diameter, the secondary electric density, and air-gap flux density are used to directly calculate the secondary thrust. Substituting the expression for the fundamental wave magnetic field of the air-gap electromagnetic field and the expression for the winding current, the fundamental thrust can be obtained as
5. Optimization Design
To compare the effect of two different secondary structures on the maximum thrust performance of the motor objectively, the experiment uses the same set of primary structures and the same space for the two secondary structures. The design of a motor’s secondary-structure parameters can be optimized by using genetic algorithms. The power supply frequency, secondary conductive-layer thickness, and secondary tooth-groove width are the variables that can be optimized. The main objective of this optimization is to maximize the motor thrust while minimizing thrust pulsation. By finding the best combination of motor-structure parameters, we can optimize the motor characteristics and achieve the desired results. According to the final optimization results, the operating characteristics of two different secondary-structure motors are compared and analyzed.
The copper-shell structure can increase the conductivity of the secondary structure and increase the induced current, but the permeability of copper is much smaller than that of iron, which will increase the equivalent air-gap of the motor and thus reduce the air-gap magnetic density. The iron teeth can reduce the equivalent air-gap, while the copper-ring structure can increase the secondary conductivity. However, the spaced arrangement of copper rings and iron teeth leads to uneven distribution of secondary material, which will make the motor air-gap magnetic-field distribution uneven and produce the cogging effect. The maximum thrust corresponds to different drive frequencies for motor motion speed conditions, so the drive frequency of the motor should be optimized to obtain the maximum motor thrust at the rated motion speed.
5.1. Determine the Range of the Optimization Variables
To shorten the genetic algorithm optimization time, the effects of secondary conductive-layer thickness, copper-ring width, copper-ring thickness, iron-tooth width and power supply frequency on the characteristics of the motor are analyzed in the preparatory stage and the range of values is estimated, respectively.
- The copper shell and copper ring are the main circulation paths of the secondary eddy current; if the thickness of the copper shell and copper ring is too small it will increase the resistance, and if too thick it will increase the equivalent air-gap, which will also increase the skin effect. Therefore, the optimization of the copper shell and the copper ring takes the value range of [0.1 mm, 3 mm].
- The alternating arrangement of copper rings and iron teeth on the secondary structure of the copper ring will affect the magnetic-field distribution inside the motor, generating harmonic components of different orders in the air-gap field and thrust characteristics; the width of the copper rings and iron teeth will affect the equivalent air-gap inside the motor and the resistivity of the secondary eddy current path. To reduce the thrust pulsation of the copper-ring secondary structure, referring to the design method of the squirrel-cage rotating motor, the width of the copper ring and iron teeth should be smaller than the primary slot pitch of the motor; at the same time, taking into account the machining difficulty of the secondary structure and the structural strength, the width of the copper ring and iron teeth should be larger than 1 mm; therefore, the range of the values of the copper ring and iron teeth in the optimization is taken as [1 mm, 16 mm].
- The power supply frequency affects the rated speed of the motor because the motor is optimized towards a high-thrust motor design and operates at low speeds. If the power supply frequency is too large it will make the power factor of the motor lower than 0.1 for a long time and produce too much reactive power [17]. Therefore, the value range of the power supply frequency for optimization is taken as [1 Hz, 200 Hz].
5.2. Optimization Results
Considering the large size of the 3D model and the long time-consuming finite-element simulation, the 2D model is used for approximate calculation in the parameter-optimization process. After iterative calculation, the optimization process and results are shown in Figure 6.
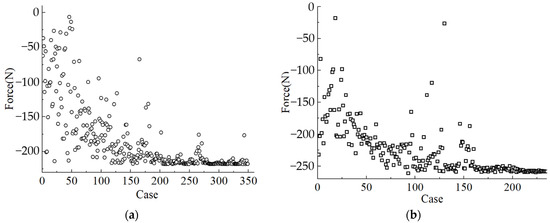
Figure 6.
Optimization result. (a) Optimization process of copper-shell secondary structure. (b) Optimization process of copper-ring secondary structure.
Based on the optimization results, the following parameter combinations Table 2 and Table 3 are approximated for the two secondary-structure motors, respectively:

Table 2.
Design parameters of copper ring.

Table 3.
Design parameters of the copper shell.
6. Performance Comparison
To objectively compare and analyze the effects of the two secondary structures on the thrust of CLIM, the article refers to the optimization results of the genetic algorithm, and selects the approximate values of the secondary-structure parameters that can output the maximum thrust, respectively. It establishes the three-dimensional finite-element analysis models of the two kinds of CLIMs by adopting the same parameters of the primary structure and the current density of the windings.
6.1. The Air-Gap Flux Density of Different Secondary Structures
The distribution of the radial component of the air-gap magnetic density along the motor axis of the two secondary structures is shown in Figure 7a. When the primary is displaced from the initial position, shows the different performance in the two secondary structures.
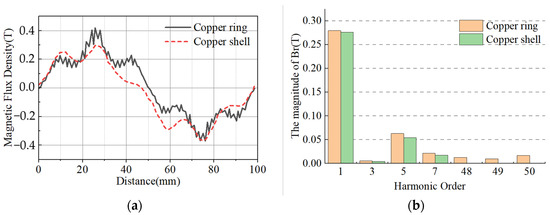
Figure 7.
The air-gap magnetic density characteristic of proposed motor topologies. (a) The air-gap magnetic-density waveform. (b) The air-gap magnetic-density harmonics.
The air-gap magnetic field components of both motors have more 5th and 7th harmonic components, due to the influence of the cogging distribution on the primary structure of the motor, as shown in Figure 7b. For the CLIM with a copper-ring secondary structure, there is a large number of sawtooth fluctuations on the air-gap magnetic density waveform, which is due to the distribution of copper rings and iron teeth on the secondary structure, which means that the air-gap magnetic density has some 48th, 49th and 50th higher harmonic components. Compared with the copper-shell secondary structure, the iron teeth on the copper-ring secondary structure reduce the equivalent air-gap of the motor and lower the equivalent reluctance. As a result, the copper-ring secondary structure still has a high air-gap flux density, despite its high harmonic content.
6.2. Comparison and Analysis of Motor Characteristics
According to the optimization results in Section 5.2, the motor-structure parameters were adjusted, and a three-phase alternating current of 28 Hz and 50 Hz was passed into the two types of motors to drive the two types of motors, respectively; the thrust waveforms of the motors were obtained after FEA. In Figure 8a, the thrust fluctuation characteristics of the two structures of CLIM are compared, and the copper-ring secondary structure of CLIM can output more thrust under the same primary structure and winding parameters. Although the air-gap flux density of the CLIM with copper-ring secondary structure contains more high harmonics, it can be seen in the thrust fluctuation of the motor output that the main harmonic orders are the 1st and 3rd harmonics, as shown in Figure 8b.

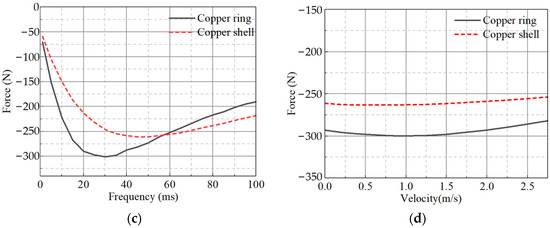
Figure 8.
Electromagnetic force for the proposed motor topologies. (a) Thrust force, (b) the harmonics of the motors, (c) thrust–frequency curves, (d) thrust–speed curves.
Figure 8c,d show the thrust with the different frequencies and velocities. The frequencies of peak thrust are different for the two CLIM configurations at the same operating speed, and the copper-ring secondary CLIM has more peak thrust. At low speeds, CLIM outputs a stable thrust that varies little with speed. The efficiency and power factor of both motor topologies are shown in Table 4. Provided that the design requirements are met, it is clear that the copper-ring secondary structure is significantly more efficient. The CLIM designed in this paper is designed with thrust maximization as the main design objective, and the motor operates at a deficient speed (0.02 m/s) with the slip rate of the motor close to 1. Therefore, the CLIM designed in this paper has a low power factor relative to conventional induction motors. Compared with rotary motor-driven, hydraulically-driven, and magnetically-driven CRDMs, the use of CLIM as a CRDM actuator eliminates the need for a complex transmission mechanism and directly generates linear motion, which simplifies the CRDM structure, reduces weight, and decreases equipment size. Therefore, applying CLIM technology to CRDM has good development prospects.

Table 4.
Comparison of motor power factor and efficiency.
7. Conclusions
Using linear motors to directly drive the nuclear-reactor control rods can overcome the disadvantages of large volume and weight, complex structure, poor reliability, and so on, which exist in hydraulic- or mechanical-transmission mechanisms. To overcome the problems of small thrust density and low efficiency of LIM, two CLIMs with different secondary topologies are proposed in this article, and the objective is to obtain a design scheme that maximizes the thrust of CLIM through optimization. To have an objective comparative analysis of the thrust characteristics of the two motors, an optimal design using a genetic algorithm is proposed to maximize the thrust of both motors by optimizing the factors affecting the thrust enhancement of the two motors. The characteristics of the secondary induced-current distribution of SLIM and CLIM are compared, and the CLIM has less additional loss and higher efficiency. The analytical calculation method of the electromagnetic thrust of CLIM is proposed; the characteristics of the air-gap flux density distribution and the thrust characteristics of the copper-ring secondary and the copper-shell secondary CLIM are comparatively analyzed, and the copper-ring secondary CLIM, which has a smaller equivalent air-gap and a larger absolute value of air-gap flux density, is capable of generating a larger electromagnetic thrust. Therefore, it can generate a larger electromagnetic thrust. The comparison results show that introducing the copper-ring secondary structure into the CLIM has a significant improvement effect on the secondary induced-current path, which greatly enhances the motor thrust density. Therefore, this article lays the foundation for promoting the application of linear motor technology in the field of nuclear reactors.
Author Contributions
Conceptualization, funding acquisition, supervision, verification, and writing—review and editing, L.Z.; methodology, formal analysis, and writing—original draft, C.D.; software and investigation, X.N. and K.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China 52077042.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lu, Q.; Li, Y.; Ye, Y.; Zhu, Z.Q. Investigation of Forces in Linear Induction Motor under Different Slip Frequency for Low-Speed Maglev Application. IEEE Trans. Energy Convers. 2013, 28, 145–153. [Google Scholar] [CrossRef]
- Boldea, I.; Tutelea, L.N.; Xu, W.; Pucci, M. Linear Electric Machines, Drives, and MAGLEVs: An Overview. IEEE Trans. Ind. Electron. 2018, 65, 7504–7515. [Google Scholar] [CrossRef]
- Yu, T.; Peng, H.; Deng, Q.; Li, W.; Wu, H.; Fu, G.; Tang, J. Study on Electromagnetic Structure Design of Control rod Drive Mechanism for Linear electric reactor. Nucl. Power Eng. 2021, 42, 213–217. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Z.; Li, H.; Yu, T.; Tang, H.; Xie, X. Electromagnetic Field Simulation Analysis of Magnetic Lifting Control rod Drive Mechanism. Mech. Des. Manuf. Eng. 2019, 48, 5. [Google Scholar]
- Zhang, Q. Study on Electromagnetic and Thrust Characteristics of Linear Induction Motor for Vertical Ejection of Microgravity Drop Tower; Beijing Jiaotong University: Beijing, China, 2022. [Google Scholar] [CrossRef]
- Wu, S.; Lu, Q. Eddy Current Analysis and Optimization Design of the Secondary of the Linear Induction Motor with an Approximation and Prediction Method. IEEE Trans. Magn. 2022, 58, 8200105. [Google Scholar] [CrossRef]
- Gomes, D.R.; Chabu, I.E. A Novel Analytical Equivalent Circuit for Single-Sided Linear Induction Motors Considering Secondary Leakage Reactance. Energies 2023, 16, 1261. [Google Scholar] [CrossRef]
- Park, S.-U.; Mok, H.-S.; Lim, J.-W.; Seo, H.-U.; Oh, S.-H. Efficiency Improvement by Deriving the Optimal Operating Slip Frequency of a Linear-Induction-Style Maglev Train. Energies 2020, 13, 6544. [Google Scholar] [CrossRef]
- Lv, G.; Zhou, T.; Zeng, D. Quasi-3D Analytic Method of the Single-Sided Linear Induction Motor with the Ladder Secondary. IEEE Trans. Ind. Electron. 2021, 68, 11817–11825. [Google Scholar] [CrossRef]
- Lv, G.; Zhou, T.; Zeng, D.; Liu, Z. Design of Ladder-Slit Secondaries and Performance Improvement of Linear Induction Motors for Urban Rail Transit. IEEE Trans. Ind. Electron. 2018, 65, 1187–1195. [Google Scholar] [CrossRef]
- Lv, G.; Zhou, T.; Zeng, D. Influence of the Ladder-Slit Secondary on Reducing the Edge Effect and Transverse Forces in the Linear Induction Motor. IEEE Trans. Ind. Electron. 2018, 65, 7516–7525. [Google Scholar] [CrossRef]
- Qin, W.; Fan, Y.; Lv, G.; Zhu, X.; Li, S. Research on the magnetic field and force characteristics of Non-magnetic secondary induction suspension motors. Electr. Mach. Control J. 2011, 15, 6. [Google Scholar] [CrossRef]
- Vaez-Zadeh, S.; Isfahani, A.H. Multiobjective design optimization of air-core linear permanent-magnet synchronous motors for improved thrust and low magnet consumption. IEEE Trans. Magn. 2006, 42, 446–452. [Google Scholar] [CrossRef]
- Huang, C.; Kou, B.; Zhao, X.; Niu, X.; Zhang, L. Multi-Objective Optimization Design of a Stator Coreless Multidisc Axial Flux Permanent Magnet Motor. Energies 2022, 15, 4810. [Google Scholar] [CrossRef]
- Huang, X.Z.; Li, J.; Tan, Q.; Qian, Z.Y.; Zhang, C.; Li, L. Sectional Combinations of the Modular Tubular Permanent Magnet Linear Motor and the Optimization Design. IEEE Trans. Ind. Electron. 2018, 65, 9658–9667. [Google Scholar] [CrossRef]
- Tan, Q.; Wang, M.; Li, L.; Li, J. Research on Noninteger Pole Number for Segmental Permanent Magnet Linear Synchronous Motor. IEEE Trans. Ind. Electron. 2021, 68, 4120–4130. [Google Scholar] [CrossRef]
- Masada, E.; Kaye, R.J. Comparison of Linear Synchronous an Induction Motors. Propulsion; SAND2004-2734P; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 2004. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).