Investigation of a Hybridized Cascade Trigeneration Cycle Combined with a District Heating and Air Conditioning System Using Vapour Absorption Refrigeration Cooling: Energy and Exergy Assessments
Abstract
1. Introduction
2. Literature Review
Gap in Knowledge, Motivation, and Objectives
- ○
- The advancement of an extensive but accurate simulation model to forecast the thermodynamic performance of a steam-to-steam cascaded waste heat recovery process and establish cohesion in similar test results and models, with emphasis on the ease of availability of steam as a working fluid.
- ○
- Testing performance under real-world operational conditions through sensitivity and optimization analyses of the gas turbine topping cycle with real gas composition.
- ○
- Identify the effects of exergetic destruction on components of the system and proffer suggestions to minimize irreversibility and propose appropriate component improvement.
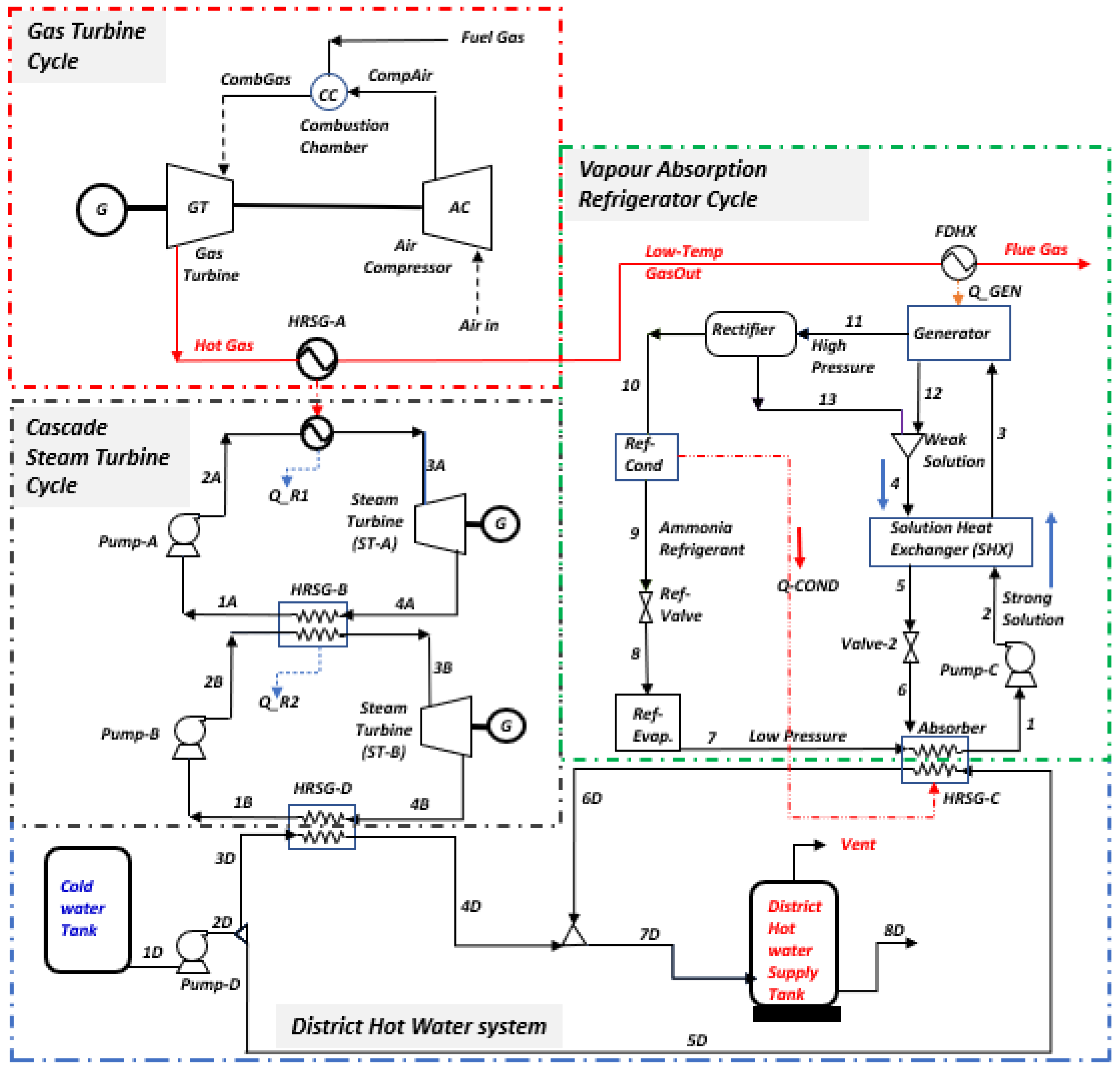
3. System Description
3.1. Process Simulation
3.2. Assumptions for the Thermodynamic System Models
- Natural gas used is 100% methane delivered at 10.1 bar and 60 °C.
- Air at 25 °C is modelled as 21% O2 and 79% N2 molar mixture. Excess air is added at 20% to reach complete state of combustion.
- No pressure drops in the heaters or between components.
- The atmospheric temperature of water is 25 °C, which transitions to steam at 264 °C, zero superheat.
- Ambient condition: pressure, = 1.013 bar; temperature, = 25 °C.
- Components of the system are at steady-state and steady-flow conditions.
- In the VAR, the pressure in the condenser and absorber are equal, just as the pressure in the generator and evaporator are also equal.
- The enthalpy, , and entropy, , are 104.83 kJ/kg and 0.3672 kJ/kg-K, respectively, in the dead-state condition.
- The VAR refrigerant leaves the generator in a pure-state condition.
- The saturated solution mixture leaving the generator and absorber have the same temperature and concentration as the mixture in both vessels.
- Saturated water is the refrigerant in the condenser and the evaporator refrigerant is the saturated vapour at condensation, with the evaporator temperature and pressure, respectively.
- The throttling work is isenthalpic and no heat loss to the environment occurs.
- Kinetic exergy, chemical exergy, and potential exergy are all negligible.
3.3. Mathematical Models of Energy and Exergy Analysis
3.4. Model Validation
| Parameter | [104] | Reference | This Work | |
|---|---|---|---|---|
| Gas turbine | Gas turbine output (MW) | 95 | 94 | 50 |
| Gas turbine exit temperature (°C) | 532 | 532 | 726 | |
| Fuel mass flow rate (kg/s) | 6.8 | 6.7 | 3.0 | |
| ORC section | Mass flow rate produced (kg/s) | 82.9 | 82.3 | N/A |
| Evaporator outflow temperature (°C) | 110.5 | 110.4 | N/A | |
| ORC turbine outflow temperature (°C) | 60.8 | 61.3 | N/A | |
| Steam section | Mass flow rate produced (kg/s) | - | - | 34.4 |
| Evaporator outlet temperature (°C) | - | - | 264 | |
| Turbine exit temperature (°C) | - | - | 100 | |
| Refrigeration system | Generator heat load (kW) | 275.1 | 275.1 | 3057 |
| Evaporator heat load (kW) | 63.2 | 62.7 | 2071 | |
| Coefficient of performance exergy | 0.23 | 0.227 | 0.206 | |
| Refrigerant mass flow rate (kg/s) | 0.05 | 3.47 | ||
| Effectiveness of heat exchanger (ε) | 0.7 | 0.7 | 0.70 | |
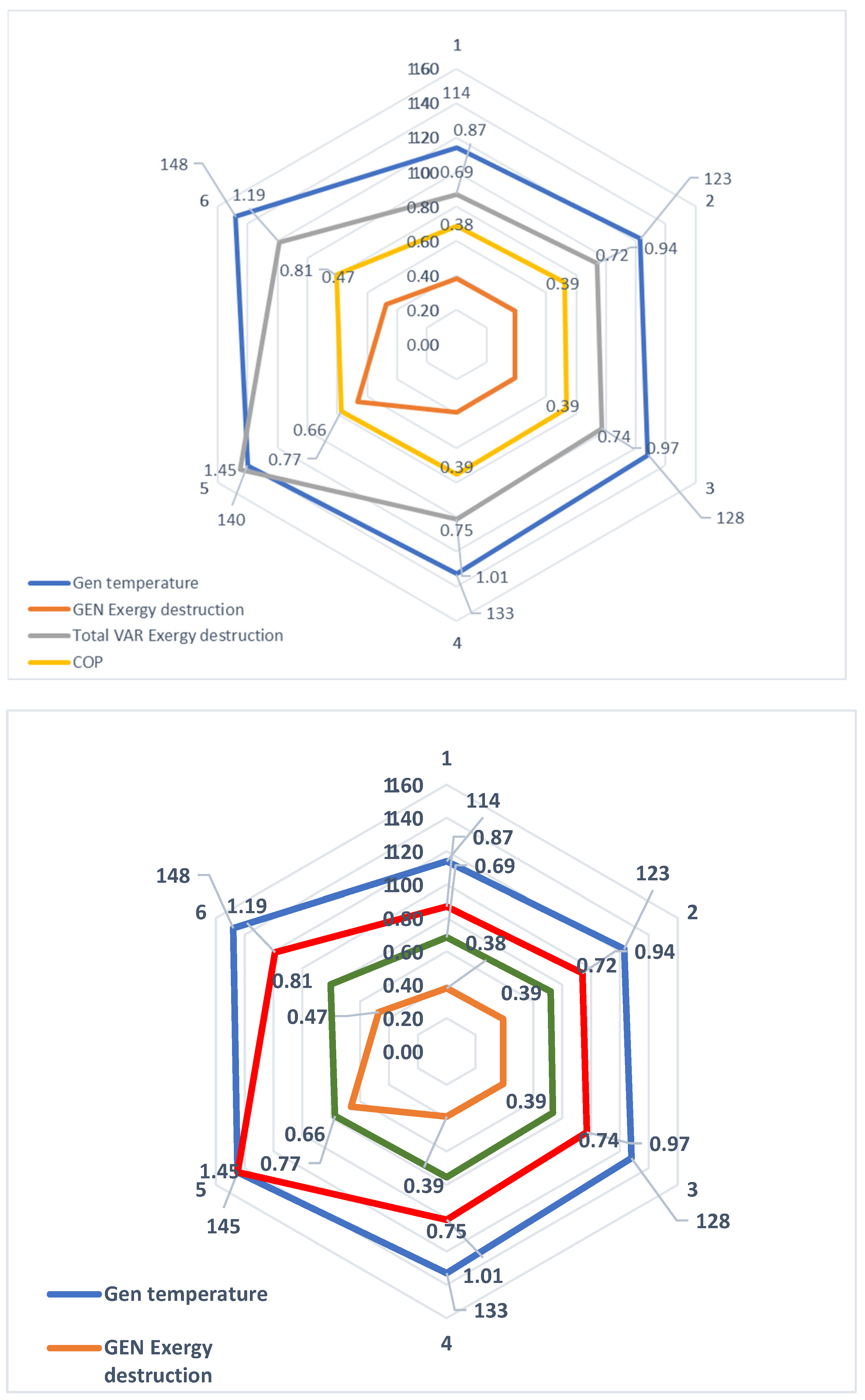
| Generator temperature (°C) | 100 | 133 | ||
| Plant Performance Cycles Data | ||
| Parameter | Gas Turbine Plant | Cascade Steam Plant |
| Thermal energy efficiency [%] | 76.68 | 38.45 |
| Cycle exergy efficiency [%] | 37.71 | 56.19 |
| Combined efficiency [%] | 85.05 | 77.99 |
| Air standard energy efficiency [%] | 48.21 | |
| Back work ratio (BWR) | 0.92 | 0.99 |
| Specific fuel consumption [kg/MWh] | 1052.36 | |
| Steam specific consumption [kg/MWh] | 1.93 | |
| Combustion efficiency [%] | 98.00 | |
| Datasets for the cooling and heating cycle performance | ||
| Parameter | VAR cooling | District Heating |
| COP [%] | 67.11 | |
| COPMAX | 1.39 | |
| Carnot Efficiency of VAR [%] | 76 | |
| COP Exergy [%] | 58.70 | |
| Circulation ratio | 2.03 | |
| Mass of strong solution [kg/s] | 3.47 | |
| Mass of Weak solution [kg/s] | 1.76 | |
| Cooling/heating capacity [MW] | 3.22 | 38.58 |
| Energy efficiency [%] | 99.87 | 100.00 |
| Exergy efficiency [%] | 92.25 | 77.66 |
| Effectiveness | 0.70 | |
4. Results and Discussions
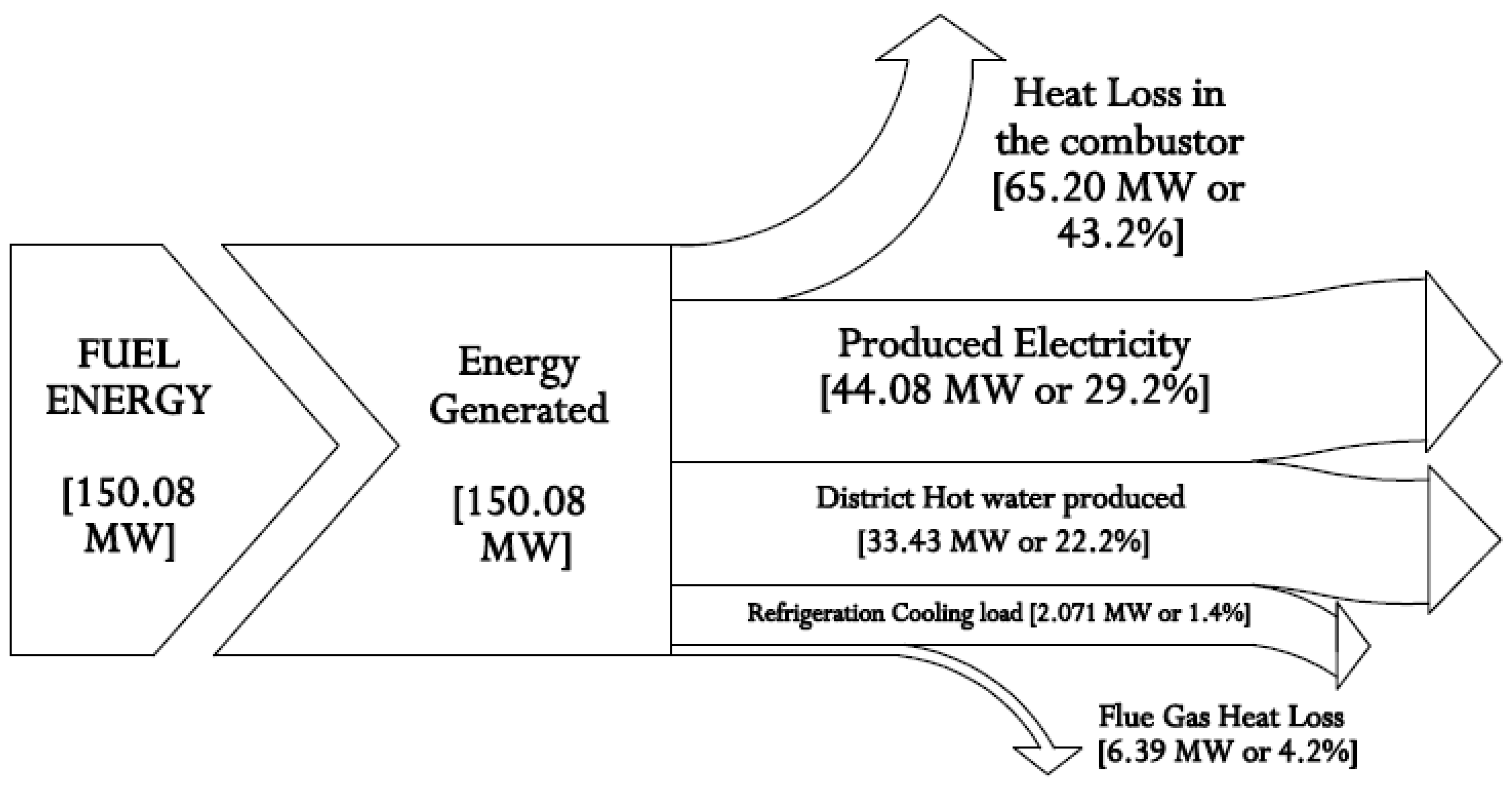
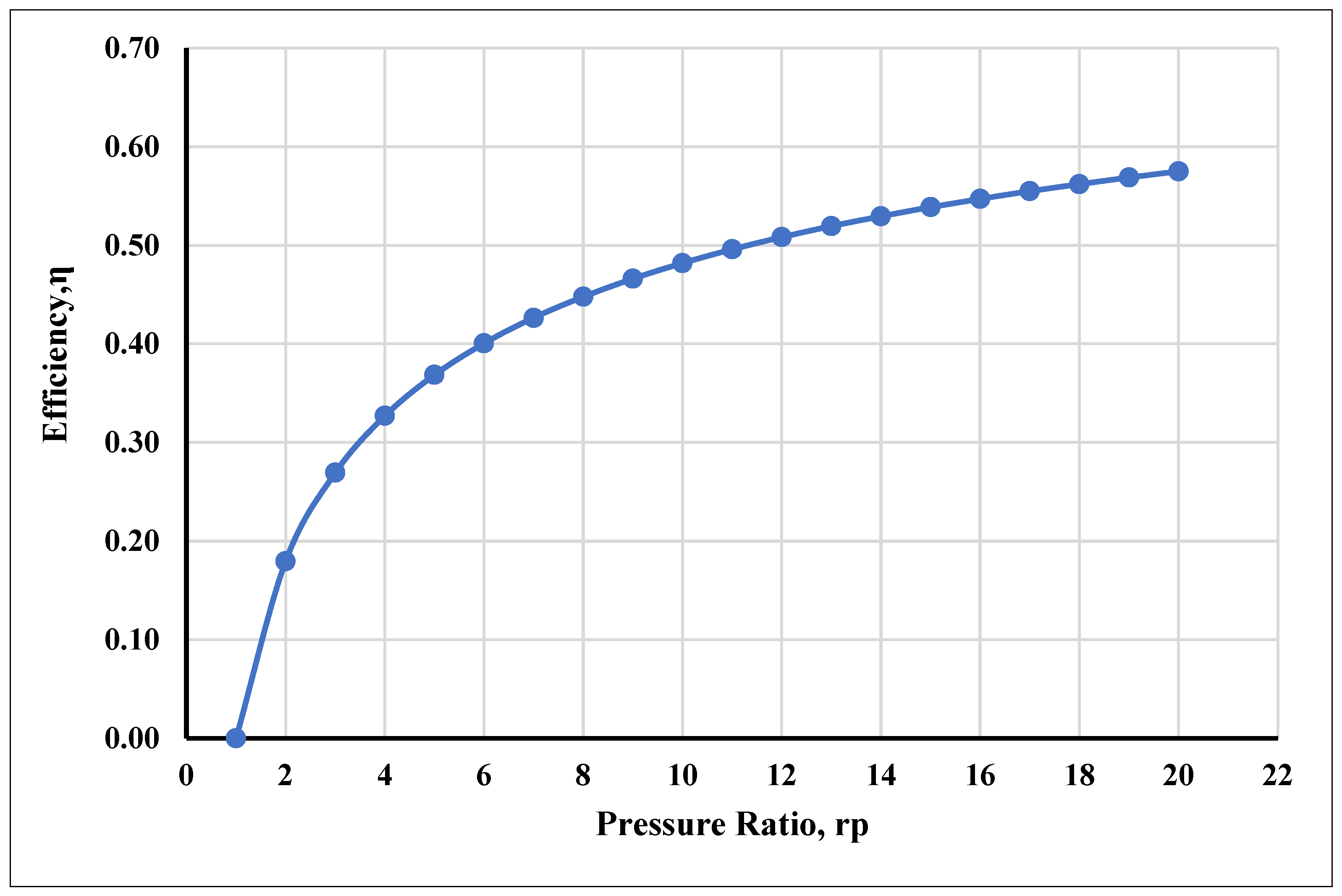
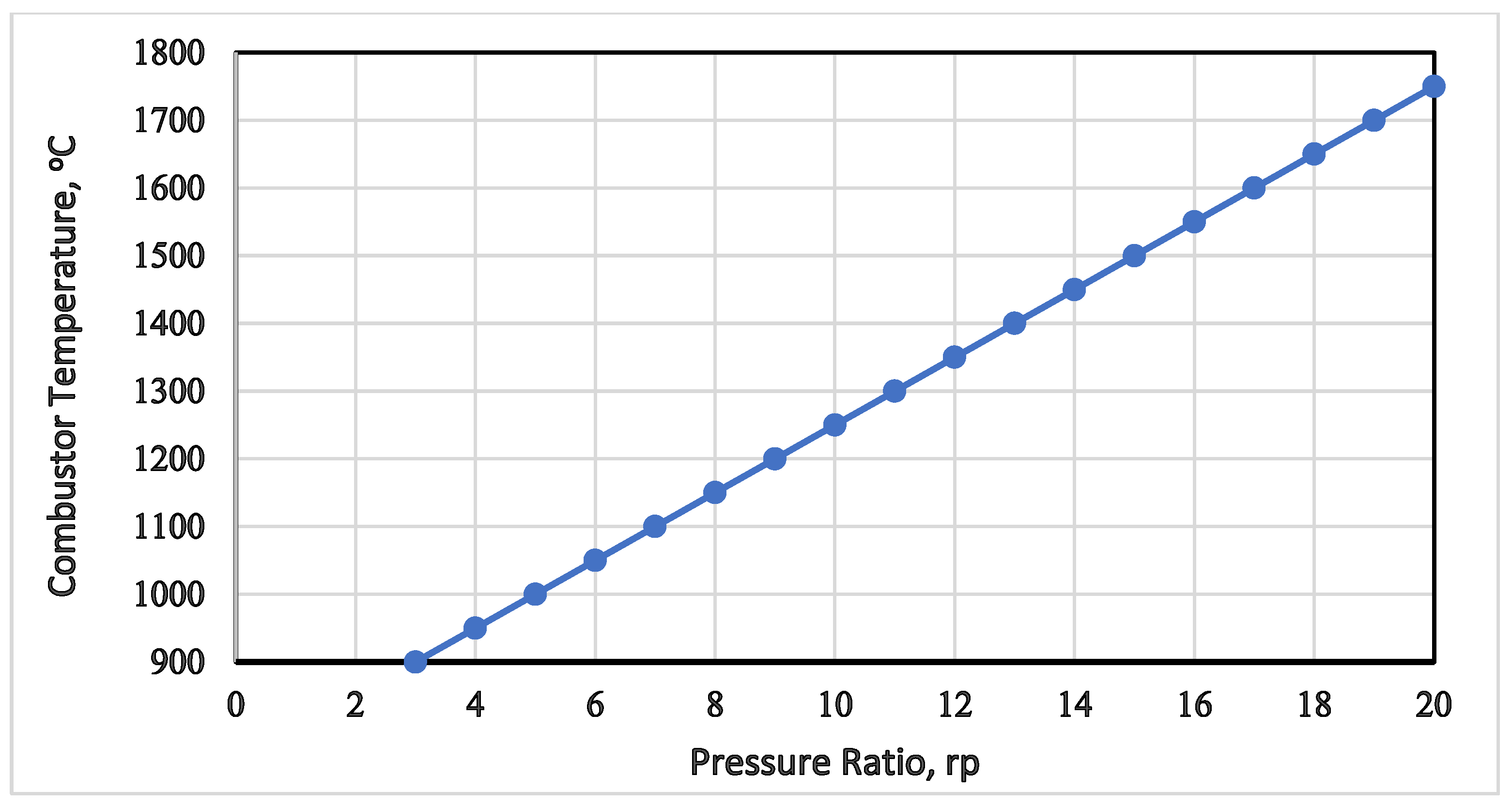
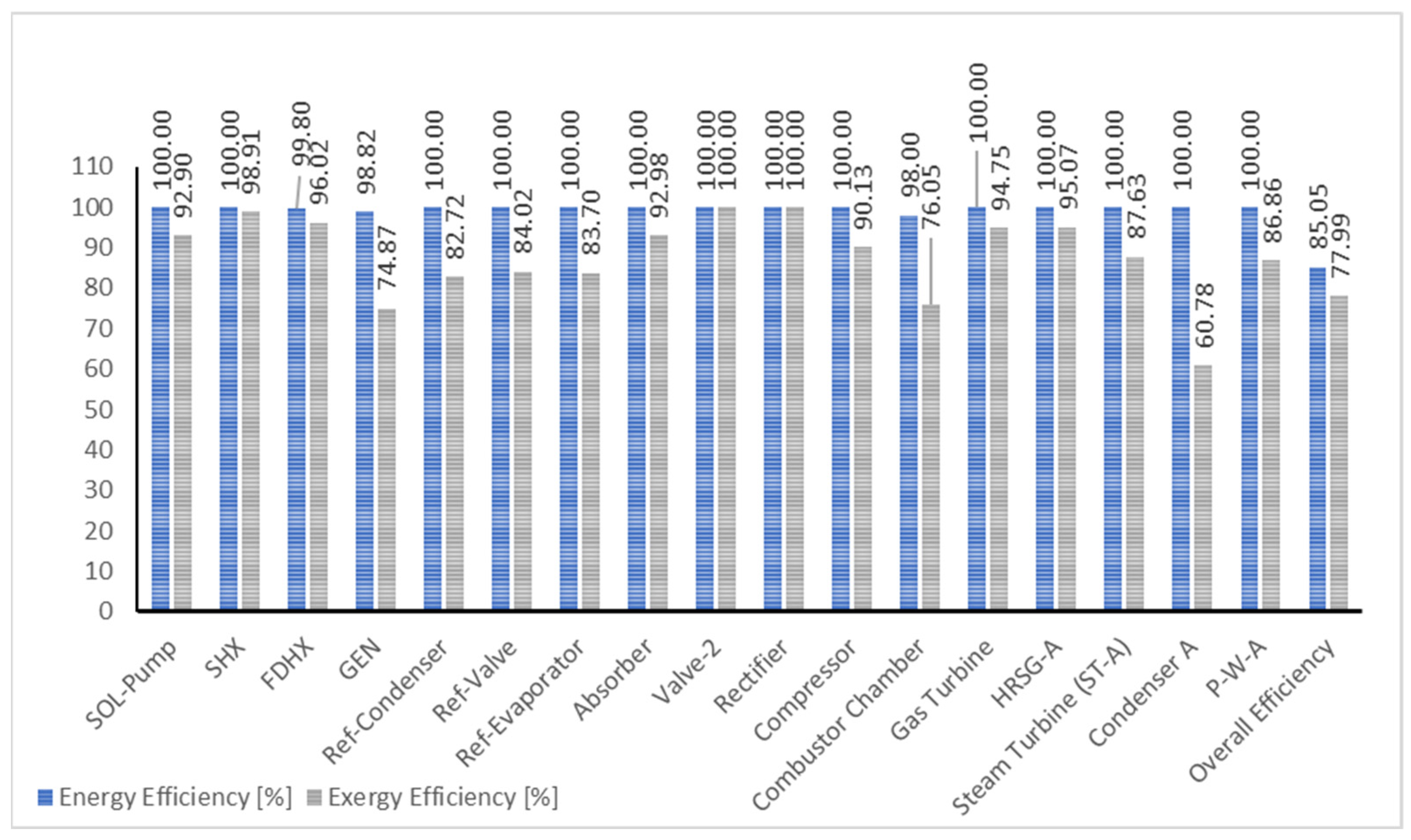
4.1. Discussions on the Energy Analysis of the Integrated Plant
4.2. Discussion on the Exergy Analysis of the Integrated Plant
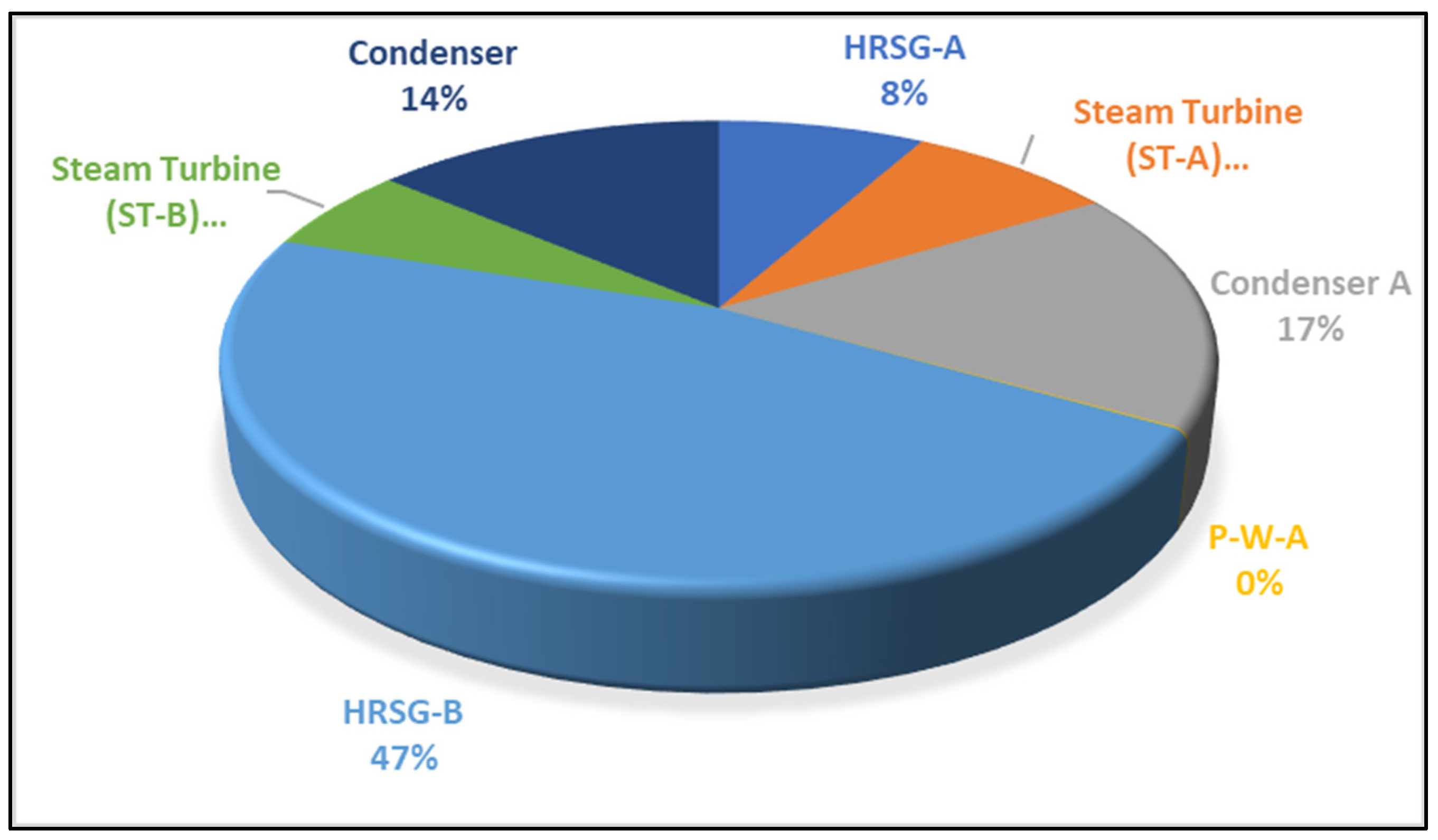
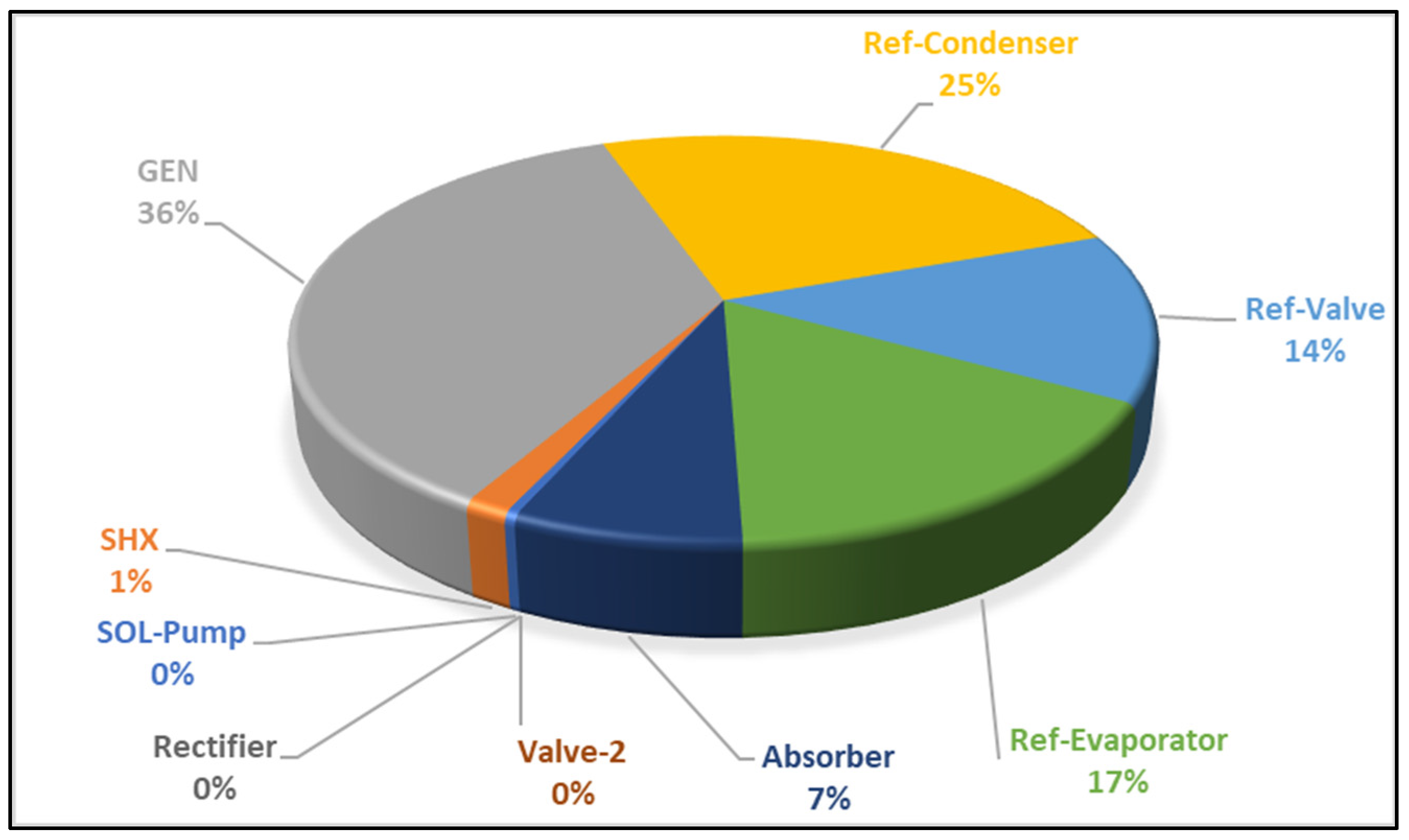
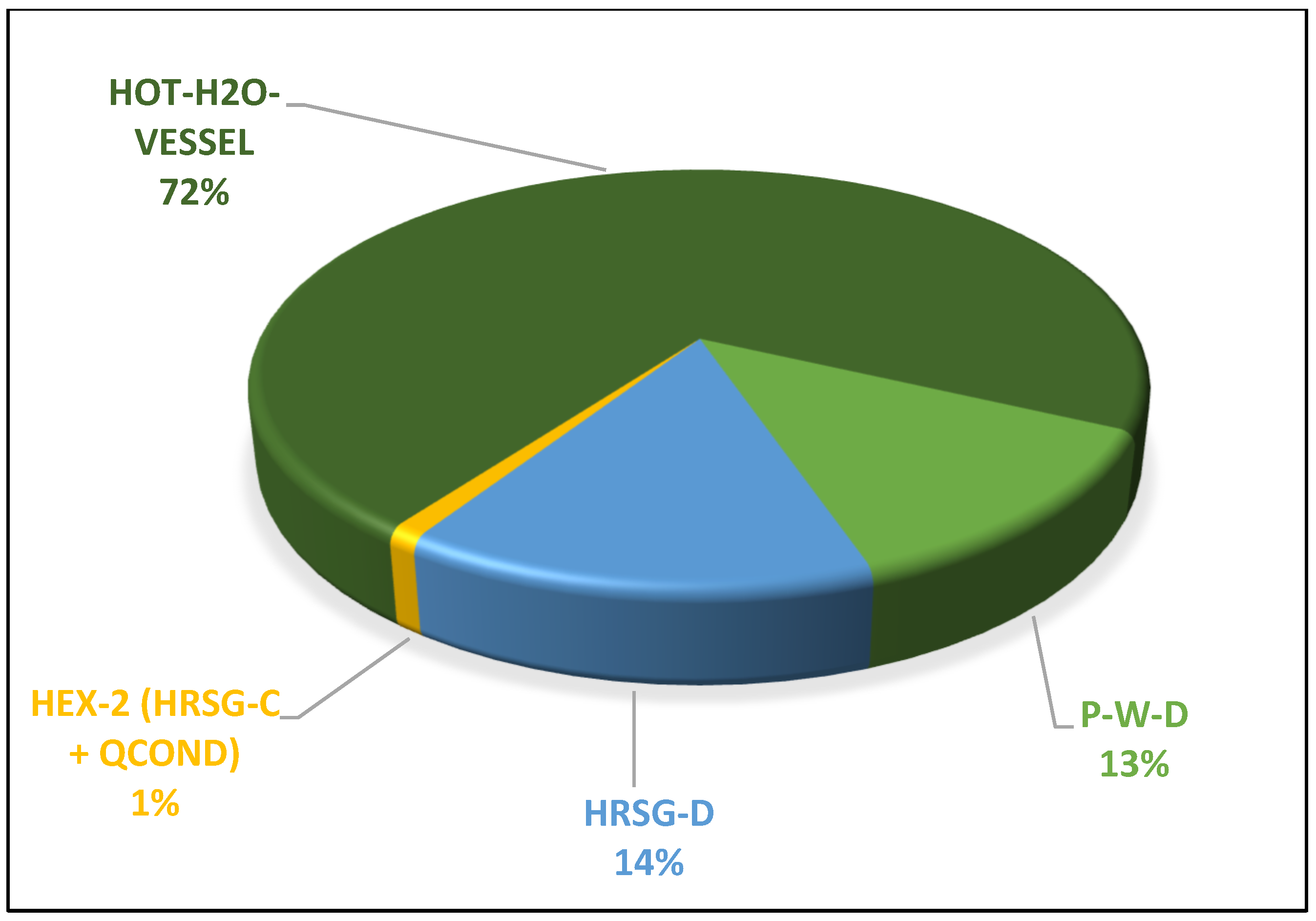
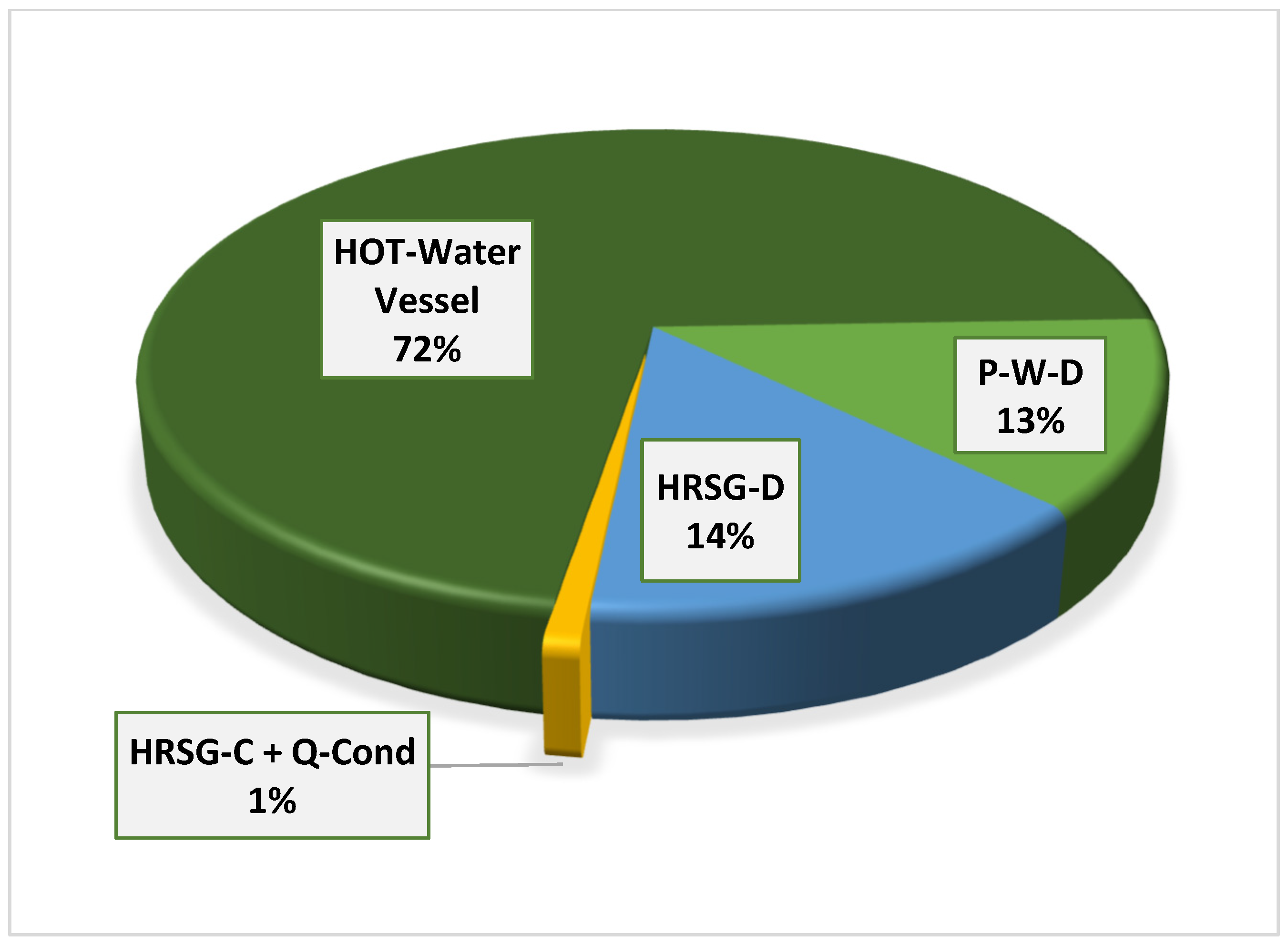
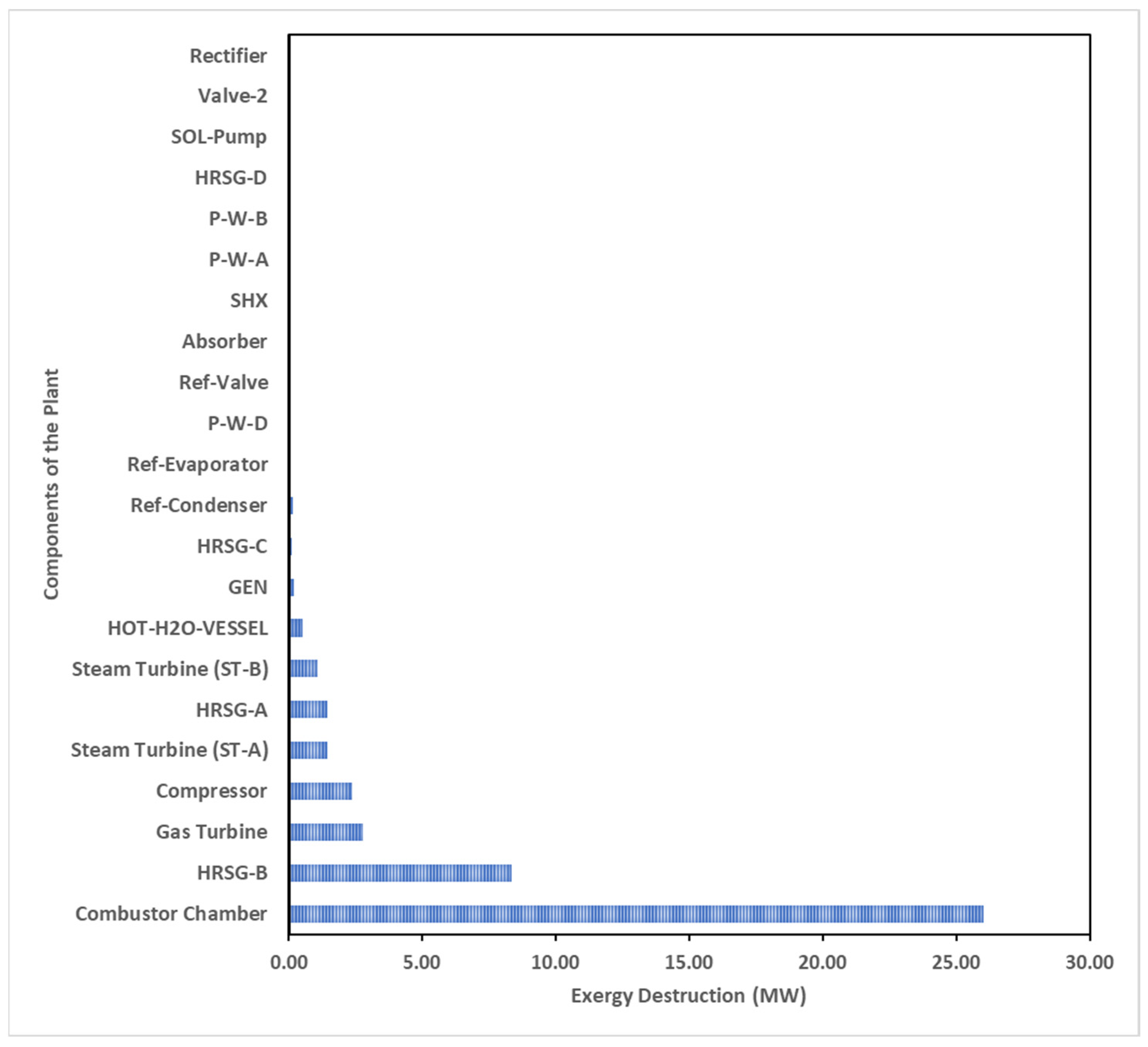
4.3. Exergetic Destruction of the Integrated Plant
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CCPP | combined-cycle power plants |
| Comp | compressor |
| COP | coefficient of performance |
| FDHX | feed heat exchangers |
| GWP | global warming potential |
| HEP | hydroelectric power |
| HEX | heat exchangers |
| HFC | hydro-fluorocarbon |
| HRSG | heat recovery steam generation |
| kBD | thousands of barrels per day |
| LNG | liquified natural gas |
| NGL | natural gas liquids |
| ORC | organic Rankine cycle |
| SHX | solution heat exchanger |
| VAR | vapour absorption refrigeration |
| VCS | vapour compression system |
| MBE | mass balance equation |
| EBE | energy balance equation |
| ExBE | exergy balance equation |
| Ref.Cond | refrigerant condenser |
| Ref.Evap | refrigerant evaporator |
| Ref.Valve | refrigerant valve |
| CV | control volume |
| LHV | lower heating value (MJ/kg) |
| HHV | higher heating value (MJ/kg) |
| Subscripts | |
| ac | air compressor |
| CHM | chemical |
| cc | combustion chamber |
| D | destruction |
| F | fuel |
| in | inlet streams |
| k | kth component of system |
| o | reference state |
| Out | outlet stream |
| P | product |
| PHY | physical |
| th | thermal |
| tot | total |
| Nomenclature | |
| Ė | energy rate [kW] |
| Ex | exergy rate [kW] |
| ex | specific exergy rate of material streams (kJ/kmol) |
| ExD | exergy destruction rate |
| ExL | exergy loss rate |
| hi | specific enthalpy at initial state (kJ/kmol) |
| ho | specific enthalpy at reference state (kJ/kmol) |
| KE | kinetic energy |
| ṁ | mass flow rate [kg/sec] |
| ṁFuel | mass flow rate of Fuel [kg/sec] |
| P | power output [kW] |
| Po | pressure at reference state (atm) |
| PE | potential energy |
| Q | heat flow rate |
| Si | specific entropy at initial state (kJ/kmol) |
| So | specific enthalpy at reference state (kJ/kmol) |
| To | temperature of reference state (K) |
| WBlowr | blower power (kW) |
| WExp | expander power (kW) |
| WNet | net power (kW) |
| WP | pump power (kW) |
| WTurb | steam turbine power (kW) |
| yD | exergy destruction rate ratio |
| Greek letters | |
| φ | coefficient from the liquid fuel expression |
| ηĖ | energy efficiency |
| ηex | exergy efficiency |
| ηPump | pump efficiency |
| ηth | thermal efficiency |
Appendix A
| Units | Temperature [C] | Pressure [bar] | Mass Flows [kg/sec] | Mass Density [kg/cum] | Mass Enthalpy [kJ/kg] | Mass Entropy [kJ/kg-K] | Heat Flow [MW] | Volume Flow [m3/s] | Mass Exergy [kJ/kg] | Exergy Flow Rate [MW] |
|---|---|---|---|---|---|---|---|---|---|---|
| VAR Cooling System | ||||||||||
| 1.00 | 31.76 | 5.98 | 3.47 | 710.25 | 8088.55 | 10.03 | 28,076.18 | 0.00 | 79.87 | 277.23 |
| 2.00 | 32.70 | 55.98 | 3.47 | 709.03 | 8080.26 | 10.00 | 28,047.43 | 0.00 | 80.45 | 279.27 |
| 3.00 | 126.72 | 55.98 | 3.47 | 305.26 | 7641.55 | 8.89 | 26,524.60 | 0.01 | 189.27 | 656.96 |
| 4.00 | 132.93 | 20.01 | 1.76 | 678.12 | 10,146.51 | 6.83 | 17,864.06 | 0.00 | 256.68 | 451.91 |
| 5.00 | 62.77 | 20.01 | 1.76 | 772.93 | 11,011.45 | 9.00 | 19,386.89 | 0.00 | 37.63 | 66.25 |
| 6.00 | 62.77 | 5.98 | 1.76 | 772.93 | 11,011.45 | 9.00 | 19,386.89 | 0.00 | 37.63 | 66.25 |
| 7.00 | 89.42 | 5.98 | 1.71 | 3.39 | 3372.36 | 5.88 | 5768.40 | 0.50 | 278.83 | 476.93 |
| 8.00 | 12.89 | 5.98 | 1.71 | 17.37 | 4583.04 | 9.79 | 7839.25 | 0.10 | 235.45 | 402.73 |
| 9.00 | 53.23 | 20.01 | 1.71 | 583.02 | 4583.04 | 9.94 | 7839.25 | 0.00 | 280.21 | 479.30 |
| 10.00 | 132.89 | 20.01 | 1.71 | 10.14 | 3275.80 | 6.21 | 5603.22 | 0.17 | 475.52 | 813.38 |
| 11.00 | 132.89 | 20.01 | 1.71 | 10.14 | 3275.80 | 6.21 | 5603.22 | 0.17 | 475.52 | 813.38 |
| 12.00 | 132.93 | 20.01 | 1.76 | 678.12 | 10,146.51 | 6.83 | 17,864.06 | 0.00 | 256.68 | 451.91 |
| 13.00 | 132.89 | 20.01 | 0.00 | 0.00 | 10,144.21 | 6.83 | 0.00 | 0.00 | 256.64 | 0.00 |
| Gas Turbine Cycle | ||||||||||
| AIR-IN | 26.85 | 1.01 | 68.39 | 1.17 | 1.60 | 0.15 | 109.26 | 58.49 | 0.01 | 0.40 |
| COMBGAS | 1250.00 | 10.00 | 71.39 | 2.19 | 769.30 | 1.29 | 54,917.63 | 32.53 | 1157.71 | 82,644.27 |
| COMPARE | 364.18 | 10.00 | 68.39 | 5.41 | 351.11 | 0.26 | 24,011.01 | 12.64 | 315.01 | 21,542.31 |
| FLUE-GAS | 120.00 | 1.01 | 71.39 | 0.86 | 2191.88 | 0.32 | 156,470.02 | 82.68 | 26.34 | 1880.08 |
| FUEL | 60.00 | 10.00 | 3.00 | 5.88 | 4575.10 | 5.98 | 13,725.29 | 0.51 | 355.16 | 1065.47 |
| GAS-OUT | 124.00 | 1.01 | 71.39 | 0.85 | 2187.44 | 0.33 | 156,152.72 | 83.52 | 27.43 | 1957.97 |
| HOTGAS | 726.13 | 0.99 | 71.39 | 0.33 | 1469.72 | 1.42 | 104,917.63 | 215.85 | 418.49 | 29,874.36 |
| Cascaded Steam-to-Steam Power System | ||||||||||
| 1A | 27.00 | 1.00 | 19.16 | 996.63 | 15,857.45 | 9.03 | 303,833.79 | 0.02 | 0.03 | 0.50 |
| 2A | 27.31 | 50.00 | 19.16 | 998.72 | 15,851.66 | 9.03 | 303,722.96 | 0.02 | 5.05 | 96.76 |
| 3A | 263.95 | 50.00 | 19.16 | 25.36 | 13,177.64 | 3.46 | 252,487.87 | 0.76 | 1017.57 | 19,496.97 |
| 4A | 99.62 | 1.00 | 19.16 | 0.73 | 13,717.90 | 3.20 | 262,839.40 | 26.40 | 401.06 | 7684.35 |
| 1B | 27.00 | 1.00 | 15.28 | 996.63 | 15,857.45 | 9.03 | 242,246.28 | 0.02 | 0.03 | 0.40 |
| 2B | 27.21 | 35.00 | 15.28 | 998.08 | 15,853.44 | 9.03 | 242,184.96 | 0.02 | 3.54 | 54.02 |
| 3B | 242.57 | 35.00 | 15.28 | 17.53 | 13,169.94 | 3.31 | 201,190.58 | 0.87 | 980.78 | 14,982.93 |
| 4B | 99.62 | 1.00 | 15.28 | 0.71 | 13,669.47 | 3.07 | 208,821.58 | 21.60 | 410.75 | 6274.82 |
| District Hot Water System | ||||||||||
| 1D | 25.00 | 2.00 | 150.00 | 997.21 | 15,865.70 | 9.06 | 2,379,855.57 | 0.15 | 0.12 | 17.64 |
| 2D | 25.23 | 40.00 | 150.00 | 998.85 | 15,861.22 | 9.06 | 2,379,183.11 | 0.15 | 4.01 | 601.02 |
| 3D | 25.23 | 40.00 | 120.00 | 998.85 | 15,861.22 | 9.06 | 1,903,346.49 | 0.12 | 4.01 | 480.82 |
| 4D | 92.01 | 40.00 | 120.00 | 965.59 | 15,582.68 | 8.22 | 1,869,921.79 | 0.12 | 31.41 | 3769.58 |
| 5D | 25.23 | 40.00 | 30.00 | 998.85 | 15,861.22 | 9.06 | 475,836.62 | 0.03 | 4.01 | 120.21 |
| 6D | 66.50 | 40.00 | 30.00 | 981.41 | 15,689.32 | 8.52 | 470,679.70 | 0.03 | 15.03 | 450.94 |
| 7D | 86.92 | 40.00 | 150.00 | 969.00 | 15,604.01 | 8.27 | 2,340,601.49 | 0.15 | 27.62 | 4143.25 |
| 8D | 87.63 | 2.00 | 150.00 | 966.77 | 15,604.01 | 8.26 | 2,340,601.49 | 0.16 | 24.29 | 3643.86 |
| Components | Balance Equations: |
|---|---|
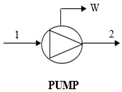 | MBE: ∑ |
| EBE: | |
| ExBE: | |
| Energy efficiency, | |
| Exergy efficiency, | |
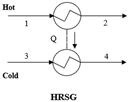 | MBE: ∑ |
| EBE: | |
| ExBE: | |
| Energy efficiency, | |
| Exergy efficiency, | |
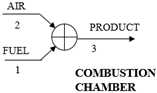 | MBE: ∑ |
| where | |
| EBE: | |
| where LHV = | |
| ExBE: | |
| Energy efficiency, | |
| Exergy efficiency, | |
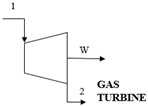 | MBE: ∑ |
| EBE: | |
| ExBE: | |
| Energy efficiency | |
| Exergy efficiency, | |
 | MBE: ∑ |
| EBE: | |
| ExBE: | |
| Energy efficiency, | |
| Exergy efficiency, | |
 | MBE: ∑ |
| EBE: | |
| ExBE: | |
 | MBE: ∑ |
| EBE: | |
| ExBE: | |
| Energy efficiency | |
| Exergy efficiency, | |
 | MBE: ∑ |
| EBE: | |
| ExBE: | |
| Energy efficiency, | |
| Exergy efficiency, | |
 | MBE: ∑ |
| EBE: | |
| ExBE: | |
| Energy efficiency, | |
| Exergy efficiency, | |
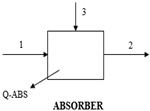 | MBE: ∑ |
| EBE: | |
| ExBE: | |
| Energy efficiency, | |
| Exergy efficiency, | |
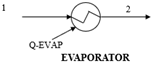 | MBE: ∑ |
| EBE: | |
| ExBE: | |
| Energy efficiency, | |
| Exergy efficiency, | |
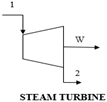 | MBE: ∑ |
| EBE: | |
| ExBE: | |
| Energy efficiency, | |
| Exergy efficiency, | |
| Total exergy destruction in the VAP |

References
- IEA. Gas Market Report, Q1-2022; International Energy Agency: Paris, France, 2022. [Google Scholar]
- Dale, S. BP Statistical Review of World Energy, 71st ed.; BP Publications: Kolkata, India, 2022. [Google Scholar]
- IEA. COP26 Climate Pledges Could Help Limit Global Warming to 1.8 °C, but Implementing Them Will Be the Key; IEA: Paris, France, 2021. [Google Scholar]
- Holz, F.; Richter, P.M.; Egging, R. The Role of Natural Gas in a Low-Carbon Europe: Infrastructure and Regional Supply Security in the Global Gas Model; DIW Berlin—German Institute for Economic Research: Berlin, Germany, 2013. [Google Scholar]
- Petrakopoulou, F.; Boyano, A.; Cabrera, M.; Tsatsaronis, G. Exergoeconomic and exergoenvironmental analyses of a combined cycle power plant with chemical looping technology. Int. J. Greenh. Gas Control 2011, 5, 475–482. [Google Scholar] [CrossRef]
- Aigba, P.A.; Emovon, I.; Samuel, O.D.; Chintua, E.C.; Abdeljawad, T.; Al-Mdallal, Q.M.; Afzal, A. Exergetic Assessment of Waste Gas to Energy in a Novel Integrated NGL Recovery and Power Generation Plant. Front. Energy Res. 2022, 9, 798896. [Google Scholar] [CrossRef]
- Poullikkas, A. An overview of current and future sustainable gas turbine technologies. Renew. Sustain. Energy Rev. 2005, 9, 409–443. [Google Scholar] [CrossRef]
- Gonzalez-Salazar, M.A.; Kirsten, T.; Prchlik, L. Review of the operational flexibility and emissions of gas- and coal-fired power plants in a future with growing renewables. Renew. Sustain. Energy Rev. 2018, 82, 1497–1513. [Google Scholar] [CrossRef]
- Ibrahim, T.K.; Rahman, M.M.; Abdalla, A.N. Optimum Gas Turbine Configuration for Improving the Performance of Combined Cycle Power Plant. Procedia Eng. 2011, 15, 4216–4223. [Google Scholar] [CrossRef]
- González-Salazar, M.A. Recent developments in carbon dioxide capture technologies for gas turbine power generation. Int. J. Greenh. Gas Control 2015, 34, 106–116. [Google Scholar] [CrossRef]
- Bracco, S.; Silvia, S. Exergetic Optimization of Single Level Combined Gas Steam Power Plants Considering Different Objective Functions. Energy 2010, 35, 5365–5373. [Google Scholar] [CrossRef]
- Xiang, W.; Chen, Y. Performance Improvement of Combined Cycle Power Plant Based on the Optimization of the Bottom Cycle and Heat, Recuperation. Therm. Sci. 2007, 16, 84–89. [Google Scholar] [CrossRef]
- Briesch, M.S.; Bannister, R.L.; Diakunchak, I.S.; Huber, D.J. A Combined Cycle Designed to Achieve Greater than 60 Percent Efficiency. ASME J. Eng. Gas Turbines Power 1995, 117, 734–741. [Google Scholar] [CrossRef]
- Bassily, A.M. Modeling, Numerical Optimization, and Irreversibility Reduction of a Dual-Pressure Reheat Combined-Cycle. Appl. Energy 2005, 81, 127–151. [Google Scholar] [CrossRef]
- Koch, C.; Cziesla, F.; Tsatsaronis, G. Optimization of combined cycle power plants using evolutionary algorithms. Chem. Eng. Process. Process Intensif. 2007, 46, 1151–1159. [Google Scholar] [CrossRef]
- Ibrahim, T.K.; Mohammed, M.K.; Awad, O.I.; Rahman, M.; Najafi, G.; Basrawi, F.; Alla, A.N.A.; Mamat, R. The optimum performance of the combined cycle power plant: A comprehensive review. Renew. Sustain. Energy Rev. 2017, 79, 459–474. [Google Scholar] [CrossRef]
- Woudstra, N.; Woudstra, T.; Pirone, A.; Van Der Stelt, T. Thermodynamic Evaluation of Combined Cycle Plants. Energy Convers. Manag. 2010, 51, 1099–1110. [Google Scholar] [CrossRef]
- Khaleel, O.J.; Ismail, F.B.; Ibrahim, T.K.; Hassan, S.H.B.A. Energy and exergy analysis of the steam power plants: A comprehensive review on the Classification, Development, Improvements, and configurations. Ain Shams Eng. J. 2022, 13, 101640. [Google Scholar] [CrossRef]
- Elhelw, M.; Al Dahma, K.S.; Attia, A.E.H. Utilizing exergy analysis in studying the performance of steam power plant at two different operation mode. Appl. Therm. Eng. 2019, 150, 285–293. [Google Scholar] [CrossRef]
- Akiba, M.; Thani, E.A. Thermodynamic Analysis of New Combination of Supercharged Boiler Cycle and Heat Recovery Cycle for Power Generation. ASME J. Eng. Gas Turbines Power 1996, 118, 453–460. [Google Scholar] [CrossRef]
- Jericha, H.; Hoeller, F. Combined Cycle Enhancement. J. Eng. Gas Turbines Power 1991, 113, 198. [Google Scholar] [CrossRef]
- Bolland, O. A Comparative Evaluation of Advanced Combined Cycle Alternatives. ASME J. Eng. Gas Turbines Power 1991, 113, 190–197. [Google Scholar] [CrossRef]
- Seyedan, B.; Dhar, P.L.; Gaur, R.R.; Bindra, G.S. Optimization of Waste Heat Recovery Boiler of a Combined Cycle Power Plant. ASME J. Eng. Gas Turbines Power 1996, 118, 561–564. [Google Scholar] [CrossRef]
- Vidal, A.; Best, R.; Rivero, R.; Cervantes, J. Analysis of a combined power and refrigeration cycle by the exergy method. Energy 2006, 31, 3401–3414. [Google Scholar] [CrossRef]
- Walraven, D.; Laenenb, B.; D’haeselee, W. Minimizing the levelized cost of electricity production from low-temperature geothermal heat sources with ORCs: Water or air cooled. Appl. Energy 2015, 142, 144–153. [Google Scholar] [CrossRef]
- Suna, J.; Li, W. Operation optimization of an organic Rankine cycle (ORC) heat recovery power plant. Appl. Therm. Eng. 2011, 31, 2032–2041. [Google Scholar] [CrossRef]
- Esen, H.; Inalli, M.; Esen, M. Technoeconomic appraisal of a ground source heat pump system for a heating season in eastern Turkey. Energy Convers. Manag. 2006, 47, 1281–1297. [Google Scholar] [CrossRef]
- Esen, H.; Inalli, M.; Esen, M. A techno-economic comparison of ground-coupled and air-coupled heat pump system for space cooling. Build. Environ. 2007, 42, 1955–1965. [Google Scholar] [CrossRef]
- Wang, J.; Wang, M.; Li, M.; Xia, J.; Dai, Y. Multi-objective optimization design of condenser in an organic Rankine cycle for low grade waste heat recovery using evolution aryalgorithm. Int. Commun. Heat. Mass. Transf. 2013, 45, 47–54. [Google Scholar] [CrossRef]
- Chen, H.; Goswam, D.Y.; Stefanakos, E.K. A review of thermodynamic cycle and working fluids for the conversion of low-grade heat. Renew. Sustain. Energy Rev. 2010, 14, 3059–3067. [Google Scholar] [CrossRef]
- Dai, Y.; Wang, J.; Gao, L. Parametric optimization and comparative study of organic Rankine cycle (ORC) for low grade waste heat recovery. Energy Convers. Manag. 2009, 50, 576–582. [Google Scholar] [CrossRef]
- Ahmadi, G.R.; Toghraie, D. Energy and exergy analysis of Montazeri Steam Power Plant in Iran. Renew. Sustain. Energy Rev. 2016, 56, 454–463. [Google Scholar] [CrossRef]
- Marin, A.; Dobrovicescu, A.; Grosu, L.; Gheorghian, A. Energy and exergy analysis of an Organic Rankine cycle, UPB Sci. Bull. Ser. D 2014, 76, 127–136. [Google Scholar]
- Chua, H.T.; Toh, H.K.; Ng, K.C. Thermodynamic modeling of an ammonia–water absorption chiller. Int. J. Refrig. 2002, 25, 896–906. [Google Scholar] [CrossRef]
- Tamm, G.; Goswami, D.Y.; Lu, S.; Hasan, A.A. A Novel Combined Power and Cooling Thermodynamic Cycle for Low Temperature Heat Sources: Part I—Theoretical Investigation. Sol. Energy 2003, 125, 218–222. [Google Scholar] [CrossRef]
- Xu, F.; Goswami, D.Y.; Sunil, S.; Bhagwat, A. Combined power/cooling cycle. Energy 2000, 25, 233–246. [Google Scholar] [CrossRef]
- Goswami, D.Y. Solar Thermal Power: Status of Technologies and Opportunities for Research; Tata McGraw Hill: New Delhi, India, 1995; pp. 57–60. [Google Scholar]
- Zheng, D.; Chen, B.; Qi, Y.; Jin, H. Thermodynamic analysis of a novel absorption power/cooling combined-cycle. Appl. Energy 2006, 83, 311–323. [Google Scholar] [CrossRef]
- Kwon, Y.; Kwak, H.; Oh, S. Exergoeconomic Analysis of Gas Turbine Cogeneration Systems. Int. J. Exergy 2001, 1, 31–40. [Google Scholar] [CrossRef]
- Szargut, J. Exergy Method; WIT Press: Southampton, UK, 2005. [Google Scholar]
- Zhang, N.; Lior, N. Development of a novel combined absorption cycle for power generation and refrigeration. J. Energy Resour. Technol. 2007, 129, 254–265. [Google Scholar] [CrossRef]
- Wang, J.F.; Dai, Y.P.; Gao, L. Parametric analysis and optimization for a combined power and refrigeration cycle. Appl. Energy 2008, 85, 1071–1085. [Google Scholar] [CrossRef]
- Ameri, M.; Ahmadi, P.; Khanmohammadi, S. Exergy analysis of a 420 MW combined cycle power plant. Int. J. Energy Res. 2008, 32, 175–183. [Google Scholar] [CrossRef]
- Demirkaya, G.; Padilla, R.V.; Goswami, D.Y.; Stefanakos, E.; Rahman, M. Analysis of a combined power and cooling cycle for low-grade heat sources. Int. J. Energy Res. 2011, 35, 1145–1157. [Google Scholar] [CrossRef]
- Padilla, R.; Demirkaya, G.; Goswami, D.Y.; Stefanakos, E.; Rahman, M. Analysis of power and cooling cogeneration using ammonia-water mixture. Energy 2010, 35, 4649–4657. [Google Scholar] [CrossRef]
- Barkhordarian, O.; Behbahaninia, A.; Bahrampoury, R. A novel ammonia-water combined power and refrigeration cycle with two different cooling temperature levels. Energy 2017, 120, 816–826. [Google Scholar] [CrossRef]
- Boudéhenn, F.; Demasles, H.; Wyttenbach, J.; Jobard, X.; Chèze, D.; Papillo, P. Development of a 5 kW cooling capacity ammonia-water absorption chiller for solar cooling applications. Energy Procedia 2012, 30, 35–43. [Google Scholar] [CrossRef]
- Raghuvanshi, S.; Maheshwari, G. Analysis of Ammonia–Water (NH3-H2O) Vapor Absorption Refrigeration System based on First Law of Thermodynamics. Int. J. Sci. Eng. Res. 2011, 2, 39–45. [Google Scholar]
- Ouadha, A.; El-Gotni, Y. Integration of an ammonia-water absorption refrigeration system with a marine Diesel engine: A thermodynamic study. Procedia Comput. Sci. 2013, 19, 754–761. [Google Scholar] [CrossRef]
- Lee, T.S.; Liu, C.H.; Chen, T.W. Thermodynamic analysis of optimal condensing temperature of cascade-condenser in cascade refrigeration systems. Int. J. Refrig. 2006, 29, 1100–1108. [Google Scholar] [CrossRef]
- Getu, H.M.; Bansal, P.K. Thermodynamic analysis of an R744–R717 cascade refrigeration system. Int. J. Refrig. 2008, 31, 45–54. [Google Scholar] [CrossRef]
- Ust, Y.; Karakurt, A.S. Analysis of a Cascade Refrigeration System (CRS) by Using Different Refrigerant Couples Based on the Exergetic Performance Coefficient (EPC) Criterion. Arab. J. Sci. Eng. 2014, 39, 8147–8156. [Google Scholar] [CrossRef]
- Dopazo, J.A.; Fernández-Seara, J.; Sieres, J.; Uhía, F.J. Theoretical analysis of a cascade refrigeration system for cooling applications at low temperatures. Appl. Therm. Eng. 2009, 29, 1577–1583. [Google Scholar] [CrossRef]
- Dopazo, J.A.; Fernández-Seara, J. Experimental evaluation of a cascade refrigeration system prototype with CO2 and NH3 for freezing process applications. Int. J. Refrig. 2011, 34, 257–267. [Google Scholar] [CrossRef]
- Almatrafi, E.; Khaliq, A.; Kumar, R.; Bamasag, A.; Siddiqui, M.E. Thermodynamic analysis of a solar refrigeration system based on combined supercritical CO2 power and cascaded refrigeration cycle. Int. J. Exergy 2023, 41, 182–196. [Google Scholar] [CrossRef]
- Yun, E.; Park, H.; Yoon, S.Y.; Kim, K.C. Dual parallel organic Rankine cycle (ORC) system for high efficiency waste heat recovery in marine application. J. Mech. Sci. Technol. 2015, 29, 2509–2515. [Google Scholar] [CrossRef]
- Molés, F.; Navarro-Esbrí, J.; Peris, B.; Mota-Babiloni, A.; Kontomaris, K.K. Thermodynamic analysis of a combined organic Rankine cycle and vapor compression cycle system activated with low temperature heat sources using low GWP fluids. Appl. Therm. Eng. 2015, 87, 444–453. [Google Scholar] [CrossRef]
- Sadreddini, A.; Ashjari, M.A.; Fani, M.; Mohammadi, A. Thermodynamic analysis of a new cascade ORC and transcritical CO2 cycle to recover energy from medium temperature heat source and liquefied natural gas. Energy Convers. Manag. 2018, 167, 9–20. [Google Scholar] [CrossRef]
- Lizarte, R.; Palacios-Lorenzo, M.E.; Marcos, J.D. Parametric study of a novel organic Rankine cycle combined with a cascade refrigeration cycle (ORC-CRS) using natural refrigerants. Appl. Therm. Eng. 2017, 127, 378–389. [Google Scholar] [CrossRef]
- Angelino, G.; Invernizzi, C. Binary conversion cycles for concentrating solar power technology. Sol. Energy 2008, 82, 637–647. [Google Scholar] [CrossRef]
- Sugawara, S.; Sato, T.; Minamiyama, T. On the equation of state of mercury. Jpn. Soc. Mech. 1962, 5, 711–718. [Google Scholar]
- Al-Sulaiman, F.A. Energy and sizing analyses of parabolic trough solar collector integrated with steam and binary vapor cycles. Energy 2013, 58, 561–570. [Google Scholar] [CrossRef]
- El-Maskoud, R.M.A. Binary Brayton cycle with two isothermal processes. Energy Convers. Manag. 2013, 73, 303–308. [Google Scholar]
- Zheng, W.; Zhou, H.; Xiao, Z.; Sun, D.; Song, C.; Zhang, X.; Li, J. Evaluation and optimization of a novel cascade refrigeration system driven by waste heat. Front. Energy Res. 2023, 11, 1111186. [Google Scholar] [CrossRef]
- Boyaghchi, F.A.; Heidarnejad, P. Thermoeconomic assessment and multi objective optimization of a solar micro CCHP based on Organic Rankine Cycle for domestic application. Energy Convers. Manag. 2015, 97, 224–234. [Google Scholar] [CrossRef]
- Zhao, L.; Zhang, Y.; Deng, S.; Ni, J.; Xu, W.; Ma, M.; Lin, S.; Yu, Z. Solar driven ORC-based CCHP: Comparative performance analysis between sequential and parallel system configurations. Appl. Therm. Eng. 2018, 131, 696–706. [Google Scholar] [CrossRef]
- Mohammadi, A.; Kasaeian, A.; Pourfayaz, F.; Ahmadi, M.H. Thermodynamic analysis of a combined gas turbine, ORC cycle and absorption refrigeration for a CCHP system. Appl. Therm. Eng. 2017, 111, 397–406. [Google Scholar] [CrossRef]
- El-Sattar, H.A.; Kamel, S.; Vera, D.; Jurado, F. Tri-generation biomass system based on externally fired gas turbine, organic rankine cycle and absorption chiller. J. Clean. Prod. 2020, 260, 121068. [Google Scholar] [CrossRef]
- Al-Ali, M.; Dincer, I. Energetic and exergetic studies of a multigenerational solar–geothermal system. Appl. Therm. Eng. 2014, 71, 16–23. [Google Scholar] [CrossRef]
- Khan, Y.; Mishra, R.S. Performance analysis of a solar based novel trigeneration system using cascaded vapor absorption-compression refrigeration system. Int. J. Refrig. 2023, 155, 207–218. [Google Scholar] [CrossRef]
- Chakravarty, K.H.; Sadi, M.; Chakravarty, H.; Alsagri, A.S.; Howard, T.J.; Arabkoohsar, A. A review on integration of renewable energy processes in vapor absorption chiller for sustainable cooling. Sustain. Energy Technol. Assess. 2022, 50, 101822. [Google Scholar] [CrossRef]
- Gogoi, T.K.; Saikia, S. Performance analysis of a solar heat driven organic Rankine cycle and absorption cooling system. Therm. Sci. Eng. Prog. 2019, 13, 100372. [Google Scholar] [CrossRef]
- Jain, V.; Kachhwaha, S.S.; Sachdeva, G. Thermodynamic performance analysis of a vapor compression–absorption cascaded refrigeration system. Energy Convers. Manag. 2013, 75, 685–700. [Google Scholar] [CrossRef]
- Salhi, K.; Korichi, M.; Ramadan, K.M. Thermodynamic and thermo-economic analysis of compression-absorption cascade refrigeration system using low-GWP HFO fluids powered by geothermal energy. Int. J. Refrig. 2018, 214–229, 94. [Google Scholar]
- Lee, H.Y.; Kim, K.H. Energy and Exergy Analyses of a Combined Power Cycle Using the Organic Rankine Cycle and the Cold Energy of Liquefied Natural Gas. Entropy 2015, 17, 6412–6432. [Google Scholar] [CrossRef]
- Karaali, R. Exergy Analysis of a Combined Power and Cooling Cycle. Special issue of the 2nd International Conference on Computational and Experimental Science and Engineering (ICCESEN 2015). Acta Phys. Pol. A 2016, 130, 209–214. [Google Scholar] [CrossRef]
- Boyaghchi, F.A.; Molaie, H. Sensitivity analysis of exergy destruction in a real combined cycle power plant based on advanced exergy method. Energy Convers. Manag. 2015, 99, 374–386. [Google Scholar] [CrossRef]
- Rabah, T.; Koten, H.; Fadhila, B.; Salma, S.; Mohamed, H. Energy and exergy analysis of a combined system: Cascade organic Rankine cycle and cascade refrigeration cycle. J. Therm. Eng. 2021, 7, 1139–1149. [Google Scholar] [CrossRef]
- Altarawneh, O.R.; Alsarayreh, A.A.; Al-Falahat, A.M.; Al-Kheetan, M.J.; Alrwashdeh, S.S. Energy and exergy analyses for a combined cycle power plant in Jordan. Case Stud. Therm. Eng. 2022, 31, 101852. [Google Scholar] [CrossRef]
- Mishra, R.S.; Khan, Y. Exergy analysis of orc integrated combined cycle power plant with single pressure heat recovery steam generator. Int. J. Res. Eng. Innov. 2017, 1, 155–162. [Google Scholar]
- Amjad, W.; Shahid, M.; Munir, A.; Asghar, F.; Manzoor, O. Energy Assessment of a Combined Cycle Power Plant through Empirical and Computational Approaches: A Case Study. Eng. Proc. 2021, 12, 25. [Google Scholar]
- Abdel-Moneim, S.A.; Hossin, K. Exergy analysis of a combined gas/steam turbine cycle with a supercharged boiler. Am. J. Eng. Res. 2013, 2, 321–333. [Google Scholar]
- Jamnani, M.B.; Kardgar, A. Energy-exergy performance assessment with optimization guidance for the components of the 396-MW combined-cycle power plant. Energy Sci. Eng. 2020, 8, 3561–3574. [Google Scholar] [CrossRef]
- Aghaziarati, Z.; Aghdam, A.H. Thermoeconomic analysis of a novel combined cooling, heating and power system based on solar organic Rankine cycle and cascade refrigeration cycle. Renew. Energy 2021, 164, 1267–1283. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, Q.; Xie, Z.; Liu, S.; Su, D.; Cui, Q. Energy and exergy analysis of Low GWP Refrigerants in Cascade Refrigeration System. Energy 2019, 170, 1170–1180. [Google Scholar] [CrossRef]
- Ebadollahi, M.; Rostamzadeh, H.; Pedram, M.Z.; Ghaebi, H.; Amidpour, M. Proposal and assessment of a new geothermal-based multigeneration system for cooling, heating, power, and hydrogen production, using LNG cold energy recovery. Renew. Energy 2019, 135, 66–87. [Google Scholar] [CrossRef]
- Oko, C.O.C.; Deebom, M.M.; Diemuodeke, E.O. Exergoeconomic analysis of cascaded organic power plant for the Port Harcourt climatic zone, Nigeria. Cogent Eng. 2016, 3, 1227127. [Google Scholar] [CrossRef]
- Kamari, M.L.; Maleki, A.; Nazari, M.A.; Sadeghi, M.; Rosen, M.A.P.F. Assessment of a biomass-based polygeneration plant for combined power, heat, bioethanol and biogas. Appl. Therm. Eng. 2021, 198, 117425. [Google Scholar] [CrossRef]
- Khalid, F.; Khaliq, A.; Siddiaqui, S.A. Cascade utilization of energy and exergy for the performance analysis of a solar powered cogeneration cycle. Int. J. Sci. Eng. Technol. 2017, 6, 1–33. [Google Scholar]
- Baghernejad, A.; Anvari-Moghaddam, A. Exergoeconomic and Environmental Analysis and Multi-Objective Optimization of a New Regenerative Gas Turbine Combined Cycle. Appl. Sci. 2021, 11, 11554. [Google Scholar] [CrossRef]
- Nivaldo, J.T. Chemistry: Structures and Properties, 2nd ed.; Pearson Education, Inc.: Hoboken, NJ, USA, 2021. [Google Scholar]
- Moran, M.J.; Shapiro, H.N. Fundamentals of Engineering Thermodynamics; John Wiley & Sons, Inc.: New York, NY, USA, 2010. [Google Scholar]
- Abdalla, M.E.; Pannir, S.; Mahjob, A.M.H. Performance and Efficiency of Combined Cycle Power Plants. In Proceedings of the 19th International Refrigeration and Air Conditioning Conference, West Lafayette, IN, USA, 10–14 July 2022. [Google Scholar]
- Ameri, M.; Enadi, N. Thermodynamic modelling and second law-based performance analysis of a gas turbine power plant (exergy and exergoeconomic analysis). J. Power Technol. 2012, 92, 183–191. [Google Scholar]
- Alirahmi, S.M.; Rostami, M.; Farajollahi, A.H. Multi-criteria design optimization and thermodynamic analysis of a novel multi-generation energy system for hydrogen, cooling, heating, power, and freshwater. Int. J. Hydrogen Energy 2020, 45, 15047–15062. [Google Scholar] [CrossRef]
- Zhu, L.; Gu, J. Second law-based thermodynamic analysis of ammonia/sodium thiocyanate absorption system. Renew. Energy 2010, 35, 1940–1946. [Google Scholar] [CrossRef]
- Dincer, I.; Zamfirescu, C. Advanced Power Generation Systems; Elsevier: Cambridge, MA, USA, 2014. [Google Scholar]
- Cengel, Y.; Boles, M. An Engineering Aproach, 5th ed.; McGraw-Hill Companies Inc.: New York, NY, USA, 2006. [Google Scholar]
- Hammad, M.; Habali, S. Design and performance study of a solar energy powered vaccine cabinet. Appl. Therm. Eng. 2000, 20, 1785–1798. [Google Scholar] [CrossRef]
- Shahata, A.I.; Aboelazm, M.M.; Elsafty, A.F. Energy and exergy analysis for single and parallel flow double effect water-lithium bromide vapor absorption systems. Int. J. Sci. Technol. 2012, 2, 85–94. [Google Scholar]
- Kotas, T.J. The Exergy Method of Thermal Plant Analysis; Butterworths: London, UK, 1985. [Google Scholar]
- Som, S.K.; Datta, A. Thermodynamic irreversibilities and exergy balance in combustion processes. Prog. Energy Combust. Sci. 2008, 34, 351–376. [Google Scholar] [CrossRef]
- Mohammadi, K.; Vandani, A.; Joda, F.; Bozorgmehry, B.R. Exergic, economic and environmental impacts of natural gas and diesel in operation of combined cycle power plants. Energy Convers. Manag. 2016, 109, 103–112. [Google Scholar] [CrossRef]
- Ahmadi, P.; Dincer, I. Exergo environmental Analysis and Optimization of a Cogeneration Plant System using Multimodal Genetic Algorithm (MGA). Energy 2010, 35, 5161–5172. [Google Scholar] [CrossRef]
- Szargut, J.; Morris, D.; Steward, R. Exergy Analysis of Thermal, Chemical, and Metallurgical Processes; Hemisphere Publishing Corporation: New York, NY, USA, 1988. [Google Scholar]
- Steinberg, B. Air Fuel Ratio Effect Combustion Efficiency and Air Fuel Ratio. Sagemetering.com. 8 February 2022. Available online: https://sagemetering.com/combustion-efficiency/air-fuel-ratio-effect-on-combustion-efficiency/ (accessed on 24 February 2024).
- Bejan, A.; Tsatsaronis, G.; Moran, M. Thermal Design and Optimization; J. Wiley: New York, NY, USA, 1996. [Google Scholar]
- Aljundi, I.H. Energy and exergy analysis of a steam power plant in Jordan. Appl. Therm. Eng. 2009, 29, 324–328. [Google Scholar] [CrossRef]
- Rašković, P.; Zvonimir, G.; Svetislav, C. Performance analysis of electricity generation by the medium temperature geothermal resources: Velika Ciglena case study. Energy 2013, 54, 11–31. [Google Scholar] [CrossRef]
- Rollbuhler, R.J. Combustion Characteristics of Gas Turbine Alternative Fuels; National Aeronautics and Space Administration Lewis Research Center: Cleveland, OH, USA, 1987; Volume E-3869. [Google Scholar]
- Akyol, U.; Özdemir, E. Thermodynamic Analysis of a Gas Turbine. Int. J. Environ. Trends (IJENT) 2017, 1, 6–13. [Google Scholar]
- Perpignan, A.A.V.; Rao, A.G.; Roekaerts, D.J.E.M. Flameless combustion and its potential towards gas turbines. Prog. Energy Combust. Sci. 2018, 69, 28–62. [Google Scholar] [CrossRef]
- Awaludin, M.; Prayitno, A.; Kurniawan, I.; Romy, R. Exergy analysis of gas turbine power plant 20 mw in Pekanbaru-Indonesia. Int. J. Technol. 2016, 5, 921–927. [Google Scholar]
- Soltani, S.; Mahmoudi, S.M.S.; Yari, M.; Rosen, M.A. Thermodynamic analyses of a biomass integrated fired combined cycle. Appl. Therm. Eng. 2013, 59, 60–68. [Google Scholar] [CrossRef]
- Ameri, M.; Ahmadi, P.; Khanmohamadi, S. Exergy analysis of supplementary firing effects on the heat recovery steam generator. In Proceedings of the 15th International Conference on Mechanical Eng, Tehran, Iran, 15–17 May 2007; p. 2053. [Google Scholar]
- Rosen, M.A.; Tang, R. Improving steam power plant efficiency through exergy analysis: Effects of altering excess combustion air and stack-gas temperature. Int. J. Exergy 2008, 5, 31–51. [Google Scholar] [CrossRef]
- Mahamud, R.; Khan, M.; Rasul, M.G.; Leinster, M.G. Exergy Analysis and Efficiency Improvement of a Coal Fired Thermal Power Plant in Queensland. In Thermal Power Plants: Advanced Applications; InTech: Rockhampton, QLD, Australia, 2013. [Google Scholar]
- Anjali, T.H.; Kalivarathan, G. Analysis of efficiency at a thermal power plant. Int. Res. J. Eng. Technol (IRJET) 2015, 2, 1112–1119. [Google Scholar]
- Ebrahimi-Moghadam, A.; Moghadam, A.J.; Farzaneh-Gord, M. Comprehensive techno-economic and environmental sensitivity analysis and multi-objective optimization of a novel heat and power system for natural gas city gate stations. J. Clean. Prod. 2020, 262, 121261. [Google Scholar]

| Type | Refrigeration Cycle | Heating System | Energy Analysis | Exergy Analysis | Capacity [kW] | Remarks | Refs. |
|---|---|---|---|---|---|---|---|
| Ammonia–water (VAR) refrigeration combined power cycle | ✓ | ✗ | ✓ | ✓ | ✗ | Exergetic efficiency of 38.97% with thermal efficiency of 19% attained at the base case. | [48] |
| Combined power cycle using ORC and cold energy from LNG | ✓ | ✓ | ✓ | ✗ | Highest exergetic destruction of the system components attributed to higher thermal efficiency realized from the increased in the inlet turbine pressure and working fluid temperature. | [76] | |
| Ammonia–water (VAR) power cycles | ✓ | ✗ | ✓ | ✓ | 197 kW | Heat transfer and boiling led to low exergetic efficiency in the boiler. | [77] |
| Ammonia–water (VAR) combined power | ✗ | ✗ | ✗ | ✓ | 420 MW | The loss exergy in the CCPP system’s component evaluated by the sensitivity analysis. | [78] |
| Combined ORC/CRS system (VC) with Toluene/R245fa | ✓ | ✗ | ✓ | ✓ | ✗ | Evaluation showed that the cascaded (ORC and cooling system cycle) performance was influenced by the evaporation temperature. | [79] |
| CCPP plant | ✗ | ✗ | ✓ | ✓ | 400 MW | The significant energetic losses and suggested improvements indicated by the highlighted zones. | [80] |
| CCPP plant | ✗ | ✗ | ✓ | ✓ | 240 MW | Exergetic analysis and final system design helped identify the size, causes, and source of inefficiencies in the plant. | [15] |
| ORC integrated with HRSG in CCPP plant | ✗ | ✗ | ✓ | ✓ | ✗ | The largest exergetic losses were reported at the varying loads. | [81] |
| CCPP plant | ✗ | ✗ | ✓ | ✓ | ✗ | Steam turbine overall efficiency increased by 19.3%, caused by 12.68% combined efficiency improvement in the gas turbine combined-cycle station. | [82] |
| Combined gas–steam turbine cycle | ✗ | ✗ | ✓ | ✓ | ✗ | The output power of 2.1 times and high effectiveness shown in SBCC of the combined cycle with supercharged boiler. | [83] |
| Combined gas turbine, ORC, and ammonia–water VAR cycle | ✓ | ✓ | ✓ | ✗ | 30 kW | Cooling of 8 kW and hot water of 7.2 ton at 67.6% efficiency obtained from the design condition. | [68] |
| Gas-fired CCPP plant | ✗ | ✗ | ✓ | ✓ | 396 MW | The destroyed exergy of the gas turbine was found to be 808 MW, accounting for 83.79% of total exergy destruction. | [84] |
| Solar ORC and cascade lithium Bromide–water refrigeration integrated with CCHP system | ✓ | ✓ | ✓ | ✓ | ✗ | Solar parabolic trough collector (PTC) outperformed the linear Fresnel reflector (LFR) and parabolic dish collector (PDC). Energetic and exergetic efficiencies of 89.39% and 8.70% reported for the PTC. | [85] |
| Low GWP refrigerants in cascade refrigeration system (CRS) | ✓ | ✗ | ✓ | ✓ | ✗ | R170/R161 and R41/R161 for CRS were reported to be superior compared to COP’s improvement in the 28 other refrigerants. The condenser was found to have the most destroyed exergy. | [86] |
| Geothermal-based multigeneration system for CCHP and H2 production, using LNG cold energy recovery | ✓ | ✓ | ✓ | ✓ | 1060 kW | Heating rate of 334.8 kW, 1020 kW of refrigeration capacity, and 5.43 kg/hr hydrogen for multigeneration system determined using 3E (energy, exergy, and exergoeconomic) analyses. | [87] |
| Cascaded organic power plant (COPP) | ✓ | ✗ | ✓ | ✓ | 100 kW | The energetic and exergetic efficiencies are 18.92% and 21.61%, respectively, with 352 USD/kW as the total capital investment. The payback time is 2 years 7 months for COPP, as obtained from the 3E analyses. | [88] |
| Biomass-based polygeneration plant for combined power, heat, bioethanol, and biogas | ✗ | ✓ | ✓ | ✓ | 35 MW | Found 90 MW district heating, 76 MW biogas, and 161 MW bioethanol reported under the design conditions, while an energy efficiency of 73.0 % for the CHP and 63.0 % the total polygene ration obtained. | [89] |
| Cascade performance assessment cogeneration cycle powered with solar | ✓ | ✗ | ✓ | ✓ | ✗ | Evident of variation in direct normal irradiation (DNI) of the backpressure of the turbine was reported, while no impact was found based on the 1st law; there was a 2nd law performance impact on the cogeneration system. | [90] |
| New regenerative gas turbine (NRGT)–CCPP plant | ✓ | ✗ | ✓ | ✓ | ✗ | Results of the exergy efficiency and exergy unit electricity cost produced as well as total cost rate for NRGT–CCPP plant highlighted. | [91] |
| Description | Compound | Mole Fraction |
|---|---|---|
| Gas turbine Cycle [92] | ||
| Fuel Composition | Methane | 0.788 |
| Ethane | 0.14 | |
| Carbon dioxide | 0.004 | |
| Nitrogen | 0.068 | |
| Air Composition | Nitrogen | 0.79 |
| Oxygen | 0.21 | |
| Input data for process simulation | Gas flowrate (kmol/sec) | 1 |
| Air flowrate (kmol/sec) | 11.43 | |
| % Excess air | 20 | |
| Fuel gas temperature (°C) | 60 | |
| Fuel gas pressure (bar) | 1 | |
| Inlet air temperature (°C) | 27 | |
| Pressure ratio | 10 | |
| Ideal gas specific heat capacities, air, k (kJ/kg·K) | 1.005 | |
| Property models | Aspen-Plus Simulator | P-Robinson |
| Vapour absorption refrigeration Cycle | ||
| Stream Composition | Ammonia | 0.6700 |
| Water | 0.3300 | |
| Input data for VAR process simulation | Pump inlet temperature (°C) | 32 |
| Inlet Pressure (bar) | 5.98 | |
| Mass flowrate (kmol/s) | 0.2 | |
| Pump discharge pressure (bar) | 50 | |
| Final condensation (°C) | 25 | |
| Pump adiabatic efficiency (%) | 85 | |
| Solution HX, outlet temp (°C) | 63 | |
| Generator: Reflux ratio | 1 | |
| Generator: Heat Duty (kW) | 133 | |
| Condenser Outlet temp (°C) | 53 | |
| Absorber Outlet temp (°C) | 32 | |
| Property models | Aspen-Plus Simulator | NRTL |
| Cascaded steam power plant system | ||
| Steam cycle input data for process simulation | HRSG-A temperature (°C) | 726 |
| HRSG-A heat supplied (MW) | 51.24 | |
| HRSG-B heat supplied (MW) | 40.99 | |
| HRSG-C heat supplied (MW) | 33.43 | |
| HRSG-D heat supplied (MW) | 5.16 | |
| HP steam temperature (°C) | 264 | |
| Pump discharge pressure (bar) | 50 | |
| Final condensation (°C) | 25 | |
| Pump adiabatic efficiency (%) | 85 | |
| Turbine adiabatic efficiency (%) | 85 | |
| ST-A Water Flowrate (kg/s) | 19.16 | |
| ST-A Water Flowrate (kg/s) | 15.28 | |
| Property models | Aspen-Plus Simulator | Steam-TA |
| District water heating system | ||
| Heating water cycle input data for process simulation | Mass flowrate of water (kg/s) | 150 |
| Pump discharge pressure (bar) | 40 | |
| Pump adiabatic efficiency (%) | 85 | |
| Hot water temperature (°C) | 88 | |
| Property models | Aspen-Plus Simulator | Steam-TA |
| Component | Power [MW] | Heat Transfer [MW] | ExFUEL [MW] | ExPROD [MW] | ExD [MW] | ExL [MW] | Energy Efficiency [%] | Exergy Destruction [%] | Exergy Efficiency [%] |
|---|---|---|---|---|---|---|---|---|---|
| SOL-Pump | 0.03 | 0.00 | 0.03 | 0.00 | 0.03 | 0.00 | 100.00 | 7.10 | 92.90 |
| SHX | 0.00 | 1.52 | 0.73 | 0.72 | 0.01 | 0.00 | 100.00 | 1.09 | 98.91 |
| FDHX | 0.00 | 0.32 | 1.96 | 1.88 | 0.08 | 0.00 | 99.80 | 3.98 | 96.02 |
| GEN | 0.00 | 3.06 | 0.81 | 0.61 | 0.20 | 0.00 | 98.82 | 25.13 | 74.87 |
| Ref-Condenser | 0.00 | 2.24 | 0.81 | 0.67 | 0.14 | 0.00 | 100.00 | 17.28 | 82.72 |
| Ref-Valve | 0.00 | 0.00 | 0.48 | 0.40 | 0.08 | 0.00 | 100.00 | 15.98 | 84.02 |
| Ref-Evaporator | 0.00 | 2.07 | 0.57 | 0.48 | 0.09 | 0.00 | 100.00 | 16.30 | 83.70 |
| Absorber | 0.00 | 2.92 | 0.58 | 0.54 | 0.04 | 0.00 | 100.00 | 7.02 | 92.98 |
| Valve-2 | 0.00 | 0.00 | 0.07 | 0.07 | 0.00 | 0.00 | 100.00 | 0.00 | 100.00 |
| Rectifier | 0.00 | 0.00 | 0.81 | 0.81 | 0.00 | 0.00 | 100.00 | 0.00 | 100.00 |
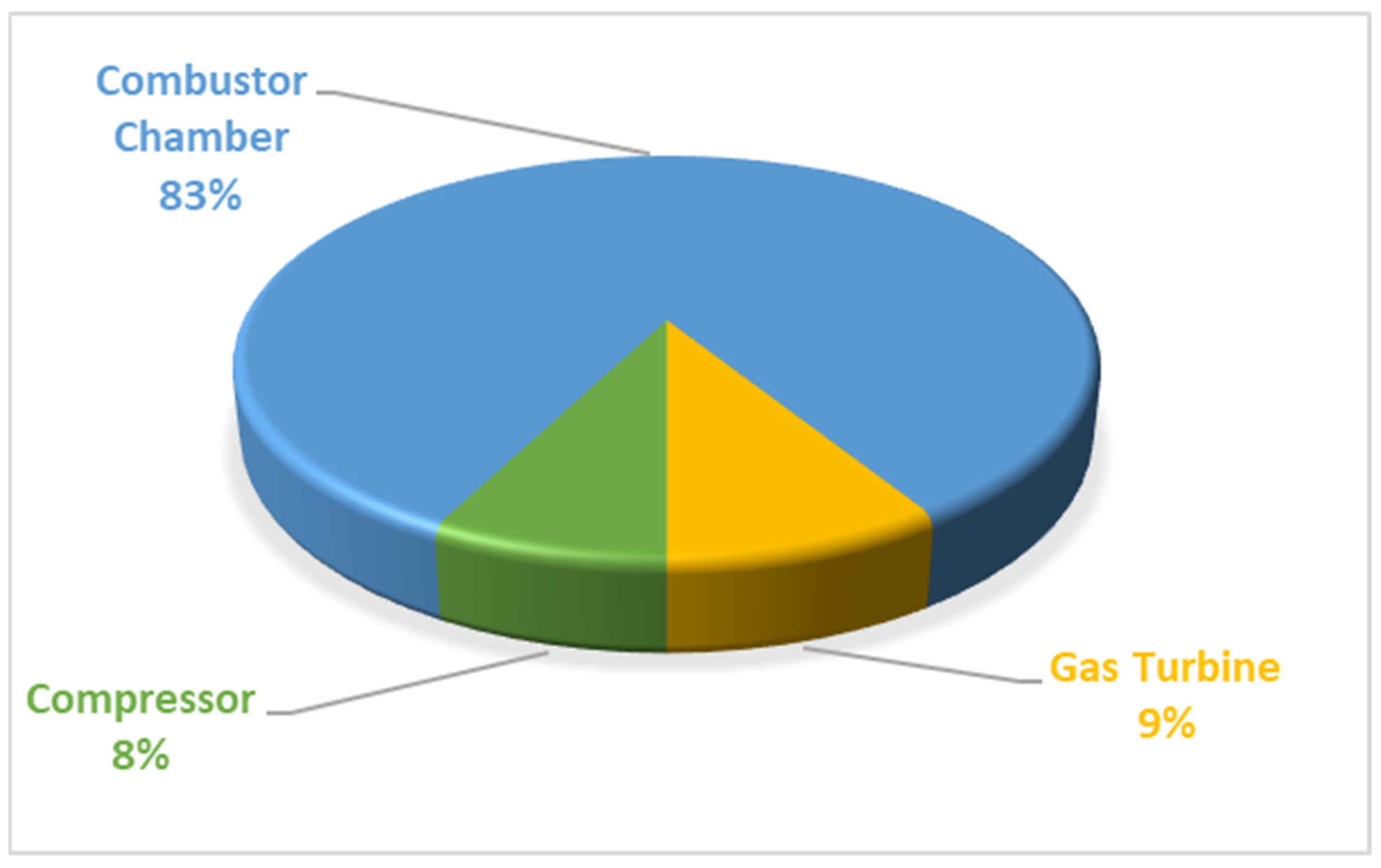
| Compressor | 23.90 | 0.00 | 23.90 | 21.54 | 2.36 | 0.00 | 100.00 | 9.87 | 90.13 |
| Combustor Chamber | 0.00 | 150.08 | 108.67 | 82.64 | 26.03 | 0.00 | 98.00 | 23.95 | 76.05 |
| Gas Turbine | 26.10 | 0.00 | 52.77 | 50.00 | 2.77 | 0.00 | 100.00 | 5.25 | 94.75 |
| HRSG-A | 0.00 | 51.24 | 29.36 | 27.92 | 1.45 | 1.88 | 100.00 | 4.93 | 95.07 |
| Steam Turbine (ST-A) | 10.35 | 0.00 | 11.81 | 10.35 | 1.46 | 0.00 | 100.00 | 12.37 | 87.63 |
| Condenser A | 0.00 | 40.99 | 7.68 | 4.67 | 3.01 | 0.00 | 100.00 | 39.22 | 60.78 |
| P-W-A | 0.11 | 0.00 | 0.11 | 0.10 | 0.01 | 0.00 | 100.00 | 13.14 | 86.86 |
| HRSG-B | 0.00 | 40.99 | 19.40 | 11.04 | 8.36 | 0.00 | 100.00 | 43.07 | 56.93 |
| Steam Turbine (ST-B) | 7.63 | 0.00 | 8.71 | 7.63 | 1.08 | 0.00 | 100.00 | 12.37 | 87.63 |
| Condenser B | 0.00 | 33.42 | 6.27 | 3.81 | 2.47 | 0.00 | 100.00 | 39.31 | 60.69 |
| P-W-B | 0.06 | 0.00 | 0.06 | 0.05 | 0.01 | 0.00 | 100.00 | 12.54 | 87.46 |
| P-W-D | 0.67 | 0.00 | 0.67 | 0.58 | 0.09 | 0.00 | 100.00 | 13.25 | 86.75 |
| HEX-1 | 0.00 | 33.42 | 3.39 | 3.29 | 0.10 | 0.00 | 100.00 | 2.95 | 97.05 |
| HEX-2 | 0.00 | 5.16 | 0.46 | 0.45 | 0.01 | 0.00 | 100.00 | 1.48 | 98.52 |
| HOT-H2O-VESSEL | 0.00 | 0.00 | 4.14 | 3.64 | 0.50 | 0.00 | 100.00 | 12.05 | 87.95 |
| Exergy Losses | 1.88 | ||||||||
| Total System | 68.86 | 242.31 | 145.26 | 113.29 | 50.36 | 1.88 | 85.05 | 52.14 | 77.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agberegha, L.O.; Aigba, P.A.; Nwigbo, S.C.; Onoroh, F.; Samuel, O.D.; Bako, T.; Der, O.; Ercetin, A.; Sener, R. Investigation of a Hybridized Cascade Trigeneration Cycle Combined with a District Heating and Air Conditioning System Using Vapour Absorption Refrigeration Cooling: Energy and Exergy Assessments. Energies 2024, 17, 1295. https://doi.org/10.3390/en17061295
Agberegha LO, Aigba PA, Nwigbo SC, Onoroh F, Samuel OD, Bako T, Der O, Ercetin A, Sener R. Investigation of a Hybridized Cascade Trigeneration Cycle Combined with a District Heating and Air Conditioning System Using Vapour Absorption Refrigeration Cooling: Energy and Exergy Assessments. Energies. 2024; 17(6):1295. https://doi.org/10.3390/en17061295
Chicago/Turabian StyleAgberegha, Larry Orobome, Peter Alenoghena Aigba, Solomon Chuka Nwigbo, Francis Onoroh, Olusegun David Samuel, Tanko Bako, Oguzhan Der, Ali Ercetin, and Ramazan Sener. 2024. "Investigation of a Hybridized Cascade Trigeneration Cycle Combined with a District Heating and Air Conditioning System Using Vapour Absorption Refrigeration Cooling: Energy and Exergy Assessments" Energies 17, no. 6: 1295. https://doi.org/10.3390/en17061295
APA StyleAgberegha, L. O., Aigba, P. A., Nwigbo, S. C., Onoroh, F., Samuel, O. D., Bako, T., Der, O., Ercetin, A., & Sener, R. (2024). Investigation of a Hybridized Cascade Trigeneration Cycle Combined with a District Heating and Air Conditioning System Using Vapour Absorption Refrigeration Cooling: Energy and Exergy Assessments. Energies, 17(6), 1295. https://doi.org/10.3390/en17061295











